Heat transfer characteristics of moving longitudinal porous fin wetted with ternary (Cu–Al₂O₃–TiO₂) hybrid nanofluid: ADM solution

Abstract

In this work, a numerical and analytical investigation of the heat transfer processes of free convection and radiation on a porous moving longitudinal fin has been carried out. A ternary hybridized nanofluid consisting of Cu, Al₂O₃, and TiO₂ is being used to wet the moving fin in this case. Both the pure water (H₂O) as a base fluid, and once again the combination of water + C₂H₆O₂ (50–50%) as a base fluid, are taken into consideration. In the process of modeling the current physical phenomena, Darcy's model is being taken into consideration. The primary equations were solved by using a technique known as the Adomian decomposition method (ADM). This solution was then verified by utilizing the HAM-based Mathematica package known as BVPh 2 as well as Runge–Kutta–Fehlberg fourth–fifth-order (RKF-45) approach. The impacts of a variety of different factors on thermal profiles and thermal gradients are depicted and analyzed. These parameters include nanoparticle volume fraction, Peclet number, wet porosity, radiative parameter, convective number, power index, and ambient temperature on ternary hybrid nanofluid is another parameter that influences thermal profiles and thermal gradients.

1 Introduction

Nanofluid is a term used to describe any fluid that contains nanoparticles. These liquids are nanoparticle dispersion in a designed colloidal solution. Nanomaterials can be nanoparticles, nanowires, nanotubes, or nanofibers, and the main fluid can be water, oil, biological fluids, lubricants, organic liquids (coolants, ethylene glycol, ethylene, or polymer solutions), or regular fluid. Nano-liquid is made when any of the above unique materials are mixed with the base liquid. Metal oxides (like MgO, SiO₂, and TiO₂), ceramic oxides (like Al₂O₃, Be₂O₃, and CuO), chemically stable metals (like gold and copper), different types of carbon (like diamonds, graphite, and carbonless nanotubes (Fullerene)), solid minerals (like SiC), and functional nanoparticles are all commonly used as nanoparticles [1,2,3].

Heat transfer is utilized to enhance thermal efficiency and cooling systems in a variety of industrial, engineering, and medical applications. Nanofluids have been found to have higher thermal conductivity and adsorption capacity than regular fluids. Because of this, nanoparticles are being used as a desirable material in the development of fluids to maximize heat transfer in automated manufacturing systems such as cooling electronic circuits and heat exchangers, and cooling heat exchange mechanisms in processors, metal tapes and radiators, car engines, welding equipment, cooling chemical reactions and car cooling systems, fuel cells, and cancer therapy [4, 5].

The ternary hybrid nanofluid is a novel term that has emerged in recent years as a result of the influence of these liquids on flow and heat transport attributes. This combination formed between molecules after extensive investigation demonstrated the influence of nanofluids on movement and heat transference capabilities [6,7,8,9].

After a lot of research into how nanoparticles affect the properties of regular fluids, it was suggested that more types of nanoparticles should be employed to improve the performing of fluid properties in manufacturing or organic settings [10,11,12,13]. Another key component that aids in heat transmission is the tying of the enlarged surface, which is the fin, to the old structure. This increases the surface available for heat transfer and, as a result, improves the cooling effect.

Gireesha et al. [14] examined heat transmission via a constant-velocity longitudinal fin and fin tip convection in a hybrid nanomaterial flow. Talbi et al. [15] observed the effects of thermic radiation and natural convection on the flowing of a hybridized nanoliquid (H₂O–C₂H₆O₂/GO–MoS₂) across a moving porous longitudinal fin using insulated and convective boundary conditions. Kezzar et al. [16] introduced a novel analytical computer methodology dubbed the Duan–Rach method (DRA) to examine longitudinal fin heat transmission with thermal conductance and temperature-dependent heat generating. Sowmya et al. [17] increased heat transfer rates in convective boundary conditions and inside heat generating using alloy-embedded nanoliquid flowing and porousness fin in wet conditions with natural convection and radiation. Goud et al. [18] employed a ternary hybrid nanofluid to observe heat transport through a totally wet dovetail fin, considering the temperature and humidity ratio. Hosseinzadeh et al. [19] analyzed the thermal efficacy of a movable porous fin moistened with a hybridized nanoliquid of varying cross sections in a magnetized force. For a longitudinal fin with a heat source and constant rapidity, Gouran et al. [20] studied convection and radiation heat transfer using LSM and MOM techniques.

When it comes to similar inertia effects, the Darcy–Forchheimer model is the most common change to the Darcy flow. The consequence of inertia is considered by the Forchheimer extension, which adds a velocity-squared factor to the momentum equation. Studying the two-dimensional Darcy–Forchheimer motion of magnetized Maxwell liquid created by a linearly stretched surface and convective heat transfer was the focus of Sadiq and Hayat [21] research. In their investigation of generalized Forchheimer flows in porous media, Ibragimov and Kiu [22] made use of an enlarged mixed finite element approach. The heat radiation in a 3D Darcy–Forchheimer rotating flow of MHD CNTs nanofluid was studied by Shah et al. [23] who conducted their research between parallel plates. The Darcy–Forchheimer viscous fluid flow over a curving extended plate was investigated by Hayat and Saif [24]. Entropy optimization in the Darcy–Forchheimer flowing of first-order slippage rapidity of the Carreau–Yasuda liquid was computed by Khan et al. [25]. Modeling the flow of a Darcy–Forchheimer hybrid nanofluid with partial slip across a spinning disk was accomplished by Li et al. [26] by using the technique of fractional simulation. Elsaid and Abdel-Aal [27] investigated the energy and mass features of a mixed convective flow of nanofluid via a porous plate that was implanted in a porous medium when a magnetic field and heat radiation were present. Their research focused on the movement of nanoliquid through the porosity plate.

The increase in heat transmission has been investigated using a wide number of approaches, and one of the most successful of these approaches is the fin technique, which examines the heat transfer properties of a system [28, 29]. Fins are often used in a wide variety of manufacturing processes to facilitate heat transmission. These applications include heat exchangers as well as microchannel heat sinks [30]. Numerous processes used in industry, including extrusion, hot rolling, and casting, apply a thermal treatment to the material that is being developed and manufactured while it is in continuous movement. This treatment is often carried out in comparison with the fluid that is surrounding the material being produced [31]. This makes it possible to get the material down to the correct temperature and cool it. The sheet area of the substance is increased by using fins that have been stretched into the environment that surrounds it. This helps to enhance the impact of cooling. Fins are solids that extend from an item to expand the heat transport rate and assist disperse heat from a hot sheet into the environment around it. Fins may be found on heat sinks, radiators, and other devices designed to transfer heat [32]. An examination of the previous research reveals that extensive effort has been done in the investigation of a variety of different types of fin designs [33,34,35]. When the cooling impact is provided by the wetted situation, heat dissipation is more efficient, and the usage of increased surfaces under moist circumstances is more prominent in cooling and refrigeration systems. Under these conditions, simultaneous heat transmission and mass transfer take place over the surface of the fin that is associated with the wet state [33]. The findings of the examination [34] demonstrate that a decrease in the thermal outlines may be achieved by increasing the surface radiative factor, and a similar pattern of interaction is seen for the surface convection parameter. In addition, liquids containing tripartite nanomaterials exhibit the highest change in temperature. In addition, in comparison with the conventional straight fin, the longitudinal trapezoidal fin has better heat transfer properties, making it the kind of fin that offers the best performance. While in the study [35] obtained that the increased thermal outline in the fin is due to a reduction in the amount of the moist variable, which is essential for the increase.

Because of its relevance to the industry, the nonlinear fin issue has garnered a significant amount of attention in recent years. Porous fins have a broad variety of uses, both in the field of engineering and in daily life. A great number of practical implementations in a variety of manufacturing, electric, and mechanical engineering fields, like gas turbine, motorbike head, aviation machines, vehicles, and heat bowls, employ fin designs to offer greater surface area and, as a consequence, to boost the efficacy of heat transmission. By using wetted porous stretched surfaces, heat transfer rates may be enhanced, and in many cases, these surfaces surpass conventional solid fins in their respective applications. Finally, the significance of this work can be summarized by examining the heat transfer of natural convection on a longitudinal permeable moving fin wetted with a ternary hybridized nanoliquid (Cu–Al₂O₃–TiO₂) numerically and analytically.

2 Governing equations

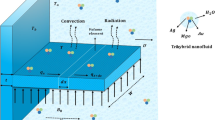
In the current study, the heat transfer of free convective and radiative consequences on a movement fin with a uniform motion $U$ and a rectangular pattern that is longitudinally porous and moist with a ternary hybrid fluid based on water is modeled. Figure 1 depicts the geometrical structure of the problem under consideration. Assuming that the fin has thickness $t$, width $w$, and length $l$, the Darcy model is used. Furthermore, the fin base is kept at a constant temperature ${T}_{b}$, while the temperature of the surrounding nanofluid is taken into account ${T}_{a}$.

Fig. 1

Schematic representation of the flow geometry

In developing the system strategy, the following presumptions were taken into consideration:

• The Darcy model is adopted.

• ${T}_{a}$ denotes the temperature of the ambient nanofluid.

• The base fin has a constant temperature ${T}_{b}$.

• adiabatic fin tip.

• The ambient nanofluid absorbs radiation from the fin's exposed surface.

The energy equation for free convective and radiative terms on a rectangular profiled longitudinal porous moving fin containing ternary hybrid nanofluid is as follows [36, 37]:

$$\begin{aligned}&\frac{{d}^{2}T}{d{x}^{2}}-\frac{2gK{\left(\rho {C}_{p}\right)}_{{Thnf}}{\left(\rho \beta \right)}_{{Thnf}}}{{\mu }_{{Thnf}}{k}_{{Thnf}}t}{\left(T-{T}_{a}\right)}^{2}-\frac{2\varepsilon \sigma {F}_{f-a}}{{k}_{{Thnf}}t}\left({T}^{4}-{T}_{a}^{4}\right)\\ &\quad -\frac{2{h}_{D}{i}_{fg}\left(1-\overline{\varphi }\right)\left(\omega -{\omega }_{a}\right)}{{k}_{{Thnf}}t}-\frac{2h\left(1-\overline{\varphi }\right)\left(T-{T}_{a}\right)}{{k}_{{Thnf}}t}-\frac{{\left(\rho {C}_{p}\right)}_{{Thnf}}U}{{k}_{{Thnf}}}\frac{dT}{dx}=0\end{aligned}$$

(1)

where ${\mu }_{{Thnf}}$, ${\rho }_{{Thnf}}$, ${({C}_{p})}_{{Thnf}}$, ${\beta }_{{Thnf}}$ and ${k}_{{Thnf}}$ are the ternary hybrid nanofluid's dynamic viscosity, density, specific heat with constant pressure, volumetric thermal expansion coefficient, and thermal conductivity.

With the boundary constraints

$$\left. {\begin{array}{*{20}c} {at \,\,x = 0 \to T\left( 0 \right) = T_{b} ,} \\ {at \,\,x = l \to \left. {\underline {\, {\frac{dT}{{dx}}} \,}}\! \right|_{x = l} = 0.} \\ \end{array} } \right\}$$

(2)

Table 1 summarizes the features of a ternary hybridized nanofluid. Whilst Table 2 demonstrates the thermophysical attributes of utilized conventional fluid and nanoparticles.

Table 1 Physical properties of ternary hybrid nanofluids [36, 37]

The heat transmission factor $h$ is given as

$$h={h}_{{a}}{\left(\frac{T-{T}_{{a}}}{{T}_{{b}}-{T}_{{a}}}\right)}^{n}$$

(3)

Introduce the following similarity transformations:

$$\left.\begin{array}{c}\theta =\frac{T}{{T}_{{b}}}, \\ {\theta }_{{a}}=\frac{{T}_{{a}}}{{T}_{{b}}}, \\ \eta =\frac{x}{l}, \\ \left(\omega -{\omega }_{{a}}\right)={b}_{2}\left(T-{T}_{{a}}\right),\end{array}\right\}$$

(4)

We get the dimensionless form by using the above-mentioned similarity transformations:

$$\frac{{d}^{2}\theta }{d{\eta }^{2}}-{Nc} \frac{{\delta }_{1}{\delta }_{2}}{\frac{1}{{\delta }_{3}}}{{\left(1-{\varphi }_{1}\right)}^{2.5}{\left(1-{\varphi }_{2}\right)}^{2.5}{\left(1-{\varphi }_{3}\right)}^{2.5}\left(\theta -{\theta }_{a}\right)}^{2}-{Nr}{\delta }_{3}\left({\theta }^{4}-{{\theta }_{a}}^{4}\right)-{m}_{2}{\delta }_{3}\frac{{\left(\theta -{\theta }_{a}\right)}^{n+1}}{{\left(1-{\theta }_{a}\right)}^{n}}-{Pe}{\delta }_{1}{\delta }_{3}\frac{d\theta }{d\eta }=0$$

(5)

here,

$$\left.\begin{array}{c}{\delta }_{1}=\left(1-{\varphi }_{3}\right)\left\{\left(1-{\varphi }_{2}\right)\left[\left(1-{\varphi }_{1}\right)+{\varphi }_{1}\frac{{\left(\rho {C}_{p}\right)}_{p_{1}}}{{\left(\rho {C}_{p}\right)}_{f}}\right]+{\varphi }_{2}\frac{{\left(\rho {C}_{p}\right)}_{p_{2}}}{{\left(\rho {C}_{p}\right)}_{f}}\right\}+{\varphi }_{3}\frac{{\left(\rho {C}_{p}\right)}_{p_{3}}}{{\left(\rho {C}_{p}\right)}_{f}},\\ {\delta }_{2}=\left(1-{\varphi }_{3}\right)\left\{\left(1-{\varphi }_{2}\right)\left[\left(1-{\varphi }_{1}\right)+{\varphi }_{1}\frac{{\left(\rho \beta \right)}_{p_{1}}}{{\left(\rho \beta \right)}_{f}}\right]+{\varphi }_{2}\frac{{\left(\rho \beta \right)}_{p_{2}}}{{\left(\rho \beta \right)}_{f}}\right\}+{\varphi }_{3}\frac{{\left(\rho \beta \right)}_{p_{3}}}{{\left(\rho \beta \right)}_{f}}, \\ {\delta }_{3}=\frac{{k}_{f}}{{k}_{{Thnf}}}, \end{array}\right\}$$

(6)

The corresponding dimensionless boundary constraints are:

$$\begin{array}{*{20}c} {at\,\, \eta = 0 \to \theta \left( 0 \right) = 1, } \\ {at \,\,\eta = 1 \to \left. {\underline {\, {\frac{d\theta }{{d\eta }}} \,}}\! \right|_{\eta = 1} = 0.} \\ \end{array}$$

(7)

where $\eta$ is the dimensionless axial distance, $\theta$ is nondimensional temperature, ${\theta }_{a}$ is the nondimensional ambient temperature, $Pe={\left(\rho {C}_{p}\right)}_{f}Ul/{k}_{f}$ is the Peclet quantity, $Nr=2\varepsilon \sigma {l}^{2}{{T}_{b}}^{3}/{k}_{f}t$ is the radiative factor, $Nc=2{\left(\rho \beta \right)}_{f}gK{\left(\rho {C}_{p}\right)}_{f}{T}_{b}{l}^{2}/{\mu }_{f}{k}_{f}t$ is the convective number, $m_{2} = \underbrace {{2h_{a} l^{2} \left( {1 - \overline{\varphi }} \right)/k_{f} t}}_{{m_{0} }} + \underbrace {{2h_{a} l^{2} i_{fg} \left( {1 - \overline{\varphi }} \right)b_{2} /k_{f} t\left( {C_{p} } \right)_{f} {\text{Le}}^{2/3} }}_{{m_{1} }}$ is the wet porous number, and $n$ is the power index.

Table 2 Thermophysical attributes of conventional fluid and nanoparticles [12, 13, 38]

3 Application of ADM

In ADM method [39], Eq. (5) can be written.

$${\mathcal{L}}\theta^{\prime\prime} = {{Nc }}\frac{{\delta_{1} \delta_{2} }}{{\frac{1}{{\delta_{3} }}}}\left( {1 - \varphi_{1} } \right)^{2.5} \left( {1 - \varphi_{2} } \right)^{2.5} \left( {1 - \varphi_{3} } \right)^{2.5} \left( {\theta - \theta_{a} } \right)^{2} + {{Nr}}\delta_{3} \left( {\theta^{4} - \theta_{a}^{4} } \right) + m_{2} \delta_{3} \frac{{\left( {\theta - \theta_{a} } \right)^{n + 1} }}{{\left( {1 - \theta_{a} } \right)^{n} }} + {{Pe}}\delta_{1} \delta_{3} \theta^{\prime}$$

(8)

Here, the differential operator $\mathcal{L}$ and the inverse operator ${\mathcal{L}}^{-1}$ are specified, respectively, by

$$\left. {\begin{array}{*{20}c} {{\mathcal{L}}_{\theta } = \frac{{d^{2} }}{{d\eta^ 2}},~} \\ {{\mathcal{L}}_{\theta } ^{{ - 1}} \left( \blacksquare \right) = \mathop \smallint \limits_{0}^{\eta } \mathop \smallint \limits_{0}^{\eta } \left( \blacksquare \right)d\eta d\eta .} \\ \end{array} } \right\}$$

(9)

With

$$\left.\begin{array}{c}{\delta }_{1}=\left(1-{\varphi }_{3}\right)\left\{\left(1-{\varphi }_{2}\right)\left[\left(1-{\varphi }_{1}\right)+{\varphi }_{1}\frac{{\left(\rho {C}_{p}\right)}_{p_{1}}}{{\left(\rho {C}_{p}\right)}_{f}}\right]+{\varphi }_{2}\frac{{\left(\rho {C}_{p}\right)}_{p_{2}}}{{\left(\rho {C}_{p}\right)}_{f}}\right\}+{\varphi }_{3}\frac{{\left(\rho {C}_{p}\right)}_{p_{3}}}{{\left(\rho {C}_{p}\right)}_{f}},\\ {\delta }_{2}=\left(1-{\varphi }_{3}\right)\left\{\left(1-{\varphi }_{2}\right)\left[\left(1-{\varphi }_{1}\right)+{\varphi }_{1}\frac{{\left(\rho \beta \right)}_{p_{1}}}{{\left(\rho \beta \right)}_{f}}\right]+{\varphi }_{2}\frac{{\left(\rho \beta \right)}_{p_{2}}}{{\left(\rho \beta \right)}_{f}}\right\}+{\varphi }_{3}\frac{{\left(\rho \beta \right)}_{p_{3}}}{{\left(\rho \beta \right)}_{f}}, \\ {\delta }_{3}=\frac{{k}_{f}}{{k}_{{Thnf}}}.\end{array}\right\}$$

(10)

Operational with ${\mathcal{L}}^{-1}$ in Eq. (8) and subsequent to exerting boundary constraints on it, we get

$$\theta =\theta \left(0\right)+{\theta }^{\prime}\left(0\right){\eta}+\underset{0}{\overset{\eta }{\iint }}\langle Nc \frac{{\delta }_{1}{\delta }_{2}}{\frac{1}{{\delta }_{3}}}{{(1-{\varphi }_{1})}^{2.5}{(1-{\varphi }_{2})}^{2.5}{(1-{\varphi }_{3})}^{2.5}\left(\theta -{\theta }_{a}\right)}^{2}+Nr{\delta }_{3}\left({\theta }^{4}-{\theta }_{a}^{4}\right)+{m}_{2}{\delta }_{3}\frac{{\left(\theta -{\theta }_{a}\right)}^{n+1}}{{\left(1-{\theta }_{a}\right)}^{n}}+{Pe}{\delta }_{1}{\delta }_{3}{\theta }^{\prime}\rangle .$$

(11)

Alternatively, taking into account the boundary constraints (7), Eq. (11) becomes:

$${{\theta}}\left( {{\eta}} \right) = 1 + {a\eta } + \iint {_{{_{0} }}^{{^{{{\eta}}} }} }\left\langle {{{Nc}}} \right.{ }\frac{{{{\delta}}_{1} {{\delta}}_{2} }}{{\frac{1}{{{{\delta}}_{3} }}}}\left( {1 - {\varphi }_{1} } \right)^{2.5} \left( {1 - {\varphi }_{2} } \right)^{2.5} \left( {1 - {\varphi }_{3} } \right)^{2.5} \left( {{{\theta}} - {{\theta}}_{{{a}}} } \right)^{2} + {{Nr}}{{\delta}}_{3} \left( {{{\theta}}^{4} - {{\theta}}_{{{a}}}^{4} } \right) + {{m}}_{2} {{\delta}}_{3} \frac{{\left( {{{\theta}} - {{\theta}}_{{{a}}} } \right)^{{{{n}} + 1}} }}{{\left( {1 - {{\theta}}_{{{a}}} } \right)^{{{n}}} }} + \left. {{{Pe}}{{\delta}}_{1} {{\delta}}_{3} {{\theta}}^\prime } \right\rangle$$

(12)

In conclusion, the elements of the solution that were derived through the use of the ADM method are outlined below:

$$\theta \left(\eta \right)={\theta }_{0}\left(\eta \right)+\underset{0}{\overset{\eta }{\iint }}\langle {Nc }\frac{{\delta }_{1}{\delta }_{2}}{\frac{1}{{\delta }_{3}}}{{(1-{\varphi }_{1})}^{2.5}{(1-{\varphi }_{2})}^{2.5}{(1-{\varphi }_{3})}^{2.5}\left(\theta -{\theta }_{a}\right)}^{2}+{Nr}{\delta }_{3}\left({\theta }^{4}-{{\theta }_{a}}^{4}\right)+{m}_{2}{\delta }_{3}\frac{{\left(\theta -{\theta }_{a}\right)}^{n+1}}{{\left(1-{\theta }_{a}\right)}^{n}}+{Pe}{\delta }_{1}{\delta }_{3}{\theta }^{{^{\prime}}}\rangle$$

(13)

Where.

$${\theta }_{0}=1+a\eta$$

(14)

The constant ${{a}}$ could be determined using boundary conditions. The two components' terms of Adomian polynomials are obtained as follows:

$${{{A}}}_{0}={{{\xi}}}_{3}{{{m}}}_{2}+\frac{1}{{{{\xi}}}_{3}}\left({{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}+2{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{a}}{{\eta}}+{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{{a}}}^{2}{{{\eta}}}^{2}\right)+{{{\xi}}}_{3}{N}{r}+{{{\xi}}}_{3}{{{m}}}_{2}{\space{a}}{{\eta}}+{{{\xi}}}_{1}{{{\xi}}}_{3}{P}{e}{\space{a}}+6{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{2}{{{\eta}}}^{2}+4{{{\xi}}}_{3}{N}{r}{\space{a}}{{\eta}}+4{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{3}{{{\eta}}}^{3}+{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{4}{{{\eta}}}^{4}-{{{\xi}}}_{3}{{{m}}}_{2}{{{\theta}}}_{{{a}}}+\frac{{{{\xi}}}_{4}}{{{{\xi}}}_{3}}\left(-2{{{\xi}}}_{1}{{{\xi}}}_{2}{N}{c}{{{\theta}}}_{{{a}}}-2{{{\xi}}}_{1}{{{\xi}}}_{2}{N}{c}{{a}}{{{\theta}}}_{{{a}}}{{\eta}}+{{{\xi}}}_{1}{{{\xi}}}_{2}{N}{c}{{{\theta}}}_{{{a}}}^{2}\right)-{{{\xi}}}_{3}{N}{r}{{{\theta}}}_{{{a}}}^{4}$$

(15a)

$$\begin{aligned}{{{A}}}_{1}&={{{\xi}}}_{1}{{{\xi}}}_{3}{{P}} {{e}}{{a}}+\frac{{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}} {{{{\xi}}}_{3}}\Big({{N}}{{c}}+2{N}{c}{\space{a}} {{\eta}}+{N}{c}{\space{{a}}}^{2}{{{\eta}}}^{2}-2{N} {c}{{{\theta}}}_{{{a}}}-2{N}{c}{{a}}{{\eta}} {{{\theta}}}_{{{a}}}+{{N}}{{c}} {{{\theta}}}_{{{a}}}^{2}\Big)+{{{\xi}}}_{3} \Big({{{m}}}_{2}+{N}{r}+{{m}}2{{a}}{{\eta}} +4{N}{r}{\space{a}}{{\eta}}+6{N}{r}{\space{{a}}}^{2} {{{\eta}}}^{2}\\ &\quad +4{N}{r}{\space{{a}}}^{3}{{{\eta}}}^{3} +{N}{r}{\space{{a}}}^{4}{{{\eta}}}^{4}-{{{m}}}_{2} {{{\theta}}}_{{{a}}}-{N}{r}{{{\theta}}}_{{{a}}}^{4} +{N}{r}+4{N}{r}{\space{a}}{{\eta}}+6{N}{r} {\space{{a}}}^{2}{{{\eta}}}^{2}+4{N}{r}{\space{{a}}}^{3} {{{\eta}}}^{3}+{N}{r}{\space{{a}}}^{4}{{{\eta}}}^{4} -{N}{r}{{{\theta}}}_{{{a}}}^{4}\Big)\end{aligned}$$

(15b)

Now using ADM, the first terms of the solution are given as.

$${{{\theta}}}_{1}={{{\xi}}}_{3}\left(\frac{1}{2}{{{m}}}_{2}{{{\eta}}}^{2}+\frac{1}{2}{N}{r}{\space{{\eta}}}^{2}+\frac{1}{2}{{{\xi}}}_{1}{P}{e}{\space{a}}{{{\eta}}}^{2}+\frac{1}{6}{{{m}}}_{2}{{a}}{{{\eta}}}^{3}+\frac{2}{3}{N}{r}{\space{a}}{{{\eta}}}^{3}+\frac{1}{2}{N}{r}{\space{{a}}}^{2}{{{\eta}}}^{4}+\frac{1}{5}{N}{r}{\space{{a}}}^{3}{{{\eta}}}^{5}+\frac{1}{30}{N}{r}{\space{{a}}}^{4}{{{\eta}}}^{6}-\frac{1}{2}{{{m}}}_{2}{{{\eta}}}^{2}{{{\theta}}}_{{{a}}}-\frac{1}{2}{N}{r}{\space{{\eta}}}^{2}{{{\theta}}}_{{{a}}}^{4}\right)+\frac{{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}}{{{{\xi}}}_{3}}\left(\frac{1}{2}{{N}}{{c}}{{{\eta}}}^{2}+\frac{1}{3}{N}{c}{\space{a}}{{{\eta}}}^{3}+\frac{1}{12}{N}{c}{{{a}}}^{2}{{{\eta}}}^{4}-{N}{c}{\space{{\eta}}}^{2}{{{\theta}}}_{{{a}}}-\frac{1}{3}{N}{c}{\space{a}}{{{{\theta}}}_{{{a}}}{{\eta}}}^{3}+\frac{1}{2}{N}{c}{\space{{\theta}}}_{{{a}}}^{2}{{{\eta}}}^{2}\right)$$

(16a)

$${{{\theta}}}_{2}=\frac{1}{2}{{{\xi}}}_{3}{{{m}}}_{2}{{{\eta}}}^{2}+\frac{1}{2{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{{\eta}}}^{2}+{{{\xi}}}_{3}{N}{r}{\space{{\eta}}}^{2}+\frac{1}{2}{{{\xi}}}_{1}{{{\xi}}}_{3}{P}{e}{\space{a}}{{{\eta}}}^{2}+\frac{1}{6}{{{\xi}}}_{3}{{{m}}}_{2}{{a}}{{{\eta}}}^{3}+\frac{1}{3{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{{a}}{{{\eta}}}^{3}+\frac{4}{3}{{{\xi}}}_{3}{N}{r}{\space{a}}{{{\eta}}}^{3}+\frac{1}{12{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{{a}}}^{2}{{{\eta}}}^{4}+{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{2}{{{\eta}}}^{4}+\frac{2}{5}{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{3}{{{\eta}}}^{5}+\frac{1}{15}{{{\xi}}}_{3}{N}{r}{\space{{a}}}^{4}{{{\eta}}}^{6}-\frac{1}{2}{{{\xi}}}_{3}{{{m}}}_{2}{{{\eta}}}^{2}{{{\theta}}}_{{{a}}}-\frac{1}{{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{{\eta}}}^{2}{{{\theta}}}_{{{a}}}-\frac{1}{3{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{a}}{{{\eta}}}^{3}{{{\theta}}}_{{{a}}}+\frac{1}{2{{{\xi}}}_{3}}{{{\xi}}}_{1}{{{\xi}}}_{2}{{{\xi}}}_{4}{N}{c}{\space{{\eta}}}^{2}{{{\theta}}}_{{{a}}}^{2}-{{{\xi}}}_{3}{N}{r}{\space{{\eta}}}^{2}{{{\theta}}}_{{{a}}}^{4}$$

(16b)

With ${\xi }_{1}={\delta }_{1}$, ${\xi }_{2}={\delta }_{2}$, ${\xi }_{3}=1/{\delta }_{3}$, and ${\xi }_{4}={\delta }_{4}$.

4 Graphical interpretations and outcomes

The influence of the quantities of the sundry factors on the temperature profile $\theta (\eta )$ is heeded in Figs. 2, 3, 4, 5, 6, 7, 8, 9. The effect of ternary hybrid nanofluid on temperature profile $\theta (\eta )$ of the fin is shown in Fig. 2 when $n={m}_{2}=1$, $Nr=Nc=2$, ${\theta }_{a}=0.3,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=0\%$,$3\%, 6\%$ and $Pe=1$. This confirms that from a physical point of view, the solid nanoparticles, if it is increased inside the fluid, raise the thermal energy stored in these molecules, and thus, raise the temperature of the fluid accordingly. Increasing ${\varphi }_{\mathrm{Cu+A{l}_{2}{O}_{3}+Ti{O}_{2}}}$ causes a boost in the temperature outline. Figure 3 is presented to see the influence of the nature of the base fluid on the temperature outline $\theta (\eta )$ of the fin. It is noticed that pure water (H₂O) has a higher temperature than the ethylene glycol–water (50–50%) base fluid when $n={m}_{2}=1,{Nr}={Nc}=2,{\theta }_{a}=0.2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${Pe}=4$. Physically, the hybrid liquid consisting of ethylene glycol and water has a higher heat transfer rate than pure water. Therefore, we found from the analysis that the pure liquid has a higher temperature than the hybrid liquid.

Fig. 2

Effect of ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}$ on $\theta (\eta )$ when $n={m}_{2}=1,Nr=Nc=2,{\theta }_{a}=0.3$ and $Pe=1$

Fig. 3

Effect of nature of the base fluid on $\theta (\eta )$ when $n={m}_{2}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and ${Pe}=4$

Figure 4 depicts the result of the power index $n$ on the temperature profile $\theta (\eta )$ of the fin when ${m}_{2}=1,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and ${Pe}=1$. It is seen that temperature has an increasing trend for larger values of power index $n$. The main reason behind this is that by increasing the power index $n$, the heat transference factor $h$ increases, which in turn increases the temperature outlines $\theta (\eta )$. Figure 5 is outlined to visualize the effect of ${\theta }_{a}$ on temperature profile $\theta (\eta )$ of the fin when $n={m}_{2}=1,{Nr}=3,{Nc}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${Pe}=1$. It is remarked that the temperature for the increasing parametric amounts of ${\theta }_{a}$ is increased. This implies that as the surrounding temperature rises, heat transference from the fin surface to the surrounding environment diminishes. Rising the temperature of the ambient medium ${\theta }_{a}$ raises the temperature of the fluid because of the convection process, which in turn slows down the rate of heat transport.

Fig. 4

Effect of power index $n$ on $\theta (\eta )$ when ${m}_{2}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and $\mathrm{Pe}=1$

Fig. 5

Consequence of ${\theta }_{a}$ on $\theta (\eta )$ when $n={m}_{2}=1,{Nr}=3,{Nc}=2 ,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${Pe}=1$

Figure 6 is plotted to perceive the influence of the Peclet number on the temperature profile $\theta (\eta )$ of the fin when $n={m}_{2}=1,{Nr}={Nc}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${\theta }_{a}=0.2$. It is found that an increase in Peclet quantity $Pe$ shows an upsurge in temperature profile $\theta (\eta )$. On the other side, the greater the speed, the less time there is for the fin to interact with its environment. As a result, as $P$ e increases, heat transfer diminishes. Whereas, from a physical point of view, the Peclet amount $Pe$ depends on the heat capacity ${\left(\rho {C}_{p}\right)}_{f}$. The greater heat capacity causes in enhance the Peclet quantity. On the contrary, regarding the thermal conductivity of the fluid ${k}_{f}$, this causes an enhancement in the temperature outlines. Figure 7 displays the consequences of ${m}_{2}$ (the wet porous variable) on the temperature outline θ $(\eta )$ of the fin when $n=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and $Pe=2$. Here, we note that with a surge in ${m}_{2}$, the temperature declines. Physically, the higher number of wet porous results in a great heat transference rate, and thus, the temperature of the fluid begins to decline gradually. Figure 8 depicts the consequences of convective parameters on the temperature outlines $\theta (\eta )$ of fins when $n={m}_{2}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}=2,{\theta }_{a}=0.2$ and ${Pe}=1$. There is a decrease in $\theta (\eta )$ of the fin when $Nc$ increases. The realize of radiative variable $Nr$ on the temperature outline is shown in Fig. 9 when $n=0$, ${m}_{2}=1$, ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$, ${Nc}=1$, ${\theta }_{a}=0.1$ and ${Pe}=1$. It is observed that a rise in $Nr$ produces a boost in the temperature profile. The improvements in the convective number and radiative parameter raise the rate of heat transport inside the fluid because of the work of the wetted fin with the trihybrid nanofluid, which makes the thermal energy stored inside the fluid begin to dissipate, which reduces the temperature of the nanofluid. Effects of ambient temperature and nature of nanofluid (i.e., ternary hybrid nanofluid, hybrid nanofluid, and Pure water) on a thermal gradient are shown in Fig. 10 when $n={m}_{2}=1,{Nr}={Nc}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${Pe}=1$. As visualized, the thermal gradient decreases with the augment of both ambient temperature and the nature of nanofluid, Therefore, in the working fluid, we discover that a water-based ternary hybrid nanofluid (Cu + Al₂O₃ + TiO₂) exhibits promising heat transfer. In addition, it can be said that one of the most important results of the current study is that when ethylene glycol is added to pure water to make the base fluid as a hybrid fluid, this results in a better heat transport rate than in the case of pure water only as conventional fluid. This result can be applied as a basis for industrial cooling processes in addition to the work of the fin during cooling.

Fig. 6

Consequence of ${Pe}$ on $\theta (\eta )$ when $n={m}_{2}=1,{Nr}={Nc}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${\theta }_{a}=0.2$

Fig. 7

Consequence of ${m}_{2}$ on $\theta (\eta )$ when $n=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and ${Pe}=2$

Fig. 8

Effect of $\mathrm{Nc}$ on $\theta (\eta )$ when $n={m}_{2}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}=2,{\theta }_{a}=0.2$ and $Pe=1$

Fig. 9

Effect of $\mathrm{Nr}$ on $\theta (\eta )$ when $n=0,{m}_{2}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nc}=1,{\theta }_{a}=0.1$ and ${Pe}=1$

Fig. 10

Effects of ${\theta }_{a}$ and nature of nanofluid on $-\theta^{{\prime}}(\eta )$ when $n={m}_{2}=1,{Nr}={Nc}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$ and ${Pe}=1$

The comparison of the water-based ternary hybrid nanofluid (Cu + Al₂O₃ + TiO₂/H₂O) with Ethylene glycol–water (50–50%)-based ternary hybrid nanofluid (Cu + Al₂O₃ + TiO₂/H₂O (50%)-C₂H₆O₂(50%)) is highlighted in Fig. 11 when $n={m}_{2}=1,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and ${Pe}=1$. When compared to Ethylene glycol–water (50–50%)-based, water-based exhibits greater heat transport. Alternatively, The thermic gradient decreases with the augment of the volume fraction of nanoparticle ${\varphi }_{\mathrm{Cu}-{\mathrm{Al}}_{2}{\mathrm{O}}_{3}-{\mathrm{TiO}}_{2}}$.

Fig. 11

Effects of ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}$ and nature of the base fluid on $-\theta^{{\prime}}(\eta )$ when $n={m}_{2}=1,{Nr}={Nc}=2,{\theta }_{a}=0.2$ and $Pe=1$

The converges of ADM method are illustrated in Fig. 12 for temperature profile θ(η) of the fin when $n={m}_{2}=1,{Nr}={Nc}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{\theta }_{a}=0.1$ and ${Pe}=1$. It is observed that the ADM analytical solution converges quickly to the RK45 numerical solution at the 19th-order of approximation. When $n=1$, ${m}_{2}=2$, ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%$, $Nr=Nc=2$, ${\theta }_{a}=0.1$ and ${Pe}=2$, the comparison of the HAM-based Mathematica software BVPh 2 with the ADM approach and the Runge–Kutta–Fehlberg fourth–fifth order (RKF-45) is shown in Fig. 13 and Table 3. The findings show that there is a remarkable degree of concordance between the two sets of data.

Fig. 12

Order of approximation of ADM solution when $n={m}_{2}=1,{Nr}={Nc}=1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{\theta }_{a}=0.1$ and ${Pe}=1$

Fig. 13

Comparison among the obtained outcomes and HAM-based Mathematica package calculations $\theta (\eta )$ when $n=1,{m}_{2}=2,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=6\%,{Nr}={Nc}=2,{\theta }_{a}=0.1$ and ${Pe}=2$

Table 3 The comparison between ADM results and HAM solution for $\theta (\eta )$ when $n=1$, ${m}_{2}={Nr}={Nc}=2$, ${\theta }_{a}=0.1,{\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}=0\%,$ and $Pe=2$

5 Concluding remarks

The following are the primary important points of the requested issue:

• Increasing, ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}$, power index $n$, ambient temperature ${\theta }_{a}$, and Peclet quantity $Pe$ increases temperature profile $\theta (\eta )$.

• Improving wet porous variable ${m}_{2}$, convective variable ${Nc}$, and radiation factor $Nr$ decreases temperature profile $\theta (\eta )$.

• Pure water has a higher temperature than the ethylene glycol–water (50–50%) base fluid.

• The thermal gradient is found to decrease by increasing ${\varphi }_{\mathrm{Cu}+{\mathrm{Al}}_{2}{\mathrm{O}}_{3}+{\mathrm{TiO}}_{2}}$ and ${\theta }_{a}$.

• Comparisons and convergence tests have proven that the HAM approach is highly resilient and trustworthy.