Introduction

It has been shown that monospecific biologics that bind to a single target receptor with high affinity is not optimal for many therapeutic applications. For example, multivalent binding is needed for optimal IgG antibody-dependent cellular cytotoxicity (ADCC) and complement-dependent cytotoxicity (CDC) to improve target cell killing [1, 2]. Furthermore, biologics that can bind to multiple receptors can neutralize pathogens, diseased cells, and soluble proteins much better than monospecific biologics [3, 4]. As a result, many avidity-based biologics that can bind multiple receptors have been developed to overcome the therapeutic limitation of monospecific biologics [4, 5].

A commonly used target-mediated drug disposition (TMDD) model [6] and its approximations [7, 8] assume that both, the drug and the target have only one binding site (one-to-one binding). In [9], the TMDD model and its approximations were derived for drugs that have two identical binding sites (two-to-one binding). This was an important extension as most therapeutic monoclonal IgG antibodies (mAbs) belong to this class [10, 11]. Here we extend the TMDD model and its approximations to drugs that have more than two (N > 2) identical binding sites (N-to-one binding). This extension can be helpful for modeling IgA antibodies that have 2 or 4 binding sites [12], IgM antibodies that have 10 or 12 binding sites [13], or engineered antibodies or other biologics with more than 2 binding sites [2, 5, 14].

While the TMDD model with one-to-one binding assumption describes biologics sufficiently accurately in most cases, development of mathematical models that describe N-to-one binding more mechanistically may facilitate understanding of drug-target interactions and their influence on pharmacokinetic and pharmacodynamic properties of the system. To simplify notations, the models for N-to-one binding will be referred to as N-to-one TMDD, N-to-one quasi-steady state (QSS), N-to-one quasi-equilibrium (QE), N-to-one irreversible binding (IB), and N-to-one Michaelis–Menten (MM) models.

Theoretical

TMDD model for a drug with N binding sites

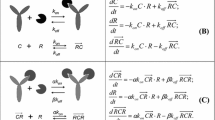
A schematic representation of binding interactions for the drug that has N = 4 identical binding sites with the target that has one binding site is presented in Fig. 1. We assume that all sites are identical, i.e. binding constants kon and koff are the same for all sites and are independent of the number of occupied sites. The free drug (C) and the free target (R) are defined as the drug and the target that are not bound to each other. The binding processes form drug-target complexes, RkC, k = 1, …, N, where k is the number of drug binding sites occupied by the target. When k < N, these complexes correspond to the partially bound drug. The complex RNC corresponds to the fully bound drug, with all binding sites occupied by the target. For future derivations it is convenient to extend the notation to k = 0 and k = N + 1 and define R0C = C and RN+1C = 0.

Fig. 1
figure 1

Schematic representation of 4-to-one binding

Full size image

Concentrations of the total drug (Ctot) and the total target (Rtot) can be then expressed as

$${C}_{tot}=C+\sum\nolimits_{k=1}^{N}{R}_{k}C,$$
(1)
$${R}_{tot}=R+\sum\nolimits_{k=1}^{N}{k\cdot R}_{k}C.$$
(2)

We assume that the drug is described by a two-compartment model with combined linear elimination and target-mediated drug disposition/elimination following intravenous (IV) and subcutaneous (SC) dosing and that elimination rate of all drug-target complexes (kint) is the same and is independent of the type of the complex (number of binding sites occupied). We also assume that binding constants are the same for all binding sites and they do not depend on the occupancy of the other binding sites. Then, equations of the system can be written as 4 equations that describe total drug and total target concentrations:

$$\frac{d{A}_{d}}{dt}=-{k}_{a}{\cdot A}_{d};\begin{array}{cc}{A}_{d}\left(0\right)={F}_{SC}\cdot {D}_{1};& {C}_{tot}\left(0\right)=\frac{{D}_{2}}{{V}_{c}};\end{array}$$
(3)
$$\frac{d{C}_{tot}}{dt}=\frac{In\left(t\right)+{k}_{a}{\cdot A}_{d}+{k}_{tp}\cdot {A}_{T}}{{V}_{c}}-\left({k}_{el}+{k}_{pt}\right)\cdot C-{k}_{int}{\cdot (C}_{tot}-C);$$
(4)
$$\frac{d{A}_{T}}{dt}={k}_{pt}\cdot C\cdot {V}_{c}-{k}_{tp}{\cdot A}_{T};\begin{array}{cc}{A}_{T}\left(0\right)=0;& \begin{array}{cc}{R}_{tot}\left(0\right)=\frac{{k}_{syn}}{{k}_{deg}};& \end{array}\end{array}$$
(5)
$$\frac{d{R}_{tot}}{dt}={k}_{syn}-{k}_{deg}\cdot R-{k}_{int}{\cdot (R}_{tot}-R);$$
(6)

and N equations that describe drug-target complexes:

$$\frac{d{R}_{k}C}{dt}={\left(N-k+1\right)\cdot k}_{on}\cdot {R}_{k-1}C\cdot R-(k\cdot {k}_{off}+{{k}_{int}+{\left(N-k\right)\cdot k}_{on}\cdot R)\cdot R}_{k}C+\left(k+1\right)\cdot {k}_{off}{\cdot R}_{k+1}C; k=1,\dots ,N.$$
(7)

Here kel is the linear elimination rate constant, kpt and ktp are inter-compartment rate constants, kon, koff, and kint are the binding, dissociation, and internalization (elimination of the complex) rate constants; kdeg and ksyn are the degradation (elimination of the target) and target production rate constants; Vc is the central compartment volume; In(t) is the infusion rate; FSC is the absolute bioavailability of the subcutaneous dose. Initial conditions correspond to the case where the free drug that is not present endogenously is administered as a subcutaneous dose D1 and bolus dose D2.

Quasi-steady-state approximation

Similarly to TMDD equations with one-to-one binding, the quasi-steady-state approximation of the TMDD N-to-one system can be derived by assuming that the free (unbound) drug C, the free (unbound) target R, and the drug-target complexes RkC are in quasi-steady-state [8], where binding rates are balanced by the sum of dissociation and internalization rates on the scale of the other processes:

$$\frac{d{R}_{k}C}{dt}={\left(N-k+1\right)\cdot k}_{on}\cdot {R}_{k-1}C\cdot R-(k\cdot {k}_{off}+{{k}_{int}+{\left(N-k\right)\cdot k}_{on}\cdot R)\cdot R}_{k}C+\left(k+1\right)\cdot {k}_{off}{\cdot R}_{k+1}C=0; k=1,\dots ,N.$$
(8)

The QSS approximation is then described by Eqs. (3)-(6) supplemented by the algebraic Eqs. (1)-(2) and (8).

A recent work by Ng and Bauer [15] demonstrated that the QSS system of differential and algebraic equations can be successfully solved numerically. However, it is rather challenging and requires significant expertise in numerical methods. Here we demonstrate an example of analytical solution of algebraic part of the system, allowing for simple and fast numerical implementation.

We aim to find the algebraic solution of Eqs. (1)-(2) and (8), that is, to express all quantities C, R, RkC, k = 1,…,N as functions of Ctot and Rtot defined in (1)-(2).

First, we will derive equation for R. To do this, we compute the sum of Eqs. (8) multiplying each by the respective k (number of binding sites occupied by the target). The resulting equation is:

$$\sum_{k=1}^{N}k\cdot \frac{d{R}_{k}C}{dt}=0.$$
(9)

Then, tedious but straightforward calculations presented in Appendix 1 result in the equation:

$${R}_{tot}=R+\frac{N{\cdot C}_{tot}\cdot R}{{K}_{D}+{K}_{IB}+R}.$$
(10)

Here KD = koff/kon is the dissociation rate constant and KIB = kint/kon is the irreversible binding rate constant introduced in [9].

This equation is identical to the corresponding expression for one-to-one binding if we interpret \(N{\cdot C}_{tot}\) as the total number of binding sites in the system. One can solve this equation for R to find:

$$R=\frac{1}{2}\left[-\left(N\cdot {C}_{tot}+{K}_{IB}+{K}_{D}-{R}_{tot}\right)+\sqrt{{\left(N{\cdot C}_{tot}+{K}_{IB}+{K}_{D}-{R}_{tot}\right)}^{2}+4\cdot ({K}_{IB}+{K}_{D}){\cdot R}_{tot}}\right]$$
(11)

This is the key equation of the QSS approximation, but it is only half of the solution. We also need expressions for C and RkC as functions of R, Ctot, and Rtot.

As shown in Appendix 2, RNC can be expressed as

$${R}_{N}C=\frac{N!{\cdot C}_{tot}\cdot {R}^{N}}{\prod_{k=1}^{N}{({K}_{IB}+k\cdot K}_{D}+k\cdot R)}$$
(12)

while the remaining elements can be found recursively as follows:

$${R}_{N-1}C={R}_{N}C\cdot \frac{{K}_{IB}+N\cdot {K}_{D}}{R},$$
(13)
$${R}_{k}C={R}_{k+1}C\cdot \frac{{K}_{IB}+\left({\text{k}}+1\right)\cdot {K}_{D} +\left({\text{N}}-{\text{k}}-1\right)\cdot {\text{R}}}{\left({\text{N}}-{\text{k}}\right)\cdot R} -{R}_{k+2}C\cdot \frac{\left({\text{k}}+2\right)\cdot {K}_{D}}{\left({\text{N}}-{\text{k}}\right)\cdot R}, k=(N-2), \dots , 0$$
(14)

Note that free drug concentration C can be found from (14) when k = 0, or, equivalently, from the equation:

$$C={C}_{tot}-\sum\nolimits_{k=1}^{N}{R}_{k}C.$$
(15)

Thus, the N-to-one QSS approximation is described by differential Eqs. (3)-(6) supplemented by algebraic Eqs. (11)-(15). Equations (12)-(14) are explicitly written for N = 4 in Appendix 3.

When internalization rate of the complexes kint is equal to the degradation rate of the free target kdeg, the total target concentration Rtot is a constant parameter of the system, and the Eq. (6) is not needed.

Quasi-equilibrium approximation

QE equations can be obtained from the corresponding QSS equations by setting KIB = 0. They can be used to resolve binding equation for the in-vitro experiment with known drug and target concentrations, Ctot and Rtot, respectively. In this case, distribution of species is described by the system:

$$R=\frac{1}{2}\left[-\left(N{\cdot C}_{tot}+{K}_{D}-{R}_{tot}\right)+\sqrt{{\left(N{\cdot C}_{tot}+{K}_{D}-{R}_{tot}\right)}^{2}+4{\cdot K}_{D}{\cdot R}_{tot}}\right]$$
(16)
$${R}_{N}C= \frac{{C}_{tot}\cdot {R}^{N}}{{{(K}_{D}+R)}^{N}}$$
(17)
$${R}_{N-1}C={R}_{N}C\cdot \frac{N\cdot {K}_{D}}{R},$$
(18)
$${R}_{k}C={R}_{k+1}C\cdot \frac{\left({\text{k}}+1\right)\cdot {K}_{D} +\left({\text{N}}-{\text{k}}-1\right)\cdot {\text{R}}}{\left({\text{N}}-{\text{k}}\right)\cdot R} -{R}_{k+2}C\cdot \frac{\left({\text{k}}+2\right)\cdot {K}_{D}}{\left({\text{N}}-{\text{k}}\right)\cdot R}, k=N-2,\dots ,0$$
(19)
$$C={C}_{tot}-\sum_{k=1}^{N}{R}_{k}C$$

In fact, in this case the system can be simplified (Appendix 4) and presented in the form:

$${R}_{k}C=\frac{{C\left(n,k\right)\cdot C}_{tot}\cdot {{K}_{D}}^{N-k}{\cdot R}^{k}}{({{K}_{D}+R)}^{N}}, C\left(n,k\right)=\frac{N!}{k!\cdot \left(N-k\right)!}, k=0,\dots ,N.$$
(20)

This solution is intuitively obvious. When probability of the binding site being occupied in equal to R/(KD + R), and probability of the site being free is KD/(KD + R), then Eqs. (20) show the probability of k sites being occupied and (N-k) sites being free.

Irreversible binding approximation

The irreversible binding approximation can be obtained from the QSS approximation by assuming koff = 0 (resulting in KD = 0). Binding equations in this case have the form

$$R=\frac{1}{2}\left[-\left(N\cdot {C}_{tot}+{K}_{IB}-{R}_{tot}\right)+\sqrt{{\left(N\cdot {C}_{tot}+{K}_{IB}-{R}_{tot}\right)}^{2}+4\cdot {K}_{IB}{\cdot R}_{tot}}\right]$$
(21)
$${R}_{N}C=\frac{N!{\cdot C}_{tot}\cdot {R}^{N}}{\prod_{k=1}^{N}{(K}_{IB}+k\cdot R)}$$
(22)
$${R}_{N-1}C={R}_{N}C\cdot \frac{{K}_{IB}}{R},$$
(23)
$${R}_{k}C={R}_{k+1}C\cdot \frac{{K}_{IB} +\left({\text{N}}-{\text{k}}-1\right)\cdot {\text{R}}}{\left({\text{N}}-{\text{k}}\right)\cdot R} , k=N-2,\dots ,0$$
(24)
$$C={C}_{tot}-\sum\nolimits_{k=1}^{N}{R}_{k}C$$

In this case the system can be simplified and presented in the form (see Appendix 5):

$${R}_{k}C={\frac{N!}{\left(N-k\right)!}\cdot C_{tot}}\cdot \frac{{K}_{IB}{\cdot R}^{k}}{\prod_{i=N-k}^{N}{(K}_{IB}+i\cdot R)} , k=0,\dots ,N.$$
(25)

Michaelis–Menten approximation

To further simplify the QSS equations, we will assume that the free drug concentration is approximately equal to the total drug concentration and that the free target concentration R is small relative to \({({K}_{IB}+K}_{D})\). In this case, we can derive (see Appendix 6)

$${R}_{k}C\approx \frac{N!{\cdot {K}_{IB}\cdot C}_{tot}\cdot {R}^{k}}{(N-k)!\prod_{i=0}^{k}{({K}_{IB}+i\cdot K}_{D}+i\cdot R)}, k= 0,..,N$$
(26)

Since R is small and RkC is of the order Rk, we can conclude that

$${C}_{tot}-C\approx { R}_{tot}-R\approx {R}_{1}C,$$
(27)

and that there is negligible concentration of complexes with k > 1.

Disregarding the quadratic term when solving Eq. (10) for R we get:

$$R\approx \frac{({K}_{IB}+{K}_{D}){\cdot R}_{tot}}{N{\cdot C}_{tot}+{K}_{IB}+{K}_{D}}$$
(28)

and then

$${R}_{1}C\approx \frac{{N{\cdot C}_{tot}\cdot R}_{tot}}{ N{\cdot C}_{tot}+{K}_{IB}+{K}_{D}}\approx \frac{{N\cdot C\cdot R}_{tot}}{ N\cdot C+{K}_{IB}+{K}_{D}}$$
(29)

Substituting Ctot – C and Rtot – R by R1C in (4) and (6), keeping only the terms up to the order of R, and assuming that Ctot is approximately equal to C, we can arrive at equations of the Michaelis–Menten approximation:

$$\frac{dC}{dt}=\frac{In\left(t\right)+{k}_{a}{A}_{d}+{k}_{tp}{A}_{T}}{{V}_{c}}-\left({k}_{el}+{k}_{pt}\right)C-{k}_{int}\frac{{R}_{tot}\cdot C}{\frac{\left({K}_{D}+{K}_{IB}\right)}{N}+C},$$
(30)
$$\frac{d{R}_{tot}}{dt}={k}_{syn}-{k}_{deg}\cdot R-{k}_{int}\frac{{R}_{tot}\cdot C}{\frac{\left({K}_{D}+{K}_{IB}\right)}{N}+C}.$$
(31)

These equations are equivalent to the MM approximation of the standard TMDD system where KSS = (KD + KIB)/N.

As before, if kint is equal to kdeg, the total target concentration is a constant parameter of the system, and the last equation can be removed. Then, the system is described by the two-compartment model with parallel linear and Michaelis–Menten elimination.

Investigation of the N-to-one model

To investigate the N-to-one model and its approximations, several simulation studies were performed for N = 4 binding sites. NONMEM 7.5.1® software [16] was used for simulations, estimation of parameters, and computation of predictions. FOCEI estimation method was used for model fitting.

First, the case of “slow elimination of complexes”, with parameters typical for mAbs and soluble targets was evaluated with two examples.

In example 1, typical predictions of the free drug, the free target, the total drug, the total target, and each of the 4 drug target complexes were computed for the full 4-to-one TMDD model and the 4-to-one QSS approximation to compare the curves at different doses and times. Four consecutive intravenous (IV) doses of 10, 50, 100, and 500 nmol were administered 21 days apart. The parameters from Table 1 (“True” values of fixed-effect parameters) were used for simulation; all variance parameters were set to zero.

Table 1 “Slow elimination of complexes” case: true values and estimated population parameters of 4-to-one binding models. Log normal (that is, normal in the log-transformed parameter space) inter-subject variability was assumed. Log normal residual variability was implemented as additive residual errors in the log-transformed dependent variables space. The true values were used as initial values for estimation
Full size table

In example 2, population PK simulation/estimation was performed. The population PK data set that imitated data from combined typical phase 1 and phase 2 studies (Table 2) was used to simulate concentrations of various quantities from the full 4-to-one TMDD model. The parameters from Table 1 (“True” values) were used for simulations. The simulated concentrations of the free drug and of the total target were then used to fit the following models:

  1. a.

    Full 4-to-one TMDD model with kon parameter estimated.

  2. b.

    Full 4-to-one TMDD model with kon parameter fixed at the true value.

  3. c.

    QSS 4-to-one approximation.

Table 2 Dosing and sampling scheme in the simulated study
Full size table

For these models, the estimated parameters were compared with the true values. Predictions of all quantities (including unobserved ones) were also computed and compared with the true (i.e. simulated from the full 4-to-one TMDD model) values. Conversion times were recorded. For all estimations, the true values were used as the initial values, thus the ability of models to converge was not tested and conversion times may have been optimistic (especially for the full model).

Then, the case of “fast elimination of complexes”, with parameters typical for mAbs and membrane-bound targets where Michaelis–Menten equations should be valid was evaluated. The same simulations as in example 1 of the “slow elimination of complexes” case were performed for the 4-to-one full TMDD, QSS, and MM models. The parameters from Table 3 were used in the simulations.

Table 3 “Fast elimination of complexes” case: true model parameters of 4-to-one binding models. Parameters not listed in this table coincide with those in Table 1
Full size table

Results

For the “slow elimination of complexes” case, typical predictions of the full 4-to-one TMDD model and the 4-to-one QSS approximation (Fig. 2) were almost identical for all quantities.

Fig. 2
figure 2

‘Slow Elimination of Complexes’ Case: Comparison of Full TMDD 4-to-one and QSS 4-to-one Model Predictions. Black: full TMDD model, gray: QSS approximation. Vertical dash lines: 10, 50, 100, 500 nmol IV doses

Full size image

In the “fast elimination of complexes” case, kint is equal to kdeg, so Rtot is constant and only C, R, and R1C are changing with time. As shown in Fig. 3, both 4-to-one QSS and the 4-to-one Michaelis–Menten models were able to reproduce the predictions of the full 4-to-one TMDD model for all these quantities.

Fig. 3
figure 3

‘Fast Elimination of Complexes’ Case: Comparison of Model Predictions for 4-to-one Models for Full TMDD, QSS, and MM. Black: full TMDD model, gray: QSS approximation, thin black: Michaelis–Menten approximation. Vertical dash lines: 10, 50, 100, 500 nmol IV doses

Full size image

In the population study for the “slow elimination of complexes” case, the full 4-to-one TMDD model (Model a) converged and provided accurate estimates for all model parameters except kon (Table 1). Model b. where kon was fixed to the true value converged and provided accurate estimates for all the other model parameters. The 4-to-one QSS model provided accurate estimates for all the parameters of the QSS model.

Model fit (objective function value [OFV]) and run times of all the models are shown in Table 1. The run time of the full 4-to-one TMDD model with the fixed kon value was approximately 8 times longer than that of the 4-to-one QSS model. The run time of the full 4-to-one TMDD model with the estimated kon value was approximately 21 times longer than that of the 4-to-one QSS model. Each function evaluation of the full model was taking approximately 9–10 times longer of the QSS model due to longer model integration time.

Discussion

Equations of the TMDD model and its QSS, QE, IB, and MM approximations were derived for drugs with N > 2 binding sites. The N-to-one QSS model was the most general approximation. The N-to-one QE and N-to-one IB approximations can be obtained from N-to-one QSS by setting KIB = 0 or KD = 0, respectively. The QSS 4-to-one model correctly estimated model parameters and predicted drug and target concentrations over time when it was fitted to the data simulated from the full 4-to-one TMDD model.

While advances in computer power and the software made numerical solution of the full N-to-one TMDD model possible, they did not (and could not) resolve the identifiability issue: binding parameters of the system cannot be determined from the routinely available data. Therefore, when the parameter kon was fixed at the true value, the full model converged much faster and was able to estimate all parameters correctly, while the model with the estimated value of kon took 2.5 times longer time to converge and was not able to estimate this parameter precisely even though dense sampling in the range of interest (immediately after the end of infusion) was available.

The system of Eqs. (1)-(4) was presented using differential equations for the total drug and total target concentrations rather than in the (equivalent and more traditional) form that uses differential equations for free drug and free target concentrations. The advantage of this form is that the large terms (terms that contain the parameter kon) are localized in equations for the RkC complexes rather than distributed throughout the entire system. We demonstrated that this is convenient for theoretical analysis of the system. Authors’ experience with numerical investigations using the full TMDD model indicated that this version is also more stable numerically. We speculate that this is because the processes with high derivatives (that involve fast binding) are localized in Eq. (7) while derivatives in Eqs. (1)-(4) are relatively small. This may allow more stable integration of the part of the system that describes slow-changing variables.

The run time of the 4-to-one QSS model was about 8 times faster than that of the full 4-to-one TMDD model with fixed kon, and it was about 21 times faster than that of the full 4-to-one TMDD model with the estimated kon value. All estimations used the true values as initial values. Further study is needed to determine and compare the ability of these models to obtain precise and robust parameter estimates from the real study data. The NONMEM code of the full 4-to-1 TMDD model, the QSS approximation of this model, and the corresponding Michelis-Menten approximation are provided in Appendix 7, 8, and 9, respectively.

We should repeat the limitation of the suggested analytical approach. We assumed that binding constants kon and koff are the same for all sites and they are independent of the number of occupied sites. Indeed, the parameters kon and koff are expected to be similar due to structural symmetry (as in most cases they are replicas of the same structure). However, it is unknown how much these parameters (and other parameters of the drug-target complexes, including kint) change when some or many of the binding sites are occupied, thus changing the structure (protein folding) of the drug-target complexes and their molecule weight. If this assumption does not hold, the analytical approach is intractable. For example, this approach does not describe systems with cooperative or allosteric binding.