MPBPK-TMDD models for mAbs: alternative models, comparison, and identifiability issues

Abstract

The aim of the present study was to evaluate model identifiability when minimal physiologically-based pharmacokinetic (mPBPK) models are integrated with target mediated drug disposition (TMDD) models in the tissue compartment. Three quasi-steady-state (QSS) approximations of TMDD dynamics were explored: on (a) antibody-target complex, (b) free target, and (c) free antibody concentrations in tissue. The effects of the QSS approximations were assessed via simulations, taking as reference the mPBPK-TMDD model with no simplifications. Approximation (a) did not affect model-derived concentrations, while with the inclusion of approximation (b) or (c), target concentration profiles alone, or both drug and target concentration profiles respectively deviated from the reference model profiles. A local sensitivity analysis was performed, highlighting the potential importance of sampling in the terminal pharmacokinetic phase and of collecting target concentration data. The a priori and a posteriori identifiability of the mPBPK-TMDD models were investigated under different experimental scenarios and designs. The reference model and QSS approximation (a) on antibody-target complex were both found to be a priori identifiable in all scenarios, while under the further inclusion of QSS approximation (b) target concentration data were needed for a priori identifiability to be preserved. The property could not be assessed for the model including all three QSS approximations. A posteriori identifiability issues were detected for all models, although improvement was observed when appropriate sampling and dose range were selected. In conclusion, this work provides a theoretical framework for the assessment of key properties of mathematical models before their experimental application. Attention should be paid when applying integrated mPBPK-TMDD models, as identifiability issues do exist, especially when rich study designs are not feasible.

Introduction

Physiologically-based pharmacokinetic (PBPK) models are compartmental models which aim to describe in detail the pharmacokinetic of a compound by including compartments for all tissues and organs that are considered biologically relevant.

PBPK models were initially developed for describing small molecule pharmacokinetics and were subsequently extended to monoclonal antibodies (mAbs) from the mid 80s [1, 2]. Due to the specific PK/PD characteristics of large molecules, in the following generation of whole body PBPK models the lymphatic flow has been included and each tissue compartment presents the interstitial space, the endosomal space, where the FcRn recycling occurs [3], and could present cellular subcompartments [4,5,6]. Shah and Betts built a PBPK platform for mAbs, based on extensive literature data, able to predict the PK concentration in plasma and tissues in different species utilizing a limited number of parameters of the compound to be studied [6]. In general the validation of a whole body PBPK model, e.g. for compounds with novel mechanisms, may require a substantial amount of information. In the presence of limited data, but also for reducing model complexity, techniques that lump tissues with similar kinetic characteristics were proposed both for small [7,8,9,10] and large molecules [11,12,13]. In particular, Cao et al reduced the mAb PBPK model [3, 6] into what they defined a minimal PBPK model (mPBPK) [11], which divides tissue spaces according to their vascular endothelial structure (i.e. leaky and tight), maintaining parameters with a physiological meaning. Target mediated drug disposition (TMDD) [14], either in plasma or in tissue, was subsequently incorporated in the model [15], giving rise to mPBPK-TMDD models. TMDD is the phenomenon in which a drug is bound with high affinity to its pharmacologic target to an extent able to influence its disposition kinetics [16]. The mathematical description of TMDD was introduced by Mager and Jusko [17], but given the difficulty in estimating the model parameters from generally available data, simplifications of the full TMDD model were subsequently proposed [18,19,20]. Practical identifiability of the full TMDD model and the quasi equilibrium (QE), quasi-steady-state (QSS), and Michaelis-Menten (MM) approximations has been investigated by Gibiansky et al. [19], who proposed an identifiability analysis algorithm for avoiding use of incorrect parameter estimates of TMDD models. Additionally, identification of TMDD parameters has been studied by Peletier and Gabrielsson, who mathematically demonstrated the parameter influence over the different portions of the TMDD signature profile and evaluated the MM approximation adequacy [16]. An analysis conducted by Eudy and colleagues has nevertheless concluded that full TMDD, QE/rapid binding (RB), QSS, and MM models were a priori fully identifiable and that the difficulties in achieving model convergence a posteriori originate from inadequate experimental design [21].

The present work investigates mPBPK-TMDD models for mAbs, under the assumption that target sites are located in tissue, with particular attention to the case when limited data are available.

In the following, four mPBPK-TMDD models are introduced: the full one (see [15] and related Supplementary Material), and three different approximated models including quasi-steady-state (QSS) conditions on TMDD dynamics. The impact of such approximations is comparatively assessed through simulations of plasma and tissue concentration profiles with reference to the full mPBPK-TMDD model. A sensitivity test is also performed on meaningful parameters. Furthermore, identifiability of the full and approximated models is investigated, with respect to both data richness and sampling design optimization; both a priori and a posteriori identifiability issues are explored. Definitions and specific implementation issues related to a priori and a posteriori identifiability, and optimal sampling are detailed in Supplementary Materials (S1–S3).

The full mPBPK-TMDD model

The full mPBPK-TMDD model is built incorporating the so-called full TMDD model [17, 19, 20] into the mPBPK model for mAbs (see Supplementary Material of [15]), supposing that the binding occurs in the leaky tissue. Similar methodology can be applied with binding occurring in the tight tissue, or in both tight and leaky tissues. The ordinary differential equations (ODEs) of such model (see Fig. 1), reported in Appendix (Eq. 4), describe the dynamics of drug concentrations in plasma, lymph and tissues, and of target and drug-target complex concentrations in the binding tissue. In particular, ${In(t)}$ is the input function in the ODEs, $C_p$ and $C_{lymph}$ represent free antibody concentrations in plasma volume ($V_p$) and lymph volume ($V_{lymph}$) respectively, while $C_{tight}$ and $C_{leaky_{free}}$ are antibody free concentrations in system interstitial fluid (ISF) volume of tissues with continuous endothelium ($V_{tight}$) and in ISF volume of tissues with fenestrated or discontinuous endothelium ($V_{leaky}$), respectively. Cao and colleagues [11] have assigned the muscle, skin, adipose and brain to $V_{tight}$, and all other tissues to $V_{leaky}$ (liver, kidney, heart, etc.). Free target concentration is expressed as $R_{leaky_{free}}$, while antibody-target concentration is $C\! R_{leaky}$. The total lymph flow L equals the sum of the flows for leaky tissue, $L_1$, and tight tissue, $L_2$. Vascular reflection coefficients for tight and leaky tissue are $\sigma _1$ and $\sigma _2$ (constrained to be $<1$), while $\sigma _L$ is the lymphatic capillary reflection coefficient. Rate constants are $k_{syn}$ for target biosynthesis, $k_{deg}$ for target degradation, $k_{int}$ for antibody-target complex internalization, $k_{on}$ for antibody-receptor association and $k_{off}$ for antibody-receptor dissociation. Finally, $C \!L_p$ is clearance from plasma. All initial conditions of the ODEs are set to zero, except for $R_{leaky_{free}}(0) = k_{syn}/k_{deg}$.

Fig. 1

Representation of the full mPBPK-TMDD model with binding in the leaky tissue. A and T represent, respectively, antibody and target

Other mPBPK-TMDD models: quasi-steady-state approximations

Considering that the molecular (microscopic) processes are usually much more rapid than the pharmacokinetic (macroscopic) processes, the mechanistic description of TMDD can be approximated exploiting a series of quasi-steady-state conditions formulated at microscopic level. Gibiansky and colleagues proposed the quasi-steady-state approximation of the drug-target complexes in the central compartment [19]. Grimm evaluated a second scenario where the approximation of the target was also added in the central compartment, assuming that there is an equilibrium between target synthesis and degradation which is shifted by the formation and dissociation of antibody-target complexes [22]. Furthermore, Grimm proposed a third scenario where complex, target and drug were all at steady state at the target site: this approximation may be applied when the target site is not in rapid exchange with plasma, and therefore the antibodies binding to the target are assumed to be balanced by the antibodies entering the target site [22].

Here, the three scenarios proposed in [19] and [22] will be all evaluated in the leaky tissue included in the mPBPK model, instead of the central compartment. In particular, we considered the quasi-steady-state approximations on:

• antibody-target complex concentration in binding tissue, assuming that the right-hand side of the differential equation for the complex ($C\! R_{leaky}$, see Eq. 4 in Appendix) equals zero:

  $$\begin{aligned} k_{int} C\! R_{leaky} = k_{on} C_{leaky_{free}} R_{leaky_{free}}- k_{off} C\! R_{leaky} \end{aligned}$$

  (1)

• free target concentration in binding tissue, assuming that target zero-order synthesis ($k_{syn}$) is balanced by first-order elimination ($k_{deg}$), and antibody-target complex association ($k_{on}$) and dissociation ($k_{off}$):

  $$\begin{aligned} k_{syn} - k_{deg} R_{leaky_{free}} = k_{on} C_{leaky_{free}} R_{leaky_{free}} - k_{off} C\! R_{leaky} \end{aligned}$$

  (2)

• free antibody concentration in binding tissue, assuming that the net amount of antibody binding to the target must be balanced by the amount entering the target site (here, the leaky tissue):

  $$\begin{aligned} C_p L_2 (1-\sigma _2) - C_{leaky_{free}} L_2 (1-\sigma _L)= & {} (k_{on} C_{leaky_{free}} R_{leaky_{free}} \nonumber \\&- k_{off} C\! R_{leaky}) V_{leaky} \end{aligned}$$

  (3)

All the three approximations on the mechanism of target mediated drug disposition can be considered for inclusion in the full mPBPK-TMDD model (Fig. 2). Note that, by virtue of the adoption of such an approximation, the differential equation for the variable at quasi-steady-state is replaced by an algebraic one.

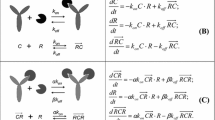
A mPBPK model with a TMDD component including the approximation on antibody-target complex concentration (Eq. 1) and expressed in terms of total drug concentration in the leaky tissue ($C_{leaky_{total}}=C_{leaky_{free}}+C\! R_{leaky}$) and total target concentration in the leaky tissue ($R_{leaky_{total}}=R_{leaky_{free}}+C\! R_{leaky}$) was already considered in [15]. In the present work, such mPBPK-TMDD model will be called Model A; model equations are reported in Appendix (Eqs. 5 and 6). Adding this QSS simplification, the model is reduced by one parameter: instead of the association and dissociation constants ($k_{on}$ and $k_{off}$), the quasi-steady-state constant $k_{ss}=(k_{int}+k_{off})/k_{on}$ is introduced. If also the approximation on target concentration in leaky tissue (Eq. 2) is added, Model B is obtained: equations are again reported in Appendix (Eqs. 7 and 8). The number of model parameters is not reduced with respect to Model A. Finally, equations for Model C (see Appendix, Eqs. 9 and 10) are computed by adding also the approximation on free antibody concentration in leaky tissue (Eq. 3); again, the number of model parameters do not decrease. In the next sections, a detailed analysis of the four mPBPK-TMDD models (Full, A, B, C) is illustrated.

Fig. 2

Structure of Models A (left panel), B (central panel) and C (right panel) obtained adding progressively the quasi-steady-state approximations on antibody-target complex, free target and free antibody in leaky tissue as described respectively by Eqs. 1, 2 and 3. The red dashed circles indicate the variable at quasi-steady-state [23]

A simulated study: comparison of the four models and sensitivity test

A simulated study of the models presented above was carried out with the software for statistical computing and graphics R (version 3.1.2), using the deSolve package for solving the ODEs systems.

First of all, taking as a reference the Full Model (as it does not make simplifying assumptions), the four models were simulated and compared. The aim was to see what changes are entailed by the addition of the quasi-steady-state approximations, both in terms of antibody and target concentrations.

Simulation of the four models was performed using mPBPK and TMDD model parameters estimated in [15] for the case study of romosozumab [24] assuming a representative value of the dissociation constant $k_D$ of about 1 nM for the Full Model ($k_D=k_{off}/k_{on}$, see Supplementary Material of [25]), and a body weight of 70 kg in order to derive $CL_p$ in L/h (see Table 1). The remaining required values, $L_1$, $L_2$, $V_{tight}$, and $V_{leaky}$, are derived with the following assumptions:

$$\begin{aligned} L_1&= 0.33 \, L\\ L_2&= 0.67 \, L\\ V_{tight}&= 0.65 \, I\! S\! F \, K_p\\ V_{leaky}&= 0.35 \, I\! S\! F \, K_p \end{aligned}$$

where $I\! S\! F = 15.6$ L is the total interstitial fluid volume for a 70 kg body weight person, 0.33 and 0.67 are the relative fractions to L of $L_1$ and $L_2$ respectively, 0.65 and 0.35 are the relative fractions to available total ISF of $V_{tight}$ and $V_{leaky}$ respectively [3, 6], and $K_p = 0.8$ is the available fraction of ISF for antibody distribution [15].

Table 1 Parameters for mPBPK-TMDD simulations

Simulations were performed at the same dose levels of the case study reported in [24], which were administered intravenously: one low, 1 mg/kg, and one high, 5 mg/kg. At low doses the mechanism of target mediated drug disposition significantly contributes to the overall clearance, while at higher doses, when the target is saturated, the overall clearance is mainly governed by the typical catabolism process for mAbs (i.e. $C\!L_{p}$).

In the simulations, one virtual 70 kg body weight subject was considered per each dose level, with samples simulated every 5 h up to 84 days. The input dose per subject was expressed in nM assuming a molecular weight of the monoclonal antibody equal to 150 kDa.

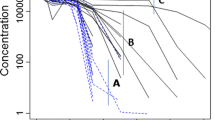
It was found that Model A generates the closest profiles to the full mPBPK-TMDD model in plasma and target site for both compound and receptor variables, free and total. Model B deviates from the Full Model in free and total target concentration profiles, while Model C systematically deviates from the Full one for both drug and target concentrations (see Fig. 3).

Fig. 3

Simulations of the two IV doses, with binding in the leaky tissue with Full Model (Indian red) and approximations of the binding process (olive), binding process and target turnover (sea green), binding process, receptor turnover and drug concentration at the target site (orchid). Upper left panel: free drug concentration in plasma. Upper right panel: total drug concentration in leaky tissue. Lower left panel: free receptor concentration in leaky tissue. Lower right panel: total receptor concentration in leaky tissue

For all the four models, also a univariate sensitivity test was performed on $\sigma _1$, $\sigma _2$, $k_{int}$, $C\!L_p$, $k_{syn}$, and $k_{deg}$. For the approximated models only, the test was carried out also on $k_{ss}$, while for the Full Model $k_{on}$ and $k_{off}$ were tested. The aim was to study parameters’ influence on the antibody and target concentration profiles. In particular, the sensitivity of $C_{p}$, $C_{leaky_{total}}$ and $R_{leaky_{total}}$ profiles with respect to the considered parameters is here of interest. Usually, the plasma concentrations of the drug (and target, when it resides in plasma) are indeed available; less frequently, measurements in tissue (e.g. total drug and target concentrations) are also collected.

More in detail, a minimum and a maximum value were defined for the tested parameters as the nominal value in Table 1 divided and multiplied by 10, respectively. This rule was not applied on $\sigma _{1}$ and $\sigma _{2}$, to respect the constraints $0<\sigma _1,\sigma _2<1$, and $\sigma _1>\sigma _2$ (Table 2).

The four models were simulated varying one parameter at a time, in order to compare the results obtained with the minimum value to the ones obtained with the maximum value.

Table 2 Parameter ranges for the sensitivity test (units as reported in Table 1)

All tested parameters have a detectable impact at both doses on all the concentration profiles considered (see Figs. 1–3 in Supplementary Material S4), with similar magnitude in the four mPBPK-TMDD models. The influence of $\sigma _{1}$ and $\sigma _2$ is less evident in respect to the other parameters because the variability ranges chosen for permeability coefficients are smaller (see Table 2). Of note is the fact that, with this choice of parameter ranges, drug and target concentration profiles corresponding to the minimum $k_{on}$ are very similar to those obtained with the maximum $k_{off}$, and viceversa (see Fig. 4). The same “mirroring” behavior does not hold when assuming 100 fold lower nominal value of $k_{off}$ (data not shown), this result highlighting the importance of simulation as a tool to show the presence of local collinearities. Furthermore, it can be observed that the variation of certain parameters has an impact only in the terminal phase of the drug concentration curves ($C_{p}$ and $C_{leaky_{total}}$), but its influence is evident throughout all the simulation time interval of the target concentration curve, $R_{leaky_{total}}$ (see Supplementary Material S4). This may indicate that target concentration data, irrespective of the sampling time selection, could help in discriminating between parameter values. In particular, it can be noticed that $k_{ss}$ and $k_{deg}$ show similar $C_{p}$ and $C_{leaky_{total}}$ profiles while they differ in $R_{leaky_{total}}$ concentration, suggesting that target concentration in the binding tissue might be needed for discriminating between the two parameters (Fig. 5).

Fig. 4

Plasma drug concentration, drug concentration in binding tissue and target concentration in binding tissue obtained with the Full Model varying: (i) $k_{on}$ (red lines), from its minimum, i.e. 0.0018 (solid line), to its maximum, i.e. 0.18 (dashed line), (ii) $k_{off}$ (blue lines), from its minimum, i.e. 0.0017 (solid line), to its maximum, i.e. 0.17 (dashed line). Left panels: simulations at 1 mg/kg; right panels: simulations at 5 mg/kg

Fig. 5

Left: plasma drug concentration, drug concentration in binding tissue and target concentration in binding tissue obtained with the three approximated models (A, B, and C) at both doses (1 and 5 mg/kg) varying $k_{ss}$, from its minimum (solid line) to its maximum (dashed line). Right: Plasma drug concentration, drug concentration in binding tissue and target concentration in binding tissue obtained with all four models (Full, A, B, and C) at both doses (1 and 5 mg/kg) varying $k_{deg}$, from its minimum (solid line) to its maximum (dashed line)

Identifiability issues

While a univariate sensitivity analysis can help detecting major model issues, like the presence of not influential model parameters, it cannot give precise information on parameter collinearities, model over-parametrization, and parameter identifiability. For this reason, we studied the identifiability of the four models, both structural (a priori) and practical (a posteriori).

Identification scenarios

The measurements of total mAb and target concentrations in the binding tissue ($C_{leaky_{total}}$ and $R_{leaky_{total}}$, respectively) are in general quite invasive, hence only few samples may be generally available. Considering this constraint, the identifiability (both a priori and a posteriori) of the four models was studied in three realistic scenarios, in which:

• i. Only $C_p$ is measured

• ii. $C_p$ and $C_{leaky_{total}}$ are measured

• iii. $C_p$ and $R_{leaky_{total}}$ are measured

A priori identifiability

A priori identifiability is a theoretical property of the model structure; it ensures that model parameters can be uniquely (globally or locally) determined from knowledge of the input-output behaviour assuming perfect experimental data (see Supplementary Material S1). Hence, the fulfillment of this property is independent of experimental design conditions. A priori identifiability is a prerequisite for parameter estimation in practice. Its study is therefore important to establish whether parameter estimation difficulties are due either to the particular experimental design or the mathematical structure of the model.

This property was studied via the IdentifiabilityAnalysis package of Mathematica, exploiting the algorithm detailed in [26], in scenarios i., ii. and iii. for the first three models. The a priori identifiability of Model C could not be assessed due to a limitation of the algorithm exploited.

Full Model and Model A were found to be a priori identifiable in every scenario. Model B turned out to be a priori identifiable only with the output choice iii. (see Table 3); in cases i. and ii. $k_{deg}$ and $k_{ss}$ are the non-identifiable parameters.

Table 3 Local a priori identifiability results for all models in all scenarios: “yes/no” indicates that there is/there is not a priori identifiability, while the “–” indicates that it’s not possible to assess the theoretical property using available software

For more details on theory and implementation, see Supplementary Material S1.

A posteriori identifiability

A posteriori identifiability refers to the ability of practically estimating an unknown parameter vector; it is inherently related to the type and amount of experimental data available (see Supplementary Material S2). Since a priori identifiability is a necessary, yet not sufficient condition for a posteriori identifiability, the latter property was analyzed only for the cases where a priori identifiability is met. The Fisher Information Matrix (FIM) [27] can provide insight into the amount of information available in the data (i.e. their quality), and a Monte Carlo (MC) procedure can be exploited for the exploration of fitting results, as far as it regards both the parameter estimates and the adherence of estimated concentration profiles on the data.

Table 4 Condition number of the Fisher Information Matrix

The condition number of the FIM for all a priori identifiable mPBPK-TMDD models and scenarios was computed (see Table 4). When the condition number is large, the matrix is close to singular or, more precisely, ill-conditioned; this entails a large uncertainty along some directions in the parameter space. The condition numbers result to be particularly elevated for all models, in all scenarios explored. The MC procedure comprises the following steps (see Fig. 6):

• Simulation from the Full Model of 100 datasets per each output choice (i., ii. and iii.), using a sampling schedule mimicking the clinical practice and a proportional residual error model with coefficient of variation equal to 0.2 for $C_p$ ($C\! V_{C_{p}}$) and $C_{leaky_{total}}$ ($C\! V_{C_{tot}}$), and 0.3 for $R_{leaky_{total}}$ ($C\! V_{R_{tot}}$).

• Fitting of the mPBPK-TMDD models on each simulated dataset, with initial parameter values equal to the true ones with a perturbation of $\pm 15\%$.

• Examination of the distribution of parameter estimates via boxplots, and computation of outliers, sample variance, confidence intervals, bias, percent coefficient of variation (CV$\%$) and Root Mean Square Error (RMSE). Furthermore, the parameters were ranked on the basis of an index, $\delta$, equal to the percent RMSE with respect to the true value of the parameter.

• Exploration of fitting quality by plotting: ODEs states vs. time, Conditional Weighted Residuals (CWRES) vs. Time, CWRES vs. the dependent variable (DV) [28], and Goodness Of Fit (GOF) plots. Furthermore, Predictive Plots (PP) are used to compare the noise-free simulated data with the percentiles of the predicted noise-free curves, computed from the 100 estimates obtained.

Fig. 6

Diagram of the MC a posteriori identifiability analysis. Datasets were simulated with the Full Model and used to identify the mPBPK-TMDD models. NONMEM output tables were obtained and analysed

In particular, in the simulation step, the following sampling scheme was considered: for plasma concentration, sampling time $t \in \mathcal {T}_{p}=\{0, 1, 2, 3, 4, 8, 16, 24, 48, 72, 96, 120, 168, 336, 504, 672, 840, 1008, 1176, 1344, 2016\}$ (i.e. rich sampling schedule on the first day, then gradually more sparse), and for total antibody and target concentration in binding leaky tissue, $t \in \mathcal {T}_{leaky}=\left\{ 72, 336, 672, 2016\right\}$ (i.e. day 3, 14, 28, 84).

R version 3.1.2 (https://www.r-project.org/) was used for FIM condition number computation and for implementing the MC procedure described above. Estimation on all simulated datasets was performed via NONMEM 7.3 (http://www.iconplc.com/innovation/nonmem/) with FOCE method. For more details about theory, implementation and the software tools exploited, see Supplementary Material S2.

From the results of the a posteriori identifiability analysis, it can be observed that the parameters with the maximum CV$\%$ and $\delta$ are the ones linked to the processes of binding, degradation and internalization of the complex. In Fig. 7 the distributions of the parameter estimates are reported, for the scenario with the Full Model and plasma drug concentration as output measure (scenario i.).

Fig. 7

Boxplots of the estimates obtained by fitting the Full Model on the 100 datasets with only $C_p$ measurements (scenario i.). The bottom and top of the box represent the first and third quartiles, while the band inside the box is the median; whiskers extend till $\pm 1.5$ IQR (Inter Quartile Range). The horizontal red line indicates the true value of the parameter

Table 5 Parameter ranking based on $\delta$ obtained after fitting Model A on drug plasma concentration and total drug concentration in binding tissue (scenario ii.)

The ranking of the parameters based on $\delta$ allowed the quantification of the sensitivity of parameter estimates to noise in the data: it is worth noticing that, regardless of the scenario considered, the “worst” parameters are, for the Full Model, $k_{on}$, $k_{off}$ and $k_{deg}$ (with $\delta$ often exceeding $120\%$), and, for Models A and B, $k_{deg}$ and $k_{ss}$ (with rank greater than $700\%$). In Table 5, an example of parameter ranking, for Model A estimated on $C_p$ and $C_{leaky_{total}}$ data, is reported (scenario ii.). The maximum CV$\%$ obtained for the estimates for the different scenarios are also proposed in Table 6. Unlike $\delta$, maximum CV$\%$ can be computed also from fitting on real data, with unknown true parameter values. For all scenarios maximum CV$\%$ is above $60\%$, this percentage is below $90\%$ only in the scenario where both plasma drug concentration and tissue target concentration are measured, and either Model A or B are used.

Table 6 Maximum CV$\%$ for each identification scenario; the third column indicates the parameter that leads to the maximum CV$\%$

As for CWRES and GOF plots, they did not show significant trends in any scenario (see e.g. Fig. 8). Indeed, the distribution of the residuals always appears compatible with a Gaussian with null mean and unitary variance; while the GOF plots, representing the simulated data (DV) compared to the population prediction (PRED), show a behavior in accordance with the residual error model. Despite the great variability in parameter estimates, in every scenario the PPs show that the corresponding predicted curves agree well with the noise-free measurable outputs considered. These plots were produced by overlapping the noise-free simulated data to the percentiles of the noise-free predicted curves obtained in each “100 runs set”. An example is reported in Fig. 9, for the scenario which presented the highest parameter CV$\%$ (see Table 6), i.e. Model A and plasma drug concentration as output measure.

Fig. 8

An example of CWRES vs time (left panel) and GOF plot (right panel) obtained for the Full Model estimated on plasma data (scenario i.). On the left, the residuals for all 100 NONMEM runs are grouped together: they are often comprised between $-2$ and 2 as it should be for their supposed distribution and do not show particular trends. On the right, the data (DV) are compared to the predictions (PRED) for both doses and all runs (units: mg/L). This scatterplot is concentrated around the identity line and, since the residual error model is proportional, the dispersion appears to be greater for higher concentrations

Since the results obtained for a posteriori identifiability depend on data richness, alternative and possibly more informative sampling designs were considered.

Fig. 9

Predictive plot (PP) with the profiles of plasma concentration obtained with all the combinations of parameters estimated for Model A on plasma data. 5th, 50th and 95th percentiles of estimated profiles (area and line) are reported, together with noise-free simulated data (points)

Alternative designs

The two other sampling schedules considered were:

• an optimal one, in order to minimize the variance of parameter Maximum-Likelihood (ML) estimators;

• a more frequent one, in order to increase the amount of information.

More in detail, the more frequent sampling schedule was obtained assuming that each output variable (i., ii., iii.) can be measured every 5 h up to day 84. The aim is to see if by collecting more data it is possible to improve the a posteriori identifiability. The optimal sampling schedule instead was obtained via PFIM (version 4.0), a software tool which evaluates and/or optimizes population designs based on the expression of the FIM in nonlinear mixed effects models [29]. Each possible output (i.e. $C_p$, $C_{leaky_{total}}$, and $R_{leaky_{total}}$) was considered separately in the optimization process using the Fedorov–Wynn algorithm [30], due to a limitation of the tool. The schedules obtained via optimal sampling still contain a feasible number of sample times; the results of all optimizations are represented in Fig. 10. More details about the settings implemented in PFIM are reported in Supplementary Material S3.

Fig. 10

Optimal sampling schedules obtained with PFIM, for high (upper panels) and low (lower panels) dose level. The 21 optimal drug samples in plasma (left) and 4+4 optimal drug and target samples in leaky tissue (right) for each a priori identifiable model, compared with the initial schedule (Start), are represented

The a posteriori identifiability analysis procedure (Fig. 6) was repeated using datasets generated with the more frequent sampling and with the optimal sampling.

As an illustrative example, in Table 7 a comparison of CV$\%$ for Model A estimates identified on plasma data is reported. It can be observed that the use of an optimal sampling schedule does not improve significantly the estimates precision with respect to the original realistic sampling schedule used for the analysis. The more frequent sampling seems to provide a better identification of the model parameters, maintaing the CV$\%$ of all parameter estimates below $45\%$. This does not hold for all models in all scenarios: for the Full Model, the dispersion in $k_{on}$ and $k_{off}$ estimates remains high even with the more frequent sampling (CV$\%>55\%$ in scenario ii. and iii., greater than $85\%$ in scenario i.).

In summary, the identifiability issues cannot be considered resolved by the realistic optimal design, while the unrealistic frequent sampling provides an appreciable improvement in parameter estimates dispersion, especially for simplified models; these observations would point to an overall over-parametrization issue.

Table 7 CV$\%$ of Model A parameter estimates obtained from plasma data (scenario i.) with the three sampling schedules

Target saturating dose

The previous sections have shown that the addition of tissue data improves the identification of some critical parameters and that more frequent sampling improves precision on estimates, but not the optimal design. Here, a third dose of 20 mg/kg has been considered to assess potential improvements in practical identifiability. Data for the three scenarios i., ii. and iii. were again simulated with the Full Model, at doses: 1, 5 and 20 mg/kg. Full Model and Model A were tested for a posteriori identifiability on all the three scenarios, while Model B only on scenario iii. CV$\%$ and $\delta$ were computed for comparison with the two doses conditions.

When considering only plasma concentrations (scenario i.), both for Full Model and Model A, the CV$\%$ generally decrease (with the exception of $k_{ss}$ for Model A), but they do not go below $60\%$ (see Table 8).

By adding tissue concentrations (scenario ii. and iii.), CV$\%$ reduction becomes more significant. In particular, for Model A in scenario iii., $\delta$ on average is equal to $15\%$ and it is always below $40\%$ (see Table 8), which is reasonable, since in data simulation a $20\%$ and a $30\%$ proportional residual errors were included, respectively, for drug in plasma or tissue, and target tissue concentration. For the Full Model instead, $\delta$ upper limit is around $80\%$ for both scenarios, while for Model B (scenario iii.) the maximum $\delta$ is approximately $50\%$.

Table 8 CV$\%$ and $\delta$ of Model A parameter estimates obtained from scenarios i. and iii., using either the two doses (1 and 5 mg/kg) or three doses (1, 5, and 20 mg/kg) datasets

Conclusions

In this paper the integration of mPBPK and TMDD models has been studied in depth for mAbs binding to their pharmacological target in tissues with leaky vasculature. First, a full mPBPK-TMDD model was considered. Secondly, since the molecular processes are usually more rapid than pharmacokinetic processes, different approximations of TMDD dynamics based on quasi-steady-state (QSS) conditions were investigated. Three additional mPBPK-TMDD models (Model A, B and C) were hence derived adding sequentially QSS approximations, respectively on: (a) antibody-target complex concentration, (b) target concentration, and (c) free antibody concentration.

The four mPBPK-TMDD models have been simulated and compared to assess the effects of quasi-steady-state assumptions on both drug and target concentration-time profiles. The simulations have shown that Model A generates the closest profiles to the Full Model, while Model B differs mainly in the target concentration profiles, and Model C systematically deviates from the Full one for both drug and target concentrations at the site of action.

A sensitivity test focused on plasma drug concentration, and drug and target concentration in binding tissue, highlighted the potential value of adding target binding data to help parameter estimation when drug data in plasma or tissue compartments are insufficient for their differentiation. Furthermore, such differentiation was demonstrated to be more evident in the terminal PK phase, thus suggesting the importance of data collection in this phase. It is however important to be aware that the results of such an analysis are dependent on the ranges considered for dosing amounts and model parameters. Therefore, it would be advisable to perform a sensitivity test after mPBPK-TMDD models identification to understand the possible impact of variations in the estimated values on the prediction of both observed and not measured variables.

A priori and a posteriori identifiability of the four mPBPK-TMDD models were explored in three experimental scenarios: (i) when measurements of drug in plasma are available, and with possible addition of (ii) total drug in tissue or (iii) total target in tissue data.

A priori identifiability is always met for the Full Model and for Model A, while such property is valid in Model B only when both total target concentration in binding tissue and drug plasma concentration can be assessed. A priori identifiability cannot be assessed for Model C using available software.

The study of the a posteriori identifiability by an MC method highlighted practical identifiability issues, especially when only measurements relative to the drug, either in tissue or in plasma, are available. To overcome identifiability issues, three possible solutions have been attempted, by enriching the experimental design: (i) the use of optimal design methods, performed on the sampling scheme, (ii) the resort to a non-realistic high number of sampling instants, equally spaced, (iii) the addition of an informative dose. While the use of an optimal or more frequent sampling schedule could not improve significantly the practical identifiability of all parameters, the addition of data at a dose which leads to full target saturation, especially when target in tissue data were considered available, was able to bear noticeable improvements in terms of CV$\%$. Appropriate dose range selection based on target expression, target turnover, drug distribution in the target tissues, and affinity is recommended when designing experiments for characterizing mAbs PK.

As reported in [15], mPBPK-TMDD models can handle TMDD at the target-expressing tissues, thus extending the usual TMDD modeling framework, where target-binding is considered only in vascular space. Nevertheless, in contrast with what was suggested in the same work [15], mPBPK-TMDD models with binding occurring in the ISF (specifically, in our case, in leaky tissues), do present parameter identifiability issues, especially when only plasma data, collected with a realistic sampling, are available. Noticeably, in this respect, the Full Model and Model A can be deemed equivalent, as the inclusion of the QSS approximation appears to be not enough to provide reliable PK parameter estimates and both models are over-parametrized.

Besides providing explicitly the equations of four mPBPK-TMDD models, pointing out their behaviour in terms of drug and target concentration profiles, this work addressed the potential identifiability issues of these models, indicating possible solutions (via informative study designs). In particular, the a priori identifiability of Full Model and Model A in three scenarios, and of Model B in the presence of target concentration in binding tissue measurements was analytically demonstrated. For all the four models, practical identifiability issues were highlighted in all scenarios and two possible solutions were proposed. In fact, the inclusion of target data in tissue and the addition of a saturating dose can reduce identifiability uncertainty, especially if both remedies are applied.

However, these solutions may not be always viable. Target concentration in tissue is not easily measurable, hence it may not be always assessed. Furthermore, the evaluation of sufficiently high doses may not be possible: a dose providing enough target saturation to improve parameter identification could also lead to toxicity episodes.

Further development of the present work may consist in a thorough investigation of possible alternative scenarios which may provide additional solutions for practical identifiability issues. Here, it was assumed that no prior information on model parameters was available; however, information on e.g. target baseline, binding affinity, or internalization rate might be retrieved from previous studies or literature. Some parameter may therefore be fixed, thus facilitating model identification. Alternative approaches including use of priors (in a Bayesian framework), or additional assumptions (e.g., constant total target amount) could also be explored.

In conclusion, mPBPK-TMDD models provide a powerful tool to integrate the molecular processes associated to monoclonal antibodies pharmacology. Their use may be key in mAbs discovery and development as they allow the inclusion in a mechanistic framework of PK and PK/PD information as it becomes available. However, attention should be paid to the existence of practical identifiability issues, especially when the use of rich experimental designs is not feasible.

Appendix

Model equations for the four mPBPK-TMDD models (Full, A, B, and C) are here provided. Parameter and variables notations are as introduced in the sections The full mPBPK-TMDD model and Other mPBPK-TMDD models: quasi-steady-state approximations.

Full Model

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L_1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}= & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{free}}}{dt}= & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] \nonumber \\&-k_{on} C_{leaky_{free}} R_{leaky_{free}} + k_{off} C\! R_{leaky} \nonumber \\ \frac{dR_{leaky_{free}}}{dt}=\, & {} k_{syn} - k_{deg} R_{leaky_{free}} - k_{on} C_{leaky_{free}} R_{leaky_{free}}+ k_{off} C\! R_{leaky} \nonumber \\ \frac{dC\! R_{leaky}}{dt}=\, & {} k_{on} C_{leaky_{free}} R_{leaky_{free}}- k_{off} C\! R_{leaky} - k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}[L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L] \end{aligned}$$

(4)

Model A

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{total}}}{dt}=\, & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] -k_{int} C\! R_{leaky} \nonumber \\ \frac{dR_{leaky_{total}}}{dt}=\, & {} k_{syn} - k_{deg} R_{leaky_{free}} - k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L\right] \end{aligned}$$

(5)

where $C_{leaky_{free}}$ and $C\! R_{leaky}$ are computed as:

$$\begin{aligned} C_{leaky_{free}}= & {} \frac{1}{2}(C_{leaky_{total}}-R_{leaky_{total}} - k_{ss} \nonumber \\&+ \sqrt{(C_{leaky_{total}}-R_{leaky_{total}}-k_{ss})^{2}+4 k_{ss} C_{leaky_{total}}}) \nonumber \\ C\! R_{leaky}= & {} \frac{R_{leaky_{total}} C_{leaky_{free}}}{k_{ss}+C_{leaky_{free}}} \end{aligned}$$

(6)

Model B

$$\begin{aligned} C_p= \,& {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{total}}}{dt}=\, & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] -k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L\right] \end{aligned}$$

(7)

where:

$$\begin{aligned} \alpha&= k_{int} \nonumber \\ \beta&= k_{ss} k_{deg} - k_{int} C_{leaky_{total}} + k_{syn} \nonumber \\ \gamma&= -k_{ss} k_{deg} C_{leaky_{total}} \nonumber \\ C_{leaky_{free}}&= \frac{1}{2 \alpha }\left( -\beta + \sqrt{\beta ^2 - 4\alpha \gamma }\right) \nonumber \\ R_{leaky_{free}}&= \frac{k_{syn} k_{ss}}{(k_{ss} k_{deg}+k_{int} C_{leaky_{free}})} \nonumber \\ C\! R_{leaky}&= \frac{R_{leaky_{free}} C_{leaky_{free}}}{k_{ss}} \end{aligned}$$

(8)

Model C

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t) + C_{lymph} L - C_p L_1 (1 - \sigma _1) - C_p L_2 (1 - \sigma _2) - C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ C_p L_1 (1-\sigma _1) - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1-\sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}} - C_{lymph} L \right] \end{aligned}$$

(9)

where $C_{leaky_{free}}$, $R_{leaky_{free}}$ and $C\! R_{leaky}$ are obtained as:

$$\begin{aligned} \alpha&= -k_{int} L_2 (1-\sigma _L) \nonumber \\ \beta&= k_{int} C_p L_2 (1-\sigma _2)-k_{ss} k_{deg} L_2 (1-\sigma _L)-k_{int} V_{leaky} k_{syn} \nonumber \\ \gamma&= k_{ss} k_{deg} C_p L_2 (1-\sigma _2) \nonumber \\ C_{leaky_{free}}&= \frac{1}{2\alpha }\left( -\beta - \sqrt{\beta ^2 - 4\alpha \gamma }\right) \nonumber \\ R_{leaky_{free}}&= \frac{k_{syn} k_{ss}}{(k_{ss} k_{deg}+k_{int} C_{leaky_{free}})} \nonumber \\ C\! R_{leaky}&= \frac{R_{leaky_{free}} C_{leaky_{free}}}{k_{ss}}\end{aligned}$$

(10)