Target-mediated drug disposition model for drugs with two binding sites that bind to a target with one binding site

Abstract

The paper extended the TMDD model to drugs with two identical binding sites (2-1 TMDD). The quasi-steady-state (2-1 QSS), quasi-equilibrium (2-1 QE), irreversible binding (2-1 IB), and Michaelis–Menten (2-1 MM) approximations of the model were derived. Using simulations, the 2-1 QSS approximation was compared with the full 2-1 TMDD model. As expected and similarly to the standard TMDD for monoclonal antibodies (mAb), 2-1 QSS predictions were nearly identical to 2-1 TMDD predictions, except for times of fast changes following initiation of dosing, when equilibrium has not yet been reached. To illustrate properties of new equations and approximations, several variations of population PK data for mAbs with soluble (slow elimination of the complex) or membrane-bound (fast elimination of the complex) targets were simulated from a full 2-1 TMDD model and fitted to 2-1 TMDD models, to its approximations, and to the standard (1-1) QSS model. For a mAb with a soluble target, it was demonstrated that the 2-1 QSS model provided nearly identical description of the observed (simulated) free drug and total target concentrations, although there was some minor bias in predictions of unobserved free target concentrations. The standard QSS approximation also provided a good description of the observed data, but was not able to distinguish between free drug concentrations (with no target attached and both binding site free) and partially bound drug concentrations (with one of the binding sites occupied by the target). For a mAb with a membrane-bound target, the 2-1 MM approximation adequately described the data. The 2-1 QSS approximation converged 10 times faster than the full 2-1 TMDD, and its run time was comparable with the standard QSS model.

Introduction

Equations that describe the pharmacokinetic and pharmacodynamic behavior of drugs with target-mediated drug disposition (TMDD) were introduced in [1]. A quasi-equilibrium (QE) or rapid binding (RB) approximation of the general TMDD model was developed in [2]. A quasi-steady-state (QSS) approximation and a Michaelis–Menten approximation were proposed in [3]. In these works it was assumed that both, the drug and the target have only one binding site. Here we extend the TMDD model and its approximations to drugs that have two identical binding sites (two-to-one binding). This is an important extension as most therapeutic monoclonal antibodies (mAbs) belong to this class [4, 5]. While the TMDD model with one-to-one binding assumption describes mAbs sufficiently accurately, development of mathematical models that describe two-to-one binding more mechanistically may facilitate the understanding of drug-target interactions and their influence on pharmacokinetic and pharmacodynamic properties of the system. To simplify notations, the models for two-to-one binding will be referred to as 2-1 TMDD, 2-1 QSS, 2-1 QE, 2-1 IB, and 2-1 MM.

Theoretical

Binding equations for a drug with two binding sites

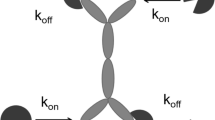
A schematic representation of binding interactions of the drug that has two identical binding sites with the target that has one binding site is presented in Fig. 1. In this section, we distinguish drug binding sites (by calling them left and right). Figure 1a, b depict binding of the right (a) and left (b) binding sites of the free drug C to the free target R. We assume that the left and right sites are identical, i.e. binding constants k_on and k_off are the same for both sites. The free drug and the free target are defined as the drug and the target that are not bound to each other. These two processes (further called C–R and R–C interactions) form two drug-target complexes, $\overrightarrow {CR}$ and $\overrightarrow {RC}$. These complexes correspond to the partially bound drug, with one binding site occupied by the target. Figure 1c, d depict binding of these complexes to the target, forming the complex that is further called $\overrightarrow {RCR}$. This complex corresponds to the fully bound drug, with both binding sites occupied by the target.

Fig. 1

Schematic representation of binding interactions. Y-shaped and round-shaped forms represent the drug and the target respectively

First, we consider a more general case where binding constants of the R–C and C–R interactions differ from those of the $R - \overrightarrow {CR}$ and $\overrightarrow {RC} - R$ interactions. The lower panel of Fig. 1 shows differential equations that describe each binding/dissociation process, assuming that other processes (distribution, elimination, etc.) are not active. Equations (1) combine all binding processes together:

$$ \begin{aligned} & \frac{dC}{dt} = - 2k_{on} C \cdot R + k_{off} (\overrightarrow {CR} + \overrightarrow {RC} ); \\\ & \frac{dR}{dt} = - 2k_{on} C \cdot R - \alpha k_{on} (\overrightarrow {CR} + \overrightarrow {RC} ) \cdot R + k_{off} (\overrightarrow {CR} + \overrightarrow {RC} ) + 2\beta k_{off} \overrightarrow {RCR} ; \\\ & \frac{{d(\overrightarrow {CR} + \overrightarrow {RC} )}}{dt} = 2k_{on} C \cdot R - k_{off} (\overrightarrow {CR} + \overrightarrow {RC} ) - \alpha k_{on} (\overrightarrow {CR} + \overrightarrow {RC} ) \cdot R + 2\beta k_{off} \overrightarrow {RCR} ; \\\ & \frac{{d\overrightarrow {RCR} }}{dt} = \alpha k_{on} (\overrightarrow {CR} + \overrightarrow {RC} ) \cdot R - 2\beta k_{off} \overrightarrow {RCR} . \end{aligned} $$

(1)

Here $C$, $R$, $\overrightarrow {CR}$, $\overrightarrow {RC}$, and $\overrightarrow {RCR}$ denote concentrations of the respective moieties.

The complexes $\overrightarrow {RC}$ and $\overrightarrow {CR}$ in these equations are identical and indistinguishable. To simplify the notation, RC will be used for the sum of $\overrightarrow {RC}$ and $\overrightarrow {CR}$ complexes, and R₂C will be used to denote the $\overrightarrow {RCR}$ complex. Equations (1) can then be re-written as

$$ \begin{aligned} & \frac{dC}{dt} = - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{dR}{dt} = - 2k_{on} C \cdot R - \alpha k_{on} RC \cdot R + k_{off} RC + 2\beta k_{off} R_{2} C; \\ & \frac{dRC}{dt} = 2k_{on} C \cdot R - k_{off} RC - \alpha k_{on} RC \cdot R + 2\beta k_{off} R_{2} C; \\ & \frac{{dR_{2} C}}{dt} = \alpha k_{on} RC \cdot R - 2\beta k_{off} R_{2} C. \end{aligned} $$

(2)

Note coefficients of 2 in front of several terms. They appear when more than one binding process described in Fig. 1 involves the same quantities.

Parameters α and β describe interaction between drug binding sites. When α < 1, occupancy of one binding site negatively interferes with binding to the other binding site. In the extreme case of α = 0, the second binding site is blocked if the first binding site is occupied. Binding equations would then degenerate to the one-to-one binding, where the definition of k_on parameter differs by a factor of 2 from the standard TMDD:

$$ \begin{aligned} & \frac{dC}{dt} = - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{dR}{dt} = - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{dRC}{dt} = 2k_{on} C \cdot R - k_{off} RC; \end{aligned} $$

(3)

When α = 1, the association constants of the drug-target binding are independent of the occupancy of the binding sites. The binding equations then take the following form:

$$ \begin{aligned} & \frac{dC}{dt} = - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{dR}{dt} = - 2k_{on} C \cdot R - k_{on} RC \cdot R + k_{off} RC + 2\beta k_{off} R_{2} C; \\ & \frac{dRC}{dt} = 2k_{on} C \cdot R - k_{off} RC - k_{on} RC \cdot R + 2\beta k_{off} R_{2} C; \\ & \frac{{dR_{2} C}}{dt} = k_{on} RC \cdot R - 2\beta k_{off} R_{2} C. \end{aligned} $$

(4)

The parameter β defines the dissociation constant of the R₂C binding. Values β > 1 indicate that the dissociation increases when the second binding site of the drug is occupied by the target.

In this work, we investigate the simplest case of α = β = 1. Then, binding equations are:

$$ \begin{aligned} & \frac{dC}{dt} = - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{dR}{dt} = - 2k_{on} C \cdot R - k_{on} RC \cdot R + k_{off} RC + 2k_{off} R_{2} C; \\ & \frac{dRC}{dt} = 2k_{on} C \cdot R - k_{off} RC - k_{on} RC \cdot R + 2k_{off} R_{2} C; \\ & \frac{{dR_{2} C}}{dt} = k_{on} RC \cdot R - 2k_{off} R_{2} C. \end{aligned} $$

(5)

In order to derive equations of target-mediated drug disposition, Eq. (5) need to be supplemented by terms for target production and elimination, drug input and elimination, and by equations that describe distribution of the drug to tissues.

General target-mediated drug disposition model for drug with two binding sites

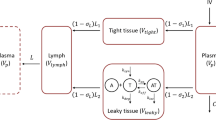
In this section, mathematical formulation of the TMDD model is extended to drugs with two binding sites. The drug is described by a two-compartment model with combined linear elimination and target-mediated drug disposition/elimination following intravenous (IV) and subcutaneous (SC) dosing. Extending the system (5), one can arrive at

$$ \begin{aligned} & \frac{{dA_{d} }}{dt} = - k_{a} A_{d} ;\begin{array}{*{20}c} {} & {A_{d} (0) = F_{SC} D_{1} } \\ \end{array} ;C(0) = D_{2} /V_{c} ; \\ & \frac{dC}{dt} = \frac{{In(t) + k_{a} A_{d} + k_{tp} A_{T} }}{{V_{c} }} - (k_{el} + k_{pt} )C - 2k_{on} C \cdot R + k_{off} RC; \\ & \frac{{dA_{T} }}{dt} = k_{pt} C \cdot V_{c} - k_{tp} A_{T} ;\begin{array}{*{20}c} {} & {A_{T} (0) = 0;\begin{array}{*{20}c} {} & {R(0) = k_{syn} /k_{\deg } ;} \\ \end{array} } \\ \end{array} \\ & \frac{dR}{dt} = k_{syn} - k_{\deg } R - 2k_{on} C \cdot R - k_{on} RC \cdot R + k_{off} RC + 2k_{off} R_{2} C; \\ & \frac{dRC}{dt} = 2k_{on} C \cdot R - (k_{\text{int}} + k_{off} )RC - k_{on} R \cdot RC\begin{array}{*{20}c} { + 2k_{off} R_{2} C;} & {} \\ \end{array} \\ & \frac{{dR_{2} C}}{dt} = k_{on} R \cdot RC - (k_{\text{int}} + 2k_{off} )R_{2} C\begin{array}{*{20}c} ; & {RC(0) = RC_{2} (0) = 0} \\ \end{array} . \end{aligned} $$

(6)

Here C, R, RC, and R ₂ C are the concentrations of the free (unbound) drug, the target, the drug-target complex with one target molecule, and the drug-target complex with two target molecules in the central (serum) compartment; k _el is the linear elimination rate constant, k_pt and k_tp are inter-compartment rate constants, k _on , k _off , and k _int are the binding, dissociation, and internalization (elimination of the complex) rate constants; k _deg and k _syn are the degradation (elimination of the target) and target production rate constants; V _c is the central compartment volume; In(t) is the infusion rate; F_SC is the absolute bioavailability of the subcutaneous dose. Initial conditions correspond to the case where the free drug that is not present endogenously is administered as a subcutaneous dose D ₁ and bolus dose D ₂ . It is assumed that the drug binding to each binding site is independent of the other site. Moreover, internalization (elimination) rate of two drug-target complexes is assumed to be the same (although generalization to the case of two different internalization rates is straightforward).

Following the procedure developed for TMDD equations with one-to-one binding, one can introduce total drug and total target concentrations as follows:

$$ C_{tot} = C + RC + R_{{^{2} }} C;\;R_{tot} = R + RC + 2R_{{^{2} }} C $$

(7)

Then, Eqs. (6) can be re-written as equations for C_tot and R_tot:

$$ \begin{aligned} & \frac{{dA_{d} }}{dt} = - k_{a} A_{d} ;\begin{array}{*{20}c} {} & {A_{d} (0) = F_{SC} D_{1} } \\ \end{array} \begin{array}{*{20}c} ; & {C(0) = D_{2} /V_{c} ;} \\ \end{array} \\ & \frac{{dC_{tot} }}{dt} = \frac{{In(t) + k_{a} A_{d} + k_{tp} A_{T} }}{{V_{c} }} - (k_{el} + k_{pt} )C - k_{\text{int}} (RC + R_{{^{2} }} C); \\ & \frac{{dA_{T} }}{dt} = k_{pt} CV_{c} - k_{tp} A_{T} ;\begin{array}{*{20}c} {} & {A_{T} (0) = 0;} \\ \end{array} \\ & \frac{{dR_{tot} }}{dt} = k_{syn} - k_{\deg } R - k_{\text{int}} (RC + 2R_{{^{2} }} C);\begin{array}{*{20}c} {} & {R_{tot} (0) = k_{syn} /k_{\deg } .} \\ \end{array} \end{aligned} $$

(8)

and two equations that describe two types of drug-target complexes:

$$ \begin{aligned} & \frac{dRC}{dt} + \frac{{dR_{2} C}}{dt} = 2k_{on} C \cdot R - (k_{\text{int}} + k_{off} )RC\begin{array}{*{20}c} { - k_{\text{int}} R_{2} C;} & {} \\ \end{array} \\ & \frac{{dR_{2} C}}{dt} = k_{on} R \cdot RC - (k_{\text{int}} + 2k_{off} )R_{2} C\begin{array}{*{20}c} ; & {RC(0) = RC_{2} (0) = 0} \\ \end{array} . \end{aligned} $$

(9)

The advantage of this form is that the large terms (terms that contain the parameter k_on) are localized in two Eq. (9) rather than distributed throughout the entire system. This is convenient for both, the theoretical analysis of the system and for solving the differential equations numerically.

Quasi-steady-state approximation

Similarly to TMDD equations with one-to-one binding, the quasi-steady-state approximation of the TMDD 2-1 system can be derived by assuming that the free (unbound) drug C, the free (unbound) target R, and the drug-target complexes RC and R ₂ C are in quasi-steady-state [3], where binding rates are balanced by the sum of dissociation and internalization rates on the scale of the other processes:

$$ \begin{aligned} & 2k_{on} C \cdot R - (k_{\text{int}} + k_{off} )RC - k_{\text{int}} R_{2} C\begin{array}{*{20}c} { = 0;} & {} \\ \end{array} \\ & k_{on} R \cdot RC - (k_{\text{int}} + 2k_{off} )R_{2} C = 0. \end{aligned} $$

(10)

By introducing the dissociation rate constant K _D  = k _off /k _on and irreversible binding rate constant K _IB  = k _int /k _on one can arrive at

$$ \begin{aligned} & 2 \cdot C \cdot R = (K_{D} + K_{IB} )RC + K_{IB} R_{{^{2} }} C, \\ & R \cdot RC = (2K_{D} + K_{IB} )R_{{^{2} }} C \end{aligned} $$

(11)

Supplementing these two equations by the definition of total drug concentration $C_{tot} = C + RC + R_{{^{2} }} C$ one can solve for C, RC and R ₂ C to arrive at

$$ \begin{aligned} & C = C_{tot} \frac{{(K_{D} + K_{IB} )(K_{D} + K_{IB} /2) + K_{IB} R/2}}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}}; \\ & RC = C_{tot} \frac{{R(2K_{D} + K_{IB} )}}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}}; \\ & R_{{^{2} }} C = C_{tot} \frac{{R^{2} }}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}}. \end{aligned} $$

(12)

Finally, substituting terms in the definition of the total target concentration

$$ R_{tot} = R + RC + 2R_{{^{2} }} C $$

by these expressions, one can get an implicit equation that defines R as a function of R _tot :

$$ R_{tot} = R + \frac{{2C_{tot} R}}{{K_{D} + K_{IB} + R}}. $$

(13)

Resolving this equation for R will get

$$ R = \frac{1}{2}\left[ { - \left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right) + \sqrt {\left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right)^{2} + 4(K_{D} + K_{IB} )R_{tot} } } \right] $$

(14)

This is remarkably similar to the expression for C through C _tot for the QSS approximation of the standard TMDD system.

The QSS approximation can then be re-written in the form:

$$ \begin{aligned} & \frac{{dA_{d} }}{dt} = - k_{a} A_{d} ;\begin{array}{*{20}c} {} & {A_{d} (0) = F_{SC} D_{1} } \\ \end{array} \begin{array}{*{20}c} ; & {C_{tot} (0) = D_{2} /V_{c} ;} \\ \end{array} \\ & \frac{{dC_{tot} }}{dt} = \frac{{In(t) + k_{a} A_{d} + k_{tp} A_{T} }}{{V_{c} }} - (k_{el} + k_{pt} )C \\ & \begin{array}{*{20}c} {} & {} & {} \\ \end{array} - k_{\text{int}} C_{tot} \frac{{R \cdot (2K_{D} + K_{IB} + R)}}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}}; \\ & \frac{{dA_{T} }}{dt} = k_{pt} C \cdot V_{c} - k_{tp} A_{T} ;\begin{array}{*{20}c} {} & {A_{T} (0) = 0;} & {R_{tot} (0) = k_{syn} /k_{\deg } .} \\ \end{array} \\ & \frac{{dR_{tot} }}{dt} = k_{syn} - k_{\deg } R_{tot} - \left( {k_{\text{int}} - k_{\deg } } \right) \cdot C_{tot} \cdot \frac{2R}{{K_{D} + K_{IB} + R}}. \end{aligned} $$

(15)

where C is expressed as in (12) through R and C _tot , and R is expressed as in (14) through C _tot and R _tot .

When internalization rate of the complexes k _int is equal to the degradation rate of the free target k _deg , the total target concentration is a constant parameter of the system and the last equation can be removed.

Michaelis–Menten approximation

To further simplify these equations, the total concentration of the target is assumed to be low compared to free drug concentration. In this case, in expressions for R (14), and RC and R ₂ C (12), C _tot can be replaced by C, resulting in

$$ R \approx \frac{{\left( {K_{D} + K_{IB} } \right)/2 \cdot R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}};\begin{array}{*{20}c} {} & {RC \approx \frac{{C \cdot R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}};} & {R_{2} C \approx 0,} & {} \\ \end{array} $$

if the terms of the order of R ² or R ² _tot are disregarded (see “Appendix” for the derivation). Then the last terms of equations for C _tot and R _tot in (15) can be simplified (see “Appendix”) as follows:

$$ \begin{aligned} & \frac{{R \cdot (2K_{D} + K_{IB} + R)}}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}} \approx \frac{{R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}} \\ & \frac{2R}{{K_{D} + K_{IB} + R}} \approx \frac{{R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}}; \end{aligned} $$

(16)

allowing to arrive at the Michaelis–Menten approximation:

$$ \begin{aligned} & \frac{{dA_{d} }}{dt} = - k_{a} A_{d} ;\begin{array}{*{20}c} {} & {A_{d} (0) = F_{SC} D_{1} } \\ \end{array} \begin{array}{*{20}c} ; & {C_{tot} (0) = D_{2} /V_{c} ;} \\ \end{array} \\ & \frac{dC}{dt} = \frac{{In(t) + k_{a} A_{d} + k_{tp} A_{T} }}{{V_{c} }} - (k_{el} + k_{pt} )C - k_{\text{int}} \frac{{R_{tot} \cdot C}}{{\left( {K_{D} + K_{IB} } \right)/2 + C}}; \\ & \frac{{dA_{T} }}{dt} = k_{pt} C \cdot V_{c} - k_{tp} A_{T} ; \\ & \frac{{dR_{tot} }}{dt} = k_{syn} - k_{\deg } R_{tot} - \left( {k_{\text{int}} - k_{\deg } } \right) \cdot \frac{{R_{tot} \cdot C}}{{\left( {K_{D} + K_{IB} } \right)/2 + C}}; \\ & \begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{d} (0) = D_{1} ;} & {C(0) = D_{2} /V_{c} } \\ \end{array} ;} & {A_{T} (0) = 0;} & {R_{tot} (0) = k_{syn} /k_{\deg } .} \\ \end{array} \end{aligned} $$

(17)

These equations are equivalent to the MM approximation of the standard TMDD system where K_SS = (K_D + K_IB)/2.

As before, if k _int is equal to k _deg , the total target concentration is a constant parameter of the system, and the last equation can be removed. Then, the system is described by the two-compartment model with parallel linear and Michaelis–Menten elimination.

Quasi-equilibrium approximation

Derivation of the QE approximation is identical to the QSS approximation with the only change that QSS conditions are replaced by QE conditions, where the free drug, the target, and the two drug target complexes are assumed to be in quasi-equilibrium [3]. All QE equations can be obtained from the corresponding QSS equations by setting K _IB  = 0. Then, C, RC, and R ₂ C are expressed through C _tot and R as follows:

$$ C = \frac{{K_{D}^{2} C_{tot} }}{{\left( {K_{D} + R} \right)^{2} }}; \quad {RC = \frac{{2K_{D} C_{tot} R}}{{\left( {K_{D} + R} \right)^{2} }};} \quad {R_{{^{2} }} C = \frac{{C_{tot} R^{2} }}{{\left( {K_{D} + R} \right)^{2} }}.} $$

(18)

while R is expressed as the following function of C _tot and R _tot :

$$ R = \frac{1}{2}\left[ { - \left( {2C_{tot} + K_{D} - R_{tot} } \right) + \sqrt {\left( {2C_{tot} + K_{D} - R_{tot} } \right)^{2} + 4K_{D} R_{tot} } } \right] . $$

(19)

Equations for the quasi-equilibrium approximation can then be re-written in the form:

$$ \begin{aligned} & \frac{{dA_{d} }}{dt} = - k_{a} A_{d} ;\begin{array}{*{20}c} {} & {A_{d} (0) = F_{SC} D_{1} } \\ \end{array} \begin{array}{*{20}c} ; & {C_{tot} (0) = D_{2} /V_{c} ;} \\ \end{array} \\ & \frac{{dC_{tot} }}{dt} = \frac{{In(t) + k_{a} A_{d} + k_{tp} A_{T} }}{{V_{c} }} - (k_{el} + k_{pt} )C - k_{\text{int}} C_{tot} \frac{{R \cdot (2K_{D} + R)}}{{\left( {K_{D} + R} \right)^{2} }}; \\ & \frac{{dA_{T} }}{dt} = k_{pt} C \cdot V_{c} - k_{tp} A_{T} ; \\ & \frac{{dR_{tot} }}{dt} = k_{syn} - k_{\deg } R_{tot} - \left( {k_{\text{int}} - k_{\deg } } \right) \cdot C_{tot} \cdot \frac{2R}{{K_{D} + R}}; \\ & \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{d} (0) = D_{1} ;} & {C_{tot} (0) = D_{2} /V_{c} } \\ \end{array} ;} & {A_{T} (0) = 0;} & {R_{tot} (0) = k_{syn} /k_{\deg } .} \\ \end{array} } & {} \\ \end{array} \end{aligned} $$

(20)

As before, the last equation can be removed if k _int is equal to k _deg .

The MM approximation for this system has the same form as the MM approximation for the standard TMDD system where K_SS = K_D/2.

Irreversible binding approximation

The irreversible binding approximation can be obtained from the QSS approximation by assuming k _off  = 0 (resulting in K _D  = 0). Then

$$ \begin{aligned} & C = \frac{{C_{tot} K_{IB} /2}}{{(K_{IB} /2 + R)}};\quad {RC = \frac{{C_{tot} K_{IB} R}}{{\left( {K_{IB} + R} \right)(K_{IB} /2 + R)}};} \\ & R_{{^{2} }} C = \frac{{C_{tot} R^{2} }}{{\left( {K_{IB} + R} \right)(K_{IB} /2 + R)}}; \end{aligned} $$

(21)

and

$$ R = \frac{1}{2}\left[ { - \left( {2C_{tot} + K_{IB} - R_{tot} } \right) + \sqrt {\left( {2C_{tot} + K_{IB} - R_{tot} } \right)^{2} + 4K_{IB} R_{tot} } } \right] $$

(22)

The MM approximation for this system has the same form as the MM approximation for the standard TMDD system where K_SS = K_IB/2.

Investigation of the two-to-one model

To investigate the two-to-one model and its approximations, several simulation studies were performed. NONMEM 7.3.0^® software [6] was used for simulations, estimation of parameters, and computation of predictions. FOCEI estimation method was used for model fitting.

First (Case 1), the full 2-1 TMDD model and the 2-1 QSS approximation were used to compute and compare typical predictions of the free drug, the free target, the total drug, the total target, and each of the two drug target complexes over time for 3 dosing scenarios (single doses of 100 or 600 nmol IV, or 2 doses of 1000 nmol SC 28 days apart). Parameters from Table 2 (“True” values in “Slow internalization”), typical for mAbs and soluble targets, were used in simulation.

In Case 2, a population PK data set was simulated that imitated a typical design of a phase 1 and phase 2 studies (Table 1). Concentrations of various quantities were simulated from the full 2-1 TMDD model using the parameters from Table 2 (“True” values in “Slow internalization”). The simulated concentrations of the free drug and of the total target were then used to fit the following models:

• Full 2-1 TMDD model written in its original form (1);

• Full 2-1 TMDD model written as in (3);

• QSS 2-1 approximation (10);

• Standard TMDD model;

• QSS approximation of the standard TMDD model.

Table 1 Dosing and sampling scheme in the simulated studies

Table 2 True and estimated model parameters

For all models estimated parameters were compared with the true values. Predictions of all quantities (including unobserved) were also computed and compared with the true (i.e. simulated from the full 2-1 TMDD model) values.

Assays for the free drug often can’t distinguish between the free and partially bound drug (where one binding site is occupied by the target) and what is reported is the sum of them. Thus, the same simulations as in Case 2 were performed for Case 3, where the sum of the free and partially bound drug (C_partial) was used in estimation instead of the free drug concentrations. In the standard TMDD and QSS models (where there is no C_partial), this sum (“measured” drug concentration) was assumed to represent the free drug.

The QSS approximation is most useful for drugs that bind to soluble target, where elimination of the drug-target complex is slow. For drugs with membrane-bound target, where internalization rate is fast, the Michaelis–Menten approximation is expected to perform best. To test whether this applies for drugs with two binding sites, simulations performed for Case 2 were repeated for Case 4, where parameters typical for membrane-bound targets were used in simulations (Table 2, “True” values in “Fast Internalization”). The full 2-1 TMDD, 2-1 QSS, and MM models were then used to estimate the parameters. Since concentrations of the target are not usually available for membrane-bound targets, only free drug concentrations were used for estimation.

Results

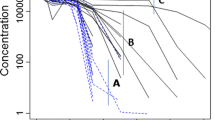
In Case 1, predictions of the full 2-1 TMDD model and the 2-1 QSS approximation (Fig. 2) were almost identical for all quantities.

Fig. 2

Case 1: Comparison of full TMDD 2-1 and QSS 2-1 model predictions

In Case 2, the 2-1 TMDD model was able to reproduce the true values (Fig. 3) for all quantities. The 2-1 QSS model also demonstrated good prediction of the true values (Fig. 4) for all quantities, except for a minor bias in predictions of low unobserved free target concentrations. The corresponding results were similar in Case 3 (where C + C_partial was used for estimation).

Fig. 3

Case 2: 2-1 TMDD model predictions versus true (simulated) values. Free drug and total target concentrations used in estimation

Fig. 4

Case 2: 2-1 QSS model predictions versus true (simulated) values. Free drug and total target concentrations used in estimation

In Case 2, the standard QSS approximation correctly predicted observed quantities (Fig. 5), but provided biased predictions of the active drug (C + C_partial) and the free target. In Case 3, the standard QSS model provided biased predictions of the free drug concentration but correctly predicted the observed quantities (Fig. 6) and provided reasonable predictions of the free target concentration. This explains why the standard QSS approximation works reasonably well in the majority of real clinical data sets.

Fig. 5

Case 2: Standard QSS model predictions versus true (simulated) values. Free drug and total target concentrations used in estimation

Fig. 6

Case 3: Standard QSS model predictions versus true (simulated) values. Sum of free and partially bound drug, and total target concentrations used in estimation

In Case 2 and Case 3 (soluble target, slow elimination rate of the complex), the full 2-1 TMDD models converged and provided accurate estimates for all model parameters, except for k_on and k_off rates (Table 2). The 2-1 QSS models provided accurate estimates of all parameters, except K_D and K_IB. K_IB was estimated with large uncertainty, and fixing it to zero provided the identical fit.

Model fit [objective function value (OF)] and run times for all models in Case 2 and Case 3 are shown in Table 3. The run time of the full 2-1 TMDD models was approximately 10 times longer than that of the 2-1 QSS models. The run time of the standard QSS approximations was comparable to the 2-1 QSS models with K_IB fixed to 0 (Table 3). The OF values were higher for the standard TMDD model and its QSS approximation compared to all 2-1 models.

Table 3 Comparisons of model fit (OF) and run times

In Case 4 (membrane-bound target), full 2-1 TMDD models failed, 2-1 QSS models were unstable, while the model with parallel linear and Michaelis–Menten elimination provided a nearly identical fit, much faster convergence, and accurate estimates of relevant model parameters (Tables 2, 3).

Discussion

Equations of the TMDD model and its QSS, QE, IB, and MM approximations were derived for drugs with two binding sites. The 2-1 QSS model was the most general approximation. The 2-1 QE and 2-1 IB approximations can be obtained from 2-1 QSS by setting K_IB = 0 or K_D = 0, respectively. The QSS 2-1 model correctly estimated model parameters (except K_IB and K_D) and predicted concentration–time course of drug and target concentrations when it was fitted to the data simulated from the full 2-1 TMDD model. Similarly to the case of the standard QSS approximation, the largest discrepancy between true and predicted values were observed for the free target concentrations at time of rapid changes of drug concentrations due to binding, when the equilibrium was not yet attained.

It was shown that numerical properties of the full 2-1 TMDD model were influenced by the specific form of the equations. In its original form (1), the NONMEM output indicated numerical difficulties. To overcome them, precision of differential equation computations, the TOL parameter, had to be increased from TOL = 9 to TOL = 11.When the form (3–4) was used, where fast-changing terms appeared in only two equations, the model was more stable, at least for the investigated simulated data, and there was no need to increase TOL.

While advances in computer power and the software made numerical solution of the full 2-1 TMDD model possible, they did not (and could not) resolve the identifiability issue: binding parameters of the system cannot be determined from the routinely available data. Indeed, the parameters k_on and k_off were estimated with low precision and high bias.

The 2-1 QSS approximation provided a good fit, with model predictions in a good agreement with the simulated (true) data. The only noticeable discrepancy was in free target concentrations during the first few hours after the first dose, when the binding processes were not yet completed.

Unlike the QSS approximation of the standard TMDD model, the 2-1 QSS approximation has the same number of parameters as the full 2-1 TMDD model, and thus it may also be prone to the identifiability problem. When K_D and K_IB were estimated, K_IB was estimated with high uncertainty. The fit was nearly identical when K_IB was fixed to zero, thus reducing the 2-1 QSS approximation to the corresponding 2-1 QE approximation even though K_IB was not zero in the simulated data. The problem of parameter identifiability can be handled on case by case basis. One possible option is to test three models: with estimated K_IB and K_D, with K_IB fixed to zero, and with K_D fixed to zero. If one of the simpler models (with one of the parameters fixed to zero) provides the same fit as a more complex model (with both parameters estimated), this model can be used for further development.

While the 2-1 QSS approximation does not reduce the number of estimated parameters, its equations have better numerical properties since they do not need to describe fast binding processes.

The standard QSS model was able to reproduce observed data (simulated from the full 2-1 TMDD model), independently on whether the free drug or free and partially bound drug was measured. The model, obviously, could not distinguish between different types of drug-target complexes, but when the combination of the free and partially bound drug was treated as the free drug concentration, the model provided reasonable estimates of free target concentrations.

As expected, in the example with fast internalization rate (i.e. fast elimination of the drug-target complex), the best results were obtained by the model with parallel linear and Michaelis–Menten elimination, and the parameter estimates of this model were consistent with true (simulated) values.

The run time of the 2-1 QSS model with K_IB set to zero was only about 30–40% longer than that of the standard QSS approximation. In return, the model allowed more granularity in describing the underlying biological system. When the computer power is available, it could be beneficial to use a more mechanistic 2-1 QSS model to describe the observed data. Even though the full 2-1 TMDD model successfully converged in our simulated examples, it required at least tenfold more time than the 2-1 QSS model, making its use impractical when the data set is large.

Applicability and precision of the 2-1 QSS approximation was numerically evaluated for two specific sets of parameters. It would be expected that conditions for applicability of the standard QSS approximation [3, 7] should also be valid for 2-1 QSS equations. However, further research may be needed to explore and confirm parameter ranges where the 2-1 QSS approximation is applicable.

The standard one-to-one TMDD model has been successfully used to describe pharmacokinetic and pharmacodynamic properties of monoclonal antibodies. However, it was a lingering question about the discrepancy between the known structure of mAbs (that have two binding sites) and the assumption of one-to-one binding. The model proposed here resolves this discrepancy by providing a more mechanistic description of mAbs/target binding. With relatively small numerical overhead, the model provides a more precise description for this important class of drugs.

Appendix

Expression for R

From (14), using the formula a − b = (a² − b²)/(a + b) with

$$ \begin{aligned} & a = \sqrt {\left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right)^{2} + 4(K_{D} + K_{IB} )R_{tot} } , \\ & b = \left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right) \end{aligned} $$

(23)

one arrives at

$$ R = \frac{{2(K_{D} + K_{IB} )R_{tot} }}{{\left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right) + \sqrt {\left( {2C_{tot} + K_{D} + K_{IB} - R_{tot} } \right)^{2} + 4(K_{D} + K_{IB} )R_{tot} } }} $$

(24)

Assuming that R_tot is small compared to C_tot and disregarding the terms of the order of R ²_tot , one can approximate the dependence of R on R_tot by the first term of the Taylor expansion of R as the function of R_tot. Specifically,

$$ R \approx R_{tot} \left( {\frac{dR}{{dR_{tot} }}} \right)_{{R_{tot} = 0}} = R_{tot} \frac{{(K_{D} + K_{IB} )}}{{2C_{tot} + K_{D} + K_{IB} }} = \frac{{\left( {K_{D} + K_{IB} } \right)/2 \cdot R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}}. $$

(25)

One can observe that use of the first term of the Taylor expansion is equivalent to setting R_tot = 0 in the denominator of (24).

Expression for RC

From (12), disregarding the terms of the order of R² and R ²_tot (equivalent to setting R = 0 in the denominator of (12)) and then using the expression (25) for R, one can get

$$ RC \approx \frac{{R \cdot C_{tot} }}{{\left( {K_{D} + K_{IB} } \right)/2}} \approx \frac{R \cdot C}{{\left( {K_{D} + K_{IB} } \right)/2}} \approx \frac{{R_{tot} \cdot C}}{{C + \left( {K_{D} + K_{IB} } \right)/2}}. $$

Expression for R₂C

From (12), disregarding the terms of the order of R ²_tot one immediately arrives at $R_{{^{2} }} C \approx 0.$

Expressions (16)

Disregarding the terms of the order of R ²_tot and using (25) for R, one can get:

$$ \frac{{R \cdot (2K_{D} + K_{IB} + R)}}{{\left( {K_{D} + K_{IB} + R} \right)(K_{D} + K_{IB} /2 + R)}} \approx \frac{2R}{{K_{D} + K_{IB} }} \approx \frac{{R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}}. $$

$$ \frac{2R}{{K_{D} + K_{IB} + R}} \approx \frac{2R}{{K_{D} + K_{IB} }} \approx \frac{{R_{tot} }}{{C + \left( {K_{D} + K_{IB} } \right)/2}} $$