Linearly Implicit and High-Order Energy-Conserving Schemes for Nonlinear Wave Equations

Abstract

A key issue in developing efficient numerical schemes for nonlinear wave equations is the energy-conserving. Most existing schemes of the energy-conserving are fully implicit and the schemes require an extra iteration at each time step and considerable computational cost for a long time simulation, while the widely-used q-stage (implicit) Gauss scheme (method) only preserves polynomial Hamiltonians up to degree 2q. In this paper, we present a family of linearly implicit and high-order energy-conserving schemes for solving nonlinear wave equations. The construction of schemes is based on recently-developed scalar auxiliary variable technique with a combination of classical high-order Gauss methods and extrapolation approximation. We prove that the proposed schemes are unconditionally energy-conserved for a general nonlinear wave equation. Numerical results are given to show the energy-conserving and the effectiveness of schemes.

1 Introduction

The paper focuses on developing linearly implicit and high-order energy-conserving schemes for a general nonlinear wave equation defined by

$$\begin{aligned} \phi _{tt}=\triangle \phi -F'(\phi ),~~(x,t) \in \Omega \times (0,T] \end{aligned}$$

(1.1)

subject to homogeneous Dirichlet or homogeneous Neumann boundary conditions and the following initial conditions

$$\begin{aligned} \phi (x,0)=\phi _0(x),\ \ \phi _t(x,0)=\phi _1(x),\ \ { x}\in \Omega , \end{aligned}$$

(1.2)

where $\Omega$ is a bounded domain in ${\mathcal R}^d$$(d=1,2,3)$, $\phi _0({x})$ and $\phi _1({ x})$ are given initial conditions, and F(u) is a nonlinear smooth potential.

Nonlinear wave equations provide a powerful tool to model complicated natural phenomena in variety of scientific fields, such as solid state physics, nonlinear optics, and quantum field theory [4, 10, 18, 19, 44]. A remarkable feature of the wave Eq. (1.1) is its energy-conserving

$$\begin{aligned} E(t)= \int _\Omega \phi _t^2+ |\nabla \phi |^2 + 2F(\phi ) d x =E(0). \end{aligned}$$

For long time simulations, it is highly desirable that numerical algorithms can preserve the conservative structures of the corresponding systems in discrete analogs.

In the past several decades, numerous effort has been devoted to developing efficient energy-conserving numerical schemes for nonlinear wave equations. Explicit schemes are easier to be implemented, but less effective due to their conditional stability. The most popular numerical schemes for solving nonlinear wave equations in a long time period are fully implicit in general. Roughly speaking, the construction of implicit energy-conserving schemes can be divided into two categories. One is based on multi-step energy-conserving schemes with certain modification of the approximations to nonlinear term $F'(\phi )$, see e.g., [24, 34, 41]. The other one is to reformulate the equations as an abstract Hamiltonian system and then, apply implicit schemes for the Hamiltonian system, such as the discrete gradient methods [30, 31, 42], the boundary-value methods [6, 7, 9] and the average vector field methods [14, 15, 35]. For a more detailed description of the energy-conserving schemes, we refer readers to the books [21, 45] and the references [8, 13, 20, 23, 26, 27, 40, 43, 46, 47]. Fully implicit schemes have shown their better performance than those explicit ones in the long time integrations due to the unconditional stability and conservation of schemes. However, these schemes require an extra iterative algorithm for solving a system of nonlinear equations at each time step, which leads to a considerable computational cost in the long time integrations.

Compared with fully nonlinear and implicit schemes, linearly implicit schemes are more attractive since the schemes only require the solution of a linear system at each time step. However, classical linearly implicit schemes may not be energy-conserved in general. Recently much attention has been paid to developing energy-stable linearly implicit schemes. Shen et al. [38] first proposed a linearly implicit scheme based on SAV approach for a parabolic type gradient flow equation with emphasis on the energy stability. Physically, the energy for this parabolic type equation does not increase as the time increases. In [38], authors proved that the SAV type scheme is energy-stable in the parabolic sense for the gradient flow model. Subsequent works can be found in [1, 11, 16, 28, 37, 39] for some different models. More recently, Cai and Shen presented a linearly implicit energy-conserving scheme for a Hamiltonian system of ODEs [12]. The construction is based on the invariant energy quadratization and the second-order time discrete approximations were studied. It is noted that nonlinear wave equations own different analytical properties. Some numerical schemes may be energy-stable for the gradient flow equation but not energy-conserved for nonlinear wave equations, e.g., the linearly implicit Euler method, the linearized two-step backward difference formula and the linearized Radau methods.

In the present paper, we present a family of high-order linearly implicit and energy-conserving schemes for solving the nonlinear wave equations. The main idea is as follows. First we introduce a scalar auxiliary variable and rewrite the nonlinear wave equation into a system of nonlinear equations. Then, the linearly implicit schemes are developed by combining the Gauss methods and some extrapolated techniques for nonlinear terms. The proposed schemes have the following advantages:

• The schemes are linearly implicit. At each step, the schemes only require the solution of a linear system.

• The schemes are generated with an arbitrary high-order accuracy in time direction and can be easily combined with existing approximations in spatial direction.

• The proposed schemes are unconditionally energy-conserved for more general problems, while some fully implicit schemes ( Gauss methods, Hamiltonian boundary value methods and line integral methods) are energy-conserved only for polynomial type nonlinear systems.

The rest of papers are organized as follows. In Sect. 2, we propose a class of time-discrete schemes and prove the energy-conserving property of schemes for the nonlinear wave Eq. (1.1). Fully discrete schemes with classical FE approximations in spatial direction are presented in Sect. 3. In Sect. 4, we present two numerical examples to confirm the theoretical results. Finally, conclusions are presented in Sect. 5.

2 Discrete Schemes and Energy Conservation

In this section, we present our linearly implicit schemes based on the SAV approach as well as their energy-conserving property for the nonlinear wave Eq. (1.1).

2.1 Linearly Implicit Schemes

We denote

$$\begin{aligned} \eta (t)=\sqrt{G(\phi )},\ \ G(\phi )=\int _{\Omega } F(\phi ) d{ x}+ C_0, \end{aligned}$$

where $C_0$ is a constant guaranteeing $\int _{\Omega } F(\phi ) d{ x}+ C_0>0$ and rewrite (1.1) as

$$\begin{aligned} \phi _t= & {} \psi ,\end{aligned}$$

(2.1)

$$\begin{aligned} \psi _t= & {} \triangle \phi -\eta w(\phi ),\end{aligned}$$

(2.2)

$$\begin{aligned} \eta _t= & {} \frac{1}{2}\int _{\Omega } w(\phi )\psi d{ x}, \end{aligned}$$

(2.3)

where $w(\phi )=\frac{F'(\phi )}{\sqrt{G(\phi )}}$. Taking the inner product of Eq. (2.1) with $\psi _t$ and Eq. (2.2) with $-\phi _t$, multiplying both sides of Eq. (2.3) with respect to $-2\eta$, and adding them together, we obtain immediately

$$\begin{aligned} \frac{d}{dt} E_s(\phi ,\psi ,\eta )=0. \end{aligned}$$

Here $E_s(\phi ,\psi ,\eta )=\Vert \psi \Vert +\Vert \nabla \phi \Vert +2\eta ^2$, where $|| \cdot ||$ denotes the $L^2$-norm. Noting that $\psi =\phi _t$ and $\eta =\sqrt{\int _{\Omega } F(\phi ) d{ x}+ C_0}$, the modified and the original energy functional have the following relation

$$\begin{aligned} E(t) =E_s(\phi ,\psi ,\eta )-C_0. \end{aligned}$$

Let $\tau :=T/N$ be the time step with N being a positive integer, $t_n:=n\tau , n=0,\dotsc ,N,$ be a uniform partition of the time interval [0, T] and $t_{ni}:=t_n+c_i\tau , i=1,\dotsc ,q, n=0,\dotsc ,N-1,$ be the internal Gauss nodes. Donote by $\{\phi _n, \psi _n, \eta _n, \phi _{ni}, \psi _{ni}, \eta _{ni}\}$ numerical approximations to $\{\phi (t_n, x), \psi (t_n, x), \eta (t_n, x), \phi (t_{ni}, x), \psi (t_{ni}, x), \eta (t_{ni}, x)\}$, respectively. Let $\phi ^*_{ni}$ be a numerical approximation to $\phi (t_{ni}, x)$, which will be given later in terms of some extrapolation technique.

Based on a q-stage Gauss method, we present a general semi-discrete numerical scheme for the system (2.1)–(2.3) by

$$\begin{aligned}&\phi _{ni}=\phi _{n}+ \tau \sum _{j=1}^q a_{ij}\psi _{nj}, \end{aligned}$$

(2.4)

$$\begin{aligned}&\left\{ \begin{array}{ll} \bar{\psi }_{ni}=\varDelta \phi _{ni} - \eta _{ni} w(\phi ^*_{ni}) &{} \quad \text {in}\,\,\,\varOmega ,\quad i=1,\dotsc ,q, \\ \psi _{ni}=\psi _{n}+ \tau \sum _{j=1}^q a_{ij} \bar{\psi }_{nj}, &{} \quad \text {in}\,\,\,\varOmega ,\quad i=1,\dotsc ,q,\\ \partial _{n}\phi _{ni}=0, \text {on}\,\,\,\partial \varOmega , &{} \quad i=1,\dotsc ,q, \end{array} \right. \end{aligned}$$

(2.5)

$$\begin{aligned}&\eta _{ni}=\eta _{n}+ \frac{\tau }{2} \sum _{j=1}^q a_{ij}\int _\Omega w(\phi ^*_{nj})\psi _{nj} d{ x}. \end{aligned}$$

(2.6)

With $\phi _{ni}, \psi _{ni}, \psi _{ni}, \eta _{ni}$, $(\phi _{n+1},\psi _{n+1},\eta _{n+1})$ can be calculated by

$$\begin{aligned} \left\{ \begin{aligned} \phi _{n+1}&:=\phi _{n}+ \tau \sum _{i=1}^q b_i \psi _{ni}, \\ \psi _{n+1}&:=\psi _{n}+ \tau \sum _{i=1}^q b_i \bar{\psi }_{ni}, \\ \eta _{n+1}&:=\eta _{n}+ \frac{\tau }{2} \sum _{i=1}^q b_i \int _\Omega w(\phi ^*_{ni})\psi _{ni} d{ x}. \end{aligned} \right. \end{aligned}$$

(2.7)

In the above formulas, $\bar{\psi }_{ni}$ is a temporary variable, which is introduced to simplify the formulations. $\phi ^*_{ni}$ is an (explicit) extrapolation approximation to $\phi (t_{ni}, x)$ of the order $\mathcal {O}(\tau ^{q+1})$, which can be generated in the following way.

We denote by $\phi _{n-1}^{\tau }(t)$ a Lagrange interpolation polynomial of degree at most q satisfying

$$\begin{aligned} \phi _{n-1}^{\tau }(t_{n-1,i})=\phi _{n-1,i},\quad i=1,\dotsc ,q , \end{aligned}$$

and

$$\begin{aligned} \phi _{n-1}^{\tau }(t_{n-1})=\phi _{{n-1}}, \quad \text{ or } \quad \phi _{n-1}^{\tau }(t_n)=\phi _n \, . \end{aligned}$$

Then, we define

$$\begin{aligned} \phi _{ni}^*:=\phi ^{\tau }_{n-1}(t_{ni}) \, . \end{aligned}$$

Remark 2.1

The q-stage Gauss method can be viewed as a special class of Runge–Kutta methods, defined by the Butcher tableau

$$\begin{aligned} \begin{array}{c|ccc} c_1 &{} a_{11} &{} \dots &{} a_{1q} \\ \vdots &{} \vdots &{} \; &{} \vdots \\ c_q &{}a_{q1} &{} \dots &{} a_{qq} \\ \hline &{}b_1 &{} \dots &{} b_q \; \\ \end{array} \end{aligned}$$

(2.8)

with $c_1,\dotsc , c_q\in (0,1)$, satisfying the condition

$$\begin{aligned} b_i a_{ij}+b_ja_{ji}-b_ib_j=0,\qquad i,j=1,\dotsc ,q \, . \end{aligned}$$

(2.9)

For the more detailed description, we refer readers to the classical book [22].

Remark 2.2

As proved in [29, 33, 36], when q-stage fully implicit Gauss methods are applied to solve the nonlinear partial differential equations with the homogeneous Dirichlet or homogeneous Neumann boundary conditions, the attained order of convergence turns out to be at most $q+1$. For this reason, here only the extrapolation with q internal nodes and one ending point in the previous time interval $[t_{n-1},t_{n}]$ is used. The extrapolation also provides the approximation of the order $\mathcal {O}(\tau ^{q+1})$.

Remark 2.3

The proposed linearly implicit methods require the starting values $\phi _{0i}, \psi _{0i}, \eta _{0i}$,

$i=1,2,\cdots , q$, which can be obtained by the Gauss methods of the same stage. We shall show numerically and theoretically the energy-conserving property from $n=1$.

Remark 2.4

For a Hamiltonian system of ODEs

$$\begin{aligned} q'(t)= & {} p(t), \\ p'(t)= & {} -\mathcal {A}q(t)-F'(q(t)), \end{aligned}$$

where $q(t)\in R^n, p(t)\in R^n$ and $\mathcal {A}$ is a positive definite operator, we can introduce a scalar auxiliary variable

$$\begin{aligned} \eta (t)=\sqrt{G(q(t))},\ \ G(q(t))= \langle F(q(t), e\rangle + C_0, \end{aligned}$$

(2.10)

with which the above system can be rewritten by

$$\begin{aligned} q'(t)= & {} p(t),\\ p'(t)= & {} -\mathcal {A}q(t)-\eta (t) w(q(t)),\\ \eta _t= & {} \frac{1}{2}\langle w(q(t)), p(t)\rangle , \end{aligned}$$

where $w(x)=\frac{F'(x)}{\sqrt{G(x)}}$, $\langle \cdot \rangle$ denotes the inner product on [0, T], $e=(1,1,\cdots ,1)^T\in R^n$ and $C_0$ is a constant guaranteeing $\langle F(q(t), e\rangle + C_0>0$. The proposed linearly implicit methods can be easily extended to the above system. One can show the energy-preserving of methods by following the proof in the present paper.

2.2 Energy Conservation

In this subsection, we show the unconditional energy-conserving property of the discrete schemes in (2.4)–(2.7). We define the time discrete energy by

$$\begin{aligned} E_\tau (\phi _{n},\psi _n,\eta _n) = \Vert \psi _n\Vert ^2+\Vert \nabla \phi _n\Vert ^2+2|\eta _n|^2, \end{aligned}$$

where $|| \cdot ||$ denotes the $L^2$-nom. Noting that $\psi =\phi _t$ and $\eta =\sqrt{\int _{\Omega } F(\phi ) d{ x}+ C_0}$, the discrete energy $E_\tau (\phi _{n},\psi _n,\eta _n)-C_0$ is an approximation to the continuous energy E(t).

Theorem 1

The numerical solution defined in (2.4)–(2.7) preserves the energy

$$\begin{aligned} E_\tau (\phi _{n+1},\psi _{n+1},\eta _{n+1} )=E_\tau (\phi _{n},\psi _n,\eta _n), \quad n=1,2,\ldots ,N-1 \, . \end{aligned}$$

(2.11)

Proof

It follows from the first equation of (2.7) that

$$\begin{aligned} \nabla \phi _{n+1}=\nabla \phi _{n}+ \tau \sum _{i=1}^q b_i \nabla \psi _{ni} . \end{aligned}$$

Taking the $L^2$-norm of both sides of the above equation yields

$$\begin{aligned} \begin{aligned} \Vert \nabla \phi _{n+1}\Vert ^2&{}=\Big (\nabla \phi _{n}+ \tau \sum _{i=1}^q b_i \nabla \psi _{ni},\nabla \phi _{n}+ \tau \sum _{j=1}^q b_j \nabla \psi _{nj}\Big )\\&{}=\Vert \nabla \phi _{n}\Vert ^2 +2\tau \sum _{i=1}^q b_i (\nabla \psi _{ni},\nabla \phi _{n}) +\tau ^2 \sum _{i,j=1}^q b_i b_j(\nabla \psi _{ni},\nabla \psi _{nj}). \end{aligned} \end{aligned}$$

whee $(\cdot , \cdot )$ denotes the inner product on $L^2(\Omega )$. Substituting $\phi _n=\phi _{ni}-\tau \sum _{j=1}^q a_{ij} \psi _{nj}$ (Eq. (2.4)) into the second term on the right-hand side of the last equation, we obtain

$$\begin{aligned} \Vert \!\nabla \! \phi _{n+1}\!\Vert ^2\!=\! & {} \Vert \nabla \phi _{n}\Vert ^2 \!+\!2\tau \!\sum _{i=1}^q b_i \!\big (\nabla \psi _{ni},\! \nabla \phi _{ni}\!-\!\tau \sum _{j=1}^q a_{ij}\! \nabla \! \psi _{nj}\big ) +\tau ^2 \sum _{i,j=1}^q b_i b_j\!(\nabla \psi _{ni},\nabla \! \psi _{nj})\nonumber \\= & {} \Vert \nabla \phi _{n}\Vert ^2 +2\tau \sum _{i=1}^q b_i \big (\nabla \psi _{ni}, \nabla \phi _{ni}\big ) -\tau ^2 \sum _{i,j=1}^q m_{ij}(\nabla \psi _{ni},\nabla \psi _{nj})\nonumber \\= & {} \Vert \nabla \phi _{n}\Vert ^2 +2\tau \sum _{i=1}^q b_i \big (\nabla \psi _{ni}, \nabla \phi _{ni}\big ), \end{aligned}$$

(2.12)

where we have noted (2.9).

Again taking the $L^2$-norms of both sides of the second equation of (2.7) gives

$$\begin{aligned} \Vert \psi _{n+1}\Vert ^2= & {} \Vert \psi _{n}\Vert ^2 +2\tau \sum _{i=1}^q b_i \big ( \bar{\psi }_{ni}, \psi _n\big )+ \tau ^2 \sum _{i,j=1}^q b_i b_j(\bar{\psi }_{ni},\bar{\psi }_{nj}). \end{aligned}$$

Substituting $\psi _n=\psi _{ni}-\tau \sum _{j=1}^q a_{ij} \bar{\psi }_{nj}$ (second equation of (2.5)) into the second term on the right-hand side of the above equation and noting (2.9), we obtain

$$\begin{aligned} \Vert \psi _{n+1}\Vert ^2= & {} \Vert \psi _{n}\Vert ^2 +2\tau \sum _{i=1}^q b_i \big ( \bar{\psi }_{ni}, \psi _{ni}\big ). \end{aligned}$$

(2.13)

Similarly, we have

$$\begin{aligned} 2|\eta _{n+1}|^2= & {} 2|\eta _{n}|^2 +2\tau \sum _{i=1}^q b_i \eta _{ni}\int _\Omega W(I_{n-1}^{\tau }\phi _{ni})\psi _{ni} d x. \end{aligned}$$

(2.14)

Moreover, from the first equation of (2.5), we can see that

$$\begin{aligned} ( \bar{\psi }_{ni}, \psi _{ni}\big )= & {} (\triangle \phi _{ni}, \psi _{ni})-\eta _{ni}\int _\Omega W(I_{n-1}^{\tau }\phi _{ni})\psi _{ni}dx \nonumber \\= & {} -(\nabla \phi _{ni}, \nabla \psi _{ni})-\eta _{ni}\int _\Omega W(I_{n-1}^{\tau }\phi _{ni})\psi _{ni} dx. \end{aligned}$$

(2.15)

Finally, we substitute (2.15) into the last term on the right-hand side of (2.13), and add (2.12) and (2.13) tegother to get

$$\begin{aligned} \Vert \psi _{n+1}\Vert ^2+\Vert \nabla \phi _{n+1}\Vert ^2+2|\eta _{n+1}|^2= \Vert \psi _{n}\Vert ^2+\Vert \nabla \phi _{n}\Vert ^2+2|\eta _{n}|^2, \end{aligned}$$

which completes the proof. $\square$

3 Fully Discrete Schemes

Let $\mathcal {T}_h$ be a quasi-uniform partition of $\Omega$ into intervals $T_i$ ($i=1,\cdots ,N_x$) in $\mathbb {R}$, or triangles in $\mathbb {R}^2$ or tetrahedra in $\mathbb {R}^3$, $\triangle x=\max _{1\le i \le N_x}\{\text {diam}\;T_i\}$ be the mesh size. Let $V_h$ be the finite-dimensional subspace of $H_0^1(\Omega )$, which consists of continuous piecewise polynomials of degree r ($r\ge 1$) on $\mathcal {T}_h$.

For given $\psi _h^n, \phi _h^n \in V_h$ and $\varvec{\eta }_0^n \in \mathbb {R}$, the Finite element solutions $\psi _{hj}^n, \bar{\psi }_{hj}^n, \phi _{ji}^n, \phi ^n_h, \psi ^n_h \in V_h$, $j=1,2,\ldots ,q$ and $\eta _h^{n+1}\in \mathbb {R}$, satisfy the system

$$\begin{aligned} ( \bar{\psi }_{hj}^n, v_h)= & {} - (\nabla \phi _{hj}^n, \nabla v_h) - \eta _j^n (w(\phi _{hj}^{n*}), v_h) , \qquad v_h \in V_h,\\ (\psi _{hj}^n, v_h)= & {} (\psi _h^n, v_h) + \tau \sum _{k=1}^q a_{jk} (\bar{\psi }_{hk}^n, v_h) , \qquad v_h \in V_h,\\ (\phi _{hj}^n, v_h)= & {} (\phi _h^n, v_h) + \tau \sum _{j=1}^q a_{jk} (\psi _{hk}^n, v_h), \qquad v_h \in V_h,\\ \eta _j^n= & {} \eta ^n_0 + \frac{\tau }{2} \sum _{k=1}^q a_{jk} (w(\phi _{hk}^{n*}), \psi _{hk}^n) , \qquad j=1,2,\ldots ,q ,\\ (\phi _h^{n+1},v_h)= & {} (\phi _h^{n},v_h)+ \tau \sum _{i=1}^q b_i (\psi _{hi}^n, v_h), \qquad v_h \in V_h, \\ (\psi _h^{n+1},v_h)= & {} (\psi _h^{n},v_h)+ \tau \sum _{i=1}^q b_i (\bar{\psi }_{hi}^n,v_h),\qquad v_h \in V_h, \\ \eta _h^{n+1}= & {} \eta _h^{n}+ \frac{\tau }{2} \sum _{i=1}^q b_i \int _\Omega w(\phi ^*_{ni})\psi _{ni} d{ x} \end{aligned}$$

and $\phi ^{n*}_{hi}$ is an (explicit) extrapolation approximation to $\phi (t_{ni}, x)$ (The extrapolation is similar to that in the previous section).

Let $\{ \alpha _i(x) \}_{i=1}^{N_x}$ be a base of $V_h$ and

$$\begin{aligned} \psi _{hj}^n(x)= & {} \sum _{i=1}^{N_x} \psi ^n_{ij} \alpha _i(x), \quad \phi _{hj}^n (x) = \sum _{i=1}^{N_x} \phi ^n_{ij} \alpha _i(x), \quad \bar{\psi }_{hj}^n(x) = \sum _{i=1}^{N_x} \bar{\psi }^n_{ij} \alpha _i(x),\\ \phi _h^n(x)= & {} \sum _{i=1}^{N_x} \phi ^n_{hi} \alpha _i(x),\quad \psi _h^n(x)= \sum _{i=1}^{N_x} \psi ^n_{hi} \alpha _i(x). \end{aligned}$$

Then in a matrix form, the above system can be rewritten by

$$\begin{aligned} ( I_q \otimes M )\bar{\varvec{\Psi }}^n= & {} - (I_q \otimes S) \varvec{\Phi }^n - D_w ( \varvec{\eta }^n \otimes \mathbf{e}), \end{aligned}$$

(3.1)

$$\begin{aligned} (I_q \otimes M) \varvec{\Psi }^n= & {} I_q\otimes (M\varvec{\Psi }_0^n) + \tau (A \otimes M) \bar{\varvec{\Psi }}^n, \end{aligned}$$

(3.2)

$$\begin{aligned} (I_q \otimes M) \varvec{\Phi }^n= & {} I_q \otimes (M \varvec{\Phi }^n_0) + \tau (A \otimes M) \varvec{\Psi }^n, \end{aligned}$$

(3.3)

$$\begin{aligned} \eta ^n= & {} \varvec{\eta }_0^n + \frac{\tau }{2} (A \otimes \mathbf{e}^T) D_w \varvec{\Psi }^n, \end{aligned}$$

(3.4)

$$\begin{aligned} \varvec{\Phi }_0^{n+1}= & {} \varvec{\Phi }_0^{n} + \tau (b^T \otimes I_{N_x} )\varvec{\Psi }^n , \end{aligned}$$

(3.5)

$$\begin{aligned} \varvec{\Psi }_0^{n+1}= & {} \varvec{\Psi }_0^{n} + \tau (b^T \otimes I_{N_x} )\bar{\varvec{\Psi }}^n , \end{aligned}$$

(3.6)

$$\begin{aligned} \eta _h^{n+1}= & {} \eta _h^{n}+ \frac{\tau }{2} \sum _{i=1}^q b_i \int _\Omega w(\phi ^*_{ni})\psi _{ni} d{ x} , \end{aligned}$$

(3.7)

where $\otimes$ denotes the kronecker product, $A=(a_{ij})_{q \times q}$, $b=(b_1,b_2,\cdots ,b_q)^T$, $I_{p}$ denotes the $p \times p$ identity matrix with $p=q$ or $N_x$, M and S define the mass matrix and stiffness matrix, respectively, $\varvec{\Psi }^n, \varvec{\Phi }^n, \bar{\varvec{\Psi }}^n \in {\mathbb R}^{qN_x}$ and $\varvec{\eta }^n \in {\mathbb R}^q$,

$$\begin{aligned}&D_w = diag(w_{11}^n, w_{12}^n, \ldots , w_{1N_x}^n, w_{21}^n, \ldots , w_{q1}^n, \ldots , w_{qN_x}^n ), \quad \mathbf{e}= (1,1,\ldots ,1)^T \in {\mathbb R}^{N_x}, \\&\varvec{\Phi }^n_0 = (\phi _{h1}^n,\phi _{h2}^n,\ldots ,\phi _{hN_x}^n)^T , \quad \varvec{\Psi }^n_0 = (\psi _{h1}^n,\psi _{h2}^n,\ldots ,\psi _{hN_x}^n)^T, \quad \eta _0^{n}=(\eta _h^n,\cdots ,\eta _h^n)\in {\mathbb R}^q \end{aligned}$$

and $w_{ij}^n = ((w(\phi _{nj}^*), \alpha _i)$.

Remark 3.1

The fully discrete scheme is energy-conserving, i.e., $E_{\tau }(\phi _h^{n+1}, \psi _h^{n+1}, \eta _h^{n+1})=E_{\tau }(\phi _h^{n}, \psi _h^{n}, \eta _h^{n})$, where

$$\begin{aligned} E_{\tau }(\phi _h^n, \psi _h^n, \eta _h^n) = \Vert \psi _h^n \Vert ^2 + \Vert \nabla \phi _h^n \Vert ^2 + 2 | \eta ^n_h|^2=(\varvec{\Psi }^n_0)^TM\varvec{\Psi }^n_0+(\varvec{\Phi }^n_0)^TS\varvec{\Phi }^n_0 +2 | \eta ^n_h|^2. \end{aligned}$$

The proof is similar to that in the previous section by multiplying both sides of Eqs. (3.5) and (3.6) by the matrices S and M, respectively.

From (3.1) and (3.2) and noting $A \otimes M = (A \otimes I)(I_q \otimes M)$ where I denotes the $N_x \times N_x$ identity matrix, we have

$$\begin{aligned} (I_q \otimes M) \varvec{\Psi }^n= & {} I_q \otimes (M \varvec{\Psi }_0^n) - \tau (A \otimes I) [ (I_q \otimes S) \varvec{\Phi }^n + D_w (\varvec{\eta }^n \otimes \mathbf{e}) ] \\= & {} I_q \otimes (M \varvec{\Psi }_0^n) - \tau (A \otimes S) \varvec{\Phi }^n - \tau (A \otimes I) D_w (\varvec{\eta }^n \otimes \mathbf{e}) \end{aligned}$$

and by (3.3),

$$\begin{aligned} (I_q\otimes M) \varvec{\Psi }^n= & {} I_q \otimes (M\varvec{\Psi }_0^n) - \tau (A \otimes S) [ \varvec{\Phi }^n_0 + \tau (A \otimes I) \varvec{\Psi }^n ] - \tau (A \otimes I) D_w ( \varvec{\eta }^n \otimes \mathbf{e}) \\= & {} I_q \otimes (M \varvec{\Psi }_0^n) - \tau A \otimes (S \varvec{\Phi }^n_0) - \tau ^2 (A^2 \otimes S) \varvec{\Psi }^n - \tau (A \otimes I) D_w (\varvec{\eta }^n \otimes \mathbf{e}) \, . \end{aligned}$$

Moreover, by (3.4),

$$\begin{aligned} (I_q \otimes M) \varvec{\Psi }^n= & {} I_q \otimes (M \varvec{\Psi }_0^n) - \tau A \otimes (S \varvec{\Phi }^n_0) - \tau ^2 ( A^2 \otimes S) \varvec{\Psi }^n \\&\quad - \tau (A\otimes I) D_w [ \varvec{\eta }_0^n \otimes \mathbf{e}+ \frac{\tau }{2} ( (A \otimes \mathbf{e}^T)D_w \varvec{\Psi }^n) \otimes e] \\= & {} I_q \otimes (M \varvec{\Psi }_0^n) - \tau A \otimes (S \varvec{\Phi }^n_0) - \tau ^2 ( A^2 \otimes S) \varvec{\Psi }^n - \tau ( A \otimes I ) D_w (\varvec{\eta }_0^n \otimes e) \\&\quad - \frac{\tau ^2}{2} (A\otimes I) D_w (A \otimes ( \mathbf{e}^T \otimes \mathbf{e})) D_w \varvec{\Psi }^n. \nonumber \end{aligned}$$

Finally, we have the system

$$\begin{aligned} \mathbf{B} \varvec{\Psi }^n = \mathbf{f}, \end{aligned}$$

(3.8)

where

$$\begin{aligned}&\mathbf{B} = I_q \otimes M + \tau ^2 A^2 \otimes S + \frac{\tau ^2}{2} (A \otimes I) D_w (A \otimes (\mathbf{e}^T \otimes \mathbf{e}) )D_w, \\&\mathbf{f} = I_q \otimes (M \varvec{\Psi }_0^n) - \tau A \otimes (S \varvec{\Phi }^n_0) - \tau ( A \otimes I) D_w (\varvec{\eta }_0^n \otimes \mathbf{e}). \end{aligned}$$

The eigenvalue of the matrix $\mathbf{B}$ can be written by

$$\begin{aligned} \lambda _\mathbf{B} = 1 + \tau ^2 \lambda _A^2 \lambda _{M,S} + O(\tau ^2), \end{aligned}$$

(3.9)

where $\lambda _\mathbf{B}, \lambda _A, \lambda _{M,S}$ denote the eigenvalue of $\mathbf{B}, A, M^{-1}S$, respectively. Since both the matrices M and S are symmetric positive definite, $\lambda _{M,S} >0$. A straightforward calculation shows that

$$\begin{aligned} |1+ \lambda \lambda _A^2|> \lambda _0>0,\qquad \text{ for } \text{ any } \lambda > 0, \end{aligned}$$

where $\lambda _0$ is a constant. Then there exists $\tau _0>0$, $|\lambda _\mathbf{B}| \ne 0$ when $\tau \le \tau _0$ and the system (3.8) has a unique solution. Therefore, at each time step, the finite element system defined in (3.1)–(3.4) has a unique solution $\varvec{\Psi }^n, \varvec{\Phi }^n, \eta ^n$.

4 Numerical Simulation

In this section, we present three numerical examples to confirm the theoretical findings. Numerical computations are performed in Matlab for a 1D problem and by Freefem for a 2D problem.

To test the energy-conserving property of methods, at each time step we calculate the discrepancies of the discrete energy

$$\begin{aligned} D_n = | E_{\tau }(\phi _h^n, \psi _h^n, \eta _h^n) - E_{\tau }(\phi _h^1, \psi _h^1, \eta _h^1)|, \qquad n = 1, 2,\ldots N \, . \end{aligned}$$

For comparison, we also apply the standard q-stage Gauss method (GM) and the q-stage linearized Gauss method (LGM) to the problem

$$\begin{aligned} \phi _t= & {} \psi ,\\ \psi _t= & {} \Delta \phi - F'(\phi ) . \end{aligned}$$

The same spatial approximations as in our proposed method are used together with these two time discrete schemes. The corresponding discrete energy and the energy change are also calculated. Since the standard GM is fully implicit, the Newton iterative algorithm is applied for solving the system of nonlinear equations at each time step, in which the convergence tolerance for the standard Newton algorithm is $10^{-13}$. Also the extrapolation technique with $q+1$ points is applied in the approximation to nonlinear terms in the LGM.

Example 1

In the first example, we consider the following 1D Klein-Gordon equation

$$\begin{aligned} \phi _{tt}= \phi _{xx} - \phi + \phi ^3, ~~~~~~(x,t)\in [0,\pi ] \times [0,100] \end{aligned}$$

(4.1)

with homogeneous Dirichlet boundary conditions and the following initial conditions

$$\begin{aligned} \phi (x,0)=\sin ^3(x), \quad \phi _t(x,0)=0,~~~~~~x\in [0,\pi ]. \end{aligned}$$

We solve this equation by the proposed method with a piecewise linear finite element approximation in spatial direction and the energy conserving schemes in time direction, where we take $\triangle x=\pi /256$ and $\tau = 1/40, 1/60, 1/80,1/100$, respectively. Since no exact solution is available, we take the numerical solution obtained by using the temporal stepsize $\tau =1/2560$ as the reference solution. The maximum numerical errors and convergence orders for $q=2,3,4$ are presented in Table 1. It can be seen from Table 1 that the q-stage SAV GM has the $q+1$-order convergence rate in the temporal direction.

Table 1 Maximum errors at $T=1$ and convergence rates in temporal direction

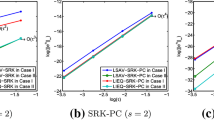
To test the energy-conserving property of methods, we solve the equation by these three type methods, q-stage GM, q-stage LGM and the proposed q-stage SAV GM in the time interval [0, 100] and calculate the discrete energy $E_{\tau }(\phi _h^n, \psi _h^n, \eta _h^n)$ and the energy discrepancies $D_n$ at each time step. We present in Figs. 1, 2 and 3 the energy discrepancies with different methods. One can observe that for GM and LGM, the discrepancies $D_n$ of the discrete energy changes with different temporal stepsizes. While for SAV-GM, the discrepancies $D_n$ are the order of the machine precision. There results confirm the energy-conserving properties of the SAV GM methods.

Fig. 1

Two-stage methods with $M=20$ (left) and $M=40$ (right) for Eq. (4.1)

Fig. 2

Three-stage methods with $M=24$ (left) and $M=48$ (right) for Eq. (4.1)

Fig. 3

Four-stage methods with $M=10$ (left) and $M=20$ (right) for Eq. (4.1)

Fig. 4

Two-stage methods with $M=20$ (left) and $M=40$ (right) for Eq. (4.2)

Fig. 5

Three-stage methods with $M=20$ (left) and $M=40$ (right) for Eq. (4.2)

Fig. 6

Four-stage methods with $M=10$ (left) and $M=20$ (right) for Eq. (4.2)

Fig. 7

Numerical simulation of the 2D SG Eq. (4.3) with ICs (i)

Fig. 8

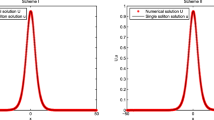
Numerical simulation of the 2D SG Eq. (4.3) with ICs (ii)

Fig. 9

GMs (left) and SAV-GMs (right) for the 2D SG Eq. (4.3) with ICs (i)

Fig. 10

GMs (left) and SAV-GMs (right) for the 2D SG Eq. (4.3) with ICs (ii)

Example 2

In the second example, we consider the following 1D nonlinear wave equation

$$\begin{aligned} \phi _{tt}= \phi _{xx} +\exp (-\phi ), \quad [0,\pi ] \times [0,100] \end{aligned}$$

(4.2)

with homogeneous Dirichlet boundary conditions and the following initial conditions

$$\begin{aligned} \phi (x,0)=0.5x(\pi -x), \quad \phi _t(x,0)=0, \quad x\in [0,\pi ]. \end{aligned}$$

The equation arises from Johnson–Mehl–Avrami–Kolmogorov theory, which characterizes the growth phenomenon of nuclei and the nucleation [2, 25, 43]. We still solve the equation by using two-, three- and four-stage GM, LGM and the proposed SAV GM, respectively. The discrepancies $D_n$ of the discrete energy are shown in Figs. 4, 5 and 6 for various stepsizes. We can see that the discrepancies of the discrete energy changed for both GMs and LGMs with different stepsizes. In contrast, the ones for SAV GMs with different stepsizes are sufficiently small and remain nearly unchanged. The results further confirm the theoretical findings in the present paper.

Example 3

We consider the 2D Sine-Gorden(SG) equation

$$\begin{aligned} \phi _{tt}= \triangle \phi -\sin (\phi ), ~~~~~~\Omega \times [0,100] \end{aligned}$$

(4.3)

with homogeneous Neumann boundary conditions, where $\Omega$ is a unit circle. The following two type initial conditions (ICs) will be tested.

$$\begin{aligned}&\text {(i) } \quad \phi (x,y,0)=4\arctan \Big (\exp \Big (1-2\sqrt{x^2+y^2}\Big )\Big ),~~\phi _t(x,y,t)=0; \end{aligned}$$

(4.4)

$$\begin{aligned}&\text {(ii) } \quad \phi (x,y,0)=4\arctan \Big ( \exp (6x)+\exp (6y)\Big ),~~\phi _t(x,y,t)=0. \end{aligned}$$

(4.5)

The SG equation with the initial conditions (4.4)–(4.5) was investigated by many authors, e.g., see [3, 5, 17], to study the behavior of ring solitons and the superposition of line solitons. Here, we solve the SG equation by the proposed energy-conserving method and the 2-stage GM, respectively, with a quadratic finite element approximation in spatial direction. A quasi-uniform triangulation is made by FreeFEM++ with M nodes uniformly distributed on the boundary of the circular domain and a uniform partition with $\tau = 1/N$ is made in time direction. We solve numerically the problem two different initial solutions defined in (4.4-(4.5) by setting $M=N=20$ . The numerical results are presented in Figs. 7 and 8, respectively. From Fig. 7, we can see that with ring solitons at the beginning, the solitons shrink ($t=2$) and expand ($t=4$) as the time increases. At the meanwhile, some oscillations at the boundary occur at $t=4$ and $t=6$ and then, disappear at $t=8$. Finally. two ring solitons can be observed at $t=10$. With the initial condition (4.5), we can see from Fig. 8 that the numerical solutions behave like line solitons at the beginning ($t=0$) and then, more line type solitons appear around the boundary ($t=2$). These line solitons move from lower-left to upper-right and change their shapes as the time increases ($t=4,t=6,t=8$ and $t=10$).

Moreover, we present in Figs. 9 and 10 the discrete energy discrepancies $D_n$ for the problem with different stepsizes and initial conditions given in (4.4) and (4.5). It can be observed clearly that the energy discrepancies $D_n$ of the GM increases dramatically for the problem with the initial condition (i) for both $\tau =0.1, 0.05$, while for the second initial condition the energy change increase quickly for $\tau =0.1$ and is stably around $0.1--0.2$ for $\tau =0.05$. Generally speaking, GM is not energy-conserved for the SG equation since it is not a polynomial type Hamiltonian. Meanwhile, the SAV GM show extremely good performance in the energy conserving. The energy discrepancies $D_n$ is constantly in the scale of $10^{-12}$, which shows that the proposed SAV GM schemes own the energy-conserving property for more general cases and which further confirms our theoretical results.

5 Conclusions

We have proposed a family of linearly implicit numerical schemes for solving the nonlinear wave equations. It is shown theoretically and numerically that the proposed schemes are unconditionally energy-conserved for more general models and the schemes are of arbitrarily high-order accuracy. Numerical results on nonlinear wave equations are given to confirm the effectiveness of the methods. The present paper brings a navel way to find high-order energy-conserving numerical methods, while based on the SAV approach, we believe more linearly implicit and energy-conserving numerical methods can be developed for solving the nonlinear wave equations. At present, there are some convergence results on SAV time discretization for parabolic problems, e.g, [1, 37]. It is possible to extend the analysis to the nonlinear wave equations. However, spatial discretization of the partial differential equations yields a stiff ODE system. As pointed out in [29, 32, 33, 48], the coefficients of the asymptotic error expansions of Runge–Kutta methods or other higher-order methods depend on stiffness of the problems and order reduction may appear. Therefore, a careful analysis is highly required. We leave the problem to the future work.