Two structure-preserving schemes with fourth-order accuracy for the modified Kawahara equation

Abstract

In this article, we present two high-order structure-preserving difference schemes for the modified Kawahara equation, which are named as Scheme I and Scheme II, respectively. Scheme I is a compact fourth-order difference scheme with a seven-point stencil and preserves discrete mass, while Scheme II is a standard fourth-order difference scheme with a nine-point stencil and preserves discrete energy. The proposed two schemes are three-level implicit and the numerical convergence order is $O(\tau ^{2}+h^{4})$. The unconditional stability of Scheme I and Scheme II is proven by von Neumann’s analysis. According to the Lax equivalence theorem, the convergence of the two schemes is also presented. The errors and rates of convergence, the discrete conservative mass $Q^{n}$ and energy $E^{n}$ are compared with those from other schemes. At last, some numerical experiments are given to demonstrate that the two proposed schemes are accurate and efficient for handling the single and multi-solitary waves propagating over a long period.

1 Introduction

The dynamics of shallow water waves is a significantly developing research area in the field of fluid mechanics. There are several models that are studied in this context, such as the KdV equation, RLW equation, Boussinesq equation, Kawahara equation and several others (Ak et al. 2016). The KdV equation

$$\begin{aligned} u_{t}+uu_{x}+u_{xxx}=0, \end{aligned}$$

was firstly introduced by Boussinesq Boussinesq (1871) and again derived by Korteweg and de Vires Korteweg and de Vries (1895), which is used to describe long waves traveling in canals (Bruzon et al. 2019). There are many KdV-type equations and one of the fifth-order KdV equations is (Kawahara 1972)

$$\begin{aligned} u_{t}+uu_{x}+u_{xxx}-u_{xxxxx}=0, \end{aligned}$$

which is called as the standard Kawahara equation. Moreover, the modified Kawahara equation is

$$\begin{aligned} u_{t}+u^{2}u_{x}+u_{xxx}-u_{xxxxx}=0, \end{aligned}$$

which is also called the singularly perturbed KdV equation (Kawahara 1972).

The modified Kawahara equation has wide applications in physics such as plasma waves, capillary-gravity water waves, water waves with surface tension, shallow water waves and so on (Jin 2009). It plays an important role in the theory of fluid mechanics, optical fibers, biology, solid-state physics, chemical kinematics, chemical physics, and geochemistry (Marinov and Marinova 2018). In this article, we consider the following modified Kawahara equation (Marinov and Marinova 2018)

$$\begin{aligned} u_{t}+\alpha u^{2}u_{x}+\beta u_{xxx}-\gamma u_{xxxxx}=0, \end{aligned}$$

(1.1)

where $\alpha >0$, $\beta >0$, $\gamma >0$. Eq. (1.1) has wide applications in the theory of shallow water waves (Hunter and Scheurle 1998; Bridges and Derks 2002). Here, u(x, t) represents the wave profile and has the asymptotic values as follows (Burde 2011; Wang and Dai 2018a):

$$\begin{aligned} u\rightarrow 0,~~\partial _{x}^{n}u\rightarrow 0,~~x\rightarrow {\pm \infty },~~n\ge 1. \end{aligned}$$

Under these assumptions, Eq. (1.1) possesses the following two conservative quantities (Zara et al. 2022; Chousurin et al. 2020; Ghiloufi and Omrani 2018):

$$\begin{aligned} Q(t)&=\int _{-\infty }^{+\infty }u(x,t)\textrm{d}x=\int _{-\infty }^{+\infty }u(x,0)\textrm{d}x=Q(0), \end{aligned}$$

$$\begin{aligned} E(t)&=\int _{-\infty }^{+\infty }u^{2}(x,t)\textrm{d}x=\Vert u(\cdot ,t)\Vert ^{2}_{L^{2}}=E(0),~~t\in (0,T]. \end{aligned}$$

In the past several decades, some types of exact and approximate analytic solutions have been proposed to solve the Kawahara and modified Kawahara equations. Considering the boundary condition $u\rightarrow 0$ as $x\rightarrow \pm \infty$, Ak et al. Ak and Karakoc (2018) obtained the following solitary wave solution of Eq. (1.1) as

$$\begin{aligned} u(x,t)=\frac{3}{\sqrt{10}}\sqrt{\frac{\beta ^{2}}{\alpha \gamma }}{{\,\textrm{sech}\,}}^{2}\Big [\sqrt{\frac{\beta }{20\gamma }}\Big (x-\frac{4\beta ^{2}}{25\gamma }t\Big )\Big ],~~x\rightarrow \pm \infty ,~~t>0. \end{aligned}$$

Applying the Adomian decomposition method (ADM), Polat et al. (2006) presented a traveling wave solution of Eq. (1.1). Wazwaz (2007) derived new solitons solutions and periodic solutions for Eq. (1.1) with the tanh method. Yusufoğlu et al. (2008) constructed periodic and solitary wave solutions for Eq. (1.1) with the sine-cosine method. Besides these, numerical solutions of the modified Kawahara equation were investigated by many researchers. Jin (2009) considered the approximate solutions of Eq. (1.1) by using the variational iteration method and homotopy perturbation method. Yuan et al. (2008) proposed the numerical scheme for Eq. (1.1) by using the dual-Petrov-Galerkin method. In Başhan (2021), Başhan investigated two different forms of the modified Kawahara equation via the differential quadrature method (DQM) by the contribution of the Crank-Nicolson technique. However, these numerical methods lack the necessary theoretical analysis, such as the stability and conservation of the numerical schemes.

On the other hand, conservative numerical schemes have attracted more and more interest in nonlinear partial differential equations (PDEs). Some of the most interesting features of physical systems are hidden in the nonlinear behavior of the nonlinear PDEs, such as mass and energy conservation laws (Soliman 2006; He 2016). Better approximated solutions can be expected from the numerical schemes which have effective conservative properties rather than the ones which have nonconservative properties, and the nonconservative schemes may easily show nonlinear blow-ups (Wongsaijai and Poochinapan 2014; Nanta et al. 2021). Also, the computational stability of the conservative scheme is totally different from that of the nonconservative scheme. The computational stability of the conservative scheme is only concerned with the structure of the scheme. The computational stability of the nonconservative scheme depends not only on the structure of the scheme, but also on the form of the initial values and their partial derivatives (Lin et al. 2003). Thus, the main purpose of this article is to construct two conservative difference schemes for the modified Kawahara equation (1.1) and give a detailed description of the stability and conservation of the two schemes.

To implement the numerical method, we choose the following initial and boundary value conditions

$$\begin{aligned} u(x,0)=u_{0}(x),~~x\in \Omega =[x_{l},x_{r}], \end{aligned}$$

(1.2)

$$\begin{aligned} u(x_{l},t)=u(x_{r},t)=0,~~u_{x}(x_{l},t)=u_{x}(x_{r},t)=0,~~u_{xx}(x_{l},t)=u_{xx}(x_{r},t)=0, \end{aligned}$$

(1.3)

where $u_{0}(x)$ is a known smooth function.

Theorem 1.1

Suppose that $u_{0}\in H_{0}^{2}(\Omega )$, then the modified Kawahara equation (1.1)–(1.3) is well-posed.

Proof

Assume that $u_{1}$ and $u_{2}$ are two solutions of the modified Kawahara equation (1.1)–(1.3) satisfying the initial conditions $u_{0}^{(1)}$ and $u_{0}^{(2)}$, respectively. Let $\eta =u_{1}-u_{2}$, then $\eta$ satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \eta _{t}=-\alpha [u_{1}^{2}(u_{1})_{x}-u_{2}^{2}(u_{2})_{x}]-\beta \eta _{xxx}+\gamma \eta _{xxxxx},\\ \eta (x,0)=u_{0}^{(1)}-u_{0}^{(2)},~~x\in \Omega ,\\ \eta (x_{l},t)=\eta (x_{r},t)=0,~~\eta _{x}(x_{l},t)=\eta _{x}(x_{r},t)=0,~~\eta _{xx}(x_{l},t)=\eta _{xx}(x_{r},t)=0.\\ \end{array}\right. \end{aligned}$$

Letting $\displaystyle G(t)=\int _{x_{l}}^{x_{r}}\eta ^{2}\textrm{d}x$, we obtain

$$\begin{aligned} \frac{d G(t)}{d t}=-2\alpha \int _{x_{l}}^{x_{r}}\eta [u_{1}^{2}(u_{1})_{x}-u_{2}^{2}(u_{2})_{x}]\textrm{d}x-2\beta \int _{x_{l}}^{x_{r}}\eta \eta _{xxx}\textrm{d}x+2\gamma \int _{x_{l}}^{x_{r}}\eta \eta _{xxxxx}\textrm{d}x \end{aligned}$$

$$\begin{aligned} ~~~~~~~~~~=-2\alpha \int _{x_{l}}^{x_{r}}\eta [u_{1}^{2}(\eta +u_{2})_{x}-u_{2}^{2}(u_{2})_{x}]\textrm{d}x-2\beta \Big [\eta \eta _{xx}-\frac{1}{2}(\eta _{x})^{2}\Big ]\Big |_{x_{l}}^{x_{r}} \end{aligned}$$

$$\begin{aligned} ~~~~~~~~~~+2\gamma \Big [(\eta \eta _{xxxx}-\eta _{x}\eta _{xxx}) +\frac{1}{2}(\eta _{xx})^{2}\Big ]\Big |_{x_{l}}^{x_{r}} \end{aligned}$$

$$\begin{aligned} ~~~~~~~~=-2\alpha \int _{x_{l}}^{x_{r}}\eta u_{1}^{2}\eta _{x}\textrm{d}x-2\alpha \int _{x_{l}}^{x_{r}}\eta (u_{1}^{2}-u_{2}^{2})(u_{2})_{x}\textrm{d}x \end{aligned}$$

$$\begin{aligned} ~~~~~~~~=2\alpha \int _{x_{l}}^{x_{r}}\eta ^{2} u_{1}(u_{1})_{x}\textrm{d}x-2\alpha \int _{x_{l}}^{x_{r}}\eta ^{2} (u_{1}+u_{2})(u_{2})_{x}\textrm{d}x. \end{aligned}$$

(1.4)

Suppose

$$\begin{aligned} C_{0}=\max _{(x,t)\in \Omega \times [0,T]}|u|,~~C_{1}=\max _{(x,t)\in \Omega \times [0,T]}|\partial u/\partial x|, \end{aligned}$$

we obtain

$$\begin{aligned} \Big |\int _{x_{l}}^{x_{r}}\eta ^{2} u_{1}(u_{1})_{x}\textrm{d}x\Big |\le C_{0}C_{1}\Big |\int _{x_{l}}^{x_{r}}\eta ^{2}\textrm{d}x\Big |, \end{aligned}$$

(1.5)

$$\begin{aligned} \Big |\int _{x_{l}}^{x_{r}}\eta ^{2}(u_{1}+u_{2})(u_{2})_{x}\textrm{d}x\Big |\le 2C_{0}C_{1}\Big |\int _{x_{l}}^{x_{r}}\eta ^{2}\textrm{d}x\Big |. \end{aligned}$$

(1.6)

We further obtain from Eqs. (1.4)–(1.6) that $\textrm{d}G(t)/\textrm{d}t\le 6\alpha C_{0}C_{1}G(t)$, $t\in [0,T]$, which yields $G(t)\le e^{6\alpha C_{0}C_{1}T}G(0)$, $0\le t\le T$. Thus, if $u_{0}^{(1)}=u_{0}^{(2)}$, we have $\eta (x,0)=0$ and hence $G(0)=0$, implying that $G(t)=0$. By the Sobolev inequality (Wang and Dai 2018b), we then obtain $\Vert \eta \Vert _{L_{\infty }}=0$ and $u_{1}=u_{2}$. Furthermore, if $\eta (x,0)<\varepsilon$, we obtain $G(0)<\varepsilon$ and hence $G(t)\le e^{6\alpha C_{0}C_{1}T}G(0)\le \varepsilon e^{6\alpha C_{0}C_{1}T}$, $0\le t\le T$. Thus, we obtain that the solution of Eqs. (1.1)–(1.3) is continuously dependent on the initial condition, implying that the modified Kawahara equation (1.1)–(1.3) is well-posed. $\square$

The remainder of the article is arranged as follows: In Section 2, a linear compact difference scheme (Scheme I) with fourth-order accuracy is derived. In Section 3, a standard fourth-order difference scheme (Scheme II) is constructed. Discrete mass and discrete energy are discussed for Scheme I and Scheme II, respectively. The unconditional stability of the two schemes is proven by von Neumann’s analysis. In Section 4, some numerical examples are provided to show the effectiveness of the proposed schemes. Concluding remarks and comments are presented in the last section.

2 Compact fourth-order difference scheme

In this section, we propose a compact fourth-order finite difference scheme (Scheme I) for the problem (1.1)–(1.3). The solution domain $\Omega =\{(x,t)|x_{l}\le x\le x_{r},~0\le t\le T\}$ is covered by the following uniform grid

$$\begin{aligned} \Omega _{h}=\{(x_{j},t^{n})|x_{j}=x_{l}+jh,~t^{n}=n\tau ,~0\le j\le J,~0\le n\le N\}, \end{aligned}$$

where $h=(x_{r}-x_{l})/J$ and $\tau =T/N$ are the spatial and temporal step sizes, respectively. Denote $U^{n}_{j}\approx u(x_{j},t^{n})$, $u^{n}_{j}\equiv u(x_{j},t^{n})$ and further let

$$\begin{aligned} Z_{h}^{0}=\{U=(U_{j})|U_{-2}=U_{-1}=U_{0}=U_{1}=U_{J-1}=U_{J}=U_{J+1}=U_{J+2}=0\}, \end{aligned}$$

where $j=-2,-1,0,...,J,J+1,J+2$. For convenience, the following notations are introduced:

$$\begin{aligned} (U_{j}^{n})_{\hat{t}}=\frac{1}{2\tau }(U_{j}^{n+1}-U_{j}^{n-1}),~(U_{j}^{n})_{\tilde{x}}=\frac{1}{h}(U_{j+1}^{n}-U_{j}^{n}),~(U_{j}^{n})_{\bar{x}}=\frac{1}{h}(U_{j}^{n}-U_{j-1}^{n}), \end{aligned}$$

$$\begin{aligned} (U_{j}^{n})_{\hat{x}}=\frac{1}{2h}(U_{j+1}^{n}-U_{j-1}^{n}),~(U_{j}^{n})_{\ddot{x}}=\frac{1}{4h}(U_{j+2}^{n}-U_{j-2}^{n}),~\bar{U}^{n}_{j}=\frac{1}{2}(U^{n+1}_{j}+U^{n-1}_{j}), \end{aligned}$$

$$\begin{aligned} \langle U^{n},V^{n}\rangle =h\sum ^{J-1}_{j=1}U^{n}_{j}V^{n}_{j},~\Vert U^{n}\Vert ^{2}=\langle U^{n},U^{n}\rangle ,~\Vert U^{n}\Vert _{\infty }=\max _{0\le j\le J}|U^{n}_{j}|. \end{aligned}$$

By setting

$$\begin{aligned} w=-\alpha u^{2}u_{x}-\beta u_{xxx}+\gamma u_{xxxxx}, \end{aligned}$$

(2.1)

we have

$$\begin{aligned} \gamma (\partial ^{7}_{x}u)^{n}_{j}=(\partial ^{2}_{x}w)^{n}_{j}+\frac{\alpha }{3}(\partial ^{3}_{x}u^{3})^{n}_{j}+\beta (\partial ^{5}_{x}u)^{n}_{j}, \end{aligned}$$

$$\begin{aligned} w^{n}_{j}=(\partial _{t}u)^{n}_{j}=(U^{n}_{j})_{\hat{t}}+O(\tau ^{2}),~~(\partial ^{2}_{x}w)^{n}_{j}=(U^{n}_{j})_{\tilde{x}\bar{x}\hat{t}}+O(\tau ^{2}+h^{2}). \end{aligned}$$

We then consider Eq. (2.1) at the grid point $(x_{j},t_{n})$ as

$$\begin{aligned} w^{n}_{j}=-\frac{\alpha }{3}[(u^{3})_{x}]^{n}_{j}-\beta (u^{n}_{j})_{xxx}+\gamma (u^{n}_{j})_{xxxxx} \end{aligned}$$

$$\begin{aligned}&=-\frac{\alpha }{3}\Big \{[(U^{n}_{j})^{3}]_{\hat{x}}-\frac{h^{2}}{6}(\partial ^{3}_{x}u^{3})^{n}_{j}+O(h^{4})\Big \}-\beta \Big [(U^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}-\frac{h^{2}}{4}(\partial ^{5}_{x}u)^{n}_{j}+O(h^{4})\Big ]\\&\quad +\gamma \Big [(U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{h^{2}}{3}(\partial ^{7}_{x}u)^{n}_{j}+O(h^{4})\Big ] \end{aligned}$$

$$\begin{aligned}&=-\frac{\alpha }{3}[(U^{n}_{j})^{3}]_{\hat{x}}-\beta (U^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}+\gamma (U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}+\frac{\alpha h^{2}}{18}(\partial ^{3}_{x}u^{3})^{n}_{j}+\frac{\beta h^{2}}{4}(\partial ^{5}_{x}u)^{n}_{j}\\&\quad -\frac{h^{2}}{3}\Big [(\partial ^{2}_{x}w)^{n}_{j}+\frac{\alpha }{3}(\partial ^{3}_{x}u^{3})^{n}_{j}+\beta (\partial ^{5}_{x}u)^{n}_{j}\Big ]+O(h^{4}) \end{aligned}$$

$$\begin{aligned}&=-\frac{\alpha }{3}[(U^{n}_{j})^{3}]_{\hat{x}}-\beta (U^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}+\gamma (U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{h^{2}}{3}(\partial ^{2}_{x}w)^{n}_{j}-\frac{\alpha h^{2}}{18}(\partial ^{3}_{x}u^{3})^{n}_{j}\nonumber \\&\quad -\frac{\beta h^{2}}{12}(\partial ^{5}_{x}u)^{n}_{j}+O(h^{4}). \end{aligned}$$

(2.2)

Thus, we obtain the following compact finite difference scheme (Scheme I) with fourth-order accuracy to solve the problem (1.1)–(1.3):

$$\begin{aligned}&(U^{n}_{j})_{\hat{t}}+\frac{h^{2}}{3}(U^{n}_{j})_{\tilde{x}\bar{x}\hat{t}}+\beta (\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}+\frac{\alpha }{3}[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\hat{x}}+\frac{\alpha h^{2}}{18}[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\tilde{x}\bar{x}\hat{x}}\nonumber \\&\quad +(\frac{\beta h^{2}}{12}-\gamma )(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}=0, \end{aligned}$$

(2.3)

$$\begin{aligned} U^{0}_{j}=u_{0}(x_{j}),~~~0\le j\le J, \end{aligned}$$

(2.4)

$$\begin{aligned} U^{n}_{0}=U^{n}_{J}=0,~(U^{n}_{0})_{\hat{x}}=(U^{n}_{J})_{\hat{x}}=0,~(U^{n}_{0})_{\tilde{x}\bar{x}}=(U^{n}_{J})_{\tilde{x}\bar{x}}=0,~1\le n\le N. \end{aligned}$$

(2.5)

Letting $e^{n}_{j}=u^{n}_{j}-U^{n}_{j}$, we obtain the following error equation:

$$\begin{aligned} r^{n}_{j}=(e^{n}_{j})_{\hat{t}}+\frac{h^{2}}{3}(e^{n}_{j})_{\tilde{x}\bar{x}\hat{t}}+\beta (\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}+\frac{\alpha }{3}[(u^{n}_{j})^{2}\bar{u}^{n}_{j}-(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\hat{x}}+(\frac{\beta h^{2}}{12}-\gamma )(\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}} \end{aligned}$$

$$\begin{aligned} ~~~~~+\frac{\alpha h^{2}}{18}[(u^{n}_{j})^{2}\bar{u}^{n}_{j}-(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\tilde{x}\bar{x}\hat{x}}. \end{aligned}$$

By using the Taylor expansion, we can see that $r^{n}_{j}=O(\tau ^{2}+h^{4})$ holds as $\tau , h\rightarrow 0$. The following two-level Crank-Nicolson difference scheme is chosen to compute $U^{1}$:

$$\begin{aligned}{} & {} (U^{0}_{j})_{\tilde{t}}+\frac{h^{2}}{3}(U^{0}_{j})_{\tilde{x}\bar{x}\tilde{t}}+\beta (U^{\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\hat{x}}+\frac{\alpha }{3}[(U^{0}_{j})^{2}U^{\frac{1}{2}}_{j}]_{\hat{x}}+\frac{\alpha h^{2}}{18}[(U^{0}_{j})^{2}U^{\frac{1}{2}}_{j}]_{\tilde{x}\bar{x}\hat{x}}\\{} & {} \quad +(\frac{\beta h^{2}}{12}-\gamma )(U^{0+\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}=0, \end{aligned}$$

where

$$\begin{aligned} (U_{j}^{0})_{\tilde{t}}=\frac{1}{\tau }(U_{j}^{1}-U_{j}^{0}),~~U^{\frac{1}{2}}_{j}=\frac{1}{2}(U^{n+1}_{j}+U^{n}_{j}). \end{aligned}$$

Theorem 2.1

The difference scheme (2.3) is unconditionally stable in the linearized sense.

Proof

For wave propagation cases, the solutions are often bounded. We assume that the quantity $U^{2}$ in the non-linear term $U^{2}\bar{U}$ is locally constant (Nanta et al. 2021). Thus, for simplicity, we substitute $U^{2}\equiv M$ into the nonlinear term in Eq. (2.3) and consider the scheme (2.3) only at interior points as follows:

$$\begin{aligned} ~~~A_{0}(U^{n+1}_{j+3}-U^{n+1}_{j-3})+B_{0}(U^{n+1}_{j+2}-U^{n+1}_{j-2})+\frac{1}{6\tau }(U^{n+1}_{j+1}+U^{n+1}_{j}+U^{n+1}_{j-1})-C_{0}(U^{n+1}_{j+1}-U^{n+1}_{j-1}) \end{aligned}$$

$$\begin{aligned} =-A_{0}(U^{n-1}_{j+3}-U^{n-1}_{j-3})-B_{0}(U^{n-1}_{j+2}-U^{n-1}_{j-2})+\frac{1}{6\tau }(U^{n-1}_{j+1}+U^{n-1}_{j}+U^{n-1}_{j-1}) \end{aligned}$$

$$\begin{aligned} ~~~+C_{0}(U^{n-1}_{j+1}-U^{n-1}_{j-1}), \end{aligned}$$

(2.6)

where

$$\begin{aligned} A_{0}=\frac{1}{4h^{5}}\Big (\frac{\beta h^{2}}{12}-\gamma \Big ),~~B_{0}=\frac{\beta }{4h^{3}}+\frac{\alpha M}{72h}-4A_{0},~~C_{0}=\frac{\beta }{2h^{3}}-\frac{\alpha M}{18h}-5A_{0}. \end{aligned}$$

(2.7)

Thus, we can simply use the von Neumann analysis (Chousurin et al. 2020; Yang et al. 2021) for Eq. (2.6). To this end, we let $U^{n}_{j}=\xi ^{n}e^{ij\theta h}$, where $\xi$ is the amplification factor for $U^{n}_{j}$ and $i=\sqrt{-1}$. Thus, we obtain

$$\begin{aligned} U^{n}_{j+1}-U^{n}_{j-1}=2i\sin (\theta h)\xi ^{n}e^{ij\theta h},~~U^{n}_{j+2}-U^{n}_{j-2}=2i\sin (2\theta h)\xi ^{n}e^{ij\theta h}, \end{aligned}$$

(2.8)

$$\begin{aligned} U^{n}_{j+3}-U^{n}_{j-3}=2i\sin (3\theta h)\xi ^{n}e^{ij\theta h},~~U^{n}_{j+1}+U^{n}_{j}+U^{n}_{j-1}=[1+2\cos (\theta h)]\xi ^{n}e^{ij\theta h}. \end{aligned}$$

(2.9)

Substituting Eqs. (2.7)–(2.9) into Eq. (2.6), we obtain the following amplification factor $\xi ^{2}=(A-\tau iB)/(A+\tau iB)$, where

$$\begin{aligned} A=1+2\cos (\theta h),~~B=12[A_{0}\sin (3\theta h)+B_{0}\sin (2\theta h)-C_{0}\sin (\theta h)]. \end{aligned}$$

Thus, we see that $|\xi |=1$. Therefore, the difference scheme (2.3) is unconditionally stable in the linearized sense. $\square$

Theorem 2.2

The solution $U^{n}$ of the difference scheme (2.3) satisfies the following discrete conservation: $Q^{n}=Q^{n-1}=\cdot \cdot \cdot =Q^{0}$, where

$$\begin{aligned} Q^{n}=\frac{h}{2}\sum _{j=1}^{J-1}(U_{j}^{n+1}+U_{j}^{n}). \end{aligned}$$

(2.10)

Proof

Multiplying Eq. (2.3) by h, summing up for j from 1 to $J-1$, and considering the discrete boundary conditions (2.5), we obtain

$$\begin{aligned} \frac{h}{2\tau }\sum _{j=1}^{J-1}(U_{j}^{n+1}-U_{j}^{n-1})=0. \end{aligned}$$

Thus, this gives

$$\begin{aligned} Q^{n}=\frac{h}{2}\sum _{j=1}^{J-1}(U_{j}^{n+1}+U_{j}^{n})=\frac{h}{2}\sum _{j=1}^{J-1}(U_{j}^{n-1}+U_{j}^{n})=Q^{n-1}=\cdot \cdot \cdot =Q^{0}. \end{aligned}$$

Hence, we complete the proof. $\square$

Since the present scheme (2.3) is a linearized difference scheme for solving the well-posed modified Kawahara equation, the stability of the scheme is equivalent to the convergence of the scheme by the Lax equivalence theorem (Morton and Mayers 1994; Wang et al. 2021). Thus, we obtain the following theorem.

Theorem 2.3

The solution of the numerical scheme (2.3)–(2.5) converges to the solution of the initial-boundary-value problem (1.1)–(1.3), and the rate of convergence is $O(\tau ^{2}+h^{4})$.

3 Standard fourth-order difference scheme

In this section, we present a standard fourth-order finite difference scheme (Scheme II) for the problem (1.1)–(1.3).

Lemma 3.1

(Chousurin et al. 2020; Bayarassou et al. 2019) For any smooth function u, we have

$$\begin{aligned} (\partial _{x}u)^{n}_{j}=\frac{4}{3}(U^{n}_{j})_{\hat{x}}-\frac{1}{3}(U^{n}_{j})_{\ddot{x}}+O(h^{4}), \end{aligned}$$

$$\begin{aligned} (\partial ^{3}_{x}u)^{n}_{j}\approx \frac{3}{2}(U^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}-\frac{1}{2}(U^{n}_{j})_{\tilde{x}\bar{x}\ddot{x}}+O(h^{4}),~~(\partial ^{5}_{x}u)^{n}_{j}\approx \frac{5}{3}(U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{2}{3}(U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}}+O(h^{4}). \end{aligned}$$

To develop a linear conservative difference scheme, the nonlinear term $u^{2}u_{x}$ is re-written as follows (Ghiloufi and Omrani 2018; He 2016):

$$\begin{aligned} u^{2}u_{x}=\frac{1}{4}[u^{2}u_{x}+(u^{3})_{x}]. \end{aligned}$$

Then, Eq. (1.1) can be changed as

$$\begin{aligned} u_{t}+\frac{\alpha }{4}[u^{2}u_{x}+(u^{3})_{x}]+\beta u_{xxx}-\gamma u_{xxxxx}=0. \end{aligned}$$

The nonlinear term $u^{2}u_{x}+(u^{3})_{x}$ is approximated as

$$\begin{aligned}{}[u^{2}u_{x}+(u^{3})_{x}]^{n}_{j}=\frac{4}{3}\Big \{(U^{n}_{j})^{2}(\bar{U}^{n}_{j})_{\hat{x}}+[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\hat{x}}\Big \}-\frac{1}{3}\Big \{(U^{n}_{j})^{2}(\bar{U}^{n}_{j})_{\ddot{x}}+[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\ddot{x}}\Big \}, \end{aligned}$$

where the accuracy is $O(\tau ^{2}+h^{4})$. The other terms are discretizated as follows:

$$\begin{aligned} (u_{xxx})^{n}_{j}=\frac{3}{2}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}-\frac{1}{2}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\ddot{x}}+O(\tau ^{2}+h^{4}), \end{aligned}$$

$$\begin{aligned} (u_{xxxxx})^{n}_{j}=\frac{5}{3}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{2}{3}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}}+O(\tau ^{2}+h^{4}). \end{aligned}$$

Thus, we propose a standard fourth-order finite difference scheme (Scheme II) for the modified Kawahara equation (1.1) as follows:

$$\begin{aligned} ~~~(U^{n}_{j})_{\hat{t}}+\frac{4\alpha }{3}\Phi _{1}(U^{n}_{j},\bar{U}^{n}_{j})-\frac{\alpha }{3}\Phi _{2}(U^{n}_{j},\bar{U}^{n}_{j}) +\beta \Big [\frac{3}{2}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}-\frac{1}{2}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\ddot{x}}\Big ] \end{aligned}$$

$$\begin{aligned} -\gamma \Big [\frac{5}{3}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{2}{3}(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}}\Big ]=0, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \Phi _{1}(U^{n}_{j},\bar{U}^{n}_{j})=\frac{1}{4}\Big \{(U^{n}_{j})^{2}(\bar{U}^{n}_{j})_{\hat{x}}+[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\hat{x}}\Big \},~~~\Phi _{2}(U^{n}_{j},\bar{U}^{n}_{j})=\frac{1}{4}\Big \{(U^{n}_{j})^{2}(\bar{U}^{n}_{j})_{\ddot{x}}+[(U^{n}_{j})^{2}\bar{U}^{n}_{j}]_{\ddot{x}}\Big \}. \end{aligned}$$

The initial and boundary conditions are discretized as similar to Eqs. (2.4) and (2.5), respectively. The truncation error of the difference scheme (3.1) is

$$\begin{aligned} r^{n}_{j}=(e^{n}_{j})_{\hat{t}}+\beta \Big [\frac{3}{2}(\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\hat{x}}-\frac{1}{2}(\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\ddot{x}}\Big ]-\gamma \Big [\frac{5}{3}(\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{2}{3}(\bar{e}^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}}\Big ] \end{aligned}$$

$$\begin{aligned} ~~~~~~~~~~~~~~~~~~~~~~+\Big [\frac{4\alpha }{3}\Phi _{1}(u^{n}_{j},\bar{u}^{n}_{j})-\frac{\alpha }{3}\Phi _{2}(u^{n}_{j},\bar{u}^{n}_{j})\Big ]-\Big [\frac{4\alpha }{3}\Phi _{1}(U^{n}_{j},\bar{U}^{n}_{j})-\frac{\alpha }{3}\Phi _{2}(U^{n}_{j},\bar{U}^{n}_{j})\Big ]. \end{aligned}$$

By using the Taylor expansion, we can see that $r^{n}_{j}=O(\tau ^{2}+h^{4})$ holds as $\tau , h\rightarrow 0$. We choose the following two-level Crank-Nicolson difference scheme for $U^{1}$

$$\begin{aligned}{} & {} (U^{0}_{j})_{\tilde{t}}+\frac{4\alpha }{3}\psi _{1}(U^{0}_{j},U^{\frac{1}{2}}_{j})-\frac{\alpha }{3}\psi _{2}(U^{0}_{j},U^{\frac{1}{2}}_{j}) +\beta \Big [\frac{3}{2}(U^{\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\hat{x}} -\frac{1}{2}(U^{\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\ddot{x}}\Big ]\\{} & {} \quad -\gamma \Big [\frac{5}{3}(U^{\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}}-\frac{2}{3}(U^{\frac{1}{2}}_{j})_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}}\Big ]=0, \end{aligned}$$

where

$$\begin{aligned} \psi _{1}(U^{0}_{j},U^{\frac{1}{2}}_{j})=\frac{1}{4}\Big \{(U^{0}_{j})^{2}(U^{\frac{1}{2}}_{j})_{\hat{x}}+[(U^{0}_{j})^{2}U^{\frac{1}{2}}_{j}]_{\hat{x}}\Big \},~\psi _{2}(U^{0}_{j},U^{\frac{1}{2}}_{j})=\frac{1}{4}\Big \{(U^{0}_{j})^{2}(U^{\frac{1}{2}}_{j})_{\ddot{x}}+[(U^{0}_{j})^{2}U^{\frac{1}{2}}_{j}]_{\ddot{x}}\Big \}. \end{aligned}$$

Theorem 3.2

The difference scheme (3.1) is unconditionally stable in the linearized sense.

Proof

Similar to Theorem 2.1, we substitute $U^{2}\equiv M$ into the nonlinear term in Eq. (3.1) and consider the scheme (3.1) only at interior points as follows:

$$\begin{aligned} ~~~A_{0}(U^{n+1}_{j+4}-U^{n+1}_{j-4})-B_{0}(U^{n+1}_{j+3}-U^{n+1}_{j-3})-C_{0}(U^{n+1}_{j+2}-U^{n+1}_{j-2})+D_{0}(U^{n+1}_{j+1}-U^{n+1}_{j-1})+\frac{1}{\tau }U^{n+1}_{j} \end{aligned}$$

$$\begin{aligned} =-A_{0}(U^{n-1}_{j+4}-U^{n-1}_{j-4})+B_{0}(U^{n-1}_{j+3}-U^{n-1}_{j-3})+C_{0}(U^{n-1}_{j+2}-U^{n-1}_{j-2}) \end{aligned}$$

$$\begin{aligned} ~~~-D_{0}(U^{n-1}_{j+1}-U^{n-1}_{j-1})+\frac{1}{\tau }U^{n-1}_{j}, \end{aligned}$$

(3.2)

where

$$\begin{aligned} A_{0}=\frac{\gamma }{6h^{5}},~~B_{0}=\frac{\beta }{16h^{3}}+\frac{3\gamma }{2h^{5}},~~C_{0}=\frac{\alpha M}{48h}-\frac{\beta }{2h^{3}}-\frac{13\gamma }{3h^{5}},~~D_{0}=\frac{\alpha M}{6h}-\frac{13\beta }{16h^{3}}-\frac{29\gamma }{6h^{5}}. \end{aligned}$$

The amplification factor for Eq. (3.2) is $\xi ^{2}=(A-\tau iB)/(A+\tau iB)$, where

$$\begin{aligned} A=1,~~B=2[A_{0}\sin (4\theta h)-B_{0}\sin (3\theta h)-C_{0}\sin (2\theta h)+D_{0}\sin (\theta h)], \end{aligned}$$

implying that $|\xi |=1$, therefore, the difference scheme (3.1) is unconditionally stable. $\square$

Lemma 3.3

(Chousurin et al. 2020; He 2016) For any two mesh functions $U, V\in Z_{h}^{0}$, we have

$$\begin{aligned} \langle U_{\tilde{x}},V\rangle =-\langle U,V_{\bar{x}}\rangle ,~~\langle U_{\hat{x}},V\rangle =-\langle U,V_{\hat{x}}\rangle ,~~\langle U_{\ddot{x}},V\rangle =-\langle U,V_{\ddot{x}}\rangle , \end{aligned}$$

$$\begin{aligned} \langle U_{\tilde{x}\bar{x}\hat{x}},U\rangle =0,~~\langle U_{\tilde{x}\bar{x}\ddot{x}},U\rangle =0,~~\langle U_{\tilde{x}\bar{x}\tilde{x}\bar{x}\hat{x}},U\rangle =0,~~\langle U_{\tilde{x}\bar{x}\tilde{x}\bar{x}\ddot{x}},U\rangle =0. \end{aligned}$$

Lemma 3.4

For any mesh function $U^{n}\in Z_{h}^{0}$, we have

$$\begin{aligned} \langle \Phi _{1}(U^{n},\bar{U}^{n}),\bar{U}^{n}\rangle =0,~~\langle \Phi _{2}(U^{n},\bar{U}^{n}),\bar{U}^{n}\rangle =0,. \end{aligned}$$

Proof

For any mesh function $U^{n}\in Z_{h}^{0}$, according to Lemma 3.3, we obtain

$$\begin{aligned} \langle \Phi _{1}(U^{n},\bar{U}^{n}),\bar{U}^{n}\rangle =\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n}_{\hat{x}}+[(U^{n})^{2}{\bar{U}}^{n}]_{\hat{x}},{\bar{U}}^{n}\rangle =\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n},{\bar{U}}^{n}_{\hat{x}}\rangle -\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n},{\bar{U}}^{n}_{\hat{x}}\rangle =0. \end{aligned}$$

Similarly, we get

$$\begin{aligned} \langle \Phi _{2}(U^{n},\bar{U}^{n}),\bar{U}^{n}\rangle =\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n}_{\ddot{x}}+[(U^{n})^{2}{\bar{U}}^{n}]_{\ddot{x}},{\bar{U}}^{n}\rangle =\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n},{\bar{U}}^{n}_{\ddot{x}}\rangle -\frac{1}{4}\langle (U^{n})^{2}{\bar{U}}^{n},{\bar{U}}^{n}_{\ddot{x}}\rangle =0. \end{aligned}$$

$\square$

Theorem 3.5

The solution $U^{n}$ of the difference scheme (3.1) satisfies the following discrete conservation:

$$\begin{aligned} E^{n}\equiv \frac{1}{2}(\Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2})=E^{n-1}=\cdot \cdot \cdot =E^{0},~~0\le n\le N-1. \end{aligned}$$

(3.3)

Proof

Taking the inner product of Eq. (3.1) with 2${\bar{U}}^{n}$, and applying Lemmas 3.3 and 3.4, we obtain $\Vert U^n\Vert ^2_{\hat{t}}=0$, that is $\Vert U^{n+1}\Vert ^2=\Vert U^{n-1}\Vert ^2$, which yields

$$\begin{aligned} \frac{1}{2}(\Vert U^{n+1}\Vert ^2+\Vert U^{n}\Vert ^2)=\frac{1}{2}(\Vert U^{n}\Vert ^2+\Vert U^{n-1}\Vert ^2), \end{aligned}$$

this shows $E^n=E^{n-1}=\cdot \cdot \cdot =E^{0}$. $\square$

Similar to Theorem 2.3, we have the following theorem for Scheme II.

Theorem 3.6

The solution of the numerical scheme (3.1) with the discrete conditions (2.9)–(2.10) converges to the solution of the initial-boundary-value problem (1.1)–(1.3), and the rate of convergence is $O(\tau ^{2}+h^{4})$.

4 Numerical experiments

In this section, we compute some numerical experiments to validate our theoretical analysis in the previous sections. The accuracy of the numerical solutions is defined as (Cheng and Wang 2021)

$$\begin{aligned} \Vert e^{n}\Vert =\Big [h\sum ^{J-1}_{j=1}|u_{j}^{n}-U_{j}^{n}|^{2}\Big ]^{\frac{1}{2}},~~\Vert e^{n}\Vert _{\infty }=\max _{1\le j\le J-1}|u_{j}^{n}-U_{j}^{n}|. \end{aligned}$$

Example 1

Consider the following modified Kawahara equation (Ak and Karakoc 2018)

$$\begin{aligned} u_{t}+u^{2}u_{x}+u_{xxx}-u_{xxxxx}=0, \end{aligned}$$

(4.1)

with the initial condition

$$\begin{aligned} u_{0}(x)=\frac{3}{\sqrt{10}}{{\,\textrm{sech}\,}}^{2}\Big (\frac{\sqrt{5}}{10}x\Big ). \end{aligned}$$

The exact solitary wave solution for Eq. (4.1) has the following form

$$\begin{aligned} u(x,t)=\frac{3}{\sqrt{10}}{{\,\textrm{sech}\,}}^{2}\Big [\frac{\sqrt{5}}{10}\Big (x-\frac{4}{25}t\Big )\Big ]. \end{aligned}$$

Table 1 Comparison of errors and rate of convergence at $T=1$ using $\tau =h^{2}$, $x_{l}=-50$ and $x_{r}=50$ for Example 1

Table 2 Comparison of error estimates in $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms for Example 1

Table 3 Discrete conservative mass and energy computed by Scheme I and Scheme for Example 1

In this experiment, we choose $x_{l}=-50$ and $x_{r}=50$. First, to investigate the accuracy of the proposed difference schemes, we take $\tau =h^{2}$ and compute the $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norm errors of the numerical solutions. From Table 1, we can see that Scheme I and Scheme II are about fourth-order of accuracy. Furthermore, we observe from Table 1 that the errors obtained from Scheme I are a little smaller than that obtained from Scheme II. Table 2 gives the comparison of error results in $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms at different times for the proposed schemes and the septic B-spline collocation method (Ak and Karakoc 2018). From Table 2, we can see that our difference schemes have relatively small errors than those obtained by the method (Ak and Karakoc 2018).

To show that Scheme I (2.3) and Scheme II (3.1) have the mass and energy conservative properties, respectively, we then list some values of discrete mass $Q^{n}$ for Scheme I and discrete energy $E^{n}$ for Scheme II at various times T in Table 3. From Table 3, we can see that Scheme I and Scheme II preserve the discrete conservative properties very well.

Fig. 1

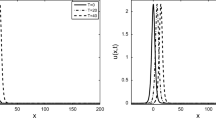
Comparison of the numerical solutions and single solitary wave solution of Example 1 computed by Scheme I (left) and Scheme II (right) with $h=0.1$ and $\tau =h^{2}$

In Fig. 1, we show the comparison of the numerical solutions and single solitary wave solution with $h=0.1$ and $\tau =h^{2}$. In Fig. 2, we draw the absolute error distributions obtained from Scheme I and Scheme II, respectively. From Figs. 1 and 2, we can see that these numerical approximations obtained by Scheme I and Scheme II are in good agreement with the single solitary wave solutions. Fig. 3 shows the plot of single solitary waves at different time levels $T=10$, 20, 30 and 40 with $h=0.5$ and $\tau =h^{2}$. From Fig. 3, we can see that the numerical solutions obtained from Scheme I and Scheme II can keep the same shape as time increases. Thus, we can say that our difference schemes are effective for studying the solitary wave traveling for a long time.

Fig. 2

Absolute error distribution of Example 1 computed by Scheme I (left) and Scheme II (right) with $h=0.1$ and $\tau =h^{2}$

Fig. 3

Single solitary wave computed by Scheme I (left) and Scheme II (right) at different time levels with $h=0.5$ and $\tau =h^{2}$

Fig. 4

Comparison of numerical solutions obtained by Scheme I with various values of the coefficients $\alpha$, $\beta$ and $\gamma$

Fig. 5

Comparison of numerical solutions obtained by Scheme II with various values of the coefficients $\alpha$, $\beta$ and $\gamma$

At last, to investigate the influence of the coefficients $\alpha$, $\beta$ and $\gamma$ on the numerical results, we plot the numerical solutions obtained from Scheme I and Scheme II with various values of the coefficients in Figs. 4 and 5, respectively, where $x_{l}=-50$, $x_{r}=50$, $h=0.1$, $\tau =0.01$ and $T=10$. We see from Figs. 4 and 5 that different values of the coefficients $\alpha$, $\beta$ and $\gamma$ of Scheme I and Scheme II can change the numerical results conspicuously.

Example 2

We consider the interaction of two separated solitary waves with different amplitudes and traveling in the same direction. In this case, we consider Eq. (4.1) with the initial condition as follows

$$\begin{aligned} u(x,0)=\sum _{i=1}^{2}\sqrt{\frac{9c_{i}}{10}}{{\,\textrm{sech}\,}}^{2}\Big [\sqrt{\frac{c_{i}}{20}}(x-\chi _{i})\Big ],~~i=1,2. \end{aligned}$$

Fig. 6

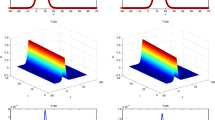
Interaction of two solitary waves for Scheme I (left) and Scheme II (right) of Example 2 at different times

First, we choose the domain $\Omega =[-50,100]$ and show the interaction of two separated at different time levels in Fig. 6, where $h=0.1$, $\tau =0.05$, $c_{1}=0.85$, $c_{2}=0.35$, $\chi _{1}=0$ and $\chi _{2}=20$. We can see that the larger solitary wave has passed the smaller solitary wave as time increases up to $T=95$. After the interaction, the two separated solitary waves regain their original shape again. The calculated values of the conservative invariants $Q^{n}$ and $E^{n}$ obtained by Scheme I and Scheme II are tabulated in Table 4. It is seen that the values of the invariants $Q^{n}$ and $E^{n}$ remain almost constant during the computer run.

Example 3

We consider the interaction of three separated solitary waves with different amplitudes and traveling in the same direction. In this case, we consider Eq. (4.1) with the following initial condition

$$\begin{aligned} u(x,0)=\sum _{i=1}^{3}\sqrt{\frac{45c_{i}}{8}}{{\,\textrm{sech}\,}}^{2}\Big [\sqrt{\frac{5c_{i}}{16}}(x-\chi _{i})\Big ],~~i=1,2,3. \end{aligned}$$

Here, we choose the parameters $x_{l}=-50$, $x_{r}=100$, $h=0.1$, $\tau =0.05$, $c_{1}=0.85$, $c_{2}=0.5$, $c_{3}=0.35$, $\chi _{1}=-25$, $\chi _{2}=0$, $\chi _{2}=20$. Fig. 7 shows the interaction of three separated solitary waves at different time levels $T=30\sim 150$. As it is seen from Fig. 7, the interaction started about at time $T=80$ and the overlapping processes occurred between $T=80$ and 100. Then, to verify the solutions of Scheme I and Scheme II are stable for the initial value, we solve Eq. (4.1) with the following initial condition

$$\begin{aligned} u(x,0)=\sum _{i=1}^{3}\sqrt{\frac{45c_{i}}{8}}{{\,\textrm{sech}\,}}^{2}\Big [\sqrt{\frac{5c_{i}}{16}}(x-\chi _{i})\Big ]+\epsilon ,~~i=1,2,3. \end{aligned}$$

Table 4 Discrete conservative mass and energy computed by Scheme I and Scheme II for Example 2

Fig. 7

Numerical solutions of Example 3 computed by Scheme II at different times

Fig. 8

Effects of the initial conditions to the solutions of Scheme I (left) and Scheme II (right) at $T=1$ with $x_{l}=-50$, $x_{r}=100$, $h=0.1$ and $\tau =0.01$

Here, $\epsilon$ is chosen as 0, $\pm 0.001$, $\pm 0.002$ and $\pm 0.003$, respectively. We can see from Fig. 8 that no significant difference exists with a slight change in the initial condition $u_{0}$, which confirms that both Scheme I and Scheme II are stable with respect to the initial condition $u_{0}$ and convergent to stationary solutions.

Example 4

We consider Eq. (4.1) with the Maxwellian initial condition (Ghiloufi and Omrani 2018)

$$\begin{aligned} u(x,0)=\exp [-(x-40)^2]. \end{aligned}$$

Table 5 Comparison of the invariants $Q^{n}$ and $E^{n}$ obtained by different methods

In this case, we calculate the solution at the region $[-100,100]$ with $h=0.25$ and $\tau =0.25$. Table 5 contains the comparison of the discrete mass $Q^{n}$ and energy $E^{n}$ obtained by our schemes and those obtained by the septic B-spline collocation method (Ak and Karakoc 2018). We can see that the values of the invariants $Q^{n}$ and $E^{n}$ obtained by our schemes are relatively more stable than the values obtained in Ak and Karakoc (2018).

Example 5

We consider Eq. (4.1) with the following initial condition

$$\begin{aligned} u(x,0)=\alpha e^{-|x-c_{1}|}+\beta {{\,\textrm{sign}\,}}(x)e^{-|x|}-\gamma e^{-|x-c_{2}|}. \end{aligned}$$

Fig. 9

Space-time graph of the interaction in the domain $[-100,100]$ at various times with $h=0.1$, $\tau =0.05$

Fig. 10

Initial condition and numerical simulation for the interaction at various times with $h=0.1$, $\tau =0.05$ in the domain $[-100,100]$

In this example, we choose $c_{1}=-5$, $c_{2}=5$ and represent the numerical results at various times with $h=0.1$, $\tau =0.05$, in the domain $[-100,100]$ in Figs. 9 and 10. As shown in the figures, we can observe the interaction of the Kawahara equation.

5 Conclusion

We have developed two conservative finite difference schemes with fourth-order accuracy for the modified Kawahara equation. The compact fourth-order difference scheme (Scheme I) and standard fourth-order difference scheme (Scheme II) are both unconditionally convergent and the convergence order is $O(\tau ^{2}+h^{4})$. To demonstrate the efficiency of the numerical schemes, the convergence errors and conserved quantities $Q^{n}$ and $E^{n}$ have been calculated for the test problems. Numerical experiments verify that the proposed difference schemes simulate the conservative quantities ($Q^{n}$ and $E^{n}$) well in single soliton and colliding soliton evolutions. It is also shown that the compact difference scheme (Scheme I) is more efficient than the non-compact numerical scheme (Scheme II). With suitable variations, the technique of analysis used in this article can be applied to study the single or multi-solitary waves propagating over a long period. Further work can be done by performing numerical approximations of other models in traffic flow modeling with the proposed schemes.