Linear High-Order Energy-Preserving Schemes for the Nonlinear Schrödinger Equation with Wave Operator Using the Scalar Auxiliary Variable Approach

Abstract

In this paper, we develop two classes of linear high-order conservative numerical schemes for the nonlinear Schrödinger equation with wave operator. Based on the method of order reduction in time and the scalar auxiliary variable technique, we transform the original model into an equivalent system, where the energy is modified as a quadratic form. To construct linear high-order conservative schemes, we first adopt the extrapolation strategy to derive a linearized PDE system, which approximates the transformed model with high precision and inherits the modified energy conservation law. Then we employ the symplectic Runge–Kutta method in time to arrive at a class of linear high-order energy-preserving schemes. This numerical strategy presents a paradigm for developing arbitrarily high-order linear structure-preserving algorithms which could be implemented simply. In order to complement the new linear schemes, the prediction-correction method is presented to obtain another class of energy-preserving algorithms. Furthermore, the trigonometric pseudo-spectral method is applied for the spatial discretization to match the order of accuracy in time. We provide ample numerical results to confirm the convergence, accuracy and conservation property of the proposed schemes.

1 Introduction

In this paper, we are concerned with the following nonlinear Schrödinger equation with wave operator (NLSW) in a bounded domain as

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{tt}u(\mathbf {x},t)-\nabla ^{2} u(\mathbf {x},t)+\text {i}\alpha \partial _{t}u(\mathbf {x},t)+\beta |u|^{2}u(\mathbf {x},t)=0\quad \text {for }\mathbf {x}\in \Omega \text { and } 0<t\le T,\\&u(\mathbf {x},0)=u_{0}(\mathbf {x}),\quad \partial _{t}u(\mathbf {x},0)=u_{1}(\mathbf {x})\quad \text {for } \mathbf {x}\in \Omega , \end{aligned} \right. \end{aligned}$$

(1.1)

where $u(\mathbf {x},t)$ is a complex function, $\alpha , \beta$ are real constants and $\text {i}=\sqrt{-1}$. $\nabla ^{2}=\Delta$ is the d-dimensional Laplace operator. $\Omega \in \mathbb {R}^{d}$ is a bounded interval ($d=1$), rectangle ($d=2$) or cube ($d=3$). The NLSW is widely used in many physical fields, such as the nonrelativistic limit of the Klein-Gordon equation [1,2,3], the Langmuir wave envelope approximation in plasma [4, 5] and the modulated planar pulse approximation of the sine-Gordon equation for light bullets [6, 7].

An intrinsic property of this equation is energy conservation. Computing the inner product of Eq. (1.1) with $\partial _{t}u(\mathbf {x},t)$ and then taking the real part, we can derive the energy conservation law

$$\begin{aligned} \frac{\,\mathrm {d}\mathcal {E}}{\,\mathrm {d}t} = 0 \quad \text {with} \quad \mathcal {E}[u]:=\int _{\Omega }\big (|\nabla u(\mathbf {x},t)|^{2} +|\partial _{t}u(\mathbf {x},t)|^{2}+\frac{\beta }{2}|u(\mathbf {x},t)|^{4}\big ) \,\mathrm {d}\mathbf {x}. \end{aligned}$$

(1.2)

It is well known that the energy conservation property plays an important role in Hamiltonian partial differential equations (PDEs). Therefore, a great deal of numerical studies on the energy-preserving discretization of this equation have been developed in the literatures. Bao and Cai [8] applied the finite difference method and presented two second-order conservative schemes for solving the NLSW numerically. The authors in [9] developed a conservative compact difference scheme for this equation and improved the spatial accuracy to fourth-order. Guo and Xu [10] utilized a fully-discrete energy-preserving scheme by discretizing the space with the local discontinuous Galerkin method and the time with the Crank-Nicolson scheme to simulate the NLSW. Wang et al. [11] addressed this issue with the help of the orthogonal spline collocation method and the proposed scheme inherited the energy conservation property well. Although the schemes mentioned above are effective, most of them have only second-order accuracy in time and there are few references considering high-order energy-preserving schemes for the NLSW.

Over the past decade, numerous high-order energy-preserving methods have been developed, such as average vector field method [12, 13], Hamiltonian boundary value methods [14], continuous stage Runge–Kutta (RK) method [15, 16], time finite element method [17] etc. These existing methods always require the computation of integrals. More recently, two energy quadratization strategies, the invariant energy quadratization (IEQ) [18, 19] and the scalar auxiliary variable (SAV) [20,21,22], are proposed and widely used in gradient flow models. The essential idea of both approaches is to transform the energy into a quadratic form by adopting a new variable and the advantage of such a reformulation is that all nonlinear terms could be treated semi-explicitly, which in turn leads to a linear system. The later approach can be seen as a modification of the former one and overcomes some of its shortcomings. Most importantly, the SAV systems are calculated just by solving the linear equations with constant coefficients in each time level, which is extremely efficient and easy to implement. As we know, all RK methods preserve arbitrary linear invariants [23], and the symplectic RK methods preserve arbitrary quadratic invariants [24]. Based on the idea of energy quadratization, the authors employ a special kind of diagonally implicit RK methods [25,26,27] and a special class of RK methods [28,29,30,31] to develop high-order energy-preserving or energy stable numerical schemes. By comparison, one can find that the latter methods can reach desired high order with the optimal RK stages, which needs fewer internal stage nodes than the former ones. Unfortunately, these schemes are nonlinear which requires nonlinear iteration in each time step. Linear high-order unconditionally energy stable schemes are recently presented and analyzed for gradient flow models [32, 33] to improve the computational efficiency. More recently, we have successfully extended their approaches to develop linear high-order mass-conserving schemes for the generalized nonlinear Schrödinger equation [34]. However, to the best of our knowledge, there has been no reference considering linear high-order energy-preserving algorithms for conservative systems.

In this paper, we will address the NLSW issue and strive to develop two classes of linear high-order energy-preserving schemes for it. More precisely, with the help of the method of order reduction and the SAV approach, we reformulate the original problem (1.1) by transforming the energy functional into a quadratic form, which leads to an new equivalent system with a modified energy conservation law. Based on the extrapolation technique, we derive a high-precision linearized conservative model to approximate the reformulated system by using the given numerical solutions up to $t_{n}=n\tau$, where $\tau$ is the time step. Subsequently, the linearized model is discretized in $(t_{n},t_{n+1}]$ by employing a special kind of RK methods, namely, Gauss collocation method in time and the trigonometric pseudo-spectral method in space to produce a family of linear high-order conservative schemes. Moreover, the prediction-correction (PC) strategy is utilized to develop another kind of linear PC schemes to complement the former ones. The resulting fully discrete schemes enjoy the following two advantages.

• (i) These schemes are all linear such that they could be easy to implement and computed efficiently with the help of fast Fourier or Sine transform.

• (ii) These schemes are energy-preserving and can reach arbitrarily high-order of accuracy spatial-temporally such that relatively large meshes can guarantee the desired accuracy of numerical solutions.

The rest of this paper is organized as follows. We present an equivalent model reformulation of the NLSW with energy conservation property in Sect. 2. In the next section, the symplectic RK method is briefly introduced and two classes of semi-discrete arbitrarily high-order linear energy-preserving schemes are developed. For the spatial discretization, we apply the high-order trigonometric pseudo-spectral method in Sect. 4 to arrive at fully discrete schemes, which are still energy-preserving. Numerical tests of convergence, accuracy and energy conservation law are given in Sect. 5, followed by some concluding remarks in Sect. 6.

2 Model Reformulation Using the SAV Approach

In this section, the NLSW is reformulated into an equivalent form by adopting the method of order reduction and energy quadratization technique. Specifically, we introduce auxiliary variables and use the SAV approach to transform the energy functional into a quadratic form. This strategy not only inherits the modified energy conservation law, but also provides an elegant platform for the next development of arbitrarily high-order numerical schemes.

Firstly, we introduce an intermediate variable $v=\partial _{t} u$ and utilize the method of order reduction in time, Eq. (1.1) leads to

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}u(\mathbf {x},t)=v(\mathbf {x},t),\\&\partial _{t}v(\mathbf {x},t)=\Delta u(\mathbf {x},t)-\text {i}\alpha v(\mathbf {x},t)-\beta |u|^{2}u(\mathbf {x},t), \end{aligned} \right. \end{aligned}$$

(2.1)

and the nonlinear energy functional (1.2) reads

$$\begin{aligned} \mathcal {E}[u,v]=\int _{\Omega }\big (|\nabla u(\mathbf {x},t)|^{2}+|v(\mathbf {x},t)|^{2}+\frac{\beta }{2}|u(\mathbf {x},t)|^{4}\big ) \,\mathrm {d}\mathbf {x}. \end{aligned}$$

(2.2)

Invoking to the definition of complex variational derivative in [35], it is readily to derive that

$$\begin{aligned} \frac{\delta \mathcal {E}}{\delta u}=\frac{\partial \mathcal {E}}{\partial u}-\nabla \cdot \big (\frac{\partial \mathcal {E}}{\partial \nabla u}\big )=-\Delta \overline{u}+\beta |\overline{u}|^{2}\overline{u}\quad \text {and}\quad \frac{\delta \mathcal {E}}{\delta \overline{u}}=\frac{\partial \mathcal {E}}{\partial \overline{u}}-\nabla \cdot \big (\frac{\partial \mathcal {E}}{\partial \nabla \overline{u}}\big )=-\Delta u+\beta |u|^{2}u, \end{aligned}$$

where $\frac{\delta \mathcal {E}}{\delta u}$ and $\frac{\delta \mathcal {E}}{\delta \overline{u}}$ denote the variational derivative of $\mathcal {E}$ with respect to u and $\overline{u}$ ($\overline{u}$ is the complex conjugate of u), respectively. Similarly, one has $\frac{\delta \mathcal {E}}{\delta v}=\overline{v}$ and $\frac{\delta \mathcal {E}}{\delta \overline{v}}=v$. Let ${\varvec{\Phi }}=(u,v)^{T}$, Eq. (2.1) can be rewritten mathematically as a compact form

$$\begin{aligned} \frac{\partial {\varvec{\Phi }}}{\partial t}=\mathcal {D}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}, \end{aligned}$$

where $\mathcal {D}=\left( \begin{array}{cc} 0 &{} 1 \\ -1 &{} -\text {i}\alpha \\ \end{array} \right)$ is a skew-adjoint matrix. From the calculation of complex variational derivative, we obtain the energy conservation law

$$\begin{aligned} \frac{\,\mathrm {d}\mathcal {E}}{\,\mathrm {d}t}&=\big (\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}, \frac{\partial {\varvec{\Phi }}}{\partial t}\big )+\big (\frac{\delta \mathcal {E}}{\delta {\varvec{\Phi }}}, \frac{\partial \overline{{\varvec{\Phi }}}}{\partial t}\big )=\big (\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}, \mathcal {D}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}\big )+\big (\frac{\delta \mathcal {E}}{\delta {\varvec{\Phi }}}, \overline{\mathcal {D}}\frac{\delta \mathcal {E}}{\delta {\varvec{\Phi }}}\big )\\&=\big (\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}, \mathcal {D}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}\big )+\big (\mathcal {D}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}},\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}\big )=\big (\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}, \mathcal {D}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}\big )+\big (\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}},\mathcal {D}^{H}\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}\big )=0, \end{aligned}$$

where the relation $\overline{\frac{\delta \mathcal {E}}{\delta {\varvec{\Phi }}}}=\frac{\delta \mathcal {E}}{\delta \overline{{\varvec{\Phi }}}}$ was used. $\overline{\mathcal {D}}$ and $\mathcal {D}^{H}$ are the complex conjugate and conjugate transpose of the matrix $\mathcal {D}$, respectively. $(u,w):=\int _{\Omega }u\cdot \overline{w}\,\mathrm {d}\mathbf{x}$ is the continuous inner product with the corresponding $L^{2}$-norm $\Vert u\Vert _{L^{2}}:=\sqrt{(u,u)}$.

Next, we apply the SAV approach to reformulate the system (2.1). Denote

$$ F(u)=\frac{1}{2}\int _{\Omega }|u(\mathbf {x},t)|^{4}\,\mathrm {d}\mathbf{x} ,$$

and assume that F(u) is bounded from below, i.e., $F(u)\ge -C_{0}$. In the SAV approach, a scalar auxiliary variable $r(t):=\sqrt{F(u)+C_{0}}$ is introduced and

$$\begin{aligned} r_{t}=\frac{1}{2\sqrt{F(u)+C_{0}}}\int _{\Omega }\big (|u|^{2}\overline{u}u_{t}+|u|^{2}u\overline{u}_{t}\big )\,\mathrm {d}\mathbf{x} =\big (\frac{|u|^{2}}{2\sqrt{F(u)+C_{0}}}, \overline{u}u_{t}+u\overline{u}_{t}\big ). \end{aligned}$$

The energy functional (2.2) is then rewritten as

$$\begin{aligned} E[u,v,r]=\int _{\Omega }\big (|\nabla u(\mathbf {x},t)|^{2}+|v(\mathbf {x},t)|^{2}\big )\,\mathrm {d}\mathbf{x} +\beta (r^{2}-C_{0}), \end{aligned}$$

which is a quadratic functional with respect to the new variables. Resorting to energy variational, Eq. (2.1) can be reformulated into the following equivalent form

$$\begin{aligned} \left\{ \begin{aligned}&u_{t}=v,\\&v_{t}=\Delta u-\text {i}\alpha v-\frac{\beta r}{\sqrt{F(u)+C_{0}}}|u|^{2}u,\\&r_{t}=\big (\frac{|u|^{2}}{2\sqrt{F(u)+C_{0}}}, \overline{u}u_{t}+u\overline{u}_{t}\big ), \end{aligned} \right. \end{aligned}$$

(2.3)

with consistent initial conditions

$$\begin{aligned} u(\mathbf {x},0)=u_{0}(\mathbf {x}),\quad v(\mathbf {x},0)=u_{1}(\mathbf {x}),\quad r(0)=\sqrt{\int _{\Omega }\frac{1}{2}|u_{0}(\mathbf {x})|^{4}\,\mathrm {d}\mathbf{x} +C_{0}}\quad \text {for }\mathbf {x}\in \Omega . \end{aligned}$$

Always, we can verify that the reformulated system (2.3) preserves a similar quadratic energy conservation law described below.

Theorem 2.1

The SAV system (2.3) satisfies the following energy conservation law

$$\begin{aligned} \frac{\,\mathrm {d}E[u,v,r]}{\,\mathrm {d}t}=0, \end{aligned}$$

where the energy functional $E[u,v,r]=\Vert \nabla u\Vert _{L^{2}}^{2}+\Vert v\Vert _{L^{2}}^{2}+\beta (r^{2}-C_{0})$.

Proof

In terms of the first and third equations in (2.3), we apply the complex variational derivative again and obtain

$$\begin{aligned} \frac{\,\mathrm {d}E}{\,\mathrm {d}t}&=\big (\frac{\delta E}{\delta u}, \overline{u}_{t}\big )+\big (\frac{\delta E}{\delta \overline{u}}, u_{t}\big )+\big (\frac{\delta E}{\delta v}, \overline{v}_{t}\big )+\big (\frac{\delta E}{\delta \overline{v}}, v_{t}\big )+\big (\frac{\delta E}{\delta r}, r_{t}\big )\\&=(-\Delta \overline{u}, \overline{u}_{t})+(-\Delta u, u_{t})+(\overline{v}, \overline{v}_{t})+(v, v_{t})+\big (\frac{\beta r}{\sqrt{F(u)+C_{0}}}|u|^{2}\overline{u}, \overline{u}_{t}\big )+\big (\frac{\beta r}{\sqrt{F(u)+C_{0}}}|u|^{2}u,u_{t}\big )\\&=\big (-\Delta \overline{u}+\overline{v}_{t}+\frac{\beta r}{\sqrt{F(u)+C_{0}}}|u|^{2}\overline{u}, \overline{v}\big )+\big (-\Delta u+v_{t}+\frac{\beta r}{\sqrt{F(u)+C_{0}}}|u|^{2}u,v\big ). \end{aligned}$$

Substituting the second relation in (2.3) into the above equality on the right-hand side, one easily derives the claimed result and completes the proof of Theorem 2.1. $\square$

3 Linear High-Order Energy-Preserving Schemes

Based on the extrapolation technique, a linear SAV system is derived for the reformulated model (2.3). Note that it still retains the energy conservation law. Then, we introduce symplectic Runge–Kutta method to discretize this linear system in time for arbitrarily high-order accuracy, and develop a class of linear semi-discrete SRK schemes, named LSAV-SRK scheme. In order to improve the accuracy and stability, we employ the prediction-correction method and present a family of linear semi-discrete SRK-PC schemes. New schemes are proved to inherit the corresponding energy conservation law.

3.1 Symplectic Runge–Kutta Method

The Runge–Kutta method discretizes an initial value problem for a general ODE model:

$$\begin{aligned} y'=f(t,y),\quad t\in (0,T],\quad y(0)=y_{0}. \end{aligned}$$

For a given approximation $y^{n}$ of the nodal value $y(t_{n})$, we utilize the general s-stage Runge–Kutta method to deduce $y^{n+1}$ as follows:

$$\begin{aligned} \left\{ \begin{aligned}&k_{i}^{n}=f(t_{n,i}, y^{n}+\tau \sum _{j=1}^{s}a_{ij}k_{j}^{n}),\ \ i=1,\dots ,s,\\&y^{n+1}=y^{n}+\tau \sum _{i=1}^{s}b_{i}k_{i}^{n}, \end{aligned} \right. \end{aligned}$$

where $b_{i}$, $c_{i}$, $a_{ij}\ (i,j=1,\dots ,s)$ are RK coefficients and satisfy $c_{i}=\sum _{j=1}^{s}a_{ij}$, $t_{n,i}:=t_{n}+c_{i}\tau$ are the internal RK stage nodes. The RK coefficients are usually displayed by a Butcher table

$$ \begin{array}{c|c} \mathbf {c} &{} \mathbf {A} \\ \hline &{} \mathbf {b}^{T} \end{array}=\begin{array}{c|ccc} c_{1} &{} a_{11} &{} \cdots &{} a_{1s} \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ c_{s} &{} a_{s1} &{} \cdots &{} a_{ss} \\ \hline &{} b_{1} &{} \cdots &{} b_{s} \end{array},$$

where $\mathbf {A}\in \mathbb {R}^{s,s}$, $\mathbf {b}\in \mathbb {R}^{s}$ and $\mathbf {c}=\mathbf {A}\mathbf {1}$ with $\mathbf {1}=(1,1,\dots ,1)^{T} \in \mathbb {R}^{s}$.

Definition 3.1

[36] If the coefficients of the RK method satisfy the following relationship

$$\begin{aligned} b_{i}a_{ij}+b_{j}a_{ji}-b_{i}b_{j}=0, \end{aligned}$$

(3.1)

then this method is symplectic.

Furthermore, if the RK coefficients $c_{1},\dots ,c_{s}$ are chosen as the Gaussian quadrature nodes, i.e., the zeros of the s-th shifted Legendre polynomial $\frac{\,\mathrm {d}^{s}}{\,\mathrm {d}x^{s}}\big (x^{s}(x-1)^{s}\big )$, it yields a special class of RK methods named Gauss collocation methods. In [37, Theroem 1.5], the authors have proved that the Gauss collocation method has the same order 2s as the Gaussian quadrature formula. In this paper, we focus on the 2-stage and 3-stage Gauss methods with the RK coefficients

$$ \begin{array}{c|cc} \frac{1}{2}-\frac{\sqrt{3}}{6} &{} \frac{1}{4} &{}\frac{1}{4}-\frac{\sqrt{3}}{6}\\ \frac{1}{2}+\frac{\sqrt{3}}{6} &{} \frac{1}{4}+\frac{\sqrt{3}}{6} &{}\frac{1}{4}\\ \hline &{} \frac{1}{2} &{}\frac{1}{2} \end{array}\quad \text {and}\quad \begin{array}{c|cccc} \frac{1}{2}-\frac{\sqrt{15}}{10} &{} \frac{5}{36} &{} \frac{2}{9}-\frac{\sqrt{15}}{15} &{} \frac{5}{36}-\frac{\sqrt{15}}{30} \\ \frac{1}{2} &{} \frac{5}{36}+\frac{\sqrt{15}}{24} &{} \frac{2}{9} &{}\frac{5}{36}-\frac{\sqrt{15}}{24} \\ \frac{1}{2}+\frac{\sqrt{15}}{10} &{} \frac{5}{36}+\frac{\sqrt{15}}{30} &{} \frac{2}{9}+\frac{\sqrt{15}}{15} &{} \frac{5}{36} \\ \hline &{} \frac{5}{18} &{} \frac{4}{9} &{} \frac{5}{18} \end{array},$$

respectively. For more details about the higher order Gauss method, we refer the readers to [37].

3.2 Linear SAV-SRK Schemes

Assume that the solutions of u up to $t_{n}$ have been given. We choose the time nodes and internal stage nodes $t_{m}$, $t_{m,i}\ (m<n)$ and $t_{n}$ as the interpolation points to construct N-th order Lagrange interpolation polynomial $u_{N}(t,x,y)$, which approximates to u(t, x, y) in time. Subsequently, the SAV system (2.3) in $(t_{n},t_{n+1}]$ is approximated by the following linearized conservative system

$$\begin{aligned} \left\{ \begin{aligned}&u_{t}=v,\\&v_{t}=\Delta u-\text {i}\alpha v-\frac{\beta r}{\sqrt{F(u_{N})+C_{0}}}|u_{N}|^{2}u_{N},\\&r_{t}=\big (\frac{|u_{N}|^{2}}{2\sqrt{F(u_{N})+C_{0}}}, u_{N}\overline{u}_{t}+\overline{u}_{N}u_{t}\big ). \end{aligned} \right. \end{aligned}$$

(3.2)

Recalling the proof of Theorem 2.1, it is readily to prove that this linearized system (3.2) also satisfies the energy conservation law, namely

$$\begin{aligned} \frac{\,\mathrm {d}E}{\,\mathrm {d}t}=\big (-\Delta \overline{u}+\overline{v}_{t}+\frac{\beta r}{\sqrt{F(u_{N})+C_{0}}}|u_{N}|^{2}\overline{u}_{N}, \overline{v}\big )+\big (-\Delta u+v_{t}+\frac{\beta r}{\sqrt{F(u_{N})+C_{0}}}|u_{N}|^{2}u_{N},v\big )=0. \end{aligned}$$

Applying the s-stage symplectic RK method mentioned above for system (3.2), one has the following semi-discrete s-stage LSAV-SRK scheme.

Scheme 1

(semi-discrete s-stage LSAV-SRK scheme). Let $b_{i}$, $a_{ij}\ (i,j=1,\dots ,s)$ and $c_{i}=\sum _{j=1}^{s}a_{ij}$ be symplectic RK coefficients and $\tau$ is the time-step. For given $U^{n},V^{n},R^{n}$ and $U_{N}(t)$, the following intermediate values are first calculated by

$$\begin{aligned} \left\{ \begin{aligned}&U_{i}^{n}=U^{n}+\tau \sum _{j=1}^{s}a_{ij}K_{j}^{n},\quad K_{i}^{n}=V_{i}^{n},\\&V_{i}^{n}=V^{n}+\tau \sum _{j=1}^{s}a_{ij}L_{j}^{n},\quad \ L_{i}^{n}=\Delta U_{i}^{n}-\mathrm {i}\alpha V_{i}^{n}-\frac{\beta R_{i}^{n}}{\sqrt{F(U_{i}^{n,*})+C_{0}}}|U_{i}^{n,*}|^{2}U_{i}^{n,*},\\&R_{i}^{n}=R^{n}+\tau \sum _{j=1}^{s}a_{ij}M_{j}^{n},\quad M_{i}^{n}= \big (\frac{|U_{i}^{n,*}|^{2}}{2\sqrt{F(U_{i}^{n,*})+C_{0}}}, U_{i}^{n,*}\cdot \overline{K}_{i}^{n}+\overline{U}_{i}^{n,*}\cdot {K}_{i}^{n}\big ), \end{aligned} \right. \end{aligned}$$

(3.3)

where $U_{i}^{n,*}=U_{N}(t_{n,i})$. Then the numerical solutions $U^{n+1}, V^{n+1}$ and $R^{n+1}$ are updated by

$$\begin{aligned} \left\{ \begin{aligned}&U^{n+1}=U^{n}+\tau \sum _{i=1}^{s}b_{i}K_{i}^{n},\\&V^{n+1}=V^{n}+\tau \sum _{i=1}^{s}b_{i}L_{i}^{n},\\&R^{n+1}=R^{n}+\tau \sum _{i=1}^{s}b_{i}M_{i}^{n}. \end{aligned} \right. \end{aligned}$$

(3.4)

The next theorem shows that the semi-discrete LSAV-SRK methods still maintain the energy conservation law.

Theorem 3.1

The semi-discrete LSAV-SRK scheme (3.3)-(3.4) preserve the energy at the discrete time level, that is,

$$\begin{aligned} E^{n+1}=E^{n}, \end{aligned}$$

where $E^{n}=\Vert \nabla U^{n}\Vert _{L^{2}}^{2}+\Vert V^{n}\Vert _{L^{2}}^{2}+\beta \big ((R^{n})^{2}-C_{0}\big )$.

Proof

From the first equation of (3.4), we obtain

$$\begin{aligned} \nabla U^{n+1}=\nabla U^{n}+\tau \sum _{i=1}^{s}b_{i}\nabla K_{i}^{n}. \end{aligned}$$

Taking the square of $L^{2}$-norm on both sides of the above equality, it is readily to check

$$\begin{aligned} \Vert \nabla U^{n+1}\Vert _{L^{2}}^{2}=\Vert \nabla U^{n}\Vert _{L^{2}}^{2}+\tau \sum _{i=1}^{s}b_{i}\Big (\big (\nabla K_{i}^{n},\nabla U^{n}\big )+\big (\nabla U^{n},\nabla K_{i}^{n}\big )\Big ) +\tau ^{2}\sum _{i,j=1}^{s}b_{i}b_{j}\big (\nabla K_{i}^{n},\nabla K_{j}^{n}\big ). \end{aligned}$$

The first relation of the first row of (3.3) yields $\nabla U^{n}=\nabla U_{i}^{n}-\tau \sum _{j=1}^{s}a_{ij}\nabla K_{j}^{n}$. Plugging it into the second term on the right-hand side of the last equality, one has

$$\begin{aligned} \Vert \nabla U^{n+1}\Vert _{L^{2}}^{2}=&\Vert \nabla U^{n}\Vert _{L^{2}}^{2}+\tau \sum _{i=1}^{s}b_{i}\Big (\big (\nabla K_{i}^{n},\nabla U_{i}^{n}\big )+\big (\nabla U_{i}^{n},\nabla K_{i}^{n}\big )\Big )-\tau ^{2}\sum _{i,j=1}^{s}\varpi _{ij}\big (\nabla K_{i}^{n},\nabla K_{j}^{n}\big ), \end{aligned}$$

where $\varpi _{ij}=b_{i}a_{ij}+b_{j}a_{ji}-b_{i}b_{j}$. The relationship of RK coefficients in Lemma 3.1 leads to

$$\begin{aligned} \Vert \nabla U^{n+1}\Vert _{L^{2}}^{2}=\Vert \nabla U^{n}\Vert _{L^{2}}^{2}+\tau \sum _{i=1}^{s}b_{i}\big (\nabla K_{i}^{n},\nabla U_{i}^{n}\big )+\tau \sum _{i=1}^{s}b_{i}\big (\nabla U_{i}^{n},\nabla K_{i}^{n}\big ). \end{aligned}$$

Similarly, the second and third equations of (3.4) imply that

$$\begin{aligned}&\Vert V^{n+1}\Vert _{L^{2}}^{2}=\Vert V^{n}\Vert _{L^{2}}^{2}+\tau \sum _{i=1}^{s}b_{i}\big (L_{i}^{n},V_{i}^{n}\big ) +\tau \sum _{i=1}^{s}b_{i}\big (V_{i}^{n},L_{i}^{n}\big ),\\&\quad (R^{n+1})^{2}=(R^{n})^{2}+2\tau \sum _{i=1}^{s}b_{i}M_{i}^{n}R_{i}^{n}. \end{aligned}$$

Multiplying the last equality by $\beta$ and adding these three results together, we apply the first and third relations of the second column of (3.3) to obtain

$$\begin{aligned} E^{n+1}=&E^{n}+\tau \sum _{i=1}^{s}b_{i}\big (V_{i}^{n},-\Delta U_{i}^{n}+L_{i}^{n}+\frac{\beta R_{i}^{n}}{\sqrt{F(U_{i}^{n,*})+C_{0}}}|U_{i}^{n,*}|^{2}U_{i}^{n,*}\big )\\&+\tau \sum _{i=1}^{s}b_{i}\big (-\Delta U_{i}^{n}+L_{i}^{n}+\frac{\beta R_{i}^{n}}{\sqrt{F(U_{i}^{n,*})+C_{0}}}|U_{i}^{n,*}|^{2}U_{i}^{n,*},V_{i}^{n}\big ). \end{aligned}$$

Replacing $L_{i}^{n}$ by the middle equality of the second column of (3.3), we arrive at the final result and complete the proof of Theorem 3.1. $\square$

Remark 1

Note that $U_{i}^{n,*}$ of Scheme 1 is the approximation of $U(t_{n,i})$. Theoretically, we can choose $t_{m}$, $t_{m,i}\ (m<n)$ and $t_{n}$ as the interpolation points to obtain the Lagrange polynomial $U_{N}(t)$. However, too many interpolation points will lead to high oscillations for the interpolation polynomial and make $U_{N}(t_{n,i})$ an inaccurate extrapolation for $U(t_{n,i})$. In the following calculations, we consider two different scenarios (denoted as Cases I and II):

• I. interpolation points are determined by the internal RK stage nodes $t_{n-1,i}\ (i=1,\dots ,s)$,

• II. interpolation points are determined by the above stage nodes as well as the time node $t_{n-1}$.

Taking the 2-stage Gauss method for example, we utilize the interpolation points $(t_{n-1,1}, U_{1}^{n-1})$ and $(t_{n-1,2}, U_{2}^{n-1})$ to derive the corresponding interpolation polynomial of Case I as

$$\begin{aligned} U_{N}(t_{n,\text {i}})=\frac{c_{\text {i}}-c_{2}+1}{c_{1}-c_{2}}U_{1}^{n-1}+ \frac{c_{\text {i}}-c_{1}+1}{c_{2}-c_{1}}U_{2}^{n-1}\quad \text {for } \text {i}=1,2, \end{aligned}$$

where $c_{1}=\frac{1}{2}-\frac{\sqrt{3}}{6}$ and $c_{2}=\frac{1}{2}+\frac{\sqrt{3}}{6}$. Then one has

$$\begin{aligned} U_{N}(t_{n,1})=(1-\sqrt{3})U_{1}^{n-1}+\sqrt{3}U_{2}^{n-1}\quad \text {and}\quad U_{N}(t_{n,2})=-\sqrt{3}U_{1}^{n-1}+(1+\sqrt{3})U_{2}^{n-1}. \end{aligned}$$

The interpolation polynomials of Case II and 3-stage Gauss method can be obtained in the same spirit. For convenience, we list the coefficients of interpolation polynomials for the 2-stage and 3-stage Gauss collocation methods in Tables 1 and 2, respectively.

Table 1 Coefficients of the interpolation polynomials with $s=2$

Table 2 Coefficients of the interpolation polynomials with $s=3$

3.3 Linear SAV-SRK-PC Schemes

To improve the accuracy as well as the stability of the schemes proposed above, we employ the prediction-correction technique [31, 38, 39] to develop the following semi-discrete LSAV-SRK-PC scheme for the linearized system (3.2).

Prediction 1

Let $\lambda$ and $\Lambda$ be iteration variable and iteration step, respectively. For given $U^{n}, V^{n}, R^{n}$ and $U_{N}(t_{n,i}), R_{N}(t_{n,i})\ (i=1,\ldots ,s)$, we set $U_{i}^{n(0)}=U_{N}(t_{n,i})$ and $R_{i}^{n(0)}=R_{N}(t_{n,i})$, then compute $U_{i}^{n(\lambda +1)}, V_{i}^{n(\lambda +1)}, K_{i}^{n(\lambda +1)}, L_{i}^{n(\lambda +1)}$ and $M_{i}^{n(\lambda +1)},R_{i}^{n(\lambda +1)}$ from $\lambda =0$ to $\Lambda -1$ by

$$\begin{aligned} \left\{ \begin{aligned}&U_{i}^{n(\lambda +1)}=U^{n}+\tau \sum _{j=1}^{s}a_{ij}K_{j}^{n(\lambda +1)},\quad K_{i}^{n(\lambda +1)}=V_{i}^{n(\lambda +1)},\\&V_{i}^{n(\lambda +1)}=V^{n}+\tau \sum _{j=1}^{s}a_{ij}L_{j}^{n(\lambda +1)},\quad \ L_{i}^{n(\lambda +1)}=\Delta U_{i}^{n(\lambda +1)}-\mathrm {i}\alpha V_{i}^{n(\lambda +1)}-\frac{\beta R_{i}^{n(\lambda )}|U_{i}^{n(\lambda )}|^{2}}{\sqrt{F(U_{i}^{n(\lambda )}) +C_{0}}}U_{i}^{n(\lambda )},\\&M_{i}^{n(\lambda +1)}= \left( \frac{|U_{i}^{n(\lambda +1)}|^{2}}{2\sqrt{F(U_{i}^{n(\lambda +1)})+C_{0}}}, U_{i}^{n(\lambda +1)}\cdot \overline{K}_{i}^{n(\lambda +1)}+\overline{U}_{i}^{n(\lambda +1)}\cdot {K}_{i}^{n(\lambda +1)}\right) ,\\&R_{i}^{n(\lambda +1)}=R^{n}+\tau \sum _{j=1}^{s}a_{ij}M_{j}^{n(\lambda +1)}. \end{aligned} \right. \end{aligned}$$

For a given error tolerance $TOL>0$, if $\max \limits _{1\le i\le s}\Vert U_{i}^{n(\lambda +1)}-U_{i}^{n(\lambda )}\Vert _{\infty }<TOL$, we terminate the iteration procedure and set $U_{i}^{n,*}=U_{i}^{n(\lambda +1)}$; otherwise, we set $U_{i}^{n,*}=U_{i}^{n(\Lambda )}$.

Correction 1

In terms of the prediction value $U_{i}^{n,*}$, we apply Scheme 1 to update the numerical solutions $U^{n+1}, V^{n+1}$ and $R^{n+1}$.

Actually, LSAV-SRK schemes are the special cases of LSAV-SRK-PC schemes with the iteration step $\Lambda =0$. We can also obtain the energy conservation law of this PC method below.

Theorem 3.2

The semi-discrete LSAV-SRK-PC scheme preserves the energy at the discrete time level, where $E^{n}=\Vert \nabla U^{n}\Vert _{L^{2}}^{2}+\Vert V^{n}\Vert _{L^{2}}^{2}+\beta \big ((R^{n})^{2}-C_{0}\big )$.

Proof

As can be seen, the prediction procedure provides a general way to calculate the value of $U_{i}^{n,*}$ and the correction procedure is the key to energy conservation. Based on Correction 1 and the proof of Theorem 4.1, one can demonstrate the energy conservation property in the same spirit. $\square$

4 Spatial Discretization

The boundary conditions of Eq. (1.1) are often set to be homogenous or periodic. In order to make the spatial accuracy compatible with the high-order accuracy in time as well as compute efficiently, we adopt the Sine or Fourier pseudo-spectral methods for spatial discretization, which is shown to preserve the fully discrete energy conservation law.

For simplicity of notations, we here derive the sine spectral differentiation matrix (SSDM) on the interval $\Omega =[a,b]$ in 1D, as extensions to higher dimensions are straightforward. For a positive integer H, we denote the spatial mesh size $h:=(b-a)/H$. Then the spatial grid points are given by $\Omega _{h}=\{x_{j}|x_{j}=a+jh,\ 0\le j\le H$}. Define

$$\begin{aligned} \mathcal {S}_H:=\mathrm {span}\Big \{\sin \big (\mu _{\ell }(x-a)\big ):\ \mu _{\ell }=\frac{\pi \ell }{b-a},\ \ell =1,2,\ldots ,H-1\Big \}. \end{aligned}$$

Let $I_{H}$ be the trigonometric interpolation operator onto $\mathcal {S}_{H}$, that is,

$$\begin{aligned} (I_{H} u)(x):=\sum _{\ell =1}^{H-1}\widetilde{u}_{\ell }\sin \big (\mu _{\ell }(x-a)\big ), \end{aligned}$$

(4.1)

with the corresponding coefficient

$$\begin{aligned} \widetilde{u}_{\ell }:=\frac{2}{H}\sum _{j=1}^{H-1}u_{j}\sin \big (\mu _{\ell }(x_{j}-a)\big ), \end{aligned}$$

(4.2)

where $u_{j}$ is interpreted as $u(x_{j})$. Substituting (4.2) into (4.1), one has

$$\begin{aligned} (I_{H}u)(x)=\sum _{j=1}^{H-1}u_{j}\mathrm {X}_{j}(x), \end{aligned}$$

where the interpolation basis function $\text {X}_{j}(x):=\frac{2}{H}\sum _{\ell =1}^{H-1}\sin \big (\mu _{\ell }(x_{j}-a)\big ) \sin \big (\mu _{\ell }(x-a)\big ).$

To obtain the SSDM for the approximation of Laplacian operator, we differentiate $\text {X}_{j}(x)$ two times, then evaluate the resulting expressions of $\text {X}_{j}''(x)$ at the collocation points $x_{k}$. As a result, we derive the second-order SSDM $\mathbf{S} _{2}$ with the elements given by [40]

$$\begin{aligned} (\mathbf{S} _{2})_{j,k}=\left\{ \begin{aligned} (-1)^{j+k+1}&\frac{\pi ^{2}}{2(b-a)^{2}}\Big [\csc ^{2}\big (\frac{h}{2}(\mu _{j}-\mu _{k})\big )- \csc ^{2}\big (\frac{h}{2}(\mu _{j}+\mu _{k})\big )\Big ], \ \&j\ne k,\\&\frac{\pi ^{2}}{6(b-a)^2}\big (3\csc ^{2}(\mu _{j}h)-2H^2-1\big ),\ \&j=k. \end{aligned} \right. \end{aligned}$$

Moreover, from [40, Lemma 3.1], one has the following decomposition property

$$\begin{aligned} \mathbf{S} _{2}=\mathbf{S} _{H}^{T}\Lambda _{x}{} \mathbf{S} _{H}, \end{aligned}$$

where $\mathbf{S} _{H}$ is the discrete Sine transform matrix with elements $(\mathbf{S} _{H})_{j,k}=\sqrt{\frac{2}{H}}\sin \frac{jk\pi }{H}$, $\mathbf{S} _{H}^{T}$ is the transpose of $\mathbf{S} _{H}$. $\lambda _\mathbf{S _{2},j}=-(\frac{j\pi }{b-a})^{2}\ (j=1,2,\ldots ,H-1)$ are the eigenvalues of $\mathbf{S} _{2}$ and $\Lambda _{x}=\mathrm {diag}(\lambda _\mathbf{S _{2},1}, \lambda _\mathbf{S _{2},2},\ldots ,\lambda _\mathbf{S _{2},H-1})$. It is noteworthy that we can develop fast algorithm by incorporating the decomposition.

Denote $\mathbb {V}_{h}=\{{\mathbf {U}}=(U_{0},U_{1},\dots ,U_{H})^{T}|\ U_{0}=U_{H}=0\}$ is the space of gird functions on $\Omega _{h}$. For any $\mathbf{U} , \mathbf{V} \in \mathbb {V}_{h}$, we define the discrete inner product

$$\begin{aligned} \langle \mathbf{U} , \mathbf{V} \rangle :=h\sum _{j=1}^{H-1}U_{j}\overline{V_{j}}, \end{aligned}$$

and the associated $l^{2}$-norm $\Vert \mathbf{U} \Vert :=\sqrt{\langle \mathbf{U} , \mathbf{U} \rangle }$. In addition, we also denote the componentwise product of vectors as $\mathbf{U} \cdot \mathbf{V} =(U_{1}V_{1},U_{2}V_{2},\dots ,U_{H-1}V_{H-1})^{T}$. Applying the Sine pseudo-spectral method to Scheme 1 in space, we obtain the following fully-discrete s-stage LSAV-SRK scheme.

Scheme 2

(fully discrete s-stage LSAV-SRK scheme) Let $b_{i}$, $a_{ij}\ (i,j=1,\dots ,s)$ and $c_{i}=\sum _{j=1}^{s}a_{ij}$ be symplectic RK coefficients and $\tau$ is the time-step. For $\mathbf{U} ^{n},\mathbf{V} ^{n}\in \mathbb {V}_{h}$ and $R^{n}$, $\mathbf{U} _{N}(t)$, the following intermediate values are first calculated by

$$\begin{aligned} \left\{ \begin{aligned}&\mathbf{U} _{i}^{n}=\mathbf{U} ^{n}+\tau \sum _{j=1}^{s}a_{ij}{} \mathbf{K} _{j}^{n},\quad \mathbf{K} _{i}^{n}=\mathbf{V} _{i}^{n},\\&\mathbf{V} _{i}^{n}=\mathbf{V} ^{n}+\tau \sum _{j=1}^{s}a_{ij}{} \mathbf{L} _{j}^{n},\quad \ \mathbf{L} _{i}^{n}=\mathbf{S} _{2} \mathbf{U} _{i}^{n}-\mathrm {i}\alpha \mathbf{V} _{i}^{n}-\frac{\beta R_{i}^{n}}{\sqrt{F(\mathbf{U} _{i}^{n,*})+C_{0}}}|\mathbf{U} _{i}^{n,*}|^{2}{} \mathbf{U} _{i}^{n,*},\\&R_{i}^{n}=R^{n}+\tau \sum _{j=1}^{s}a_{ij}M_{j}^{n},\quad M_{i}^{n}= \big \langle \frac{|\mathbf{U} _{i}^{n,*}|^{2}}{2\sqrt{F(\mathbf{U} _{i}^{n,*})+C_{0}}}, \mathbf{U} _{i}^{n,*}\cdot \overline{\mathbf{K }}_{i}^{n}+\overline{\mathbf{U }}_{i}^{n,*}\cdot \mathbf{K} _{i}^{n}\big \rangle , \end{aligned} \right. \end{aligned}$$

(4.3)

where $\mathbf{U} _{i}^{n,*}=\mathbf{U} _{N}(t_{n,i})$. Then the numerical solutions $\mathbf{U} ^{n+1}, \mathbf{V} ^{n+1}$ and $R^{n+1}$ are updated by

$$\begin{aligned} \left\{ \begin{aligned}&\mathbf{U} ^{n+1}=\mathbf{U} ^{n}+\tau \sum _{i=1}^{s}b_{i}{} \mathbf{K} _{i}^{n},\\&\mathbf{V} ^{n+1}=\mathbf{V} ^{n}+\tau \sum _{i=1}^{s}b_{i}{} \mathbf{L} _{i}^{n},\\&R^{n+1}=R^{n}+\tau \sum _{i=1}^{s}b_{i}M_{i}^{n}. \end{aligned} \right. \end{aligned}$$

(4.4)

Remark 2

It is not difficult to find (4.3) is a system of linear equations with respect to the variables $\mathbf{U} _{i}^{n}, \mathbf{V} _{i}^{n}, R_{i}^{n}, \mathbf{K} _{i}^{n}, \mathbf{L} _{i}^{n}, M_{i}^{n}$. This implies that Scheme 2 is linear-implicit and we can use the fast sine transform to solve it efficiently.

Theorem 4.1

The fully discrete LSAV-SRK scheme (4.3)-(4.4) inherit the following energy conservation law

$$\begin{aligned} E_{h}^{n+1}=E_{h}^{n}, \end{aligned}$$

where $E_{h}^{n}=\Vert \nabla _{h} \mathbf{U} ^{n}\Vert ^{2}+\Vert \mathbf{V} ^{n}\Vert ^{2}+\beta \big ((R^{n})^{2}-C_{0}\big )$ and $\Vert \nabla _{h} \mathbf{U} \Vert =\sqrt{\langle \mathbf{U} , -\mathbf{S} _{2}{} \mathbf{U} \rangle }$ for $\mathbf{U} \in \mathbb {V}_{h}$.

Proof

From the first equation of (4.4), we obtain

$$\begin{aligned} -\mathbf{S} _{2}{} \mathbf{U} ^{n+1}=-\mathbf{S} _{2}{} \mathbf{U} ^{n}- \tau \sum _{i=1}^{s}b_{i}{} \mathbf{S} _{2}{} \mathbf{K} _{i}^{n}. \end{aligned}$$

Taking the discrete inner product with $\mathbf{U} ^{n+1}$, it is readily to check

$$\begin{aligned} \Vert \nabla _{h} \mathbf{U} ^{n+1}\Vert ^{2}&=\big \langle \mathbf{U} ^{n}+\tau \sum _{i=1}^{s}b_{i}{} \mathbf{K} _{i}^{n}, -\mathbf{S} _{2}{} \mathbf{U} ^{n}- \tau \sum _{i=1}^{s}b_{i}{} \mathbf{S} _{2}{} \mathbf{K} _{i}^{n}\big \rangle \\&=\Vert \nabla _{h} \mathbf{U} ^{n}\Vert ^{2}- \tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{U} _{i}^{n}, \mathbf{S} _{2}{} \mathbf{K} _{i}^{n}\big \rangle -\tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{K} _{i}^{n}, \mathbf{S} _{2}{} \mathbf{U} _{i}^{n}\big \rangle -\tau ^{2}\sum _{i,j=1}^{s}\varpi _{ij}\big \langle \mathbf{K} _{i}^{n},\mathbf{S} _{2}{} \mathbf{K} _{j}^{n}\big \rangle \\&=\Vert \nabla _{h} \mathbf{U} ^{n}\Vert ^{2}- \tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{U} _{i}^{n}, \mathbf{S} _{2}{} \mathbf{K} _{i}^{n}\big \rangle -\tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{K} _{i}^{n}, \mathbf{S} _{2}{} \mathbf{U} _{i}^{n}\big \rangle , \end{aligned}$$

where the first relation of the first row of (4.3) and the relationship of RK coefficients in Lemma 3.1 were used. Similarly, the second and third equations of (4.4) yield

$$\begin{aligned}&\Vert \mathbf{V} ^{n+1}\Vert ^{2}=\Vert \mathbf{V} ^{n}\Vert ^{2}+\tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{L} _{i}^{n},\mathbf{V} _{i}^{n}\big \rangle +\tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{V} _{i}^{n},\mathbf{L} _{i}^{n}\big \rangle ,\\&\quad (R^{n+1})^{2}=(R^{n})^{2}+2\tau \sum _{i=1}^{s}b_{i}M_{i}^{n}R_{i}^{n}. \end{aligned}$$

Multiplying the last equality by $\beta$ and adding these three results together, we apply the first and third relations of the second column of (4.3) to find

$$\begin{aligned} E_{h}^{n+1}&=E_{h}^{n}+\tau \sum _{i=1}^{s}b_{i}\big \langle \mathbf{V} _{i}^{n},-\mathbf{S} _{2} \mathbf{U} _{i}^{n}+\mathbf{L} _{i}^{n}+\frac{\beta R_{i}^{n}}{\sqrt{F(\mathbf{U} _{i}^{n,*})+C_{0}}}|\mathbf{U} _{i}^{n,*}|^{2}{} \mathbf{U} _{i}^{n,*}\big \rangle \\&\quad +\tau \sum _{i=1}^{s}b_{i}\big \langle -\mathbf{S} _{2} \mathbf{U} _{i}^{n}+\mathbf{L} _{i}^{n}+\frac{\beta R_{i}^{n}}{\sqrt{F(\mathbf{U} _{i}^{n,*})+C_{0}}}|\mathbf{U} _{i}^{n,*}|^{2}{} \mathbf{U} _{i}^{n,*},\mathbf{V} _{i}^{n}\big \rangle . \end{aligned}$$

Replacing $\mathbf{L} _{i}^{n}$ by the middle equality of the second column of (4.3), we arrive at the final result and complete the proof of Theorem 4.1. $\square$

Analogously, one has the fully discrete s-stage LSAV-SRK-PC scheme and its energy conservation law.

Prediction 2

Let $\lambda$ and $\Lambda$ be iteration variable and iteration step, respectively. For given $\mathbf{U} ^{n},\mathbf{V} ^{n},R^{n}$ and $\mathbf{U} _{N}(t_{n,i}), R_{N}(t_{n,i})\ (i=1,\ldots ,s)$, we set $\mathbf{U} _{i}^{n(0)}=\mathbf{U} _{N}(t_{n,i})$ and $R_{i}^{n(0)}=R_{N}(t_{n,i})$, then compute $\mathbf{U} _{i}^{n(\lambda +1)}, \mathbf{V} _{i}^{n(\lambda +1)}, \mathbf{K} _{i}^{n(\lambda +1)}, \mathbf{L} _{i}^{n(\lambda +1)}$ and $M_{i}^{n(\lambda +1)},R_{i}^{n(\lambda +1)}$ from $\lambda =0$ to $\Lambda -1$ by

$$\begin{aligned} \left\{ \begin{aligned}&\mathbf{U} _{i}^{n(\lambda +1)}=\mathbf{U} ^{n}+\tau \sum _{j=1}^{s}a_{ij}{} \mathbf{K} _{j}^{n(\lambda +1)},\quad \mathbf{K} _{i}^{n(\lambda +1)}=\mathbf{V} _{i}^{n(\lambda +1)},\\&\mathbf{V} _{i}^{n(\lambda +1)}=\mathbf{V} ^{n}+\tau \sum _{j=1}^{s}a_{ij}{} \mathbf{L} _{j}^{n(\lambda +1)},\quad \ \mathbf{L} _{i}^{n(\lambda +1)}=\mathbf{S} _{2} \mathbf{U} _{i}^{n(\lambda +1)}-\mathrm {i}\alpha \mathbf{V} _{i}^{n(\lambda +1)}-\frac{\beta R_{i}^{n(\lambda )}|\mathbf{U} _{i}^{n(\lambda )}|^{2}}{\sqrt{F(\mathbf{U} _{i}^{n(\lambda )}) +C_{0}}}{} \mathbf{U} _{i}^{n(\lambda )},\\&M_{i}^{n(\lambda +1)}= \big \langle \frac{|\mathbf{U} _{i}^{n(\lambda +1)}|^{2}}{2\sqrt{F(\mathbf{U} _{i}^{n(\lambda +1)})+C_{0}}}, \mathbf{U} _{i}^{n(\lambda +1)}\cdot \overline{\mathbf{K }}_{i}^{n(\lambda +1)}+\overline{\mathbf{U }}_{i}^{n(\lambda +1)}\cdot \mathbf{K }_{i}^{n(\lambda +1)}\big \rangle ,\\&R_{i}^{n(\lambda +1)}=R^{n}+\tau \sum _{j=1}^{s}a_{ij}M_{j}^{n(\lambda +1)}. \end{aligned} \right. \end{aligned}$$

For a given error tolerance $TOL>0$, if $\max \limits _{1\le i\le s}\Vert \mathbf{U} _{i}^{n(\lambda +1)}-\mathbf{U} _{i}^{n(\lambda )}\Vert _{\infty }<TOL$, we terminate the iteration procedure and set $\mathbf{U} _{i}^{n,*}=\mathbf{U} _{i}^{n(\lambda +1)}$; otherwise, we set $\mathbf{U} _{i}^{n,*}=\mathbf{U} _{i}^{n(\Lambda )}$.

Correction 2

In terms of the prediction value $\mathbf{U} _{i}^{n,*}$, we apply Scheme 2 to update the numerical solutions $\mathbf{U} ^{n+1}, \mathbf{V} ^{n+1}$ and $R^{n+1}$.

Theorem 4.2

The fully discrete LSAV-SRK-PC scheme inherits the energy conservation law, where $E_{h}^{n}=\Vert \nabla _{h} \mathbf{U} ^{n}\Vert ^{2}+\Vert \mathbf{V} ^{n}\Vert ^{2}+\beta \big ((R^{n})^{2}-C_{0}\big )$.

Proof

It is similar to the proof of Theorems 3.2 and 4.1, so it is omitted. $\square$

Remark 3

The prediction system of PC method is also linear with constant coefficients and we can still use the fast algorithm to solve it.

Remark 4

If the boundary conditions are set to be periodic, we shall use the Fourier spectral differentiation matrix and fast Fourier transform for spatial discretization and computations, respectively. More details are referred to [41].

Remark 5

The invariant energy quadratization (IEQ) approach can also be employed to reformulate the original system (2.1) and the corresponding LIEQ-SRK schemes and LIEQ-SRK-PC schemes can be developed in the same spirit. We omit the details here to save space but give some numerical results in the next section.

5 Numerical Examples

In this section, a collection of numerical tests are reported to show the convergence, accuracy and energy conservation law of the proposed schemes. Moreover, we always set $TOL=1e-12$ in the prediction-correction calculations without further declaration.

Example 1

The problem (1.1) in 1D with the periodic boundary conditions are considered. We choose the parameter values $\alpha =1$ and $\beta =-2$ to test the convergence orders. The exact solution is $u(x,t)=A\mathrm {sech}(Jx)\exp (\text {i} \theta t)$, where $A=|J|$ and $\theta =\frac{1}{2}(-1\pm \sqrt{1-4J^{2}})$.

Define the discrete maximum norm solution error $e(\tau ,h)=\Vert U^{N}-u(t_{N})\Vert _{\infty }$. The convergence rate in time is computed by

$$\begin{aligned} \mathrm {Order }\approx \log _{2}\big (e(\tau ,h)/e(\tau /2,h)\big ). \end{aligned}$$

In computations, we set $J=\frac{1}{4}$ and $\theta =-\frac{1}{4}(2+\sqrt{3})$, then investigate the spatial and temporal orders separately on the interval $\Omega =[-128,128]$ until $T=1$. The spatial accuracy is checked by fixing a sufficiently small $\tau =1e-06$ to avoid contamination of the temporal error. Solution errors of the fully-discrete LSAV schemes (LSAV-SRK and LSAV-SRK-PC) in different scenarios are drawn in Table 3, where the spatial errors are very small and almost negligible. It indicates that the Fourier pseudo-spectral method is of arbitrary order of accuracy for the sufficiently smooth problem.

Table 3 Spatial errors of the LSAV schemes of Example 1

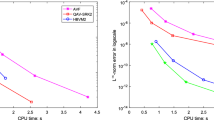
The temporal accuracy is examined on the halving time-steps with the space size $h=1/4$. The solution errors of various numerical schemes are calculated and summarized in Fig. 1. Since the interpolation polynomials with degree k has $(k+1)$th-order accuracy, the LSAV-SRK schemes with $s=2$ reach second- and third-order accuracy in Cases I and II, respectively, see Fig. 1a. In order to test the validity and capability of the prediction-correction strategy, we use a one-step ($\Lambda =1$) prediction iteration and adopt the LSAV-SRK-PC schemes with $s=2$ to address this issue. Relevant results are drawn in Fig. 1b. Observation from Fig. 1b shows that both two cases reach fourth-order accuracy which is beyond our expectations. In our numerical experience, one-step prediction iteration normally improve the accuracy by one order. However, it may have better results on this issue. We next choose this PC schemes with $s=3$ and further test the convergence rates in Fig. 1c. We are pleased to find that the results are consistent with our conjecture, i.e., the LSAV-SRK-PC schemes with $s=3$ have fifth- and sixth-order accuracy in Cases I and II, respectively. Numerical results of the IEQ approach are also tested and similar conclusion can be drawn.

Fig. 1

Temporal convergence rates of various linear SRK schemes of Example 1

Table 4 Spatial errors of the LSAV schemes of Example 2

Fig. 2

Temporal convergence rates of various linear SRK schemes of Example 2

Example 2

We consider another example of NLSW in 2D subject to the homogeneous Dirichlet boundary conditions on the domain $\Omega =[-4,4]^{2}$ with the parameter values $\alpha =\beta =1$. To better check the errors and orders for mesh refinement tests, an exact solution

$$\begin{aligned} u(x,y,t)=\sin (\pi x)\sin (\pi y)\exp (-\sqrt{2}\pi \mathrm {i}t) \end{aligned}$$

is constructed by adding a nonhomogeneous term $f(x,y)u=(\sqrt{2}\pi +\sin ^{2}(\pi x)\sin ^{2}(\pi y))u$ on the right-hand side of Eq. (1.1).

Always, we set $T=1$ and take the time-step $\tau =1e-06$ and the same space size $h=h_{x}=h_{y}=1/4$ to test the errors and orders in space and time, respectively. Table 4 confirms that, for the sufficiently smooth problem, the Sine pseudo-spectral method can reach arbitrarily high-order accuracy in space. Temporal orders of various linear RK schemes in two different scenarios are plotted in Fig. 2. Numerical results in three subfigures again witness the conclusion in Example 1, i.e., a one-step prediction-correction strategy achieves great performance for the NLSW and improves the temporal accuracy by two orders.

Table 5 Minimum iteration steps of the NSAV-SRK schemes of Examples 1 and 2

To better illustrate the advantages of PC strategy, we apply the nonlinear SAV-SRK (NSAV-SRK) schemes as well as the fixed-point iteration method to solve the problems in Examples 1 and 2 with the same parameters $h=1/4$ and $TOL=1e-12$. Solution errors, convergence orders and the minimum iteration steps are recorded in Table 5. It is readily to see that the iteration steps decrease as the time-step halves. Compared with the results of LSAV-SRK-PC schemes in Figs. 1 and 2, we find the nonlinear schemes have almost the same errors, but need more iterations to reach the desired order. It again confirms the effectiveness of PC strategy.

On the other hand, conservation property is verified with $\tau =h=1/8$ when the running time hits $T=10$. Energy errors of linear SRK schemes in different cases are shown in Fig. 3. Numerical results state clearly that the discrete energy of all schemes conserves well during a long period of time, which are in agreement with the continuous case.

Fig. 3

Energy errors of various linear SRK schemes of Example 2

Fig. 4

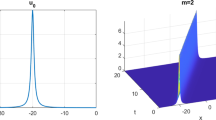
Contour figures of the soliton |u| (left) and section views figures (right) at different times of Example 3

Example 3

We choose another 2D problem and simulate the dynamics of the solutions on the domain $\Omega =[-32,32]^{2}$ with the parameter values $\alpha =\beta =1$. The initial conditions are

$$\begin{aligned} u_{0}(x,y)=(1+\mathrm {i})(x+y)\exp (-10(1-x-y)^{2}),\quad u_{1}(x,y)=0. \end{aligned}$$

Here, we use the zero Dirichlet boundary conditions as before.

We take $h=\tau =1/20$ and display the simulation results of LSAV-SRK-PC schemes with $s=2$ in Case I. The movement contour figures of soliton |u| at $t=0,5,10$ are shown on the left-hand side of Fig. 4. On the other part, we give the section views when $x = y$ in the domain $[-15,15]$ to illustrate the effectiveness and stability of this scheme. Due to the high resolution and energy-preserving, we use less meshes to capture the oscillation precisely, which indicates that this scheme is stable and do not occur blow-up. Numerical results of other linear SRK schemes are the same, which are omitted here for brevity. All these results show that the proposed schemes work well in a given large steps for the long time simulations of NLSW.

Table 6 Temporal errors and orders of the LSAV schemes with $\gamma =2$ of Example 4

Table 7 Temporal errors and orders of the LSAV schemes with $\gamma =0$ of Example 4

Table 8 Temporal errors and orders of the LSAV schemes of Example 4

Example 4

Lastly, we strive to compute the NLSW with a perturbation strength. This equation in 1D is described by a dimensionless parameter $\varepsilon \in (0,1]$ as

$$\begin{aligned} \left\{ \begin{aligned}&\varepsilon ^{2}\partial _{tt}u^{\varepsilon }(x,t)-\partial _{xx} u^{\varepsilon }(x,t)+\mathrm {i}\alpha \partial _{t}u^{\varepsilon }(x,t) +\beta |u^{\varepsilon }|^{2}u^{\varepsilon }(x,t)=0\quad \text {for }x\in \Omega \text { and }0<t\le T,\\&u^{\varepsilon }(x,0)=u_{0}(x),\quad \partial _{t}u^{\varepsilon }(x,0)=u_{1}^{\varepsilon }(x)\quad \text {for } x\in \Omega . \end{aligned} \right. \end{aligned}$$

As $\varepsilon \rightarrow 0^{+}$, it collapses to the standard nonlinear Schrödinger equation (NLS). In the small perturbation parameter regime, i.e., $0<\varepsilon \ll 1$, highly oscillations arise in time with $O(\varepsilon ^{2})$-wavelength [8]. Here, the boundary conditions are also set to be homogenous and the initial data $u_{1}^{\varepsilon }$ is assumed to satisfy the following condition

$$\begin{aligned} u_{1}^{\varepsilon }(x)=u_{1}(x)+\varepsilon ^{\gamma }\omega ^{\varepsilon }(x)=\frac{\mathrm {i}}{\alpha }\big (-\partial _{xx}u_{0}(x)+\beta |u_{0}(x)|^{2} u_{0}(x)\big )+\varepsilon ^{\gamma }\omega ^{\varepsilon }(x), \end{aligned}$$

where $\Vert \omega ^{\varepsilon }\Vert _{H^{2}}$ is uniformly bounded with $\lim \inf _{\varepsilon \rightarrow 0^{+}}\Vert \omega ^{\varepsilon }\Vert _{H^{2}}>0$ and $\gamma \ge 0$ is a parameter describing the consistency of the initial data about NLS. Moreover, the initial data can be classified into well-prepared $(\gamma \ge 2)$ and ill-prepared $(0\le \gamma < 2)$ cases.

In the practical computations, we set the parameter values $\alpha =-1, \beta =1$ and $\Omega =[-16,16]$. The initial data $u_{0}(x)=\pi ^{-1/4}e^{-x^2/2}$ and $\omega ^{\varepsilon }(x)=e^{-x^2/2}$. Due to the analytical solution is not available, we estimate the experimental temporal order by assuming that $u(T)-U^{N}\approx C_{u}\tau ^{\beta }$ and compute the order $\beta$ by

$$\begin{aligned} \text {Order}\approx \log _{2}\big (\Vert U^{N}-U^{2N}\Vert _{\infty }/\Vert U^{2N}-U^{4N}\Vert _{\infty }\big ). \end{aligned}$$

We still choose $h=1/4$ to ignore the spatial error and show the temporal rates of LSAV schemes with different $\gamma$ in Tables 6- 8. According to the error estimates in [8], one knows that the temporal order is $O(\tau ^{\beta }/\varepsilon ^2)$. The upper parts of Tables 6 and 7 list the errors and orders of the SRK schemes with $s=2$ in Case I. We take different $\varepsilon$ and $\tau$ with $\varepsilon =O(\tau )$ and observe that this scheme is of second-order accuracy no matter in well-prepared case ($\gamma =2$) or in ill-prepared case ($\gamma =0$). When the mesh strategy is adjusted to $\varepsilon =O(\tau ^2)$ and $\varepsilon =O(\tau ^3)$, the SRK-PC schemes with $s=2$ in Case I and the SRK-PC schemes with $s=3$ in Case II reach fourth- and sixth-order accuracy, respectively, see the middle and lower parts of Tables 6 and 7. In Table 8, the SRK schemes with $s=2$ in Case II and the SRK-PC schemes with $s=3$ in Case I are applied to examine the temporal rates combined with the mesh strategies $\varepsilon =O(\tau ^{3/2})$ and $\varepsilon =O(\tau ^{5/2})$, respectively. Relevant results state that the former is of third-order accuracy in time and the latter has fifth-order accuracy. In general, convergence order tests are exactly consistent with the previous ones.

The profiles of solution |u| with different cases are shown in Fig. 5, which are solved by the LSAV-SRK-PC schemes with $s=2$ in Case I with $h=\tau =1/20$. By comparison, it is not hard to see the solutions of ill-prepared case change more dramatically with different $\varepsilon$. Relevant results indicate the proposed schemes are also feasible and effective in handling the NLSW with small perturbation parameter.

6 Conclusion

In this paper, we present two classes of fully discrete structure-preserving algorithms for solving the NLSW. The proposed schemes have two advantageous properties: (1) they are linear and can be computed simply and efficiently; (2) they inherit the energy conservation property and can reach arbitrarily high order. Numerical examples illustrate that these methods are suitable for dealing with a serious of NLSW problems with proper boundary conditions, and numerous results verify the effectiveness and high accuracy of methods. It is noteworthy that the numerical strategy given in this paper can be extended to general conservative system for developing arbitrarily high-order linear structure-preserving schemes. The authors in [33] established the error analysis of the energy-decaying extrapolated RK-SAV methods for the dissipative system and the error estimates of conservative system are still open. In addition, PC schemes show tremendous performance in numerical computations whereas the mechanism of prediction-correction is still unknown. These will be considered further in our future works.

Fig. 5

Profiles of the solution |u| with different $\gamma$ and $\varepsilon$ of Example 4