A Modular Grad-Div Stabilization for the 2D/3D Nonstationary Incompressible Magnetohydrodynamic Equations

Abstract

In this paper, we study an efficient and modular grad-div stabilization algorithm for the 2D/3D nonstationary incompressible magnetohydrodynamic equations. The considered algorithm is a fully discrete first-order scheme based on the mixed finite element method and does not increase computational time for increasing stabilization parameters. Also, both unconditional stability and convergence analysis are given. Finally, numerical experiments are presented to verify both the numerical theory and efficiency of the presented algorithm.

1 Introduction

The magnetohydrodynamic (MHD) model is mainly used to describe the interaction of an electrically conducting fluid with an external magnetic field, which has been widely applied in industry and engineering, such as for liquid metal cooling of nuclear reactors, electromagnetic pumping, stirring of liquid metals and so on [11, 31]. The governing equations of the MHD model include the incompressible Navier–Stokes equations of hydrodynamics coupled with the Maxwell system of electromagnetism (including divergence-free constraint for the magnetic field) via the Lorentz force and Ohm’s law. Due to the widely practical application and computational complexity of the MHD model, much effort has been spent on the development of some efficient numerical methods to investigate this problem.

Based on a conservative formulation to ensure the local divergence-free condition of the magnetic field weakly, a finite element method has been proposed in [39] for 3D nonstationary incompressible MHD flows with both high and low magnetic Reynolds numbers. Amari et al. [3] have developed a more general anisotropic semi-implicit scheme for the MHD problem. This scheme can deal with domains that do not allow the use of direct methods. In [4], a term-by-term stabilized finite element formulation based on orthogonal subscales for the numerical approximation of the incompressible MHD system has been proposed and analyzed. In order to stabilize the unresolved scales in MHD simulations, Belenli et al. [5] have studied a subgrid stabilization finite element method. In [36], Prohl has discussed some coupling and decoupling fully discrete schemes and verified convergence of these schemes towards weak solutions for vanishing discretization parameters. Case et al. [8] have presented an energy, cross-helicity and magnetic helicity preserving method for the considered equations which is a semi-implicit Galerkin finite element discretization and enforces pointwise solenoidal constraints by employing the Scott–Vogelius finite elements.

Additionally, a finite element spatial approximation of the MHD system under smooth domains and data has been considered [24], and the optimal $L^2$-norm error estimates are obtained by using a new negative-norm technique without the standard duality argument. Applying the implicit Euler scheme to discretize the two-dimensional MHD equations in time, $H^2$-uniform stability has been obtained [40]. In addition, He and Zhang [23, 46] have studied the unconditional stability and convergence of the first order Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. Moreover, compared to the semi-implicit scheme [23, 46], Yang and He [43] have analysed the implicit/explicit scheme. This scheme only needs to solve the constant matrix equations, but it is conditionally stable. Furthermore, in order to increase convergence order in time, based on the Crank–Nicolson extrapolation scheme, Zhang et al. [47] have considered the temporal discretization while Dong and He [15] have considered the full discretization. In [44], a second order backward difference Newton scheme has been designed, which is a combination of the second order backward difference approximation for time terms and the Newton treatment for nonlinear terms. However, mass conservation law is often ignored or not strongly enforced by most schemes for the MHD model. In fact, if mass conservation is correctly accounted for in the numerical schemes, then resulting numerical solutions have greater physical accuracy. Due to the importance of mass conservation, there is a natural interest to study how to design numerical schemes to keep this law.

The grad-div stabilization [35], which is studied in [18] initially, is a simple, useful and popular technique for incompressible flow problems. It adds a penalty term with respect to the continuity equation to the momentum equation and can penalize for lack of mass conservation and improve solution accuracy by reducing the effect of the pressure on the velocity error [26]. Hence, this tool has been widely studied for the incompressible flows over the past decade. In particular, for the Oseen equations, de Frutos et al. [13] have proved that adding a grad-div stabilization term to the Galerkin approximation has a stabilizing effect for small viscosity. Further, they have extended the previous work to the Navier–Stokes equations with high Reynolds number [14]. In [19], the grad-div stabilized finite element discretizations of the singularly perturbed Oseen equations on properly layer-adapted meshes have been considered.

Combination of grad-div stabilization with other algorithms has been investigated by many authors. Within the viewpoints of variational multiscale methods and stabilization procedures of least-square type, the grad-div stabilization as a pressure subgrid model has been studied [34]. A combination of the streamline-upwind/Petrov–Galerkin formulation and the grad-div stabilization applied to the stationary Navier–Stokes equations has been considered [33]. In [10], the local projection stabilization method which combines the idea of streamline upwinding with the grad-div stabilization has been proposed. Based on the Yosida splitting methods, Rebholz and Xiao [37] have analyzed the accuracy of divergence free elements together with grad-div stabilization. All above algorithms together with the grad-div stabilization are based on conforming finite element methods in space. For grad-div stabilization with discontinuous finite element method, Akbas et al. [2] have designed and tested broken grad-div stabilization for incompressible flows in order to get the desired pressure robustness effect.

Although the grad-div stabilization term is consistent for continuous equations, the finite element solution depends on the stabilization parameter. As is known, too large values of the stabilization parameter overstabilize the problem, make the corresponding linear algebraic system poorly conditioned and cost lots of computational time resulting from decreased sparsity and increased coupling. Hence, the choice of the stabilization parameter has drawn attention. Jenkins et al. [25] have given an analytic support for the numerical observation from [20] that the use of large stabilization parameters is appropriate in certain situations, and found that the optimal stabilization parameter could range from being very small to very large. Ahmed [1] has extended the idea presented for the Stokes problem in [25] to the Oseen equations. In [12], a restricted range of possible values for the parameter in 3D turbulent flows away from walls has been provided. Besides, a better understanding of grad-div stabilization is achieved, when the limit behavior for arbitrarily large stabilization parameter is investigated [7]. As it is claimed in [7], with the stabilization parameter tending to infinity, the limit of the grad-div stabilized Taylor–Hood solution of the Navier–Stokes problem converges to the Scott–Vogelius solution. Further, the convergence rate is improved in [30]. Also, if the stabilization parameter tends to infinity, then the solution of the Chorin/Temam projection methods for Navier–Stokes equations equipped with the grad-div stabilization converges to the associated coupled method solution [28]. In addition, in order to understand how small changes in the stabilization parameter could affect the solution, Neda et al. [32] have presented a numerical study of the sensitivity of the parameter for mixed finite element discretizations of incompressible flow problems. They have found that the solutions are the most sensitive for small values of the stabilization parameter in certain situations.

Recently, in order to increase sparsity and decrease coupling of coefficient matrices for velocity created by grad-div stabilization, Linke and Rebholz [29] have proposed sparse grad-div stabilization, which has similar advantages as grad-div stabilization but is more efficient because of a sparser structure of its matrices. Furthermore, Çıbık [9] has extended the idea to the optimal control of an incompressible stationary flow problem. A combination of the projection methods and the sparse grad-div stabilization applied to the Navier–Stokes equations has been considered [6]. Besides, as it is found by many authors [20, 25, 32], the use of large stabilization parameters is unavoidable in certain situations. However, the solver for large stabilization parameters may slow down and even lead breakdown. To address this issue, an effective variant of the grad-div stabilization, called modular grad-div stabilization [17], is presented for calculating solutions to the Navier–Stokes equations. This stabilization is found to be unaffected by variations of the stabilization parameters whereas the cost of the standard technique grows rapidly as the parameter grows. Later, Rong and Fiordilino [38] have improved this modular grad-div stabilization with the first order backward Euler time discretization to the second order backward difference time discretization.

Since the modular grad-div stabilization have proven useful for a large range of stabilization parameters, we apply it to the MHD model to improve mass conservation of numerical solutions. Inspired by [17], we develop an Euler semi-implicit time-discrete, modular grad-div stabilization algorithm for the 2D/3D MHD problem and give the corresponding numerical analysis and numerical tests. The remainder of this paper is as follows. In Sect. 2, we introduce nonstationary incompressible MHD equations and notation, lemmas and necessary preliminaries. In the next section, we show the modular grad-div stabilization algorithm for the considered equations and prove unconditional stability and convergence. Then, in Sect. 4, numerical experiments show that the presented method is efficient. Section 5 is the conclusion of this paper.

2 Preliminaries

This work is concerned with the following 2D/3D nonstationary incompressible MHD system that couples the incompressible Navier–Stokes equations with Maxwell equations under the influence of body forces and currents [22, 23, 31]:

$$\begin{aligned} \left\{ \begin{aligned}&{\mathbf {u}}_{t}+({\mathbf {u}}\cdot \nabla ){\mathbf {u}}-\nu \Delta {\mathbf {u}}+\mu {\mathbf {H}}\times \text {curl}{\mathbf {H}}+\nabla {p}={\mathbf {f}},\\&\text{ div }{\mathbf {u}}=0,\\&\mu {\mathbf {H}}_{t}+\sigma ^{-1} \text {curl} \text {curl}{\mathbf {H}}- \mu \text {curl}({\mathbf {u}}\times {\mathbf {H}})=\sigma ^{-1} \text {curl}{\mathbf {J}},\\&\text{ div }{\mathbf {H}}=0, \end{aligned} \right. \end{aligned}$$

(1)

which holds for all $(\mathbf {x},t)\in \Omega \times (0,T]$, where $T\in (0,\infty )$ is a final time and $\Omega$ is an open bounded domain in $\mathbb {R}^{d},\; d=2, 3$, together with the following homogeneous boundary and initial conditions [22, 27]:

$$\begin{aligned} \left\{ \begin{aligned}&{\mathbf {u}}|_{S_{T}}=0\;(\text {no-slip condition}),\\&({\mathbf {H}}\cdot \mathbf {n})|_{S_{T}}=0,\;(\mathbf {n}\times \text {curl} {\mathbf {H}})|_{S_{T}}=0\;(\text {perfectly conducting wall}),\\&{\mathbf {u}}(\mathbf {x},0)={\mathbf {u}}_{0}(\mathbf {x}),\; {\mathbf {H}}(\mathbf {x},0)={\mathbf {H}}_{0}(\mathbf {x}),\;\text {in}\;\Omega , \end{aligned} \right. \end{aligned}$$

(2)

with $\text{ div }{\mathbf {u}}_{0}(\mathbf {x})=0$ and $\text{ div }{\mathbf {H}}_{0}(\mathbf {x})=0$. Here $S_{T}:=\partial \Omega \times [0,T]$ and $\mathbf {n}$ is the unit exterior normal to $\partial \Omega .$ Besides, ${\mathbf {u}},$${\mathbf {H}}$ and p represent the velocity field, magnetic field and pressure, respectively. Three parameters appearing in (1) are the kinematic viscosity $\nu ,$ the magnetic permeability $\mu$ and the electric conductivity $\sigma .$ Furthermore, ${\mathbf {f}}$ denotes the known body force and ${\mathbf {J}}$ is the known current with $\mathbf {n}\times {\mathbf {J}}|_{S_{T}}=0$.

For the mathematical setting of problem (1) with the boundary and initial conditions (2), we introduce the usual $L^{2}(\Omega )$ norm and its inner product by $\Vert \cdot \Vert _{0,2}$ and $(\cdot ,\cdot ),$ respectively. The $L^{p}(\Omega )$ norm and $W^{m,p}(\Omega )$ norm are denoted by $\Vert \cdot \Vert _{0,p}$ and $\Vert \cdot \Vert _{m,p}$, respectively, for $m\in \mathbb {N^{+}}$, $1\le p\le \infty$. In particular, $H^{m}(\Omega )$ is used to represent the space $W^{m,2}(\Omega )$ and $\Vert \cdot \Vert _{m,2}$ denotes the norm in $H^{m}(\Omega )$. Besides, for X being a normed function space in $\Omega$, $L^{p}(0,T;X)$ is the space of all functions defined on $[0,T]\times \Omega$ for which the norm

$$\begin{aligned} \Vert u\Vert _{L^{p}(0,T;X)}=\left( \int _{0}^{T}\Vert u\Vert _{X}^{p}dt\right) ^{\frac{1}{p}}, \quad p\in [1,\infty ), \end{aligned}$$

is finite.

We define the following particular subspaces of $H^{1}(\Omega )^d$ that satisfy specific boundary conditions [16, 22, 23]:

$$\begin{aligned} \mathbf {X}&:={H}_{0}^{1}(\Omega )^d=\{{\mathbf {v}}\in {H}^{1}(\Omega )^{d}:{\mathbf {v}}|_{\partial \Omega }=0\},\quad \\ {\mathbf {W}}&:={H}_{n}^{1}(\Omega )^d=\{{\mathbf {B}}\in {H}^{1}(\Omega )^{d}:{\mathbf {B}}\cdot \mathbf {n}|_{\partial \Omega }=0\}, \end{aligned}$$

and subspaces with (weakly) divergence-free functions:

$$\begin{aligned} \mathbf {X}_{0}:=\{{\mathbf {v}}\in \mathbf {X}:\text{ div }{\mathbf {v}}=0\},\quad {\mathbf {W}}_{0}:=\{{\mathbf {B}}\in {\mathbf {W}}:\text{ div }{\mathbf {B}}=0\}, \end{aligned}$$

and subspace of $L^{2}(\Omega )$:

$$\begin{aligned} M:=L_{0}^{2}(\Omega )=\{q\in L^{2}(\Omega ):(1,q)=0\}. \end{aligned}$$

To derive the variational formulation of problem (1)–(2), we introduce two bilinear forms:

$$\begin{aligned}&a({\mathbf {u}},{\mathbf {v}})=\nu (\nabla {\mathbf {u}},\nabla {\mathbf {v}})\quad \forall {\mathbf {u}},{\mathbf {v}}\in \mathbf {X},\qquad d({\mathbf {v}},q)=(\text{ div }{\mathbf {v}},q)\quad \forall {\mathbf {v}}\in \mathbf {X},\;q\in M, \end{aligned}$$

the skew-symmetric form:

$$\begin{aligned} b({\mathbf {u}},{\mathbf {v}},\mathbf {w})&=(({\mathbf {u}}\cdot \nabla ){\mathbf {v}},\mathbf {w})+\frac{1}{2}((\text{ div }{\mathbf {u}})\mathbf {w},{\mathbf {v}})\nonumber \\&=\frac{1}{2}(({\mathbf {u}}\cdot \nabla ){\mathbf {v}},\mathbf {w})-\frac{1}{2}(({\mathbf {u}}\cdot \nabla )\mathbf {w},{\mathbf {v}})\quad \forall {\mathbf {u}},{\mathbf {v}},\mathbf {w}\in \mathbf {X}, \end{aligned}$$

(3)

which satisfies following properties [17, 24, 41]:

$$\begin{aligned} |b({\mathbf {u}},{\mathbf {v}},\mathbf {w})|&\le C_{0}\Vert \nabla {\mathbf {u}}\Vert _{0,2}\Vert \nabla {\mathbf {v}}\Vert _{0,2}\Vert \nabla \mathbf {w}\Vert _{0,2}, \end{aligned}$$

(4)

$$\begin{aligned} |b({\mathbf {u}},{\mathbf {v}},\mathbf {w})|&\le C_{1}\Vert {\mathbf {u}}\Vert _{0,2}^{\frac{1}{2}}\Vert \nabla {\mathbf {u}}\Vert _{0,2}^{\frac{1}{2}}\Vert \nabla {\mathbf {v}}\Vert _{0,2}\Vert \nabla \mathbf {w}\Vert _{0,2}, \end{aligned}$$

(5)

for all ${\mathbf {u}},{\mathbf {v}},\mathbf {w}\in \mathbf {X}$. Moreover, if ${\mathbf {v}}\in H^2(\Omega )^d,$ then there exists $C_2$ such that [16]

$$\begin{aligned} |b({\mathbf {u}},{\mathbf {v}},\mathbf {w})|\le C_2\Vert {\mathbf {u}}\Vert _{0,2}\Vert {\mathbf {v}}\Vert _{2,2}\Vert \nabla \mathbf {w}\Vert _{0,2}. \end{aligned}$$

(6)

Additionally, from [15, 23], we have the following bounds

$$\begin{aligned}&|({\mathbf {v}}\times {\mathbf {H}},\text {curl}{\mathbf {B}})|\le C_{3}\Vert \nabla {\mathbf {v}}\Vert _{0,2}\Vert \text {curl}{\mathbf {H}}\Vert _{0,2} \Vert \text {curl}{\mathbf {B}}\Vert _{0,2}, \end{aligned}$$

(7)

$$\begin{aligned}&|({\mathbf {v}}\times {\mathbf {H}},\text {curl}{\mathbf {B}})|\le C_{4}\Vert {\mathbf {v}}\Vert _{2,2}\Vert {\mathbf {H}}\Vert _{0,2}\Vert \text {curl}{\mathbf {B}}\Vert _{0,2}, \end{aligned}$$

(8)

$$\begin{aligned}&|({\mathbf {v}}\times {\mathbf {H}},\text {curl}{\mathbf {B}})|\le C_{5}\Vert \nabla {\mathbf {v}}\Vert _{0,2}\Vert {\mathbf {B}}\Vert _{2,2}\Vert {\mathbf {H}}\Vert _{0,2}, \end{aligned}$$

(9)

for all ${\mathbf {v}}\in \mathbf {X}$ and ${\mathbf {B}},{\mathbf {H}}\in {\mathbf {W}}$ or ${\mathbf {v}},{\mathbf {B}}\in H^2(\Omega )^d$. Here and after, we denote C (with or without a subscript) as a general positive constant depending on $(\nu ,\mu ,\sigma ,\Omega ,T,{\mathbf {u}}_{0},{\mathbf {H}}_{0},{\mathbf {f}},{\mathbf {J}}),$ which may stand for different values at different occurrences.

Then, based on the above definitions of functional spaces, we have the following variational formulation of problem (1)–(2): Find $({\mathbf {u}},p,{\mathbf {H}})\in L^{2}(0,T;\mathbf {X})\times L^{2}(0,T;M)\times L^{2}(0,T;{\mathbf {W}})$ such that, for all $({\mathbf {v}},q,{\mathbf {B}})\in \mathbf {X}\times M\times {\mathbf {W}}$ and for almost all $t\in (0,T)$,

$$\begin{aligned}&({\mathbf {u}}_{t},{\mathbf {v}})+a({\mathbf {u}},{\mathbf {v}})+b({\mathbf {u}},{\mathbf {u}},{\mathbf {v}})+\mu ({\mathbf {H}}\times \text {curl}{\mathbf {H}},{\mathbf {v}})-d({\mathbf {v}},p)+d({\mathbf {u}},q)=({\mathbf {f}},{\mathbf {v}}), \end{aligned}$$

(10)

$$\begin{aligned}&\mu ({\mathbf {H}}_{t},{\mathbf {B}})+\sigma ^{-1}(\text {curl}{\mathbf {H}},\text {curl}{\mathbf {B}})-\mu ({\mathbf {u}}\times {\mathbf {H}},\text {curl}{\mathbf {B}})=\sigma ^{-1}({\mathbf {J}},\text {curl}{\mathbf {B}}), \end{aligned}$$

(11)

$$\begin{aligned}&{\mathbf {u}}(0)={\mathbf {u}}_{0},\;{\mathbf {H}}(0)={\mathbf {H}}_{0}. \end{aligned}$$

(12)

Throughout this paper we need the following assumptions as in [23] on the prescribed data for problem (1)–(2). :

Assumption A0

The initial data ${\mathbf {u}}_{0}\in \mathbf {X}_{0}\cap H^{2}(\Omega )^{d}$, ${\mathbf {H}}_{0}\in {\mathbf {W}}_{0}\cap H^{2}(\Omega )^{d}$, the force ${\mathbf {f}}$ and the current ${\mathbf {J}}$ satisfy the bound

$$\begin{aligned} \sup _{0\le t\le T}\Big (\Vert {\mathbf {f}}(t)\Vert _{0,2}+\Vert {\mathbf {f}}_{t}(t)\Vert _{0,2}+\Vert {\mathbf {J}}(t)\Vert _{1,2} +\Vert {\mathbf {J}}_{t}(t)\Vert _{1,2}\Big )+\Vert {\mathbf {u}}_{0}\Vert _{2,2}+\Vert {\mathbf {H}}_{0}\Vert _{2,2}\le C. \end{aligned}$$

Assumption A1

The problem (10)–(12) has a weak solution $({\mathbf {u}}(t),p(t),{\mathbf {H}}(t))$ satisfying ${\mathbf {u}}\in L^{2}(0,T;\mathbf {X}_{0})$, ${\mathbf {H}}\in L^{2}(0,T;{\mathbf {W}}_{0})$ and $p\in L^{2}(0,T;M)$ such that

$$\begin{aligned} \int _{0}^{T}(\Vert \nabla {\mathbf {u}}(t)\Vert _{0,2}^{4}+\Vert \text {curl}{\mathbf {H}}(t)\Vert _{0,2}^{4})dt\le C. \end{aligned}$$

Assumption A2

Assume that the boundary of $\Omega$ is smooth so that the unique solution $({\mathbf {v}},q)$ of the steady Stokes problem

$$\begin{aligned} -\Delta {\mathbf {v}}+\nabla q=\mathbf {f_u},\quad \nabla \cdot {\mathbf {v}}=0\;\text {in}\; \Omega , \quad {\mathbf {v}}|_{\partial \Omega }=0, \end{aligned}$$

for prescribed $\mathbf {f_u}\in L^{2}(\Omega )^{d}$ satisfies

$$\begin{aligned} \Vert {\mathbf {v}}\Vert _{2,2}+\Vert q\Vert _{1,2}\le C\Vert \mathbf {f_u}\Vert _{0,2}; \end{aligned}$$

and Maxwell’s equations

$$\begin{aligned} \text {curl}\text {curl}{\mathbf {B}}=\mathbf {f_H},\quad \nabla \cdot {\mathbf {B}}=0\;\text {in}\; \Omega , \quad \mathbf {n}\times \text {curl}{\mathbf {B}}=0,\quad {\mathbf {B}}\cdot \mathbf {n}=0\;\text {on}\;\partial \Omega , \end{aligned}$$

for the prescribed $\mathbf {f_H}\in L^{2}(\Omega )^{d}$ admits a unique solution ${\mathbf {B}}\in {\mathbf {W}}_{0}$ which satisfies

$$\begin{aligned} \Vert {\mathbf {B}}\Vert _{2,2}\le C\Vert \mathbf {f_H}\Vert _{0,2}. \end{aligned}$$

Besides, we recall some a priori energy estimates of the solution to the problem (10)–(12) in the following, which are proved in [23].

Lemma 2.1

[23] Assume that Assumption (A0)–(A2) hold, then the solution $({\mathbf {u}}(t),p(t),{\mathbf {H}}(t))$ of the problem (10)–(12) satisfies the estimate

$$\begin{aligned} \begin{aligned}&\sup _{0\le t\le T}(\Vert {\mathbf {u}}_{t}(t)\Vert _{0,2}^{2}+\Vert {\mathbf {H}}_{t}(t)\Vert _{0,2}^{2} +\Vert {\mathbf {u}}(t)\Vert _{2,2}^{2}+\Vert {\mathbf {H}}(t)\Vert _{2,2}^{2}+\Vert p(t)\Vert _{1,2}^2)\\&\quad +\,\int _{0}^{T}(\Vert {\mathbf {u}}_{tt}\Vert _{-1,2}^{2}+\Vert {\mathbf {H}}_{tt}\Vert _{-1,2}^{2}+\Vert \nabla {\mathbf {u}}_{t}\Vert _{0,2}^{2}+\Vert \nabla {\mathbf {H}}_{t}\Vert _{0,2}^{2})dt\le C, \end{aligned} \end{aligned}$$

where $\Vert {\mathbf {u}}_{tt}\Vert _{-1,2}=\sup _{{\mathbf {v}}\in \mathbf {X}}\frac{|({\mathbf {u}}_{tt},{\mathbf {v}})|}{\Vert \nabla {\mathbf {v}}\Vert _{0,2}}$ and $\Vert {\mathbf {H}}_{tt}\Vert _{-1,2}=\sup _{{\mathbf {B}}\in {\mathbf {W}}}\frac{| ({\mathbf {H}}_{tt},{\mathbf {B}})|}{\Vert \nabla {\mathbf {B}}\Vert _{0,2}}.$

From now on, $\pi _{h}$ is a uniform partition of the domain $\Omega$ into triangular ($d=2$) or tetrahedral ($d=3$) element K with diameters bounded by a real positive parameter $h=\max _{K\in \pi _h}\{\text{ diam }(K)\}.$

Next, we introduce the following finite element subspaces:

$$\begin{aligned} \mathbf {X}_{h}&=\{{\mathbf {v}}_{h}\in C^{0}(\Omega )^{d}\cap \mathbf {X}:{\mathbf {v}}_{h}|_{K}\in P_{2}(K)^{d},\forall K\in \pi _{h}\},\\ M_{h}&=\{q_{h}\in C^{0}(\Omega )\cap M:q_{h}|_{K}\in P_{1}(K),\forall K\in \pi _{h}\},\\ {\mathbf {W}}_{h}&=\{{\mathbf {B}}_{h}\in C^{0}(\Omega )^{d}\cap {\mathbf {W}}:{\mathbf {B}}_{h}|_{K}\in P_{2}(K)^{d},\forall K\in \pi _{h}\}. \end{aligned}$$

Furthermore, we need the subspace $\mathbf {X}_{0h}$ of $\mathbf {X}_{h}$ which is defined as

$$\begin{aligned} \mathbf {X}_{0h}=\{{\mathbf {v}}_{h}\in \mathbf {X}_{h}: d({\mathbf {v}}_{h},q)=0,\forall q_h\in M_h\}. \end{aligned}$$

Let $P_h : L^2(\Omega )^d\rightarrow \mathbf {X}_{h}$ and $R_h : L^2(\Omega )^d\rightarrow {\mathbf {W}}_{h}$ be $L^2$-orthogonal projections. For ${\mathbf {v}}\in H^{2}(\Omega )^{d}\cap \mathbf {X}$ and ${\mathbf {B}}\in H^{2}(\Omega )^{d}\cap {\mathbf {W}}$, these projections satisfy the following properties [23]

$$\begin{aligned}&\Vert P_{h}{\mathbf {v}}\Vert _{1,2}\le C\Vert {\mathbf {v}}\Vert _{1,2},\qquad \Vert {\mathbf {v}}-P_{h}{\mathbf {v}}\Vert _{0,2}+h\Vert \nabla ({\mathbf {v}}-P_{h}{\mathbf {v}})\Vert _{0,2}\le Ch^{3}\Vert {\mathbf {v}}\Vert _{3,2}, \end{aligned}$$

(13)

$$\begin{aligned}&\Vert R_{h}{\mathbf {B}}\Vert _{1,2}\le C\Vert {\mathbf {B}}\Vert _{1,2},\qquad \Vert {\mathbf {B}}-R_{h}{\mathbf {B}}\Vert _{0,2}+h\Vert \nabla ({\mathbf {B}}-R_{h}{\mathbf {B}})\Vert _{0,2}\le Ch^{3}\Vert {\mathbf {B}}\Vert _{3,2}. \end{aligned}$$

(14)

As is known, the following discrete Gronwall lemma will play an important role in analysis of convergence, so we list it in the following lemma.

Lemma 2.2

[17, 23] Let $a_{n},b_{n}$ and $d_{n}$ for the integer $n\ge 0$ be nonnegative numbers such that

$$\begin{aligned} a_{m}+{\tau }\sum _{n=0}^{m}b_{n}\le {\tau }\sum _{n=0}^{m-1}a_{n}d_{n}+C_*,\quad m\ge 1, \end{aligned}$$

then

$$\begin{aligned} a_{m}+{\tau }\sum _{n=0}^{m}b_{n}\le C_* \exp \left( {\tau }\sum _{n=0}^{m-1}d_{n}\right) ,\quad m\ge 1. \end{aligned}$$

3 A Modular Grad-Div Stabilization for the MHD Equations

Let $N >0$ be a fixed integer number and $\{t_{_{n}}\}_{n=0}^{N}$ be a uniform partition of [0, T] and $t_{n}=n\tau$ with time step $\tau =\frac{T}{N}$. Besides, we define $({\mathbf {u}}_{h}^{n},p_{h}^{n},{\mathbf {H}}_{h}^{n})$ to be an approximate solution of (1)–(2) at $t=t_{n}.$ Then, we construct a modular grad-div stabilization algorithm of the problem (1)–(2) applying the finite element discretization and a semi-implicit backward Euler scheme as the temporal-spatial discretization.

Algorithm 3.1

Step I: Given $({\mathbf {u}}_{h}^{n},{\mathbf {H}}_{h}^{n})\in \mathbf {X}_{h}\times {\mathbf {W}}_{h}$, find $(\hat{{\mathbf {u}}}_{h}^{n+1},p_{h}^{n+1},\hat{{\mathbf {H}}}_{h}^{n+1})\in \mathbf {X}_{h}\times M_{h}\times {\mathbf {W}}_{h}$ such that, for all $0 <n \le N-1$ and $({\mathbf {v}}_{h},q_{h},{\mathbf {B}}_{h})\in \mathbf {X}_{h}\times M_{h}\times {\mathbf {W}}_{h},$

$$\begin{aligned}&(d_{t}{\hat{{\mathbf {u}}}}_{h}^{n+1},{\mathbf {v}}_{h}) +a({\hat{{\mathbf {u}}}}_{h}^{n+1},{\mathbf {v}}_{h}) +b({\mathbf {u}}_{h}^{n},{\hat{{\mathbf {u}}}}_{h}^{n+1},{\mathbf {v}}_{h}) +\mu ({{\mathbf {H}}}_{h}^{n}\times \text {curl}{\hat{{\mathbf {H}}}}_{h}^{n+1},{\mathbf {v}}_{h})-d({\mathbf {v}}_{h},p_{h}^{n+1})\nonumber \\&\qquad +\,d({\hat{{\mathbf {u}}}}_{h}^{n+1},q_{h}) =({\mathbf {f}}^{n+1},{\mathbf {v}}_{h}), \end{aligned}$$

(15)

$$\begin{aligned}&\mu (d_{t}{\hat{{\mathbf {H}}}}_{h}^{n+1},{\mathbf {B}}_{h}) +\sigma ^{-1}(\text {curl}\hat{{\mathbf {H}}}_{h}^{n+1},\text {curl}{\mathbf {B}}_{h}) -\mu ({\hat{{\mathbf {u}}}}_{h}^{n+1}\times {\mathbf {H}}_{h}^{n},\text {curl}{\mathbf {B}}_{h}) \nonumber \\&\quad =\sigma ^{-1}({\mathbf {J}}^{n+1},\text {curl}{\mathbf {B}}_{h}), \end{aligned}$$

(16)

$$\begin{aligned}&\hat{{\mathbf {u}}}_{h}^{0}=P_h{\mathbf {u}}_0,\quad \hat{{\mathbf {H}}}_{h}^{0}=R_h{\mathbf {H}}_0, \end{aligned}$$

(17)

where $d_{t}\hat{\mathbf {s}}_{h}^{n+1}=\frac{1}{{\tau }}(\hat{\mathbf {s}}_{h}^{n+1}-\mathbf {s}_{h}^{n})$ with $\mathbf {s}={\mathbf {u}}$ or ${\mathbf {H}},$ and $\mathbf {g}^{n+1}=\frac{1}{{\tau }}\int _{t_{n}}^{t_{n+1}}\mathbf {g}(t)dt$ with $\mathbf {g}={\mathbf {f}}$ or ${\mathbf {J}}$.

Step II: Given $(\hat{{\mathbf {u}}}_{h}^{n+1},\hat{{\mathbf {H}}}_{h}^{n+1})\in \mathbf {X}_{h}\times {\mathbf {W}}_{h}$ from (15)–(17), find $({\mathbf {u}}_{h}^{n+1},{\mathbf {H}}_{h}^{n+1})\in \mathbf {X}_{h}\times {\mathbf {W}}_{h}$ such that, for all $0 <n \le N-1$ and $({\mathbf {v}}_{h},{\mathbf {B}}_{h})\in \mathbf {X}_{h}\times {\mathbf {W}}_{h},$

$$\begin{aligned}&\left( d_{t}{\mathbf {u}}_{h}^{n+1}-d_{t}\hat{{\mathbf {u}}}_{h}^{n+1},{\mathbf {v}}_{h}\right) +\beta _{1}\left( \nabla \cdot d_{t}{\mathbf {u}}_{h}^{n+1},\nabla \cdot {\mathbf {v}}_{h}\right) +\gamma _{1}(\nabla \cdot {\mathbf {u}}_{h}^{n+1},\nabla \cdot {\mathbf {v}}_{h})=0, \end{aligned}$$

(18)

$$\begin{aligned}&\left( d_t{\mathbf {H}}_{h}^{n+1}-d_t\hat{{\mathbf {H}}}_{h}^{n+1},{\mathbf {B}}_{h}\right) +\beta _{2}\left( \nabla \cdot d_t{\mathbf {H}}_{h}^{n+1},\nabla \cdot {\mathbf {B}}_{h}\right) +\gamma _{2}(\nabla \cdot {\mathbf {H}}_{h}^{n+1},\nabla \cdot {\mathbf {B}}_{h})=0, \end{aligned}$$

(19)

with ${\mathbf {u}}_{h}^{0}=\hat{{\mathbf {u}}}^0_h,$${\mathbf {H}}_{h}^{0}=\hat{{\mathbf {H}}}^0_h$ and stabilization parameters $\beta _i\ge 0,$$\gamma _i\ge 0,$$i=1,2,$ recalling $d_{t}\mathbf {s}_{h}^{n+1}=\frac{1}{\tau }(\mathbf {s}_{h}^{n+1}-\mathbf {s}_{h}^{n}).$

In the following part of this section, we analyze the stability and convergence of the modular grad-div stabilization algorithm for the MHD equations.

3.1 Stability Analysis

In this subsection, we show that Algorithm 3.1 is unconditionally stable. In fact, choosing ${\mathbf {v}}_{h}=2\tau {\mathbf {u}}_{h}^{n+1}$ in (18) and ${\mathbf {B}}_{h}=2\tau {\mathbf {H}}_{h}^{n+1}$ in (19), we have, on using the equality $2(\mathbf {a}-\mathbf {b},\mathbf {a})=|\mathbf {a}|^2-|\mathbf {b}|^2 +|\mathbf {a}-\mathbf {b}|^2$ for $\mathbf {a},\mathbf {b}\in \mathbb {R}^{d},$ that

$$\begin{aligned} \begin{aligned}&\Vert {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} -(\Vert \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}+\beta _1\Vert \nabla \cdot {\mathbf {u}}_{h}^{n}\Vert _{0,2}^{2}) +\Vert {\mathbf {u}}_{h}^{n+1}-\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} \\&\quad +\,2\gamma _{1}{\tau }\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}+ \beta _1\tau ^2\Vert \nabla \cdot d_t{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}=0,\\&\Vert {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}+\beta _2\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2} -(\Vert \hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}+\beta _2\Vert \nabla \cdot {\mathbf {H}}_{h}^{n}\Vert _{0,2}^{2}) +\Vert {\mathbf {H}}_{h}^{n+1}-\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2} \\&\quad +\,2\gamma _{2}{\tau }\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}+ \beta _2\tau ^2\Vert \nabla \cdot d_t{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}=0. \end{aligned} \end{aligned}$$

(20)

Then, we establish the unconditional stability of Algorithm 3.1 in the following theorem.

Theorem 3.1

Suppose that Assumption (A0)–(A2) hold, then Algorithm 3.1 is unconditionally stable. That is,

$$\begin{aligned}&\beta _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}^{2} +\mu \beta _{2}\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}^{2} +\sum _{n=0}^{N-1}\Big (\Vert {\mathbf {u}}_{h}^{n+1} -\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +\mu \Vert {\mathbf {H}}_{h}^{n+1}-\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Big ) \\&\qquad +\,\Vert {\mathbf {u}}_{h}^{N}\Vert _{0,2}^{2}+\tau \sum _{n=0}^{N-1}\Big (\nu \Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +2\gamma _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} +\sigma ^{-1}\Vert \mathrm {curl}{\hat{{\mathbf {H}}}}_{h}^{n+1}\Vert _{0,2}^{2}\\&\qquad +\,2\gamma _{2}\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}\Big ) \\&\qquad +\,\mu \Vert {\mathbf {H}}_{h}^{N}\Vert _{0,2}^{2} +\tau ^2\sum _{n=0}^{N-1}\Big (\Vert d_t\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +\beta _{1}\Vert \nabla \cdot d_t{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} +\mu \Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\\&\qquad +\,\beta _{2}\Vert \nabla \cdot d_t{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}\Big )\\&\quad \le C. \end{aligned}$$

Proof

First, we set $({\mathbf {v}}_{h},q_h)=2{\tau }(\hat{{\mathbf {u}}}_{h}^{n+1},p_h^{n+1})$ and ${\mathbf {B}}_{h}=2{\tau }\hat{{\mathbf {H}}}_{h}^{n+1}$ in (15) and (16), respectively, then add the ensuing equations. Finally, applying (3) and the identity $(\mathbf {a}\times \text {curl}\mathbf {b},\mathbf {c})=(\mathbf {c}\times \mathbf {a},\text {curl}\mathbf {b})$ for $\mathbf {a},\mathbf {b}\in H^1(\Omega )^{d}$ yield

$$\begin{aligned}&\Vert \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}-\Vert {\mathbf {u}}_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +\mu (\Vert \hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}-\Vert {\mathbf {H}}_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\quad +\,2\nu {\tau }\Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +2\sigma ^{-1}{\tau }\Vert \text {curl}\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2} =2{\tau }(({\mathbf {f}}^{n+1},\hat{{\mathbf {u}}}_{h}^{n+1})+\sigma ^{-1}({{\mathbf {J}}^{n+1}},\text {curl}\hat{{\mathbf {H}}}_{h}^{n+1})). \end{aligned}$$

(21)

Inserting (20) in (21) to obtain

$$\begin{aligned}&\Vert {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}-\Vert {\mathbf {u}}_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} +\Vert \hat{{\mathbf {u}}}_{h}^{n+1}-{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} +2{\tau }\nu \Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\mu (\Vert {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}-\Vert {\mathbf {H}}_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}+\Vert \hat{{\mathbf {H}}}_{h}^{n+1} -{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\qquad +\,2\sigma ^{-1}{\tau }\Vert \text {curl}\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\beta _{1}(\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot {\mathbf {u}}_{h}^{n}\Vert _{0,2}^{2}+\tau ^2\Vert \nabla \cdot d_t{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}) +2\gamma _{1}{\tau }\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\beta _{2}\mu (\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot {\mathbf {H}}_{h}^{n}\Vert _{0,2}^{2}+\tau ^2\Vert \nabla \cdot d_t{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2})+2\gamma _{2}{\tau }\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\quad =2{\tau }({\mathbf {f}}^{n+1},\hat{{\mathbf {u}}}_{h}^{n+1}) +2\sigma ^{-1}{\tau }({{\mathbf {J}}}^{n+1},\text {curl}\hat{{\mathbf {H}}}_{h}^{n+1}). \end{aligned}$$

(22)

Further, employing the Cauchy–Schwarz and Young inequalities, we get the bound of the right hand side (RHS) of (22)

$$\begin{aligned} 2{\tau }({\mathbf {f}}^{n+1},\hat{{\mathbf {u}}}_{h}^{n+1})&\le C\int ^{t_{n+1}}_{t_n}\Vert {\mathbf {f}}(t)\Vert ^{2}_{0,2}dt+\nu {\tau }\Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\sigma ^{-1}{\tau }({\mathbf {J}}^{n+1},\text {curl}{\hat{{\mathbf {H}}}}_{h}^{n+1})&\le C\int ^{t_{n+1}}_{t_n}\Vert {\mathbf {J}}(t)\Vert _{0,2}^{2}dt+\sigma ^{-1}{\tau }\Vert \text {curl}{\hat{{\mathbf {H}}}}_{h}^{n+1}\Vert _{0,2}^{2}. \end{aligned}$$

Together with the above estimates, summing (22) over n from 0 to $N-1$ gives

$$\begin{aligned}&\Vert {\mathbf {u}}_{h}^{N}\Vert ^{2}+\mu \Vert {\mathbf {H}}_{h}^{N}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}^{2}+\mu \beta _{2}\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}^{2}\\&\qquad +\,{\tau }\sum _{n=0}^{N-1}\left( \nu \Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}+\sigma ^{-1}\Vert \text {curl}{\hat{{\mathbf {H}}}}_{h}^{n+1}\Vert _{0,2}^{2}+2\gamma _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2} \right. \\&\left. \qquad +\,2\gamma _{2}\Vert \nabla \cdot {\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}\right) \\&\qquad +\,\sum _{n=0}^{N-1}\left( \Vert \hat{{\mathbf {u}}}_{h}^{n+1} -{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}+\tau ^2\Vert d_t\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2} \right. \\&\left. \qquad +\,\mu \Vert \hat{{\mathbf {H}}}_{h}^{n+1}-{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2} +\,\tau ^2\mu \Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\right) \\&\qquad +\,\tau ^2\sum _{n=0}^{N-1}\left( \beta _{1}\Vert \nabla \cdot d_t{\mathbf {u}}_{h}^{n+1}\Vert _{0,2}^{2}+\beta _{2}\mu \Vert \nabla \cdot d_t{\mathbf {H}}_{h}^{n+1}\Vert _{0,2}^{2}\right) \\&\quad \le \Vert {\mathbf {u}}_{h}^{0}\Vert _{0,2}^{2}+\mu \Vert {\mathbf {H}}_{h}^{0}\Vert _{0,2}^{2} +\beta _{1}\Vert \nabla \cdot {\mathbf {u}}_{h}^{0}\Vert _{0,2}^{2}+\beta _{2}\mu \Vert \nabla \cdot {\mathbf {H}}_{h}^{0}\Vert _{0,2}^{2}\\&\qquad +\,C\int ^T_0\left( \Vert {\mathbf {f}}(t)\Vert _{0,2}^{2}+\Vert {\mathbf {J}}(t)\Vert _{0,2}^{2}\right) dt \\&\quad \le C, \end{aligned}$$

where we have used (13), (14) and Assumption (A0). The proof is thus complete. $\square$

3.2 Error Estimates of the Modular Algorithm

We are now in a position to state and prove the error estimate for the modular grad-div stabilization algorithm (15)–(19). In order to obtain the error equation, let $({\mathbf {v}},q)=({\mathbf {v}}_{h},q_h)$ in (10) and ${\mathbf {B}}={\mathbf {B}}_{h}$ in (11) with $t=t_{n+1}$, and use integration by parts to get

$$\begin{aligned}&(d_{t}{\mathbf {u}}(t_{n+1}),{\mathbf {v}}_{h}){+}a({\mathbf {u}}(t_{n+1}),{\mathbf {v}}_{h}) {+}b({\mathbf {u}}(t_{n+1}),{\mathbf {u}}(t_{n+1}),{\mathbf {v}}_{h})+\mu ({\mathbf {H}}(t_{n+1})\times \text {curl}{\mathbf {H}}(t_{n+1}),{\mathbf {v}}_{h})\nonumber \\&\qquad -\,d({\mathbf {v}}_h,p(t_{n+1}))+d({\mathbf {u}}(t_{n+1}),q_h)=({\mathbf {f}}(t_{n+1}),{\mathbf {v}}_{h})-\frac{1}{{\tau }}\int ^{t_{n+1}}_{t_{n}}(t-t_{n})({\mathbf {u}}_{tt}(t),{\mathbf {v}}_{h})dt, \end{aligned}$$

(23)

$$\begin{aligned}&\mu (d_{t}{\mathbf {H}}(t_{n+1}),{\mathbf {B}}_{h})+\sigma ^{-1}(\text {curl}{\mathbf {H}}(t_{n+1}),\text {curl}{\mathbf {B}}_{h})-\mu ({\mathbf {u}}(t_{n+1})\times {\mathbf {H}}(t_{n+1}),\text {curl}{\mathbf {B}}_{h})\nonumber \\&\quad =\sigma ^{-1}({\mathbf {J}}(t_{n+1}),\text {curl}{\mathbf {B}}_{h})-\frac{\mu }{{\tau }}\int ^{t_{n+1}}_{t_{n}}(t-t_{n})({\mathbf {H}}_{tt}(t),{\mathbf {B}}_{h})dt. \end{aligned}$$

(24)

Here we define $d_{t}\mathbf {s}(t_{n+1})=\frac{1}{{\tau }}(\mathbf {s}(t_{n+1})-\mathbf {s}(t_{n}))$ with $\mathbf {s}={\mathbf {u}}$ or ${\mathbf {H}}.$

Then, subtract (15) and (16) from (23) and (24), respectively, to get

$$\begin{aligned}&(d_{t}\hat{{\mathbf {e}}}_{u}^{n+1},{\mathbf {v}}_{h}){+}a(\hat{{\mathbf {e}}}_{u}^{n+1},{\mathbf {v}}_{h}){+}b({\mathbf {u}}(t_{n}),{\mathbf {u}}(t_{n+1}),{\mathbf {v}}_{h}){-}b({\mathbf {u}}_{h}^{n},\hat{{\mathbf {u}}}_{h}^{n+1},{\mathbf {v}}_{h}){-}d({\mathbf {v}}_h,p(t_{n+1})-p_h^{n+1})\nonumber \\&\quad +\,d(\hat{{\mathbf {e}}}_{u}^{n+1},q_h)+\mu ({\mathbf {H}}(t_{n})\times \text {curl}{\mathbf {H}}(t_{n+1}),{\mathbf {v}}_{h})-\mu ({\mathbf {H}}_{h}^{n}\times \text {curl}\hat{{\mathbf {H}}}_{h}^{n+1},{\mathbf {v}}_{h})=({\mathbf {E}}_{1}^{n+1},{\mathbf {v}}_{h}), \end{aligned}$$

(25)

$$\begin{aligned}&\mu (d_{t}\hat{{\mathbf {e}}}_{H}^{n+1},{\mathbf {B}}_{h}) +\sigma ^{-1}(\text {curl}\hat{{\mathbf {e}}}_{H}^{n+1},\text {curl}{\mathbf {B}}_{h}) -\mu ({\mathbf {u}}(t_{n+1})\times {\mathbf {H}}(t_{n}),\text {curl}{\mathbf {B}}_{h})\nonumber \\&\quad +\,\mu (\hat{{\mathbf {u}}}_{h}^{n+1}\times {\mathbf {H}}_{h}^{n},\text {curl}{\mathbf {B}}_{h})=({\mathbf {E}}_{2}^{n+1},{\mathbf {B}}_{h}), \end{aligned}$$

(26)

where

$$\begin{aligned} ({\mathbf {E}}_{1}^{n+1},{\mathbf {v}}_{h})&=-\frac{1}{{\tau }}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\mathbf {u}}_{tt}(t),{\mathbf {v}}_{h})dt +\frac{1}{{\tau }}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\mathbf {f}}_{t}(t),{\mathbf {v}}_{h})dt\nonumber \\&+\,\,b({\mathbf {u}}(t_{n})-{\mathbf {u}}(t_{n+1}),{\mathbf {u}}(t_{n+1}),{\mathbf {v}}_{h})+\mu (({\mathbf {H}}(t_{n})-{\mathbf {H}}(t_{n+1}))\times \text {curl}{\mathbf {H}}(t_{n+1}),{\mathbf {v}}_{h}), \end{aligned}$$

(27)

and

$$\begin{aligned} ({\mathbf {E}}_{2}^{n+1},{\mathbf {B}}_{h})&=-\frac{\mu }{{\tau }}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\mathbf {H}}_{tt}(t),{\mathbf {B}}_{h})dt +\frac{1}{{\sigma \tau }}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\mathbf {J}}_{t}(t),\text {curl}{\mathbf {B}}_{h})dt\nonumber \\&-\,\mu ({\mathbf {u}}(t_{n+1})\times ({\mathbf {H}}(t_{n})-{\mathbf {H}}(t_{n+1})),\text {curl}{\mathbf {B}}_{h}), \end{aligned}$$

(28)

and $\hat{{\mathbf {e}}}_{s}^{n}=\mathbf {s}(t_{n})-\hat{\mathbf {s}}_{h}^{n}$ with $\mathbf {s}={\mathbf {u}}$ or ${\mathbf {H}}$. Split the errors as $\hat{{\mathbf {e}}}_{u}^{n}=\varvec{\eta }_{u}^{n}-\varvec{\hat{\psi }}_{h}^{n}$ where $\varvec{\eta }_{u}^{n}={\mathbf {u}}(t_{n})-\tilde{{\mathbf {u}}}^{n}$ and $\varvec{\hat{\psi }}_{h}^{n}=\hat{{\mathbf {u}}}_{h}^{n}-\tilde{{\mathbf {u}}}^{n},$ and $\hat{{\mathbf {e}}}_{H}^{n}=\varvec{\eta }_{H}^{n}-\varvec{\hat{\phi }}_{h}^{n}$ where $\varvec{\eta }_{H}^{n}={\mathbf {H}}(t_{n})-\tilde{{\mathbf {H}}}^{n}$ and $\varvec{\hat{\phi }}_{h}^{n}=\hat{{\mathbf {H}}}_{h}^{n}-\tilde{{\mathbf {H}}}^{n},$ respectively. Here, $\tilde{{\mathbf {u}}}^{n}$ denotes interpolation of ${\mathbf {u}}(t_{n})$ in $\mathbf {X}_h,$ and $\tilde{{\mathbf {H}}}^{n}$ denotes interpolation of ${\mathbf {H}}(t_{n})$ in ${\mathbf {W}}_h.$

Moreover, in order to derive estimate for error, we need establish bounds of ${\mathbf {E}}_{1}^{n+1}$ and ${\mathbf {E}}_{2}^{n+1}$. In fact, according to (4), (7) and Cauchy–Schwarz inequality, it follows from (27) and (28) that

$$\begin{aligned} \Vert {\mathbf {E}}_{1}^{n+1}\Vert ^2_{-1,2}&=\left( \sup _{{\mathbf {v}}_{h}\in \mathbf {X}_{h}}\frac{|({\mathbf {E}}_{1}^{n+1}, {\mathbf {v}}_{h})|}{\Vert \nabla {\mathbf {v}}_{h}\Vert _{0,2}}\right) ^2\nonumber \\&\le C\tau \Big (\int _{t_{n}}^{t_{n+1}}(\Vert {\mathbf {f}}_{t}(t)\Vert _{0,2}^{2} +\Vert {\mathbf {u}}_{tt}\Vert ^2_{-1,2})dt\nonumber \\&\quad +\,\Vert \nabla {\mathbf {u}}(t_{n+1})\Vert _{0,2}^2\int _{_{t_{n}}}^{t_{n+1}}\Vert \nabla {\mathbf {u}}_{t}(t)\Vert _{0,2}^{2}dt \nonumber \\&\quad +\,\Vert \nabla {\mathbf {H}}(t_{n+1})\Vert _{0,2}^2\int _{_{t_{n}}}^{t_{n+1}}\Vert \nabla {\mathbf {H}}_{t}(t)\Vert _{0,2}^{2}dt\Big ), \end{aligned}$$

(29)

and

$$\begin{aligned} \Vert {\mathbf {E}}_{2}^{n+1}\Vert ^2_{-1,2}&=\left( \sup _{{\mathbf {B}}_{h}\in {\mathbf {W}}_{h}}\frac{|({\mathbf {E}}_{2}^{n+1},{\mathbf {B}}_{h})|}{\Vert \text {curl} {\mathbf {B}}_{h}\Vert _{0,2}}\right) ^2 \le C{\tau }\Big (\int _{_{t_{n}}}^{t_{n+1}}(\Vert {\mathbf {J}}_{t}(t)\Vert _{0,2}^{2} \quad +\Vert {\mathbf {H}}_{tt}\Vert _{-1,2}^2)dt\nonumber \\&\quad +\,\Vert \nabla {\mathbf {u}}(t_{n+1})\Vert _{0,2}^2\int _{_{t_{n}}}^{t_{n+1}}\Vert \nabla {\mathbf {H}}_{t}(t)\Vert _{0,2}^{2}dt\Big ). \end{aligned}$$

(30)

Further, add (29) and (30). Then, summing the ensuing inequality with respect to n from $n=0$ to $n=N-1,$ we arrive at

$$\begin{aligned}&\sum _{n=0}^{N-1}(\Vert {\mathbf {E}}_{1}^{n+1}\Vert ^{2}_{-1,2} +\Vert {\mathbf {E}}_{2}^{n+1}\Vert ^{2}_{-1,2}) \\&\quad \le C{\tau } \int _{0}^{T}(\Vert {\mathbf {f}}_{t}(t)\Vert _{0,2}^{2}+\Vert {\mathbf {u}}_{tt}\Vert _{-1,2}^2 +\Vert {\mathbf {J}}_{t}(t)\Vert _{0,2}^{2}+\Vert {\mathbf {H}}_{tt}\Vert _{-1,2}^2)dt\\&\qquad +\,C{\tau } (\Vert \nabla {\mathbf {u}}(t_{n+1})\Vert ^2_{0,2}+\Vert \nabla {\mathbf {H}}(t_{n+1})\Vert ^2_{0,2})\int _{0}^{T}(\Vert \nabla {\mathbf {u}}_{t}(t)\Vert _{0,2}^{2}+\Vert \nabla {\mathbf {H}}_{t}(t)\Vert _{0,2}^{2})dt. \end{aligned}$$

Based on Assumption (A0) and Lemma 2.1, we arrive at

$$\begin{aligned} \tau \sum _{n=0}^{N-1}(\Vert {\mathbf {E}}_{1}^{n+1}\Vert ^{2}_{-1,2}+\Vert {\mathbf {E}}_{2}^{n+1}\Vert ^{2}_{-1,2}) \le C{\tau }^2. \end{aligned}$$

(31)

Finally, we consider the effect of step II of Algorithm 3.1. Note that

$$\begin{aligned} \left( \frac{{\mathbf {u}}(t_{n+1})-{\mathbf {u}}(t_{n+1})}{\tau },{\mathbf {v}}_{h}\right) +\beta _{1}\left( \nabla \cdot d_t{\mathbf {u}}(t_{n+1}),\nabla \cdot {\mathbf {v}}_{h}\right)&=-\gamma _{1}(\nabla \cdot {\mathbf {u}}(t_{n+1}),\nabla \cdot {\mathbf {v}}_{h}), \end{aligned}$$

(32)

$$\begin{aligned} \left( \frac{{\mathbf {H}}(t_{n+1})-{\mathbf {H}}(t_{n+1})}{\tau },{\mathbf {B}}_{h}\right) +\beta _{2}\left( \nabla \cdot d_t{\mathbf {H}}(t_{n+1}), \nabla \cdot {\mathbf {B}}_{h}\right)&=-\gamma _{2}(\nabla \cdot {\mathbf {H}}(t_{n+1}),\nabla \cdot {\mathbf {B}}_{h}). \end{aligned}$$

(33)

Subtract (18) and (19) from (32) and (33), respectively, which in turn imply that

$$\begin{aligned}&\left( \frac{{\mathbf {e}}_{u}^{n+1}-\hat{{\mathbf {e}}}_{u}^{n+1}}{\tau },{\mathbf {v}}_{h}\right) +\beta _{1}\left( \nabla \cdot d_t{\mathbf {e}}_{u}^{n+1}, \nabla \cdot {\mathbf {v}}_{h}\right) +\gamma _{1}(\nabla \cdot {\mathbf {e}}_{u}^{n+1},\nabla \cdot {\mathbf {v}}_{h})=0 \end{aligned}$$

(34)

$$\begin{aligned}&\left( \frac{{\mathbf {e}}_{H}^{n+1}-\hat{{\mathbf {e}}}_{H}^{n+1}}{\tau },{\mathbf {B}}_{h}\right) +\beta _{2}\left( \nabla \cdot d_t{\mathbf {e}}_{H}^{n+1},\nabla \cdot {\mathbf {B}}_{h}\right) +\gamma _{2}(\nabla \cdot {\mathbf {e}}_{H}^{n+1},\nabla \cdot {\mathbf {B}}_{h})=0, \end{aligned}$$

(35)

where $\mathbf {{e}}_{s}^{n}=\mathbf {s}(t_{n})-\mathbf {{s}}_{h}^{n}$. Split the errors as $\mathbf {{e}}_{u}^{n}=\varvec{\eta }_{u}^{n}-\varvec{{\psi }}_{h}^{n}$ and $\mathbf {{e}}_{H}^{n}=\varvec{\eta }_{H}^{n}-\varvec{{\phi }}_{h}^{n}$ where $\varvec{{\psi }}_{h}^{n}=\mathbf {{u}}_{h}^{n}-\tilde{{\mathbf {u}}}^{n}$ and $\varvec{{\phi }}_{h}^{n}=\mathbf {{H}}_{h}^{n}-\tilde{{\mathbf {H}}}^{n}.$ Let $\tilde{{\mathbf {u}}}^{0}=\mathbf {{u}}_{h}^{0}$ and $\tilde{{\mathbf {H}}}^{0}={\mathbf {H}}_{h}^{0}.$

Selecting ${\mathbf {v}}_{h}=2\tau \varvec{\psi }_{h}^{n+1}$ in (34) and decomposing the errors give the estimate,

$$\begin{aligned}&\Vert \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} +\Vert \varvec{\psi }_{h}^{n+1}-\varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} +2\gamma _{1}{\tau }\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} \\&\qquad +\,\beta _{1}\left( \Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert \nabla \cdot d_t\varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2}\right) \\&\quad =2\beta _{1}\tau ^2(\nabla \cdot d_t\varvec{\eta }_{u}^{n+1}, \nabla \cdot d_t\varvec{\psi }_{h}^{n+1}) +2\beta _{1}\tau (\nabla \cdot d_t\varvec{\eta }_{u}^{n+1}, \nabla \cdot \varvec{\psi }_{h}^{n}) \\&\qquad +\,2\gamma _{1}{\tau }(\nabla \cdot \varvec{\eta }_{u}^{n+1}, \nabla \cdot \varvec{\psi }_{h}^{n+1}) +\Vert \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}\\&\quad \le C\beta _{1}\tau \int _{t_{n}}^{t_{n+1}}\Vert \nabla \varvec{\eta }_{ut}\Vert _{0,2}^2dt +\frac{\beta _{1}\tau ^2}{4}\Vert \nabla \cdot d_t\varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} +C\beta _{1}\int _{t_{n}}^{t_{n+1}}\Vert \nabla \varvec{\eta }_{ut}\Vert _{0,2}^2dt \\&\qquad +\,\frac{\beta _{1}{\tau }}{2}\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +C\gamma _{1}{\tau }\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2} +\frac{\gamma _{1}{\tau }}{2}\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} +\Vert \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}, \end{aligned}$$

where we have apply the Cauchy–Schwarz and Young inequality. Reorganizing the above inequality it follows that

$$\begin{aligned} \Vert \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}&\ge \Vert \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} +\Vert \varvec{\hat{\psi }}_{h}^{n+1}-\varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} +\gamma _{1}{\tau }\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} -\beta _{1}{\tau }\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}\nonumber \\&\quad +\,\beta _{1}(\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert ^{2} +\frac{\tau ^2}{2}\Vert \nabla \cdot d_t\varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\quad -\,C\beta _{1}(1+{\tau })\int _{t_{n}}^{t_{n+1}}\Vert \nabla \varvec{\eta }_{ut}\Vert _{0,2}^2dt -C\gamma _{1}{\tau }\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}. \end{aligned}$$

(36)

Arguing in exactly the same way as in the proof of (36), we obtain

$$\begin{aligned} \Vert \varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}&\ge \Vert \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}+\Vert \varvec{\hat{\phi }}_{h}^{n+1} -\varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2} +\gamma _{2}{\tau }\Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2} -\beta _{2}{\tau }\Vert \nabla \cdot \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}\nonumber \\&\quad +\,\beta _{2}(\Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2} +\frac{\tau ^2}{2}\Vert \nabla \cdot d_t\varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\quad -\,C\beta _{2}(1+{\tau })\int _{t_{n}}^{t_{n+1}}\Vert \nabla \varvec{\eta }_{Ht}\Vert _{0,2}^2dt -C\gamma _{2}{\tau }\Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}. \end{aligned}$$

(37)

Theorem 3.2

Suppose that Assumption (A0)–(A2) are satisfied, then the following estimate holds

$$\begin{aligned} \begin{aligned}&\Vert {\mathbf {e}}_{u}^{N}\Vert _{0,2}^{2}+\mu \Vert {\mathbf {e}}_{H}^{N}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot {\mathbf {e}}_{u}^{N}\Vert _{0,2}^{2}+\mu \beta _{2}\Vert \nabla \cdot {\mathbf {e}}_{H}^{N}\Vert _{0,2}^{2}+\nu {\tau }\sum _{n=0}^{N-1}\Vert \nabla \hat{{\mathbf {e}}}_{u}^{n+1}\Vert _{0,2}^{2}\\&\qquad +\,\sigma ^{-1}{\tau }\sum _{n=0}^{N-1}\Vert \nabla {\hat{{\mathbf {e}}}}_{H}^{n+1}\Vert _{0,2}^{2}+2\gamma _{1}{\tau }\sum _{n=0}^{N-1}\Vert \nabla \cdot {\mathbf {e}}_{u}^{n+1}\Vert _{0,2}^{2}+2\gamma _{2}{\tau }\sum _{n=0}^{N-1}\Vert \nabla \cdot {\mathbf {e}}_{H}^{n+1}\Vert _{0,2}^{2}\\&\quad \le C(h^{4}+\tau h^{3}+{\tau }^{2}). \end{aligned} \end{aligned}$$

(38)

Proof

Setting ${\mathbf {v}}_{h}=2{\tau }\varvec{\hat{\psi }}_{h}^{n+1}\in \mathbf {X}_{0h}$ and $q_h=0$ in (25), and ${\mathbf {B}}_{h}=2{\tau }\varvec{\hat{\phi }}_{h}^{n+1}$ in (26), adding the two equations and decomposing the errors, we deduce that

$$\begin{aligned}&\Vert \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}+\tau ^2\Vert d_t\varvec{\hat{\psi }}_{h}^{n+1} \Vert _{0,2}^{2} +\mu (\Vert \varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}+\tau ^2\Vert d_t\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\qquad +\,2\nu {\tau }\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} +2\sigma ^{-1}{\tau }\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\quad =2\tau (d_t\varvec{\eta }_{u}^{n+1}, \varvec{\hat{\psi }}_{h}^{n+1})+2\tau (d_t\varvec{\eta }_{H}^{n+1},\varvec{\hat{\phi }}_{h}^{n+1}) +2\nu {\tau }(\nabla \varvec{\eta }_{u}^{n+1},\nabla \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad +\,2\sigma ^{-1}{\tau }(\text {curl}\varvec{\eta }_{H}^{n+1}, \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) +2{\tau }b({\mathbf {u}}(t_{n}),{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1}) -2{\tau }b({\mathbf {u}}_{h}^{n},\hat{{\mathbf {u}}}_{h}^{n+1}, \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad +\,2\mu {\tau }({\mathbf {H}}(t_{n})\times \text {curl}{\mathbf {H}}(t_{n+1}), \varvec{\hat{\psi }}_{h}^{n+1})-2\mu {\tau } ({\mathbf {H}}_{h}^{n}\times \text {curl}\hat{{\mathbf {H}}}_{h}^{n+1}, \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad -\,2\mu {\tau }({\mathbf {u}}(t_{n+1})\times {\mathbf {H}}(t_{n}), \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) +2\mu {\tau }(\hat{{\mathbf {u}}}_{h}^{n+1}\times {\mathbf {H}}_{h}^{n}, \text {curl}\varvec{\hat{\phi }}_{h}^{n+1})\nonumber \\&\qquad -\,2{\tau }({\mathbf {E}}_{1}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1}) -2{\tau }({\mathbf {E}}_{2}^{n+1},\varvec{\hat{\phi }}_{h}^{n+1}). \end{aligned}$$

(39)

Inserting $\pm 2{\tau }b({\mathbf {u}}_{h}^{n},{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})$, $\pm 2{\tau }b(\hat{{\mathbf {u}}}_{h}^{n+1},\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})$, $\pm 2\mu {\tau }({\mathbf {H}}_{h}^{n}\times \text {curl}{\mathbf {H}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})$, $\pm 2\mu {\tau }(\hat{{\mathbf {H}}}_{h}^{n+1}\times \text {curl}\varvec{\eta }_{H}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})$, $\pm 2\mu {\tau }({\mathbf {u}}(t_{n+1})\times {\mathbf {H}}_{h}^{n},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1})$ and $\pm 2\mu {\tau }(\varvec{\eta }_{u}^{n+1}\times \hat{{\mathbf {H}}}_{h}^{n+1}, \text {curl}\varvec{\hat{\phi }}_{h}^{n+1})$ into the RHS of (39) and using (3), equation (39) is rewritten as

$$\begin{aligned}&\Vert \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} +\mu (\Vert \varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}+\tau ^2\Vert d_t\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\qquad +\,2\nu {\tau }\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}+2\sigma ^{-1}{\tau }\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\quad =2\tau (d_t\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1}) +2\tau (d_t\varvec{\eta }_{H}^{n+1}, \varvec{\hat{\phi }}_{h}^{n+1})+2\nu {\tau }(\nabla \varvec{\eta }_{u}^{n+1},\nabla \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad +\,2\sigma ^{-1}{\tau }(\text {curl}\varvec{\eta }_{H}^{n+1},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) +2{\tau }b(\varvec{\eta }_{u}^{n},{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1}) \nonumber \\&\qquad -\,2{\tau }b(\varvec{\psi }_{h}^{n},{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1}) +2{\tau }b(-\tau d_t\hat{{\mathbf {u}}}_{h}^{n+1},\varvec{\eta }_{u}^{n+1}, \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad -\,2{\tau }b(\hat{{\mathbf {u}}}_{h}^{n+1},\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1}) +2\mu {\tau }(\varvec{\eta }_{H}^{n}\times \text {curl}{\mathbf {H}}(t_{n+1}), \varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad -\,2\mu {\tau }(\varvec{\phi }_{h}^{n}\times \text {curl}{\mathbf {H}}(t_{n+1}), \varvec{\hat{\psi }}_{h}^{n+1}) +2\mu {\tau }(-\tau d_t\hat{{\mathbf {H}}}_{h}^{n+1}\times \text {curl}\varvec{\eta }_{H}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1}) \nonumber \\ {}&\qquad +\,2\mu {\tau }(\hat{{\mathbf {H}}}_{h}^{n+1}\times \text {curl}\varvec{\eta }_{H}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1}) -2{\tau }({\mathbf {E}}_{1}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})\nonumber \\&\qquad -\,2\mu {\tau }({\mathbf {u}}(t_{n+1})\times \varvec{\eta }_{H}^{n},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) +2\mu {\tau }({\mathbf {u}}(t_{n+1})\times \varvec{\phi }_{h}^{n},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) -2{\tau }({\mathbf {E}}_{2}^{n+1}, \varvec{\hat{\phi }}_{h}^{n+1})\nonumber \\&\qquad -\,2\mu {\tau }(\varvec{\eta }_{u}^{n+1}\times (-\tau d_t\hat{{\mathbf {H}}}_{h}^{n+1}), \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}) -2\mu {\tau }(\varvec{\eta }_{u}^{n+1}\times \hat{{\mathbf {H}}}_{h}^{n+1},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1}), \end{aligned}$$

(40)

in which we have used the fact that $(\mathbf {a}\times \text {curl}\mathbf {b},\mathbf {c})=(\mathbf {c}\times \mathbf {a},\text {curl}\mathbf {b})$ for $\mathbf {a},\mathbf {b}\in H^1(\Omega )^{d}$.

We now estimate each terms of the RHS of (40) separately. Applying the Cauchy–Schwarz and Young inequalities, we have the following bounds,

$$\begin{aligned} 2\tau |(d_t\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|&\le C\int _{t_{n}}^{t_{n+1}}\Vert \varvec{\eta }_{ut}\Vert _{0,2}^2dt+\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\tau |(d_t\varvec{\eta }_{H}^{n+1},\varvec{\hat{\phi }}_{h}^{n+1})|&\le C\int _{t_{n}}^{t_{n+1}}\Vert \nabla \varvec{\eta }_{Ht}\Vert _{0,2}^2dt+\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\nu {\tau }|(\nabla \varvec{\eta }_{u}^{n+1},\nabla \varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2} +\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\sigma ^{-1}{\tau }|(\text {curl}\varvec{\eta }_{H}^{n+1}, \text {curl}\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert \text {curl}\varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2} +\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}, \end{aligned}$$

Next, making use of (4), (5), (6), the inverse inequality, the Cauchy–Schwarz and Young’s inequalities, we arrive at

$$\begin{aligned} 2{\tau }|b(\varvec{\eta }_{u}^{n},{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert \nabla {\mathbf {u}}(t_{n+1})\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n}\Vert _{0,2}^{2}+\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2{\tau }|b(\varvec{\psi }_{h}^{n},{\mathbf {u}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {u}}(t_{n+1})\Vert _{2,2}^{2}\Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2{\tau }|b({\mathbf {u}}_{h}^{n}-\hat{{\mathbf {u}}}_{h}^{n+1},\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }h^{-\frac{1}{2}}\Vert {\mathbf {u}}_{h}^{n}-\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}\\&\le C{\tau }h^{-1}\Vert {\mathbf {u}}_{h}^{n}-\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}+\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2{\tau }|b(\hat{{\mathbf {u}}}_{h}^{n+1},\varvec{\eta }_{u}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}+\frac{\nu {\tau }}{12}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}, \end{aligned}$$

Further, combining (7), (8) and (9) with the Cauchy–Schwarz and Young’s inequalities shows that

$$\begin{aligned} 2\mu {\tau }|(\varvec{\eta }_{H}^{n}\times \text {curl}{\mathbf {H}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {H}}(t_{n+1})\Vert _{2,2}^{2}\Vert \varvec{\eta }_{H}^{n}\Vert _{0,2}^{2}+\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|(\varvec{\phi }_{h}^{n}\times \text {curl}{\mathbf {H}}(t_{n+1}),\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {H}}(t_{n+1})\Vert _{2,2}^{2}\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2} +\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|(({\mathbf {H}}_{h}^{n}-\hat{{\mathbf {H}}}_{h}^{n+1})\times \text {curl}\varvec{\eta }_{H}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {H}}_{h}^{n}-\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}h^{-1}\Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}\\&\quad +\,\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|(\hat{{\mathbf {H}}}_{h}^{n+1}\times \text {curl}\varvec{\eta }_{H}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|&\le C{\tau }\Vert \mathrm {curl}\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \text {curl}\varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}\\&\quad +\,\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|({\mathbf {u}}(t_{n+1})\times \varvec{\eta }_{H}^{n},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {u}}(t_{n+1})\Vert _{2,2}^{2}\Vert \varvec{\eta }_{H}^{n}\Vert _{0,2}^{2}+\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|({\mathbf {u}}(t_{n+1})\times \varvec{\phi }_{h}^{n},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {u}}(t_{n+1})\Vert _{2,2}^{2}\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}+\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|(\varvec{\eta }_{u}^{n+1}\times ({\mathbf {H}}_{h}^{n}-\hat{{\mathbf {H}}}_{h}^{n+1}),\text {curl}\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {H}}_{h}^{n}-\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}h^{-1} \Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}\\&\quad +\,\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2},\\ 2\mu {\tau }|(\varvec{\eta }_{u}^{n+1}\times \hat{{\mathbf {H}}}_{h}^{n+1},\text {curl}\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert \mathrm {curl}\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}\\&\quad +\,\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}. \end{aligned}$$

Finally, the consistency error terms are bounded as

$$\begin{aligned} 2{\tau }|({\mathbf {E}}_{1}^{n+1},\varvec{\hat{\psi }}_{h}^{n+1})|+2{\tau }|({\mathbf {E}}_{2}^{n+1},\varvec{\hat{\phi }}_{h}^{n+1})|&\le C{\tau }\Vert {\mathbf {E}}_{1}^{n+1}\Vert _{-1,2}^{2}+C{\tau }\Vert {\mathbf {E}}_{2}^{n+1}\Vert _{-1,2}^{2}\\&\quad +\,\frac{\sigma ^{-1}{\tau }}{7}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}+\frac{\nu {\tau }}{11}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}. \end{aligned}$$

Use above estimates, insert (36) and (37) into (40) and rearrange. Then,

$$\begin{aligned}&\Vert \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}+\Vert \varvec{\psi }_{h}^{n+1} -\varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2} +\tau ^2\Vert d_t\varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}+\nu {\tau }\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\mu (\Vert \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}{-}\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2} {+}\Vert \varvec{\phi }_{h}^{n+1}{-}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2} {+}\tau ^2\Vert d_t\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2})+\sigma ^{-1}{\tau }\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\beta _{1}\left( \Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +\frac{\tau ^2}{2}\Vert \nabla \cdot d_t\varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2}\right) +\gamma _{1}{\tau }\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\beta _{2}\mu \left( \Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2} -\Vert \nabla \cdot \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2} +\frac{\tau ^2}{2}\Vert \nabla \cdot d_t\varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}\right) +\mu \gamma _{2}{\tau }\Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\quad \le C{\tau }\left( \Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2} +\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2} +\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}+\mu \beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}\right) \nonumber \\&\qquad +\,C{\tau }(\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}+\Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2})\nonumber \\&\qquad +\, C\left( \int ^{t_{n+1}}_{t_n}\Vert \varvec{\eta }_{ut}\Vert _{0,2}^{2}dt +\int ^{t_{n+1}}_{t_n}\Vert \varvec{\eta }_{Ht}\Vert _{0,2}^{2}dt+{\tau }\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}+{\tau }\mu \Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}\right) \nonumber \\&\qquad +\,C(1+{\tau })\left( \beta _{1} \int ^{t_{n+1}}_{t_n}\Vert \nabla \varvec{\eta }_{ut}\Vert _{0,2}^{2}dt+\beta _{2}\mu \int ^{t_{n+1}}_{t_n}\Vert \nabla \varvec{\eta }_{Ht}\Vert _{0,2}^{2}dt\right) \nonumber \\&\qquad +\,C{\tau } \left( \Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}{+}\Vert \nabla \hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2}{+}\Vert \nabla \hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}\right) \nonumber \\&\qquad +\,C{\tau } \left( \tau ^2h^{-1}\Vert d_t\hat{{\mathbf {u}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2} +\tau ^2h^{-1}\Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{H}^{n+1}\Vert _{0,2}^{2}\right) \nonumber \\&\qquad +\,C{\tau } \left( \tau ^2h^{-1}\Vert d_t\hat{{\mathbf {H}}}_{h}^{n+1}\Vert _{0,2}^{2}\Vert \nabla \varvec{\eta }_{u}^{n+1}\Vert _{0,2}^{2} +\Vert {\mathbf {E}}_{1}^{n+1}\Vert _{-1,2}^{2}+\Vert {\mathbf {E}}_{2}^{n+1}\Vert _{-1,2}^{2}\right) , \end{aligned}$$

(41)

where we have used Lemma 2.1.

Sum (41) from $n=0$ to $N-1$ and use Theorem 3.1, (31) and the accuracy of the interpolation to yield

$$\begin{aligned}&\Vert \varvec{\psi }_{h}^{N}\Vert _{0,2}^{2}+\mu \Vert \varvec{\phi }_{h}^{N}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{N}\Vert _{0,2}^{2}+\beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{N}\Vert _{0,2}^{2}+\nu {\tau }\sum _{n=0}^{N-1}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}\nonumber \\&\qquad +\,\frac{{\tau }}{\sigma }\sum _{n=0}^{N-1}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}+{\tau }\sum _{n=0}^{N-1}\left( \gamma _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2}+\gamma _{2}\mu \Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}\right) \nonumber \\&\quad \le C{\tau }\sum _{n=0}^{N-1}\left( \Vert \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}+\Vert \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{n}\Vert _{0,2}^{2}+\beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{n}\Vert _{0,2}^{2}\right) \nonumber \\&\qquad +\,C(h^{4}+{\tau }^{2}+\tau h^3+\Vert \varvec{\psi }_{h}^{0}\Vert _{0,2}^{2}+\mu \Vert \varvec{\phi }_{h}^{0}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{0}\Vert _{0,2}^{2}+\beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{0}\Vert _{0,2}^{2}). \end{aligned}$$

(42)

In view of Lemma 2.2, we have

$$\begin{aligned} \begin{aligned}&\Vert \varvec{\psi }_{h}^{N}\Vert _{0,2}^{2}+\mu \Vert \varvec{\phi }_{h}^{N}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{N}\Vert _{0,2}^{2}+\beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{N}\Vert _{0,2}^{2}+\nu {\tau }\sum _{n=0}^{N-1}\Vert \nabla \varvec{\hat{\psi }}_{h}^{n+1}\Vert _{0,2}^{2}\\&\qquad +\,\frac{{\tau }}{\sigma }\sum _{n=0}^{N-1}\Vert \text {curl}\varvec{\hat{\phi }}_{h}^{n+1}\Vert _{0,2}^{2}+{\tau }\sum _{n=0}^{N-1}\left( \gamma _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{n+1}\Vert _{0,2}^{2}+\gamma _{2}\mu \Vert \nabla \cdot \varvec{\phi }_{h}^{n+1}\Vert _{0,2}^{2}\right) \\&\quad \le C(h^{4}+\tau h^{3}+{\tau }^{2}+\Vert \varvec{\psi }_{h}^{0}\Vert _{0,2}^{2}+\mu \Vert \varvec{\phi }_{h}^{0}\Vert _{0,2}^{2}+\beta _{1}\Vert \nabla \cdot \varvec{\psi }_{h}^{0}\Vert _{0,2}^{2}+\beta _{2}\Vert \nabla \cdot \varvec{\phi }_{h}^{0}\Vert _{0,2}^{2}). \end{aligned} \end{aligned}$$

Then we have completed the proof by using $\varvec{\psi }_{h}^{0}=\varvec{\phi }_{h}^{0}=0$ and applying the triangle inequality. $\square$

4 Numerical Experiments

In this section, we give some numerical examples to illustrate the theoretical results proven in the previous sections and to show the effectiveness of Algorithm 3.1 for the 2D/3D unsteady incompressible MHD problem. Convergence will be checked against problems with known analytical solutions and a classical benchmark problem, Hartmann flow, which is the MHD version of classical Poiseuille flow. In the given experiments, the velocity, pressure and magnetic are approximated by the $P_{2}-P_{1}-P_{2}$ element pair.

4.1 Analytical Solutions

The prescribed solutions are in $\Omega =(0,1)^{d}$ and $d=2,3$. The right hand sides of problem (1) are determined by the following exact solutions with $\alpha$ an arbitrary positive constant

$$\begin{aligned} u_{1}&=\alpha \pi \sin ^2(\pi x)\sin (\pi y)\cos (\pi y)\cos (t),\quad u_{2}=-\alpha \pi \sin (\pi x)\sin ^2(\pi y)\cos (\pi x)\cos (t),\\ H_{1}&=\alpha \sin (\pi x)\cos (\pi y)\cos (t),\quad H_{2}=-\alpha \cos (\pi x)\sin (\pi y)\cos (t),\\ p&=\alpha \cos (\pi x)\cos (\pi y)\cos (t), \end{aligned}$$

for $d=2$ and

$$\begin{aligned} u_{1}&=-\frac{1}{2}\alpha \pi \sin ^2(\pi x)\sin (\pi y)\cos (\pi y)\sin (\pi z)\cos (\pi z)\cos (t),\\ u_{2}&=\alpha \pi \sin (\pi x)\cos (\pi x)\sin ^2(\pi y)\sin (\pi z)\cos (\pi z)\cos (t),\\ u_{3}&=-\frac{1}{2}\alpha \pi \sin (\pi x)\cos (\pi x)\sin (\pi y)\cos (\pi y)\sin ^2(\pi z)\cos (t),\\ p&=\alpha \cos (\pi x)\cos (\pi y)\cos (\pi z)\cos (t),\\ H_{1}&=-\frac{1}{2}\alpha \pi \sin (\pi x)\cos (\pi y)\cos (\pi z)\cos (t),\\ H_{2}&=\alpha \pi \cos (\pi x)\sin (\pi y)\cos (\pi z)\cos (t),\\ H_{3}&=-\frac{1}{2}\alpha \pi \cos (\pi x)\cos (\pi y)\sin (\pi z)\cos (t), \end{aligned}$$

for $d=3$. Besides, choose equation parameters $\nu =1$, $\mu =1$ and $\sigma =1$, the stabilization parameters $\gamma _{1}=\gamma _{2}=1$ and $\beta _{1}=\beta _{2}=0.2$, $\alpha =0.01$ and the final time $T=1$.

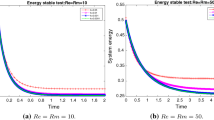
Firstly, we implement the numerical tests to verify the unconditional stability of the presented method. In order to verify Theorem 3.1, we compute the values of $\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}$, $\Vert \nabla \hat{{\mathbf {u}}}_{h}^{N}\Vert _{0,2}$, $\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \hat{{\mathbf {H}}}_{h}^{N}\Vert _{0,2}$ for the 2D/3D MHD problems with different time steps, which are listed in Tables 1, 2, 3 and 4. From these tables, we find that the values of $\Vert \nabla \hat{{\mathbf {u}}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \hat{{\mathbf {H}}}_{h}^{N}\Vert _{0,2}$ approach constants, which shows that no time-step restriction is needed. Besides, the values of $\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}$ are small, which shows that the numerical solutions have better conservation.

Table 1 $\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}$ of the considered scheme for 2D problem

Table 2 $\Vert \nabla \hat{{\mathbf {u}}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \hat{{\mathbf {H}}}_{h}^{N}\Vert _{0,2}$ of the considered scheme for 2D problem

Table 3 $\Vert \nabla \cdot {\mathbf {u}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \cdot {\mathbf {H}}_{h}^{N}\Vert _{0,2}$ of the considered scheme for 3D problem

Table 4 $\Vert \nabla \hat{{\mathbf {u}}}_{h}^{N}\Vert _{0,2}$ and $\Vert \nabla \hat{{\mathbf {H}}}_{h}^{N}\Vert _{0,2}$ of the considered scheme for 3D problem

Secondly, we implement the numerical tests to verify the error convergence rate of Algorithm 3.1, which is presented in Theorem 3.2. Here, we pick several values of ${\tau }$: 1/4, 1/8, 1/16, 1/32, 1/64 for the 2D problem and 1/2, 1/4, 1/6, 1/8, 1/10, 1/12 for the 3D problem. Let $Err({\mathbf {e}}_s)$ denote the error by

$$\begin{aligned} Err({\mathbf {e}}_s)&=\left( \tau \sum _{n=0}^{N-1}\Vert {\mathbf {e}}^{n+1}_s\Vert _{0,2}^2\right) ^{1/2}. \end{aligned}$$

We present the error results of the velocity and magnetic field in Tables 5, 6, 7 and 8. From these numerical results, the expected first-order time accuracy (or better) is seen for all relevant quantities. Moreover, we show the spatial convergence rates of the velocity and magnetic field for 2D and 3D problems in Tables 9, 10, 11 and 12. From these tables, we find that the desired second-order accuracy (or better) for $Err(\nabla \cdot {\mathbf {e}}_u)$, $Err(\nabla \cdot {\mathbf {e}}_H)$, $Err(\nabla \hat{{\mathbf {e}}}_u)$ and $Err(\nabla \hat{{\mathbf {e}}}_H)$ are obtained. As expected, the values of $Err(\nabla \cdot {\mathbf {e}}_u)$ and $Err(\nabla \cdot {\mathbf {e}}_H)$ are small, which shows that the numerical solutions of the presented method has better mass conservation.

Table 5 Errors and convergence rates of the considered scheme with ${h}=\mathcal {O}(\tau )$ for 2D problem

Table 6 Errors and convergence rates of the considered scheme with ${h}=\mathcal {O}(\tau )$ for 2D problem

Table 7 Errors and convergence rates of the considered scheme with ${h}=\mathcal {O}(\tau )$ for 3D problem

Table 8 Errors and convergence rates of the considered scheme with ${h}=\mathcal {O}(\tau )$ for 3D problem

Table 9 Errors and convergence rates of the considered scheme with ${\tau }=\mathcal {O}(h^{2})$ for 2D problem

Table 10 Errors and convergence rates of the considered scheme with ${\tau }=\mathcal {O}(h^{2})$ for 2D problem

Table 11 Errors and convergence rates of the considered scheme with ${\tau }=\mathcal {O}(h^{2})$ for 3D problem

Table 12 Errors and convergence rates of the considered scheme with ${\tau }=\mathcal {O}(h^{2})$ for 3D problem

Thirdly, for the timing test, we compare our algorithm with the standard grad-div algorithm. We set ${\tau }=h=1/32$, and vary the grad-div parameters such that $0\le \beta _{1},\beta _{2}\le 8000$ and $0<\gamma _{1},\gamma _{2}\le 20{,}000$ at $T=1$ for 2D problem. For the standard grad-div algorithm and Step $\text {I}$ of the modular grad-div algorithm, we use GMRES to solve. For Step $\text {II}$ of the modular grad-div algorithm, at each time step, we use UMFPACK to solve. We list the computational times in Table 13. We see that the computational time cost by the modular grad-div algorithm does not increase as the stabilization parameters increase. However, for the standard grad-div algorithm, increasing stabilization parameters increases computational time. In addition, we can find that the present method costs less computational time, which is not surprising since Step I of the presented algorithm requires solution of a standard system without the added coupling or ill-conditioning of the grad-div terms and Step II is the same uncoupled and simple grad-div system at every timestep.

Table 13 Computational time by different grad-div algorithms

4.2 Hartmann Flow

Hartmann flow is a classical benchmark problem for the MHD model which involves a steady unidirectional flow. It describes the flow of a liquid metal through a channel under an external transverse magnetic field [21] and has been investigated in [42, 44, 45, 48]. The related physical parameters $R_{e}$ (fluid Reynolds number), $R_{m}$ (magnetic Reynolds number) and the coupling coefficient s are given by

$$\begin{aligned} R_{e}=\frac{1}{\nu },\quad R_{m}=\mu \sigma ,\quad s=\frac{1}{\mu }, \end{aligned}$$

in our numerical examples. We consider both 2D/3D Hartmann flows with Hartmann number $H_{a}=\sqrt{R_{e}R_{m}s}$.

Firstly, we consider the domain $\Omega =(0,2)\times (-1,1)$ under the influence of the transverse magnetic field ${\mathbf {H}}^{d}=(0,1)$. The exact solutions to the 2D MHD problem are given by [21]

$$\begin{aligned} {\mathbf {u}}(x,y)&=\left( \frac{GRe}{H_{a}\tanh (H_{a})}\Big (1-\frac{\cosh (yH_{a})}{\cosh (H_{a})}\Big ),0\right) ,\\ p(x,y)&=-Gx-\frac{G^{2}}{2s}\left( \frac{\sinh (yH_{a})}{\sinh (H_{a})}-y\right) ^{2}+p_0,\\ {\mathbf {H}}(x,y)&=\left( \frac{G}{s}\Big (\frac{\sinh (yH_{a})}{\sinh (H_{a})}-y\Big ),1\right) . \end{aligned}$$

We impose no-slip boundary conditions on the wall and Neumann boundary conditions on the inlet and the outlet:

$$\begin{aligned}&{\mathbf {u}}=0\quad \text {on}\; y=\pm 1,\\&(p\mathbf {I}-R_{e}^{-1}\nabla {\mathbf {u}})\mathbf {n}=p\mathbf {n}\quad \text {on}\;x=0,2\\&\mathbf {n}\times {\mathbf {H}}=\mathbf {n}\times {\mathbf {H}}^d\quad \text {on} \;\partial \Omega , \end{aligned}$$

where I is the identity matrix.

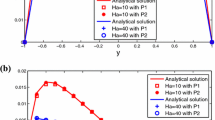
For the 2D problem, we set $G=1,$$p_0=10,$$s=25$ with $R_{e}=R_{m}=0.1$ and $R_{e}=R_{m}=1.$ We select $h=1/60$, ${\tau }=1$ and $\gamma _{1}=\gamma _{2}=1$, $\beta _{1}=\beta _{2}=0.2$. The numerical solutions are computed at $T=50$ for the these cases, respectively. The analytical solutions ${\mathbf {u}}(1,y)$ and ${\mathbf {H}}(1,y)$ are presented in Figs. 1 and 2 alongside the numerical ones ${\mathbf {u}}(1,y_{k})$ and ${\mathbf {H}}(1,y_{k})$ ($y_{k}=-1+0.1k,k=0,\ldots ,20$) obtained by Algorithm 3.1. From the figures, we find that the numerical solutions of our scheme are consistent with the exact solutions of Hartmann flow.

Fig. 1

$H_{a}=0.5$, $R_{e}=R_{m}=0.1$ (left: velocity; right: magnetic field)

Fig. 2

$H_{a}=5$, $R_{e}=R_{m}=1$ (left: velocity; right: magnetic field)

Secondly, we consider the 3D Hartmann flow with the rectangular duct $\Omega =(0,2)\times (-y_0,y_0)\times (-z_0,z_0)$ under the influence of the uniform magnetic field ${\mathbf {H}}^{d}=(0,1,0)$. The solutions of this model are of the following form [21, 42, 48]:

$$\begin{aligned} {\mathbf {u}}(x,y,z)&=({H}_{u}(y,z),0,0),\;{\mathbf {H}}(x,y,z)=({H}_{H}(y,z),1,0),\\ p(x,y,z)&=-Gx-s{H}^{2}_{H}(y,z)/2+p_{0}, \end{aligned}$$

with

$$\begin{aligned} {H}_{u}(y,z)=-\frac{1}{2}GR_{e}(z^{2}-z_{0}^{2})+\sum _{i=0}^{+\infty }a_{i}(y)\cos (\lambda _{i}z),\;{H}_{H}(y,z)=\sum _{i=0}^{+\infty }b_{i}(y)\cos (\lambda _{i}z), \end{aligned}$$

where

$$\begin{aligned} a_{i}&=A_{i}\cosh (p_{1}y)+B_{i}\cosh (p_{2}y),\\ b_{i}&=\frac{1}{R_{e}s}\left( A_{i}\frac{\lambda _{i}^{2}-p_{1}^{2}}{p_{1}}\sinh (p_{1}y)+B_{i}\frac{\lambda _{i}^{2}-p_{2}^{2}}{p_{2}}\sinh (p_{2}y)\right) ,\\ A_{i}&=\frac{-\,p_{1}(\lambda _{i}^{2}-p_{2}^{2})}{\gamma _{i}}{u}_{i}(y_{0})\sinh (p_{2}y_{0}),\;B_{i}=\frac{p_{2}(\lambda _{i}^{2}-p_{1}^{2})}{\gamma _{i}}{u}_{i}(y_{0})\sinh (p_{1}y_{0}),\\ \lambda _{i}&=\frac{(2i+1)\pi }{2z_{0}},\;p_{1,2}^{2}=\lambda _{i}^{2}+H_{a}^{2}/2\pm H_{a}\sqrt{\lambda _{i}^{2}+H_{a}^{2}/4},\;{u}_{i}(y_{0})=\frac{-2GR_e}{\lambda ^3z_0}\sin (\lambda _iz_0),\\ \gamma _{i}&=p_{2}(\lambda _{i}^{2}-p_{1}^{2})\sinh (p_{1}y_{0})\cosh (p_{2}y_{0})-p_{1}(\lambda _{i}^{2}-p_{2}^{2})\sinh (p_{2}y_{0})\cosh (p_{1}y_{0}). \end{aligned}$$

The boundary conditions are imposed by

$$\begin{aligned}&{\mathbf {u}}=0\quad \text {on} \;y=\pm y_0\quad \text {and}\quad z=\pm z_0,\\&(p\mathbf {I}-R_{e}^{-1}\nabla {\mathbf {u}})\mathbf {n}=p\mathbf {n}\quad \text {on}\; x=0 \quad \text {and}\quad x=2,\\&\mathbf {n}\times {\mathbf {H}}=\mathbf {n}\times {\mathbf {H}}^{d}\quad \text {on}\; \partial \Omega . \end{aligned}$$

We take $G=1$, $y_0=\frac{1}{2}$ and $z_0=\frac{1}{4}$. Besides, we design this investigation with the parameters $R_{e}=R_{m}=30$, $s=1$, $\gamma _{1}=\gamma _{2}=1$ and $\beta _{1}=\beta _{2}=0.2$. The numerical results of the presented method, Zhang’s method [48] and the Linearized Crank–Nicolson method at final time $T=10$ are shown in Table 14. From this table, we can find that the presented method has the best accuracy among these methods.

Table 14 Errors for the different methods of 3D Hartmann flow at T = 10

5 Conclusions

In this work, we have presented an Euler semi-implicit time-discrete, modular grad-div stabilization algorithm for the time-dependent MHD equations. Then, we theoretically establish the unconditional stability and provide rigorous error estimates of the algorithm. The presented algorithm is unaffected by variations of grad-div stabilization parameters whereas the cost of standard implementations grow rapidly as the parameters grow. Numerical tests illustrate the theoretical results and computational efficiency.

In the future, we will consider some second order in time numerical schemes with grad-div stabilization to solve the time-dependent MHD equations, such as the BDF2 scheme or the Crank–Nicolson scheme.