A Numerical Framework for Integrating Deferred Correction Methods to Solve High Order Collocation Formulations of ODEs

Abstract

Recent analysis and numerical experiments show that the deferred correction methods are competitive numerical schemes for time dependent differential equations. These methods differ in the mathematical formulations, choices of collocation points, and numerical integration or differentiation strategies. Existing analyses of these methods usually follow traditional ODE theory and study each algorithm’s convergence and stability properties as the step size $\varDelta t$ varies. In this paper, we study the deferred correction methods from a different perspective by separating two different concepts in the algorithm: (1) the properties of the converged solution to the collocation formulation, and (2) the convergence procedure utilizing the deferred correction schemes to iteratively and efficiently reduce the error in the provisional solution. This new viewpoint allows the construction of a numerical framework to integrate existing techniques, by (1) selecting an appropriate collocation discretization based on the physical properties of the solution to balance the time step size and accuracy of the initial approximate solution; and by (2) applying different deferred correction strategies for reducing different components in the error of the provisional solution. This paper discusses properties of different components in the numerical framework, and presents preliminary results on the effective integration of these components for ODE initial value problems. Our results provide useful guidelines for implementing “optimal” time integration schemes for general time dependent differential equations.

1 Introduction

The accurate and efficient solution of time dependent differential equations has been an active research area for more than 50 years. For ordinary differential equation (ODE) initial value problems (IVPs), the linear multistep methods and Runge–Kutta methods have been extensively studied in both theory and implementation and have become standard topics in entry level numerical analysis textbooks [1, 2, 23, 39]. Widely used ODE IVP solvers include the backward differentiation formula (BDF) based DASPK [7, 34] and Runge–Kutta method based Radau5 [20]. Instead of detailed descriptions and references in this paper, we refer interested readers to [37] for existing theoretical results, different algorithms, and software packages. Many of these numerical simulation tools have been successfully applied in research studies and have significantly advanced our knowledge in science and engineering. However, these advances in turn also revealed the limitations of existing numerical algorithms. For example, to understand the biological cycles of a typical ion channel consisting of thousands of particles, current molecular dynamics simulation tools usually require millions of time steps to fully resolve the opening and closing dynamics using existing low order time stepping schemes (e.g., the Verlet integration scheme). Even with the acceleration of the fast N-body solvers [18, 36] for each time step, most simulations require weeks or longer to get any biologically relevant results. In recent years, several schemes were introduced to address the challenges in designing accurate and efficient algorithms for large-scale long-time simulations. Examples include the parareal algorithm and its variants for efficient parallelization in time [14, 35]; the high order temporal discretization using an orthogonal basis and pseudo-spectral formulations for each time step, to allow larger step sizes [6, 24, 32]; the spectral deferred correction (SDC), integral deferred correction (InDC), iterated defect correction (IDeC) and Krylov deferred correction (KDC) methods for their efficient solutions [3, 11, 12, 25]; and the parallel full approximation scheme in space and time (PFASST) which combines different preconditioning techniques [13].

In this paper, we focus on the high order temporal collocation discretization and deferred correction methods, and describe how to integrate these techniques to construct an “optimal” numerical framework for solving ordinary differential equations. In existing literature, each involved technique usually only addresses a particular aspect of this framework. In [19, 21], the Gauss collocation formulations using only 2, 4, and 6 nodes were implemented as geometric integrators for Hamiltonian systems, however without the deferred correction or other acceleration techniques, numerical results suggest that the resulting solvers are not as efficient as other linear multistep methods (see Fig. 5.1 in [19]). Also, when analyzing the iterated, integral, and spectral deferred (defect) correction methods, most existing results follow traditional numerical ODE theory and study the convergence and stability region properties for varying step size $\varDelta t$. However, note that when the magnitude of the error is large in the deferred correction iterations, one wouldn’t accept such results in the numerical implementation, implying that most of the existing analyses are not applicable. Instead, it is more appropriate to consider the mathematical and numerical properties of the underlying collocation formulation. Another commonly encountered problem in the deferred correction methods is the order reduction and divergence of the numerical procedure for stiff ODE and DAE systems.

We present a different perspective to understand and integrate these methods in a numerical framework for solving ODE systems. In this framework, we consider the deferred correction techniques as efficient iterative schemes to reduce the error in the convergence procedure, and different deferred correction strategies can be applied to reduce different error components in the provisional solution. Within the prescribed convergence criterion, we analyze the mathematical properties of the solution by studying the underlying collocation formulations. In the optimal numerical implementation of this framework, the collocation formulation is selected based on the physical properties of the solution. We treat each low order deferred correction scheme as a preconditioner, and integrate these preconditioning techniques with existing iterative solvers (e.g., fixed point iterations or Jacobian-free Newton–Krylov methods) for better convergence.

This paper is organized as follows. In Sect. 2, we study the converged solution by developing the “collocation formulations database” for the numerical framework for solving ODE initial value problems and by discussing the properties of each formulation. In Sect. 3, we start from the backward Euler based spectral deferred correction methods and their convergence properties, and then study different deferred correction methods to form the “deferred correction methods database” in the convergence procedure, an iterative procedure to reduce the errors in the provisional solution. In Sect. 4, we discuss several algorithm design guidelines to integrate different components to efficiently converge to the solution of an “optimal” discretization in the numerical framework. We provide preliminary numerical experiments to validate each guideline, and demonstrate the performance of the framework by comparing a very primitive implementation with some existing techniques. This paper is our first step to design optimal space–time parallel adaptive numerical methods for time dependent differential equations, and in Sect. 5, we summarize our results and discuss several related research topics to further improve the efficiency of our numerical framework for large-scale long-time simulations of differential equations.

2 Collocation Formulations and Properties

For long time simulations, it is in general impractical to use one single step for the entire interval from $t=0$ to $t_{\textit{final}}$ (e.g., by using a spectral formulation for $[0, t_{\textit{final}}]$). We therefore follow the standard practice of adaptively dividing the whole interval into a sequence of subintervals (time steps) based on the properties of the solution and any step size constraints. In this section, we discuss different collocation formulations for each time step. These formulations differ in the mathematical formulations, choices of collocation points, and numerical integration or differentiation strategies. We leave the discussions of their accurate and efficient solutions to later sections.

Spectral and pseudo-spectral methods have been widely used for solving spatial differential equations in simple geometries (i.e., Fourier series for periodic solutions, or Chebyshev polynomials for rectangular or cubic geometries) [8, 16, 17]. One advantage of these methods is that when the number of expansion terms (in the spectral formulation) or node points (in the pseudo-spectral type collocation formulation) increases, the approximation error decays very rapidly for smooth functions; and unlike traditional linear multistep methods or low order explicit Runge–Kutta methods for the temporal initial value problems, the stability region constraint is in general not a big concern. Not surprisingly, as time is only one dimensional and there is no complex geometry involved, these methods have also been applied for solving time dependent differential equations in the past. In this section, we first discuss the Legendre polynomial based Gauss collocation formulation, and then discuss other collocation formulations for initial value problems. Clearly, when an iterative scheme is applied to a specific collocation formulation and is convergent (up to a prescribed precision), the numerical properties of the solution are then determined by the properties of the collocation formulation, not the convergence procedure. Unlike existing analysis of the deferred correction methods, this new viewpoint allows us to study the mathematical properties of the framework (e.g., order and stability) by focusing on the converged solution of the collocation formulation, and to consider the convergence procedure (describing how the iterations converge) separately.

2.1 Gauss Collocation Method

We first present a variant of the well-studied Gauss collocation formulation (also referred to as the Gauss Runge–Kutta (GRK) method) for ODE initial value problems $y'(t)=f(t,y(t))$ with given initial data y(0) [21, 23]. To march one step from $t=0$ to $t=\varDelta t$, we define ${Y}(t)=y'(t)$ as the new unknown function and recover y(t) using $y(t)=y(0)+\int _0^t {Y}(\tau ) d\tau$. This will give what we call the “yp-formulation” as

$$\begin{aligned} {Y}(t)=f(t, y(0)+\int _0^t {Y}(\tau ) d \tau ). \end{aligned}$$

(1)

In the Gauss collocation formulation, p Gaussian quadrature nodes $\mathbf{t}=[t_1, t_2, \ldots , t_p]^T$ are used to discretize the yp-formulation in $[0, \varDelta t]$. For the given function values $\mathbf{{Y}}=[{Y}_1, {Y}_2, \ldots , {Y}_p]^T$ at the Gaussian nodes, we can construct the $(p-1){th}$ degree Legendre polynomial expansion to approximate ${Y}(t)=y'(t)$ where the coefficients are computed using the Gaussian quadrature rules. We can integrate this interpolating polynomial analytically from 0 to $t_m$, $m=1, \ldots , p$, to form a linear mapping that maps the function values $\mathbf{{Y}}$ to the integrals of ${Y}(t)$ at the node points. Taking out the scalar factor $\varDelta t$ in this mapping, the integral $\int _0^t {Y}(\tau ) d \tau$ can be approximated by $\varDelta t S \mathbf{{Y}}$, where S is called the “spectral integration matrix” [17] which can be precomputed. The discretized Gauss collocation formulation using p node points in the time interval $[0, \varDelta t]$ is given by

$$\begin{aligned} \mathbf{{Y}}=\mathbf{F}(\mathbf{t}, \mathbf{y}_0+\varDelta t S \mathbf{{Y}}). \end{aligned}$$

(2)

The following theorem, mostly from [23], summarizes several nice properties of this formulation, assuming it is solved exactly.

Theorem 1

For ODE initial value problems, the Gauss collocation formulation in Eq. (2) with p nodes is of order 2p (super convergence), A-stable, B-stable, symplectic (structure preserving), and symmetric (time reversible). In addition, the error decays exponentially when p increases.

Interested readers are referred to [5, 22] for the proof of the theorem. These nice properties allow the use of very large time step sizes when solving ordinary differential equation initial value problems.

Comment The yp-formulation can be easily generalized to differential algebraic equations (DAEs) of the form $F(t,y,y')=0$, and the discretized system becomes

$$\begin{aligned} \mathbf{F}(\mathbf{t}, \mathbf{y}_0+\varDelta t S \mathbf{{Y}}, \mathbf{{Y}}) = \mathbf{0}. \end{aligned}$$

Similar to the ODE case, the pseudo-spectral type collocation formulation allows much larger time step sizes in the numerical simulation. In Fig. 1, we compare the Gauss collocation formulation with traditional BDF methods for the DAE system from [1]

$$\begin{aligned} \left( \begin{array}{l} x'_1 \\ x'_2 \\ 0 \end{array} \right) =\left( \begin{array}{lll} 10-\frac{1}{2-t} &{}\quad 0 &{} \quad 10(2-t)\\ \frac{9}{2-t} &{}\quad -1 &{}\quad 9\\ t+2 &{}\quad t^2-4 &{}\quad 0\\ \end{array}\right) \left( \begin{array}{l} x_1 \\ x_2 \\ z \end{array} \right) + \left( \begin{array}{l} \frac{3-t}{2-t} e^t \\ 2e^t \\ e^t(2-t-t^2) \\ \end{array}\right) \end{aligned}$$

(3)

whose analytical solution is given by $(x_1,x_2,z)=\left( e^t,e^t,-e^t/(2-t)\right)$ and can be resolved to machine precision using a 15-term Legendre polynomial expansion for each component when $t \in [0,1]$. It can be observed that the fourth order BDF method requires a time step size of $10^{-3}$ for 10 digits of accuracy, as shown in (a) of Fig. 1 (also see [1], p. 268). On the other hand, the Gauss collocation discretization using a step size of $10^{-1}$ and 5 Gaussian nodes gives 14 digits accuracy [see (b) in Fig. 1]. The step size differences are further studied by comparing the accuracy regions of the Gauss collocation and BDF schemes. For a given error tolerance $\epsilon >0$, the accuracy region associated with a numerical scheme is defined to be the subset of the complex plane $\mathbb {C}$ consisting of all $\lambda$ such that when the scheme is applied to the model problem $y'(t)= \lambda y(t)$, $y(0)=1$ on the interval [0, 1], the error between the numerical solution $\tilde{y}$ and analytical solution y satisfies the relation $|\tilde{y}(1)-y(1)|<\epsilon$. For the $q_{th}$ order BDFq scheme, exact values are used at nodes $t_k=k/q$, $k=0, \ldots , q-1$ to derive the numerical solution at $t_q=1$. In Fig. 2, we plot the accuracy regions of the 4-node Gauss collocation and BDF4 schemes for $\epsilon =10^{-10}$. It can be observed that the Gauss collocation formulation has a much larger accuracy region than BDF4.

Fig. 1

Accuracy in $x_1$ for different step sizes using a traditional BDF methods, orders 2, 3, 4 (from [1]) and b Gauss collocation methods using 3, 4, 5 Gaussian nodes

Fig. 2

Accuracy regions of 4-node Gauss collocation and 4th order BDF schemes

We refer interested readers to [20] and references therein for further analysis of different collocation formulations for DAE systems, and to [24, 25] for more numerical examples demonstrating the step size-accuracy relations of the pseudo-spectral type collocation formulations for both ODE and DAE problems.

2.2 Different Collocation Formulations

In the Gauss collocation formulation discussed in the previous section, the Legendre polynomial based Gaussian quadrature nodes are used and the spectral integration matrix is constructed accordingly for the yp-formulation. Other types of formulations, quadrature nodes, and numerical differentiation or integration techniques have also been studied in the literature. In this subsection, we present different collocation formulations to form our “collocation formulation database” for ODE initial value problems.

Mathematical Formulations For the ODE initial value problem $y'=f(t,y)$, most existing collocation formulations use y as the unknown and solve the differential equation directly. In the “differential quadrature method” [10] and other traditional pseudo-spectral collocation formulations, the “spectral differentiation matrix” is constructed by differentiating the interpolating polynomial of y at the collocation points and evaluating the derivative polynomial to form the spectral differentiation matrix D mapping $\mathbf {y}$ at the collocation points to $\mathbf {y'}$. We refer to this class of formulations as the “differential formulation”, and the discretized ODE system can be represented as $D \mathbf {y} = \mathbf {f}(\mathbf {t}, \mathbf {y})$. An alternative formulation is to use the equivalent Picard integral equation formulation $y(t)=y_0+\int _0^t f(\tau , y(\tau )) d \tau$ and discretize the ODE system as in $\mathbf {y} = \mathbf {y_0} + \varDelta t S \mathbf {f} (\mathbf {t}, \mathbf {y})$ where $\mathbf {y}$ are the unknowns at the collocation points, and S is the (scaled) spectral integration matrix. We refer to this formulation as the “integral formulation”. When this formulation is coupled with uniform collocation points, the resulting deferred correction methods are called the integral deferred correction methods (InDC) [11]. In the previous subsection, we also presented the “yp-formulation” using $y'$ as the unknown and using the spectral integration matrix to form the discretized collocation formulation given by $\mathbf {Y} = \mathbf {f} (\mathbf {t}, \mathbf {y_0} + \varDelta t S \mathbf {Y})$.

Although these formulations are equivalent mathematically, they have very different numerical properties as will be discussed in Sect. 3.5. For example, for non-stiff problems, the yp-formulation can be one order higher (in $\varDelta t$) than the integral formulation. However for stiff problems, when $|\varDelta t \lambda | \gg 1$, the integral formulation is preferred due to the additional $\varDelta t \lambda$ factor in the yp-formulation (see Eqs. 18, 19). Also, it is not easy to generalize some of these formulations to more complicated differential equation systems. For example, for a general DAE system $F(t, y, y')=0$, it is nontrivial to derive the standard Picard integral equation for y in the integral formulation, and one may prefer the differential formulation or yp-formulation.

Collocation Points, Integration and Differentiation Matrices Instead of Gaussian quadrature nodes, other node points have also been studied in the literature: when Radau Ia nodes are used, the left end-point $t=0$ is added when constructing the numerical integration or differentiation matrices; when Radau IIa nodes are used, the right end-point $t=\varDelta t$ is added; in the Gauss-Lobatto scheme, both end points are added in the collocation formulation; and one can also use the Chebyshev polynomial based Clenshaw–Kurtis quadrature and corresponding spectral differentiation or integration matrices to take advantage of the “near-minimax” approximation properties of the Chebyshev polynomial expansion and the fast Fourier transform [40]. As these collocation points are closely related with the underlying orthogonal polynomials, one can very stably construct the least squares polynomial using the corresponding Gaussian-type quadratures, and differentiate or integrate the resulting polynomial to construct the spectral differentiation or integration matrices. Note that for ODE problems, when considering the errors at both the interior and boundary collocation points, these collocation formulations have similar order properties as shown in traditional ODE analysis. However, when only considering the solution at the right end point $t=\varDelta t$, the Legendre polynomial based collocation formulations are preferred due to their relatively higher order of convergence. Also, for DAE problems, the orders at $t=\varDelta t$ will be different for the “differential” and “algebraic” components (see, e.g. [23]) for different choices of nodes, and the Radau IIa or Gauss-Lobatto nodes are usually preferred due to their relative higher order properties for the algebraic components.

More recently, assuming the solution can be better approximated by exponential sums as in the case for linear homogeneous ODEs, collocation nodes and spectral integration matrices are designed using skeletonization techniques by Rokhlin et. al. for ODE systems [15, 32]. When the solution can be approximated by the so-called “band-limited” functions, in [6], quadrature nodes and the corresponding spectral integration matrix using the “prolate spheroidal wave functions” were applied to initial value problems. These collocation formulations only differ in the set of node points and precomputed spectral differentiation matrix D or integration matrix S. It is therefore possible to precompute and form the collocation formulation database. For a given ODE system, based on the physical properties of the solution and different measures of the error, one can choose a particular set of nodes and the corresponding matrix to form the “optimal” formulation. Also note that unlike traditional ODE solvers, for better accuracy, in addition to changing to a smaller step size and reducing the error using the “order of convergence” concept, one can also add more points to the interval in the collocation formulation to take full advantage of the convergence properties in the orthogonal basis based pseudo-spectral methods. The latter option may be more favorable if the resulting system can be solved efficiently, and usually allows much larger step sizes in the simulation.

Comment When a smaller number of nodes (e.g., less than 10 node points) is preferred (e.g., due to memory constraints), in the existing integral deferred correction methods [11], the uniform nodes are usually applied as they show better convergence properties in the deferred correction iterations as will be discussed in the next section. However, such uniform collocation formulations may have serious numerical problems (especially when the number of nodes increases) due to the stability and accuracy issues from the underlying uniform polynomial interpolation schemes, such as the well-known Runge’s phenomenon. We believe such collocation formulations should be avoided in the final converged solution, however one may want to take advantage of their fast convergence in the deferred correction iterations as will be discussed in Sect. 4. Also, generalization of the collocation schemes to partial differential equations is straightforward and interested readers are referred to [9, 26, 27] for preliminary results along this direction.

3 Deferred Correction Methods and Properties

Despite the aforementioned excellent properties of many of the high order collocation formulations, the higher order ($p\ge 10$ node points) collocation formulation is rarely used in most of today’s numerical simulations. The main reason is the efficiency of the solution algorithms. Assuming an ODE system with N equations is resolved using p Gaussian nodes in the Gauss collocation formulation, as the spectral differentiation matrix D or integration matrix S is dense (solutions at current time depend both on history data and solutions at future times), the Newton’s method and direct Gauss elimination (for each linearized system) will require $O((Np)^3)$ operations. This number increases cubicly as p increases. In most BDF type methods, the operation is only $N^3$ for each time step. Also, when the step size is large, the initial value may no longer serve as a good initial guess for the solution in the time interval, resulting in convergence problems in the nonlinear solver.

Instead of direct Gauss elimination, in recent years, different deferred correction methods were proposed to improve the efficiency when solving the discretized collocation formulations iteratively. We first present the backward Euler based spectral deferred correction (SDC) methods for the yp-Gauss collocation formulation.

3.1 Backward Euler Preconditioned SDC for yp-Gauss Collocation Formulation

We consider the yp-formulation in Eq. (2) using the Gaussian nodes. The first step in a SDC method is to use a low order “predictor” to find an approximate solution of ${Y}(t)$ at the collocation points in $[0, \varDelta t]$, denoted by $\tilde{\mathbf{Y}}= [ \tilde{Y}_1, \tilde{Y}_2, \ldots \tilde{Y}_p ]^T$. When the backward Euler’s method is applied, the predictor solves the low order discretized system given by

where $\varDelta t_i = t_i-t_{i-1}$ ($t_0=0$) is the time step size from $t_{i-1}$ to $t_i$. In matrix form, this is equivalent to solving

$$\begin{aligned} \tilde{\mathbf{Y}}=\mathbf{F}(\mathbf{t}, \mathbf{y}_0+\varDelta t \tilde{S} \tilde{\mathbf{Y}}) \end{aligned}$$

(4)

where

$$\begin{aligned} \varDelta {t}\tilde{\mathbf{S }}=\begin{bmatrix} \varDelta {t}_1&\quad 0&\quad \cdots&\quad 0&\quad 0\\ \varDelta {t}_1&\quad \varDelta {t}_2&\quad \cdots&\quad 0&\quad 0 \\ \varDelta {t}_1&\quad \varDelta {t}_2&\quad \cdots&\quad 0&\quad 0 \\ \vdots \\ \varDelta {t}_1&\quad \varDelta {t}_2&\quad \cdots&\quad \varDelta {t}_{p-1}&\quad \varDelta {t}_p \end{bmatrix} \end{aligned}$$

(5)

is the first order rectangular rule (using the right end point) for approximating $\int _0^{t_i} {Y}(\tau ) d\tau$. Unlike the spectral integration matrix $\mathbf S$ where solutions at current time depend on both the history and future data, in the low order discretization represented succinctly in Eq. (4), solutions are “decoupled” due to the lower triangular structure of $\tilde{\mathbf{S }}$, reducing the solution time to $O( N^3 p )$ for ODE systems of size N, assuming Gauss elimination is used for each step of the Newton iterations when solving the nonlinear system $\tilde{Y}_k = f(t_k, y_0 + \varDelta t_1 \tilde{Y}_1 + \varDelta t_2 \tilde{Y}_2 +\cdots + \varDelta t_k \tilde{Y}_k)$ when marching from $t_{k-1}$ to $t_k$. We use $\tilde{Y}(t)$ to represent the corresponding Legendre interpolating polynomial of $\tilde{\mathbf{Y}}$, where the expansion coefficients are stably computed using the Gaussian quadrature.

In the second step of the SDC method, define the error as $\delta (t)= {Y}(t)-\tilde{Y}(t)$. We can find the “error’s equation” given by

$$\begin{aligned} \tilde{Y}(t)+ \delta (t) = f\left( t, y_0+\int _0^{t} \left( \tilde{Y}(\tau )+ \delta (\tau )\right) d\tau \right) \end{aligned}$$

(6)

with initial value $\delta (0)=0$. As $\tilde{Y}$ at the Gaussian nodes is given, we can apply the spectral integration matrix to $\int _0^{t} \tilde{Y}(\tau ) d \tau$ to accurately evaluate its integral. For the unknown $\delta (t)$, similar to the predictor step, the backward Euler’s method can be applied to obtain a low order approximation of the error $\delta (t)$ by solving the equation system

$$\begin{aligned} \tilde{\mathbf{Y}}+ \tilde{\varvec{\delta }}=\mathbf{F}\left( \mathbf{t}, \mathbf{y}_0+\varDelta t S \tilde{\mathbf{Y}}+ \varDelta t \tilde{S} \tilde{\varvec{\delta }}\right) \end{aligned}$$

(7)

where $\tilde{\varvec{\delta }}= [ \tilde{\delta }_1, \tilde{\delta }_2, \ldots , \tilde{\delta }_p]^T$ is the low order solution at each collocation node. Next, we can add $\tilde{\varvec{\delta }}$ to $\tilde{\mathbf{Y}}$ to obtain an “improved” approximation of ${Y}(t)$, define the new error, and repeat the second step. We refer to each such iteration as one SDC correction. In the SDC methods, this procedure is stopped either when $\tilde{\varvec{\delta }}$ is smaller than a prescribed accuracy requirement or after a fixed number of iterations. In the latter case, if the error is still large, one reduces the step size and solves the collocation formulation in a smaller interval. In other words, one accepts the SDC results only when $\tilde{\varvec{\delta }}$ in Eq. (7) is within certain error tolerance. Notice that in this case, $\tilde{\mathbf{Y}}$ approximately satisfies (up to $O(\tilde{\varvec{\delta }})$ error) $\tilde{\mathbf{Y}}=\mathbf{F}(\mathbf{t}, \mathbf{y}_0+\varDelta t S \tilde{\mathbf{Y}})$ which is exactly the Gauss collocation formulation in Eq. (2). Therefore, SDC is simply an iterative scheme trying to converge to the Gauss collocation formulation.

Comment When analyzing the deferred correction methods, most existing results follow traditional numerical ODE theory and study the convergence and stability region properties for varying step size $\varDelta t$. However, note that when the error is large in the deferred correction iterations, the results will not be accepted and smaller step sizes have to be used until the error is small enough. This implies that most existing analyses cover inapplicable numerical regimes which never appear in real implementations. It is therefore more appropriate to separate the study of the convergence procedure from that of the converged solutions. When the corrections are convergent, the numerical properties of the algorithm are determined by the underlying collocation formulation.

Comment Generalization of the SDC methods to the DAE problems is straightforward. When the backward Euler’s method is applied, the corresponding low order discretization for the error is given by $\mathbf{F}(\mathbf{t}, \mathbf{y}_0+\varDelta t S \tilde{\mathbf{Y}}+ \varDelta t \tilde{S} \tilde{\varvec{\delta }}, \tilde{\mathbf{Y}}+\tilde{\varvec{\delta }})=\mathbf{0}.$ For a given provisional solution, only $O( N^{3}p )$ operations are required to get the low order error approximation $\tilde{\varvec{\delta }}$ in each SDC correction due to the lower triangular structure of $\tilde{S}$.

3.2 Understanding Deferred Correction Iterations

To get further insight of the deferred correction iterations, we first consider the SDC scheme in matrix form applied to a linear ODE of the form $y'(t) = \lambda y +f(t)$ with given initial condition $y(0) = y_0$, and the corresponding collocation formulation becomes $\mathbf{{Y}}=\lambda (\mathbf{y}_0+\varDelta t S \mathbf{{Y}}) +\mathbf{F}$ with given $\mathbf{y}_0=[y_0, y_0, \ldots , y_0]^T$ and $\mathbf{F}=[f(t_1), f(t_2), \ldots , f(t_p)]^T$. Therefore the linear system for $\mathbf{{Y}}$ is given by

$$\begin{aligned} (I-\lambda \varDelta t S) \mathbf{{Y}}= \lambda \mathbf{y}_0 +\mathbf{F}. \end{aligned}$$

(8)

In the first step, using the backward Euler’s method as the predictor to solve the low order discretization

$$\begin{aligned} \left( I-\lambda \varDelta t \tilde{S}\right) \mathbf{{Y}}= \lambda \mathbf{y}_0 + \mathbf{F}, \end{aligned}$$

(9)

we get the initial provisional solution

$$\begin{aligned} \tilde{\mathbf{Y}}^{[0]} = \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} (\lambda \mathbf{y}_0 + \mathbf{F}). \end{aligned}$$

(10)

In each SDC correction, assuming the provisional solution from the previous correction step is denoted by $\tilde{\mathbf{Y}}^{[n]}$, the discretized low order error’s equation in Eq. (7) becomes

$$\begin{aligned} \tilde{\mathbf{Y}}^{[n]} + \tilde{\varvec{\delta }}=\lambda \left( \mathbf{y}_0+\varDelta t S \tilde{\mathbf{Y}}^{[n]} + \varDelta t \tilde{S} \tilde{\varvec{\delta }}\right) + \mathbf{F}. \end{aligned}$$

(11)

Using Eq. (10) to write $(\lambda \mathbf{y}_0 + \mathbf{F})$ as $(I-\lambda \varDelta t \tilde{S}) \tilde{\mathbf{Y}}^{[0]}$, $\tilde{\varvec{\delta }}$ is then given by

$$\begin{aligned} \tilde{\varvec{\delta }}= \tilde{\mathbf{Y}}^{[0]} - \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} \left( I-\lambda \varDelta t S\right) \tilde{\mathbf{Y}}^{[n]}. \end{aligned}$$

(12)

Therefore we have the recursive relation

$$\begin{aligned} \tilde{\mathbf{Y}}^{[n+1]} = \tilde{\mathbf{Y}}^{[n]} + \tilde{\varvec{\delta }}= \tilde{\mathbf{Y}}^{[0]} + \mathbf{C}\tilde{\mathbf{Y}}^{[n]} \end{aligned}$$

(13)

where the matrix $\mathbf{C}$ is given by

$$\begin{aligned} \mathbf{C}= & {} I-\left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} \left( I-\lambda \varDelta t S\right) =I-\left( I-\lambda \varDelta t\tilde{S}\right) ^{-1} \left( I-\lambda \varDelta t \tilde{S} + \lambda \varDelta t\tilde{S}-\lambda \varDelta tS\right) \\= & {} \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} \lambda \varDelta t (S-\tilde{S}), \end{aligned}$$

and is called the “correction matrix” in this paper. Solving the recursive equation in Eq. (13), we get

$$\begin{aligned} \tilde{\mathbf{Y}}^{[n]} = \tilde{\mathbf{Y}}^{[0]} + \mathbf{C}\tilde{\mathbf{Y}}^{[0]} + \mathbf{C}^2 \tilde{\mathbf{Y}}^{[0]} + \cdots + \mathbf{C}^n \tilde{\mathbf{Y}}^{[0]}. \end{aligned}$$

(14)

Instead of the above step-by-step analysis of the SDC method, a more straightforward viewpoint is to consider the collocation formulation in Eq. (8) and apply the low-order preconditioner $(I-\lambda \varDelta t \tilde{S})^{-1}$ to get a preconditioned system

$$\begin{aligned} \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} \left( I-\lambda \varDelta t S\right) \mathbf{{Y}}= \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1}\left( \lambda \mathbf{y}_0 +\mathbf{F}\right) = \tilde{\mathbf{Y}}^{[0]}. \end{aligned}$$

(15)

Notice that as $\tilde{S}$ is a low order approximation of S (or when $\lambda \varDelta t$ is small), $(I-\lambda \varDelta t \tilde{S})^{-1} (I-\lambda \varDelta t S) = I-\mathbf{C}$ is close to the Identity matrix. Applying Neumann series to the equation $(I-\mathbf{C}) \mathbf{{Y}}= \tilde{\mathbf{Y}}^{[0]}$, we can derive Eq. (14) directly. Therefore, for linear ODE problems, we conclude that the SDC method is simply a Neumann series expansion for solving the optimal collocation formulation preconditioned by the low order methods. The convergence of the deferred correction methods is then determined by the following theorem.

Theorem 2

For linear ODE initial value problems, the spectral deferred correction iterations in Eq. (14) are convergent if and only if the spectral radius $\rho (\mathbf{C})$ (the supremum among the absolute values of all the eigenvalues) of the correction matrix $\mathbf{C}$ is less than 1.

For nonlinear problems, the SDC approach can be considered as a simplified Newton’s method. For a given input provisional solution $\mathbf{{Y}}^{[k]}$, denoting the low order approximation of the error $\tilde{\varvec{\delta }}$ as an implicit function of $\mathbf{{Y}}^{[k]}$ as $\tilde{\varvec{\delta }}= \mathbf{H}({\tilde{\mathbf{Y}}}^{[\mathbf{k}]})$, one can apply the Newton’s method to find the zero of $\mathbf {H}$,

$$\begin{aligned} \mathbf{{Y}}^{[k+1]} = \mathbf{{Y}}^{[k]} - J_H^{-1} \mathbf{H}\left( {\tilde{\mathbf{Y}}}^{[\mathbf{k}]}\right) =\mathbf{{Y}}^{[k]} - J_H^{-1} \tilde{\varvec{\delta }}. \end{aligned}$$

Applying the implicit function theorem to Eq. (7), and it is straightforward to show that the Jacobian matrix is close to the negative Identity matrix $-I$ when the low-order preconditioner is effective, therefore the Newton’s method is simplified to $\mathbf{{Y}}^{[k+1]} = \mathbf{{Y}}^{[k]} + \tilde{\varvec{\delta }}.$

3.3 Properties of Deferred Correction Iterations

Our numerical results (also see [12]) show that for many ODE initial value problems, the properly implemented deferred correction methods outperform many existing commonly used solvers in efficiency for the same accuracy requirement, especially when very high accuracy (i.e., more than 6 digits accuracy) is required. However, we also observe the “order reduction” phenomenon when deferred correction iterations are applied to very stiff ODE systems. For some DAE systems, the deferred correction scheme becomes divergent, independent of the selected step size. We refer interested readers to Fig. 7 in [25], where the SDC method is applied to Andrews’ squeezing problem (see [37] for the full description of this DAE system) and becomes divergent after a few iterations for different step sizes. One observation is that when the Gauss collocation formulation is solved exactly, “order reduction” or divergence is never a concern in the converged solution. This observation means that the order reduction or divergence is not caused by the final converged solution, but by the deferred correction convergence procedure, in particular, the spectral radius $\rho (\mathbf{C})$ of the correction matrix $\mathbf{C}$ and the error in the initial provisional solution.

3.3.1 $\rho (\mathbf{C})$ and Convergence Region

We first define the “convergence region” to measure when the deferred correction methods are convergent for linear problems.

Definition 1

For linear ODE initial value problems, we define the “convergence region” $\varOmega$ of a deferred correction method as $\varOmega = \{ \lambda \varDelta t:\ \rho (\mathbf{C}(\lambda \varDelta t)) < 1, \ \lambda \in \mathbb {C} \}.$ The method is called “A-convergent” if $\varOmega$ contains the left half complex plane. It is called “L-convergent” if it is “A-convergent” and $\lim _{|\lambda \varDelta t| \rightarrow \infty } \rho (\mathbf{C}(\lambda \varDelta t)) \rightarrow 0$ for $\lambda \varDelta t$ on the left half complex plane.

For the backward Euler preconditioned SDC methods for yp-Gauss collocation formulation, the correction matrix is

$$\begin{aligned} \mathbf C = \left( I - \lambda \varDelta {t}\tilde{\mathbf{S }}\right) ^{-1}\left( \lambda \varDelta {t}\right) \left( \mathbf S - \tilde{\mathbf{S }}\right) . \end{aligned}$$

(16)

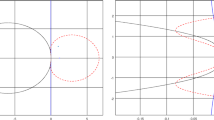
In Fig. 3, we plot the numerically computed convergence region (contour = 1) and other contour lines of $\rho (\mathbf{C})$ for (a) $p=4$ and (b) $p=10$. Both seem to be A-convergent.

Fig. 3

Contour of $\rho (\mathbf{C}(\lambda \varDelta t))$ for a $p=4$ and b $p=10$ for SDC, $\lambda \varDelta t = x+ iy$

For the correction matrix $\mathbf{C}(\lambda \varDelta t)$, we are particularly interested in two regimes to understand the properties of the deferred correction iterations: when $|\lambda \varDelta {t}| \ll 1$ (non-stiff systems), and when $|\lambda \varDelta t| \rightarrow \infty$ (“strongly stiff limit” for stiff systems). For non-stiff systems where $|\lambda \varDelta {t}| \ll 1$, after each iteration, clearly the error will decay approximately by the factor $(\lambda \varDelta {t})(\mathbf S - \tilde{\mathbf{S }})$ as

$$\begin{aligned} \mathbf C _{\text {ns}} = \left( I + \left( \lambda \varDelta {t}\tilde{\mathbf{S }}\right) + \left( \lambda \varDelta {t}\tilde{\mathbf{S }}\right) ^2 + \cdots \right) \left( \lambda \varDelta {t}\right) \left( \mathbf S - \tilde{\mathbf{S }}\right) . \end{aligned}$$

(17)

However in the strongly stiff limit, the correction matrix becomes $\mathbf C _{\text {s}} = I - \tilde{\mathbf{S }}^{-1}{} \mathbf S$. The convergence of the iterations will then depend on how accurate the low order integration rule in $\tilde{\mathbf{S }}$ approximates the high order rule in $\mathbf S$. In Table 1, we list $\rho (\mathbf C _{\text {s}})$ for different numbers of node points. It can be seen that “order reduction” becomes a serious problem as the number of nodes increases. For 8 points, the modulus of the largest eigenvalue of the correction matrix is 0.8448. This means that for general stiff ODE systems, one error component will decay asymptotically by the factor 0.8448 after each SDC iteration due to the “unresolved” stiff components (as $|\lambda \varDelta {t}| \gg 1$) in the iterations. When $p=16$, the SDC method becomes divergent as $\rho (\mathbf C _{\text {s}})=1.0105$. Clearly, when $p>15$, the methods are not A-convergent, and the error will eventually start to increase when the number of iterations increases. For several cases when $p \le 15$, our numerical results show that the methods are A-convergent. Also, from Table 1, we see that none of these methods are L-convergent. In Fig. 4, we also plot the eigenvalue distributions of $\mathbf C _{\text {s}}$ for $p=10$ and $p=40$.

Table 1 $\rho (\mathbf C _{\text {s}})$ for different numbers of Gaussian nodes, stiff case, SDC

Fig. 4

Distributions of correction matrix eigenvalues for $p=10$ and $p=40$, stiff case, SDC

Comment We want to point out that “L-convergence” is different from the classical “L-stability” concept. “L-convergence” studies the convergence properties of the SDC and other iterative methods, while the classical “L-stability” concept shows the “amplification factor” $Am(\lambda )$ (see [12]) in the SDC methods after a fixed number of iterations. More specifically, a careful study of the error formulas in Eqs. (18, 19) in Sect. 3.5 shows that the integral formulation based SDC methods are $L(\alpha )$-stable due to the factor $(I-\lambda \varDelta t \tilde{S})^{-1}$ (also see [33]). The yp-formulation based SDC methods, on the other hand, are mostly not $L(\alpha )$-stable, but they have the same correction matrix as their integral formulation based counterparts and hence have the same convergence behaviors.

3.3.2 Eigenvectors of $\mathbf{C}$ and Initial Error

In addition to spectral radius $\rho (\mathbf{C})$ which determines the asymptotic convergence properties of the deferred correction iterations, the initial error (and its corresponding eigen-decomposition) in the provisional solution also plays an important role in the “convergence procedure”. This will be explained in this subsection by comparing the SDC iterations with standard Picard iterations for non-stiff linear ODE systems (Picard iterations are divergent for stiff systems). In the SDC iterations, a low order method is applied to precondition the original formulation as in Eq. (15), while in the “standard” Picard iteration, the solution is derived by applying the Neumann series directly (without any preconditioner) to $(I-\lambda \varDelta t S) \mathbf{{Y}}= b \equiv (\lambda \mathbf{y}_0 + \mathbf{F})$ as $\mathbf{{Y}}= b+ \mathbf C _{\text {ns}}^{\text {P}} b + (\mathbf C _{\text {ns}}^{\text {P}})^2 b + \cdots$ where the new correction matrix is given by $\mathbf C _{\text {ns}}^{\text {P}} = \lambda \varDelta {t}\mathbf{S }.$ The “standard” Picard iteration can be considered as the discretized version of the Picard iteration $y^{[k+1]}(t)=y_0+\int _0^t f(\tau , y^{[k]}(\tau )) d \tau$ for ODE initial value problems.

Fig. 5

Modulus of the a largest and b second largest eigenvalues for different numbers of nodes, SDC versus Picard for the Gauss collocation formulation

To understand the asymptotic convergence properties, we notice that after each standard Picard iteration, similar to the SDC iterations, the error will be reduced by a factor of $O(\lambda \varDelta {t})$. We therefore compare the constant prefactor determined by the spectral radius of $\mathbf S - \tilde{\mathbf{S }}$ in the SDC correction matrices $\mathbf C _{\text {ns}}$ and the radius of $\mathbf S$ in the Picard correction matrix $\mathbf C _{\text {ns}}^{\text {P}}$. In (a) of Fig. 5, we compare the spectral radius (modulus of the largest eigenvalue $|\lambda |_{max}$) of $\mathbf S$ for Picard iteration and that of $\mathbf S - \tilde{\mathbf{S }}$ for SDC. It can be seen that asymptotically the SDC iterations have a similar convergence rate as the Picard iterations when $\lambda \varDelta {t}$ is small. In (b) of Fig. 5, we also show how the second largest eigenvalues change as a function of the number of Gaussian nodes for the SDC and Picard iterations. In Fig. 6, we plot the eigenvalue distributions of the matrix $\mathbf S - \tilde{\mathbf{S }}$ in the SDC method and $\mathbf S$ in the Picard iterations for (a) $p=10$ and (b) $p=20$, respectively. In Fig. 7, we plot the normalized eigenvectors of the matrix $\mathbf S - \tilde{\mathbf{S }}$, and in Fig. 8, the normalized eigenvectors of $\mathbf S$, both for $p=15$. These vectors can be considered as the discretized eigenfunctions. Each component $v_j$ in the eigenvector $\mathbf {v}$ is considered as the eigenfunction value at $t_j$.

Fig. 6

Eigenvalue distributions of SDC and Picard iterations for a 10 nodes and b 20 nodes

Fig. 7

$\mathbf S - \tilde{\mathbf{S }}$: Real (o) and imaginary ($+$) components of each eigenvector at the collocation points, non-stiff case, $p=15$, SDC

Fig. 8

$\mathbf S$: Real (o) and imaginary ($+$) components of each eigenvector at the collocation points, non-stiff case, $p=15$, Picard iteration

Fig. 9

How errors decay after each SDC or Picard iteration

One interesting observation is that even though the spectral radii of the two correction matrices are similar in magnitude (which implies similar convergence rates for a large number of iterations), the eigenvalue distributions and structures of the eigenvectors are very different. For example, for the matrix $\mathbf S -\tilde{\mathbf{S }}$ in the SDC iterations, zero is an eigenvalue and the corresponding eigenvector is the constant vector. Notice that for both methods, when a Taylor expansion is applied to the error term in the initial provisional solution, the constant component is usually the largest term, followed by linear, then quadratic, and then higher degree terms. So one should expect smaller initial error when using the SDC method and SDC can effectively eliminate the dominating “low-frequency” error components. This is validated numerically in Fig. 9, by implementing both the SDC and Picard iterations for the model problem $y'(t)=y(t)+f(t)$, where f(t) is chosen so that the analytical solution is given by $y(t)=\frac{1}{1+t}$. The figure shows how the errors decay after each SDC or Picard iteration in one time step [0, 0.6]. In the simulation, $p=15$ is used for both methods, and the spectral radius of $\mathbf S - \tilde{\mathbf{S }}$ is approximately 0.049. It can be seen that the error from the SDC iterations is smaller than that of the Picard iterations, and the asymptotic decay slope of the Picard iterations approaches that of the SDC method. Also, the numerical value of the slope of the SDC curve is approximately $-3.37$, which is very close to the theoretical value $-3.53 \approx \log (0.6 \cdot 0.049)$.

Fig. 10

Real (o) and imaginary ($+$) components of each eigenvector at the collocation points, stiff case, $p=15$, backward Euler preconditioned Gauss collocation formulation

When the SDC methods are applied to the stiff systems where $|\lambda \varDelta {t}| \gg 1$, in Fig. 10, we plot all the eigenvectors of the correction matrix $\mathbf C _{\text {s}}$ for $p=15$. It can be observed that higher frequency errors decay slower than the lower frequency errors because the moduli of the corresponding eigenvalues are larger. Recall that for the initial provisional solution in the SDC iterations, the low frequency errors are usually the dominating components. The overall errors will therefore decay rapidly in the first few iterations, but “order reduction” or even “divergence” is expected eventually for a large number of corrections due to the asymptotic convergence properties determined by the spectral radius $\rho (\mathbf C _{\text {s}})$. One interesting numerical example can be found in Fig. 7 in [25], where the SDC method is applied to Andrews’ squeezing DAE system. For this specific example and different step sizes, the errors decay in the first few iterations and start to increase once the dominating error becomes the high frequency component corresponding to the largest eigenvalue. In existing deferred correction implementations, such divergence (and order reduction for smaller p) was usually controlled by fixing the total number of iterations to bound the growth of the eigenvectors corresponding to eigenvalues of large moduli, and by using smaller step sizes to reduce the magnitude of the coefficients of these eigenvectors in the initial error.

Comment For general DAE systems, it is usually expected that in the discretized algebraic equations, as $\tilde{\mathbf{S }}^{-1}$ is applied to precondition $\mathbf S$ directly by applying the implicit function theorem, the convergence of the SDC method for DAE systems will most likely depend on the spectral radius of $I- \tilde{\mathbf{S }}^{-1} \mathbf S$, especially for higher index DAE systems, and the numerical properties of the SDC methods will be similar to the strongly stiff limit case for ODEs.

3.4 Different Deferred Correction Methods

In this subsection, we discuss several deferred correction strategies and present their properties. We focus on the “yp-formulation” but other formulations have also been studied and can be included in the “deferred correction methods database”. In the “convergence procedure”, appropriate deferred correction schemes will be selected to reduce different error components in the initial solution for faster convergence to the collocation formulation.

3.4.1 Backward Euler for Radau and Lobatto Collocation Formulations

We also studied the backward Euler preconditioned SDC type methods for the Radau IIa collocation formulation (SDC-Radau) where the right end point $t=\varDelta t$ is included in the spectral integration, and the Lobatto formulation (SDC-Lobatto) with both end points $t=0$ and $t=\varDelta t$ used in the formulation.

For Radau IIa nodes, we found that the convergence behaviors of the SDC-Radau schemes are similar to those of the Gaussian nodes in both the non-stiff ($|\lambda \varDelta t|$ small) and stiff ($|\lambda \varDelta t|$ large) cases. In Table 2, we show the spectral radius $\rho (\mathbf{C})$ of the correction matrices for different numbers of Radau IIa nodes for the stiff case. It can be seen that when $p \ge 12$, the SDC-Radau methods become divergent. We also plot the convergence region of the SDC-Radau in Fig. 11. Similar to the Gauss collocation case, our numerical results show that the methods are A-convergent for smaller p, but become divergent when p is large. Also, none of these formulations are L-convergent.

Table 2 $\rho (\mathbf{C})$ for different numbers of nodes, SDC-Radau

Fig. 11

Contour of $\rho (\mathbf{C})$ for a $p=4$ and b $p=10$ for SDC-Radau, $\lambda \varDelta t = x+ iy$

For Lobatto nodes, the left end point ($t=0$) is included in the integration quadrature and we also add $t_0 = 0$ to the collocation formulation. It is easy to see that all entries in the first row of the integration matrix S (representing $\int _0^0 Y(\tau ) d \tau$) will be zero. We denote

$$\begin{aligned} S=\left[ \begin{array}{ll} 0_{1 \times 1} &{} \quad \mathbf{0}_{1 \times (p-1)} \\ S_{21} &{} \quad S_{22} \end{array}\right] , \end{aligned}$$

where $S_{21}$ is the $(p-1) \times 1$ vector and $S_{22}$ is the $(p-1)\times (p-1)$ submatrix. The equation at $t=0$ is simply the initial consistency condition $\tilde{Y}_0 = f(t_0, y_0)$. The low order quadrature rule can be represented in a similar way as

$$\begin{aligned} \tilde{S} = \left[ \begin{array}{ll} 0_{1 \times 1} &{} \quad \mathbf{0}_{1 \times (p-1)} \\ \tilde{S}_{21} &{} \quad \tilde{S}_{22} \end{array}\right] . \end{aligned}$$

When the backward Euler’s method (rectangular rule using the right end point) is used, $\tilde{S}_{21}$ is a zero vector, and $\tilde{S}_{22}$ contains the lengths of the subintervals between adjacent Lobatto quadrature nodes similar to Eq. (5). Applying the Woodbury matrix identity, the correction matrix can be simplified as

$$\begin{aligned} \mathbf{C}= & {} I-\left[ \begin{array}{ll} 1 &{} \quad \mathbf{0}\\ (I- \varDelta t \lambda \tilde{S}_{22})^{-1} \varDelta t \lambda \tilde{S}_{21} &{}\quad (I- \varDelta t \lambda \tilde{S}_{22})^{-1} \end{array}\right] \left[ \begin{array}{ll} 1 &{} \quad \mathbf{0}\\ - \lambda \varDelta t S_{21} &{}\quad (I- \lambda \varDelta t S_{22}) \end{array}\right] \\= & {} \left[ \begin{array}{ll} 0 &{}\quad \mathbf{0}\\ (I- \lambda \varDelta t \tilde{S}_{22})^{-1} \lambda \varDelta t (S_{21}-\tilde{S}_{21}) &{}\quad I- (I- \lambda \varDelta t \tilde{S}_{22})^{-1} (I- \lambda \varDelta t S_{22}) \end{array}\right] . \end{aligned}$$

One therefore only needs to study the “sub-correction matrix” $I- (I- \lambda \varDelta t \tilde{S}_{22})^{-1} (I- \lambda \varDelta t S_{22})$ to understand the convergence properties of the original correction matrix. For stiff systems when $|\lambda \varDelta t|$ is large, one needs to study the matrix $I-\tilde{S}_{22}^{-1} S_{22}$. In Table 3, we show the spectral radius of this matrix for stiff ODE systems. Similar to the Gaussian and Radau IIa cases, the SDC-Lobatto methods become divergent when $p>14$ and order reduction is expected for smaller numbers of nodes. For comparison, we also plot the convergence regions of SDC-Lobatto methods in Fig. 12.

Table 3 $\rho (\mathbf{C})$ for different numbers of nodes, SDC-Lobatto methods

Fig. 12

Contour of $\rho (\mathbf{C})$ for a $p=4$ and b $p=10$, SDC-Lobatto methods, $\lambda \varDelta t = x+ iy$

Comment In most existing analysis and implementations of deferred correction methods, a fixed number of iterations is performed and the resulting “solution” may still be far away from the converged solution in each time step, hence one should expect a relatively large error in the initial value $y_0$ for the next step. For stiff problems, the large error may accumulate rapidly when the number of time steps increases in any yp-formulation using the left end point $t=0$. This can be shown by studying the initial provisional solution $\tilde{\mathbf{Y}}^{[0]} = (I-\lambda \varDelta t \tilde{S})^{-1} (\lambda \mathbf{y}_0 + \mathbf{F})$ [also see Eq. (10)]. When the left end point is used in the collocation formulation, as

$$\begin{aligned} \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} = \left[ \begin{array}{ll} 1 &{}\quad \mathbf{0}\\ \left( I- \varDelta t \lambda \tilde{S}_{22}\right) ^{-1} \varDelta t \lambda \tilde{S}_{21} &{}\quad \left( I- \varDelta t \lambda \tilde{S}_{22}\right) ^{-1} \end{array}\right] , \end{aligned}$$

the error in the first entry (corresponding to the left end point) of $\tilde{\mathbf{Y}}^{[0]}$ will be $\lambda$ times the error from the initial value $y_0$. When this entry is used in the spectral integration scheme, this error will propagate to other collocation points and magnify the overall error by $O(\lambda )$ in the final solution at each time step, resulting in an unstable numerical time marching scheme. Therefore, the yp-formulation with the left end point $t=0$ should be avoided in the standard deferred correction methods.

3.4.2 Backward Euler for Uniform Collocation Formulations

It is well-known that the uniform interpolations suffer from the Runge phenomena when a large number of interpolation points are used, so in existing implementations, only low order uniform collocation formulations (e.g., $p<10$) are considered in the integral deferred correction (InDC) methods [11]. In this subsection, we analyze the backward Euler preconditioned deferred correction methods for the uniform yp-collocation formulations (denoted as InDC-yp). In Fig. 13, we show the convergence regions for $p=4$ and $p=5$. The numerically computed convergence regions show that when $p=4$, the method is A-convergent. However, the method is no longer A-convergent when $p>4$.

Fig. 13

Contour of $\rho (\mathbf{C})$ for a $p=4$ and b $p=5$ for InDC-yp, $\lambda \varDelta t = x+ iy$

The most interesting feature of the InDC-yp is the following theorem for stiff systems.

Theorem 3

For the InDC-yp method, when $|\lambda \varDelta t| \rightarrow \infty$, the correction matrix $\tilde{S}^{-1} S - I$ has eigenvalues equal to zero; and its Jordan canonical form consists of one Jordan block.

The proof is sketched in the “Appendix”. Because there only exist zero eigenvalues, we conclude that the InDC-yp methods are L-convergent for $p<5$. Clearly, the InDC methods have better convergence properties, but larger error is expected from the converged solution due to the uniform collocation points for large p.

3.4.3 Higher Order Preconditioners

In this subsection, we study the convergence properties of the second order trapezoidal rule preconditioned yp-formulations.

We first consider the non-stiff case. The left end point ($t=0$) is used in the first subinterval by the trapezoidal rule. We add it to the collocation formulation to compare the trapezoidal rule preconditioned Lobatto collocation formulation (denoted as SDC-Lobatto-T and the corresponding correction matrix is denoted as $C_{ns}^{T}$) with the backward Euler preconditioned Lobatto collocation formulation SDC-Lobatto. From Fig. 14, it can be seen that the spectral radius of $S-\tilde{S}$ from $C_{ns}^{T}$ is smaller than that from the SDC-Lobatto. Therefore for non-stiff problems, the second order trapezoidal rule preconditioned SDC-Lobatto-T should converge asymptotically faster. Also, using the trapezoidal rule predictor, the initial low order solution should have much better accuracy (smaller error). One interesting observation is that as the spectral radius of the trapezoidal rule preconditioned SDC-Lobatto-T method is non-zero, one should only expect the error to decay by the factor $\lambda \varDelta t$ after each iteration, assuming the initial error has all eigenmodes. This disagrees with some existing claims that the error decays by a factor $\varDelta t^2$ after each 2nd order SDC correction. Such disagreements were also pointed out in [11], where the integral deferred correction methods are studied as special Runge–Kutta approaches.

Fig. 14

Spectral radius $\rho (S-\tilde{S})$ for different numbers of nodes, SDC-Lobatto and SDC-Lobatto-T

For stiff problems, the second order trapezoidal rule preconditioned SDC-Lobatto-T iterations show worse convergence properties. In Table 4, we show the spectral radius of the correction matrix in this regime. It can be seen that the trapezoidal rule preconditioned SDC iterations become divergent when $p>5$. Therefore, without resolving the “order reduction” and divergence problems, the higher order trapezoidal rule preconditioner is usually not recommended for solving the pseudo-spectral discretization for stiff ODE and DAE systems.

Table 4 $\rho (\mathbf{C})$ of SDC-Lobatto-T, strongly stiff limit case

Another interesting observation is obtained when the trapezoidal rule preconditioner is applied to the uniform collocation formulation (denoted as InDC-yp-T) of non-stiff problems, described in the following theorem, and the proof is given in the “Appendix”.

Theorem 4

For a non-stiff ODE system and its uniform collocation discretization, after each trapezoidal rule preconditioned InDC-yp-T iteration, the error decays by the factor $(\varDelta t)^2$ before reaching its discretization order $(\varDelta {t})^{p+1}$.

Therefore, higher order preconditioners are more effective to reduce the non-stiff errors when the uniform nodes are used. However many of these schemes show worse convergence properties for stiff systems in the standard deferred correction iterations, e.g., we found that for $p=6$, the trapezoidal rule preconditioned iterations are divergent. For smaller p, severe order reduction is observed.

3.4.4 Krylov Deferred Correction Methods

For non-stiff problems, existing numerical results show that the Neumann-series type deferred correction methods are very effective in the solution procedure to converge to the corresponding collocation formulation. This is unfortunately not true for stiff problems, and one has to deal with the divergence and order reduction for stiff ODE systems in the convergence procedure. One effective solution in existing literature is to search for the optimal solution in the Krylov subspace. One can use the Krylov deferred correction (KDC) methods [24, 25] to solve the preconditioned formulation in Eq. (15). For linear stiff problems, instead of the Neumann series solution in Eq. (14), one can search for the optimal least squares solution in the Krylov subspace $\mathbb {K}_k(\mathbf{C}, \tilde{\mathbf{Y}}^{[0]})=span \{ \tilde{\mathbf{Y}}^{[0]}, \mathbf{C}\tilde{\mathbf{Y}}^{[0]}, \mathbf{C}^2 \tilde{\mathbf{Y}}^{[0]}, \ldots , \mathbf{C}^{k-1} \tilde{\mathbf{Y}}^{[0]} \}$ using existing Krylov subspace methods such as the GMRES or BiCGStab as the matrix $\mathbf{C}$ is usually non-symmetric [4, 28, 38].

For nonlinear stiff problems, one can apply the Jacobian-free Newton Krylov (JFNK) methods to find the root of the low-order method preconditioned system $\tilde{\varvec{\delta }}= \mathbf{H}( \tilde{\mathbf{Y}})$, where the “input” variable $\tilde{\mathbf{Y}}$ is the approximate solution and the “output” $\tilde{\varvec{\delta }}$ is the low-order estimate of the error in the SDC correction. Note that when $\tilde{\mathbf{Y}}$ solves the original collocation formulation in Eq. (2), the output $\tilde{\varvec{\delta }}=\mathbf{0}$. Also, when the output is a good estimate of the error in the input variable $\tilde{\mathbf{Y}}$, by applying the implicit function theorem, one can show that the Jacobian matrix of $\mathbf{H}$ is close to $-\mathbf{I}$. We refer interested readers to [29, 31] for details of the JFNK methods. In the following we present the algorithmic structure of one step of the KDC methods marching from 0 to $\varDelta t$ using existing implementations of the JFNK methods.

Krylov deferred correction method: Subroutine OneStep($y(t_0+\varDelta t)$, $\mathbf{{Y}}$, $y(t_0)$, $t_0$, $\varDelta t$)

In the JFNK method, the function evaluation $\tilde{\varvec{\delta }}= \mathbf{H}( \tilde{\mathbf{Y}})$ is simply one SDC iteration for the given provisional solution $\tilde{\mathbf{Y}}$, and such a function evaluation module should be provided by the user. We refer interested readers to [24–26] for details of the KDC algorithm and preliminary numerical results. Though KDC is a promising method, we do find that straightforward application of existing JFNK packages in KDC is not optimal. For small $\varDelta t$, existing JFNK methods often encounter difficulty converging to the collocation formulation even though the original deferred correction approaches converge satisfactorily. Also, for some settings, the deferred correction approach converges faster than the JFNK. We believe the reason is that the general purpose JFNK solvers are unaware of the special structures in the preconditioned system implicitly given by the function $\mathbf{H}$. Modification and optimization of the JFNK methods for the numerical framework will be further addressed in Sect. 4.

3.5 Integral Formulation, yp-Formulation, and Convergence

Our analysis also shows that using different formulations will also change the convergence properties of the deferred correction iterations. In this subsection, we compare the integral formulation with the yp-formulation for the linear ODE $y'(t)= \lambda y(t) +f(t)$ for both non-stiff and stiff cases. In the yp-formulation, we use $Y(t)=y'(t)$ as the unknown and solve the discretized system in Eq. (8). The iterations for the yp-formulation are given in Eq. (14) and the converged solution $\mathbf{{Y}}$ is explicitly given by $\mathbf{{Y}}= (I-\lambda \varDelta t S)^{-1} (\lambda \mathbf{y}_0 +\mathbf{F}).$ After finding $\mathbf{{Y}}$, the solution $\mathbf {y}$ is constructed using $\mathbf {y} = \mathbf {y_0} + \varDelta t S \mathbf{{Y}}$. In the integral formulation, one computes y(t) directly by solving the Picard integral equation $y(t)=y_0+ \int _0^t \left( \lambda y(\tau ) +f(\tau ) \right) d \tau$. The discretized system is given by $\mathbf {y} = \mathbf {y_0} + \varDelta t S \left( \lambda \mathbf {y} + \mathbf{F}\right)$, and the converged solution is given explicitly by $\mathbf {y} = (I-\lambda \varDelta t S)^{-1} (\mathbf{y}_0 + \varDelta t S \mathbf{F}).$ The Neumann series expansion for the preconditioned formulation

$$\begin{aligned} \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} (I-\lambda \varDelta t S) \mathbf {y} = \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} (\mathbf{y}_0 + \varDelta t S \mathbf{F}) ={\tilde{\mathbf {y}}}^{[0]} \end{aligned}$$

is given by

$$\begin{aligned} {\tilde{\mathbf {y}}}^{[n]} = {\tilde{\mathbf {y}}}^{[0]} + \mathbf{C}{\tilde{\mathbf {y}}}^{[0]}+ \mathbf{C}^2 {\tilde{\mathbf {y}}}^{[0]} + \cdots + \mathbf{C}^n {\tilde{\mathbf {y}}}^{[0]} \end{aligned}$$

where $\mathbf{C}$ is the same correction matrix as in the yp-formulation. It is easy to verify that

$$\begin{aligned} \mathbf {y_0} + \varDelta t S \mathbf{{Y}}= \mathbf {y_0} + \varDelta t S \left( (I-\lambda \varDelta t S)^{-1} (\lambda \mathbf{y}_0 +\mathbf{F}) \right) = (I-\lambda \varDelta t S)^{-1} (\mathbf{y}_0 + \varDelta t S \mathbf{F}), \end{aligned}$$

therefore when convergent, the yp-formulation gives the same solution (left of the identity) as that from the integral formulation (right of the identity).

However, after a fixed number K iterations, the truncated expansions will have different properties. Assuming both series expansions are convergent, the error from the truncated yp-formulation is then given by

$$\begin{aligned} err_{yp}=\varDelta t S \left( \sum _{k=K+1}^{\infty } C^k \tilde{\mathbf{{Y}}}^{[0]}\right) = \varDelta t S \left( \sum _{k=K+1}^{\infty } C^k \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1}(\lambda \mathbf{y}_0 +\mathbf{F}) \right) , \end{aligned}$$

(18)

and the error from the integral formulation is given by

$$\begin{aligned} err_{integral}=\sum _{k=K+1}^{\infty } C^k {\tilde{\mathbf {y}}}^{[0]} = \sum _{k=K+1}^{\infty } C^k \left( I-\lambda \varDelta t \tilde{S}\right) ^{-1} \left( \mathbf{y}_0 + \varDelta t S \mathbf{F}\right) . \end{aligned}$$

(19)

Comparing the error terms, we can see that for non-stiff problems when $|\varDelta t \lambda | \ll 1$, the error from the yp-formulation should be one order higher (in $\varDelta t$) than the integral formulation due to the additional $\varDelta t$ factor. However for stiff problems when $|\varDelta t \lambda | \gg 1$, the integral form is preferred. Also, when the deferred correction methods are applied to the integral formulations with the left end point $t=0$, the numerical schemes should be more stable in time marching than the corresponding yp-formulation case discussed in Sect. 3.4.1, as the term $\lambda \mathbf{y}_0$ doesn’t exist in the integral formulation.

4 Algorithm Design Guidelines and Numerical Experiments

In most existing deferred correction implementations, one applies a particular deferred correction method for the corresponding collocation formulation. For stiff systems, when the estimated error is still large after a fixed number of iterations due to the order reduction or divergence, a commonly used strategy is to reduce the step size as the error components corresponding to the “bad eigenvalue” in the provisional solution become smaller when $\varDelta t$ decreases. One can therefore “control” the growth of the divergent or slowly convergent components in the Neumann series expansion by stopping the iterations before they become significant. The drawback of this strategy is that this approach only works when the step size is reasonably small (due to the divergence or order reduction), and one can no longer take advantage of the large step size in the optimal collocation formulations.

In the new numerical framework, instead of using one single deferred correction method for a particular collocation formulation, different deferred correction techniques can be applied to reduce different components in the error of the provisional solution, to more efficiently converge to the solution of the “optimal” collocation formulation for the underlying ODE system. In the following, we provide some guidelines for each step of the numerical framework. Preliminary numerical experiments are also performed to support these guidelines. We want to mention that the new perspective of looking at the deferred correction methods as iterative schemes to converge to the optimal collocation formulation also allows the introduction of other existing effective preconditioning techniques for faster convergence, e.g., domain decomposition or multigrid techniques commonly used in today’s spatial solvers.

4.1 Optimal Collocation Formulation

A good collocation formulation can be selected from the “collocation formulation database” based on the physical properties of the system. For ODE systems, our default choice is the Legendre polynomial based Gauss collocation formulation. In general, the orthogonal basis functions based collocation formulations are recommended, as it is a widely accepted fact that they outperform the uniform nodes based formulations, by allowing larger step sizes and better accuracy. This is demonstrated by comparing the solutions from the Gauss and uniform collocation formulations for the non-stiff ODE system $y'(t)=y(t)+f(t)$ with analytical solution $y(t)=\frac{1}{1+5(t-0.5)^2}$ (and f(t) is determined accordingly). In Table 5, we list the errors for different numbers of nodes for both formulations, where the numerical solution is derived by solving the collocation formulations directly using Gauss elimination (instead of deferred correction iterations) in one time step [0, 1], and the $L_2$ error (at all collocation points) is used for both cases. Similar experiments are performed for the functions $y(t)=t^{20}$, $y(t)=e^{4t}$, $y(t)=\cos (4t)$, and $y(t)=e^{-t^2}$, and results are presented in Fig. 15. Except for the case $y(t)=t^{20}$ and $n=20$ where both formulations achieve machine precision, it can be seen that for all other cases, the results from the Gauss collocation formulations are more accurate than those from the uniform collocation formulations.

Table 5 Errors from Gauss and uniform collocation formulations, $y(t)=\frac{1}{1+5(t-0.5)^2}$

Fig. 15

Accuracy comparisons of Gauss and uniform collocation formulations

There are several factors in finding the optimal formulation for a specific ODE system. One may need to know the properties of the solution to determine which formulation will need fewer points for the same accuracy requirement. In general the orthogonal basis based collocation formulations or the skeletonization based schemes should give good results for most problems, and uniform collocation formulations should be avoided, especially when one wants to use a big time step size with a large number of nodes for efficiency considerations.

4.2 Techniques for Convergence Procedure

Existing studies of the deferred correction methods show that it is more efficient to solve the collocation formulation using an iterative approach instead of the direct Gauss elimination, and the low-order methods are good preconditioners for the pseudo-spectral collocation formulation. In the “convergence procedure” of the numerical framework, different preconditioning techniques can be integrated to eliminate the errors of the provisional solutions efficiently. In this section, we compare different strategies for stiff and non-stiff problems, and provide guidelines for faster convergence.

Table 6 Errors and Orders of the backward Euler and trapezoidal rule preconditioned deferred correction iterations for different collocation formulations, non-stiff case

We first compare different schemes for the non-stiff model problem $y'(t)=y(t)+f(t)$ with analytical solution $y(t)=\frac{1}{1+t}$ (and f(t) determined accordingly). In Table 6, we show how the errors change for different numbers of deferred correction iterations using different low-order preconditioners and collocation schemes. We march from $t=0$ to $t_{\textit{final}}=3$ using “nsteps” time steps, and set the number of node points to $p=7$ for each time step in all cases. In the “Uniform+B(oth)” collocation formulation, both end points are used in the formulation. We also tested the Radau IIa nodes and Gaussian nodes and results are very similar to those from the Lobatto collocation formulation for the non-stiff case in Table 6. We therefore neglect those results in the table. It can be seen that:

• (a) The order of the yp-formulation is 1 order higher than the corresponding integral formulation.

• (b) After each correction, the backward Euler preconditioned deferred correction methods improve the convergence order by 1 for both the yp-formulation and integral formulation.

• (c) For both the yp-formulation and integral formulation, the trapezoidal rule preconditioned deferred correction methods improve the convergence order by 2 after each iteration for the uniform collocation formulations. This is not true for the Lobatto nodes.

• (d) For all cases in this table, the trapezoidal rule preconditioner outperforms the backward Euler preconditioner for this non-stiff linear problem after the same amount of iterations.

These results agree with our analysis in previous sections, and suggest the following strategies to start the iteration procedure: (1) one should apply a high order “predictor” to uniform collocation formulations to derive a more accurate initial provisional solution $\mathbf{{Y}}^{[0]}$ using the yp-formulation; (2) to reduce the non-stiff error components in the provisional solution, the higher order method (e.g., trapezoidal rule) preconditioned deferred correction schemes for the yp-formulation with uniform grids are preferred as they show better convergence properties; (3) one should compare the result $\tilde{\varvec{\delta }}^{[0]}$ from the first deferred correction iteration to the initial provisional solution, to check if $\mathbf{{Y}}^{[0]}$ is an acceptable initial guess for the Newton’s method to converge to the collocation formulation solution. One possible measure is to check if the ratio $||\tilde{\varvec{\delta }}^{[0]}||/||\mathbf{{Y}}^{[0]}||$ is sufficiently small; and (4) for the first several deferred correction iterations, as the dominating error comes from the non-stiff part, it is probably unnecessary to search for the solution in the Krylov subspace, and the fixed point type iterations (Neumann series for linear problems) should provide good convergence properties. This can be measured by the ratio of $||\tilde{\mathbf{\delta }}^{[n+1]}||/||\tilde{\varvec{\delta }}^{[n]}||$. When the ratio is small, standard deferred correction iterations should still be acceptable.

A relatively large ratio $||\tilde{\mathbf{\delta }}^{[n+1]}||/||\tilde{\varvec{\delta }}^{[n]}||$ (e.g. $>1/2$) suggests that the dominating error no longer comes from the non-stiff components, and algorithms which can efficiently reduce the errors from the stiff components should be applied. It is unfortunately still an open problem what the optimal strategy should be to reduce the errors from the stiff components. In this paper, we consider possible strategies for two scenarios: (1) when only the Neumann series type iterations are used as in standard deferred correction procedures, and (2) when the Krylov subspace based iterative methods can be applied to further accelerate the convergence. Note that many researchers prefer the standard deferred correction methods in the first scenario as it doesn’t require additional overhead operations (e.g., solving the least squares problem using the Krylov subspace methods) or additional memory to store the vectors in the Krylov subspace. However when scenario (1) is used to solve stiff ODE systems, serious order reduction (or even divergence) is expected unless very small time step sizes are used. In the remainder of this subsection, we provide some guidelines for scenario (1), and in Sect. 4.4, we show preliminary implementation of the numerical framework for scenario (2) based on the Jacobian-free Newton–Krylov methods, which we believe are more appropriate for reducing the stiff error components.

In Table 7, we check the numerical properties of different deferred correction schemes for the stiff model problem $y'(t)=\lambda y(t)+f(t)$ with analytical solution $y(t)=\frac{1}{1+t}$ (and f(t) determined accordingly). We set $\lambda =-10^5$ and use the same settings for other parameters as in the non-stiff case. We show how the errors change for different numbers of deferred corrections in a time marching scheme. In the table, we add the “uniform+R” collocation formulation where only the right hand side is included in the spectral integration. We focus on the first order backward Euler preconditioner, and neglect results from the trapezoidal rule based schemes due to their poor convergence properties in the “strongly stiff limit” case as summarized in Table 4. The purpose of this experiment is not to identify which method should be used to reduce the stiff components errors, but to find out which methods should be avoided when standard deferred correction methods are preferred, especially when one doesn’t require the iteration procedure to converge to the collocation formulation and hence allows the existence of relatively large errors in the solution.

Table 7 Errors and orders of the backward Euler preconditioned deferred correction iterations for different collocation formulations, stiff case

Our observations can be summarized as follows:

• (a) Without converging to the collocation formulation, the deferred correction schemes for the yp-formulation using the left end point should be avoided, as the large error in the initial value will be magnified by the factor $\lambda$ and will propagate to later steps when marching in time, as discussed in Sect. 3.5 (see results from $Uniform+B$ and Lobatto).

• (b) When the iterations converge to an acceptable accuracy, the yp-formulation without the left end point will become acceptable (see the case yp, Radau IIa, 2 SDC Iters).

• (c) When there are large errors in the initial solution, the integral formulations give more stable results than the yp-formulation, as discussed in Sect. 3.5 (see Eqs. 18, 19).

• (d) After two SDC iterations, the best results are from the integral formulation with uniform grids without the left end point (Uniform+R). The better accuracy is the result of smaller initial error (without using the left end point) and faster convergence due to the “close-to-zero” eigenvalues in the correction matrix as studied in Theorem 3 in Sect. 3.4.2.

• (e) Order reduction is observed for the $Uniform+B$, Lobatto, and Radau cases using the integral formulation, due to one or both of the following two reasons: (1) slower convergence due to the spectral radius of the correction matrix (Lobatto and Radau cases, see Sects. 3.3.1 and 3.4), and (2) large initial error from using the left end point ($Uniform+B$ and Lobatto cases, see Sect. 3.4.1).

Fig. 16

Convergence rate for backward Euler preconditioned Gauss (left) and uniform (right) collocation formulations for different stiffness parameters $\lambda$

Note that in the previous numerical experiments, we follow the standard deferred correction schemes and consider both the converged and non-converged solutions in the simulations. Also, in the initial error, we have both stiff and non-stiff components. In the new numerical framework, as we first reduce the errors from the non-stiff components, it is therefore more appropriate to focus on the rate of convergence (determined by the spectral radius of the correction matrix discussed in Sect. 3) for different schemes for stiff problems (instead of checking the errors in the first few iterations that also include the initial errors as in the previous experiments). In Fig. 16, we compare the rate of convergence for the backward Euler preconditioned deferred correction iterations for the integral formulations using the Gauss collocation points to that using the uniform collocation points. Both schemes are applied to the model problem $y'(t)+\sin (t) = \lambda \left( y(t)-\cos (t) \right)$ with initial value $y(0)=1$. We march from $t=0$ to $t=1$ using one big step, and use 10 node points in the discretization. We only test real $\lambda$ values for $\lambda =-10^{k}$, $k=1, \ldots , 6$. Our numerical results show that the scheme using the uniform nodes converges at a faster rate compared to that using the Gauss type nodes. For $\lambda =-1e+6$, the error decays rapidly when the uniform nodes are used. This is consistent with the analysis in Theorem 3. We therefore conclude that when the standard deferred correction scheme is preferred, the backward Euler preconditioned integral deferred correction schemes for the uniform collocation formulation are acceptable schemes to reduce the stiff error components. However order reduction (and divergence for large numbers of nodes) is still expected, e.g., the case when $\lambda =-1e+2$ in the numerical experiments. However as we discussed in Sect. 4.1, when the accuracy of the converged solution of the collocation formulation is considered, the Gauss type nodes based collocation formulations are preferred.

4.3 Mapping Between Different Node Points

Analysis and numerical experiments in previous sections show that when the uniform nodes are used in the “convergence procedure”, better convergence properties are usually expected compared with deferred correction schemes using other types of nodes. However the converged solutions are less accurate and may suffer from the Runge phenomenon. In this subsection, we show how to use different nodes for the provisional solution $\tilde{Y}$ and error $\delta$ for both the yp- and integral formulations, so that when the deferred correction iterations for the uniform collocation formulations are convergent, the converged solution will solve the orthogonal basis based collocation formulations.

We first consider the yp-formulation given in Eq. (6), and its error’s equation is given by

$$\begin{aligned} \delta (t) = \left( f(t, y_0+\int _0^{t} \left( \tilde{Y}(\tau )+ \delta (\tau )) d\tau \right) - f\left( t, y_0+\int _0^{t} \tilde{Y}(\tau ) d\tau \right) \right) + \varphi (t) \end{aligned}$$

where $\varphi (t)=\left( f(t, y_0+\int _0^{t} \tilde{Y}(\tau ) d\tau ) - \tilde{Y}(t) \right)$ is usually referred to as the residual function in the spectral deferred correction methods. Introducing the linear mapping $P_{uG}$ which maps the polynomial values at the Gauss nodes to those at the uniform nodes, we can discretize the error’s equation at uniform node points as

$$\begin{aligned} \tilde{\varvec{\delta }}_{u} \!=\! \left( \mathbf{F}\left( \mathbf{t}_{u}, \mathbf{y}_0\!+\! P_{uG} \left( \varDelta t S_{G} \tilde{\mathbf{Y}}_{G} \right) \!+\! \varDelta t \tilde{S_{u}} \tilde{\varvec{\delta }}_{u} \right) - \mathbf{F}\left( \mathbf{t}_{u}, \mathbf{y}_0+ P_{uG}\left( \varDelta t S_{G} \tilde{\mathbf{Y}}_{G} \right) \right) \right) \!+\! P_{uG} {\varvec{\varphi }}_{G}\nonumber \\ \end{aligned}$$

(20)

where ${\varvec{\varphi }}_{G}= \mathbf{F}(\mathbf{t}_{g}, \mathbf{y}_0+\varDelta t S_{G} \tilde{\mathbf{Y}}_{G}) - \tilde{\mathbf{Y}}_{G}$ is the discretized residual at the Gauss collocation nodes, the sub-indices u and G represent that the corresponding vectors or integration matrices are defined on the uniform (u) or Gauss (G) nodes, respectively. Once the low order estimate of the error $\tilde{\varvec{\delta }}_{u}$ is available, it can be mapped to the Gauss nodes using a precomputed linear mapping $P_{Gu}=P^{-1}_{uG}$, and $P_{Gu} \tilde{\varvec{\delta }}_{u}$ can be added to the provisional solution $\tilde{\mathbf{Y}}_{G}$ defined on the Gauss nodes in the deferred correction procedure. Note that when the residual ${\varvec{\varphi }}_{G}=\mathbf{0}$ (meaning that $\tilde{\mathbf{Y}}_{G}$ solves the Gauss collocation formulation), $\tilde{\varvec{\delta }}_{u}=\mathbf{0}$. Similar to Sect. 3.2, for a linear ODE of the form $y'(t) = \lambda y +f(t)$ with given initial condition $y(0) = y_0$, detailed matrix analysis shows that this mapping procedure, if applied from the beginning of the deferred correction iterations, is equivalent to solving the Gauss collocation formulation $\mathbf{{Y}}_{G}=\lambda (\mathbf{y}_0+\varDelta t S_{G} \mathbf{{Y}}_{G}) +\mathbf{F}_{G}$ (with given $\mathbf{y}_0=[y_0, y_0, \dots , y_0]^T$ and $\mathbf{F}=[f(t_1), f(t_2), \dots , f(t_p)]^T$) using the preconditioner $P_{Gu} (I-\lambda \varDelta t \tilde{S}_{u})^{-1} P_{uG}$. The preconditioned system is given by

$$\begin{aligned} P_{Gu} \left( I\!-\!\lambda \varDelta t \tilde{S}_{u}\right) ^{-1} P_{uG} \left( I\!-\!\lambda \varDelta t S_{g}\right) \mathbf{{Y}}_{G}\!=\! P_{Gu} \left( I-\lambda \varDelta t \tilde{S}_{u}\right) ^{-1} P_{uG} \left( \lambda \mathbf{y}_0 +\mathbf{F}_{G}\right) \!=\! \tilde{\mathbf{Y}}^{[0]}.\nonumber \\ \end{aligned}$$

(21)

This mapping procedure can be applied in the same way to the integral Gauss collocation formulation represented by $\mathbf {y}_{G} = \mathbf {y_0} + \varDelta t S_{G} \mathbf {f} (\mathbf {t}_{G}, \mathbf {y}_{G})$. Defining the residual function as ${\varvec{\varphi }}_{G}= \mathbf {y_0} + \varDelta t S_{G} \mathbf {f} (\mathbf {t}_{G}, \mathbf {y}_{G}) - \mathbf {y}_{G}$, the discretized error’s equation at uniform nodes is then given by

$$\begin{aligned} \tilde{\varvec{\delta }}_{u} = \varDelta t \tilde{S}_{u} \left( \mathbf {f} \left( \mathbf {t}_{u}, P_{uG} \mathbf {y}_{G} + \tilde{\varvec{\delta }}_{u}\right) - \mathbf {f} \left( \mathbf {t}_{u}, P_{uG} \mathbf {y}_{G}\right) \right) + P_{uG} {\varvec{\varphi }}_{G}, \end{aligned}$$

(22)

where the operators $P_{Gu}$ and $P_{uG}$ are the same operators as the yp-formulation. Clearly when ${\varvec{\varphi }}_{G}=\mathbf{0}$, the error $\tilde{\varvec{\delta }}_{u}=0$.

4.4 Revisit the Jacobian-Free Newton–Krylov Methods

The new numerical framework allows many different strategies to be applied to the “convergence procedure”. In the previous sections, we mainly focused on the standard deferred correction type schemes and their impacts to the convergence properties. There are other techniques which can be introduced to further accelerate the convergence, e.g., the multigrid (or multi-order) techniques. These additional techniques are currently being actively studied and tested numerically for different scenarios. The purpose of this paper is to present the new perspective of studying existing deferred correction methods, and to introduce a numerical framework for more accurate and efficient solutions of time dependent differential equation problems. There are many open questions on the “optimal” strategies to accelerate the “convergence procedure” for different types of problems. In the following, we present a preliminary implementation of the numerical framework utilizing the Krylov deferred correction methods presented in Sect. 3.4.4, where a modified version of existing Jacobian-free Newton–Krylov method is adopted to accelerate the convergence procedure in the second step of the KDC algorithm.

In the algorithm, we will continue using the deferred correction type function evaluations $\tilde{\varvec{\delta }}^{[k]}=H(\tilde{\mathbf{Y}}^{[k-1]}+\tilde{\varvec{\delta }}^{[k-1]})$ as they effectively control the growth of the non-stiff errors, even though the Jacobian matrix of the low order techniques preconditioned system is no longer close to $-I$ for the stiff components. We introduce a predefined but adjustable parameter $\eta _1<1$ to check if the initial provisional solution provided by the predictor can serve as a good initial guess for the Newton’s method when solving the nonlinear collocation formulation, and another parameter $\eta _2<1$ to check if the standard deferred correction schemes are still effective. When order reduction or divergence is observed, we search for the optimal solution in the Krylov subspace using a modified Jacobian-free Newton–Krylov method, where the Krylov subspace is updated when the low order estimate $\tilde{\varvec{\delta }}^{[k]}=H(\tilde{\mathbf{Y}}^{[k-1]}+\tilde{\varvec{\delta }}^{[k-1]})$ shows no significant improvement compared with previous step results, and the optimal solution for the linearized equation $J_{H} \mathbf {x} = - \tilde{\varvec{\delta }}^{[k]}$ in each Newton’s iteration is sought in the recycled and updated Krylov subspace. In the modified JFNK, instead of the finite difference approximation as used in standard JFNK methods, the matrix-vector product $J_{H} \tilde{\varvec{\delta }}^{[k-1]}$ is computed using the Taylor expansion

$$\begin{aligned} \tilde{\varvec{\delta }}^{[k]}=H\left( \tilde{\mathbf{Y}}^{[k-1]}+\tilde{\varvec{\delta }}^{[k-1]}\right) \approx H\left( \tilde{\mathbf{Y}}^{[k-1]}\right) + J_{H} \tilde{\varvec{\delta }}^{[k-1]}, \end{aligned}$$

which is valid when $O(|| \tilde{\varvec{\delta }}^{[k]} ||) \approx O(|| \tilde{\varvec{\delta }}^{[k-1]} ||)$, i.e., when the result from one deferred correction iteration no longer converges efficiently for stiff systems. We stop the iterations in the “convergence procedure” when the solution is sufficiently close to that of the collocation formulation, measured by a prescribed error tolerance. The algorithm is described in detail by the following pseudo-code.

JFNK based “convergence procedure”

We demonstrate the performance of this numerical framework by comparing its preliminary implementation with the standard SDC method and an existing JFNK implementation from [28]. We apply these methods to a nonlinear ODE system which models the behavior of vacuum tube circuits. It was proposed by B. Van der Pol in the 1920’s, and is often referred to as the Van der Pol oscillator described by

$$\begin{aligned} \left\{ \begin{array}{l} y'_1(t) = y_2(t), \\ y'_2(t) = \left( 1-y_1^2(t) y_2(t)-y_1(t) \right) /\varepsilon . \end{array}\right. \end{aligned}$$

(23)

This is a stiff ODE system when $\varepsilon$ is small for relatively large time step sizes. In our simulation, following the work in [30] (see page 156, Sec. 7.2), we set the initial values as $[y(0),y'(0)]=[2, -0.6666654321121172]$ and focus on one time step $[0, \varDelta t]$. We use the Lobatto nodes based collocation formulation with 10 node points, and test different $\varepsilon$ and $\varDelta t$ values. In Fig. 17, we set $\varepsilon =0.01$ and show how the relative errors decay after each “function evaluation” $\tilde{\varvec{\delta }}=H(\tilde{\mathbf{Y}})$ for three different time step sizes $\varDelta t = \pi$ (stiff), $\varDelta t = \pi /10$ (mildly stiff), and $\varDelta t = \pi /100$ (non-stiff). For the stiff case ($\varDelta t = \pi$), our implemented framework requires approximately 50 iterations to converge to machine precision, while the general purpose JFNK and standard SDC method require 200 and 400 iterations, respectively. For the mildly stiff case ($\varDelta t=\pi /10$), these numbers become 50, 140, and 200, and for the non-stiff case, they are 20, 90, and 45. In the non-stiff case, the SDC method outperforms the general purpose JFNK method, due to the additional overhead operations required by the JFNK methods. For all three cases, the new framework (jfnk-new) outperforms other methods. Very similar results are derived for the settings $\varepsilon =10^{-6}$, $\varDelta t = \pi \cdot 10^{-4}$ (stiff), $\varDelta t = \pi \cdot 10^{-5}$ (mildly stiff), and $\varDelta t = \pi \cdot 10^{-6}$ (non-stiff) and these results are neglected in this paper.

Fig. 17

Comparison of the new framework with other methods, a $\varDelta t= \pi$, b $\varDelta t= \pi /10$, c $\varDelta t= \pi /100$, and d comparison of converged solutions for $\varDelta t= \pi /10$

In (d) of Fig. 17, we compare the converged solutions from different methods with the results from the backward Euler method based predictor (“b. Euler” in the figure) for the mildly stiff case $\varDelta t = \pi /10$ in one step. It can be seen that when different iteration schemes are convergent, they all converge to the solution of the collocation formulation.

Finally, we want to emphasize that our current implementation is by no means optimal, but it is an acceptable scheme which integrates different techniques presented in the algorithm design guidelines in previous sections, and it shows great potential for large-scale long-time differential equation simulations. We are currently testing different strategies to further improve the performance of the modified JFNK solver specifically designed for finding the roots of the function $\tilde{\varvec{\delta }}=H(\tilde{\mathbf{Y}})$, where most components of the output $\tilde{\varvec{\delta }}$ are good estimates of the errors in the input provisional solution $\tilde{\mathbf{Y}}$. Results will be reported in future papers.

5 Summary and Future Work

In this paper, we introduce a new perspective to understand the classical deferred correction methods, which separates the analysis of the “convergence procedure” from that of the “converged solution” to the collocation formulations. In the resulting numerical framework, an “optimal” collocation formulation is first selected based on the properties of the solution from the “collocation formulation database”, and different deferred corrections schemes can be selected from the “deferred correction methods database” to effectively reduce different error components in the provisional solution. Numerical results from a very preliminary implementation integrating different techniques presented in this paper show that the new framework is very promising for long-time large-scale simulations of differential equation initial value problems.

In the “convergence procedure”, this paper only focuses on how to apply different schemes from the “deferred correction methods database” to accelerate the convergence. We are also studying how to further improve the efficiency of the framework by introducing new preconditioning techniques for the “convergence procedure”. Examples include the multi-grid multi-order preconditioners, operator splitting techniques, semi-implicit discretization schemes for nonlinear differential equations, and domain decomposition based parareal-type preconditioners for time parallelization. These techniques will form a more general “convergence procedure toolbox”. After analyzing the properties of the solution, a proper tool or tools can be selected from the toolbox to effectively reduce the errors for faster convergence to the optimal collocation formulation. Finally, the new numerical framework can be coupled with fast elliptic equations solvers or fast N-body problem solvers to allow space–time parallel solution of time dependent partial differential equations. Research results along these directions will be reported in future papers.

Appendix

Proof of Theorem 3

Assuming p points $\{ 1/p, 2/p, \dots , (p-1)/p, 1 \}$ are used in the uniform collocation formulation, then $\tilde{S}$ is a lower triangular matrix and all non-zero entries (including diagonal entries) are 1 / p. Simple calculation shows that $\tilde{S}^{-1}$ has zero entries everywhere except along the diagonal and subdiagonal, with nonzero entries p on the diagonal and $-p$ on the subdiagonal,

$$\begin{aligned} \tilde{S}^{-1} = \left[ \begin{array}{llllll} p &{}\quad 0 &{} \quad 0 &{} \quad \cdots &{}\quad 0 &{}\quad 0 \\ -p &{}\quad p &{} \quad 0 &{}\quad \cdots &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad -p &{} \quad p &{} \quad \cdots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -p &{}\quad \cdots &{} \quad 0 &{}\quad 0 \\ \cdots &{} \quad \cdots &{}\quad \cdots &{} \quad \cdots &{}\quad \cdots &{}\quad \cdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad -p &{}\quad p \end{array} \right] . \end{aligned}$$

Consider the vector $\mathbf{V}_j = [ (p-1)^j, (p-2)^j, \dots , 2^j, 1^j, 0]^T$ ($j=1,\dots ,p-1$) and $\mathbf{V}_0=[1,1, \ldots , 1,1]^T$. As S integrates polynomials of degree $\le p-1$ exactly, one can show

$$\begin{aligned} \left( \tilde{S}^{-1} S - I\right) \mathbf{V}_j = \frac{1}{j+1} \sum _{l=0}^{j-1} \left( {\begin{array}{c}l\\ j+1\end{array}}\right) \mathbf{V}_l \quad and \quad \left( \tilde{S}^{-1} S - I\right) \mathbf{V}_0 = \mathbf{0}. \end{aligned}$$

Define $\mathbf{W}_0=\mathbf{V}_0$. The basis for the Jordan canonical form can be constructed recursively by solving $(\tilde{S}^{-1} S - I) \mathbf{W}_j = \mathbf{W}_{j-1}$, where $\mathbf{W}_j$ consists of a linear combination of $\mathbf{V}_k$, $k=0, \ldots , j$. $\square$

To prove Theorem 4, we start from the following Lemma:

Lemma 1

For the trapezoidal rule preconditioned uniform collocation formulation (InDC-yp-T), the matrix $S-\tilde{S}$ maps the vector $[ (\frac{j}{p})^k ]_{j=0}^p := [ (\frac{0}{p})^k, (\frac{1}{p})^k, (\frac{2}{p})^k, \dots , (\frac{p-1}{p})^k, 1 ]^T$ ($k \le p$) to a linear combination of vectors $[ (\frac{j}{p})^m ]_{j=0}^p$, $m=0, \dots , k-1$.

Proof

Assume $p+1$ points $\{ 0/p, 1/p, 2/p, \dots , (p-1)/p, 1 \}$ are used in the uniform collocation formulation. As the integration matrix S integrates polynomials of degree p or less exactly, we have

$$\begin{aligned} S \left[ \left( \frac{j}{p}\right) ^k \right] _{j=0}^p = \left[ \int _0^{\frac{j}{p}} x^k dx \right] _{j=0}^p = \frac{1}{k+1} \left[ \left( \frac{j}{p}\right) ^{k+1} \right] _{j=0}^p. \end{aligned}$$

Now consider the $j^{th}$ entry of the vector $\tilde{S} [ (\frac{j}{p})^k ]_{j=0}^p$ given by

$$\begin{aligned} \tilde{S} \left[ \left( \frac{j}{p}\right) ^k \right] _j= & {} \frac{1}{p} \left( \frac{1}{2} \left( \frac{0}{p}\right) ^k + \sum _{n=1}^{j-1} \left( \frac{n}{p}\right) ^k + \frac{1}{2} \left( \frac{j}{p}\right) ^k \right) =\frac{1}{p^{k+1}}\left( \sum _{n=1}^j n^k - \frac{1}{2} j^k\right) \\= & {} \frac{1}{p^{k+1}}\left( \frac{j^{k+1}}{k+1} + \frac{1}{2} j^k + \text{ lower } \text{ order }\,(<k)\hbox { terms }-\frac{1}{2} j^k\right) . \end{aligned}$$

Therefore, after cancelling the $j^{k+1}$ and $j^k$ terms, we have

$$\begin{aligned} (S-\tilde{S})\left[ \left( \frac{j}{p}\right) ^k \right] _{j=0}^p = \sum _{m=0}^{k-1} c_m \left[ \left( \frac{j}{p}\right) ^m \right] _{j=0}^p. \end{aligned}$$

$\square$

Proof of Theorem 4

We will Apply Lemma 1 and the Taylor expansion of the initial provisional solution in the trapezoidal rule preconditioned deferred correction iterations for the uniform collocation formulation (InDC-yp-T). From Eq. (17), we see that the correction matrix has the expansion

$$\begin{aligned} C^t_{ns}=(\lambda \varDelta {t})\left( \mathbf S - \tilde{\mathbf{S }}\right) + (\lambda \varDelta {t})^2 \tilde{\mathbf{S }}\left( \mathbf S - \tilde{\mathbf{S }}\right) + (\lambda \varDelta {t})^3 \tilde{\mathbf{S }}^2\left( \mathbf S - \tilde{\mathbf{S }}\right) + \cdots , \end{aligned}$$

and the initial provisional solution b has the expansion of the form (neglecting all $(\varDelta {t})^{p+1}$ and higher order terms)

$$\begin{aligned} b \approx \sum _{m=0}^{p} (\lambda \varDelta {t})^m c_m \left[ \left( \frac{j}{p}\right) ^m \right] . \end{aligned}$$

By induction and Lemma 1, it is straightforward to show that

$$\begin{aligned} \left( C^t_{ns}\right) ^k b \approx (\lambda \varDelta {t})^{2k} \sum _{m=0}^{p} c_{m,k} \left[ \left( \frac{j}{p}\right) ^m \right] , \end{aligned}$$

neglecting $(\varDelta {t})^{p+1}$ and higher order terms. Therefore, after each trapezoidal rule preconditioned SDC iteration for the uniform collocation formation, the order will increase by $(\varDelta {t})^2$, until it reaches $(\varDelta {t})^{p+1}$. $\square$