1 Introduction

From the latter half of the 20th century onwards, many authors have contributed to the development of time integration methods for the solution of ordinary and partial differential equations – by the methods of lines. A main objective was to develop A-stable methods with an order of accuracy larger than 2 to tackle efficiently the numerical solution of stiff problems arising, among others, from the modelling of viscous fluid flows. In this context, we recall that many fluid flows are unsteady (e.g., vortex shedding downstream of a circular cylinder) and require substantial computational resources to carry out the simulation.

Regardless of the time integration method accuracy (order), the difficulty of choosing the optimal time step size to capture the time-sensitive variations of physical phenomena limits the predictive efficiency of any discretized model. As a result, several studies proposed a conservative time step value based on the minimum size of the spatial discretization and an estimate of the maximum fluid velocity [9], or through the Courant-Friedrichs-Lewy condition [16] of an explicit time integration method. Nevertheless, this approach leads to poor use of allocated computational resources to undertake the simulations. In response to this problem Ouyang and Tamma [30], Gresho et al. [13], Birken et al. [1], John and Rang [19], and Mayr et al. [27] introduced time integrators with a variable time step size (VS) that only require the initial time step size and tolerance for local error.

Past contributions from several authors (including ours) to the modelling of incompressible fluid flows and fluid-structure interaction relied primarily on finite element and finite differences (among which, Backward Difference Formulae – BDF), respectively, for spatial and temporal discretizations. In particular, Euler and Gear’s implicit methods remain frequently used for solving complex problems by many researchers and in commercial codes (e.g., Fluent, COMSOL). It is well known that these are, within the theoretical framework of Dahlquist, the only A-stable methods in the BDF family. BDF methods with an order greater than 2 are not A-stable, and one must dynamically adjust the order and time step size according to the evolution of the simulation, as popularized and implemented in the DASSL code by Petzold [31] and co-workers [10, 20]. Of particular relevance to incompressible flows, we also acknowledge the work of Skelboe [34], Brenan et al. [2] and Hay et al. [17, 18] for the integration of Hessenberg index-2 differential-algebraic equations (DAEs).

Admittedly, these variable-step variable-order BDF heuristics (VSVO) allow solving with efficiency relatively simple physical phenomena such as the Von Kármán vortex street. However, when simulating breaking waves [38], large bubble deformations [29] or the chaotic motion of submerged devices [4], we found that the order of the BDF method rarely exceeds order 2; this is a disappointing outcome limiting the reach of the VSVO adaptivity. Hence, to improve the computational efficiency of multiscale physical problems, this suggests using higher order non-LMM (Linear Multistep Method) time discretizations that are A-stable beyond the second Dahlquist barrier.

To this end, we investigated two alternatives to BDF for temporal integration based on finite difference formulae: Implicit Runge-Kutta (IRK) and deferred corrections for the simulation of the Navier-Stokes equations. In this context, IRK methods proved to be very accurate and robust [3]. However, they require more storage space and more computing time per time step than BDF discretizations, at least for fully implicit IRK (non-DIRK). On the other hand, we found that our deferred correction method [26] was as accurate as the third-order BDF discretization without requiring much more storage space for the system of algebraic equations. This approach used the methodology proposed by Guermond and Minev [14], iteratively improving the first-order BDF discretizations to construct second and third-order solutions – but limited to constant time step integration.

We have therefore chosen the methodology of deferred corrections to elaborate time integration methods with variable time steps. More specifically, we are interested in designing arbitrary order A-stable methods based on finite difference formulae (BDF) to benefit from the experience gained in this specific research area. While we recognize the possibilities of spectral deferred corrections [6, 28, 36], this choice certainly facilitates the adaptation of existing finite element simulation software – based on BDF time integration formulae – to take advantage of these improved computational methods.

Within this research framework, we identify the work of Gustafsson and Kress as the most relevant to our study. In [15], Gustafsson and Kress developed a family of deferred correction methods for linear initial value problems. In this paper, they apply the implicit midpoint rule p/2 times in each time step to obtain an accurate solution of even order p. Subsequently, they studied and applied this methodology to linear boundary value problems [25], where they derive error estimates for time-dependent coefficients and performed numerical experiments to confirm the theoretical results. More recently, Kress [24] has enriched these results by substituting the Gear method (BDF2) for the midpoint rule as the building block in the deferred correction methodology. Furthermore, she also proposed modifications to the standard Dirichlet boundary to avoid the order reduction phenomenon. We mention that these implicit midpoint DC methods were extended to nonlinear initial value problems [23] and reaction-diffusion equations [22]. Finally, we note that Gustafsson and Kress developed their methodology only for constant time step integration deferred correction methods.

In this paper, we obtain from the second-order backward difference method (BDF2) a family of deferred correction methods of arbitrary order p (DCp). We introduce and analyze these new methods in the context of variable time step integration for solving initial value problems. In doing so, we establish the 0-stability of the BDF2 building block as a main ingredient of our DCp methodology. We also show that the usual stability conditions are sufficient for the maximal increase of order of accuracy to hold for the cascade BDF2 \(\rightarrow \) DC3 \(\rightarrow \) DC4, etc., but not for the direct construction from BDF2 to DC4. An extra condition on the ratio of consecutive time step sizes is introduced for the jump from DCp to DC\(p+2\) to reach maximal order increase. This analysis is an original contribution. Finally, we prove the A-stability for these methods. Accordingly, we present in Sect. 2 the variable time integration algorithm and the construction of the deferred correction methods. We study the 0-stability and A-stability of these methods and derive their error estimates in Sect. 3. And, finally, in Sect. 4, we make use of the manufactured solution method to confirm the results of the theoretical analysis.

2 Deferred correction methods

In this section, we build a suite of time integration methods – of increasing accuracy – based on the second-order backward differentiation formula. This is part of the general development of higher-order implicit A-stable methods to allow adaptive time-stepping for better control of the computational accuracy. It falls within the scope of the seminal work of Fox [8], Keller and Pereyra [21], and extends the Difference Corrected BDF framework of Söderlind [35] and the results of Kress [24] to variable step size integration.

Notation 2.1

We adopt the following conventions for the solutions of the model ordinary differential equation (ODE) (2.1):

  • \({\mathcal {I}} = [0,T]\), solution time interval;

  • \(0=t^0< t^1< ... < t^N = T\), N+1 discrete solution times;

  • \(k_n = t^n - t^{n-1}\) and \(\{k_n\}_{n=1}^N\), time steps;

  • \(\omega _n= k_n/k_{n-1}\), ratio of successive time steps;

  • \(k = \max \{k_n\}_{n=1}^N\), maximum time step;

  • \(u=u(t)\), an exact solution;

  • \(u_n \equiv u(t^n)\), shorthand for the solution \(u=u(t)\) at time \(t^n\);

  • \(u^n \approx u(t^n)\), a numerical approximation of the solution \(u=u(t)\) at time \(t^n\);

  • \(u_k = \{u^n\}_{n=0}^N\), a vector of numerical solution;

  • \(F_n = F(t^n,u(t^n))\), r.h.s. exact value at time \(t^n\);

  • \(F^n = F(t^n,u^n)\), r.h.s. approximation at time \(t^n\).

Let us begin this exposé with the initial value problem for the first-order differential equation

$$\begin{aligned} \begin{aligned} \frac{du}{dt}&= F(t,u), \\ u(0)&= u_0, \end{aligned} \end{aligned}$$
(2.1)

with solution \(u \in {\mathcal {C}}^{p+1}({\mathcal {I}};{{\mathbb {R}}})\) – see Sect. 3 for appropriate values of p – and initial value \(u_0\). To simplify notations, we assume that we have a scalar ODE, but u(t) can be taken in \({{\mathbb {R}}}^d\) or any Hilbert space H with appropriate assumptions on \(F(t,\cdot ):H\rightarrow H\).

Using the second-order backward difference approximation (BDF2) of the time derivative, the differential equation is transformed into the following implicit algebraic formula

$$\begin{aligned} \frac{d}{dt}u(t^n) \approx \boxed {\sum _{i=0}^2 c_i^n u^{n-i} = F(t^n,u^n)} \end{aligned}$$
(2.2)

with

$$\begin{aligned} \left. \begin{aligned} c_0^n&= \frac{1}{k_n}+ \frac{1}{k_n+k_{n-1}} = \frac{2\,\omega _n+1}{k_n \,(\omega _n+1)}\\ c_1^n&= -\frac{1}{k_n} - \frac{1}{k_{n-1}} = - \frac{(\omega _n+1)^2}{k_n \,(\omega _n+1)}\\ c_2^n&= \frac{k_n}{k_{n-1}} \frac{1}{k_n+k_{n-1}} = \frac{(\omega _n)^2}{k_n \,(\omega _n+1)} \end{aligned} \right\} \, , \end{aligned}$$
(2.3)

where we seek the solution at \(t^n\) knowing the solutions at \(t^{n-1}\) and \(t^{n-2}\). By substituting the exact solution u(t) into the BDF2 algebraic formula (2.2), we obtain

$$\begin{aligned} \left. \begin{aligned} c_0^n u(t^n) + c_1^n u(t^{n-1}) + c_2^n u(t^{n-2}) - F(t^n,u(t^n)) - E(t^n)&= 0 \\ E(t^n) = \sum _{j=3}^{\infty } (-1)^j \frac{u^{(j)}(t^n)}{j!} \, (c_1^n \, k_n^j + c_2^n (k_n+k_{n-1})^j) \end{aligned} \,\right\} . \end{aligned}$$
(2.4)

At this point, let us emphasize that the proper approximation of the truncation error \(E(t^n)\) is central to the development of the deferred correction methods of this study.

To obtain higher-order methods, it is often sufficient to modify the algebraic formula (2.2) by adding one or more terms borrowed from the expression of the truncation error (2.4). We carried out this process in two steps. First, we replace in (2.4) the unknown values of the solution \(u(t^n)\), \(u(t^{n-1})\) and \(u(t^{n-2}\)) by their known numerical approximations \(u^n\), \(u^{n-1}\) and \(u^{n-2}\). Finally, we replace the analytical error \(E(t^n)\) with a numerical approximation \({\mathcal {D}}_p(u^n)\), where we approximate the derivatives of the unknown solution \(u^{(j)}(t^n)\) by well-chosen finite difference formulas, noted \(u^{(j),n}\), involving known numerical values at \(t^n\), \(t^{n-1}\), \(t^{n-2}\), and so on. For example, we write

$$\begin{aligned} \left. \begin{aligned} \sum _{i=0}^2 c_i^n u^{n-i} +{\mathcal {D}}_p(u^n) = F(t^n,u^n) \\ {\mathcal {D}}_p(u^n) = \sum _{j=3}^{p} (-1)^{j+1} \frac{u^{(j), n}}{j!} \, (c_1^n \, k_n^j + c_2^n (k_n+k_{n-1})^j) \end{aligned} \right\} \, . \end{aligned}$$
(2.5)

This results in the family of BDF methods which are conditionally stable above BDF2 [39], i.e., the second-order approximation. However, in the deferred correction, we replace \(u^n\) in \({\mathcal {D}}_p(u^n)\) with a known lower-order approximation \(v^n\), such that \({\mathcal {D}}_p(u^n) \approx {\mathcal {D}}_p(v^n)\), to enhance the stability of the high-order numerical solution \(u^n\). To illustrate this approach, consider the following set of equations:

$$\begin{aligned} \left. \begin{aligned} \sum _{i=0}^2 c_i^n {\bar{u}}^{n-i} = F(t^n,{\bar{u}}^n) \\ \sum _{i=0}^2 c_i^n {\hat{u}}^{n-i} + {\mathcal {D}}_3({\bar{u}}^n) = F(t^n,{\hat{u}}^n) \end{aligned} \right\} \,\, , \end{aligned}$$
(2.6)

where \({\bar{u}}\) and \({\hat{u}}\) are the BDF2 and the high-order deferred correction solution, respectively. This results in a third-order deferred correction (DC3) with \({\mathcal {D}}_3({\bar{u}}^n)\), i.e., with one term in this correction series. This is written as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}_3({\bar{u}}^n) = \frac{{\bar{u}}^{(3), n}}{3!} \, (c_1^n \, k_n^3 + c_2^n (k_n+k_{n-1})^3) \\ {\bar{u}}^{(3), n} = 2 \, \delta ^{{\bar{F}}}_{12} \end{aligned} \end{aligned}$$
(2.7)

where \(\delta ^{{\bar{F}}}_{12} \overset{\text {def }}{=}{\bar{F}}[t^n, t^{n-1}, t^{n-2}]\) stands for the second backward divided difference through the data points

$$\begin{aligned} (t^n, {\bar{F}}^n), ..., (t^{n-2}, {\bar{F}}^{n-2} ) \end{aligned}$$
(2.8)

with \({\bar{F}}^n = F(t^n, {\bar{u}}^n))\), i.e., the best available \(\dot{u}(t^n)\) time derivative. Finally, to complete this description, we put in Table 1 the divided difference through these data points. Then the usual Newton polynomial through these points,

$$\begin{aligned} {\bar{p}}_2(t) = {\bar{F}}^n + \delta ^{{\bar{F}}}_{11} \, (t-t^n) + \delta ^{{\bar{F}}}_{12} \, (t-t^n) \,(t-t^{n-1}) \,\,\, , \end{aligned}$$
(2.9)

yields

$$\begin{aligned} {\bar{u}}^{(3)}(t^n) \approx \frac{d^2 {\bar{p}}_2}{dt^2}(t^n) = {\bar{u}}^{(3),n} = 2 \, \delta ^{{\bar{F}}}_{12} \end{aligned}$$
(2.10)

This overall procedure is a natural generalization of the Difference Corrected BDF framework [35, 39] to encompass variable step size integration. Moreover, note that it is also possible to use a higher degree polynomial to enhance the third derivative approximation.

Table 1 Divided difference based on \({\bar{F}}(t,{\bar{u}})\)
Full size table

We repeat this procedure, to sequentially construct fourth-order (DC4 method) and fifth-order (DC5 method) solutions, etc. We summarize this process with the following set of equations starting with BDF2 up to DC5:

$$\begin{aligned}&\left. \begin{aligned} \boxed { \sum _{i=0}^2 c_i^n {\bar{u}}^{n-i} = F(t^n,{\bar{u}}^n) } \end{aligned} \right\} \,\, \text {BDF2} \,\, , \end{aligned}$$
(2.11)
$$\begin{aligned}&\left. \begin{aligned} {\bar{F}}^{n-i} = F(t^{n-i}, {\bar{u}}^{n-i} ) \,\,\,\, \forall \,i \in \{0,1,2\} \\ {\bar{u}}^{(3),n} = 2\, \delta _{12}^{{\bar{F}}} \\ \boxed { \sum _{i=0}^2 c_i^n {\hat{u}}^{n-i} + {\mathcal {D}}_3({\bar{u}}^n) = F(t^n,{\hat{u}}^n) } \end{aligned} \right\} \,\, \text {DC3}, \end{aligned}$$
(2.12)
$$\begin{aligned}&\left. \begin{aligned} {\hat{F}}^{n-i} = F(t^{n-i}, {\hat{u}}^{n-i} ) \,\,\,\, \forall \,i \in \{0,1,2,3\} \\ {\hat{u}}^{(3),n} = 2\, \delta _{12}^{{\hat{F}}} + 2 \, \delta _{13}^{{\hat{F}}} \, ( 2\,k_n+k_{n-1} ) \\ {\hat{u}}^{(4),n}(t^n) = 6 \, \delta _{13}^{{\hat{F}}} \\ \boxed { \sum _{i=0}^2 c_i^n {\tilde{u}}^{n-i} + {\mathcal {D}}_4({\hat{u}}^n) = F(t^n,{\tilde{u}}^n) } \end{aligned} \right\} \,\, \text {DC4}, \end{aligned}$$
(2.13)

and

$$\begin{aligned} \left. \begin{aligned} {\tilde{F}}^{n-i} = F(t^{n-i}, {\tilde{u}}^{n-i} ) \,\,\,\, \forall \,i \in \{0,1,2,3,4\} \\ {\tilde{u}}^{(3),n} = 2\, \delta _{12}^{{\tilde{F}}} + 2 \, \delta _{13}^{{\tilde{F}}} \, ( 2\,k_n+k_{n-1} ) \\ + 2 \, \delta _{14}^{{\tilde{F}}} \, ( 3\,k_n^2 + 4\,k_n\,k_{n-1} + 2\,k_{n-2}\,k_n + k_{n-1}^2 + k_{n-2}\,k_{n-1} ) \\ {\tilde{u}}^{(4),n} = 6 \, \delta _{13}^{{\tilde{F}}} + 6 \, \delta _{14}^{{\tilde{F}}} \, ( 3\,k_n + 2\, k_{n-1} + k_{n-2}) \\ {\tilde{u}}^{(5),n} = 24\, \delta _{14}^{{\tilde{F}}} \\ \boxed { \sum _{i=0}^2 c_i^n u^{n-i} + {\mathcal {D}}_5({\tilde{u}}^n) = F(t^n, u^n) } \end{aligned} \right\} \,\, \text {DC5}. \end{aligned}$$
(2.14)

We immediately observe the computational cascade. At time \(t^n\), we use the second-order solution (2.11) – BDF2 – to calculate the third-order solution (2.12), and so on until we reach the fifth-order solution (2.14). Obviously, this example is limited to the fifth-order approximation only to illustrate the construction sequence and to show the intricate interaction explicitly with the divided difference and the time steps.

3 Stability and error estimates

In this section, we prove the stability and obtain error estimates for our DC methods. Since our analysis depends in an essential way on the 0-stability of the BDF2 method, we must first review and discuss the conditions to reach this stability. Our proof of 0-stability is inspired by Crouzeix and Mignot [5,  chap.7], but the developments specific to BDF2 and some of the strategies to select varying time steps are not discussed and regrouped in this form in the literature. In the following subsections, we derive the error estimates for our DC methods of order 3 and 4 with variable time steps, and indicate how these estimates can be generalized to higher-order DC methods. It is a deliberate choice to make explicit the difficulties encountered in the proofs of theorems and propositions.

We first prove that one correction step from BDF2 to DC3, then an other from DC3 to DC4 lead, respectively, to third and fourth-order of accuracy, with no constraint on the ratio \(\omega _n\) of successive time steps beyond the requirements for 0-stability. We also investigate the possibility to construct a variant of DC4 directly from BDF2 in one correction step to reduce the computational cost, as was done by [24] with constant time steps. We show that this is possible, but under a severe restriction on the ratio of the form \(|\omega _n-\omega _{n-1}|\le {\mathcal {C}}k\), as the maximal time step k is reduced. This section ends with a proof of the A-stability of our DC methods of arbitrary orders with constant time steps, since this notion applies in this case only.

3.1 BDF2 with variable steps – 0-stability and error estimate

Given \(u^j\), \(j=0,1\), the BDF2 method with variable time steps (2.2) can be rewritten as:

$$\begin{aligned} u^n - \frac{(\omega _n+1)^2}{2\,\omega _n+1} u^{n-1} + \frac{\omega _n^2}{2\,\omega _n+1} u^{n-2} = \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,F(t^n,u^n),\quad n\ge 2,\qquad \end{aligned}$$
(3.1)

The 0-stability consists in a uniform bound on the error between the solution \(u^n\) of the original problem and the solution \(z^n\) of a perturbed problem, solved with the same method

$$\begin{aligned} z^n - \frac{(\omega _n+1)^2}{2\,\omega _n+1} z^{n-1} + \frac{\omega _n^2}{2\,\omega _n+1} z^{n-2} = \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,F(t^n,z^n) + \delta ^n,\quad n\ge 2,\qquad \end{aligned}$$
(3.2)

with initial conditions \(z^j=u^j+e^j\), \(j=0,1\), and perturbations \(\delta ^n\), \(n\ge 2\). For this purpose, we define \(e^n=z^n-u^n\), and substract (3.1) from (3.2):

$$\begin{aligned} \left[ 1-\frac{g^n\,k_n\,(\omega _n+1)}{2\,\omega _n+1}\right] \,e^n = \frac{(\omega _n+1)^2}{2\,\omega _n+1}\,e^{n-1} - \frac{\omega _n^2}{2\,\omega _n+1}\,e^{n-2} + \delta ^n, \end{aligned}$$
(3.3)

where

$$\begin{aligned} F(t^n,z^n)-F(t^n,u^n)=g^n\,(z^n-u^n) \quad \text{ with }\quad g^n=\int _0^1 F_u(t^n,u^n+s\,(z^n-u^n))\,ds, \end{aligned}$$

and \(F_u\) is the partial derivative of F with respect to variable u. It follows that if F is globally Lipschitz with respect to the variable u, then \(|g^n|\le L\), for all n. In matrix form, this gives

$$\begin{aligned} \underbrace{ \begin{bmatrix} \displaystyle 1-\frac{g^n\,k_n\,(\omega _n+1)}{2\,\omega _n+1} &{} \displaystyle 0 \\ 0 &{}1 \end{bmatrix} }_{\displaystyle D_n} \underbrace{ \begin{bmatrix} \displaystyle e^n\\ e^{n-1} \end{bmatrix} }_{\displaystyle U_n} = \underbrace{ \begin{bmatrix} \displaystyle \frac{(\omega _n+1)^2}{2\,\omega _n+1} &{} \displaystyle - \frac{\omega _n^2}{2\,\omega _n+1} \\ 1 &{}0 \end{bmatrix} }_{\displaystyle R_n} \underbrace{ \begin{bmatrix} e^{n-1}\\ e^{n-2} \end{bmatrix} }_{\displaystyle U_{n-1}} + \underbrace{ \begin{bmatrix} \delta ^n\\ 0 \end{bmatrix} }_{\displaystyle E_n} \, .\nonumber \\ \end{aligned}$$
(3.4)

Shortly, this reads as \(D_n U_n=R_n U_{n-1}+E_n\) or \(U_n=S_n U_{n-1}+{\bar{E}}_n\), with \(S_n=D_n^{-1}R_n\), \({\bar{E}}_n=D_n^{-1}E_n\) and the matrices and vectors given in the previous equation.

Definition 3.1

(S-condition) [5,  p.152] The method (3.1) satisfies the S-condition for stability if \(\exists \, {\mathcal {C}}>0\) such that \(\forall k,\forall n\) with \(1\le k \le n \le N-1\), we have:

$$\begin{aligned} \Vert R_n R_{n-1} \cdots R_k \Vert _1 \le {\mathcal {C}}. \end{aligned}$$
(3.5)

Theorem 3.1

[5,  th.7.6] If the method (3.1) satisfies the S-condition and F is globally Lipschitz in the variable u with constant L, then (3.1) is 0-stable, i.e., there exists a constant \({\mathcal {K}}>0\) independent from \(k_n\) but depending on T and L, and such that

$$\begin{aligned} | z^n-u^n | \le {\mathcal {K}}\, \left( |e_0| + |e_1| + \sum _{j=2}^{n-1} |\delta ^j| \right) . \end{aligned}$$
(3.6)

Theorem 3.2

Assume that the solution of (2.1) is such that \(u\in {\mathcal {C}}^3([0,T],{{\mathbb {R}}})\). If the BDF2 method is 0-stable for sequences of steps \(\{k_n\}_{n=1}^N\), with \(k=\max _{n} k_n\rightarrow 0\) when \(N\rightarrow \infty \), and \(|e_0|,|e_1|=O(k^2)\), then the following error estimate holds

$$\begin{aligned} |u(t^n)-u^n| \le {\mathcal {C}}\,k^2, \quad \forall n=1,\dots , N, \end{aligned}$$
(3.7)

where the constant \({\mathcal {C}}\) is independent from the numerical solution \(u^n\) and the steps \(k_n\).

Proof

To simplify notations, the exact solution is noted as \(u_n=u(t^n)\) and the r.h.s. of the ODE as \(F_n=F(t^n,u(t^n))\). From Sect. 2, the truncation error for (3.1) is

$$\begin{aligned} E_2^n = \sum _{i=0}^2 c_i^n u_{n-i} -F_n = -\frac{u_n'''}{6} \, k_n \, (k_n + k_{n-1}) +O(k^3). \end{aligned}$$
(3.8)

In (3.2), we set \(z_n=u_n=u(t^n)\), thus

$$\begin{aligned} \delta ^n=\frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,E_2^n \quad \Rightarrow \quad |\delta ^n| \le {\mathcal {C}}\,k_n\,k^2\,\Vert u'''\Vert _{\infty ,(0,T)}. \end{aligned}$$

From this bound on \(|\delta ^n|\), the hypothesis \(|e_0|,|e_1|=O(k^2)\) and \(\sum _{n=1}^N k_n=T\), the 0-stability bound (3.6) directly gives the error estimate (3.7). \(\square \)

In the rest of this section, we investigate for which sequences of steps \(\{ k_n \}_{n\ge 1}\) the BDF satisfies the S-condition and is 0-stable. We first present the following sufficient condition.

Proposition 3.1

If \(\omega _n \le \gamma < 1+\sqrt{2}\), \(\forall n\), the BDF2 method satisfies the S-condition and is 0-stable.

Proof

Let us introduce the following change of basis

$$\begin{aligned} H = \begin{bmatrix} 1 &{} 0 \\ 1 &{} \epsilon \end{bmatrix} \qquad \text{ and }\qquad H^{-1} = \begin{bmatrix} 1 &{} 0 \\ -1/\epsilon &{} 1/\epsilon \end{bmatrix}. \end{aligned}$$

We note that for all matrices \(R_n\), \(u_1=[1\;\; 1]^t\) is an eigenvector with eigenvalue \(\lambda _1=1\). This gives

$$\begin{aligned} H^{-1} R_n H = \begin{bmatrix} 1 &{} 0 \\ -1/\epsilon &{} 1/\epsilon \end{bmatrix} \begin{bmatrix} \frac{(\omega _n+1)^2}{2\,\omega _n+1} &{} - \frac{\omega _n^2}{2\,\omega _n+1} \\ 1 &{}0 \end{bmatrix} \begin{bmatrix} 1 &{} 0 \\ 1 &{} \epsilon \end{bmatrix} = \begin{bmatrix} 1 &{} - \frac{\epsilon \,\omega _n^2}{2\,\omega _n+1} \\ 0 &{} \frac{\omega _n^2}{2\,\omega _n+1} \end{bmatrix}. \end{aligned}$$

We recall that \(\displaystyle \Vert M\Vert _1=\max _{1\le j \le q} \sum _{i=1}^p |M_{ij}|\), for any matrix M of size \(p\times q\), hence

$$\begin{aligned} \Vert H^{-1} R_n H \Vert _1 = \max \left( 1, \frac{(1+|\epsilon |)\,\omega _n^2}{2\,\omega _n+1} \right) . \end{aligned}$$
(3.9)

It results that

$$\begin{aligned} \Vert R_n R_{n-1}\cdots R_k \Vert _1= & {} \Vert H (H^{-1} R_n H) (H^{-1} R_{n-1} H) \cdots (H^{-1} R_k H) H^{-1} \Vert _1 \nonumber \\\le & {} \Vert H \Vert _1 \Vert H^{-1} R_n H \Vert _1 \Vert H^{-1} R_{n-1} H \Vert _1 \cdots \Vert H^{-1} R_k H \Vert _1 \Vert H^{-1} \Vert _1 \nonumber \\\le & {} \Vert H \Vert _1 \, \Vert H^{-1} \Vert _1 = {\mathcal {C}}, \end{aligned}$$
(3.10)

if \(\Vert H^{-1} R_n H \Vert _1 \le 1\) for all n.

Imposing this condition for each n is one step selection strategy among others, see remark 3.1 below. This condition is satisfied if

$$\begin{aligned} \max \left( 1, \frac{(1+|\epsilon |)\,\omega _n^2}{2\,\omega _n+1} \right) = 1,\;\forall n \qquad \Longleftrightarrow \qquad (1+|\epsilon |)\,\omega _n^2 \le 1+2\,\omega _n. \end{aligned}$$
(3.11)

Inequality (3.11) is true under the following conditions:

  • The limit case occurs for \(|\epsilon |=0\) \(\Rightarrow \) \(\omega _n^2 \le 1+2\,\omega _n\) \(\Leftrightarrow \) \(\omega _n^2-2\,\omega _n-1\le 0\). Since \(\omega _\pm = 1\pm \sqrt{2}\), we must have \(\omega _n\le \omega _+=1+\sqrt{2}\).

  • \(|\epsilon |>0\) is essential, since the matrix H must be invertible. A sufficient condition to have (3.11) is \(\omega _n\le \gamma < 1+\sqrt{2}\). Since \(1-\sqrt{2}<0<\gamma <1+\sqrt{2}\), one gets \(1+2\gamma -\gamma ^2>0\) and the largest \(|\epsilon |\) must be such that \((1+|\epsilon |)\,\gamma ^2 = 1+2\gamma \) \(\Leftrightarrow \) \(|\epsilon |=\frac{1+2\gamma -\gamma ^2}{\gamma ^2}>0\). We note that \(\gamma \rightarrow 1+\sqrt{2}\) \(\Rightarrow \) \(|\epsilon |\rightarrow 0\) \(\Rightarrow \) \(\Vert H^{-1}\Vert \rightarrow +\infty \), then we must impose \(\omega _n\le \gamma < 1+\sqrt{2}\) to have \(\Vert H^{-1} R_n H \Vert _1 \le 1\) and be able to pick the same \(|\epsilon |>0\), for all n.

\(\square \)

Remark 3.1

From (3.9), we have \(\Vert H^{-1} R_n H \Vert _1\ge 1\). For the S-condition to hold, \(\Vert H^{-1} R_n H \Vert _1= 1\) was enforced for all n. We could still get (3.10) while allowing a maximum of p steps for which \(1<\Vert H^{-1} R_n H \Vert _1\le M\), with M fixed, and by imposing \(\Vert H^{-1} R_n H \Vert _1= 1\) for all the other steps. This would then yield

$$\begin{aligned} \Vert R_n R_{n-1}\cdots R_k \Vert _1 \le M^p\,\Vert H \Vert _1 \Vert H^{-1} \Vert _1 \le {\mathcal {C}},\quad \forall n\ge k\ge 1. \end{aligned}$$

Multistep methods are sensitive to abrupt changes of the time step, both in terms of accuracy and stability. In particular, Gear and Tu [11, 37] showed that p time steps must be taken between changes of the size of \(k_n\) in order to ensure the 0-stability of certain classes of order p methods. Alternating sequences of the form \(k_{2j+1}=k_1\) and \(k_{2j}=k_2\) lead to the instability of these classes of multistep methods beyond order 2. We now show that BDF2 is 0-stable for any alternating sequence of this type. Since our DC methods are stable under the same conditions as BDF2, they are 0-stable for all alternating sequences.

Proposition 3.2

The BDF2 method satisfies the S-condition and is 0-stable for all alternating sequences \(k_1\)-\(k_2\), for any pair of steps \(k_1\) and \(k_2\), even if one of \(\omega \) or \(1/\omega \) is larger than \(1+\sqrt{2}\).

Proof

Let

$$\begin{aligned} \omega =k_1/k_2, \qquad \gamma _1=\frac{\omega ^2}{1+2\omega } \quad \text{ and }\quad \gamma _2=\frac{1/\omega ^2}{1+2/\omega }, \end{aligned}$$

and use the matrices \(R_n\) and H introduced above to define

$$\begin{aligned} {\bar{R}}_n = H^{-1} R_n H = \begin{bmatrix} 1 &{} -\epsilon \,\gamma _n \\ 0 &{} \gamma _n \end{bmatrix}, \qquad n=1,2. \end{aligned}$$

This gives

$$\begin{aligned} \Vert R_n R_{n-1}\cdots R_k \Vert _1 \le \Vert H \Vert _1 \Vert {\bar{R}}_1 {\bar{R}}_2\Vert _1^\frac{n-k}{2} \Vert H^{-1} \Vert _1 \le {\mathcal {C}}, \end{aligned}$$

as long as \(\Vert {\bar{R}}_1 {\bar{R}}_2\Vert \le 1\). Noting that

$$\begin{aligned} {\bar{R}}_1 {\bar{R}}_2 = \begin{bmatrix} 1 &{} -\epsilon \,\gamma _1 \\ 0 &{} \gamma _1 \end{bmatrix} \begin{bmatrix} 1 &{} -\epsilon \,\gamma _2 \\ 0 &{} \gamma _2 \end{bmatrix} = \begin{bmatrix} 1 &{} -\epsilon \,\gamma _2\,(1+\gamma _1) \\ 0 &{} \gamma _1\,\gamma _2 \end{bmatrix}, \end{aligned}$$

the 0-stability holds if

$$\begin{aligned} \Vert {\bar{R}}_1 {\bar{R}}_2\Vert = \max \left( 1, \gamma _1\,\gamma _2\,(1+|\epsilon |)+\gamma _2\,|\epsilon | \right) \le 1. \end{aligned}$$

We set and notice that

$$\begin{aligned} r= & {} \gamma _1\,\gamma _2\,(1+|\epsilon |)+\gamma _2\,|\epsilon | = \frac{1}{(1+2\omega )\,(1+2/\omega )} + |\epsilon |\, \underbrace{ \frac{(1+\omega )^2}{\omega ^2\,(1+2\omega )\, (1+2/\omega )}}_{\displaystyle A_\omega } \\= & {} \frac{1}{1+4+2\omega +2/\omega )} + |\epsilon |\,A_\omega \,\,\,\, \le \frac{1}{9} + |\epsilon |\,A_\omega \,\,\,\, \le 1, \end{aligned}$$

for all \(|\epsilon | \le 8/(9A_\omega )\). \(\square \)

3.2 DC3 – Error estimate

We now obtain an error estimate for the variable-step DC3 method, by first proving the following lemma. In this lemma, \({\mathcal {D}}_3({\bar{u}})\) is defined in (2.7) and \({\mathcal {D}}_3(u)\) refers to the same finite difference operator applied to the exact solution evaluated at the discrete times \(t^n\). This convention also applies to higher order approximations analyzed below.

Lemma 3.1

Assume that the hypotheses from Theorem 3.2 hold so that we have the error estimate (3.7) for the solution \({\bar{u}}^n\) of BDF2. Then, for a maximal step k small enough,

$$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|{\mathcal {D}}_3(u) -{\mathcal {D}}_3({\bar{u}})| \le {{{\mathcal {C}}}}\, k^4, \end{aligned}$$
(3.12)

with a constant \({{\mathcal {C}}}\) independent from k and the numerical solutions.

Proof

The proof proceeds by extending the idea from [23] to variable time steps and corrections \({\mathcal {D}}(u)\) defined in F rather than u.

We first define \(D_-F_n= \frac{F_n-F_{n-1}}{k_n}\) (using \(k_{n-1}\) for \(D_-F_{n-1}\) and so forth) and write

$$\begin{aligned} {\mathcal {D}}_3(u)-{\mathcal {D}}_3({\bar{u}})= & {} \frac{k_n\,(k_n+k_{n-1})}{3} (\delta _{12}^{F}-\delta _{12}^{{\bar{F}}}) \nonumber \\= & {} \frac{k_n}{3} \left( D_-(F_n-{\bar{F}}^n) - D_-(F_n-{\bar{F}}^{n-1}) \right) . \end{aligned}$$
(3.13)

We get the estimate in three steps:

  1. 1.

    Let us define

    $$\begin{aligned} h_n= F_n-{\bar{F}}^n = \int _0^1 F'(K_1^n)\,{\bar{e}}_n\,ds_1, \end{aligned}$$
    (3.14)

    where \(K_1^n=u_n+s_1\,({\bar{u}}^n-u_n)=u_n-s_1\,{\bar{e}}_n\). We note that

    $$\begin{aligned} |K_1^n|\le |u_n|+s_1\,|{\bar{e}}_n| \le {{{\mathcal {C}}}}\,(1+k^2) \le \bar{{{\mathcal {C}}}}, \qquad \text{ for } k\le {\bar{k}}_0, \end{aligned}$$

    since the exact solution \(u=u(t)\) is continuous, thus bounded on [0, T], and the BDF2 method converges with order 2. Hence \(|F'(K_1^n)|\le {\bar{L}}\), provided \(F\in C^1\) (we are not using here the fact that F is globally Lipschitz). It results that \(|h_n|\le {{{\mathcal {C}}}}\,k^2\), for \(k\le {\bar{k}}_0\). The conditions for the 0-stability of BDF2 and \(|{\bar{e}}_i|\le {{{\mathcal {C}}}}k^2\), \(i=0,1\), apply to warrant the error estimate on \({\bar{u}}_n\), which conditions must also hold to prove items (2) and (3) below.

  2. 2.

    The bound \(|D_-h_n|\le {{{\mathcal {C}}}}\,k^2\) is obtained using the fact that

    $$\begin{aligned} D_-h_n = D_-(F_n-{\bar{F}}^n) = \int _0^1 F'(K_1^n)\,D_-{\bar{e}}_n\,ds_1 \nonumber \\ +\,\int _0^1\int _0^1 F''(K_2^n)\,(D_-K_1^n)\,{\bar{e}}_n\,ds_1ds_2, \end{aligned}$$
    (3.15)

    where \(K_2^n=K_1^{n-1}+s_2\,(K_1^n-K_1^{n-1})\). We have that \(K_2^n\) is bounded, since \(K_1^n\) is bounded, thus \(|F''(K_2^n)|\le {{{\mathcal {C}}}}\) if \(F\in C^2\).

    We show that \(|D_-{\bar{e}}_n|\le {{{\mathcal {C}}}}\,k^2\). From BDF2,

    $$\begin{aligned} \frac{2\,\omega _n+1}{\omega _n+1}\,D_-{\bar{e}}_n - \frac{\omega _n}{\omega _n+1}\,D_-{\bar{e}}_{n-1} = h_n + E_2^n, \end{aligned}$$
    (3.16)

    \(\Rightarrow \)

    $$\begin{aligned} |D_-{\bar{e}}_n| \le \frac{\omega _n+1}{2\,\omega _n+1} \left( |h_n| + |E_2^n| \right) + \frac{\omega _n}{2\,\omega _n+1}\,|D_-{\bar{e}}_{n-1}|. \end{aligned}$$
    (3.17)

    For \(\omega _n \ge 0\), the inequalities \(0\le \omega _n/(2\,\omega _n+1)\le 1/2\) and \(1/2\le (\omega _n+1)/(2\,\omega _n+1) \le 1\) hold and give

    $$\begin{aligned} |D_-{\bar{e}}_n|\le & {} \left( |h_n| + |E_2^n| \right) + \frac{1}{2}\,|D_-{\bar{e}}_{n-1}| \quad \le \frac{1}{2^{n-1}} \,|D_-{\bar{e}}_1| + \sum _{j=2}^n \frac{|h_j| + |E_2^j|}{2^{n-j}} \nonumber \\\le & {} \frac{1}{2^{n-1}} \,|D_-{\bar{e}}_1| + \sum _{j=2}^n \frac{{{{\mathcal {C}}}}\,k^2}{2^{n-j}} \quad \le \bar{{{\mathcal {C}}}}\,k^2, \end{aligned}$$

    using \(|h_j|=O(k^2)\), \(|E_2^j|=O(k^2)\) and \(|D_-{\bar{e}}_1|=O(k^2)\) (which results from a startup with a second-order method).

    Finally, \(|D_-K_1^n| \le |D_-u_n| + s_1 |D_-{\bar{e}}_n| \le {{{\mathcal {C}}}}\) for \(s_1 \in [0,1]\), and we are done bounding \(|D_-h_n|\).

  3. 3.

    From (3.13), we get directly

    $$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|{\mathcal {D}}_3(u) -{\mathcal {D}}_3({\bar{u}})| = \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1} \,\frac{k_n}{3}\,|D_-h_n-D_-h_{n-1}| \le {{{\mathcal {C}}}}\, k^4. \end{aligned}$$

\(\square \)

Theorem 3.3

Assume that the solution of (2.1) is such that \(u\in {\mathcal {C}}^4([0,T],{{\mathbb {R}}})\). For \(j=0,1\), let be given initial solutions \({\bar{u}}^j\) and \({\hat{u}}^j\) that approach the exact solution \(u(t^j)\) with second and third-order accuracy, respectively. Consider \({\bar{u}}^n\) and \({\hat{u}}^n\), respectively, solutions of (2.11) and (2.12), for \(n=2,\dots ,N\). Assume that the hypotheses on 0-stability of BDF2 from Theorem 3.2 hold. Then the solution of DC3 satisfies the following error estimate

$$\begin{aligned} |{\hat{e}}_n|= |u_n-{\hat{u}}^n|\le {\mathcal {C}}\,k^3, \qquad n\ge 0, \end{aligned}$$
(3.18)

where the constant \({\mathcal {C}}\) is independent from the numerical solutions \({\bar{u}}^n\), \({\hat{u}}^n\), and the steps \(k_n\).

Proof

Using (2.4), the truncation error for DC3 is obtained by sustituting the exact solution \(u_n=u(t^n)\):

$$\begin{aligned} E_{3}^n= & {} \sum _{i=0}^2 c_i^n u_{n-i} + {\mathcal {D}}_3(u) -F_n \nonumber \\= & {} \left[ u_n' - \frac{k_n\,(2\,k_n^2+3\,k_n\,k_{n-1}+k_{n-1}^2)}{72}\,u_n^{(4)} +O(k^4)\right] -F_n \nonumber \\= & {} -\frac{k_n\,(2\,k_n^2+3\,k_n\,k_{n-1}+k_{n-1}^2)}{72}\,u_n^{(4)} +O(k^4), \end{aligned}$$
(3.19)

where \(u_n^{(4)}=u^{(4)}(t^n)\).

We obtain a recurrence relation for \({\hat{e}}_n\) by substracting (2.12) from (3.19):

$$\begin{aligned}&\frac{2\,\omega _n+1}{k_n\,(\omega _n+1)} {\hat{e}}_n - \frac{(\omega _n+1)^2}{k_n\,(\omega _n+1)} {\hat{e}}_{n-1} + \frac{\omega _n^2}{k_n\,(\omega _n+1)} {\hat{e}}_{n-2} + ({\mathcal {D}}_3(u)-{\mathcal {D}}_3({\bar{u}}))\nonumber \\&\quad = (F_n-{\hat{F}}^n) +E_3^n. \end{aligned}$$
(3.20)

We rewrite the recurrence as in (3.3):

$$\begin{aligned} \left[ 1-\frac{{\hat{g}}^n\,k_n\,(\omega _n+1)}{2\,\omega _n+1}\right] \,{\hat{e}}_n = \frac{(\omega _n+1)^2}{2\,\omega _n+1}\,{\hat{e}}_{n-1} - \frac{\omega _n^2}{2\,\omega _n+1}\,{\hat{e}}_{n-2} + \delta _n, \end{aligned}$$
(3.21)

with

$$\begin{aligned} \delta ^n=\frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,\left[ E_3^n - ({\mathcal {D}}_3(u)-{\mathcal {D}}_3({\bar{u}})) \right] . \end{aligned}$$

The terms in \(\delta ^n\) do not depend on the solution \({\hat{u}}^n\) of the DC3 method, but only on the solution \({\bar{u}}^n\) of BDF2 and the exact solution. The first term is easily bounded by assuming that k is sufficiently small,

$$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|E_3^n|\le & {} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,\frac{k_n\,(2\,k_n^2+3\,k_n\,k_{n-1} +k_{n-1}^2)}{72}\,|u_n^{(4)}| +O(k^5) \\\le & {} {{{\mathcal {C}}}}\,k^4\, \Vert u^{(4)}\Vert _{\infty ,[0,T]}. \end{aligned}$$

From Lemma 3.1, we then get that \(|\delta ^n|\le {{{\mathcal {C}}}}\,k^4\). The recurrence (3.21) is the same as for BDF2 (with a different \(\delta _n\)), and the 0-stability of BDF2 gives

$$\begin{aligned} |{\hat{e}}_n|=|u(t^n)-{\hat{u}}^n|\le {{{\mathcal {C}}}}_1\,(|{\hat{e}}_0|+|{\hat{e}}_1|)+{{{\mathcal {C}}}}_2\,k^3\le {{{\mathcal {C}}}}\,k^3, \end{aligned}$$

assuming that \(|{\hat{e}}_0|,|{\hat{e}}_1|\le {{{\mathcal {C}}}}k^3\) and any of the conditions for the 0-stability of BDF2 holds. The constants \({{{\mathcal {C}}}}\), \({{{\mathcal {C}}}}_1\) and \({{{\mathcal {C}}}}_2\) are independent from k and the numerical solution \({\hat{u}}^n\), but depend on the exact solution.

\(\square \)

Remark 3.2

The DC3 method is 0-stable since it is convergent. Any step selection strategy, e.g., \(\omega _n\le \omega <1+\sqrt{2}\), alternating steps or any other, that makes BDF2 0-stable is sufficient for obtaining error estimates for DC3 or higher-order DC methods presented in this paper.

3.3 DC4 – Error estimate

We first obtain an error estimate for the variable-step DC4 method, part of the three-substep approach BDF2 \(\rightarrow \) DC3 \(\rightarrow \) DC4.

Theorem 3.4

Assume that the solution of (2.1) is such that \(u\in {\mathcal {C}}^5([0,T],{{\mathbb {R}}})\), and that \({\bar{u}}^n\), \({\hat{u}}^n\) are obtained as in Theorem 3.3. For \(j=0,1,2\), let be given initial solutions \({\tilde{u}}^j\) that are fourth-order accurate. Consider \({\tilde{u}}^n\) solution of (2.13), for \(n=3,\dots ,N\). Then, under any of the conditions for 0-stability of BDF2 and assuming that the maximal step k is small enough, the solution of DC4 satisfies the following error estimate

$$\begin{aligned} |{\tilde{e}}_n|= | u_n-{\tilde{u}}^n|\le {\mathcal {C}}\,k^4, \qquad n\ge 0, \end{aligned}$$
(3.22)

where the constant \({\mathcal {C}}\) is independent from the numerical solutions \({\bar{u}}^n\), \({\hat{u}}^n\), \(u^n\), and the steps \(k_n\).

Proof

We obtain the same recurrence as in (3.21) with \({\hat{e}}_n\) replaced by \({\tilde{e}}_n\), \({\hat{g}}^n\) by \({\tilde{g}}^n\) and

$$\begin{aligned} \delta ^n=\frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,\left[ E_4^n - ({\mathcal {D}}_4(u)-{\mathcal {D}}_4({\hat{u}})) \right] . \end{aligned}$$

The estimate (3.22) follows as in the proof of Theorem 3.3, from the hypothesis \(|{\tilde{e}}_1|,|{\tilde{e}}_2| \le {{{\mathcal {C}}}}\, k^4\) and by noting that for k sufficiently small,

$$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|E_4^n| \le {{{\mathcal {C}}}}\,k^5\, \Vert u^{(5)}\Vert _{\infty ,[0,T]}, \end{aligned}$$

and

$$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|{\mathcal {D}}_4(u) -{\mathcal {D}}_4({\hat{u}})| \le {{{\mathcal {C}}}}\, k^5. \end{aligned}$$
(3.23)

The bound (3.23) is derived as follows:

  1. 1.

    Let us define

    $$\begin{aligned} h_n= F_n-{\hat{F}}^n = \int _0^1 F'(K_1^n)\,{\hat{e}}_n\,ds_1, \end{aligned}$$
    (3.24)

    where \(K_1^n=u_n-s_1\,{\hat{e}}_n\) is also bounded for k sufficiently small, and \(|h_n|\le {{{\mathcal {C}}}}\,k^3\) results from \(|{\hat{e}}_n|=O(k^3)\).

  2. 2.

    We get the bound \(|D_-h_n|\le {{{\mathcal {C}}}}\,k^3\) by just noticing that (3.17) becomes

    $$\begin{aligned} |D_-{\hat{e}}_n| \le \frac{\omega _n+1}{2\,\omega _n+1} \left( |h_n| + |E_3^n| + |{\mathcal {D}}_3(u)-{\mathcal {D}}_3({\bar{u}})|\right) + \frac{\omega _n}{2\,\omega _n+1}\,|D_-{\hat{e}}_{n-1}|,\nonumber \\ \end{aligned}$$
    (3.25)

    with the first three terms at the right being \(O(k^3)\), and by assuming that \(|D_-{\hat{e}}_1|=O(k^3)\) (a natural assumption if we initialize the computations with a third-order method).

  3. 3.

    From the definition of \({\mathcal {D}}_4(u)\),

    $$\begin{aligned}&\frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|{\mathcal {D}}_4(u) -{\mathcal {D}}_4({\hat{u}})| \\&\quad \le \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\left\{ |{\mathcal {D}}_3(u)-{\mathcal {D}}_3({\hat{u}})| + \frac{k_n\,(k_n+k_{n-1})\,(2\,k_n+k_{n-1})}{12}\,|\delta _{13}^{F} -\delta _{13}^{{\hat{F}}}| \right\} \\&\quad \le \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1} \,\frac{k_n}{3}\, |D_-h_n-D_-h_{n-1}| \\&\qquad + \frac{(\omega _n+1)\, k_n^2\, (k_n+k_{n-1})\, (2\,k_n+k_{n-1})}{12\,(2\,\omega _n+1)} \left| \frac{(\delta _{12}^{F}-\delta _{12}^{{\hat{F}}})(t^n) - (\delta _{12}^{F}-\delta _{12}^{{\hat{F}}})(t^{n-1})}{k_n+k_{n-1}+k_{n-2}} \right| \\&\quad \le {{{\mathcal {C}}}}\, k^5 + \frac{(\omega _n+1)\, k_n^2\, (k_n+k_{n-1})}{6\,(2\,\omega _n+1)} \left\{ |(\delta _{12}^{F}-\delta _{12}^{{\hat{F}}})(t^n)| + |(\delta _{12}^{F}-\delta _{12}^{{\hat{F}}})(t^{n-1})| \right\} \\&\quad \le {{{\mathcal {C}}}}\, k^5 + \frac{(\omega _n+1)\, k_n^2\, (1+\sqrt{2})}{6\,(2\,\omega _n+1)} \left\{ |D_-h_n-D_-h_{n-1}| + |D_-h_{n-1}-D_-h_{n-2}| \right\} \\&\quad \le {{{\mathcal {C}}}}\, k^5, \end{aligned}$$

    using the fact that \((k_n+k_{n-1})/(k_n+k_{n-1}+k_{n-2})< 1\), \((k_n+k_{n-1})\,\delta _{12}^{F} = D_-F^n - D_-F^{n-1}\), \(k_n+k_{n-1}\le (1+\sqrt{2})\,(k_{n-1}+k_{n-2})\) and the bound \(|D_-h_n|\le {{{\mathcal {C}}}}\,k^3\) obtained in item 2.

\(\square \)

It was shown in [24] that the two-substep approach BDF2 \(\rightarrow \) DC4 leads to fourth-order accuracy when constant time steps are used. We present numerical experiments in Sect. 4.4 where only third-order accuracy can be recovered with this approach in the general setting of variable time steps, even if the condition \(\omega _n\le \gamma \le 1+\sqrt{2}\) for 0-stability is imposed at each time step. The method consists in computing \({\bar{u}}^n\) solution of (2.11) directly followed by the computation of \({\tilde{u}}^n\) solution of

$$\begin{aligned} \left. \begin{aligned} {\bar{F}}^{n-i} = F(t^{n-i}, {\bar{u}}^{n-i} ) \,\,\,\, \forall \,i \in \{0,1,2,3\} \\ {\bar{u}}^{(3),n} = 2\, \delta _{12}^{{\bar{F}}} + 2 \, \delta _{13}^{{\bar{F}}} \, ( 2\,k_n+k_{n-1} ) \\ {\bar{u}}^{(4),n}(t^n) = 6 \, \delta _{13}^{{\bar{F}}} \\ \boxed { \sum _{i=0}^2 c_i^n {\tilde{u}}^{n-i} + {\mathcal {D}}_4({\bar{u}}^n) = F(t^n,{\tilde{u}}^n) } \end{aligned} \right\} \,\, \text {DC4}. \end{aligned}$$
(3.26)

Fourth-order accuracy can be reached under a more restrictive rule for selecting variable time steps.

Theorem 3.5

Assume that the solution of (2.1) is such that \(u\in {\mathcal {C}}^5([0,T],{{\mathbb {R}}})\), and that \({\bar{u}}^n\) is obtained as in Theorem 3.2. For \(j=0,1,2\), let be given initial solutions \({\tilde{u}}^j\) that are fourth-order accurate. Consider \({\tilde{u}}^n\) solution of (3.26), for \(n=3,\dots ,N\). Then, under any of the conditions for 0-stability of BDF2, the condition \(|\omega _n-\omega _{n-1}|\le {\mathcal {C}}k\) and assuming that the maximal step k is small enough, the solution of DC4 satisfies the following error estimate

$$\begin{aligned} |{\tilde{e}}_n|= |u_n-{\tilde{u}}^n|\le {\mathcal {C}}\,k^4, \qquad n\ge 0, \end{aligned}$$
(3.27)

where the constant \({\mathcal {C}}\) is independent from the numerical solutions \({\bar{u}}^n\), \(u^n\), and the steps \(k_n\).

Proof

The estimate on \({\tilde{e}}_n\) is obtained as in theorem 3.4, replacing all \({\hat{u}}^n\) by \({\bar{u}}^n\). The only bound that requires a new analysis is

$$\begin{aligned} \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,|{\mathcal {D}}_4(u_n) -{\mathcal {D}}_4({\bar{u}}^n)| \le {{{\mathcal {C}}}}\, k^5, \end{aligned}$$
(3.28)

which relies on the estimate \(|D_-h_n-D_-h_{n-1}|\le {\mathcal {C}}\,k^3\).

This time, \(h_n\) is defined as for DC3, with estimates \(h_n=O(k^3)\) and \(D_-h_n=O(k^3)\) rather than \(O(k^2)\). From (3.15), we calculate:

$$\begin{aligned}&D_-h_n-D_-h_{n-1}= \int _0^1 F'(K_1^n)\,D_-{\bar{e}}_n\,ds_1 \,+\, \int _0^1\int _0^1 F''(K_2^n)\,(D_-K_1^n)\,{\bar{e}}_n\,ds_1ds_2 \\&\quad -\int _0^1 F'(K_1^{n-1})\,D_-{\bar{e}}_{n-1}\,ds_1 - \int _0^1\int _0^1 F''(K_2^{n-1})\,(D_-K_1^{n-1})\,{\bar{e}}_{n-1}\,ds_1ds_2 \\&\quad = \int _0^1 F'(K_1^n)\,[D_-{\bar{e}}_n-D_-{\bar{e}}_{n-1}]\,ds_1 + \int _0^1 [F'(K_1^n)-F'(K_1^{n-1})]\,D_-{\bar{e}}_{n-1}\,ds_1 \\&\quad +\,\int _0^1\int _0^1 [F''(K_2^n)-F''(K_2^{n-1})]\,(D_-K_1^n)\, {\bar{e}}_n\,ds_1ds_2 \\&\quad + \int _0^1\int _0^1 F''(K_2^{n-1})\,[(D_-K_1^n)-(D_-K_1^{n-1})]\, {\bar{e}}_n\,ds_1ds_2 \\&\quad +\,\int _0^1\int _0^1 F''(K_2^{n-1})\,(D_-K_1^{n-1})\,[{\bar{e}}_n-{\bar{e}}_{n-1}]\,ds_1ds_2 \end{aligned}$$

where \(K_{j+1}^n=K_j^{n-1}+s_{j+1}\,(K_j^n-K_j^{n-1})\), \(j\ge 1\). This gives

$$\begin{aligned} D_-h_n-D_-h_{n-1}= & {} \int _0^1 F'(K_1^n)\,[D_-{\bar{e}}_n-D_-{\bar{e}}_{n-1}]\,ds_1\nonumber \\&+ k_n\int _0^1\int _0^1 [F''(K_2^n)\,(D_-K_1^n)\,(D_-{\bar{e}}_{n-1})\,ds_1ds_2\nonumber \\&+\,k_n\int _0^1\int _0^1\int _0^1 F'''(K_3^n)\,(D_-K_2^n)\,(D_-K_1^n)\,{\bar{e}}_n\,ds_1ds_2ds_3\nonumber \\&+\, \int _0^1\int _0^1 F''(K_2^{n-1})\,[(D_-K_1^n)-(D_-K_1^{n-1})]\,{\bar{e}}_n\,ds_1ds_2\nonumber \\&+\,k_n\int _0^1\int _0^1 F''(K_2^{n-1})\,(D_-K_1^{n-1})\,(D_-{\bar{e}}_n)\,ds_1ds_2 \nonumber \\= & {} A+B+C+D+E . \end{aligned}$$
(3.29)

Each of these terms can be bounded in \(O(k^3)\):

  1. 1.

    \(|{\bar{e}}_n|=O(k^2)\), as expected for the solution \({\bar{u}}_n\) of BDF2.

  2. 2.

    \(|K_j|\le {\mathcal {C}}\), \(\forall j\ge 1\), for the same reasons as above. Assuming \(F\in C^3\), this gives \(|F'(K_1^n)|,|F''(K_2^n)|,|F'''(K_3^n)|\le {\mathcal {C}}\).

  3. 3.

    From the proof of Theorem 3.3, \(|D_-{\bar{e}}_n|\le {\mathcal {C}}\,k^2\) and \(|D_-K_1^n|\le {\mathcal {C}}\), when \(k\le {\bar{k}}_1\) with \({\bar{k}}_1\) small enough. Hence

    $$\begin{aligned} |D_-K_2^n| \le |D_-K_1^{n-1}|+s_2\,(|D_-K_1^n|+|D_-K_1^{n-1}| \le {{{\mathcal {C}}}}, \qquad \text{ for } k\le {\bar{k}}_1.\nonumber \\ \end{aligned}$$
    (3.30)
  4. 4.

    Combining items 1, 2 and 3, it follows that \(|B|,|C|,|E|\le {\mathcal {C}}\,k^3\), for \(k\le {\bar{k}}_1\).

  5. 5.

    To get \(|D|\le {\mathcal {C}}\,k^3\), we note that

    $$\begin{aligned} |D_-K_1^n-D_-K_1^{n-1}|\le & {} |D_-u_n-D_-u_{n-1}|+s_1\,|D_-{\bar{e}}_n -D_-{\bar{e}}_{n-1}| \\\le & {} {{{\mathcal {C}}}}_1\,k\,\Vert u''\Vert _{\infty ,(0,T)}\,+\,{{{\mathcal {C}}}}_2\,k^2 \le {{{\mathcal {C}}}}\,k, \text{ for } k\le {\bar{k}}_2\le {\bar{k}}_1. \end{aligned}$$
  6. 6.

    We are left bounding |A|, in particular \(|D_-{\bar{e}}_n-D_-{\bar{e}}_{n-1}|\le {\mathcal {C}}\,k^3\). From substracting (3.16) at consecutive steps,

    $$\begin{aligned}&D_-{\bar{e}}_n-D_-{\bar{e}}_{n-1} \\&\quad = \frac{k_n\,(\omega _n+1)}{2\,\omega _n+1}\,[D_-h_n + D_-E_2^n] +\frac{\omega _{n-1}-\omega _n}{(2\,\omega _{n-1}+1)(2\,\omega _n+1)}\,[h_{n-1} + E_2^{n-1}] \\&\qquad + \frac{\omega _n}{2\,\omega _n+1}\,[D_-{\bar{e}}_{n-1}-D_-{\bar{e}}_{n-2}] + \frac{\omega _n-\omega _{n-1}}{(2\,\omega _{n-1}+1)(2\,\omega _n+1)}\,D_-{\bar{e}}_{n-2}. \end{aligned}$$

    From \(|D_-h_n|,|h_n|,|D_-E_2^n|,|E_2^n|\le {\mathcal {C}}\,k^2\), the inequalities \(0\le \omega _n/(2\,\omega _n+1)\le 1/2\) and \(1/2\le (\omega _n+1)/(2\,\omega _n+1) \le 1\) and \((2\,\omega _{n-1}+1)(2\,\omega _n+1)\ge 1\), for \(\omega _n \ge 0\), and using the hypothesis \(|\omega _n-\omega _{n-1}|\le {\mathcal {C}}\,k\), we deduce that:

    $$\begin{aligned}&|D_-{\bar{e}}_n-D_-{\bar{e}}_{n-1}| \le {\mathcal {C}}\,k^3 + \frac{1}{2} \,|D_-{\bar{e}}_{n-1}-D_-{\bar{e}}_{n-2}| \nonumber \\&\quad \le {\mathcal {C}}\,k^3\,\sum _{j=3}^n\frac{1}{2^{n-j}} + \frac{1}{2^{n-2}}\,|D_-{\bar{e}}_2-D_-{\bar{e}}_1| \quad \le {\mathcal {C}}\,k^3, \end{aligned}$$
    (3.31)

    as long as \(|D_-{\bar{e}}_2-D_-{\bar{e}}_1|=O(k^3)\).

\(\square \)

Remark 3.3

The DC4 method with variable steps (2.11)+(3.26) is fourth-order accurate if \(\omega _n\le \omega <1+\sqrt{2}\) and \(|\omega _n-\omega _{n-1}|\le {\mathcal {C}}k\). If \(\omega _n\) is constant, this last condition is satisfied. An other possibility is to impose for \(\omega \) fixed the bounds \(\omega -mk\le \omega _n\le \omega +Mk\), \(\forall n\), in which case \(|\omega _n-\omega _{n-1}|\le (m+M)\,k\) and the convergence is fourth-order whenever \(k\rightarrow 0\). Since the goal of adaptive methods is to be able to reduce or increase the time step from one step to the next, this restricts \(\omega \) to be 1. This then puts a relatively severe constraint on the variation of the step \(k_n\), since \(k_{n-1}(1-mk)\le k_n \le k_{n-1}(1+Mk)\) and the increment on \(k_n\) must be \(O(k^2)\). The alternating sequence \(k_1\)–\(k_2\) discussed above does not comply with this criteria, and the order of convergence is reduced to 3 in this case. In fact, \(k_1=k\) and \(k_2=\omega \,k\) \(\Rightarrow \) \(\omega _n-\omega _{n-1}=\omega -1/\omega =\text{ const }\ne 0\), for all \(k>0\) and \(\omega \ne 1\).

We state the following general theorem on the order of accuracy of the DCp method. The proof is a mixture of the techniques used above for studying DC3 and DC4, and the general notations introduced in [23] to handle the multilinear forms \(D_-^jh_n\) in the general setting.

Theorem 3.6

Assume that the solution of (2.1) is such that \(u\in {\mathcal {C}}^{p+1}([0,T],{{\mathbb {R}}})\), and that \(u^{l,n}\), \(l=2,\ldots ,p-1\), are solutions of DC methods of order l built from BDF2 with variable time steps as in Sect. 2. For \(j=0,1,\ldots ,p-2\), let be given initial solutions \(u^{p,j}\) that are p-th order accurate. For \(n=p-1,\dots ,N\), consider \(u^{p,n}\) solution of the DC method built from the correction \({{{\mathcal {D}}}}_p(u^{p-1,n})\). Then, under any of the conditions for 0-stability of BDF2 and assuming that the maximal step k is small enough, the solution of DCp satisfies the following error estimate

$$\begin{aligned} | u_n-u^{p,n}|\le {\mathcal {C}}\,k^p, \qquad n\ge 0, \end{aligned}$$
(3.32)

where the constant \({\mathcal {C}}\) is independent from all numerical solutions \(u^{j,n}\) and steps \(k_n\).

Remark 3.4

We have the following equivalences between the notation of Theorem 3.6 and the notation introduced previously in Sect. 2: \(u^{2,j} \equiv {\bar{u}}^j\), \(u^{3,j} \equiv {\hat{u}}^j\), \(u^{4,j} \equiv {\tilde{u}}^j\), and \(u^{5,j} \equiv u^j\).

3.4 A-stability

We first prove the A-stability of our DC methods, then investigate the absolute stability of two closely related methods and show how these two methods lack the mechanism to achieve A-stability.

The notion of A-stability applies to multistep methods with constant time steps. We consider the differential equation

$$\begin{aligned} \frac{du}{dt}=\lambda u, \qquad \lambda \in {{\mathbb {C}}}. \end{aligned}$$
(3.33)

A time-stepping method is absolutely stable for a \(\lambda \in {{\mathbb {C}}}\) provided its numerical solution of (3.33) for this \(\lambda \) is such that \(u^n\rightarrow 0\) whenever \(n\rightarrow \infty \). A method is A-stable if the region of absolute stability contains all \({{\mathbb {C}}}^-=\{\lambda \in {{\mathbb {C}}}\,|\, Re(\lambda ) < 0\}\).

3.4.1 DC methods

The BDF2 method with constant time step applied to (3.33) gives the homogeneous difference equation

$$\begin{aligned} a\,{{\bar{u}}}^n +b\,{{\bar{u}}}^{n-1}+ c\,{{\bar{u}}}^{n-2}=0,\quad n\ge 2, \end{aligned}$$
(3.34)

with \(a=3/2-z\), \(b=-2\), \(c=1/2\) and \(z=\lambda k\). The general solution is given by \({{\bar{u}}}^n=c_1 \xi _1^n + c_2 \xi _2^n\), where \(\xi _i\), \(i=1,2\), are the roots of the characteristic equation \(a\,\xi ^2+b\,\xi +c=0\), \(c_1\) and \(c_2\) are coefficients to fit the initial conditions. BDF2 is A-stable because \(|\xi _i|<1\), \(i=1,2\), for \(Re(\lambda ) < 0\), which implies \({{\bar{u}}}^n\rightarrow 0\) as \(n\rightarrow \infty \). To simplify notations in the proof below, we order the roots according to \(|\xi _1|\le |\xi _2|<1\).

To prove the A-stability of our DC methods, we consider the non-homogeneous difference equation

$$\begin{aligned} a\,u^n +b\,u^{n-1}+ c\,u^{n-2}=g_n,\quad n\ge 2, \end{aligned}$$
(3.35)

where \(g_n\) is a given function of n independent from \(u^n\). The general solution is given by \(u^n={{\bar{u}}}^n+v^n\), where \({{\bar{u}}}^n\) is the solution of the homogeneous difference equation given above and \(v^n\) is the particular solution of the non-homogeneous equation given by

$$\begin{aligned} v^n = \sum _{j=2}^n g_j\,(a_1\,\xi _1^{n-j}+a_2\,\xi _2^{n-j}),\quad n\ge 2. \end{aligned}$$
(3.36)

See [7, chap.2] for a review of linear difference equations.

The fact that \(u^n\rightarrow 0\) is controlled by \(v^n\). It results from the following lemma:

Lemma 3.2

Assume that there exist \(K>0\) and fixed integers \(\alpha ,\beta \ge 0\) such that \(|g_j|\le K\,j^\alpha \, |\xi _2|^{j-\beta }\), \(\forall j\). Then there exists \({{\bar{K}}}>0\) such that

$$\begin{aligned} |v^n|\le {{\bar{K}}}\,n^{\alpha +1}\,|\xi _2|^{n-\beta },\quad n\ge \max (2,\beta ). \end{aligned}$$
(3.37)

Proof

$$\begin{aligned} |v^n| \le \max (|a_1|,|a_2|) \sum _{j=2}^n |g_j|\,|\xi _2|^{n-j} \le K_1\,|\xi _2|^{n-\beta } \sum _{j=2}^n j^\alpha =K_1\,|\xi _2|^{n-\beta }\,\varPi _{\alpha +1}(n), \end{aligned}$$

where \(n\ge \max (2,\beta )\), \(K_1=K\,\max (|a_1|,|a_2|)\) and \(\varPi _{\alpha +1}(n)\) is a polynomial of degree \(\alpha +1\) in n from the formulae for the sums of powers of integers. The result follows from \(|\varPi _{\alpha +1}(n)|\le {\mathcal {C}}\,n^{\alpha +1}\), which holds for \(n\ge 1\) and consequently for \(n\ge \max (2,\beta )\). \(\square \)

Theorem 3.7

The DC method of order p built from BDF2 is A-stable.

Proof

We detail the proof for DC3 and present the main steps for DCp, \(p\ge 4\), in the sequence BDF2 \(\rightarrow \) DC3 \(\rightarrow \) DC4 \(\rightarrow \) \(\ldots \) \(\rightarrow \) DCp.

The application of DC3 to (3.33) gives a difference equation of the form (3.35) with

$$\begin{aligned} g_n=-\sum _{i=1,2} c_i\,z\,\frac{\xi _i^2 -2 \xi _i + 1}{3}\,\xi _i^{n-2}. \end{aligned}$$

We apply lemma 3.2 with \(\alpha =0\), \(\beta =2\) and

$$\begin{aligned} K=\sum _{i=1,2} |c_i\,z|\,\frac{|\xi _i^2 -2 \xi _i + 1|}{3}, \end{aligned}$$

which gives \(|v^n|\le {{\bar{K}}}\,n\,|\xi _2|^{n-2} \rightarrow 0\) as \(n\rightarrow \infty \).

Through an induction, it is seen that the application of DCp to (3.33) gives a difference equation of the form (3.35), where \(g_n\) is a polynomial \(\varPi (\xi _1,\xi _2;n,z)\) in \(\xi _1^{\beta _1}\,\xi _2^{\beta _2}\) with \(n-N+1\le \beta _1+\beta _2\le n\) and whose coefficients are polynomials of degree at most \(N-3\) in n. We apply lemma 3.2 with \(\alpha =N-3\), \(\beta =N-1\) and K that results from bounding the coefficients in \(\varPi (\xi _1,\xi _2;n,z)\), which gives \(|v^n|\le {{\bar{K}}}\,n^{N-2}\,|\xi _2|^{n-N+1}\rightarrow 0\) as \(n\rightarrow \infty \).

For the sequence BDF2 \(\rightarrow \) DC4 \(\rightarrow \) \(\ldots \) \(\rightarrow \) DCp, p even, the proof for DC4 proceeds as for DC3 above, using \(\alpha =0\) and \(\beta =3\) in lemma 3.2. An induction and the application of the lemma with \(\alpha =N/2-2\) and \(\beta =N-1\) proves the result for DCp. \(\square \)

3.4.2 Related methods

We now present and briefly analyze two DC3 methods where the correction is more tightly coupled with the solution of the DC3 method, rather than being computed from the solution of BDF2 that evolves independently from the solution of DC3. This illustrates how important this is to evaluate the correction from an independently evolving numerical solution to maintain A-stability at arbitrary orders.

We first consider a “most extreme” variant of the DC3 method (with constant time step to simplify) where the correction \({\mathcal {D}}_3(u)\) is evaluated from the solution u of DC3:

$$\begin{aligned}&\frac{3u^n-4u^{n-1}+u^{n-2}}{2k} = F(t^n,u^n) \nonumber \\&\qquad - \frac{k^2}{3}\frac{F(t^n,u^n) -2 F(t^{n-1},u^{n-1}) + F(t^{n-2},u^{n-2})}{k^2}. \end{aligned}$$
(3.38)

This variant, here called the modified BDF2 method, is third-order accurate, but unfortunately far from being A-stable. This scheme applied to (3.33) gives the following homogeneous difference equation

$$\begin{aligned} (3/2-2z/3) u^n - (2+2z/3) u^{n-1}+ (1/2+z/3) u^{n-2}=0,\quad n\ge 2. \end{aligned}$$
(3.39)

The absolute stability region is much smaller than for BDF3, see Fig. 1.

Fig. 1
figure 1

Boundary of the absolute stability regions. At left: modified BDF2 – Eq. (3.38) – (black dotted line), BDF3 (red dashed line) and DC3 method from (3.40) (blue plain line). At right: zoom near the origin of the graph at left. In all cases, the stability region lies immediately at the left of the origin (color figure online)

Full size image

We next consider a variant of the DC3 method where the correction \({\mathcal {D}}_3\) is evaluated from \(u^{n-1}\) and \(u^{n-2}\), the solution of DC3, and a “prediction” \({{\bar{u}}}^n\) obtained from BDF2:

$$\begin{aligned}&\frac{3 {{\bar{u}}}^n-4u^{n-1}+u^{n-2}}{2k} = F(t^n,{{\bar{u}}}^n), \nonumber \\&\frac{3u^n-4u^{n-1}+u^{n-2}}{2k} = F(t^n,u^n) \nonumber \\&\qquad - \frac{k^2}{3}\frac{F(t^n,{{\bar{u}}}^n) -2 F(t^{n-1},u^{n-1}) + F(t^{n-2},u^{n-2})}{k^2}. \end{aligned}$$
(3.40)

This can be seen as a hybrid between the DC methods investigated in this paper and the method (3.38) that we just discussed. Note that a family of similar DC methods built from BDF methods with constant time steps was proposed in [12].

One would expect that, since \(u^{n-1}\) and \(u^{n-2}\) are more accurate than \({{\bar{u}}}^{n-1}\) and \({{\bar{u}}}^{n-2}\) obtained from BDF2, the solution \(u^n\) of (3.40) would be more accurate than the solution of (2.12). It turns out that this is not the case, at least in the preliminary numerical tests that we performed (not shown here). Moreover, the A-stability is lost, see Fig. 1. The absolute stability region is obtained from applying the method to (3.33) and solving the so-obtained homogeneous difference equation

$$\begin{aligned} (3/2-z) u^n + \frac{4z^2+10z-18}{9-6z} u^{n-1}+ \frac{9/2-z-2z^2}{9-6z} u^{n-2}=0,\quad n\ge 2.\qquad \end{aligned}$$
(3.41)

This method is more stable than BDF3 in the vicinity of the origin, but the boundary of the absolute stability region has a vertical asymptote at the left of the imaginary axis. Hence, except at the origin, there is a neighbourhood of the imaginary axis where this DC method is unstable, while this is not the case for BDF3 when \(z=i\,y\), |y| gets large enough.

Computing the correction \({\mathcal {D}}_3\) directly from the solution of the DC method (completely or partially) has dramatic impact on the stability. For instance, the resulting method (3.38) is a third-order linear multistep method, hence there is no surprise that it is not A-stable from the second Dahlquist barrier. In case of \({\mathcal {D}}_3\) partially evaluated from the DC solution, the resulting method (3.40) is a third-order general linear multistep method, yet not A-stable. The BDF2-based DC methods proposed in this paper are not general linear methods. They maintain A-stability at arbitrary order from the fact that an A-stable method (here BDF2) is slightly perturbed with a correction term \({\mathcal {D}}_p\) evaluated from a completely independent solution obtained with an other A-stable method (here DCp to get DC\(p+1\) or DC\(p+2\)). For equation (3.33), the characteristic roots of BDF2 are then preserved, leading to \(u^n\rightarrow 0\), \(n\rightarrow \infty \), while these roots are modified for the last two DC variants proposed and studied in this subsection.

4 Numerical tests

To assess the numerical behaviour of the deferred corrections integration methods – DC3 to DC5 –, we will make use of the method of manufactured solutions (MMS) [32, 33] and carry out simulations with constant and alternating step size [11, 37]. When used with time-stepping systematic refinement studies, which are remarkably sensitive, the MMS produces robust code verifications in comparison with the theoretical error estimates obtained previously in Sect. 3. Moreover, when used with alternating step size verification strategy, MMS often reveals unsuspected weaknesses such as the reduction of the order of convergence of the time integration method, and thus its inability to effectively adjust the step size within an adaptive error control strategy.

In this context, we have selected two manufactured solutions whose results are representative of all the numerical tests carried out. Table 2 summarizes the parameters of these manufactured solutions in relationship with the model ODE (2.1). This allows us to measure the integration error \({\mathcal {E}}(k)\) between the numerical and exact solutions as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {E}}(k)&= \Vert u_k - u_\text {ms} \Vert _\infty = \max _n | u^n - u_\text {ms}(t^n) |\\ {\mathcal {E}}(k)&\le {\mathcal {C}} \, k^{p} \end{aligned} \end{aligned}$$
(4.1)

where k, \(u_k\) and \(u_\text {ms}(t)\) are, respectively, the time step, the vector of numerical solution and the manufactured (or closed-form) solution. Finally, we recall that the objective of the systematic time step refinement studies is to measure the rate of convergence p of the time integration method and then to compare the result with the theory.

Table 2 Manufactured solutions
Full size table

The family of BDF integration methods requires, in addition to the initial solution \(u_0\), one or more additional solutions to start the computation [39]. For example, BDF2 requires \(u^0 = u(t^0)\) and \(u^1=u(t^1)\) to predict \(u^2\). The same is true for the deferred correction methods. In this study, these values are initialized using the manufactured solution. In doing so, we measure the accuracy of the discretization scheme without mitigating the effect of the initialization of these additional values. This ensures compliance with the accuracy requirements for the initial conditions as stated in Theorems 3.2–3.5.

The specific objectives of the numerical tests are fourfold: i) – Sect.4.1 – to measure the convergence rate of the deferred correction methods with constant step size, ii) – Sect. 4.2 – to measure the convergence rate of the deferred corrections methods with alternating step size, iii) – Sect. 4.3 – to estimate the error of a low order deferred correction method with a higher-order method, and iv) – Sect. 4.4 – to assess the convergence rate of the DC4 variant (3.26) under constant and alternating step sizes.

Finally in Sect. 4.5 we assess the numerical behaviour of the deferred corrections methods with a stiff system of linear ODEs.

4.1 Constant time step refinement studies

We integrate the model Eq. (2.1), stepping through the time integration interval \({\mathcal {I}}\) in N time steps of constant size. The computation is then repeated by systematically doubling the number of time steps. We then calculate the rate of convergence p in the usual manner by considering the ratio of two successive errors,

$$\begin{aligned} \frac{{\mathcal {E}}(k)}{{\mathcal {E}}(k/2)} \approx 2^{p}. \end{aligned}$$

Tables 3 and 4 show the results of this convergence study for the manufactured solutions described in Table 2.

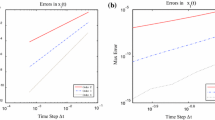
For the first manufactured solution (MMS-1), we reach rapidly and monotonically the theoretical convergence rates established in Sect. 3. Beyond 640 time steps, the precision of higher-order integration methods (DC4 and more rapidly so for DC5) lies within floating-point arithmetic accuracy, and the computation of the convergence rate p becomes meaningless. On the other hand, the solutions of the second manufactured problem (MMS-2) show oscillatory convergence towards their theoretical convergence rates. Beyond 5120 time steps, the computational error of DC5 is again within floating-point arithmetic accuracy.

Table 3 MMS-1, constant step size refinement
Full size table
Table 4 MMS-2, constant step size refinement
Full size table

4.2 Alternating time step refinement studies

We now integrate Eq. (2.1) by stepping through the time integration interval in \(2\,N\) time steps and alternating between two steps \(k_1=k_{\max }\) and \(k_2=k_{\min }\) – per Proposition 3.2. More precisely, we assume that the ratio \(\omega \),

$$\begin{aligned} \frac{k_{2\,i}}{k_{2\,i-1}} = \frac{k_{\max }}{k_{\min }} = {\omega }, \forall i \in \{1,2,...,N\}, \end{aligned}$$

between two consecutive time steps of even and odd indices is constant and independent of the number of steps. This implies that the ratio between two consecutive time steps of odd and even indices is also constant and equal to

$$\begin{aligned} \frac{k_{2\,i+1}}{k_{2\,i}} = \frac{k_{\min }}{k_{\max }} = \frac{1}{\omega }, \forall i \in \{1,2,...,N-1\}. \end{aligned}$$

The computations are repeated by systematically doubling the number of time steps while keeping the ratio \(\omega \) constant – \(k_{\max }\) and \(k_{\min }\) are thus divided by two. Finally, note that k in \({\mathcal {E}}(k)\) is \(k_{\max }\).

Tables 5 and 6 show the results for the manufactured solutions described in Table 2. For this refinement studies we choose \(\omega =4\) which is above the recommended theoretical 0-stability limit of the BDF2 integration – Proposition 3.1. Nevertheless, as shown previously in Proposition 3.2, this alternating time-stepping strategy yields stable solutions. Hence, a comparative study between the results of Tables  5 and 6 and those of Tables  3 and 4 does not reveal any significant change. The ability to achieve the theoretical convergence rates seems not to be hampered by the extreme variation of the time step.

Table 5 MMS-1, alternating step size \(k_{2i}/k_{2i-1}= 4\) refinement
Full size table
Table 6 MMS-2, alternating step size \(k_{2i}/k_{2i-1}= 4\) refinement
Full size table

4.3 Error estimation

In this study, we have, so far, used the manufactured solutions of Table 2 to measure the integration error of the numerical solutions. In practice, these closed-form solutions are replaced by appropriate alternatives denoted \(u^*\). A possibility is to use a high-order solution \(u^*\) as a substitute to the exact solution in the computation of \({\mathcal {E}}\). This allows us to compute an integration error \({\mathcal {E}}^*(k)\) between the numerical solution and the surrogate solution \(u^*\),

$$\begin{aligned} \left. \begin{aligned} {\mathcal {E}}^*(k)&= \Vert u_k - u^* \Vert _\infty \\ {\mathcal {E}}^*(k)&\le {\mathcal {C}} \, k^{p} \end{aligned} \right\} \,\, , \end{aligned}$$
(4.2)

and the efficiency ratio,

$$\begin{aligned} \eta = \frac{{\mathcal {E}}^*(k)}{{\mathcal {E}}(k)}, \end{aligned}$$
(4.3)

a measure of its reliability as an error estimation technique. Thus an estimation technique is reliable and robust if the efficiency is close to 100%, repeatedly, for different problems. Specifically, we propose to test the efficiency of the solution from DC3, as \(u^*\), to estimate the discretization error of BDF2, and the solution from DC4, to estimate the discretization error of DC3, and so on.

In Tables 7 and 8, we present the results of these numerical experiments for the BDF2, DC3 and DC4 methods, for the first and the second manufactured problem. We observe that the effectiveness of the error estimation is almost optimal over a wide range of time integration steps, integration methods and manufactured problems. Note that we carried out these tests with alternating time steps, i.e., the most challenging integration scenario of this study.

Table 7 MMS-1, alternating step size \(k_{2i}/k_{2i-1}= 4\) refinement, error estimate efficiency
Full size table
Table 8 MMS-2, alternating step size \(k_{2i}/k_{2i-1}= 4\) refinement, error estimate efficiency
Full size table

4.4 BDF2 to DC4 numerical assessment

In this section, we study the convergence rate of the DC4 method described by Eq. (3.26). Recall that this version constructs a fourth-order approximation directly from the second-order solution obtained from the BDF2 method. It, therefore, avoids the use of the DC3 method, thus reducing the computational cost.

We present in Table 9 the results of three convergence studies for the second manufactured solution (MMS-2) of the model Eq. (2.1), i.e., (i) a constant time step convergence study, (ii) an alternating time step convergence study, and (iii) an asymptotic convergence study – note that the parameters of the first two studies are described in Sects. 4.1 and 4.2 , respectively. In the asymptotic study, we integrate the solution by stepping through the time interval \({\mathcal {I}}\) in N time steps of increasing size according to a geometric progression. For this purpose, the ratio between the maximum and minimum time step is kept constant regardless of the number of time steps. Specifically, we set

$$\begin{aligned} \left. \begin{aligned} \frac{k_N}{k_1}&= \frac{k_{\max }}{k_{\min }} = \gamma = 2 \\ k_{max}&= T/N \end{aligned} \right\} . \end{aligned}$$
(4.4)

This intrinsically defines a geometric progression such that

$$\begin{aligned} \left. \begin{aligned} r&= \gamma ^{1/(N-1)} \\ k_1&= T \, (r-1)/(r^N-1) \\ k_i&= k_1 \, r^{i-1}\quad \,\,\, \forall i \in \{1,2,...,N\} \end{aligned} \right\} , \end{aligned}$$
(4.5)

with r the common ratio. With this construction, \(k_{\max }\) decreases by two as the number of time steps doubles, and the ratio \(\omega _n\), between two successive time steps, satisfies

$$\begin{aligned} \lim _{N \rightarrow \infty } \omega _n \rightarrow 1, \end{aligned}$$
(4.6)

thus respecting the condition \(|\omega _n-\omega _{n-1}| \le {\mathcal {C}}\, k\), where \(k = k_{\max }\), of Theorem 3.5 – see also Remark 3.3.

The results in Table 9 confirm the theoretical results of Theorem 3.5: at constant time step, the method is fourth-order; at alternating time step, the method is third-order; and if the ratio converges asymptotically to unity then the method converges again to fourth-order. However, in the context of adaptive time step control, the occurrence of asymptotic time step convergence is exceptional. In practice, it is more likely to experience a loss of convergence order, making this method unsuitable for this purpose.

Table 9 MMS-2, BDF2 to DC4 numerical assessment
Full size table

4.5 Stiff linear ODEs numerical assessment

We conclude these tests by studying the convergence of the numerical solution for a system of stiff linear differential equations. To this end, we use the procedure described in Sect. 4.1 by systematically doubling the number of time steps. We apply this procedure to compute the solution of the following first-order system of differential equations

$$\begin{aligned} \begin{aligned} \frac{d{{\mathbf {u}}}}{dt}&= \underbrace{ \begin{pmatrix} -1 &{} 1 &{} +100 \\ 0 &{} 0 &{} +100 \\ 0 &{} -100 &{} 0 \end{pmatrix} }_{A} \, {\mathbf {u}} \\ \mathbf{u}(0)&= \begin{pmatrix} 2&1&1 \end{pmatrix}^t \end{aligned} \,\,\, , \end{aligned}$$
(4.7)

on the interval \({\mathcal {I}}=[0,5]\). Once again, we use (4.1) to measure the integration error between the numerical and the exact solution of (4.7) given by

$$\begin{aligned} \begin{aligned} {\mathbf {u}}(t)&= e^{-t} \begin{pmatrix} 1 \\ 0\\ 0 \end{pmatrix} + \cos (100\,t) \begin{pmatrix} 1 \\ 1\\ 1 \end{pmatrix} + \sin (100\,t) \begin{pmatrix} 1 \\ 1\\ -1 \end{pmatrix}. \end{aligned} \end{aligned}$$
(4.8)

Note that the ratio of the largest to the smallest eigenvalue of A is 100 (in modulus). Moreover, this simple system would be hard to solve by BDF methods of order 3 and higher (if possible at all) because of the pair of imaginary eigenvalues.

In Table 10, we show the results of this comparative study between the DC3 method and the first and second-order BDF methods. These BDF methods are used, in particular, for the solution of stiff differential equations. Note that we selected DC3 as a representative of our DC methodology.

Table 10 Stiff ODEs system with constant step size refinement
Full size table

The results collected in Table 10 confirm that the DC3 method can capture the solution of a system of stiff ordinary differential equations. Above 4000 time steps, DC3 outclasses the BDF methods. We believe that higher-order DC methods (such as DC4 and DC5) would require significantly fewer time steps to reach a target accuracy. This without losing stability and convergence order.

5 Conclusion

We first described in Sect. 2 a novel deferred correction methodology based on the second-order backward differentiation formula (BDF2) as its building block, where we established these algebraic relations to allow variable time-stepping to ultimately control the local truncation error. This approach is implicit and improves the previous solution by one order of accuracy from one iteration to the next such as DCp \(\rightarrow \) DC\(p+1\) for \(p\ge 2\) with DC2 standing for BDF2.

To prove on solid grounds the stability of our DC methods, we began by examining and discussing the 0-stability specific to the BDF2 building block, as it is essential to establish the theorems and propositions of Sect. 3. We proved that one correction step from BDF2 to DC3 – Theorem 3.3 – , then an other from DC3 to DC4 – Theorem 3.4 – lead, respectively, to third and fourth-order of accuracy, with no constraint on the ratio \(\omega _n\) of successive time steps beyond the requirements for 0-stability. We then indicated how these estimates can be generalized to higher-order DC methods through Theorem 3.6.

To challenge the robustness and efficiency of our DC methodology, we also investigated a variant of DC4 built directly from BDF2 in one correction step in the manner of Kress [24] with constant time steps. In Theorem 3.5 we showed that this is possible, but under a severe restriction on the time step ratio of the form \(|\omega _n-\omega _{n-1}|\le {\mathcal {C}}k\), as the maximal time step k is reduced. Finally, Theorem 3.7 proves the A-stability of our DC methods of arbitrary orders.

We selected in Sect. 4 two representative manufactured solutions from a collection of numerical tests to verify and validate the implementation of the deferred corrections methods (DC3 to DC5) described previously in Sect. 2. The consistency between the simulations and the theoretical predictions ensures the quality of the implementation and the sharpness of all the error estimates obtained in Sect. 3. We observed that the convergence rate of these methods does not seem to be hampered significantly by the extreme variation of the time step beyond the bound \(\omega _n\le 1+\sqrt{2}\) commonly used for 0-stability, at least within the scope of the alternating time step scenario. These deferred corrections methods can then be exploited to control a local truncation as well as global error estimates. For this purpose, we demonstrated that it is reliable to use the solution of a higher-order method to estimate the integration error of a lower-order solution. In particular, the computation of one extra correction step provides a reliable estimate of the global error, but this comes with a computational overhead. In situations where optimal time steps are not known a priori, this additional computational effort due to adaptivity should make the integration process robust in the sense of guaranteeing the accuracy aimed for. Assuming that one has a good strategy to adapt the time step based on a global error estimator, it would then be worth paying the price of one more DC step. More work is needed here to assess this adaptation strategy.

In Sects. 4.1 to 4.3, we investigated the robustness of the computational cascade of Eqs. (2.11) to (2.14) in the presence of a non-constant time step for applications related to adaptive time step control. This approach improves the accuracy of the solution by one order by stepping through the integration methods for a linear increase in computational cost. On the other hand, in Sect. 4.4, we have verified that it is possible to reduce the computational cost considerably by using an alternative construction that allows a two-order increase in computational accuracy. However, the possibility to adapt the time step is reduced.