Cost-reduction implicit exponential Runge–Kutta methods for highly oscillatory systems

Abstract

In this paper, two novel classes of implicit exponential Runge–Kutta (ERK) methods are studied for solving highly oscillatory systems. First of all, symplectic conditions for two kinds of exponential integrators are derived, and we present a first-order symplectic method. High accurate implicit ERK methods (up to order four) are formulated by comparing the Taylor expansion of the exact solution, it is shown that the order conditions of two new kinds of exponential methods are identical to the order conditions of classical Runge–Kutta (RK) methods. Moreover, we investigate the linear stability properties of these exponential methods. Numerical examples not only present the long time energy preservation of the first-order symplectic method, but also illustrate the accuracy and efficiency of these formulated methods in comparison with standard ERK methods.

1 Introduction

It is well known that classical Runge–Kutta methods have a wide range of applications in scientific computing. Especially, symplectic methods can preserve the symplecticity of the original systems, and symplectic or symmetric methods provide long time energy preservation applied to a Hamiltonian system. Symplectic algorithms for Hamiltonian systems appeared in 1980s, and the earliest significant contribution to this field were due to Feng Kang (see [1, 2]). It is worth noting the earlier important work on symplectic integration by Sanz-Serna, who first found and analyzed symplectic Runge–Kutta schemes for Hamiltonian systems (see [3]). Symplectic exponential Runge–Kutta methods for solving Hamiltonian systems were proposed by Mei et al. [4], and shown better performance than classical symplectic Runge–Kutta schemes. However, the coefficients of these exponential integrators are strongly dependent on the computing or approximating the product of a matrix exponential function with a vector. As a consequence, we try to design two novel classes of implicit exponential Runge–Kutta methods with lower computational cost.

In this work, we consider the first-order initial value problem

$$\begin{aligned} \left\{ \begin{array}{l} y'(t)+My(t)=f(y(t)),\quad t\in [t_0,t_\textrm{end}],\\ y(t_0)=y_0, \end{array} \right. \end{aligned}$$

(1)

where the matrix $M\in {\mathbb {R}}^{m\times m}$ is symmetric positive definite or skew-Hermitian with eigenvalues of large modulus. Problems of the form (1) arise frequently in a variety of applied science such as quantum mechanics, flexible mechanics, and electrodynamics. Some highly oscillatory problems (see, e.g. [5, 6]), Schrödinger equations (see, e.g. [7,8,9]) and KdV equations (see, e.g. [10]) can be converted into (1) with appropriate spatial discretizations. Using the Volterra integral formula

$$\begin{aligned} y(t_0+h)=e^{-hM}y(t_0)+h\int _0^1 e^{-(1-\tau )hM}f(y(t_0+h\tau ))d\tau , \end{aligned}$$

(2)

Hochbruch and Ostermann [11] formulated exponential Runge–Kutta methods of collocation type. It is noted that exponential Runge–Kutta (ERK) methods were based on the stiff-order conditions (comprise the classical order conditions) [5, 11,12,13]. In formula (2), $e^{-hM}$ is generally the matrix exponential function, and exponential integrators can exactly integrate the linear equation $y^{\prime }(t)+My(t)=0$, which indicates that exponential integrators have unique advantages for solving highly oscillatory problems than non-exponential integrators. Exponential integrators have received more attention [5, 14,15,16,17,18,19,20,21,22]. It is also worth mentioning that extended Runge–Kutta-Nyström (ERKN) methods [23,24,25,26,27,28,29,30], as the exponential integrators, which were formulated for effectively solving second-order oscillatory systems.

On the other hand, (1) frequently possesses some important geometrical or physical properties. When $f(y)=J^{-1}\nabla U(y)$ and $-M=J^{-1}Q$, with the skew-symmetric

$$\begin{aligned} J=\left( \begin{array}{cc} 0&{}I\\ -I&{}0\\ \end{array} \right) , \end{aligned}$$

where U(y) is a smooth potential function, Q is a symmetric matrix and I is the identity matrix, the problem (1) can be converted into a Hamiltonian system. Owing to this, our study starts by deriving symplectic conditions of these methods. In this paper, the coefficients of implicit exponential methods are real constants, therefore our study is related to the classical order, not satisfy the stiff order conditions. We have presented that two new kinds of explicit ERK methods up to order four reduce to classical Runge–Kutta (RK) methods once $M\rightarrow {\textbf{0}}$ [31, 32]. In what follows, we will study the implicit ERK methods.

The paper is organized as follows. In Sect. 2, we investigate symplectic conditions for the simplified version of ERK (SVERK) and modified version of ERK (MVERK) methods, respectively, and present a first-order symplectic SVERK method. The order conditions of implicit SVERK and MVERK methods are derived in Sect. 3, which are identical to the order conditions of RK methods. Section 4 is devoted to linear stability regions of implicit SVERK and MVERK methods. In Sect. 5, numerical experiments are carried out to show the structure-preserving property of the symplectic method, and present the comparable accuracy and efficiency of these implicit ERK methods. The last section is concerned with concluding remarks.

2 Symplectic conditions for two new classes of ERK methods

In [31], we have formulated the modified and simplified versions of explicit ERK methods for stiff or highly oscillatory problems, and analyzed the convergence of explicit exponential methods. Meanwhile, it has been pointed out that the internal stages and update of SVERK methods preserve some properties of matrix-valued functions, and MVERK methods inherit the internal stages and modify the update of classical RK methods, but their coefficients are independent of matrix exponentials $\varphi _k(-hM)$ defined by (30).

Definition 2.1

([31]) An s-stage SVERK method for the numerical integration (1) is defined as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_i=e^{-c_ihM}y_0+h\sum \limits _{j=1}^sa_{ij}f(Y_j), \quad i=1,\ldots ,s,\\ \displaystyle y_{1}=e^{-hM}y_0+h\sum \limits _{i=1}^sb_{i}f(Y_i)+w_s(z), \end{array} \right. \end{aligned}$$

(3)

where $a_{ij}$, $b_i$ are real constants for $i,j=1,\ldots , s$, $Y_i\approx y(t_0+c_ih)$ for $i=1,\ldots ,s$, $w_s(z)$ depends on h, M, and $w_s(z)\rightarrow 0$ when $M\rightarrow {\textbf{0}}$.

Definition 2.2

([31]) An s-stage MVERK method for the numerical integration (1) is defined as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\bar{Y}}_i=y_0+h\sum \limits _{j=1}^s{\bar{a}}_{ij}(-M{\bar{Y}}_j+f({\bar{Y}}_j)), \quad i=1,\ldots ,s,\\ \displaystyle {\bar{y}}_{1}=e^{-hM}y_0+h\sum \limits _{i=1}^s{\bar{b}}_{i}f({\bar{Y}}_i)+{\bar{w}}_s(z), \end{array} \right. \end{aligned}$$

(4)

where ${\bar{a}}_{ij}$, ${\bar{b}}_i$ are real constants for ${i,j=1,\ldots , s}$, ${\bar{Y}}_i\approx y(t_0+{\bar{c}}_ih)$ for $i=1,\ldots ,s$, ${\bar{w}}_s(z)$ is related to h and M, and ${\bar{w}}_s(z)\rightarrow 0$ once $M\rightarrow {\textbf{0}}$.

The $w_s(z)$ and ${\bar{w}}_s(z)$ also depend on the term $f(\cdot )$ and initial value $y_0$ once we consider the order of SVERK and MVERK methods which satisfies $p\ge 2$. If we consider the first-order methods, then $w_s(z)=0$ and ${\bar{w}}_s(z)=0$. It should be noted that the SVERK or MVERK methods with the same order share the same $w_s(z)$ or ${\bar{w}}_s(z)$, and $w_s(z)$ is different from ${\bar{w}}_s(z)$ when $p\ge 3$ in [31, 32]. It is clear that SVERK and MVERK methods reduce to classical RK methods when $M\rightarrow {\textbf{0}}$, and these methods exactly integrate the first-order homogeneous linear system

$$\begin{aligned} y'(t)=-My(t), \quad y(0)=y_0, \end{aligned}$$

(5)

with the exact solution

$$\begin{aligned} y(t)=e^{-tM}y_0. \end{aligned}$$

The SVERK method (3) can be displayed by the following Butcher Tableau

(6)

where $c_i=\sum _{j=1}^sa_{ij}$ for $i=1,\ldots ,s$. Similarly, the MVERK method (4) also can be expressed in the Butcher tableau

(7)

with ${\bar{c}}_i=\sum _{j=1}^s {\bar{a}}_{ij}$ for $i=1,\ldots ,s$.

It is true that (1) becomes a Hamiltonian system when $f(y)=J^{-1}\nabla U(y)$ and $M=-J^{-1}Q$, where U(y) is a smooth potential function and Q is a symmetric matrix. Thus, we consider the following Hamiltonian system

$$\begin{aligned} \left\{ \begin{array}{l} y'(t)-J^{-1}Qy(t)=J^{-1}\nabla U(y),\quad t\in [t_0,t_\textrm{end}],\\ y(t_0)=y_0. \end{array} \right. \end{aligned}$$

(8)

Under the assumptions of $w_s(z)=0$ and ${\bar{w}}_s(z)=0$, we will analyze symplectic conditions for SVERK and MVERK methods. In fact, $w_s(z)=0$ and ${\bar{w}}_s(z)=0$ mean that the order of SVERK and MVERK methods satisfies $p\le 1$. Since $w_s(z)\ne 0$ and ${\bar{w}}_s(z)\ne 0$, the $w_s(z)$ and ${\bar{w}}_s(z)$ will break the formal conservation of the symplectic invariant, hence the following analysis does not involve high order methods.

Theorem 2.3

Suppose that the coefficients of an s-stage SVERK method with $w_s(z)=0$, which satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{array}{l} e^{-(1-c_k)hM}G^{-1}_{k}=G^{-1}_{k}(e^{-(1-c_k)hM})^{\intercal }, \quad k=1,\ldots ,s,\\ b_{k}b_{l}=b_{k}a_{kl}Je^{-(1-c_k)hM}J^{-1}+b_{l}a_{lk}(e^{-(1-c_k)hM})^{\intercal }, \quad k,l=1,\ldots ,s, \end{array} \right. \end{aligned}$$

(9)

where $G^{-1}_k=\nabla ^2U(y_n+h\sum _{l=1}^s a_{kl}\xi _l)$ and $\xi _k =f(y_n+h\sum _{l=1}^s a_{kl}\xi _l)$, then the SVERK method is symplectic.

Proof

A numerical method is said to be symplectic if the numerical solution $y_{n+1}$ satisfies $(\frac{\partial y_{n+1}}{\partial y_0})^{\intercal }J(\frac{\partial y_{n+1}}{\partial y_0})$ $=(\frac{\partial y_{n}}{\partial y_0})^{\intercal }J(\frac{\partial y_{n}}{\partial y_0})$. Under the assumption $w_s(z)=0$, we rewrite the SVERK method as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \xi _{k}=f\big (e^{-c_khM}y_n+h\sum \limits _{l=1}^sa_{kl}\xi _l\big ), \ k=1,\ldots ,s,\\ \displaystyle y_{n+1}=e^{-hM}y_n+h\sum \limits _{k=1}^sb_{k}\xi _{k}. \end{array} \right. \end{aligned}$$

(10)

Letting $\Xi _k=\frac{\partial \xi _k}{\partial y_0}$, $\Psi _{n+1}=\frac{\partial y_{n+1}}{\partial y_0}$, and $G_k=\nabla ^2U\big (e^{-c_khM}y_n+h\sum _{l=1}^sa_{kl}\xi _l\big )$ for $k=1, \ldots , s$. Moreover, assuming the symmetric matrices $G_1, \ldots , G_s$ are nonsingular, we apply (10) to a Hamiltonian system (8), the derivative of $y_{n+1}$ with respect to $y_0$ is

$$\begin{aligned} \Psi _{n+1}=e^{-hM}\Psi _n+h\sum \limits _{k=1}^s b_k\Xi _k. \end{aligned}$$

(11)

It is easy to obtain

$$\begin{aligned} \Psi _{n+1}^{\intercal }J \Psi _{n+1}&=\Big (e^{-hM}\Psi _n+h\sum \limits _{k=1}^s b_k\Xi _k\Big )^{\intercal }J\Big (e^{-hM}\Psi _n+h\sum \limits _{k=1}^s b_k\Xi _k\Big )\nonumber \\&=(e^{-hM}\Psi _n)^{\intercal }J(e^{-hM}\Psi _n)+h\sum \limits _{k=1}^sb_k(e^{-hM}\Psi _n)^{\intercal }J\Xi _k\nonumber \\&\quad +h\sum \limits _{k=1}^s b_k\Xi _{k}^{\intercal }Je^{-hM}\Psi _n\nonumber \\&\quad +h^2\sum \limits _{k=1}^s\sum \limits _{l=1}^sb_kb_l\Xi _{k}^{\intercal }J\Xi _l. \end{aligned}$$

(12)

It follows from (10) that

$$\begin{aligned} \Xi _k=J^{-1}G_k\big (e^{-c_khM}\Psi _n+h\sum \limits _{l=1}^s a_{kl}\Xi _l\big ), \quad k=1, \ldots , s, \end{aligned}$$

(13)

thus

$$\begin{aligned} \Psi _n=e^{c_khM}G_{k}^{-1}J\Xi _k-h\sum \limits _{l=1}^s a_{kl}e^{c_khM}\Xi _l, \quad k=1, \ldots , s. \end{aligned}$$

(14)

In view of (14), we have

$$\begin{aligned} \begin{aligned} h\sum \limits _{k=1}^sb_k(e^{-hM}\Psi _n)^{\intercal }J\Xi _k&=h\sum \limits _{l=1}^s b_l\big (e^{c_lhM}G_l^{-1}J\Xi _l-h\sum \limits _{k=1}^s a_{lk}e^{c_lhM}\Xi _k\big )^{\intercal }(e^{-hM})^{\intercal }J\Xi _l\\&=h\sum \limits _{k=1}^s b_k\Xi _{k}^{\intercal } J^{\intercal } G_{k}^{-1} (e^{-(1-c_k)hM})^{\intercal }J\Xi _{k}\\&\quad - h^2\sum \limits _{k=1}^s \sum \limits _{l=1}^s b_la_{lk}\Xi _{k}^{\intercal }(e^{-(1-c_k)hM})^{\intercal }J\Xi _{l}, \end{aligned} \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{aligned} h\sum \limits _{k=1}^sb_k\Xi _{k}^{\intercal } Je^{-hM}\Psi _n&=h\sum \limits _{k=1}^s b_k\Xi _k^{\intercal }Je^{-hM}\big (e^{c_khM}G_{k}^{-1}J\Xi _k-h\sum \limits _{l=1}^s a_{kl}e^{c_khM}\Xi _l\big )\\&=h\sum \limits _{k=1}^s b_k\Xi _{k}^{\intercal } J e^{-(1-c_k)hM} G_{k}^{-1}J\Xi _{k}\\&\quad - h^2\sum \limits _{k=1}^s \sum \limits _{l=1}^s b_ka_{kl}\Xi _{k}^{\intercal }Je^{-(1-c_k)hM}\Xi _{l}. \end{aligned} \end{aligned}$$

(16)

Inserting (15) and (16) into (12) yields

$$\begin{aligned} \Psi _{n+1}^{\intercal }J \Psi _{n+1}&=\Psi _{n}^{\intercal } J\Psi _{n}+h\sum \limits _{k=1}^s b_k\Xi _{k}^{\intercal } \Big (J^{\intercal }G_{k}^{-1}(e^{-(1-c_k)hM})^{\intercal }+J e^{-(1-c_k)hM} G_{k}^{-1}\Big )J\Xi _{k}\\&-h^2\sum \limits _{k=1}^s \sum \limits _{l=1}^s b_la_{lk}\Xi _{k}^{\intercal }(e^{-(1-c_k)hM})^{\intercal }J\Xi _{l}\\ {}&- h^2\sum \limits _{k=1}^s \sum \limits _{l=1}^s b_ka_{kl}\Xi _{k}^{\intercal }Je^{-(1-c_k)hM}\Xi _{l} \\&+h^2\sum \limits _{k=1}^s\sum \limits _{l=1}^sb_kb_l\Xi _{k}^{\intercal }J\Xi _l \\&=\Psi _{n}^{\intercal } J\Psi _{n}+h\sum \limits _{k=1}^s b_k\Xi _{k}^{\intercal }J \Big ( e^{-(1-c_k)hM} G_{k}^{-1}-G_{k}^{-1}(e^{-(1-c_k)hM})^{\intercal }\Big )J\Xi _{k}\\&+h^2\sum \limits _{k=1}^s \sum \limits _{l=1}^s \Xi _{k}^{\intercal } \big (b_kb_l-b_ka_{kl}Je^{-(1-c_k)hM}J^{-1}-b_la_{lk}(e^{-(1-c_k)hM})^{\intercal }\big )J\Xi _l. \end{aligned}$$

As the coefficients of a SVERK method satisfy the conditions (9), a direct calculation leads to

$$\begin{aligned} \Psi _{n+1}J\Psi _{n+1}=\Psi _{n}J\Psi _{n}. \end{aligned}$$

Therefore the SVERK method is symplectic. The proof is complete. $\square$

Remark 2.4

It can be observed that symplectic conditions of SVERK methods with $w_s(z)=0$ reduce to symplectic conditions of classical RK methods once $M\rightarrow {\textbf{0}}$. A choice is that $b_1=1$, $c_1=1$ and $a_{11}=1/2$, we can obtain the first-order symplectic SVERK method

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=e^{-hM}y_n+\frac{h}{2}f(Y_1), \\ \displaystyle y_{n+1}=e^{-hM}y_n+hf(Y_1). \end{array} \right. \end{aligned}$$

(17)

For (1), the method (17) reduces to the implicit midpoint method when $M\rightarrow {\textbf{0}}$. Unfortunately, there is no existing the symplectic SVERK method with order $p\ge 2$ due to $w_s(z)\ne 0$.

The next theorem will present symplectic conditions of MVERK methods with ${\bar{w}}_s(z)=0$.

Theorem 2.5

Suppose that the coefficients of an s-stage MVERK method with ${\bar{w}}_s(z)=0$, which satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{array}{l} D_i^{\intercal }Je^{-hM}+(e^{-hM})^{\intercal }JD_i=0, \ i=1,\ldots , s,\\ {\bar{b}}_i{\bar{b}}_j={\bar{b}}_i{\bar{a}}_{ij}Je^{-hM}J^{-1}+{\bar{b}}_j{\bar{a}}_{ji}e^{-hM}, \ i,j=1,\ldots ,s,\\ {\bar{b}}_j{\bar{a}}_{ji}M^{\intercal }(e^{-hM})^{\intercal }JD_j+{\bar{b}}_i{\bar{a}}_{ij}D_i^{\intercal }Je^{-hM}M=0,\ i,j=1,\ldots ,s, \end{array} \right. \end{aligned}$$

(18)

with $D_i=\frac{\partial f({\bar{Y}}_i)}{\partial y_0}$, then the MVERK method is symplectic.

Proof

Setting $D_i=\frac{\partial f({\bar{Y}}_i)}{\partial y}$, $X_i=\frac{\partial {\bar{Y}}_i}{\partial y_0}$, and $\Psi _{n+1}=\frac{\partial {\bar{y}}_{n+1}}{y_0}$. Similarly, we apply the MVERK method (4) with ${\bar{w}}_s(z)=0$ to a Hamiltonian system (8), the derivative of this scheme with respect to $y_0$ is

$$\begin{aligned} \left\{ \begin{array}{l} X_i=\frac{\partial {\bar{Y}}_i}{\partial y_0}=\Psi _{n}+h\sum \limits _{j=1}^s {\bar{a}}_{ij}(-MX_j+D_jX_j),\\ \Psi _{n+1}=e^{-hM}\Psi _n+h\sum \limits _{i=1}^s {\bar{b}}_iD_iX_i. \end{array} \right. \end{aligned}$$

(19)

Then, we have

$$\begin{aligned} \begin{aligned} \Psi _{n+1}^{\intercal }J \Psi _{n+1}&=\Big (e^{-hM}\Psi _n+h\sum \limits _{i=1}^s {\bar{b}}_iD_iX_i\Big )^{\intercal }J\Big (e^{-hM}\Psi _n+h\sum \limits _{i=1}^s {\bar{b}}_iD_iX_i\Big )\\&=(e^{-hM}\Psi _n)^{\intercal }J(e^{-hM}\Psi _n)+h\sum \limits _{i=1}^s{\bar{b}}_i(e^{-hM}\Psi _n)^{\intercal }JD_iX_i\\&\quad +h\sum \limits _{i=1}^s {\bar{b}}_i(D_iX_i)^{\intercal }Je^{-hM}\Psi _n\\&\quad +h^2\sum \limits _{i=1}^s\sum \limits _{j=1}^s{\bar{b}}_i{\bar{b}}_j(D_iX_i)^{\intercal }JD_jX_j. \end{aligned} \end{aligned}$$

(20)

Using the first formula of (19), we obtain

$$\begin{aligned} X_i^{\intercal }(e^{-hM})^{\intercal } JD_iX_i= & {} \Psi _n^{\intercal }(e^{-hM})^{\intercal } JD_iX_i\nonumber \\ {}{} & {} +h\sum \limits _{j=1}^s {\bar{a}}_{ij}(-MX_j+D_jX_j)^{\intercal }(e^{-hM})^{\intercal }JD_iX_i,\nonumber \\ (D_iX_i)^{\intercal } Je^{-hM}X_i= & {} (D_iX_i)^{\intercal } Je^{-hM}\Psi _n\nonumber \\ {}{} & {} +h\sum \limits _{j=1}^s {\bar{a}}_{ij}(D_iX_i)^{\intercal } Je^{-hM}(-MX_j+D_jX_j), \end{aligned}$$

(21)

thus

$$\begin{aligned} \Psi _n^{\intercal }(e^{-hM})^{\intercal } JD_iX_i= & {} X_i^{\intercal }(e^{-hM})^{\intercal } JD_iX_i\nonumber \\ {}{} & {} -h\sum \limits _{j=1}^s {\bar{a}}_{ij}(-MX_j+D_jX_j)^{\intercal }(e^{-hM})^{\intercal }JD_iX_i,\nonumber \\ (D_iX_i)^{\intercal } Je^{-hM}\Psi _n= & {} (D_iX_i)^{\intercal } Je^{-hM}X_i\nonumber \\ {}{} & {} -h\sum \limits _{j=1}^s {\bar{a}}_{ij}(D_iX_i)^{\intercal } Je^{-hM}(-MX_j+D_jX_j). \end{aligned}$$

(22)

Inserting (22) into (20) leads to

$$\begin{aligned} \begin{aligned} \Psi _{n+1}^{\intercal }J \Psi _{n+1}&=\Psi _{n}^{\intercal } J\Psi _{n}+h\sum \limits _{i=1}^s {\bar{b}}_iX_i^{\intercal } (e^{-hM})^{\intercal }JD_iX_i\\&-h^2\sum \limits _{i=1}^s \sum \limits _{j=1}^s {\bar{b}}_j{\bar{a}}_{ji}(-MX_i+D_iX_i)^{\intercal }(e^{-hM})^{\intercal }JD_j \\ {}&\times X_j +h\sum \limits _{i=1}^s {\bar{b}}_i(D_iX_i)^{\intercal }Je^{hM}X_i\\&-h^2\sum \limits _{i=1}^s \sum \limits _{j=1}^s {\bar{b}}_i{\bar{a}}_{ij}(D_iX_i)^{\intercal }JS(-MX_j+D_jX_j)\\&+h^2\sum \limits _{i=1}^s \sum \limits _{j=1}^s{\bar{b}}_i{\bar{b}}_j(D_iX_i)^{\intercal }J(D_jX_j) \\&=\Psi _{n}^{\intercal } J\Psi _{n}+h\sum \limits _{i=1}^s {\bar{b}}_iX_i^{\intercal }\big (D_i^{\intercal }Je^{hM}+(e^{hM})^{\intercal }JD_i\big )X_i\\&+h^2\sum \limits _{i=1}^s \sum \limits _{j=1}^s (D_iX_i)^{\intercal }\big ({\bar{b}}_i{\bar{b}}_j-{\bar{b}}_j{\bar{a}}_{ij}(e^{-hM})^{\intercal } -{\bar{b}}_i{\bar{a}}_{ij}JSJ^{-1}\big )JD_jX_j\\ \\&+h^2\sum \limits _{i=1}^s \sum \limits _{j=1}^s X_i^{\intercal }\big ({\bar{b}}_j{\bar{a}}_{ji}M^{\intercal } (e^{-hM})^{\intercal } JD_j+{\bar{b}}_i{\bar{a}}_{ij}D_i^{\intercal } Je^{-hM}M\big )X_j. \end{aligned} \end{aligned}$$

As the coefficients of the MVERK method satisfy conditions (18), it can be verified that

$$\begin{aligned} \Psi _{n+1}^{\intercal }J\Psi _{n+1}=\Psi _{n}^{\intercal }J\Psi _{n}, \end{aligned}$$

whence the MVERK method is symplectic. The proof is complete. $\square$

Remark 2.6

Theorem 2.5 presents symplectic conditions of MVERK methods with $w_s(z)=0$. However, when $b_i$ ($i=1,\ldots ,s$) are constants, the second formula of (18) can never be satisfied. Symplectic conditions of MVERK methods with $w_s(z)\ne 0$ can be analyzed by the same way, unfortunately, the MVERK methods with ${\bar{w}}_s(z)\ne 0$ can not preserve the symplectic invariant.

Corollary 2.7

There does not exist any symplectic MVERK methods.

3 Highly accurate implicit ERK methods

Section 2 is concerned with symplectic conditions for SVERK and MVERK methods. However, the symplectic SVERK method only has order one, and there is no existing symplectic MVERK methods. In practice, we need some highly accurate and effective numerical methods, hence the high order implicit SVERK (IMSVERK) and implicit MVERK (IMMVERK) methods are studied in this section.

We now consider a one-stage IMSVERK method with $w_2(z)=-\frac{h^2Mf(y_0)}{2!}$

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=e^{-c_1hM}y_0+ha_{11}f(Y_1), \\ \displaystyle y_{1}=e^{-hM}y_0+hb_{1}f(Y_1)-\frac{h^2Mf(y_0)}{2!}, \end{array} \right. \end{aligned}$$

(23)

and one-stage IMMVERK method with ${\bar{w}}_2(z)=-\frac{h^2Mf(y_0)}{2!}$

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\bar{Y}}_1=y_0+h{\bar{a}}_{11}(-M{\bar{Y}}_1+f({\bar{Y}}_1)), \\ \displaystyle {\bar{y}}_{1}=e^{-hM}y_0+h{\bar{b}}_1f({\bar{Y}}_1)-\frac{h^2Mf(y_0)}{2!}. \end{array} \right. \end{aligned}$$

(24)

A numerical method is said to be of order p if the Taylor expansion of the numerical solution $y_1$ or ${\bar{y}}_1$ and the exact solution $y(t_0+h)$ coincides up to $h^p$ about $y_0$. For convenience, we denote $g(t_0)=-My(t_0)+f(y(t_0))$, the Taylor expansion for the exact solution $y(t_0+h)$ is

$$\begin{aligned} \displaystyle y(t_0+h)&=y(t_0)+hy'(t_0)+\frac{h^2}{2!}y''(t_0)+\frac{h^3}{3!}y'''(t_0)+\frac{h^4}{4!}y^{(4)}(t_0) +{\mathcal {O}}{(h^5)}\\&=y(t_0)+hg(t_0)+\frac{h^2}{2!}(-M+f'_y(y_0))g(t_0)\\&\quad +\frac{h^3}{3!}\big (M^2g(t_0)+(-M+f'_y(y(t_0)))f'_y(y(t_0))g(t_0) \\&\quad -f'_y(y(t_0))Mg(t_0)+f''_{yy}(y(t_0))(g(t_0),g(t_0))\big )\\&\quad +\frac{h^4}{4!}\big (-M^3g(t_0)+M^2f'_y(y(t_0))g(t_0)-Mf'_y(y(t_0))\\&\quad \times (-M+f'_y(y(t_0)))g(t_0)-Mf''_{yy}(y(t_0))(g(t_0),g(t_0))\\&\quad +f'''_{yyy}(y(t_0))(g(t_0),g(t_0),g(t_0))+3f''_{yy}(y(t_0))\\&\quad \times ((-M+f'_y(y(t_0)))g(t_0),g(t_0))\\&\quad +f'_y(y(t_0))(-M+f'_y(y(t_0)))(-M+f'_y(y(t_0)))g(t_0)\\&\quad +f'_y(y(t_0))f''_{yy}(y(t_0))(g(t_0),g(t_0))\big )+{\mathcal {O}}{(h^5)}. \end{aligned}$$

Under the assumption $y_0=y(t_0)$, the Taylor expansions for numerical solutions $y_1$ and ${\bar{y}}_1$ are

$$\begin{aligned} y_1&=(I-hM+\frac{h^2M^2}{2!}+{\mathcal {O}}{(h^3)})y_0+hb_1f(y_0-c_1hMy_0\\&\quad +a_{11}hf(y_0) +{\mathcal {O}}(h^2)) -\frac{h^2Mf(y_0)}{2!}\\&=y_0-hMy_0+\frac{h^2M^2}{2!}y_0+hb_1f(y_0)\\&\quad +h^2b_1c_1f'_y(y_0)(-My_0+f(y_0)) -\frac{h^2Mf(y_0)}{2!}+{\mathcal {O}}{(h^3)}\\&=y_0-hMy_0+hb_1f(y_0)+\frac{h^2}{2!}(-M)(-My_0+f(y_0))\\&\quad +h^2b_1c_1f'_y(y_0)(-My_0+f(y_0))+{\mathcal {O}}{(h^3)}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\bar{y}}_1&=(I-hM+\frac{h^2M^2}{2!}+{\mathcal {O}}{(h^3)})y_0\\&\quad +h{\bar{b}}_1\big [f(y_0)+h{\bar{a}}_{11}f'_y(y_0)(-My_0 +f(y_0)+{\mathcal {O}}{(h)})\big ]-\frac{h^2Mf(y_0)}{2!}\\&=y_0-hMy_0+h{\bar{b}}_1f(y_0)+\frac{h^2M^2}{2!}y_0\\&\quad +h^2{\bar{b}}_1{\bar{a}}_{11}f'_y(y_0)(-My_0+f(y_0))-\frac{h^2Mf(y_0)}{2!}+{\mathcal {O}}{(h^3)}\\&=y_0-hMy_0+h{\bar{b}}_1f(y_0)+\frac{h^2}{2!}(-M)(-My_0+f(y_0))\\&\quad +h^2{\bar{b}}_1{\bar{a}}_{11}f'_y(y_0)(-My_0+f(y_0))+{\mathcal {O}}(h^3). \end{aligned} \end{aligned}$$

If we consider the implicit second-order ERK methods with one stage, then $b_1={\bar{b}}_1=1$ and $a_{11}={\bar{a}}_{11}=\frac{1}{2}$. Therefore, the second-order IMSVERK method with one stage is given by

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=e^{-\frac{1}{2}hM}y_0+\frac{h}{2}f(Y_1),\\ \displaystyle y_{1}=e^{-hM}y_0+hf(Y_1)-\frac{h^2Mf(y_0)}{2!}, \end{array} \right. \end{aligned}$$

(25)

which can be denoted by the Butcher tableau

(26)

The second-order IMMVERK method with one stage is shown as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\bar{Y}}_1=y_0+\frac{h}{2}(-M{\bar{Y}}_1+f({\bar{Y}}_1)), \\ \displaystyle y_{1}=e^{-hM}y_0+hf({\bar{Y}}_1)-\frac{h^2Mf(y_0)}{2!}, \end{array} \right. \end{aligned}$$

(27)

which also can be indicated by the Butcher tableau

(28)

ERK methods of collocation type were formulated by Hochbruck and Ostermann, and their convergence properties also were analyzed in [11]. Using the collocation code $c_1=1/2$, then the implicit second-order (stiff) ERK method with one stage is

(29)

with

$$\begin{aligned} \varphi _{ij}(-hM)=\varphi _i(-c_jhM)=\int _0^1 e^{-(1-\tau )c_jhM}\frac{\tau ^{i-1}}{(i-1)!}d\tau . \end{aligned}$$

(30)

We notice that when $M\rightarrow {\textbf{0}}$, the methods (26), (28), and (29) reduce to the implicit midpoint rule.

Now, we consider fourth-order IMSVERK and IMMVERK methods with two stages. The order conditions for the implicit fourth-order RK method with two stages are

(31)

Under the assumptions $c_1=a_{11}+a_{12}$ and $c_2=a_{21}+a_{22}$, it has a unique solution [33, 34]. The following theorem verifies that the order conditions of fourth-order IMSVERK methods with two stages are identical to (31).

Theorem 3.1

Suppose that the coefficients of a two-stage IMSVERK method with $w_4(z)$

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=e^{-c_1hM}y_0+h\big [a_{11}f(Y_1)+a_{12}f(Y_2)\big ],\\ Y_2=e^{-c_2hM}y_0+h\big [a_{21}f(Y_1)+a_{22}f(Y_2)\big ],\\ \displaystyle y_{1}=e^{-hM}y_0+h(b_1f(Y_1)+b_2f(Y_2))+w_4(z), \end{array} \right. \end{aligned}$$

(32)

where

$$\begin{aligned} \begin{aligned} w_4(z)&=-\frac{h^2}{2!}Mf(y_0)+\frac{h^3}{3!}\big ((M-f'_y(y_0))Mf(y_0) -Mf'_y(y_0)g(y_0)\big )\\&\quad +\frac{h^4}{4!}\Big ((-M+f'_y(y_0))M^2f(y_0)\\&\quad +M^2f'_y(y_0)g(y_0)-Mf''_{yy}(y_0)\big (g(y_0),g(y_0)\big )\\&\quad -Mf'_y(y_0)(-M+f'_y(y_0))g(y_0)-f'_y(y_0)Mf'_y(y_0)\\&\quad \times g(y_0)-f'_y(y_0)f'_y(y_0)Mf(y_0)+3f''_{yy}(y_0)\big (-Mf(y_0),g(y_0)\big )\Big ), \end{aligned} \end{aligned}$$

which satisfy (31), then the IMSVERK method has order four.

Proof

Ignoring the term ${\mathcal {O}}(h^5)$, and the Taylor expansion for numerical solution $y_1$ is shown by

$$\begin{aligned} y_1&=e^{-hM}y_0+hb_1f\big ((I-c_1hM+\frac{(c_1hM)^2}{2!}- \frac{(c_1hM)^3}{3!}\nonumber \\&\quad +{\mathcal {O}}(h^4))y_0+ha_{11}f(Y_1)+ha_{12}f(Y_2)\big )+hb_2\nonumber \\&\quad \times f\big ((I-c_2hM+\frac{(c_2hM)^2}{2!}-\frac{(c_2hM)^3}{3!}+{\mathcal {O}}(h^4))y_0\nonumber \\&\quad +ha_{21}f(Y_1)+ha_{22}f(Y_2) \big )+w_4(z)+{\mathcal {O}}(h^5)\nonumber \\&=(I-hM+\frac{h^2M^2}{2}-\frac{h^3M^3}{3!}+\frac{h^4M^4}{4!}+{\mathcal {O}}(h^5))y_0\nonumber \\&\quad +h(b_1+b_2)f(y_0) +h^2b_1f^{\prime }_y(y_0)(-c_1My_0 +a_{11} \nonumber \\&\quad \times f(Y_1)+a_{12}f(Y_2)+\frac{h(c_1M)^2}{2}y_0-\frac{h^2(c_1M)^3}{3!}y_0\nonumber \\&\quad +{\mathcal {O}}(h^3))+h^2b_2f^{\prime }_y(y_0)(-c_2My_0+a_{21}f(Y_1)\nonumber \\&\quad +a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0-\frac{h^2(c_2M)^3}{3!}y_0+{\mathcal {O}}(h^3))\nonumber \\&\quad +\frac{h^3}{2}b_1f''_{yy}(y_0)\big (-c_1My_0+a_{11}f(Y_1) +a_{12}\nonumber \\&\quad \times f(Y_2) +\frac{h(c_1M)^2}{2}y_0,-c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2)+\frac{h(c_1M)^2}{2}y_0\big )\nonumber \\&\quad +\frac{h^3}{2}b_2f''_{yy}(y_0)\Bigg (-c_2My_0 \nonumber \\&\quad +a_{21}f(Y_1)+a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0,-c_2My_0+a_{11}f(Y_1)\nonumber \\&\quad +a_{12}f(Y_2)+\frac{h(c_2M)^2}{2}y_0\Bigg )+\frac{h^4}{3!}b_1\nonumber \\&\quad \times f'''_{yyy}(y_0)\big (-c_1M y_0+a_{11}f(Y_1)+a_{12}f(Y_2),\nonumber \\&\quad -c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2),-c_1My_0+a_{11}\nonumber \\&\quad \times f(Y_1)+a_{12}f(Y_2)\big )+\frac{h^4}{3!}b_2f'''_{yyy}(y_0)(-c_2My_0\nonumber \\&\quad +a_{21}f(Y_1)+a_{22}f(Y_2),-c_2My_0+a_{21}f(Y_1)\nonumber \\&\quad +a_{22}f(Y_2),-c_2My_0+a_{21}f(Y_1)+a_{22}f(Y_2))+w_4(z)+{\mathcal {O}}(h^5). \end{aligned}$$

(33)

Under the appropriate assumptions $c_i=\sum _{j=1}^s a_{ij}$ for $i=1,\ldots ,s$, we have

$$\begin{aligned} \begin{aligned} y_1&=e^{-hM}y_0+h(b_1+b_2)f(y_0)+h^2b_1f^{\prime }_y(y_0)\big (-c_1My_0\\&\quad +a_{11}f(Y_1)+a_{12}f(Y_2)+\frac{h(c_1M)^2}{2}y_0 \\&\quad -\frac{h^2(c_1M)^3}{3!}y_0\big )+h^2b_2f^{\prime }_y(y_0)\big (-c_2My_0+a_{21}f(Y_1)\\&\quad +a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0 -\frac{h^2(c_2M)^3}{3!}y_0\big )\\&\quad +\frac{h^3}{2}b_1f''_{yy}(y_0)\big (-c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2)\\&\quad +\frac{h(c_1M)^2}{2}y_0, -c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2) \\&\quad +\frac{h(c_1M)^2}{2}y_0\big )+\frac{h^3}{2}b_2f''_{yy}(y_0)\big (-c_2My_0+a_{21}f(Y_1)\\&\quad +a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0, -c_2My_0+a_{21}\\ {}&\quad \times f(Y_1)+a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0\big )\\&\quad +\frac{h^4}{3!}b_1f'''_{yyy}(y_0)\big (c_1(-My_0+f(y_0)),c_1(-My_0+f(y_0)),c_1\\&\quad \times (-My_0+f(y_0))\big ) +\frac{h^4}{3!}b_2f'''_{yyy}(y_0)\big (c_2(-My_0\\&\quad +f(y_0)),c_2(-My_0+f(y_0)),c_2(-My_0+f(y_0))\big )\\&\quad +w_4(z)+{\mathcal {O}}(h^5). \end{aligned} \end{aligned}$$

Inserting $Y_1$ and $Y_2$ of (32) into $f(Y_1)$ and $f(Y_2)$ yields

$$\begin{aligned} a_{11}f(Y_1)&=a_{11}f\left( y_0-c_1hMy_0+ha_{11}f(Y_1)+ha_{12}f(Y_2)+\frac{(c_1hM)^2}{2!}y_0\right) \\&=a_{11}f(y_0)+hf^{\prime }_y(y_0)\big (-c_1My_0+a_{11}f(y_0)\\&\quad +ha_{11}f^{\prime }_y(y_0)(-c_1My_0+a_{11}f(y_0)+a_{12}f(y_0))\\&\quad +a_{12}f(y_0)+ha_{12}f^{\prime }_y(y_0)\left( -c_2My_0\right. \\&\quad \left. +a_{21}f(y_0)+a_{22}f(y_0))+\frac{h(c_1M)^2}{2}y_0\right) +\frac{h^2}{2}a_{11}c_1^2 \\ {}&\quad \times f''_{yy}(y_0)(g(y_0),g(y_0))\\&=a_{11}f(y_0)+ha_{11}c_1f^{\prime }_{y}(y_0)g(y_0)\\&\quad +h^2(a_{11}^2c_1+a_{11}a_{12}c_2)f^{\prime }_{y}(y_0)f^{\prime }_{y}(y_0)g(y_0)\\&\quad +\frac{h^2}{2}a_{11}c_1^2f^{\prime }_{y}(y_0)\\&\quad \times M^2y_0+\frac{h^2}{2}a_{11}c_1^2f''_{yy}(y_0)(g(y_0),g(y_0)), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} a_{12}f(Y_2)&=a_{12}f(y_0)+ha_{12}c_2f^{\prime }_{y}(y_0)g(y_0)\\&\quad +h^2(a_{12}a_{21}c_1+a_{12}a_{22}c_2)f^{\prime }_{y}(y_0)f^{\prime }_{y}(y_0)g(y_0) +\frac{h^2}{2}a_{12}c_2^2\\ {}&\quad \times f^{\prime }_{y}(y_0)M^2y_0+\frac{h^2}{2}a_{12}c_2^2f''_{yy}(y_0)(g(y_0),g(y_0)). \end{aligned} \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \begin{aligned}&h^2b_1f^{\prime }(y_0)\left( -c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2)+\frac{h(c_1M)^2}{2}y_0 -\frac{h^2(c_1M)^3}{3!}y_0\right) \\&\quad =h^2b_1c_1f^{\prime }_y(y_0)g(y_0)\\&\qquad +\frac{h^3}{2}b_1c_1^2f^{\prime }_y(y_0) M^2y_0-\frac{h^4}{3!}b_1c_1^3f^{\prime }_y(y_0)M^3y_0\\&\qquad +h^3b_1(a_{11}c_1+a_{12}c_2)f^{\prime }_y(y_0)f^{\prime }_y(y_0)g(y_0)+h^4b_1(a_{11}^2c_1 \\&\qquad +a_{11}a_{12}c_2+a_{12}a_{21}c_1+a_{12}a_{22}c_2)f^{\prime }_y(y_0)f^{\prime }_y(y_0)f^{\prime }_y(y_0)g(y_0)\\&\qquad +\frac{h^4}{2}b_1(a_{11}c_1^2+a_{12}c_2^2)\big (f^{\prime }_y(y_0)f^{\prime }_y(y_0)M^2\\&\qquad \times y_0+f^{\prime }_y(y_0)f''_{yy}(y_0)(g(y_0),g(y_0))\big ), \end{aligned} \end{aligned}$$

and

$$\begin{aligned}&h^2b_2f^{\prime }(y_0)\left( -c_2My_0+a_{21}f(Y_1)+a_{22}f(Y_2)+\frac{h(c_2M)^2}{2}y_0 -\frac{h^2(c_2M)^3}{3!}y_0\right) \\&\quad =h^2b_2c_2f^{\prime }_y(y_0)g(y_0)\\&\qquad +\frac{h^3}{2}b_2c_2^2f^{\prime }_y(y_0) M^2y_0-\frac{h^4}{3!}b_2c_2^3f^{\prime }_y(y_0)M^3y_0\\&\qquad +h^3b_2(a_{21}c_1+a_{22}c_2)f^{\prime }_y(y_0)f^{\prime }_y(y_0)g(y_0)+h^4b_1(a_{22}^2c_2 \\&\qquad +a_{22}a_{21}c_1+a_{21}a_{12}c_2+a_{21}a_{11}c_1)f^{\prime }_y(y_0)f^{\prime }_y(y_0)f^{\prime }_y(y_0)g(y_0)\\&\qquad +\frac{h^4}{2}b_2(a_{21}c_1^2+a_{22}c_2^2)\big (f^{\prime }_y(y_0)f^{\prime }_y(y_0)M^2\\&\qquad \times y_0+f^{\prime }_y(y_0)f''_{yy}(y_0)(g(y_0),g(y_0))\big ). \end{aligned}$$

Likewise, a direct calculation leads to

$$\begin{aligned} \begin{aligned}&\frac{h^3}{2}b_1f''_{yy}(y_0)\left( -c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2)\right. \\&\qquad \left. +\frac{h(c_1M)^2}{2}y_0,-c_1My_0+a_{11}f(Y_1)+a_{12}f(Y_2) +\frac{h(c_1M)^2}{2}y_0\right) \\&\quad =\frac{h^3}{2}b_1f''_{yy}(y_0)\left( c_1g(y_0)+h(a_{11}c_1+a_{12}c_2)f^{\prime }_y(y_0)g(y_0)\right. \\&\qquad +\frac{h(c_1M)^2}{2}y_0,c_1g(y_0)+h(a_{11}c_1+a_{12}c_2)\\&\qquad \times \left. f^{\prime }_y(y_0)g(y_0)+\frac{h(c_1M)^2}{2}y_0)\right) \\&\quad =\frac{h^3}{2}b_1c_1^2f''_{yy}(y_0)(g(y_0),g(y_0))+h^4b_1(a_{11}c_1+a_{12}c_2)\\&\qquad c_1f''_{yy}(y_0)(f^{\prime }_y(y_0)g(y_0),g(y_0)) +\frac{h^4}{2}b_1c_1^3f''_{yy}(y_0)(M^2y_0,g(y_0)), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\frac{h^3}{2}b_2f''_{yy}(y_0)\left( -c_2My_0+a_{21}f(Y_1)+a_{22}f(Y_2)\right. \\&\qquad \left. +\frac{h(c_2M)^2}{2}y_0,-c_2My_0+a_{21}f(Y_1)+a_{22}f(Y_2) +\frac{h(c_2M)^2}{2}y_0\right) \\&\quad =\frac{h^3}{2}b_2c_2^2f''_{yy}(y_0)(g(y_0),g(y_0))+h^4b_2(a_{21}c_1+a_{22}c_2)c_2f''_{yy}(y_0)(f^{\prime }_y(y_0)g(y_0),g(y_0))\\&\qquad +\frac{h^4}{2}b_2c_2^3f''_{yy}(y_0)(M^2y_0,g(y_0)). \end{aligned} \end{aligned}$$

To sum up, the Taylor expansion for the numerical solution $y_1$ is

$$\begin{aligned} y_1&=y_0-hMy_0+h(b_1+b_2)f(y_0)-\frac{h^2Mg(y_0)}{2!}\\&\quad +h^2(b_1c_1+b_2c_2)f^{\prime }_y(y_0)g(y_0)-\frac{h^3}{3!}f^{\prime }_y(y_0)Mf(y_0) \\&\quad +\frac{h^3}{3!}M(M-f^{\prime }_y(y_0))g(y_0)+\frac{h^3}{2}(b_1c_1^2+b_2c_2^2)\big (f^{\prime }_y(y_0)M^2y_0+f''_{yy}(y_0)(g(y_0),g(y_0))\big )\\&\quad +h^3(b_1(a_{11}c_1+a_{12}c_2)+b_2(a_{21}c_1+a_{22}c_2)) f^{\prime }_y(y_0)f^{\prime }_y(y_0)g(y_0)\\&\quad +\frac{h^4}{4!}\big (-M^3g(y_0)+M^2f^{\prime }_y(y_0)g(y_0)\\&\quad -Mf^{\prime }_y(y_0)(-M+f^{\prime }_y(y_0))g(y_0)-Mf''_{yy}(y_0)(g(y_0),g(y_0))\\&\quad -f^{\prime }_y(y_0)Mf^{\prime }_y(y_0)g(y_0)-f^{\prime }_y(y_0)f^{\prime }_y(y_0)Mf(y_0)\\&\quad +f^{\prime }_y(y_0)M^2f(y_0)+3f''_{yy}(y_0)(-Mf(y_0),g(y_0))\big )\\&\quad +h^4(b_1c_1^3+b_2c_2^3)\big (\frac{1}{3!}f'''_{yyy}(y_0)(g(y_0),g(y_0),g(y_0)\\&\quad +\frac{1}{2}f''_{yy}(y_0)(M^2y_0,g(y_0))-\frac{1}{3!}f^{\prime }_y(y_0)M^3y_0\big )\\&\quad +h^4(b_1c_1(a_{11}c_1+a_{12}c_2)+b_2c_2(a_{21}c_1+a_{22}c_2))f''_{yy}(y_0)(f^{\prime }_y(y_0)g(y_0),g(y_0))\\&\quad +\frac{h^4}{2}\big (b_1(a_{11}c_1^2+a_{12}c_2^2)+b_2(a_{21}c_1^2+a_{22}c_2^2)\big )f^{\prime }_y(y_0)(f''_{yy}(y_0)(g(y_0),g(y_0))\\&\quad +f^{\prime }_y(y_0)f^{\prime }_y(y_0)M^2y_0)\\&\quad +h^4\big (b_1(a_{11}^2c_1+(a_{11}+a_{22})a_{12}c_2+a_{12}a_{21}c_1)\\&\quad +b_2(a_{22}^2c_2+(a_{11}+a_{22})a_{21}c_1+a_{21}a_{12}c_2)\big )(f^{\prime }_y(y_0))^3\\&\quad \times g(y_0)+{\mathcal {O}}(h^5). \end{aligned}$$

By comparing with the Taylor expansion of the exact solution $y(t_0+h)$, it can be verified that the IMSVERK method with coefficients satisfying the order conditions (31) has order four. The proof of the theorem is complete. $\square$

Theorem 3.1 indicates that there exists a unique fourth-order IMSVERK method with two stages:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=e^{-\frac{3-\sqrt{3}}{6}hM}y_0+h\big [\frac{1}{4}f(Y_1)+\frac{3-2\sqrt{3}}{12}f(Y_2)\big ],\\ \displaystyle Y_2=e^{-\frac{3+\sqrt{3}}{6}hM}y_0+h\big [\frac{3+2\sqrt{3}}{12}f(Y_1)+\frac{1}{4}f(Y_2)\big ],\\ \displaystyle y_{1}=e^{-hM}y_0+\frac{h}{2}(f(Y_1)+f(Y_2))-\frac{h^2}{2!}Mf(y_0)\\ \displaystyle \qquad \quad +\frac{h^3}{3!}\big ((M-f'_y(y_0))Mf(y_0)-Mf'_y(y_0)g(y_0)\big ) \\ \displaystyle \qquad \quad +\frac{h^4}{4!}\Big ((-M+f'_y(y_0))M^2f(y_0)+M^2f'_y(y_0)g(y_0)-Mf''_{yy}(y_0)\big (g(y_0),g(y_0)\big )\\ \displaystyle \qquad \quad -Mf'_y(y_0)(-M+f'_y(y_0))g(y_0)-f'_y(y_0)Mf'_y(y_0)g(y_0)\\ \qquad \quad -f'_y(y_0)f'_y(y_0)Mf(y_0)+3f''_{yy}(y_0)\big (-Mf(y_0),g(y_0)\big )\Big ). \end{array} \right. \end{aligned}$$

(34)

The method (34) can be displayed by the Butcher tableau

(35)

The following theorem shows the order conditions of the fourth-order IMSVERK method with two stages are exactly identical to (31) as well.

Theorem 3.2

Suppose that the coefficients of a two-stage IMMVERK method with ${\bar{w}}_4(z)$

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\bar{Y}}_1=y_0+h\big [{\bar{a}}_{11}(-M{\bar{Y}}_1+f({\bar{Y}}_1))+{\bar{a}}_{12}(-M{\bar{Y}}_2+f({\bar{Y}}_2))\big ],\\ {\bar{Y}}_2=y_0+h\big [{\bar{a}}_{21}(-M{\bar{Y}}_1+f({\bar{Y}}_1))+{\bar{a}}_{22}(-M{\bar{Y}}_2+f({\bar{Y}}_2))\big ],\\ \displaystyle {\bar{y}}_{1}=e^{-hM}y_0+h({\bar{b}}_1f({\bar{Y}}_1)+{\bar{b}}_2f({\bar{Y}}_2))+{\bar{w}}_4(z), \end{array} \right. \end{aligned}$$

(36)

where

$$\begin{aligned} \begin{aligned} {\bar{w}}_4(z)&=-\frac{h^2}{2!}Mf(y_0)+\frac{h^3}{3!}(M^2f(y_0)-Mf'_y(y_0)g(y_0))\\&\quad +\frac{h^4}{4!}(-M^3f(y_0)+M^2f'_y(y_0)g(y_0)-Mf''_{yy}(y_0)\\&\quad \times (g(y_0),g(y_0)) -Mf'_y(y_0)(-M+f'_y(y_0))g(y_0)), \end{aligned} \end{aligned}$$

which satisfy (31), then the IMMVERK method has order four.

Proof

Under the assumptions ${\bar{c}}_1={\bar{a}}_{11}+{\bar{a}}_{12}$ and ${\bar{c}}_2={\bar{a}}_{21}+{\bar{a}}_{22}$, by comparing the Taylor expansion of numerical solution ${\bar{y}}_1$ with exact solution $y(t_0+h)$, the result can be proved in a same way as Theorem 3.1. Therefore, we omit the details. $\square$

Then, we present the unique fourth-order IMMVERK method with two stages

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle Y_1=y_0+h\Big [\frac{1}{4}(-MY_1+f(Y_1))+\frac{3-2\sqrt{3}}{12}(-MY_2+f(Y_2))\Big ],\\ \displaystyle Y_2=y_0+h\Big [\frac{3+2\sqrt{3}}{12}(-MY_1+f(Y_1))+\frac{1}{4}(-MY_2+f(Y_2))\Big ],\\ \displaystyle y_{1}=e^{-hM}y_0+\frac{h}{2}(f(Y_1)+f(Y_2))-\frac{h^2}{2!}Mf(y_0)+\frac{h^3}{3!}(M^2f(y_0)-Mf'_y(y_0)g(y_0))\\ \qquad \quad +\frac{h^4}{4!}(-M^3f(y_0) +M^2f'_y(y_0)g(y_0)-Mf''_{yy}(y_0)(g(y_0),g(y_0))\\ \displaystyle \quad \qquad -Mf'_y(y_0)(-M+f'_y(y_0))g(y_0)), \end{array} \right. \nonumber \\ \end{aligned}$$

(37)

with $g(y_0)=-My_0+f(y_0)$, which can be denoted by the Butcher tableau

(38)

In view of (34) and (37), two methods reduce to the classical implicit fourth-order RK method with two stages by Hammer and Hollingsworth (see, e.g. [33]) once $M\rightarrow {\textbf{0}}$. It should be noted that (34) and (37) use the Jacobian matrix and Hessian matrix of f(y) with respect to y at each step, however, to our knowledge, the idea for stiff problems is no by means new (see, e.g. [35,36,37]). Using the Gaussian points $c_1=\frac{1}{2}-\frac{\sqrt{3}}{6}$ and $c_2=\frac{1}{2}+\frac{\sqrt{3}}{6}$, the ERK method of collocation type with two stages has been formulated by Hochbruck et al. [11], which can be represented by the Butcher tableau

(39)

It is clear that the coefficients of (39) are matrix exponentials $\varphi _k(-hM)$ $(k>0)$, their implementation depends on the computing or approximating the product of a matrix exponential function with a vector. As we consider the variable stepsize technique, the coefficients of these exponential integrators are needed to recalculate at each step. In contrast, the coefficients of SVERK and MVERK methods are the real constants, their operations can reduce the computation of matrix exponentials to some extent. On the other hand, compared with standard RK methods, these ERK methods possess some properties of matrix-valued functions and exactly integrate the homogeneous linear equation (5).

4 Linear stability

In what follows we investigate the linear stability properties of IMMVERK and IMSVERK methods. For classical RK methods, the linear stability analysis is related to the Dahlquist test equation [34]

$$\begin{aligned} y^{\prime }=\lambda y,\ \lambda \in {\mathbb {R}}. \end{aligned}$$

When we consider exponential integrators, the stability properties of an exponential method are analyzed by applying the method to the partitioned Dalquist equation [38]

$$\begin{aligned} y^{\prime }=i\lambda _1y+i\lambda _2y, \qquad y(t_0)=y_0, \qquad \qquad \lambda _1, \ \lambda _2 \in {\mathbb {R}}. \end{aligned}$$

(40)

i.e., solving (40) by a partitioned exponential integrator, and treating the $i\lambda _1$ exponentially and the $i\lambda _2$ explicitly, then we have the explicit scalar form

$$\begin{aligned} y_{n+1}=R(ik_1,ik_2)y_n, \quad \quad \quad k_1=h\lambda _1, \ k_2=h\lambda _2. \end{aligned}$$

(41)

Definition 4.1

For an exponential method with $R(ik_1,ik_2)$ given by (41), the set S of the stability function $R(ik_1,ik_2)$

$$\begin{aligned} S=\big \{(k_1,k_2)\in {\mathbb {R}}^2: |R(ik_1,ik_2)|\le 1 \big \}, \end{aligned}$$

is called the stability region of the exponential method.

Applying the IMMVERK method (27) and IMSVERK method (25) to (40), the stability regions of implicit second-order ERK methods are respectively depicted in Fig. 1b and c, and we also plot the stability region of the explicit second-order MVERK method with two stages (see, e.g. [31]) in Fig. 1a. For fourth-order ERK methods, we select the IMMVERK method (37), IMSVERK method (34) and the explicit SVERK method with four stages (see, e.g. [32]) to make a comparison, the stability regions of these methods are shown in Fig. 2. It can be observed that implicit exponential methods possess the comparable stability regions than explicit exponential methods.

Fig. 1

a Stability region for explicit second-order MVERK (EXMVERK21) method with two stages. b Stability region for implicit second-order MVERK (IMMVERK12) method. c Stability region for implicit second-order SVERK (IMSVERK12) method

Fig. 2

a Stability region for explicit fourth-order SVERK (EXSVERK41) method with four stages. b Stability region for implicit fourth-order MVERK (IMMVERK24) method. c Stability region for implicit fourth-order SVERK (IMSVERK24) method

5 Numerical Experiments

In this section, we apply the symplectic method (17) and high accurate IMSVERK and IMMVERK methods to highly oscillatory problems. In order to illustrate the accuracy and efficiency of these exponential methods, we select implicit ERK methods to make comparison. These methods are implicit, and we use the fixed-point iteration, the iteration will be stopped once the norm of the difference of two successive approximations is smaller than $10^{-14}$. Matrix exponentials $\varphi _k(-hM)$ $(k>0)$ are evaluated by the Krylov subspace method [39], which possesses the fast convergence. In all numerical experiments, the explicit fourth-order (stiff) ERK method with five stages in [13] with smaller time stepsize is employed as the reference solutions, and we take the Euclidean norm for global errors (GE) and denote by GEH the global error of Hamiltonian. The following numerical methods are chosen for comparison:

• First-order methods:

  • IMSVERK1: the 1-stage implicit SVERK method (17) of order (classical) one presented in this paper;

  • EEuler: the 1-stage explicit exponential Euler method of order (stiff) one proposed in [13];

  • IMEEuler: the 1-stage implicit exponential Euler method of order (stiff) one proposed in [11].

• Second-order methods:

  • IMMVERK12: the 1-stage implicit MVERK method (27) of order (classical) two presented in this paper;

  • IMSVERK12: the 1-stage implicit SVERK method (25) of order (classical) two presented in this paper;

  • IMERK12: the 1-stage implicit ERK method (29) of order (stiff) two proposed in [11].

• Fourth-order methods:

  • IMMVERK24: the 2-stage implicit MVERK method (37) of order (classical) four presented in this paper;

  • IMSVERK24: the 2-stage implicit SVERK method (34) of order (classical) four presented in this paper;

  • IMERK24: the 2-stage implicit ERK method (39) proposed in [11].

Problem 1

The Hénon–Heiles Model is used to describe the stellar motion (see, e.g. [34]), which has the following identical form

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{c} x_1 \\ x_2 \\ y_1 \\ y_2\\ \end{array} \right) '+\left( \begin{array}{cccc} 0 &{} 0 &{} -1 &{}0\\ 0 &{} 0 &{} 0 &{}-1\\ 1 &{} 0 &{} 0 &{}0 \\ 0 &{} 1 &{} 0 &{}0\\ \end{array} \right) \left( \begin{array}{c} x_1 \\ x_2 \\ y_1\\ y_2\\ \end{array} \right) = \left( \begin{array}{c} 0\\ 0\\ -2x_1x_2\\ -x_1^2+x_2^2\\ \end{array} \right) . \end{aligned}\end{aligned}$$

The Hamiltonian of this system is given by

$$\begin{aligned} H(x,y)=\frac{1}{2}(y_1^2+y_2^2)+\frac{1}{2}(x_1^2+x_2^2)+x_1^2x_2-\frac{1}{3}x_2^3. \end{aligned}$$

We select the initial values as

$$\begin{aligned} \big (x_1(0),x_2(0),y_1(0),y_2(0)\big )^{\intercal }=\left( \sqrt{\frac{11}{96}},0,0,\frac{1}{4}\right) ^{\intercal }. \end{aligned}$$

At first, Fig. 3a presents the problem is solved on the interval [0, 10] with stepsizes $h=1/2^{k},\ k=2,\ldots ,6$ for IMSVERK1s1, EEuler, IMEEuler, it can be observed that the IMSVERK1s1 method has higher accuracy than first-order exponential Euler methods. We integrate this problem with stepsize $h=1/30$ on the interval [0, 100], the relative errors $RGEH=\frac{GEH}{H_0}$ of Hamiltonian energy for IMSVERK1s1, EEuler and IMEEuler are presented by Figs. 3b and 4, which reveals the structure-preserving properties of the symplectic method. Finally, we integrate this system over the interval [0, 10] with stepsizes $h=1/2^{k}$ for $k=2,\ldots ,6$, Figs. 5 and 6 display the global errors against the stepszies and the CPU time (seconds) for IMMVERK12, IMSVERK12, IMERK12, IMMVERK24, IMSVERK24, IMERK24.

Fig. 3

Results for Problem 1. a The $\log$–$\log$ plots of global errors (GE) against h. b The energy preservation for method IMSVERK1s1

Fig. 4

Results for Problem 1: the energy preservation for methods EEuler (a) and IMEEuler (b)

Fig. 5

Results for Problem 1. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Fig. 6

Results for Problem 1. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Problem 2

Consider the Duffing equation [4]

$$\begin{aligned} \left\{ \begin{array}{c} \ddot{q}+\omega ^2q=k^2(2q^3-q), \\ q(0)=0, \ {\dot{q}}(0)=\omega , \end{array} \right. \end{aligned}$$

(42)

where $0\le k <\omega$.

Set $p={\dot{q}}$, $z=(p,q)^{\intercal }$. We rewrite the Duffing equation as

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{c} p\\ q\\ \end{array} \right) '+\left( \begin{array}{cc} 0&{} \omega ^2\\ -1 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} p \\ q \\ \end{array} \right) = \left( \begin{array}{c} k^2(2q^3-q)\\ 0 \end{array} \right) . \end{aligned}\end{aligned}$$

It is a Hamiltonian system with the Hamiltonian

$$\begin{aligned} H(p,q)=\frac{1}{2}p^2+\frac{1}{2}\omega ^2q^2+\frac{k^2}{2}(q^2-q^4). \end{aligned}$$

Let $\omega =30$, $k=0.01$. This problem is solved on the interval [0, 100] with the stepsize $h=1/30$, Figs. 7 and 8 show the energy preservation behaviour for IMSVERK1s1, EEuler and IMEEuler. We also integrate the system over the interval [0, 10] with stepsizes $h=1/2^k,\ k=4,\ldots ,8$ for IMSVERK1s1, EEuler, IMEEuler, IMMVERK12, IMSVERK12, IMERK12, IMMVERK24, IMSVERK24, IMERK24, which are shown in Figs. 7a, 9 and 10.

Fig. 7

Results for Problem 2. a The $\log$–$\log$ plots of global errors (GE) against h. b the energy preservation for method IMSVERK1s1

Fig. 8

Results for Problem 2: the energy preservation for methods EEuler (a) and IMEEuler (b)

Fig. 9

Results for Problem 2. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Fig. 10

Results for Problem 2. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Problem 3

Consider the sine-Gorden equation with periodic boundary conditions [4]

$$\begin{aligned}\left\{ \begin{array}{l} \dfrac{\partial ^2u}{\partial t^2}=\dfrac{\partial ^2u}{\partial x^2}-\sin (u), \quad -1<x<1, \ t>0,\\ u(-1,t)=u(1,t).\\ \end{array}\right. \end{aligned}$$

Discretising the spatial derivative $\partial _{xx}$ by the second-order symmetric differences, which leads to the following Hamiltonian system

$$\begin{aligned}\frac{d}{dt}\left( \begin{array}{c} U^{\prime }\\ U\\ \end{array}\right) +\left( \begin{array}{cc} \textbf{0}&{}M\\ -I&{}\textbf{0}\\ \end{array}\right) \left( \begin{array}{c} U^{\prime }\\ U\\ \end{array}\right) =\left( \begin{array}{c} -\sin (U)\\ \textbf{0}\\ \end{array}\right) , \quad t\in [0,t_{\textrm{end}}], \end{aligned}$$

whose Hamiltonian is shown by

$$\begin{aligned} H(U^{\prime },U)=\frac{1}{2}{U^{\prime }}^{\intercal }U^{\prime }+\frac{1}{2}U^{\intercal }MU^{\intercal }-(\cos u_1+\cdots +u_N). \end{aligned}$$

In here, $U(t)=(u_1(t),\ldots ,u_N(t))^T$ with $u_i(t)\approx u(x_i,t)$ for $i=1,\ldots ,N$, with $\Delta x=2/N$ and $x_i=-1+i\Delta x$, $F(t,U)=-\sin (u)=-(\sin (u_1),\ldots ,\sin (u_N))^T$, and

$$\begin{aligned}M=\dfrac{1}{\Delta x^2} \left( \begin{array}{ccccc} 2 &{} -1 &{} &{} &{}-1 \\ -1 &{} 2&{} -1 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} -1 &{} 2 &{} -1\\ -1&{} &{} &{} -1&{}2 \\ \end{array} \right) . \end{aligned}$$

In this test, we choose the initial value conditions

$$\begin{aligned}U(0)=(\pi )^N_{i=1}, \ U'(0)=\sqrt{N}\left( 0.01+\sin \Big (\dfrac{2\pi i}{N}\Big )\right) _{i=1}^N\end{aligned}$$

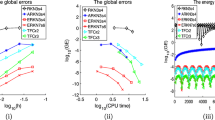
with $N=48$, and solve the problem on the interval [0, 1] with stepsizes $h=1/2^k,\ k=4,\ldots ,8$. The global errors GE against the stepsizes and the CPU time (seconds) for IMSVERK1s1, EEuler, IMEEuler, IMMVERK12, IMSVERK12, IMERK12, IMMVERK24, IMSVERK24, IMERK24, which are respectively presented in Figs. 11a, 12 and 13. Then we integrate this problem on the interval [0, 100] with stepsize $h=1/40$, the energy preservation behaviour for IMSVERK1s1, EEuler, IMEEuler are shown in Figs. 11b and 14.

Fig. 11

Results for Problem 3. a The $\log$–$\log$ plots of global errors (GE) against h. b the energy preservation for method IMSVERK1s1

Fig. 12

Results for Problem 3. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Fig. 13

Results for Problem 3. a The $\log$–$\log$ plots of global errors (GE) against h. b The $\log$–$\log$ plots of global errors against the CPU time

Fig. 14

Results for Problem 3: the energy preservation for methods EEuler (a) and IMEEuler (b)

6 Conclusion

Exponential Runge–Kutta methods have the unique advantage for solving highly oscillatory problems, however the implementation of ERK methods generally requires the evaluations of products of matrix functions with vectors. To reduce the computational cost, two new classes of explicit ERK integrators were formulated in [31, 32], and we studied the implicit ERK methods in this paper. Firstly, we analyzed symplectic conditions and verified the existence of the symplectic method, however, the symplectic method only had order one. Then we designed some practical and effective numerical methods (up to order four). Furthermore, we plotted linear stability regions for implicit ERK methods. Numerical results presented the energy preservation behaviour for IMSVERK1s1, and demonstrated the comparable accuracy and efficiency for IMSVERK1s1, IMMVERK12, IMMVERK24, IMSVERK12, IMSVERK24, when applied to the Hénon–Heiles Model, the Duffing equation and the sine-Gordon equation.

Exponential integrators show the better performance than non-exponential integrators. High accuracy and structure preservation for exponential integrators can be further investigated.