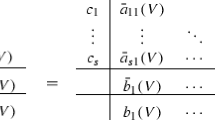Explicit multi-frequency symmetric extended RKN integrators for solving multi-frequency and multidimensional oscillatory reversible systems

Abstract

This paper studies explicit multi-frequency symmetric extended Runge–Kutta–Nyström (ERKN) integrators tailored to numerically computing the multi-frequency and multidimensional oscillatory reversible second-order differential equations $q''(t)+Mq(t)=f\big (q(t)\big )$. We establish the symmetry conditions in a simplified way for multi-frequency ERKN integrators. Five explicit multi-frequency symmetric ERKN integrators are derived based on the simplified symmetry conditions. The arbitrary high-order explicit multi-frequency symmetric ERKN integrators can be achieved by the application of the symmetric composition. The stability and phase properties of the new integrators are discussed. Five numerical experiments are carried out and the numerical results demonstrate the remarkable numerical behavior of the new explicit multi-frequency symmetric integrators when applied to the multi-frequency and multidimensional oscillatory reversible second-order differential equations.

1 Introduction

Reversible systems have the property that inverting the initial direction of the velocity vector and keeping the initial position only inverts the direction of motion but it does not change the solution trajectory. In applications, it is quite natural to search for the numerical methods that produce a reversible numerical flow when they are applied to a reversible differential equation [10]. The structure of time reversibility is preserved by symmetric integrators. Moreover, for Hamiltonian systems, when the long-term energy preservation of numerical methods is considered, the symmetry of numerical methods plays an essential role as pointed out by the authors in [2]. Hence the design and analysis of symmetric integrators is an important aspect in geometric numerical integration. This paper is concerned with multi-frequency symmetric integrators for the following multi-frequency and multidimensional oscillatory reversible differential equations

$$\begin{aligned} q''(t)+Mq(t)=f\big (q(t)\big ), \qquad q(t_0)=q_0,\ \ q'(t_0)=q'_0,\qquad t\in [t_0,t_{\mathrm {end}}], \end{aligned}$$

(1)

where $M$ is a $d\times d$ symmetric and positive semi-definite matrix which implicitly preserves the dominant frequencies of the system (1) and $f: \mathbb {R}^{d}\rightarrow \mathbb {R}^{d}$ is sufficiently smooth. The solution of (1) is a nonlinear multi-frequency oscillator given by the linear term $Mq$. These kind of problems arise in a wide variety of applications such as mechanics, astronomy, quantum physics, molecular dynamics, theoretical physics, semi-discrete wave equations via the method of lines.

Over the last one decade and earlier, some novel approaches to modifying the classical Runge–Kutta–Nyström (RKN) methods have been proposed for the single-frequency problem

$$\begin{aligned} q''(t)+\omega ^2q(t)=f\big (q(t)\big ), \qquad q(t_0)=q_0,\ \ q'(t_0)=q'_0,\qquad t\in [t_0,t_{\mathrm {end}}], \end{aligned}$$

(2)

where the main frequency $\omega >0$ may be known or accurately estimated in advance. For the related work to this topic, readers are referred to [1, 3–6, 8, 15, 16, 18] and references contained therein. All these methods have coefficients which are analytic functions of $\nu ^2$ ($\nu =h\omega$) and thus they cannot be applied to the multi-frequency and multidimensional oscillatory system (1). This point can be shown by the following nonlinear oscillator with two different frequencies [19]

$$\begin{aligned} \begin{array}{ll} q_1^{\prime \prime }+q_1=2\epsilon q_1q_2,\qquad \qquad \ q_1(0)=1,\ \ q'_1(0)=0,\\ q_2^{\prime \prime }+2q_2=\epsilon q_1^2+4\epsilon q_2^3,\qquad \ q_2(0)=1,\ \ q'_2(0)=0.\\ \end{array} \end{aligned}$$

(3)

It can be observed that such oscillators with coupled frequencies do not fit the scheme of (2) and thence all the methods for single-frequency problems given in previous publications are not directly applicable to the coupled oscillators. Moreover, the analysis and conclusions of the methods for single-frequency problems cannot be directly extended to multi-frequency integrators, which will be shown further by Remark 2.6 of this paper.

In order to solve (1) effectively, many researches have been done and readers are referred to [2, 12, 20–23, 26–29] for example. Among them, a standard form of multi-frequency extended Runge–Kutta–Nyström (ERKN) integrators is formulated in [28] and the corresponding order conditions are also derived in that paper based on a tri-colored rooted tree theory. Multi-frequency ERKN integrators exactly preserve the oscillatory feature of the unperturbed multi-frequency oscillators $q''(t)+Mq(t)=0$, not only for the updates but also for the internal stages. Therefore, multi-frequency ERKN integrators are deserved to behave better than the classical RKN methods when applied to the multi-frequency and multidimensional oscillatory reversible system (1) and this point has been shown numerically by the numerical results in [28]. Symplectic and symmetric ERKN integrators are formulated in [29]. However, it should be noted that requiring a multi-frequency ERKN method to be symplectic and symmetric simultaneously brings many restrictions in the construction of numerical methods, which weakens the variety of symmetric multi-frequency ERKN integrators for the multi-frequency and multidimensional oscillatory reversible system (1). Moreover, symmetric methods themselves have excellent longtime behaviour when applied to reversible differential equations and a theoretical explanation of this property has been given in [10]. Therefore, symmetric integrators play a central role in geometric numerical integration of reversible differential equations. However, multi-frequency symmetric ERKN integrators have not been especially and well developed so far, and the research is required for the application of multi-frequency ERKN integrators as an efficient approach to solving the multi-frequency and multidimensional oscillatory reversible system (1). Motivated by the point stated above, this paper is devoted to the construction of explicit multi-frequency symmetric ERKN integrators.

We proceed as follows. We briefly overview the main results of multi-frequency ERKN integrators and derive the symmetry conditions of multi-frequency ERKN integrators in Sect. 2. Section 3 is devoted to proposing five novel practical explicit multi-frequency symmetric ERKN integrators based on the symmetry conditions of the multi-frequency ERKN integrators. In Sect. 4, we carry out five numerical experiments and the numerical results demonstrate the remarkable efficiency of the new integrators in comparison with some existing methods in the scientific literature. The concluding comments of this paper are presented in Sect. 5.

2 Multi-frequency symmetric ERKN integrators

2.1 Multidimensional ERKN integrators

In [28], multi-frequency ERKN integrators for solving (1) are formulated and their order conditions are also derived. Here we restate the main results of multi-frequency ERKN methods [28].

Definition 2.1

An $s$-stage multi-frequency ERKN integrator for solving (1) is defined by

$$\begin{aligned} Q_{i}&= \phi _{0}(c_{i}^{2}V)q_{n}+hc_{i}\phi _{1}(c_{i}^{2}V)q'_{n}+h^{2}\textstyle \sum \limits _{j=1}^{s}\bar{a}_{ij}(V)f(Q_{j}),\ \ \ i=1,\ldots ,s,\nonumber \\ q_{n+1}&= \phi _{0}(V)q_{n}+h\phi _{1}(V)q'_{n}+h^{2}\textstyle \sum \limits _{i=1}^{s}\bar{b}_{i}(V)f(Q_{i}),\\ q'_{n+1}&= -hM\phi _{1}(V)q_{n}+\phi _{0}(V)q'_{n}+h\textstyle \sum \limits _{i=1}^{s}b_{i}(V)f(Q_{i}),\nonumber \end{aligned}$$

(4)

where $c_i, \ i=1,\ldots ,s$ are real constants, $b_{i}(V)$, $\bar{b}_{i}(V),\ i=1,\ldots ,s$, and $\bar{a}_{ij}(V),\ i,j=1,\ldots ,s$ are matrix-valued functions of $V\equiv h^{2}M$, and

$$\begin{aligned} \phi _{j}(V):=\sum \limits _{k=0}^{\infty }\dfrac{(-1)^{k}V^{k}}{(2k+j)!},\qquad j=0,1,\ldots . \end{aligned}$$

(5)

Usually, the coefficients of (4) can be displayed in a Butcher tableau:

It is noted that when $V=\mathbf {0}_{d\times d}$, (4) reduces to the classical $s$-stage RKN method represented by the Butcher tableau

It can be observed from (4) that multi-frequency ERKN methods revise both the internal stages and updates of the classical RKN methods.

The next theorem gives the order conditions of multi-frequency ERKN methods [28].

Theorem 2.2

The necessary and sufficient conditions for an $s$-stage multi-frequency ERKN integrator to be of order $r$ are given by

$$\begin{aligned} \bar{b}^{T}(V)\Phi (\tau )&= \dfrac{\rho (\tau )!}{\gamma (\tau )}\phi _{\rho (\tau )+1}(V)+\mathcal {O}(h^{r-\rho (\tau )}),\ \ \ \rho (\tau )=1,\ldots ,r-1,\nonumber \\ b^{T}(V)\Phi (\tau )&= \dfrac{\rho (\tau )!}{\gamma (\tau )}\phi _{\rho (\tau )}(V)+\mathcal {O}(h^{r+1-\rho (\tau )}),\ \ \ \rho (\tau )=1,\ldots ,r, \end{aligned}$$

(6)

where $\tau$ is an extended Nyström tree associated with an elementary differential $\mathcal {F}(\tau )(q_{n})$ of the function $f(q)$ at $(q_{n})$.

The analysis of the order conditions based on a tri-colored rooted tree theory for the multi-frequency ERKN integrators can be found in [28].

In what follows, we are concerned with the stability and phase properties of the multi-frequency ERKN integrators. This has been analyzed in [24] and thence we just briefly recall here the definitions.

Consider the revised test equation:

$$\begin{aligned} y^{\prime \prime }(t)+\omega ^{2}y(t)=-\epsilon y(t)\qquad \mathrm {with} \qquad \omega ^{2}+ \epsilon >0, \end{aligned}$$

(7)

where $\omega$ represents an estimation of the dominant frequency $\lambda$ and $\epsilon =\lambda ^{2}-\omega ^{2}$ is the error of that estimation. Applying a multi-frequency ERKN integrator to (7) produces

$$\begin{aligned} \left( \begin{array}{l} q_{n+1}\\ hq_{n+1}^{\prime } \end{array} \right) =S(V,z)\left( \begin{array}{l} q_{n}\\ hq_{n}^{\prime } \end{array} \right) , \end{aligned}$$

where the stability matrix $S(V,z)$ is given by

$$\begin{aligned} S(V,z)=\left( \begin{array}{l@{\quad }l} \phi _{0}(V)-z\bar{b}^{T}(V)N^{-1}\phi _{0}(c^{2}V) &{} \phi _{1}(V)-z\bar{b} ^{T}(V)N^{-1}\big (c\cdot \phi _{1}(c^{2}V)\big )\\ -V\phi _{1}(V)-zb^{T}(V)N^{-1}\phi _{0}(c^{2}V) &{} \phi _{0}(V)-zb^{T} (V)N^{-1}\big (c\cdot \phi _{1}(c^{2}V)\big ) \end{array}\right) \end{aligned}$$

with $V=h^{2}\omega ^{2},\ z=h^{2}\epsilon$ and $N=I+z\bar{A}(V)$.

Definition 2.3

(See [24].) $R_{s}=\{(V,z)|\ V>0\ and \ \rho (S)<1\}$ is called the stability region of a multi-frequency ERKN integrator and $R_{p}=\{(V,z)|\ V>0,\ \rho (S)=1\ and \ \mathrm {tr}(S)^{2}<4\det (S)\}$ is called the periodicity region of a multi-frequency ERKN integrator.

Definition 2.4

(See [24].) The quantities

$$\begin{aligned} \phi (\eta )=\eta -\arccos \left( \dfrac{\mathrm {tr}(S(V,z))}{2\sqrt{\det (S(V,z))}}\right) ,\ \ d(\eta )=1-\sqrt{\det (S(V,z))} \end{aligned}$$

are called the dispersion error and the dissipation error of the multi-frequency ERKN integrators, respectively, where $\eta =h\lambda$. Accordingly, a method is said to be dispersive of order $r$ and dissipative of order $s$, if $\phi (\eta )=O(\eta ^{r+1})$ and $d(\eta )=O(\eta ^{s+1})$, respectively. If $\phi (\eta )=0$ and $d(\eta )=0$, then the method is said to be zero dispersive and zero dissipative, respectively.

2.2 Symmetry conditions of multi-frequency ERKN integrators

In this subsection, we analyze and derive the symmetry conditions of multi-frequency ERKN integrators.

An integrator $y_{n+1}=\Phi _h(y_n)$ is symmetric if exchanging $y_n\leftrightarrow y_{n+1}$ and $h\leftrightarrow -h$ does not change the integrator.

Theorem 2.5

An $s$-stage multi-frequency ERKN integrator for integrating (1) is symmetric if its coefficients satisfy

$$\begin{aligned} c_i&= 1-c_{s+1-i},\quad \ i=1,2,\ldots ,s,\nonumber \\ \bar{b}_{i}(V)&= \phi _{1}(V)b_{s+1-i}(V)-\phi _{0}(V)\bar{b}_{s+1-i}(V),\quad i=1,2,\ldots ,s,\nonumber \\ \bar{a}_{ij}(V)&= \phi _{0}(c_{s+1-i}^{2}V)\bar{b}_{j}(V)-c_{s+1-i}\phi _{1}(c_{s+1-i}^{2}V)b_{j}(V)+\bar{a}_{s+1-i,s+1-j}(V),\nonumber \\&\quad i, j=1,2,\ldots ,s. \end{aligned}$$

(8)

Proof

(a) For an $s$-stage multi-frequency ERKN integrator (4), exchanging $(q_{n},q'_{n})$ $\leftrightarrow (q_{n+1},q'_{n+1})$ and replacing $h$ by $-h$ yields

$$\begin{aligned}&\hat{Q}_{i} = \phi _0(c_i^2 V)q_{n+1}-hc_i\phi _1(c_i^2 V)q'_{n+1}+h^2\sum \limits _{j=1}^{s}\bar{a}_{ij}(V)f(\hat{Q}_{j}),\ \ i=1,2,\ldots ,s,&\nonumber \\&q_{n} = \phi _0(V)q_{n+1}-h\phi _1(V)q'_{n+1}+h^2\sum \limits _{i=1}^s\bar{b}_i(V)f(\hat{Q}_{i}),&\nonumber \\&q'_{n} = hM\phi _1(V)q_{n+1}+\phi _0(V)q'_{n+1}-h\sum \limits _{i=1}^sb_i(V)f(\hat{Q}_{i}).&\end{aligned}$$

(9)

It follows from (5) that $\phi _0(V)+V\phi ^2_1(V)=I$. According to this property and (9), we obtain

$$\begin{aligned} \hat{Q}_{i}&= \phi _0((1-c_i)^2 V)q_n+h(1-c_i)\phi _1((1-c_i)^2 V)q'_n+h^2\sum \limits _{j=1}^{s} \big [\phi _0(c_i^2 V)\big (\phi _1(V)b_j(V)\nonumber \\&\quad -\phi _0(V)\bar{b}_j(V)\big )-c_i\phi _1(c_i^2 V)\big (V\phi _1(V)\bar{b}_j(V)+ \phi _0(V)b_j(V)\big )+\bar{a}_{ij}(V)\big ]f(\hat{Q}_{j}), \nonumber \\ q_{n+1}&= \phi _0(V)q_n+h\phi _1(V)q'_n+h^2\sum \limits _{i=1}^s\big [\phi _{1}(V)b_{i}(V)-\phi _{0}(V)\bar{b}_{i}(V)\big ]f(\hat{Q}_{i}),\nonumber \\ q'_{n+1}&= -hM\phi _1(V)q_n+\phi _0(V)q'_n+h\sum \limits _{i=1}^s\big [V\phi _{1}(V)\bar{b}_{i}(V)+\phi _{0}(V)b_{i}(V)\big ]f(\hat{Q}_{i}). \end{aligned}$$

(10)

Replace all indices $i$ and $j$ in (10) by $s + 1 - i$ and $s + 1 - j$, respectively, and then an $s$-stage multi-frequency ERKN integrator is symmetric if its coefficients satisfy the following conditions

$$\begin{aligned} c_i&= 1-c_{s+1-i},\quad \ i=1,2,\ldots ,s,\nonumber \\ \bar{b}_{i}(V)&= \phi _{1}(V)b_{s+1-i}(V)-\phi _{0}(V)\bar{b}_{s+1-i}(V),\quad \ i=1,2,\ldots ,s,\nonumber \\ b_{i}(V)&= V\phi _{1}(V)\bar{b}_{s+1-i}(V)+\phi _{0}(V)b_{s+1-i}(V), \quad i=1,2,\ldots ,s,\nonumber \\ \bar{a}_{ij}(V)&= \phi _{0}(c_{s+1-i}^{2}V)\bar{b}_{j}(V)-c_{s+1-i}\phi _{1}(c_{s+1-i}^{2}V)b_{j}(V)+\bar{a}_{s+1-i,s+1-j}(V),\nonumber \\&\quad i,\ j=1,2,\ldots ,s. \end{aligned}$$

(11)

(b) We now show that the second condition in (11) implies the third one.

For the symmetric and positive semi-definite matrix $M$, there exists an orthogonal matrix $P$ and a positive semi-definite diagonal matrix $\tilde{M}$ such that

$$\begin{aligned} M=P^T \tilde{M} P. \end{aligned}$$

Then we have

$$\begin{aligned} \bar{b}_{i}(V)&= \phi _{1}(V)b_{s+1-i}(V)-\phi _{0}(V)\bar{b}_{s+1-i}(V)\Leftrightarrow \bar{b}_{i}(\tilde{V})\nonumber \\&= \phi _{1}(\tilde{V})b_{s+1-i}(\tilde{V})-\phi _{0}(\tilde{V})\bar{b}_{s+1-i}(\tilde{V}),\nonumber \\ b_{i}(V)&= V\phi _{1}(V)\bar{b}_{s+1-i}(V)+\phi _{0}(V)b_{s+1-i}(V)\Leftrightarrow b_{i}(\tilde{V})\nonumber \\&= \tilde{V}\phi _{1}(\tilde{V})\bar{b}_{s+1-i}(\tilde{V})+\phi _{0}(\tilde{V})b_{s+1-i}(\tilde{V}), \end{aligned}$$

where $i=1,2,\ldots ,s$ and $\tilde{V}=h^2 \tilde{M}$.

With this result, in order to prove that the second condition in (11) implies the third one for the matrix $V$, we just need to verify that conclusion is true when $V$ is a nonnegative real number.

In fact, let $V=x\ge 0$. When $V=x>0$, the second condition in (11) becomes

$$\begin{aligned}&\bar{b}_{i}(x)=\phi _{1}(x)b_{s+1-i}(x)-\phi _{0}(x)\bar{b}_{s+1-i}(x),\ \ \ i=1,2,\ldots ,s, \end{aligned}$$

(12)

which delivers

$$\begin{aligned} \bar{b}_{s+1-i}(x)&= \phi _{1}(x)b_{i}(x)-\phi _{0}(x)\bar{b}_{i}(x)\nonumber \\&= \phi _{1}(x)b_{i}(x)-\phi _{0}(x)\big (\phi _{1}(x)b_{s+1-i}(x) -\phi _{0}(x)\bar{b}_{s+1-i}(x)\big )\\&= \phi _{1}(x)b_{i}(x)-\phi _{0}(x)\phi _{1}(x)b_{s+1-i}(x)\!+\!\phi _{0}^2(x)\bar{b}_{s+1-i}(x),\ i=1,2,\ldots ,s.\quad \nonumber \end{aligned}$$

(13)

Using $\phi _0^2(x)+x\phi _1^2(x)=1$, it follows from (13) that

$$\begin{aligned} \phi _{1}(x)b_{i}(x)-\phi _{0}(x)\phi _{1}(x)b_{s+1-i}(x)&= \big (1-\phi _{0}^2(x)\big )\bar{b}_{s+1-i}(x)\nonumber \\&= x\phi _1^2(x)\bar{b}_{s+1-i}(x),\ \ \ i=1,2,\ldots ,s, \end{aligned}$$

which can be simplified as (the third condition in (11) when $V=x$)

$$\begin{aligned} b_{i}(x)=x\phi _{1}(x)\bar{b}_{s+1-i}(x)+\phi _{0}(x)b_{s+1-i}(x),\ \ \ \ \ i=1,2,\ldots ,s. \end{aligned}$$

(14)

On the other hand, it follows from the condition (14) that

$$\begin{aligned} b_{s+1-i}(x)&= x\phi _{1}(x)\bar{b}_{i}(x)+\phi _{0}(x)b_{i}(x)\\&= x\phi _{1}(x)\bar{b}_{i}(x)+\phi _{0}(x)\big (x\phi _{1}(x)\bar{b}_{s+1-i}(x)+\phi _{0}(x)b_{s+1-i}(x)\big )\nonumber \\&= x\phi _{1}(x)\bar{b}_{i}(x)\!+\!x\phi _{0}(x)\phi _{1}(x)\bar{b}_{s+1-i}(x)\!+\!\phi _{0}^2(x)b_{s+1-i}(x),\; i\!\!=\!\!1,2,\ldots ,s. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} x\phi _{1}^2(x)b_{s+1-i}(x)=x\phi _{1}(x)\bar{b}_{i}(x)+x\phi _{0}(x)\phi _{1}(x)\bar{b}_{s+1-i}(x),\ \ \ \ \ i=1,2,\ldots ,s, \end{aligned}$$

which give (12). The above analysis shows that the second condition in (11) is equivalent to the third one when $V=x>0$.

When $V=x=0$, the second condition in (11) becomes

$$\begin{aligned} \bar{b}_{i}(0)=b_{s+1-i}(0)-\bar{b}_{s+1-i}(0),\ \ \ i=1,2,\ldots ,s \end{aligned}$$

(15)

and the third one is

$$\begin{aligned} b_{i}(0)=b_{s+1-i}(0), \ \ \ i=1,2,\ldots ,s. \end{aligned}$$

(16)

It follows from (15) that

$$\begin{aligned} b_{s+1-i}(0)=\bar{b}_{i}(0)+\bar{b}_{s+1-i}(0),\ \ b_{i}(0)=\bar{b}_{s+1-i}(0)+\bar{b}_{i}(0),\ \ i=1,2,\ldots ,s. \end{aligned}$$

This shows $b_{i}(0)=b_{s+1-i}(0)$, namely, the second condition in (11) implies the third one when $V=x=0$.

In conclusion, the symmetry conditions in (11) can be simplified as (8). The proof is complete. $\square$

Remark 2.6

We note that [1] gives the symmetry conditions of single-frequency methods for the single-frequency problem (2). However, it is very important to note that the symmetry conditions of multi-frequency ERKN integrators when applied to a multi-frequency problem and their proof are different from those of single-frequency methods in [1]. This fact shows that the analysis and conclusions of single-frequency methods cannot be directly applied to multi-frequency integrators. It is also noted that the symmetry conditions (11) are derived in [29] but they can be simplified as (8) as shown in the proof of Theorem (2.5).

2.3 Approximate energy conservation

If $f(q)$ in (1) is the negative gradient of a differentiable function $U(q)$, then the system (1) is a multi-frequency and multidimensional oscillatory Hamiltonian system with the Hamiltonian

$$\begin{aligned} H(q,q')=\frac{1}{2}q'^{T}q'+\dfrac{1}{2}q^{T}Mq+U(q). \end{aligned}$$

With regard to the approximate energy conservation of multi-frequency ERKN integrators, we have the following result.

Theorem 2.7

Under the local assumptions of $q_{n-1}=q(t_{n-1})$ and $q_{n-1}^{\prime }=q^{\prime }(t_{n-1})$, the energy of a $r$th order multi-frequency ERKN integrator satisfies

$$\begin{aligned} H(q_n,q_n')=H(q_0,q'_0)+\mathcal {O}(h^{r+1}). \end{aligned}$$

(17)

Proof

A $r$th order multi-frequency ERKN integrator means

$$\begin{aligned} q_{n}-q(t_{n})=\mathcal {O}(h^{r+1}),\quad q_{n}^{\prime }-q^{\prime }(t_{n})=\mathcal {O}(h^{r+1}). \end{aligned}$$

Accordingly, we have

$$\begin{aligned} H(q_n,q_n')&= \frac{1}{2}q_n'^{T}q_n'+\dfrac{1}{2}q_n^{T}Mq_n+U(q_n)\\&= \frac{1}{2}\big (q^{\prime }(t_{n})+\mathcal {O}(h^{r+1})\big )^{T}\big (q^{\prime }(t_{n})+\mathcal {O}(h^{r+1})\big )\\&+\dfrac{1}{2}\big (q(t_{n})+\mathcal {O}(h^{r+1})\big )^{T}M\big (q(t_{n})\!+\!\mathcal {O}(h^{r+1})\big )+U\Big (\big (q(t_{n})\!+\!\mathcal {O}(h^{r+1})\big )\Big )\\&= \frac{1}{2}q'(t_{n})^{T}q'(t_{n})+\dfrac{1}{2}q(t_{n})^{T}Mq(t_{n})+U\big (q(t_{n})\big )+\mathcal {O}(h^{r+1})\\&= H(q(t_{n}),q'(t_{n}))+\mathcal {O}(h^{r+1})=H(q_0,q'_0)+\mathcal {O}(h^{r+1}). \end{aligned}$$

$\square$

3 Practical explicit multi-frequency symmetric ERKN integrators

In this section we only consider explicit multi-frequency symmetric ERKN integrators since explicit integrators avoid the necessity of solving a system of nonlinear equations at each step.

3.1 One-stage explicit symmetric integrators

Consider the one-stage explicit multi-frequency ERKN integrator displayed in a Butcher tableau

It follows from the symmetry conditions (8) that this integrator is symmetric if

$$\begin{aligned}&c_1=1/2,\quad \bar{b}_{1}(V)=\phi _{1}(V)b_{1}(V)-\phi _{0}(V)\bar{b}_{1}(V),\nonumber \\&\phi _{0}(c_{1}^{2}V)\bar{b}_{1}(V)-c_{1}\phi _{1}(c_{1}^{2}V)b_{1}(V)=\mathbf {0}_{d\times d}. \end{aligned}$$

(18)

By (6), the necessary and sufficient conditions for this method of order two are

$$\begin{aligned}&b_1(V)=\phi _1(V)+O(h^2),\quad b_1(V)c_1=\phi _2(V)+O(h),\quad \bar{b}_1(V)=\phi _2(V)+O(h).\nonumber \\ \end{aligned}$$

(19)

By (19), we choose $b_1(V)=\phi _1(V)$. Then solving the second condition in (18) yields that $\bar{b}_1(V)=\phi _2(V)$ and under the results of $b_1(V)$ and $\bar{b}_1(V)$, it is verified that the third condition in (18) is satisfied. This gives an explicit multi-frequency symmetric ERKN method of order two presented by

$$\begin{aligned} Q_{1}&= \phi _{0}(V/4)q_{n}+\frac{h}{2}\phi _{1}(V/4)q'_{n},\\ q_{n+1}&= \phi _{0}(V)q_{n}+h\phi _{1}(V)q'_{n}+h^{2}\phi _2(V)f(Q_{1}),\\ q'_{n+1}&= -hM\phi _{1}(V)q_{n}+\phi _{0}(V)q'_{n}+h\phi _1(V)f(Q_{1}), \end{aligned}$$

which is denoted by MSERKN1s2. It is noted that MSERKN1s2 reduces to the Störmer-Verlet formula when $V\rightarrow \mathbf {0}_{d\times d}.$

3.2 Two-stage explicit symmetric integrators

We turn to considering the two-stage explicit multi-frequency symmetric ERKN integrator denoted by the Butcher tableau

It follows from (6) that the necessary and sufficient conditions for two-stage explicit multi-frequency ERKN integrators of order two are

$$\begin{aligned} b_1(V)+b_2(V)=\phi _1(V)+O(h^2),\quad b_1(V)c_1+b_2(V)c_2=\phi _2(V)+O(h),\nonumber \\ \quad \bar{b}_1(V)+\bar{b}_2(V)=\phi _2(V)+O(h).\qquad \quad \end{aligned}$$

(20)

Solving the symmetric conditions (8) of this two-stage explicit integrator as well as the first condition in (20) yields

$$\begin{aligned} c_1&= 1-c_2,\nonumber \\ b_1(V)&= \bar{b}_1(V)\phi _0(c_2^2V)\big (c_2\phi _1(c_2^2V)\big )^{-1}, \quad b_2(V)=\bar{b}_2(V)\phi _0(c_1^2V)\big (c_1\phi _1(c_1^2V)\big )^{-1},\nonumber \\ \bar{b}_2(V)&= -c_1c_2\phi _1(V)\phi _1(c_1^2V)\phi _1(c_2^2V)\nonumber \\&\quad \Big (c_1\phi _0(V)\phi _0(c_2^2V)\phi _1(c_1^2V)-\phi _0(c_1^2V) \big (\phi _0(c_2^2V)\phi _1(V)+c_2\phi _1(c_2^2V)\big )\Big )^{-1},\nonumber \\ \bar{b}_1(V)&= b_2(V)\phi _1(V)-\bar{b}_2(V)\phi _0(V),\nonumber \\ \bar{a}_{21}(V)&= \phi _{0}(c_{1}^{2}V)\bar{b}_{1}(V)-c_{1}\phi _{1}(c_{1}^{2}V)b_{1}(V). \end{aligned}$$

(21)

A careful calculation can verify that the integrators determined by (21) are a family of explicit multi-frequency symmetric ERKN integrators of order two, where $c_2$ is a free parameter. We note that the coefficients $b_1(V),\ b_2(V),\ \bar{b}_2(V)$ are well-defined even for a singular matrix $V$ and their Taylor series expansions are

$$\begin{aligned} b_1(V)&= \frac{1}{2}I+\frac{6c_1-5}{24}V+\frac{1+10c_1-30c_1^2+20c_1^3}{240}V^2 +\cdots ,\\ b_2(V)&= \frac{1}{2}I+\frac{1-6c_1}{24}V+\frac{1-10c_1+30c_1^2-20c_1^3}{240}V^2 +\cdots ,\\ \bar{b}_2(V)&= \frac{c_1}{2}I+\frac{c_1(1-6c_1+4c_1^2)}{24}V+\frac{c_1(3-30c_1+100c_1^2-120c_1^3+48c_1^4)}{720}V^2 +\cdots . \end{aligned}$$

We give an example. We chose $c_{2}$ such that the coefficient of the first term in the Taylor expansion of the dissipation error $d(\eta )$ of this integrator is minimal. This yields $c_{2}=\frac{3+\sqrt{3}}{6}$ and this case gives a practical multi-frequency symmetric ERKN integrator of order two, which is denoted by MSERKN2s2.

We then are concerned with two-stage explicit multi-frequency symmetric ERKN integrator with FSAL properties (the last evaluation at any step is the same as the first evaluation at the next step), which can be expressed in Butcher tableau as

According to the symmetric conditions (8) and the second order conditions (20), we choose

$$\begin{aligned}&c_1=0,\ \ c_2=1,\ \ \bar{a}_{21}(V)= \phi _2(V),\ \ \bar{b}_1(V)=\phi _2(V),\ \ \bar{b}_2(V)=\mathbf {0}_{d\times d},\nonumber \\&b_1(V)=\phi _0(V)\phi _2(V)\phi _1(V)^{-1},\ \ b_2(V)=\phi _2(V)\phi _1(V)^{-1}, \end{aligned}$$

(22)

which gives the following multi-frequency symmetric ERKN integrator of order two (denoted by FMSERKN2s2)

$$\begin{aligned} q_{n+1}&= \phi _{0}(V)q_{n}+h\phi _{1}(V)q'_{n}+h^{2}\phi _2(V)f(q_{n}),\nonumber \\ q'_{n+1}&= -hM\phi _{1}(V)q_{n}+\phi _{0}(V)q'_{n}+h\phi _2(V)\phi _1(V)^{-1}\big (\phi _0(V)f(q_{n})+f(q_{n+1})\big ). \end{aligned}$$

It is noted that the coefficients $b_1(V),\ b_2(V)$ are well-defined even for a singular matrix $V$ and their Taylor series expansions are

$$\begin{aligned} b_1(V)&= \frac{1}{2}I-\frac{5}{24}V+\frac{1}{240}V^2-\frac{5}{8064}V^3 +\cdots ,\\ b_2(V)&= \frac{1}{2}I+\frac{1}{24}V+\frac{1}{240}V^2+\frac{17}{40320}V^3 +\cdots . \end{aligned}$$

3.3 Three-stage explicit symmetric integrators

A three-stage explicit multi-frequency ERKN integrator can be denoted by

Solving the symmetric conditions (8) of this three-stage explicit integrator yields

$$\begin{aligned}&c_3=1-c_1,\ \ c_2=1/2,\nonumber \\&\bar{b}_1(V)=c_3b_1(V) \phi _1(c_3^2V)\big (\phi _0(c_3^2V)\big )^{-1},\nonumber \\&\bar{b}_2(V)=c_2b_2(V) \phi _1(c_2^2V)\big (\phi _0(c_2^2V)\big )^{-1},\nonumber \\&\bar{b}_3(V)=c_1b_3(V) \phi _1(c_1^2V)\big (\phi _0(c_1^2V)\big )^{-1},\nonumber \\&b_3(V)=\ c_3b_1(V) \phi _0(c_1^2V)\phi _1(c_3^2V)\Big ( \phi _0(c_3^2V)\nonumber \\&\quad \times \big (\phi _0(c_1^2V)\phi _1(V)-c_1\phi _0(V)\phi _1(c_1^2V)\big )\Big )^{-1},\nonumber \\&\bar{a}_{21}(V)= \phi _{0}(c_{2}^{2}V)\bar{b}_{1}(V)-c_{2}\phi _{1}(c_{2}^{2}V)b_{1}(V),\nonumber \\&\bar{a}_{31}(V)= \phi _{0}(c_{1}^{2}V)\bar{b}_{1}(V)-c_{1}\phi _{1}(c_{1}^{2}V)b_{1}(V),\nonumber \\&\bar{a}_{32}(V)= \phi _{0}(c_{1}^{2}V)\bar{b}_{2}(V)-c_{1}\phi _{1}(c_{1}^{2}V)b_{2}(V). \end{aligned}$$

(23)

The necessary and sufficient conditions for this integrator of order four are given by (6)

$$\begin{aligned} \begin{array}{l} b^T(V)(e\otimes I)=\phi _1(V)+\mathcal O(h^4),\quad b^T (V)(c\otimes I)=\phi _2(V)+\mathcal O(h^3),\\ b^T (V)\big ((c^2)\otimes I\big )=2\phi _3(V)+\mathcal O(h^2),\quad b^T (V)\big ((c^3)\otimes I\big )=6\phi _4(V)+\mathcal O(h),\\ b^T(V)\big (\bar{A}(\mathbf {0})(e\otimes I)\big )=\phi _3(V)+\mathcal O(h^2),\quad b^T(V)\big (\bar{A}(\mathbf {0})(c \otimes I)\big )=\phi _4(V)+\mathcal O(h),\\ b^T(V)\big ((c\otimes I)\cdot ( \bar{A}(\mathbf {0})(e \otimes I))\big )=3\phi _4(V)+\mathcal O(h),\quad \bar{b}^T(V)(e\otimes I)=\phi _2(V)+\mathcal O(h^3),\\ \bar{b}^T(V)(c\otimes I)=\phi _3(V)+\mathcal O(h^2),\quad \bar{b}^T(V)\big ((c^2)\otimes I\big )=2\phi _4(V)+\mathcal O(h),\\ \bar{b}^T(V)\big (\bar{A}(\mathbf {0})(e \otimes I)\big )=\phi _4(V)+\mathcal O(h), \end{array} \end{aligned}$$

(24)

where $I$ is a $d\times d$ identity matrix and $e=(1,1,1)^T.$

3.3.1 Case one

We solve the first two equations with the terms $\mathcal {O}(h^{4})$, $\mathcal {O}(h^{3})$ ignored

$$\begin{aligned} b^T(V)(e\otimes I)=\phi _1(V),\ \ \ b^T (V)(c\otimes I)=\phi _2(V) \end{aligned}$$

and obtain

$$\begin{aligned}&b_1(V)=\frac{c_2b_3(V)-c_3b_3(V)-c_2\phi _1(V)+ \phi _2(V)}{c_1-c_2},\end{aligned}$$

(25)

$$\begin{aligned}&b_2(V)=\frac{c_1b_3(V)-c_3b_3(V)-c_1\phi _1(V) +\phi _2(V)}{c_2-c_1}. \end{aligned}$$

(26)

Based on the formula (25) and the result of $b_3(V)$ in (23), we obtain

$$\begin{aligned} b_1(V)=&\phi _0(c_3^2V)(\phi _0(c_1^2V)\phi _1(V)-c_1\phi _0(V)\phi _1(c_1^2V))(\phi _1(V)-2\phi _2(V))\nonumber \\&\quad \times \Big (c_1(-1+2c_1)\phi _0(V)\phi _0(c_3^2V)\phi _1(c_1^2V)+\phi _0(c_1^2V)\nonumber \\&\quad \times \big ((1-2c_1)\phi _0(c_3^2V)\phi _1(V)+(1-2c_3)c_3\phi _1(c_3^2V)\big )\Big )^{-1}.\qquad \quad \end{aligned}$$

(27)

Inserting (23), (26) and (27) into the order conditions (24) gives that $c_1=\frac{4+2 \root 3 \of {2}+ \root 3 \of {4}}{12}$. Then the value of $c_1$ as well as (23), (26) and (27) determines a three-stage explicit multi-frequency symmetric ERKN integrator of order four (denoted by 1MSERKN3s4).

Let $a=\root 3 \of {2},\ b=\root 3 \of {4}$ and the Taylor series expansions (the first four terms) of $b_1(V),\ b_3(V),\ \bar{b}_1(V),\ \bar{b}_2(V),\ \bar{b}_3(V)$ are

$$\begin{aligned} b_1(V)&= \left( \frac{143\, a}{4{,}665{,}600} + \frac{359\, b}{6{,}531{,}840} - \frac{2{,}431}{16{,}329{,}600}\right) \, V^3 + \left( \frac{271}{45{,}360} - \frac{137}{90{,}720\, b} - \frac{b}{560}\right) V^2\, \\&+ \left( \frac{b}{60} - \frac{a}{120} - \frac{41}{360}\right) \, V + \frac{4+2a+b}{6}I,\\ b_3(V)&= \left( - \frac{3{,}859\, a}{32{,}659{,}200} - \frac{613\, b}{6{,}531{,}840} - \frac{2{,}431}{16{,}329{,}600}\right) \, V^3 + \left( \frac{871\, a}{181{,}440} + \frac{19\, b}{5{,}040} + \frac{271}{45{,}360}\right) V^2\, \\&+ \left( - \frac{11\, a}{120} - \frac{b}{15} - \frac{41}{360}\right) \, V + \frac{4+2a+b}{6}I,\\ \bar{b}_1(V)&= \left( \frac{139\, a}{32{,}659{,}200} + \frac{481\, b}{65{,}318{,}400} - \frac{619}{32{,}659{,}200}\right) \, V^3 + \left( \frac{37}{36{,}288} - \frac{b}{2{,}880} - \frac{13\, a}{72{,}576}\right) V^2\, \\&+ \left( \frac{a}{720} + \frac{b}{144} - \frac{7}{240}\right) \, V + \frac{4+a}{12}I,\\ \bar{b}_2(V)&= \, \left( \frac{11\, a}{1{,}020{,}600} + \frac{149\, b}{32{,}659{,}200} + \frac{107}{8{,}164{,}800}\right) V^3 - \, \left( \frac{b}{3{,}360} + \frac{23}{18{,}144\, b} + \frac{59}{90{,}720}\right) V^2\\&+\, \left( \frac{a}{45} + \frac{b}{90} + \frac{1}{60}\right) V - \frac{{\left( a + 1\right) }^2 }{6}I,\\ \bar{b}_3(V)&= \left( - \frac{491\, a}{32{,}659{,}200} - \frac{779\, b}{65{,}318{,}400} - \frac{619}{32{,}659{,}200}\right) \, V^3 + \left( \frac{59\, a}{72{,}576} + \frac{13\, b}{20{,}160} + \frac{37}{36{,}288}\right) \, V^2 \\&+ \left( - \frac{17\, a}{720} - \frac{13\, b}{720} - \frac{7}{240}\right) \, V + \frac{4+3a+b}{12}I. \end{aligned}$$

3.3.2 Case two

Similarly, according to the result of $b_3(V)$ in (23) and the following two equations [obtained by modifying some conditions in (24)]

$$\begin{aligned} b^T(V)(e\otimes I)=\phi _1(V),\ \ \ b^T (V)(c^2\otimes I)=2\phi _3(V), \end{aligned}$$

we obtain

$$\begin{aligned} b_1(V)&= -\phi _0(c_3^2V)(\phi _0(c_1^2V)\phi _1(V)-c_1\phi _0(V)\phi _1(c_1^2V))(c_2^2\phi _1(V)-2\phi _3(V))\nonumber \\&\quad \times \Big ((c_1^2-c_2^2)(-1+c_3)\phi _0(V)\phi _0(c_3^2V)\phi _1(c_1^2V)+\,\,\phi _0(c_1^2V)\nonumber \\&\quad \times \big ((c_1^2-c_2^2)\phi _0(c_3^2V)\phi _1(V) +c_3(c_3^2-c_2^2)\phi _1(c_3^2V)\big )\Big )^{-1},\nonumber \\ b_2(V)&= \frac{(c_3^2-c_1^2)b_3(V)+c_1^2\phi _1(V) -2\phi _3(V)}{c_1^2-c_2^2}. \end{aligned}$$

(28)

Inserting (23) and (28) into the fourth order conditions (24) yields that $c_3=\frac{8-2 \root 3 \of {2}- \root 3 \of {4}}{12}$ and then we obtain a three-stage explicit multi-frequency symmetric ERKN integrator of order four determined by (23) and (28). Let $a=\root 3 \of {2},\ b=\root 3 \of {4}$ and the Taylor series expansions (the first four terms) of $b_1(V),\ b_3(V),\ \bar{b}_1(V),\ \bar{b}_2(V),\ \bar{b}_3(V)$ are

$$\begin{aligned} b_1(V)&= \left( - \frac{247\, a}{60{,}480} - \frac{73\, b}{48{,}384} - \frac{7}{1{,}440}\right) \, V^3 + \left( \frac{17\, a}{1{,}890} + \frac{25\, b}{12{,}096} + \frac{523}{30{,}240}\right) V^2 \\&\quad + \left( \frac{b}{120} - \frac{a}{40} - \frac{2}{15}\right) \, V + \frac{4+2a+b}{6}I, \\ b_3(V)&= \left( - \frac{953\, a}{181{,}440} - \frac{2377\, b}{725{,}760} - \frac{1}{162}\right) \, V^3 + \left( \frac{31\, a}{1{,}890} + \frac{643\, b}{60{,}480} + \frac{593}{30{,}240}\right) V^2 \\&\quad - \left( \frac{13\, a}{120}+ \frac{3\, b}{40} + \frac{2}{15}\right) \, V + \frac{4+2a+b}{6}I,\\ \bar{b}_1(V)&= \left( - \frac{20{,}681\, a}{14{,}515{,}200} - \frac{8{,}843\, b}{43{,}545{,}600} - \frac{6{,}913}{4{,}354{,}560}\right) V^3\\&\quad + \left( \frac{199\, a}{60{,}480} + \frac{b}{8{,}640} + \frac{299}{60{,}480}\right) V^2\,\\&\quad + \left( \frac{5\, b}{864} - \frac{11\, a}{2{,}160} - \frac{79}{2{,}160}\right) \, V + \frac{4+a}{12}I,\\ \bar{b}_2(V)&= \, \left( \frac{881\, a}{226{,}800} + \frac{3{,}629\, b}{1{,}814{,}400}+ \frac{8{,}171}{1{,}814{,}400}\right) V^3 \\&\quad - \, \left( \frac{5\, a}{504} + \frac{5\, b}{1{,}008} + \frac{29}{2{,}520}\right) V^2 +\, \left( \frac{7\, a}{180} + \frac{7\, b}{360} + \frac{13}{360}\right) V - \frac{{\left( a + 1\right) }^2\, }{6}I,\\ \bar{b}_3(V)&= \left( - \frac{3{,}967\, a}{1{,}612{,}800} - \frac{11{,}179\, b}{6{,}220{,}800} - \frac{64{,}027}{21{,}772{,}800}\right) V^3\\&\quad + \left( \frac{401\, a}{60{,}480} + \frac{293\, b}{60{,}480} + \frac{481}{60{,}480}\right) \, V^2\\&\quad +\,\, \left( - \frac{73\, a}{2{,}160} - \frac{109}{2{,}160\, a} - \frac{89}{2{,}160}\right) \, V + \frac{4+3a+b}{12}I. \end{aligned}$$

3.4 Stability and phase properties

The stability regions for the new integrators are depicted in Fig. 1 and it can be observed that the stability region of MSERKN2s2 is smaller than those of the others.

Fig. 1

Stability regions (shaded regions) for the obtained integrators

The dissipation errors and dispersion errors of the new integrators are as follows.

• MSERKN1s2: $d(\eta ) =0$, $\phi (\eta ) = \dfrac{\epsilon (-2\epsilon +\omega ^{2})}{48(\epsilon +\omega ^{2})^{2}}\eta ^{3}+O(\eta ^{5})$.

• MSERKN2s2: $d(\eta ) =0$, $\phi (\eta ) = -\dfrac{\epsilon ^2}{24 (2+\sqrt{3})(\epsilon +\omega ^{2})^{2}}\eta ^{3}+O(\eta ^{5})$.

• FMSERKN2s2: $d(\eta ) =0$, $\phi (\eta ) = -\dfrac{ \epsilon }{24 (\epsilon +\omega ^{2})}\eta ^{3}+O(\eta ^{5})$.

• 1MSERKN3s4:

  $$\begin{aligned} d(\eta )&= 0,\\ \phi (\eta )&= - \dfrac{ \epsilon \Big (48(10-13\root 3 \of {2}+4\root 3 \of {4}) \epsilon ^2-4(46-49\root 3 \of {2}+10 \root 3 \of {4})\epsilon \omega ^2+(250-17\root 3 \of {2}-144 \root 3 \of {4})\omega ^4\Big )}{320(-2+2\root 3 \of {2}+ \root 3 \of {4})^4(-26+3\root 3 \of {2}+ 14\root 3 \of {4}) (\epsilon +\omega ^{2})^{3}}\eta ^{5}\nonumber \\&\quad +\,O(\eta ^{6}). \end{aligned}$$

• 2MSERKN3s4:

  $$\begin{aligned} d(\eta )&= 0,\\ \phi (\eta )&= - \epsilon \Big (48(-1658 + 215\root 3 \of {2}+871\root 3 \of {4}) \epsilon ^2-12(-12634 + 907\root 3 \of {2}\\&\quad +7241 \root 3 \of {4})\epsilon \omega ^2+5(4878 - 22165\root 3 \of {2}+14519 \root 3 \of {4})\omega ^4\Big ) \\&\quad \big /\Big (1920(-1+2\root 3 \of {2})(28-22\root 3 \of {2}+ \root 3 \of {4})^3 (\epsilon +\omega ^{2})^{3}\Big ) \eta ^{5}+O(\eta ^{6}). \end{aligned}$$

Remark 3.1

It is noted that when $V\rightarrow \mathbf {0}_{d\times d}$, the multi-frequency symmetric ERKN integrators derived in this section reduce to the classical symmetric RKN methods for solving the important second-order ODEs $q''=f(q)$. For example, as pointed out in Sect. 3.1 when $V\rightarrow \mathbf {0}_{d\times d}$, the the integrator MSERKN1s2 reduces to the Störmer-Verlet formula

$$\begin{aligned} Q_{1}&= q_{n}+\dfrac{h}{2}q_{n}^{\prime },\nonumber \\ q_{n+1}&= q_{n}+hq_{n}^{\prime }+\frac{h^{2}}{2}f(Q_{1}),\nonumber \\ q_{n+1}^{\prime }&= q_{n}^{\prime }+hf(Q_{1}), \end{aligned}$$

(29)

which is wildly employed in practice. When $V\rightarrow \mathbf {0}_{d\times d}$, the integrators 1MSERKN3s4 and 2MSERKN3s4 become the same symmetric RKN method displayed in the following Butcher tableau:

with $c_3=\frac{8-2 \root 3 \of {2}-\root 3 \of {4}}{12}$. This method has been given in [11, 14] and we denote it by SSRKN3s4.

Remark 3.2

We note that the order conditions together with the symmetry conditions for a higher-order multi-frequency ERKN integrator are huge. Therefore, the derivation of a high-order multi-frequency symmetric ERKN integrator based on the order conditions and the symmetry conditions is not easy. However, high-order symmetric integrators are easily obtained by symmetric composition methods. We do not discuss it further in this paper and refer the reader to V.3 of Chapter V in [10] for the details.

Remark 3.3

We do not discuss the non-autonomous problem $q''(t)+Mq(t)=f(t,q(t))$ in this paper because by appending the equation $t''=0$, it can be transformed into the autonomous form

$$\begin{aligned} u^{\prime \prime }(t) + \widetilde{M}u(t)=g\big (u(t)\big ), \end{aligned}$$

where

$$\begin{aligned} u(t)=\Big (t, q^T(t)\Big )^T,\ g\big (u(t)\big )=\Big (t, f^T\big (t,q(t)\big ) \Big )^T \end{aligned}$$

and

$$\begin{aligned} \widetilde{M}=\left( \begin{array}{ll} 1 &{} 0_{1\times d}\\ 0_{d\times 1} &{} M \\ \end{array} \right) . \end{aligned}$$

Therefore, all the analysis and the proposed integrators in this paper are applicable to the non-autonomous problem $q''(t)+Mq(t)=f\big (t,q(t)\big )$.

4 Numerical experiments

This section presents five numerical experiments and the numerical results show the remarkable efficiency of the new integrators as compared with some existing methods, The integrators for comparisons are:

• C: the symmetric and symplectic method of order two given in [7];

• E: the symmetric method of order two given in [9];

• ARKN3s4: the three-stage ARKN method of order four given in [25];

• SSRKN3s4: the three-stage symmetric and symplectic RKN method of order four given in [11, 14];

• MSERKN1s2: the one-stage multi-frequency symmetric ERKN integrator of order two derived in Sect. 3.1;

• MSERKN2s2: the two-stage multi-frequency symmetric ERKN integrator of order two derived in Sect. 3.2;

• FMSERKN2s2: the two-stage multi-frequency symmetric ERKN integrator of order two derived in Sect. 3.2;

• 1MSERKN3s4: the three-stage multi-frequency symmetric ERKN integrator of order four derived in Sect. 3.3;

• 2MSERKN3s4: the three-stage multi-frequency symmetric ERKN integrator of order four derived in Sect. 3.3.

In the numerical experiments, we use Taylor expansions (the first four terms) to evaluate the coefficients of the new integrators. In each experiment, we show the efficiency curve (accuracy versus the computational cost measured by the number of function evaluations required by each method), as well as the energy conservation for a Hamiltonian system. Since the exact solutions of some problems are not available, a reference solution is obtained by choosing a very small stepsize.

Problem 1. Consider a nonlinear wave equation (see [17])

$$\begin{aligned}&\dfrac{\partial ^2u}{\partial t^2}-gd(x)\dfrac{\partial ^2u}{\partial x^2}=\dfrac{1}{4}\lambda ^2(x,u)u,\ \ \ \ \ 0<x\le b,\ \ \ \ \ t>0,\\&\dfrac{\partial u}{\partial x}(t,0)=\dfrac{\partial u}{\partial x}(t,b)=0, \ \ \ u(0,x)=\sin \Big (\dfrac{\pi x}{b}\Big ),\ \ \ u_t(0,x)=-\dfrac{\pi }{b}\sqrt{g d(x)}\cos \Big (\dfrac{\pi x}{b}\Big ), \end{aligned}$$

where $d(x)$ is the depth function given by $d(x)=d_0\Big [2+\cos (\dfrac{2\pi x}{b})\Big ]$, $g$ denotes the acceleration of gravity, and $\lambda (x,u)$ is the coefficient of bottom friction defined by $\lambda (x,u)=\dfrac{g|u|}{C^2d(x)}$ with Chezy coefficient $C$.

By using second-order symmetric differences, this problem is converted into a system of ODEs

$$\begin{aligned}&\dfrac{d^2U}{dt^2}+MU=F(t,U),\ \ \ 0<t\le t_{end}.\nonumber \\&U(0)=\Big (\sin \Big (\dfrac{\pi x_1}{b}\Big ),\ldots ,\sin \Big (\dfrac{\pi x_N}{b}\Big )\Big )^T,\nonumber \\&U'(0)=\Big (-\dfrac{\pi }{b}\sqrt{g d(x_1)}\cos \Big (\dfrac{\pi x_1}{b}\Big ),\ldots ,-\dfrac{\pi }{b}\sqrt{gd(x_N)}\cos \Big (\dfrac{\pi x_N}{b}\Big )\Big )^T, \end{aligned}$$

(30)

where $x_i = i\Delta x$ with $\Delta x= \frac{1}{N}$, $U(t)$ denotes the $N$-dimensional vector with entries $u_i(t)\approx u(x_i,t)$,

$$\begin{aligned} M=\dfrac{g}{\Delta x^2}\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -2d(x_1)&{}d(x_1) &{}&{} &{}\\ d(x_2) &{}-2d(x_2) &{} d(x_2)&{} &{} \\ &{}\ddots &{}\ddots &{}\ddots &{} \\ &{}&{}d(x_{N-1}) &{}-2d(x_{N-1}) &{} d(x_{N-1})\\ &{} &{} &{}d(x_N)&{}-2d(x_N) \\ \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} F(t,U)=\left( \dfrac{1}{4}\lambda ^2(x_1,u_1)u_1, \ldots , \dfrac{1}{4}\lambda ^2(x_N,u_N)u_N\right) ^T. \end{aligned}$$

We choose $b=100,\ g=9.81,\ d_0=10,\ C=50$ for solving this problem. It is integrated in the interval $[0,100]$ with $N=32$ and the stepsizes $h=1/(2^{j}\times 3)$ for the methods C, E, MSERKN1s2, FMSERKN2s2, $h=1/(2^{j-1}\times 3)$ for MSERKN2s2, and $h=1/(2^{j})$ for the other methods, where $j=2,3,4,5$. The global errors are shown in Fig. 2a. The matrix $M$ is diagonalizable and its smallest eigenvalue is about 0.00 and the largest eigenvalue is about 10,472.80. It is noted that some errors of some methods are quite large and we do not plot the corresponding points in the figure. Similar situation occurs in the following problems.

Fig. 2

Results for Problem 1 (a) and Problem 2 (b). The logarithm of the global error ($GE$) over the integration interval against the logarithm of the number of function evaluations

Problem 2. Consider the wave equation

$$\begin{aligned} \begin{array}{ll} \dfrac{\partial ^2u}{\partial t^2}-a(x)\dfrac{\partial ^2u}{\partial x^2}+92u=f(t,x,u),\ \ \ 0<x<1,\ \ t>0,\\ \\ u(0,t)=0,\ \ \ u(1,t)=0,\ \ \ u(x,0)=a(x),\ \ \ u_t(x,0)=0, \end{array} \end{aligned}$$

with $a(x) = 4x(1-x),\ \ \ f(t,x,u)=u^5-a^2(x)u^3+\dfrac{a^5(x)}{4}\sin ^2(20t)\cos (10t).$ The exact solution is $u(x,t) = a(x) \cos (10t).$

Using semi-discretization on the spatial variable with second-order symmetric differences, we obtain

$$\begin{aligned} \dfrac{d^2U}{dt^2}+MU&= F(t,U),\ \ U(0)=\big (a(x_1),\ldots ,a(x_{N-1})\big )^T,\nonumber \\ U'(0)&= \mathbf{0}, \ \ 0<t\le t_{\mathrm {end}}, \end{aligned}$$

(31)

where $U(t)=\big (u_{1}(t),\ldots ,u_{N-1}(t)\big )^{T}$ with $u_{i}(t)\approx u(x_{i},t)$, $x_i = i\Delta x$, $\Delta x= 1/N$, $i=1,\ldots ,N-1,$

$$\begin{aligned} M=92I_{N-1}+\dfrac{1}{\Delta x^2}\left( \begin{array}{lllll} 2a(x_1)&{}-a(x_1) &{}&{} &{}\\ -a(x_2) &{}2a(x_2) &{} -a(x_2)&{} &{} \\ &{}\ddots &{}\ddots &{}\ddots &{} \\ &{}&{}-a(x_{N-2}) &{}2a(x_{N-2}) &{} -a(x_{N-2})\\ &{} &{} &{}-a(x_{N-1})&{}2a(x_{N-1}) \\ \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} F(t,U)=\big ( f(t,x_1,u_1), \ldots , f(t,x_{N-1},u_{N-1})\big )^T. \end{aligned}$$

The system is integrated in the interval $[0,20]$ with $N=40$ and the integration stepsizes $h=1/(2^j\times 30)$ for the methods C, E, MSERKN1s2, FMSERKN2s2, $h=1/(2^j\times 15)$ for MSERKN2s2, and $h=1/(2^j\times 10)$ for the other methods, where $j=0,1,2,3.$ The efficiency curves are shown in Fig. 2b. We note that the matrix $M$ is diagonalizable and its smallest eigenvalue is about 100.00 and the largest eigenvalue is about 6,332.00.

Problem 3. Consider the nonlinear Klein–Gordon equation [13]

$$\begin{aligned} \dfrac{\partial ^{2}u}{\partial t^{2}}-\dfrac{\partial ^{2}u}{\partial x^{2}}=-u^3-u,\ \ \ 0<x<L,\ \ t>0,\\ u(x,0)=A\left( 1+\cos \left( \frac{2\pi }{L}x\right) \right) ,\ \ u_{t}(x,0)=0,\ \ u(0,t)=u(L,t), \end{aligned}$$

where $L=1.28$, $A=0.9$. Carrying out a semi-discretization on the spatial variable by using second-order symmetric differences yields

$$\begin{aligned} \dfrac{d^2U}{dt^2}+ MU=F(t,U),\ \ \ 0<t\le t_{\mathrm {end}}, \end{aligned}$$

where $U(t)=\big (u_1(t),\ldots ,u_N(t)\big )^T$ with $u_i(t)\approx u(x_i,t),i=1,\ldots ,N$,

$$\begin{aligned} M=\dfrac{1}{\Delta x^2}\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 2 &{}-1 &{}&{} &{}-1\\ -1 &{}2 &{} -1&{} &{} \\ &{}\ddots &{}\ddots &{}\ddots &{} \\ &{}&{}-1 &{}2 &{} -1\\ -1 &{} &{} &{}-1&{}2 \\ \end{array} \right) _{N\times N} \end{aligned}$$

with $\Delta x= L/N, \, x_i = i\Delta x, \, F(t,U)=\big (-u_1^3-u_1,\ldots ,-u_N^3-u_N\big )^T$ and $N=32$. The corresponding Hamiltonian of this system is

$$\begin{aligned} H(U',U)=\dfrac{1}{2}U'^{T}U'+\dfrac{1}{2}U^{T}MU+\frac{1}{2}u^2_{1}+\frac{1}{4}u^4_{1}+\cdots + \frac{1}{2}u^2_{N}+\frac{1}{4}u^4_{N}. \end{aligned}$$

We solve this problem in $[0,500]$ with $N=32$ and stepsizes $h=1/(2^{j}\times 150)$ for the methods C, E, MSERKN1s2, FMSERKN2s2, $h=1/(2^{j}\times 75)$ for MSERKN2s2, and $h=1/(2^{j}\times 50)$ for the other methods, where $j=0,1,2,3.$ Figure 3a shows the error in the positions at $t_{\mathrm {end}}=10$ versus the computational effort. Then this problem is integrated with a fixed stepsize $h=1/50$ in the interval $[0,t_{\mathrm {end}}],\ t_{\mathrm {end}}=10^{i},\ i=0,1,2,3$. The results of energy conservation are presented in Fig. 3b. The smallest eigenvalue of the matrix $M$ is about 0.00 and the largest eigenvalue is about 2,500.00.

Fig. 3

Results for Problem 3. a The logarithm of the global error ($GE$) over the integration interval against the logarithm of the number of function evaluations. b The logarithm of the maximum global error of Hamiltonian $GEH=\max |H_{n}-H_{0}|$ against $\log _{10}(t_{\mathrm {end}})$

Problem 4. Consider the sine-Gordon equation with periodic boundary conditions ([12])

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial ^{2}u}{\partial t^{2}}=\dfrac{\partial ^{2}u}{\partial x^{2}}-\sin u,\ \ \ -1<x<1,\ \ t>0, &{} \\ u(-1,t)=u(1,t). &{} \end{array}\right. \end{aligned}$$

We carry out a semi-discretization on the spatial variable by using second-order symmetric differences and obtain the following system of second-order ODEs in time:

$$\begin{aligned} \dfrac{d^{2}U}{dt^{2}}+MU=F(t,U),\ \ \ 0<t\le t_{\mathrm {end}}, \end{aligned}$$

where $U(t) =(u_{1}(t),\ldots ,u_{N}(t))^{T}\ \text {with}u_{i}(t)\approx u(x_{i},t),\ i=1,2,\ldots ,N,$ ${\Delta x} =2/N{,\ x_{i}=-1+i\Delta x},$ $F(t,U) =-\sin (U)=-\big (\sin u_{1},\ldots ,\sin u_{N}\big )^{T},$

$$\begin{aligned} M&=\dfrac{1}{\Delta x^{2}}\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 2 &{} -1 &{} &{} &{} -1\\ -1 &{} 2 &{} -1 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} -1 &{} 2 &{} -1\\ -1 &{} &{} &{} -1 &{} 2 \end{array} \right) . \end{aligned}$$

The Hamiltonian of this system is

$$\begin{aligned} H(U',U)=\dfrac{1}{2}U'^{T}U'+\dfrac{1}{2}U^{T}MU-\cos (u_{1})-\cos (u_{2})-\cdots -\cos (u_{N}). \end{aligned}$$

The initial conditions are chosen as

$$\begin{aligned} U(0)=(\pi )_{i=1}^{N},\ \ \ U_{t}(0)=\sqrt{N}\left( 0.01+\sin \left( \dfrac{2 \pi i}{N}\right) \right) _{i=1}^{N} \end{aligned}$$

with $N=32$. The problem is integrated in the interval $[0,500]$ with stepsizes $h=1/(30\times {2^{j}})$ for the methods C, E, MSERKN1s2, FMSERKN2s2, $h=1/(15\times 2^{j})$ for MSERKN2s2, and $h=1/(10\times {2^{j}})$ for the other methods, where $j=0,1,2,3.$ Figure 4a shows the global errors. We integrate this problem with a fixed stepsize $h=1/40$ in the interval $[0,t_{\mathrm {end}}],\ t_{\mathrm {end}} =10^{i},\ i=0,1,2,3$. The results of energy conservation are presented in Fig. 4b. The smallest eigenvalue of the matrix $M$ is about 0.00 and the largest eigenvalue is about 1,024.00.

Fig. 4

Results for Problem 4. a The logarithm of the global error ($GE$) over the integration interval against the logarithm of the number of function evaluations. b The logarithm of the maximum global error of Hamiltonian $GEH=\max |H_{n}-H_{0}|$ against $\log _{10}(t_{\mathrm {end}})$

Problem 5. Consider a Fermi-Pasta-Ulam Problem [10].

Fermi-Pasta-Ulam Problem is a Hamiltonian system with the Hamiltonian

$$\begin{aligned} H(y,x)&=\dfrac{1}{2}\textstyle \sum \limits _{i=1}^{2m}y_{i}^{2}+\dfrac{\omega ^{2}}{2}\textstyle \sum \limits _{i=1}^{m}x_{m+i}^{2}+\dfrac{1}{4} [(x_{1}-x_{m+1})^{4}\\&\quad +\textstyle \sum \limits _{i=1}^{m-1}(x_{i+1}-x_{m+i-1}-x_{i}-x_{m+i} )^{4}+(x_{m}+x_{2m})^{4}], \end{aligned}$$

where $x_{i}$ is a scaled displacement of the $i$th stiff spring, $x_{m+i}$ represents a scaled expansion (or compression) of the $i$th stiff spring, and $y_{i},\ y_{m+i}$ are their velocities (or momenta).

Therefore, we have

$$\begin{aligned} x^{\prime \prime }(t)+Mx(t)=-\nabla U(x),\qquad t\in [t_{0},t_{\mathrm {end}}], \end{aligned}$$

where

$$\begin{aligned} M&= \left( \begin{array}{l@{\quad }l} \mathbf {0}_{m\times m} &{} \mathbf {0}_{m\times m}\\ \mathbf {0}_{m\times m} &{} \omega ^{2}I_{m\times m} \end{array}\right) ,\\ U(x)&= \dfrac{1}{4}\Big [(x_{1}-x_{m+1})^{4}+\textstyle \sum \limits _{i=1} ^{m-1}(x_{i+1}-x_{m+i-1}-x_{i}-x_{m+i})^{4}+(x_{m}+x_{2m})^{4}\Big ]. \end{aligned}$$

Following [10], we choose

$$\begin{aligned} m=3,\ x_{1}(0)=1,\ y_{1}(0)=1,\ x_{4}(0)=\dfrac{1}{\omega },\ y_{4}(0)=1, \end{aligned}$$

with zero for the remaining initial values and $\omega =50$. The system is integrated in the interval $[0,10]$ with stepsizes $h=1/(120\times {2^{j}})$ for the methods C, E, MSERKN1s2, FMSERKN2s2, $h=1/(60\times {2^{j}})$ for MSERKN2s2, and $h=1/(40\times {2^{j}})$ for the other methods, where $j=0,1,2,3.$ The efficiency curves are shown in Fig. 5a. We integrate this problem with a fixed stepsize $h=1/500$ in the interval $[0,t_{\mathrm {end}}],\ t_{\mathrm {end}} =10^{i},\ i=0,1,2,3$. The results of energy conservation are presented in Fig. 5b.

Fig. 5

Results for Problem 5. a The logarithm of the global error ($GE$) over the integration interval against the logarithm of the number of function evaluations. b The logarithm of the maximum global error of Hamiltonian $GEH=\max |H_{n}-H_{0}|$ against $\log _{10}(t_{\mathrm {end}})$

It follows from the numerical results that our novel integrators are very promising as compared with the classical RKN methods, ARKN methods, and Gautschi-type trigonometric or exponential integrators.

5 Conclusions and discussions

In this paper, in order to solve multi-frequency and multidimensional oscillatory reversible differential Eq. (1) efficiently, we first present the symmetry conditions for multi-frequency ERKN integrators in a simplified way. Then five novel explicit multi-frequency symmetric ERKN integrators are derived based on the simplified symmetry conditions. The stability and phase properties of the new multi-frequency symmetric ERKN integrators are discussed. Furthermore, the remarkable efficiency of the new integrators are shown by the numerical results from five numerical experiments in comparison with existing methods in the literature.