1 Introduction

Microwave-based heat treatment is a strategy of high interest to both industry and academia. One of the reasons rests on the features that separate it from conventional heating. This type of processing has relevant features such as high efficiency of converting electrical to thermal energy, savings in processing time, the appearance of temperature profiles opposite to those achieved with conventional heating (conduction, convection, and thermal radiation), focused heating, and instant shutdown [1,2,3,4,5]. Even so, there are properties that must be well defined prior to designing processes where microwaves and matter interact. Some examples include the magnetic permeability, the permittivity, and the electrical conductivity, along with the thermodynamic properties (thermal conductivity, specific heat and density).

In general, both types of properties depend on temperature, and their relationship is found through experimentation. Most case studies assume that these properties are either constant or that they only change in a polynomial way. However, there are situations in which they depend particularly on the position and direction in which they are measured, which is frequently observed with the continuous development of new materials. On the other hand, microwave-sensitive spheres coated with different layers (forming a core–shell structure) have extensive applications, especially in medicine. For example, Tang et al. [6] prepared mPEG-PLGA microspheres with microwave sensitivity for the treatment of hepatocellular carcinoma. This core–shell morphology was achieved using the double emulsion technique. They found that microspheres coated with MoS2 nanosheets dispersed in saline can increase their temperature by 8.5 °C under microwave irradiation. Likewise, Mao et al. [7] developed a system made of zirconium oxide microspheres along with an ionic liquid that interacts with microwave energy. By rapidly heating this substance, a drug is progressively released aimed at removing cancerous tissues. Conversely, Paruch used 3D numerical simulations as a tool to correctly select the control parameters of artificial hyperthermia during the ablation of cancerous cells [8]. The author analyzed a system composed of two external electrodes, which induce an electromagnetic field and a temperature profile resulting from electrodes action. In tumor excision procedures, two parameters are of paramount importance. The first one is the biocompatibility of the material used for heating purposes. The other one is the precise direction of the heat flow generated within it. Biocompatibility is linked to the chemical nature of the material. Heat flow direction, instead, is related to the uniform heating of all surrounding tissues (3D). The idea is to destroy the tumor while avoiding damaging any healthy tissue that may be present. One way to satisfy these two basic requirements is to use particles with a core–shell structure. The core should efficiently absorb the energy present in the electromagnetic field. At the same time, the layer (or layers) that surrounds it must diffuse heat uniformly and should have a well-defined chemical structure (biocompatible). Similar studies to those described above are found in the literature [9,10,11,12].

Given such a particular application for this type of spherical material with core–shell structure, it is relevant to be able to predict the temperature profile created within them. In doing so, the effect on heating uniformity of healthy and cancerous tissues can be estimated. It is for this reason that we propose this work. Our goal is to simulate such a situation, and in particular, when thermal conductivity changes with the direction in which it is measured. We assume here that there is anisotropy in the directions of the unit vectors, i.e., orthotropic variation of the thermal conductivity of two layers surrounding a core. Similarly, having an orthotropic variation of the thermal conductivity at the industrial level leads to undesirable temperature profiles. From the point of view of the estimation and experimental determination of conductivity with orthotropic variation, there are several works recently reported. For example, Cao et al. proposed a numerical estimation of the thermal conductivity of orthotropic materials based on knowledge of internal temperature profiles [13]. They solved a classic inverse problem considering a regular two-dimensional geometry. Their thermal model consisted of a two-dimensional partial differential equation valid for a square plate of negligible thickness and uniform density. Once the direct and inverse problems were raised, they minimized the estimates with the slightest variance, i.e., the ordinary least squares norm, which is also known as the sum of squared residuals. The optimization procedure was carried out using the conjugate gradient method, together with the method of finite differences. Their results indicated that this approach is a valid strategy for finding thermal conductivity values. The work carried out by Mahmood et al. [14] also focused on estimating (identifying) the thermal conductivity of a non-homogeneous and possibly anisotropic medium from internal temperature measurements. They discretized the heat equation by including orthotropic thermal conductivity coefficients and using the finite differences method. For the solution of the objective function, the MATLAB lsqnonlin toolbox was employed. The authors concluded that their results were accurate and stable, even with noisy input temperature data. In a similar report, Zhou et al. used the differential transformation dual reciprocity boundary element method combined with the Levenberg–Marquardt algorithm and estimated the thermal conductivity of a 2D orthotropic material [15]. It is worth mentioning the existence of new methods proposed for experimental measurements of the orthotropic thermal conductivity tensor. Chen et al. proposed an extension of the conventional method of measuring thermal conductivities to include measurement in orthotropic materials [16]. This new version was validated by comparing with the guarded hot-plate method, based on the results from a test on cherry wood specimens. Results were reported by the authors under certain operational conditions. Wojciech et al. [17] developed a new non-destructive technique to measure the thermal conductivity of isotropic and orthotropic materials. Their method is based on the inverse heat transfer problem solution. They used a commercial CFD solver combined with the traditional Levenberg–Marquardt algorithm. Conversely, knowledge about the thermal conductivity is paramount for processes involving conduction heat transfer. But we will not delve into it. Instead, we will focus on the second-order thermal conductivity tensor, which is symmetric. Such tensor exhibits components that vary with direction. So, it must be included in the global energy balance. A common scenario for this behavior rests on the thermal variation across orthogonal coordinate axes. This is known as orthotropic thermal conductivity and has three components. Recently, Mahmood et al. [14] numerically solved an inverse problem aimed at estimating components of the orthotropic thermal conductivity in heterogeneous media and using temperature profile measurements. The authors used a traditional finite difference approach. They stated that their solutions were precise and stable, despite adding errors into the measurements.

In this work, we formulate the mathematical model that describes a medium with multiple phases, where said phases exhibit thermal conductivities that vary in an orthogonal fashion. We analyzed its effect over the global temperature profile, and thus, over the heat generation of the system. Such an effect becomes essential when analyzing tumor destruction using nanoparticles that exhibit thermal conductivities with this variation. As will be shown in the results section, if heating is asymmetrical, it would eliminate tissue in a non-uniform way. This may be a highly desirable feature in some scenarios. For example, imagine the case where you have a tumor next to an organ, or the case where you have a tumor with a non-uniform shape. In both cases, it would be desirable to have the means for generating a heterogeneous temperature profile centered on cancer tissue, and that closely resembles its geometry. To that end, we focus on analyzing the effect of varying thermal conductivities in the heat generation of heterogeneous systems. Such heat comes from nanoparticles that absorb microwaves, and which can be used in processes such as tumor ablation. We use simulations to visualize generation asymmetry. As mentioned, the desirability of such a feature is subjective. Since we already mentioned a desirable scenario, let us focus on an undesirable one. Imagine that you need to thermally treat a material, such as rubber. It would be desirable to generate a uniform temperature profile that covered the whole sample. Otherwise, the material will be untreated at some points or overly treated at others. Therefore, asymmetry would have negative consequences for the process. Due to space restrictions, throughout this work, we only show the generated temperature profiles for some exemplary cases.

Despite the number of works dealing with thermal simulations, we found no evidence about the effect of orthotropic thermal conductivities in heat generation. So, this work fills that knowledge gap by providing a way for easily simulating such an effect. Besides, we show the impact that these properties have when dealing with nanoparticles that absorb microwaves. To this end, we present temperature profiles for four examples. In the first one, we considered shells exhibiting an isotropic condition, i.e., identical thermal conductivities. Moreover, we assume that the core has a dielectric constant that is ten times higher than those of the shells. In the second scenario, however, we consider different thermal conductivities, so that we can study the effect of orthotropic shells. In the third one, we analyze a scenario similar to the first one. This time, however, the shells exhibit a thermal conductivity with a higher value in the \(\theta\) direction than in the \(r\) and \(\phi\) directions. Conversely, the last scenario shows the inverse case. Hence, values for the \(r\) and \(\phi\) directions are quite higher than the value for the \(\theta\) direction. In doing so, we aim at generating a high contrast in the temperature profiles and heat flows across scenarios. We organized this article as follows: after this brief, introduction appears with the mathematical model of the thermal system and its numerical solution. Some simulation findings arise in the results section. In the end, the most relevant conclusions are included.

2 Thermal Model

The model that we tackled in this work is given by a heat transfer problem in a heterogeneous medium, where thermal conductivities vary in the direction of each axis of the spherical coordinates. For this reason, we formulated the mathematical model based on the heat diffusion equation for each phase of the system in a transitory state, including the internal generation of heat, which represents heating utilizing microwaves. We now provide more details about the problem and the model.

2.1 Thermal Problem

The problem is to evaluate the effect of the orthotropic conductivity tensor in a nano-sphere with core–shell morphology, on the generation of temperature profiles, and therefore, on its homogeneous and symmetrical heat release.

2.2 Thermal System in 3D

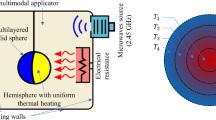
As mentioned, the modified core–shell system has one core and two layers. The core absorbs microwaves. It will be assumed that the thermophysical properties of the two layers are time, position, and temperature invariant; the only exception being thermal conductivities. They will vary in all three orthogonal directions (orthotropy). For simplicity, in this work, we disregarded contact thermal resistances between shells. Also, we assume high conductivities and a great amount of energy is transformed into heat, so such an assumption seems feasible, at least for initial calculations. In addition, the whole sphere hangs inside an electromagnetic cavity and slowly rotates. The system receives uniform radiation from microwaves due to a mode stirrer included within the cavity.

2.3 Thermal Model

Consider a heat transfer process ruled by

$$\alpha \frac{{\partial T\left( {x;y;z;t} \right)}}{\partial t} - \varvec\nabla \cdot \left( {\varvec{K}\left( {x;y;z} \right)\varvec\nabla T\left( {x;y;z;t} \right)} \right) + c\left( {x;y;z} \right)T\left( {x;y;z;t} \right) = \dot{g}\left( {x;y;z;t} \right)$$
(1)

where \(\left( {x;y;z;t} \right) \in {\varvec{\Omega}}\), and \({\varvec{\Omega}}\) is a domain limited to a plane (2D) or to a region (3D). Likewise, \(\alpha \left[ {{\text{J}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1} } \right]\) is a constant coefficient dependent on either temperature or position, known as the volumetric coefficient of thermal expansion. It represents the product of density (\(\rho \left[ {{\text{kg}} \cdot {\text{m}}^{ - 3} } \right]\)) and specific heat capacity (\(c \left[ {{\text{W}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1} } \right]\)) for the solid, in the case of the energy equation. \(\varvec{K}\left( {x;y;z} \right) \left[ {{\text{W}} \cdot {\text{m}}^{ - 1} \cdot {\text{K}}^{ - 1} } \right]\) is the thermal conductivity tensor,

$$\varvec{K}\left( {x;y;z} \right) = \left[ {\begin{array}{*{20}c} {\varvec{k}_{11} \left( {x;y;z} \right)} & {k_{12} \left( {x;y;z} \right)} & {k_{13} \left( {x;y;z} \right)} \\ {k_{21} \left( {x;y;z} \right)} & {\varvec{k}_{22} \left( {x;y;z} \right)} & {k_{21} \left( {x;y;z} \right)} \\ {k_{31} \left( {x;y;z} \right)} & {k_{31} \left( {x;y;z} \right)} & {\varvec{k}_{33} \left( {x;y;z} \right)} \\ \end{array} } \right].$$
(2)

For this work, components outside the main diagonal are zero. Also, \(\varvec{k}_{11} \left( {x;y;z} \right) \ne \varvec{ k}_{22} \left( {x;y;z} \right) \ne \varvec{ k}_{33} \left( {x;y;z} \right).\)\(c\left( {x;y;z} \right) \left[ {{\text{W}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1} } \right]\) is a constant or variable factor. \(\dot{g}\left( {x;y;z;t} \right) \left[ {{\text{W}}\cdot{\text{m}}^{ - 3} } \right]\) represents the internal volumetric generation term, which is due to electromagnetic radiation. For all cases, \(T \left[ {\text{K}} \right]\) represents temperature.

2.4 Thermal Model in Spherical Coordinates

After some manipulations, the mathematical model describing heat conduction in the system is given by a set of three coupled time-variable partial differential equations. The solution allows generation of temperature profiles as a function of position (3D) and time, for each component of the system. The model is given by the energy balance (also known as heat diffusion equation) shown in (3), which is valid for \(r_{i} \le r \le r_{i + 1}\), \(0 \le \theta \le \pi\), and \(0 \le \phi \le 2\pi\) with \(i = 1, 2, 3\),

$$\rho_{i} c_{i} \frac{{\partial T_{i} \left( {r;\mu ;\phi ;t} \right)}}{\partial t} = \frac{1}{{ r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} k_{ii} \left( {r;\theta ;\phi } \right)\frac{{\partial T_{i} \left( {r;\mu ;\phi ;t} \right)}}{\partial r}} \right) + \frac{ 1 }{{r^{2} { \sin }^{2} \theta }}\frac{\partial }{\partial \phi }\left( {k_{jj} \left( {r;\theta ;\phi } \right)\frac{{\partial T_{i} \left( {r;\mu ;\phi ;t} \right)}}{\partial \phi }} \right)+ \frac{ 1 }{{r^{2} \sin \theta }}\frac{\partial }{\partial \theta }\left( {\sin \theta k_{kk} \left( {r;\theta ;\phi } \right)\frac{{\partial T_{i} \left( {r;\mu ;\phi ;t} \right)}}{\partial \theta }} \right) + P_{av}^{'''} \left( {r;\theta ;\phi ;t} \right).$$
(3)

Through a variable change common in literature (\(\mu = { \cos \theta}\)), the initial and boundary conditions are set as detailed below.

Initial conditions:

$$T_{i} \left( {r;\mu ;\phi ;t = 0} \right) = {\mathfrak{F}}_{i} \left( {r;\mu ;\phi } \right),$$
(4)

since \({\mathfrak{F}}_{i} ,\) is the initial temperature distribution function of the \(i\)th sphere or shell.

Boundary conditions:

  1. 1.

    Direction \(r\) and for the core \(\left( {i = 1} \right)\):

    $$\frac{{\partial T_{1} \left( {r_{1} ;\mu ;\phi ;t} \right)}}{\partial r} = 0.$$
    (5)
  2. 2.

    Direction \(r\) for the outermost shell \(\left( {i = 3} \right)\):

    $$k_{33} \frac{{\partial T_{3} \left( {r_{3} ;\mu ;\phi ;t} \right)}}{\partial r} = q^{\prime\prime}\left( {r = r_{3 } ;\mu ;\phi } \right),$$
    (6)

    where \(q^{\prime\prime}\left( {r = r_{3} ;\mu ;\phi } \right)\) [\({\text{W}} \cdot {\text{m}}^{ - 2}\)] is the heat flow per unit area released through the outer surface.

  3. 3.

    Temperature continuity on the same sphere \(\left( {\forall i \in \left\{ {1, 2, 3} \right\}} \right)\):

    $$T_{i} \left( {r;\mu = - 1;\phi ;t} \right) = T_{i} \left( {r;\mu = 1;\phi ;t} \right).$$
    (7)
  4. 4.

    Heat flow continuity on the same sphere \(\left( {\forall i \in \left\{ {1, 2, 3} \right\}} \right)\):

    $$\frac{{\partial T_{i} \left( {r;\mu = - 1;\phi ;t} \right)}}{\partial \mu } = \frac{{\partial T_{i} \left( {r;\mu = 1;\phi ;t} \right)}}{\partial \mu }.$$
    (8)
  5. 5.

    Temperature continuity \(\left( {\forall i \in \left\{ {1, 2, 3} \right\}} \right)\):

    $$T_{i} \left( {r;\mu ;\phi = 0;t} \right) = T_{i} \left( {r;\mu ;\phi = 2\pi ;t} \right).$$
    (9)
  6. 6.

    Heat Flow continuity \(\left( {\forall i \in \left\{ {1, 2, 3} \right\}} \right)\):

    $$\frac{{\partial T_{i} \left( {r;\mu ;\phi = 0;t} \right)}}{\partial \phi } = \frac{{\partial T_{i} \left( {r;\mu ;\phi = 2\pi ;t} \right)}}{\partial \phi }.$$
    (10)
  7. 7.

    Temperature continuity at the interface between core and first shell, as well as between shells \(\left( {1:2;2:3} \right)\):

    $$T_{i} \left( {r_{i} ;\mu ;\phi ;t} \right) = T_{i + 1} \left( {r_{i + 1} ;\mu ;\phi ;t} \right).$$
    (11)
  8. 8.

    Heat flow continuity at the interface between core and first shell, as well as between shells \(\left( {1:2;2:3} \right)\):

    $$k_{ii} \frac{{\partial T_{i} \left( {r_{i} ;\mu ;\phi ;t} \right)}}{\partial \phi } = k_{ii + 1} \frac{{\partial T_{i + 1} \left( {r_{i + 1} ;\mu ;\phi ;t} \right)}}{\partial \phi },$$
    (12)

Conditions 3 and 4 belong to the \(\theta\) direction, while conditions 5 and 6 belong to \(\phi .\) In this case, the internal energy generation (i.e., volumetric heat generation) exists for the core (\(i = 1\)). It is assumed to be constant with time and position and is modeled as a constant energy flow. Other components of the system are described further on.

2.5 Power Generated by Microwaves

Microwave heating implies direct conversion of electromagnetic energy into heat [1,2,3]. The average power per unit volume (\(P_{av}^{'''} \left[ {{\text{W}} \cdot {\text{m}}^{ - 3} } \right]\)) dissipated by microwaves is given by

$$P_{av}^{'''} \left( {r;\theta ;\phi ;t} \right) = \pi f\left[ {\varepsilon_{0} \varepsilon_{ef}^{''} \left( T \right)E_{rms}^{2} + \mu_{0} \mu_{ef}^{''} \left( T \right)H_{rms}^{2} } \right],$$
(13)

which considers electric (\(\varepsilon_{0} \varepsilon_{ef}^{''} \left( T \right)E_{rms}^{2}\)) and magnetic (\(\mu_{0} \mu_{ef}^{''} \left( T \right)H_{rms}^{2}\)) losses on the material. In this equation, \(f~\) [GHz] is the microwave frequency. We used \(f = 2.45\) GHz in the simulations because it is the standard frequency employed by microwave ovens. Recall that \(\varepsilon_{0} \approx 8.85 \times 10^{ - 12} {\text{F}} \cdot {\text{m}}^{ - 1}\) and \(\mu_{0} \approx 1.256 \times 10^{ - 6} {\text{H}} \cdot {\text{m}}^{ - 1}\) correspond to vacuum permittivity and permeability, respectively. Likewise, \(\varepsilon_{ef}^{''}\) and \(\mu_{ef}^{''}\) are the imaginary parts of the effective values of permittivity and permeability, which are also known as effective loss factors. Last, \(E_{rms} \left[ {{\text{V}} \cdot {\text{m}}^{ - 1} } \right]\) and \(H_{rms} \left[ {{\text{A}} \cdot {\text{m}}^{ - 1} } \right]\) stand for the electrical and magnetic field strength, respectively. Here, we consider that both fields interact with the material of the inner sphere, and that the permittivity and permeability coefficients are temperature independent.

2.6 Heat Transfer Due to Natural Convection

This mechanism is modeled through Newton’s cooling law,

$$\dot{Q}_{conv} = h \cdot A_{s} \left( {T_{S} - T_{\infty } } \right),$$
(14)

where \(\dot{Q}_{conv}\) [W] represents the energy per time unit being exchanged between a solid and a fluid. The convection heat transfer coefficient is given by \(h\)\(\left[ {{\text{W}} \cdot {\text{m}}^{ - 2} \cdot {\text{K}}^{ - 1} } \right].\)\(A_{s} \left[ {{\text{m}}^{2} } \right]\) is the surface area for convection heat transfer, \(T_{s}\)  [K] is the corresponding temperature and \(T_{\infty }\)  [K] is the temperature of the fluid away from the surface. It is evident that \(h\) is not a property of the fluid. Hence, determining it experimentally is complex as it depends on many variables. Some of them include geometry, orientation of the solid, surface features, nature of the fluid, thermophysical properties, and velocity.

3 Methodology and Results

This section includes scenarios simulating microwave irradiation of the core–shell morphology. Temperature profiles and heat flows through the second layer are included in the resulting data.

Numerical solution: All numerical procedures carried out in this work were performed in a MacBook Pro (2016), 256 GB SSD, i5-i7 Quad Core, 2133 MHz, 8 GB RAM Intel Iris Graphics 550. Furthermore, scripts and plots were developed and implemented on MATLAB (R2019a).

Simulation procedure: Since each thermal conductivity is a property represented by a vector with three elements (one for each of the \(r, \theta\) and \(\phi\) directions), and considering that each component is real-valued, there is an infinite number of values it can take. Hence, there are infinite parameter combinations (i.e., examples). We selected some of them as different illustrative scenarios. For starters, we considered that the shells had identical thermal conductivities, i.e., an isotropic condition, and that the dielectric constant of the core was ten times higher. Such a condition was not preserved for the second scenario. To study the effect of orthotropic shells, we assumed different thermal conductivities. Subsequently, for the third scenario we analyzed the impact of possessing a core with high thermal conductivity, while the shells shared, once again, the same conductivity values. This time, however, the value for the \(\theta\) direction is quite high when compared with those in the \(r\) and \(\phi\) directions. For the last scenario that we analyzed, we reversed such situation. So, this time around values for the \(r\) and \(\phi\) directions are quite higher than the value for the \(\theta\) direction. In doing so, we were able to generate high contrast in the temperature profiles and heat flows across scenarios.

The physical system: An internal solid sphere surrounded by two layers with different thermophysical properties and with orthotropic conductivities is heated within an electromagnetic cavity. Heating is assumed as homogeneous along the whole surface. The inner sphere absorbs all microwave energy and transforms it into heat. The composite sphere exchanges heat uniformly along the whole surface of the external layer, as it is immersed into a liquid at 36 °C. As an initial approximation, a constant convection heat transfer coefficient was assumed. Furthermore, the surrounding liquid is presumed to be a microwave transparent material.

Simulation conditions: Here, the core is isotropic and it converts all energy from electromagnetic waves (at 2.45 GHz) into heat (thermal energy). The core is surrounded by two layers of materials of different thicknesses. The internal volumetric heat generation can be adjusted depending on the required temperature level, and therefore, of the amount of heat needed. Ideally, for an application such as the complete destruction of cancerous tissue, for example, controlled and homogeneous conditions will be mandatory. The release of heat will be homogeneous, if the nano-spheres have a homogeneous (symmetric) temperature profile in all three directions. Table 1 includes all the simulation parameters, which were kept constant for all tests. Note that we use dimensionless values for the radii so that the effect of their ratio can be more easily assessed. Striving for repeatability, the value of each radius was \(r_{1} = 0.02{\text{ m}}, r_{2} = 0.06 {\text{ m}}, r_{3} = 0.12 {\text{ m}}\). Besides, the thermophysical property values were chosen to analyze different simulation scenarios of an orthotropic core–shell system. Temperature corresponds to the lower limit of the normal human body temperature range.

Table 1 Simulation parameters for steady and transient states
Full size table

It is essential to highlight that this is a first analysis that relates the simultaneous effect of nanoparticles, microwaves, and thermal conductivities with orthotropic variation of a core–shell morphology on temperature profiles and heat flows. So, we found no experimental values where the thermodynamic and physical properties were like the ones used in this work. Nonetheless, we observed that they match with the tendencies reported in [14, 17, 18]. Also, note that we neglected the interphase region properties between spheres for all simulations. This is mainly due to the presence of high thermal conductivities in the model, and because of the massive amounts of thermal energy transported.

3.1 Scenario 1

The composite sphere is inserted in a medium that is at a nearly constant temperature of 36 °C. The power of the microwave generator was adjusted in such a way that the maximum temperature within the thermal system did not exceed 70 °C for an irradiation time from 0 s to 250 s. Both, generator power and irradiation time, are tunable parameters. The steady and transient states of the system are analyzed.

3.1.1 Steady-State

The ratio of each of the components of the conductivity tensor to the thermal conductivity of the core is \(k_{11} = 1.0,\) and for the two shells are \(\varvec{k}_{22} = \left[ {0.1;0.1;0.1} \right],\) and \(\varvec{k}_{33} = \left[ {0.1;0.1;0.1} \right]\). Each position represents the value of the conductivity \(\varvec{k}_{{{ii}}} \left( {r;\theta ;\phi } \right)\) in spherical coordinates. Figure 1 shows the main result for the isotropic case, considering a view in the \(\left( {r;\pi /2;\phi } \right)\) direction. As noted, both heat flow (Fig. 1a) and temperature profile (Fig. 1b) are symmetrical. The uniform level curves in the latter illustrate such homogeneously distributed core temperatures, while the concentration of colored elements in the former shows the effect of higher temperature values.

Fig. 1
figure 1

Heat flow and temperature profile for the composite sphere (one isotropic core with two isotropic layers) at steady-state, with \(r_{1}\): \(r_{2}\) = 1:3 and \(r_{1}\): \(r_{3}\) = 1:6

Full size image

The corresponding heat flow that is released when heating the core with microwaves is simulated as shown in Fig. 2. As observed, the heat flow is also symmetric in all three dimensions. The heat flow in each direction is simply the first partial derivative of the temperature profile multiplied by the thermal conductivity as shown

Fig. 2
figure 2

Heat flow distribution at steady-state when the isotropic composite sphere is heated by microwaves. Left: whole sphere. Right: zoom into a smaller region

Full size image
$$q_{r}^{''} = - \varvec{k}_{iir} \frac{{\partial T_{i} \left( {r;\theta ;\phi ;t} \right)}}{\partial r}, q_{\theta }^{''} = - \frac{{\varvec{k}_{ii\theta } }}{r}\frac{{\partial T_{i} \left( {r;\theta ;\phi ;t} \right)}}{\partial \theta } , {\text{and}} \, q_{\phi }^{''} = - \frac{{\varvec{k}_{ii\phi } }}{r\sin \theta }\frac{{\partial T_{i} \left( {r;\theta ;\phi ;t} \right)}}{\partial \phi }.$$
(15)

3.1.2 Transient State

The mathematical model was now solved including the temperature variation over time. Figure 3 shows some symmetrical temperature profiles in the isotropic system for \(t = 50\) s (Fig. 3a) and \(250\) s (Fig. 3b). In this figure, we observe that a specific temperature value was reached guaranteeing a symmetrical temperature profile. Keep in mind that this will ensure that all surrounding elements (e.g., tissues) will receive the same amount of thermal energy.

Fig. 3
figure 3

Transient temperature profile within the isotropic thermal system after: (a) 5 s and (b) 250 s

Full size image

Now, Fig. 4 shows the symmetrical variation of temperature and heat flow over time. The inner sphere, with a higher temperature, irradiates thermal energy uniformly. The reason is conductivities on all three perpendicular dimensions \(\left( {r;\theta ;\phi } \right)\) are the same. The components of thermal conductivity can be observed in the cone given by the \(\theta\) variation, at a distance \(r\) from the center, and by the azimuth planes \(\phi\). Figure 4a shows that steady-state heat flow is reached by the whole sphere around the 40 s mark. Moreover, Fig. 4b shows the homogeneous distribution of temperature throughout the transient state of the composite sphere. Ranges and thermophysical properties considered for this simulation are given in Table 1. Our data corroborate that the developed software generates the expected profiles for limit scenarios, independently of the magnitude of thermal conductivities. Heat flow per unit area changes directions due to the heating process. The initial temperature of the system is 25 °C. Since the surrounding liquid begins at 36 °C, spheres begin receiving energy from the fluid (−). After the core transforms enough microwaves into heat, the temperature of the composite sphere increases above 36 °C and begins delivering energy to the fluid (+). As expected, after reaching a steady-state, heat flow remains stable.

Fig. 4
figure 4

Thermal behavior in the core of the isotropic sphere with \(k_{11} = 100\) and \(\varvec{k}_{22} = \varvec{k}_{33} = \left[ {200; 200; 200} \right]\)

Full size image

3.2 Scenario 2

Most of the simulation conditions of the previous scenario were maintained. The conductivities of the first layer (of radius \(r_{2}\)) in the orthogonal directions were changed to \(\varvec{k}_{22} = \left[ {0.2;10;5} \right]\) and \(\left[ {10;0.2;5} \right]\).

3.2.1 Steady-State Performance

In this section, we present simulation data after the system has reached its steady-state. For illustrative purposes and clarity, some 3D figures are included. Figure 5 shows the temperature profile for two scenarios with different properties at the inner layer: \(\left[ {0.2;10;5} \right]\) (Fig. 5a) and \(\left[ {10;0.2;5} \right]\) (Fig. 5b). Bear in mind that this figure also shows the heat flux generated by the temperature difference but affected by the orthotropy present in its two layers. Arrows in Fig. 5 indicate the preferential direction of heat flow. In Fig. 5b, the \(x\)-axis temperature of a point on layer two is about 40 °C, but, for that same point, the y-axis temperature is about 75 °C. Since there is a temperature difference, the heating of neighboring points across both axes will differ. Thus, heating due to the composite sphere will be affected, as shown by its temperature profiles and heat flow preferential direction.

Fig. 5
figure 5

Steady-state temperature profiles (top) and heat fluxes (bottom) for two different configurations of the thermal conductivity at the inner layer

Full size image

3.2.2 Transient State

The thermal mathematical model was solved numerically but randomly changing a few parameters. Figure 6 shows the corresponding temperature profile and the contour plots after 5 s and 150 s have elapsed (Fig. 6a, b, respectively). As observed, the orthotropy characteristics of the shells have a crucial effect on the temperature profiles, and consequently, on the preferential directions of the heat flow. This last aspect impacts the applications of this type of morphology.

Fig. 6
figure 6

Transient temperature profiles for \(k_{11} = 200,\varvec{k}_{22} = \left[ {10; 0.2; 5} \right],\) and \(\varvec{k}_{33} = \left[ {40; 80; 120} \right]\)

Full size image

Figure 7 shows two examples for determining heat flow per unit area of a couple of orthotropic shells, with different volumetric heating (microwaves) conditions that are kept constant with time and position (250 \({\text{W}} \cdot {\text{m}}^{ - 3}\) and 200 \({\text{W}} \cdot {\text{m}}^{ - 3}\)). For both cases, \(\varvec{k}_{22} = \left[ {10;0.2;5} \right]\). But, in the first case (Fig. 7a) both \(k_{11}\) and \(k_{33}\) are smaller than for the second one (Fig. 7b). Since the composite sphere has an initial temperature below that of the liquid, heat will initially flow into the former. It is observed in the concavity of both heat flow curves. It is worth remarking that we adopted the thermodynamic convention where heat output is given by (+) and heat input is provided by (−). Also, the core always generates heat because of its interaction with the energy being transported by the electromagnetic field. As an example of the effects that orthotropy may have, we decided to plot the temperature profiles corresponding to Fig. 7a in Fig. 8. Note that the effect is consistently observed in the profiles, and thus, in the heat flow direction. Here, we selected four instants of time for better assessing the evolution of the profiles: 5 s (Fig. 8a), 75 s (Fig. 8b), 150 s (Fig. 8c), and 350 s (Fig. 8d).

Fig. 7
figure 7

Heat flux rate for two composite spheres

Full size image
Fig. 8
figure 8

Temperature profiles for \(k_{11} = 100, \varvec{k}_{22} = \left[ {10;0.2;5} \right],\varvec{k}_{33} = \left[ {6;0.8;4} \right]\) generated after (a) 5 s, (b) 75 s, (c) 150 s, and (d) 350 s

Full size image

3.3 Scenario 3

As before, some of the simulation conditions of the previous scenario were maintained. While \(k_{11} = 1000,\) the conductivities of the first and second layers are kept equal, \(\varvec{k}_{22} = \varvec{k}_{33} = \left[ {1;140;1} \right]\). Figure 9 includes the simulated transient state temperature profiles, as well as the preferred heat flow direction for this scenario, and at two different time instants: after 5 s (Fig. 9a) and after 250 s (Fig. 9b). Starting at this figure, it becomes evident that having orthotropy in the conductivities affects the preferential direction of heat flow to its surroundings. Bear in mind that the inner sphere considers constant thermophysical properties, including thermal conductivity across its volume.

Fig. 9
figure 9

Temperature profiles for \(k_{11} = 1000, \varvec{k}_{22} = \varvec{k}_{33} = \left[ {1;140;1} \right]\), after (a) 5 s and (b) 250 s. The lower figures show the heat flow preferred direction

Full size image

3.4 Scenario 4

Simulation conditions of previous scenarios were maintained. While \(k_{11} = 1000,\) the conductivities of the first and second shells are kept equal, \(\varvec{k}_{22} = \varvec{k}_{33} = \left[ {140;1;140} \right]\). As in past cases, Fig. 10 includes the simulated transient state temperature profiles, and the preferred heat flow direction after 5 s (Fig. 10a) and after 250 s (Fig. 10b). This scenario clearly shows the variation of the temperature profile due to the orthotropic variation of thermal conductivity. We assume that the core possesses a single thermal conductivity, while the layers exhibit the same orthotropic anisotropy. Regarding temperature profiles of the composite sphere, Fig. 11a shows the variation as a function of time and radius. It can be observed that the system reaches a steady-state after 150 s. Likewise, the outer layer loses heat toward its surroundings, and hence, temperature varies. Figure 11b shows a 3D plot of the preferential heat flow direction.

Fig. 10
figure 10

Temperature profiles for \(k_{11} = 1000, \varvec{k}_{22} = \varvec{k}_{33} = \left[ {140;1;140} \right]\), and after (a) 5 s and (b) 250 s

Full size image
Fig. 11
figure 11

(a) Temperature profiles and (b) heat flow inside the compound sphere with \(\rho_{1} = 35\), \(\rho_{2} = 15\), \(\rho_{3} = 5\), \(c_{p1} :c_{p3} = 6:1, c_{p1} :c_{p2} = 2:1\), and \(k_{11} = 1000,\varvec{k}_{22} = \varvec{k}_{33} = \left[ {54; 54; 54} \right].\)

Full size image

4 Conclusions

This article tackled the mathematical model of a thermal system that included the effect of orthotropy in heterogeneous conditions. Such a system included a composite sphere with two layers (or shells) and a core with high magnetic permeability and electric permittivity. It allows the core to absorb an electromagnetic field and to transform it into thermal energy. The outer layers have known thermodynamic properties, but their thermal conductivities vary in the direction of perpendicular unitary vectors. We observed that a previous determination of this property is paramount, especially when a homogeneous and uniform thermal energy distribution is required. For the analyzed scenarios, our developed software generated expected results, under several simulated experimental conditions. Consequently, our contribution is twofold. On the one hand, we provided a way for easily simulating the effect of orthotropic thermal conductivities in heat generation. On the other, we showed the impact that such kind of properties has for nanoparticles that absorb microwaves. It was shown through temperature profiles, and heat flows for some selected scenarios.