1 Introduction

Natural convection (NC) is a fundamental method for heat transfer (HT) that represents the heat displacement between the mobile fluid and the surface with different temperatures. There are two main objectives for studying this phenomenon: comprehending the physical mechanisms and considering the calculation approaches. In HT enhancement, various shapes and novel materials have helped many researchers. For instance, a porous medium with vast applications contains a solid network connected by empty pores or spaces. Furthermore, adding solid materials with nanometer dimensions is among the solutions that have attracted significant attention. With higher thermal conductivity, such materials improve HT in various thermal systems.

Walker and Homsy [1] primarily studied NC in a cavity in this regard. Hussein and Mustafa [2] investigated NC in a fully open parallelogram cavity for the first time by using water as the base fluid and copper nanoparticles. It was revealed that by increasing the volume fraction and Rayleigh number (Ra) of the nanoparticles, the average Nusselt number (Nu) is increased. Parvin and Akter [3] examined the impact of magnetic parameters on NC HT in a prismatic enclosure with an uneven temperature distribution on the bottom wall. They revealed a direct relation between the Hartmann number (Ha) and temperature while observing an inverse relation to velocity variation. Sivaraj and Sheremet [4] quantitatively studied the NC HT in a porous medium with downward slopes and a solid heater in the middle. They found that non-linear changes in the average Nusselt number (Nu) are caused by incrementing the applied magnetic field (B) angle.

Motlagh and Soltanipour [5] used the non-homogeneous two-phase Buongiorno's model to assess the NC HT within an inclined square cavity. According to their findings, the average Nusselt number (Nu) remains almost constant at low Rayleigh number (Ra), with the increase of the slope angle, regardless of the volume fraction of the nanoparticles. Janagi et al [6] identified the NC flow and HT of cold water in a square porous cavity. They revealed that by increasing the Darcy number and porosity increases the HT rate. The effect of the baffle on NC HT in a C-shaped cavity with a magnetic field was quantitatively evaluated by Abedini et al [7]. Their simulations indicated that by increasing the cavity dimensions ratio, Nu increases. Forced convection HT of water–copper nanofluid was assessed by Hassanpour et al [8] through a magnetic field using the finite volume method. Rashad et al [9] investigated the effect of the location and size of the heat source and heat sink on entropy generation and NC HT in a sloping porous cavity. It was revealed that by increasing the volume fraction of nanofluids, the entropy generation reduces, thus decreasing the irreversibility of HT.

Salari et al [10] numerically simulated the NC of two immiscible fluids within a rectangular container utilising aluminium oxide nanofluid and water. NC HT was examined by Ahmed et al [11] for two porous finned triangular cavities under a magnetic field. Copper was used as the nanoparticle and water as the base fluid. They also considered Darcy's model for the porous media. Alnaqi et al [12] quantitatively investigated the effects of magnetic field and radiation on the nanofluid-generated entropy and HT rate in a diagonal square cavity with conductive fins. They revealed that by addition of nanofluid with a concentration of 6% in the absence of radiation results in an HT rate increase by about 5.9% and entropy generation by 16.6%.

Yu et al [13] studied the HT of molten salt and SiO2 nanoparticles within a cylindrical cavity was simultaneously using experimental and numerical approaches. Moreover, Dogonchi et al [14] assessed the effect of nanoparticles' shape numerically on NC HT in a square-shaped porous medium with an oval-shaped cavity. Geridonmez et al [15] studied the MHD water–Al2O3 nanofluid flow numerically under a heater. They found that by increasing the heater's length, Ra and nanoparticle concentration, the HT rate increases. Dogonchi et al [16] used the finite element approach to examine the MHD NC of water–copper fluid in a square chamber using a wavy circular heater. Sadeghi et al [17] numerically investigated NC HT of the water as the base fluid and Al2O3 as nanoparticles using the finite element technique in a chamber with innovative geometry and a wavy wall such as a trapezoidal heater. They observed that the highest HT rate was achieved with a higher Ra and lower Hartmann numbers. Sivasankaran et al [18] numerically studied the Casson fluid HT in a square cavity with a porous material considering the thermal radiation parameter (Rd). It was revealed that the characteristics of HT improve by raising the Caisson fluid parameter. However, by increasing the thermal radiation parameter, the HT becomes less favorable [19,20,21,22,23,24,25,26].

The present study deals with the fluid flow and heat transfer in porous media. For this purpose, the effects of TiO2–Al2O3 hybrid nanoparticles on these concentrates and processes were investigated on a base fluid containing water and ethylene glycol (50\(/\)50). The nanoparticle is calculated with a constant volume fraction of 0.05 and a shape factor of 5.7. Considering the problem conditions, the governing equations comprising momentum, continuity and energy equations were obtained. The similarity solutions were used to transform the resulting partial differential equations (PDEs) into ordinary differential equations (ODEs) describing the flow and energy functions. Then considering the boundary conditions, the problem was solved. The ODEs were solved using the non-commercial software Flex PDE using the finite numerical solution and element discretisation techniques.

2 Problem formulation and numerical approach

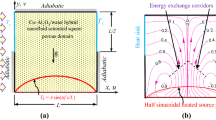
Figure 1a displays the geometry of the problem with associated boundary circumstances. The base fluid was water–ethylene glycol (50\(/\)50) with TiO2–Al2O3 as the hybrid nanoparticles. Using the non-commercial Flex PDE software, the ODEs were discretised and solved based on the finite element method. The effect of magnetic field, porosity and heat radiation was identified based on the HT rate and fluid flow, thus determining the average Nusselt magnitude.

Fig. 1
figure 1

(a) The geometry and boundary conditions and (b) adaptive mesh refinement.

Full size image

The momentum, continuity and energy equations are presented as follows [27]:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$
(1)
$$ \frac{{\mu_{nf} }}{K}u - \sigma_{hnf} B_{0}^{2} \left[ {v\left( {{\text{sin}}\gamma } \right)\left( {{\text{cos}}\gamma } \right) - u\left( {{\text{sin}}\gamma } \right)^{2} } \right] = - \frac{\partial p}{{\partial x}}, $$
(2)
$$\begin{aligned} &\frac{{\mu_{nf} }}{K}v - \sigma_{hnf} B_{0}^{2} \left[ {u\left( {{\text{sin}}\gamma } \right)\left( {{\text{cos}}\gamma } \right) - v\left( {{\text{cos}}\gamma } \right)^{2} } \right]\\ &\quad = - \frac{\partial p}{{\partial x}} + g\left( {\rho \beta } \right)_{hnf} \left( {T - T_{c} } \right), \end{aligned}$$
(3)
$$ \begin{aligned} & \frac{1}{\varepsilon }\left[ {\left( {\rho c_{p} } \right)_{hnf}^{ - 1} \frac{{\partial q_{r} }}{\partial y} + \left( {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right)} \right]\\ &\quad = k_{hnf} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)\left( {\rho c_{p} } \right)_{hnf}^{ - 1} , \\ & q_{r} = - \left( {\frac{{4\sigma_{e} }}{{3\beta_{r} }}} \right)\left( {\frac{{\partial T^{4} }}{\partial y}} \right),\;T^{4} \cong - 3T_{c}^{4} + {4}T_{c}^{3} {\text{T}}. \\ \end{aligned} $$
(4)

Here, \(\beta \) is the thermal expansion coefficient, K is the permeability, \({\sigma }_{e}\) is the electrical conductivity, \(\varepsilon \) is the porosity of the medium, \(\rho \) is the density and \({q}_{r}\) is the radiative heat flux.

The formulation for hybrid nanoparticles is also presented below [27]. The hybrid nanofluid (hnf) viscosity and thermal conductivity are given in eqs (9) and (10) [28]:

$${\rho }_{hnf}={\rho }_{f}\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+{\phi }_{1}\left(\frac{{\rho }_{{s}_{1}}}{{\rho }_{f}}\right)\right]+{\phi }_{2}{\rho }_{{s}_{2}},$$
(5)
$$\begin{aligned}{(\rho \beta )}_{hnf}&={(\rho \beta )}_{f}\left(1-{\phi }_{2}\right)\left[\left(1-{\phi }_{1}\right)+{\phi }_{1}\left(\frac{{(\rho \beta )}_{{s}_{1}}}{{(\rho \beta )}_{f}}\right)\right]\\\ &\quad +{\phi }_{2}{(\rho \beta )}_{{s}_{2}},\end{aligned}$$
(6)
$$\begin{aligned}{(\rho {c}_{p})}_{hnf}&={(\rho {c}_{p})}_{f}(1{-}{\phi }_{2})\left[\!(1{-}{\phi }_{1}){+}{\phi }_{1}\left(\!\frac{{(\rho {c}_{p})}_{{s}_{1}}}{{(\rho {c}_{p})}_{f}}\!\right)\!\right]\\ &\quad +{\phi }_{2}{(\rho {c}_{p})}_{{s}_{2}},\end{aligned}$$
(7)
$$\frac{{\sigma }_{hnf}}{{\sigma }_{bf}}=1+\frac{3\phi [{\sigma }_{1}{\phi }_{1}+{\sigma }_{2}{\phi }_{2}-{\sigma }_{bf}\left({\phi }_{1}+{\phi }_{2}\right)]}{\left[ \left({\sigma }_{1}{\phi }_{1}+{\sigma }_{2}{\phi }_{2}+2\phi {\sigma }_{bf}\right)-\phi {\sigma }_{bf}(\left({\sigma }_{1}{\phi }_{1}+{\sigma }_{2}{\phi }_{2}\right)-{\sigma }_{bf}({\phi }_{1}+{\phi }_{2}))\right]},^{\phantom{\dfrac{\sum}{2}}}$$
(8)
$$\begin{aligned}&\frac{{k}_{hnf}}{{k}_{bf}} =\frac{{k}_{{s}_{2}}+\left(s-1\right){k}_{bf}-(s-1){\phi }_{2}({k}_{bf}-{k}_{{s}_{2}})}{{k}_{{s}_{2}}+\left(s-1\right){k}_{bf}+{\phi }_{2}({k}_{bf}-{k}_{{s}_{2}})}, \\ &\frac{{k}_{bf}}{{k}_{f}}=\frac{{k}_{{s}_{1}}+\left(s-1\right){k}_{f}-(s-1){\phi }_{1}({k}_{f}-{k}_{{s}_{1}})}{{k}_{{s}_{1}}+\left(s-1\right){k}_{f}+{\phi }_{1}({k}_{f}-{k}_{{s}_{1}})},\end{aligned}$$
(9)
$${\mu }_{hnf}=\frac{{\mu }_{f}}{{(1-{\phi }_{1})}^{2.5}{(1-{\phi }_{2})}^{2.5}}.$$
(10)

Here, \(\phi \) is the nanoparticle volume fraction, \(\mu \) is the dynamic viscosity, \({c}_{p}\) is the specific heat capacity, \({s}_{1}\) is the first solid nanoparticle, \({s}_{2}\) is the second solid nanoparticle and k is the thermal conductivity.

The thermo-physical properties of the nanoparticles and base fluid are shown in table 1 [29,30].

Table 1 The thermo-physical features of ethylene glycol–water and hybrid nanoparticles [29,30].
Full size table

Equation (11) displays the dimensionless parameters and stream function (\(\Psi \)).

$${\begin{aligned} & v = - \frac{\partial \psi }{{\partial x}}, \quad\;\; u = \frac{\partial \psi }{{\partial y}}, \quad\;\;{\Delta }T = \frac{{Lq^{\prime\prime}}}{{k_{f} }}, \\ & \theta = \frac{{\left( {T - T_{c} } \right)}}{{{\Delta }T}},\quad\;\; \left( {X,Y} \right) = \frac{{\left( {x,y} \right)}}{L},\quad\;\; {\Psi } = \frac{\psi }{{\alpha_{nf} }}. \\ \end{aligned}}$$
(11)

Here, \(\theta \), X and Y correspond to the dimensionless temperature and Cartesian coordinates, respectively.

Equations (12) and (13) represent the concluding terms for the governing equations. The considered constant parameters are described by eq. (14). Furthermore, the conditions for inner and outer walls are obtained by eq. (15) [27].

$$\begin{aligned} &\frac{{\partial^{2} {\Psi }}}{{\partial X^{2} }} + \frac{{\partial^{2} {\Psi }}}{{\partial Y^{2} }} \\&\quad = - \frac{{A_{6} }}{{A_{5} }}Ha\left[\frac{{\partial^{2}{\Psi }}}{{\partial Y^{2} }}\left( {\sin^{2} \gamma } \right) +\frac{{\partial^{2} {\Psi }}}{{\partial X^{2} }}\left( {\cos^{2}\gamma } \right)\right.\\ &\qquad + \left. 2\frac{{\partial^{2}{\Psi }}}{\partial X\partial Y}\left( {{\text{sin}}\gamma }\right)\left( {{\text{cos}}\gamma } \right) \right] -\frac{{A_{3} A_{2} }}{{A_{4} A_{5} }}\frac{\partial \theta }{{\partial X}}Ra, \end{aligned}$$
(12)
$$\begin{aligned} &\varepsilon \left[\left(\frac{{\partial }^{2}\theta }{\partial {X}^{2}}\right)+\left(1+\frac{4}{3}\left(\frac{{k}_{f}}{{k}_{hnf}}\right)Rd\right)\left(\frac{{\partial }^{2}\theta }{\partial {Y}^{2}}\right)\right]\\ &\quad =-\frac{\partial \theta }{\partial X}\frac{\partial\Psi }{\partial X}+\frac{\partial\Psi }{\partial Y}\frac{\partial \theta }{\partial X},\end{aligned}$$
(13)
$$ \begin{aligned} A_{1} & = \frac{{\rho_{hnf} }}{{\rho_{f} }},\quad A_{2} = \frac{{\left( {\rho c_{p} } \right)_{hnf} }}{{\left( {\rho c_{p} } \right)_{f} }},\quad A_{3} = \frac{{\left( {\rho \beta } \right)_{hnf} }}{{\left( {\rho \beta } \right)_{f} }},\\ A_{4} &= \frac{{k_{hnf} }}{{k_{f} }},\quad A_{5} = \frac{{\mu_{hnf} }}{{\mu_{f} }},\quad A_{6} = \frac{{\sigma_{hnf} }}{{\sigma_{f} }}, \\ Ra & = \left( {\frac{{gK\left( {\rho \beta } \right)_{f} }}{{\mu_{f} \alpha_{f} }}} \right)L{\Delta }T,\quad Ha = \frac{{\sigma_{f} KB_{0}^{2} }}{{\mu_{f} }},\\ \delta_{s} &= \frac{{k_{hnf} }}{{\left[ {k_{s} \left( {1 - \varepsilon } \right)} \right]}}, \\ \end{aligned} $$
(14)
$${\begin{aligned} & {\Psi } = 0.0,\;{\text{on}}\;{\text{all}}\;{\text{the}}\;{\text{walls}} \\ & \theta_{nf} = \theta_{s} = 0.0,\;{\text{on}}\;{\text{the}}\;{\text{outer}}\;{\text{wall}} \\ & \theta_{nf} = \theta_{s} = {1}.0,\;{\text{on}}\;{\text{the}}\;{\text{inner}}\;{\text{wall}}. \\ \end{aligned}}$$
(15)

The local (Loc) and average Nusselt numbers are obtained as

$${Nu}_{\text{Loc}}=\left(\frac{{k}_{hnf}}{{k}_{f}}\right)\left(\frac{1}{\theta }\right)\left[1+\frac{4}{3}Rd\left(\frac{{k}_{hnf}}{{k}_{f}}\right)\right]$$
(16)
$${Nu}_{\text{av}}=\frac{1}{2\pi }{\int }_{0}^{2\pi }{Nu}_{\text{Loc}}{\text{d}}r.$$
(17)

Here, \({\delta }_{s}\), x and y correspond to the modified thermal conductivity ratio and Cartesian coordinates, respectively.

NuLoc is calculated on the surface of the geometry (S).

FlexPDE is oriented by Galerkin's standard finite element method (GFEM), which works with linear or cubical second-order interpolation among the quadrilaterals and triangles. To reach accurate meshing and target accuracy, the software continually calculates the solution error thus refining the meshing structure.

3 Grid independence testing, meshing and validation

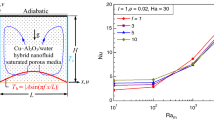
Figure 1b shows the final modified meshing. As can be seen, meshing is more adaptive in the edge zones. The validity of final unstructured and adaptive meshing was proved by the grid independence test. The grid analysis is shown in figure 2a for three various grid sizes. NuLoc was determined for each grid size. Finally, the grid = 24,966 was utilised to decrease the CPU computation time.

Fig. 2
figure 2

(a) The comparison of NuLoc for various grid sizes when Ra = 200, Ha = 10, Rd = 0.5, \(\varepsilon =0.7\) and (b) the validation of ongoing study with Khanfar et al [31]. \(\phi = 0.01\) and \(\Pr = 6.2\) (Cu–water).

Full size image

To validate the results, the findings of the survey were compared with those of Khanfar et al [31] (figure 2b), with a correct comparative overlap in the Nuav values. Nanofluids are used to promote heat transmission in a two-dimensional cavity and several relevant parameters are examined. A model is created to examine how well nanofluids in a cavity transfer heat while accounting for solid particle dispersion by Khanfar et al Consider CuO nanofluid and the percentage of volume fraction is equal to 0.01.

4 Results and discussion

This section deals with the effect of different physical factors on the fluid flow behaviour and HT rate of the nanofluid.

The variation of different parameters in this study is shown in table 2.

Table 2 The variation of different parameters in this study.
Full size table

4.1 Effect of porosity parameter on HT features

The analysis of streamlines and the isotherm condition is shown in figure 3 for different porosity parameters. The porosity parameters (ε) were chosen as 0.5, 0.7 and 0.9. Moreover, Ra, Rd and Ha are 200, 0.5 and 10, respectively. According to the results, by increasing ε, the temperature is reduced within the cavity. The streamlined contour is also displayed for different sides of the cavity (figure 3). The integrated effects of temperature gradient and gravitational force were obtained for the formation of the vortices. As observed, both the intensity and velocity of the vortices within the cavity are reduced by the increased ε. Besides, by increasing ε, the size of the vortices decreases.

Fig. 3
figure 3

(a) The streamlines and (b) isotherms for ε = 0.5, 0.7 and 0.9.

Full size image

NuLoc within the cavity concerning different porosities is displayed in figure 4a. As seen, the maximum Nu occurs for porosity = 0.5. Thus, the reduced porosity and increased convective flow and the HT rate resulted in a higher Nu. According to the energy equation, an increase in epsilon results in a decrease in the ratio of convective heat transfer to conductive heat transfer, consequently leading to a reduction in Nu. The temperature distribution for various porosities is displayed in figure 4b. It was found that the temperature increased close to the inner wall. Moreover, the increased temperature and ε were directly related.

Fig. 4
figure 4

(a) The NuLoc plot and (b) the temperature plot for ε = 0.5, 0.7 and 0.9.

Full size image

4.2 Effect of magnetic field on HT characteristics

Figure 5 displays the isotherm condition (b) and streamlines (a) for Ha = 0, 10 and 20. The values of the ε, Ra and Rd were 0.7, 200 and 0.5, respectively. According to the results, the absence or existence of the magnetic field results in various flow patterns inside the cavity. Taking into account the streamlines within the cavity, it was found that the strength of the vortices in both the clockwise and counterclockwise directions significantly decreased with increasing magnetic field. Conversely, electric vortices were induced in the current by incrementing the magnetic field resulting in the incremented resistance. Therefore, the HT penetration is reduced from the hot to the cold wall thus reducing HT. The mixture is electrically conductive due to the presence of ions from the hybrid nanofluid that produces electric vortices due to the Lorentz force in the presence of a magnetic field as governed by eqs (2) and (3).

Fig. 5
figure 5

(a) The streamlines and (b) isotherms for Ha = 0, 10 and 20.

Full size image

The effect of Ha on NuLoc is presented in figure 6a. As observed, an inverse relationship exists between HT and Ha owing to Lorentz forces and electrical vortices resisting the convective flow. Therefore, NuLoc is reduced by increasing Ha. Figure 6b shows the temperature distribution for different values of Ha. According to the acquired data, without a magnetic field, a completely different temperature profile was developed. As the intensity of the magnetic field increases due to increased friction work, the temperature profile increases.

Fig. 6
figure 6

(a) The NuLoc plot and (b) the temperature plot for Ha = 0, 10 and 20.

Full size image

4.3 Effects of Ra on the HT characteristics

Figure 7 represents the streamlines (a) and isotherm condition (b) for Ra = 100, 200 and 300. Here, ε, Ha and Rd are 0.7, 10 and 0.5, respectively. It is worth stating that Ra is the ratio of the thermal diffusivity to the buoyancy force. Therefore, the effect of buoyancy forces is negligible at low Ra and HT is associated with higher conductivity. According to figure 7, by increasing Ra, both fluid flow and molecular motion increase. Based on the streamlines, the value of the stream function significantly increases at the centre of the vortices by the increased Ra. The stream function is maximum at Ra = 300. The vortex strength and the chamber fluid flow velocity are incremented by the increase in buoyancy force in this situation.

Fig. 7
figure 7

(a) The streamlines and (b) isotherms for Ra = 100, 200 and 300.

Full size image

As seen in figure 8a, the HT rate is improved by the augmentation of Ra as well as the increased buoyancy forces. Thus, NuLoc is also incremented. Figure 8b shows the temperature distribution for various Ra. From the findings, it can be seen that the temperature graph's curvature grows as Ra rises. Furthermore, the irregularity increases with the increased Ra, thus increasing the HT rate.

Fig. 8
figure 8

(a) The NuLoc plot and (b) the temperature plot for Ra = 100, 200 and 300.

Full size image

4.4 Effect of radiation parameter on HT features

Figure 9 represents the isotherm condition (b) and streamlines (a) based on different values of Rd (0, 0.5 and 1). The Ha, porosity parameter and Ra for the simulation in this part were 0.7, 10 and 200, respectively. According to the results, without Rd, the streamlines appear to be denser. However, they have comparatively lower intensity. Moreover, the results revealed that for all three Rd values, the temperature profile increases.

Fig. 9
figure 9

(a) The streamlines and (b) isotherms for Rd = 0, 0.5 and 1.

Full size image

The NuLoc for different radiation settings is shown in figure 10a. HT is reduced by augmentation of this parameter owing to radiant energy losses thus decrementing NuLoc. The temperature distribution for various values of Rd is shown in figure 10b. According to the results, the temperature profile is less affected by altering Rd.

Fig. 10
figure 10

(a) The NuLoc plot and (b) the temperature plot for Rd = 0, 0.5 and 1.

Full size image

4.5 Optimisation, variance analysis and correlation

As a test design, the Taguchi method is used to achieve a state where the return characteristic tends to have the least fluctuation and the ideal state [32,33]. Generally, based on the intended objective, three definable and desirable design features in the Taguchi technique include the highest, the nominal value and the lowest values. Rd, Ha, ε and Ra are the considered variables. Table 3 presents the information on the included variables. It should be noted that the number of tests was reduced from 81 to 9 using the Taguchi approach.

Table 3 The tests designed by the Taguchi method.
Full size table

The problem is modelled by response surface methodology (RSM) as an optimisation technique, through a set of statistical and mathematical methods. The reduced calculation cost is one of the benefits of this technique. First, this method was utilised for laboratory data, which was later expanded for modelling and numerical research. The two approaches are different based on the type of errors. This method highly required a correlation to assess the effects of variable parameters on the objective function. The general quadratic polynomial relation in RSM is as follows:

$$\begin{aligned} y&={a}_{0}+\sum\limits_{i=1}^{n}{a}_{i}{x}_{i}+\sum\limits_{i=1}^{n}{a}_{ii}{x}_{i}^{2}+\sum_{i=1}^{n}\sum_{j=1}^{n}{a}_{ij}{x}_{i}{x}_{j}+\xi ,\\ &\quad i<j. \end{aligned}$$
(18)

  • The predicted response, linear, constant and quadratic coefficient and interaction factor are defined as y, ai, a0, aii and aij.

  • The error is represented by the design parameters described as \({x}_{i}\), \({x}_{j}\) and \(\xi \).

The examination of parameters in the prediction regression utilising variance analysis (ANOVA) is shown in table 4. ANOVA helps to comprehend and assess the discrepancy scale of the actual results and estimated outcomes. In the present work, a proper overlap is shown by this differentiation between real results and predicted outcomes with the R-squared value of 89.9% (figure 11).

Table 4 The variance analysis (ANOVA).
Full size table
Fig. 11
figure 11

The predicted vs. actual of Nuav.

Full size image

For this purpose, the maximum Nuav in the obtained correlation is

$$\begin{aligned}{Nu}_{\text{av}}&=20.099-5.04\left(\varepsilon \right)-0.714(Ha)+0.033(Ra)\\ &\quad -0.236(Rd).\end{aligned}$$
(19)

The optimum values for the operating variables in the correlation are listed in table 5, which results in the maximum Nu.

Table 5 The outcome of the optimisation procedure by RSM.
Full size table

Figure 11 shows the actual and predicted values for the Nuav relative to the hypothetical line.

The combined effect of the involved operating factors on Nu is also shown in figure 12.

Fig. 12
figure 12

The effects of various operating parameters on Nuav by RSM

Full size image

These values are presented using the response surface technique. As observed, the Nu increases as Ra increases. It should be noted that Nuav decreases as Ha, Rd and ε increase.

5 Conclusions

In the present paper, the fluid flow and HT in a porous medium were numerically examined. An investigation was also performed on the effect of thermal radiation field, porosity and magnetic parameters on the flow pattern and HT rate. Moreover, using the appropriate correlations, Nuav was determined. Using the RSM, the optimal values were also determined. Mainly, in the present work, the following findings were obtained:

  • The velocity and strength of the vortices within the cavity are reduced by increasing ε. Moreover, by raising the porosity value, the size of the vortices is reduced.

  • The increased Ha significantly amplifies the intensity of the vortices.

  • The co-flowing streamlines and HT rate are caused by the higher Ha owing to Lorentz forces and resistance from vortices induced electrically. Thus, NuLoc is decreased by incrementing the Ha.

  • The HT by convection is improved with an increased Ra, associated with the intensified buoyancy forces. Therefore, NuLoc correspondingly increases.

  • For Nuav, the optimal values are ε = 0.52, Ra = 299.4, Ha = 1.0 and Rd = 0.133.

In future, the influence of other parameters on vortex dynamics and heat transfer may be studied and the experimental validation of the numerical results is important.