1 Introduction

Lasers can cause damage to optical materials. Numerous theoretical and experimental works on this subject have been conducted over the past fifty years. Since pulsed laser systems are extensively employed in engineering materials, non-destructive detection, and material description, the stimulation of thermoelastic plane waves in materials by a pulsed laser is of considerable significance. The absorption of a laser pulse raises the temperature of a solid at a specific point, leading to thermal expansion and the production of a thermoelastic waves. There are two things to consider when using ultra-short pulsed lasers to heat materials [1]. Materials can be heated to hundreds of Kelvin degrees with the help of a powerful and focused laser beam. Adapting the spectrum illumination to the black body model allows for high-resolution remote temperature monitoring of continuous wave laser heat generation. There are several benefits to heat materials with a pulsed laser. However, this method also necessitates fast electronics and labor-intensive temperature determination processes, as the temprature change occurs in nanoseconds [2].

Laser heating has several uses, including but not limited to softening and hardening materials, annealing crystals or polycrystalline materials, diffusing dopants in semiconductors, synthesizing compounds and thin films, and polymerizing polymers. Laser processing has been used to remove energy barriers for phase transitions, promote thermally driven reactions, and increase bulk diffusion. The ability to spatially and temporally localize the laser illumination has significant benefits. When the thermal gradients are generated, sample temperatures can be increased to levels much higher than those that can be maintained in the sample chamber. Materials in diamond anvil cells, for instance, can be heated to high temperatures [3].

The pulse duration is crucial in pulsed laser heating because it determines whether or not the material is in thermodynamic equilibrium when the temperature is measured. Due to the length and duration of the pulse, several phenomena may occur. For example, a high-energy pulsed laser is used to create shock waves. In this case, the leading edge of the laser pulse ionizes the sample, causing the laser energy to be absorbed into the surface of the sample and creating a shock wave that travels deeper into the sample [4]. Now, laser pulses with a time scale of femtoseconds can be used to make non-thermal and nonlinear conditions inside a material and remove particles from its surface [5, 6]. High-impact and short laser pulses are widely used in the diamond cutting and semiconductor industries, among many other applications. In such cases, the temperature measurement is not important, but the rapid deposition of the concentrated energy is. After when a semiconductor material or metal absorbs the laser energy, the leading edge deposits that energy into the electrons, after which the excited electrons collide with each other and turn into phonons. The phonons are then heated and diffused so that they can be used to determine the lattice temperature [7, 8]. The practical importance of the end result of laser treatment cannot be overemphasized. Laser heat transfer offers several advantages compared to traditional methods, including accuracy, localized treatment, and low cost [9].

The concept of thermoelasticity is the framework under which the semiconductor materials can be classified as elastic materials. Semiconductors have recently come to the forefront of interest due to their application in solar-powered electricity generation combined with exposure to laser pulses [10]. Some examples include solar cells, displays, transistors, and the increasing industrial applications of nanostructures derived from semiconductor materials. These applications can be found in various sub-fields of electrical and mechanical engineering. Recently, the idea of photo-thermal energy has been applied to semiconductor materials to find appropriate ways to generate energy that is beneficial to our environment. Several physical and mathematical frameworks were examined to provide an accurate description of the overlap between thermo-photometric and thermoelastic frameworks. Gordon et al. [11] began their investigation on photoelectron spectroscopy using elastic electron deformation. The photoacoustic spectroscopy method is a technique for determining the speed of sound in a semiconductor by using laser pulses as its light source. This technique is considered as one of the most sensitive analytical procedures in the field [12]. Numerous applications in modern engineering take the advantage of wave propagation induced by electrical deformations of flexible semiconductors by photo-thermal processing [13].

Photo-excited carriers routinely cause elastic and electro-mechanical sample distortion. Photo-induced plasmas in semiconductors cause crystal lattice distortion, also known as conductive voltage distortion and valence bands in semiconductors, which is the basic hypothesis underlying the electronic distortion process. For this reason, the specimen may experience local pressure due to photo-stimulated mounts. In contrast, this strain can cause plasma waves in semiconductors through a uniform elastic and local generation process, similar to the heat wave formation method [14]. Our ever-growing industries are widely using semiconductor materials in different areas, thanks to their superior features. However, the intrinsic properties of a semiconductor material also differ when it is subjected to external stimulus, such as temperature change and resistance. This is because some materials resist the internal passage of electrons and do not usually conduct electricity.

The excited electrons on the surface of semiconductor material, known as the carrier density, travel freely and produce plasma waves. When the material body temperature changes due to exposure to internal and external heat supplies and process deformations that occur throughout the microinertia mechanism of microelements, these differences appear during the thermoelasticity and electron deformation processes, respectively (TD and ED) [15]. Mechanical and thermal waves and plasma waves may be required to be studied during these operations. On the other hand, the internal particles of the elastic semiconductor move and collide, producing thermal and mechanical waves. In this case, the stresses and strains occurring in the flexible semiconductor body are related to thermomechanical effects [16]. The impact of the body microstructure is crucial in this case because it produces new wave scattering that is not possible according to the hypothesis of thermal elasticity of conventional photo-thermoelasticity.

The study of applying the traditional theory of calculus to derivatives and integrals of non-integer orders is known as fractional calculus and has recently received a lot of interest from academics in various fields. Its success stems from its demonstrated ability to properly describe a wide variety of physical processes, spanning from biophysics to astrophysics, and is not limited to mathematicians. During the development of this theory, several formulations for non-integer order operators have been made. Each of these tries to go beyond the traditional ideas of integral and derivative. The famous works of Bernhard Riemann and Joseph Liouville, as well as the improvements put out by Mkhitar Dzhrbashyan, are approaches that have stood the test of time and are now generally recognized. Also, when the standard Laplace transform was used on fractional derivatives, it was found that the second one was the same as the operator that Michele Caputo found on his own [17].Please note citation of Table 7 has been changed to Table 6. Kindly check and confirm.ok

Numerous kinds of fractional derivatives appear in published studies. They are used to deal with various engineering and scientific issues and to design the dynamic behavior of numerous systems in diverse scientific fields, including mechanics, chemical engineering, financial management, ecosystems, biological sciences, and control theory. For example, Caputo and Fabrizio [18] introduced a fractional derivative with a nonsingular kernel to characterize material heterogeneity and differences at different scales. Conventional local models of singular kernel fractional theories cannot fully explain them. However, this fractional operator had some problems: it was not local. Furthermore, the fractional order derivative's symmetric integral is not fractional. Atangana and Baleanu [19, 20] presented an expansion of [18] using the Mittag–Lefler function with a single parameter. Al-Refai [21] presented the weighted Atangana–Baleanu fractional operators and explored their characteristics due to the significance of weighted fractional derivatives for solving numerous forms of integral equations in attractive ways. In [22], a generalized model of all fractional derivative operators that come before it with a nonsingular kernel has been made. These definitions have introduced several models (see, for example, [23,24,25,26,27]).

Humans have faced the problem of heat transfer within materials since ancient times. Fourier's early writings established the mathematical roots of this phenomenon more than two centuries ago. During this time, equations explaining heat transfer in solids have proven to be effective methods for discovering heat transfer and a wide range of diffusion-like problems that arise in physical, chemical, biotechnological, earth science, and even economic problems, as well as in finance and engineering. This is due to the fact that the theoretical mathematical structure of the non-stationary heat equation, also known as the thermal diffusion equation, clearly influenced the mathematical formulation of several different physical systems in the scattering concept. These physical systems include electric current flows, mass transfer, fluid mechanics, and photon transmission [28, 29].

Coupling thermoelasticity was developed by Biot [30] to address the first problem in non-paired thermoelasticity. Due to the parabolic nature of both the heat equation and the coupled model, the second drawback still exists in both models. Many new formulations have superseded the coupled bio-theory of thermoelasticity [30]. With the help of hyperbolic heat equations, these systems overcome the problem that the thermoelastic theories of both unpaired and paired thermoelasticity have infinite diffusion rates. The concept of extended thermoelasticity with a single relaxation period for isotropic materials was established by Lord and Schulman [31], using a modified Maxwell-Catagneo law of heat transfer (termed LS theory). This model ensures that heat and distorted waves travel at a finite pace because their heat equation is of the wave type. The idea of thermoelasticity with two relaxation periods was generated by Green and Lindsay [32] by positing a unique thermoelasticity variation (called the GL model). This theory changes the heat equation and associated theoretical equations. When the medium under study has a center of symmetry, the classical Fourier equation to explain thermal conductivity remains valid. In order to consider a more comprehensive class of heat flow issues known as GN-I, GN-II, and GN-III, Green and Naghdi [33,34,35] make efforts to modify the constitutive equations. Green and Naghdi's models present a concept known as "thermal displacement gradient" in the independent constitutive variables. As a result of linearization, the thermal transfer equation for GN-I is identical to the conventional heat conduction equation, while GN-II and GN-III allow for the transmission of limited heat signals [35]. The GN-III model incorporates a thermal dampening aspect, which facilitates the dispersion of thermal energy [36,37,38,39,40].

Numerous research studies devoted to analyse and interpret the Moore-Gibson-Thompson (MGT) equation emphasizing how it is important in various fields, over the past few years. Most models are built as a third-order differential equation and have been applied to many fluid flow problems [41]. Recently, Quintanilla [42, 43] used the MGT equation to create a new model to describe the heat transfer process. Abouelregal et al. [37, 44,45,46,47] established the proposed revised heat equation after incorporating the relaxation coefficient into the GN-III framework and using the energy equation. Many papers have been written on this hypothesis since the concept of the MGT equation and other types of thermoelasticity [48,49,50,51,52,53,54,55]. When examined at different temperatures, the semiconductor materials' mechanical, electrical, and thermal properties will all show characteristic transitions. In flexible semiconductor materials, the generation of a temperature gradient due to light absorption generates an electric potential difference between the two ends of the semiconductor. Multiple authors have used conventional models to investigate topics like uncoupled and coupled plasma processes, heat transfer, and elasticity equations, as well as the numerous consequences of thermal and electrical deformation in semiconductors.

This paper is dedicated to discuss the temperature-dependent properties of semiconductor materials heated by an ultrashort pulsed laser and photo-generated plasma. The governing equations is developed by considering the concept of photo-thermal induction in semiconductor materials. The role of thermal and optical parameters in the proposed model and its practical applications in the field of thermal and optical characterization are the main objectives behind this study. To this end, the modified Moore-Gibson-Thompson (MGT) thermoelastic model is employed. Different aspects of thermoelectric deformation have been studied in semiconductors, such as coupled plasmas, thermoelastic processes and elastic waves. The set of systems’ equation with fractional derivatives are solved by applying the Laplace transform technique under some suitable boundary conditions.

2 Mathematical formulation of the model

For thermoelastic, homogeneous and isotropic semiconductors with electrical and thermal characteristics, the system of coupled hyperbolic plasma and thermo-elastic equations are as follows:

The equation of motion:

$$S_{{{{ij}},j}} + R_{i} = \varrho \ddot{u}_{i}$$
(1)

The equation that describes the constitutive relations is given by

$$S_{{{{ij}}}} = C_{{{{ijkl}}}} e_{{{{kl}}}} - \beta_{{{{ij}}}} \theta - d_{{{{nij}}}} N$$
(2)

The relations between strain and displacement are take the form:

$$2e_{{{{ij}}}} = u_{i,j} + u_{j,i} .$$
(3)

In Eqs. (1) to (3), \({S}_{\mathrm{ij}}\) denotes the stress tensor, \(N\) is the carrier density, \(\varrho\) denotes the material’s density, \({u}_{i}\) represents the displacements, \({R}_{i}\) symbolizes the body forces, and \(i,j,k\) equals \(\mathrm{1,2},3\). Additionally, \({e}_{\mathrm{ij}}\) represents the strain tensor, \({e=e}_{\mathrm{kk}}\) represents the cubical dilatation, \({d}_{\mathrm{nij}}={d}_{\mathrm{ni}}{\delta }_{\mathrm{ij}}\) represents the variance in deformation potential between the con Additionally, the thermodynamical temperature is denoted by \(\theta =T-{T}_{0}\), where \({T}_{0}\) is the location temperature.

The equation that describes the linked plasma and the thermo-elastic wave is given by [14, 16]

$$\left( {D_{{{{Eij}}}} N_{,j} } \right)_{,i} = \varrho \frac{\partial N}{{\partial t}} + \frac{1}{\tau }N + \kappa \theta + G$$
(4)

where \({D}_{\mathrm{Eij}}\) represents the diffusion constants, \(\kappa\) represents the thermal activation coupling coefficient, \(\tau\) represents the lifespan of photo-generated electron–hole pairs, and G represents the "source" term for carrier photogeneration. For example, Vasilev and Sandomirskii [56] tentatively demonstrated that the thermal activation reaction value in harmonic modulation lasers is not feasible at low temperatures. However, they later retracted this conclusion.

Cattaneo–Vernotte in [57,58,59] developed a revised Fourier law by comprising the idea of the thermal relaxation \({\tau }_{0}\) to the heat transfer rate \(\vec{F}\). This allowed for a more accurate representation of the Fourier law. The improved form of Fourier's law in this proposal can be written as follows:

$$\vec{F} + \tau_{0} { }\frac{{\partial \vec{F}}}{\partial t} = - K_{{{{ij}}}} \vec{\nabla }\theta$$
(5)

In Eq. (5), the thermal conductivity tensor is denoted by the symbol \({K}_{ij}\) which is assumed to be positive. Since the time derivative component is included here, the speed of heat propagation is limited. According to Eq. (16), the heat flow does not immediately become apparent; rather, it develops gradually throughout the growth period.

Instead of the more common entropy inequality, Green and Naghdi [33,34,35] introduced three new thermal elasticity theories based on entropy inequality. These theories were an alternative to the more common inequality of entropy. One possible representation of the enhanced Fourier law, which is based on the third kind of Green and Naghdi theory (GN-III), is as follows [34]:

$$\vec{F} = - K_{{{{ij}}}} \,\vec{\nabla }\theta - K_{{{{ij}}}}^{*} \vec{\nabla }\vartheta , \dot{\vartheta } = \theta$$
(6)

where \(\vartheta\) symbolizes the thermal displacement and the values \(K_{{{{ij}}}}^{*}\) relate to the rates of thermal conductivity. The fluctuation in the amount of internal energy \(E_{{{{in}}}}\) over time may be stated as

$$\frac{\partial }{\partial t}\left( {E_{{{{in}}}} } \right) = \varrho C_{E} \frac{\partial \theta }{{\partial t}},$$
(7)

The final equation that describes energy conservation may be stated as follows:

$$\varrho C_{E} \frac{\partial \theta }{{\partial t}} + T_{0} \frac{\partial }{\partial t}\left( {\beta_{ij} e_{ij} } \right) = - \vec{\nabla } \cdot \vec{F} + S,$$
(8)

where \(C_{E}\) denotes the specific, and \(S\) refers to the supply of the heat.

The definition of derivatives and integrals for arbitrary real orders distinguishes fractional calculus from conventional calculus. In some cases, fractional operators are more effective at simulating a phenomenon than traditional integrals and derivatives. They can also describe systems with complicated nonlinear phenomena and high-order dynamics more effectively. This is due to two primary factors. First, we are not limited to integer order and can select any order for the derivative and integral operators. Second, when the system has long-term memory, fractional order derivatives can be helpful since they depend not only on current circumstances but also on the past.

Riemann–Liouville described the type of the fractional integral of the function \(y\left( t \right)\) as order \(\alpha > 0\) as follows [60]:

$${}_{{{{RL}}}}^{{}} D_{t}^{\alpha } y\left( t \right) = \frac{1}{{{\Gamma }\left( {1 - \alpha } \right)}}\frac{{{d}}}{{{{d}}t}}\mathop \int \limits_{0}^{t} \frac{y\left( \zeta \right)}{{\left( {t - \zeta } \right)^{\alpha } }}{{d}}\zeta$$
(9)

For any function \(y\left( t \right)\) and \(\alpha \in \left( {0,1} \right)\) has the following definition for the Caputo fractional derivative:

$${}_{C}^{{}} D_{t}^{\alpha } y\left( t \right) = \mathop \int \limits_{0}^{t} \frac{{\left( {t - \zeta } \right)^{ - \alpha } }}{{{\Gamma }\left( {1 - \alpha } \right)}}y^{\prime}\left( \zeta \right){{d}}\zeta$$
(10)

The most important ideas concerning fractional operators didn't enter practical use outside of pure mathematics until the twentieth century. Today, not just mathematics but also engineering, economics, and other scientific disciplines heavily rely on this topic. In fact, by using these broader concepts, we can describe some real-world events in a way that the derivative of the correct order cannot.

Several models have lately been examined in the nonsingular kernel. Such models have attracted the attention of many scientists in the field in recent years. The basic definitions of both Riemann–Liouville and Caputo are based on a singular kernel. Caputo and Fabrizio [18, 61] can solve the singular kernel problem found in previous definitions of fractional order derivatives by using an exponential function. The formula to calculate the updated fractional derivative introduced by Caputo-Fabrizio (CF) is given in the equation below [18]:

$${}_{{{{CF}}}}^{{}} D_{t}^{\alpha } y\left( t \right) = \frac{1}{1 - \alpha }\mathop \int \limits_{0}^{t} {{e}}^{{ - \frac{\alpha }{1 - \alpha }\left( {t - \zeta } \right)}} \frac{\partial y\left( \zeta \right)}{{\partial \zeta }}{{d}}\xi ,{ }\alpha \in \left( {0,1} \right).$$
(11)

Unfortunately, various criticisms have been expressed about the fractional derivatives developed by Caputo and Fabrizio. The integral kernel in the definition of CF was nonsingular but non-local, which led to one of the criticisms made about this concept. Atangana and Baleanu (AB) [19, 20] developed two fractional derivatives that were dependent on a modified version of the Mittag–Leffler function \({E}_{\alpha }\). These fractional derivatives solved the non-singularity and non-localization of the kernel. These fractional derivatives are mainly based on the concepts of Caputo and Riemann–Liouville. In the context of the Caputo idea, the definition of the Atangana–Baleanu fractional operator of order is as follows [19, 20]:

$${}_{{{{AB}}}}^{{}} D_{t}^{\alpha } y\left( t \right) = \frac{1}{1 - \alpha }\mathop \int \limits_{0}^{t} E_{\alpha } \left[ { - \mu_{\alpha } \left( {t - \zeta } \right)^{\alpha } } \right]\frac{\partial y\left( \zeta \right)}{{\partial \zeta }}{{d}}\xi$$
(12)

where \(\mu_{\alpha } = \frac{\alpha }{1 - \alpha }\). The Laplace transform method is well-known for its significance in the field of differential equations research. The Laplace transform equation for the Atangana-Baleanu partial operator is as follows [19, 20]:

$${\mathcal{L}}\left[ {{}_{{{{AB}}}}^{{}} D_{t}^{\alpha } y\left( t \right)} \right] = \frac{{\mu_{\alpha } \left( {s^{\alpha } {\mathcal{L}}\left[ {y\left( t \right)} \right] - s^{\alpha - 1} y\left( 0 \right)} \right)}}{{\alpha \left( {s^{\alpha } + \mu_{\alpha } } \right)}},{ }s > 0$$
(13)

As a result, it is abundantly evident that the Atangana–Baleanu fractional derivative will need to use the Laplace transform at some point during the mathematical operations.

Previous research has shown that using the fractional Atangana–Baleanu derivative, denoted by (\({}_{\mathrm{AB}}{D}_{t}^{\alpha }\), rather than the conventional derivative, denoted by \(\frac{\partial }{\partial t}\), is a more reasonable alternative. On this basis, Fourier’s law (5) can be modified from a mathematical perspective to include the fractional derivative as follows:

$$\left( {1 + \tau_{0} { }{}_{{{{AB}}}}^{{}} D_{t}^{\alpha } } \right)\vec{F} = - K_{{{{ij}}}} \vec{\nabla }\theta$$
(14)

Following the incorporation of the relaxation coefficient into the GN-III model (6), Quintanilla [42, 43] and Abouelregal et al. [44,45,46] modified the heat transfer model. Based on these suggestions and with the introduction of the fractional operator, the Green and Naghdi versions of the third type will have the following modified structure:

$$\vec{F} + \tau_{0} { }{}_{{{{AB}}}}^{{}} D_{t}^{\alpha } \vec{F} = - K_{{{{ij}}}} \,\vec{\nabla }\theta - K_{{{{ij}}}}^{*} \vec{\nabla }\vartheta$$
(15)

Carrier-free charge density is produced by free electrons excited with semiconductor gap energy in fabrication when the flexible semiconductor medium is exposed to light beams from the outside. The element's electrical deformation and elastic vibrations change when light is absorbed. The overall shape of the heat equation in this scenario would be affected by the thermal flexible plasma waves. As a result, Fourier's fractional law can be modified to include plasma effects in semiconductors to become more general, as follows:

$$\left( {1 + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } } \right)\vec{F} = - K_{{{{ij}}}} \,\vec{\nabla }\theta - K_{{{{ij}}}}^{*} \vec{\nabla }\vartheta - \int {\frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}{{d}}\vec{x}}$$
(16)

The impact of photoexcitation is denoted by the concluding term \(\begin{gathered} \hfill \\ \int {\frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}{{d}}\vec{x}} \hfill \\ \end{gathered}\) in Eq. (16).

From this point forward, we will presume that the constitutive constants meet the conditions: \(C_{E} > 0\), \(K_{{{{ij}}}} > 0\), \(K_{{{{ij}}}}^{*} > 0\) and \(\tau_{0} > 0\). Also, its assumed that \(K_{{{{ij}}}} > \tau_{0} K_{{{{ij}}}}^{*}\).

The following is the solution that is obtained by differentiating the equation given above concerning the position vector \(\vec{x}\):

$$\vec{\nabla } \cdot \vec{F} + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } \left( {\vec{\nabla } \cdot \vec{F}} \right) = - \vec{\nabla } \cdot \left( {K_{ij} \,\vec{\nabla }\theta + K_{ij}^{*} \vec{\nabla }\vartheta } \right) - \frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}.$$
(17)

When Eq. (17) is substituted into Eq. (8), the improved fractional MGT heat transfer equation with a fractional operator describing the interplay between the thermal-plasma-elastic waves can be obtained as follows:

$$\left( {1 + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } } \right)\left[ {\varrho C_{E} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + T_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\beta_{{{{ij}}}} u_{i,j} } \right) - \varrho \frac{\partial Q}{{\partial t}}} \right] = \left( {K_{{{{ij}}}} \dot{\theta }_{,j} } \right)_{,i} + \left( {K_{{{{ij}}}}^{*} \theta_{,j} } \right)_{,i} + \frac{{E_{g} }}{\tau }\frac{{\partial^{2} N}}{{\partial t^{2} }}$$
(18)

We assumed that the space is flooded with an elementary magnetic field, denoted by \(\vec{H}\). This magnetic field will generate an induced electric field \(\vec{E}\) and an induced magnetic field \(\vec{h}\). In the case of slow-moving medium, Maxwell's magnetic equations will take the following form

$$\nabla \times \vec{h} = \vec{J},{ }\mu_{0} \frac{{\partial \vec{h}}}{\partial t} = - \nabla \times \vec{E},{ }\mu_{0} \left( {\frac{{\partial \vec{u}}}{\partial t} \times \vec{H}} \right) = - \vec{E},{{ div}}\left( {\vec{h}} \right) = 0$$
(19)
$$\tau_{{{{ij}}}} = \mu_{0} \left[ {H_{j} h_{i} + H_{i} h_{j} - H_{k} h_{k} \delta_{{{{ij}}}} } \right]$$
(20)

where \(\mu_{0}\) signifies the magnetic reluctivity, \(\vec{J}\) represents the density of an electric current and \(\tau_{{{{ij}}}}\) denotes the Maxwell stress tensor.

3 Problem formulation

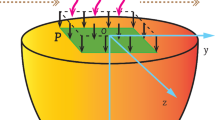
In this section, the proposed model will be applied to study plasmonic, thermal, and elastic surface waves on semiconductors during the process of photo thermoplastic interactions. The material has been assumed to be an infinitely flexible, cylindrical-cavity semiconductor with isotropic thermal properties and a uniform composition. As a result of the heat flux generated by the laser pulse, the photogeneration of carrier concentration was restricted to the inner boundary of the cylindrical gap. To study the problem, the cylindrical coordinates \(\left(\rho , \phi , z\right)\) are taken into account, with the z-axis pointing in the same direction as the cylindrical axis. At first, the body is not stressed or deformed, and the temperature inside the cylinder is constant and stable. As a result of the symmetry of the problem, the different system variables will depend on the instantaneous time t and the radial distance. Also, for the sake of the consistency requirement, all physical domain variables are assumed to be bounded within the medium. The displacement components, as well as their connections to strain, are as follows:

$$\vec{u} = \left( {u, 0, 0} \right),{ }e_{\rho \rho } = \frac{u}{\rho },{ }e_{\phi \phi } = \frac{\partial u}{{\partial \rho }}.$$
(21)

The equations that describe the relationships between stress, strain, temperature, and carrier are as follows:

$$\begin{array}{*{20}c} {S_{\rho \rho } = 2\mu \frac{\partial u}{{\partial \rho }} + \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right),} \\ {S_{\phi \phi } = 2\mu \frac{u}{\rho } + \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right)} \\ {S_{zz} = \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + d_{n} N} \right),} \\ \end{array} ,$$
(22)

where \({\alpha }_{t}\) stands for the linear thermal expansion factor, \({\delta }_{n}\) stands for the electronic deformation parameter, \(\lambda\), \(\mu\) stand for Lame's constants, and \(e=\frac{1}{\rho }\frac{\partial (\rho u)}{\partial \rho }\). If we incorporate the Lorentz force \({R}_{\rho }\) in the equation that describes dynamic motion, then we get the following::

$$\frac{{\partial S_{\rho \rho } }}{\partial \rho } + \frac{1}{\rho }\left( {S_{\rho \rho } - S_{\phi \phi } } \right) + R_{\rho } = \varrho \frac{{\partial^{2} u}}{{\partial t^{2} }}.$$
(23)

Assume that the cylinder is entirely surrounded by a magnetic field of constant intensity, given by \({\overrightarrow{H}}_{0}=\left(\mathrm{0,0},{H}_{0}\right)\). Then we get the following results according to Eq. (19)

$${ }\vec{E} = \left( {0,\mu_{0} H_{0} \frac{\partial u}{{\partial t}},0} \right),{ }\vec{J} = \left( {0,\frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right),0} \right),\vec{h} = \left( {0,0,\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right).$$
(24)

The magnetic field \(\vec{H}_{0}\) is the source of the Lorentz force component, which is designated by the symbol \(R_{\rho }\) and can be represented as

$$R_{\rho } = \mu_{0} \left( {\vec{J} \times \vec{H}_{0} } \right)_{\rho }$$
(25)

As a result, we may deduce \(R_{\rho }\) and Maxwell's stress \(\tau_{\rho \rho }\) from (20) and (24), respectively, as

$$R_{\rho } = \mu_{0} H_{0}^{2} \frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right),{ }\tau_{\rho \rho } = \mu_{0} H_{0}^{2} \frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }$$
(26)

Putting Eqs. (22) and (26) into Eq. (23), we obtain:

$$\left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right) = \gamma \frac{\partial \theta }{{\partial \rho }} + d_{n} \frac{\partial N}{{\partial \rho }} + \varrho \frac{{\partial^{2} u}}{{\partial t^{2} }},$$
(27)

where \(\left\{ {\gamma ,{ }d_{n} } \right\} = \left\{ {\left( {3\lambda + 2\mu } \right)\alpha_{t} ,\left( {3\lambda + 2\mu } \right)\delta_{n} } \right\}\).

By applying the factor \(\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }\), Eq. (27) can be rewritten as follows

$$\left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\nabla^{2} e - \gamma \nabla^{2} \theta - d_{n} \nabla^{2} N = \varrho \frac{{\partial^{2} e}}{{\partial t^{2} }}.$$
(28)

When the heat source is absence (\(Q = 0\)), the proposed MGTE photo-thermal heat transfer Eq. (18) may be written as:

$$\left( {1 + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } } \right)\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\varrho C_{E} \theta + \gamma T_{0} {{e}}} \right] = \left[ {K\frac{\partial }{\partial t} + K^{*} } \right]\nabla^{2} \theta + \frac{{E_{g} }}{\tau }\frac{{\partial^{2} N}}{{\partial t^{2} }}.$$
(29)

It is easy to reduce the system of equations to their dimensionally reduced forms. Therefore, the following dimensionless quantities are provided:

$$\begin{array}{*{20}c} {\left\{ {\rho ^{\prime},{ }u^{\prime}} \right\} = v_{0} \eta \left\{ {\rho ,u} \right\},{ }\left\{ {t^{\prime},\tau_{0}^{^{\prime}} ,\tau ^{\prime}} \right\} = v_{0}^{2} \eta \left\{ {t,\tau_{0} ,\tau } \right\},\left\{ {\theta {^{\prime}},N^{\prime}} \right\} = \frac{1}{{\rho v_{0}^{2} }}\left\{ {\gamma \theta ,d_{{{n}}} n} \right\},} \\ {\left\{ {S_{{{{ij}}}}^{^{\prime}} ,\tau_{\rho \rho }^{^{\prime}} } \right\} = \frac{1}{{\rho v_{0}^{2} }}\left\{ {S_{{{{ij}}}} ,\tau_{\rho \rho } } \right\},{ }\eta = \frac{{\rho C_{E} }}{K},{ }v_{0} = \sqrt {v_{1}^{2} + v_{a}^{2} } .} \\ \end{array} { }$$
(30)

In Eq. (30), the \(v_{1} = \sqrt {\frac{\lambda + 2\mu }{\varrho }}\) indicates the dilatational wave speed while \(v_{0} = \sqrt {\mu_{0} H_{0}^{2} /\varrho }\) represents the medium Alfven wave speed. If the primes are not taken into account, the basic equations can be rewritten as follows:

$$\left( {1 + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } } \right)\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\theta + \varepsilon_{1} {{e}}} \right] = \nabla^{2} \frac{\partial \theta }{{\partial t}} + \omega^{*} \nabla^{2} \theta + \varepsilon_{2} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( N \right),$$
(31)
$$\nabla^{2} \left( {e - \theta - {\rm N}} \right) = \frac{{\partial^{2} }}{{\partial t^{2} }}\left( e \right)$$
(32)
$$\left( {\nabla^{2} - g_{1} \frac{\partial }{\partial t} - g_{2} } \right){\rm N} = - g_{3} \theta ,$$
(33)
$$\begin{array}{*{20}l} {S_{\rho \rho } = 2\beta^{2} \frac{\partial u}{{\partial \rho }} + \left( {1 - 2\beta^{2} } \right)e - \left( {\theta + {\rm N}} \right),} \hfill \\ {S_{\phi \phi } = 2\beta^{2} \frac{u}{\rho } + \left( {1 - 2\beta^{2} } \right)e - \left( {\theta + {\rm N}} \right),} \hfill \\ {S_{{{{zz}}}} = \left( {1 - 2\beta^{2} } \right)e - \left( {\theta + {\rm N}} \right)} \hfill \\ \end{array}$$
(34)

where

$$\begin{array}{*{20}c} {\beta^{2} = \mu /\left( {\lambda + 2\mu } \right),{ }\varepsilon_{1} = \gamma^{2} T_{0} /\left( {c_{0}^{2} \rho^{2} C_{e} } \right),{ }\omega^{*} = K^{*} /\left( {Kc_{0}^{2} } \right),\varepsilon_{2} = \frac{{\gamma E_{g} v_{0}^{2} \eta }}{{\tau d_{{{n}}} \varrho C_{E} }}{ },} \\ {\eta_{0} = \left( {\eta c_{0} } \right)^{2} ,{ }g_{1} = \rho /\left( {\eta_{0} D_{E} } \right),{ }g_{2} = 1/\left( {\eta_{0} D_{E} \tau_{1} } \right),{ }g_{3} = \kappa d_{n} /\left( {D_{E} \gamma \eta_{0} } \right).} \\ \end{array}$$
(35)

It is assumed that the problem started with the following specific initial conditions

$$\begin{array}{*{20}c} {u\left( {\rho ,t} \right) = 0,\frac{{\partial u\left( {\rho ,t} \right)}}{\partial t} = 0,{ }{\rm N}\left( {\rho ,t} \right) = 0,\frac{{\partial {\rm N}\left( {\rho ,t} \right)}}{\partial t} = 0,{ }} \\ {\theta \left( {\rho ,t} \right) = 0,\frac{{\partial \theta \left( {\rho ,t} \right)}}{\partial t} = 0{{ at }}t = 0} \\ \end{array}$$
(36)

We also suppose that there is no traction on the inner boundary of the cavity (\(\rho = \rho_{0}\)). Consequently, the following mechanical condition can be introduced

$$S_{\rho \rho } \left( {\rho_{0} ,t} \right) = 0$$
(37)

Furthermore, it is assumed that an exponentially laser-pulsed heat flow is applied to the surrounding boundary \(\rho = \rho_{0}\). As a direct consequence of this, the thermal condition may be implemented as [41]:

$$q_{\rho } = q_{0} \frac{{t^{2} }}{{16t_{p}^{2} }}{ }e^{{ - t/t_{p} }} , {{at}} \rho = \rho_{0} ,$$
(38)

where the constant \(q_{0}\) denotes the intensity of the heat flow and \(t_{p}\) symbolizes the duration of the pulsating heat flow. When using dimensionless variables (23) after applying modified Fourier's law (8), then we get:

$$\dot{q}_{\rho } + \tau_{0} { }{}_{AB}^{{}} D_{t}^{\alpha } \dot{q}_{\rho } = - \,\left( {\frac{\partial }{\partial t} + \omega^{*} } \right) \frac{\partial \theta }{{\partial \rho }}$$
(39)

Combining Eqs. (38) and (39) results in

$$\frac{{q_{0} }}{{16t_{p}^{2} }}\left( {1 + \tau_{0} { }_{{{{AB}}}} D_{t}^{\alpha } } \right)\frac{\partial }{\partial t}\left( {t^{2} { }e^{{ - t/t_{p} }} } \right) = - \,\left( {\frac{\partial }{\partial t} + \omega^{*} } \right) \frac{\partial \theta }{{\partial \rho }} {{at}} \rho = \rho_{0}$$
(40)

Even if carriers can reach the surface of the sample while the process is in the diffusion phase, there is still the possibility that they will recombine. This fact has a direct bearing on the fact that the condition of the carrier density restriction can be stated as:

$$D_{E} \frac{\partial N}{{\partial \rho }} = s_{v} N{{ at}} \rho = \rho_{0} ,$$
(41)

where the symbol \({s}_{v}\) denotes the surface recombination velocity.

4 Solution technique

A linear system of differential equations can be solved with the help of the different numerical and semi-analytical methods [62,63,64,65,66] and one of the most powerful methods is Laplace transform [49]. Laplace transforms of several functions are needed to analyze the controller system thoroughly. Laplace and inverse Laplace transform aspects are used for a comprehensive. The following equation is used to perform the Laplace transform

$${\mathcal{L}}\left[ {g\left( t \right){ }} \right] = \overline{g}\left( s \right) = \mathop \int \limits_{0}^{\infty } g\left( t \right)e^{{ - {{st}}}} {{d}}t, s > 0$$
(42)

By means of the Laplace transform, Eqs. (31) through (34) can be written in the following forms:

$$\left( {\nabla^{2} - \psi } \right)\overline{\theta } = \psi \varepsilon_{1} \overline{e} - \varepsilon_{2} s^{2} \overline{N},$$
(43)
$$\left( {\nabla^{2} - s^{2} } \right)\overline{e} = \nabla^{2} \overline{\theta } + \nabla^{2} \overline{\rm N}$$
(44)
$$\left( {\nabla^{2} - g_{4} } \right)\overline{\rm N} = g_{3} \overline{\theta },$$
(45)
$$\left[ {\begin{array}{*{20}c} {\overline{S}_{\rho \rho } } \\ {\overline{S}_{\phi \phi } } \\ {\overline{S}_{zz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2\beta^{2} } & 0 & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ 0 & {2\beta^{2} } & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ 0 & 0 & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\partial \overline{u}}}{\partial \rho }} \\ {\frac{{\overline{u}}}{\rho }} \\ {\overline{\theta }} \\ {\overline{\rm N}} \\ \end{array} } \right]{ }.{ }$$
(46)

where \(\psi = \frac{{s^{2} \left( {1 + \tau_{0} \omega_{0} } \right)}}{{\left( {s + \omega^{ * } } \right)}}\) and \(\omega_{0} = \frac{{s^{\alpha } }}{{s^{\alpha } \left( {1 - \alpha } \right) + \alpha }}\). After the Eqs. (43)-(45) have been decoupled, we obtain

$$\left( {\nabla^{6} - \alpha_{2} \nabla^{4} + \alpha_{1} \nabla^{2} - \alpha_{0} } \right)\left\{ {\overline{\theta },\overline{N},\overline{e}} \right\} = 0,$$
(47)

where \(\alpha_{2}\), \(\alpha_{1}\) and \(\alpha_{0}\) are provided by

$$\begin{array}{*{20}c} {\alpha_{2} = s^{2} + g_{7} + \frac{{g_{6} }}{{g_{3} }},\alpha_{1} = s^{2} g_{7} + g_{8} + \frac{{g_{6} g_{5} }}{{g_{3} }},\alpha_{0} = s^{2} g_{8} ,} \\ {g_{4} = sg_{1} + g_{2} ,{ }g_{5} = g_{4} - g_{3} ,{ }g_{6} = { }g_{3} \psi \varepsilon_{1} ,} \\ {g_{7} = g_{4} + \psi , g_{8} = g_{4} \psi + { }s^{2} g_{3} \varepsilon_{2} .} \\ \end{array}$$
(48)

With the use of Eq. (47) and the variables \(\lambda_{i} ,\) \(\left( {i = 1,2,3} \right)\), then we have

$$\left( {\nabla^{2} - \lambda_{1}^{2} } \right)\left( {\nabla^{2} - \lambda_{2}^{2} } \right)\left( {\nabla^{2} - \lambda_{3}^{2} } \right)\left\{ {\overline{\theta },\overline{N},\overline{e}} \right\} = 0,$$
(49)

where \(\lambda_{1}^{2}\), \(\lambda_{2}^{2}\) and \(\lambda_{3}^{2}\) represent the roots corresponding to the following equation

$$\lambda^{6} - \alpha_{2} \lambda^{3} + \alpha_{1} \lambda^{2} - \alpha_{0} = 0,$$
(50)

which are presented by

$$\begin{array}{*{20}c} {\lambda_{1}^{2} = \frac{1}{3}\left[ {2\beta_{0} \sin \left( {\gamma_{0} } \right) + \alpha_{2} } \right],} \\ {\lambda_{2}^{2} = - \frac{1}{3}\beta_{0} \left[ {\sin \left( {\gamma_{0} } \right) + \sqrt 3 \cos \left( {\gamma_{0} } \right)} \right] + \frac{1}{3}\alpha_{2} ,} \\ {\lambda_{2}^{2} = \frac{1}{3}\beta_{0} \left[ {\sqrt 3 \cos \left( {\gamma_{0} } \right) - \sin \left( {\gamma_{0} } \right)} \right] + \frac{1}{3}\alpha_{2} ,} \\ \end{array}$$
(51)

with

$$\beta_{0} = \sqrt {\alpha_{2}^{2} - 3\alpha_{1} } ,{ }\gamma_{0} = \frac{1}{3}\sin^{ - 1} \left( { - \frac{{2\alpha_{2}^{3} - 9\alpha_{2} \alpha_{1} + 27\alpha_{0} }}{{2\beta_{0}^{3} }}} \right).$$
(52)

Solving Eq. (49), we get:

$$\left\{ {\overline{e}, \overline{\theta },\overline{\rm N}} \right\} = \mathop \sum \limits_{i = 1}^{3} \left\{ {1,L_{i} ,H_{i} } \right\}A_{i} K_{0} \left( {\lambda_{i} \rho } \right)$$
(53)

where \({K}_{\mathrm{n}}( . )\) symbolizes the second kind of modified Bessel functions of order\(n\). The Bessel function \({K}_{\mathrm{n}}( . )\) has an exponentially declining behavior, in contrast to the typical Bessel functions, which have an oscillating pattern. The value of the three coefficients\({A}_{i}\), with\(i=1\),\(2\), and\(3\), can be obtained from the assumed boundary conditions. By introducing Eq. (53) into Eqs. (42)-(45), we obtain the following relations: (45)

$$H_{i} = g_{3} \left( {\lambda_{i}^{2} - s^{2} } \right)/\left( {\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} } \right),{ }L_{n} = \left( {\lambda_{i}^{2} - s^{2} } \right)\left( {\lambda_{i}^{2} - g_{4} } \right)/\left( {\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} } \right), i = 1,2,3.$$
(54)

The Laplace transform allows the cubic dilatation \(\overline{e}\) to be expressed as

$$\overline{e} = \frac{1}{\rho }\frac{\partial }{\partial \rho }\left( {\rho \overline{u}} \right) = \mathop \sum \limits_{i = 1}^{3} A_{i} K_{0} \left( {\lambda_{i} \overline{\rho }} \right).$$
(55)

After integrating Eq. (55) with respect to \(\rho\), we get:

$$\overline{u} = - \mathop \sum \limits_{i = 1}^{3} \frac{1}{{m_{i} }}A_{i} K_{1} \left( {\lambda_{i} \rho } \right).$$
(56)

Equation (56) can be differentiated with respect to \(\rho\) to yield

$$\frac{{{{d}}\overline{u}}}{{{{d}}\rho }} = \mathop \sum \limits_{i = 1}^{3} A_{i} \left( {K_{0} \left( {\lambda_{i} \rho } \right) + \frac{1}{{\rho { }\lambda_{i} }}K_{1} \left( {\lambda_{i} \rho } \right)} \right).$$
(57)

The general solutions to thermal stresses are as follows:

$$\begin{array}{*{20}l} {\overline{S}_{\rho \rho } = \mathop \sum \limits_{i = 1}^{3} A_{i} \left( {{\Omega }_{i} K_{0} \left( {\lambda_{i} \rho } \right) + \frac{{2\beta^{2} }}{{\rho { }\lambda_{i} }}K_{1} \left( {\lambda_{i} \rho } \right)} \right),} \hfill \\ {\overline{S}_{\phi \phi } = \mathop \sum \limits_{i = 1}^{3} A_{i} \left( {{\Phi }_{i} K_{0} \left( {\lambda_{i} \rho } \right) + \frac{{2\beta^{2} }}{{\rho { }\lambda_{i} }}K_{1} \left( {\lambda_{i} \rho } \right)} \right),} \hfill \\ {\overline{S}_{{{{zz}}}} = \mathop \sum \limits_{i = 1}^{3} A_{i} {\Phi }_{i} K_{0} \left( {\lambda_{i} \rho } \right)} \hfill \\ \end{array}$$
(58)

where

$${\Omega }_{i} = 1 - L_{i} - H_{i,} { ,}\;\phi_{i} = 1 - 2\beta^{2} - L_{i} - H_{i}$$
(59)

The formula for Maxwell's stress \(\overline{\tau }_{\rho \rho }\) in a non-dimensional space is as follows:

$$\overline{\tau }_{\rho \rho } = \frac{{v_{a}^{2} }}{{v_{0}^{2} }}e = \frac{{v_{a}^{2} }}{{v_{0}^{2} }}\mathop \sum \limits_{i = 1}^{3} A_{i} K_{0} \left( {\lambda_{i} \rho } \right)$$
(60)

The following transformations are applied to the boundary conditions (37), (40), and (41) after the Laplace transform has been applied:

$$\begin{array}{*{20}l} {\left. {\frac{{\partial \overline{\theta }}}{\partial \rho }} \right|_{{\rho = \rho_{0} }} = - \frac{{sq_{0} \left( {1 + s{{t}}0} \right){{tp}}^{3} }}{{8t_{p}^{2} \left( {s + \omega^{*} } \right)\left( {1 + s{{tp}}} \right)^{3} }} = - \overline{G}\left( s \right)} \hfill \\ {\overline{\sigma }_{\rho \rho } \left( {\rho_{0} ,{{s}}} \right) = 0} \hfill \\ {D_{E} \left. {\frac{{\partial \overline{N}}}{\partial \rho }} \right|_{{\rho = \rho_{0} }} = s_{f} \overline{N}\left( {\rho_{0} ,s} \right)} \hfill \\ \end{array}$$
(61)

When replacing Eqs. (53) and (58) in Eq. (61), the following results are obtained:

$$\begin{array}{*{20}l} {\mathop \sum \limits_{i = 1}^{3} \lambda_{i} A_{i} K_{1} \left( {\rho_{0} { }\lambda_{i} } \right) = \overline{G}\left( s \right)} \hfill \\ {\mathop \sum \limits_{i = 1}^{3} \frac{1}{{m_{i} }}A_{i} K_{1} \left( {\rho_{0} { }\lambda_{i} } \right) = 0} \hfill \\ {\mathop \sum \limits_{i = 1}^{3} A_{i} H_{i} \left( {\left( {D_{E} - s_{v} } \right)K_{0} \left( {\lambda_{i} \rho_{0} } \right) + \frac{{D_{E} }}{{\rho_{0} { }\lambda_{i} }}K_{1} \left( {\lambda_{i} \rho_{0} } \right)} \right) = 0} \hfill \\ \end{array}$$
(62)

By solving (62), we are able to obtain the values for the coefficients \({A}_{i}\), where \(i=\mathrm{1,2},3\).

5 Numerical method

Since the Laplace transforms are used in different areas of science and engineering, several numerical algorithms have been proposed to inverse the solutions from the Laplace domain. This research successfully acquired the inversion of Laplace transforms by using an efficient and accurate computational approach based on the expansion of the Fourier series [67]. Using the following procedure, it is possible to transform any function \(\overline{\Gamma }\left(\rho ,s\right)\) into the space–time domain \(\Gamma \left(\rho ,t\right)\):

$$\Gamma \left( {\rho ,t} \right) = \frac{{e^{\varpi t} }}{t}\left( {\frac{1}{2}\overline{\Gamma }\left( {\rho ,\varpi } \right) + {{Re}}\mathop \sum \limits_{j = 1}^{{m_{n} }} \overline{\Gamma }\left( {\rho ,\varpi + \frac{{i{{j}}\pi }}{t}} \right)\left( { - 1} \right)^{j} } \right)$$
(63)

The symbol \({m}_{n}\) represents the total number of terms that give the best approximation, \(\mathrm{Re}\) represents the complex number's real part, and \(i=\sqrt{-1}\) mean the imaginary part. A number of studies led the researchers to conclude that the value of the coefficient \(\varpi\) must satisfy the relation \(t\cong 4.7\) to promote faster convergence [59] if the previous algorithm is used [68].

6 Special cases

In Sect. 2 of this article, it is proposed to use the concept of the Atangana-Baleanu fractional operator with a nonsingular nucleus to construct a fractional MGT framework that describes the photothermoelastic behaviour. The proposed model is based mainly on the values of the thermal parameters \({K}_{ij}^{*}\) and \({\tau }_{0}\). Two distinct sets of models may be constructed depending on whether or not fractional order is included.

6.1 Photothermoelastic models

In the case where the fractional derivatives are taken into account (\(\alpha =1\)), the following of photo-thermoelastic models can be derived:

  • If the parameters \({\tau }_{0}\) and \({K}_{\mathrm{ij}}^{*}\) are not taken into account, the conventional photo-thermoelastic theory, also known as C-PT, may be derived.

  • In the case when the parameter \({K}_{\mathrm{ij}}^{*}\) does not exist, the photo-thermoelastic theory with a single relaxation (LS-PT) is utilized.

  • If the term in Eq. (18) that holds the parameters \({K}_{\mathrm{ij}}\) is removed, the photo-thermal model that includes the second kind of Green and Naghdi theories, which is referred to as GNII-PT, can be obtained.

  • In the absence of the previously stated relaxation time \({\tau }_{0}\), it is possible to construct the third photo-thermal type of the Green and Naghdi theories, which is abbreviated as GNIII-PT.

  • When both of these factors (\({\tau }_{0}\) and \({K}_{\mathrm{ij}}^{*}\)) are greater than zero, the MGT photo-thermal model, abbreviated MGT-PT, is applied.

6.2 Photo-thermoelasticity with a fractional operator

This fractional photo-thermal elasticity model uses the fractional derivative Atangana-Baleanu without a singular kernel. As in the previous case, four more photocurrent models can be derived if fractional differentiation is present (\(0<\alpha <1\)) based on the presence or absence of the constants \({\tau }_{0}\) and \({K}_{\mathrm{ij}}^{*}\). The abbreviations for the four different model names are indicated by the symbols LS-FPT, GNII-FPT, GNIII-FPT, and MGT-FPT.

7 Numerical results

We will present some numerical data in the next section to provide concrete evidence of the importance of the theoretical conclusions reached in the previous chapters. The calculated values of the physical fields under consideration will be determined with the aid of the Mathematica program. The effect of the modified fractional photo-thermal equation (MGT-FPT), which was introduced by introducing the MGT equation on the different fields, will be shown in illustrations and tables. The following properties of silicon (Si) will be used in theoretical studies and numerical calculations as semiconducting solids [15]:

$$\begin{array}{*{20}c} {\lambda = 3.64 \times 10^{10} {{kg }}/{{m}}^{1} {{s}}^{2} ,{ }\mu = 5.46 \times 10^{10} {{kg }}/{{m}}^{1} {{s}}^{2} ,K = 1.51{{ W }}/{{m}}^{1} {{K}}^{1} ,{ }} \\ {{ }\varrho = 2330{{ kg}}/{{ m}}^{3} ,{ }C_{E} = 6.95 \times 10^{2} {{ J kg}}/{{ K}}^{1} ,{ }s_{f} = 2{{ m}}/{{ s}}^{1} ,{ }d_{n} = - 9 \times 10^{ - 31} {{ m}}^{3} ,{ }} \\ {T_{0} = 300{{ K }},E_{g} = 1.11{{ eV}},{ }D_{E} = 2.5 \times 10^{ - 3} {{ m}}^{2} /{{ s}}^{1} ,{ }\tau = 5 \times 10^{ - 5} {{ s}}.} \\ \end{array}$$

The approximate numerical algorithm described in (57) will be applied to find the numerical values of the variance in the behavior of the system domains such as non-dimensional temperature \(\theta\), thermal deformation \(u\), radial and circumference stresses \({\sigma }_{\rho \rho }\) and \({\sigma }_{\phi \phi }\), the radial component of Maxwell stress (\({\tau }_{\rho \rho }\)) and the change in carrier density \(N\) with the variation of the radial direction \(\rho\). The numerical results were calculated at instant time \(t=0.12\mathrm{s}\) and when \({\rho }_{0}=1\), and this is visually represented in Tables 1, 2, 3, 4, 5 and 6. Three different scenarios will be carried out in which numerical calculations of field variables are made for the purpose of clarification and discussion to reach the most important conclusions from this study.

Table 1 The temperature \(\theta\) under different photo-thermoelastic models
Full size table
Table 2 The displacement \(u\) under different photo-thermoelastic models
Full size table
Table 3 The variation in stress \({S}_{\mathrm{rr}}\) under different photo-thermoelastic models
Full size table
Table 4 The variation of carrier density \(N\) under different photothermoelasticity models
Full size table
Table 5 The variation of Maxwell's stress \({\tau }_{rr}\) via different photo-thermoelastic models
Full size table
Table 6 Photo-thermoelastic studied fields under the influence of the laser pulse duration and carrier lifetime factors
Full size table

7.1 The impact of fractional photo-thermoelastic models

The standard derivative of integer order has been generalized into the form known as the fractional derivative. Recent research has used it to examine the influence of memory on the dynamics of various emerging systems across several subjects. The scientific establishment was quickly interested in the new concept of a fractional derivative, and during the past two years, several publications have been released. This section aims to quickly summarize the features of these new derivatives (fractional operators) and recent findings inspired by the idea proposed in [19, 20]. This subsection places an emphasis, in particular, on paying attention to heat equations.

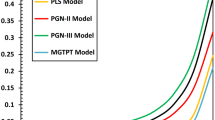
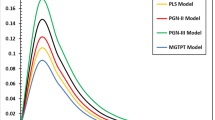
As explained in Sect. 5, the MGT photo-thermal concept (MGT-PT) combines several thermoelectric and fractional thermoelectric models. A comparison will be made between four photo-thermal models in the absence of fractional differentiation (LS-PT, GNII-PT, GNIII-PT, and MGT-PT) and the other four fractional models in the absence of fractional differentiation (LS-FPT, GNII-FPT, GNIII-FPT, and MGT-FPT). The parameters of the carrier lifetime, denoted by \(\tau\), and the length time of the pulsed heat flow, denoted by \({t}_{p}\), with values of 0.01 and 0.15, respectively, were considered in the study. The variation in the behavior of the considered field variables is explained in Tables 1, 2, 3, 4, 5 and 6 by the change in the radial distance \(r\) and the constancy of time. The following major considerations are highlighted in the tables:

  • The numerical analysis reveals that the boundary criteria imposed on the edges of the cavity can be considered satisfactory. This is true when compared to theoretical predictions that have been proposed previously.

  • All models, except for the GNIII-PT model, provide identical findings at the beginning of heat and light wave propagation at the surface of the gap. The waves then move at various speeds through the turbulence zone until they converge again, after which they fade out.

  • It has been observed that as the structural size grows, the radial pressure is restricted close to the surface of the hollow cylinder, where heat flux is applied. Physically, this is thought to be possible.

  • Although the magnitudes are different, the behavior of the distribution of each studied variable is similar.

  • There are significant differences in the variance between fractional photo-thermoelastic and non-fractional photo-thermal models.

  • The fractional order parameter \(\alpha\) of the Atangana-Baleanu fractional derivative operator has a significant influence on the distribution progress with time.

  • he results indicate how the material behaves when optical, mechanical, and heat waves pass through it: it is more flexible in the fractional photo-thermoelastic model with the Atangana-Baleanu model operator than in the classical photo-thermoelastic. This is because the Atangana-Baleanu fractional model is an evolution of the classical models.

  • The body temperature rises in the transmission plane of the heat flux transfer rate and decreases gradually as we move away from the surface of the responsive cylinder. This is because the surface of the cylinder is more sensitive to temperature changes in that plane.

  • The distributions of temperature change \(\theta\) and carrier density \(N\) are only slightly affected by fractional derivatives, and they may be absent entirely within the medium.

  • The parameters \({\tau }_{0}\) and \({K}^{*}\) including in the heat conduction equation, significantly impacts every one of the investigated domains.

  • The parameters \({\tau }_{0}\) and \({K}^{*}\), which are included in the heat conduction equation, have a significant impact on all of the investigated domains.

  • With the help of the current thermodynamic model, researchers can classify thermoelastic materials and their properties according to the choice of the fractional order of the differential derivatives. Because of this, the fractional parameter is becoming increasingly important to measure how well a material can move heat.

  • The optical and mechanical thermal diffusion rates are slowed down considerably inside the medium due to the photo-thermoelastic properties that photo-thermoelastic materials possess.

  • In the case of thermo-optical versions with non-fractional derivatives (LS-PT, GNII-PT, GNIII-PT, and MGT-PT), the temperature distribution is more significant than in the case of modified fractional thermo-optical versions (LS-FPT, GNII-FPT, GNIII-FPT, and MGT-FPT). This phenomenon is quite consistent with reports by Quintanilla [42, 43], in addition to the observations emphasized by Abouelregal et al. in several papers, as in [37, 44,45,46,47].

  • In the case of the LS-PT, LS-FPT, MGT-PT, and MGT-FPT models, adding a relaxation constant \({\tau }_{0}\). In this case, the modified Fourier law of Greene and Naghdi's theorems may slow down the velocity of the different waves faster, even if the fractional operators with fractional orders exist.

  • The photo-thermal models that include fractional derivatives provide displacement values that are less extreme than those produced by the photo-thermal models that do not include fractional derivatives. Because of this, the fractional parameter should make the displacement less affect the elastic photo-thermal waves.

  • When the mechanical boundary condition is met, the radial stress \({\sigma }_{rr}\) values at the surrounding surface vanish. This also demonstrates another degree of accuracy on the part of the numerical method which has been introduced to solve the proposed problem.

  • Because a fractional parameter was included in the model, the magnitude of the stress component \({\sigma }_{rr}\) was reduced, which makes more sense.

  • The compressive nature of heat stress distributions is more pronounced near the body's surface. The surface of the solid is due to a constant heat flux, which is organized in such a way that the compressive nature of the stress wave corresponds to the real case.

  • Maxwell stress \({\tau }_{rr}\) variance starts at its lowest surface value, rises rapidly to a peak point, and then rises monotonously until it disappears.

  • There was a good agreement between the fractional derivatives used to describe semiconductor materials and the experimental data when integral derivatives were used instead of fractional derivatives. In addition, it is shown that memory of matter affects the behavior of the studied domains.

  • When modelling the thermo-photophysical interactions, fractal calculus should be seen as one of the most influential mathematical techniques that should be taken into account. It is particularly suitable for developing time-dependent constitutive models [69]. The use of fractional calculus is also largely inspired by the fact that fewer parameters are necessary to construct an approximate solution suitable for experimental data. This is one of the main motives behind the use of fractional calculus, which is further explained in [70].

  • It was found that the fractional derivative is a better way to model the process of designing machines and devices than the traditional models. This means that it should be taken into account [71].

  • The Atangana–Baleanu fractional derivative effect is superior to the traditional type, allowing for a more reliable depiction of various events in the real world. An increase in the fractional differential order leads to a decrease in the value of the physical variables. When the fractional Atangana–Baleanu derivative is used, the modes inside the elastic semiconductor go away faster.

  • Different semiconductor components that are exposed to optical, thermal fields can be designed and manufactured based on the results of these investigations. Furthermore, in the case of developing new materials, the interaction between thermoplastics, plasma waves, various materials science, and mechanical design is critical to meeting the requirements of the innovative application.

7.2 The impact of laser pulse length and carrier lifetime

In recent years, the discovery of lasers has been useful in understanding the properties of the internal structure of some materials. Therefore, these important developments paved the way for a wide range of modern applications throughout physics, engineering, technology, and the medical sciences. In previous publications in the field of thermoelasticity, the focus was on the thermal influence of a non-Gaussian laser on the behavior of photothermal matters.

Optically produced brief elastic pulses (high mechanical waves) in a wide range of technical physics applications are also gaining traction. When a beam of light from a laser source falls on a sample, the laser pulses cause the temperature of the sample to rise. After the optical excitation of all the excited electrons, the intensity of the free carrier charge will become obvious and play a prominent role. Since optically produced ultrasound carries information about both the generating medium and the media surrounding it, it has become possible to create one-dimensional theoretical concepts based on these waves and pulses.

When studying semiconductor materials, it is crucial to have both theoretical and applied approaches to obtaining data on the carrier's intrinsic concentrations and extended lifespan. This is done to identify the mechanics of the device, enhance its functions, and improve its performance. Even though the minority carrier mobility and effective carrier lifetime factor of the solar cell adsorbent material affect the open circuit voltage, they have a much bigger effect on the photo-generated carrier concentration N.

This subsection examines the phenomenon of heating semiconductor materials using pulsed lasers. Considering that the material is an unbounded solid body with a cylindrical cavity made of silicon, it was exposed to a non-Gaussian pulsed laser with a duration of \({t}_{p}\). When temperature meets tension, energy dissipation occurs. This results in the conversion of potential mechanical energy into stable thermal energy. The combination of these two factors reduces vibration by utilizing thermal elasticity. In Table 6, it is shown how the laser pulse length, denoted by \({t}_{p}\), as well as the lifetime parameter, denoted by \(\tau\), affect the non-dimensional thermophysical fields being studied. The numerical discussion was done using \(\rho =1.1\) in light of the MGT photo-thermoelastic model with fractional differentiation.

Table 6 shows that the studied variables, which comprise temperature, deformation, carrier density, and thermal stresses, are strongly dependent not just on distance and time but also on the laser pulse duration \({t}_{p}\) and the lifetime factor \(\tau\) of photo-generated carriers. This is true regardless of the amount of time that has passed. Furthermore, the change in laser duration \({t}_{p}\), has a greater sensitivity to thermal and mechanical waves than the change in lifespan \(\tau\).

It is clear from the table that with increasing laser pulse duration \({t}_{p}\), it has been proven that the values of change in temperature \(\theta\), carrier density variation \(N\), and thermal displacement \(u\) will all decrease. On the other hand, the values of radial stress \({\sigma }_{\rho \rho }\) and Maxwell stress \({\tau }_{\rho \rho }\) are shown to rise with the increase of this pulse. Also, when increasing the values of the carrier life constant \(\tau\) resulting from the carrier, it was discovered that there is a rise in the temperature in addition to the other studied fields. On the other hand, when the value of the lifetime parameter \(\tau\) increases, the radial displacement distribution \(u\) shows a downward trend.

The carrier lifetime parameter is expected to play a major role in examining the macroscopic outputs of some materials related to thermophotovoltaic materials, which dominate the determination of material properties. Several thin-film photovoltaic materials may have an inaccurately measured carrier life or inadequate knowledge of their material characteristics. Taken together, these data suggest that the idea of restricting heat dissipation rates is correct [72]. The conclusions acquired from this illustration may apply to developing novel materials and other materials science and physical engineering fields where plasma waves and elasticity are present. Temperature fluctuations in materials subjected to the conduction pattern of heat transfer occur when there is a rapid change in contraction or expansion [10]. The wide use of pulsed laser techniques in the fields of material processing, non-destructive testing, and characterization has brought a lot of attention to this mechanism. Surface layers of metallic materials have been successfully hardened using a modern process called laser thermal hardening. The loss of heat from the interior cold layers of metals and alloys during thermal hardening allows the heated irradiation surface area to instantly cool [73].

There are many reasons why this technology has been the focus of intensive industry and scientific study. Numerous experimental, theoretical, mathematical and optimization studies have been conducted to better comprehend and optimize the laser cutting process with regard to several parameters, including quality performance, cost, efficiency, cutting duration, etc. [74].

8 Conclusion

The current paper presented a new photo-thermal conductivity model using the Moore-Gibson-Thompson equation. In the modified framework, the Lord and Shulman heat transfer equation was combined with the Green-Naghdi theory of type III (GN-III) to solve the issue of infinite velocities of thermal signals. Atangana and Baleanu’s operator, which uses an extended Mittag–Leffler function as a nonlocal and non-singular kernel, was employed to capture the properties of the fractional derivatives. The improved model allowed us to study the interplay between heat, plasma, and elastic waves in semiconductor materials. Although the conventional GNIII-PT framework differs from the extended LS-PT, GNIII-PT, and MGT-PT photo-thermal models, the numerical results clearly demonstrated that the behaviour of photothermoelastic models is comparable regardless of whether the fractional operators are included or not. In addition, the values of physical fields were lower than those expected by the photo-thermal elastic models if the fractional derivatives are used, and therefore, the selection of the fractional parameter is important as a measure of a material's thermal and optical conductivity. The discussions showed that the effects of laser pulse’s length and lifetime are also important. In the modified fractional photothermoelasticity MGT-FPT theory, heat signals move through the medium as waves with a finite speed instead of the infinite speed predicted by Fourier’s law. The photo-thermoelastic process is easy to understand by employing the generalized fractional MGT-FPT model compared to the fractional GNIII-FPT model. It is worth mentioning that for long periods, the outcomes from the coupled photo-thermoelastic and generalized models eventually converge to each other.