Analytical Solutions of Gravity Vector and Gravity Gradient Tensor Caused by a 2D Polygonal Body with a 2D Polynomial Density Contrast

Abstract

In this paper, analytical solutions are presented for the gravity vector and gravity gradient tensor at any point produced by a 2D body whose cross-section is an arbitrary polygon and the density contrast is a 2D arbitrary-order polynomial function varying in both horizontal and vertical directions. In addition, we analyze the singularity of our expressions. For the gravity vector, the singularity points only exist at the vertices of the polygon. But for the gravity gradient tensor, there are two situations: (1) if every side of the polygon is not parallel to z-axis, the singularity points will only exist at the vertices of the polygon; (2) if there is any side parallel to z-axis in the polygon, all the points on the line passing through the side parallel to z-axis will become singularity points. To avoid this singularity, observation points can be moved from the singularity points by a minimal distance. Besides, the analytic expressions are validated compared with conventional method that sums up the gravity effects of a series of units with uniform densities, with the numerical stability also being evaluated through numerical tests. What is more, applications with some numerical examples and effective models show that our analytical solution within the range of numerical stability is superior in computational accuracy and efficiency to the conventional method that sums up the gravity effects of a series of units with uniform densities. In a word, our expressions provide an effective method for computing the gravity vector and gravity gradient tensor of an irregular 2D body with complicated density variation.

1 Introduction

The forward gravity problem is the foundation of gravity exploration (Wu 2018). Since the geological bodies in reality generally have complex density contrasts and complex shapes, they are often approximated by a collection of simple regular-shaped bodies whose density contrasts are assumed to be constant (Conway 2015; D’Urso 2015; Jiang et al. 2018; Werner 2017). The analytical solutions of gravity effects induced by some regular-shaped bodies with uniform densities have been reached, such as a rectangular prism (Nagy 1966; Nagy et al. 2000; Okabe 1979), a polyhedron (D’Urso 2013,2014a; Petrović 1996; Tsoulis and Petrović 2001), a polygonal prism (Cady 1980; Kwok 1991; Chen et al. 2018) and a cylinder (Kwok 1991; Rim and Li 2016).

Although geological bodies in reality all have three dimensions, there are some linear geologic structures whose strike extension is far greater than the cross-section dimension (Grant and West 1965) (e.g., fault zones, intrusive rock walls, etc.). For reducing the computation of gravity effects, this kind of structures can be often approximated by 2D bodies extending infinitely along the strike to replace the actual distribution of original sources, and the corresponding inversion algorithm is easier to be established. In fact, the study of 2D bodies is earlier than that of 3D bodies due to easier computation. In 1948, a line integral for calculating the gravity anomaly of a 2D mass with uniform density was presented (Hubbert 1948). On this basis, a classic computational scheme for rapid computation of gravity anomaly resulting from a 2D homogenous body whose cross-section is a polygon was proposed (Talwani et al. 1959) and was applied to sedimentary basins (Bott 1960). Until now, the analytical solutions of gravity potential and its first-order, second-order, third-order derivatives caused by a 2D homogeneous body with polygonal cross-section have already been obtained (Jia and Wu 2011; Okabe 1979; Won and Bevis 1987), and some singularities of the formulas have been solved (Jia and Wu 2011).

The above studies only involve constant densities. While most mass sources have a non-uniform density, the uniform-density assumption is not applicable to most geological structures in practical applications (Jiang et al. 2018; Sykes 1996). Therefore, different kinds of functions were used to simulate the variation of density contrast in bodies for computing the gravity effects of the variable-density bodies.

Gravity vector fields caused by 3D regular-shaped variable-density bodies have been extensively studied: solutions of some density-depth functions including linear (D’Urso 2014b; Hamayun and Tenzer 2009; Hansen 1999; Holstein 2003; Pohanka 1998), quadratic (Gallardo et al. 2005; Gallardo-Delgado et al. 2003), cubic (García-Abdeslem 2005), parabolic (Chakravarthi et al. 2002) and arbitrary-order polynomial (Jiang et al. 2017) have been considered. However, there are still more complex density variations not only related to depth existing in real geological bodies (e.g., dipping layered intrusions, sedimentary beds, etc.). As a consequence, the general polynomial density contrast which not only varies in depth but also varies in the horizontal direction was proposed by Zhang et al. (2001). It is a significant for approximating complicated density distributions of geological bodies due to its superiority over the depth-dependent density function (Ren et al. 2018), which has been clearly proved by Jiang et al. (2017). Zhou (2009a) utilized line-integral method to compute the gravity anomaly of a rectangular prism with the density contrast varies with horizontal and vertical directions. Then, Zhang and Jiang (2017) obtained the closed-form expressions of gravity vector field produced by a 3D rectangular prism whose density is a linear combination of arbitrary-order polynomial functions in three directions of x, y and z. Ren et al. (2017a, b) derived singularity-free analytic formulas of gravity potential and gravity vector caused by a polyhedron whose density contrast is described by λ = ax^m + byⁿ + cz^t, but for the solution of gravity potential, the maxima of m, n, t are 2; and for the solution of gravity vector, m ≤ 1, n ≤ 1, t ≤ 1. Soon afterward, the maximum order of gravity vector’s solution was expanded up to 3 (Ren et al. 2017a, b). At the same time, D’Urso and Trotta (2017) deduced singularity-free expressions for calculating gravity anomaly of a polyhedral body with cubic polynomial density contrast in both horizontal and vertical directions at any point, and indicated that the general approach can be easily extended to higher-order polynomial functions.

Similarly, a few achievements have also been made in gravity anomalies of 2D variable-density bodies: sources with some density-depth or density-distance functions have been considered, such as linear (Gendzwill 1970; Murthy and Rao 1979; Pan 1989), quadratic (Rao 1985,1986,1990; Ruotoistenmäki 1992), cubic (García Abdeslem 2003), parabolic (Visweswara Rao et al. 1994), hyperbolic(Litinsky 1989; Rao et al. 1994; Visweswara Rao et al. 1994, 1995), exponential (Chai and Hinze 1988; Chappell and Kusznir 2008; Cordell 1973; Litinsky 1989), and any types of depth-dependent functions (Zhou 2008). Compared with these above functions only varying in one direction, density contrast which changes with horizontal and vertical directions offers a more flexible way to approximate arbitrary variable-density distributions (Ren et al. 2018). When the density function of a 2D body varies in both horizontal and vertical directions, we can model the gravity anomaly of it rapidly by using numerical integration method (Martín Atienza and García Abdeslem 1999; Zhou 2009b). Nevertheless, using numerical methods inevitably reduces the accuracy of data and leads to numerical errors in forward computing, which can be completely avoided by using analytical solutions (Ren et al. 2018). Hence, the derivation of corresponding analytical solutions is still essential. Zhang et al. (2001) firstly made a contribution of deducing an analytical solution of gravity anomaly produced by a 2D polygonal body with an arbitrary-order polynomial density function varying in horizontal and vertical directions at Cartesian coordinate system. Furthermore, Zhou (2010) extended the solution and solved some singularities of it. D’Urso (2015) presented analytical expressions for calculating gravity anomaly resulting from a 2D polygonal body whose density contrast is a polynomial in horizontal and vertical directions, but the order of the polynomial is not more than 3.

It is well known that gravity gradient data have better resolution than the gravity measurement data since they contain higher frequency information (Jiang et al. 2018). Therefore, the study about gravity gradient tensors of sources with variable-density contrast has aroused the attention of geophysicists in recent years. D’Urso (2014b) made an analytical solution of gravity gradient tensor induced by a polyhedron whose density contrast varies linearly with a position vector. Yet, when the observation point is aligned with an edge of a face of the polyhedron, the expressions exhibit a singularity. Wu and Chen (2016) modeled gravity vector and gravity gradient anomalies of 2D and 3D prisms with density-depth functions by using a Fourier-domain method, bringing about the inevitable truncation errors. Moreover, Wu (2018) modeled the gravity potential, gravity vector and gravity gradient tensor of arbitrary 2D and 3D bodies with arbitrary density contrast varying in horizontal and vertical directions by using Fourier-domain solutions, but the unavoidable numerical error is still one of the greatest drawbacks. Correspondingly, Jiang et al. (2018) obtained closed-form expressions for computing gravity gradient of a right rectangular prism with an arbitrary-order polynomial density contrast related to depth, dealing with the singularities. Ren et al. (2018) reached an analytic solution of gradient tensor of a polyhedron whose density contrast varies with horizontal and vertical directions, but the order of density function cannot exceed 3. To the best of our knowledge, the analytic expressions about gravity gradient and the horizontal component of gravity vector produced by 2D variable-density bodies have not been proposed so far.

To this end, we derive space-domain analytic solutions of gravity vector and gradient tensor of a 2D body whose cross-section is a polygon and the density contrast is a 2D arbitrary-order polynomial function varying in horizontal and vertical directions. Actually, it is a remarkable fact that polygonal models with arbitrary-order polynomial densities can provide a very general solution for 2D bodies. On the one hand, when the order of polynomial function is high enough, any 2D density distribution can be approximated well. On the other hand, when the number of sides of the polygon is large enough, any continuous boundary can also be well approximated (Wu 2018). In this paper, we draw on the strategy which was used in the derivation of gravity anomaly of 2D variable-density bodies (Zhang et al. 2001; Zhou 2010) to derive the spatial analytic expressions of both gravity vector and gravity gradient tensor. We also discuss the singularity problem of the derived analytic expressions here. In addition, we validate our expressions by comparing with the result of conventional method in which the variable-density source is divided into a series of constant-density units. We also evaluated the numerical stability, the efficiency and the RMS error of our expressions under different-order polynomial density functions.

2 Derivation of the Gravity Vector and Gravity Gradient Tensor

2.1 Basic Expressions

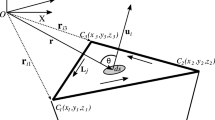
Figure 1 defines the right-handed Cartesian coordinate system and shows a 2D body whose cross-section is approximated by a polygon. The y-axis is parallel to the strike of the body, and observations lie along a profile contained within the x–z plane. The z-axis is positive downward.

Fig. 1

A 2D body with a polygonal cross-section and a density contrast following a 2D polynomial function, σ(x, z) is the density contrast, (x_k, z_k) and (x_{k +1}, z_k+1) represent the coordinates of vertices of the polygon, (x₀, z₀) are the coordinates of any observation point P in space, r_k and r_k+1 represent the distances between P and vertices

Let U denote the gravitational potential of a 2D body, the gravity vector can be expressed as (Jia and Wu 2011)

$$\varvec{g} = \left[ {\begin{array}{*{20}c} {U_{x} } \\ {U_{z} } \\ \end{array} } \right]$$

(1)

in which U_x and U_z are the gravity components in x and z directions, respectively. U_x and U_z at any observation point (x₀, z₀) can be minutely described by one generalized equation as

$$U_{x/z} \left( {e,f} \right){\,=\,}U_{x/z} \left( {x_{0} ,z_{0} } \right){\,=\,}2G\iint\limits_{s} {\sigma (x,z)\frac{{\left( {x - x_{0} } \right)^{e} \left( {z - z_{0} } \right)^{f} }}{{\left( {x - x_{0} } \right)^{2} + \left( {z - z_{0} } \right)^{2} }}{\text{d}}x{\text{d}}z}$$

(2)

where e is either 0 or 1, and so does f. Besides, G is gravitational constant, s denotes cross-sectional area of the 2D body, and σ(x, z) represents the density contrast. Specifically, U_x/z(1, 0) = U_x(x₀, z₀), and U_x/z(0, 1) = U_z(x₀, z₀).

The gravity gradient tensor of this 2D body can be expressed as (Jia and Wu 2011)

$${\mathbf{T}} = \left[ {\begin{array}{*{20}c} {U_{xx} } & {U_{xz} } \\ {U_{zx} } & {U_{zz} } \\ \end{array} } \right]$$

(3)

in which each component at (x₀, z₀) can be minutely described by

$$\left\{ {\begin{array}{*{20}l} {U_{xz} \left( {x_{0} ,z_{0} } \right) = U_{zx} \left( {x_{0} ,z_{0} } \right) = 4G\iint\limits_{s} {\sigma \left( {x,z} \right)\frac{{\left( {x - x_{0} } \right)\left( {z - z_{0} } \right)}}{{\left[ {\left( {x - x_{0} } \right)^{2} + \left( {z - z_{0} } \right)^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \hfill \\ {U_{zz} \left( {x_{0} ,z_{0} } \right) = - U_{xx} \left( {x_{0} ,z_{0} } \right) = 2G\iint\limits_{s} {\sigma \left( {x,z} \right)\frac{{\left( {z - z_{0} } \right)^{2} - \left( {x - x_{0} } \right)^{2} }}{{\left[ {\left( {x - x_{0} } \right)^{2} + \left( {z - z_{0} } \right)^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \hfill \\ \end{array} } \right.$$

(4)

where G is gravitational constant, s denotes the cross-sectional area, and σ(x, z) represents the density contrast.

Here, we assume the 2D body has an arbitrary polygonal cross-section and a density variation following a 2D arbitrary-order polynomial function (Zhang et al. 2001)

$$\sigma (x,z) = \sum\limits_{i = 0}^{{N_{x} }} {\sum\limits_{j = 0}^{{N_{z} }} {D_{i,j} x^{i} z^{j} } }$$

(5)

where N_x and N_z, respectively, represent the maximum order of x and z, while D_{i, j} represent the coefficients of the polynomial.

By substituting Eq. (5) into Eq. (2), the expression of gravity components becomes

$$U_{x/z} \left( {e,f} \right){\,=\,}U_{x/z} \left( {x_{0} ,z_{0} } \right){\,=\,}2G\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } } \iint\limits_{s} {x^{i} z^{j} \frac{{(x - x_{0} )^{e} (z - z_{0} )^{f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}}{\text{d}}x{\text{d}}z .$$

(6)

By substituting Eq. (5) into Eq. (4), the expressions of gravity gradient components become

$$\left\{ {\begin{array}{*{20}l} {U_{xz} \left( {x_{0} ,z_{0} } \right) = U_{zx} \left( {x_{0} ,z_{0} } \right) = 4G\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } } \iint\limits_{s} {x^{i} z^{j} \frac{{\left( {x - x_{0} } \right)\left( {z - z_{0} } \right)}}{{\left[ {\left( {x - x_{0} } \right)^{2} + \left( {z - z_{0} } \right)^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \hfill \\ {U_{zz} \left( {x_{0} ,z_{0} } \right) = - U_{xx} \left( {x_{0} ,z_{0} } \right) = 2G\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } } \iint\limits_{s} {x^{i} z^{j} \frac{{\left( {z - z_{0} } \right)^{2} - \left( {x - x_{0} } \right)^{2} }}{{\left[ {\left( {x - x_{0} } \right)^{2} + \left( {z - z_{0} } \right)^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \hfill \\ \end{array} } \right..$$

(7)

Among them, the analytical solution of the vertical component of gravity vector has already been obtained (Zhang et al. 2001; Zhou 2010), while in the following sections, we use a unified method to derive all the analytic expressions of both gravity vector and gravity gradient tensor.

2.2 U _x and U _z

As shown in Fig. 1, it is assumed that the coordinates of observation point are (x₀, z₀) and those of the two endpoints of kth side of the polygon are (x_k, z_k) and (x_k+1, z_k+1).

According to Binomial theorem (Singh 2017), we can easily get

$$x^{i} z^{j} = [(x - x_{0} ) + x_{0} ]^{i} [(z - z_{0} ) + z_{0} ]^{j} = \sum\limits_{n = 0}^{i} {C_{i}^{n} \left( {x - x_{0} } \right)^{i - n} x_{0}^{n} \sum\limits_{m = 0}^{j} {C_{j}^{m} \left( {z - z_{0} } \right)^{j - m} z_{0}^{m} } }$$

(8)

where C ⁿ _i and C ^m _j are the binomial expansion coefficients, which means 0 ≤ n ≤ i and 0 ≤ m ≤ j.

Substituting Eq. (8) into Eq. (6), the integral becomes

$$\iint\limits_{s} {\frac{{x^{i} z^{j} (x - x_{0} )^{e} (z - z_{0} )^{f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}x{\text{d}}z} = \sum\limits_{n = 0}^{i} {\sum\limits_{m = 0}^{j} {C_{i}^{n} C_{j}^{m} x_{0}^{n} z_{0}^{m} } } \iint\limits_{s} {\frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}x{\text{d}}z} .$$

(9)

According to Eq. (4) in the paper of Zhou (2010), we know that

$$\begin{aligned} & \frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }} \\ & \quad = \frac{1}{i + j - m - n + e + f}\left\{ {\frac{\partial }{\partial x}\left[ {\frac{{\left( {x - x_{0} } \right)^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} \right] + \frac{\partial }{\partial z}\left[ {\frac{{\left( {x - x_{0} } \right)^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} \right]} \right\} \\ \end{aligned}$$

(10)

where e and f are constants, with i + j − m − n + e + f ≠0.

Using Stokes’ theorem for a plane (Riley et al. 2010)

$$\iint\limits_{s} {\left( {\frac{\partial }{\partial z}A_{x} - \frac{\partial }{\partial x}A_{z} } \right)}{\text{d}}x{\text{d}}z = \oint_{c} {\left( {A_{x} {\text{d}}x + A_{z} {\text{d}}z} \right)} ,$$

(11)

We convert the surface integral in the result of Eq. (9) into a sum of line integrals calculated on the boundary of the polygon in a counterclockwise direction. Since the closed boundary of the polygon is connected by its N_e sides end to end, we can sum up integrals on each side of the polygon followed by a counterclockwise direction. In this way, we arrive at

$$\begin{aligned} & \iint\limits_{s} {\frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}x{\text{d}}z} \\ & \quad = \frac{1}{i + j - m - n + e + f}\oint_{c} {\left[ {\frac{{\left( {x - x_{0} } \right)^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}x - \frac{{\left( {x - x_{0} } \right)^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}z} \right]} \\ & \quad = \frac{1}{i + j - m - n + e + f}\sum\limits_{k = 1}^{{N_{e} }} {\left[ {\int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} {\text{d}}x - \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} {\text{d}}z} \right]} \\ \end{aligned}$$

(12)

where e and f are constants, N_e is the number of polygon’s sides, and k denotes that it is kth side being calculated followed by a counterclockwise direction with its two endpoints being (x_k, z_k) and (x_k+1, z_k+1) as shown in Fig. 1. Obviously, e + f ≡ 1 whether for U_x or U_z. So that i + j − m − n + e + f = i + j − m − n + 1 ≥1 with 0 ≤ n ≤ i and 0 ≤ m ≤ j.

We note that

$$E_{x/z} (e,f) = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}x} - \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} {\text{d}}z$$

(13)

to stand for the integrals calculated on the kth side. Then, taking Eqs. (9), (12) and (13) into Eq. (6), the expression of gravity vector becomes

$$U_{x/z} \left( {e,f} \right) = U_{x/z} \left( {x_{0} ,z_{0} } \right) = 2G\frac{{\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } \sum\limits_{n = 0}^{i} {\sum\limits_{m = 0}^{j} {C_{i}^{n} C_{j}^{m} x_{0}^{n} z_{0}^{m} } } } }}{{i + j - m - n + {\text{e}} + f}}\sum\limits_{k = 1}^{{N_{e} }} {E_{x/z} (e,f)}$$

(14)

where U_x/z(1, 0) = U_x(x₀, z₀), U_x/z(0, 1) = U_z(x₀, z₀), (x₀, z₀) are the coordinates of observation point, G is gravitational constant, N_x and N_z, respectively, represent the maximum order of x and z in density function, D_{i, j} represents the coefficient of the polynomial density function, C ⁿ _i and C ^m _j are the binomial expansion coefficients with 0 ≤ n ≤ i and 0 ≤ m ≤ j which means i + j − m − n + e + f = i + j − m − n + 1 ≥1, N_e is the number of polygon’s sides, and k denotes that it is the kth side being calculated followed by a counterclockwise direction.

Since we have to get the value of function E_x/z (e, f), which becomes a problem about calculating line integrals on straight lines, we should unify the variables of the integrals first. Two cases must be considered, respectively: one is the kth side in not parallel to z-axis, and the other is the kth side in parallel to z-axis. If the kth side is not parallel to z-axis, which means x_k ≠ x_k+1, the slope of the line this side located exists and the equation of this line can be described by z = px + q where p =(z_k+1− z_k)/(x_{k +1}− x_k) and q =(z_kx_{k +1}− z_{k +1}x_k)/(x_{k +1}− x_k). Then, we can substitute this equation into Eq. (13) and replace variable z with variable x, making Eq. (13) an integral only related to the coordinates of x. In the other case, that means x_k = x_k+1, the slope of the line doesn’t exist, so does the equation of the line, while the integral of x in Eq. (13) is 0 in this time, just leaving the latter integral about z which is easy to be calculated.

Then, we show the details in the two cases, respectively:

• 1. When x_k ≠ x_{k +1},substituting the linear equation z = px + q into Eq. (13) and combining similar terms, we have

  $$E_{x/z} (e,f) = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{(px_{0} + q - z_{0} )\left( {x - x_{0} } \right)^{i - n + e} (px + q - z_{0} )^{j - m + f} }}{{(1 + p^{2} )x^{2} + 2[p(q - z_{0} ) - x_{0} ]x + [(q - z_{0} )^{2} + x_{0}^{2} ]}}{\text{d}}x}$$

  (15)

  with p =(z_k+1− z_k)/(x_k+1− x_k) and q =(z_kx_k+1− z_k+1x_k)/(x_k+1− x_k). After noting Q = px₀ + q − z₀, a =(q − z₀)² + x ²₀ , b = p(q − z₀)− x₀, c =1 + p², and using Binomial theorem (Singh 2017) on the terms (x − x₀)^i−n+e and (px + q − z₀)^j−m+f, Eq. (15) becomes

  $$E_{x/z} (e,f) = Q\sum\limits_{{l_{1} = 0}}^{i - n + e} {\sum\limits_{{l_{2} = 0}}^{j - m + f} {C_{i - n + e}^{{l_{1} }} C_{j - m + f}^{{l_{2} }} ( - x_{0} )^{{l_{1} }} p^{{j - m + f - l_{2} }} (q - z_{0} )^{{l_{2} }} } } \cdot I_{l}$$

  (16)

  where ${C_{i - n + e}^{{l_{1} }}}$ and ${C_{j - m + f}^{{l_{2} }}}$ are the binomial expansion coefficients, and

  $$I_{l} = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{x^{l} }}{{cx^{2} + 2bx + a}}{\text{d}}x}$$

  (17)

  with l = i + j − m − n − l₁− l₂ + e + f.

  Obviously, once we want to get the value of integral I_l, we need to consider another two cases according to the discriminant

  $$\begin{aligned} \Delta & = 4ac - 4b^{2} \\ & = 4\left( {1 + p^{2} } \right)\left[ {\left( {q - z_{0} } \right)^{2} + x_{0}^{2} } \right] - 4\left[ {p\left( {q - z_{0} } \right) - x_{0} } \right]^{2} \\ & = \left( {4 + 4p^{2} } \right)\left( {q - z_{0} } \right)^{2} + 4x_{0}^{2} + 4p^{2} x_{0}^{2} - 4p^{2} \left( {q - z_{0} } \right)^{2} + 8px_{0} \left( {q - z_{0} } \right) - 4x_{0}^{2} \\ & = 4\left[ {\left( {q - z_{0} } \right)^{2} + 2px_{0} \left( {q - z_{0} } \right) + p^{2} x_{0}^{2} } \right] \\ & = 4\left( {px_{0} + q - z_{0} } \right)^{2} \\ & = 4Q^{2} \\ \end{aligned}$$

  (18)

  of the quadratic polynomial cx²+2bx + a, which include Δ = 0 and Δ > 0.

  • 1) When Δ = 0,we have Q = 0. By setting Q = 0 in Eq. (16), we reach

    $$E_{x/z} (e,f) = 0 .$$

    (19)

  • 2) When Δ > 0,the result of integral I_l has already been calculated by Zhou (2010) as

    $$\left\{ {\begin{array}{*{20}l} {I_{0} = \frac{1}{\left| Q \right|}\left( {\tan^{ - 1} \frac{{c \cdot x_{k + 1} + b}}{\left| Q \right|} - \tan^{ - 1} \frac{{c \cdot x_{k} + b}}{\left| Q \right|}} \right)} \hfill \\ {I_{1} = \frac{1}{c}\ln \frac{{r_{k + 1} }}{{r_{k} }} - \frac{b}{c}I_{0} } \hfill \\ {I_{l} = \frac{{x_{k + 1}^{l - 1} - x_{k}^{l - 1} }}{c(l - 1)} - \frac{2b}{c}I_{l - 1} - \frac{a}{c}I_{l - 2} \begin{array}{*{20}c} {} & {(l \ge 2)} \\ \end{array} } \hfill \\ \end{array} } \right.$$

    (20)

    where r_k+1=[(x_k+1− x₀)² + (z_k+1− z₀)²]^1/2 and r_k=[(x_k− x₀)² + (z_k− z₀)²]^1/2.

• 2. When x_k = x_k+1,the integral of x in Eq. (13) is 0, just leaving the integral with respect to z to be calculated. Hence, Eq. (13) can be expressed as

  $$E_{x/z} \left( {e,f} \right) = - \left( {x_{k} - x_{0} } \right)^{i - n + e + 1} \cdot K_{l}$$

  (21)

  where

  $$K_{l} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(z - z_{0} )^{l} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} dz$$

  (22)

  with l = j − m + f. When using the Binomial theorem, we have 0 ≤ m ≤ j, so that f ≤ j − m + f ≤ j + f. In accordance, there is l ≥ 0 for E_x (1, 0) and l ≥ 1 for E_z (0, 1).

Referring to Eq. (57), we can obtain the result of K₀, while those of K₁, K₂ and K_l (l > 2) have already been calculated by Zhou (2010). So the result of integral K_l is

$$\left\{ {\begin{array}{*{20}l} {K_{0} = \frac{1}{{x_{k} - x_{0} }}\left( {\tan^{ - 1} \frac{{z_{k + 1} - z_{0} }}{{x_{k + 1} - x_{0} }} - \tan^{ - 1} \frac{{z_{k} - z_{0} }}{{x_{k} - x_{0} }}} \right)} \hfill \\ {K_{1} = \ln \frac{{r_{k + 1} }}{{r_{k} }}} \hfill \\ {K_{l} = \frac{{(z_{k + 1} - z_{0} )^{l - 1} - (z_{k} - z_{0} )^{l - 1} }}{l - 1} - (x_{k} - x_{0} )^{2} K_{l - 2} \;\;(l \ge 2)} \hfill \\ \end{array} } \right.$$

(23)

where r_k+1=[(x_k+1− x₀)² + (z_k+1− z₀)²]^1/2 and r_k=[(x_k− x₀)² + (z_k− z₀)²]^1/2.

However, it should be noted that the value of recursive integral K_l cannot be calculated according to Eq. (23) when x₀ = x_k = x_k+1 with z₀ ≠ z_k and z₀ ≠ z_k+1, because the first term K₀ cannot be calculated. While taking actual meanings of those functions into account, we can find that the value of K₀ under this condition is 0. Since tan ⁻¹[(z_k+1− z₀)/(x_k+1− x₀)] and tan ⁻¹[(z_k− z₀)/(x_k− x₀)], respectively, represent the angle between horizontal direction and a line through observation point and endpoint of the side parallel to z-axis, they are all π/2, and hence the difference between them is 0. Moreover, the factor 1/(x_k− x₀) can be reduced actually. Considering that calculating K_l is aiming to obtain the value of function E_x/z (e, f) shown in Eq. (21), and there is a factor (x_k− x₀)^{i − n+e+1} in Eq. (21) with i − n + e + 1 ≥ 1, the factor 1/(x_k− x₀) can always be canceled. So we can assign K₀ directly to 0 under this condition, and the value of other terms of recursive integral K_l can also be obtained.

Until now, the calculation of function E_x/z (e, f) shown in Eq. (13) has been completed, which means the analytical solutions of gravity vector have also been achieved. To sum up, Eqs. (16)–(23) comprise the result of E_x/z (e, f), which works for U_x(x₀, z₀) with E_x (1, 0) and works for U_z(x₀, z₀) with E_z (0, 1). Moreover, Eqs. (14) and (16)–(23) constitute the complete analytical expression system of the gravity vector (U_x and U_z).

2.3 U _xz, U _zx, U _xx and U _zz

Because U_xz = U_zx and U_zz = − U_xx, we just take U_xz and U_zz for example.

Using the Binomial theorem, (Singh 2017), we put the expanded Eq. (8) into Eq. (7) and do some sorting, and then we can get the analytic expressions of U_xz and U_zz as

$$\left\{ {\begin{array}{*{20}l} {U_{xz} (x_{0} ,z_{0} ) = 4G\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } \sum\limits_{n = 0}^{i} {\sum\limits_{m = 0}^{j} {C_{i}^{n} C_{j}^{m} x_{0}^{n} z_{0}^{m} } } } E_{xz} } \hfill \\ {U_{zz} (x_{0} ,z_{0} ) = 2G\sum\limits_{i = 0}^{N_{x}} {\sum\limits_{j = 0}^{N_{z}} {D_{i,j} } \sum\limits_{n = 0}^{i} {\sum\limits_{m = 0}^{j} {C_{i}^{n} C_{j}^{m} x_{0}^{n} z_{0}^{m} } } } E_{zz} } \hfill \\ \end{array} } \right.$$

(24)

with

$$\left\{ {\begin{array}{*{20}l} {E_{xz} = \iint\limits_{s} {\frac{{(x - x_{0} )^{i - n + 1} (z - z_{0} )^{j - m + 1} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \hfill \\ {E_{zz} = \iint\limits_{s} {\frac{{(x - x_{0} )^{i - n} (z - z_{0} )^{j - m + 2} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z - \iint\limits_{s} {\frac{{(x - x_{0} )^{i - n + 2} (z - z_{0} )^{j - m} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}}} \hfill \\ \end{array} } \right.$$

(25)

where (x₀, z₀) are the coordinates of observation point, G is gravitational constant, N_x and N_z, respectively, represent the maximum order of x and z in density function, D_{i, j} represents the coefficient of the polynomial density function, and C ⁿ _i and C ^m _j are the binomial expansion coefficients with 0 ≤ n ≤ i and 0 ≤ m ≤ j.

Thanks to the law shown in Eq. (10), we can further infer that

$$\begin{aligned} & \frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }} \\ & \quad = \frac{1}{i + j - m - n + e + f - 2}\left\langle {\frac{\partial }{\partial x}\left\{ {\frac{{(x - x_{0} )^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}} \right\} + \frac{\partial }{\partial z}\left\{ {\frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}} \right\}} \right\rangle \\ \end{aligned}$$

(26)

where e and f are constants, and i + j − m − n + e + f − 2 ≠ 0.

According to Eq. (26) and Stokes’ theorem for a plane (Riley et al. 2010) mentioned in Eq. (11), we convert the surface integrals in Eq. (25) into a sum of line integrals calculated on the boundary of the polygon in a counterclockwise direction. Considering that the closed boundary is connected by N_e sides end to end, we reach

$$\iint\limits_{s} {\frac{{(x - x_{0} )^{i - n + e} (z - z_{0} )^{j - m + f} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z} = \frac{1}{i + j - m - n + e + f - 2}\sum\limits_{k = 1}^{{N_{e} }} {T_{xz/zz} (e,f)}$$

(27)

with

$$T_{xz/zz} (e,f) = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e} (z - z_{0} )^{j - m + f + 1} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}} {\text{d}}x - \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{\left( {x - x_{0} } \right)^{i - n + e + 1} (z - z_{0} )^{j - m + f} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}} {\text{d}}z$$

(28)

where i + j − m − n + e + f − 2 ≠ 0, N_e is the number of polygon’s sides, and k denotes that it is the kth side being calculated followed by a counterclockwise direction with its two endpoints being (x_k, z_k) and (x_k+1, z_k+1) as shown in Fig. 1.

In terms of Eqs. (27) and (28), one premise must be met above all, that is i + j − m − n + e + f − 2 ≠ 0. However, as we can see in Eq. (25), e + f ≡2. Since 0 ≤ n ≤ i and 0 ≤ m ≤ j, it is obvious that i + j − m − n + e + f − 2 = 0 if and only if n = i with m = j. Under this condition, Eqs. (27) and (28) are meaningless, making this situation needed to be discussed separately.

Nevertheless, let’s begin with the general situation.

• 1. When i + j ≠ m + n, the conclusions in Eqs. (27) and (28) are tenable. Taking them into Eq. (25), we have

  $$\left\{ {\begin{array}{*{20}l} {E_{xz} = \frac{1}{i + j - m - n}\sum\limits_{k = 1}^{{N_{e} }} {T_{xz} \left( {1,1} \right)} } \hfill \\ {E_{zz} = \frac{1}{i + j - m - n}\sum\limits_{k = 1}^{{N_{e} }} {\left[ {T_{zz} (0,2) - T_{zz} (2,0)} \right]} } \hfill \\ \end{array} } \right.$$

  (29)

  where N_e is the number of polygon’s sides and k denotes that it is the kth side being calculated followed by a counterclockwise direction.

  The problem about calculating function T_xz/zz (e, f) is also a problem about calculating linear integrals on straight lines. When we unify the integral variables, two cases must be considered, respectively: one is that the kth side is not parallel to z-axis, and the other is that the kth side is parallel to z-axis. If the kth side is not parallel to z-axis, which means x_k ≠ x_k+1, the equation of the line this side located can be described by z = px + q where p =(z_k+1− z_k)/(x_k+1− x_k) and q =(z_kx_k+1− z_k+1x_k)/(x_k+1− x_k). Then, we can substitute this equation into Eq. (28) and replace variable z with variable x, making Eq. (28) an integral only depend on the coordinates of x. In the other case, that means x_k = x_k+1, the slope of this line doesn’t exist, while the integral of x in Eq. (28) is 0 in this case, just leaving the latter integral about z to be calculated.

  Here are the details:

  • 1) When x_k≠ x_{k +1},substitute the linear equation z = px + q into Eq. (28) and merge similar terms, then we have

    $$T_{xz/zz} \left( {e,f} \right) = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{(px_{0} + q - z_{0} )\left( {x - x_{0} } \right)^{i - n + e} (px + q - z_{0} )^{j - m + f} }}{{\left\{ {(1 + p^{2} )x^{2} + 2[p(q - z_{0} ) - x_{0} ]x + [(q - z_{0} )^{2} + x_{0}^{2} ]} \right\}^{2} }}{\text{d}}x} .$$

    (30)

    After noting Q = px₀ + q − z₀, a =(q − z₀)² + x ²₀ , b = p(q − z₀)− x₀, c =1 + p², and using the Binomial theorem (Singh 2017) on the terms (x − x₀)^{i − n+e} and (px + q − z₀)^{j − m+f}, Eq. (30) becomes

    $$T_{xz/zz} (e,f) = Q\sum\limits_{{l_{1} = 0}}^{i - n + e} {\sum\limits_{{l_{2} = 0}}^{j - m + f} {C_{i - n + e}^{{l_{1} }} C_{j - m + f}^{{l_{2} }} ( - x_{0} )^{{l_{1} }} p^{{j - m + f - l_{2}}} (q - z_{0} )^{{l_{2} }} } } \cdot J_{l}$$

    (31)

    where $C_{i - n + e}^{{l_{1} }}$ and $C_{j - m + f}^{{l_{2} }}$ are the binomial expansion coefficients, and

    $$J_{l} = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{x^{l} }}{{\left( {cx^{2} + 2bx + a} \right)^{2} }}{\text{d}}x}$$

    (32)

    with l = i + j − m − n − l₁− l₂ + e + f.

    Similarly, in order to get the value of integral J_l, we consider two cases according to the discriminant Δ =4ac − 4b²=4Q² [which is proved in Eq. (18)] of the quadratic polynomial cx²+2bx + a, which include Δ = 0 and Δ > 0.

    • ① When Δ = 0, we have Q = 0. By setting Q = 0 in Eq. (31), we reach

      $$T_{xz/zz} (e,f) = 0$$

      (33)

    • ② When Δ > 0,we can refer to some mathematical formulas to get the value of integral J_l. Specifically, we can obtain J₀ according to Eq. (58), J₁ according to Eq. (59), J₂ according to Eq. (60), J₃ according to Eq. (61) and J_l (l ≥ 4) according to Eq. (60). The final results can be easily reached without further description as

      $$\left\{ {\begin{array}{*{20}l} {J_{0} = \frac{1}{{2Q^{2} }}\left[ {\frac{{cx_{k + 1} + b}}{{r_{k + 1}^{2} }} - } \right.\left. {\frac{{cx_{k} + b}}{{r_{k}^{2} }}} \right] + \frac{c}{{2Q^{2} }}I_{0} } \hfill \\ {J_{1} = - \frac{1}{{2Q^{2} }}\left[ {\frac{{bx_{k + 1} + a}}{{r_{k + 1}^{2} }} - } \right.\left. {\frac{{bx_{k} + a}}{{r_{k}^{2} }}} \right] - \frac{b}{{2Q^{2} }}I_{0} } \hfill \\ {J_{2} = - \frac{1}{c}\left( {\frac{{x_{k + 1} }}{{r_{k + 1}^{2} }} - \frac{{x_{k} }}{{r_{k}^{2} }}} \right) + \frac{a}{c}J_{0} } \hfill \\ \begin{aligned} J_{3} = \frac{1}{{2c^{2} }}\ln \frac{{r_{k + 1}^{2} }}{{r_{k}^{2} }} + \frac{{\left( {3bQ^{2} - b^{3} } \right)x_{k + 1} + aQ^{2} - ab^{2} }}{{2c^{2} Q^{2} r_{k + 1}^{2} }} - \frac{{\left( {3bQ^{2} - b^{3} } \right)x_{k} + aQ^{2} - ab^{2} }}{{2c^{2} Q^{2} r_{k}^{2} }} - \frac{{3bQ^{2} + b^{3} }}{{2c^{2} Q^{2} }} \cdot I_{0} \hfill \\ J_{l} = \frac{1}{c(l - 3)}\left( {\frac{{x_{k + 1}^{l - 1} }}{{r_{k + 1}^{2} }} - \frac{{x_{k}^{l - 1} }}{{r_{k}^{2} }}} \right) - \frac{l - 2}{l - 3} \cdot \frac{2b}{c}J_{l - 1} - \frac{l - 1}{l - 3} \cdot \frac{a}{c}J_{l - 2} \;\;(l \ge 4) \hfill \\ \end{aligned} \hfill \\ \end{array} } \right.$$

      (34)

      with

      $$I_{0} = \frac{1}{\left| Q \right|}\left( {\tan^{ - 1} \frac{{c \cdot x_{k + 1} + b}}{\left| Q \right|} - \tan^{ - 1} \frac{{c \cdot x_{k} + b}}{\left| Q \right|}} \right)$$

      (35)

      where r_k+1=[(x_k+1− x₀)² + (z_k+1− z₀)²]^1/2 and r_k=[(x_k− x₀)² + (z_k− z₀)²]^1/2. Besides, Q = px₀ + q − z₀, a =(q − z₀)² + x ²₀ , b = p(q − z₀)− x₀, c =1 + p², p =(z_k+1− z_k)/(x_k+1− x_k) and q =(z_kx_k+1− z_k+1x_k)/(x_k+1− x_k).Until now, the calculation about function T_xz/zz (e, f) shown in Eq. (28) for the time x_k ≠ x_k+1 has been completed.

  • 2) When x_k= x_k+1,the integral of x in Eq. (28) is 0, just leaving the latter integral of z to be calculated. Hence, Eq. (28) can be expressed as

    $$T_{xz/zz} (e,f) = - \left( {x_{k} - x_{0} } \right)^{i - n + e + 1} \cdot H_{l}$$

    (36)

    where

    $$H_{l} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(z - z_{0} )^{l} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}} {\text{d}}z$$

    (37)

    with l = j − m + f.

    Likewise, we can also refer to some mathematical formulas to get the value of integral H_l. Specifically, we can obtain H₀ according to Eq. (62), H₁ according to Eq. (63) and H_l (l ≥ 2) according to Eq. (64). The final results can be easily reached without further description as

    $$\left\{ {\begin{array}{*{20}l} {H_{0} = \frac{1}{{2(x_{k} - x_{0} )^{3} }}\left[ {\frac{{(x_{k + 1} - x_{0} )\left( {z_{k + 1} - z_{0} } \right)}}{{r_{k + 1}^{2} }} - \frac{{(x_{k} - x_{0} )\left( {z_{k} - z_{0} } \right)}}{{r_{k}^{2} }} + \tan^{ - 1} \frac{{z_{k + 1} - z_{0} }}{{x_{k + 1} - x_{0} }} - \tan^{ - 1} \frac{{z_{k} - z_{0} }}{{x_{k} - x_{0} }}} \right]} \hfill \\ {H_{1} = - \frac{1}{2}\left( {\frac{1}{{r_{k + 1}^{2} }} - \frac{1}{{r_{k}^{2} }}} \right)} \hfill \\ {H_{l} = - \frac{1}{2}\left( {\frac{{\left( {z_{k + 1} - z_{0} } \right)^{l - 1} }}{{r_{k + 1}^{2} }} - \frac{{\left( {z_{k} - z_{0} } \right)^{l - 1} }}{{r_{k}^{2} }}} \right) + \frac{l - 1}{2}K_{l - 2} \;\;(l \ge 2)} \hfill \\ \end{array} } \right.$$

    (38)

    where

    $$K_{l} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(z - z_{0} )^{l} }}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} {\text{d}}z$$

    (39)

    whose result is shown in Eq. (23).

    Until now, the calculation about function T_xz/zz (e, f) shown in Eq. (28) for the time x_k = x_k+1 has been completed, which means the calculation about functions E_xz and E_zz shown in Eq. (25) for the time i + j ≠ m + n has been completed too. The entire result of T_xz/zz (e, f) is comprised of Eqs. (31)–(39).

• 2. When i + j = m + n, the conclusions in Eqs. (27) and (28) are meaningless. Thus, we put n = i and m = j into Eq. (25) directly, making

  $$\left\{ {\begin{array}{*{20}c} {E_{xz} = \iint\limits_{s} {\frac{{(x - x_{0} )(z - z_{0} )}}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \\ {E_{zz} = \iint\limits_{s} {\frac{{(z - z_{0} )^{2} - (x - x_{0} )^{2} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }}{\text{d}}x{\text{d}}z}} \\ \end{array} } \right.$$

  (40)

  where s denotes the cross-sectional area and (x₀, z₀) are the coordinates of observation point.

  Considering the strategy above, we transform the integrands of Eq. (40) into

  $$\left\{ {\begin{array}{*{20}l} {\frac{{(x - x_{0} )(z - z_{0} )}}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }} = - \frac{1}{2}\left\{ {\frac{\partial }{\partial x}\left[ {\frac{{(z - z_{0} )}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} \right]{ + }\frac{\partial }{\partial z}0} \right\}} \hfill \\ {\frac{{(z - z_{0} )^{2} - (x - x_{0} )^{2} }}{{\left[ {(x - x_{0} )^{2} + (z - z_{0} )^{2} } \right]^{2} }} = \frac{\partial }{\partial x}\left[ {\frac{{(x - x_{0} )}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}} \right]{ + }\frac{\partial }{\partial z}0} \hfill \\ \end{array} } \right. .$$

  (41)

  Then, applying Stokes’ theorem for a plane (Riley et al. 2010) mentioned in Eq. (11), we convert the surface integral into a sum of line integrals calculated on the sides of the polygon in a counterclockwise direction. Thus, Eq. (40) becomes

  $$\left\{ {\begin{array}{*{20}c} {E_{xz} = \frac{1}{2}\sum\limits_{k = 1}^{{N_{e} }} {F_{xz} } } \\ {E_{zz} = - \sum\limits_{k = 1}^{{N_{e} }} {F_{zz} } } \\ \end{array} } \right.$$

  (42)

  with

  $$\left\{ \begin{aligned} F_{xz} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(z - z_{0} )}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}z} \hfill \\ F_{zz} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(x - x_{0} )}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}z} \hfill \\ \end{aligned} \right.$$

  (43)

  where N_e is the number of polygon’s sides and k denotes that it is the kth side being calculated followed by a counterclockwise direction with its two endpoints being (x_k, z_k) and (x_k+1, z_k+1) as shown in Fig. 1.

  Two cases must be considered when calculating Eq. (43): one is the kth side is not parallel to z-axis, and the other is the kth side is parallel to z-axis. When the kth side is not parallel to z-axis, x_k ≠ x_k+1. The equation of the line this side located is z = px + q where p =(z_k+1− z_k)/(x_k+1− x_k) and q =(z_kx_k+1− z_k+1x_k)/(x_k+1− x_k). So we need to unify variables in integrals before calculating. In the other case, that means x_k = x_k+1, the slope of this line doesn’t exist. So we can directly get the result with the variation range of variable z.

  • 1) When x_k ≠ x_k+1, substituting the linear equation z = px + q into Eq. (43) for sorting, we have

    $$\left\{ {\begin{array}{*{20}l} {F_{xz} = p^{2} \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{x}{{cx^{2} + 2bx + a}}{\text{d}}x} + p(q - z_{0} )\int_{{x_{k} }}^{{x_{k + 1} }} {\frac{1}{{cx^{2} + 2bx + a}}{\text{d}}x} } \hfill \\ {F_{zz} = p\int_{{x_{k} }}^{{x_{k + 1} }} {\frac{x}{{cx^{2} + 2bx + a}}{\text{d}}x} - px_{0} \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{1}{{cx^{2} + 2bx + a}}{\text{d}}x} } \hfill \\ \end{array} } \right.$$

    (44)

    where a =(q − z₀)² + x ²₀ ,  p(q − z₀)− x₀\,=\, p(q − z₀)− x₀ and c =1 + p².

    Another two cases needed to be considered according to the discriminant Δ =4ac − 4b²=4Q² [which is proved in Eq. (18)] with Q = px₀ + q − z₀ of the quadratic polynomial cx²+2bx + a, which include Δ = 0 and Δ > 0.

    • ① When Δ = 0,the factor cx²+2bx + a can be expressed as c(x + b/c)² due to the method of completing the square. After noting a′ = b/c = [p(q − z₀)− x₀]/(1 + p²) and X′ = c(x + a′)² = cx²+2bx + a, we define a new integral M_l as

      $$M_{l} = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{x^{l} }}{{X^{\prime }}}} {\text{d}}x = \frac{1}{c}\int_{{x_{k} }}^{{x_{k + 1} }} {\frac{{x^{l} }}{{\left( {x + a^{\prime }} \right)^{2} }}} {\text{d}}x$$

      (45)

      with the value of M₀ and M₁ that can be obtained according to Eq. (65) and Eq. (66), respectively, as

      $$\left\{ {\begin{array}{*{20}l} {M_{0} = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{1}{{X^{\prime }}}} {\text{d}}x = - \frac{1}{c}\left( {\frac{1}{{x_{k + 1} + a^{\prime }}} - \frac{1}{{x_{k} + a^{\prime }}}} \right)} \hfill \\ {M_{1} = \int_{{x_{k} }}^{{x_{k + 1} }} {\frac{x}{{X^{\prime }}}} {\text{d}}x = \frac{1}{c}\ln \frac{{x_{k + 1} + a^{\prime }}}{{x_{k} + a^{\prime }}} + \frac{{a^{\prime }}}{c}\left( {\frac{1}{{x_{k + 1} + a^{\prime }}} - \frac{1}{{x_{k} + a^{\prime }}}} \right)} \hfill \\ \end{array} } \right.$$

      (46)

      Thanks to integral M_l, Eq. (44) can be briefly expressed as

      $$\left\{ {\begin{array}{*{20}l} {F_{xz} = p^{2} M_{1} + p(q - z_{0} )M_{0} } \hfill \\ {F_{zz} = pM_{1} - px_{0} M_{0} } \hfill \\ \end{array} } \right.$$

      (47)

    • ② When Δ > 0,the factor cx²+2bx + a doesn’t need to be changed, and the integrals in Eq. (44) are the same as I₀ and I₁ mentioned in Eq. (20). Hence, Eq. (44) can be expressed as

      $$\left\{ {\begin{array}{*{20}l} {F_{xz} = p^{2} I_{1} + p\left( {q - z_{0} } \right)I_{0} } \hfill \\ {F_{zz} = pI_{1} - px_{0} I_{0} } \hfill \\ \end{array} } \right.$$

      (48)

      with

      $$I_{0} = \frac{1}{\left| Q \right|}\left( {\tan^{ - 1} \frac{{c \cdot x_{k + 1} + b}}{\left| Q \right|} - \tan^{ - 1} \frac{{c \cdot x_{k} + b}}{\left| Q \right|}} \right)$$

      (49)

      and

      $$I_{1} = \frac{1}{c}\ln \frac{{r_{k + 1} }}{{r_{k} }} - \frac{b}{c}I_{0}$$

      (50)

      where Q = px₀ + q −z₀, b =  p(q − z₀)− x₀, c = 1 + p², r_k+1=[(x_k+1 − x₀)² + (z_k+1− z₀)²]^1/2 and r_k = [(x_k− x₀)² + (z_k − z₀)²]^1/2.

      Until now, the calculation of functions F_xz and F_zz shown in Eq. (43) for the time x_k ≠ x_k+1 has been completed.

  • 2) When x_k= x_k+1, the integrated line is parallel to z-axis without a slope, so we don’t have to unify variable z into variable x. On the contrary, we can directly get the value of Eq. (43) with the variation range of variable z.

    Under this condition, the integrals in Eq. (43) are the same as K₀ and K₁ mentioned in Eq. (23). Hence, Eq. (43) becomes

    $$\left\{ {\begin{array}{*{20}l} {F_{xz} = \int_{{z_{k} }}^{{z_{k + 1} }} {\frac{{(z - z_{0} )}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}z} = K_{1} } \hfill \\ {F_{zz} = (x_{k} - x_{0} )\int_{{z_{k} }}^{{z_{k + 1} }} {\frac{1}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}{\text{d}}z} = (x_{k} - x_{0} )K_{0} } \hfill \\ \end{array} } \right.$$

    (51)

    with

    $$K_{0} = \frac{1}{{x_{k} - x_{0} }}\left( {\tan^{ - 1} \frac{{z_{k + 1} - z_{0} }}{{x_{k + 1} - x_{0} }} - \tan^{ - 1} \frac{{z_{k} - z_{0} }}{{x_{k} - x_{0} }}} \right)$$

    (52)

    and

    $$K_{1} = \ln \frac{{r_{k + 1} }}{{r_{k} }}$$

    (53)

    where r_k+1 = [(x_k+1 − x₀)² + (z_k+1 − z₀)²]^1/2 and r_k = [(x_k − x₀)² + (z_k − z₀)²]^1/2.

    Until now, the calculation about F_xz and F_zz shown in Eq. (43) for the time x_k = x_k+1 has been completed, which means the calculation about E_xz and E_zz shown in Eq. (25) for the time i + j = m + n has been completed. With the results we got for the time i + j ≠ m + n, we have finished all the derivation of analytic expressions of U_xz and U_zz so far.

    In summary, Eqs. (24), (29), (31)–(39), (42) and (46)–(53) constitute a complete analytical expression system for U_xz and U_zz.

3 Singularity and Numerical Error

Because of the domain limits of elementary functions, our expressions are meaningless at some points in the plane. These points are called singularity points. And due to the limited floating-point precision in numerical calculations, numerical stability has always been a desirable attribute for every algorithm.

In this section, we analyze the singularity of our expressions in different situations and propose corresponding solutions. We also use another conventional method whose result is taken as a standard to get the relative error and the range of numerical stability of our expressions, in which the model with different-order polynomial density function is divided into a collection of constant-density units. Finally, we test the numerical stability of our expressions with practical density variation, and prove its validity for high-order polynomial density cases.

3.1 Singularity Analysis

Singularity is essentially caused by the domain limitations of some elementary functions in our expressions. As an example, the denominator cannot be 0 for fractional functions; N needs to be greater than 0 for a logarithmic function lnN. In other words, these functions may have meaningless conditions such as 0/0, 1/0, or ln0 at certain points in the plane, making the anomalies at these singularity points unable to be calculated.

According to the derivation above, two cases need to be considered before analysis: one is that all sides of the model are not parallel to z-axis, and the other is that the model contains any side parallel to z-axis. The reason of this consideration is the recursive integrals used in the two cases are not the same. Besides, as long as one of the previous terms of a recursive integral cannot be calculated, the latter terms of it cannot be calculated.

On the one hand, when all sides of the model are not parallel to z-axis, the calculation of U_x and U_z only involves the recursive integral I_l. As can be seen in Eq. (20), I₁ as a second term of I_l contains function ln(r_k+1/r_k), making the anomalies of U_x and U_z at vertices of the model unable to be calculated, while the calculation of U_xz and U_zz involves recursive integrals I_l, J_l and M_l. As can be seen in Eq. (34), J₀ as a first term of J_l, contains functions (cx_k+1 + b)/r ² _k+1 and (cx_k + b)/r ² _k , which also makes the anomalies of U_xz and U_zz at vertices unable to be calculated. To sum up, the singularity points only locate at vertices of the polygon in this situation.

On the other hand, once one of the sides of the model is parallel to z-axis, the calculation of U_x and U_z not only involves integral I_l (which means the anomalies of U_x and U_z at vertices of the model cannot be calculated), but also needs the recursive integral K_l. As can be seen in Eq. (23), there are two factors in the first term K₀, those are 1/(x_k− x₀) and {tan ⁻¹[(z_k+1− z₀)/|x_k+1− x₀|]− tan ⁻¹[(z_k− z₀)/|x_k− x₀|]}. Their denominators require that the horizontal coordinate of observation point couldn’t be equal to that of vertex. However, as we explained earlier, if the observation point locates on the line through the parallel side but is not coincide with two endpoints, we can assign K₀ directly to 0, so that other terms of integral K_l could be calculated continually. To sum up, the singularity points of U_x and U_z still locate at vertices of the polygon under this condition.

But for U_xz and U_zz, the situation is different. Under this circumstance, the calculation about U_xz and U_zz not only involves integral J_l (which means the anomalies of U_xz and U_zz at vertices cannot be calculated), but also involves integral H_l. As can be seen in Eq. (38), the first term H₀ is quite similar to K₀. Yet unlike K₀, the factor 1/(x_k− x₀)³ of H₀ cannot be reduced. The reason is that, in order to calculate function T_xz/zz (e, f) shown in Eq. (36), H₀ needs to be multiplied by factor (x_k− x₀)^{i − n+e+1}, while i − n + e + 1 ≥ 1 with the value of e becoming 0, 1, 2, which cannot make 1/(x_k− x₀)³ reduced completely. For recursive integral H_l, once the first term H₀ cannot be calculated, the latter terms of it cannot be calculated, so does the anomalies of U_xz and U_zz. As a result, the domain of observation points is limited into {(x₀, z₀)|x₀ ≠ x_k}. To sum up, all points on the line through the side parallel to z-axis are singularity points of U_xz and U_zz under this condition.

Comparing the analysis of these two cases above, it is obvious that the latter one is much more complicated. Therefore, if we can make all the sides of the polygon not parallel to z-axis when modeling, we can control the singularity points of our expressions to just locate at the vertices of the polygon whether for the gravity vector or for the gravity gradient tensor. Furthermore, two methods can be used to remove the singularity in numerical calculation. One is to move the computation points away from the singularity points by an infinitesimal distance (Jiang et al. 2017) which is used in later model testing, and the other is to exclude an extremely small sphere around the singularity points (Tsoulis and Petrovic 2001; Zhou 2009a, 2010). Generally, the radius of the exclusive infinitesimal sphere can be specified as ε = μR_m, where μ is a dimensionless, infinitely smaller number and R_m is the maximum size of the mass body (Zhou 2010).

3.2 Numerical Error

Another problem is the analytical numerical error of the expression. The rounding error in calculations may be magnified, even if your algorithm is derived correctly. Holstein and Ketteridge (1996) claimed that numerical calculation of analytic expressions was plagued by limited floating-point precision. Certainly, the gravitational field decreases as the distance between the target and observation increases, while the numerical error increases.

In order to evaluate the stability of our expressions, consider a square object {[x, z]:− 1 ≤ x ≤ 1, 0 ≤ z ≤ 2} shown in Fig. 2, whose density contrast is $\sigma \left( {x,z} \right) = \sum\nolimits_{i = 0}^{3} {x^{i} z^{i} }$ where σ(x, z) is in g/cm³ and where x and z are in meters. The observation points are along line z = − x + 1 at a length interval of √2 from point (2, − 1) to point (300, − 299). According to Holstein and Ketteridge (1996), we define the dimensionless target distance as the ratio of a distance between observation point and target body to a typical linear size of the target.

Fig. 2

A square object {[x, z]:− 1 ≤ x ≤ 1, 0 ≤ z ≤ 2} with density contrast $\sigma \left( {x,z} \right) = \sum\nolimits_{i = 0}^{3} {x^{i} z^{i} }$ where σ(x, z) is in g/cm³ and where x and z are in meters. The observation points are along line z = − x + 1 at a length interval of √2 from point (2, − 1) to point (300, − 299)

In the meantime, we also take another conventional method called constant-density method to compare, in which the model is divided into a collection of constant-density units. And the gravity effects of these constant-density units are calculated according to the analytic expressions presented by Jia and Wu (2011). It is said the conventional method has better stability when calculating. In this model, we set the constant-density unit into a small square whose side length is 0.02 m, and replace the density of it with an average of those at vertices and center point, and then sum up the contributions of all units calculated by analytic Eqs. (20a)–(20f) in the paper presented by Jia and Wu (2011). Figure 3 shows the various differences between the anomalies of gravity vector and gravity gradient tensor calculated by the two methods versus dimensionless target distance, using MATLAB software on a computer with Intel (R) Core(TM) i5-2400, frequency 3.10 GHz, and RAM of 4.00 GB.

Fig. 3

The anomalies of U_x (a), U_z (b), U_xz and U_zx (c), U_xx and U_zz (d) for the model shown in Fig. 2 calculated by constant-density method and present approach versus the dimensionless target distance of observation point

As can be seen in Fig. 3, when observation point is close to target body, the results of two methods match well. But beyond a certain distance, the result of present approach is destroyed by the calculation of closure difference. Since the result of constant-density method is always stable in this range, it can be taken as a standard to evaluate the relative error of present approach. Figure 4 reflects how a base-10 logarithm of the relative error of present approach compared with constant-density method changes with the dimensionless target distance along observation line.

Fig. 4

A base-10 logarithm of the relative error of present approach compared with constant-density method for the gravity vector and gravity gradient tensor produced by the model shown in Fig. 2 versus the dimensionless target distance of observation point. Besides, the horizontal dashed line indicates the 100% relative error

In Fig. 4, the horizontal dashed line indicates a relative error of 100%, which means the calculated floating-point error is the same order as the solution of gravity effects. Correspondingly, the dimensionless target distance at this time is called critical target distance, which reflects the range of numerical stability of present approach. Beyond the critical target distance, the fluctuation of our curve becomes more and more severe with the increase of distance. What’s more, according to those anomalies shown in Fig. 3, if we take the absolute value less than 0.001 mgal as the criterion for the disappearance of U_x and U_z, and the absolute value less than 1 E as the criterion for the disappearance of U_xz and U_zz, the corresponding dimensionless target distances of their disappearance (also called the maximum target distances of anomalies) become: U_x, 18.46 times; U_z, 18.46 times; U_xz, 10 times; U_zz, 3.34 times. And according to Fig. 4, we can know that their critical target distances, respectively, becomes: U_x, 65 times; U_z, 63 times; U_xz, 48.3 times; U_zz, 27.2 times. It is quite obvious that the critical target distances of present approach are much greater than the maximum target distances of anomalies, proving the practicability of our expressions.

Furthermore, we evaluate the numerical stability ranges of present approach with different-order polynomial density function $\sigma (x,z) = \sum\nolimits_{i = 0}^{n} {x^{i} z^{i} } , \, (n = 1,2,3, \ldots ,7)$ plotting the variety of critical target distances of gravity vector and gravity gradient tensor versus the maximum order of density function in Fig. 5. Besides, the units of density are g/cm³, and those of x and z are meters. There are several facts in Fig. 5: first, as the order increases, the critical target distances are always decreasing; second, the critical target distances of gravity gradient tensor are smaller than those of gravity vector, for the increasing errors due to higher order in differentiation; third, the critical target distance of U_zz is smaller than U_xz, because the repeated calculations of function T_xz/zz (e, f) shown in Eq. (29) inevitably increase the numerical error of U_zz.

Fig. 5

Critical target distances of present approach for gravity vector and gravity gradient tensor produced by the model shown in Fig. 2 with the density contrast being $\sigma (x,z) = \sum\nolimits_{i = 0}^{n} {x^{i} z^{i} } ,\quad (n = 1,2,3, \ldots ,7)$. The horizontal axis is the maximum order of density function

Finally, in order to test numerical stability of present approach with actual density contrast, we take a density function σ (x, z) = − 700 + 254.8z − 27.3z² shown in Eq. (54) for example, which represents the density contrast of Sebastián Vizcaíno basin in Mexico. Besides, the units of density are kg/m³, and those of x and z are kilometers. We calculate the critical target distances of gravity vector and gravity gradient tensor produced by the model shown in Fig. 2 with this actual density contrast, in which the critical target distance of U_zz is 2650 times, and those of U_x, U_z, U_xz are larger than 200,000 times. These values are much larger than those of same order calculated before, because smaller coefficients in actual density function can suppress the amplified closure differences. To this end, for the cases of higher-order polynomial densities in practical applications, the range of numerical stability of our expressions is sufficient.

4 Model Test

In this section, our expressions are coded in MATLAB programs for different models to check the correctness and stabilities. We chiefly consider about three cases of density contrast: first, the density only varies in vertical direction; second, the density only varies in horizontal direction; third, the density varies in both horizontal and vertical directions. And all observation points in these three examples are set near the targets, within the range of numerical stability. Necessarily, we also use constant-density method to make a comparison with present approach.

In these examples, the universal gravitational constant G = 6.67408 × 10⁻¹¹ m³/(kg·s²). Besides, all codes are run in MATLAB R2012b software on a computer with an Intel(R) Core(TM) i5-2400, a frequency of 3.10 GHz, and a RAM of 4.00 GB.

4.1 Density only Varies in Vertical Direction

This model is quoted from the paper of D’Urso (2015), representing the Sebastián Vizcaíno basin in Mexico. It was first considered by García-Abdeslem et al. (2005) and later discussed by Zhou (2008). As shown in Fig. 6, the cross-section of this 2D model is a heptagon with coordinates of vertices being (0, 0), (0.22, 0.1), (0.68, 0.19), (0.9, 0.22), (1.1, 0.23), (1.5, 0.18) and (1.8, 0). And the density contrast is a quadratic polynomial function only varies in vertical direction as

$$\sigma (x,z) = \begin{array}{*{20}l} { - 700} \hfill \\ \end{array} + 254.8z - 27.3z^{2}$$

(54)

where the units of density are kg/m³ and those of x and z are kilometers. We set the observation line on z = 0, and put an observation point every 0.043 km from x = − 0.5 km to x = 2.5 km. To validate the result of present approach, we adopt the constant-density method for a comparison, in which this model is evenly divided into 230 long strips along z-axis. And the gravitational contribution of every unit whose density is replaced by the average of those at vertices and center point is calculated according to analytic Eqs. (20a)–(20f) in the paper of Jia and Wu (2011).

Fig. 6

A 2D model quoted from the paper of D’Urso (2015) whose cross-section is a heptagon with vertices being (0, 0), (0.22, 0.1), (0.68, 0.19), (0.9, 0.22), (1.1, 0.23), (1.5, 0.18), (1.8, 0) and the density contrast is σ (x, z) = − 700 + 254.8z − 27.3z², representing the Sebastián Vizcaíno basin in Mexico. The units of density are kg/m³ and those of x and z are kilometers. Besides, the observation points are set every 0.043 km from x = − 0.5 km to x = 2.5 km along z = 0

Figure 7(a) shows the results of gravity vector along the observation line obtained by two methods, while (b) shows those of gravity gradient tensor. Since the results of two methods are well matched, the correctness of present approach is proved completely. Furthermore, Fig. 8 shows root mean square (RMS) error of the result of constant-density method compared with present approach versus the number of divided units, where gravity vector is in black and gravity gradient tensor is in pink. Besides, the absolute values of U_xx and U_zz are equal, so does their RMS errors. There are several facts in Fig. 8: first, if there is only 1 unit, the RMS errors reach maximum with 0.0406 mgal of U_x, 0.0474 mgal of U_z, 1.2378 E of U_xz and 1.1511 E of U_xx/U_zz; second, the RMS error is getting smaller with the increasing number of divided units, which means the result of constant-density method is getting closer to that of present approach; third, dividing 200 units can make the RMS error of U_x and U_z below 10⁻⁶ mgal; fourth, dividing 140 units can make the RMS error of U_xz and U_zz below 10⁻⁴ E. These data definitely exhibit the advantage of present approach in terms of accuracy.

Fig. 7

The anomalies of gravity vector (a) and gravity gradient tensor (b) along observation line due to the model shown in Fig. 6, obtained by constant-density method and present approach

Fig. 8

The RMS error of constant-density method compared with present approach versus the number of divided units, for gravity vector (in black) and gravity gradient tensor (in pink) along the observation line produced by the model shown in Fig. 6

4.2 Density only Varies in Horizontal Direction

This model was used by D’Urso (2015). It was first considered by Martín Atienza and García Abdeslem (1999) and later studied by Zhou (2009b, 2010). As shown in Fig. 9, the cross-section of this 2D model is a trapezoid with vertices being (− 2, 0.1), (− 3.8, 3.1), (4.6, 3.1) and (1, 0.1). Its density contrast is a quadratic polynomial function only varies in horizontal direction as

$$\sigma (x,z) = \begin{array}{*{20}l} {500} \hfill \\ \end{array} + 20x - 20x^{2}$$

(55)

where the units of density are kg/m³ and those of x and z are kilometers. We set the observation line on z = 0 and put an observation point every 0.223 km from x = − 5 km to x = 5 km. To validate the result of present approach, we also adopt constant-density method for a comparison, in which this model is evenly divided into 250 vertical strips along x-axis. And the gravitational contributions of every unit whose density is replaced by the average of those at vertices and center point are calculated according to analytic Eqs. (20a)–(20f) in the paper of Jia and Wu (2011). Since these equations have singularities at vertices of the model (Jia and Wu 2011), we make the depth of this model 0.1 km deeper than that of D’Urso (2015), so that observation points are not coincide with vertices of units.

Fig. 9

A 2D model whose cross-section is a trapezoid with vertices being (− 2, 0.1), (− 3.8, 3.1), (4.6, 3.1), (1, 0.1) and the density contrast is σ (x, z) = 500 + 20x − 20x². The units of density are kg/m³ and those of x and z are kilometers. Besides, the observation points are set every 0.223 km from x = − 5 km to x = 5 km along z = 0

In Fig. 10, picture (a) shows the results of gravity vector along the observation line obtained by two methods, while picture (b) shows those of gravity gradient tensor. Since the results of two methods are well matched, the correctness of present approach is proved again. In Fig. 11, picture (a) shows RMS error of the result of constant-density method compared with the present approach versus the number of divided units, where gravity vector is in black and gravity gradient tensor is in pink, and picture (b) shows the CPU time consumed by the two methods accordingly. Besides, the absolute values of U_xx and U_zz are equal, so does their RMS errors. From picture (a) in Fig. 11, we know some facts: first, if there is only 1 unit, the RMS errors reach maximum with 4.9938 mgal of U_x, 6.4777 mgal of U_z, 23.6375 E of U_xz and 23.3345 E of U_xx/U_zz; second, the RMS error is getting smaller with the increasing number of divided units, which means the result of constant-density method is getting closer to that of present approach. Although the result of constant-density method is becoming more and more accurate, the CPU time it consumed is becoming longer and longer, which can be seen in picture (b) of Fig. 11. Specifically, 140 and 150 units are needed, respectively, to make the RMS error of U_x and U_z below 0.001mgal, while the CPU time consumed by constant-density method accordingly is 1.33 times and 1.22 times of that of present approach; and 250 units are needed to make the RMS error of U_xz and U_xx/U_zz below 0.001E, while the CPU time consumed by constant-density method accordingly is 2.16 times and 1.4 times of that of present approach. These data illustrate the advantages of present approach in both accuracy and efficiency.

Fig. 10

The anomalies of gravity vector (a) and gravity gradient tensor (b) along observation line due to the model shown in Fig. 9, obtained by constant-density method and present approach

Fig. 11

a The RMS error of constant-density method compared with present approach versus the number of divided units, for gravity vector (in black) and gravity gradient tensor (in pink) along the observation line produced by the model shown in Fig. 9; b The corresponding CPU time consumed by the two methods, respectively, versus the number of divided units

4.3 Density Varies in both Horizontal and Vertical Directions

This model is a long valley model which was first considered by Murthy and Rao (1979) and later analyzed by Zhang et al. (2001). As shown in Fig. 12, the cross-section of this 2D model is a hexagon with vertices being (5, 0.1), (8, 1.6), (10, 1.8), (12, 1.6), (13.5, 0.6) and (15, 0.1). Its density contrast is a polynomial function varying in both horizontal and vertical direction as

Fig. 12

A 2D model whose cross-section is a hexagon with vertices being (5, 0.1), (8, 1.6), (10, 1.8), (12, 1.6), (13.5, 0.6), (15, 0.1) and the density contrast is a polynomial varies with both x and z shown in Eq. (56). The units of density are kg/m³ and those of x and z are kilometers. Besides, the observation points are set every 0.433 km from x = 0 km to x = 20 km along z = 0

$$\begin{aligned} \sigma (x,z) & = \begin{array}{*{20}l} {-\,602.4} \hfill \\ \end{array} - 18.22z + \begin{array}{*{20}l} {7.16} \hfill \\ \end{array} z^{2} + 44.55z^{3} + 21.25z^{4} + \begin{array}{*{20}l} {0.027} \hfill \\ \end{array} xz + 0.0049xz^{2} \\ & \quad \begin{array}{*{20}l} { -\,0.0091} \hfill \\ \end{array} xz^{3} \begin{array}{*{20}l} { - 0.06} \hfill \\ \end{array} x^{2} + \begin{array}{*{20}l} {0.11} \hfill \\ \end{array} x^{2} z + 0.097x^{2} z^{2} + \begin{array}{*{20}l} {0.017} \hfill \\ \end{array} x^{3} \begin{array}{*{20}l} { -\,0.0028} \hfill \\ \end{array} x^{3} z \\ \end{aligned}$$

(56)

where the units of density are kg/m³ and those of x and z are kilometers. We set the observation line on z = 0 and put an observation point every 0.433 km from x = 0 km to x = 20 km. To validate the result of present approach, we adopt constant-density method for a comparison, in which this model needed to be divided along both x-axis and z-axis. Here, we design a grid with a step size of 0.1 km in x-axis and 0.01 km in z-axis to cut apart the model into 10,747 polygonal units with constant densities. And then, the gravitational contributions of every unit whose density is replaced by the average of those at vertices and center point are calculated according to analytic Eqs. (20a)–(20f) in the paper of Jia and Wu (2011). Since these equations unavoidably have singularities at vertices of the model Jia and Wu (2011), we make the depth of this model 0.1 km deeper than original, so that observation points are not coincide with vertices of units.

In Fig. 13, picture (a) shows the results of gravity vector along the observation line obtained by two methods, while picture (b) shows those of gravity gradient tensor. The results of two methods are well matched continuously, proving the correctness of present approach. In Fig. 14, picture (a) shows RMS error of the result of constant-density method compared with present approach versus the number of divided units, where gravity vector is in black and gravity gradient tensor is in pink, and picture (b) shows the CPU time consumed by the two methods accordingly. Besides, the absolute values of U_xx and U_zz are equal, so does their RMS errors. From picture (a) in Fig. 14, we conclude some facts: first, if there is only 1 unit, the RMS errors reach maximum with 3.0232 mgal of U_x, 3.4227 mgal of U_z, 10.0244 E of U_xz and 9.8536 E of U_xx/U_zz; second, the RMS error is getting smaller with the increasing number of divided units, which means the result of constant-density method is getting closer to that of present approach. However, with the improvement in the accuracy of constant-density method, the efficiency of it is gradually decreasing on the contrast, which can be seen in picture (b) of Fig. 14. Specifically, 2743 units are needed to make the RMS error of U_x and U_z below 0.001mgal, while the CPU time consumed by constant-density method is almost 1.2 times of that of present approach; and 7739 units are needed to make the RMS error of U_xz and U_xx/U_zz below 0.001E, while the CPU time consumed by constant-density method accordingly is 2.71 times and 1.56 times of that of present approach, respectively. With no doubt, present approach is superior in accuracy and efficiency.

Fig. 13

The anomalies of gravity vector (a) and gravity gradient tensor (b) along observation line due to the model shown in Fig. 12, obtained by constant-density method and present approach

Fig. 14

a The RMS error of constant-density method compared with present approach versus the number of divided units, for gravity vector (in black) and gravity gradient tensor (in pink) along the observation line produced by the model shown in Fig. 12; b The corresponding CPU time consumed by the two methods, respectively, versus the number of divided units

In order to make further test on the efficiency of present approach, we change the density contrast function into σ (x, z) = xⁿzⁿ (n = 0, 1,…,7) and record corresponding CPU time consumed by the present approach on the observation line which includes 47 observation points under different orders of density function. Figure 15 shows the variation of corresponding CPU time versus the order n of density function. It can be seen that CPU time increases as the order n increases. Besides, U_zz increases sharply while U_x and U_z increasing at the same speed. Taking the model in Fig. 2 into consideration, we also find that the efficiency of present approach is also related to the number of vertices of model. In one case where the density contrast is $\sigma \left( {x,z} \right) = \sum\nolimits_{i = 0}^{3} {x^{i} z^{i} }$ with the same number of observation points, the CPU times consumed by the model shown in Fig. 13 on the observation line are 3.3156 s of U_x, 3.3267 s of U_z, 4.3707 s of U_xz and 7.7145 s of U_zz, while those of the model shown in Fig. 2 are 1.3018 s of U_x, 1.2994 s of U_z, 1.6634 s of U_xz, and 2.7823 s of U_zz.

Fig. 15

The corresponding CPU time consumed by present approach on the observation line, for gravity vector and gravity gradient tensor produced by a 2D model whose cross-section is shown in Fig. 12 and the density contrast is σ (x, z) = xⁿzⁿ (n = 0, 1,…,7) where the units of density are kg/m³ and those of x and z are kilometers. Besides, the observation points are set every 0.433 km from x = 0 km to x = 20 km along z = 0. The horizontal axis is the order n of density function

Obviously, when the density contrasts are the same, the fewer the number of vertices of the model is, the less the corresponding CPU time is. In summary, the time complexity of the present approach is affected by two factors: one is the order of density function, and the other is the number of vertices of polygon.

5 Conclusions

We derive the analytical solutions of gravity vector and gravity gradient tensor at any point produced by a 2D body whose cross-section is an arbitrary polygon and the density contrast is a 2D arbitrary-order polynomial function varying in horizontal and vertical directions. The analytical solutions are just related to the coordinates of vertices of the polygon and the polynomial density function. When the polygonal model doesn’t contain a side parallel to z-axis, the singularity points of gravity vector and gravity gradient tensor only exist at vertices of the polygon. While if there is any side parallel to z-axis in the model, the singularity points of gravity gradient tensor correspondingly extend to the straight line passing through this side. Two methods can be used to remove the singularity in numerical calculation: one is to move the computation points away from the singularity points by an infinitesimal distance; the other is to exclude an extremely small sphere around the singularity points. Due to limited floating-point precision of computer, our analytical solution inevitably has numerical errors. Accordingly, the numerical stability range decreases as the order of density contrast function increases. While under a same order, the numerical stability range of gravity gradient tensor is smaller than that of gravity vector. Even so, all the ranges of numerical stability are always sufficient in practical applications. The result of model test shows that, within the range of numerical stability, our expressions have higher accuracy than the conventional constant-density method of stacking the gravity effects of units with uniform densities. On the one hand, when the order of polynomial function is high enough, any 2D density distribution can be approximated well. On the other hand, when the number of sides of the polygon is large enough, any continuous boundary can also be well approximated. As a consequence, the analytical solutions we derived of gravity vector and gravity gradient tensor produced by a polygonal model with arbitrary-order polynomial densities provide a very general and accurate solution for the gravity effects of 2D bodies.

Appendix

We provide the solutions of some indefinite integrals, which are necessary for the derivation of the analytic expressions referred to above. In the solutions below, a, b, c, m are constants, x is the integral variable, X = cx²+ bx + a and Q = 4ac − b².

$$\int {\frac{{{\text{d}}x}}{{c^{2} + x^{2} }} = \frac{1}{c}\tan^{ - 1} \frac{x}{c}}$$

(57)

$$\int {\frac{{{\text{d}}x}}{{X^{2} }}} = \frac{2cx + b}{QX} + \frac{2c}{Q}\int {\frac{{{\text{d}}x}}{X}}$$

(58)

$$\int {\frac{x}{{X^{2} }}} {\text{d}}x = - \frac{2a + bx}{QX} - \frac{b}{Q}\int {\frac{{{\text{d}}x}}{X}}$$

(59)

$$\int {\frac{{x^{m} }}{{X^{2} }}} {\text{d}}x = \frac{{x^{m - 1} }}{(m - 3)cX} - \frac{m - 2}{m - 3} \cdot \frac{b}{c} \cdot \int {\frac{{x^{m - 1} }}{{X^{2} }}{\text{d}}x} - \frac{m - 1}{m - 3} \cdot \frac{a}{c}\int {\frac{{x^{m - 2} }}{{X^{2} }}} {\text{d}}x\;\;(m \ge 2)$$

(60)

$$\int {\frac{{x^{3} }}{{X^{2} }}} {\text{d}}x = \frac{1}{{2c^{2} }}\ln \left| x \right| + \frac{{a\left( {2ac - b^{2} } \right) + bx\left( {3ac - b^{2} } \right)}}{{c^{2} QX}} - \frac{{b\left( {6ac - b^{2} } \right)}}{{2c^{2} Q}}\int {\frac{{{\text{d}}x}}{X}}$$

(61)

$$\int {\frac{1}{{\left( {c^{2} + x^{2} } \right)^{2} }}{\text{d}}x = \frac{1}{{2c^{3} }}\left( {\frac{cx}{{c^{2} + x^{2} }} + \tan^{ - 1} \frac{x}{c}} \right)}$$

(62)

$$\int {\frac{x}{{\left( {c^{2} + x^{2} } \right)^{2} }}{\text{d}}x = - \frac{1}{{2(c^{2} + x^{2} )}}}$$

(63)

$$\int {\frac{{x^{m} }}{{\left( {c^{2} + x^{2} } \right)^{2} }}{\text{d}}x} = - \frac{{x^{m - 1} }}{{2(c^{2} + x^{2} )}} + \frac{m - 1}{2}\int {\frac{{x^{m - 2} }}{{c^{2} + x^{2} }}{\text{d}}x} \;\;(m \ge 2)$$

(64)

$$\int {\frac{1}{{\left( {a + bx} \right)^{2} }}{\text{d}}x = - \frac{1}{b(a + bx)}}$$

(65)

$$\int {\frac{x}{{\left( {a + bx} \right)^{2} }}{\text{d}}x = \frac{1}{{b^{2} }}\left[ {\ln (a + bx) + \frac{a}{a + bx}} \right]}$$

(66)