Efficient Modeling of Gravity Fields Caused by Sources with Arbitrary Geometry and Arbitrary Density Distribution

Abstract

We present a brief review of gravity forward algorithms in Cartesian coordinate system, including both space-domain and Fourier-domain approaches, after which we introduce a truly general and efficient algorithm, namely the convolution-type Gauss fast Fourier transform (Conv-Gauss-FFT) algorithm, for 2D and 3D modeling of gravity potential and its derivatives due to sources with arbitrary geometry and arbitrary density distribution which are defined either by discrete or by continuous functions. The Conv-Gauss-FFT algorithm is based on the combined use of a hybrid rectangle-Gaussian grid and the fast Fourier transform (FFT) algorithm. Since the gravity forward problem in Cartesian coordinate system can be expressed as continuous convolution-type integrals, we first approximate the continuous convolution by a weighted sum of a series of shifted discrete convolutions, and then each shifted discrete convolution, which is essentially a Toeplitz system, is calculated efficiently and accurately by combining circulant embedding with the FFT algorithm. Synthetic and real model tests show that the Conv-Gauss-FFT algorithm can obtain high-precision forward results very efficiently for almost any practical model, and it works especially well for complex 3D models when gravity fields on large 3D regular grids are needed.

1 Introduction

The gravity forward problem is the foundation of gravity exploration in geophysics. It can be formulated either in spherical coordinate system for global- and regional-scale problems, or in Cartesian coordinate system for local problems when the planar approximation of the earth surface is acceptable. In the former case, the forward problem can be solved either in the spectral domain using fast algorithms for spherical harmonic expansions (Driscoll and Healy 1994; Mohlenkamp 1999; Rokhlin and Tygert 2005; Tygert 2006; Gruber et al. 2011), or in the space domain using solutions of a spherical prism, i.e., a tesseroid (Asgharzadeh et al. 2007; Heck and Seitz 2007; Grombein et al. 2013; Uieda et al. 2016; Deng et al. 2016). In the latter case, analogously, the forward problem is usually solved in the Fourier domain based on the FFT algorithm (Parker 1973; Pedersen 1978; Forsberg 1985; Hansen and Wang 1988; Sideris and Li 1993; Li and Sideris 1994; Wu and Tian 2014), or in the space domain using solutions of a rectangular prism (Nagy 1966; Li and Chouteau 1998; Nagy et al. 2000).

Many authors have made contributions to the gravity forward problem, presenting various approaches involving both analytical, numerical and hybrid analytical–numerical (seminumerical) algorithms. In our opinion, these contributions may be assigned to four main aspects:

• 1. to model sources with more arbitrary geometries;

• 2. to model sources with more general density distributions;

• 3. to model the gravity potential and its first-order (the gravity vector), second-order (the gravity gradient tensor) and higher-order derivative components;

• 4. to model the gravity effects listed above in all space, both outside and within the source body, and to clarify singularity problems.

Obviously, it is a universal solution which can be used for sources with arbitrary complicated geometry and arbitrary variable density distribution that we are pursuing. Moreover, we always prefer algorithms with higher accuracy and lower computational costs, though most of the time we have to find a reasonable trade-off between these two factors. In the following, we provide a brief review of existing forward algorithms formulated in the Cartesian coordinate system, as the method we present in this paper generally falls into this category. However, it should be mentioned that some models, e.g., the polyhedron, which is originally formulated in the Cartesian coordinate system, can also be well applied in the spherical coordinate system through a coordinate system transformation.

Historically, space-domain solutions have played a major role in the gravity modeling theory. Both analytical and numerical techniques are used whenever they are well suited for the model under consideration. Analytical solutions are very useful; they are considered as the most accurate algorithm and they can provide references to numerical or seminumerical algorithms. However, they are available only when the source body is assumed to have relatively simple geometry and density distribution. When some complicated models are to be calculated, e.g., sources with their boundaries or density distributions described by some arbitrary functions, numerical or seminumerical solutions become necessary.

For the general 2D gravity forward problem, a source body with its cross section represented by an arbitrary polygon is usually considered as the general case of source geometry. Analytical expressions of the gravity anomaly due to 2D polygonal sources with homogeneous density were derived by Talwani et al. (1959). Later, analytical solutions of variable density models, including linear models (Murthy and Rao 1979), quadratic polynomial models (Rao 1986), hyperbolic models (Rao et al. 1994) and general 2D polynomial models (Zhang et al. 2001; Zhou 2010), were also derived. Jia and Wu (2011) revised forward modeling of the gravity-field components and their first- and second-order partial derivatives due to homogeneous 2D polygonal sources and addressed some singularity cases. D’Urso (2015) provided a nice review of gravity forward algorithms due to a 2D polygonal source whose density contrast is a 2D polynomial function.

In addition to analytical solutions, numerical solutions are also provided for polygonal sources with variable density. Numerical techniques become indispensable when a certain density function, like the exponential function (Cordell 1973), or some other more arbitrary functions are used (Zhou 2008, 2009b). They also provide a simple solution when sources with continuous boundaries are studied (Martin-Atienza and Garcia-Abdeslem 1999; Garcia-Abdeslem 2003). Although analytical solutions are not available under these conditions, it should be mentioned that the polygonal model with 2D polynomial density function has in fact provided a quite general solution for 2D models, because any continuous boundary can be well approximated by a n-sided polygon when n is sufficiently large, and any 2D density distribution can be well approximated by a 2D polynomial density function when the order of the polynomial is sufficiently high.

For the general 3D gravity forward problem, previous works mainly focus on two models: the right rectangular prism and the polyhedron. A combination of the two, namely the rectangular prism with inclined top and bottom faces, has also been studied by several authors (Smith 2000; Tsoulis et al. 2003; D’Urso and Trotta 2015).

The right rectangular prism is probably the most widely used model in gravity exploration. A collection of prisms provides a simple way to approximate a source body with complex geometry and arbitrary variable density contrast. Nagy et al. (2000) presented closed-form expressions of the gravity potential, and its derivatives, up to the third order for a prism, in a unified manner, and provided a detailed singularity analysis of these expressions when they are generalized to the whole space. Later, analytical solutions due to the rectangular prism with several depth-dependent variable density contrast, including the parabolic model (Chakravarthi et al. 2002), the quadratic polynomial model (Gallardo-Delgado et al. 2003; Gallardo et al. 2005) and the cubic polynomial model (Garcia-Abdeslem 2005), were also studied. Recently, Jiang et al. (2017) derived analytical solution of gravity anomalies due to a right rectangular prism with an arbitrary order of polynomial density-contrast function of depth. Soon after, Zhang and Jiang (2017) further extended the solution to a linear combination of three arbitrary-order polynomial density functions in x-, y- and z-directions. Although these models can already cover a wide range of density distributions, when more complex models are considered, such as depth-dependent density models described by arbitrary functions, or density models vary both horizontally and vertically following some arbitrary functions, numerical or hybrid solutions are still useful (Garcia-Abdeslem 1992; Zhou 2009a).

Comparing to the right rectangular prism, the polyhedron offers a more general geometric representation at the expense of a more complicated derivation for the analytical solutions. Closed-form solutions for the gravity anomaly due to homogeneous polyhedral bodies have been studied by many authors (Barnett 1976; Okabe 1979; Holstein and Ketteridge 1996; Guptasarma and Singh 1999; Tsoulis and Petrovic 2001; Tsoulis 2012; D’Urso 2013, 2014a; Conway 2015; Werner 2017). Polyhedral bodies with linear density distribution have also received considerable attention during the past decade (Pohanka 1998; Hansen 1999; Holstein 2003; Hamayun and Tenzer 2009; D’Urso 2014b, 2016). Ren et al. (2017a) derived singularity-free analytic formula of the gravity potential caused by polyhedral bodies with its density varies in the case of $\lambda =ax^m+by^n+cz^t$, $m\,\le\, 2, n\,\le\, 2, t\,\le\, 2$, and analytic formula of the gravity potential due to a rectangular prism with $m\,\le\, 3, n\,\le\, 3, t\,\le\, 3$. Recently, D’Urso and Trotta (2017) and Ren et al. (2017c) presented singularity-free expressions for evaluating the gravity anomaly due to polyhedral bodies with its density contrast described by a third-order polynomial, and indicated that the general approach can be easily extended to higher-order polynomial functions. Analogous to the 2D case, such a model may provide a quite general solution for 3D forward problems since a polyhedron with increasing number of facets can be used to approximate a 3D source with arbitrary geometry, and a 3D polynomial density function with increasing order can be used to approximate as closely as desired any smooth density distribution.

In addition to space-domain methods, Fourier-domain methods have also been developed. Compared to analytical solutions, Fourier-domain solutions are considered to be less accurate. However, they are far more computationally efficient, thanks to the fast Fourier transform algorithm (Cooley and Tukey 1965), especially when gravity fields on large regular grids are to be calculated. Besides, Fourier-domain expressions of the gravity potential and its derivatives are related through very simple multiplicative factors. Therefore, computational costs can be further reduced for Fourier-domain algorithms when multiple gravity fields, including vector and tensor components, or even higher-order derivatives, are calculated simultaneously (Wu and Chen 2016).

Fourier-domain solutions are available for a single rectangular prism with homogeneous density distribution (Bhattacharyya 1966), depth-dependent linear or exponential density distributions (Chai and Hinze 1988; Chenot and Debeglia 1990; Lee and Biehler 1991), and general 3D polynomial density distributions (Wu and Chen 2016). They are also available for 2D prismatic bodies with general 2D polynomial density distributions (Wu and Chen 2016), and arbitrary 2D polygonal bodies with homogeneous density distribution (Pedersen 1978). Fourier-domain solutions due to arbitrary 3D polyhedral bodies in the case of homogeneous density contrast were derived by Wu (1981) and Pedersen (1978), and later simplified by Hansen and Wang (1988). For variable polyhedral models, Wu (1983) derived Fourier-domain expressions of the gravity anomaly caused by an arbitrary polyhedron with linear and exponential depth-dependent density function.

In addition to single-source bodies, Fourier-domain algorithms work especially efficiently for large-scale combined models, e.g., a 2D layer with horizontally variable density distribution (Blakely 1996), a general 3D source with arbitrarily variable density distribution (Tontini et al. 2009; Sanso and Sideris 2013; Zhang and Wong 2015) and topographic models with density variations both horizontally and vertically, following exponential, parabolic or polynomial functions (Parker 1973; Forsberg 1985; Granser 1987; Chai and Hinze 1988; Chai and Jia 1990; Guspi 1992; Sideris and Li 1993; Li and Sideris 1994; Chappell and Kusznir 2008; Zhang et al. 2015; Wu 2016). These models are frequently used in forward problems such as gravity terrain correction, isostatic compensation and inverse problems such as equivalent source construction, 3D density imaging, and sediment–basement interface or crust–mantle interface determinations. Wu (2016) provided a brief review of Fourier-domain algorithms for the modeling of topographic masses, in which they were divided into three categories, namely Chai-type algorithms (Chai and Hinze 1988), Parker-type algorithms (Parker 1973) and Forsberg-type algorithms (Forsberg 1985).

Alternatively, the gravity forward problem can also be solved by finite differences method (Farquharson and Mosher 2009), finite element methods (Cai and Wang 2005), Cauchy-type integrals (Zhdanov and Liu 2013; Cai and Zhdanov 2015) and fast multipole method (FMM) (Casenave et al. 2016; Ren et al. 2017b).

In this paper, we focus on solving the general 2D and 3D gravity forward problems in Cartesian coordinate system using Fourier-domain algorithms. It is well known that the general gravity forward problem can be expressed as continuous convolution-type integrals (Bhattacharyya and Navolio 1975; Blakely 1996). The gravity potential and its derivatives, including the gravity vector, the gravity gradient tensor, and higher-order components like the gravitational curvatures, can all be written as the convolution of the density distribution function and the corresponding kernel function, that is, Newton’s integral kernel, or its derivative of certain order.

To evaluate the continuous convolution integral using the discrete FFT algorithm, there are two different approaches; both involve two major steps. The first approach begins by transforming the continuous convolution in the space domain to the equivalent point-wise multiplication in the Fourier domain based on the convolution theorem. Then both the forward and inverse continuous Fourier transforms are calculated approximately using the forward and inverse discrete FFT algorithms, respectively. As the continuous Fourier transform of Newton’s integral kernel or its derivatives can be obtained analytically, the forward transform is applied only to the density function, while the inverse transform is applied to the Fourier-domain product of the density and kernel functions. Since the discrete FFT algorithm is in fact the rectangle rule of the continuous Fourier transform after truncating at finite integral limits (Wu and Tian 2014), the forward results contain both truncation and quadrature errors (Wu and Chen 2016). The second approach begins by approximating the continuous convolution integral using a uniformly sampled discrete convolution, which is also the rectangle rule. Then the discrete convolution, which is intrinsically a Toeplitz matrix–vector product, is embedded into a circulant matrix–vector product and evaluated efficiently and accurately, to almost machine precision, through the FFT algorithm (Vogel 2002). Likewise, the approximation of the continuous convolution using a discrete one will inevitably produce quadrature errors.

Fourier-domain algorithms including Parker-type algorithms (Parker 1973; Wu 2016) for topographic models, and the 3D FFT-based algorithm introduced in Tontini et al. (2009) for general 3D models, generally belong to the first approach; while Forsberg-type algorithms (Forsberg 1985) and those introduced in Sanso and Sideris (2013) and Zhang and Wong (2015) generally belong to the second approach. It should be mentioned that when a prism-stacked model is used, as is the case in Sanso and Sideris (2013), the continuous convolution integral reduces to a discrete convolution after integrating within each grid cell and replacing the point mass kernel function with the rectangular prism kernel function. Then the results obtained by the second approach mentioned above agree with the classical prism summation results to almost machine precision. However, when continuous density models are considered, that is, the density varies not only from prism to prism, but also within each prism element, both approaches involve a discretization step where the rectangle rule is applied to approximate a continuous integral, i.e., the continuous convolution integral or the continuous Fourier transform integral, and this discretization step produces numerical errors, which becomes one of the greatest drawbacks of Fourier-domain solutions.

To improve the numerical accuracy of Fourier-domain approaches, numerical quadrature errors need to be reduced. For the first approach mentioned above, we have already introduced a Gauss-FFT algorithm to calculate more accurately the forward and inverse continuous Fourier transforms (Wu and Tian 2014; Wu and Chen 2016; Wu 2016; Wu and Lin 2017). The Gauss-FFT algorithm is based on a hybrid rectangle-Gaussian sampling of the function to be transformed. It converges to the precise results much faster than the standard FFT algorithm with grid expansion, which is in fact the rectangle rule with smaller steps (Wu and Tian 2014). Here in this paper, we try to focus on the second Fourier-domain approach. Inspired by the Gauss-FFT algorithm, a Conv-Gauss-FFT algorithm is introduced by applying the hybrid rectangle-Gaussian grid directly to the continuous convolution integral. Instead of using a classical rectangle rule, we first approximate the continuous convolution integral using a weighted sum of a series of shifted rectangle rules, with the weights and offsets determined by a Gaussian quadrature rule. Then each shifted rectangle rule, which is basically a discrete convolution, is evaluated efficiently and accurately, to almost machine precision, through the FFT algorithm (Vogel 2002).

The Conv-Gauss-FFT algorithm is rigorously the hybrid rectangle-Gaussian quadrature rule for the continuous convolution integral, with its numerical accuracy controlled by both the step length of the rectangle grid and number of Gaussian nodes within each rectangle interval. Together with a point-in-polygon or a point-in-polyhedron algorithm, it can be easily applied to solve general 2D and 3D gravity forward problems involving sources with arbitrary geometry and arbitrary variable density distribution. Generally speaking, the algorithm can achieve high accuracy for field points considerably far from the source, but it may introduce some observable errors for field points close to the source’s boundary.

This paper is organized as follows: Section 2 introduces a hybrid rectangle-Gaussian grid for continuous convolutions. The 1D, 2D and 3D continuous convolutions are calculated using a weighted sum of a series of discrete convolutions. Section 3 provides some details on how to evaluate discrete convolutions efficiently and accurately by combining circulant embedding with the FFT algorithm. Section 4 presents expressions of the 1D, 2D and 3D Conv-Gauss-FFT algorithms based on the results obtained in Sects. 2 and 3 and provides some general discussions on the numerical accuracy and computational complexity of the presented algorithm. In Sect. 5, the 2D and 3D gravity forward problems are studied in the form of convolution-type integrals, and more details on how to solve general gravity forward problems of sources with versatile geometries and density distributions using the Conv-Gauss-FFT algorithm are provided. In Sect. 6, many synthetic and real models are implemented to test the accuracy and efficiency of the presented algorithm. Section 7 provides a brief discussion on combining the Conv-Gauss-FFT algorithm with analytical solutions or some properly designed quadrature methods to evaluate the long-range and close-range contributions separately. Finally in Sect. 8, we draw some conclusions and suggest some possible future works.

2 A Hybrid Rectangle-Gaussian Grid for Continuous Convolutions

2.1 1D Continuous Convolutions

The 1D continuous convolution of two functions t and f, denoted as $h=t * f$, is written as:

$$\begin{aligned} h(x)=\int _{-\infty }^{\infty } f(\tilde{x}) t(x-\tilde{x}) {\mathrm{d}} \tilde{x}. \end{aligned}$$

(1)

In the following, we call t the kernel function, f the source function and h the field function, based on their meanings in a forward modeling problem.

In a practical evaluation, the infinite integral usually reduces to a finite one due to the finite extent of the function f, indicating a finite length of the source body in a modeling problem:

$$\begin{aligned} h(x)=\int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}} f(\tilde{x}) t(x-\tilde{x}) {\mathrm{d}} \tilde{x}. \end{aligned}$$

(2)

Now we use a hybrid rectangle-Gaussian grid to evaluate Eq. 2, that is, we divide the integration region $[\tilde{x}_{0},\tilde{x}_{\tilde{L}}]$ into $\tilde{L}$ equal subintervals of length $\Delta \tilde{x}=\frac{\tilde{x}_{\tilde{L}}-\tilde{x}_{0}}{\tilde{L}}$, after which we apply the Gaussian quadrature rule to each subinterval $[\tilde{x}_{\tilde{l}},\tilde{x}_{\tilde{l}+1}]$, $\tilde{l}=0,1,2,\,\ldots ,\,\tilde{L}-1$; thus, we have:

$$\begin{aligned} \begin{aligned} h(x)&=\int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}} f(\tilde{x}) t(x-\tilde{x}) {\mathrm{d}} \tilde{x}=\sum _{\tilde{l}=0}^{\tilde{L}-1}\int _{\tilde{x}_{\tilde{l}}}^{\tilde{x}_{\tilde{l}+1}} f(\tilde{x}) t(x-\tilde{x}) {\mathrm{d}} \tilde{x}\\&= \Delta \tilde{x}\sum _{\tilde{l}=0}^{\tilde{L}-1} \sum _{i=1}^{I} \mu _{i}^{(I)} f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}) t\left( x-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}\right) , \end{aligned} \end{aligned}$$

(3)

where $\mu _{i}^{(I)}$ and $\tilde{\alpha }_i$ are the weights and nodes of a I-nodes Gauss–Legendre quadrature rule over the integration area [0, 1], and $\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}=\tilde{x}_{0}+(\tilde{l}+\tilde{\alpha }_i)\Delta \tilde{x}$.

Suppose that h(x) is needed on a size L regular grid: $x_l=x_0+l\Delta x$, $l=0,1,2,\ldots ,L-1$, by changing the order of the two summations in Eq. 3, we have:

$$\begin{aligned} h(x_l)= \Delta \tilde{x}\sum _{i=1}^{I} \mu _{i}^{(I)} \sum _{\tilde{l}=0}^{\tilde{L}-1} f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}) t(x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}). \end{aligned}$$

(4)

If we choose identical grid interval for the source function f and the field function h, that is, $\Delta x=\Delta \tilde{x}$, then the value of the expression $x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}=x_0-\tilde{x}_{0}+(l-\tilde{l}-\tilde{\alpha }_i)\Delta x$ depends solely on the value of $l-\tilde{l}$. Therefore, the kernel $t(x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i})$ becomes a function of $l-\tilde{l}$, and the second summation on the RHS of Eq. 4 becomes a discrete convolution.

Let

$$\begin{aligned} {\mathbf {h}}=[h(x_l)], \quad l=0,1,2,\ldots ,L-1 \end{aligned}$$

(5)

be the size L field vector containing values of the field function,

$$\begin{aligned} {\mathbf {f}}_{\tilde{\alpha }_i}=[f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i})], \quad \tilde{l}=0,1,2,\ldots ,\tilde{L}-1 \end{aligned}$$

(6)

be the size $\tilde{L}$ source vector containing values of the source function on a $\tilde{\alpha }_i$-shifted grid, and

$$\begin{aligned} {\mathbf {t}}_{\tilde{\alpha }_i}=[t(x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i})], \quad l-\tilde{l}=1-\tilde{L},\ldots ,-\,1,0,1,\ldots ,L-1 \end{aligned}$$

(7)

be the size $L+\tilde{L}-1$ kernel vector containing values of the kernel function on a $\tilde{\alpha }_i$-shifted grid, then Eq. 4 can be written in vector form as:

$$\begin{aligned} {\mathbf {h}}=\Delta x \sum _{i=1}^{I} \mu _{i}^{(I)} {\mathbf {t}}_{\tilde{\alpha }_i} \star {\mathbf {f}}_{\tilde{\alpha }_i}, \end{aligned}$$

(8)

where ${\mathbf {t}}_{\tilde{\alpha }_i} \star {\mathbf {f}}_{\tilde{\alpha }_i}$ denotes the discrete convolution:

$$\begin{aligned}{}[{\mathbf {t}}_{\tilde{\alpha }_i} \star {\mathbf {f}}_{\tilde{\alpha }_i}]_{l} =\sum _{\tilde{l}=0}^{\tilde{L}-1}[{\mathbf {t}}_{\tilde{\alpha }_i}]_{l-\tilde{l}}[{\mathbf {f}}_{\tilde{\alpha }_i}]_{\tilde{l}},\quad l=0,1,\ldots ,L-1, \end{aligned}$$

(9)

and it can be evaluated accurately and efficiently through the FFT algorithm. This will be discussed in detail in Sect. 3.

2.2 2D and 3D Continuous Convolutions

Applying a 2D or 3D hybrid rectangle-Gaussian grid, the above derivation can be easily extended to 2D and 3D continuous convolutions.

For a 2D finite continuous convolution:

$$\begin{aligned} h(x,z)=\int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}}\int _{\tilde{z}_{0}}^{\tilde{z}_{\tilde{N}}} f(\tilde{x},\tilde{z}) t(x-\tilde{x},z-\tilde{z}) {\mathrm{d}} \tilde{x}{\mathrm{d}} \tilde{z}, \end{aligned}$$

(10)

we have:

$$\begin{aligned} {\mathbf {h}}_{2D}=\Delta x \Delta z \sum _{i=1}^{I} \sum _{k=1}^{K} \mu _{i}^{(I)} \omega _{k}^{(K)} {\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k} \star {\mathbf {f}}_{\tilde{\alpha }_i \tilde{\gamma }_k}, \end{aligned}$$

(11)

where $(\mu _{i}^{(I)},\omega _{k}^{(K)})$ and $(\tilde{\alpha }_i,\tilde{\gamma }_k)$ are the weights and nodes of a $I \times K$ nodes 2D Gauss–Legendre quadrature rule over the integration area $[0,1] \times [0,1]$, and

$$\begin{aligned}&{\mathbf {h}}_{2D}=[h(x_l,z_n)], \nonumber \\&l=0,1,2,\ldots ,L-1, \quad n=0,1,2,\ldots ,N-1 \end{aligned}$$

(12)

is the size $L \times N$ matrix containing values of the field function,

$$\begin{aligned}&{\mathbf {f}}_{\tilde{\alpha }_i \tilde{\gamma }_k}=[f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i},\tilde{z}_{\tilde{n}+\tilde{\gamma }_k})], \nonumber \\&\tilde{l}=0,1,2,\ldots ,\tilde{L}-1, \quad \tilde{n}=0,1,2,\ldots ,\tilde{N}-1 \end{aligned}$$

(13)

is the size $\tilde{L}\times \tilde{N}$ matrix containing values of the source function on a $(\tilde{\alpha }_i,\tilde{\gamma }_k)$-shifted grid, and

$$\begin{aligned}&{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}=[t(x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i},z_n-\tilde{z}_{\tilde{n}+\tilde{\gamma }_k})], \nonumber \\&l-\tilde{l}=1-\tilde{L},\ldots ,-1,0,1,\ldots ,L-1, \nonumber \\&n-\tilde{n}=1-\tilde{N},\ldots ,-1,0,1,\ldots ,N-1 \end{aligned}$$

(14)

is the size $(L+\tilde{L}-1)\times (N+\tilde{N}-1)$ matrix containing values of the kernel function on a $(\tilde{\alpha }_i,\tilde{\gamma }_k)$-shifted grid.

Analogously, for a 3D finite continuous convolution:

$$\begin{aligned} h(x,y,z)=\int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}}\int _{\tilde{y}_{0}}^{\tilde{y}_{\tilde{M}}}\int _{\tilde{z}_{0}}^{\tilde{z}_{\tilde{N}}} f(\tilde{x},\tilde{y},\tilde{z}) t(x-\tilde{x},y-\tilde{y},z-\tilde{z}) {\mathrm{d}} \tilde{x}{\mathrm{d}} \tilde{y}{\mathrm{d}} \tilde{z}, \end{aligned}$$

(15)

we have

$$\begin{aligned} {\mathbf {h}}_{3D}=\Delta _{x}\Delta _{y}\Delta _{z} \; \sum _{i=1}^{I} \sum _{j=1}^{J} \sum _{k=1}^{K} \mu _{i}^{(I)} \nu _{j}^{(J)} \omega _{k}^{(K)} {\mathbf {t}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k} \star {\mathbf {f}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k}. \end{aligned}$$

(16)

where $(\mu _{i}^{(I)},\nu _{j}^{(J)},\omega _{k}^{(K)})$ and $(\tilde{\alpha }_i,\tilde{\beta }_j,\tilde{\gamma }_k)$ are the weights and nodes of a $I \times J \times K$ nodes 3D Gauss–Legendre quadrature rule over the integration volume $[0,1]^3$, and

$$\begin{aligned}&{\mathbf {h}}_{3D}=[h(x_l,y_m,z_n)], \nonumber \\&l=0,1,2,\ldots ,L-1, \quad m=0,1,2,\ldots ,M-1, \quad n=0,1,2,\ldots ,N-1 \end{aligned}$$

(17)

is the size $L \times M \times N$ matrix containing values of the field function,

$$\begin{aligned}&{\mathbf {f}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k}=[f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i},\tilde{y}_{\tilde{m}+\tilde{\beta }_j},\tilde{z}_{\tilde{n}+\tilde{\gamma }_k})], \nonumber \\&\tilde{l}=0,1,2,\ldots ,\tilde{L}-1, \quad \tilde{m}=0,1,2,\ldots ,\tilde{M}-1, \quad \tilde{n}=0,1,2,\ldots ,\tilde{N}-1 \end{aligned}$$

(18)

is the size $\tilde{L}\times \tilde{M}\times \tilde{N}$ matrix containing values of the source function on a $(\tilde{\alpha }_i,\tilde{\beta }_j,\tilde{\gamma }_k)$-shifted grid, and

$$\begin{aligned}&{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k}=[t(x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i},y_m-\tilde{y}_{\tilde{m}+\tilde{\beta }_j},z_n-\tilde{z}_{\tilde{n}+\tilde{\gamma }_k})], \nonumber \\&l-\tilde{l}=1-\tilde{L},\ldots ,-1,0,1,\ldots ,L-1, \nonumber \\&m-\tilde{m}=1-\tilde{M},\ldots ,-1,0,1,\ldots ,M-1, \nonumber \\&n-\tilde{n}=1-\tilde{N},\ldots ,-1,0,1,\ldots ,N-1 \end{aligned}$$

(19)

is the size $(L+\tilde{L}-1)\times (M+\tilde{M}-1)\times (N+\tilde{N}-1)$ matrix containing values of the kernel function on a $(\tilde{\alpha }_i,\tilde{\beta }_j,\tilde{\gamma }_k)$-shifted grid.

3 Discrete Convolutions Via the FFT Algorithm

We have reduced the 1D, 2D and 3D continuous convolutions to the weighted sum of a series of discrete convolutions using 1D, 2D or 3D hybrid rectangle-Gaussian grids. It can be observed from Eqs. 8, 11 and 16 that the efficiency of the algorithm relies on the fast calculation of discrete convolutions. It is well known that discrete convolutions can be evaluated efficiently and accurately, to almost machine precision, through the FFT algorithm (Vogel 2002). In the following, we provide some basic concepts of the relationships between discrete convolutions, Toeplitz systems and the FFT algorithm.

The derivation here is a bit different from those provided in Vogel (2002) in several aspects: (1) we deal with the more general case when the vectors ${\mathbf {h}}$ and ${\mathbf {f}}$ are of the same or different sizes L and $\tilde{L}$, respectively. The size of the kernel vector ${\mathbf {t}}$ is then $L+\tilde{L}-1$, as has been discussed above; (2) we add no extra zeros when embedding the Toeplitz matrix T into its circulant extension; and (3) we use slightly different symbols to simplify expressions.

The 1D discrete convolution of a source vector ${\mathbf {f}}=(f_0,f_1,\ldots ,f_{\tilde{L}-1})$ and a kernel vector ${\mathbf {t}}=(t_{1-\tilde{L}},t_{2-\tilde{L}},\ldots ,t_{-1},t_0,t_1,\ldots ,t_{L-2},t_{L-1})$ is written as:

$$\begin{aligned}{}[{\mathbf {h}}]_{l}=\left[ {\mathbf {t}} \star {\mathbf {f}}\right] _{l}=\sum _{\tilde{l}=0}^{\tilde{L}-1}t_{l-\tilde{l}}f_{\tilde{l}},\quad l=0,1,\ldots ,L-1. \end{aligned}$$

(20)

Let

$$\begin{aligned} T=\begin{bmatrix} t_{0}&\quad t_{-1}&\quad \ldots&\quad t_{2-\tilde{L}}&\quad t_{1-\tilde{L}} \\ t_{1}&\quad t_{0}&\quad t_{-1}&\quad \ddots&\quad t_{2-\tilde{L}} \\ \vdots&\quad \ddots&\quad \ddots&\quad \ddots&\quad \vdots \\ t_{L-2}&\quad \ddots&\quad t_{L-\tilde{L}+1}&\quad t_{L-\tilde{L}}&\quad t_{L-\tilde{L}-1} \\ t_{L-1}&\quad t_{L-2}&\quad \ldots&\quad t_{L-\tilde{L}+1}&\quad t_{L-\tilde{L}} \\ \end{bmatrix}, \end{aligned}$$

(21)

$$\begin{aligned} {\mathbf {f}}= \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots \\ f_{\tilde{L}-2} \\ f_{\tilde{L}-1} \end{bmatrix}, \quad {\mathbf {h}}= \begin{bmatrix} h_{0} \\ h_{1} \\ \vdots \\ h_{L-2} \\ h_{L-1} \end{bmatrix}, \end{aligned}$$

(22)

then the discrete convolution can be written in matrix–vector product form as:

$$\begin{aligned} {\mathbf {h}}=T{\mathbf {f}}, \end{aligned}$$

(23)

where $T={\text {toeplitz}}({\mathbf {t}})$.

Toeplitz matrix–vector products can be efficiently computed by combining circulant embedding with FFTs (Vogel 2002). Denote $C={{\text {circulant}}}(\mathbf {c})$ as the $n \times n$ circulant matrix

$$\begin{aligned} C=\begin{bmatrix} c_{0}&\quad c_{n-1}&\quad \ldots&\quad c_{2}&\quad c_{1} \\ c_{1}&\quad c_{0}&\quad c_{n-1}&\quad \ddots&\quad c_{2} \\ \vdots&\quad c_{1}&\quad c_{0}&\quad \ddots&\quad \vdots \\ c_{n-2}&\quad \ddots&\quad \ddots&\quad \ddots&\quad c_{n-1} \\ c_{n-1}&\quad c_{n-2}&\quad \ldots&\quad c_{1}&\quad c_{0} \\ \end{bmatrix}, \end{aligned}$$

(24)

with $\mathbf {c}=(c_0,c_1,\ldots ,c_{n-1})$. The Toeplitz matrix T can be embedded in a size $(L+\tilde{L}-1) \times (L+\tilde{L}-1)$ circulant matrix $\hat{T}={\text {circulant}}(\hat{\mathbf {t}})$, with $\hat{\mathbf {t}}=(t_0,t_1,\ldots ,t_{L-1},t_{1-\tilde{L}},\ldots ,t_{L-\tilde{L}-2},t_{L-\tilde{L}-1})$. Therefore, the Toeplitz matrix–vector product $T{\mathbf {f}}$ can be embedded in a circulant matrix–vector product $\hat{T}\hat{\mathbf {f}}$ and then evaluated through the FFT algorithm:

$$\begin{aligned}&\hat{\mathbf {h}}=\hat{T}\hat{\mathbf {f}}=\hat{T} \begin{bmatrix} {\mathbf {f}} \\ \mathbf {0}_{(L-1)\times 1} \end{bmatrix}= \begin{bmatrix} T{\mathbf {f}} \\ A{\mathbf {f}} \end{bmatrix} ={\mathbf {F}}^{-1}\left[ {\mathbf {F}}(\hat{\mathbf {f}}) {\mathbf {F}}(\hat{\mathbf {t}}) \right] , \nonumber \\&{\mathbf {h}}=[\hat{\mathbf {h}}]_{L \times 1}, \end{aligned}$$

(25)

where ${\mathbf {F}}$ and ${\mathbf {F}}^{-1}$ represent the 1D forward and inverse discrete Fourier transform operators, respectively. The vector $\hat{\mathbf {f}}=(f_0,f_1,\ldots ,f_{\tilde{L}-1},\underbrace{0,\ldots ,0}_{L-1})$ is obtained by a zero-padding extension of the original source vector ${\mathbf {f}}$, and $\hat{\mathbf {t}}={\text {circshift}}({\mathbf {t}},L)$ is obtained by circularly shifting the elements in the original kernel vector ${\mathbf {t}}$ by L positions. Finally, the field vector ${\mathbf {h}}$ can be obtained by extracting the first L elements in the extended field vector $\hat{\mathbf {h}}$.

Analogously, the derivation above can be extended to the evaluation of 2D and 3D discrete convolutions using the 2D and 3D FFT algorithms.

For the 2D discrete convolution:

$$\begin{aligned}&[{\mathbf {h}}]_{l,n}=[{\mathbf {t}} \star {\mathbf {f}}]_{l,n} =\sum _{\tilde{l}=0}^{\tilde{L}-1}\sum _{\tilde{n}=0}^{\tilde{N}-1}t_{l-\tilde{l},n-\tilde{n}}f_{\tilde{l},\tilde{n}}, \nonumber \\&l=0,1,\ldots ,L-1, \quad n=0,1,\ldots ,N-1, \end{aligned}$$

(26)

the algorithm can be written as:

$$\begin{aligned}&\hat{\mathbf {h}}_{2D}={\mathbf {F}}^{-1}\left[ {\mathbf {F}}(\hat{\mathbf {f}}_{2D}) {\mathbf {F}}(\hat{\mathbf {t}}_{2D}) \right] , \nonumber \\&{\mathbf {h}}_{2D}=[\hat{\mathbf {h}}_{2D}]_{L \times N}. \end{aligned}$$

(27)

Here ${\mathbf {F}}$ and ${\mathbf {F}}^{-1}$ represent the 2D forward and inverse discrete Fourier transform operators, respectively. The extended source matrix $\hat{\mathbf {f}}_{2D}$ is obtained by a zero-padding extension of the original source matrix $[f_{\tilde{l},\tilde{n}}]$ of size $\tilde{L}\times \tilde{N}$ to the size $(L+\tilde{L}-1) \times (N+\tilde{N}-1)$, and $\hat{\mathbf {t}}_{2D}={\text {circshift}}({\mathbf {t}}_{2D},L,N)$ is obtained by circularly shifting the elements in the original kernel matrix $[t_{l-\tilde{l},n-\tilde{n}}]$ by L and N positions along two dimensions, respectively. Finally, the field matrix ${\mathbf {h}}_{2D}$ can be obtained by extracting the first $L \times N$ elements in the extended field matrix $\hat{\mathbf {h}}_{2D}$.

Similarly, the algorithm for the 3D discrete convolution:

$$\begin{aligned}&[{\mathbf {h}}]_{l,m,n}=[{\mathbf {t}} \star {\mathbf {f}}]_{l,m,n} =\sum _{\tilde{l}=0}^{\tilde{L}-1}\sum _{\tilde{m}=0}^{\tilde{M}-1}\sum _{\tilde{n}=0}^{\tilde{N}-1} t_{l-\tilde{l},m-\tilde{m},n-\tilde{n}}f_{\tilde{l},\tilde{m},\tilde{n}}, \nonumber \\&l=0,1,\ldots ,L-1, \quad m=0,1,\ldots ,M-1, \quad n=0,1,\ldots ,N-1, \end{aligned}$$

(28)

is written as:

$$\begin{aligned}&\hat{\mathbf {h}}_{3D}={\mathbf {F}}^{-1}\left[ {\mathbf {F}}(\hat{\mathbf {f}}_{3D}) {\mathbf {F}}(\hat{\mathbf {t}}_{3D}) \right] , \nonumber \\&{\mathbf {h}}_{3D}=[\hat{\mathbf {h}}_{3D}]_{L \times M \times N}, \end{aligned}$$

(29)

where ${\mathbf {F}}$ and ${\mathbf {F}}^{-1}$ represent the 3D forward and inverse discrete Fourier transform operators, respectively. The extended 3D source matrix $\hat{\mathbf {f}}_{3D}$ is obtained by a zero-padding extension of the original 3D source matrix $[f_{\tilde{l},\tilde{m},\tilde{n}}]$ of size $\tilde{L}\times \tilde{M}\times \tilde{N}$ to the size $(L+\tilde{L}-1) \times (M+\tilde{M}-1) \times (N+\tilde{N}-1)$, and $\hat{\mathbf {t}}_{3D}={\text {circshift}}({\mathbf {t}}_{3D},L,M,N)$ is obtained by circularly shifting the elements in the original kernel matrix $[t_{l-\tilde{l},m-\tilde{m},n-\tilde{n}}]$ by L, M and N positions along three dimensions, respectively. Finally, the 3D field matrix ${\mathbf {h}}_{3D}$ can be obtained by extracting the first $L \times M \times N$ elements in the extended 3D field matrix $\hat{\mathbf {h}}_{3D}$.

4 The Conv-Gauss-FFT Algorithm

Based on the derivations in the previous two sections, we introduce here an efficient algorithm, namely the Conv-Gauss-FFT algorithm, for the calculation of continuous convolution-type integrals by a combined use of hybrid rectangle-Gaussian grids and the FFT algorithm.

For 1D continuous convolutions, by combining Eqs. 8 and 25, we have:

$$\begin{aligned} \hat{\mathbf {h}}&= \Delta x \sum _{i=1}^{I} \mu _{i}^{(I)} {\mathbf {F}}^{-1}\left[ {\mathbf {F}}(\hat{\mathbf {f}}_{\tilde{\alpha }_i}) {\mathbf {F}}(\hat{\mathbf {t}}_{\tilde{\alpha }_i}) \right] \nonumber \\&= \Delta x \; {\mathbf {F}}^{-1}\left[ \sum _{i=1}^{I} \mu _{i}^{(I)} {\mathbf {F}}(\hat{\mathbf {f}}_{\tilde{\alpha }_i}) {\mathbf {F}}(\hat{\mathbf {t}}_{\tilde{\alpha }_i}) \right] , \nonumber \\ {\mathbf {h}}&= [\hat{\mathbf {h}}]_{L \times 1}. \end{aligned}$$

(30)

We call this approach the 1D Conv-Gauss-FFT algorithm.

The 2D and 3D Conv-Gauss-FFT algorithms for the evaluations of the 2D and the 3D continuous convolutions can be obtained analogously. Combining Eqs. 11 and 27, we have the 2D Conv-Gauss-FFT algorithm:

$$\begin{aligned} \hat{\mathbf {h}}_{2D}&= \Delta _{x}\Delta _{z} \; {\mathbf {F}}^{-1}\left[ \sum _{i=1}^{I} \sum _{k=1}^{K} \mu _{i}^{(I)} \omega _{k}^{(K)} {\mathbf {F}}(\hat{\mathbf {f}}_{\tilde{\alpha }_i \tilde{\gamma }_k}) {\mathbf {F}}(\hat{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}) \right] , \nonumber \\ {\mathbf {h}}_{2D}&= [\hat{\mathbf {h}}_{2D}]_{L \times N}. \end{aligned}$$

(31)

Similarly, by combining Eqs. 16 and 29, we have the 3D Conv-Gauss-FFT algorithm:

$$\begin{aligned} \hat{\mathbf {h}}_{3D}&= \Delta _{x}\Delta _{y}\Delta _{z} \; {\mathbf {F}}^{-1}\left[ \sum _{i=1}^{I} \sum _{j=1}^{J} \sum _{k=1}^{K} \mu _{i}^{(I)} \nu _{j}^{(J)} \omega _{k}^{(K)} {\mathbf {F}}(\hat{\mathbf {f}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k}) {\mathbf {F}}(\hat{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\beta }_j \tilde{\gamma }_k}) \right] , \nonumber \\ {\mathbf {h}}_{3D}&= [\hat{\mathbf {h}}_{3D}]_{L \times M \times N}. \end{aligned}$$

(32)

The complexity of the algorithm depends on several parameters, including the source grid size, the field grid size, and the number of Gaussian nodes used in each direction. Take the 3D Conv-Gauss-FFT algorithm for instance, the numerical complexity of the algorithm is $O(IJKS\log {S})$, with I, J, K the number of Gaussian nodes along three directions, and $S=(L+\tilde{L}-1) \times (M+\tilde{M}-1) \times (N+\tilde{N}-1)$ is determined by the sizes of both the source grid ($\tilde{L}\times \tilde{M}\times \tilde{N}$) and the field grid ($L \times M \times N$). The total number of discrete Fourier transforms needed is $2IJK+1$.

The accuracy of the algorithm also depends on several aspects, among which the well-behavedness of the source and the kernel functions, i.e., how well can continuous polynomials approximate these functions, plays the central role. When the source and the kernel functions are well-behaved, that is, smooth enough and with no singularity, the algorithm can achieve high accuracy as long as a sufficiently large number of Gaussian nodes are used. However, when the source function is only piecewise continuous, as is usually the case in a gravity forward problem, the density function changes discontinuously across the boundary of the source body, the algorithm may introduce some observable errors for field points close to the source’s boundary. Furthermore, when the kernel function has a strong singularity, as is the case for high-order derivatives of Newton’s integral kernel, the algorithm fails if the convolution integral becomes singular and cannot be properly solved using a regular quadrature method, including the hybrid rectangle-Gaussian quadrature method used here.

The Conv-Gauss-FFT algorithm, including the 2D and 3D cases, has been coded in MATLAB language. Together with a point-in-polygon algorithm and a point-in-polyhedron algorithm, the method can be used to solve general 2D and 3D gravity forward problems including sources with arbitrary geometry and arbitrary density distribution. Moreover, the algorithm may also be useful in solving other convolution-type integrals in geophysics and geodesy (Hirt et al. 2011). The efficiency, accuracy and robustness of the algorithm will be assessed by numerical comparisons with examples derived from the literature.

5 General Gravity Forward Modeling Using the Conv-Gauss-FFT Algorithm

5.1 The 2D Forward Problem

The general 2D gravity forward problem can be written as a continuous convolution-type integral:

$$\begin{aligned} \frac{\partial ^{i+k}}{\partial x^i \partial z^k} \phi (x,z)= 2 G \; \int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}}\int _{\tilde{z}_{0}}^{\tilde{z}_{\tilde{N}}} \rho (\tilde{x},\tilde{z}) \frac{\partial ^{i+k}}{\partial x^i \partial z^k} \left[ \log {\frac{1}{{\mathrm{d}} (x-\tilde{x},z-\tilde{z})}} \right] {\mathrm{d}} \tilde{x}{\mathrm{d}} \tilde{z}, \end{aligned}$$

(33)

where G is the gravitational constant, $\rho (\tilde{x},\tilde{z})$ is the 2D density distribution within the integration region, $\phi$ is the gravity potential and $\frac{\partial ^{i+k}}{\partial x^i \partial z^k}$ represent its derivative components, and

$$\begin{aligned} {\mathrm{d}} (x-\tilde{x},z-\tilde{z})=\sqrt{(x-\tilde{x})^2+(z-\tilde{z})^2} \end{aligned}$$

(34)

is the 2D Euclidean distance between a field point (x, z) and a source point $(\tilde{x},\tilde{z})$.

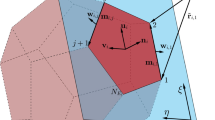
Figure 1 shows some basic concepts of the 2D Conv-Gauss-FFT algorithm. The region covered by filed points (the red grid) is denoted as:

$$\begin{aligned} {\varOmega }_{{\mathrm{field}}}=\left\{ (x,z)\big |x_0 \,\le\, x \,\le\, x_{L-1}, z_0 \,\le\, z \,\le\, z_{N-1}\right\} . \end{aligned}$$

(35)

The source region (the green grid) is defined as:

$$\begin{aligned}&{\varOmega }_{{\mathrm{source}}}=\left\{ (\tilde{x},\tilde{z})|\tilde{x}_0 \,\le\, \tilde{x}\,\le\, \tilde{x}_{\tilde{L}}, \tilde{z}_0 \,\le\, \tilde{z}\,\le\, \tilde{z}_{\tilde{N}}\right\} , \nonumber \\&\tilde{x}_0=x_0+\left\lfloor \frac{\tilde{x}_{\mathrm{min}}-x_0}{\Delta x}\right\rfloor \Delta x, \quad {\mathrm{d}} \tilde{x}_{\tilde{L}}=x_0+\left\lceil \frac{\tilde{x}_{\mathrm{max}}-x_0}{\Delta x}\right\rceil \Delta x, \nonumber \\&\tilde{z}_0=z_0+\left\lfloor \frac{\tilde{z}_{\mathrm{min}}-z_0}{\Delta z}\right\rfloor \Delta z, \quad {\mathrm{d}} \tilde{z}_{\tilde{N}}=z_0+\left\lceil \frac{\tilde{z}_{\mathrm{max}}-z_0}{\Delta z}\right\rceil \Delta z, \end{aligned}$$

(36)

where $\tilde{x}_{\mathrm{min}},\tilde{x}_{\mathrm{max}},\tilde{z}_{\mathrm{min}},\tilde{z}_{\mathrm{max}}$ are the upper and lower limits of the coordinate values of the source polygon’s (the blue polygon’s) vertices, and the symbols $\lfloor \; \rfloor$ and $\lceil \; \rceil$ represent the floor and ceiling functions, respectively.

We mention here that although we have drawn the source grid contained within the field grid in Fig. 1, there is no limitation on the geometrical relationship between these two regions. They can either be separated (${\varOmega }_{\mathrm{field}}\cap {\varOmega }_{\mathrm{source}}=\varnothing$), overlapped (${\varOmega }_{\mathrm{field}}\cap {\varOmega }_{\mathrm{source}}\ne \varnothing$), or with one contained in another (${\varOmega }_{\mathrm{field}}\cap {\varOmega }_{\mathrm{source}}={\varOmega }_{\mathrm{field}} \; \text {or} \; {\varOmega }_{\mathrm{source}}$). However, to make the Conv-Gauss-FFT algorithm work, the grid intervals of these two regions along each direction must be the same, that is, the condition $\Delta \tilde{x}= \Delta x, \Delta \tilde{y}= \Delta y, \Delta \tilde{z}= \Delta z$ is met.

Fig. 1

Illustration of the 2D gravity forward model based on the 2D Conv-Gauss-FFT algorithm

Now we use the 2D Conv-Gauss-FFT algorithm (Eq. 31) to evaluate Eq. 33. Obviously, the kernel function t can be evaluated analytically for the gravity potential and its derivatives of arbitrary order. Taking the vertical component of the gravity vector for instance, we have:

$$\begin{aligned} t(x-\tilde{x},z-\tilde{z})=\frac{\partial }{\partial z} \left[ \log {\frac{1}{{\mathrm{d}} (x-\tilde{x},z-\tilde{z})}} \right] = \frac{-(z-\tilde{z})}{(x-\tilde{x})^2+(z-\tilde{z})^2}. \end{aligned}$$

(37)

Then for each pair of shift parameters $(\tilde{\alpha }_i,\tilde{\gamma }_k)$, the kernel matrix $\hat{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}$ can be obtained by circularly shifting the elements in the original kernel matrix ${\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}$ by L and N positions along two dimensions, respectively, with ${\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}$ defined in Eq. 14.

The kernel functions correspond to the gravity vector, and the gravity gradient tensor components caused by a 2D source body are written as:

$$\begin{aligned} \begin{bmatrix} \phi _{x},\, \phi _{z} \end{bmatrix} \longleftrightarrow \begin{bmatrix} \frac{-(x-\tilde{x})}{{\mathrm{d}}^2},\, \frac{-(z-\tilde{z})}{\mathrm{d}^2} \end{bmatrix}, \end{aligned}$$

(38)

$$\begin{aligned} \begin{bmatrix} \phi _{xx},\,\phi _{xz},\, \phi _{zz} \end{bmatrix} \longleftrightarrow \begin{bmatrix} \frac{2(x-\tilde{x})^2-{\mathrm{d}}^{2}}{{\mathrm{d}}^{4}},\, \frac{2(x-\tilde{x})(z-\tilde{z})}{{\mathrm{d}}^{4}},\, \frac{2(z-\tilde{z})^2-{\mathrm{d}}^{2}}{{\mathrm{d}}^{4}} \end{bmatrix}. \end{aligned}$$

(39)

Similarly, for each pair of shift parameters $(\tilde{\alpha }_i,\tilde{\gamma }_k)$, the source matrix $\hat{\mathbf {f}}_{\tilde{\alpha }_i \tilde{\gamma }_k}$ is obtained by the zero-padding extension of the original source matrix ${\mathbf {f}}_{\tilde{\alpha }_i \tilde{\gamma }_k}$, which is defined in Eq. 13 by the source function $f(\tilde{x}_{\tilde{l}+\tilde{\alpha }_i},\tilde{z}_{\tilde{n}+\tilde{\gamma }_k})$. For the polygonal model in Fig. 1, values of the source function can be determined by both the density distribution $\rho (\tilde{x},\tilde{z})$ within the polygon and a point-in-polygon algorithm. Denote the region covered by the source polygon as ${\varOmega }_{{\rm polygon}}$, we then have:

$$f(\tilde{x},\tilde{z})= \left\{ \begin{array}{ll} \rho (\tilde{x},\tilde{z}), &\quad {\text {if}}\, (\tilde{x},\tilde{z}) \in {\varOmega }_{{\mathrm{polygon}}}, \\ 0, &\quad {\text {if}}\,(\tilde{x},\tilde{z}) \notin {\varOmega }_{{\rm polygon}}. \\ \end{array}\right.$$

(40)

As shown in Fig. 1, the source function is sampled on a hybrid rectangle-Gaussian grid (cross symbols) with the number of Gaussian nodes chosen as $I=K=2$. For each pair of shift parameters $(\tilde{\alpha }_i,\tilde{\gamma }_k)$, the point-in-polygon algorithm is used to determine whether a grid point lies inside (blue cross symbols) or outside of (green cross symbols) the source polygon. For the point-in-polygon test, we use the MATLAB function inpoly.m downloaded from the MATLAB central. The function is provided by Darren Engwirda at http://cn.mathworks.com/matlabcentral/fileexchange/10391-fast-points-in-polygon-test.

In addition to polygonal models, the source region can also be defined by analytical functions. Martin-Atienza and Garcia-Abdeslem (1999) studied 2D gravity modeling with source body bounded either laterally by functions of depth:

$$\begin{aligned} {\varOmega }_{{\mathrm{2D}}}=\left\{ (\tilde{x},\tilde{z}){:}\,h_1(\tilde{z}) \,\le\, \tilde{x}\,\le\, h_2(\tilde{z}), \tilde{z}_1 \,\le\, \tilde{z}\,\le\, \tilde{z}_2\right\} , \end{aligned}$$

(41)

or vertically by functions of the horizontal position:

$$\begin{aligned} {\varOmega }_{{\mathrm{2D}}}=\left\{ (\tilde{x},\tilde{z}){:}\,\tilde{x}_1 \,\le\, \tilde{x}\,\le\, \tilde{x}_2, g_1(\tilde{x}) \,\le\, \tilde{z}\,\le\, g_2(\tilde{x})\right\} . \end{aligned}$$

(42)

For these analytically defined geometries, it is simpler to determine whether a source point lies within the source region or not. The point-in-polygon algorithm is no longer necessary; a simple comparison to the two analytical boundary functions would immediately tell.

5.2 The 3D Forward Problem

We have discussed in detail the 2D Conv-Gauss-FFT solution for a general 2D gravity forward problem. The 3D forward problem can be solved in a very similar way based on the 3D Conv-Gauss-FFT algorithm (Eq. 32) and a point-in-polyhedron algorithm.

The general 3D gravity forward problem can be written as:

$$\begin{aligned} \frac{\partial ^{i+j+k}}{\partial x^i \partial y^j \partial z^k} \phi (x,y,z) =G \; \int _{\tilde{x}_{0}}^{\tilde{x}_{\tilde{L}}}\int _{\tilde{y}_{0}}^{\tilde{y}_{\tilde{M}}}\int _{\tilde{z}_{0}}^{\tilde{z}_{\tilde{N}}} \rho (\tilde{x},\tilde{y},\tilde{z}) \frac{\partial ^{i+j+k}}{\partial x^i \partial y^j \partial z^k} \left[ \frac{1}{r(x-\tilde{x},y-\tilde{y},z-\tilde{z})} \right] {\mathrm{d}} \tilde{x}{\mathrm{d}} \tilde{y}{\mathrm{d}} \tilde{z}, \end{aligned}$$

(43)

where

$$\begin{aligned} r(x-\tilde{x},y-\tilde{y},z-\tilde{z})=\sqrt{(x-\tilde{x})^2+(y-\tilde{y})^2+(z-\tilde{z})^2} \end{aligned}$$

(44)

is the 3D Euclidean distance between a field point (x, y, z) and a source point $(\tilde{x},\tilde{y},\tilde{z})$, and $\rho (\tilde{x},\tilde{y},\tilde{z})$ is the 3D density distribution within the integration volume.

Again, kernel functions of the gravity potential and its derivatives of arbitrary order can be obtained analytically. The kernels correspond to the most frequently used gravity vector, and gravity gradient tensor components are:

$$\begin{aligned} \begin{bmatrix} \phi _{x}\, \phi _{y}\, \phi _{z} \end{bmatrix} \longleftrightarrow \begin{bmatrix} \frac{-(x-\tilde{x})}{r^{3}}\, \frac{-(y-\tilde{y})}{r^{3}}\, \frac{-(z-\tilde{z})}{r^{3}} \end{bmatrix}, \end{aligned}$$

(45)

$$\begin{aligned} \begin{bmatrix} \phi _{xx}\, \phi _{yy}\, \phi _{zz} \\ \phi _{xy}\, \phi _{xz}\, \phi _{yz} \end{bmatrix} \longleftrightarrow \begin{bmatrix} \frac{3(x-\tilde{x})^2-r^2}{r^5}\, \frac{3(y-\tilde{y})^2-r^2}{r^5}\, \frac{3(z-\tilde{z})^2-r^2}{r^5} \\ \frac{3(x-\tilde{x})(y-\tilde{y})}{r^{5}}\, \frac{3(x-\tilde{x})(z-\tilde{z})}{r^{5}}\, \frac{3(y-\tilde{y})(z-\tilde{z})}{r^{5}} \end{bmatrix}. \end{aligned}$$

(46)

Clearly all kernel functions listed above have very simple expressions and can be evaluated very quickly with almost negligible computational cost.

Analogous to the 2D case, for each group of shift parameters $(\tilde{\alpha }_i,\tilde{\beta }_j,\tilde{\gamma }_k)$, the point-in-polyhedron algorithm is used to determine whether a grid point lies within or out of the source polyhedron. Figure 2 shows a point-in-polyhedron test of a regular grid of points using an Octahedron source body. The MATLAB function inpolyhedron.m downloaded from the MATLAB central provided by Sven Holcombe is used for the test. Denote the region occupied by the source polyhedron as ${\varOmega }_{{\rm polyhedron}}$, we then have:

$$f(\tilde{x},\tilde{y},\tilde{z})= \left\{ \begin{array}{ll} \rho (\tilde{x},\tilde{y},\tilde{z}), &\quad {\text {if}}\,(\tilde{x},\tilde{y},\tilde{z}) \in {\varOmega }_{\mathrm{polyhedron}}, \\ 0, &\quad {\text {if}}\,(\tilde{x},\tilde{y},\tilde{z}) \notin {\varOmega }_{\mathrm{polyhedron}}. \\ \end{array}\right.$$

(47)

Fig. 2

A point-in-polyhedron test of a regular grid of points using an Octahedron

In addition to polyhedral bodies, a 3D source region can also be described by a layer with uneven top and bottom surfaces, like those frequently used in a terrain correction problem (Parker 1973; Wu 2016):

$$\begin{aligned} {\varOmega }_{3D}=\left\{ (\tilde{x},\tilde{y},\tilde{z}){:}\,\tilde{x}_1 \,\le\, \tilde{x}\,\le\, \tilde{x}_2, \, \tilde{y}_1 \,\le\, \tilde{y}\,\le\, \tilde{y}_2, \, \tilde{z}_1(\tilde{x},\tilde{y}) \,\le\, \tilde{z}\,\le\, \tilde{z}_2(\tilde{x},\tilde{y})\right\} . \end{aligned}$$

(48)

The top and bottom surfaces can be step functions, piecewise triangular interpolated functions, or smooth functions as discussed in Wu (2016). When these topographic models are considered, the point-in-polyhedron algorithm is no longer necessary, and a simple comparison to the top and bottom surface functions would directly tell if a point lies within or outside the source region.

6 Numerical Tests

In this section, we use both 2D and 3D synthetic and real models, with versatile geometries, constant or variable density distributions, to test the Conv-Gauss-FFT algorithm. For each model, space-domain analytical solutions are used as precise references. Numerical accuracy and computational efficiency of the Conv-Gauss-FFT algorithm are then tested by comparing to space-domain solutions.

For comparison of numerical accuracy, we provide difference maps between the Conv-Gauss-FFT algorithm and space-domain analytical solutions. Alternatively, we also use several different criteria, including the absolute error, the relative error and the relative root-mean-square (rrms) error. The absolute error and the relative error are used when comparison is made at a single field point, e.g., at the origin of the coordinate system. The relative root-mean-square error is used for comparison of fields on profiles or on the whole 2D or 3D regular grid.

We also include the computing times of both algorithms for all synthetic and real models. We use $T_{{\mathrm{space}}}$ as the computing time for space-domain methods and $T_{\mathrm{CGF}}$ for the Conv-Gauss-FFT algorithm. It should be mentioned that in the numerical examples we provided, $T_{\mathrm{space}}$ usually represents the time cost of the space-domain solution calculating gravity anomalies at one single point or on one single profile, while $T_{\mathrm{CGF}}$ usually represents the time cost of the Conv-Gauss-FFT algorithm calculating gravity anomalies on the whole 2D or 3D grid. The algorithms were coded in MATLAB language and executed on a Intel core PC with 8 GB of RAM and a i5-3470 CPU having a clock speed of 3.20 GHz.

6.1 2D Examples

First we test our algorithm using a simple 2D model, an infinitely extended horizontal cylinder. The cylinder is of uniform density contrast $\rho =1000$ kg m$^{-3}$. It is centered at the origin of the coordinate system, and its radius is $a=10$ km. Field points on a regular grid $x=-20{:}1{:}20$ km, $z=-20{:}1{:}20$ km are evaluated using both methods. Figure 3 compares forward results of the gravity component $\phi _z$ caused by the cylinder using both space-domain analytical solution and the 2D Conv-Gauss-FFT algorithm with different numbers of Gaussian nodes.

Fig. 3

a Space-domain forward gravity anomaly $\phi _z$ (mGal) due to an infinitely extended horizontal cylinder and the associated error maps of the 2D Conv-Gauss-FFT algorithm with different number of Gaussian nodes, b $I=K=10$, c $I=K=20$, d $I=K=30$

Space-domain solution of the $\phi _z$ anomaly due to this model is easily obtained:

$$\phi _z(x,z)= \left\{ \begin{array}{ll} -2G \frac{\pi a^2 \rho z}{x^2+z^2}, &\quad {\text {if}}\, (x,z) \notin {\varOmega }_{\mathrm{cylinder}}, \\ -2G \pi \rho z, &\quad {\text {if}}\, (x,z) \in {\varOmega }_{\mathrm{cylinder}}, \\ \end{array}\right.$$

(49)

where ${\varOmega }_{\mathrm{cylinder}}$ denotes the area covered by the cylinder: ${\varOmega }_{{\mathrm{cylinder}}}=\{(x,z) | x^2+z^2 \,\le\, a^2\}$. Figure 3a shows space-domain forward results of the $\phi _z$ anomaly. As indicated in Eq. 49, the $\phi _z$ anomaly is symmetric with respect to the x-axis and antisymmetric with respect to the z axis. Inside the cylinder, it is linearly dependent on the value of z.

Figure 3b–d shows the associated error maps of the 2D Conv-Gauss-FFT algorithm with numbers of Gaussian nodes $I=K=10,20,30$. For most part of the field region, the Conv-Gauss-FFT algorithm with a small number of Gaussian nodes can already generate forward results almost identical to the space-domain solutions. However, the difference between these two algorithms becomes noticeable near the boundary of the cylinder, and it cannot be fully suppressed by increasing the number of Gaussian nodes. The reason for this, as has been discussed before, is that the density function changes discontinuously across the boundary of the source body, producing a discontinuous source function that cannot be well approximated by continuous polynomials. The space-domain solution costs only about 0.0004 s because the analytical expressions are very simple. The Conv-Gauss-FFT algorithm with $I=K=10,20,30$ costs about 0.10, 0.38 and 0.85 s, respectively.

Figure 4 provides more details of the differences between these two algorithms. Figure 4a plots the absolute errors of the $I=K=30$ Conv-Gauss-FFT algorithm against the point–cylinder distance, i.e., the minimum distance from each field point to the boundary of the cylinder: $\delta =|\sqrt{x^2+z^2}-a|$. Apparently the point–cylinder distance in general controls the upper bound of the error. The larger the distance, the smaller the error’s upper bound. Figure 4b shows histogram of the error. Most of the errors lie within the range $[-0.01,0.01]$ mGal. Figure 4c shows absolute error changes at five randomly picked field points: A, B, C, D and E with increasing number of Gaussian nodes. In general, the errors decrease with increasing number of Gaussian nodes. However, they do not decrease monotonically due to unknown reasons. Figure 4d shows the overall rrms errors of the Conv-Gauss-FFT algorithm with increasing number of Gaussian nodes for the modeling of the $\phi _x$ and $\phi _z$ components on the whole 2D grid. These two components have exactly the same rrms error because both their analytical expressions and kernel functions are mathematically equivalent. The changing of rrms errors has similar behaviors with those observed in Fig. 4c. In general, they also decrease, but not monotonically, with increasing number of Gaussian nodes.

Fig. 4

a Absolute errors of the $I=K=30$ Conv-Gauss-FFT algorithm against the point–cylinder distance, b histogram of the error, c absolute error changes with increasing number of Gaussian nodes at five field points, d the overall rrms error of the Conv-Gauss-FFT algorithm with increasing number of Gaussian nodes for the modeling of the $\phi _x$ and $\phi _z$ components

Next we test our method using a variable density model, a 2D prism with linear depth-dependent density function $\rho (\tilde{z})=100+60\tilde{z}$ kg m$^{-3}$. As shown in Fig. 5, the prism extends from $-\,5$ to 5 km horizontally and 0 to 15 km vertically. For the Conv-Gauss-FFT algorithm, a 2D grid of field points: $x=-20{:}1{:}20$ km, $z=-20{:}1{:}20$ km are calculated. For the space-domain analytical solution, only five profiles A, B, C, D and E at different heights $z=-\,1$ km (solid line), $z=-\,2$ km (dashed line), $z=-\,4$ km (dotted line), $z=-\,8$ km (cross), and $z=-\,16$ km (asterisk) in the upper half-space are evaluated. Therefore, the comparison between these two methods is carried out only on these five profiles.

Fig. 5

A 2D prism model with linear depth-dependent density function $\rho =100+60\tilde{z}$ kg m$^{-3}$. Five field profiles A–E at different heights $z=-\,1,-\,2,-\,4,-\,8,-\,16$ km in the upper half-space are calculated and compared using space-domain analytical solutions and the 2D Conv-Gauss-FFT algorithm

Unlike the horizontal cylinder model we have studied above, the geometry of the 2D prism model chosen here fits perfectly with the rectangle-Gaussian grid used in the Conv-Gauss-FFT algorithm. As a result, the density function changes smoothly within each small rectangle area, leading to integral kernels that can be well approximated by continuous polynomials, which then ensures the high accuracy of the Gaussian quadrature rule.

Figure 6 compares space-domain and Conv-Gauss-FFT forward results of the gravity vector component $\phi _z$ and the gravity gradient tensor component $\phi _{zz}$ on the five profiles A, B, C, D, E listed above caused by the linear variable density model in Fig. 5. It can be observed that for both the $\phi _z$ and $\phi _{zz}$ components, the Conv-Gauss-FFT algorithm agrees very well, to almost machine precision, to the space-domain analytical solutions. The Conv-Gauss-FFT algorithm converges faster for profiles higher above the source because gravity anomalies generated farther from the source are smoother and can be better approximated by lower-order polynomials. The space-domain solution costs about 0.0015 s modeling these five profiles, while the Conv-Gauss-FFT algorithm with $I=K=10$ costs about 0.09 s modeling the whole 2D grid.

Fig. 6

Comparison of space-domain and Conv-Gauss-FFT forward results of the gravity vector component $\phi _z$ and the gravity gradient tensor component $\phi _{zz}$ on five profiles A, B, C, D and E caused by the linear variable density model in Fig. 5. a Space-domain forward results of $\phi _z$, b rrms errors of $\phi _z$ calculated by the Conv-Gauss-FFT algorithm with increasing number of Gaussian nodes, c the corresponding errors of the $I=K=10$ Conv-Gauss-FFT algorithm, d space-domain forward results of $\phi _{zz}$, e rrms errors of $\phi _{zz}$ calculated by the Conv-Gauss-FFT algorithm with increasing number of Gaussian nodes, f the corresponding errors of the $I=K=10$ Conv-Gauss-FFT algorithm

Finally, we test our algorithm using four 2D models in the literature. They have been studied by several authors using versatile variable density distributions. Figure 7 compares space-domain analytical solutions and the Conv-Gauss-FFT forward results of the $\phi _z$ anomaly caused by these four models.

Fig. 7

2D variable density models previously studied by other authors. a A 2D prism with quadratic depth-dependent density, b a 2D polygon with quadratic depth-dependent density, c a 2D polygon with quadratic horizontally dependent density, d source body bounded laterally by functions of depth with a second-order polynomial density function

Figure 7a shows forward results of a 2D rectangular prism, which extends vertically from 1 to 2 km, and horizontally from 3 to 9 km; it has been studied by Rao (1986), Zhang et al. (2001) and D’Urso (2015), by assuming a depth-dependent density function

$$\begin{aligned} \rho (\tilde{z})=1.54+0.24\tilde{z}-0.035\tilde{z}^2. \end{aligned}$$

(50)

Space-domain results are extracted from table 1 in D’Urso (2015). The Conv-Gauss-FFT algorithm with $I=K=2$ is applied to calculate a 2D grid of field points: $x=0{:}0.01{:}12$ km, $z=0{:}1{:}3$ km, after which field values on the profile $z=0$ km with horizontal positions coincide with those in D’Urso (2015) are extracted for comparison. The Conv-Gauss-FFT algorithm costs about 0.02 s evaluating the whole 2D grid.

Figure 7b shows forward results of a 2D polygon; it has been studied by Garcia-Abdeslem et al. (2005), Zhou (2008) and D’Urso (2015). It refers to the Sebastián Vizcaíno Basin in Mexico for which the density contrast has been assumed in the form

$$\begin{aligned} \rho (\tilde{z})=-0.7+0.2548\tilde{z}-0.0273\tilde{z}^2. \end{aligned}$$

(51)

Space-domain results are extracted from table 2 in D’Urso (2015). The Conv-Gauss-FFT algorithm with $I=2$, $K=4$ is applied to calculate gravity anomalies on the 2D grid: $x=-0.4{:}0.01{:}2.2$ km, $z=0{:}0.05{:}3$ km, after which field values on the profile $z=0$ km with horizontal positions coincide with those in D’Urso (2015) are extracted for comparison. The Conv-Gauss-FFT algorithm costs about 0.05 s evaluating the whole 2D grid.

Figure 7c shows forward results of a 2D polygon with horizontally dependent density function; it has been studied by Martin-Atienza and Garcia-Abdeslem (1999), Zhou (2010) and D’Urso (2015), by assuming a density function

$$\begin{aligned} \rho (\tilde{x})=0.5+0.02\tilde{x}-0.02\tilde{x}^2. \end{aligned}$$

(52)

Space-domain results are extracted from table 4 in D’Urso (2015). The Conv-Gauss-FFT algorithm with $I=K=2$ is applied to calculate gravity anomalies on the 2D grid: $x=-5.5{:}0.01{:}5.5$ km, $z=0{:}0.1{:}3$ km, after which field values on the profile $z=0$ km with horizontal positions coincide with those in D’Urso (2015) are extracted for comparison. The Conv-Gauss-FFT algorithm costs about 0.3 s evaluating the whole 2D grid.

Figure 7d shows forward results of a 2D model bounded laterally by functions of depth. It can be defined in the form of Eq. 41, with $\tilde{z}_1=0$ km, $\tilde{z}_2=3$ km the upper and bottom depths, and $h_1(\tilde{z})=-4-0.07\tilde{z}+0.3\tilde{z}^2+0.01\tilde{z}^3$ km, $h_2(\tilde{z})=4.5+0.5\tilde{z}-0.2\tilde{z}^2$ km the left and right boundary functions; it has been studied by Martin-Atienza and Garcia-Abdeslem (1999), Zhou (2009b, 2010) and D’Urso (2015), by assuming a 2D variable density function

$$\begin{aligned} \rho (\tilde{x},\tilde{z})=-0.7-0.05\tilde{x}\tilde{z}+0.04\tilde{x}^2+0.06\tilde{z}^2. \end{aligned}$$

(53)

Space-domain results are extracted from table 5 in D’Urso (2015). The Conv-Gauss-FFT algorithm with $I=2$, $K=4$ is applied to calculate gravity anomalies on the 2D grid: $x=-5.5{:}0.01{:}5.5$ km, $z=0{:}0.1{:}3$ km, after which field values on the profile $z=0$ km with horizontal positions coincide with those in D’Urso (2015) are extracted for comparison. The Conv-Gauss-FFT algorithm costs about 0.25 s evaluating this model.

In all density functions, the coordinates $\tilde{x},\tilde{z}$ are expressed in kilometers and the density expressed in g cm$^{-3}$. Figure 7 shows a perfect agreement between the analytical solutions (red and blue lines) and those computed by means of the proposed Conv-Gauss-FFT approach (black dots).

6.2 3D Examples

Now we test the 3D Conv-Gauss-FFT algorithm using 3D models. We choose the triangulated shape model of the asteroid 433 EROS (approximate size $13 \times 13 \times 33$ km), which was mapped by the NEAR Shoemaker probe from April to October 2000 and has been investigated in depth by Zuber et al. (2000), Tsoulis et al. (2009), D’Urso (2014a, b) and Fukushima (2017). Several models of this body at various resolutions have been made available by the Planetary Science Institute (USA) at the address http://www.psi.edu/pds/archive/shape.html. Data can be downloaded at the address http://sbn.psi.edu/pds/asteroid/NEAR_A_5_COLLECTED_MODELS_V1_0/data/msi/ for all resolutions. We compare our results based on the 3D Conv-Gauss-FFT algorithm with space-domain solutions provided in D’Urso (2014a, b) using both constant and variable density functions for the asteroid 433 EROS.

Figure 8 shows forward results of the gravity potential $\phi$ (units in $\hbox {m}^2\,\hbox {s}^{-2}$) and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ (units in mGal) on a surface 0.2 km above the surface of the asteroid 433 EROS using the 3D Conv-Gauss-FFT algorithm with $I=J=K=2$. Here the asteroid 433 EROS is characterized by 1708 faces and 856 vertices. The results are obtained by assuming $G = 6.67259\times 10^{-11}$ m$^3$ kg$^{-1}$ s$^{-2}$ and a constant density $\rho =2670$ kg m$^{-3}$ of the model.

Fig. 8

Forward results of the gravity potential $\phi$ (units in $\hbox {m}^2\,\hbox {s}^{-2}$) and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ (units in mGal) on a surface 0.2 km above the surface of the asteroid 433 EROS using the 3D Conv-Gauss-FFT algorithm with $I=J=K=2$

The computation surface contains 856 vertices, with each vertex 0.2 km above a corresponding vertex of the asteroid 433 EROS. The local normal vector for each vertex is obtained by taking the average direction of the normal vectors of the triangular surfaces sharing this vertex. That is, for each vertex P of the asteroid 433 EROS, suppose P is shared by N surrounding triangular surfaces whose unit normal vectors are ${\mathbf {n}}_i$, $i=1,2,\ldots ,N$, then the local unit normal vector corresponding to the vertex P is calculated as: ${{\mathbf {n}}}_P=\sum _{i=1}^{N}{{\mathbf {n}}}_i/|\sum _{i=1}^{N}{{\mathbf {n}}}_i|$, and a computation point Q with ${\mathbf {r}}_Q={\mathbf {r}}_P+0.2{\mathbf {n}}_P$ is evaluated, where ${\mathbf {r}}_P$ and ${\mathbf {r}}_Q$ are position vectors for the vertices P and Q, respectively.

Figure 9 shows the corresponding difference maps between space-domain analytical solutions and the 3D Conv-Gauss-FFT algorithm. For space-domain analytical solution, we have coded the algorithm introduced in D’Urso (2014a) for the gravity potential and its first-order derivatives in MATLAB language and evaluated these components on the computation surface directly. For the 3D Conv-Gauss-FFT algorithm, we first calculate the gravity potential and its first derivatives on the 3D regular grid: $x=-\,20{:}0.25{:}20$ km, $y=-10{:}0.25{:}10$ km, $z=-10{:}0.25{:}10$ km, and then, field values on the computation surface are obtained through a linear interpolation. The space-domain algorithm costs about 97 s evaluating 856 points. The Conv-Gauss-FFT algorithm costs about 22 s calculating the whole 3D grid, which is of size $81 \times 161 \times 81$ and in all contains 1,056,321 points.

Fig. 9

Difference maps of the gravity potential $\phi$ (units in $\hbox {m}^2\,\hbox {s}^{-2}$) and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ between space-domain analytical solutions and the 3D Conv-Gauss-FFT algorithm with $I=J=K=2$

It can be observed that the errors for the gravity potential $\phi$ and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ are all very small comparing to the referenced fields. The gravity potential exhibits smaller errors than the gravity vector components because the corresponding integral kernel is smoother and can be better approximated by low-order polynomials. The largest misfits between two algorithms for all three gravity vector components are only about 2 mGal, which proves the accuracy and efficiency of the Conv-Gauss-FFT algorithm, especially when fields on a regular grid are needed.

Some further comparisons between the Conv-Gauss-FFT algorithm and space-domain analytical solutions for the asteroid 433 EROS with constant and variable density contrasts are implemented and summarized in Tables 1 and 2. In all cases, the comparison is made at the origin of the coordinate system, i.e., the point (0, 0, 0). The relative error is used to test the accuracy of the algorithm. Time costs of both algorithms, with $T_{\mathrm{space}}$ represents the computation time of the space-domain solution calculating the gravity anomalies at a single point, i.e., the origin, and $T_{\mathrm{CGF}}$ represents the computation time of the Conv-Gauss-FFT algorithm evaluating the whole 3D grid mentioned above, are provided.

Table 1 Comparison of values of the gravity potential $\phi$ and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ at the origin caused by the asteroid 433 Eros with constant density and different numbers of faces ($N_{{\rm F}}$) calculated by the Conv-Gauss-FFT algorithm ($I=J=K=2$) and the space-domain algorithm in D’Urso (2014a)

Table 2 Comparison of values of the gravity potential $\phi$, three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$, and three off-diagonal gravity gradient tensor components $\phi _{xy}$, $\phi _{xz}$, $\phi _{yz}$ at the origin caused by the asteroid 433 Eros with variable density $\rho =2670+\tilde{x}+\tilde{y}+\tilde{z}$ kg m$^{-3}$ and different numbers of faces ($N_\mathrm{F}$) calculated by the Conv-Gauss-FFT algorithm ($I=J=K=2$) and the space-domain results from D’Urso (2014b)

Table 1 summarizes forward results of both algorithms for the gravity potential $\phi$ and three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$ caused by the asteroid 433 EROS with constant density $\rho =2670$ kg m$^{-3}$ and characterized by 1708, 7790, 10,152, 22,540, 89,398 and 200,700 faces. For the gravity potential, relative errors for all six models are below $10^{-4}$; for vector gravity components, the largest relative error among all six models is about $0.4\%$. The computation time for the space-domain solution increases significantly when the number of faces of the polyhedral model becomes larger, while the computation time of the Conv-Gauss-FFT algorithm changes little. This is because in the Conv-Gauss-FFT algorithm, only the point-in-polyhedron algorithm depends on the geometry of the source, and it runs very fast for test points on a regular grid, with the computation time increases very slowly when the polyhedron is characterized by larger numbers of faces.

Table 2 summarizes forward results of both algorithms caused by the asteroid 433 EROS with linear variable density $\rho =2670+\tilde{x}+\tilde{y}+\tilde{z}$ kg m$^{-3}$ and characterized by 1708, 7790, 10,152 and 22,540 faces. The model has been studied in D’Urso (2014b) using several linear density functions. Forward results in table 2 in D’Urso (2014b) are extracted for comparison. It should be noted that since the origin of the coordinate system lies inside the source body, the integral in Eq. 43 for three diagonal gravity gradient tensor components $\phi _{xx}$, $\phi _{yy}$, $\phi _{zz}$ suffers from singularity problems which cannot be properly solved by regular quadrature methods, including the rectangle-Gaussian quadrature rule embedded in the Conv-Gauss-FFT algorithm, we provide only forward results of the gravity potential $\phi$, three gravity vector components $\phi _{x}$, $\phi _{y}$, $\phi _{z}$, and three off-diagonal gravity gradient tensor components $\phi _{xy}$, $\phi _{xz}$, $\phi _{yz}$ here. For the gravity potential, relative errors for all models are below $10^{-4}$; for vector gravity components, the largest relative error is about $0.4\%$; for tensor gravity components, the largest relative error is about $2\%$. Time costs of the Conv-Gauss-FFT algorithm for all models are less than 40 s modeling the whole 3D grid, which confirms its efficiency for 3D variable density models.

7 Discussion

Numerical examples have shown that in general, the Conv-Gauss-FFT algorithm achieves high accuracy. However, it may introduce some observable errors under certain conditions. For example, when the computation point lies near the boundary of the source, and when the geometry of the source does not fit perfectly with a rectangular mesh. A possible way to solve this problem may be the combination of the Conv-Gauss-FFT algorithm with analytical solutions or some properly designed quadrature methods to evaluate the long-range and close-range contributions separately. Similar techniques have been used in Parker (1995) and Tsoulis (1998, 2001) in solving terrain correction problems where the combination of analytical solutions for an inner zone surrounding the computation point with modified FFT for the computation of the effect of the rest of the DTM are discussed.

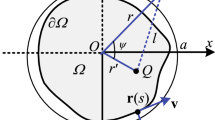
Take the general 2D forward problem for example, let $\mathscr {P}$ be the set of all field points, then for a field point $P(x_P,z_P) \in {\mathscr {P}}$ , denote the rectangular region close to P by

$$\begin{aligned} {\varOmega }(P)=\left\{ (x,z) \big | |x-x_P|\,\le\, L_c \Delta x,\; |z-z_P|\,\le\, N_c \Delta z\right\} , \end{aligned}$$

(54)

where $L_c, N_c$ specify the distances along two dimensions within which a close range is defined. As shown in Fig. 1 by setting $L_c=N_c=1$, field points can be classified into three categories based on three different relations between the source body region ${\varOmega }_{\mathrm{polygon}}$ and the region ${\varOmega }(P)$:

$$P \in \left\{ \begin{array}{ll} {\mathscr {P}}_{\mathrm{in}}, &\quad {\text {if}}\,{\varOmega }(P) \cap {\varOmega }_{\mathrm{polygon}} = {\varOmega }(P), \\ {\mathscr {P}}_{\mathrm{out}}, &\quad {\text {if}}\,{\varOmega }(P) \cap {\varOmega }_{\mathrm{polygon}} = \varnothing , \\ {\mathscr {P}}_{\mathrm{bnd}}, &\quad {\text {otherwise}}. \\ \end{array}\right.$$

(55)

Then we can evaluate the long-range contribution by applying the Conv-Gauss-FFT algorithm with a slightly modified kernel $\hat{\mathbf {t}}_{\tilde{\alpha }_i \tilde{\gamma }_k}^{\mathrm{long}}$:

$$\hat{{\mathbf{t}}}_{\tilde{\alpha }_i \tilde{\gamma }_k}^{\mathrm{long}}= \left\{ \begin{array}{ll} 0, &\quad {\text {if}}\,|x_l-\tilde{x}_{\tilde{l}+\tilde{\alpha }_i}| \,\le\, L_c \Delta x\,{\text { and }}\,|z_n-{\tilde{z}}_{{\tilde{n}}+\tilde{\gamma }_k}| \,\le\, N_c \Delta z, \\ \hat{{\mathbf{t}}}_{\tilde{\alpha}_i \tilde{\gamma }_k}, &\quad {\text{otherwise}}, \\ \end{array}\right.$$

(56)

and evaluate the close-range contribution using either analytical solutions or some properly designed quadrature methods. For example, if $P \in {\mathscr {P}}_{\mathrm{out}}$, clearly the close-range contribution is zero; if $P \in {\mathscr {P}}_{\mathrm{in}}$, close-range contribution can be accurately evaluated using analytical solution of a 2D prism; if $P \in {\mathscr {P}}_{\mathrm{bnd}}$, analytical solution or some properly designed quadrature methods can be applied once the region ${\varOmega }(P) \cap {\varOmega }_{\mathrm{polygon}}$ is rigorously defined.

The 3D case can be understood analogously. However, in order to use analytical solutions, an efficient algorithm for the calculation of the geometric intersection of a rectangular prism and a polyhedron is needed, which may cause some extra computational efforts. Besides, analytical solutions can be used only when they are available for the density model under consideration, and they also require considerable computational costs. An optimal trade-off between numerical accuracy and computational efficiency may be obtained by choosing optimal values of the parameters $L_c, M_c, N_c$.

8 Conclusions

We have reviewed briefly space-domain and Fourier-domain gravity forward algorithms in Cartesian coordinate system, based on which we introduced a Conv-Gauss-FFT algorithm for the accurate and efficient evaluation of continuous convolution-type integrals, and applied it to solve general 2D and 3D gravity forward problems.

The contribution of the Conv-Gauss-FFT algorithm can be summarized as follows:

• 1. The algorithm can be applied to source bodies with arbitrary geometry, with their boundaries represented either by discrete or continuous functions. Therefore, the algorithm can be applied to almost any 2D or 3D model, including single-source bodies like sphere, ellipsoid, cylinder, prism and general polyhedron, combined models like a 2D layer, a 3D terrain, or a general 3D model.

• 2. Although no numerical example of a prism-staked model is provided here, we mention that in fact the algorithm achieves best numerical accuracy and efficiency for this kind of models. On the one hand, since the source is a 3D mesh of prisms, a prefect match of the rectangle-Gaussian grid and the source’s boundaries can be obtained. On the other hand, the point-in-polyhedron algorithm is no longer needed, which can further accelerate the algorithm.

• 3. The algorithm can be applied to arbitrary density distribution that are defined either by discrete or by continuous functions, including polynomial, exponential, hyperbolic, parabolic, or any other analytically defined function. For the 3D prism-stacked model that is widely applied in both forward and inverse problems, since IJK sample points are picked within each prism element when an $I \times J \times K$ nodes 3D Conv-Gauss-FFT algorithm is applied, the density function can vary not only from prism to prism, but also within each prism element. This adds more flexibility to the 3D prism-stacked model.

• 4. Theoretically, the algorithm can be extended to any higher-order derivatives of the gravitational potential simply by replacing the kernel function with the corresponding derivative component of Newton’s integral kernel. For the gravity potential and its first-order derivatives, the algorithm can obtain high-precision forward results in the whole 2D or 3D space. For gravity gradient tensor components, the algorithm can provide reliable forward results outside the source body, but may fail or need special treatment inside the source body due to singularity problems. For gravity curvature components and higher-order derivatives, we have not done any numerical example, a reasonable guess is that the algorithm works well for field points outside the source body, and it may fail for those lying within.

• 5. Efficiency of the algorithm is guaranteed by the fast computations of the kernel functions of a mass point, a fast point-in-polyhedron algorithm, and the FFT algorithm. For 3D prism-stacked models, the algorithm presented here is more efficient than the mass-prism-based algorithm in Sanso and Sideris (2013) by avoiding the numerous, time-consuming evaluations of the logarithmic and arctangent terms. Besides, the algorithm presented here is more accurate than the algorithm in Tontini et al. (2009) since edge effects now can be completely eliminated. It is also more accurate than the algorithm in Zhang et al. (2015) because instead of a pure rectangle mesh of mass points, we use a hybrid rectangle-Gaussian grid of mass points.

Future works may be dedicated to the application of appropriate numerical quadrature methods for the evaluation of close-range contribution. Further applications of the algorithm for other convolution-type integrals in geophysics and geodesy, like the modeling of magnetic fields, upward and downward continuation of potential fields, and the evaluation of many geodetic integrals under planar assumption, may also be studied.