Effects of secondary current and stratification on suspension concentration in an open channel flow

Abstract

In this work, a mathematical model on concentration distribution is developed for a steady, uniform open channel turbulent flow laden with sediments by incorporating the effect of secondary current through velocity distribution together with the stratification effect due to presence of sediments. The effect of particle-particle interaction at reference level and the effect of incipient motion probability, non-ceasing probability and pick-up probability of the sediment particles at reference concentration are taken into account. The proposed model is compared with the Rouse equation as well as verified with existing experimental data. Good agreement between computed value and experimental data indicates that secondary current influences the suspension of particles significantly. The direction and magnitude (strength) of secondary current lead to different patterns of concentration distribution and theoretical analysis shows that type II profile (where maximum concentration appears at significant height above channel bed surface) always corresponds to upward direction and greater magnitude of secondary current.

1 Introduction

Transportation of sediment particles in a turbulent flow through open-channels is of fundamental importance in hydraulics. The knowledge of suspension concentration distribution helps us to model sediment transport in river. Many theories have been used in the problem of vertical distribution of suspended sediment out of which advection-diffusion approach is the mostly considered one. The advection-diffusion theory points that the rate of upward transfer of suspended particles due to turbulent diffusion is balanced by downward settlement due to gravitational force.

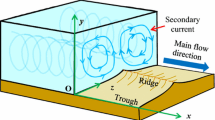
Open channel flow such as river flow often possesses lateral variation in bed topology forming sand ‘troughs’ and ‘ridges’. Sand ‘ridges’ are longitudinal bed forms that are aligned parallel to main flow direction [1] and are separated by sand ‘troughs’. This phenomenon has been widely observed in natural rivers [2] and deserts [3]. Researchers have observed that the occurrence of sand ‘troughs’ and ‘ridges’ are always associated with secondary current and in turn secondary current modifies bed forms [4–6]. Prandtl [7] mentioned that there are two types of secondary current in fluid flow. Secondary current of the first kind is produced from the main flow and driven by curvature effect [8]. Secondary current of the second kind is generated by turbulence and related to formation of sand ‘ridges’. In this study secondary current of the second kind is considered and its influence on concentration distribution is analyzed. Previous studies were only concerned about the change of velocity profile in open channels with the effect of secondary current [9–11]. Authors have proposed models to compute the SSCD [12–15] but did not consider the effect of secondary current in their models. Using the two-phase flow concept, Cao et al. [16] proposed a general(from Fick’s diffusion equation) diffusion equation and derived different explicit and independent models for SSCD depending on the choice of the eddy viscosity distribution. Although their model modifies Rouse equation, they did not consider the effect of secondary current on SSCD. Few works have been done incorporating the effect of secondary current on concentration distribution. From a semi-theoretical study, Chiu et al. [17] showed that secondary currents have significant effect on the distribution of suspended material. Later on, Yang [18] considered the effect of secondary current and proposed models for velocity and concentration distribution.

In this study we consider advection-diffusion equation which contains an additional mass flux term $Cv$ ($C$ is the mean volumetric sediment concentration and $v$ is the mean vertical velocity of the mixture). The necessity of the additional term $Cv$ in the governing equation for concentration distribution in open channel flow was realized long ago by different researchers [19, 20]. They pointed out that presence of sediment particles influences the upward velocity and suggested that the mass flux $Cv$ together with the sediment settling flux $C\omega$ (where $\omega$ is the settling velocity of sediment particles) should be balanced by turbulent diffusion. Fu et al. [21] also pointed out the necessity of the term $Cv$.

The existence of two types of concentration profiles was experimentally observed both in pipe and open-channel flow by several researchers [22–25]. These two types of profiles differ by the position of maximum sediment concentration from channel bed surface. Although different authors have defined these two types of profiles in different way, in this study we define type I profile to be that profile where the location of maximum sediment concentration is at the channel bed surface or in other words, sediment concentration gradually decreases from bed surface to the water surface and type II profile is defined where the location of maximum sediment concentration is significantly above the channel bed surface at some distance from channel bed or in other words, sediment concentration increases at first then begins to decrease when the height from the bed reaches a critical value. This phenomenon of location of maximum sediment concentration above the channel bed in the near-bed region cannot be explained by traditional gradient diffusion theory. Several research results show that near-bed hydraulic lift force on particle by surrounding fluid, particle fluctuating intensity, particle-particle collisions and viscous-turbulent interface effects are important for particle suspension in the near-bed region [25–28]. This study provides an attempt to describe different patterns of concentration distribution as an effect of secondary current generated by variation of bed texture.

Main objectives of this study are: (1) to analyze the effect of secondary current and stratification on distribution of suspended matters, (2) to develop a more general model for SSCD incorporating the influence of secondary current and stratification, (3) to provide a new explanation for the mechanism of two types of sediment concentration profiles.

2 Governing equation in three-dimensional sediment-laden flow

For a channel flow, the mass conservation equations of the solid phases can be written as follows after taking the Reynolds decomposition as

$$\begin{aligned} \frac{\partial C}{\partial t}+\frac{\partial (C u_s+\overline{C'u_s'})}{\partial x}+\frac{\partial (C v_s+\overline{C'v_s'})}{\partial y}+\frac{\partial (C w_s+\overline{C'w_s'})}{\partial z} = 0 \end{aligned}$$

(1)

where $t$ denotes time, $x$, $y$ and $z$ are longitudinal, vertical and lateral co-ordinates respectively, $u_s$, $v_s$ and $w_s$ are mean longitudinal, vertical and lateral velocities of the particle respectively with corresponding fluctuations $u_s'$, $v_s'$ and $w_s'$, $C$ is mean sediment concentration by volume and $C'$ is the fluctuation of sediment concentration. Under gravitational action a solid particle is considered to have an effective settling velocity $\omega$ (time-independent) in the vertical direction i.e., the vertical velocity $v_s$ of sediment particles is the sum of vertical velocity $v$ together with the fall velocity $-\omega$ of sediment particles [16, 29, 30]. Thus after taking time average, followings are obtained

$$\begin{aligned} v_s = v-\omega \quad \text{ and } \quad v_s'=v' \end{aligned}$$

(2)

In this study, a steady, uniform (along longitudinal $x$-direction) two dimensional (2D) turbulent open-channel flow with a bed slope angle $\theta$ (Fig. 1) is considered. In that case, the sediment concentration varies only in the $y$-direction perpendicular to the bed. Substitution of Eq. 2 into Eq. 1 gives the governing equation of sediment transport as follows

$$\begin{aligned} \frac{\partial (Cv+\overline{C'v'})}{\partial y} = \frac{\partial (C\omega )}{\partial y} \end{aligned}$$

(3)

Integration of Eq. 3 with respect to $y$ gives the governing equation for vertical distribution of sediment particles as

$$\begin{aligned} Cv+\overline{C'v'}-C\omega = 0 \end{aligned}$$

(4)

where the integration constant is determined as zero using the zero mass flux condition at the free surface. Equation 4 reverts to the conventional diffusion equation if one considers $v\approx 0$. In this study we consider Eq. 4 as the governing equation as it considers the effect of mean vertical velocity induced by secondary current. The importance of the term $Cv$ was realized by several researchers [19–21] where they pointed out that apart from settling flux and sediment diffusion, vertical velocity helps sediment particles to remain in suspension in the flow.

Fig. 1

Schematic diagram of uniform two-dimensional sediment-laden flow

Generally sediment diffusion can be expressed as

$$\begin{aligned} -\overline{C'v'} = \varepsilon _{s}\frac{dC}{dy} \end{aligned}$$

(5)

where $\varepsilon _{s}$ is the sediment diffusivity. Substituting Eq. 5 into Eq. 4 the governing equation for suspension concentration becomes

$$\begin{aligned} \varepsilon _{s}\frac{dC}{dy} = -C\omega +Cv \end{aligned}$$

(6)

Equation 6 is the diffusion equation. The second term on the right hand side (RHS) of Eq. 6 represents the effect of secondary current on suspension distribution in vertical direction. If $v=0$, Eq. 6 reduces to the conventional diffusion equation

$$\begin{aligned} \varepsilon _{s}\frac{dC}{dy} = -C\omega \end{aligned}$$

(7)

Generally Reynolds shear stress varies linearly over the flow depth in open channel flows. Yang [10] first pointed that in clear water flows, shear stress deviates from its linear profile in the outer region and accordingly he proposed a modification. Later on Yang [18] studied the effect of sediment concentration on turbulent characteristics and pointed out that the measured Reynolds shear stress in sediment-laden flows is systematically higher than that of clear water flows. The measured Reynolds shear stress for sediment-laden flows is plotted in Fig. 2 from experimental data of Muste and Patel [35], Cellino and Graf [36] and Muste et al. [37]. From the figure one can observe that there is no significant changes in the Reynolds stress distribution with the presence of sediment particles. Similar results were reported by Best et al. [38], Graf and Cellino [39], and Righetti and Romano [40]. Therefore in this study, linear variation of shear stress over the flow depth $h$ is considered. Under this assumption the governing equation for velocity becomes

$$\begin{aligned} \varepsilon _{f}\frac{du}{dy} = u_*^2\left( 1-\frac{y}{h}\right) \end{aligned}$$

(8)

where $u$ is the mean flow velocity in the main flow direction, $\varepsilon _f$ is the eddy diffusivity of the mixture and $u_*(=\sqrt{gJh})$ is the shear velocity in which $g$ is the gravitational acceleration and $J$ denotes channel slope.

Fig. 2

Reynolds shear stress distribution with sediment in open channel flows

Many researchers considered the effect of stratification due to concentration of suspended sediment, but most of them brought the stratification effect either through the variability of the von Karman coefficient or by introducing buoyancy term into the governing equation. Smith and McLean [41] first introduced the effect of sediment induced stratification through reduction in eddy diffusivity. In this study, following Smith and MeLean [41] and Herrmann and Madsen [42], eddy viscosity and sediment diffusivity in a stratified flow are expressed as

$$\begin{aligned} \varepsilon _{f} = \varepsilon _{fn}(1-\beta R_i) \\ \nonumber \varepsilon _{s} = \varepsilon _{sn}(1-\beta R_i) \end{aligned}$$

(9)

where $\varepsilon _{fn}$ and $\varepsilon _{sn}$ are the eddy diffusivity and sediment diffusivity under neutral condition (where the effect due to presence of suspended sediment is negligible) respectively, $\beta$ is the stratification correction parameter and $R_i$ denotes flux Richardson number. The stratification correction parameter $\beta$ is a constant and the value was found to be $4.7\pm 0.5$ by Businger et al. [43] from the data of Kansas experiment. Herrmann and Madsen [42] suggested the value of $\beta$ to be $4$. According to Monin and Yaglom [44] the flux Richardson number is defined as

$$\begin{aligned} R_i = -\frac{g(s_p-1)\varepsilon _s\frac{dC}{dy}}{\varepsilon _f\left( \frac{du}{dy}\right) ^2} \end{aligned}$$

(10)

where $s_p(=\rho _s/\rho _f)$ is the specific gravity of sediment and $u$ is the flow velocity in the main flow direction. Substitution of Eqs. 7–9 into Eq. 10 and after algebraic manipulation, the flux Richardson number can be expressed as

$$\begin{aligned} R_i = \frac{l \xi }{1-\xi +\beta l \xi } \end{aligned}$$

(11)

where $\xi =y/h$ is the dimensionless depth, $l=hL^{-1}$ is a parameter in which $L$ is the Monin–Obukov length scale which denotes the effect of buoyancy on turbulent flow [45] where $\kappa (=0.4)$ denotes the von Karman coefficient.

According to Reynolds analogy, under the neutral flow condition the sediment diffusivity coefficient $\varepsilon _{sn}$ is usually taken to be proportional to the fluid eddy viscosity $\varepsilon _{fn}$ as

$$\begin{aligned} \varepsilon _{sn} = \gamma \varepsilon _{fn} \end{aligned}$$

(12)

where $\gamma$ is the proportionality constant which is inverse of the turbulent Schmidt number. Several investigations regarding the variation of parameter $\gamma$ with various flow characteristics, bed forms, particle diameter, sediment quantity have been carried out so far. Carstens [46] discussed the value of $\gamma$ by analyzing measured data for the oscillatory motion of a spherical particle in fluid and obtained $\gamma \le 1$ for all experimental cases. Jobson and Sayre [47] reported experimental evidence that in an open channel flow $\gamma$ depends on turbulent characteristics and suggested possibilities of both $\gamma <1$ and $\gamma >1$. Einstein and Chien [33] suggested $\gamma >1$ by experimental data from flume and field measurements. In their experiments, Graf and Cellino [39] found that in suspension flow over a moveable bed without bed forms, $\gamma <1$ and for moveable bed with bed forms $\gamma >1$. Recently, Yoon and Kang [48] found that $\gamma$-value depends on sediment quantity and size. With higher sediment quantity, $\gamma$ increases; with higher sediment size $\gamma$ decreases. The above explanation indicates that $\gamma$ is not a universal constant and the value may be smaller, equal or greater than unity. Therefore in the present study the value of this parameter is calculated from experimental data.

To derive the suspension concentration profile, logarithmic velocity profile is generally used. Hunag et al. [49] showed that vertical gradient of suspended concentration is affected by bed roughness height $k_s$. The logarithmic profile for velocity distribution for rough wall is expressed as [50]

$$\begin{aligned} \frac{u}{u_*} = \frac{1}{\kappa }\ln \left( \frac{y}{k_s}\right) +B_s \end{aligned}$$

(13)

where $B_s$ is the constant which depends on bed roughness and expressed as $B_s = -2.5\ln (y_0/k_s)$ [50]. Here $y_0$ denotes the movable bed roughness height (hypothetical bed level). The disadvantage of Eq. 13 is that it loses its validity as $y\rightarrow 0$ in the near-bed viscous wall region, since $\ln (y/k_s)\rightarrow -\infty$ as $y\rightarrow 0$. Consequently, corresponding concentration profile derived using Eq. 13 shows an infinite sediment concentration in the near-bed region. But sediment concentration must be a finite quantity everywhere including the near-bed region. To overcome this drawback, a modification to Eq. 13 is needed. Therefore Jasmund-Nikuradse’s logarithmic velocity profile is used [51] which is given as

$$\begin{aligned} \frac{u}{u_*} = \frac{1}{\kappa }\ln \left( 1+\frac{y}{k_s}\right) \end{aligned}$$

(14)

where $k_s$ is the Nikuradse equivalent sand roughness. Using Boussinesq’s formula and Eq. 14, the sediment diffusion coefficient under neutral condition can be written as

$$\begin{aligned} \varepsilon _{sn} = \gamma \kappa u_* h \left( \xi +\frac{k_s}{h}\right) (1-\xi ) = \gamma \kappa u_* h(\xi +l_r)(1-\xi ) \end{aligned}$$

(15)

where $l_r=k_s/h$ ia a parameter related to bed roughness. Consequently sediment diffusivity can be expressed from Eqs. 9, 11 and 15 as

$$\begin{aligned} \varepsilon _{s} = \frac{\gamma \kappa u_* h(1-\xi )^2 (\xi +l_r)}{1-\xi +\beta l \xi } \end{aligned}$$

(16)

When sediment transport takes place as bed-load, due to movement of sediment particles on the bed surface, bed roughness varies. As the parameter $l_r$ is related to bed roughness, it is more reasonable to relate $l_r$ with the variable bed roughness $y_0$. Therefore one can further express $l_r$ as

$$\begin{aligned} l_r = \frac{k_s}{h} = \left( \frac{y_0}{h}\right) \Big / \left( \frac{y_0}{k_s}\right) \end{aligned}$$

(17)

The moveable bed roughness $y_0$ can be calculated from the formula proposed by Herrmann and Madsen [42] for neutral (N) and stratified (S) flow respectively as

$$\begin{aligned} (y_0)_N = \frac{d}{30}[4.5(\tau -\tau _*)+1.7]\pm 0.36 \end{aligned}$$

(18)

and

$$\begin{aligned} (y_0)_S = \frac{d}{30}[7.4(\tau -\tau _*)+1.6]\pm 0.29 \end{aligned}$$

(19)

where $d$ is the particle diameter, $\tau =u_*^2/[(s_p-1)gd]$ is the Shields Parameter and $\tau _*$ is the critical Shields Parameter. The critical Shields Parameter is calculated from the formula proposed by Soulsby [52] as

$$\begin{aligned} \tau _* = 0.095S_*^{-2/3}+0.056\left[ 1-\exp \left( -\frac{S_*^{3/4}}{20}\right) \right] \end{aligned}$$

(20)

where $S_*=\frac{d\sqrt{(s_p-1)gd}}{4\nu _f}$ is the fluid-sediment parameter in which $\nu _f$ is the kinematic viscosity of fluid.

From the experimental data of Nikuradse [53], Jan et al. [54] proposed various relations to calculate $y_0/k_s$ depending on the parameter $Re_*$ which are given as follows

$$\begin{aligned}&\displaystyle \frac{y_0}{k_s} = \frac{0.11}{Re_*}, \quad Re_*\le 4\end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \frac{y_0}{k_s} = 0.0275-0.007\sqrt{\sin \left( \frac{Re_*-4}{14}\right) \pi }, \quad 4<Re_*\le 11\end{aligned}$$

(22)

$$\begin{aligned}&\displaystyle \frac{y_0}{k_s} = 0.0205+\frac{0.0125}{\sqrt{2}}\sqrt{1+\sin \left( \frac{Re_*-40.5}{59}\right) \pi }, \quad 11<Re_*<70\end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle \frac{y_0}{k_s} = 0.033, \quad Re_*\ge 70 \end{aligned}$$

(24)

where $Re_* = \frac{u_* k_s}{\nu _f}$ is the roughness Reynolds number.

2.1 Mean vertical velocity induced by secondary current

The existence of secondary current in laboratory and field measurements was reported a century ago [55]. From various experimental investigations it is found that both in narrow (where the aspect ratio i.e. the ratio of channel width to flow depth is less than $5$) and wide open channels, secondary current is generated by side wall effect, free surface effect and variation of bed topology [56]. When the flow starts, sediment particles start moving with flow and due to lateral transport of sediment particles, ‘ridges’ and ‘troughs’ are made along longitudinal direction (parallel to main flow direction) in an alternative manner (in lateral direction, see Fig. 3) which in turn influences the secondary current. This indicates that there is a relation between bedforms and secondary current. Experiments of Wang and Cheng [6] help us to find the distribution of vertical velocity generated in the flow from secondary currents. They showed that secondary current appears as paired-cells in the cross-sectional plane in a cellular fashion. From the pattern of vertical velocity it is found that at the channel bed vertical velocity is zero and initially it increases and reaches to a maximum value and after that it begins to decrease towards the free surface with a zero vertical velocity at free surface [6]. This phenomenon suggests that this type of distribution can be modeled using the boundary condition $v = 0$ at $y = 0$ and $y = h$. Following Yang [57] the vertical velocity profile can be described as

$$\begin{aligned} \frac{v}{u_*} = \alpha \kappa \xi ^{m}(1-\xi )^{p} \end{aligned}$$

(25)

where $m$ and $p$ are exponents which depends on channel geometry such as aspect ratio, roughness etc. to be determined from experimental data and $\alpha$ is a parameter. Variation of vertical velocity for different values of parameters $m$ and $p$ are plotted in Fig. 4 with the value of parameters $\alpha = 0.5$. From Fig. 4, one can observe that the magnitude of vertical velocity decreases with increase of value of parameter $m$ or $p$. Experimental data from Wang and Cheng’s [6] (test case S$75$) at different distances from side wall are plotted in Fig. 5 together with Eq. 25 with values of parameters $\alpha = 2$, $m = 1$ and $p = 1$; and $\alpha = -1.88$, $m=1$ and $p=1$ for upward and downward direction of vertical velocity respectively. In the figure, $\lambda$ denotes the width of secondary cell. The value of shear velocity $u_*$ is calculated as $u_* = \sqrt{gJh}$. From Fig. 5, one can observe that Eq. 25 predicts the measured data well and mean vertical velocity may be positive/upward or negative/downward corresponding to $\alpha >0$ or $<0$ respectively. Experimental data of Ohmoto et al. [31] is plotted in Fig. 6 which also validate this conclusion where they found both upward and downward vertical velocity as secondary current appears in a cellular fashion. The value of the parameters are taken as: $\alpha = 0.35$, $m = 1.3$ and $p = 1.2$, and $\alpha = -0.14$, $m=1.2$ and $p=0.8$ for upward and downward direction of vertical velocity respectively. From Fig. 6 one can observe that maximum magnitude of downward vertical velocity appears near the free surface and it gradually decreases towards free surface. The proposed equation i.e., Eq. 25 predicts this downward velocity up to $70\,\%$ of the total flow depth and near the free surface it deviates from experimental data. From the comparisons one can conclude that the parameter $\alpha$ may be greater, equal or less than zero according to the direction of vertical velocity in upward, parallel to lateral direction or downward respectively (see Fig. 3). Also from the examples it is observed that value of parameters $m$ and $p$ is either one or varies around one.

Fig. 3

Direction of secondary current and different patterns of concentration distribution

Fig. 4

Variation of vertical velocity $v$ for different values of parameters $m$ and $p$

Fig. 5

Verification of Eq. 25 with experimental data from Wang and Cheng [6]

Fig. 6

Mean vertical velocity profile (experimental data from Ohmoto et al. [31])

Theoretically $m$ and $p$ can be determined. For simplicity it is assumed that shape of secondary cells appears to be symmetric with respect to its circulation center, which locates at the middle of the flow depth above the interface of rough and smooth strips. Under this assumption mean vertical velocity can be expressed as [6]

$$\begin{aligned} \frac{v}{u_*} = - \frac{v_{max}}{u_*}\sin (\pi \xi )\cos \left( \pi \frac{b-z}{\lambda }\right) \end{aligned}$$

(26)

where $b$ is the width of the channel. According to Yang et al. [58], parameter $\alpha$ changes in lateral direction and can be expressed as

$$\begin{aligned} \alpha = m_1\alpha _0 \eta _*^{m_1-1}\left( 1-\frac{m_1+1}{m_1}\eta _*\right) \end{aligned}$$

(27)

where $m_1 = \lambda _1/(\lambda -\lambda _1)$, $\alpha _0$ denotes the strength of secondary current [58], $\lambda _1$ is the half width of rough strip and $\eta _* = (b-z)/\lambda$. Substituting Eq. 27 into Eq. 25 and at the central section vertical velocity can be expressed as

$$\begin{aligned} \frac{v}{u_*} = m_1 \alpha _0 \kappa \left( \frac{b}{2\lambda }\right) ^{m_1-1}\left[ 1-\frac{m_1+1}{m_1}\frac{b}{2\lambda }\right] \xi ^m(1-\xi )^p \end{aligned}$$

(28)

Similarly from Eq. 26, using the approximation $\sin (\pi \xi ) \thickapprox 4\xi (1-\xi )$, in the region $0\leqslant \pi \xi \leqslant \pi$ one obtains

$$\begin{aligned} \frac{v}{u_*} \thickapprox - 4\frac{v_{max}}{u_*} \cos \left( \frac{\pi b}{2\lambda }\right) \xi (1-\xi ) \end{aligned}$$

(29)

Comparing Eqs. 28 and 29 as a first approximation one gets

$$\begin{aligned} m = p = 1 \end{aligned}$$

(30)

and

$$\begin{aligned} \alpha _0 = - \frac{m_1 \kappa \left( \frac{b}{2\lambda }\right) ^{m_1-1}\left[ 1-\frac{m_1+1}{m_1}\frac{b}{2\lambda }\right] }{4\frac{v_{max}}{u_*} \cos \left( \frac{\pi b}{2\lambda }\right) } \end{aligned}$$

(31)

Therefore from both theoretical and experimental considerations, the case of $m=p=1$ is considered in this study. In general, substitution of Eq. 25 into the governing equation Eq. 4 gives the sediment concentration distribution equation for different values of $m$ and $p$.

3 Solution of concentration distribution equation

Substitution of Eqs. 5, 9 and 25 into Eq. 4 gives the sediment concentration distribution equation as

$$\begin{aligned} \frac{1}{C}\frac{dC}{d\xi } = \left[ \frac{-\omega }{\varepsilon _{sn}/h}+\frac{v}{\varepsilon _{sn}/h}\right] \Big /(1-\beta R_i) \end{aligned}$$

(32)

Substituting Eqs. 11 and 15 into Eq. 32 one obtains

$$\begin{aligned} \!\!\frac{1}{C}\frac{dC}{d\xi } {=} -\frac{\omega }{\kappa \gamma u_*(\xi +l_r)(1-\xi )}{+}\frac{\alpha \xi }{ \gamma (\xi +l_r)}+\beta l \left( \frac{\xi }{1-\xi }\right) \left[ \frac{-\omega +\alpha u_* \xi (1-\xi )}{\kappa \gamma u_*(\xi +l_r)(1-\xi )}\right] \end{aligned}$$

(33)

In this equation, second term on right hand side (RHS) denotes the effect of secondary current on concentration distribution and the third term considers the effect of stratification. Integration of Eq. 32 between the reference level $\xi _a$ to $\xi$ gives the sediment concentration distribution equation as

$$\begin{aligned} \frac{C}{C_a} = \underbrace{\left( \frac{1{-}\xi }{\xi +l_r}\frac{\xi _a{+}l_r}{1{-}\xi _a}\right) ^{Z_1}}_{\text{ Rouse } \text{ function }}\underbrace{\left( \frac{1{-}\xi _a}{1-\xi }\right) ^{Z_2\beta l}\exp \left[ \left\{ Z_2(1{-}\beta l){-}\frac{Z_1 \beta l}{(1{-}\xi )(1{-}\xi _a)}\right\} (\xi -\xi _a)\right] }_{\text{ Extra } \text{ terms }} \end{aligned}$$

(34)

where the following approximations are used for smaller values of $l_r$ as

$$\begin{aligned} \int \limits _{\xi _a}^{\xi }\frac{1}{(\xi +l_r)(1-\xi )}d\xi \approx \ln \left( \frac{\xi +l_r}{1-\xi }\frac{1-\xi _a}{\xi _a+l_r}\right) \end{aligned}$$

(35)

and

$$\begin{aligned} \int \limits _{\xi _a}^{\xi }\frac{\xi }{\xi +l_r}d\xi \approx \xi -\xi _a \end{aligned}$$

(36)

The parameter $Z_1 = \omega /(\kappa \gamma u_*)$ is the Rouse number, $Z_2 = \alpha S_c$ is a parameter that considers the effect of secondary current and $S_c$ is the Schmidt number, $\xi _a$ and $C_a$ denote the reference level and reference concentration respectively. The calculation of reference level and reference concentration is discussed later in Sects. 3.2 and 3.3 respectively. From Eq. 34 one can observe that first term on the RHS is the Rouse function when $l_r\approx 0$, and the extra terms occur from the consideration of the effect of secondary current and sediment induced stratification. Here the parameter $\beta$ denotes the effect of stratification and the terms containing both the parameters $\beta$ and $Z_2$ denote the combined effect of secondary current and stratification.

To show the effects of stratification and secondary currents on concentration profile, examples are considered. The results corresponding to the effect of stratification is shown in Fig. 7 where the values of the parameters are kept as: $\beta = 0$(neutral case) and $4$(stratified case), $Z_1 = 0.9$, $Z_2 = 1.5$, $\xi _a = 0.005$, $l_r = 0.006$. Figure clearly indicates that stratification causes a decrease in sediment concentration compared to the neutral case. This causes because stratification decreases the sediment diffusivity $\varepsilon _s$ by the factor $1-\beta R_i$ as expressed by Eq. 9(as $R_i>0$ and $\beta >0$), which leads to a decrease in concentration. One can rewrite Eq. 34 as

$$\begin{aligned} \frac{C}{C_a} = \frac{\displaystyle \left( \frac{1-\xi }{\xi +l_r}\frac{\xi _a+l_r}{1-\xi _a}\right) ^{Z_1}\exp [Z_2(\xi -\xi _a)]}{\displaystyle \left( \frac{1-\xi }{1-\xi _a}\right) ^{Z_2\beta l}\exp \left[ \beta l \left\{ Z_2+\frac{Z_1}{(1-\xi )(1-\xi _a)}\right\} (\xi -\xi _a)\right] }=\frac{C_N}{F_s(\xi )} \end{aligned}$$

(37)

where $C_N$ denotes the sediment concentration at neutral nonstratified condition and function $F_s(\xi )$ denotes the effect of stratification which can be expressed as

$$\begin{aligned} F_s(\xi ) = \frac{(1-\xi )^{Z_2 \beta l} \exp \left[ \beta l \left\{ Z_2 \xi +\frac{Z_1}{1-\xi }\right\} \right] }{(1-\xi _a)^{Z_2 \beta l} \exp \left[ \beta l \left\{ Z_2 \xi _a+\frac{Z_1}{1-\xi _a}\right\} \right] }\ge 1 \quad \text{ for } \quad 1>\xi \ge \xi _a \end{aligned}$$

(38)

Equations 37 and 38 clearly indicate that stratification results in a decrease in concentration compared with neutral nonstratified flow as $C\le C_N$.

Fig. 7

Concentration profiles for neutral and stratified uniform sediment-laden flow. a Concentration, b difference between neutral and stratified concentration. Input values: $Z_1 = 0.9,\, Z_2 = 1.5,\, \xi _a = 0.005,\, l_r = 0.006$

Similarly to show the effect of secondary current on concentration distribution, curves are plotted in Fig. 8 with $Z_1=1.65$, $l = 0.01$, $l_r=7\times 10^{-3}$, $\xi _a=0.005$, $C_a=0.002$, $\gamma =0.2$ and for seven different values of parameter $\alpha$. Here we assume that magnitude of upward vertical velocity is smaller compared to the particle settling velocity which otherwise leads to inverse variation of sediment concentration in the near-bed region (discussed in Sect. 5). The value of parameter $\alpha$ has the range from $-0.3$ to $0.3$ which is consistent with obtained value from experimental results in Table 1 where $\alpha$ varies between $-1.7$ and $0.32$. This variation of parameter $\alpha$ can be attributed to the strength of secondary current and from Eq. 27 one can observe that $\alpha$ varies in lateral $z$-direction. Conclusion of Eq. 27 is consistent with the configuration of Fig. 3 where one can obtain a negligible effect of secondary current at the section 1–1 where $\alpha =0$ and between the section 1–1 and 2–2 the value of parameter $\alpha$ gradually decreases as the direction of secondary current is vertically downward. Similarly between section 2–2 and 3–3 the value gradually increases and approaches to a maximum value at the section 3–3. Therefore how much secondary current one expects for different values of parameter $\alpha$ depends on the location of the section in lateral direction. From Fig. 8 one can observe that sediment concentration increases with the increase of magnitude of upward vertical velocity, this occurs as more sediment particles come to suspension from bed surface and due to upward vertical velocity net settlement of sediment is smaller; and it decreases with increase of magnitude of downward vertical velocity as sediment particles gravitate to the bed surface due to additional mass flux in vertically downward direction. Therefore high sediment flow (which is known as ‘line of boil’) occurs over sand ridges where secondary velocity is upward and less sediment flow occurs over sand troughs where secondary current is downward. This clearly indicates why Coleman [59] observed longitudinal boil lines in Brahmaputra River. Figures 7 and 8 suggest that both secondary current and stratification has significant effect on suspended concentration distribution. The advantages of Eq. 34 are it reverts to Rouse equation if one considers $Z_2=0$, $\beta =0$ and $l_r\approx 0$; and it reverts to an equation proposed by Ghoshal and Kundu [60] if $\beta =0$. Although Rouse equation is good enough but it cannot be extrapolated to the bed surface where $\xi$ approaches to zero as it possess an infinite concentration at bed surface layer; whereas the proposed model possess a finite concentration at bed surface level which demonstrates the superiority of the proposed model.

Table 1 Detailed flow characteristics for selected test cases ($^*$ denotes minimum error)

Fig. 8

Effect of vertical velocity(or secondary current) on concentration profile. a Vertical velocity upward, b vertical velocity downward

To compute sediment concentration distribution from the above proposed formula the value of the parameters: particle settling velocity $\omega$; reference level $\xi _a$; and reference concentration $C_a$ should be known. The formulae for calculating these parameters are discussed in the following sections.

3.1 Particle settling velocity

The sediment settling velocity $\omega$ is an important parameter in determination of suspended concentration profile and it depends on the sediment and flow parameters. Based on the relationship between Reynolds number and the dimensionless particle diameter, Zhiyao et al. [61] proposed a formula for calculating the settling velocity of natural sediment particle. They compared the formula with several existing formulas in literature and found that this formula has higher prediction accuracy than other published formulas and it is applicable to all Reynolds numbers less than $2 \times 10^5$. Therefore settling velocity of the sediment particles is calculated from the formula given by Zhiyao et al. [61] as

$$\begin{aligned} \omega = \frac{\nu _f}{d}d_*^3(38.1+0.93d_*^{12/7})^{-7/8} \end{aligned}$$

(39)

where $d_*$ is the dimensionless sediment particle diameter defined as $d_* \!=\! [\{(s_p-1) g\}/\nu _f^2]^{1/3}d$. It is important to mention herein that hindered effect due to inter particle collisions on settling velocity has not been considered in this section. Particle-particle interaction is mainly important in the near-bed region. As a result the near-bed suspension profile is affected by interactions effects and suspension profile other than the near-bed region is less affected by interaction effects. The effect of particle-particle interaction on settling velocity and on concentration distribution is discussed in detail in Sect. 5.

3.2 Bed-load layer thickness

The reference level denotes the thickness of the bed-load layer or in other words, it is taken as the common boundary of bed-load and suspended-load layer. In literature, authors have provided many formulae to calculate the reference level where reference level is related to specific gravity $s_p$ of sand particles, dimensionless shear stress $\tau [= u_*^2/\{(s_p-1) g d\}]$ and nature of bed. A brief literature survey can be found in Sun et al. [62]. Since the reference level is measured very near to channel bed, near-bed flow characteristics such as particle-particle interactions has to be considered. Including particle-particle collision effect Cheng [63] proposed an analytical model for computing reference level which we have considered in this study. The formula is given by

$$\begin{aligned} \xi _a = \frac{\tau d d_*^3}{h\left( \sqrt{25+1.2d_*^2}-5\right) ^{1.5}} \int \limits _{0}^{C_m}\frac{\lambda _2}{C(C^{-1/3}-1)^2 \mu _r \omega _r}dC \end{aligned}$$

(40)

where $C_m$ is the maximum concentration, $\lambda _2$ is a parameter varies from $0.005$ to $0.5$, $\mu _r$ and $\omega _r$ are relative viscosity and relative settling velocity of sediment particles respectively which are as follows [63]

$$\begin{aligned} \mu _r = \exp \left[ \frac{2.5}{\beta _1}\left\{ \frac{1}{(1-C)^{\beta _1}}-1\right\} \right] \end{aligned}$$

(41)

and

$$\begin{aligned} \omega _r = \frac{\mu _r}{1+(s_p-1)C}\left( \frac{\sqrt{25+1.2d_*^2(1-C)^{2/3}[1+(s_p-1)C]^{2/3}\mu _r^{-4/3}}-5}{\sqrt{25+1.2d_*^2}-5}\right) ^{1.5} \end{aligned}$$

(42)

where value of parameters $\beta _1$ and $C_m$ are taken as $2.5$ and $0.6$ as mentioned by Cheng [63].

3.3 Reference concentration $C_a$

Reference concentration $C_a$ is the value of sediment concentration at reference level $\xi _a$. It is assumed that the bed load transport takes place in the bed-load layer and in this layer, there is a constant sediment concentration $C_a$. Therefore reference concentration is taken as the concentration at the top of the bed-load layer. It can be calculated from the entrainment function defined at the bed surface. Many formulae are available in literature to compute reference concentration [42, 62, 64, 65]. In this study the formula proposed by Sun et al. [62] is used as it considers three basic probabilities: incipient motion probability, non-ceasing probability and pick-up probability of the sediment particle. The reference concentration is given by

$$\begin{aligned} C_a = M_0 P_0 \frac{F(\cdot )}{1+F(\cdot )} \end{aligned}$$

(43)

where $M_0$ denotes the density coefficient of bed material, $P_0$ denotes the grain size class percentage of bed material and equal to unity for uniform sediments and the function $F(\cdot )$ is expressed as

$$\begin{aligned} F(\cdot ) = \frac{10^{-5} \tau ^2 d_*^{1.84}\alpha _n \lambda _n}{(1-\gamma _n)(1-\lambda _n)(1+\gamma _n \lambda _n)} \end{aligned}$$

(44)

where $\alpha _n,\, \gamma _n$ and $\lambda _n$ are incipient motion probability, non-ceasing probability and pick-up probability of sediment particles which are given by

$$\begin{aligned} \alpha _n = 1-\frac{1}{\sqrt{2 \pi }}\int \limits _{-2.7(\sqrt{0.0822/\tau }+1)}^{2.7(\sqrt{0.0822/\tau }-1)}e^{-x^2/2}dx\end{aligned}$$

(45)

$$\begin{aligned} \gamma _n = 1-\frac{1}{\sqrt{2 \pi }}\int \limits _{-2.7(\sqrt{0.0571/\tau }+1)}^{2.7(\sqrt{0.0571/\tau }-1)}e^{-x^2/2}dx\end{aligned}$$

(46)

$$\begin{aligned} \lambda _n = \frac{2}{\sqrt{2 \pi }}\int \limits _{\omega /u_*}^{\infty }e^{-x^2/2}dx \end{aligned}$$

(47)

respectively.

Reference level and reference concentration are calculated from Eqs. 40 and 43 respectively.

4 Comparison of model and experimental data

To validate the proposed model in this study, existing laboratory experimental data have been used. As in this study the effect of secondary current is considered, therefore it is necessary to consider those experimental data in which the effect of secondary current is present. Therefore experimental data of Coleman [32], Einstein and Chien [33] and Wang and Qian [34] have been used. The following test cases (or RUN) have been selected to verify the model: test cases 7, 13, 25, 30, 36 and 40 from Coleman [32]; test cases S5, S10, S12, S14, S15 and S16 from Einstein and Chien [33]; and test cases SQ1, SQ2 and SQ3 from Wang and Qian [34]. In all the selected test cases aspect ratio has the range from $2.08$ to $3.75$ and maximum volumetric sediment concentration varies from $0.027$ to $23.32\,\%$. Detail flow characteristics are shown in Table 1.

Figure 9 compares the proposed model with the experimental data of Coleman [32]. The experiments were carries out in a $15$ m long smooth flume. The flow conditions i.e. $h\approx 1.69$ mm, $b = 356$ mm, $J = 0.002$, $u_*=0.041$ m/s were kept same for all test cases. The aspect ratios are small and has the range from $2.046$ to $2.132$ including all test cases. This clearly indicates that secondary currents exists. Sediment concentration gradually increases in different test cases and reaches high values (up to $625$ kg/m$^3$) in some test cases which indicates that large density gradient was present in the experiment. Therefore this is an ideal data set to verify the proposed model for the present study. To compare the proposed model with Rouse equation and Coleman’s [32] data, selected test cases are plotted in Fig. 9. All test cases are plotted in a semilog graph paper to show the results clearly. In all the cases, the parameters in Rouse equation are calculated in the following way: settling velocity is calculated from Eq. 39, $\kappa = 0.4$ and $u_*$ is taken from experimental data and the proportionality parameter is calculated from experimental data by minimizing $S_1$ the sum of the residuals i.e., solving $\partial S_1/\partial \gamma =0$ where $S_1$ is expressed as

$$\begin{aligned} S_1 = \sum _{i=1}^n \left[ \gamma \ln \left( \frac{C_i}{C_a}\right) -\frac{\omega }{\kappa u_*}\ln \left( \frac{1-\xi _i}{\xi _i}\frac{\xi _a}{1-\xi _a}\right) \right] ^2 \end{aligned}$$

(48)

where $n$ is total number of data points $(\xi _i,C_i)$. $\partial S_1/\partial \gamma =0$ implies that

$$\begin{aligned} \gamma = \frac{\omega }{\kappa u_*}\frac{\sum _{i=1}^n \ln \left( \frac{1-\xi _i}{\xi _i}\frac{\xi _a}{1-\xi _a}\right) \ln \left( \frac{C_i}{C_a}\right) }{\sum _{i=1}^n\left\{ \ln \left( \frac{C_i}{C_a}\right) \right\} ^2} \end{aligned}$$

(49)

A MATLAB programme has been written to compute the value of $\gamma$. The Rouse equation is plotted as a best fitting line with the experimental data. The proposed model consists of only two free parameters $\gamma$ and $\alpha$ which are calculated using least square method by minimizing the sum of residuals. From the figure it can be observed that Rouse equation predicts concentration well but in the near surface region it deviates from data points where effect of secondary current is present. Also one can observe from Fig. 9 that proposed model significantly improves Rouse equation and gives more accurate prediction of suspended concentration throughout the flow depth. It is important to mention herein that proposed model slightly deviates from experimental data near the free surface in RUN 25, 30, 36 and 40 in Fig. 9. This deviation can be attributed to the deviation of vertical velocity profile near the free surface. In this study we have assumed as a first approximation that $m=p=1$ i.e. vertical velocity follows a parabolic type profile. Under this consideration maximum magnitude of vertical velocity occurs at $y/h=0.5$. From Ohmoto et al. [31] experimental data one can observe that maximum magnitude occurs at $y/h=0.85$ for downward velocity profile. Also in RUN 25 and 30 Rouse profile provides a better prediction at the free surface as the ‘Extra terms’ presents in the proposed model decreases the concentration near the free surface as $\xi$ approaches to one. But throughout the flow depth proposed model gives better result than Rouse profile.

Fig. 9

Comparison of proposed model with experimental data of Coleman [32]. Circles denote Coleman’s [32] experimental data, dash doted lines denote Rouse profile and continuous lines denote proposed model

Similarly the data set of Einstein and Chien [33] has been used for the verification of the proposed model. The experiments were carried out in a $0.3$ m wide channel. Characteristics of the flow and natural sediments are shown in Table 1 for selected test cases. The mean size of sediment were $1.3$ mm for run S$5$, $0.94$ mm for run S$10$, and $0.274$ mm for runs S$12$, S$14$, S$15$ and S$16$. The aspect ratio has the range from $2.273$ to $2.727$. Figure 10 shows that comparison of the proposed model with experimental data of Einstein and Chien [33] together with the Rouse equation. The parameters present in Rouse equation and parameters in proposed model were calculated similarly as mentioned earlier. From the figure one can observe that Rouse equation predicts suspended sediment concentration up to $20\,\%$ of the flow depth from channel bed whereas proposed model predicts the concentration well throughout the flow depth.

Fig. 10

Comparison of proposed model with experimental data of Einstein and Chien [33]. Squares denote Einstein and Chien’s [33] experimental data, dash doted lines denote Rouse profile and continuous lines denote proposed model

Wang and Qian’s [34] experimental data with natural sand particles have been used to verify the proposed model. The experiments were conducted in a recirculating, tilting flume $20$ m long, $30$ cm wide, and $40$ cm high and the bed slope was $J = 0.01$. The aspect ratio is $3.75$ for all selected test cases. Other flow characteristics are shown in Table 1. Figure 11 shows the comparison between computed and observed concentration profiles together with the Rouse equation. From the figure one can observe that Rouse profile predicts concentration well in the near-bed region and it deviates in the outer region. The deviation gradually increases with the increase of height from bed as the effect of secondary current is more in the outer region than in the inner region. The proposed model predicts sediment concentration well throughout the flow depth as this includes the effect of secondary current. This indicates that Rouse equation can be significantly modified by proposed model where the presence of secondary circulation and density stratification effects are included.

Fig. 11

Comparison of proposed model with experimental data of Wang and Qian [34]. Crosses denote Wang and Qian’s [34] experimental data, dash doted lines denote Rouse profile and continuous lines denote proposed model

4.1 Error analysis

To get an quantitative idea about the accuracy of the fitting between computed and observed values, the weighted relative errors $E$ were calculated from the formula

$$\begin{aligned} E = \sqrt{\sum \frac{(S_c-S_0)^2}{S_0T}} \end{aligned}$$

(50)

where $S_c$ and $S_0$ are computed and observed values of suspended concentration at various height in weight percentage and $T$ denotes the total value observed which is equal to $100$. In Eq. 50, the sum is performed over all available data points throughout the flow depth. The value of errors (for all selected test cases) corresponding to the Rouse equation and the proposed model has been calculated and shown in Table 1 where $E_R$ and $E_1$ denote errors corresponding to the Rouse equation and the proposed model respectively. From the table it can be observed that minimum error corresponds to the proposed model which indicates that Rouse equation can be significantly improved by proposed model including the effects of secondary current and density gradient using flux Richardson number. From Table 1 it can also be observed that the value of parameter $\alpha$ may be positive or negative.

5 Mechanism of different profiles of sediment concentration

Two types of vertical suspension profiles of sediment particles are observed by researchers [22–25]. The commonly occurred profile is the type I profile. The occurrence of type II profile can be described from the view point of secondary current considered in this present study. Secondary current helps to put sediment particles in suspension after their ejection from bed surface due to fluid uplift force. For steady, uniform and one dimensional (in vertical $y$-direction) case, transport equation can be written from Eqs. 3 and 5 as

$$\begin{aligned} \left( \frac{\varepsilon _s}{h}\right) \frac{d C}{d\xi } = C(v-\omega ) \end{aligned}$$

(51)

In this Eq. 51, the fall velocity $\omega$ and the sediment diffusivity $\varepsilon _s$ are always positive. But the vertical velocity may be positive, zero or negative. Figure 3 presents the occurrence of secondary currents (in paired-cells) in a cross sectional plane over the bed forms. From the figure it can be observed that the upward vertical velocity occurs above the bed ridges (along line 3–3) whereas downward vertical velocity always corresponds to the bed troughs (along line 2–2). This shows that the vertical velocity is always negative along the 2–2 line and it is always positive along 3–3 line and along line 1–1, vertical velocity is directed to lateral direction and therefore $v=0$ can be considered. It can be observed from Eq. 51 that when $v=0$ i.e. along 1–1 profile in Fig. 3, Rouse equation can be obtained which indicates that in that case $dC/dy<0$ throughout the flow depth and type I profile always occurs. When $v<0$ (along 2–2 profile in Fig. 3) or direction of secondary flow is downward, from Eq. 51 we have $dC/dy<0$ throughout the depth i.e., sediment concentration systematically decreases with height from its maximum value at the channel bed and the type I profile is obtained. Alternatively when $v>0$ (along 3–3 profile in Fig. 3) or direction of secondary flow is upward, from Eq. 51 we have $dC/dy<0$ when $v-\omega <0$ and $dC/dy>0$ when $v-\omega >0$ over the flow depth i.e., the concentration gradient $dC/dy$ changes its sign accordingly the function $v-\omega$ changes its sign. In the former case magnitude of secondary current is small compared to settling velocity of particles throughout the flow depth and therefore type I profile is obtained and in the latter case magnitude of secondary current is larger compared to the settling velocity and type II profile is obtained. In real flow situations, the settling velocity decreases with the increase of sediment concentration which is often described by Richardson and Zaki’s [66] formula. Therefore with increase of distance from channel bed, both vertical velocity and settling velocity increases and if $v>\omega$, concentration gradient increases with height. After a certain height, when upward vertical velocity balances settling velocity i.e., $v=\omega$ then concentration reaches to a maximum value and thereafter if $v<\omega$, concentration gradient decreases with height and type II profile is formed.

As the type II profile is limited in the near-bed region, it is more appropriate to consider the hindering effect due to concentration and particle size in the settling velocity of particles. Experimental data shows that settling velocity is smaller at higher concentrations and can be described by Richardson and Zaki’s [66] formula as

$$\begin{aligned} \omega = \omega _0 \left( 1-\frac{C}{C_{max}}\right) ^n \end{aligned}$$

(52)

where $\omega _0$ is particle settling velocity in clear water, $n$ is an exponent and its value varies from $4.65$ to $2.4$ with increase of particle Reynolds number. As concentration depends on depth $y$, following Absi [67], one can write settling velocity as a $y$ dependent function as

$$\begin{aligned} \omega = \omega _0 \phi (\xi ) \end{aligned}$$

(53)

where $\phi = 1$ at the free surface and decreases to zero at channel bed. In this study we assumed that $\omega = \omega _0$, so in this case $\phi (\xi ) = 1$. The inverse variation of sediment concentration in the near-bed region could be attributed to the behavior of the function $\phi$ and vertical velocity. Therefore to evaluate the function $\phi$, experimental data from Bouvard and Petkovic’s [22] experiment is used. The data for function $\phi$ is obtained from

$$\begin{aligned} \phi (\xi )|_{data} = \frac{\omega }{\omega _0}\Big |_{data} = \left( 1-\frac{C}{C_{max}}\right) ^n\Big |_{data} \end{aligned}$$

(54)

Experimental data obtained from Eq. 54 are plotted in Fig. 12. The value of the parameter $n$ is kept as $4.65$. It can be observed that a polynomial function can be fitted with the data points. Therefore settling velocity in the near-bed region could be written as a function of $y$ as

$$\begin{aligned} \omega = \omega _0 \xi ^2(2-\xi )^2 \end{aligned}$$

(55)

The variation of settling velocity with vertical distance $\xi$ is plotted in Fig. 13a together with vertical velocity for different values of parameter $\alpha$. It can be observed that both vertical velocity and settling velocity increase with $\xi$ in the near-bed region. In the region $0\le \xi \le 0.2$, the magnitude of settling velocity is greater compared to the magnitude of secondary current when $\alpha =0.1$ and the magnitude of secondary current increases with increase of parameter $\alpha$ which is shown in the subplot inside Fig. 13a. This indicates that for $\alpha =0.1$, we have $v<\omega$ and therefore $dC/dy<0$ throughout the flow depth and type I profile is obtained. With increase of parameter $\alpha$, $v>\omega$ in the near-bed region $0\le \xi \le \xi _{max}$ and $v<\omega$ in the region $\xi _{max} \le \xi \le 1$ where $\xi _{max}$ denotes the location of maximum concentration from bed. Therefore in the former region $dC/dy>0$ and in the latter region $dC/dy<0$ i.e. initially concentration gradient increases with $\xi$ and then begins to decrease and thus type II profile is obtained in such situations. Similarly the variation of concentration gradient with depth is related to the variation of the function $\Psi = v-\omega$ in the flow. From Eqs. 25 and 55 we can write the function $\Psi$ as

$$\begin{aligned} \Psi (\xi ,\alpha ,m,n,d) = \alpha \kappa u_* \xi ^m (1-\xi )^n-\omega _0 \xi ^2(2-\xi )^2 \end{aligned}$$

(56)

From this equation it can be observed that the value of the function depends on the strength of secondary current $\alpha$, particle diameter $d$ and parameters $m$ and $n$.

Fig. 12

Prediction of the damping function $\phi$ (data taken from Bouvard and Patkovic [22])

Fig. 13

a Variation of vertical velocity and hindered settling velocity with height for different strength of secondary current, and b variation of the function $\Psi$ with height

To demonstrate the variation of concentration gradient with vertical distance more clearly, an example is considered. The function $\Psi$ is plotted for $m = n = 1$, $d = 9$ mm and for six different values of parameter $\alpha$. This value of particle diameter corresponds to typical laboratory conditions (observed in Bouvard and Petkovic’s [22] experiment). The results are shown in Fig. 13b. From the figure it can be observed that for $\alpha = 0.1$, $\Psi <0$ throughout the flow depth (type I profile occurs) and with increase of $\alpha$, function $\Psi$ initially increases i.e., $\Psi >0$ in a region adjacent to bed and thereafter $\Psi <0$ (type II profile occurs). It indicates that secondary current influences the suspension of sediment particles i.e., the occurrence of type I and type II profile is related to the magnitude of secondary current in the near-bed region. It is also clear from the above discussion that type II profile may not occur although secondary current exists in the flow and type II profile is attributed to a greater value of the parameter $\alpha$ i.e. for higher magnitude of secondary current.

6 Conclusions

Theoretical analysis has been carried out to study the effect of vertical velocity influenced by secondary current on concentration distribution. Good agreement between the proposed model and experimental data leads to the following conclusions:

• 1. Starting with the mass conservation equation, this study presents a mathematical model for suspension distribution which includes the effects of density stratification and mean vertical velocity induced by secondary current. The proposed model generalizes Rouse profile by including the aforementioned effects.

• 2. The proposed model is verified with experimental data of Coleman [32], Einstain and Chien [33], and Wang and Qian [34]. Verification shows that proposed model gives more accurate result than Rouse equation and produces least weighted errors.

• 3. From the computed results it is obtained that the value of parameter $\alpha$ may be positive or negative according to upward or downward direction of vertical velocity respectively which is consistent with the theoretical consideration.

• 4. Stratification results a decrease in sediment concentration relative to the neutral case. On the other hand, increase or decrease of sediment concentration is related to the direction and strength of vertical velocity induced by secondary current. Suspended concentration increases in the flow with upward vertical velocity and decreases with downward vertical velocity.

• 5. Furthermore the mechanism of different types of suspended concentration profile has been analyzed. It is found that vertical velocity has significant effect for the occurrence of different types of concentration profiles and type II profile always corresponds to strong upward vertical velocity.