Effect of lateral bed roughness variation on particle suspension in open channels

Abstract

In this paper the effect of variation of bed roughness along lateral direction on suspension concentration distribution in open channel turbulent flows was investigated. Starting from the mass and momentum conservation equations, this study demonstrates that both the Reynolds shear stress $(-\overline{u'v'})$ and sediment diffusivity depends on bed roughness. From the theoretical analysis, it is found that both the Reynolds shear stress and the sediment diffusivity increase over smooth bed surfaces and decrease over rough bed surfaces. At the junction of smooth and rough bed surface, the effect of bed roughness on the Reynolds shear stress and sediment diffusion is almost negligible. Including this effect, suspension concentration distribution is also studied and from the Hunt’s diffusion equation, an analytical model for predicting suspension concentration is proposed. Apart from this effect, the effects of moveable bed roughness and stratification are also considered in the model. It is observed that the Rouse equation is obtained from the proposed model as a special case when the flow is considered as single phase and there is no effect of secondary current, stratification and bed roughness variation. On the basis of experimental data available in literature, the proposed model is validated and also compared with the Rouse equation. To get a quantitative idea about the goodness of fit, weighted relative error is calculated. The comparison results and calculated errors indicate that the present model is capable of describing the suspension concentration distribution more accurately than Rouse model throughout the flow depth in open channel flow.

Introduction

Most of the flows in natural environment occurs over erodible sediment bed. During the flow, sediment particles on the bed surface are transported by fluid. In this process, bed characteristics such as bed shear stress, bed roughness, bed elevation, etc. changes continuously along longitudinal and lateral direction. It is therefore necessary to obtain an idea of how the sediment particles are entrained into the water column and to get the resulting form of the suspended sediment concentration profile. Open channel flow such as river flow often possesses the lateral variation in bed topology forming sand ‘troughs’ and ‘ridges’ (Fig. 1). Sand ‘ridges’ are longitudinal bed forms that are aligned parallel to main flow direction and are separated by sand ‘troughs’ (Karcz 1981). This phenomenon has been widely observed in natural rivers (Sambrook Smith and Ferguson 1996) and deserts (Liao et al. 2010). Several investigations suggest that the construction mechanism of sand ‘troughs’ and ‘ridges’ is due to secondary current and in turn sand ‘troughs’ and ‘ridges’ also influence the secondary current (Colombini 1993; Nezu et al. 1988; Wang and Cheng 2006).

Fig. 1

Schematic diagram of cellular secondary current according to Karcz (1981)

Fig. 2

Pattern of multicellular secondary current in straight wide river as envisaged by Nezu and Nakagawa (1993) after Kinoshita (1967)

Fig. 3

Secondary circulations due to lateral variation of bed roughness (after Wang and Cheng 2006)

Prandtl (1925) first proposed two classification of secondary current. These are Prandtl’s secondary current of the first kind and Prandtl’s secondary current of the second kind. First kind of secondary current is generally observed in curved pipe, river bends and in meandering channels. The driving force for this kind of secondary current is centrifugal and it is observed in laminar as well as in turbulent flow. The second kind is a result of turbulence non-homogeneity and anisotropy without any effect of channel curvature and this type is observed in turbulent flow through straight open-channels. Often, this type of secondary current is called turbulence- induced secondary current. There are a variety of turbulence-driven secondary flow in natural streams, which are caused by asymmetry of channel boundaries, free surface effects, variations in bed conditions and instabilities in turbulent flow. In this study, we focus on turbulence-driven secondary flow or Prandtl secondary current of second kind that are particularly associated with side wall effect or variation of bed roughness.

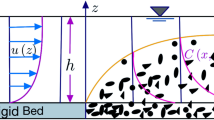
Though secondary current is observed in narrow and wide open-channels, there is difference in the mechanism of secondary current in these channels. In narrow open-channel flows, at secondary current occurs due to anisotropy of turbulence caused by side-wall and free surface effects. In case of wide open-channels, it is generated by variation of bed elevation or bed roughness along lateral direction (Vanoni 1946; Karcz 1981; Coleman 1969). Nezu and Rodi (1985) pointed out that in wide open channels, flow at the central section is free from side wall effect, whereas flow in the regions near to the side wall is affected by the side walls. By observing the periodic variation of suspension concentration along spanwise direction, Vanoni (1946) suggested that secondary current might exist in wide open-channels. This fact is supported by the observation of Karcz (1981) and Kinoshita (1967). To describe formation of sand ribbons in wide open-channels, Karcz (1981) imagined the pattern of cellular secondary current which is shown in Fig. 1. Kinoshita (1967) mentioned that secondary current may exist in the form of longitudinal vortex in straight open-channels and rivers which consists of paired counter-rotating stream-wise vortices with diameter equal to flow depth and having spanwise spacing of twice the flow depth. From the analysis of Kinoshita (1967), Nezu and Nakagawa (1993) proposed a pictorial representation of this concept which is shown in Fig. 2. In the figure, the ‘line of boil’ denotes high sediment flow zone. Coleman (1969) observed boil lines on arial photographs of the Brahmaputra River, India. Colombini (1993) studied the secondary current driven by turbulence and formation of bed ridges using the RANS equation with non-linear turbulence model. He found that for the formation of longitudinal sand strips, instability of the erodible bottom is important rather than the secondary vortices. Falcomer and Armenio (2002) carries out large-eddy simulations of a turbulent channel flow with longitudinal, large-amplitude, ridges. They found that when the Reynolds number is large enough near-wall cellular flows appear. Therefore it is clear that apart from the effects of bed forms and sidewall effects, several other factors are important for the generation of secondary current in open channel flows.

Fig. 4

Variation of Reynolds shear stress with the effect of secondary current due to lateral bed roughness variation; dash-dot line denotes linear profile of shear stress and continuous line denotes proposed model [data taken from Wang and Cheng (2006)]

Fig. 5

Variation of Reynolds shear stress at $\eta = -0.5$; dash-dot line denotes linear profile of shear stress and continuous line denotes proposed model [data taken from Wang and Cheng (2006)]

Fig. 6

Effect of bed roughness variation on sediment diffusion

The effect of secondary current on concentration profile has been considered by few researchers. From a semi-theoretical study, Chiu and McSparran (1966) showed that secondary currents have significant effect on the distribution of suspended material. Yang (2007) considered the effect of secondary current and proposed recurring models for velocity and concentration distribution. Later on, Kundu and Ghoshal (2014) mentioned that secondary current has significant effect on the types of suspension concentration profile and therefore its effect cannot be neglected. Previous studies were only concerned about the change of velocity profile in open channels with the effect of secondary current (Guo and Julien 2001; Kundu and Ghoshal 2012; Yang et al. 2004). Authors have proposed models to compute the sediment suspension concentration distribution (SSCD) but did not consider the effect of secondary current in their models (Rouse 1937; Umeyama 1992; Mazumder and Ghoshal 2006; Bose and Dey 2009). Using the two-phase flow concept, Cao et al. (1995) proposed a general (from Fick’s diffusion equation) diffusion equation and derived different explicit and independent models for SSCD depending on the choice of the eddy viscosity distribution. Although their model modifies Rouse equation, they did not consider the effect of secondary current on SSCD.

It is clear from the above discussion that though some authors considered the effect of secondary current in their models, but the effects of secondary current on the Reynolds shear stress and sediment diffusion has not been considered explicitly. Though Yang et al. (2004) considered the effect of secondary current on the Reynolds shear stress but they did not consider this effect on diffusion process. The novelty of this study is that it gives a picture how this Reynolds shear stress and sediment diffusion gradually changes with the strength and direction of secondary current. Apart from this, the present study also gives emphasis on the fact that how the Reynolds shear stress and diffusion process are affected by the change of bed roughness along lateral direction.

Therefore in this study the concentration distribution in turbulent flow through open-channels is revisited. The main purpose is to study the effect of bed roughness variation along lateral direction (which generates secondary circulations) on the suspension concentration distribution over the whole water column. First we consider the effect of secondary current on the Reynolds shear stress distribution and proposed a modified model for the Reynolds shear stress closure. Then the effect of bed roughness on the sediment diffusion is investigated. Including this effect a modified model for concentration distribution is proposed which includes the effects of secondary current, stratification and moveable bed roughness. The effect of bed roughness at the reference concentration is also considered which makes the study more effective. The reference level and reference concentration is also calculated from formula proposed by Cheng (2003) and Sun et al. (2003) respectively rather than taking from experimental data. Finally, the proposed model is validated with experimental data from literature and the accuracy of the model and the Rouse equation is also calculated by comparing the weighted relative error.

Theoretical considerations

To investigate the effect of bed roughness on the Reynolds shear stress and to develop a theoretical model for suspension concentration distribution a steady, uniform (along longitudinal direction) and fully developed turbulent flow over sediment-laden bed through a straight rectangular open channel was considered. Guo and Julien (2001) showed that under such flow conditions governing equations in clear water flow is also valid well in sediment-laden flow. Therefore time-averaged mass and momentum equation in the x-direction for sediment-laden flow can be written as

$$\begin{aligned} \frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} = 0 \end{aligned}$$

(1)

and

$$\begin{aligned} v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} = g\sin \theta +\frac{\mu }{\rho _{\rm f}}\left( \frac{\partial ^2 u}{\partial y^2}+\frac{\partial ^2 u}{\partial z^2}\right) -\frac{\partial }{\partial y}(\overline{u'v'})+\frac{\partial }{\partial z}(\overline{u'w'}) \end{aligned}$$

(2)

where (x, y, z) denotes longitudinal, vertical and lateral coordinates, (u, v, w) denotes mean velocity components corresponding to x, y and z coordinates respectively, g is the gravitational acceleration, $\rho _{\rm f}$ denotes fluid density, $\mu$ is dynamic viscosity, $-\rho _{\rm f}\overline{u'v'}$ and $-\rho _{\rm f}\overline{u'w'}$ are the Reynolds shear stresses where overbar denotes time-averaged quantities. Adding Eqs. 1 and 2 one gets the governing equation as

$$\begin{aligned} \frac{\partial (\rho _{\rm f}uv-\tau _{xy})}{\partial y}+\frac{\partial (\rho _{\rm f}uw-\tau _{xz})}{\partial z} = \rho _{\rm f} g S \end{aligned}$$

(3)

where S is energy slope, $\tau _{xy}=\mu \partial u/\partial y-\rho _{\rm f} \overline{u'v'}$, $\tau _{xz}=\mu \partial u/\partial z-\rho _{\rm f} \overline{u'w'}$, uv and uw are momentum fluxes caused by mean velocities. Equation 3 shows that wall-normal and wall-tangential gradient terms are balanced by gravitational term. Tracy (1965) showed that both the wall-normal and wall-tangential gradient terms are important in different regions of open channels. He also concluded that near a wall (either bed or sidewall), wall-normal gradient term has more significant effect compared to the wall-tangential gradient term. Therefore at the central section, near to bed, the first term on the left hand side (LHS) of Eq. 3 is dominant and second term on LHS is negligible (as wall-normal direction is y-direction). Integration of Eq. 3 with respect to y along with the boundary condition: at $y=h$, $v=0$, $\tau =0$ yields

$$\begin{aligned} \mu \frac{\partial u}{\partial y}-\rho _{\rm f} \overline{u'v'} = \rho _{\rm f}ghS\left( 1-\frac{y}{h}\right) +\rho _{\rm f}uv \end{aligned}$$

(4)

where h is flow depth. Here we assume that the effect of wind on the free surface is negligible and zero shear stress boundary condition is applied. If the fluid surface is affected by wind, the shear stress at free surface is given by White (1991, p. 149)

$$\begin{aligned} \tau |_{\xi =1} = C_{\rm d}\rho _{\rm air}(V_{\rm wind}-u_{\rm surf})^2 \end{aligned}$$

(5)

where $C_{\rm d}$ is the water surface drag coefficient, $\rho _{\rm air}$ is the density of air, $V_{\rm wind}$ is the wind velocity over fluid surface and $u_{\rm surf}$ is the fluid surface velocity. The zero shear boundary condition is also observed by Immamoto and Ishigaki (1988) in their experiment where the experiment was performed in a rectangular open channel of aspect ratio 5. They observed zero Reynolds shear stress at the central section and the point of zero shear stress tends toward the bed with the increase of distance from the central section which may be attributed as an effect of side wall. Nezu and Rodi (1985) proposed that for wide open channels where ${\rm Ar}(=b/h)>5$ (where b and h are channel width and height respectively), at the central region where $|z/h|<({\rm Ar}-5)/2$ (z denotes the measured lateral distance from central section) the effect of side wall can be neglected. Therefore a zero Reynolds shear stress boundary condition can be applied at the central section of wide open channels. The term uv denotes the effect of secondary current on shear stress distribution. Equation 4 can be simplified by ignoring the viscous effect since after some distant from channel bed turbulent effects overinfluenced the viscous effects and introducing global shear velocity $u_*(=\sqrt{ghS})$ as follows:

$$\begin{aligned} -\frac{\overline{u'v'}}{u_*^2} = \frac{\tau }{\tau _{\rm b}} = \left( 1-\frac{y}{h}\right) +\frac{uv}{u_*^2} \end{aligned}$$

(6)

where $\tau _{\rm b}$ is the bed shear stress.

Yang et al. (2004) proposed an empirical closure model for uv term using data of Immamoto and Ishigaki (1988) which is given as

$$\begin{aligned} \frac{uv}{u_*^2} = -\alpha \frac{y}{h} \end{aligned}$$

(7)

where $\alpha (>0)$ is an empirical constant. From Eqs. 6 and 7 it is observed that near the free surface when $y/h\rightarrow 1$, the Reynolds shear stress $\tau /\tau _0\rightarrow -\alpha$. In the dataset of Immamoto and Ishigaki (1988), the aspect ratio of their experiment was ${\rm Ar} = 5$. Therefore the data of Reynolds shear stress can be affected by the side wall effect. Since in this study we generally taken wide open channel with bed roughness variation, therefore the data of Immamoto and Ishigaki (1988) is not applicable. The dataset of Wang and Cheng (2005) found to be more appropriate for the present study and therefore the data of experiments by Wang and Cheng (2005) is considered. The Reynolds shear stress data from Wang and Cheng (2005) are re-plotted in Fig. 4. From Fig. 4 it is observed that near the free surface shear stress approaches to zero which is not compatible to the assumption used in Eq. 7. Therefore the proposed empirical model, i.e., Eq. 7 cannot be applied to wide open-channels where the effect of secondary current due to variation of bed roughness is present. Also it is obvious that at the free surface $y/h=1$, $v=0$ and therefore the product $uv\rightarrow 0$ at the free surface. This influence of the secondary current on Reynolds shear stress distribution from bed roughness variation can be related to the term uv on the right hand side of Eq. 6. Therefore Eq. 7 has been modified by a parabolic type profile as

$$\begin{aligned} \frac{uv}{u_*^2} = \beta \left( \frac{y}{h}\right) \left( 1-\frac{y}{h}\right) \end{aligned}$$

(8)

where $\beta$ is a parameter and its value can be determined from experimental data and $\beta >0$ or $\beta <0$ according to upward or downward direction of secondary current respectively.

Effect of bed roughness on shear stress distribution

In an open channel flow secondary current occurs due to sidewall effect, lateral variation of bed roughness, change of bed elevation (Wang and Cheng 2005, 2006), instability of erodible bottom (Colombini 1993) and for large Reynolds number (Falcomer and Armenio 2002). As the present study concerns about the effect of bed roughness variation only, therefore the experiments by Wang and Cheng (2005) is considered where secondary circulations were generated artificially creating lateral bed roughness variation. The experiments were carried out in a straight rectangular tilting flume of 18 m long, 0.6 m wide and 0.6 m deep. The bed comprised of five rough and four smooth longitudinal strips, placed in an alternate manner as shown in Fig. 3. Each strip was 0.075 m wide except to two sidewall strips which has half of the original wide. The rough strips were prepared with fine gravels packed densely of uniform medium diameter of 2.55 mm. The flow depth was 0.075 m and the aspect ratio Ar was maintained to 8 (wide open channel). As the aspect ratio ${\rm Ar}=8$ is greater than the critical value (${\rm Ar}_{\rm crit}\approx 5$, Nezu and Rodi 1985), the region $-1.5<\eta (=z/h)<1.5$ around the central section of the channel can be considered as unaffected by sidewall effects. Flow measurements were conducted with a two-dimensional (2D) Laser Doppler Anemometer (LDA). Using the LDA, streamwise and vertical instantaneous velocities are measured simultaneously in a vertical plane. Then measured instantaneous velocities were analyzed together with information of seeding particle arrival time and transit time. The data analysis results the mean velocities and other statistical quantities like correlation of velocity fluctuations such as $-\overline{u'v'}$. After computing the Reynolds shear stress, the dimensionless Reynolds shear stress $-\rho _{\rm f}\overline{u'v'}/\tau _{\rm b}$ is calculated where $\tau _{\rm b}$ is computed from $\rho _{\rm f} g h S$. The data were measured at 14 m downstream from the channel entrance, where the flow was considered fully developed. Measured Reynolds shear stress data are re-plotted in Fig. 4 (except $\eta =-0.5$ which is plotted in Fig. 5 separately) for ten distinct positions from the central section for $\eta = 0, -0.1, -0.2, \ldots , -0.9, -1$. As the maximum measurement distance ($\eta =-1$) from central section is inside the above mentioned central region, i.e. $-1.5<\eta <1.5$, it can be considered that all measured data are not affected by sidewall effects. Equation 6 with the proposed assumption in Eq. 8 is also plotted in Fig. 4. In Fig. 4, continuous lines denotes the proposed model in this study and dash-dotted lines indicate linear profiles for $\beta =0$. The proposed model lines are plotted as best fitting lines in MATLAB. From Fig. 4 it is observed that both the measured data and the proposed model show a concave type profile for $\eta =0$ to $\eta =-0.4$ and show a convex type profile for $\eta =-0.6$ to $\eta =-1$. The Reynolds shear stress at $\eta = -0.5,$ i.e. at the joint section of rough and smooth bed region, is plotted separately in Fig. 5. Continuous line denotes the proposed model which is plotted as a best fitting curve with data for $\beta =0.048$. From the figure it is clear that the profile is almost linear. At $\eta =-0.5$, the measured data and proposed model show almost a linear profile for the Reynolds shear stress. This variation in Reynolds shear stress profile can be attributed to the direction of vertical component of secondary current induced by only bed roughness effect. Corresponding to the downward direction of secondary current where $v<0$ (Fig. 4), causes a downward deviation of Reynolds shear stress from linear profile. Similarly, corresponding to the upward direction of secondary current where $v>0$, causes a upward deviation of Reynolds shear stress from linear profile. Also it is observed from Fig. 4 that as $\eta$ approaches from 0 to $-0.5$, the profile gradually approaches to the linear profile and at $\eta =-0.5$ the profile becomes almost linear. Similarly, at the section from $\eta =-0.6$ to $\eta = -1$, the Reynolds shear stress profiles gradually becomes convex. Therefore, the Reynolds shear stress distribution deviates from linear distribution except at the section where $v\approx 0$ and this deviation causes due to direction of secondary current which appears due to lateral bed roughness variation as no effect of side wall was present in the experimental data.

Fig. 7

Change in sediment diffusion with secondary current by variation of bed roughness; a cross section view, b upward view

Fig. 8

Effect of secondary current induced by bed roughness variation on concentration distribution

Fig. 9

Test of the proposed model in the near bed region with the experimental data of Coleman (1986)

Fig. 10

Comparison of proposed model with experimental data of Vanoni (1940) and the Rouse equation. Blue diamonds denote data points, green dash dotted lines denote Rouse equation and red continuous lines denote proposed model

These Figs. 4 and 5 indicate that the secondary current which is induced by bed roughness variation along lateral direction has significant effect on the Reynolds shear stress.

Sediment suspension distribution equation

In steady, uniform and fully developed open channel flows, carrying suspended load, the volume fraction of sediment concentration C is described by the convection-diffusion equation. Taking the x-axis along the bed in the main direction of flow and the y-axis vertically upwards, the steady-state equation can be expressed by Hunt’s diffusion equation as follows (Graf 1971):

$$\begin{aligned} \varepsilon _{\rm s}\frac{{\rm d}C(y)}{{\rm d}y}+C(y)\left[ \varepsilon _{\rm m}-\varepsilon _{\rm s}\right] \frac{{\rm d}C(y)}{{\rm d}y}+C(y)\left[ 1-C(y)\right] \omega _{0}=0 \end{aligned}$$

(9)

where $\omega _{0}$ is the settling velocity of sediment particle, C(y) is the sediment concentration at y, $\varepsilon _{\rm s}$ and $\varepsilon _{\rm m}$ are the sediment and momentum diffusion coefficient respectively. This equation is a sediment mass conservation equation, where the mass flux $[\varepsilon _{\rm s}+C(y)(\varepsilon _{\rm s}-\varepsilon _{\rm m})]{\rm d}C/{\rm d}y$ in y-direction is balanced by sediment settling flux $-\omega _0C(y)[1-C(y)]$. Equation 9 shows that different mathematical models of the distribution of sediment concentration may be derived by using different models of sediment diffusion coefficient.

According to the Reynolds analogy, the sediment diffusion coefficient $\varepsilon _{\rm s}$ is assumed to be proportional to the momentum diffusion coefficient $\varepsilon _{\rm m}$ as

$$\begin{aligned} \varepsilon _{\rm s}=\gamma \varepsilon _{\rm m} \end{aligned}$$

(10)

where $\gamma$ is the proportionality constant. In this equation, $\gamma$ describes the difference between diffusivity of momentum (diffusivity of a fluid particle) and diffusivity of sediment particles. The momentum diffusion coefficient $\varepsilon _{\rm m}$ in fluid sediment mixture is given by Einstein and Chien (1955) as

$$\begin{aligned} \varepsilon _{\rm m} = \frac{\tau }{\rho _{\rm f} (1 + AC) \frac{{\rm d}u}{{\rm d}y}} \end{aligned}$$

(11)

where $A(=\frac{\rho _{\rm s}}{\rho _{\rm f}}-1)$ is a constant. This equation reduces to Boussinesq’s formula $\tau = \rho _{\rm f}\varepsilon _{\rm m}{\rm d}u/{\rm d}y$ for clear water flow.

To derive the suspension concentration profile, logarithmic velocity profile is generally used. Huang et al. (2008) showed that vertical gradient of suspended concentration is affected by bed roughness height $k_{\rm s}$. The logarithmic profile for velocity distribution for rough wall is expressed as Bonakdari et al. (2008)

$$\begin{aligned} \frac{u}{u_*} = \frac{1}{\kappa }\ln \left( \frac{y}{k_{\rm s}}\right) +B_{\rm s} \end{aligned}$$

(12)

where $B_{\rm s}$ is the constant which depends on bed roughness and expressed as $B_{\rm s} = -2.5\ln (y_0/k_{\rm s})$ (Bonakdari et al. 2008). Here $y_0$ denotes the movable bed roughness height (hypothetical bed level). The disadvantage of Eq. 12 is that it loses its validity as $y\rightarrow 0$ in the near-bed viscous wall region, since $\ln (y/k_{\rm s})\rightarrow -\infty$ as $y\rightarrow 0$. Consequently, corresponding concentration profile derived using Eq. 12 shows an infinite sediment concentration in the near-bed region. But sediment concentration must be a finite quantity everywhere including the near-bed region. To overcome this drawback, a modification to Eq. 12 is needed. Therefore Jasmund-Nikuradse’s logarithmic velocity profile is used which is given as (Bogardi 1974)

$$\begin{aligned} \frac{u}{u_*} = \frac{1}{\kappa }\ln \left( 1+\frac{y}{k_{\rm s}}\right) \end{aligned}$$

(13)

where u is the velocity in main flow direction, $\kappa (=0.4)$ is the von Karman coefficient in clear water and $k_{\rm s}$ is the Nikuradse equivalent sand roughness. Using Eqs. 11 and 13, the sediment diffusion coefficient can be written as

$$\begin{aligned} \varepsilon _{\rm s} = \frac{\gamma \kappa u_* h(\xi +l_{\rm r})\{1-\xi +\beta \xi (1-\xi )\}}{1+AC} \end{aligned}$$

(14)

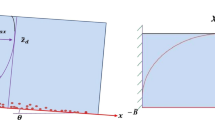
where $l_{\rm r}=k_{\rm s}/h$ ia a parameter related to relative bed roughness height. From Eq. 14 it can be observed that sediment diffusion changes with the relative bed roughness height and with the effect of secondary current caused by variation of bed roughness. The variation of sediment diffusion with change of various bed roughness is plotted in Fig. 6 for four different values of parameter $l_{\rm r} = 0.21\times 10^{-2}$, $1.27\times 10^{-2}$, $1.9\times 10^{-2}$ and $2.75\times 10^{-2}$ and for each of these four cases, five different values of parameter $\beta = -0.4$, $-0.2$, 0, 0.2 and 0.4 has been considered. From the Fig. 6 it is observed that for all fixed values of parameter $\beta$, sediment diffusion slightly increases with the increase of bed roughness height. Whereas, for a fixed value of parameter $l_{\rm r}$, sediment diffusion is greatly affected by the variation of parameter $\beta$. More precisely, sediment diffusion increases with the increase of $\beta$ and decreases with the decrease of $\beta$. This fact is described in Fig. 7. In Fig. 7a the cross section of the rectangular channel, in Fig. 7b the view of bed from up and in Fig. 7c how the secondary current affects the particle diffusion have been shown. In Fig. 7a, along the section 1–1 the direction of secondary current is vertically downward; along the section 2–2, the direction is from rough bed surface to smooth bed surface; and along section 3–3 the direction is vertically upward. Along section 3–3, the upward direction of secondary current influence particles to lift in upward direction. When a particle moves upward by influence vertical turbulent velocity fluctuation with additional effect of secondary current, it interacts more rapidly with its close neighboring particles (black colored particles surrounding red target particle in Fig. 7c below). Thereafter, these neighboring particles interacts with other particles which are close to them. In this process the surrounding particles of each particular particle is affected and gradually interaction increases by kick-out and interstitial mechanism and as a result diffusion of sediment particles increases. Also at the section 3–3, the particles near to bed surface of section 2–2 has been shifted to the smooth bed region by the secondary current (Fig. 7b). When a particle of bigger size come in interact with smaller particle over smooth bed surface it dislodges smaller particles from bed and as a consequence sediment diffusivity increases. Similarly, along section 2–2, where $v\approx 0,$ i.e. there is no additional effective force on particles along vertical direction and all particles are shifted from section 2–2 to section 3–3. Therefore along this section, effect of secondary current on sediment diffusivity in vertical direction is almost negligible as $\beta \approx 0$. Along the section 1–1, sediment diffusion along vertical direction decreases as the downward secondary current moves sediment particles from suspension region towards rough bed surface and which are again moved along the section 2–2. As a result along 1–1 section sediment diffusion decreases over vertical water column.

When sediment transport takes place over erodible bed, due to movement of sediment particles on the bed surface, bed roughness and bed shear stress continuously changes. As the parameter $l_{\rm r}$ is related to bed roughness, it is more appropriate to relate the parameter $l_{\rm r}$ with the variable bed roughness hight $y_0$. Therefore $l_{\rm r}$ can be expressed as

$$\begin{aligned} l_{\rm r} = \frac{k_{\rm s}}{h} = \left( \frac{y_0}{h}\right) \Big / \left( \frac{y_0}{k_{\rm s}}\right) \end{aligned}$$

(15)

where $y_0$ is the movable bed roughness height (hypothetical bed level). The moveable bed roughness $y_0$ can be calculated from the formula proposed by Herrmann and Madsen (2007) as

$$\begin{aligned} y_0= \frac{d}{30}[4.5(\psi -\psi _*)+1.7]\pm 0.36 \end{aligned}$$

(16)

where d is the particle diameter, $\psi =u_*^2/(Agd)$ is the shields parameter and $\psi _*$ is the critical shields parameter. The critical shields parameter is calculated from the formula proposed by Soulsby (1997) as

$$\begin{aligned} \psi _* = 0.095S_*^{-2/3}+0.056\left[ 1-\exp \left( -\frac{S_*^{3/4}}{20}\right) \right] \end{aligned}$$

(17)

where $S_*=\frac{d\sqrt{Agd}}{4\nu _{\rm f}}$ is the fluid-sediment parameter in which $\nu _{\rm f}$ is fluid kinematic viscosity.

From the experimental data of Nikuradse (1933) and Jan et al. (2006) proposed relations to calculate $y_0/k_{\rm s}$ depending on the parameter ${\rm Re}_*$ as follows:

$$\begin{aligned} \frac{y_0}{k_{\rm s}} = \frac{0.11}{{\rm Re}_*}, \quad {\rm Re}_*\le 4 \end{aligned}$$

(18)

$$\begin{aligned} \frac{y_0}{k_{\rm s}} = 0.0275-0.007\sqrt{\sin \left( \frac{{\rm Re}_*-4}{14}\right) \pi }, \quad 4<{\rm Re}_*\le 11 \end{aligned}$$

(19)

$$\begin{aligned} \frac{y_0}{k_{\rm s}} = 0.0205+\frac{0.0125}{\sqrt{2}}\sqrt{1+\sin \left( \frac{{\rm Re}_*-40.5}{59}\right) \pi },\quad 11<{\rm Re}_*<70 \end{aligned}$$

(20)

$$\begin{aligned} \frac{y_0}{k_{\rm s}} = 0.033, \quad {\rm Re}_*\ge 70 \end{aligned}$$

(21)

where ${\rm Re}_* = (u_* k_{\rm s})/\nu _{\rm f}$ is the roughness Reynolds number.

Substitution of Eqs. 14 and 10 into Eq. 9 gives the sediment suspension distribution equation as

$$\begin{aligned} \frac{S_{\rm c}C+(1-C)}{C(1-C)(1+AC)}\frac{{\rm d}C}{{\rm d}\xi } = -\frac{\omega _0/(\kappa \gamma u_*)}{(\xi +l_{\rm r})\{1-\xi +\beta \xi (1-\xi )\}} \end{aligned}$$

(22)

where $S_{\rm c}(=1/\gamma )$ is the Schmidt number. Equation 22 is a modified diffusion equation which includes the effect of bed roughness and secondary current; and it reduces to the conventional diffusion equation if one considers that $l_{\rm r}\approx 0$, $\beta =0$ and apply Boussinesq’s formula for momentum diffusion coefficient. Naturally in river flows, bed roughness changes as bed particles are eroded by flow which is a important factor. Equation 22 considers the effect of variation of bed roughness in two ways. The parameter $l_{\rm r}$ directly includes the effect of moveable bed roughness variation due to erosion of bed materials and the other parameter $\beta$ includes the effect of secondary current causes as an effect of lateral variation of bed roughness. The effect of secondary current on concentration profile has been considered by only few researchers (Chiu and McSparran 1966; Kundu and Ghoshal 2014). Kundu and Ghoshal (2014) has mentioned that secondary current has significant effect on the types of suspension concentration profile and therefore it cannot be neglected. Inclusion of these effects makes the study more appropriate than previous studies because in natural flows these effects are always present and cannot be neglected. This makes the present study more effective than previous studies.

Integration of Eq. 22 between the reference level $\xi _{\rm a}$ to $\xi$ and simplification gives the sediment concentration distribution equation as

$$\begin{aligned} \frac{C}{C_{\rm a}}\cdot \left( \frac{1-C_{\rm a}}{1-C}\right) ^{\lambda _1}\cdot \left( \frac{1+AC_{\rm a}}{1+AC}\right) ^{1-\lambda _1} = \varPhi (\xi )\cdot \varPsi (\xi ) \end{aligned}$$

(23)

where the functions $\varPhi (\xi )$ and $\varPsi (\xi )$ are given as follows:

$$\begin{aligned} \varPhi (\xi ) = \left( \frac{1-\xi }{\xi +l_{\rm r}}\cdot \frac{\xi _{\rm a}+l_{\rm r}}{1-\xi _{\rm a}}\right) ^{\frac{Z_1}{(1+l_{\rm r})(1+\beta )}}, \end{aligned}$$

(24)

$$\begin{aligned} \varPsi (\xi ) = \left( \frac{\xi +l_{\rm r}}{\xi _{\rm a}+l_{\rm r}}\cdot \frac{1+\beta \xi _{\rm a}}{1+\beta \xi }\right) ^{\frac{Z_1\chi }{1+l_{\rm r}}}, \end{aligned}$$

(25)

$$\begin{aligned} \chi = \frac{1}{1+\beta }-\frac{1}{1-\beta l_{\rm r}} \quad \text{ and } \quad \lambda _1 = \frac{S_{\rm c}}{1+A} \end{aligned}$$

(26)

in which parameter $Z_1 = \omega _0/(\kappa \gamma u_*)$ denotes the Rouse number, $\xi _{\rm a}$ and $C_{\rm a}$ denotes the reference level and reference concentration respectively. From Eq. 23 it can be observed that concentration of sediment is best described by product of two functions $\varPhi (\xi )$ and $\varPsi (\xi )$. Function $\varPhi (\xi )$ is a Rouse type function and another function $\varPsi (\xi )$ considers the effects of bed roughness on sediment suspension. Although Rouse equation is good enough but it cannot be extrapolated to the bed surface where $\xi$ approaches to zero as it possess an infinite concentration at bed surface layer; whereas the proposed model possess a finite concentration at bed surface level which demonstrates the superiority of the proposed model.

Rouse equation can be obtained from Eq. 23 if one considers that $A\approx 0$, $l_{\rm r}\approx 0$ and $\beta =0$. The condition $A\approx 0$ indicates that the density of particle is approximately equal to the density of fluid, i.e., there is no change in density of solid phase and fluid phase. This indicates that there is no sediment induced effect present in the flow. The condition $l_{\rm r}\approx 0$ indicates no change in movable bed roughness which occurs due to erosion of particles over bed surface. Generally, this happens when flow velocity is low; and in low fluid velocity, particles with relatively bigger size will not be able to move to suspension layer from bed-load layer. As a consequences, over all suspension concentration will be low. And the condition $\beta =0$ indicates absence of secondary current as a result of bed roughness variation. These indicate that Rouse equation is applicable only in single phase flow and when there is no effect of bed roughness and secondary current, i.e. only along the section 2–2 in Fig. 9a where secondary current is parallel to lateral direction.

From the discussion about the combined effects of secondary current and bed roughness on sediment diffusivity, it can be summarized that diffusivity increases over the smooth bed surfaces and decreases over rough bed surfaces. At the junction of smooth and rough bed surface diffusivity is unaffected by those effects. Figure 8 shows the variation of concentration with secondary current induced by bed roughness variation. In figure $\beta =0$ corresponding to the case of no secondary current. It can be observed from Fig. 8 that when $\beta >0$, concentration increases in suspension. This happens because upward secondary occurs over smooth bed surface where sediment diffusivity increases. Alternately when $\beta <0$, concentration decreases in suspension as downward secondary occurs over rough bed surface where sediment diffusivity decreases along vertical upward direction.

Fig. 11

Comparison of proposed model with experimental data of Einstein and Chien (1955) and the Rouse equation. Blue squares denote data points, green dash dotted lines denote Rouse equation and red continuous lines denote proposed model

Fig. 12

Comparison of proposed model with experimental data of Wang and Qian (1989) and the Rouse equation. Blue crosses denote data points, green dash dotted lines denote Rouse equation and red continuous lines denote proposed model

Fig. 13

Influence of stratification and secondary current caused by bed roughness variation on suspension distribution

Sediment concentration at some given height from bed can be calculated from the above proposed equation if the value of the parameters, i.e. particle settling velocity $\omega _0$; reference level $\xi _{\rm a}$; and reference concentration $C_{\rm a}$ are known. The following sections describe how these parameters can be calculated.

Particle settling velocity

The sediment settling velocity $\omega _0$ is an important parameter in determination of suspended concentration profile and it depends on the sediment and flow parameters. In still and clear fluid, a falling particle accelerates in the downward direction due to gravitational force. When the sum of upward drag and buoyancy force equals to the weight of the particle, the particle reaches a constant velocity which is called the fall or settling velocity and it is denoted by $\omega _0$. Several models are available in literature to compute fall velocity of particles and a comprehensive summary can be found in Zhiyao et al. (2008). Based on the relationship between particle Reynolds number and the dimensionless particle diameter, Zhiyao et al. (2008) also proposed a formula for calculating the settling velocity of a single particle. Their model provides much appropriate results than others and is applicable for a wide range of particle Reynolds number. Therefore to compute settling velocity of the sediment particles, the formula given by Zhiyao et al. (2008) is used which is given as

$$\begin{aligned} \omega _0 = \frac{\nu _{\rm f}}{d}d_*^3(38.1+0.93d_*^{12/7})^{-7/8} \end{aligned}$$

(27)

where $d_*$ is the dimensionless sediment particle diameter defined as $d_*=[(Ag)/\nu _{\rm f}^2]^{1/3}d$. It should be mentioned here that the above formula for settling velocity has been used by other researchers (Kundu and Ghoshal 2014).

Reference level

The reference level denotes the thickness of the bed-load layer. It is also considered as the common boundary of bed-load and suspended-load layer. In literature, authors have provided many formulae to calculate the reference level. A brief literature survey can be found in Sun et al. (2003). Since the reference level is measured very near to sediment bed, nearbed flow characteristics such as particle-particle interactions are important and to be considered. Considering this effect Cheng (2003) proposed an analytical model for computing reference level. Among various models in literature, those effects are incorporated in the model of Cheng (2003) which gives good estimation when compared to the experimental data. Therefore in this study we have considered it to compute bed-load layer thickness or reference level. The formula is as follows:

$$\begin{aligned} \xi _{\rm a} = \frac{\tau d d_*^3 L}{h\left( \sqrt{25+1.2d_*^2}-5\right) ^{1.5}} \end{aligned}$$

(28)

where L is given as

$$\begin{aligned} L = \int _{0}^{C_{\rm m}}\frac{\lambda }{C(C^{-1/3}-1)^2 \mu _* \omega _*}{\rm d}C, \end{aligned}$$

(29)

$C_{\rm m}$ is the maximum concentration, $\lambda$ is a parameter varies from 0.005 to 0.5, $\mu _*$ and $\omega _*$ are relative viscosity and relative settling velocity of sediment particles respectively which are as follows (Cheng 2003):

$$\begin{aligned} \mu _* = \exp \left[ \frac{2.5}{\beta _*}\left\{ \frac{1}{(1-C)^{\beta _*}}-1\right\} \right] \end{aligned}$$

(30)

and

$$\begin{aligned} \omega _* = \frac{\mu _*}{1+AC}\left( \frac{\phi -5}{\sqrt{25+1.2d_*^2}-5}\right) ^{1.5} \end{aligned}$$

(31)

where

$$\begin{aligned} \phi = \sqrt{25+1.2d_*^2(1-C)^{2/3}[1+AC]^{2/3}\mu _*^{-4/3}} \end{aligned}$$

(32)

and value of parameters $\beta _*$ and $C_{\rm m}$ are taken as 2.5 and 0.6 as mentioned by Cheng (2003). Computed reference level for selected test cases are listed in Table 1.

Table 1 Detailed flow characteristics for selected test cases

Reference concentration

Reference concentration $C_{\rm a}$ is the value of sediment concentration at reference level $\xi _{\rm a}$. Since concentration is calculated close to bed, pick-up and incipient motion of particles affect the concentration and therefore these effects should be considered in the model. Several authors proposed formula to compute reference concentration. Among several models, the model proposed by Sun et al. (2003) considers three basic probabilities: incipient motion probability, non-ceasing probability and pick-up probability of the sediment particle in the model for reference concentration. Therefore the reference concentration is computed from the model of Sun et al. (2003) which is given by

$$\begin{aligned} C_{\rm a} = M_* P_* \frac{F(\cdot )}{1+F(\cdot )} \end{aligned}$$

(33)

where $M_*$ denotes the density coefficient of bed material, $P_*$ denotes the grain size class percentage of bed material and equal to unity for uniform sediments and the function $F(\cdot )$ is expressed as

$$\begin{aligned} F(\cdot ) = \frac{10^{-5} \tau ^2 d_*^{1.84}\alpha _n \lambda _n}{(1-\gamma _n)(1-\lambda _n)(1+\gamma _n \lambda _n)} \end{aligned}$$

(34)

where $\alpha _n$, $\gamma _n$ and $\lambda _n$ are incipient motion probability, non-ceasing probability and pick-up probability of sediment particles which are given by

$$\begin{aligned} \alpha _n = 1-\frac{1}{\sqrt{2 \pi }}\int _{-2.7(\sqrt{0.0822/\tau }+1)}^{2.7(\sqrt{0.0822/\tau }-1)}{\rm e}^{-x^2/2}{\rm d}x \end{aligned}$$

(35)

$$\begin{aligned} \gamma _n = 1-\frac{1}{\sqrt{2 \pi }}\int _{-2.7(\sqrt{0.0571/\tau }+1)}^{2.7(\sqrt{0.0571/\tau }-1)}{\rm e}^{-x^2/2}{\rm d}x \end{aligned}$$

(36)

$$\begin{aligned} \lambda _n = \frac{2}{\sqrt{2 \pi }}\int _{\omega _0/u_*}^{\infty }{\rm e}^{-x^2/2}{\rm d}x \end{aligned}$$

(37)

respectively. Calculated values of reference concentration are shown in Table 1 for selected test cases.

Comparison with experimental data

To test the validity of the model near the bed region as well as over the whole flow depth in different types of flow, existing experimental data from Coleman (1986), Einstein and Chien (1955), Wang and Qian (1989) and Vanoni (1940) are selected. The following sections describe the cases in details. Since in this study we propose a significant modified form of the Rouse equation; therefore we also compare our model with the Rouse equation. This comparison also helps to determine how the proposed model improves the prediction of suspension concentration distribution.

Verification of model in near-bed region

To test the validity of the proposed model in near bed region, experimental data of Coleman (1986) is selected. The experiments were carries out in a 15 m long flume. The flow conditions, i.e. height $h\approx 1.69$ mm, width of the channel $b = 356$ mm, channel slope $S = 0.002$ and $u_*=0.041$ m/s were kept same for all test cases. The aspect ratios are small and has the range from 2.046 to 2.132 including all test cases. This clearly indicates that secondary currents exists. Sediment concentration gradually increases in different test cases and reaches high values (up to 625 kg/m$^3$) in some test cases. In Fig. 9, data corresponding to Run 36 is plotted together with the proposed model and the Rouse equation. From the Fig. 9, it is observed that disagreement among these two equations occurs in the region near the bed where no observed data can be obtained since the region is very close to the bed to allow measurements. More precisely one sees from Fig. 9 that when $\xi _{\rm a}=10^{-4}$, the value of $C/C_{\rm a}$ computed from the Rouse equation and proposed model are 121.11 and 3.02 respectively. These values indicate that proposed model is more appropriate than the Rouse equation which gives a high value of sediment concentration in the near bed region.

Verification of model over the whole flow depth

To validate the proposed model over the total flow depth, existing laboratory experimental data have been used. As in this study the effect of secondary current as a result of bed roughness variation is included, the experimental data which have the effect of bed roughness and secondary current is considered. Therefore experimental data of Einstein and Chien (1955), Wang and Qian (1989) and Vanoni (1940) (wide channel) have been used in this study. The following test cases (or RUN) have been selected to verify the model: test cases S5, S10, S12, S14, S15 and S16 from Einstein and Chien (1955); test cases SQ1, SQ2 and SQ3 from Wang and Qian (1989) and all test cases (S1 to S22) from Vanoni (1940). In all the selected test cases aspect ratio has the range from 2.27 to 11.9 and maximum volumetric sediment concentration varies from 0.027 to 74 %. Detail flow characteristics of all test cases or runs are shown in Table 1.

Figure 10 shows the verification of the proposed concentration model with the experimental data of Vanoni (1940). Vanoni (1940) performed experiments in two series (series I and II). The experiments were done in a flume which is 33.25 inches wide and 60 feet long with adjustable bed slope. The bottom of the channel was made of steel sheet plate with artificially roughened by sand particles. In series I, experiments on three clear water (test cases 1, 2 and 3) and 13 sediment-water mixture (test cases 1–13) were performed where the slope was kept as $S=0.0025$. In series II, experiments on three clear water (test cases 14a, 14b, 21) and nine sediment-water mixture (test cases 14–22) were performed. In all the test cases aspect ratio is greater than 5. Therefore the flow at the central section is free from side wall effects and due to rough bed surface, secondary currents are generated in the flow. The model is verified with all 22 sets of experimental data and for comparison purpose results of selected test cases S5, S11, S17, S19, S20 and S22 are plotted in Fig. 10. In Fig. 10, the Rouse equation for suspension concentration is also plotted to compare it with the present model. The parameters present in the Rouse equation are calculated in the following way: settling velocity is calculated from Eq. 27, $\kappa = 0.4$ and $u_*$ is taken from experimental data and the proportionality parameter $\gamma$ is calculated from experimental data by minimizing $S_1$ the sum of the residuals, i.e., solving $\partial S_1/\partial \gamma =0$ where $S_1$ is expressed as

$$\begin{aligned} S_1 = \sum _{i=1}^n \left[ \gamma \ln \left( \frac{C_i}{C_{\rm a}}\right) -\frac{\omega _0}{\kappa u_*}\ln \left( \frac{1-\xi _i}{\xi _i}\frac{\xi _{\rm a}}{1-\xi _{\rm a}}\right) \right] ^2 \end{aligned}$$

(38)

where n is total number of data points $(\xi _i,C_i)$. $\partial S_1/\partial \gamma =0$ implies that

$$\begin{aligned} \gamma = \frac{\omega _0}{\kappa u_*}\frac{\sum _{i=1}^n \ln \left( \frac{1-\xi _i}{\xi _i}\frac{\xi _{\rm a}}{1-\xi _{\rm a}}\right) \ln \left( \frac{C_i}{C_{\rm a}}\right) }{\sum _{i=1}^n\left\{ \ln \left( \frac{C_i}{C_{\rm a}}\right) \right\} ^2} \end{aligned}$$

(39)

A MATLAB programme has been written to compute the value of $\gamma$. The Rouse equation is plotted as a best fitting line with the experimental data. The proposed model consists of only two free parameters $\gamma$ and $\beta$ which are calculated using least square method by minimizing the sum of residuals in MATLAB. From the Fig. 10 it is observed that Rouse equation predicts suspended sediment concentration correctly up to 20 % of the flow depth from channel bed in all cases except S11 where it predicts concentration correctly over whole flow depth. It can also be observed from the figure, that the proposed model predicts the concentration well throughout the flow depth in most of the test cases. The errors corresponding to the Rouse equation and the proposed model for all test cases of Vanoni, are shown in Table 1. From the Table 1 it can be observed that present model is more appropriate in predicting suspension concentration than the Rouse model as in most of the test cases it gives minimum error. This comparison results show that proposed model can be applied for wide open channel flows to predict sediment concentration distribution where bed roughness effect influences the sediment concentration over full water column.

Apart from the wide open channels, the application of the proposed model is extended for narrow open channel flows. The model is compared to the experimental data of Einstein and Chien (1955) and Wang and Qian (1989) for this purpose.

Figure 11 compares the proposed model with the experimental data of Einstein and Chien (1955). The experiments were carried out in a 0.3 m wide channel. Characteristics of the flow and natural sediments are shown in Table 1 for selected test cases. The mean size of sediment were 1.3 mm for run S5, 0.94 mm for run S10, and 0.274 mm for runs S12, S14, S15 and S16. The aspect ratio has the range from 2.273 to 2.727. Therefore, at the central section both the effects of side wall and bed roughness are present. In the figure the Rouse equation is also plotted to compare it with the study. From the Fig. 11 it is observed that the Rouse equation predicts suspended sediment concentration up to $20\%$ of the flow depth from channel bed whereas proposed model predicts the concentration well throughout the flow depth. It is also important to notice that data of Einstein and Chien (1955) present up to half of the flow depth from bed. Therefore to show the validity of the proposed model throughout the flow depth, data of Wang and Qian Wang and Qian (1989) is also taken.

In Fig. 12 the verification with Wang and Qian Wang and Qian (1989) experimental data is shown. The experiments were conducted in a recirculating and tilting flume 20 m long, 30 cm wide, and 40 cm high with sediment bed with the bed slope $S = 0.01$. The aspect ratio is 3.75 for all selected test cases. Other flow characteristics are shown in Table 1. Figure 12 also shows the comparison between proposed model and the Rouse equation. From the Fig. 12 it is observed that Rouse profile predicts concentration well in the inner region (region adjacent to bed and comprise 20 % of the total flow depth, i.e. $0\le \xi \le 0.2$) and it deviates in the outer region (region above the inner region where $\xi >0.2$). The deviation gradually increases with the increase of height from bed as the effect of secondary current is more effective in the outer region than in the inner region. The proposed model predicts sediment concentration well throughout the flow depth as this includes the effect of secondary current. This indicates that Rouse equation can be significantly modified by proposed model considering the effect of bed roughness.

Accuracy of the model

To get an quantitative idea about the accuracy of the fitting between computed and observed values, the weighted relative errors E were calculated from the formula

$$\begin{aligned} E = \sqrt{\sum \frac{(S_{\rm co}-S_{\rm o})^2}{S_{\rm o}T}} \end{aligned}$$

(40)

where $S_{\rm co}$ and $S_{\rm o}$ are computed and observed values of suspended concentration at various height in weight percentage and T denotes the total value observed which is equal to 100. In Eq. 40, the sum is performed over all available data points throughout the flow depth. The value of errors (for all selected test cases) corresponding to the Rouse equation and the proposed model has been calculated and shown in Table 1 where $E_{\rm R}$ and $E_1$ denotes errors corresponding to the Rouse equation and the proposed model respectively.

Discussion

In their analysis of experimental results, Vanoni (1946) and Einstein and Chien (1955) observed the reduction of the von Karman coefficient $\kappa$ in flows with presence of suspended sediment. Later on, many scientists hypothesized that the presence of suspended particles modify the turbulent structures and they often related it with the stratification effect (Smith and McLean 1977; Herrmann and Madsen 2007; Armenio and Sarkar 2002; Wright and Parker 2004a, b; Taylor et al. 2005).

Many researchers considered the effect of stratification due to concentration of suspended sediment, but most of them brought the stratification effect either through the variability of the von Karman coefficient or by introducing buoyancy term into the governing equation. Smith and McLean (1977) first found that the presence of sediment particles reduces the diffusion process and they proposed the effect of sediment induced stratification through reduction in eddy diffusivity. The Miles theorem states that if the Richardson number ${\rm R}_i$ is greater than 0.25 everywhere, then a stratified flow is stable. Later on, Armenio and Sarkar (2002) studied the boundary-forced stratified turbulence using large-eddy simulation approach. They found that under such flow the range of Richardson number falls in the range $0.15 < {\rm R}_i < 0.25$. The gradient Richardson number appears to be the important to determine the buoyancy effects (Armenio and Sarkar 2002). Also Dallali and Armenio (2015) showed that for fine particles stratification effect is not negligible. Therefore the effect of stratification is also considered in the present model. To show it, following Smith and McLean (1977) and Herrmann and Madsen (2007), momentum diffusivity in a stratified flow is expressed as

$$\begin{aligned} \varepsilon _{\rm m} = \varepsilon _{\rm mn}(1-\beta _1 R_i) \end{aligned}$$

(41)

where $\varepsilon _{\rm mn}$ is the momentum diffusivity under neutral condition (where the effect due to presence of suspended sediment is negligible), $\beta _1$ is the stratification correction parameter and $R_i$ denotes the Richardson number which denotes the effect of stratification in sediment mixed flow. The stratification correction parameter $\beta _1$ is a parameter (Businger et al. 1971). According to Wright and Parker (2004a) and Monin and Yaglom (1971), the Richardson number is defined as

$$\begin{aligned} R_i = \left( \frac{\rho _{\rm s}}{\rho _{\rm f}}-1\right) \frac{g\omega _0 C}{u_*^2(1-\xi )\frac{{\rm d}u}{{\rm d}y}} \end{aligned}$$

(42)

Using the momentum diffusivity $\varepsilon _{\rm mn}$ under neutral condition, momentum diffusivity $\varepsilon _{\rm m}$ in mixture is expressed in terms of $\varepsilon _{\rm mn}$ from Eq. 11 as

$$\begin{aligned} \varepsilon _{\rm m} = \frac{\tau }{\rho _{\rm f} (1 + AC) \frac{{\rm d}u}{{\rm d}y}} = \frac{\varepsilon _{\rm mn}}{1+AC} \end{aligned}$$

(43)

Substitution of Eq. 42 into Eq. 43 results

$$\begin{aligned} \varepsilon _{\rm m} = \frac{\varepsilon _{\rm mn}}{1+aR_i} \end{aligned}$$

(44)

where a is a factor which is independent of sediment concentration and $a=u_*^2(1-\xi )({\rm d}u/{\rm d}y) /(g\omega _0)$ (Yang 2007). If the Taylor series expansion is applied, the Eq. 44 can be expressed as

$$\begin{aligned} \varepsilon _{\rm m} = \frac{\varepsilon _{\rm mn}}{1+aR_i} = \varepsilon _{\rm mn}\left[ 1-aR_i+\left( aR_i\right) ^2-\left( aR_i\right) ^3+\cdots \right] \end{aligned}$$

(45)

If the first two terms in Eq. 45 are kept, one obtains

$$\begin{aligned} \varepsilon _{\rm m} = \varepsilon _{\rm mn}(1-aR_i) \end{aligned}$$

(46)

and consequently the sediment diffusion coefficient in stratified flow is expressed as

$$\begin{aligned} \varepsilon _{\rm s} = \gamma \varepsilon _{\rm m} = \gamma \varepsilon _{\rm mn}(1-aR_i) = \varepsilon _{\rm sn}(1-aR_i) \end{aligned}$$

(47)

where $\varepsilon _{\rm sn}$ denotes sediment diffusion coefficient in neutral flow. Equation 46 was similar to Eq. 41 and developed by both Smith and McLean (1977) and Herrmann and Madsen (2007) and was applied by Wright and Parker (2004a). Thus one can conclude that the present model is consistent with previous studies, and the effect of density stratification has been included in the model.

Because the present model hypothesizes that bed roughness and stratification effects jointly deviates the suspension concentration from the Rouse equation, it would be useful to identify clearly the relative importance of these two causes. Figure 13 is plotted for this purpose and experimental data of Run 18 of Vanoni (1940) has been selected. First the parameter A and $\beta$ is set to zero, it means that the effect of stratification and secondary current due variation of bed roughness are neglected which gives the Rouse equation in neutrally buoyant flow. Second, $A=1.65$ and $\beta =0$ are used, this means that only stratification effect is included. It can be sheen from Fig. 13 that lower suspension concentration is obtained than Rouse equation. This happens because stratification decreases the sediment diffusivity $\varepsilon _{\rm s}$ by the factor $1-aR_i$ as expressed by Eq. 47 (as $R_i > 0$ and $a> 0$), which leads to a decrease in concentration. Third by adjusting the parameter $\beta$, one can fit the measured data point with good agreement as shown in Fig. 13, which indicates that the effect of secondary current due to the bed roughness effect on concentration distribution should not be underestimated.

Conclusions

In this study the effect of variation of bed roughness along lateral direction on suspension concentration distribution over the whole water depth is investigated. Besides this, the effect of bed roughness on the Reynolds shear stress and sediment diffusivity also studied. The main findings are as follows:

• 1. The Reynolds shear stress depends on bed roughness in open channel flows. More precisely, the Reynolds shear stress increases over smooth bed surfaces and decreases over rough bed surfaces. It is also found that the Reynolds shear stress profile follows a convex type profile when bed is rough and a concave type profile when bed is smooth which also agrees with previous existing results. At the junction of smooth and rough bed, the Reynolds shear stress does not depend on bed roughness and follow the conventional linear profile of open channel flows.

• 2. Since due to the variation of bed roughness, cellular secondary current is generated over the whole flow region, therefore 3D flow appears also at the central section of open channels.

• 3. The effect of variation of bed roughness along lateral direction on sediment diffusion is also investigated. From the analysis it is found that along vertical direction sediment diffusion increases over smooth bed and decreases over rough bed surfaces. It is also found that at the junction of smooth and rough bed surface, diffusion is not affected by the roughness effect.

• 4. It is known that due to change of bed roughness, near bed sediment concentration changes. In this study it is found that lateral variation in bed roughness also changes the suspension concentration distribution over the whole water column. More precisely, sediment concentration increases over smooth bed surfaces and decreases over rough bed surfaces.

• 5. Combining the effects of secondary current induced by bed roughness variation, stratification and moveable bed roughness, an analytical model for predicting suspension concentration is proposed from Hunt’s diffusion equation. The model is validated with several experimental results and it is found that present model gives more appropriate result to predict sediment concentration near to bed layer as well as throughout the whole flow depth for narrow and wide open channel flows. Computed weighted relative errors also indicate the superiority of this model than the Rouse equation. As a result near bed sediment concentration can be calculated from the model by numerically extrapolating the curve.

• 6. Due to the effect of stratification induced by the presence of sediment particles, sediment suspension concentration decreases.

• 7. This study also gives emphasis of the fact that the Rouse model is applicable in single phase flow when there if no effect of secondary current and stratification in the flow.