1 Introduction

Turbulent velocity distribution in a sediment-laden flow is an important topic of research in the field of sediment transport. Different theoretical analyses proved that the behaviour of velocity profile in sediment-laden flow is similar to that of clear water but not the same. Several factors like density, viscosity are changed due to the presence of particles in the flow, and these become functions of concentration. Regarding the study of turbulent velocity profiles, von Karman [49] and Prandtl [39] were the pathfinders whose law of wall is till now used in the study of turbulence. After that, a number of researchers examined the law of wall, including various factors of turbulence and many of these studies also include the effect of sediment presence. For example, Vanoni and Nomicos [48], Elata and Ippen [14] also showed the validity of log-law in sediment-mixed fluid, with a decrement in the value of the von-Karman constant. Einstein and Chien [13] proved that the main effect of sediment occurs near the bottom boundary. Coleman [7, 8] showed that only log-law is not sufficient to describe the velocity throughout the channel depth and near the free surface, the velocity profile deviates from log-law, which is to be corrected using a wake parameter. He claimed that von Karman constant of clear water flow does not change in sediment-laden flow, but the wake parameter changes. Muste and Patel [35] experimentally studied the log-law in the presence of sediments and showed that low concentration hardly affects the log-law near the bed. Umeyama and Gerritsen [46] studied the vertical distribution of velocity in a sediment-laden flow from the mixing length point of view. A number of studies (Coles [10], Coleman [7], Sarma et al. [43], Coleman [8], Guo [16], Sarma et al. [44], Absi [1], Kundu and Ghoshal [25]) can be found in the literature that studied velocity distribution in turbulent flow for clear and sediment-laden flows. Mohan et al. [32] studied the simultaneous distribution of fluid velocity and concentration by considering the effect of sediment presence through the stratification concept. However, all these studies mainly focused on the one-dimensional distribution of longitudinal velocity. Study of two-dimensional distribution of stream-wise mean velocity in the presence of sediments has not been paid equal attention.

One crucial aspect in open-channel flow is secondary current which is always present and independent of the channel geometry (Yang [53]). Study of secondary current has been a very important topic of research to the science community as it not only helps to understand the flow geometry but also explains the variation in sediment bed texture and bed topography (Yang et al. [55]). Several researchers (Nezu and Rodi [37], Nezu and Nakagawa [36], Wang and Cheng [50], Yang et al. [55]) studied the causes of the generation of secondary current. Many researchers included the effect of secondary current while modelling stream-wise mean velocity distribution along a vertical in an open-channel flow. Lassabatere et al. [28] studied velocity distribution for the outer region and the central part of the open channel focusing on an analytical approach. Their model is capable of explaining different kinds of flows, including dip-phenomenon, which arises due to the presence of secondary current in narrow channels where the maximum velocity occurs below the free surface. Focusing on the dip-position and the centreline wake strength coefficient, quite a number of works have been done by Guo and Julien [18,19,20,21]. Kundu and Ghoshal [25] developed a complete analytical model for stream-wise mean velocity distribution along a vertical, known as total-dip-modified-log-wake law. Apart from these works, several works (Yang et al. [54], Guo [17], Kundu et al. [27]) can be found in the literature that worked on dip-phenomenon to study velocity distribution. Nevertheless, these works are also mainly based on the one-dimensional distribution of stream-wise mean velocity that too mostly for clear water flow only, leaving a scope to explore the case of two-dimensional.

Out of the very few works on two-dimensional velocity, Sarma et al. [43] studied velocity distribution in a smooth rectangular channel by dividing the channel into four regions though dip-phenomenon was not addressed there. Coleman and Alonso [9] introduced Cole’s wake function to the velocity distribution formula for narrow-deep open channels; but the verification was conducted only for the perpendicular bisectors of cross sections. Tominaga et al. [45] experimentally measured the three-dimensional turbulent structure in straight open-channel flows and showed that the secondary current affects the primary mean flow. They classified their experiments into three groups—(i) smooth rectangular open channel, (ii) trapezoidal open channel and (iii) rectangular rough open channel. Though in the last group, they considered roughness in the bed, the roughness was not due to erodible sediment bed and the roughness elements were glass beads that were densely attached to the wall. Lu [31] studied steady uniform flow through open channels deriving a two-dimensional velocity expression though it needed modification for application in rivers with narrow-deep cross section. Yang et al. [54], Bonakdari et al. [3], Absi [1] studied the effect of secondary current on the centreline vertical shear stress distribution. Guo and Julien [18] started from the Navier–Stokes equation in order to study the turbulent velocity profile for sediment-laden flow but ultimately reduced the equation to a one-dimensional form only. Pu [41] proposed a velocity profile representing steady, uniform and fully developed turbulent open-channel flow. The model contains the effect of secondary current and is valid for both smooth and rough bed flows. Guo [17] studied the modified log-wake law for cross-sectional and centreline velocity distribution for smooth rectangular open-channel flow by including dip-phenomenon, ignoring the transverse and vertical velocity components. A recent study of Lu et al. [30] started from the Reynolds equation for turbulent flow and analytically solved the two-dimensional velocity distribution along vertical and transverse directions. Though their model showed dip effects, they neither kept all the important terms of the Reynolds equation nor included the effect of sediment presence. Recently, Mohan et al. [33] developed a model for the two-dimensional distribution of stream-wise mean velocity starting from the RANS equation and taking into account the terms neglected by Lu et al. [30]. Secondary flows along the vertically upward direction and the lateral direction were considered in the model, which were taken as functions of lateral and vertical co-ordinates. Their model is capable of predicting dip phenomenon that occurs in a narrow open-channel flow and can also explain the periodic nature of transverse velocity for wide open-channel flow. But they did not take into account the effect of sediment presence in the flow and they themselves mentioned it as a possible future extension of their model.

From the aforementioned literature review, it can be noted that existing studies on velocity distribution were mostly on the vertical distribution of stream-wise mean velocity, i.e. a one-dimensional study. Our motivation for the present study comes from the fact that the distribution of stream-wise mean velocity along vertical and lateral directions in an open-channel turbulent flow incorporating the effects of sediment concentration, secondary current and dip-phenomenon has not been studied yet. For limited two-dimensional studies available in the literature, either dip-phenomenon is not included in the model or the transverse/vertical component of velocity is not taken into account or relevant terms are neglected from the governing equation or sediment suspension effect is not incorporated. The present study aims to develop a model starting from the RANS equation for stream-wise mean velocity distribution, which considers the transverse and vertical velocity components for a steady and uniform flow along the main flow direction. The model includes the dip effect and most importantly, unlike the existing researches, includes the effect of sediment suspension. This work can be considered as an extension of Mohan et al.’s [33] work who developed a similar model for clear water flow. So the main objectives of the present study are (i) starting from the RANS equation, to develop a two-dimensional distribution model of longitudinal mean velocity for a steady, uniform turbulent flow; (ii) to include the effect of secondary current and dip-phenomenon; (iii) to consider the effect of sediment presence in suspension through modified density and viscosity; (iv) to solve the developed partial differential equation by numerical method; and (v) to validate the model under limited conditions by comparing it with available experimental data.

2 Mathematical modelling

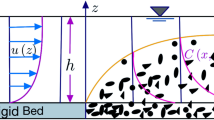
We consider a steady, uniform (along stream-wise direction), sediment-laden turbulent flow through a rectangular open channel of width 2B and height H. Let u be the mean velocity of the flow along the longitudinal (stream-wise) direction x, v be the mean velocity of the flow along the transverse direction y and w be the mean velocity of the flow along the vertical direction z in the cartesian co-ordinate system, i.e. u, v and w are the stream-wise, transverse and vertical components of mean velocity, respectively (Fig. 1). Since the flow is uniform in the longitudinal direction, the velocity components u, v and w are independent of x. Let \(u^\prime \), \(v^\prime \) and \(w^\prime \) be the fluctuation components of u, v, w, respectively. For steady, uniform, sediment-laden turbulent flow in an open channel, the continuity equation and the Reynolds-averaged Navier–Stokes (RANS) equation in the x-direction can be expressed as (Guo and Julien [18])

$$\begin{aligned}&\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 \end{aligned}$$
(1)
$$\begin{aligned}&v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} =\frac{\rho _m}{\overline{\rho }}g\sin \theta +\nu _m\left( \frac{\partial ^2 u}{\partial y^2}+\frac{\partial ^2 u}{\partial z^2}\right) +\left[ \frac{\partial }{\partial y}\left( -\overline{u^\prime v^\prime }\right) +\frac{\partial }{\partial z}\left( -\overline{u^\prime w^\prime }\right) \right] \end{aligned}$$
(2)

where \(\theta \) is the angle between the channel bed and the horizontal line; g is gravitational acceleration; \(\nu _m(=\frac{\mu _m}{\overline{\rho }})\) is the kinematic viscosity of sediment–fluid mixture; \(\mu _m\) is the dynamic viscosity of sediment–fluid mixture; \(\rho _m\) is the density of sediment–fluid mixture; \(\overline{\rho }\) is the domain averaged density of sediment–fluid mixture which can be expressed as

$$\begin{aligned} \bar{\rho }=\frac{1}{A}\int \int \rho _m dA \end{aligned}$$
(3)

considering \(\rho _m\) does not change along the stream-wise direction. Here \(A=2B\times H\) be the cross-sectional area of the channel and \(dA=dydz\). Let \(S=\sin \theta \) be the bed slope of the channel.

Fig. 1
figure 1

Schematic diagram of two-dimensional velocity distribution along vertical (z) and transverse (y) directions

Full size image

Rearranging the terms and substituting \(S=\sin \theta \) into Eq. (2), one gets

$$\begin{aligned} v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=\frac{\rho _m}{\overline{\rho }}gS+\frac{1}{\overline{\rho }}\frac{\partial }{\partial y}(\tau _{ty})+ \frac{1}{\overline{\rho }}\frac{\partial }{\partial z}(\tau _{tz}) \end{aligned}$$
(4)

where \(\tau _{ty}\) and \(\tau _{tz}\) are the total shear stresses given by

$$\begin{aligned}&\tau _{ty}=\mu _m\frac{\partial u}{\partial y}+(-\bar{\rho }\overline{u^\prime v^\prime }) \end{aligned}$$
(5a)
$$\begin{aligned}&\tau _{tz}=\mu _m\frac{\partial u}{\partial z}+(-\bar{\rho }\overline{u^\prime w^\prime }) \end{aligned}$$
(5b)

The first terms of the right hand sides of Eqs. (5a) and (5b) are the shear stresses due to viscosity, and the second terms of the right hand sides of Eqs. (5a) and (5b) are the shear stresses due to turbulence or Reynolds shear stresses. According to the Boussinesq hypothesis,

$$\begin{aligned}&-\overline{u^\prime v^\prime }=\varepsilon _{ty}\frac{\partial u}{\partial y} \end{aligned}$$
(6a)
$$\begin{aligned}&-\overline{u^\prime w^\prime }=\varepsilon _{tz}\frac{\partial u}{\partial z} \end{aligned}$$
(6b)

where \(\varepsilon _{ty}\) and \(\varepsilon _{tz}\) are the coefficients of turbulent diffusivity or eddy viscosity along transverse and vertical directions, respectively. Then, from Eqs. (5a) and (5b) with the help of Eqs. (6a) and (6b), we get

$$\begin{aligned} \tau _{ty}=\bar{\rho }(\nu _m+\varepsilon _{ty})\frac{\partial u}{\partial y} \end{aligned}$$
(7a)
$$\begin{aligned} \tau _{tz}=\bar{\rho }(\nu _m+\varepsilon _{tz})\frac{\partial u}{\partial z} \end{aligned}$$
(7b)

Inserting the values of \(\tau _{ty}\) and \(\tau _{tz}\) in Eq. (4), the RANS equation can be expressed as:

$$\begin{aligned}&(\nu _m + \varepsilon _{ty})\frac{\partial ^2 u}{\partial y^2}\ +\ \frac{\partial u}{\partial y} \frac{\partial (\nu _m +\varepsilon _{ty})}{\partial y}\ +\ (\nu _m + \varepsilon _{tz})\frac{\partial ^2 u}{\partial z^2}\ +\ \frac{\partial u}{\partial z} \frac{\partial (\nu _m +\varepsilon _{tz})}{\partial z}\ \nonumber \\&\quad -\ v\frac{\partial u}{\partial y}\ -\ w\frac{\partial u}{\partial z} =-\frac{\rho _m}{\bar{\rho }}gS \end{aligned}$$
(8)

An approximate formulation of the eddy viscosity \(\varepsilon _{ty}\) of Eq. (8) is obtained by Ikeda [22] from the logarithmic law as

$$\begin{aligned} \varepsilon _{ty}=\frac{\kappa }{6}\overline{u}_*H \end{aligned}$$
(9)

in which \(\kappa \) is the von Karman constant and \(\bar{u}_*\) is the spatially averaged shear velocity. \(\bar{u}_*\) varies sinusoidally in the transverse direction in a wide channel due to the secondary currents. A parabolic distribution of the eddy viscosity \(\varepsilon _{tz}\) is often modelled by using the linear law of fluid shear stress and the logarithmic law of stream-wise mean velocity as (Graf [15], Yang [52])

$$\begin{aligned} \varepsilon _{tz}=\kappa u_{*b}z\ \left( 1-\frac{z}{H} \right) \end{aligned}$$
(10)

in which \(u_{*b}\) is the local bed shear velocity. Wang and Cheng [50] developed a relation between the spatially averaged shear velocity \(\bar{u}_*\) and the local bed shear velocity \(u_{*b}\) in narrow open channels as follows:

$$\begin{aligned} \bar{u}_*=\frac{1}{2B}\int _{-B}^B u_{*b} \left[ 1+0.18\ cos\left( \frac{\pi y}{H}\right) \right] ^{-1/2} dy =\frac{u_{*b}}{Ar/2} \int _0^{Ar/2} [1+0.18\ cos(\pi t)]^{-1/2} dt \end{aligned}$$
(11)

where \(Ar=2B/H\) is the aspect ratio of the channel. Using Eq. (11), the eddy viscosity \(\varepsilon _{tz}\) can be expressed as

$$\begin{aligned} \varepsilon _{tz}=\kappa \lambda \bar{u}_*z \left( 1-\frac{z}{H} \right) \end{aligned}$$
(12)

where \(\lambda =Ar/[2\int _{0}^{Ar/2}[1+0.18\ cos(\pi t)]^{-1/2}\ dt]\) is a constant.

The density \(\rho _m\) of fluid–sediment mixture depends on the volumetric concentration, densities of fluid and sediment particles and can be expressed as [12]

$$\begin{aligned} \rho _m=\rho _s C+\rho _f(1-C) \end{aligned}$$
(13)

where \(\rho _s\) is the density of sediment; \(\rho _f\) is the density of fluid; C is the volumetric concentration of sediment; \((1-C)\) is the volumetric concentration of fluid. When the accelerating or decelerating sediment particles transport through the fluid, the surrounding fluid also moves. As the sediment particles and fluid cannot occupy the same physical space simultaneously, we need to include the added fluid mass in the density of sediment particles. The modified density of sediment particle \(\rho _s\) becomes (Montes [34])

$$\begin{aligned} \rho _s=\rho _s + K \rho _f \end{aligned}$$
(14)

where K is the coefficient of added fluid mass. Substituting the modified value of \(\rho _s\) in Eq. (13), the modified density of fluid–sediment mixture becomes

$$\begin{aligned} \rho _m=(\rho _s+K\rho _f)C+\rho _f(1-C) =\rho _f[1+(R+K)C] \end{aligned}$$
(15)

where \(R=\frac{\rho _s}{\rho _f}-1\) is the submerged specific gravity of sediment particles.

Pal and Ghoshal [38] studied the effect of suspension concentration on the kinematic viscosity of the fluid–sediment mixture and suggested that the kinematic viscosity of fluid–sediment mixture \(\nu _m\) can be expressed as

$$\begin{aligned} \frac{\nu _m}{\nu _f}=\frac{\mu _r}{1+RC} \end{aligned}$$
(16)

where \(\nu _f\) is the kinematic viscosity of the fluid, \(\mu _r\) is the relative viscosity of the sediment–fluid mixture, R is the submerged specific gravity of sediment particle, C is the volumetric concentration of sediment particle. Many expressions of \(\mu _r\) are available in the literature. Here, one of the most widely cited expressions of \(\mu _r\) suggested by Barnes et al. [2] has been considered which is given by

$$\begin{aligned} \mu _r=\left( 1-\frac{C}{C_{max}}\right) ^{-[\mu ]C_{max}} \end{aligned}$$
(17)

where [\(\mu \)] is the intrinsic viscosity which can be taken as 3 following Leighton and Acrivos [29] and \(C_{max}\) is the maximum volumetric concentration of suspended sediment particles, taken as 2/3 following Cheng [5]. Then, the expression of \(\mu _r\) can be written as

$$\begin{aligned} \mu _r=\left( 1-\frac{3C}{2}\right) ^{-2} \end{aligned}$$
(18)

Combining Eqs. (16), (17) and (18), \(\nu _m\) can be written as

$$\begin{aligned} \nu _m=\frac{\nu _f\left( 1-\frac{3C}{2}\right) ^{-2}}{1+RC} \end{aligned}$$
(19)

In order to compute the stream-wise mean velocity distribution, a two-dimensional expression of concentration distribution, i.e. an expression of concentration in the yz plane, needs to be considered. To the best of the authors’ knowledge, no significant expression of concentration in the yz plane is available in the literature. So to find C(y, z), we apply the concept of secondary circulation in yz plane with a simple liberalization of the flow field [11]. According to Coleman [6] and Kundu and Ghoshal [26], for upward secondary current, concentration increases and downward secondary current, it decreases and the concentration varies periodically along the lateral direction with periodicity 2H of the span of counter rotating secondary cells. Generally, for the vertical distribution of sediment concentration, the Rouse equation is considered [42]. Therefore, the final expression of concentration can be taken as the superposition of the Rouse model and the periodic sine function as

$$\begin{aligned} \frac{C(y,z)}{C_a}=\left( \frac{z_a/H}{1-z_a/H} \frac{1-z/H}{z/H} \right) ^{R_*} + sin\left( \frac{\pi }{2} \frac{y/H}{Ar} \right) \end{aligned}$$
(20)

where \(C_a\) is the reference concentration; \(R_*=\frac{\omega _s}{\beta \kappa u_*}\) is the Rouse no. in which \(\omega _s\) is the settling velocity of a sediment particle in clear fluid, \(\beta\) is the ratio of sediment diffusion coefficient to momentum diffusion coefficient and \(u_*\) is the shear velocity of the flow; \(z_a\) is the reference vertical height of the channel; \(Ar=2B/H\) is the aspect ratio of the channel.

In three-dimensional flow, the flow is comprised of primary flow, which is parallel to the main flow and secondary flows or currents that are transverse to the main flow. The secondary currents are minor flow compared to the main flow. Secondary currents of Prandtl’s second kind are induced by the turbulence and occur due to the flow non-uniformities near the walls by anisotropic turbulence [40]. The maximum velocity of these kinds of secondary currents is less than \(5\%\) of the maximum velocity of the mean longitudinal velocity. The structures of secondary current in wide and narrow open channels are different, which is shown in Fig. 2. In open-channel flow, the sidewalls strongly influence velocity profile in narrow channels, whereas there is less influence in wide channels. Due to the sidewall effect, the maximum velocity in narrow open channels occurs below the free surface, known as dip-phenomenon [17]. It can be seen from Fig. 2 that due to the presence of the free surface vortex in narrow open channels, secondary current w(y, z) at the central section acts along the vertically downward direction. In the case of wide open channels with alternate rough and smooth fixed beds (attached to the channel bottom), w(y, z) acts along the vertically downward direction over the rough bed surface at the central section of the channel. Under such assumptions, the vertical secondary current component w(y, z) can be modelled according to Wang and Cheng [51] as

$$\begin{aligned} w(y,z)=-w_{max} \ sin\left( \frac{\pi z}{H}\right) cos\left( \frac{\pi y}{H}\right) \end{aligned}$$
(21)

where \(w_{max}\) is the maximum velocity of w. Putting this value of w(y, z) in Eq. (1) and then integrating, we get

$$\begin{aligned} v(y,z)=w_{max} \ cos\left( \frac{\pi z}{H}\right) sin\left( \frac{\pi y}{H}\right) \end{aligned}$$
(22)

To non-dimensionalize Eq. (8), we use the following variables

$$\begin{aligned} \widetilde{z}&=\frac{z}{H},&\widetilde{y}&=y/H,&\widetilde{u}&=\frac{u}{\overline{u}_*},&\widetilde{v}&=\frac{v}{\overline{u}_*},\\ \widetilde{w}&=\frac{w}{\overline{u}_*},&\widetilde{\varepsilon }_{ty}&=\frac{\varepsilon _{ty}}{\overline{u}_* H},&\widetilde{\varepsilon }_{tz}&=\frac{\varepsilon _{tz}}{\overline{u}_* H},&\widetilde{\nu }_m&=\frac{\nu _m}{\overline{u}_* H} \end{aligned}$$

and then the governing equation becomes

$$\begin{aligned}&(\widetilde{\nu }_m+\widetilde{\varepsilon }_{ty})\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{y}^2} + (\widetilde{\nu }_m+\widetilde{\varepsilon }_{tz})\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{z}^2} +\left[ \frac{\partial }{\partial \widetilde{y}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{ty})-\widetilde{v}\right] \frac{\partial \widetilde{u}}{\partial \widetilde{y}}\nonumber \\&\quad +\left[ \frac{\partial }{\partial \widetilde{z}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{tz})-\widetilde{w}\right] \frac{\partial \widetilde{u}}{\partial \widetilde{z}}=-\frac{\rho _m}{\overline{\rho }} \frac{gSH}{\overline{u}_*^2} \end{aligned}$$
(23)

Here, \(\widetilde{u}(\widetilde{y},\widetilde{z})\) is the primary mean velocity along the cross-sectional yz direction. The secondary currents \(\widetilde{v}(\widetilde{y},\widetilde{z})\) and \(\widetilde{w}(\widetilde{y},\widetilde{z})\) are given in Eqs. (22) and (21), respectively.

Fig. 2
figure 2

Schematic pattern of secondary current- a in narrow open channel ([37]) and b in wide open channel for both smooth and rough non-erodible bed surface ([23, 51])

Full size image

To solve the governing Eq. (23), boundary conditions along vertical and boundary conditions along transverse direction both are needed. Boundary conditions along the vertical direction are given as follows:

$$\begin{aligned}&\widetilde{u}(\widetilde{y},\widetilde{z})\Big |_{\widetilde{z}=0}=\widetilde{u}_a \end{aligned}$$
(24)
$$\begin{aligned}&\widetilde{u}(\widetilde{y},\widetilde{z})\Big |_{\widetilde{z}=1}=\widetilde{u}_b \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\partial \widetilde{u}}{\partial \widetilde{z}}\Bigg |_{\widetilde{z}=\widetilde{z}_d}=0 \end{aligned}$$
(26)

where \(\widetilde{u}_a(=u_a/\overline{u}_*)\) is the primary mean velocity at the bottom of the channel. Its value is very small and dependent on the bed roughness (in plane bed, its value is zero). Here, \(\widetilde{u}_b(=u_b/\overline{u}_*)\) is the primary mean velocity at the free surface and \(\widetilde{z}_d=z_d/H\) is the dimensionless distance from channel bed to velocity dip position.

Boundary conditions along the transverse direction are given as follows:

$$\begin{aligned}&\frac{\partial \widetilde{u}}{\partial \widetilde{y}}\Bigg |_{\widetilde{y}=0}=0 \end{aligned}$$
(27)
$$\begin{aligned}&\widetilde{u}(\widetilde{y},\widetilde{z})\Big |_{\widetilde{y}=|B/H|}=\widetilde{u}_w \end{aligned}$$
(28)

where \(\widetilde{u}_w(=u_w/\overline{u}_*)\) is the sidewall velocity of the flow. In the next section, the governing Eq. (23) is solved numerically with the help of boundary conditions Eqs. (24) to (28) using the finite difference method.

3 Numerical Solution

The governing equation given by Eq. (23) can be written as follows:

$$\begin{aligned} M\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{y}^2} + N\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{z}^2} +P\frac{\partial \widetilde{u}}{\partial \widetilde{y}} +Q\frac{\partial \widetilde{u}}{\partial \widetilde{z}} + R = 0 \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned}&M=(\widetilde{\nu }_m+\widetilde{\varepsilon }_{ty})\\&N=(\widetilde{\nu }_m+\widetilde{\varepsilon }_{tz})\\&P=\left[ \frac{\partial }{\partial \widetilde{y}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{ty})-\widetilde{v}\right] \\&Q=\left[ \frac{\partial }{\partial \widetilde{z}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{tz})-\widetilde{w}\right] \\&R=\frac{\rho _m}{\overline{\rho }} \frac{gSH}{\overline{u}_*^2} \end{aligned} \end{aligned}$$
(30)

Here, the explicit expressions of P and Q are given as

$$\begin{aligned} \begin{aligned} P&= \left[ \frac{\partial }{\partial \widetilde{y}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{ty})-\widetilde{v}\right] =\frac{\nu _f}{\overline{u}_* H} \frac{\partial }{\partial \widetilde{y}} \left\{ \frac{ \left( 1-3C/2 \right) ^{-2}}{1+RC} \right\} + \frac{\partial }{\partial \widetilde{y}} \left( \frac{\kappa }{6} \right) - \frac{w_{max}}{\overline{u}_*} cos (\pi \widetilde{z}) sin (\pi \widetilde{y})\\&=\frac{\nu _f}{\overline{u}_* H} \frac{\left( 1-3C/2 \right) ^{-2} \left\{ 3 \left( 1- 3C/2\right) ^{-1} \ (1+RC) - R \right\} }{(1+RC)^2} \frac{\partial C}{\partial \widetilde{y}} - \frac{w_{max}}{\overline{u}_*} cos (\pi \widetilde{z}) sin (\pi \widetilde{y}) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Q&= \left[ \frac{\partial }{\partial \widetilde{z}} (\widetilde{\nu }_m+\widetilde{\varepsilon }_{tz}) -\widetilde{w}\right] = \frac{\nu _f}{\overline{u}_* H} \frac{\partial }{\partial \widetilde{z}} \left\{ \frac{ \left( 1-3C/2 \right) ^{-2}}{1+RC} \right\} + \frac{\partial }{\partial \widetilde{z}} ( \kappa \lambda \widetilde{z} (1-\widetilde{z})) + \frac{w_{max}}{\overline{u}_*} sin (\pi \widetilde{z}) cos(\pi \widetilde{y}) \\&= \frac{\nu _f}{\overline{u}_* H} \frac{\left( 1-3C/2 \right) ^{-2} \left\{ 3 \left( 1- 3C/2\right) ^{-1} \ (1+RC) - R \right\} }{(1+RC)^2} \frac{\partial C}{\partial \widetilde{z}} + \kappa \lambda (1-2\widetilde{z}) + \frac{w_{max}}{\overline{u}_*} sin (\pi \widetilde{z}) cos(\pi \widetilde{y}) \end{aligned} \end{aligned}$$

in which

$$\begin{aligned} &C=c_a \left\{ \left( \frac{\widetilde{z}_a}{1-\widetilde{z}_a} \frac{1-\widetilde{z}}{\widetilde{z}} \right) ^{R_*} + sin \left( \frac{\pi }{2} \frac{\widetilde{y}}{Ar} \right) \right\} , \ \ \ \widetilde{z}_a=z_a/H \\ &\frac{\partial C}{\partial \widetilde{y}} = \frac{c_a \pi }{2\ Ar} cos \left( \frac{\pi \widetilde{y}}{2\ Ar} \right) \\ &\frac{\partial C}{\partial \widetilde{z}} = -c_a R_* \frac{\widetilde{z}_a}{1-\widetilde{z}_a} \left( \frac{\widetilde{z}_a}{1-\widetilde{z}_a} \frac{1-\widetilde{z}}{\widetilde{z}} \right) ^{R_* -1} \frac{1}{\widetilde{z}^2} \end{aligned}$$

In the present study, the finite difference method has been adopted to solve the governing equation. Considering \(L_y\) and \(L_z\) as the lengths of the domain in \(\widetilde{y}\) and \(\widetilde{z}\) direction, respectively, the whole domain can be divided into \(s-1\) number of equal parts of length \(\varDelta \widetilde{y}=\frac{L_y}{s-1}\) at \(\widetilde{y}\) direction and \(t-1\) number of equal parts of length \(\varDelta \widetilde{z}=\frac{L_z}{t-1}\) at \(\widetilde{z}\) direction. The coordinates of the grid points are defined as \(\widetilde{y}_i=\widetilde{y}_1 +(i-1)\varDelta \widetilde{y}\) for \(i=1,2,...,s\) and \(\widetilde{z}_j=\widetilde{z}_1 +(j-1)\varDelta \widetilde{z}\) for \(j=1,2,...,t\) in \(\widetilde{y}\) and \(\widetilde{z}\) direction, respectively. Here, \(\widetilde{y}_1=0\) and \(\widetilde{z}_1=\widetilde{z}_a\) are the reference heights in \(\widetilde{y}\) and \(\widetilde{z}\) direction, respectively. Assuming \(\widetilde{u}_{i,j}\) be the numerical value of \(\widetilde{u}(\widetilde{y},\widetilde{z})\) at the (i, j)-th grid point, second-order finite difference approximations of \(\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{y}^2}\), \(\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{z}^2}\), \(\frac{\partial \widetilde{u}}{\partial \widetilde{y}}\) and \(\frac{\partial \widetilde{u}}{\partial \widetilde{z}}\) at the same grid point can be written as follows:

$$\begin{aligned}&\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{y}^2}\Bigg |_{i,j} = \frac{\widetilde{u}_{i+1,j}-2 \widetilde{u}_{i,j}+\widetilde{u}_{i-1,j}}{(\varDelta \widetilde{y})^2} \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial ^2 \widetilde{u}}{\partial \widetilde{z}^2}\Bigg |_{i,j} = \frac{\widetilde{u}_{i,j+1}-2 \widetilde{u}_{i,j}+\widetilde{u}_{i,j-1}}{(\varDelta \widetilde{z})^2} \end{aligned}$$
(32)
$$\begin{aligned}&\frac{\partial \widetilde{u}}{\partial \widetilde{y}}\Bigg |_{i,j}=\frac{\widetilde{u}_{i+1,j}-\widetilde{u}_{i-1,j}}{2\varDelta \widetilde{y}} \end{aligned}$$
(33)
$$\begin{aligned}&\frac{\partial \widetilde{u}}{\partial \widetilde{z}}\Bigg |_{i,j}=\frac{\widetilde{u}_{i,j+1}-\widetilde{u}_{i,j-1}}{2\varDelta \widetilde{z}} \end{aligned}$$
(34)

Discretizing Eq. (29) with the help of second-order difference approximations given by Eqs. (31–34) and rearranging the terms, discretized equation at the grid point (i, j) can be written as follows:

$$\begin{aligned}&\left[ \frac{N_{i,j}}{(\varDelta \widetilde{z})^2}-\frac{Q_{i,j}}{2\varDelta \widetilde{z}}\right] \widetilde{u}_{i,j-1} +\left[ \frac{M_{i,j}}{(\varDelta \widetilde{y})^2}-\frac{P_{i,j}}{2\varDelta \widetilde{y}}\right] \widetilde{u}_{i-1,j} -\left[ \frac{2N_{i,j}}{(\varDelta \widetilde{z})^2} +\frac{2M_{i,j}}{(\varDelta \widetilde{y})^2}\right] \widetilde{u}_{i,j}\nonumber \\&\quad + \left[ \frac{M_{i,j}}{(\varDelta \widetilde{y})^2}+\frac{P_{i,j}}{2\varDelta \widetilde{y}}\right] \widetilde{u}_{i+1,j}+ \left[ \frac{N_{i,j}}{(\varDelta \widetilde{z})^2}+\frac{Q_{i,j}}{2\varDelta \widetilde{z}}\right] \widetilde{u}_{i,j+1} + R_{i,j}=0, \end{aligned}$$
(35)

for \(i=2,3,4,....,s-1\) and \(j=2,3,4,....,t-1\).

The boundary conditions given by Eqs. (24–28) can be discretized as

$$\begin{aligned}&\widetilde{u}_{i,1}=\widetilde{u}_a, \ \text {for}\ \ i=1,2,...,s \end{aligned}$$
(36)
$$\begin{aligned}&\widetilde{u}_{i,t}=\widetilde{u}_b, \ \text {for}\ \ i=1,2,...,s \end{aligned}$$
(37)
$$\begin{aligned}&\frac{\widetilde{u}_{i,l+1}-\widetilde{u}_{i,l-1}}{2\varDelta \widetilde{z}}=0,\ \text {for} \ \ i=1,2,...,s \end{aligned}$$
(38)

where l is the grid point in \(\widetilde{z}\) direction where \(\widetilde{z}=\widetilde{z}_d\) i.e. \(\widetilde{z}_l=\widetilde{z}_d\).

$$\begin{aligned} \frac{-3\widetilde{u}_{1,j}+4\widetilde{u}_{2,j}-\widetilde{u}_{3,j}}{2\varDelta \widetilde{y}}=0,\ \text {for} \ \ j=1,2,...,t \end{aligned}$$
(39)

and

$$\begin{aligned} \widetilde{u}_{s,j}=\widetilde{u}_w, \ \text {for} \ \ j=1,2,...,t \end{aligned}$$
(40)

respectively. The above defined equations have double index notations. However, it will be easier to understand and solve these equations if one converts them into single index notations. So using the transformation given by \(n=i+(j-1)s\), the governing equation and the boundary conditions in single index notation can be written as follows:

$$\begin{aligned}&\left[ \frac{N_n}{(\varDelta \widetilde{z})^2}-\frac{Q_n}{2\varDelta \widetilde{z}}\right] \widetilde{u}_{n-s} +\left[ \frac{M_n}{(\varDelta \widetilde{y})^2}-\frac{P_n}{2\varDelta \widetilde{y}}\right] \widetilde{u}_{n-1} -\left[ \frac{2N_{n}}{(\varDelta \widetilde{z})^2} +\frac{2M_{n}}{(\varDelta \widetilde{y})^2}\right] \widetilde{u}_{n}\nonumber \\&\quad + \left[ \frac{M_{n}}{(\varDelta \widetilde{y})^2}+\frac{P_{n}}{2\varDelta \widetilde{y}}\right] \widetilde{u}_{n+1}+ \left[ \frac{N_{n}}{(\varDelta \widetilde{z})^2}+\frac{Q_{n}}{2\varDelta \widetilde{z}}\right] \widetilde{u}_{n+s} + R_{n}=0, \end{aligned}$$
(41)

for \(n=s+2,s+3,..,2s-1,2s+2,...,3s-1,.....,(t-2)s+2,...,(t-1)s-1.\)

$$\begin{aligned}&\widetilde{u}_{n}=\widetilde{u}_a, \ \text {for}\ \ n=1,2,...,s \end{aligned}$$
(42)
$$\begin{aligned}&\widetilde{u}_{n}=\widetilde{u}_b, \ \text {for}\ \ n=(t-1)s+1,(t-1)s+2,...,st \end{aligned}$$
(43)
$$\begin{aligned}&\widetilde{u}_{n+s}-\widetilde{u}_{n-s}=0,\ \text {for} \ \ n=i+(l-1)s \ \text {where} \ \ i=1,2,...,s \end{aligned}$$
(44)
$$\begin{aligned}&-3\widetilde{u}_{n}+4\widetilde{u}_{n+1}-\widetilde{u}_{n+2}=0,\ \text {for} \ \ n=1,1+s,1+2s,...,1+(t-1)s \end{aligned}$$
(45)
$$\begin{aligned}&\widetilde{u}_{n}=\widetilde{u}_w, \ \text {for} \ \ n=s,2s,...,st \end{aligned}$$
(46)

Finally, one has an algebraic system of equations with st number of variables as \((\widetilde{u}_1, \widetilde{u}_2,..., \widetilde{u}_{st})\) to be solved and to that purpose, a MATLAB code has been written. In the next section, the solution of the problem has been validated with existing experimental data under different conditions.

4 Result and discussion

This section discusses the distribution of the stream-wise mean velocity along the directions of vertical, transverse and yz plane of the flow. The centreline velocity distribution indicates the distribution of the stream-wise mean velocity along the vertical direction, which is measured at \(y=0\), i.e. at the middle point of the width of the channel. Cross-sectional velocity distribution indicates the distribution of the stream-wise mean velocity along the yz plane of the flow and transverse velocity distribution is along the y direction, measured at different heights of the open channel.

Determination of the centreline velocity, cross-sectional velocity and transverse velocity from the above described numerical scheme has been done in the following way. From Eqs. (41–46), one can understand that these equations represent st numbers of an algebraic system of equations with st number of variables. Solving this system of equations, one can get \(u_n\), for all values of n, \(n=1,2,..,st\). Then, using the transformation \(n=i+(j-1)s\), one gets u for all the grid points of \(\widetilde{y}\) and \(\widetilde{z}\). This whole distribution of the stream-wise mean velocity, i.e. u(i, j) for all values of i and j represents the cross-sectional velocity distribution in yz cross-sectional plane. Centreline velocity distribution is the velocity distribution along the vertical direction corresponding to the grid point \(i=1\), i.e. u(1, j), for all values of j. Here, transverse velocity distribution is the distribution of stream-wise mean velocity along the transverse direction at a particular vertical grid point j, i.e. \(u(i,j=p)\) for all values of i and considering \(j=p\) grid point corresponds to that required vertical height where our interest lies in finding transverse distribution.

In the following subsections, validation of the proposed model is discussed by comparing it with existing experimental data for both wide and narrow open channels. As the proposed model considers the effect of secondary current, the experimental data are chosen so that it contains this effect. Here, the maximum value of secondary current (\(w_{max}\)) is taken as \(1.5\%\) of the stream-wise mean velocity \((u_{max})\) (Tominaga et al. [45]).

4.1 Considered experimental data

To validate the model, experimental data of Coleman [7], Vanoni [47], Tominaga et al. [45] and Sarma et al. [43] are considered, a short description of which follows.

Coleman [7] did experiments in a smooth flume which was 356 mm wide and 15 m long. In this experiment, flow depth was nearly constant and about 1.71 m. The experiment contained 40 test cases where energy slope S was kept 0.002 for \(1-37\) tests (runs) and 0.0022 for the rest. All tests were performed for sediment-mixed flow except tests 1, 21 and 32, which were performed for clear water flow.

Vanoni [47] performed experiments in two series in a 33.25-inches-wide and 60-feet-long flume which had adjustable bed slope. In series I, test cases 1, 2 and 3 were performed for clear water and the rest of the test cases \((1-13)\) for sediment-mixed flow in which S was kept to be 0.0025. In series II, test cases 14a, 14b and 21 were performed for clear water flow and the rest of the test cases \((14-22)\) for sediment-mixed flow. In all these test cases, maximum velocity occurs at the free surface and the aspect ratio varies from 5 to 11.90.

Tominaga et al. [45] measured the three-dimensional turbulent structure with hot-film anemometers in three straight open channels, including a smooth rectangular flume which was 12.5-m-long and 40 cm \(\times \) 40 cm cross section. The bed wall was a painted iron plate, and the sidewalls were made with glass. Filters were set up in the settling tank to exclude any suspended impurities. At the entrance of the channel, honeycomb and mesh screens were set up to regulate the flow. A tripping wire was set up at the channel entrance to enhance the turbulent flow. A fully developed, uniform flow was established at the test section 7.5 m downstream from the channel entrance by adjusting the bed slope and the movable weir at the channel end. In these experiments, width was kept fixed and flow depth H was changed.

Sarma et al. [43] studied the velocity distribution in a smooth rectangular channel by dividing the channel into four regions. The experiments were conducted in a smooth, straight, horizontal rectangular flume of smooth walls of length 15.25 m, width 61 cm and height 30 cm, in which the channel bed was kept very nearly horizontal. The experiments were conducted in two stages. The first stage was carried out in a 61-cm -wide flume, and the second stage was in a 30.5-cm-wide flume. The experiments covered specific aspect ratios and Froude numbers in each stage where Ar varied from 1 to 8. A parabolic law was considered to determine the velocity distribution in region 1, i.e. in the inner region of the bed and the outer region of the sidewall, which is of the following form:

$$\begin{aligned} \frac{u_{max}-u}{u_*}=K_w\left( 1-\frac{y}{B}\right) ^2 \end{aligned}$$
(47)

in which \(K_w\) is the coefficient in the law for the outer region of the sidewall very close to the bed, whose value was found as 2.4.

4.2 Variation of velocity profile with concentration

4.2.1 Cross-sectional velocity distribution

Figure 3 shows the variation of the velocity contour in the cross-sectional yz plane due to the presence of sediment particles. The figure considers three channels with aspect ratios 2.01, 3.94 and 8, as mentioned in Tominaga et al. [45]. Here, we assume that the sediment particles are mixed over the whole domain and transported with the flow without forming any beds. The values of other parameters are taken from the experiments of [45]. Three different reference concentrations, 0.001, 0.05 and 0.1, are considered to show the difference among the contour lines clearly. It can be observed from the figure that contour lines are open for wide channels with an aspect ratio 8. As the aspect ratio decreases, contour lines gradually close. This occurs due to the effects of sidewalls in narrow channels. Throughout the cross section of the narrow channel, maximum velocity appears below the free surface and as a result, contour lines around the dip-position shift vertically towards the mid-depth of the channel. Apart from this, it is also found that with the increase in the sediment concentration in the flow, contour lines shift towards the boundary wall, showing the importance of including the effects of concentration in the velocity model. It is also to be noted that the effect of presence of sediment particles towards bottom and sidewall boundaries gradually decreases as no significant difference in contour lines is observed. This can be explained as follows: Yang [52] analyzed the data of [4] and found that the Reynolds shear stress increases in the presence of sediment particles. According to a similar analogy with viscous shear stress, it is known that the Reynolds shear is proportional to the velocity gradient, i.e. \(\overline{u'w'} \sim du/dz\). As a result, the velocity gradient increases in the presence of sediment particles, increasing the velocity in the main flow domain that shifts the contour lines towards boundary regions. Also, near the boundaries, Reynolds shear stress does not show any significant change due to sediment particles [52]; consequently, no significant change in the velocity contour lines occurs.

Fig. 3
figure 3

Effect of concentration on cross-sectional velocity distribution in three different cases—a \(Ar = 8\), b \(Ar = 3.94\) and c \(Ar = 2.01\)

Full size image

4.2.2 Transverse velocity distribution

The effect of concentration on the transverse velocity profile is shown in Fig. 4. This figure presents three transverse velocity profiles, one without the sediment, i.e. for clear water flow and the other two for sediment-mixed flow. The transverse velocity profiles are evaluated at \(\frac{z}{H}=0.1\) and for \(Ar=2\) [43]. As already mentioned, the sediment-mixed flow is considered the flow where sediment particles are mixed throughout the whole flow domain and moving with the flow without deposition at the channel bottom. The required parameters are given inside the figure. In the figure, the red dashed line represents the velocity profile in the absence of sediment concentration in the flow, i.e., when \(C_a=0\). The green dotted line and the blue line represent the velocity profiles with the presence of concentration in the flow, where \(C_a\) has been taken as 0.1 and 0.5, respectively. It can be observed from the figure that the difference is prominent in the main flow region and as the curves reach the sidewall, the difference fades away. This behaviour can be explained as follows—near the sidewall, the sediment concentration is low compared to the main flow region; as a result, the effect of the presence of sediments on velocity near the sidewall is almost negligible. Also, at the centreline, the velocity slightly increases with the increase in sediment particles. This occurs due to the increase in the Reynolds shear stress in the presence of sediment particles.

Fig. 4
figure 4

Effect of concentration on transverse velocity profile

Full size image

4.3 Application to laboratory data

4.3.1 Centreline velocity distribution

In this section, validation of the proposed model at the centreline along the vertical direction is discussed by considering experimental data for wide and narrow open channels for both sediment-mixed and clear water flow. To that purpose, the experimental data of Coleman [7] are considered for narrow open channels and the experimental data of Vanoni [47] are considered for wide open channels.

To validate the proposed model, six different test cases of Coleman [7] have been considered; test cases 10, 17 and 31 are chosen for sediment-mixed flow, and test cases 1, 21 and 32 are chosen for clear water flow. In all the test cases, aspect ratio Ar ranges from 2.07 to 2.11. Experimental data of Coleman [7] and computed velocity from the proposed model are plotted in Figs. 5 and 6. Values of the different flow parameters for these cases are given inside the figures. Good agreement in all six cases shows that the proposed model can predict the distribution of stream-wise mean velocity along the vertical direction in narrow open channels for both sediment-mixed and clear water flow.

Fig. 5
figure 5

Comparing experimental data of Coleman [8] for centreline velocity with test result for sediment-mixed fluid

Full size image
Fig. 6
figure 6

Comparing experimental data of Coleman [8] for centreline velocity with test result for clear fluid

Full size image

Out of all the test cases of Vanoni [47], test cases 5, 10 and 19 are selected for sediment-mixed flow and test cases 1, 2 and 14a are selected for clear water flow to validate the proposed model. Computed velocity from the proposed model and experimental data of Vanoni [47] are plotted in Figs. 7 and 8. Related flow parameters are shown inside the figure. Both figures show that the proposed model can also predict stream-wise velocity distribution in the vertical direction for wide channels.

Fig. 7
figure 7

Comparing experimental data of Vanoni [47] for centreline velocity with test results for sediment-mixed fluid

Full size image
Fig. 8
figure 8

Comparing experimental data of Vanoni [47] for centreline velocity with test results for clear fluid

Full size image

4.3.2 Cross-sectional velocity distribution

The experimental data of Tominaga et al. [45] have been used to validate the cross-sectional velocity of this proposed model for clear water flow. Though the proposed model is for sediment-mixed flow, due to the unavailability of relevant data in the literature, the model has been validated for clear water flow by removing the concentration related terms. Comparison of the cross-sectional velocity distribution of experimental data of Tominaga et al. [45] with the present model converted for clear fluid is shown in Fig. 9 for three different aspect ratios (\(Ar=2.01\), 3.94, and 8). Flow parameters are shown in Table 1. The left column of Fig. 9 shows the left-half of the cross-sectional velocity data of Tominaga et al. [45], and the right column of the figure shows the right half of the cross-sectional velocity data of the proposed model. An appropriate calculation is needed to accurately predict the velocity dip position in the computed solution for narrow open channels. The model of Kundu [24] has been chosen for the prediction of velocity dip position as his model accurately predicts the velocity dip position with the least error compared to other models available in the literature. The formula of Kundu [24] for the prediction of velocity dip-position is given as follows-

$$\begin{aligned} \widetilde{z}_d=0.5+\frac{1}{2L} ln[1+(e^L -1)(1-e^{-0.07 Ar^{1.88}})], \end{aligned}$$
(48)

where \(L=0.724\). From Fig. 9, it can be observed that the proposed model characterizes the dip-phenomenon and cross-sectional velocity qualitatively well for clear water flow.

Fig. 9
figure 9

Comparing computed cross-sectional velocity distribution from numerical solution for clear fluid (in right column) with experimental data of Tominaga et al. [45] (in left column) as \(u/u_{max}\) for a \(Ar=2.01\), b \(Ar=3.94\) and c \(Ar=8\)

Full size image
Table 1 Values of the parameters for experiment of Tominaga et al. [45]
Full size table

4.3.3 Transverse velocity distribution

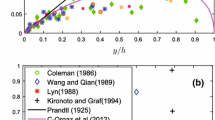
The distribution of velocity along the transverse direction at different heights and for different aspect ratios has been validated with the experimental data of Sarma et al. [43] for clear water flow by removing the concentration related terms in the model as there are no relevant data available for sediment-mixed flow. For \(Ar=2,\) 4 and 8, the experimental data and the computed transverse velocity from the proposed model are plotted in Fig. 10 at heights \(\widetilde{z}=0.1\) and 0.04, respectively. The distribution of stream-wise velocity along the transverse direction from Sarma et al. [43], which is of parabolic pattern, is also plotted in Fig 8. Here also, the model of Kundu [24] has been used for predicting an accurate velocity dip position which is essential for the determination of the transverse velocity distribution. Values of different flow parameters are shown in Table 2. Figure 10 shows that the proposed model can predict the transverse velocity distributions in clear fluid for both narrow and wide open channels. Also, one can observe from the figures that for a higher aspect ratio, the proposed model slightly deviates from the parabolic profile of Sarma et al. [43], and as the aspect ratio increases, the deviation also increases. The existence and the structures of the secondary currents play a significant role in the transverse velocity distribution. Generally, the second kind of cellular secondary current occurs periodically along the transverse direction with the periodicity 2H, which can be seen from Eq. (21). Only one pair of counter rotating circular cells exist for case (a) in Fig. 10, where \(Ar=2\) or \(B=H\). As a result, the periodicity does not occur and the numerical solution of the proposed model matches exactly with the parabolic profile of velocity distribution of Sarma et al. [43]. For cases (b) and (c) in Fig. 10 where \(Ar=4\) and 8, two and four pairs of secondary current cells exist, respectively, and the transverse velocity distribution becomes periodic. Therefore, we notice slight deviations for cases (b) and (c) in Fig. 10.

Fig. 10
figure 10

Comparison of computed transverse velocity distribution of the proposed model with the experimental data and model of Sarma et al. [43] for a \(Ar = 2\) ; b \(Ar = 4\) ; and c \(Ar = 8\)

Full size image
Table 2 Values of parameters for transverse velocity distribution
Full size table

To show the variation of the primary mean velocity along the transverse direction together with the secondary circulation for different aspect ratios for clear water flow, Fig. 11 is plotted. The transverse velocity distributions are plotted in the left column of the figure where non-dimensionalization of y has been done by half of the width of the channel (B) and in the right column, the cross-sectional velocity vectors are plotted from Eqs. (21) and (22) for four different aspect ratios, \(Ar=2\), 4, 6 and 8. Here \(z/H=0.1\) and \(\widetilde{u}_a=16\) and all other parameters are from the experimental data of Sarma et al. [43]. From the figure, it can be seen that when \(Ar=2\), only one circular vortex exists in the secondary circulation and as the aspect ratio increases, the number of the circular vortex also increases due to alternate smooth and rough bed surface and the corresponding transverse velocity distribution becomes periodic [51].

Fig. 11
figure 11

Variation of transverse velocity with secondary circulations for different aspect ratios for clear water flows. Left column represents the transverse velocity distribution, and right column represents the circular secondary currents in half cross-sectional plane for different aspect ratios

Full size image

5 Conclusion

Based on RANS equation, a model for the two-dimensional distribution of stream-wise mean velocity in the presence of sediments has been derived. This model includes the transverse and vertical components of secondary velocity, and the effects of sediment particles have been incorporated through the density and viscosity of the sediment–fluid mixture. As the secondary current has been taken into consideration, the model is capable of addressing dip-phenomenon, which is commonly observed in narrow open channels. The model is validated at the centreline with existing experimental data for both wide and narrow channels, and satisfactory results are obtained. Due to the lack of two-dimensional experimental data of stream-wise mean velocity with sediments, the model has been validated with existing clear water data. It has been found that the presence of sediment particles increases the velocity in the main flow zone and as a result, velocity contour lines shift towards the boundary regions. Also that, for higher aspect ratios, contour lines are open and for smaller aspect ratio, contour lines are closed which shows a similar pattern like clear water flow. Apart from these, the validity of the model has also been tested for transverse velocity distributions in clear water flow and in this case also satisfactory results are obtained. From the variation of transverse velocity with sediment concentration, it is found that the velocity follows a similar pattern as of clear water flow and the effects of concentration are prominent in the main flow region that gradually diminishes towards the sidewall region. The periodic secondary current, which was lacking in previous studies, has been included in this study as the periodic variation of the secondary current is often found in natural rivers. In a broad sense, this study gives an idea about the pattern and variation of stream-wise mean velocity as a two-dimensional distribution in the presence of sediments through an open-channel turbulent flow.