Unsteady two-dimensional distribution of suspended sediment transport in open channels

Abstract

The current work presents a two-dimensional (2D) unsteady suspended sediment transport model for an open channel turbulent flow. Unlike most of the existing similar works in literature who describes either the spatial change or the temporal change in concentration along with vertical distribution, the present study describes spatial, temporal and vertical variation of concentration together. The model is developed from the mixing length point of view, which is an important feature of turbulent flow. It also incorporates the effect of hindered settling velocity of a sediment particle resulting from the presence of other particles in the flow. The developed non-linear partial differential equation together with the most realistic boundary condition has been solved numerically. The findings indicate that the suspension region experiences a decrease in concentration value far from downstream as a result of the modified mixing length of sediment-laden flow and opposite is the case for the hindered settling velocity at any downstream position. Over all, a reduction in the concentration value occurs in the suspension due to the inclusion of these two effects. Also, the hindered settling increases the magnitude of the bottom concentration and the damping factor of mixing length decreases the magnitude of the bottom concentration both the effects being very small. The model has been validated with laboratory data under specified conditions.

1 Introduction

The transportation mechanisms of suspended sediments are observed in natural waterways, including rivers, lakes and oceans and are of significant importance in water supply systems, harbours and other man-made hydraulic structures that undergo turbulent flow. Thus, it has been studied by various branches of engineering and science disciplines, such as environmental engineering, sedimentology, fluid dynamics, ecology, etc.

For a better understanding of suspended sediment transport and the interaction between fluid and sediment particles in turbulent flow, a reliable mathematical model for concentration distribution is necessary. Though several models can be found in the literature that describe the sediment distribution in suspension, most of the available models deal with either steady or unsteady one-dimensional (1D) distribution or steady 2D distribution of sediment concentration in the suspension. Rouse [1], a pioneer in the area of sediment transport, established a 1D sediment transport model that utilized the concept of diffusion and subsequently provided an analytical solution for the model. The major drawback of the Rouse model is that it cannot predict the sediment concentration well near the channel bed and close to the free surface. In order to address the disadvantages, Hunt [2] then analysed the vertical distribution of concentration by studying the sediment phase and water phase separately. To improve the vertical concentration distribution, many works [3,4,5,6,7,8] have been done using different approaches and considering different turbulent phenomena. The literature in this regard is so vast that any survey is insufficient. Several researchers considered the changes of concentration profiles with temporal variation and variation along the main flow direction also, which makes the model more realistic and difficult to solve than the steady vertical distribution of concentration. Mei [9] and Hjelmfelt and Lenau [10], investigated the non-equilibrium sediment transport with constant advection velocity and solved the steady 2D convection-diffusion equation analytically. In their studies, Mei [9] considered a specified constant concentration at the bottom and zero sediment flux at the free surface, while Hjelmfelt and Lenau [10] used a specified constant concentration at the bottom and zero concentration at the free surface. Also, several works can be found in the literature [11,12,13] that have solved steady 2D problem by incorporating constant boundary conditions. Monin [14] and Calder [15] proposed a near-bed boundary condition where the deposition was considered and entrainment was ignored. Considering both entrainment and deposition in the bottom boundary condition, Dobbins [16] solved the unsteady 1D transport problem; but in that work, entrainment rate and deposition flux both were constant, which was an unnecessary constraint. Cheng [17] formulated the generalized boundary conditions at the bottom for non-equilibrium sediment transport in terms of two parameters - the deposition velocity and the equilibrium constant. With this more realistic bottom boundary condition, Liu and Nayamatullah [18] and Liu [19], respectively, solved the unsteady 1D transport equation and the steady 2D transport equation analytically by employing the generalized integral transform technique (GITT) for arbitrary eddy viscosity.

Majority of the previous studies on sediment concentration distribution in suspension assumed constant settling velocity of the sediments [18,19,20]. However, the presence of sediments in sediment-laden flows increases the density resulting in an increment in the buoyancy force of the fluids. This upward force leads to a significant reduction in particle settling velocity, which is referred in the literature [21] as ‘hindered settling velocity’. Various studies [22,23,24] of sediment transport in the literature, considered the effect of hindered settling of sediment to compute the vertical distribution of the sediment concentration. Richardson and Zaki [21] proposed a relation between sediment concentration and sediment settling velocity. The researchers [6, 8, 25,26,27,28] who considered Richardson and Zaki’s expression for settling velocity, mostly studied 1D steady concentration only. Jing et al. [29] proposed a 2D suspended sediment transport model by incorporating concentration-dependent settling velocity and provided a numerical solution. Mohan et al. [30] and Kumbhakar et al. [31] incorporated this effect and semi-analytically solved the unsteady 1D and the steady 2D transport model by the homotopy analysis method (HAM), respectively.

The present study analyses the unsteady 2D sediment transport on the basis of the mixing length formulation. Prandtl [32] initially developed the mixing length theory, which is based on the concept of momentum exchange between layers of fluid in clear water turbulent flow. He correlated the fluctuating velocity in turbulent flow with the momentum transfer that occurs within the flow. During assimilation of fluid parcels, the average distance that the parcels travel, is called ‘mixing length’. Prandtl [32] proposed two expressions of mixing length l: one of them is linear and the other one is parabolic. The linear type expression of mixing length leads to the well-known expression of the universal log-law of velocity distribution. In the literature, there are a number of mixing length expressions developed after Prandtl [32]; but only a few of them are concentration-dependent. Umeyama and Gerritsen [33] proposed a mixing length expression for sediment-mixed flow which was used in their work to construct a model for vertical velocity distribution. They came to the conclusion that the mixing length in high concentration flow is smaller than in low concentration flow or clear water flow. Later, by using the same mixing length, Umeyama [34] investigated the sediment concentration distribution in an open channel turbulent flow. Kovacs [4] generalized the Prandtl-von Karman mixing length expression for sediment-laden flows by including a damping factor $\left( 1 - c^{1/3}\right)$. Ghoshal et al. [35] considered a 1D unsteady advection–diffusion equation that incorporated the hindered settling and the mixing length of Kovacs [4], which made the equation non-linear and provided a numerical solution for sediment concentration in suspension.

From the above literature review, it is observed that the available models of sediment transport in an open channel turbulent flow are mostly in a one-dimensional steady and unsteady state. For two-dimensional case, most of the available models for sediment transport are in a steady state. Under the constant advection assumption, 2D steady transport models are mathematically equivalent to 1D unsteady transport model [18]. Thus, the researchers mostly considered either one of these two, but not the two together. A combination of these two, that is, 2D unsteady transport model is considered by very few researchers [36] may be due to the difficulty in tackling the problem both analytically and numerically. Also, researchers did not consider a combination of mixing length with damping factor and hindered settling effect simultaneously in a 2D unsteady transport model. Variation of sediment distributions in streamwise as well as in vertical direction with time, helps to get a better understanding of sediment transport process. This motivates to broaden the work of Ghoshal et al. [35] who developed a one-dimensional (i.e., vertical) unsteady transport framework with the previously mentioned two important effects. Hence, the present work can be considered as an extension of the work of Ghoshal et al. [35] by including one more dimension in the horizontal direction in an unsteady framework. More precisely, the objective of the present study is to develop a reliable mathematical model for unsteady 2D sediment transport by considering the modified mixing length and settling velocity due to presence of particles in the flow. Due to the inclusion of hindered settling and mixing length with damping factor in the transport model, the developed model becomes a highly non-linear partial differential equation (PDE). Finite difference method with Euler’s implicit scheme, is used to solve the PDE. The sediment concentration profiles are discussed for various cases, such as for the effects of concentration-dependent mixing length and the hindered settling. Also, the variation of concentration profiles along the streamwise direction for a fixed time and variation of the same with time for a fixed longitudinal distance are studied. In addition, the concentration at the bottom is discussed separately due to the consideration of the effects of mixing length and hindered settling. Finally, the proposed model has been verified using appropriate experimental data under specified conditions.

2 Mathematical formulation

The generalised form of the unsteady three-dimensional advection–diffusion equation in a wide open channel can be derived from the mass conservation law for sediment and is as follows:

$$\begin{aligned} \frac{\partial c}{\partial t} + \frac{\partial {(uc)}}{\partial x} + \frac{\partial {(vc)}}{\partial y} + \frac{\partial {(wc)}}{\partial z}= & {} \frac{\partial }{\partial x}\left[ {(\epsilon _{m} + \epsilon _{sx})}\frac{\partial c}{\partial x}\right] + \frac{\partial }{\partial y}\left[ {(\epsilon _{m} + \epsilon _{sy})}\frac{\partial c}{\partial y}\right] \nonumber \\{} & {} +\frac{\partial }{\partial z}\left[ {(\epsilon _{m} + \epsilon _{sz})}\frac{\partial c}{\partial z}\right] \end{aligned}$$

(1)

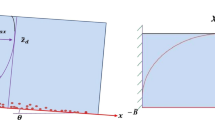
where c is the time-averaged volumetric concentration of suspended sediment; t is the time; x, y and z are the cartesian coordinates in the longitudinal (stream-wise), transverse and vertical directions, respectively; u, v and w are the time-averaged velocity components along x, y and z directions, respectively; $\epsilon _{sx}$, $\epsilon _{sy}$ and $\epsilon _{sz}$ are the sediment diffusion coefficients in the x, y and z directions, respectively; and $\epsilon _m$ is the molecular diffusion coefficient. A schematic diagram of the non-equilibrium suspended sediment concentration and flow velocity is shown in Fig. 1. This work assumes that the fluid flow is independent of time and uniform along the longitudinal direction. The concentration variation in the transverse direction is not considered and diffusion in the longitudinal direction is neglected as advection is dominant in that direction [19]. For simplification, the sediment diffusion coefficient $\epsilon _{sz}$ in the vertical direction z has been replaced by $\epsilon _s$. The vertical velocity component w is a combination of the mean velocity of fluid flow $w_f$ along the vertical direction and the downward sediment settling velocity $w_s$, i.e., $w = w_f - w_s$ in sediment-mixed fluid. The effect of settling velocity is much more prominent than the effect of fluid flow in a vertical direction; so, the term $\frac{\partial (w_f c)}{\partial z}$ is negligible compared to the term $\frac{\partial (w_s c)}{\partial z}$ [37]. Then the governing equation (1) becomes

$$\begin{aligned} \frac{\partial c}{\partial t} + u\frac{\partial c}{\partial x} - \frac{\partial {(w_{s} c)}}{\partial z} = \frac{\partial }{\partial z}\left( \epsilon _{s}\frac{\partial c}{\partial z}\right) \end{aligned}$$

(2)

To analyze the concentration profile from Eq. (2), some key parameters must be known, such as sediment settling velocity $w_s$, sediment diffusivity $\epsilon _s$ and flow velocity distribution u which are discussed subsequently.

Many authors [21, 38] proposed correlations between sediment settling velocity and concentration. It is shown in the existing literature that the magnitude of sediment settling velocity in sediment-mixed flow is lower than the clear water settling velocity due to the presence of particles in suspension as already mentioned in the introduction part. Richardson and Zaki [21] proposed a relation between settling velocity and concentration, which is as follows

$$\begin{aligned} w_s = w_0 (1-c)^{\eta _{H}} \end{aligned}$$

(3)

where $w_0$ is the settling velocity of a sediment particle in clear water and $\eta _{H}$ is the exponent of settling velocity reduction. It has been observed that the value of $\eta _H$ changes according to the particle’s Reynolds number and it ranges from 2.4 to 4.9 [21]. Few researchers [6, 30] have chosen an average value of $\eta _H = 4$ in order to minimize the mathematical computation. The present study also considers the value of $\eta _H = 4$. The expression of sediment settling velocity in clear water has been considered from Cheng [39], which is as follows:

$$\begin{aligned} w_0 = \frac{\nu _f}{d} \left( \sqrt{25+1.2d_*^2}-5 \right) ^{1.5} \end{aligned}$$

(4)

where $\nu _f$ is the kinematic viscosity of clear water; g is the gravitational acceleration; d is the sediment diameter and $d_*$ is the dimensionless diameter of the sediment, which is expressed as follows:

$$\begin{aligned} d_* = \left( \frac{\Delta g}{\nu _f^2}\right) ^{\frac{1}{3}} d \end{aligned}$$

(5)

where $\Delta = s - 1$, s is the relative density of sediment particles and the value of s is taken as 2.65.

The sediment diffusion coefficient $\epsilon _s$ can be approximated near the bed as [40]

$$\begin{aligned} \epsilon _s = u_* l \end{aligned}$$

(6)

where l is the mixing length and $u_*$ is the shear velocity. Following the work of Castro-Orgaz et al. [41], the above expression of sediment diffusion coefficient has been used in this work throughout the whole water depth. To use the expression of $\epsilon _s$, one must know the expression of mixing length. In 1933, Prandtl [32] established two expressions on normalized mixing length in clear water flow: one is of linear type as $l = \kappa z$ and the other one is of parabolic type as $l = \kappa z \sqrt{1 - \frac{z}{h}}$. Kovacs [4] modified the Prandtl’s [32] mixing length expression to provide a generalised formula for sediment-mixed flow. According to Kovacs [4], the volume occupied by the suspended particles in a unit volume can be given by their concentration c in sediment-mixed flow. Assuming that a small cube is filled with suspended particles, the length of the side of the cube is proportional to $c^{1/3}$. Since the space occupied by suspended particles is unavailable for travelling fluid particles, their mixing length l is reduced by the length taken by suspended particles. Thus, the damping function, $1-c^{1/3}$, is introduced in the mixing length expression, which is purely based on the volumetric presence of sediment particles in the sediment-laden flow [4]. Consequently, the expression of concentration-dependent mixing length becomes [4]

$$\begin{aligned} l = l_0 (1-c^{\frac{1}{3}}) \end{aligned}$$

(7)

where $l_0$ is the mixing length in clear water flow and the remaining factor, i.e., $(1-c^{\frac{1}{3}})$, is the damping factor. The findings of Umeyama and Gerritsen [33] indicated that the parabolic mixing length profile exhibited better agreement with experimental data in comparison to the linear profile. Thus, this study employs Prandtl’s [32] parabolic formulation of the clear water mixing length expression which is the following

$$\begin{aligned} l_{0}=\kappa z \sqrt{1-\frac{z}{h}} \end{aligned}$$

(8)

where $\kappa$ is the von-Karman constant. The expression of sediment diffusivity $\epsilon _s$ can be found by combining Eqs. (6), (7), and (8). Substituting the expressions of the settling velocity $w_s$ and the sediment diffusivity $\epsilon _s$ into Eq. (2), the governing equation of suspended sediment transport becomes

$$\begin{aligned} \frac{\partial c}{\partial t} + u\frac{\partial c}{\partial x} - \frac{\partial }{\partial z} \Big [ w_0 (1-c)^{\eta _{H}} c \Big ]= \frac{\partial }{\partial z}\left[ \kappa u_* z \sqrt{1- \frac{z}{h}} \left( 1-c^\frac{1}{3}\right) \frac{\partial c}{\partial z}\right] \end{aligned}$$

(9)

The following non-dimensional parameters are introduced to transform the governing equation in the non-dimensional form:

$$\begin{aligned} {\hat{C}}=\frac{c}{C_{a}}, \quad {\hat{t}}=\frac{t u_{*}}{h}, \quad {\hat{u}}=\frac{u}{u_{*}}, \quad {\hat{x}} = \frac{x}{h},\quad {\hat{z}}=\frac{z}{h}, \quad {\hat{w}}_{0}=\frac{w_{0}}{u_{*}} \end{aligned}$$

where h is the maximum flow depth and $C_a$ represents the reference concentration at the reference height $z = a$. By using the above-defined dimensionless parameters in Eq. (9), we can get the non-dimensional form of Eq. (9) as

$$\begin{aligned} \frac{\partial {\hat{C}}}{\partial {\hat{t}}} + {\hat{u}}({\hat{z}})\frac{\partial {\hat{C}}}{\partial {\hat{x}}} - \frac{\partial }{\partial {\hat{z}}}\left[ {\hat{w}}_{0} (1 - {C}_a {\hat{C}})^{\eta _H} {\hat{C}} \right] = \frac{\partial }{\partial {\hat{z}}}\left[ \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \left( 1 - {C}_a^{1/3} {\hat{C}}^{1/3}\right) \frac{\partial {\hat{C}}}{\partial {\hat{z}}}\right] \end{aligned}$$

(10)

Equation (10) represents the unsteady 2D sediment concentration distribution in suspension in an open channel turbulent flow which incorporates the effects of concentration dependent mixing length and hindered settling.

2.1 Initial and boundary conditions

The non-dimensional form of the suspended sediment transport equation given in Eq. (10) is an unsteady two-dimensional initial boundary value problem. Specific values of the initial and boundary conditions are required to achieve the numerical solution of Eq. (10). It is assumed that sediment particles occur in suspension from a particular reference height $z = a$ to the free surface $z = h$.

Several kinds of bottom boundary condition at the reference level $z = a$ has been used in the literature by many researchers ( [10, 42, 17]) in their study of sediment transport. Cheng [17] proposed a boundary condition at the bottom surface, by making the flux equal to the rate of placing the sediment into suspension and showed that all the existing bottom boundary conditions are special cases of the boundary condition proposed by him. This study considers Cheng’s [17] generalized bottom boundary condition, which can be expressed as

$$\begin{aligned} Q_a = -\left[ \epsilon _{s}\frac{\partial c}{\partial z } + w_{s} c\right] = - \gamma (c-c_{*})~~~~\text {at}~~z = a \end{aligned}$$

(11)

where $Q_a$ is the net sediment flux at the bottom surface, $\gamma$ and $c_*$ are the depth independent parameters determined by the hydraulic conditions and the characteristics of the bottom surface. In the transient process, for the adjustment of sediment concentration from an initial condition to a final equilibrium steady-state value, the net sediment flux $Q_a$ must tend to zero. In other words, as equilibrium is approached, $\lim _{t\rightarrow \infty }Q_a=0$ and $c_{*} = \lim _{t\rightarrow \infty }c_{a}$ [17]. Here, $c_a$ is referred as the value of c at $z=a$. Thus, $c_*$ can be viewed as the equilibrium sediment concentration at the bottom surface and $\gamma$ is a ratio of the deposition flux and the bottom concentration [17]. From the physical point of view, $\gamma$ is considered as reflectivity coefficient at the bottom surface. If $\gamma = 0$ then it represents a completely reflective surface, while $\gamma = \infty$ represents a completely absorbing surface ( [17, 19]). This bottom boundary condition was also used by Liu and Nayamatullah [18], Liu [19], Mohan et al. [30] and Kumbhakar et al. [31]. For the boundary condition at the free surface, it is assumed that there is no mass flux at the free surface $z = h$. Hence the boundary condition at the free surface is as follows:

$$\begin{aligned} \epsilon _{s}\frac{\partial c}{\partial z } + w_{s} c = 0~~~~~~\text {at}~~z = h \end{aligned}$$

(12)

The sediment concentration at the inlet is assumed to be uniform. So, the inlet condition can be written as

$$\begin{aligned} {\hat{C}}({\hat{x}} =0, {\hat{z}}) = {\hat{C}}_{{\hat{x}}_0}({\hat{z}}) = 1 \end{aligned}$$

(13)

In the boundary conditions, hindered settling effect or change of mixing length due to concentration has not been taken into account. Recently it has been shown by Hossain et al. [36] that inclusion of hindered settling in the boundary condition does not bring any change in the result. Replacing the expressions of $\epsilon _s$ and $w_s$ with $u_* l_0$ and $w_0$, respectively, as also done by Ghoshal et al. [35] and using dimensionless scale parameters in Eqs. (11) to (12), the boundary conditions take the form as

$$\begin{aligned}{} & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \frac{\partial {\hat{C}}}{\partial {\hat{z}}}+{\hat{w}}_{0} {\hat{C}}=0 \quad \text{ at } {\hat{z}}=1 \end{aligned}$$

(14)

$$\begin{aligned}{} & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \frac{\partial {\hat{C}}}{\partial {\hat{z}}}+{\hat{w}}_{0} {\hat{C}}={\hat{\gamma }}({\hat{C}}-{\hat{C}}_{*}) \quad \text{ at } {\hat{z}}={\hat{a}} \end{aligned}$$

(15)

where ${\hat{C}}_*=\frac{c_*}{C_{a}},$ ${\hat{\gamma }} = \frac{\gamma }{u_*}$ and ${\hat{a}}=\frac{a}{h}$ are dimensionless parameters.

The dimensionless form of the initial condition can be chosen as

$$\begin{aligned} {\hat{C}}({\hat{t}} =0, {\hat{x}},{\hat{z}}) = 1 \end{aligned}$$

(16)

Eq. (10) with the aforementioned generalized initial and boundary conditions given by Eqs.(13) to (16) is highly non-linear partial differential equation and therefore obtaining the analytical solution is not an easy task. As an alternative, the present study looks for an approximate numerical solution. In the following section, the numerical method is described, which is used to solve the problem in the present study.

3 Numerical procedure

In order to solve Eq. (10) with the conditions given in Eqs. (13) to (16), this study employs the standard finite difference method along with a fully implicit Euler time marching scheme. Equation (10) can be expressed as follows

$$\begin{aligned} \frac{\partial {\hat{C}}}{\partial {\hat{t}}} + {\hat{u}}({\hat{z}})\frac{\partial {\hat{C}}}{\partial {\hat{x}}} - \phi ({\hat{C}}) \frac{\partial {\hat{C}}}{\partial {\hat{z}}} = \frac{\partial }{\partial {\hat{z}}}\left[ \psi ({\hat{C}},{\hat{z}}) \frac{\partial {\hat{C}}}{\partial {\hat{z}}}\right] \end{aligned}$$

(17)

where

$$\begin{aligned} \phi ({\hat{C}})= & {} {\hat{w}}_0 (1 - {C}_a {\hat{C}})^{\eta _H - 1} [1 - (\eta _H + 1){C}_a {\hat{C}}] \end{aligned}$$

(18)

$$\begin{aligned} \psi ({\hat{C}},{\hat{z}})= & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \left( 1 - {C}_a^{1/3} {\hat{C}}^{1/3}\right) \end{aligned}$$

(19)

Eq. (17) can be re-written as

$$\begin{aligned} \frac{\partial {\hat{C}}}{\partial {\hat{t}}} +{\hat{u}}\frac{\partial {\hat{C}}}{\partial {\hat{x}}} - \phi \frac{\partial {\hat{C}}}{\partial {\hat{z}}} = \frac{\partial \psi }{\partial {\hat{z}}}\frac{\partial {\hat{C}}}{\partial {\hat{z}}} + \psi \frac{\partial ^2 {\hat{C}}}{\partial {\hat{z}}^2} \end{aligned}$$

(20)

By using a fully implicit backward Euler method, Eq. (20) can be expressed as a semi-discretized form:

$$\begin{aligned} \frac{{\hat{C}}^{n+1} - {\hat{C}}^n}{\Delta {\hat{t}}} +{\hat{u}}\frac{\partial {\hat{C}}^{n+1}}{\partial {\hat{x}}} - \phi ^{n+1} \frac{\partial {\hat{C}}^{n+1}}{\partial {\hat{z}}} = \frac{\partial \psi ^{n+1}}{\partial {\hat{z}}}\frac{\partial {\hat{C}}^{n+1}}{\partial {\hat{z}}} + \psi ^{n+1} \frac{\partial ^2 {\hat{C}}^{n+1}}{\partial {\hat{z}}^2} \end{aligned}$$

(21)

The superscripts n and $n+1$ stands for the previous and present time levels, ${\hat{t}}^n$ and ${\hat{t}}^{n+1}$, respectively. The variable $\Delta {\hat{t}} (={\hat{t}}^{n+1} - {\hat{t}}^n)$ specifies the time step. ${\hat{C}}^n$ represents the value of ${\hat{C}}$ at the previous time step ${\hat{t}}^n$. The values of ${\hat{C}}^{n+1}$, which represent the unknown value of ${\hat{C}}$ at the present time step ${\hat{t}}^{n+1}$, can be used to calculate the functions $\phi ^{n+1}$ and $\psi ^{n+1}$. First, the functions $\phi$ and $\psi$ are linearized, because these functions are non-linear in ${\hat{C}}$ and then the concentration equation (21) is linearized by Picard’s iterative methods. Using the most recent estimates of $\phi ^{n+1}$ and $\psi ^{n+1}$, ${\hat{C}}^{n+1}$ has been estimated successively according to Picard’s iterative approach. The superscripts n and m denote the time level and Picard’s iteration level, respectively. The linearized form of Eq. (21) is as follows:

$$\begin{aligned} \frac{{\hat{C}}^{n+1,m+1} - {\hat{C}}^n}{\Delta {\hat{t}}} +{\hat{u}}\frac{\partial {\hat{C}}^{n+1,m+1}}{\partial {\hat{x}}} - \phi ^{n+1,m} \frac{\partial {\hat{C}}^{n+1,m+1}}{\partial {\hat{z}}}= & {} \frac{\partial \psi ^{n+1,m}}{\partial {\hat{z}}}\frac{\partial {\hat{C}}^{n+1,m+1}}{\partial {\hat{z}}} \nonumber \\{} & {} + \psi ^{n+1,m} \frac{\partial ^2 {\hat{C}}^{n+1,m+1}}{\partial {\hat{z}}^2} \end{aligned}$$

(22)

where

$$\begin{aligned} \phi ^{n+1,m}= & {} {\hat{w}}_0 (1 - {\hat{C}}^{n+1,m}{C}_a)^{\eta _H - 1} [1 - (\eta _H + 1){\hat{C}}^{n+1,m}{C}_a] \end{aligned}$$

(23)

$$\begin{aligned} \psi ^{n+1,m}= & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \left( 1 - {C}_a^{1/3} ({\hat{C}}^{n+1,m})^{1/3}\right) \end{aligned}$$

(24)

The computational space domain is assumed rectangular with lengths $L_x$ and $H_z$ corresponding to the stream-wise and vertical directions, respectively. The entire space domain can be discretized into $M-1$ equally spaced grid size $\Delta {\hat{x}} = \frac{L_{{\hat{x}}}}{M-1}$ with M number of grid points in ${\hat{x}}$ direction and $N-1$ equally spaced grid size $\Delta {\hat{z}} = \frac{H_{{\hat{z}}}}{N-1}$ with N number of grid points in ${\hat{z}}$ direction. The grid point coordinates are defined as follows: $\hat{x_{i}} = x_1 + (i-1) * \Delta {\hat{x}}$ for $i = 1,2,3,...,M$ and $\hat{z_j} = a + (j-1) * \Delta {\hat{z}}$ for $j = 1,2,3,...,N$ in the ${\hat{x}}$ and in ${\hat{z}}$ directions, respectively. A second-order finite difference approximation is used to discretize the space derivatives as follows:

$$\begin{aligned} \frac{\partial {\hat{C}}}{\partial {\hat{x}}} \Big \Vert _{i,j}= & {} \frac{{\hat{C}}_{i+1,j} - {\hat{C}}_{i-1,j}}{2\Delta {\hat{x}}} \end{aligned}$$

(25)

$$\begin{aligned} \frac{\partial {\hat{C}}}{\partial {\hat{z}}}\Big \Vert _{i,j}= & {} \frac{{\hat{C}}_{i,j+1} - {\hat{C}}_{i,j-1}}{2\Delta {\hat{z}}} \end{aligned}$$

(26)

$$\begin{aligned} \frac{\partial ^2 {\hat{C}}}{\partial {\hat{z}}^2} \Big \Vert _{i,j}= & {} \frac{{\hat{C}}_{i,j+1} - 2 {\hat{C}}_{i,j} + {\hat{C}}_{i,j-1}}{(\Delta {\hat{z}})^2} \end{aligned}$$

(27)

Using Eq. (25) to Eq. (27) into Eq. (22) and rearranging the terms, one can obtain the following discretized equation:

$$\begin{aligned} A_{i,j} {\hat{C}}^{n+1,m+1}_{i,j-1} + B_{i,j} {\hat{C}}^{n+1,m+1}_{i-1,j} + D_{i,j} {\hat{C}}^{n+1,m+1}_{i,j} + E_{i,j} {\hat{C}}^{n+1,m+1}_{i+1,j} + F_{i,j} {\hat{C}}^{n+1,m+1}_{i,j+1}= R_{i,j} \end{aligned}$$

(28)

where

$$\begin{aligned} A_{i,j}= & {} \left[ \phi ^{n+1,m}_{i,j} + \frac{\partial \psi ^{n+1,m}}{\partial {\hat{z}}}\Big \Vert _{i,j} \right] \frac{\Delta {\hat{t}}}{2 \Delta {\hat{z}}} - \psi ^{n+1,m}_{i,j} \frac{\Delta {\hat{t}}}{(\Delta {\hat{z}})^2} \end{aligned}$$

(29)

$$\begin{aligned} B_{i,j}= & {} - {\hat{u}}_{i,j} \frac{\Delta {\hat{t}}}{2 \Delta {\hat{x}}} \end{aligned}$$

(30)

$$\begin{aligned} D_{i,j}= & {} 1 + 2\psi ^{n+1,m}_{i,j} \frac{\Delta {\hat{t}}}{(\Delta {\hat{z}})^2} \end{aligned}$$

(31)

$$\begin{aligned} E_{i,j}= & {} {\hat{u}}_{i,j} \frac{\Delta {\hat{t}}}{2 \Delta {\hat{x}}} \end{aligned}$$

(32)

$$\begin{aligned} F_{i,j}= & {} - \left[ \phi ^{n+1,m}_{i,j} + \frac{\partial \psi ^{n+1,m}}{\partial {\hat{z}}}\Big \Vert _{i,j} \right] \frac{\Delta {\hat{t}}}{2 \Delta {\hat{z}}} - \psi ^{n+1,m}_{i,j} \frac{\Delta {\hat{t}}}{(\Delta {\hat{z}})^2} \end{aligned}$$

(33)

$$\begin{aligned} R_{i,j}= & {} {\hat{C}}^n_{i,j} \end{aligned}$$

(34)

for $i = 2,3,4,..., M-1$ and $j = 2,3,4,..., N-1$. The boundary conditions given in Eqs. (14) to (15) can be discretized as follows:

$$\begin{aligned}{} & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \left[ \frac{-3 {\hat{C}}^{n+1,m+1}_{i,1} + 4{\hat{C}}^{n+1,m+1}_{i,2} - {\hat{C}}^{n+1,m+1}_{i,3}}{2\Delta {\hat{z}}} \right] + {\hat{w}}_0 {\hat{C}}^{n+1,m+1}_{i,1} \nonumber \\{} & {} \quad = \gamma ( {\hat{C}}^{n+1,m+1}_{i,1} - {\hat{C}}_*)~~\text {for}~~i = 2,3,...,M-1 \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \kappa {\hat{z}} \sqrt{1-{\hat{z}}} \left[ \frac{3 {\hat{C}}^{n+1,m+1}_{i,N} - 4{\hat{C}}^{n+1,m+1}_{i,N-1} + {\hat{C}}^{n+1,m+1}_{i,N-2}}{2\Delta {\hat{z}}} \right] + \nonumber \\{} & {} \quad {\hat{w}}_0 {\hat{C}}^{n+1,m+1}_{i,N} = 0 \quad \text {for}~~i = 2,3,...,M-1 \end{aligned}$$

(36)

$$\begin{aligned}{} & {} {\hat{C}}^{n+1,m+1}_{1,j} = 0 \quad \text {for}~~j = 1,2,3,...,N \end{aligned}$$

(37)

$$\begin{aligned}{} & {} {\hat{C}}^{n+1,m+1}_{M,j} = {\hat{C}}^{n+1,m+1}_{M-1,j} \quad \text {for}~~j = 1,2,3,...,N \end{aligned}$$

(38)

The discretized system of linear algebraic equations (28) is solved using the Gauss-Seidel iterative method. A MATLAB code has been developed to solve the system and obtain the numerical solution.

4 Results and discussion

This section begins with a description of the input functions that are necessary to solve Eq. (10). Then, transient sediment concentration profile, concentration profiles at different downstream positions and concentration distributions for simultaneous variations in time and downstream location, have been analyzed both theoretically and graphically. Following this, both physical phenomena of sediment transport, mixing length effect and hindered settling effect on the distribution of suspended sediment concentration are described. Additionally, the behaviour of sediment concentration near the bed has been discussed. At the end, the derived numerical solution of the present mathematical framework is validated with the available experimental data in the literature.

4.1 Expression for input function

From Eq. (10), it can be seen that apart from the expressions of $w_s$ and $\epsilon _s$, the flow velocity ${{\hat{u}}}({{\hat{z}}})$ is essential to obtain the solution of the proposed model. Since the flow is uniform in the main direction, so the flow velocity ${{\hat{u}}}({{\hat{z}}})$ can be considered a constant value as in Hjelmfelt and Lenau [10]. However, this study considers the log-law of advection velocity, which is more realistic and given as follows:

$$\begin{aligned} u(z) = \frac{u_{*}}{\kappa } ln \frac{z}{z_{0}} \end{aligned}$$

(39)

where $z_0$ is the start elevation of the log-law formula. The value of $\kappa$ is taken as 0.41 throughout the study. Equation (39) can be further rewritten into the following normalized form as [19]

$$\begin{aligned} {\hat{u}}({{\hat{z}}}) = \frac{1- {{\hat{z}}}_{0}}{{{\hat{z}}}_0 - ln {{\hat{z}}}_0 -1} ln\frac{{{\hat{z}}}}{{{\hat{z}}}_{0}} ~~~~~~~~\text {for}~~~~~{{\hat{z}}}_0 \le {{\hat{z}}} \le 1 \end{aligned}$$

(40)

where ${{\hat{z}}}_0 = \frac{z_0}{h}$. The value of ${\hat{z}}_0$ is usually small and it is considered as 0.001 [19]. The present study uses Eq. (40) to compute the velocity component ${\hat{u}}({{\hat{z}}})$ which was used by Liu [19] and Kumbhakar et al. [31] also in their 2D steady transport models.

4.2 Temporal and horizontal variation of concentration profiles

Figures 2a and b illustrates the temporal and stream-wise variations of concentration distributions, respectively. For both the figures, the initial concentration distribution is ${\hat{C}}({\hat{t}} = 0, {\hat{x}}, {\hat{z}}) = 1$. The values of required parameters are $\eta _H = 4$, $d = 0.105$ mm, ${\hat{a}} = 0.05$, $C_a = 0.014$, ${\hat{\gamma }} = 1$ and $\hat{C_*} = 1$. Figure 2a shows the transient sediment concentration profiles at various times, i.e., ${\hat{t}} = 0.5, 1.0, 2.0, 4.0, 5.0$ and 10.0 for a particular downstream ${\hat{x}} = 80$. From Fig. 2a, it can be observed that the concentration profile becomes steady at large time.

Figure 2b demonstrates the stream-wise concentration distributions for distinct downstream positions, i.e., ${\hat{x}} = 2, 3, 5, 10, 20, 50$ and 80 at a particular time ${\hat{t}} = 10$. From Fig. 2b, one can notice that, as ${\hat{x}}$ increases, the magnitude of the concentration profile increases and after some particular value of ${\hat{x}} = 80$, the concentration profile does not change and behaves like a uniform one at that specific time ${\hat{t}} = 10$. It can be seen from Fig. 2a and b that the concentration profiles exhibit the same pattern for change with time at fixed location and for change with location at fixed time.

Figure 3 demonstrates concentration profiles for simultaneous variation in times ${\hat{t}}$ and downstream locations ${\hat{x}}$. The inlet and initial concentration are ${\hat{C}}({\hat{t}}, {\hat{x}} = 0, {\hat{z}}) = 1$ and ${\hat{C}}({\hat{t}} = 0, {\hat{x}}, {\hat{z}}) = 1$, respectively. The required parameters are ${\hat{a}} = 0.035$, $C_a = 0.014$, ${\hat{\gamma }} = 1$, and $\hat{C_*} = 1$. From Fig. 3, it is clear that the magnitude of sediment concentration increases as the increase in values of time ${\hat{t}}$ and downstream location ${\hat{x}}$. The concentration profiles do not alter and behave like uniform concentration distribution from particular values of ${\hat{t}} = 20$ and ${\hat{x}} = 50$.

4.3 Influence of mixing length on vertical distribution of sediment concentration

As already mentioned, Ghoshal et al. [35] used the mixing length from Kovacs [4] to investigate 1D unsteady sediment concentration distribution in an open channel steady fluid flow. Following the study of Ghoshal et al. [35], the present study assumes the concentration-dependent mixing length in an unsteady 2D model of suspended sediment transport.

Although the effect of mixing length has been taken into account in the study of sediment transport by Ghoshal et al. [35], they could not demonstrate the change in concentration distribution along the downstream direction as their model did not include spatial variation. Present study demonstrates the impact of mixing length through the damping factor $(1 - C_a^{1/3}{\hat{C}}^{1/3})$ on sediment concentration profile at various downstream positions (${\hat{x}}$ = 1, 2, 5, 20, 30, 50) for a particular time ${\hat{t}} = 20$ in Fig. 4. Initially, uniform sediment distribution in the whole computational domain is considered. Also, the uniform sediment distribution is considered at the inlet, i.e., ${\hat{C}}({{\hat{t}}}, {{\hat{x}}=0},{\hat{z}})=1$. The values of the required parameters are $\eta _H = 4$, ${\hat{a}} = 0.035$, $C_a = 0.014$, ${\hat{\gamma }} = 2$, $u_* = 4.1$ cm, and $h = 17$ cm. The solid line represents the concentration profile, which includes the mixing length with the damping factor, i.e., $l = l_0 (1 - C_a^{1/3}{\hat{C}}^{1/3})$, whereas the dashed line represents the sediment concentration distribution corresponding to mixing length without damping factor, i.e., $l = l_0$. From Fig. 4, it is observed that the differences in concentration distributions are much more in the central suspension region compared to the region near the free surface and close to the bed. From Fig. 4a–c, it can be observed that the concentration distribution is higher in the case of mixing length with the damping factor as compared to the mixing length without damping factor. But, from Fig. 4d–f, the concentration distributions start getting lower, corresponding to mixing length with the damping factor compared to the mixing length without damping factor and as the downstream distance increases the effect stabilizes. The explanation for this can be made as follows: at a particular time, the sediment concentration close to the inlet boundary is high and as distance increases from the inlet, the magnitude of the concentration profile becomes less. In Fig. 4, the sediment concentration is greater in downstream locations close to the inlet boundaries than in downstream locations far from the boundary. More specifically, the magnitude of the concentration profile is smaller after ${\hat{x}}=5$ than it was before (Fig. 4). As shown in Fig. 4a–c, the mixing length effect is considerably less pronounced before ${\hat{x}}=5$ and has a different effect than anticipated. But, as we go away from the stream-wise distance ${\hat{x}}=5$, (Fig. 4d–f) the magnitude of concentration becomes less and here the impact of mixing length becomes more effective with a dampening in the concentration profile due to concentration-dependent mixing length. The region up to ${\hat{x}}=5$ behaves like a transition region. It can be seen from Fig. 4a–c, the magnitude of the concentration profile becomes greater than unity at some of the nodes of the computational domain. For example, in Fig. 4a, at vertical distance ${\hat{z}}=0.1508$, the magnitude of the concentration is ${\hat{C}}=1.02338$, which is greater than unity. An increment in the concentration distribution has been observed while incorporating the mixing length in Fig. 4a–c. On the other hand, from Fig. 4d–f, it can be observed that the magnitude of the concentration at any height ${\hat{z}}$ is less than unity. The mixing length effect dampens the concentration profile from these cases which is after the transition zone.

For a better understanding, the impact of mixing length with and without the damping factor has been shown in a three-dimensional (3D) concentration plot at time ${\hat{t}} = 10$ in Fig. 5. The values of the required parameters are the same as those mentioned in the above paragraph. From Fig. 5, it can be observed that there is a clear difference between the sediment concentration distribution of mixing length with the inclusion and omission of the damping component. It is pertinent to mention here that Fig. 5 has been plotted after the transition region. This is the reason why the mixing length in this case dampens the concentration values rather than raising them. Hence major significance is that this effect helps not to overestimate the magnitude of the sediment concentration in suspension.

4.4 Influence of hindered settling mechanism on distribution of sediment concentration

Although the impact of hindered settling has been taken into account in studies of 1D unsteady sediment transport by Mohan et al. [30] and 2D steady transport by Kumbhakar et al. [31], they did not demonstrate the variation in sediment concentration distribution with time or space by including the hindered settling effect. Ghoshal et al. [35] demonstrated the variation of sediment concentration distribution with time only due to the inclusion of hindered settling effect as their model did not include any spatial variation of concentration. The impact of hindered settling phenomenon on the sediment concentration profile has been demonstrated in Fig. 6 through the exponent of settling velocity reduction $\eta _H$. Figure 6 demonstrates the concentration profiles at various downstream positions (${\hat{x}}$ = 1, 2, 5, 20, 50, 80) for a particular time ${\hat{t}} = 20$. A value of $\eta _H = 4$ incorporates the effect of hindered settling whereas a value of $\eta _H = 0$ does not consider the hindered settling effect. The concentration profiles are plotted for both scenarios: with ($\eta _H = 4$) and without ($\eta _H = 0$) hindered settling effects. A uniform concentration is assumed at the inlet, i.e., ${\hat{c}}({\hat{t}}, {\hat{x}} = 0, {\hat{z}}) = {\hat{c}}_0({\hat{z}}) = 1$ and also in the initial condition, i.e., ${\hat{c}}({\hat{t}} = 0, {\hat{x}}, {\hat{z}}) = 1$. For all the cases, the required parameters are ${\hat{a}} = 0.03$, $C_a = 0.0772$, ${\hat{\gamma }} = 2$, $u_* = 10.09$ cm, $d = 0.274$ mm, $h = 13.2$ cm and $\hat{C_*} = 1$. From Fig. 6, it is observed that the concentration value increases due to inclusion of the hindered settling effect and its impact on the concentration profile is prominent in the main flow region. No significant impact is observed near the free surface and close to the bottom region. This happens because the sediment particles are much lower at the free surface than in the main flow region; whereas in the bottom region of the channel, the combination of the lower flow velocity due to the frictional forces and the higher density lead to fewer eddies, which are responsible for the transportation of momentum [43]. From Fig. 6a–c, it is observed that the differences between the sediment concentration profiles start to increase with respect to space until ${\hat{x}} = 5$, and then start to decrease until ${\hat{x}} = 50$. After downstream position ${\hat{x}} = 50$, the difference between the sediment concentrations does not alter and becomes uniform.

For a better understanding, the influence of hindered settling with and without hindered settling has been shown in Fig. 7 in a 3D concentration profile that has been plotted at ${\hat{t}} = 10$. The required parameter values are as specified in the preceding paragraph. From Fig. 7, it can be seen that there is a significant difference between the sediment concentration distribution due to inclusion and omission of hindered settling.

4.5 Overshooting effect on bottom concentration

Overshooting phenomenon is an interesting aspect of the suspended sediment transport. Overshooting means the concentration profile overshoots its equilibrium value and slowly decreases to equilibrium. Under certain inlet conditions, the bottom concentration profile at the downstream position will overshoot its equilibrium value and attain a higher concentration than equilibrium [17]. The overshooting phenomenon has been observed in experiments conducted by Jobson and Sayre [44]. Celik and Rodi [45] presented a numerical model that simulates the initial increase in the near-bed concentration and the overshooting of its equilibrium value. As far as the authors’ knowledge, the overshooting effect for the unsteady 2D suspended sediment transport model in sediment-mixed flow is yet to be addressed. Hence, the present study shows the effect of the overshooting phenomenon on bottom concentration at different downstream distances. Figure 8 plots the bottom sediment concentration at three dimensionless downstream distances (${\hat{x}}=2.5$, 5 and 10) for two different values of the depth-independent parameter ${\hat{\gamma }}=0.4$ and 1. In each of the figures, the value of the equilibrium sediment concentration $\hat{C_*}$ has been kept at 1. The values of the other required parameters are considered as ${\hat{a}}=0.03$, $\hat{w_0}=0.2$, $C_a=0.01$, $\eta _H=4$ and $\hat{C_*}=1$. Figure 8 shows the evolution of bottom concentration with time at different downstream positions, which indicates that initially bottom sediment concentration overshoots the values of $\hat{C_*}$. As the downstream distance ${\hat{x}}$ increases, the bottom sediment concentration goes closer to the equilibrium value and at the far field position, the bottom concentration converges to it. This happens as the inlet and initial concentration are not compatible with the bottom boundary condition and thus the overshooting occurs [18, 19]. Also, it can be observed from the figure that as the value of ${\hat{\gamma }}$ decreases, the peak of the bottom concentration profile increases. This happens because the bottom reflects more sediments as the value of ${\hat{\gamma }}$ decreases and as a result the sediment concentration at the bottom increases. The values of the other parameters are listed in the figure. This phenomenon has also been reported by Liu and Nayamatullah [18], Sen et al. [46] and Mohan et al. [30] in their respective studies of unsteady 1D transport of sediment concentration, whereas Hossain et al. [36] showed this effect in the study of unsteady 2D transport.

4.6 Influence of hindered settling and mixing length on bottom concentration

Figure 9 shows the effect of hindered settling on bottom concentration through the exponent of settling velocity reduction $\eta _H$ in the presence of mixing length and Fig. 10 shows the impact of mixing length on bottom concentration through the damping factor $(1-C_a^{1/3} {\hat{C}}^{1/3})$ in the presence of hindered settling. Both the figures are plotted at ${\hat{x}}=3$ and the same parameters are considered, which are taken as ${\hat{a}}=0.035$, $\hat{w_0}=0.2$, $C_a=0.02$, $\eta _H=4$, $\hat{C_*}=1$ and ${\hat{\gamma }}=1$. These effects on bottom concentration show the same characteristics as those mentioned previously in Sects. 4.3 and 4.4 on the whole suspension region. That is, the hindered settling increases the magnitude of the bottom concentration and the damping factor of mixing length decreases the magnitude of the bottom concentration. Though it has been observed that both effects on bottom concentration are very low, one can conclude from comparing Figs. 9 and 10 that the impact of hindered settling is almost negligible on the bottom. On the other hand, the concentration-dependent mixing length has a small but still significant effect on the concentration distribution which ascertains the importance of the concentration-dependent mixing length in the distribution of sediment concentration. The finding regarding the hindered settling effect is supported by the study of Hossain et al. [36] also, who considered this effect in the bottom boundary condition and showed that it has negligible effect there.

4.7 Validation with the existing experimental data

There is a lack of experimental data in the literature on the unsteady 2D distribution of sediment in suspension. Therefore, there is no direct way to examine the accuracy of the proposed model. However, plenty of experimental data is available for the distribution of suspended sediment concentration along the vertical direction in an steady uniform flow. The proposed model behaves like a one-dimensional steady uniform transport model at a large time ${{\hat{t}}}$ and far from the downstream [36]. Therefore, at a large value of ${\hat{t}}$ and far from downstream, the proposed model’s solution is validated by using proper experimental data. The present study considers the experimental data from Coleman [47], Vanoni [48] and Einstein and Chien [49].

Table 1 Experimental data of Coleman [47], Vanoni [48] and Einstein and Chien [49] and calculated value of ${\hat{w}}_0$

Coleman [47] used a 15 m long and 356 mm wide smooth flume to conduct 40 separate experiments of sediment particles of three distinct diameters 0.105, 0.210 and 0.420 mm. Out of all these experiments, three data sets—Run 4, Run 5 and Run 29 are chosen randomly. Figure 11 shows the comparison between the chosen experimental data and the proposed model. The values of the required parameters and calculated settling velocities of sediment are listed in Table 1. In Fig. 11a, the concentration distributions for different cases have been demonstrated. The impacts of hindered settling and mixing length with damping component are incorporated by $\eta _H = 4$ and $l = l_0 (1 - C_a {\hat{C}}^{1/3})$, respectively. The solid line represents these effects on the concentration profile in Fig. 11a; on the other hand, $\eta _H = 0$ and $l = l_0$ account for no hindered settling effect and the clear water mixing length effect, respectively and is shown by the dashed line. From Fig. 11a, it can be seen that the proposed model, which includes the hindered settling effect and the concentration-dependent mixing length effect, agrees well with the experimental data. But the concentration profile with the clear water mixing length and no hindered settling effect do not agree with the experimental data. This indicates the necessity of including both effects when comparing the present solution to experimental data; consequently, the remaining figures are generated by including both effects. For the sake of simplicity, the effects of hindered settling and mixing length have not been depicted separately in the remaining figures.

Vanoni [48] conducted 29 different experiments with three distinct sediment of diameters 0.16, 0.10 and 0.133 mm. For the validation purpose, three of these data sets, Run 7, Run 21 and Run 29, are chosen randomly. Figure 12 compares the present solution to the experimental data of Vanoni [48]. Table 1 contains the computed values of the sediment settling velocities ${\hat{w}}_0$ and all other necessary parameters.

Einstein and Chien [49] performed 16 different experiments near the channel bed using three different particle diameters: $d = 1.3$, $d = 0.940$, and $d = 0.274$ mm. Figure 13 depicts a comparison between the observed data of Einstein and Chien [49] and the current model solution. The obtained dimensionless sediment settling velocities corresponding to different size of particles and other values of parameters can be found in Table 1. From Figs. 11, 12, 13, It is clear that the model agrees with the experimental data quite well in every case when both the effects of hindered settling and mixing length are considered.

5 Conclusion

This study presents a mathematical framework for two-dimensional unsteady sediment transport in a sediment-mixed turbulent flow through an open channel. Unlike the most existing works in the literature that deal with either 1D unsteady or 2D steady, the present work considers the concentration variation with time, longitudinal and vertical directions all together. The model incorporates two important features of sediment-mixed flow: (i) modified mixing length and (ii) modified settling velocity of a particle due to the presence of particles in suspension. Inclusion of these effects make the governing equation non-linear which has been solved numerically.

As the model contains concentration as a function of horizontal coordinate, vertical coordinate and time, it can exhibit together all the horizontal, vertical and temporal variation of concentration. The inclusion of modified mixing length increases the concentration in the beginning and then decreases which becomes stable after a certain downstream position. Apart from that, consideration of hindered settling phenomenon increases the concentration at any downstream position and the difference in concentration first increases and then becomes stable after a certain downstream position. Both the effects are shown separately on bottom concentration and it is observed that these effects are prominent only in the main suspension region.

At the end, due to lack of similar experimental data, the model has been compared with steady and only vertically varying experimental data on concentration distribution. A close agreement between the model and observed data proves the validity of the model.

Fig. 1

Schematic diagram of suspended sediment distribution in an open channel [19]

Fig. 2

Sediment concentration profiles a for different times at a particular downstream distance and b for different downstream distances for a particular time

Fig. 3

Time-dependent and stream-wise position-specific concentration profiles

Fig. 4

Influence of mixing length on vertical distributions of sediment concentration for different downstream positions ${\hat{x}}$ at time ${\hat{t}} =20$

Fig. 5

Influence of mixing length on three-dimensional (3D) distribution of sediment concentration at time ${\hat{t}}=10$

Fig. 6

Influence of hindered settling on vertical distributions of sediment concentration for different downstream positions ${\hat{x}}$ at time ${\hat{t}} =20$

Fig. 7

Influence of hindered settling on three-dimensional (3D) distribution of sediment concentration at time ${\hat{t}}=10$

Fig. 8

Bottom concentration profiles at different downstream positions - a ${\hat{x}}=2.5$, b ${\hat{x}}=2.5$ and c ${\hat{x}}=2.5$ for two different values of ${\hat{\gamma }}=0.4$ and 1

Fig. 9

Influence of hindered settling on bottom concentration at ${\hat{x}}=3$

Fig. 10

Effect of mixing length on bottom concentration at ${\hat{x}}=3$

Fig. 11

Validation of the present numerical solution with experimental data of Coleman [47]

Fig. 12

Validation of the present numerical solution with experimental data of Vanoni [48]

Fig. 13

Validation of the present numerical solution with experimental data of Einstein and Chien [49]