1 Introduction and motivation

Motivated by the increased reliance of many applications on shared cyber-infrastructures (ranging from defense and banking to health care and power distribution systems), various notions of security and privacy have received considerable attention from researchers. A number of such notions focus on characterizing the information flow from the system to an eavesdropper (Focardi and Gorrieri 1994). Opacity falls in this category and aims at determining whether a given system’s secret behavior (i.e., a subset of the behavior of the system that is considered critical and is usually represented by a predicate) is kept opaque to outsiders (Bryans et al. 2005; Saboori and Hadjicostis 2007). More specifically, this requires that the eavesdropper (modeled as a passive observerFootnote 1 of the system’s behavior) never be able to establish the truth of the predicate.

Early works that studied notions of opacity in discrete event systems include (Bryans et al. 2005a, b; Badouel et al. 2006; Dubreil et al. 2008). The authors of Brayans et al. (2005a, b) focus on finite state Petri nets and define opacity with respect to state-based predicates. Multiple intruders that are modeled as observers with different observation capabilities are considered in Badouel et al. (2006), whereas the authors of Dubreil et al. (2008) consider a single intruder (that might observe different events than the ones observed/controlled by a supervisor that aims to control the system so as to avoid exposure of a property of interest) and establish that a minimally restrictive supervisor always exists, but might not be regular.

In Saboori and Hadjicostis (2007, 2013), the authors consider opacity with respect to state-based predicates in a discrete event system (DES) that can be modeled as a non-deterministic finite automaton with partial observation on its transitions. State-based notions of opacity exemplify the use of observers, and make more explicit the relationship between state-based notions of opacity and their verification with observers. Examples to motivate the study of current- and initial-state opacity in the context of sensor network coverage and encryption using pseudo-random number generators can be found in Saboori and Hadjicostis (2013, 2011). The authors in Wu and Lafortune (2013) showed that there exists a polynomial-time transformation between several notions of opacity, including language-based and state-based notions.

Motivated by the absence of likelihood information in most earlier work on opacity, the information-theoretic works in Millen (1987) and Wittbold and Johnson (1990), and more recently the works in Berard et al. (2010) and Brard et al. (2015), extend notions of opacity to probabilistic settings. In particular, state-based notions of opacity have been developed for probabilistic finite automata (PFA’s) in Saboori and Hadjicostis (2014) by devising appropriate measures to quantify opacity. The following three notions were defined and analyzed in Saboori and Hadjicostis (2014):

  • (i) Step-based almost current-state opacity considers the a priori probability of violating current-state opacity, following any sequence of events of length k, and requires that this probability lies below a threshold for all possible sequences of length k (for all k).

  • (ii) Almost current-state opacity considers the a priori probability of violating current-state opacity following any sequence of events, and requires that this probability lies below a threshold.

  • (iii) Probabilistic current-state opacity requires that, for each possible sequence of observations, the following property holds: the increase in the conditional probability that the system current state lies in the set of secret states (conditioned on the given sequence of observations) compared to the prior probability (that the initial state lied in the set of secret states before any observation) is smaller than a given threshold.

The above ideas were extended in Keroglou and Hadjicostis (2013) to deal with corresponding notions of initial-state opacity in PFA’s.

In this paper we study probabilistic system opacity. The setting we consider is as follows: a system is chosen at initialization among m known models, each of which is captured by a hidden Markov model (HMM). Our goal is to determine whether the true (chosen) system remains hidden from an intruder (eavesdropper). We assume that the eavesdropper observes (via a natural projection map) a subset of the events occurring in the system. We allow partial flow of information to the eavesdropper, as long as a strictly positive (nonzero) threshold of ambiguity holds, even in the worst case. In our setup, the worst case involves an eavesdropper who knows exactly the m HMMs and also knows the observation sequence that has been generated. The question is to determine whether the true (chosen) HMM remains hidden from the eavesdropper, for any observation sequence. Here, “remains hidden” should be interpreted in a probabilistic sense: the eavesdropper cannot have confidence above a certain threshold (bounded away from unity), even if she/he is willing to wait for an arbitrarily long sequence of observations.

The main contribution of this work is to provide a polynomial complexity verification algorithm for the setting of probabilistic system opacity (assuming that the HMMs can start from any initial state with nonzero probability). The probabilistic system opacity setting was introduced in our previous work (Keroglou and Hadjicostis 2016) and part of the material used to establish results in this work, was introduced in Keroglou and Hadjicostis (2014). In this paper we extend our previous works in two ways:

  1. 1)

    We validate the correctness of a polynomial complexity algorithm for probabilistic system opacity. Specifically, we provide complete proofs for Theorem 1 and Theorem 3, which were not provided in our previous papers (Keroglou and Hadjicostis 2016) and (Keroglou and Hadjicostis 2014).

  2. 2)

    We discuss (in Section 5) how probabilistic system opacity relates to (is actually a special case of) probabilistic current-state opacity in Saboori and Hadjicostis (2014). However, unlike probabilistic current-state opacity which is in general undecidable, we show that probabilistic system opacity can be verified with polynomial complexity.

The paper is organized as follows. Section 2 reviews the HMM model under consideration, as well as needed concepts and notation. Specifically, we are interested in classification among HMMs, i.e., the ability of the observer to distinguish between two (or more) HMMs. Sections 3 and 4 introduce the relevant notion of probabilistic system opacity and develop the verification algorithm. In some sense, classification can be seen as the opposite of opacity. Indeed, we prove later in the paper, that, in our specific setup, classification and opacity are exactly opposite. Note here that classification characterizes the models, but, on the other hand, opacity is dependent on the specific sequence of observations; in other words, classification depends on unconditional probabilities whereas probabilistic system opacity depends on conditional probabilities (thus, a priori, their relationship is not clear). Section 5 makes connections with probabilistic current state opacity and Section 6 summarizes the contribution of this work and briefly discusses possible future extensions.

2 Notation and background

Definition 1

(HMM Model). An HMM is described by a five-tuple S = (Q, E,Δ,Λ,π 0), where Q = {q 1, q 2,...,q |Q|} is the finite set of states; E = {e 1, e 2,...,e |E|} is the finite set of outputs; Δ : Q × Q → [01] captures the state transition probabilities; Λ : Q × E × Q → [01] captures the output probabilities associated with transitions; and π 0 is the initial state probability distribution vector. Specifically, for q, q ′∈ Q and σ ∈ E, the output probabilities associated with transitions are given by

$$\Lambda(q, \sigma, q^{\prime})\equiv \Pr(q[t + 1]=q^{\prime},E[t + 1]=\sigma \mid q[t]=q) \; , $$

and the state transition probabilities are given by

$$\Delta(q, q^{\prime}) \equiv \Pr(q[t + 1]=q^{\prime}\mid q[t]=q) \; , $$

where q[t] (E[t]) is the state (output) of the HMM at time step (or epoch) t. The output function Λ(q, σ, q ′) describes the conditional probability of observing the output σ associated with the transition to state q ′ from state q. The state transition function needs to satisfy

$$ \begin{array}{rcl} \Delta(q, q^{\prime})&=&\displaystyle\sum\limits_{\sigma \in E} \Lambda (q,\sigma,q^{\prime}),\text{ }\forall q,q^{\prime} \in Q \end{array} $$
(1)

and also

$$\displaystyle\sum\limits_{i = 1}^{|Q|} \Delta(q,q_{i})= 1, \text{ }\forall q \in Q. $$

Definition 2

(Markov chain). For any HMM model S = (Q, E,Δ,Λ,π 0), there exists an associated Markov chain M C = (Q,Δ,π 0), where Q = {q 1, q 2,...,q |Q|} is the finite set of states; Δ : Q × Q → [01] captures the state transition probabilities; and π 0 is the initial state probability distribution vector. We also denote the Markov chain by M C = (Q, A, π 0) where A is a |Q|×|Q| matrix such that A(k, j) = Δ(q j , q k ).

Given an HMM model S = (Q, E,Δ,Λ,π 0), we also define for notational convenience the |Q|×|Q| matrix A σ , associated with output σ ∈ E, as follows: the (k, j)th entry of A σ captures the probability of a transition from state q j to state q k that produces output σ, i.e., A σ (k, j) = Λ(q j , σ, q k ). Note that \({A}={\sum }_{\sigma \in E} {A}_{\sigma }\) is a column stochastic matrix whose (k, j)th entry denotes the probability of taking a transition from state q j to state q k , without regard to the output produced, i.e., A is the transition matrix of the Markov chain M C = (Q, A, π 0) that corresponds to the given HMM S = (Q, E,Δ,Λ,π 0). We denote an observation sequence of length n as ω = ω[1]ω[2]...ω[n] ∈ E ∗, where ω[t] ∈ E. We say that the observation sequence ω belongs to the language of HMM S (L(S)) iff there exists q[0],q[1],q[2],...,q[n] s.t. π 0(q[0]) > 0 and Δ(q[t],ω[t + 1],q[t + 1]) > 0,∀t = 0,1,2,...,n − 1.

Remark 1

If π[t] is the |Q|-dimensional vector whose jth entry denotes the probability of being in state q j after t steps (or epochs), then we have π[0] = π 0 and π[t + 1] = A π[t] = A t+ 1 π 0.

Next we recall the properties of irreducibility and aperiodicity for Markov chains.

Definition 3

(Irreducible or Strongly Connected Markov Chain) (Seneta 2006; Cassandras and Lafortune 2007). A Markov chain M C = (Q, A, π 0) is irreducible if for all q, q ′∈ Q, there exists some \(n \in \mathbb {N}\) such that A n(q ′, q) > 0, where A n is the n th power of A. Equivalently, ∀q ′∈ Q, q ′ is reachable from any other state q ∈ Q. In such case, we observe that the graphFootnote 2 corresponding to MC is strongly connected.

Definition 4

(Periodic Markov chain) (Seneta 2006; Cassandras and Lafortune 2007). A state q i ∈ Q of a Markov chain M C = (Q, A, π 0) is said to be periodic if the greatest common divisor d of the set {n > 0 : Pr(q[n] = q i | q[0] = q i ) > 0} is d ≥ 2. If d = 1, state q i is said to be aperiodic. The Markov chain is said to be aperiodic if all states q i ∈ Q are aperiodic.

Remark 2

(Cassandras and Lafortune 2007) If a Markov chain M C = (Q, A, π 0) is irreducible, then all its states have the same period. It follows that if d = 1 for any state of an irreducible Markov chain, then all states are aperiodic. On the other hand, if any state has period d ≥ 2, then all states have the same period and the chain is said to be periodic with period d ≥ 2.

Lemma 1

(Cassandras and Lafortune 2007) (Stationary distribution of a Markov chain). If the Markov chain is irreducible and aperiodic, then \(\displaystyle \lim _{t \rightarrow \infty }\pi [t]\) exists and is called the stationary distribution of the Markov chain denoted by π s = [π s (q 1),π s (q 2),...,π s (q |Q|)]T, where T denotes matrix/vector transposition.

Definition 5

(Stationary Emission Probabilities of HMM). Given an HMM S = (Q, E,Δ,Λ,π 0), the stationary emission probability π e (e i ), ∀e i ∈ E, can be expressed as

$$\pi_{e}(e_{i})= \mathbf{1}^{T} (A_{e_{i}} \pi_{s}), $$

where 1 T is the |Q|-dimensional row vector with all entries equal to unity. We denote the vector of stationary emission probabilities as π e = [π e (e 1)...π e (e |E|)]T.

Note that the stationary state probability vector π s for an HMM S is the same as the stationary state probability vector of its associated Markov chain M C = (Q, A, π 0).

2.1 Optimal decision rule (MAP rule)

Suppose that we are given two HMMs, captured by \(S^{(1)}=(Q^{(1)}, E^{(1)}, \Delta ^{(1)},\allowbreak \Lambda ^{(1)}, \pi ^{(1)}_{0})\) and S (2) = (Q (2), E (2),Δ(2),Λ(2), π0(2)), with prior probabilities for each model given by P 1 and P 2 = 1 − P 1, respectively. Given \(E^{(j)}=\left \{ e^{(j)}_{1},e^{(j)}_{2},...,\allowbreak e^{(j)}_{|E^{(j)}|}\right \}\), j = {1,2}, for the two HMMs, we define for notational convenience E = E (1) ∪ E (2) with E = {e 1, e 2,...,e |E|}. \(A^{(j)}_{e_{i}}\) is the transition matrix for S (j), j = {1,2}, under the output symbol e i ∈ E. The matrix \(A^{(j)}_{e_{i}}\), associated with output e i ∈ E (j), is defined as follows: the (k, l)th entry of \(A^{(j)}_{e_{i}}\) captures the probability of a transition from state q l to state q k that produces output e i , i.e., \(A^{(j)}_{e_{i}}(k,l)=\Lambda ^{(j)}(q_{l},e_{i},q_{k})\). We set A e i (j) to zero if e i ∈ E ∖ E (j). If we observe a sequence of n outputs ω = ω[1]ω[2]...ω[n], with ω[t] ∈ E, that is generated by one of the two underlying HMMs, the classifier that minimizes the probability of error needs to implement the maximum a posteriori probability (MAP) rule. Specifically, the MAP classifier compares (as done in a classical hypothesis testing problem (Neyman and Pearson 1992))

$$\Pr(S^{(1)} \mid \omega) \ \;\;_<^> \;\; \Pr(S^{(2)} \mid \omega) \Rightarrow \displaystyle \frac{\Pr(\omega \mid S^{(1)})}{\Pr(\omega \mid S^{(2)})} \;\;_<^> \;\; \frac{P_{2}}{P_{1}},$$

and decides in favor of S (1) (S (2)) if the left (right) quantity is larger. When we decide in favor of one or the other model, we incur a probability of error proportional to the probability of the model that was not selected; with some algebra, it can be shown that Pr(error,ω) = min{P 1 ⋅ Pr(ω∣S (1)),P 2 ⋅ Pr(ω∣S (2))}.

2.2 Probability of misclassification between HMMs

To calculate the a priori probability of error before any sequence of observations of length n is observed, we need to consider all possible observation sequences of length n:

$$\begin{array}{@{}rcl@{}} \Pr(\text{error} at \textit{n}) &=&\displaystyle\sum\limits_{\omega \in E^{n}}\Pr(\text{error}, \omega), \end{array} $$
(2)

where E n is the set of all sequences of length n with outputs from E. We arbitrarily index each of the d n (d = |E|) sequences of observations via ω(i), i ∈{1,2,...,d n}, and use \(P^{(j)}_{i}\) to denote \(P^{(j)}_{i}=\Pr (\omega (i)|S^{(j)})\), j ∈{1, 2}. Note that some of these sequences may have zero probability under one of the two models (or even both models). The probability of misclassification between the two systems, after n steps, can then be expressed as

$$\begin{array}{@{}rcl@{}} \Pr(\text{error at } n)&=&\displaystyle\sum\limits_{i = 1}^{d^{n}}\Pr(\text{error},{\omega(i)})\\ &=&\displaystyle\sum\limits_{i = 1}^{d^{n}}\min\left\{P_{1}\cdot P^{(1)}_{i}, P_{2}\cdot P^{(2)}_{i}\right\}. \end{array} $$
(3)

We can calculate \(P^{(j)}_{i}=\Pr (\omega (i)|S^{(j)})\) with an iterative algorithm, a detailed description of which can be found in Athanasopoulou and Hadjicostis (2008) and Fu (1982). Specifically, given sequence ω = ω[1]ω[2]...ω[n] we calculate

$$\rho^{(j)}_{n}= A^{(j)}_{\omega[n]} A^{(j)}_{\omega[n-1]} ... A^{(j)}_{\omega[1]} \pi^{(j)}_{0}, $$

which is essentially a vector whose k th entry captures the probability of reaching state q k ∈ Q (j) while generating the sequence of outputs ω (i.e., \(\rho ^{(j)}_{n}(k)=\Pr (q[n]=q_{k}, \omega | S^{(j)})\)). If we sum up the entries of \(\rho ^{(j)}_{n}\) we obtain \(P^{(j)}_{\omega }=\Pr (\omega \mid S^{(j)})={\sum }^{|Q^{(j)}|}_{k = 1} \rho _{n}^{(j)}(k)\).

Utilizing the above algorithm, we can certainly compute the probability of error at n by explicitly calculating \(P_{j}\cdot P^{(j)}_{i}\) for each sequence ω(i). However, the calculation of the a priori probability of error is computationally difficult for large values of n due to the exponential number of the possible sequences of observations ω; thus, in this paper, we are interested in obtaining easily calculable bounds for the a priori probability of error or misclassification. It is well-known that the MAP classifier described here minimizes the probability of error (misclassification); thus, any other rule, will be suboptimal in terms of minimizing the probability of error and can be used to obtain a bound on the probability of error. The following example is borrowed from Keroglou and Hadjicostis (2014).

Example 1

Suppose we are given the HMMs, \(S^{(1)}=(Q^{(1)}, E^{(1)}, \Delta ^{(1)}, \Lambda ^{(1)}, \pi ^{(1)}_{0})\) and S (2) = (Q (2), E (2),Δ(2),Λ(2), π0(2)) shown in Fig. 1, with E (1) = E (2) = E = {α, β}, \(\pi ^{(1)}_{0}=\pi ^{(2)}_{0}= \left [\begin {array}{cccccc} \par 1 & 0 \end {array} \right ]^{T},\)and P 1 = P 2 = 0.5. The corresponding \(A^{(1)}_{\alpha },A^{(1)}_{\beta },A^{(2)}_{\alpha },A^{(2)}_{\beta }\) are as follows:

$${A}^{(1)}_{\alpha} = \left[ \begin{array}{ll} 0 & 0 \\ 0.5 & 0.5 \end{array} \right] \text{, }{ A}^{(1)}_{\beta} = \left[ \begin{array}{ll} 0.5 & 0.25 \\ 0 & 0.25 \end{array} \right], $$
$${ A}^{(2)}_{\alpha} = \left[ \begin{array}{ll} 0 & 0 \\ 0.6 & 0.06 \end{array} \right]\text{, } { A}^{(2)}_{\beta} = \left[ \begin{array}{ll} 0.4 & 0.04 \\ 0 & 0.9 \end{array} \right]. $$
Fig. 1
figure 1

S (1) (top) and S (2) (bottom) used in Example 1

Full size image

If the sequence ω(ℓ) = β α β α is observed, we have \(P^{(1)}_{\ell }= \displaystyle \sum \limits _{k = 1}^{|Q^{(1)}|} \rho ^{(1)}_{4}(k)= 0.0625\), where \(\rho ^{(1)}_{4}=A^{(1)}_{\alpha }A^{(1)}_{\beta }A^{(1)}_{\alpha }A^{(1)}_{\beta } \pi _{0}^{(1)}\), and \(P^{(2)}_{\ell }=\displaystyle \sum \limits _{k = 1}^{|Q^{(2)}|}\rho ^{(2)}_{4}(k)= 0.0187\), where \(\rho ^{(2)}_{4}= A^{(2)}_{\alpha }A^{(2)}_{\beta }\allowbreak A^{(2)}_{\alpha }A^{(2)}_{\beta } \pi _{0}^{(2)}\). Thus, the probability of error between the two models when this specific sequence is observed is Pr(error,ω(ℓ)) = 0.0094 (i.e., S (1) will be selected and \(\Pr (\text {error}, \omega (\ell ))=P_{2}\cdot P^{(2)}_{\ell }\)).

3 Probabilistic system opacity

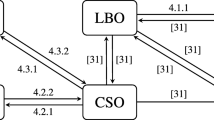
Probabilistic system opacity considers the following setting: we are given m HMMs, denoted by S (i) for i ∈{1,2,...,m}. The prior probability of S (i) is P i , P i > 0, with the prior probabilities satisfying \(\displaystyle \sum \limits _{i = 1}^{m} P_{i}= 1\). A user is supposed to choose one of these models, say S (i), and would like to keep an observer (eavesdropper) confused about the chosen HMM, for any behavior that might occur in the chosen HMM, regardless of the sequence of observations generated by it and regardless of how long the observer is willing to wait (refer to Fig. 2). This means that for any (arbitrarily long) observation sequence that can be generated by the chosen HMM, the observer must not be able to determine the chosen HMM, at least not with absolute certainty or with certainty that tends asymptotically to unity.

Fig. 2
figure 2

An HMM is chosen out of m different HMMs, S (1), S (2), …,S (m); an Eavesdropper knows the exact structure of these HMMs and also observes the observation sequence that is generated; probabilistic system opacity holds if the Eavesdropper is kept confused about which is the true HMM that generates the observation

Full size image

Definition 6

(Probabilistic System Opacity). Consider a set of m HMMs, \(S^{(i)}=\left (Q^{(i)}, E^{(i)}, \Delta ^{(i)}, \Lambda ^{(i)}, \pi ^{(i)}_{0}\right )\), for i ∈{1,...,m}, with corresponding Markov chains \(MC^{(i)}=\left (Q^{(i)},A^{(i)},\pi _{0}^{(i)}\right )\) that are irreducible and aperiodic and with initial probability distribution \(\pi ^{(i)}_{0}>0\). Probabilistic system opacity holds if there exists an α 0 > 0, such that for any chosen S (i) and for any observation sequence ω that could be generated by S (i), we have

$$\alpha(\omega):=\frac{\displaystyle\sum\limits_{k = 1,k \neq i}^{m}P_{k}P^{(k)}_{\omega}}{\displaystyle\sum\limits_{k = 1}^{m}P_{k}P^{(k)}_{\omega}}\geq \alpha_{0} \; . $$

Remark 3

Note that in Definition 6, we assume that the initial probability distribution \(\pi ^{(i)}_{0}\) is a strictly positive vector (i.e., all initial states are possible among all m HMMs). If this is the case, we will argue that probabilistic system opacity can be verified with polynomial complexity. The complexity and the verification algorithm in the more general case, where \(\pi ^{(i)}_{0}\) is not necessarily strictly positive, remains an open problem.

4 Polynomial verification of probabilistic opacity

In the following definition, we discuss the problem of probabilistic opacity for two HMMs. It will become obvious from the discussions in this section that the conditions for m HMMs, to be probabilistically opaque are based on the conditions for a pair of HMMs to be probabilistically opaque, which is defined next.

Definition 7

(Pairwise Probabilistic Opacity). Two HMMs, S (i) = (Q (i), E, Δ(i), Λ(i), \(\pi ^{(i)}_{0}\)) for i ∈{1, 2} and prior probabilitiesFootnote 3 P 1 and P 2 are probabilistically opaque if there exists α 0 (0 < α 0 < 1/2) such that for any observation sequence ω

$$(\forall \omega \in L(S^{(1)})\cup L(S^{(2)})) \text{ we have } \alpha(\omega)\geq \alpha_{0} \; , $$

with

$$\alpha(\omega)=\min\left\{\frac{P_{1}P^{(1)}_{\omega}}{P_{1}P^{(1)}_{\omega}+P_{2}P^{(2)}_{\omega}}, \frac{P_{2}P^{(2)}_{\omega}}{P_{1}P^{(1)}_{\omega}+P_{2}P^{(2)}_{\omega}}\right\} \; . $$

[Recall that \(P_{i}P^{(i)}_{\omega }\), i ∈{1, 2}, is the probability that observation ω is generated by HMM S (i).]

To determine whether two HMMs are probabilistically opaque, we will employ tools from probabilistic equivalence and HMM classification; we introduce some relevant definitions next.

Definition 8

(Probabilistic Equivalence for HMMs (Tzeng 1989)). Two HMMs, \(S^{(i)}=(Q^{(i)}, E^{(i)}, \Delta ^{(i)}, \Lambda ^{(i)}, \pi ^{(i)}_{0})\), i ∈{1, 2} with E = E (1) = E (2) are probabilistically equivalent iff for any string ω ∈ L(S) (L(S) = L(S (1)) ∪ L(S (2))) the two HMMs, accept the string with equal probability.

Remark 4

Two HMMs can be tested for probabilistic equivalence with polynomial complexity (Tzeng 1989).

Remark 5

We say that two HMMs are probabilistically equivalent from steady–state iff the two HMMs \(S^{(i)}=(Q^{(i)}, E^{(i)}, \Delta ^{(i)}, \Lambda ^{(i)},\allowbreak \pi ^{(i)}_{s})\), for i ∈{1, 2}, where \(\pi ^{(i)}_{s}\) is their respective steady–state probabilities (Definition 1), are probabilistically equivalent.

Theorem 1 (Probability of Error Among Two HMMs Tending to Zero)

Consider two HMMs, \(S^{(i)}=(Q^{(i)}, E^{(i)}, \Delta ^{(i)}, \Lambda ^{(i)}, \pi ^{(i)}_{0})\) , i ∈{1, 2}, with corresponding Markov chains \(MC^{(i)}=(Q^{(i)},A^{(i)},\pi _{0}^{(i)})\) that are irreducible and aperiodic. If S (1) and S (2) are not probabilistically equivalent from steady–state, then

$$(\forall \epsilon>0)(\exists n_{0} \in \mathbb{N}) \text{ such that for } n\geq n_{0}\; \Pr(\text{error at } n)<\epsilon, $$

where Pr(error at n) is the probability of misclassification for the two HMMs (defined in Eq. 2).

Proof

The proof is provided in Appendix. □

In other words, if the two HMMs are not probabilistically equivalent from steady–state, then the probability of error among the two HMMs tends, when n goes to infinity, to zero. The proof in Appendix relies on the fact that we are able to discriminate between the two HMM models using a suboptimal decision rule (Definition 12) based on the empirical frequencies of output symbols, as long as the two systems are characterized, at steady-state, by different statistical properties for the occurrence of output symbols or different statistical properties of finite sequences of consecutive output symbols (this occurs if and only if the two HMMs are not probabilistically equivalent from steady–state). The theoretical analysis in Appendix establishes an upper bound on the misclassification probability, which is described by a function that decreases exponentially with the length of the observation sequence (as long as the two systems are characterized, at steady-state, by different statistical properties for the stationary emission probabilities (Definition 5) or stationary emission probabilities for a finite number of consecutive output symbols).

Now, we revisit the following theorem, which was introduced and proved in Keroglou and Hadjicostis (2016). This theorem establishes the necessary and sufficient conditions needed for two HMMs to be probabilistically opaque.

Theorem 2 (Conditions for Pairwise Probabilistic Opacity (Definition 7))

Consider two HMMs \(S^{(i)}=\left (Q^{(i)}, E^{(i)}, \Delta ^{(i)}, \allowbreak \Lambda ^{(i)},\pi ^{(i)}_{0}\right )\) , i = 1,2,with corresponding Markov chains \(MC^{(i)}=\left (Q^{(i)},A^{(i)},\pi _{0}^{(i)}\right )\) that are irreducible and aperiodic. These two HMMs are pairwise probabilistically opaque iff they are probabilistically equivalent from steady-state.

Proof

Let us use the following notation:

  • ω = ω[1]ω[2]...ω[n], where ω[t] ∈ E for t ∈{1,...,n};

  • 1 T = [1...1] is a row vector with n identical elements equal to 1;

  • \(A^{(1)}_{\omega }=A^{(1)}_{\omega [n]} {\cdots } A^{(1)}_{\omega [1]}\) and \(A^{(2)}_{\omega }=A^{(2)}_{\omega [n]} {\cdots } A^{(2)}_{\omega [1]}\);

  • For a vector π, min{π} is the minimum element of the vector and max{π} is the maximum element of the vector;

  • \(\alpha (\omega )=\min \left \{\frac {P_{1}P^{(1)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }}, \frac {P_{2}P^{(2)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }} \right \}\), where \(P_{i}P^{(i)}_{\omega }\), i = 1,2, is the probability that observation ω is generated by HMM S (i).

(→) Suppose that the two HMMs are probabilistically opaque; we need to show that the two HMMs are probabilistically equivalent from steady-state. We know that if the probability of error does not tend to zero, then the two HMMs are probabilistically equivalent from steady–state according to the contraposition of Theorem 1. It remains to prove that if the two HMMs are probabilistically opaque, then the probability of error among the two HMMs does not tend to zero. If the two HMMs are probabilistically opaque, we argue that the probability of error when trying to classify between S (1) and S (2) based on a sequence of observations satisfies

$$(\exists \;0<\alpha_{0}^{\prime}<1\;)(\forall n \in \mathbb{N}) \{\Pr(\text{error at }n) \geq \alpha_{0}^{\prime}\} \; . $$

This is proved easily because we know that (∃α 0)(∀ω ∈ L(S (1)) ∪ L(S (2))), we have \(\min \left \{\frac {P_{1}P^{(1)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }}, \frac {P_{2}P^{(2)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }} \right \}\geq \alpha _{0}\). Therefore, for each \(n \in \mathbb {N}\)

$$\begin{array}{@{}rcl@{}} \Pr(\text{error at }n)&=&\displaystyle\sum\limits_{\omega: |\omega|=n}\left( \min\left\{P_{1}P^{(1)}_{\omega}, P_{2}P^{(2)}_{\omega}\right\}\right)\\ &\geq& \displaystyle\sum\limits_{\omega: |\omega|=n}\alpha_{0} \left( P_{1}P^{(1)}_{\omega}+ P_{2}P^{(2)}_{\omega}\right)\\ &=& \alpha_{0}\left( P_{1}\displaystyle\sum\limits_{\omega: |\omega|=n} P^{(1)}_{\omega}+ P_{2}\displaystyle\sum\limits_{\omega: |\omega|=n} P^{(2)}_{\omega}\right)=\alpha_{0}(P_{1}+P_{2})=a_{0}^{\prime} \; . \end{array} $$

This proves that the probability of error does not tend to zero; therefore, the two HMMs are probabilistically equivalent from steady–state.

(←) Suppose that the two HMMs are probabilistically equivalent from steady–state; then, for any ω, we have

$$\mathbf{1}^{T} A^{(1)}_{\omega} \pi^{(1)}_{s}=\mathbf{1}^{T} A^{(2)}_{\omega} \pi^{(2)}_{s}=:\pi_{\omega,s} \; . $$

We next prove that the two HMMs are Probabilistically Opaque. Four useful inequalities for i ∈{1, 2} are the following:

$$\begin{array}{@{}rcl@{}} P^{(i)}_{\omega}&=&\mathbf{1}^{T}A^{(i)}_{\omega} \pi^{(i)}_{0} \\ &\geq & \mathbf{1}^{T}A^{(i)}_{\omega}\min\{\pi^{(i)}_{0}\} \mathbf{1} \\ &\geq& \min\{\pi^{(i)}_{0} \} \pi_{\omega,s} \; , \\ \\ P^{(i)}_{\omega}&=&\mathbf{1}^{T}A^{(i)}_{\omega} \pi^{(i)}_{0} \\ &\leq & \mathbf{1}^{T}A^{(i)}_{\omega}\max\left\{\pi^{(i)}_{0}\right\}\mathbf{1} \\ &\leq & \frac{\max\left\{\pi^{(i)}_{0}\right\}}{\min\left\{\pi^{(i)}_{s}\right\}}\mathbf{1}^{T}A^{(i)}_{\omega} \pi^{(i)}_{s} \\ &\leq & \frac{\max\left\{\pi^{(i)}_{0}\right\}}{\min\left\{\pi^{(i)}_{s}\right\}}\pi_{\omega,s} \; . \end{array} $$

In summary, we have

$$\min\left\{\pi^{(i)}_{0}\right\} \pi_{\omega,s} \leq P^{(i)}_{\omega} \leq \frac{\max\left\{\pi^{(i)}_{0}\right\}}{\min\left\{\pi^{(i)}_{s}\right\}}\pi_{\omega,s} \; . $$

From the previous inequalities we can rewrite \(\alpha (\omega )=\min \left \{\frac {P_{1}P^{(1)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }},\allowbreak \frac {P_{2}P^{(2)}_{\omega }}{P_{1}P^{(1)}_{\omega }+P_{2}P^{(2)}_{\omega }}\right \}\!\geq \min \{c_{1},c_{2}\}\), where c 1 < 1 and c 2 < 1, with

$$c_{i}=\frac{P_{i}\min\{\pi^{(i)}_{0} \}}{P_{1}\frac{\max\left\{\pi^{(1)}_{0}\right\}}{\min\{\pi^{(1)}_{s}\}} + P_{2}\frac{\max\left\{\pi^{(2)}_{0}\right\}}{\min\{\pi^{(2)}_{s}\}}},$$

which proves that for any ω, of any length n, the observer is uncertain with a threshold of at least α 0 = min{c 1, c 2}. □

Theorem 3 discussed and proven in the remainder of this section, was presented without proof in Keroglou and Hadjicostis (2016). The following lemmas are useful in proving Theorem 3.

Lemma 1

If probabilistic system opacity holds then the probability of error among m HMMs with S (i) as the chosen system, does not tend to zero ( (∃0 < 𝜖 < 1)(∀n 0)(∃n ≥ n 0) (Pr(error at n, S (i)) ≥ 𝜖 ).

Proof

We have the following statements:

  1. 1.

    From Probabilistic System Opacity we have for any ω ∈ L(S):

    $$\frac{\displaystyle\sum\limits_{k = 1,k \neq i}^{m}P_{k}P^{(k)}_{\omega}}{\displaystyle\sum\limits_{k = 1}^{m}P_{k}P^{(k)}_{\omega}}\geq \alpha_{0} $$
  2. 2.

    The set of decisions is {H 0, H 1}, where H 0 : { We accept S (i)} and H 1 : { We reject S (i)}

  3. 3.

    Using the MAP rule, we decide in favor of H 0 when \(P_{i}P^{(i)}_{\omega }>\displaystyle \sum \limits _{k\neq i} P_{k}P^{(k)}_{\omega }\) and in favor of H 1 when \(P_{i}P^{(i)}_{\omega }\leq \displaystyle \sum \limits _{k\neq i} P_{k}P^{(k)}_{\omega }\)

  4. 4.

    Ω n = {ω : |ω| = n}

  5. 5.

    \({\Omega }^{n}_{a}=\left \{\omega : (|\omega |=n) \wedge \left (P_{i}P^{(i)}_{\omega }>\displaystyle \sum \limits _{k\neq i} P_{k}P^{(k)}_{\omega }\right )\right \}\)

  6. 6.

    \({\Omega }^{n}_{r}=\left \{\omega : (|\omega |=n) \wedge \left (P_{i}P^{(i)}_{\omega }\leq \displaystyle \sum \limits _{k\neq i} P_{k}P^{(k)}_{\omega }\right )\right \}\)

  7. 7.

    \((\forall \omega \in {\Omega }_{n})\!\left (\displaystyle \sum \limits _{k \neq i}P_{k}P^{(k)}_{\omega }\geq \alpha _{0}\displaystyle \sum P_{k}P^{(k)}_{\omega }\geq \alpha _{0}P_{i}P^{(i)}_{\omega }\right .\) (Definition 6)

  8. 8.

    \(\Pr (\text {error at } n,\; S^{(i)})= \displaystyle \sum \limits _{\omega \in {\Omega }^{n}_{a}} \displaystyle \sum \limits _{k\neq i} P_{k}P^{(k)}_{\omega }\allowbreak + \displaystyle \sum \limits _{\omega \in {\Omega }^{n}_{r}} P_{i}P^{(i)}_{\omega }\)

From 1–8 we have

$$\begin{array}{@{}rcl@{}} \Pr(\text{error at } n,\; S^{(i)}) & \geq& \alpha_{0}\left( \displaystyle\sum\limits_{\omega \in {\Omega}^{n}_{a}}P_{i}P^{(i)}_{\omega}+ \displaystyle\sum\limits_{\omega \in {\Omega}^{n}_{r}}P_{i}P^{(i)}_{\omega}\right)\\ &\geq& \alpha_{0}\displaystyle\sum\limits_{\omega \in {\Omega}_{n}}P_{i}P^{(i)}_{\omega}\allowbreak =\alpha_{0}P_{i}=\epsilon \end{array} $$

The proof is concluded. □

Lemma 2

For a, b 1, b 2,...,b m nonnegative real numbers, we have that

\(\min \{a,b_{1}+b_{2}+...b_{m}\}\leq \displaystyle \sum \limits ^{m}_{i = 1} \min \{a,b_{i}\}\)

Proof

We use mathematical induction:

  1. 1.

    For m = 2, we have to prove that min{a, b 1 + b 2}≤ min{a, b 1} + min{a, b 2}. We take three cases i) a > b 1 ≥ 0 and a > b 2 ≥ 0, ii) 0 ≤ a ≤ b 1 and 0 ≤ a ≤ b 2, iii) 0 ≤ a ≤ b 1 and a > b 2 ≥ 0.

    We prove only the first case, the proofs for the other cases are left to the interested reader. For the first case, min{a, b 1} + min{a, b 2} = b 1 + b 2 which implies that min{a, b 1 + b 2}≤ (b 1 + b 2) = min{a, b 1} + min{a, b 2}.

  2. 2.

    Let us suppose that for k < m, \(\min \{a,b_{1}+b_{2}+...b_{k}\}\leq \displaystyle \sum \limits ^{k}_{i = 1} \min \{a,b_{i}\}\).

  3. 3.

    We want to prove that \(\min \{a,b_{1}+b_{2}+...+b_{k}+ b_{k + 1}\}\leq \displaystyle \sum \limits ^{k + 1}_{i = 1} \min \{a,b_{i}\}\). Indeed, with B k = b 1 + ...b k we have from 1) and 2) that \(\min \{a,B_{k}+ b_{k + 1}\}\leq \min \{a,B_{k}\}+\min \{a,b_{k + 1}\}\leq \displaystyle \sum \limits ^{k}_{i = 1}\min \{a,b_{i}\} + \min \{a,b_{k + 1}\}=\displaystyle \sum \limits ^{k + 1}_{i = 1}\min \{a,b_{i}\}\). The proof is concluded.

□

Lemma 3

If the probability of error among m HMMs with S (i) as the chosen system, does not tend to zero, then there exists at least one S (j), such that S (i) and S (j) are pairwise probabilistic opaque.

Proof

We have the following statements:

  1. 1.

    The pairwise probability of error for S (i) and S (j) is defined below:

    \(\Pr (\text {pairwise error at }n,\; S^{(i)},S^{(j)})=\displaystyle \sum \limits _{\omega : |\omega |=n}\min \{P_{i}P^{(i)}_{\omega }, P_{j}P^{(j)}_{\omega }\}\)

  2. 2.

    The probability of error among m HMMs with S (i) as the chosen system can be formulated as given below:

    $$\Pr(\text{error at } n,\; S^{(i)})= \displaystyle\sum\limits_{\omega: |\omega|=n} \min\left\{P_{i}P^{(i)}_{\omega}, \displaystyle\sum\limits_{k\neq i} P_{k}P^{(k)}_{\omega}\right\}$$

We prove this lemma by contraposition. If there does not exist S (j) such that S (i) and S (j) are pairwise probabilistic opaque, then according to Definition 7 (and from Theorems 1 and 2) for any S (j) the pairwise probability of error for S (i) and S (j) tends to zero. This can be formulated as:

$$(\forall 0<\epsilon<1)(\exists n_{ij})(\forall n\geq n_{ij})$$
$$\Pr(\text{pairwise error at }n,\; S^{(i)},S^{(j)})<\epsilon.$$
$$\begin{array}{@{}rcl@{}} \Pr(\text{error at } n,\; S^{(i)}) & \overset{\mathrm{2)}}{=}& \displaystyle\sum\limits_{\omega: |\omega|=n} \min\left\{P_{i}P^{(i)}_{\omega}, \displaystyle\sum\limits_{k\neq i} P_{k}P^{(k)}_{\omega}\right\}\\ & \overset{\mathrm{ Lemma~2}}{\leq}& \displaystyle\sum\limits_{\omega: |\omega|=n}\displaystyle\sum\limits_{j \neq i}\min\left\{P_{i}P^{(i)}_{\omega}, P_{j}P^{(j)}_{\omega}\right\}\\ &\overset{\mathrm{1)}}{=}&\displaystyle\sum\limits_{j \neq i}\Pr(\text{pairwise error at }n,\; S^{(i)},S^{(j)}). \end{array} $$

From 1), 2) and from Lemma 2 and if we pick n 0 = max{n i j } we have that

$$(\forall 0<\epsilon^{\prime}<1)(\exists n_{0})(\forall n\geq n_{0}) $$
$$\Pr(\text{error at } n,\; S^{(i)})\leq \Pr(\text{pairwise error at }n,\; S^{(i)},S^{(j)})\leq (k-1)\epsilon=\epsilon^{\prime}. $$

The proof is concluded. □

Theorem 3 (Necessary and Sufficient Conditions for Probabilistic System Opacity)

Consider a set of m HMMs, S (i) = (Q (i), E (i),Δ(i), Λ(i), π0(i)), i ∈{1,...,m},with corresponding Markov chains \(MC^{(i)}=(Q^{(i)},A^{(i)},\pi _{0}^{(i)})\) that are irreducible and a periodic and with initial probability distribution \(\pi ^{(i)}_{0}>0\) . The following statements are true:

(→)If the property of probabilistic system opacity as described in Definition 6 holds, then, for any i there exists at least one HMM S (j), j ≠ i, such that S (i) and S (j) are pairwise probabilistically opaque (Definition 7).

(←)If, for any i, there exists at least one HMM S (j), j ≠ i, such that S (i) and S (j) are pairwise probabilistically opaque, then the property of probabilistic system opacity holds.

Proof

(→) We prove the statement by combining Lemma 1 and Lemma 3.

(←) We need to show that for any system S (i) and for any observation sequence ω that can be generated by S (i), we have

$$\alpha(\omega)=\frac{\displaystyle\sum\limits_{k = 1,k \neq i}^{m}P_{k}P^{(k)}_{\omega}}{\displaystyle\sum\limits_{k = 1}^{m}P_{k}P^{(k)}_{\omega}}\geq \alpha_{0} \; . $$

Suppose S (j) is the HMM that is pairwise probabilistically opaque with S (i). Then, from Definition 7, there exists an α i j , for any observation sequence ω, such that \(\min \left \{\frac {P_{i} P^{(i)}_{\omega }}{P_{i}P^{(i)}_{\omega }+P_{j}P^{(j)}_{\omega }},\allowbreak \frac {P_{j}P^{(j)}_{\omega }}{P_{i}P^{(i)}_{\omega }+P_{j}P^{(j)}_{\omega }}\right \}\geq \alpha _{ij}\). Thus, for any observation sequence ω that could be generated by S (i), we have

$$\begin{array}{@{}rcl@{}} \alpha(\omega) &= & \frac{\displaystyle\sum\limits_{k = 1,k \neq i}^{m}P_{k}P^{(k)}_{\omega}}{\displaystyle\sum\limits_{k = 1}^{m}P_{k}P^{(k)}_{\omega}} = 1-\frac{P_{i}P^{(i)}_{\omega}}{\displaystyle\sum\limits_{k = 1}^{m}P_{k}P^{(k)}_{\omega}} \\ &\geq & 1-\frac{P_{i}P^{(i)}_{\omega}}{P_{i}P^{(i)}_{\omega}+P_{j}P^{(j)}_{\omega}} = \frac{P_{j}P^{(j)}_{\omega}}{P_{i}P^{(i)}_{\omega}+P_{j}P^{(j)}_{\omega}} \geq \alpha_{ij}=\alpha_{0} \; . \end{array} $$

Therefore, probabilistic system opacity holds if, for any chosen S (i), there exists another system S (j), such that S (i) and S (j) are pairwise probabilistically opaque (Definition 7). □

Remark 6

Note that in the definition of probabilistic system opacity (Definition 7) nothing is stated about the need to have, for each system S (i) another system S (j), such that S (i) and S (j) are pairwise opaque. This is somewhat surprising, as one might think that we do not need probabilistically opaque HMMs in order to have probabilistic system opacity (e.g., we could hide some of the observation sequences generated by S (i), with an HMM S (k) and other sequences in another HMM \(S^{(k^{\prime })}\), without S (k) and \(S^{(k^{\prime })}\) needing to be probabilistically opaque with S (i)). This line of thought is not correct: if two HMMs are not probabilistically opaque, then the probability of error tends to zero eventually for all observation sequences that can be generated by S (i) (this is part of the proof of the verification of two probabilistically opaque HMMs). Thus, if there is no HMM that is probabilistically opaque with S (i), then one can always distinguish that the observed sequence is generated by S (i), with certainty that tends, at least asymptotically, to unity.

Remark 7

Probabilistic system opacity can be verified with polynomial complexity in terms of the size of the state space of the system. Indeed, according to Theorem 3, to verify the notion of probabilistic system opacity, we need to check for pairwise probabilistic opacity for all HMM pairs S (i), S (j), where i, j ∈{1,...,m} (m 2 pairs). According to Theorem 2 two HMMs are pairwise probabilistically opaque iff they are probabilistically equivalent from steady-state. Thus, we need to compute the steady-state, which can be done with polynomial complexity, and then we need to check for probabilistic equivalence from steady-state, which can also be done with polynomial complexity (Tzeng 1989).

5 Connections with probabilistic current–state opacity

Probabilistic system opacity can be seen as a special case of probabilistic current–state opacity, as introduced in Saboori and Hadjicostis (2014) for a given HMM (Q, E,Δ,Λ,π 0). In Saboori and Hadjicostis (2014) the authors defined probabilistic current–state opacity in a general setup, where there exists a secret set of states, Q s ⊆ Q, that need to remain “hidden” from an eavesdropper in the following (probabilistic) sense: the confidence of the eavesdropper, captured by the conditional probability that the system state lies in the set of secret states Q s after the execution of observation sequence ω should not exceed a threshold 𝜃. In general, the problem is proven undecidable in Saboori and Hadjicostis (2014). Probabilistic system opacity (which, as we argue below, is a special case of probabilistic current–state opacity) is shown not only to be decidable, but also verifiable with polynomial complexity.

To establish the connection between probabilistic system opacity and current–state opacity, we first reproduce the definition of probabilistic current–state opacity, with a little modification, in order to match the notation used in this paper.

Definition 9

Given an HMM S = (Q, E,Δ,Λ,π 0) and a set of secret states Q s ⊆ Q, HMM S is probabilistically current–state opaque with respect to Q s , and a parameter 𝜃 or (Q s , 𝜃)–probabilistically current–state opaque, if

$$\forall \omega \in L(S): \displaystyle\sum\limits_{\forall q_{i} \in Q_{s}}\rho_{\omega}(i) -\displaystyle\sum\limits_{\forall q_{i} \in Q_{s}}\pi_{0}(i)\leq \theta, $$

where ρ ω = A ω[n] A ω[n− 1]...A ω[1] π 0, with ω = ω[1]ω[2]...ω[n].

Our setup (assumed here to have m= 2 HMMs with prior probabilities P 1 and P 2) can be seen as a special case of probabilistic current–state opacity as follows:Footnote 4

Let S = (Q, E,Δ,Λ,π 0), be the union of two given irreducible HMMs S (1) = (Q (1), E (1),Δ(1),Λ(1), π0(1)) and \(S^{(2)}=(Q^{(2)}, E^{(2)}, \Delta ^{(2)}, \allowbreak \Lambda ^{(2)}, \pi ^{(2)}_{0})\), where

  • \(\pi _{0}=\left [ \begin {array}{l} P_{1}\pi ^{(1)}_{0} \\ P_{2}\pi ^{(2)}_{0} \end {array} \right ]\) (note π 0 > 0)

  • any \(q_{k} \in Q^{(i)}:\frac {\pi _{0}(q_{k})}{P_{i}}=\pi ^{(i)}_{0}(q_{k})\)

  • E = E (1) ∪ E (2)

  • Q = Q (1) ∪ Q (2)

  • The functions Δ and Λ are defined as follows:

    • {For any q 1 ∈ Q (1) and q 2 ∈ Q (2)}, we have {Δ(q 1, q 2) = Δ(q 2, q 1) = 0}

    • {For any i ∈{1, 2} and \(q_{k}^{(i)}, q_{k^{\prime }}^{(i)} \in Q^{(i)}\}\), we have

      $$\left\{\Delta\left( q_{k}^{(i)},q_{k^{\prime}}^{(i)}\right)=\Delta^{(i)}\left( q_{k}^{(i)},q_{k^{\prime}}^{(i)}\right)\right\} $$

    • {For any i ∈{1, 2}, \(q_{k}^{(i)}, q_{k^{\prime }}^{(i)} \in Q^{(i)}\}\) and σ ∈ E}, we have

      $$\left\{\Lambda\left( q_{k}^{(i)},\sigma,q_{k^{\prime}}^{(i)}\right)=\Lambda^{(i)}\left( q_{k}^{(i)},\sigma, q_{k^{\prime}}^{(i)}\right)\right\}. $$

In the above setup, the problem can be decomposed, from the system’s perspective, into two probabilistic current-state opacity problems. This is because we need to protect both systems (S (1) and S (2)). Thus, we need to take into consideration two cases depending on the chosen HMM. If we chose S (1) (or S (2)) then the set of secret states is Q s = Q (1) (or Q s = Q (2)) respectively.

Case 1.:

If we chose S (1), then Q s = Q (1) and probabilistic current-state opacity implies that ∀ω ∈ L(S) : α 1(ω) − P 1 ≤ 𝜃;

Case 2.:

If we chose S (2), then Q s = Q (2) and probabilistic current-state opacity implies that ∀ω ∈ L(S) : α 2(ω) − P 2 ≤ 𝜃.

We can easily prove the following for all ω ∈ L(S):

  1. 1.

    α 1(ω) = 1 − α 2(ω)

  2. 2.

    \(\alpha _{2}(\omega )\overset {\mathrm {1, Case~1}}{\geq } (1-P_{1}) - \theta =P_{2}-\theta \)

  3. 3.

    \(\alpha _{1}(\omega )\overset {\mathrm {1, Case~2}}{\geq } (1-P_{2}) - \theta =P_{1}-\theta \)

  1. 1.

    If both Case 1 and Case 2 hold with 𝜃 < min{P 1, P 2}, then for i ∈{1, 2}, we have that \(\alpha _{i}(\omega )\overset {\mathrm {2,3}}{\geq } \alpha _{0}\), where α 0 = min{P 1 − 𝜃, P 2 − 𝜃} (0 < α 0 < 1). In that case the system is also probabilistically opaque.

  2. 2.

    If the system is probabilistically opaque, then there exists some 1 > α 0 > 0 such that for all ω ∈ L(S), \(\alpha _{1}(\omega )\geq \alpha _{0} \overset {\mathrm {1}}{\Rightarrow } \alpha _{2}(\omega )-P_{2}\leq 1-(\alpha _{0}+P_{2})\) and \(\alpha _{2}(\omega )\geq \alpha _{0} \overset {\mathrm {1}}{\Rightarrow } \alpha _{1}(\omega )-P_{1}\leq 1-(\alpha _{0}+P_{1})\). This implies that S is (Q s , 𝜃)–probabilistically current–state opaque (both Case 1 and Case 2 hold), for 𝜃 ≥ max{1 − (α 0 + P 1),1 − (α 0 + P 2)}. In order to have a meaningful 𝜃 we want α 0 + P 1 < 1 and α 0 + P 2 < 1 equivalently α 0 < 1 − P 2 = P 1 and α 0 < 1 − P 1 = P 2 or α 0 < min{P 1, P 2}. This is always valid, because if a system is probabilistically opaque for a threshold \(\alpha _{0}^{\prime }\) then the system is also probabilistically opaque for all \(\alpha _{0}\leq \alpha _{0}^{\prime }\).

6 Conclusions and future work

In this work, we analyzed and verified a notion of probabilistic opacity related to distinguishing the true system among a set of possible systems, based on a sequence of observations. We established necessary and sufficient conditions under which this notion of probabilistic system opacity can be verified with polynomial complexity. In order to establish polynomial verification algorithms, we analyzed the specific case of HMMs with all initial states possible. There is an interesting feature in this case: despite the fact that the notion of probabilistic system opacity is concerned with probabilities conditioned on the observation sequence, probabilistic system opacity turns out to be the exact opposite of the notion that captures the ability to classify the system (i.e., distinguishing the correct HMM), which is a notion that relies on the ensemble of observation sequences. An open problem is to solve the general case starting with an arbitrary initial state distribution in each HMM. In the described setup, we choose an HMM out of m possible HMMs, which is essentially a multiple hypothesis testing problem, applied to the HMM setup we have. An interesting extension of this setup would be to involve a change in the behavior of the chosen HMM that occurs at an a priori unknown instant of time. In addition to detecting the underlying HMM (the one that was chosen at the switch time), an additional challenge here is the fact that the instant at which the switch occurs is also unknown. An interesting approach to overcome this challenge would be to use sequential methods i.e., repeated sequential probability ratio test (SPRT) as in Chen and Willett (2000) and Cardenas et al. (2004).