Comparative analysis of related notions of opacity in centralized and coordinated architectures

Abstract

Opacity is a confidentiality property that captures whether an intruder can infer a “secret” of a system based on its observation of the system behavior and its knowledge of the system’s structure. In this paper, we study four notions of opacity: language-based opacity, initial-state opacity, current-state opacity, and initial-and-final-state opacity. Initial-and-final-state opacity is a new opacity property introduced in this paper, motivated by secrecy considerations in anonymous network communications; the other three opacity properties have been studied in prior work. We investigate the relationships between these opacity properties. In this regard, a complete set of transformation algorithms among the four notions is provided. We also propose a new, more efficient test for initial-state opacity based on the use of reversed automata, and present a trellis-based test for the new property of initial-and-final state opacity. We then study the notions of initial-state opacity, current-state opacity, and initial-and-final-state opacity in the context of a new coordinated architecture where two intruders work as a team in order to infer the secret. In this architecture, the intruders have the capability of combining their respective state estimates at a coordinating node. In each case, a characterization of the corresponding notion of “joint opacity” and an algorithmic procedure for its verification are provided.

1 Introduction

The development of online services in network communications has led to many security and privacy problems. Many of these problems require some information about the system to be kept secret to an outside observer with malicious intentions. Various information flow properties have arisen in the literature: anonymity, non-interference, non-deductibility, and opacity; see, e.g., Schneider and Sidiropoulos (1996), Focardi and Gorrieri (1994), Hadj-Alouane et al. (2005) and Alur et al. (2006). The property that is of interest here is opacity, which characterizes whether a given “secret” about the system behavior is hidden or not from an outsider observer with malicious intentions, termed an intruder hereafter.

In this paper, we study opacity properties in discrete event systems (DES) modeled as finite-state automata (FSA). The system is partially observed. The intruder, modeled as an observer of the system, is assumed to have full knowledge of the system’s structure and to have partial observations of the system’s behavior. Based on its partial observations, the intruder constructs an estimate of the secret of the system. The system is said to be opaque if the intruder is never sure whether the secret has occurred or not. Depending on how the secret is defined, various notions of opacity emerge. Three main types of opacity properties have been considered in the literature: language-based opacity, initial-state opacity, and current-state opacity. Language-based opacity defines the secret as a sublanguage of the system; initial-state opacity and current-state opacity define the secret as a secret state set. In this paper, we define a fourth type of opacity called initial-and-final-state opacity, which is motivated by anonymous network communications (see e.g., Chaum 1981, 1988) where the identities of the senders and/or receivers need to be kept secret. We define initial-and-final-state opacity so that the initial and the final states of the system are simultaneously hidden. Regardless of how the secret is defined, an opacity property holds if whenever a secret-relevant behavior occurs, there is another non-secret-relevant behavior that looks the same to the intruder. We can think of opacity as “plausible deniability” of the given secret.

There is much prior work on existing notions of opacity. Opacity was first introduced in the computer science literature to analyze cryptographic protocols (Mazaré 2004). It was then investigated in systems modeled as Petri nets (Bryans et al. 2005). In Bryans et al. (2005), the authors defined the secret as predicates over Petri net markings (i.e., states), and formalized three opacity properties based on when the information of the system’s state is critical: initial-opaque, final opaque, and always-opaque. Extending the work in Bryans et al. (2005), the authors in Bryans et al. (2008) investigated opacity in labelled transition systems, in which the secret was defined as predicates over runs. Recently, Saboori and Hadjicostis (2007, 2008, 2009) investigated state-based opacity properties using FSA models. In particular, the notion of initial-state opacity was defined in Saboori and Hadjicostis (2007) and a trellis-based initial-state-estimator for its verification was presented in Saboori and Hadjicostis (2008). The same authors also introduced and verified in Saboori and Hadjicostis (2007, 2009) the notion of K-step opacity, which is a stronger version of current-state opacity that requires the secret to hold for K-delayed estimates of the state; we do not consider K-step opacity in this paper. Several works on opacity have considered the enforcement of opacity properties (Badouel et al. 2007; Dubreil et al. 2008, 2009, 2010; Saboori and Hadjicostis 2008; Cassez et al. 2009). Inspired by the theory of supervisory control of DES, Dubreil et al. (2008, 2010) and Saboori and Hadjicostis (2008), constructed minimally restrictive opacity-enforcing supervisory controllers. In Badouel et al. (2007), the authors solved the control problem of the so-called concurrent secrecy (as defined therein) for a language-based notion of opacity. In Cassez et al. (2009), the authors enforced opacity by modifying the set of observable events; they also provided a transformation from trace-based opacity to state-based opacity (or the current-state opacity in our terminology). Also, Dubreil et al. (2009) used techniques from diagnosis of DES (Sampath et al. 1995) to detect and predict the flow of secret information and constructs a monitor that allows an administrator to detect it. Finally, Lin (2011) compared language-based opacity with other information flow properties and with observability (Lin and Wonham 1988) and diagnosability of DES.

The first focus of this paper is to investigate relationships among the four notions of opacity in FSA models. Opacity is defined as a state property in Saboori and Hadjicostis (2007, 2008, 2009), and as a language property in Dubreil et al. (2008, 2009, 2010), Cassez et al. (2009). While they are formulated differently, trace-based opacity (in the terminology of Cassez et al. (2009)) is reduced to state-based opacity (or current-state opacity in our terminology) in Cassez et al. (2009), and an alternative language-based definition is given for initial-state opacity in Saboori and Hadjicostis (2008). However, to the best of our knowledge, transformations between other pairs of opacity properties have never been presented in the literature. In Section 4, we present a complete set of algorithms for transforming any one of the four types of opacity (language-based, initial-state, current-state, and initial-and-final-state) to any other.

The second focus of this paper is to consider the efficient verification of opacity properties. In Section 5, we review existing methods of verifying opacity properties and propose a new, more efficient one, for initial-state opacity. Our algorithm constructs an initial state estimator (ISE) called the G _R -based ISE using the reversed automaton of the system. This algorithm reduces the complexity of the ISE derived in Saboori and Hadjicostis (2008), which we call the trellis-based ISE. While the trellis-based ISE requires the complexity of $O(2^{|X|^2})$, the G _R -based ISE requires only the complexity of O(2^|X|); X is the state space of the system. We also use the trellis-based estimator to verify the new notion of initial-and-final-state opacity property.

The third focus of this paper is to extend initial-state opacity, current-state opacity, and initial-and-final-state opacity to a coordinated architecture where the system is observed by multiple observers that share their state estimates through a coordinator. The observers work as a team in trying to identify the (common) secret by reporting their estimates, based on their respective projection maps, to a coordinator where the coordinated estimate is generated. In the context of this coordinated architecture, we define three corresponding notions of joint opacity properties. We develop algorithmic procedures to verify each of the three joint opacity properties. To the best of our knowledge, this is the first study of opacity in the context of a coordinated architecture. The work in Badouel et al. (2007) also considers secrecy under multiple observers; however, our problem formulation is different. In Badouel et al. (2007), an individual secret set is associated with each observer, and concurrent secrecy holds if all secret sets are simultaneously opaque, each one with respect to its own individual observer. The problem considered in Badouel et al. (2007) is to synthesize a supervisory controller that will enforce concurrent secrecy.

The remaining sections of this paper are organized as follows. Section 2 introduces the system model and relevant notations. Section 3 gives the definitions of the four opacity properties studied in the paper. Section 4 presents the transformation procedures between each pair of opacity properties. Section 5 considers the verification of the four opacity properties. Section 6 introduces and verifies opacity properties under the coordinated architecture. Section 7 concludes the paper.

2 Preliminaries

We consider various notions of opacity in DES modeled as a finite-state automata. A deterministic finite-state automaton G = (X, E, f, X ₀, X _m ) has a set of states X = {0, 1, ..., N − 1}, a finite set of events E, a partial state transition function f: X ×E → X, a set of initial-states X ₀, and a set of marked states X _m . In opacity problems, the initial state need not be known a priori, and thus a set of initial states instead of a single initial state is used. When there are no marked states, we write G = (X, E, f, X ₀). E ^* is the set of all finite strings composed of elements of E. The function f is extended to domain X × E ^* in the usual manner. The language generated by the system G describes the system’s behavior and is defined by ${\cal L}(G, X_0) := \{s \in E^*: (\exists i \in X_0) [f(i, s) \mbox{~is def\/ined}]\}$; it is prefix-closed by definition. Also, the marked language of G is defined by ${\cal L}_m(G, X_0) := \{s \in E^*: (\exists i \in X_0,j \in X_m) [f(i, s) = j]\}$. In general, the system is partially observed. The event set is partitioned into an observable set E _o and an unobservable set E _uo . Given a string t ∈ E ^*, its observation is the output of the natural projection function $P: E^* \rightarrow E_o^*$, which is recursively defined as P(te) = P(t)P(e) where t ∈ E ^* and e ∈ E. The projection of an event P(e) = e if e ∈ E _o , while P(e) = ε if e ∈ E _uo  ∪ {ϵ} where ϵ denotes the empty string.

The reversed automaton of G, denoted by G _R , is constructed by reversing all transitions in G. Given a string t, the reverse operator Rev: E ^* →E ^* outputs a new string with events in the reversed order, t _R . Formally, the reversed automaton of G is defined as follows.

Definition 1

(Reversed automaton G _R ) Given a deterministic finite-state automaton G = (X, E, f, X ₀, X _m ), the reversed automaton G _R is the nondeterministic automaton that is obtained by reversing all the transitions in G. Specifically, G _R : = (X, E, f _R , X _R,0, X _R,m ) where the transition function has codomain 2^X and is defined as f _R (x′, e) = {x ∈ X : f(x, e) = x′}.

Similar to f, f _R is extended to domain X × E ^* in a recursive manner: $f_R(x', se)= \{x \in X : ( \exists x'' \in X) [x \in f_R(x'', e), x'' \in f_R(x',s)]\}$; or equivalently, f _R (x′, se) = {x ∈ X : [f(x, es _R ) = x′]}. The sets of initial and marked states of G _R , X _R,0 and X _R,m , respectively, are to be specified according to the context.

3 Classification of notions of opacity

In this section, we define the four notions of opacity we study in this paper. The centralized architecture, where there is one single intruder of the system, is considered. In this model, the intruder is assumed to have full knowledge of the system’s structure, but can only observe P(t) when the system executes $t \in {\cal L}(G,X_0)$. Based on its observations, the intruder constructs estimates of the system’s behavior. The secret is said to be opaque if the intruder’s estimate never reveals the system’s secret. Specifically, the secret is opaque if for any “secret behavior,” there exist at least one other “non-secret behavior” that looks the same to the intruder. Depending on the secret behavior under consideration, we classify the corresponding opacity properties into four categories, studied in the following four subsections: language-based opacity, initial-state opacity, current-state opacity, and initial-and-final-state opacity.

3.1 Language-based opacity

We start our discussion with language-based opacity (or simply LBO). In Saboori and Hadjicostis (2008), Dubreil et al. (2008, 2010) and Cassez et al. (2009), language-based opacity is defined over a system G and a secret behavior $L_S \subseteq E^*$. The secret is opaque with respect to ${\cal L}(G,X_0)$ and the projection map P if no execution leads to an estimate that is completely inside the secret behavior. Alternatively, in Lin (2011), language-based opacity is defined over two sublanguages of the system, $L_1, L_2 \subseteq {\cal L}(G, X_0)$. Sublanguage L ₁ is opaque with respect to L ₂ and an observation mapping θ if the intruder confuses every string in L ₁ with some strings in L ₂ under θ. In this paper, we follow the definition in Lin (2011) but let the general observation mapping θ be the natural projection map P.

Definition 2

(Language-based Opacity) Given system G = (X, E, f, X ₀), projection P, secret language $L_S \subseteq {\cal L}(G, X_0)$, and non-secret language $L_{NS} \subseteq {\cal L}(G, X_0)$, G is language-based opaque if for every string t ∈ L _S , there exists another string t′ ∈ L _NS such that P(t) = P(t′). Equivalently, $L_S \subseteq P^{-1}[P(L_{NS})]$.

The system is language-based opaque if for any string t in the secret language L _S , there exists at least one other string t′ in the non-secret language L _NS with the same projection. Therefore, given the observation s = P(t), intruders cannot conclude whether secret string t or non-secret string t′ has occurred. Note that L _S and L _NS need not be prefix-closed in general. Also, they need not be regular; however, we assume that they are regular in the remainder of this paper.

Example 1

Consider the system G in Fig. 1 with E _o  = {a, b, c} . It is language-based opaque when L _S  = {abd} and $L_{NS} = \{abc^*d, adb\}$ because whenever the intruder sees P(L _S ) = { ab }, it is not sure whether string abd or string adb has occurred. However, this system is not language-based opaque if L _S  = {abcd} and L _NS  = {adb}; no string in L _NS has the same projection as the secret string abcd.

Fig. 1

The system G discussed in Example 1

3.2 Initial-state opacity

The notion of initial-state opacity (or ISO) was first defined for Petri nets in Bryans et al. (2005). The authors of Saboori and Hadjicostis (2008) then introduced this notion for finite-state automata and investigated its verification and enforcement. Initial-state opacity property is a state property that relates to the membership of the system’s initial state within a set of secret states. The system is initial-state opaque if the observer is never sure whether the system’s initial state is a secret state or not.

Definition 3

(Initial-State Opacity) Given system G = (X, E, f, X ₀), projection P, set of secret initial states $X_S \subseteq X_0$, and set of non-secret initial states $X_{NS} \subseteq X_0$, G is initial-state opaque if ∀ i ∈ X _S and ∀ t ∈ L(G, i), $\exists j \in X_{NS}$, $\exists t' \in L(G, j)$, such that P(t) = P(t′).

The system is initial-state opaque if for every string t that originates from secret state i, there exists another string t′ from non-secret state j such that t and t′ are observationally equivalent. Therefore, the intruder can never determine whether the system started from a secret state i or from a non-secret state j.

The following is the same example as in Saboori and Hadjicostis (2008) that is used to demonstrate ISO. This example is used throughout this work in order to facilitate the comparison of our algorithmic procedures with those in Saboori and Hadjicostis (2008).

Example 2

Saboori and Hadjicostis (2008) Consider G in Fig. 2 with E _o  = {a, b},X _S  = {2}, and X _NS  = X ∖ X _S . G is initial-state opaque because for every string t starting from state {2}, there is another string (uo)t starting from state {0} that looks the same. However, ISO does not hold if X _S  = {0}. Whenever the intruder sees string aa, it is sure that the system originated from state {0}; no other initial states can generate strings that look the same as aa.

Fig. 2

The system G discussed in Example 2

3.3 Current-state opacity

Current-state opacity was first introduced as “final opacity” in Bryans et al. (2005) in the context of Petri nets. The definition was then adopted in the framework of labelled transition systems in Bryans et al. (2008), and further developed in finite state automata models (Dubreil et al. 2008, 2010; Saboori and Hadjicostis 2008; Cassez et al. 2009). A system is current-state opaque if the observer can never infer, from its observations, whether the current state of the system is a secret state or not.

Definition 4

(Current-State Opacity) Given system G = (X, E, f, X ₀), projection P, set of secret states $X_S \subseteq X$, and set of non-secret states $X_{NS}\subseteq X$, G is current-state opaque if ∀ i ∈ X ₀ and $\forall t \in {\cal L}(G, i)$ such that f(i, t) ∈ X _S , $\exists j \in X_0$, $\exists t' \in L(G, j)$ such that: (i) f(j, t′) ∈ X _NS and (ii) P(t) = P(t′).

Current-state opacity (or CSO) states that for every string t that goes to a secret state, there must exist another string t′ going to a non-secret state whose projection is the same. As a result, the intruder can never assert with certainty that the system’s current state is in X _S . Note that the generalized system model we use, where there can be multiple initial states, allows the two observationally equivalent strings to start from different initial states.

Example 3

Consider G in Fig. 3 and the sets of secret and non-secret states X _S  = {3} and $X_{NS} = X ~\backslash~ X_S$. If E _o  = {b}, then G is current-state opaque because the intruder is always confused between ab and cb when observing b; that is, the intruder cannot tell if the system is in state 3 or 4. However, if E _o  = {a, b}, CSO does not hold because the intruder is sure that the system is in state 3 when observing ab.

Fig. 3

The system G discussed in Example 3

3.4 Initial-and-Final-State Opacity (IFO)

Motivated by anonymous communications in security networks (Chaum 1981, 1988), we introduce a new notion of opacity called initial-and-final state opacity. In anonymous communications, the identities of both the sender and the receiver need to be hidden from the intruder. If we model a communication network as a DES, and use the initial and the final states to represent the identities of the sender and the receiver, the network is anonymous if the memberships of the initial and the final states are hidden as a pair. Formally, initial-and-final-state opacity is defined in terms of set of initial and final state pairs.

Definition 5

(Initial-and-Final-State Opacity) Given system G = (X, E, f, X ₀), projection P, set of secret state pairs $X_{sp} \subseteq X_0 \times X$, and set of non-secret state pairs $X_{nsp} \subseteq X_0 \times X$, G is initial-and-final-state opaque if ∀ (x ₀, x _f ) ∈ X _sp and $\forall t \in {\cal L}(G, x_0)$ such that f(x ₀, t) = x _f , there is a pair (x ₀′, x _f ′) ∈ X _nsp and a string t′ ∈ L(G, X ₀) such that f(x ₀′, t′) = x _f ′ and P(t) = P(t′).

Initial-and-final-state opacity (or simply IFO) requires that the occurrence of a string starting from x ₀ and ending at x _f , where (x ₀, x _f ) is a secret pair, should not reveal to the intruder the fact that x ₀ is the initial state and x _f is the final state. A system is said to be intial-and-final-state opaque if for any string t that starts from x ₀ and ends at x _f , with (x ₀, x _f ) ∈ X _sp , there exists another string t′ starting from x ₀′ and ending at x _f ′, where (x ₀′, x _f ′) ∈ X _nsp , that has the same projection. Therefore, the intruder can never determine whether the initial-and-final state pair is a secret pair or a non-secret pair.

Example 4

Consider again G in Fig. 2 and take X _sp  = {(3, 1)}. G is initial-and-final state opaque if the non-secret state pair set is X _nsp  = {(1, 0), (1, 1), (1, 2), (1, 3)}. However, initial-and-final-state opacity property does not hold if we take X _sp  = {(0, 0)} since (0, 0) is the only state pair that corresponds to string aa; no other state pairs give strings that look the same as aa.

Remark 1

ISO and CSO are both special cases of IFO. To obtain an ISO problem from an IFO problem, we set X _sp  = X _S × X and X _nsp  = X _NS × X. Also, to obtain an CSO problem, we set X _sp  = X ₀ × X _S and X _nsp  = X ₀ × X _NS .

Remark 2

In the definitions of LBO, ISO, CSO, and IFO, no assumptions are made regarding the sets of secret and non-secret languages, states, or state pairs, respectively. However, to facilitate our work, we can assume they are disjoint without loss of generality. Take ISO for example. Assume that X _S  ∩ X _NS  = X _I  ≠ ∅. Then, every state in the intersecting set X _I is a secret state as well as a non-secret state. That is, a string from a secret state in X _I is also from a non-secret state. No states in X _I results in the violation of opacity. Therefore, ISO is unchanged if X _I is removed from the secret set X _S . Therefore, we can re-define the secret state set as $X_{S}' = X_{S} ~\backslash~ X_I$, which is disjoint with X _NS , without affecting ISO. Similar results hold for LBO, CSO and IFO.

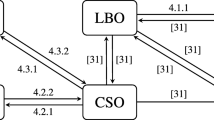
4 Transformation between different notions of opacity

While different notions of opacity have been defined in existing work, their relationships have never been completely characterized. To the best of our knowledge, the only works that consider such relationships are the alternative language-based definition for initial-state opacity in Saboori and Hadjicostis (2008), the transformations from trace-based opacity (LBO in our terminology) to state-based opacity (CSO in our terminology) in Cassez et al. (2009), and the transformations in Lin (2011) from language-based opacity to strong-secrecy and weak-secrecy (defined therein). In this section, we provide a complete characterization of the relationships between the four notions of opacity defined in the previous section. Algorithms that map among the four notions are presented in the following subsections, according to the diagram in Fig. 4. Examples are provided for most of the algorithms. Complete proofs are provided for the transformations between IFO and LBO in the corresponding subsections. The proofs for the other transformations are briefly discussed in Section 4.5. For the sake of simplicity, we will use the acronym IFO to denote both “initial-and-final-state opacity” and “initial-and-final-state opaque”; it will be clear from the context if the noun or the adjective is referred to. Similarly for LBO, CSO, and ISO.

Fig. 4

Transformations between notions of opacity (labeled by section numbers)

4.1 Transformation between IFO and LBO

4.1.1 IFO to LBO

Given an IFO problem with G = (X, E, f, X ₀) and sets of secret and non-secret state pairs X _sp and X _nsp , we transform the IFO problem into an LBO problem by the following steps:

• 1. Construct $G_{i}^s = Trim[(X, E, f, \{x_{0,i}^s\}, \{x_{f,i}^s\})]$ where $(x_{0,i}^s, x_{f,i}^s)$ is the i-th pair in X _sp , and $G_j^{ns} = Trim[(X, E, f, \{x_{0,j}^{ns}\}, \{x_{f,j}^{ns}\})]$ where $(x_{0,j}^{ns}, x_{f,j}^{ns})$ is the j-th pair in X _nsp .

• 2. Obtain G ^s by treating the set of all $G_{i}^s$ as a single automaton, with corresponding sets of initial and marked states; proceed similarly to obtain G ^ns from all $G_j^{ns}$. Define the secret and non-secret languages L _S and L _NS as

  $$\begin{array}{rll} L_{S} & =& {\cal L}_m\left(G^s\right) = \bigcup_i {\cal L}_m\big(G_i^{s}\big)\\ L_{NS} &=& {\cal L}m(G^{ns})= \bigcup_j {\cal L}_m\big(G_j^{ns}\big) \end{array}$$

• 3. Obtain G _LBO by treating G ^s and G ^ns as a single automaton.

We show that (G, X _sp , X _nsp ) is IFO if and only if (G _LBO , L _S , L _NS ) is LBO. By construction, every $G_i^s$ marks the language that corresponds to the i-th secret pair $(x^s_{0,i}, x^s_{f,i}) \in X_{sp}$. Since every secret pair has a corresponding $G_i^s$, language L _S captures the complete set of secret pairs X _sp . Similarly, L _NS captures the set of non-secret pairs X _nsp . To verify if (G, X _sp , X _nsp ) is IFO, we check if every string with a secret pair (x ₀, x _f ) ∈ X _sp has the same projection as a string associated with a non-secret pair (x ₀′, x _f ′) ∈ X _nsp , that is, if every string t ∈ L _S has the same projection as a string t′ ∈ L _NS in G _LBO . This procedure is equivalent to verify if (G _LBO , L _S , L _NS ) is LBO.

We discuss the computational complexity of this transformation. Given any input instance (G, X _sp , X _nsp ), building G ^s takes complexity $O(|X|^2|X_0|)$ because each $G_{i}^s$ is simply the trim of G with the i-th state pair in X _sp as the initial and marked state, and there are at most |X||X ₀| number of such $G_{i}^s$. Similarly, building G ^ns also takes complexity $O(|X|^2|X_0|)$. Therefore, this transformation can be obtained in polynomial time, in the cardinality of the state space of G.

4.1.2 LBO to IFO

Given an LBO problem with G, L _S , and L _NS , we construct the equivalent IFO problem by the following steps:

• 1. Build automata $G^s = (X^s, E, f_s, X_{0}^s, X_{f}^s)$ with ${\cal L}_m(G^s, X^s_0) = L_S$ and $G^{ns} = (X^{ns}, E, f_{ns}, X_{0}^{ns}, X_f^{ns})$ with ${\cal L}_m(G^{ns}, X^{ns}_0) = L_{NS}$.

• 2. Construct G _IFO by treating the two automata G ^s and G ^ns as a single one. Take the set of secret pairs to be $X_{sp} = {X_{0}^s} \times {X_{f}^s}$ and the set of non-secret pairs to be $X_{nsp} = {X_{0}^{ns}} \times {X_{f}^{ns}}$.

We show that (G, L _S , L _NS ) is LBO if and only if (G _IFO , X _sp , X _nsp ) is IFO. By construction, G ^s, which has initial states $X_{0}^s$ and marked states $X_{f}^s$, generates marked language L _S . Thus, a string is in L _S if and only if it has an initial-final state pair in $X_{sp} = X_{0}^s \times X_{f}^s$. Similarly, a string is in L _NS if and only if it has an initial-final state pair in $X_{nsp} = X_{0}^{ns} \times X_{f}^{ns}$. To verify if (G, L _S , L _NS ) is LBO, we verify if every string in L _S is always confused with a string in L _NS ; that is, if every state pair in X _sp is always confused with a state pair in X _nsp . This is the same as checking if (G, X _sp , X _nsp ) is IFO.

This transformation also requires polynomial complexity. In step 1, the complexity depends on how the languages L _S and L _NS are defined. Recall that L _S and L _NS are assumed to be regular. They could be specified using automata, in which case G ^s and G ^ns are directly obtained. More generally, L _S could be expressed as sublanguages of ${\cal L} (G)$ in terms of state and/or event ordering, in which case G ^s can be obtained in polynomial time by splitting the state space of G as necessary using standard automata procedures. Step 2 takes only constant time. Therefore, the transformation can be done in polynomial time, in the cardinality of the state space of G.

Example 5

Consider again the system in Fig. 1. Let L _S  = {abd}, $L_{NS}= abc^*d + adb$, and the set of observable events E _o  = {a, b, c}. To transform the LBO problem into an IFO problem, we first build G ^s (top in Fig. 5) and G ^ns (bottom in Fig. 5). Then, we construct G _IFO by taking the two automata as a single one, as shown in Fig. 5. Finally, we define the set of secret and non-secret pairs by X _sp  = {(0, 3)} and X _nsp  = {(4, 7), (4, 9)}, respectively.

Fig. 5

G _IFO used in Example 5

4.2 Transformation between ISO and LBO

4.2.1 ISO to LBO

Given an ISO problem with G, X _S , and X _NS , we construct the equivalent LBO problem by the following steps:

• 1. Build automata $G^s = Trim[G(X, E, f, X_S)]$ and $G^{ns} = Trim[G(X, E, f, X_{NS})]$.

• 2. Obtain G _LBO by treating G ^s and G ^ns as a single automaton. Define the secret and the non-secret languages as $L_{S} = {\cal L}(G_{LBO}, X_S)$ and $L_{NS} = {\cal L}(G_{LBO}, X_{NS})$.

Example 6

Let us go back to Example 2 and take X _S  = {0} and $X_{NS} = X ~\backslash~X_S = \{1, 2, 3\}$. Following the transformation, the secret and non-secret languages are defined by $L_S = {\cal L}(G, \{0\})$ and $L_{NS} = {\cal L}(G,X \setminus X_S)$. In this case, LBO does not hold since no string in L _NS looks the same as string aa ∈ L _S .

4.2.2 LBO to ISO

To transform from LBO to ISO, we must check if L _S and L _NS in the LBO problem are prefix-closed. This is because the languages of an ISO problem are prefix-closed by definition. If L _S and L _NS are not prefix-closed, then this transformation is not meaningful. Specifically, given an LBO problem with G, L _S , and L _NS , we construct this transformation by:

• 1. Check if L _S and L _NS are both prefix-closed. If yes, then proceed to Step 2. Otherwise, no transformation exists.

• 2. Build automata $G^s = (X^s, E, f_s, X_0^s)$ and $G^{ns} = (X^{ns}, E, f_{ns}, X_0^{ns})$ such that ${\cal L}(G^s, X^s_0) =L_S$ and ${\cal L}(G^{ns}, X^{ns}_0) = L_{NS}$.

• 3. Construct G _ISO by treating G ^s and G ^ns as a single automaton. Take the secret and non-secret initial states sets to be $X_S = X^s_0$ and $X_{NS} = X^{ns}_0$, respectively.

Example 7

Consider again the system in Fig. 1, with the set of observable events E _o  = {a, b, c}. Let the secret and non-secret languages to be prefix-closed: $L_S = \overline{\{abd\}}$ and $L_{NS} = \overline{[abc^*d + adb]}$. This LBO problem can be transformed to an ISO problem on the system in Fig. 5 (with no marked states) with secret state set X _S  = {0} and non-secret state set X _NS  = {4}. In this example, ISO holds because for every string starting from state {0}, there is another string from {4} with the same projection.

4.3 Transformation between CSO and LBO

4.3.1 CSO to LBO

Given a CSO problem with G, X _S , X _NS , the equivalent LBO problem is built in two steps. First, we build automata $G^s = Trim[G(X, E, f, X_0, X_S]$ and $G^{ns} = Trim[G(X, E, f, X_0, X_{NS} )]$. Then, we obtain G _LBO by treating G ^s and G ^ns as a single automaton, and define the secret and the non-secret languages as $L_{S} = {\cal L}_m(G_{LBO}, X_S)$ and $L_{NS}= {\cal L}_m(G_{LBO}, X_{NS})$.

Example 8

Let us go back to Example 3. Take X _S  = {3}, $X_{NS} = X ~\backslash~X_S$, and E _o  = {b}. Following the above transformation, the secret and the non-secret languages are defined by L _S  = {ab} and L _NS  = {ϵ, a, c, cb }. In this case, LBO holds because the intruder always confuses the secret string ab with the non-secret string cb.

4.3.2 LBO to CSO

Given an LBO problem with G, L _S , L _NS , we transform it to a CSO problem in two steps. First, we build $G^s = (X^s, E, f_s, X_0^s, X_f^s)$ and $G^{ns} = (X^{ns}, E, f_{ns}, X_0^{ns}, X_f^{ns})$ such that ${\cal L}_m(G^s, X^s_0) =L_S$ and ${\cal L}_m(G^{ns}, X^{ns}_0) = L_{NS}$. Then, we construct G _CSO by treating G ^s and G ^ns as a single automaton, where the initial state set is $X_0= X_0^s \cup X_0^{ns}$ and the secret and non-secret state sets are $X_S = X^s_f$ and $X_{NS} = X^{ns}_f$.

Example 9

Consider again the system in Fig. 1, with E _o  = {a, b, c}. This LBO problem is transformed to a CSO problem on the system in Fig. 5 with initial state set X ₀ = {0, 4}, secret state set X _S  = {3}, and non-secret state set X _NS  = {7, 9}. G is current-state opaque because string adb, which ends at state {9}, has the same projection as string abd, which is the only string that ends at secret state {3}.

4.4 Transformation between ISO/CSO and IFO

As explained in Remark 1, ISO and CSO are special cases of IFO, so the transformations from ISO to IFO and from CSO to IFO are already covered by that remark. On the other hand, the transformation from IFO to ISO can be obtained by first transforming IFO to LBO and then transforming LBO to ISO; similarly for the case IFO to CSO.

4.5 Discussion

The transformations between ISO/CSO and LBO can be proven using similar methods for those between IFO and LBO. For the transformation from ISO to LBO, we construct G ^s and G ^ns whose initial states are X _S and X _NS , respectively. By suitably defining L _S and L _NS as sublanguages of G ^s and G ^ns, languages L _S and L _NS completely capture X _S and X _NS . Therefore, checking if a string starts from X _S or X _NS is equivalent to checking if the string is in L _S or L _NS . That is, verifying ISO in the original automaton G is equivalent to verifying LBO in G _LBO . A similar argument holds for the transformation from CSO to LBO. The only difference is that X _S and X _NS are the marked states of G ^s and G ^ns. For the transformation from LBO to ISO, we construct G ^s and G ^ns that generate L _S and L _NS by suitably defining the initial states as X _S and X _NS . Therefore, checking if a string is in L _S or L _NS is equivalent to checking if the string starts from X _S or X _NS . That is, verifying LBO in the original automaton G is equivalent to verifying ISO in G _ISO . Similarly, by letting X _S and X _NS to be the marked states of G ^s and G ^ns, we can prove the transformation from LBO to CSO.

All the transformations are of polynomial-time computational complexity. We have seen that transformations between IFO and LBO require polynomial time. Transformations between ISO/CSO and LBO also require polynomial time because they are adapted from those between IFO and LBO. The transformations from IFO to ISO/CSO can also be done in polynomial time by transforming from IFO to LBO in polynomial time and then from LBO to ISO/CSO in polynomial time. In conclusion, we have shown that there exists a polynomial-time transformation between any pair of the four notions of opacity. The only exception is that there is no transformation from LBO to ISO when the secret or non-secret languages are not prefix-closed. Therefore, we can say that two opacity properties, OP ₁ and OP ₂, are “equivalent” in the sense that OP ₁ holds in system G if and only if OP ₂ holds in the the transformed system G′.

5 Verification of different notions of opacity

We are interested in the verification of the four notions of opacity. Based on the results of the preceding section, we can always transform one opacity property to another for the purpose of verification. However, this may not be the most efficient manner to proceed. Thus, it is still worthwhile to consider each opacity property individually. Algorithms are available in the literature for verifying ISO, CSO, and LBO. For the sake of completeness, we briefly discuss the verification of CSO and LBO at the beginning of this section. Then we present a new algorithm for the verification of ISO that has reduced computational complexity as compared with existing ones. Finally, we present an algorithm for the verification of the new property of IFO.

We mention that no polynomial-time algorithms, in the cardinality of the state space of G, exist for any of the above notions of opacity. In fact, it was shown in Cassez et al. (2009) and Dubreil (2009) that the verification of state-based opacity (CSO in our terminology) and that of trace-based opacity (LBO in our terminology) are PSPACE-complete problems. Also, ISO was shown to be PSPACE-complete in Saboori (2010), when | E _o | > 1. As a result, IFO must also be PSPACE-complete due to the polynomial-time transformations from other notions of opacity to IFO mentioned in Section 4.5.

5.1 Verification of current-state opacity

The most intuitive way to verify CSO is to build the observer automaton.¹ The observer Obs(G, X ₀) models how the intruder gains knowledge of the system through observations. More specifically, the state of Obs(G, X ₀) reached by $s\in P[{\cal L}(G, X_0)]$ is the intruder’s state estimate after observing s. Therefore, we can use Obs(G, X ₀) to capture all possible state estimates of the intruder. To verify CSO, we examine all reachable states in Obs(G, X ₀). The system is CSO if no state in Obs(G, X ₀) contains secret states but not non-secret states. Also, when constructing the observer to verify CSO, one does not assume a specific set of secret states. Thus, no reconstruction of the observer is required if the set of secret states changes.

5.2 Verification of language-based opacity

Given $L_S, ~L_{NS} \subseteq {\cal L}(G, X_0)$, the system is LBO if $L_S \subseteq P^{-1}[P(L_{NS})]$. To check the aforestated language inclusion, the author of Lin (2011) proposed Algorithm 1 therein that utilizes marked languages of automata. We use the notation of Lin (2011) to briefly review that algorithm for the sake of comparison with a transformation-based approach. In order to fit our model, Algorithm 1 of Lin (2011) needs to be slightly modified by using the natural projection instead of the more general state-based projection. In brief, the algorithm first constructs two automata, G ₁ and G ₂, that mark L _S and L _NS , respectively. Next, it constructs their observers, G ₅ and G ₈, and the product of these two observers, G ₉, that marks the joint projected marked language. Then, it compares ${\cal L}_m(G_9)$ and ${\cal L}_m(G_5)$. The system is LBO if these two marked languages are equal. That is, P(L _S ) ∩ P(L _NS ) = P(L _S ), or equivalently, $P(L_S) \subseteq P(L_{NS})$. As an alternative, we can use state-based verification by transforming the LBO problem to a CSO one. The state-based verification is based on the transformation from LBO to CSO presented in Section 4.3.2. The equivalent CSO problem is then verified as described above in Section 5.1. While the above two algorithms are constructed differently, their computational complexity is the same. In Algorithm 1, if we assume that G ₁ and G ₂ have state spaces in the order of X, then building G ₉ has worst-case complexity of O(2^2|X|). As for state-based verification, transforming from LBO to CSO doubles the state space to 2X and building the observer also has worst-case complexity of O(2^2|X|).

5.3 Verification of ISO

To verify ISO, we need to capture the intruder’s initial state estimate, which is the set of states where the observed string could have started. The definition for the initial state estimate is given below:

Definition 6

(Initial-state estimate) Given system G = (X, E, f, X ₀) and P, the initial state estimate after observing string s is defined as $\hat{X}_0(s) := \{i \in X_0: (\exists t \in E^*)(P(t) = s) [f(i, t)\; \rm{is\;defined} ]\}$

The authors of Saboori and Hadjicostis (2008) constructed a trellis-based initial state estimator to capture the initial state estimate. Motivated by the work in Saboori and Hadjicostis (2008), we propose a new algorithm using the reversed automaton to generate the estimates. Since we will use the initial state estimator of Saboori and Hadjicostis (2008) in other parts of this paper, we start with a brief review of key notations and rules from Saboori and Hadjicostis (2008). We use the acronym ISE for “initial state estimator” hereafter.

5.3.1 Trellis-based initial state estimator

The authors of Saboori and Hadjicostis (2008) used state mappings to construct the trellis-based ISE. A state mapping $m \in 2^{X^2}$ is a subset of X ² consisting of state pairs. Induced by the observed string $s \in P[{\cal L}(G,X_0)]$, the state mapping M(s) enumerates all possible pairs of starting and ending states corresponding to s. The composition operator for two state mappings $\circ: 2^{X^2} \times 2^{X^2} \rightarrow 2^{X^2}$ is defined as:

$$ m_1, m_2 \in 2^{X^2}, m_1 \circ m_2 := \{(i_1, i_3)~|~\exists i_2 \in X, (i_1, i_2) \in m_1, (i_2, i_3 )\in m_2\} $$

The operator takes the starting states of m ₁ and the ending states of m ₂ to form a new state mapping only for those sets of tuples that share the same intermediate element. Given G, the trellis-based ISE of G is a deterministic finite-state automaton where the state reached by string $s \in P[{\cal L}(G,X_0)]$ is state mapping M(s). Since intruders are assumed to have no prior knowledge about the system’s initial state, the ISE starts with a state mapping whose set of starting states is the entire state space X. More specifically, the initial state of the estimator is $\{(i,i): i\in X)\} \cup \{(i,j) \in X^2: (\exists t \in E_{uo}^*)[f(i, t) = j]\}$. The transition function is defined such that state mapping m transitions to state mapping m′ through event e _o if m′ = m ∘ M(e _o ) where M(e _o ) is the state mapping induced by e _o . The estimator relies on state mappings to relay information about the initial- and the current-state estimates. Given a state m of the trellis-based ISE reached by s, Saboori and Hadjicostis (2008) proved that the set of starting states of m is exactly the intruder’s initial-state estimate $\hat{X}_0(s)$. One can verify ISO by examining all states in the trellis-based ISE and determining if the condition on X _S and X _NS is satisfied or not.

Remark 3

To verify IFO using the trellis-based ISE in Section 5.4.1, and to help us extend notions of opacity to the coordinated architecture of Section 6, we slightly modify above the definition of the initial state of the trellis-based ISE from Saboori and Hadjicostis (2008). Specifically, the modified initial state includes the unobservable reach to account for the unobservable transitions after the system begins and before the first observable transition. This is a practical concern as the intruder does not know when the system starts. The modification does not affect the initial state estimates since the unobservable reach affects only the ending states but not the starting states. Furthermore, it affects only the initial state but not the other states of the ISE. As a result, the modification gives the same initial state estimates as those in Saboori and Hadjicostis (2008).

Example 10

Consider the system in Fig. 2. The a- and b-induced state mappings are M(a) = {(0, 0), (0, 1), (0, 2), (0, 3), (2, 1), (2, 3)} and $M(b) = \{(1,0),(1,1), (1,2), (1,3), (3,1), (3,3)\}$. To construct the trellis-based ISE, we start with the initial state mapping m ₀ as defined above. Then, we generate new state mappings by composing m ₀ with M(a), and M(b). The complete construction is shown in Fig. 6.

Fig. 6

Trellis-based ISE of the system in Fig. 2

5.3.2 G _R -based initial state estimator

One of our contributions in this paper is to propose a new algorithm to construct the initial state estimate based on the reversed automaton G _R . In the following, we first introduce the method of verifying ISO when X ₀ = X. Then we generalize the verification method to the case when X ₀ ⊂ X.

Case 1

ISO problem when X ₀ = X

To construct our ISE, we first build the reversed automaton G _R of the system G. After that, we build the observer Obs(G _R , X), with the initial state being the entire state space X. We prove below that the state of Obs(G _R , X) reached by string s _R is the initial state estimate after s, where s _R is the reversed string of string s. This explains why the initial state is taken as X. Because the observer has no prior knowledge about the system’s initial state, its estimate after observing nothing is the entire set of initial states X ₀ = X. We describe the construction of the initial state estimate in the following theorem. The subscript R applied to strings indicates the corresponding reversed string.

Theorem 1

Given system G = (X, E, f, X), map P , set of secret states $X_S \subseteq X$ , and set of non-secret states $X_{NS} \subseteq X$ , the initial state estimate after observing s is $\hat{X}_0(s) = f_{\rm obs, R}(X, s_R)$ , where f _{obs, R} is the transition function of Obs(G _R , X) = (X _{obs, R}, E _o , f _obs,R, X).

The construction of the initial state estimate relies on the structure of its reversed automaton. Before proving Theorem 1, we present three lemmas that characterize useful properties of reversed strings and automata. We use the notation Rev(·) for the operation of taking the reverse of a string or of all the strings in a set of strings.

Lemma 1

P(t _R ) = P(t _R ′) iff P(t) = P(t′).

This result is proved in a straightforward manner by using induction on the length of strings.

Lemma 2

x ₀ ∈ f _R (x, t _R ) iff x = f(x ₀, t).

Proof

This result is proved by using the extended definition of f _R ; that is, f _R (x, t _R ) = {x ₀ ∈ X: [f(x ₀, t) = x]}. □

Lemma 3

$t_R {\kern-1pt}\in{\kern-1pt} {\cal L}(G_R,X)$ iff $t {\kern-1pt}\in{\kern-1pt} {\cal L}(G,X)$ . Thus, ${\cal L}[Obs(G_R,X)] {\kern-1pt}={\kern-1pt} Rev\big(P[{\cal L}(G,X)]\big)$.

Proof

$$\begin{array}{rll} t \in {\cal L}(G, X) & \Leftrightarrow &\exists x, x' \in X, \textrm{~such that $x' = f(x,t)$} \\ & \Leftrightarrow &\exists x, x' \in X, \textrm{~such that $x \in f_R(x', t_R)$ by Lemma~2 } \\ & \Leftrightarrow &t_R \in {\cal L}(G_R, X) \end{array}$$

Furthermore, because t _R  = Rev(t), we have ${\cal L}(G_R,X) = Rev[{\cal L}(G,X)]$. By applying projection operation at both sides, we obtain $P[{\cal L}(G_R,X)] = P\big(Rev[{\cal L}(G,X)]\big)$; that is, ${\cal L}[Obs(G_R,X)] = Rev \big(P[{\cal L}(G,X)]\big)$. □

We can now present the proof of Theorem 1:

Proof

For any string $s \in P[{\cal L}(G,X)]$, if we pick any state $x_0 \in \hat{X}_0(s):= \{i \in X: (\exists t \in E^*)(P(t) = s) [f(i, t)$ is defined ]}, then we have that $\exists t \in {\cal L}(G, X)$ where P(t) = s such that f(x ₀, t) is defined.

• Using Lemma 3, we have that $\exists t \in {\cal L}(G, X) \Leftrightarrow \exists t_R \in {\cal L}(G_R, X)$.

• Using Lemma 2, we have that $x = f(x_0,t) \Leftrightarrow x_0 \in f_R(x,t_R)$.

• Using Lemma 1, we have that $P(t) = s \Leftrightarrow P(t_R) = s_R$.

Therefore, an arbitrary $x_0 \in \hat{X}_0(s)$ iff $\exists t_R \in {\cal L}(G_R, X)$, $\exists x \in X$ where P(t _R ) = s _R and x ₀ ∈ f _R (x, t _R ).

Equivalently, $x_0 {\kern1pt}\in{\kern1pt} \{i {\kern1pt}\in{\kern1pt} X:(\exists x {\kern1pt}\in{\kern1pt} X)(\exists t_R {\kern1pt}\in{\kern1pt} {\cal L}(G_R, X)) [P(t_R) {\kern1pt}={\kern1pt} s_R] \textrm{~~and~~} [i {\kern1pt}\in{\kern1pt} f_R (x, t_R)]\} =:f_{\rm obs, R}(X, s_R)$. □

Obs(G _R , X) can be interpreted as an ISE in the sense that Theorem 1 shows that the intruder’s initial state estimate after observing string s is captured by the state of Obs(G _R , X) reached by s _R . The verification of ISO can therefore be performed by examining all the states of this ISE. The system is not ISO if there exists an observation sequence that leads to an initial state estimate containing secret states but not non-secret states, as formalized by the following result, where X _{obs, R} denotes the state space of Obs(G _R , X).

Theorem 2

System G = (X, E, f, X) is ISO iff ∀ y ∈ X _{obs, R} , $y \cap X_S \neq \emptyset \Rightarrow y \cap X_{NS} \neq \emptyset$.

Proof

By definition, G is ISO if and only if the system’s initial state estimate never contains secret states but not non-secret states. Whenever there is a secret state in the estimate, there must also be a non-secret state to confuse the intruder, for all observable strings $s \in P[{\cal L}(G, X)]$. To prove the result it is sufficient to prove that the collection of all possible initial state estimates of the intruder equals to the collection of all reachable states of Obs(G _R , X). We first observe that each initial state estimate is captured by a state in Obs(G _R ,X). This is given in the result of Theorem 1 where $\hat{X}_0(s) = f_{\rm obs,R}(X, s_R)$ for all $s \in P[{\cal L}(G,X)]$. For the reverse direction, we observe that each reachable state of Obs(G _R ,X) corresponds to a valid initial state estimate. This is because Obs(G _R ,X) is deterministic and ${\cal L}[Obs(G_R,X)] = Rev\big(P[{\cal L}(G,X)]\big)$ by Lemma 3. Therefore, the ISO property is verified by examining all reachable states of Obs(G _R , X). □

Example 11

We use the G _R -based ISE to verify the ISO property of the system in Fig. 2. To build the G _R -ISE, we first build G _R , shown in Fig. 7a. Then, we build Obs(G _R , X), shown in Fig. 7b. In the G _R -ISE, the initial state is X because the intruder has no prior knowledge of the system’s initial state. The state reached by string t _R is the intruder’s initial state estimate after observing t. In this example, after observing event b, the intruder constructs initial state estimate {1, 3}, which is the state of the ISE reached by Rev(b) = b. If the intruder further observes a, its initial state estimate is updated to {1}, which is the state of the G _R -ISE reached by Rev(ba) = ab. To verify the ISO property, we examine all the states of the G _R -ISE in Fig. 7b. If the secret state is {1}, the system is not ISO because the state of the ISE reached by ab contains only state 1.

Fig. 7

Construction of the G _R -based ISE of the system in Fig. 2

Case 2

Initial-State Opacity problem when X ₀ ⊂ X

In the previous case, we verified the ISO property when X ₀ = X. Now, we consider the case when X ₀ ⊂ X, which was mentioned but not studied in Saboori and Hadjicostis (2008).

Recall that when X = X ₀, the language of the G _R -ISE is ${\cal L}[Obs(G_R, X)] = Rev(P[{\cal L}(G, X)])=Rev(P[{\cal L}(G, X_0)])$; thus, the set of initial state estimates is the set of reachable states of Obs(G _R , X). However, when X ₀ ⊂ X, we could have $Rev(P[{\cal L}(G, X_0)]) \subset Rev(P[{\cal L}(G, X)])= {\cal L}[Obs(G_R, X)]$. In this case, there exists a string t _R in ${\cal L}[Obs(G_R, X)]$ but not in $Rev(P[{\cal L}(G, X_0)])$. Thus, t _R does not correspond to a valid initial state estimate; namely, state y = f _{obs, R}(X, t _R ) ∈ X _obs,R does not give a valid initial state estimate. To verify ISO when X ₀ ⊂ X, we need to identify and examine only valid initial state estimates instead of examining all reachable states of Obs(G _R , X). For this purpose, we use marking of states. First, we construct a modified automaton G′ by marking all states in X ₀ to recognize all valid initial states. Then, we build the reversed automaton G _R ′ = (X, E, f _R , X, X ₀) and its G _R ′-based ISE. The marked language of G′ _R -ISE is therefore the reversed projection language, i.e., ${\cal L}_m[Obs(G_R', X)] = Rev \big(P[{\cal L}(G, X_0)]\big)$. A marked state corresponds to a reversed string that starts from a valid initial state. The set of valid initial state estimates is obtained by taking the intersection of X ₀ with the marked states of Obs(G _R ′, X). (Note that an observer state is marked if it contains at least one marked state.) Since only marking has been affected, we write Obs(G _R ′, X) = (X _{obs, R}, E _o , f _obs,R, X, X _{obs, R, m}). We have the following result.

Theorem 3

Given system G = (X, E, f, X ₀) with X ₀ ⊂ X, projection P, set of secret states X _S  ⊂ X, and set of non-secret states X _NS  ⊂ X, when observing $s \in P[{\cal L}(G, X_0)]$ we have:

• 1. $\hat{X_0}(s) = f_{\rm obs, R} (X, s_R) \cap X_0$

• 2. $s_R \in {\cal L}_m[Obs(G_R', X)]$

That is, there exists y _m  = f _{obs, R} (X, s _R ) ∈ X _{obs, R, m} such that the initial state estimate $\hat{X_0}(s)$ is y _m  ∩ X ₀.

Similarly to the case where X ₀ = X, before proving Theorem 3, we would like to relate the properties of Obs(G _R ′, X) to those of the original automaton G.

Lemma 4

x = f(x ₀,t) iff x ₀ ∈ f _R (x,t _R ) ∩ X ₀ . Furthermore, $\exists x \in X, x = f(x_0,t)$ if and only if x ₀ ∈ f _obs,R(X,s _R ) ∩ X ₀ , where P(t _R ) = s _R .

Proof

$$\begin{array}{rll} x = f(x_0, t) &\Leftrightarrow &x = f(x_0, t) \wedge x_0 \in X_0 \mbox{, since~} x_0 \in X_0 \mbox{~is always true}\\ & \Leftrightarrow &x_0 \in f_R(x, t_R) \wedge x_0 \in X_0 \mbox{, by Lemma 2.}\\ & \Leftrightarrow &x_0 \in f_R(x, t_R) \cap X_0 \end{array}$$

Furthermore, $\exists x \in X, x_0 \in f_R(x,t_R) \Leftrightarrow x_0 \in f_{\rm obs,R}(X,s_R)\cap X_0$ where P(t _R ) = s _R . Therefore, we have $\exists x \in X, x = f(x_0,t)$ if and only if x ₀ ∈ f _obs,R(X,s _R ) ∩ X ₀ , where P(t _R ) = s _R . □

Lemma 5

$t \in {\cal L}(G, X_0)$ iff $t_R \in {\cal L}_m(G_R', X)$.

Proof

$$\begin{array}{rll} t \in {\cal L}(G, X_0) & \Leftrightarrow &\exists x_0 \in X_0, \mbox{~and~} x \in X, \textrm{~such that $x = f(x_0,t)$} \\ & \Leftrightarrow &\exists x_0 \in X_0, x \in X, \textrm{~such that $x_0 \in f_R(x, t_R)$ by Lemma~4.} \\ & \Leftrightarrow &t_R \in {\cal L}_m(G_R', X) \textrm{~because $X_0$ is the set of marked states of $G_R'$} \end{array}$$

□

We can now prove Theorem 3.

Proof

For any string $s \in P[{\cal L}(G,X_0)]$, pick any state $x_0 \in \hat{X}_0(s):= \{i \in X_0: (\exists t \in E^*)(P(t) = s) [f(i, t)\; \rm{is\; defined} ]\}$; we have $\exists t \in {\cal L}(G, X_0)$ where P(t) = s such that f(x ₀, t) is defined.

• Using Lemma 3, we have that $t \in {\cal L}(G, X_0) \Leftrightarrow t_R \in {\cal L}_m(G_R', X)$.

• Using Lemma 2, we have that $P(t) = s \Leftrightarrow P(t_R) = s_R$

• Using Lemma 1, we have that $x = f(x_0,t) \Leftrightarrow x_0 \in f_{\rm obs,R}(X,s_R)\cap X_0$

Therefore, given an arbitrary x ₀, $x_0 \in \hat{X}_0(s)$ holds if and only if $\exists x \in X$, $\exists t_R \in {\cal L}_m(G_R', X)$ where $P(t_R) = s_R \in {\cal L}_m[Obs(G_R', X)]$, such that x ₀ ∈ f _obs,R(X,s _R ) ∩ X ₀ . That is, x ₀ ∈ f _obs,R(X, s _R ) ∩ X ₀ where $s_R \in {\cal L}_m[Obs(G_R', X)]$, which proves Theorem 3. □

Theorem 3 gives the initial state estimate of an intruder that has prior knowledge of X ₀ ⊂ X. The intruder’s estimate after observing string s is the intersection of X ₀ and the marked state of Obs(G _R , X) reached by s _R . To verify ISO when X ₀ ⊂ X, we need to examine all marked states of Obs(G _R , X).

Theorem 4

System G = (X, E, f, X ₀) is ISO if and only if ∀ y ∈ X _{obs, R, m} , $(y \cap X_0) \cap X_S \neq \emptyset \Rightarrow (y \cap X_0) \cap X_{NS} \neq \emptyset$.

Proof

To prove Theorem 4, it is sufficient to prove that the collection of all initial state estimates is equal to the collection of Z = {z = y ∩ X ₀: y ∈ X _{obs, R, m}}. By Theorem 3, we know that every initial state estimate is captured by the intersection of X ₀ and a marked state of the G _R ′-based ISE. That is, every initial state estimate is inside the set Z. As for the other direction, because ${\cal L}_m[Obs(G_R', X)] = Rev(P[{\cal L}(G, X_0)])$, we always obtain a valid initial state estimate by intersecting a marked state of the G _R ′-based ISE with X ₀. That is, every element in Z is an initial state estimate. This completes the proof. □

Corollary 1

The computational complexity of verifying ISO using the G _R -ISE in Theorems 2 and 4 is in the worst case O(2^| X|).

Corollary 1 states the advantage of using the G _R -based ISE to verify ISO. The trellis-based ISE in Saboori and Hadjicostis (2008) has complexity $O(2^{|X|^2})$ because of the use of state mappings as building blocks for the ISE.

Example 12

Consider the system in Fig. 2 with the sets X ₀ = {0, 2}, X _S  = {0}, and X _NS  = {2}. To verify if the system is ISO, we construct the modified automaton G′ by marking all initial states, and then build the G _R ′-based ISE, as shown in Fig. 8a and b. As before, the intruder’s initial state estimate after it observes string ab is the state reached by Rev(ab) = ba in the G _R ′-based ISE, {0, 2}. However, since only {0} and {2} are initial states of the system, not all states but only marked states reached in G _R ′-based ISE correspond to valid initial state estimates. For example, state {1, 3} is not a valid initial state estimate; no string starting from {0} or {2} has its reversed observable string that reaches state {1, 3} in the G _R ′-based ISE. To verify ISO, we examine all marked states of G _R ′-ISE. The system is not ISO because the marked state {0} is a valid initial state estimate that contains only secret initial state.

Fig. 8

Verifying ISO when X ₀ ⊂ X

We conclude this section with two remarks that apply to Cases 1 and 2.

Remark 4

Consider Case 1; a similar argument holds for Case 2. A state of the G _R -based ISE reached by string s _R is the initial state estimate after observing s. In fact, the state represents only the state estimate after observing s; it does not possess any physical meaning if viewed as an intermediate state or as the starting state of another string. For example, the G _R -based ISE starts from X, the state reached by ε, because the intruder’s initial state estimate after observing nothing is $\hat{X}_0(\epsilon)= X$. If event a is observed, then the intruder’s estimate moves to $\hat{X}_0(a) = f_{\rm obs,R}(X, a)$, which is the state reached by a = Rev(a). Although $\hat{X}_0(a)$ is reached from $\hat{X}_0(\epsilon)$, $\hat{X}_0(\epsilon)$ is not the final state estimate after observing a. Constructed in a reversed manner, states of G _R -based ISE along the same path share the same suffix but not prefix in general; thus, those state estimates are not the intermediate or final state estimate of one another in general. While the G _R -based ISE does not show the evolution of the intruder’s initial state estimates, it is sufficient for verifying ISO because it provides the set of all initial state estimates.

Remark 5

The construction of the G _R -based ISE does not assume a specific set of secret states. The set X _S is not considered until verification where all (marked) states of the G _R -based ISE are examined. As a result, if X _S changes, one does not need to reconstruct the ISE, but only need to test the inclusion relationship with the new X _S to verify ISO.

5.4 Verification of IFO

IFO considers the memberships of both the initial and final states of the system. To verify such a property, one needs to construct the initial-and-final state pair estimates that correspond to the intruder’s knowledge. Depending on whether X _sp and X _nsp are given in the form of a Cartesian product or not, we propose to use trellis-based ISE, the G _R -based ISE, or the observer to verify the property.

5.4.1 Verifying IFO for general X _sp and X _nsp

Let us first consider the case where X _sp and X _nsp are not expressed in the form of a Cartesian product. They may be any subset of $2^{X^2}$. In this case, enumeration of all possible starting and ending state pairs is needed to verify IFO. The trellis-based ISE of Saboori and Hadjicostis (2008) gives such an enumeration by using state mappings, as was described earlier. Therefore, we can use it in a straightforward manner to verify IFO. For all reachable states of the trellis-based ISE, if secret pairs always come along with non-secret pairs, then the system is IFO; otherwise, it is not IFO.

Example 13

Let us go back to the IFO problem in Example 4 and take the sets of secret and non-secret state pairs to be X _sp  = {(0, 0)} and X _nsp  = {(0, 1), (0, 2), (0, 3)}. To model the intruder, we use the trellis-based ISE shown in Fig. 6, which generates a set of state pairs for each observed string. In this example, the intruder would guess that the system has one of the state pairs in m ₁ = {(0, 0), (0, 1), (0, 2), (0, 3), (2, 1), (2, 3)} if observing a and it would update its estimate to m ₂ = {(0, 0), (0, 1), (0, 2), (0, 3)} upon observing an additional a (i.e, string aa). To verify the IFO property, we examine all reachable states of this ISE and notice that when the secret state pair (0, 0) is present, a non-secret state pair is also always present. Therefore, the system is IFO.

5.4.2 Verifying IFO when X _sp and X _nsp are expressed as Cartesian products

When both X _sp and X _nsp are expressed as Cartesian products, the verification can be simplified as compared to the preceding general case. In this special case, it is not necessary to remember the exact initial and final state pair. It is sufficient to remember whether the initial and the final states are secret or not. Consequently, the G _R -based ISE or the standard observer can be used to verify IFO. We write $X_{sp} = X_0^s \times X_f^{s}$ and $X_{nsp} =X_0^{ns} \times X_f^{ns}$, and use $X_0^{s}, X_0^{ns}, X_f^{s}, X_f^{ns}$ as alternative parameters for the problem.

Verifying IFO property using the G_R-based ISE

Given system G, the procedure to follow is:

• 1. Label states in $X_f^s$ with S and states in $X_f^{ns}$ with N by right-concatenating the label with the state name. (Right concatenation indicates that the labels are used for final states)

• 2. Build the G _R -based ISE. When constructing the observer, pass the label such that the successor carries the label of the predecessor.

• 3. The system is IFO if for every state containing i ₀ S where $i_0 \in X_0^s$, it also contains j ₀ N where $j_0 \in X_0^{ns}$.

Indeed, the IFO problem in this special case can be thought of as an ISO problem with marked states, which considers the ISO property with respect to a marked language. In this case, the languages of the ISO problem are not prefix-closed in general. We did not discuss this case previously in order to keep the formulation of ISO problems simple. If a system is marked-state initial-state opaque, then for every string starting from X _S and ending at a marked state in X _m , there is another string starting from X _NS and ending X _m with the same projection. That is, every state pair in X _S × X _m is confused with some state pair in X _NS × X _m , which is an IFO problem in Cartesian product form.

Verifying IFO property using observers

Similarly, we can verify the IFO problem in Cartesian product form using observers. First, label secret and non-secret initial states by left-concatenating S or N. (Left concatenation indicates that the labels are used for the initial-states). Then, build the observer and pass the label as before. The system is IFO if for every state containing Si _f where $i_f \in X_f^s$, it also contains Nj _f where $j_f \in X_f^{ns}$.

Remark 6

When verifying IFO using the trellis-based ISE, X _sp and X _nsp are part of the construction of the trellis. One can test the property without reconstructing the trellis-based ISE if X _sp or X _nsp changes. However, for the IFO in Cartesian product form, final state sets $X_f^s, X_f^{ns}$ are fixed if the G _R -based ISE is used; initial state sets $X_0^s, X_0^{ns}$ are fixed if the observer is used. While the latter two methods have only one degree of freedom in varying state sets, their complexity is lower compared to that of the trellis-based ISE. Using the G _R -based ISE or the observer has worst-case complexity of O(2^2|X|), while using the trellis-based ISE has worst-case complexity of $O(2^{|X|^2})$.

6 Joint opacity properties under coordinated architecture

6.1 A coordinated architecture

In this section, we extend the study of the three state-based opacity properties, ISO, CSO, and IFO, to a coordinated architecture where intruders work as a team to infer the secret. In the spirit of Debouk et al. (2000), we study a simplified coordinated architecture where two local intruders communicate with one coordinator, as shown in Fig. 9. Each local intruder knows the system model. They observe the system through their individual projection map, generate local state estimates, and then report the estimates to the coordinator. The coordinator has no knowledge about the system. It forms the so-called coordinated estimate by taking the intersection of the local estimates it receives. The communication from the local intruders to the coordinator is assumed to have no delay. The collaboration is restricted by the following rules: (1) local intruders do not communicate with each other about their individual estimates; (2) local intruders have no knowledge of the projection map of one another; and (3) the only collaboration between the two local intruders is through the coordinator, where the only memory available is to store the most recent coordinated estimate. The system is said to be jointly opaque if no coordinated estimate ever reveals the secret information. Because of the restricted collaboration, the coordinated estimate is no finer than the estimate of a single “system intruder” that would observe all events that are observable to some intruder. Such coordinated structures capture situations where a system intruder does not exist and where the coordination among local intruders is restricted. In the next three sections, we define and verify the generalized notions of ISO, CSO, and IFO that correspond to this specific coordinated architecture. As before, the system is modeled as a deterministic finite-state automaton G = (X, E, f, X ₀), but this time there are two sets of observable events, E _o,1 and E _o,2, one for each intruder, with associated natural projections P ₁ and P ₂ and respective sets of unobservable events E _uo,1 and E _uo,2. We form the union E _o,1 ∪ E _o,2 = E _o , and keep the notation P for the natural projection and E _uo for set of unobservable events corresponding to E _o .

Fig. 9

The coordinated architecture

6.2 Joint-Initial-State Opacity (J-ISO)

We start by proposing a definition of “joint initial state opacity” that is adapted to the coordinated architecture in Fig. 9.

Definition 7

(Joint-Initial-State Opacity (J-ISO)) Given G, projection maps P ₁ and P ₂, set of secret states $X_S\subseteq X_0$, and set of non-secret states $X_{NS}\subseteq X_0$, G is jointly initial-state opaque under the coordinated architecture if ∀ i ∈ X _S and $\forall t \in {\cal L}(G, i)$, $\exists j \in X_{NS}$, $\exists t_1 \in {\cal L}(G, j)$, $\exists t_2 \in {\cal L}(G, j)$ such that P ₁(t) = P ₁(t ₁) = s ₁, and P ₂(t) = P ₂(t ₂) = s ₂.

The system G is jointly initial-state opaque (J-ISO) if for every string t from a secret state i in X _S , there are other two strings, t ₁ and t ₂, from a common non-secret state j such that they are observationally equivalent to t to intruders 1 and 2, respectively. The common non-secret initial state j ensures that the coordinated estimate, formed by the intersection of two local estimates, contains a non-secret state whenever the real initial state is a secret state. Note that if a system is jointly initial-state opaque, it must be initial-state opaque for each intruder. However, the reverse is not true in general.

We use the G _R -based initial state estimator to model local intruders, where intruder k is represented by Obs _k (G _R , X), k = 1, 2. In addition, for analysis purposes, we consider Obs(G _R , X) which models the system intruder whose observable event set is E _o ; it is not a real intruder and its role will be explained later.

To verify the J-ISO property, we introduce a test automaton to capture the coordinated estimate. The test automaton is defined as $G_{\rm test}^{\rm ISO} := (Q, E_o, f_{\rm test}^{\rm ISO}, q_0)$. The state space is $Q \subseteq X_{\rm obs,R,1}\times X_{\rm obs,R,2}\times X_{\rm obs,R}\times X_{\rm obs,R,1\cap2}$, where X _obs,R,1, X _obs,R,2, and X _obs,R are the state spaces of the corresponding G _R -ISE and $X_{\rm obs,R,1\cap2} := \{ y \in 2^X : (\exists x_k \in X_{\rm obs,R,k}, k = 1, 2) [y = x_1 \cap x_2]\}$. A state in Q is denoted as q = (q ₁; q ₂; q _s ; q _c ) and the initial state of $G_{\rm test}^{\rm ISO}$ is q ₀ = (q ₁₀; q ₂₀; q _s0; q ₁₀ ∩ q ₂₀) = (X; X; X; X). The transition function $f_{\rm test}^{\rm ISO}$ is defined as follows:

$$\begin{array}{lll} &&f_{\rm test}^{\rm ISO}((q_1; q_2; q_s; q_c), e) \\ &&{\kern11pt} =\begin{cases} (f_{\rm obs, 1, R}(q_{1}, e);~ q_{2};~ f_{\rm obs, R}(q_{s}, e);~ f_{\rm obs, 1, R}(q_{1}, e) \cap q_{2}) \mbox{ if }e \in E_{o,1} \setminus E_{o,2}\\ (q_{1}; ~f_{\rm obs, 2, R}(q_{2}, e);~ f_{\rm obs, R}(q_{s}, e);~ q_{1} \cap f_{\rm obs, 2, R}(q_{2}, e)) \mbox{ if }e \in E_{o,2} \setminus E_{o,1}\\ (f_{\rm obs, 1, R}(q_{1}, e);~ f_{\rm obs, 2, R}(q_{2}, e);~ f_{\rm obs, R}(q_{s}, e);~ f_{\rm obs, 1, R}(q_{1}, e) \cap f_{\rm obs, 2, R}(q_{2}, e))\\ \mbox{if }e \in E_{o,1} \cap E_{o,2}\\ \end{cases} \end{array}$$

where e ∈ E _o , f _{obs, k, R} is the transition function of Obs _k (G _R , X), and f _{obs, R} is the transition function of Obs(G _R , X). Note that the fourth state q _c  = q ₁ ∩ q ₂ does not affect the behavior of $G_{\rm test}^{\rm ISO}$, and the dynamics of $G_{\rm test}^{\rm ISO}$ depend only on (q ₁; q ₂, q _s ) and are equivalent to that of Obs ₁(G _R , X) ∥ Obs ₂(G _R , X) ∥ Obs(G _R , X). With the additional parallel composition with Obs(G _R , X), the behavior of the test automaton is restricted within system’s observable behavior:

$$\begin{array}{rll}{\cal L}(G_{\rm test}^{\rm ISO}) :&= &P^{-1}_{o, 1}\big({\cal L}[Obs_1(G_R, X)] \big) \cap P^{-1}_{o, 2}\big({\cal L}[Obs_2(G_R, X)]\big) \cap {\cal L}[Obs(G_R, X)]\\ &= &{\cal L}[Obs(G_R, X)] \end{array}$$

where the inverse projection maps $P_{o, k}^{-1}: E_{o, k}^* \rightarrow 2^{E_o^*}$, for k = 1, 2, are with respect to E _o but not E.

We use the following example to show how the system intruder, Obs(G _R , X), restricts the observable behavior of $G_{\rm test}^{\rm ISO}$.

Example 14

Consider the system in Fig. 10a with E _{o, 1} = {a, c} and E _{o, 2} = {b, c}. To verify J-ISO, we build two G _R -ISEs to model intruders 1 and 2, respectively, as shown in Fig. 10b and c). Then we take parallel composition Obs ₁(G _R , X) ∥ Obs ₂(G _R , X) to synchronize the behavior of these two local intruders, as shown in Fig. 11a. This parallel composition does not give the correct system behavior; Obs ₁(G _R , X) ∥ Obs ₂(G _R , X) generates string ab while the system does not generate its reversed string ba. To restrict the behavior of the test automaton within valid observable behavior, we do an additional parallel composition with the system intruder Obs(G _R , X) that is shown in Fig. 10d, and obtain the correct $G_{\rm test}^{\rm ISO}$ shown in Fig. 11b. The resulting $G_{\rm test}^{\rm ISO}$ no longer includes string ab, and generates the system’s observable behavior ${\cal L}[Obs(G_R, X)]$.

Fig. 10

The DES and its local and system G _R -ISEs used in Example 14

Fig. 11

The $G_{\rm test}^{\rm ISO}$ in Example 14

The following lemma shows that the coordinated initial state estimate after a string $t \in {\cal L}(G, X)$ with P(t) = s, denoted by $\hat{X}_{0, {\rm coor}}(s)$, is captured by $G_{\rm test}^{\rm ISO}$. We will show later how to use $G_{\rm test}^{\rm ISO}$ to verify the J-ISO property

Lemma 6

Given G, projection maps P ₁ and P ₂ , the coordinated initial-state estimate after a string t ∈ L(G,X) with P(t) = s is captured by the state reached by s _R in $G_{\rm test}^{\rm ISO}$ . Specifically, $\hat{X}_{0, {\rm coor}}(s)= q_c$ where q _c is the fourth element in $q = (q_1; q_2; q_s; q_c) =f_{\rm test}^{\rm ISO}(q_0,s_R)$

Proof

Pick any string $s \in P[{\cal L}(G,X)]$ with P(t) = s, P ₁(s) = s ₁, and P ₂(s) = s ₂. By Theorem 1, the initial state estimates of the local intruder 1 and 2 are $\hat{X}_{0,1}(s_1)= f_{\rm obs,1,R}(X, s_{1R})$ and $\hat{X}_{0,2}(s_2)= f_{\rm obs,2,R}(X, s_{2R})$. Thus, the coordinated initial state estimate is $\hat{X}_{0, {\rm coor}}(s) = \hat{X}_{0, 1}(s_1) \cap \hat{X}_{0, 2}(s_2) = f_{\rm obs, 1, R}(X, s_{1R}) \cap f_{\rm obs, 2, R}(X, s_{2R})$. On the other hand, by construction, the state reached by s _R in $G_{\rm test}^{\rm ISO}$ is

$$\begin{array}{rll} f_{\rm test}^{\rm ISO}(q_0, s_R) &=& (q_1; q_2; q_s; q_c) \\ &=&(f_{\rm obs, 1, R}(X, s_{1R});~ f_{\rm obs, 2, R}(X, s_{2R});~ f_{\rm obs, R}(X, s_R);\\ && f_{\rm obs, 1, R}(X, s_{1R}) \cap f_{\rm obs, 2, R}(X, s_{2R})) \end{array}$$

where the fourth element q _c is $f_{\rm obs, 1, R}(X, s_{1R}) \cap f_{\rm obs, 2, R}(X, s_{2R}) = \hat{X}_{0, {\rm coor}}(s)$. Therefore, after a string $t \in {\cal L}(G, X)$ with P(t) = s, the coordinated estimate $\hat{X}_{0, {\rm coor}}(s)$ is q _c , which is the fourth element of state $q= f_{\rm test}^{\rm ISO}(q_0, s_R)$ □

We now use $G_{\rm test}^{\rm ISO}$ to verify J-ISO.

Theorem 5

G is jointly initial-state opaque if and only if: ∀ q = (q ₁; q ₂; q _s ; q _c ) reachable in $G_{\rm test}^{\rm ISO}$ , $q_c \cap X_S \neq \emptyset \Rightarrow q_c \cap X_{NS} \neq \emptyset$.

Proof

G is J-ISO if and only if $\hat{X}_{0, {\rm coor}}(\cdot)$ always contains a non-secret state whenever it contains a secret state. To prove Theorem 5, it is sufficient to prove that the collection of $\hat{X}_{0, {\rm coor}}(\cdot)$ is the collection of the fourth element of every reachable state in $G_{\rm test}^{\rm ISO}$. By Lemma 6, $\hat{X}_{0, {\rm coor}}(s)$ is captured by the fourth element of the state q reached via s _R . Since $G_{\rm test}^{\rm ISO}$ is deterministic and ${\cal L}\big(G_{\rm test}^{\rm ISO}\big) = {\cal L}[Obs(G_R,X)] = Rev\big(P[{\cal L}(G,X)]\big)$, every reachable state of $G_{\rm test}^{\rm ISO}$ corresponds to a valid $\hat{X}_{0, {\rm coor}}(\cdot)$, and vice-versa. Therefore, the J-ISO property is verified by examining the fourth element of all reachable states in $G_{\rm test}^{\rm ISO}$. □

Example 15

Let us go back to Example 14 and take the secret and non-secret state sets to be X _S  = {0} and X _NS  = X ∖ X _S . The system is initial-state opaque to each local intruder because no state in Obs ₁(G _R , X) or Obs ₂(G _R , X) contains only the secret state 0. However, the system is not jointly initial-state opaque. As seen in Fig. 11b, by collaborating under the coordinated architecture, the team of intruders generate a coordinated estimate {0} when P(t) = s = bc (s _R  = cb) has occurred.

We can extend the above verification procedure for J-ISO to the joint versions of CSO and IFO, by employing the respective estimator in the construction of the test automaton. These results are presented in the next two sections.

6.3 Joint-Current-State Opacity(J-CSO)

Definition 8

(Joint-Current-State Opacity(J-CSO)) Given G, projection maps P ₁, P ₂, set of secret states $X_S\subseteq X$, and set of non-secret states $X_{NS}\subseteq X$. G is jointly current-state opaque under the coordinated architecture if ∀ i ∈ X ₀ and $\forall t \in {\cal L}(G, i)$ where f(i, t) = x ∈ X _S , $\exists j_1,j_2 \in X_0$, $\exists t_1 \in {\cal L}(G, j_1)$, $\exists t_2 \in {\cal L}(G, j_2)$ such that (i)f(j ₁, t ₁) = f(j ₂, t ₂) = x′ ∈ X _NS and (ii)P ₁(t) = P ₁(t ₁) = s ₁, and P ₂(t) = P ₂(t ₂) = s ₂.

The system G is jointly-current-state opaque if for every string t ending at a secret state x, there are other two strings t ₁ and t ₂ ending at a common non-secret state x′ such that intruder 1 confuses t with t ₁ and intruder 2 confuses t with t ₂. Strings t ₁ and t ₂ need not start from the same initial state, but they have to end at a common non-secret state to ensure that a non-secret state exists in the coordinated estimate. Similarly to the case of J-ISO, to verify J-CSO, we build a test automaton $G_{\rm test}^{\rm CSO} := (Q, E_o, f_{\rm test}^{\rm CSO}, q_0)$ where standard observers are used to model intruders. Specifically, Obs _k (G) models the behavior of local intruder k, and Obs(G) models the system intruder who observes E _o ; the system intruder is to confine the behavior of the test automaton. The state space $Q \subseteq X_{\rm obs,1}\times X_{\rm obs,2}\times X_{\rm obs}\times X_{\rm obs,1\cap2}$ where X _obs,1,X _obs,2, and X _obs are state spaces of the corresponding observers and $X_{\rm obs,1\cap2} = \{y \in 2^X: (\exists x_k \in X_{\rm obs,k}, k = 1, 2)[y = x_1 \cap x_2]\}$. A state in Q is denoted by q = (q ₁;q ₂;q _s ;q _c ), and the initial state is q ₀ = (X; X; X; X). The transition function $f_{\rm test}^{\rm CSO}$ is defined as follows:

$$\begin{array}{lll} &&f_{\rm test}^{\rm CSO}((q_1; q_2; q_s; q_c), e) \\ &&{\kern11pt}=\begin{cases} (f_{\rm obs, 1}(q_{1}, e);~ q_{2};~ f_{\rm obs}(q_{s}, e);~ f_{\rm obs, 1}(q_{1}, e) \cap q_{2})~~ \mbox{if }e \in E_{o,1} \setminus E_{o,2}\\ (q_{1}; ~f_{\rm obs, 2}(q_{2}, e);~ f_{\rm obs}(q_{s}, e);~ q_{1} \cap f_{\rm obs, 2}(q_{2}, e))~~ \mbox{if }e \in E_{o,2} \setminus E_{o,1}\\ (f_{\rm obs, 1}(q_{1}, e);~ f_{\rm obs, 2}(q_{2}, e);~ f_{\rm obs}(q_{s}, e);~ f_{\rm obs, 1}(q_{1}, e) \cap f_{\rm obs, 2}(q_{2}, e))\\ \mbox{if }e \in E_{o,1} \cap E_{o,2}\\ \end{cases} \end{array}$$

where f _{obs, k} is the transition function of Obs _k (G), and f _obs is that of Obs(G).

Theorem 6

G is jointly current-state opaque if and only if: ∀ q = (q ₁; q ₂; q _s ; q _c ) reachable in $G_{\rm test}^{\rm CSO}$ , $q_c \cap X_S \neq \emptyset \Rightarrow q_c \cap X_{NS} \neq \emptyset$.

Due to the similarity between $G_{\rm test}^{\rm CSO}$ and $G_{\rm test}^{\rm ISO}$, we omit the proof.

6.4 Joint-Initial-and-Final-State Opacity(J-IFO)

Definition 9

(Joint-Initial-and-Final-State Opacity(J-IFO)) Given G, projection maps P ₁ and P ₂, set of secret pairs $X_{sp} \subseteq X_0 \times X$, and set of non-secret pairs $X_{nsp} \subseteq X_0 \times X$, G is jointly initial-and-final-state opaque under the coordinated architecture if ∀ (x ₀, x _f ) ∈ X _sp and $\forall t \in {\cal L}(G, x_0)$ where f(x ₀, t) = x _f , $\exists (x_0', x_f') \in X_{nsp}, \exists t_1, t_2 \in {\cal L}(G, x_0')$ such that (i)f(x ₀′, t ₁) = f(x ₀′, t ₂) = x _f ′ ∈ X _NS and (ii)P ₁(t) = P ₁(t ₁) = s ₁, and P ₂(t) = P ₂(t ₂) = s ₂.

G is jointly-initial-and-final-state opaque if for every string t that corresponds to a secret state pair, there are other two strings t ₁ and t ₂ corresponding to a common non-secret state pair (x ₀′, x _f ′) ∈ X _nsp such that intruder 1 confuses t ₁ with t and intruder 2 confuses t ₂ with t. The common non-secret state pair (x ₀′, x _f ′) ∈ X _nsp ensures that a non-secret state pair exists in the coordinated estimate.

To verify J-IFO property, we use a test automaton $G_{\rm test}^{\rm IFO} := (Q, E_o, f_{\rm test}^{\rm IFO}, q_0)$ where trellis-ISE are used to model local intruders and the system intruder. The state space is $Q \subseteq M_1\times M_2\times M \times M_{1\cap2}$, where M ₁,M ₂ and M are the state spaces of corresponding trellis-ISEs, and $M_{1\cap2} := \{y \in 2 ^{X^2}: (\exists m_k \in M_{k}, k = 1, 2)[y = m_1 \cap m_2]\}$. A state in Q is denoted as q: = (q ₁, q ₂, q _s , q _c ). The initial state of $G_{\rm test}^{\rm IFO}$ is q ₀ = (q ₁₀; q ₂₀; q _s0; q ₁₀ ∩ q ₂₀) where $q_{k0}= \{(i,i): i\in X)\} \cup \{(i,j) \in X^2: (\exists t \in E_{uo,k}^*)[f(i, t) = j]\}$ and $q_{s0}= \{(i,i): i\in X)\} \cup \{(i,j) \in X^2: (\exists t \in E_{uo}^*)[f(i, t) = j]\}$. The transition function $f_{\rm test}^{\rm IFO}$ is defined as follows:

$$\begin{array}{lll} &&f_{\rm test}^{\rm IFO}((q_1; q_2; q_s; q_c), e) \\ &&{\kern11pt} =\begin{cases} (f_{\rm tre, 1}(q_{1}, e);~ q_{2};~ f_{\rm tre}(q_{c}, e);~ f_{\rm tre, 1}(q_{1}, e) \cap q_{2}) \mbox{if }e \in E_{o,1} \setminus E_{o,2}\\ (q_{1}; ~f_{\rm tre, 2}(q_{2}, e);~ f_{\rm tre}(q_{c}, e);~ q_{1} \cap f_{\rm tre, 2}(q_{2}, e)) \mbox{if }e \in E_{o,2} \setminus E_{o,1}\\ (f_{\rm tre, 1}(q_{1}, e);~ f_{\rm tre, 2}(q_{2}, e);~ f_{\rm tre}(q_{c}, e);~ f_{\rm tre, 1}(q_{1}, e) \cap f_{\rm tre, 2}(q_{2}, e))\\ \mbox{if }e \in E_{o,1} \cap E_{o,2}\\ \end{cases} \end{array}$$

where f _{tre, k} is the transition function of trellis ISE k, and f _tre is the transition function of the system trellis-ISE.

Example 16

Consider J-IFO using system G in Fig. 12a with X _sp  = {(0, 2)}, $X_{nsp}= X^2 \setminus X_{sp}$, E _{o, 1} = {a, c}, and E _{o, 2} = {b, c}. We construct trellis-based ISE to model intruders 1 and 2 and the system intruder, as shown in Fig. 12b, c and d, respectively. The system is IFO to both local intruders. To verify J-IFO, we build tester $G_{\rm test}^{\rm IFO}$, shown in Fig. 13, by parallel composing the three trellises and adding the intersection of the two local estimates as the fourth element. The system is J-IFO because no states of $G_{\rm test}^{\rm IFO}$ contains the secret state pair (0, 2) alone.

Fig. 12

The DES and trellises used in Example 16

Fig. 13

The tester $G_{\rm test}^{\rm IFO}$ of the system in Example 16

7 Conclusion

We presented several new results regarding the property of opacity of DES in the context of centralized and coordinated architectures. Four types of opacity properties were investigated: language-based opacity, initial-state opacity, current-state opacity, and initial-and-final-state opacity; the latter one was introduced to capture situations where the secret simultaneously involves the initial and final states of the system. We also developed a set of transformation algorithms between the four notions of opacities and showed that every pair of opacity properties are equivalent through some transformation. These results unify the treatment of opacity in DES. To verify the different notions of opacities, we reviewed existing methods and proposed new algorithms. Finally, we formulated three new notions of joint opacity in the context of a coordinated architecture where a set of intruders work as a team to infer the secret. Verification algorithms were proposed for each notion of joint opacity, leveraging the centralized tests.

It would be of interest to investigate the extension of recent results on opacity-enforcing supervisory control, as in Dubreil et al. (2008, 2010) and Saboori and Hadjicostis (2008) for instance, to the coordinated architecture considered in this paper. It would also be worthwhile to continue the study of opacity under multiple cooperating intruders but examining other types of coordinated architectures. Finally, it may be possible to obtain more computationally–efficient algorithms than those presented in this paper under special structural assumptions on the automaton model of the system.