Comparing the notions of opacity for discrete-event systems

Abstract

Opacity is an information flow property characterizing whether a system reveals its secret to a passive observer. Several notions of opacity have been introduced in the literature. We study the notions of language-based opacity, current-state opacity, initial-state opacity, initial-and-final-state opacity, K-step opacity, and infinite-step opacity. Comparing the notions is a natural question that has been investigated and summarized by Wu and Lafortune, who provided transformations among current-state opacity, initial-and-final-state opacity, and language-based opacity, and, for prefix-closed languages, also between language-based opacity and initial-state opacity. We extend these results by showing that all the discussed notions of opacity are transformable to each other. Besides a deeper insight into the differences among the notions, the transformations have applications in complexity results. In particular, the transformations are computable in polynomial time and preserve the number of observable events and determinism, and hence the computational complexities of the verification of the notions coincide. We provide a complete and improved complexity picture of the verification of the discussed notions of opacity, and improve the algorithmic complexity of deciding language-based opacity, infinite-step opacity, and K-step opacity.

1 Introduction

Applications often require to keep some information about the behavior of a system secret. Properties that guarantee such requirements include anonymity (Schneider and Sidiropoulos 1996), noninterference (Hadj-Alouane et al. 2005), secrecy (Alur et al. 2006), security (Focardi and Gorrieri 1994), and opacity (Mazarė 2004).

In this paper, we are interested in opacity for discrete-event systems (DESs) modeled by finite automata. Opacity is a state-estimation property that asks whether a system prevents an intruder from revealing the secret. The intruder is modeled as a passive observer with the complete knowledge of the structure of the system, but with only limited observation of the behavior of the system. Based on the observation, the intruder estimates the behavior of the system, and the system is opaque if the intruder never reveals the secret. In other words, for any secret behavior of the system, there is a non-secret behavior of the system that looks the same to the intruder.

If the secret is modeled as a set of states, the opacity is referred to as state-based. Bryans et al. (2005) introduced state-based opacity for systems modeled by Petri nets, Saboori and Hadjicostis (2007) adapted it to (stochastic) automata, and Bryans et al. (2008) generalized it to transition systems. If the secret is modeled as a set of behaviors, the opacity is referred to as language-based. Language-based opacity was introduced by Badouel et al. (2007) and Dubreil et al. (2008). For more details, we refer the reader to the overview by Jacob et al. (2016).

Several notions of opacity have been introduced in the literature. In this paper, we are interested in the notions of current-state opacity (CSO), initial-state opacity (ISO), initial-and-final-state opacity (IFO), language-based opacity (LBO), K-step opacity (K-SO), and infinite-step opacity (INSO). Current-state opacity is the property that the intruder can never decide whether the system is currently in a secret state. Initial-state opacity is the property that the intruder can never reveal whether the computation started in a secret state. Initial-and-final-state opacity of Wu and Lafortune (2013) is a generalization of both, where the secret is represented as a pair of an initial and a marked state. Consequently, initial-state opacity is a special case of initial-and-final-state opacity where the marked states do not play a role, and current-state opacity is a special case where the initial states do not play a role.

While initial-state opacity prevents the intruder from revealing, at any time during the computation, whether the system started in a secret state, current-state opacity prevents the intruder only from revealing whether the current state of the system is a secret state. However, it may happen that the intruder realizes in the future that the system was in a secret state at some former point of the computation. For instance, if the intruder estimates that the system is in one of two possible states and, in the next step, the system proceeds by an observable event that is possible only from one of the states, then the intruder reveals the state in which the system was one step ago.

This issue has been considered in the literature and led to the notions of K-step opacity (K-SO) and infinite-step opacity (INSO) introduced by Saboori and Hadjicostis (2007, 2012). While K-step opacity requires that the intruder cannot ascertain the secret in the current and K subsequent states, infinite-step opacity requires that the intruder can never ascertain that the system was in a secret state. Notice that 0-step opacity coincides with current-state opacity by definition, and that an n-state automaton is infinite-step opaque if and only if it is (2ⁿ − 2)-step opaque (Yin and Lafortune 2017).

Comparing different notions of opacity for automata models, Saboori and Hadjicostis (Saboori and Hadjicostis 2008) provided a language-based definition of initial-state opacity, Cassez et al. (2012) transformed language-based opacity to current-state opacity, and Wu and Lafortune showed that current-state opacity, initial-and-final-state opacity, and language-based opacity can be transformed to each other. They further provided transformations of initial-state opacity to language-based opacity and to initial-and-final-state opacity, and, for prefix-closed languages, a transformation of language-based opacity to initial-state opacity.

In this paper, we extend these results by showing that, for automata models, all the discussed notions of opacity are transformable to each other. As well as the existing transformations, our transformations are computable in polynomial time and preserve the number of observable events and determinism (whenever it is meaningful). In more detail, the transformations of Wu and Lafortune (2013) preserve the determinism of transitions, but result in automata with a set of initial states. This issue can, however, be easily fixed by adding a new initial state, connecting it to the original initial states by new unobservable events, and making the original initial states non-initial. We summarize our results, together with the existing results, in Fig. 1.

Fig. 1

Overview of the transformations among the notions of opacity for automata models

There are two immediate applications of the transformations. First, the transformations provide a deeper understanding of the differences among the opacity notions from the structural point of view. For instance, the reader may deduce from the transformations that, for prefix-closed languages, the notions of language-based opacity, initial-state opacity, and current-state opacity coincide, or that to transform current-state opacity to infinite-step opacity means to add only a single state and a few transitions.

Second, the transformations provide a tool to obtain the complexity results for all the discussed opacity notions by studying just one of the notions. For an illustration, consider, for instance, our recent result showing that deciding current-state opacity for systems modeled by DFAs with three events, one of which is unobservable, is PSpace-complete (Balun and Masopust 2020). Since we can transform the problems of deciding current-state opacity and of deciding infinite-step opacity to each other in polynomial time, preserving determinism and the number of observable events, we obtain that deciding infinite-step opacity for systems modeled by DFAs with three events, one of which is unobservable, is PSpace-complete as well. In particular, combining the transformations with known results (Balun and Masopust 2020; Jacob et al. 2016), we obtain a complete complexity picture of the verification of the discussed notions of opacity as summarized in Table 1.

Table 1 Complexity of verifying the notions of opacity for DESs with Σ_o being the set of observable events following from the transformations and known results; n stands for the number of states of the input automaton, ℓ for the number of observable events of the input automaton, and m ≤ ℓn² for the number of transitions in the projected automaton of the input automaton

The fact that checking opacity for DESs is PSpace-complete was known for some of the considered notions (Jacob et al. 2016). In particular, deciding current-state opacity, initial-state opacity, and language-based opacity were known to be PSpace-complete, deciding K-step opacity was known to be NP-hard, and deciding infinite-step opacity was known to be PSpace-hard.

Complexity theory tells us that any two PSpace-complete problems can be transformed to each other in polynomial time. In other words, it gives the existence of polynomial transformations between the notions of opacity for which the verification is PSpace-complete. However, the theory and the PSpace-hardness proofs presented in the literature do not give a clue how to obtain these transformations. Therefore, from the complexity point of view, our contribution is not the existence of the transformations, but the construction of specific transformations. Since the presented transformations preserve determinism and the number of observable events, they allow us to present stronger results than those known in the literature (Jacob et al. 2016) that we summarize in Table 1.

The transformations further allow us to improve the algorithmic complexity of deciding language-based opacity, infinite-step opacity, and K-step opacity, although we do not use the transformations themselves, but rather the deeper insight into the problems they provide. For language-based opacity, Lin (2011) suggested an algorithm with complexity O(2²ⁿ), where n is the number of states of the input automaton. In this paper, we improve this complexity to O((n + mℓ)2ⁿ), where ℓ = |Σ_o| is the number of observable events and m ≤ ℓn² is the number of transitions in the projected automaton of the input automaton. For infinite-step opacity and K-step opacity, the latest results are by Yin and Lafortune (2017) who designed an algorithm for checking infinite-step opacity with complexity O(ℓ2²ⁿ), and an algorithm for checking K-step opacity with complexity $O(\min \limits \{\ell 2^{2n},\ell ^{K+1} 2^{n}\})$. In this paper, we suggest a new algorithm for deciding infinite-step opacity with complexity O((n + mℓ)2ⁿ), and a new algorithm for checking K-step opacity with complexity O((K + 1)2ⁿ(n + mℓ²)). Notice that K is bounded by 2ⁿ − 2, since an n-state automaton is infinite-step opaque if and only if it is (2ⁿ − 2)-step opaque (Yin and Lafortune 2017). Consequently, our algorithm improves the complexity if K is either very large (larger than 2ⁿ − 2) or polynomial with respect to n; otherwise, the two-way observer technique of Yin and Lafortune (2017) is more efficient, and it is a challenging open problem whether its complexity can be further improved. All our results are summarized in Table 1.

2 Preliminaries

We assume that the reader is familiar with the basic notions of automata theory (Cassandras and Lafortune 2008). For a set S, |S| denotes the cardinality of S, and 2^S the power set of S. Let $\mathbb {N}$ denote the set of all non-negative integers. An alphabet Σ is a finite nonempty set of events. A string over Σ is a sequence of events from Σ. Let Σ^∗ denote the set of all finite strings over Σ; the empty string is denoted by ε. A language L over Σ is a subset of Σ^∗. The set of all prefixes of strings of L is the set $\overline {L}=\{u \mid \text {there is } v\in {\Sigma }^{*} \text { such that } uv \in L\}$. For a string u ∈Σ^∗, |u| denotes the length of u, and $\overline {u}$ denotes the set of all prefixes of u.

A nondeterministic finite automaton (NFA) over an alphabet Σ is a structure $\mathcal {G} = (Q,{\Sigma },\delta ,I,F)$, where Q is a finite set of states, $I\subseteq Q$ is a set of initial states, $F \subseteq Q$ is a set of marked states, and δ: Q ×Σ→ 2^Q is a transition function that can be extended to the domain 2^Q ×Σ^∗ by induction. To simplify our proofs, we use the notation δ(Q, S) = ∪_s∈Sδ(Q, s), where $S\subseteq {\Sigma }^{*}$. For a set of states $Q_{0}\subseteq Q$, the language marked by $\mathcal {G}$ from the states of Q₀ is the set $L_{m}(\mathcal {G},Q_{0}) = \{w\in {\Sigma }^{*} \mid \delta (Q_{0},w)\cap F \neq \emptyset \}$, and the language generated by $\mathcal {G}$ from the states of Q₀ is the set $L(\mathcal {G},Q_{0}) = \{w\in {\Sigma }^{*} \mid \delta (Q_{0},w)\neq \emptyset \}$. The language marked by $\mathcal {G}$ is then $L_{m}(\mathcal {G})=L_{m}(\mathcal {G},I)$, and the language generated by $\mathcal {G}$ is $L(\mathcal {G})=L(\mathcal {G},I)$. The NFA $\mathcal G$ is deterministic (DFA) if |I| = 1 and |δ(q, a)|≤ 1 for every q ∈ Q and a ∈Σ. An automaton $\mathcal G$ is non-blocking if $\overline {L_{m}(\mathcal G)} = L(\mathcal G)$.

A discrete-event system (DES) G over Σ is an NFA together with the partition of the alphabet Σ into two disjoint subsets Σ_o and Σ_uo = Σ ∖Σ_o of observable and unobservable events, respectively. In the case where all states of the automaton are marked, we simply write G = (Q,Σ,δ, I) without specifying the set of marked states.

When discussing the state estimation properties, the literature often studies deterministic systems with a set of initial states. Such systems are known as deterministic DES and defined as a DFA with several initial states; namely, a deterministic DES is an NFA $\mathcal {G}=(Q,{\Sigma },\delta ,I,F)$, where |δ(q, a)|≤ 1 for every q ∈ Q and a ∈Σ.

The opacity property is based on partial observations of events described by projection $P\colon {\Sigma }^{*} \to {\Sigma }_{o}^{*}$. The projection is a morphism defined by P(a) = ε for a ∈Σ_uo, and P(a) = a for a ∈Σ_o. The action of P on a string σ₁σ₂⋯σ_n, with σ_i ∈Σ for 1 ≤ i ≤ n, is to erase all events that do not belong to Σ_o, that is, P(σ₁σ₂⋯σ_n) = P(σ₁)P(σ₂)⋯P(σ_n). The definition can be readily extended to languages.

Let G be a NFA over Σ, and let $P\colon {\Sigma }^{*} \to {\Sigma }_{o}^{*}$ be a projection. By the projected automaton of G, we mean the automaton P(G) obtained from G by replacing every transition (p, a, q) by the transition (p, P(a),q), and by eliminating the ε-transitions. In particular, if δ is the transition function of G, then the transition function γ of the automaton P(G) is defined as $\gamma (q,a)=\hat {\delta }(q,a)$, where $\hat {\delta }\colon Q\times {\Sigma }^{*} \to 2^{Q}$ is the extension of δ to the domain Q ×Σ^∗, that is, $\hat {\delta }(q,\varepsilon )=\{q\}$ and $\hat {\delta }(q,wa)=\bigcup _{p\in \hat {\delta }(q,w)} \delta (p,a)$. Then P(G) is an NFA over Σ_o, with the same set of states as G, that recognizes the language P(L_m(G)) and can be constructed in polynomial time (Hopcroft and Ullman 1979). The DFA constructed from P(G) by the subset construction is called an observer (Cassandras and Lafortune 2008). In the worst case, the observer has exponentially many states compared with the automaton G (Jirȧskovȧ and Masopust 2012; Wong 1998).

A decision problem is a yes-no question. A decision problem is decidable if there is an algorithm that solves it. Complexity theory classifies decidable problems into classes based on the time or space an algorithm needs to solve the problem. The complexity classes we consider are L, NL, P, NP, and PSpace denoting the classes of problems solvable by a deterministic logarithmic-space, nondeterministic logarithmic-space, deterministic polynomial-time, nondeterministic polynomial-time, and deterministic polynomial-space algorithm, respectively. The hierarchy of classes is L $\subseteq$ NL $\subseteq$ P $\subseteq$ NP $\subseteq$ PSpace. Which of the inclusions are strict is an open problem. The widely accepted conjecture is that all are strict. A decision problem is NL-complete (resp. NP-complete, PSpace-complete) if (i) it belongs to NL (resp. NP, PSpace) and (ii) every problem from NL (resp. NP, PSpace) can be reduced to it by a deterministic logarithmic-space (resp. polynomial-time) algorithm. Condition (i) is called membership and condition (ii) hardness.

3 Notions of opacity

In this section, we recall the definitions of the notions of opacity we discuss. The notion of initial-and-final-state opacity is recalled to make the paper self-contained.

Current-state opacity asks whether the intruder cannot decide, at any instance of time, whether the system is currently in a secret state.

Definition 1 (Current-state opacity (CSO))

Given a DES G = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$, a set of secret states $Q_{S} \subseteq Q$, and a set of non-secret states $Q_{NS} \subseteq Q$. System G is current-state opaque if for every string w such that δ(I, w) ∩ Q_S≠∅, there exists a string $w^{\prime }$ such that $P(w)=P(w^{\prime })$ and $\delta (I,w^{\prime })\cap Q_{NS} \neq \emptyset$.

The definition of current-state opacity can be reformulated as a language inclusion as shown in the following lemma. This result is similar to that of Wu and Lafortune (2013) used to transform current-state opacity to language-based opacity. We use this alternative definition to simplify proofs.

Lemma 1

Balun and Masopust (2020) Let G = (Q,Σ,δ, I) be a DES, $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$ a projection, and $Q_{S}, Q_{NS} \subseteq Q$ sets of secret and non-secret states, respectively. Let G_S = (Q,Σ,δ, I, Q_S) and G_NS = (Q,Σ,δ, I, Q_NS), then G is current-state opaque if and only if $L_{m}(P(G_{S})) \subseteq L_{m}(P(G_{NS}))$.

The second notion of opacity under consideration is language-based opacity. Intuitively, a system is language-based opaque if for any string w in the secret language, there exists a string $w^{\prime }$ in the non-secret language with the same observation $P(w)=P(w^{\prime })$. In this case, the intruder cannot conclude whether the secret string w or the non-secret string $w^{\prime }$ has occurred. We recall the most general definition by Lin (2011).

Definition 2 (Language-based opacity (LBO))

Given a DES G = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$, a secret language $L_{S} \subseteq L(G)$, and a non-secret language $L_{NS} \subseteq L(G)$. System G is language-based opaque if $L_{S} \subseteq P^{-1}P(L_{NS})$.

It is worth mentioning that the secret and non-secret languages are often considered to be regular; and we consider it as well. The reason is that, for non-regular languages, the inclusion problem is undecidable; see Asveld and Nijholt (2000) for more details.

The third notion is the notion of initial-state opacity. Initial-state opacity asks whether the intruder can never reveal whether the computation started in a secret state.

Definition 3 (Initial-state opacity (ISO))

Given a DES G = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\rightarrow {\Sigma }_{o}^{*}$, a set of secret initial states $Q_{S}\subseteq I$, and a set of non-secret initial states $Q_{NS}\subseteq I$. System G is initial-state opaque with respect to Q_S, Q_NS and P if for every w ∈ L(G, Q_S), there exists $w^{\prime } \in L(G,Q_{NS})$ such that $P(w) = P(w^{\prime })$.

The fourth notion is the notion of initial-and-final-state opacity of Wu and Lafortune (2013). Initial-and-final-state opacity is a generalization of both current-state opacity and initial-state opacity, where the secret is represented as a pair of an initial and a marked state. Consequently, initial-state opacity is a special case of initial-and-final-state opacity where the marked states do not play a role, and current-state opacity is a special case where the initial states do not play a role.

Definition 4 (Initial-and-final-state opacity (IFO))

Given a DES G = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\rightarrow {\Sigma }_{o}^{*}$, a set of secret state pairs $Q_{S}\subseteq I \times Q$, and a set of non-secret state pairs $Q_{NS}\subseteq I \times Q$. System G is initial-and-final-state opaque with respect to Q_S, Q_NS and P if for every secret pair (q₀, q_f) ∈ Q_S and every w ∈ L(G, q₀) such that q_f ∈ δ(q₀, w), there exists $(q_{0}^{\prime },q_{f}^{\prime }) \in Q_{NS}$ and $w^{\prime } \in L(G,q_{0}^{\prime })$ such that $q_{f}^{\prime } \in \delta (q_{0}^{\prime }, w^{\prime })$ and $P(w) = P(w^{\prime })$.

The fifth notion is the notion of K-step opacity. K-step opacity is a generalization of current-state opacity requiring that the intruder cannot reveal the secret in the current and K subsequent states. By definition, current-state opacity is equivalent to 0-step opacity.

We slightly generalize and reformulate the definition of Saboori and Hadjicostis (2012).

Definition 5 (K-step opacity (K-SO))

Given a system G = (Q,Σ,δ, I), a projection $P \colon {\Sigma }^{*} \to {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, a set of non-secret states $Q_{NS}\subseteq Q$, and a non-negative integer $K\in \mathbb {N}$. System G is K-step opaque with respect to Q_S, Q_NS, and P if for every string st ∈ L(G) such that |P(t)|≤ K and δ(δ(I, s) ∩ Q_S, t)≠∅, there exists a string $s^{\prime }t^{\prime } \in L(G)$ such that $P(s)=P(s^{\prime })$, $P(t)=P(t^{\prime })$, and $\delta (\delta (I,s^{\prime })\cap Q_{NS}, t^{\prime }) \neq \emptyset$.

Finally, the last notion we consider is the notion of infinite-step opacity. Infinite-step opacity is a further generalization of K-step opacity by setting K being infinity. Actually, Yin and Lafortune (2017) have shown that an n-state automaton is infinite-step opaque if and only if it is (2ⁿ − 2)-step opaque. Again, we slightly generalize and reformulate the definition of Saboori and Hadjicostis (Saboori and Hadjicostis 2011).

Definition 6 (Infinite-step opacity (INSO))

Given a system G = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\rightarrow {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, and a set of non-secret states $Q_{NS}\subseteq Q$. System G is infinite-step opaque with respect to Q_S, Q_NS and P if for every string st ∈ L(G) such that δ(δ(I, s) ∩ Q_S, t)≠∅, there exists a string $s^{\prime }t^{\prime } \in L(G)$ such that $P(s)=P(s^{\prime })$, $P(t)=P(t^{\prime })$, and $\delta (\delta (I,s^{\prime })\cap Q_{NS}, t^{\prime }) \neq \emptyset$.

4 Transformations

Although some of the transformations were previously known in the literature, Wu and Lafortune (2013) were first who studied the transformations systematically. In particular, they provided polynomial-time transformations among current-state opacity, language-based opacity, initial-state opacity, and initial-and-final-state opacity, see Fig. 1. Inspecting the reductions, it can be seen that after eliminating the unnecessary Trim operations, the transformations use only logarithmic space, preserve the number of observable events, and determinism (whenever it is meaningful). As we already pointed out, the transformations of Wu and Lafortune (2013) preserve the determinism of transitions, but they admit a set of initial states. This issue can, however, be easily eliminated by adding a new initial state, connecting it to the original initial states by new unobservable events, and making the original initial states non-initial.

However, their transformation from language-based opacity to initial-state opacity is restricted only to the case where the secret and non-secret languages of the language-based opacity problem are prefix closed. We complete the polynomial-time transformations among all the discussed notions of opacity. In particular, we provide a general transformation from language-based opacity to initial-state opacity in Section 4.1.1, transformations between infinite-step opacity and current-state opacity in Section 4.2, and transformations between K-step opacity and current-state opacity in Section 4.3. All the transformations preserve the number of observable events and determinism. Except for a few exceptions, the transformations need only logarithmic space. Our results are summarized in Fig. 1 with references to the corresponding sections.

The following auxiliary lemma states that we can reduce the number of observable events in DESs with at least three observable events without affecting current-state opacity and initial-state opacity of the DES. We make use of this lemma to preserve the number of observable events in cases where we introduce new observable events in our reductions, namely in Sections 4.1.1, 4.2.2, and 4.3.2.

Lemma 2

Let G = (Q,Σ,δ, I, F) be an NFA, and let ${\Gamma }_{o}\subseteq {\Sigma }_{o}$ contain at least three events. Let $G^{\prime }=(Q^{\prime },({\Sigma }-{\Gamma }_{o})\cup \{0,1\},\delta ^{\prime },I,F)$ be an NFA obtained from G as follows. Let $k=\lceil \log _{2}(|{\Gamma }_{o}|) \rceil$, and let $e\colon {\Gamma }_{o} \to \{0,1\}^{k}$ be a binary encoding of the events of Γ_o. We replace every transition (p, a, q) with a ∈Γ_o by k transitions

$$ (p,b_{1},p_{b_{1}}), (p_{b_{1}},b_{2},p_{b_{1}b_{2}}),\ldots, (p_{b_{1}{\cdots} b_{k-1}},b_{k},q) $$

where $e(a)=b_{1}b_{2}{\cdots } b_{k} \in \{0,1\}^{k}$, and $p_{b_{1}},\ldots ,p_{b_{1}{\cdots } b_{k-1}}$ are states that are added to the state set of $G^{\prime }$. Notice that these states are neither secret nor non-secret and that, to preserve determinism, they are newly created when they are needed for the first time, and reused when they are needed later during the replacements, cf. Figure 2 illustrating a replacement of three observable events {a₁, a₂, a₃} with the encoding e(a₁) = 00, e(a₂) = 01, and e(a₃) = 10.

Fig. 2

The replacement of three observable events {a₁, a₂, a₃} with the encoding e(a₁) = 00, e(a₂) = 01, and e(a₃) = 10, and new states p₀ and p₁

Then G is current-state (initial-state) opaque with respect to Q_S, Q_NS, and $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$ if and only if $G^{\prime }$ is current-state (initial-state) opaque with respect to Q_S, Q_NS, and $P^{\prime }\colon [({\Sigma }-{\Gamma }_{o})\cup \{0,1\}]^{*} \to [({\Sigma }_{o}-{\Gamma }_{o})\cup \{0,1\}]^{*}$.

Proof

To show that G is current-state opaque if and only if $G^{\prime }$ is current-state opaque, we define the languages L_S = L_m(Q,Σ,δ, I, Q_S), L_NS = L_m(Q,Σ,δ, I, Q_NS), $L^{\prime }_{S}=L_{m}(Q^{\prime },({\Sigma }-{\Gamma }_{o})\cup \{0,1\},\delta ^{\prime },I,Q_{S})$, and $L^{\prime }_{NS}=L_{m}(Q^{\prime },({\Sigma }-{\Gamma }_{o})\cup \{0,1\},\delta ^{\prime },I,Q_{NS})$. Using Lemma 1, we now need to show that $P(L_{S})\subseteq P(L_{NS})$ if and only if $P^{\prime }(L^{\prime }_{S})\subseteq P^{\prime }(L^{\prime }_{NS})$. To this end, we define a morphism $f\colon {\Sigma }^{*} \to (({\Sigma }-{\Gamma }_{o})\cup \{0,1\})^{*}$ so that f(a) = e(a) for a ∈Γ_o, and f(a) = a for a ∈Σ−Γ_o. By the definition of e and the construction of $G^{\prime }$, for any string w, we have that w ∈ L(G) if and only if $f(w) \in L(G^{\prime })$. In particular, P(w) ∈ P(L_S) if and only if $P^{\prime }(f(w)) \in P^{\prime }(L^{\prime }_{S})$, and P(w) ∈ P(L_NS) if and only if $P^{\prime }(f(w)) \in P^{\prime }(L^{\prime }_{NS})$, which completes this part of the proof.

To show that G is initial-state opaque if and only if $G^{\prime }$ is initial-state opaque, we define the languages L_S = L(Q,Σ,δ, Q_S), L_NS = L(Q,Σ,δ, Q_NS), $L^{\prime }_{S}=L(Q^{\prime },({\Sigma }-{\Gamma }_{o})\cup \{0,1\},\delta ^{\prime },Q_{S})$, and $L^{\prime }_{NS}=L(Q^{\prime },({\Sigma }-{\Gamma }_{o})\cup \{0,1\},\delta ^{\prime },Q_{NS})$. Since this transforms initial-state opacity to language-based opacity (Wu and Lafortune 2013), it is sufficient to show that $P(L_{S})\subseteq P(L_{NS})$ if and only if $P^{\prime }(L^{\prime }_{S})\subseteq P^{\prime }(L^{\prime }_{NS})$. However, this can be shown analogously as above. □

Notice that this binary encoding can be done in polynomial time, and that it preserves determinism.

4.1 Transformations between LBO and ISO

In this section, we discuss the transformations between language-based opacity and initial-state opacity. The transformation from initial-state opacity to language-based opacity has been provided by Wu and Lafortune (2013), as well as the transformation from language-based opacity to initial-state opacity for the case where both the secret and the non-secret language of the language-based opacity problem are prefix closed. We now extend the transformation from language-based opacity to initial-state opacity to the general case.

4.1.1 Transforming LBO to ISO

The language-based opacity problem consists of a DES G_LBO over Σ, a projection $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$, a secret language $L_{S} \subseteq L(G)$, and a non-secret language $L_{NS} \subseteq L(G)$. We transform it to a DES G_ISO in such a way that G_LBO is language-based opaque if and only if G_ISO is initial-state opaque.

Assume that the languages L_S and L_NS are represented by the non-blocking automata A_S = (Q_S,Σ_S, δ_S, I_S, F_S) and A_NS = (Q_NS,Σ_NS, δ_NS, I_NS, F_NS), respectively. Without loss of generality, we may assume that their sets of states are disjoint, that is, Q_S ∩ Q_NS = ∅.

Our transformation proceeds in two steps:

• 1. We construct a DES G_ISO with one additional observable event @.

• 2. We use Lemma 2 to reduce the number of observable events of G_ISO by one.

Since the second step follows from Lemma 2, we only describe the first step, that is, the construction of G_ISO over Σ ∪{@}, and the specification of the sets of secret states $Q^{\prime }_{S}$ and non-secret states $Q^{\prime }_{NS}$.

From the automata A_S and A_NS, we construct the automata G_S = (Q_S ∪{x_S},Σ_S, δ_S, I_S, Q_S ∪{x_S}) and G_NS = (Q_NS ∪{x_NS},Σ_NS, δ_NS, I_NS, Q_NS ∪{x_NS}) by adding two new states x_S and x_NS, and the following transitions, see Fig. 3 for an illustration of the construction:

• for every state q ∈ F_S, we add a new transition (q, @, x_S) to δ_S;

• for every state q ∈ F_NS, we add a new transition (q, @, x_NS) to δ_NS.

Fig. 3

Transforming LBO to ISO

Let $Q^{\prime }_{S} = I_{S}$ denote the set of secret initial states of G_ISO, and let $Q^{\prime }_{NS} = I_{NS}$ denote the set of non-secret initial states of G_ISO. We extend projection P to $P^{\prime }\colon ({\Sigma }\cup \{@\})^{*} \to ({\Sigma }_{o}\cup \{@\})^{*}$. Finally, let G_ISO denote the automata G_S and G_NS considered as a single NFA. Before we show that G_LBO is language-based opaque if and only if G_ISO is initial-state opaque, notice that the transformation can be done in polynomial time and that it preserves determinism.

Theorem 1

The DES G_LBO is language-based opaque with respect to L_S, L_NS, and P if and only if the DES G_ISO is initial-state opaque with respect to $Q^{\prime }_{S}$, $Q^{\prime }_{NS}$, and $P^{\prime }$.

Proof

We need to show that $P(L_{S})\subseteq P(L_{NS})$ if and only if $P^{\prime }(L(G_{S}))\subseteq P^{\prime }(L(G_{NS}))$.

However, by construction, $L(G_{S}) =\overline {L_{S}} \cup L_{S}@$ and $L(G_{NS})=\overline {L_{NS}} \cup L_{NS}@$, and hence $P(L_{S})\subseteq P(L_{NS})$ if and only if $P^{\prime }(L(G_{S}))\subseteq P^{\prime }(L(G_{NS}))$, which is if and only if G_ISO is initial-state opaque. □

We now provide an illustrative example.

Example 1

Let G₁ over Σ = {a, b, c} depicted in Fig. 4 (left) be the instance of the LBO problem with the secret language L_S = abb^∗ and the non-secret language L_NS = acb^∗. Our transformation of LBO to ISO then results in the DES $G_{1}^{\prime }$ depicted in Fig. 4 (right) with a new observable event @, a single secret initial state 1, and a single non-secret initial state 4. We distinguish two cases depending on whether event c is observable or not.

Fig. 4

An example of the transformation of the LBO problem (left) to the ISO problem (right)

In the first case, we assume that event c is unobservable. In this case, G₁ is language-based opaque, because $P(L_{S}) \subseteq P(L_{NS})$, and the reader can see that $P(L(G_{1}^{\prime },1)) = \overline {abb^{*}@} \subseteq \overline {ab^{*}@} = P(L(G_{1}^{\prime },4))$. Therefore, $G_{1}^{\prime }$ is initial-state opaque.

In the second case, we assume that event c is observable. In this case, G₁ is not language-based opaque, because ab ∈ P(L_S) whereas ab∉P(L_NS), and we can see that $ab\in L(G_{1}^{\prime },1)$ and $ab\not \in L(G_{1}^{\prime },4)$. Therefore, $G_{1}^{\prime }$ is not initial-state opaque.

4.1.2 The case of a single observable event

The second step of our construction, Lemma 2, requires that G_ISO has at least three observable events or, equivalently, that G_LBO has at least two observable events. Consequently, our transformation does not preserve the number of observable events if G_LBO has a single observable event. In fact, we show that there does not exist such a transformation unless P = NP, which is a longstanding open problem of computer science. Deciding language-based opacity for systems with a single observable event is coNP-complete (Holzer and Kutrib 2011; Stockmeyer and Meyer 1973). We show that deciding initial-state opacity for systems with a single observable event is NL-complete, and hence efficiently solvable on a parallel computer (Arora and Barak 2009). In particular, the problem can be solved in polynomial time.

Theorem 2

Deciding initial-state opacity for DESs with a single observable event is NL-complete.

Proof

Deciding initial-state opacity is equivalent to checking the inclusion of two prefix-closed languages. Namely, a DES G with Σ_o = {a} is initial-state opaque with respect to secret states Q_S and non-secret states Q_NS if and only if $K_{S}\subseteq K_{NS}$ for K_S = P(L(G, Q_S)) and K_NS = P(L(G, Q_NS)). Since the languages K_S and K_NS are prefix-closed, they are either finite, consisting of at most |Q| strings, or equal to {a}^∗.

To show that the problem belongs to NL, we show how to verify $K_{S} \not \subseteq K_{NS}$ in nondeterministic logarithmic space. Then, since NL is closed under complement (Immerman 1988; Szelepcsėnyi 1988), $K_{S} \subseteq K_{NS}$ belongs to NL. Thus, to check that $K_{S} \not \subseteq K_{NS}$ in nondeterministic logarithmic space, we guess k ∈{0,…,|Q|} in binary, store it in logarithmic space, and verify that a^k ∈ K_S and a^k∉K_NS. To verify a^k ∈ K_S, we guess a path in G step by step, storing only the current state, and counting the number of steps by decreasing k by one in each step; logarithmic space is sufficient for this. Since a^k∉K_NS belongs to the complement of NL, which coincides with NL, we can check a^k∉K_NS in nondeterministic logarithmic space as well.

To show that deciding initial-state opacity for DESs with a single observable event is NL-hard, we reduce the DAG reachability problem (Jones 1975): given a DAG G = (V, E) and nodes s, t ∈ V, the problem asks whether t is reachable from s.

From G, we construct a DES $\mathcal {A}=(V\cup \{i\},\{a\},\delta ,\{s,i\})$, where i is a new initial state and a is an observable event, as follows. With each node of G, we associate a state in $\mathcal {A}$. Whenever there is an edge from j to k in G, we add an a-transition from j to k to $\mathcal {A}$. We add a self-loop labeled by a to state t and to state i. The set of secret initial states is Q_S = {i} and the set of non-secret initial states Q_NS = {s}. Then, $\mathcal {A}$ is initial-state opaque if and only if there is a path from s to t in G. Indeed, $L(\mathcal A,i)=\{a\}^{*}$ is included in $L(\mathcal A,s)$ if and only if $L(\mathcal A,s)=\{a\}^{*}$, which is if and only if t is reachable from s. □

4.1.3 Algorithmic complexity of deciding LBO

The algorithmic complexity of deciding whether a given DES is language-based opaque with respect to given secret and non-secret languages has been investigated in the literature. Lin (2011) suggested an algorithm with the complexity O(2²ⁿ), where n is the order of the state spaces of the automata representing the secret and non-secret languages. The same complexity has been achieved by Wu and Lafortune (2013) using the transformation to current-state opacity. We improve this complexity.

Theorem 3

The time complexity of deciding whether a DES G is language-based opaque with respect to a projection P, a secret language $L_{S} \subseteq L(G)$, and a non-secret language $L_{NS} \subseteq L(G)$ is $O(m\ell 2^{n_{2}} + n_{1}2^{n_{2}})$, where n₁ is the number of states of the automaton recognizing L_S, n₂ is the number of states recognizing L_NS, $m\le \ell {n_{1}^{2}}$ is the number of transitions of an NFA recognizing P(L_S), and ℓ is the number of observable events.

Proof

Let G_S and G_NS be automata recognizing L_S and L_NS with n₁ and n₂ states, respectively. Then $P(L_{S})\subseteq P(L_{NS})$ if and only if P(L_S) ∩co-P(L_NS) = ∅, where co-P(L_NS) stands for Σ^∗− P(L_NS). We represent P(L_S) by the projected automaton P(G_S) with m transitions and at most n₁ states, and co-P(L_NS) by the complement of the observer of G_NS, denoted by co-$G_{NS}^{obs}$, which has at most $2^{n_{2}}$ states and $\ell 2^{n_{2}}$ transitions. The problem is now equivalent to checking whether the language of $P(G_{S}) \cap \text {co-}G_{NS}^{obs}$ is empty, which means to search the structure for a reachable marked state. Since P(G_S) has at most n₁ states and $m\le \ell {n_{1}^{2}}$ transitions, the structure has $O(m\ell 2^{n_{2}} + n_{1}2^{n_{2}})$ transitions and states, which completes the proof. □

4.2 Transformations between CSO and INSO

In this section, we provide the transformations between current-state opacity and infinite-step opacity. To the best of our knowledge, no transformations between current-state opacity and infinite-step opacity have been discussed in the literature so far.

4.2.1 Transforming CSO to INSO

We first focus on the transformation from current-state opacity to infinite-step opacity. The problem of deciding current-state opacity consists of a DES G_CSO = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, and a set of non-secret states $Q_{NS} \subseteq Q$. From G_CSO, we construct a DES G_INSO over the alphabet Σ ∪{u}, where u is a new unobservable event. Specifically, we construct $G_{INSO}=(Q\cup \{q^{\star }\}, {\Sigma }\cup \{u\}, \delta ^{\prime }, I)$ from G_CSO by adding a new state q^⋆ that is neither secret nor non-secret, and by defining $\delta ^{\prime }$ as follows, see Fig. 5 for an illustration:

• 1. $\delta ^{\prime } = \delta$, that is, $\delta ^{\prime }$ is initialized as δ and further extended as follows;

• 2. for each state q ∈ Q_NS, we add a transition (q, u, q^⋆) to $\delta ^{\prime }$;

• 3. for each a ∈Σ, we add a self-loop (q^⋆, a, q^⋆) to $\delta ^{\prime }$.

We extend the projection P to the projection $P^{\prime }\colon ({\Sigma }\cup \{u\})^{*} \to {\Sigma }_{o}^{*}$. The sets Q_S and Q_NS remain unchanged.

Fig. 5

Transforming CSO to INSO

Notice that the transformation preserves the number of observable events and determinism, and that it requires only logarithmic space. It remains to show that G_CSO is current-state opaque if and only if G_INSO is infinite-step opaque.

Theorem 4

The DES G_CSO is current-state opaque with respect to Q_S, Q_NS, and P if and only if the DES G_INSO is infinite-step opaque with respect to Q_S, Q_NS, and $P^{\prime }$.

Proof

Assume first that G_CSO is not current-state opaque. Since the new state q^⋆ is neither secret nor non-secret, we have that G_INSO is not current-state opaque either. Consequently, G_INSO is not infinite-step opaque.

On the other hand, assume that G_CSO is current-state opaque. Since the new state q^⋆ is neither secret nor non-secret, we have that G_INSO is current-state opaque as well. Let st ∈ L(G_INSO) be such that $\delta ^{\prime }(\delta ^{\prime }(I, s)\cap Q_{S}, t) \neq \emptyset$; in particular, $\delta ^{\prime }(I, s)\cap Q_{S} \neq \emptyset$. Then, since G_INSO is current-state opaque, there exists $s^{\prime }\in L(G_{INSO})$ such that $P^{\prime }(s^{\prime })=P^{\prime }(s)$ and $\delta ^{\prime }(I,s^{\prime })\cap Q_{NS} \neq \emptyset$. By construction, $s^{\prime }$ can be extended by the string ut using the transitions to state q^⋆ followed by self-loops in state q^⋆. Therefore, $\delta ^{\prime } (\delta ^{\prime }(I,s^{\prime })\cap Q_{NS}, ut) \neq \emptyset$ and $P^{\prime }(st) = P^{\prime }(sut)$, which shows that G_INSO is infinite-step opaque. □

We now illustrate the construction in the following example.

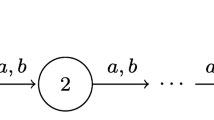
Example 2

Let G₂ over Σ = {a, b, c} depicted in Fig. 6 (left) be the instance of the CSO problem with the set of secret states Q_S = {2} and the set of non-secret states Q_NS = {5}. Our transformation of CSO to INSO then results in the DES $G_{2}^{\prime }$ depicted in Fig. 6 (right) with a new state q^⋆ and a new unobservable event u. We distinguish two cases depending on whether event c is observable or not.

Fig. 6

An example of the transformation of the CSO problem (left) to the INSO problem (right)

If event c is unobservable, then G₂ is current-state opaque, because the only string leading to a secret state, state 2, is the string a, for which the string ac leading to the non-secret state, state 5, satisfies that P(a) = P(ac). Then, the reader can see that $G_{2}^{\prime }$ is infinite-step opaque, because the only possible extensions of the string a from the secret state 2 are of the form b^k, for $k\in \mathbb {N}$, and for every such extension there is an extension ub^k of the string ac from the non-secret state 5 such that P(ab^k) = P(acub^k).

If event c is observable, then G₂ is not current-state opaque, because the only string leading to a non-secret state, string ac, has a different observation then the string a leading to the secret state, that is, P(ac)≠P(a). Consequently, the reader can verify that $G_{2}^{\prime }$ is not current-state opaque, and hence neither infinite-step opaque.

4.2.2 Transforming INSO to CSO

Transforming infinite-step opacity to current-state opacity is technically more involved. The problem of deciding infinite-step opacity consists of a DES G_INSO = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\rightarrow {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, and a set of non-secret states $Q_{NS}\subseteq Q$. From G_INSO, we construct a DES G_CSO in the following two steps:

• 1. We construct a DES G_CSO such that G_CSO is current-state opaque if and only if G_INSO is infinite-step opaque. In this step of the construction, G_CSO has one observable event more than G_INSO.

• 2. To reduce the number of observable events by one, we apply Lemma 2. Consequently, the resulting DES has the same number of observable events as G_INSO, if G_INSO has at least two observable events, is deterministic if and only if G_CSO is, and is current-state opaque if and only if G_CSO is.

We now describe the construction of $G_{CSO}=(Q\cup Q^{+}\cup Q^{-},{\Sigma }\cup \{@\},\delta ^{\prime },I)$, where Q⁺ = {q⁺∣q ∈ Q}, Q⁻ = {q⁻∣q ∈ Q}, and @ is a new observable event. To this end, we first make two disjoint copies of G_INSO, denoted by G_S and G_NS, where the set of states of G_S is denoted by $Q_{S}^{\prime }=Q^{+}$ and the set of states of G_NS is denoted by $Q_{NS}^{\prime }=Q^{-}$. The DES G_CSO is taken as the disjoint union of the automata G_INSO, G_S, and G_NS, see Fig. 7 for an illustration. Furthermore, for every state q ∈ Q_S, we add the transition (q, @, q⁺) and, for every state q ∈ Q_NS, we add the transition (q, @, q⁻). The set of secret states of G_CSO is $Q_{S}^{\prime }$ and the set of non-secret states of G_CSO is $Q_{NS}^{\prime }$. We extend projection P to $P^{\prime }\colon ({\Sigma }\cup \{@\})^{*} \to ({\Sigma }_{o}\cup \{@\})^{*}$.

Fig. 7

Transforming INSO to CSO

Notice that G_CSO is deterministic if and only if G_INSO is, and that logarithmic space is sufficient for the construction of G_CSO. As already pointed out, however, the construction does not preserve the number of observable events, which requires the second step of the construction using Lemma 2 as described above.

We now show that G_INSO is infinite-step opaque if and only if G_CSO is current-state opaque.

Theorem 5

The DES G_INSO is infinite-step opaque with respect to Q_S, Q_NS, and P if and only if the DES G_CSO is current-state opaque with respect to $Q_{S}^{\prime }$, $Q_{NS}^{\prime }$, and $P^{\prime }\colon ({\Sigma }\cup \{@\})^{*} \to ({\Sigma }_{o}\cup \{@\})^{*}$.

Proof

Assume that G_INSO is infinite-step opaque. We show that G_CSO is current-state opaque. To this end, consider a string w such that $\delta ^{\prime }(I,w)\cap Q_{S}^{\prime } \neq \emptyset$. We want to show that there exists $w^{\prime }$ such that $P^{\prime }(w)=P^{\prime }(w^{\prime })$ and $\delta ^{\prime }(I,w^{\prime })\cap Q_{NS}^{\prime } \neq \emptyset$. However, since $Q_{S}^{\prime }=Q^{+}$, w is of the form w₁@w₂. Then, by the construction, δ(I, w₁) contains a secret state of G_INSO, say q ∈ δ(I, w₁) ∩ Q_S, such that state q⁺ is a copy of state q reached under @ from state q in G_CSO, and w₂ is read from state q⁺ in the copy G_S of G_INSO. That is, w₂ can be read from state q in G_INSO, and hence δ(I, w₁w₂)≠∅. Altogether, δ(δ(I, w₁) ∩ Q_S, w₂)≠∅ and the fact that G_INSO is infinite-step opaque imply that there exists a string $w_{1}^{\prime }w_{2}^{\prime } \in L(G_{INSO})$ such that $P(w_{1})=P(w_{1}^{\prime })$, $P(w_{2})=P(w_{2}^{\prime })$, and $\delta (\delta (I,w_{1}^{\prime })\cap Q_{NS}, w_{2}^{\prime }) \neq \emptyset$. Let $w^{\prime }=w_{1}^{\prime }@w_{2}^{\prime }$. Then $P^{\prime }(w)=P^{\prime }(w^{\prime })$ and, by the construction, $\emptyset \neq \delta ^{\prime }(\delta ^{\prime }(I,w_{1}^{\prime }@)\cap Q_{NS}^{\prime }, w_{2}^{\prime }) \subseteq Q_{NS}^{\prime }$, which completes the proof.

On the other hand, assume that G_INSO is not infinite-step opaque, that is, there exists a string st ∈ L(G_INSO) such that δ(δ(I, s) ∩ Q_S, t)≠∅ and for every $s^{\prime }t^{\prime } \in L(G_{INSO})$ with $P(s)=P(s^{\prime })$ and $P(t)=P(t^{\prime })$, $\delta (\delta (I,s^{\prime })\cap Q_{NS}, t^{\prime }) = \emptyset$. But then for s@t ∈ L(G_CSO), we have that $\emptyset \neq \delta ^{\prime }(\delta ^{\prime }(I,s@)\cap Q_{S}^{\prime },t) = \delta ^{\prime }(I,s@t) \subseteq Q_{S}^{\prime }$ and, for every $s^{\prime }@t^{\prime } \in L(G_{CSO})$ such that $P^{\prime }(s@t)=P^{\prime }(s^{\prime }@t^{\prime })$, we have that $\delta ^{\prime }(I,s^{\prime }@t^{\prime }) \cap Q_{NS}^{\prime } = \delta ^{\prime } (\delta ^{\prime }(I,s^{\prime }@)\cap Q_{NS}^{\prime }, t^{\prime }) = \emptyset$, which shows that G_CSO is not current-state opaque. □

We now illustrate the construction.

Example 3

Let G₃ over Σ = {a, b, c} depicted in Fig. 8 (left) be the instance of the INSO problem with the set of secret states Q_S = {2} and the set of non-secret states Q_NS = {4}. Our transformation of INSO to CSO then results in the DES $G_{3}^{\prime }$ depicted in Fig. 8 (right) with a new observable event @, the set of secret states $Q_{S}^{\prime }$, and the set of non-secret states $Q_{NS}^{\prime }$. We again consider two cases based on the observability status of event c.

Fig. 8

An example of the transformation of the INSO problem (left) to the CSO problem (right)

If event c is unobservable, then G₃ is infinite-step opaque. Indeed, the only string leading to the single secret state, state 2, is the string a. The same string leads to the single non-secret state, state 4. Then, any possible extension of the string a from the unique secret state 2 is the string b^k, for $k\in \mathbb {N}$, which reaches state 3. However, for any such extension, there is the extension cb^k from the non-secret state 4 with P(ab^k) = P(acb^k). The reader can further see that $G_{3}^{\prime }$ is current-state opaque, because it can enter a secret state only after generating a string of the form a@b^k, $k\in \mathbb {N}$, in which case $\delta ^{\prime }(1,P^{-1}(a@))=\{2^{+},4^{-},5^{-}\}$ and $\delta ^{\prime }(1,P^{-1}(a@b^{k}))=\{3^{+},5^{-}\}$ for k ≥ 1.

If event c is observable, then G₃ is not infinite-step opaque, because after generating string ab, the intruder can deduce that the system was in the secret state 2. Similarly, after generating string a@b, system $G_{3}^{\prime }$ ends up in the only state 3⁺, which is a secret state, and hence $G_{3}^{\prime }$ is not current-state opaque.

4.2.3 The case of a single observable event

To preserve the number of observable events, our transformation of infinite-step opacity to current state opacity relies on Lemma 2. This lemma requires at least two observable events in G_INSO, and hence it is not applicable to systems with a single observable event. For these systems, we provide a different transformation that requires to add at most a quadratic number of new states.

The problem of deciding infinite-step opacity for systems with a single observable event consists of a DES G_INSO = (Q,Σ,δ, I) with Σ_o = {a}, a set of secret states $Q_{S}\subseteq Q$, a set of non-secret states $Q_{NS}\subseteq Q$, and a projection P : Σ^∗→{a}^∗.

We denote the number of states of G_INSO by n, and define a function $\varphi \colon Q \rightarrow${0,…,n} that assigns, to every state q, the maximal number k ∈{0,…,n} of observable steps that are possible from state q; formally, $\varphi (q)=\max \limits \left \{ k\in \{0,\ldots ,n\} \mid \delta (q,P^{-1}(a^{k}))\neq \emptyset \right \}$.

From G_INSO, we construct a DES $G_{CSO}=(Q^{\prime }, {\Sigma }, \delta ^{\prime }, I)$ as illustrated in Fig. 9, where $\delta ^{\prime }$ is initialized as δ and modified as follows. For every state p ∈ Q with φ(p) > 0, we add n new states p₁,…,p_n to $Q^{\prime }$ and n new transitions (p, a, p₁) and (p_i, a, p_i+ 1), for $i=1,\dots , n-1$, to $\delta ^{\prime }$. Finally, we replace every transition (p, a, r) in $\delta ^{\prime }$ by the transition (p_n, a, r). Notice that the transformation requires to add at most n² states, and hence it can be done in polynomial time. Let $Q^{\prime }_{S}=Q_{S}$ and $Q^{\prime }_{NS}=Q_{NS}$. For every state p ∈ Q_S with φ(p) = k > 0, we add the corresponding states p₁,…,p_k to $Q^{\prime }_{S}$. Analogously, for p ∈ Q_NS with φ(p) = k > 0, we add p₁,…,p_k to $Q^{\prime }_{NS}$.

Fig. 9

Transforming INSO to CSO for systems with a single observable event

Notice that the transformation can be done in polynomial time, preserves the number of observable events, and determinism. However, whether the transformation can be done in logarithmic space is open. Even if the DES had no unobservable event, to determine whether φ(⋅) = n is equivalent to the detection of a cycle. The detection of a cycle is NL-hard: We can reduce the DAG reachability problem as follows. Given a DAG G and two nodes s and t, we construct a DES $\mathcal {G}$ by associating a state with every node of G and an a-transition with every edge of G. Finally, we add an a-transition from t to s. Then t is reachable from s in G if and only if $\mathcal {G}$ contains a cycle. Since it is an open problem whether L= NL, it is an open problem whether φ can be computed in deterministic logarithmic space.

We show that G_INSO is infinite-step opaque if and only if G_CSO is current-state opaque.

Theorem 6

The DES G_INSO with a single observable event is infinite-step opaque with respect to Q_S, Q_NS, and P if and only if the DES G_CSO is current-state opaque with respect to $Q^{\prime }_{S}$, $Q^{\prime }_{NS}$, and P.

Proof

Assume that G_INSO is not infinite-step opaque. Then, there exists st ∈ L(G_INSO) with δ(δ(I, s) ∩ Q_S, t)≠∅ such that δ(δ(I, P^− 1P(s)) ∩ Q_NS, P^− 1P(t)) = ∅. Let f : Σ^∗→Σ^∗ be a morphism such that f(a) = a^n+ 1 and f(b) = b, for a≠b ∈Σ. Then, by construction, $\delta (I,s)= \delta ^{\prime }(I,f(s))$, and hence $\delta ^{\prime }(I,f(s)) \cap Q_{S}^{\prime } \neq \emptyset$. If δ(I, P^− 1P(s)) ∩ Q_NS = ∅, then $\delta (I,f(P^{-1}P(s)))\cap Q_{NS}^{\prime } = \emptyset$ because $\delta (I,s^{\prime }) = \delta ^{\prime }(I,f(s^{\prime }))$ for any $s^{\prime }\in P^{-1}P(s)$, and G_CSO is not current-state opaque. Otherwise, we denote by q_s ∈ δ(I, s) ∩ Q_S and q_ns ∈ δ(I, P^− 1P(s)) ∩ Q_NS the states with maximal φ(q_s) and φ(q_ns). Since G_INSO is not infinite-step opaque, φ(q_s) > φ(q_ns). Then, in G_CSO, q_s has exactly one outgoing observable transition and is followed by φ(q_s) = k secret states, while q_ns is followed by φ(q_ns) < k non-secret states. Therefore, $\delta ^{\prime }(I,f(s)a^{k}) \cap Q_{S}^{\prime }\neq \emptyset$ and $\delta ^{\prime }(I,f(s^{\prime })a^{k}) \cap Q_{NS}^{\prime }=\emptyset$ for any $s^{\prime }\in P^{-1}P(s)$, and hence G_CSO is not current-state opaque.

On the other hand, assume that G_INSO is infinite-step opaque, and that $\delta ^{\prime }(I,w)\cap Q_{S}^{\prime }\neq \emptyset$. We show that $\delta ^{\prime }(I,P^{-1}P(w))\cap Q_{NS} \neq \emptyset$. Consider a state $q_{s} \in \delta ^{\prime }(I,w) \cap Q_{S}^{\prime }$ and a path π in G_CSO leading to q_s under w. Denote by p the last state of π that corresponds to a state of G_INSO; that is, p is not a new state added by the construction of G_CSO. Since $q_{s}\in Q_{S}^{\prime }$, we have, by construction, that p ∈ Q_S. Then the choice of p partitions w = uv, where u, read along the path π, leads to state p, and v = a^ℓ is a suffix of length ℓ ≤ n. Let $u^{\prime }$ be a string such that $f(u^{\prime })=u$. Then $p\in \delta (I,u^{\prime })\cap Q_{S}$. Since φ(p) ≥ ℓ, there exists t such that P(t) = a^ℓ and $\delta (\delta (I,u^{\prime })\cap Q_{S},t) \neq \emptyset$ in G_INSO. Then infinite-step opacity of G_INSO implies that there exists $u^{\prime \prime }$ and $t^{\prime }$ such that $P(u^{\prime })=P(u^{\prime \prime })$, $P(t)=P(t^{\prime })$, and $\delta (\delta (I,u^{\prime \prime })\cap Q_{NS},t^{\prime }) \neq \emptyset$. In particular, there is a state $q_{ns}\in \delta (I,u^{\prime \prime })\cap Q_{NS}$ with φ(q_ns) ≥ ℓ, and $\delta ^{\prime }(I,f(u^{\prime \prime }))\cap Q_{NS}^{\prime } \neq \emptyset$. Therefore, $\delta ^{\prime }(I,f(u^{\prime \prime })a^{\ell })\cap Q_{NS}^{\prime } \neq \emptyset$ and $P(f(u^{\prime \prime })a^{\ell }) = P(uv) = P(w)$, which completes the proof. □

We now illustrate the construction.

Example 4

Let G₄ over Σ = {a, u} depicted in Fig. 10 (left) be the instance of the INSO problem with a single observable event Σ_o = {a}, the set of secret states Q_S = {1}, and the set of non-secret states Q_NS = {3}. Then, φ(1) = φ(3) = 3, and our transformation of INSO to CSO results in the DES $G_{4}^{\prime }$ depicted in Fig. 10 (right) with the set of secret states $Q_{S}^{\prime }$ and the set of non-secret states $Q_{NS}^{\prime }$. We consider two cases based on the presence of the unobservable transition (1,u,3) in G₄.

Fig. 10

An example of the transformation of the INSO problem with a single observable event (left) to the CSO problem (right)

We first assume that the transition (1,u,3) exists in G₄. Then, G₄ is infinite-step opaque, because any string a^k leading from the secret state 1 is indistinguishable from the string ua^k that leads the system to the non-secret state 3. The reader can see that $G_{4}^{\prime }$ is current-state opaque, because a secret state is reachable only under a string of the form a^k, for k ∈{0,1,2,3}, and for any such string there is an indistinguishable string ua^k reaching a non-secret state.

If the transition (1,u,3) does not exist in G₄, then G₄ is not infinite-step opaque, because it is neither current-state opaque and, obviously, neither $G_{4}^{\prime }$ is current-state opaque.

4.2.4 Improving the algorithmic complexity of deciding infinite-step opacity

Let G = (Q,Σ,δ, I, F) be a DES. We design an algorithm deciding infinite-step opacity in time O((n + mℓ)2ⁿ), where ℓ = |Σ_o| is the number of observable events, n is the number of states of G, and m is the number of transitions of P(G), m ≤ ℓn².

To decide whether G is infinite-step opaque with respect to $Q_{S},Q_{NS}\subseteq Q$, and $P\colon {\Sigma }^{*} \to {\Sigma }_{o}^{*}$, we proceed as follows:

• 1. We compute the observer $\mathcal G^{obs}$ of G in time O(ℓ2ⁿ) (Cassandras and Lafortune 2008);

• 2. We compute the projected automaton P(G) of G in time O(m + n) (Hopcroft and Ullman 1979);

• 3. We compute the product automaton $\mathcal C = P(G) \times \mathcal G^{obs}$ in time O((m + n) ⋅ ℓ2ⁿ) (Domaratzki and Salomaa 2007); – states of $\mathcal C$ are of the form Q × 2^Q;

• 4. For every reachable state X of $\mathcal G^{obs}$, we compute X_S = X ∩ Q_S and X_NS = X ∩ Q_NS;

  • (a) If X_S≠∅ and X_NS = ∅, then G is not infinite-step opaque; this is, actually, the standard check whether G is current-state opaque;

  • (b) Otherwise, for every state x ∈ X_S, we add a transition from X under @ to state (x, X_NS) of $\mathcal C$, and we add the state (x, X_NS) to set Y;

• 5. If $\mathcal C$ contains a state of the form (q, ∅) reachable from Y, then G is not infinite-step opaque; otherwise, G is infinite-step opaque.

Informally, we first make use of the standard check in the observer of G whether G is current-state opaque. If it is not, then it is neither infinite-step opaque. Otherwise, for every state X of the observer of G that contains both secret and non-secret states, we add a transition under the new event @ to a pair of a secret state x ∈ X and the set of all non-secret states X_NS of X. If a state of the form (q, ∅) is reachable from (x, X_NS), then G is not infinite-step opaque. Otherwise, G is infinite-step opaque. We now formally prove correctness.

Lemma 3

The DES G is infinite-step opaque if and only if G is current-state opaque and no state of the form (q, ∅) is reachable in $\mathcal C$ from the set Y.

Proof

Assume that G is not infinite-step opaque. Then, there exists st ∈ L(G) such that δ(δ(I, s) ∩ Q_S, t)≠∅ and δ(δ(I, P^− 1P(s)) ∩ Q_NS, P^− 1P(t)) = ∅. There are two cases:

• (i) either δ(I, P^− 1P(s)) ∩ Q_NS = ∅, in which case G is not current-state opaque, neither infinite-step opaque, and the algorithm detects this situation in the observer of G on line 4(a),

• (ii) or δ(I, P^− 1P(s)) ∩ Q_NS = Z≠∅. In this case, P(s)@ leads from the observer of G to the pairs (δ(I, P^− 1P(s)) ∩ Q_S) ×{Z} of the NFA $\mathcal {C}$. Since δ(I, st)≠∅, there exists (z, Z) ∈ (δ(I, P^− 1P(s)) ∩ Q_S) ×{Z} such that P(t) leads the projected automaton P(G) from state z to a state q. However, δ(Z, P^− 1P(t)) = ∅ implies that P(t) leads the observer of G from state Z to state ∅, and hence the pair (q, ∅) is reachable in $\mathcal {C}$ from a state of Y.

On the other hand, if G is infinite-step opaque, then it is current-state opaque, and we show that no state of the form (q, ∅) is reachable in $\mathcal C$ from a state of Y. For the sake of contradiction, assume that a state of the form (q, ∅) is reachable in $\mathcal {C}$ from a state of Y. Then, there must be a string s such that P(s) reaches a state X in the observer of G such that X_S = X ∩ Q_S contains a state z, X ∩ Q_NS = Z≠∅, there is a transition under @ from X to the pair (z, Z) of $\mathcal {C}$, and the NFA $\mathcal {C}$ reaches state (q, ∅) from (z, Z) under a string w. In particular, there must be a string t ∈ P^− 1(w) that moves G from state z to state q. But then δ(δ(I, s) ∩ Q_S, t)≠∅, and δ(δ(I, P^− 1P(s)) ∩ Q_NS, P^− 1(w)) = ∅, which means that G is not infinite-step opaque – a contradiction. □

Since our algorithm constructs and searches the NFA $\mathcal C$ that has O(n2ⁿ) states and O(mℓ2ⁿ) transitions, the overall time complexity of our algorithm is O((n + mℓ)2ⁿ).

We now illustrate the procedure in the following example.

Example 5

We consider system G₃ of Example 3 as depicted in Fig. 8 with all the events a, b, c observable, the set of secret states Q_S = {2}, and the set of non-secret states Q_NS = {4}. Then G₃ is current-state opaque, but not infinite-step opaque. To show that G₃ is not infinite-step opaque, our algorithm works as follows. First, notice that P(G₃) coincides with G₃, since there are no unobservable transitions in G₃. A relevant part of the observer of G₃ is depicted in Fig. 11 (left), and a relevant part of the automaton C, i.e., of the product of P(G₃) with the observer of G₃, is depicted in Fig. 11 (right). The only reachable state of the observer that has a nonempty intersection with Q_S = {2} is state X = {2,4}, resulting in X_S = {2} and X_NS = {4}. The algorithm then creates an @-transition from state X = {2,4} of the observer to state (2,{4}) of the product automaton C (the dashed transition in Fig. 11). Since state (3,∅) is reachable from state (2,{4}) in C, system G₃ is not infinite-step opaque; indeed, observing ab in G₃, the intruder knows for sure that the system was in a secret state.

Fig. 11

The relevant part of the observer of G₃ (left), the corresponding part of the automaton C (right), and the @-transition (dashed) added by the algorithm

On the other hand, we now assume that c is unobservable. To avoid confusion, we denote G₃ with a and b observable, c unobservable, the set of secret states Q_S = {2}, and the set of non-secret states Q_NS = {4} as $\tilde {G_{3}}$. Then $\tilde {G_{3}}$ is infinite-step opaque, and our algorithm works as follows. First, we construct $P(\tilde {G_{3}})$ as shown in Fig. 12. Relevant parts of the observer of $\tilde {G_{3}}$ and of the product of $P(\tilde {G_{3}})$ with the observer, automaton C, is depicted in Fig. 13.

Fig. 12

Projected automaton $P(\tilde {G_{3}})$

Fig. 13

The relevant part of the observer of $\tilde {G_{3}}$ (left), the corresponding part of the automaton C (right), and the @-transition (dashed) added by the algorithm

The only reachable state of the observer of $\tilde {G_{3}}$ with a nonempty intersection with Q_S = {2} is state X = {2,4,5}, resulting in X_S = {2} and X_NS = {4}. The algorithm creates an @-transition from state X = {2,4,5} of the observer to state (2,{4}) of the product automaton C (the dashed transition in Fig. 13). Since no state of the form (q, ∅) is reachable from state (2,{4}), $\tilde {G_{3}}$ is infinite-step opaque.

4.3 Transformations between CSO and K-SO

In this section, we describe the transformations between current-state opacity and K-step opacity. To the best of our knowledge, no such transformations have been considered in the literature so far.

4.3.1 Transforming CSO to K-SO

The transformation from current state opacity to K-step opacity is analogous to the transformation from current state opacity to infinite-step opacity of Section 4.2.1. Intuitively, the modification is that we need to make only K observable steps from any non-secret state instead of infinitely many such steps.

The problem of deciding current-state opacity consists of a DES G_CSO = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\to {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, and a set of non-secret states $Q_{NS} \subseteq Q$.

For a given $K\in \mathbb {N}$, from G_CSO, we construct a DES G_K-SO$=(Q\cup Q^{\star }, {\Sigma }\cup \{u\}, \delta ^{\prime }, I)$, where u is a new unobservable event, by adding K + 1 new states $Q^{\star }=\{q_{0}^{\star }, \ldots , q_{K}^{\star }\}$ that are neither secret nor non-secret, and by defining $\delta ^{\prime }$ as follows, see Fig. 14 for an illustration:

• 1. $\delta ^{\prime } = \delta$, that is, $\delta ^{\prime }$ is initialized as δ and further extended as follows;

• 2. for every state q ∈ Q_NS, we add the transition $(q,u,q_{0}^{\star })$ to $\delta ^{\prime }$;

• 3. for i = 0,…,K − 1 and every a ∈Σ_o, we add the transition $(q_{i}^{\star }, a, q_{i+1}^{\star })$ to $\delta ^{\prime }$.

We extend the projection P to the projection $P^{\prime }\colon ({\Sigma }\cup \{u\})^{*} \to {\Sigma }_{o}^{*}$. The sets Q_S and Q_NS remain unchanged.

Fig. 14

Transforming CSO to K-SO

Theorem 7

The DES G_CSO is current-state opaque with respect to Q_S, Q_NS, and P if and only if the DES G_K-SO is K-step opaque with respect to Q_S, Q_NS, $P^{\prime }$, and K.

Proof

Assume first that G_CSO is not current-state opaque. Since the new states $q_{0}^{\star },\ldots , q_{K}^{\star }$ are neither secret nor non-secret, G_K-SO is not current-state opaque either, and hence G_K-SO is not K-step opaque.

On the other hand, assume that G_CSO is current-state opaque. Since the new states $q_{0}^{\star },\ldots , q_{K}^{\star }$ are neither secret nor non-secret, G_K-SO is current-state opaque as well. Let st ∈ L(G_K-SO) be such that |P(t)|≤ K and $\delta ^{\prime }(\delta ^{\prime }(I, s)\cap Q_{S}, t) \neq \emptyset$. Then, since G_K-SO is current-state opaque, there is $s^{\prime }\in P^{-1}P(s)$ such that $\delta ^{\prime }(I,s^{\prime })\cap Q_{NS} \neq \emptyset$. By construction, we can extend $s^{\prime }$ by the string uP(t) using the transitions through the new states $q_{0}^{\star },\ldots ,q_{K}^{\star }$, that is, $\delta ^{\prime } (\delta ^{\prime }(I,s^{\prime })\cap Q_{NS}, uP(t)) \neq \emptyset$, and hence G_K-SO is K-step opaque. □

We now illustrate the construction.

Example 6

Let G₂ over Σ = {a, b, c} depicted in Fig. 15 (left) be the instance of the CSO problem from Example 2 with the set of secret states Q_S = {2} and the set of non-secret states Q_NS = {5}. Our transformation of CSO to K-SO then results in the DES $G_{2}^{\prime \prime }$ depicted in Fig. 15 (right) with K = 2, a new unobservable event u, and three new states $q_{0}^{\star }$, $q_{1}^{\star }$, and $q_{2}^{\star }$. We again distinguish two cases depending on whether event c is observable or not.

Fig. 15

An example of the transformation of the CSO problem (left) to the K-SO problem (right)

If c is unobservable, G₂ is current-state opaque as shown in Example 2. The reader can see that $G_{2}^{\prime \prime }$ is then 2-step opaque, because the only possible extensions of the string a from the secret state 2 are of the form b^k, for $k\in \mathbb {N}$, and for those extensions where k ≤ 2, there is an extension ub^k of the string ac from the non-secret state 5 such that P(ab^k) = P(acub^k).

If c is observable, then G₂ is not current-state opaque as shown in Example 2. Consequently, the reader can verify that $G_{2}^{\prime \prime }$ is not current-state opaque, and hence neither 2-step opaque.

4.3.2 Transforming K-SO to CSO

Transforming K-step opacity to current-state opacity is again similar to the transformation of infinite-step opacity to current-state opacity. Again, we only need to check K subsequent steps instead of all the subsequent steps. The problem of deciding K-step opacity consists of a DES G_K-SO = (Q,Σ,δ, I), a projection $P\colon {\Sigma }^{*}\rightarrow {\Sigma }_{o}^{*}$, a set of secret states $Q_{S}\subseteq Q$, and a set of non-secret states $Q_{NS}\subseteq Q$. From G_K-SO, we construct a DES G_CSO in the following two steps:

• 1. We construct a DES G_CSO such that G_CSO is current-state opaque if and only if G_K-SO is K-step opaque. In this step of the construction, G_CSO has one observable event more than G_K-SO.

• 2. To reduce the number of observable events by one, we apply Lemma 2. Consequently, the resulting DES has the same number of observable events as G_K-SO, if G_K-SO has at least two observable events, is deterministic if and only if G_CSO is, and is current-state opaque if and only if G_CSO is.

We now describe the construction of $G_{CSO}=(Q\cup Q^{+}\cup Q^{-}\cup Q^{\star },{\Sigma }\cup \{u,@\},\delta ^{\prime },I)$, where Q⁺ = {q⁺∣q ∈ Q}, Q⁻ = {q⁻∣q ∈ Q}, $Q^{\star }=\{q^{\star }_{0},\ldots , q^{\star }_{K+1}\}$, @ is a new observable event, and u is a new unobservable event. To this end, we first make two disjoint copies of G_K-SO, denoted by G⁺ and G⁻, where the set of states of G⁺ is denoted by Q⁺ and the set of states of G⁻ is denoted by Q⁻. The DES G_CSO is now taken as the disjoint union of the automata G_K-SO, G⁺, and G⁻, see Fig. 16 for an illustration. We now add K + 2 new states $q_{0}^{\star },\ldots , q_{K+1}^{\star }$ to G_CSO and the following transitions. For every state q ∈ Q_S, we add the transition (q, @, q⁺), for every state q ∈ Q_NS, we add the transition (q, @, q⁻), for every q⁻∈ Q⁻, we add the transition $(q^{-}, u,q_{0}^{\star })$, for every a ∈Σ_o and $i=0,\dots , K$, we add the transition $(q_{i}^{\star },a,q_{i+1}^{\star })$, and, finally, we add the self-loop $(q_{K+1}^{\star },a,q_{K+1}^{\star })$ for every a ∈Σ_o. The set of secret states of G_CSO is the $Q_{S}^{\prime }=Q^{+}$ and the set of non-secret states of G_CSO is the set $Q_{NS}^{\prime }=\{q_{0}^{\star },q_{K+1}^{\star }\}$. We extend projection P to $P^{\prime }\colon ({\Sigma }\cup \{@, u\})^{*} \to ({\Sigma }_{o}\cup \{@\})^{*}$.

Fig. 16

Transforming K-SO to CSO

Notice that G_CSO is deterministic if and only if G_K-SO is, and that logarithmic space is sufficient for the construction of G_CSO. However, as already pointed out, the construction does not preserve the number of observable events, which requires the second step of the construction using Lemma 2.

We now show that G_K-SO is K-step opaque if and only if G_CSO is current-state opaque.

Theorem 8

The DES G_K-SO is K-step opaque with respect to Q_S, Q_NS, and P if and only if the DES G_CSO is current-state opaque with respect to $Q_{S}^{\prime }$, $Q_{NS}^{\prime }$, and $P^{\prime }\colon ({\Sigma }\cup \{@,u\})^{*} \to ({\Sigma }_{o}\cup \{@\})^{*}$.

Proof

Assume that G_K-SO is K-step opaque. We show that G_CSO is current-state opaque. To this end, consider a string w such that $\delta ^{\prime }(I,w)\cap Q_{S}^{\prime } \neq \emptyset$. We want to show that there exists $w^{\prime}\in P^{\prime}{-1}P^{\prime}(w)$ such that $\delta ^{\prime }(I,w^{\prime })\cap Q_{NS}^{\prime } \neq \emptyset$. However, since $Q_{S}^{\prime }=Q^{+}$, w is of the form w₁@w₂ and, by the construction, δ(I, w₁) contains a secret state of G_K-SO. Since G is K-step opaque, there exists a string $w_{1}^{\prime } \in P^{-1}P(w_{1})$ such that $\delta (I,w_{1}^{\prime })\cap Q_{NS} \neq \emptyset$. Then, because w₂ can be read in the copy of G_K-SO from a state q⁺ for a state q ∈ δ(I, w₁) ∩ Q_S, we further have that δ(δ(I, w₁) ∩ Q_S, w₂)≠∅. If |P(w₂)|≤ K, then K-step opacity of G_K-SO implies that there exists a string $w_{1}^{\prime \prime }w_{2}^{\prime \prime } \in L(G_{\text {K-SO}})$ such that $P(w_{1}^{\prime \prime })=P(w_{1})$, $P(w_{2}^{\prime \prime })=P(w_{2})$, and $\delta (\delta (I,w_{1}^{\prime \prime })\cap Q_{NS}, w_{2}^{\prime \prime }) \neq \emptyset$. By construction, $q_{0}^{\star } \in \delta ^{\prime } (\delta ^{\prime }(I,w_{1}^{\prime \prime }@)\cap Q_{NS}, w_{2}^{\prime \prime }u)$, and hence G_CSO is current-state opaque. If |P(w₂)| > K, then $q_{K+1}^{\star } \in \delta ^{\prime } (\delta ^{\prime }(I,w_{1}^{\prime \prime }@)\cap Q_{NS}, uP(w_{2}^{\prime \prime }))$, and hence G_CSO is current-state opaque.

On the other hand, assume that G_K-SO is not K-step opaque, that is, there exists a string st ∈ L(G_K-SO) such that |P(t)|≤ K, δ(δ(I, s) ∩ Q_S, t)≠∅ and, for every $s^{\prime }\in P^{-1}P(s)$ and $t^{\prime }\in P^{-1}P(t)$, $\delta (\delta (I,s^{\prime })\cap Q_{NS}, t^{\prime }) = \emptyset$. But then, for s@t ∈ L(G_CSO), we have that $\delta ^{\prime }(\delta ^{\prime }(I,s@)\cap Q_{S}^{\prime },t) \cap Q_{S}^{\prime } \neq \emptyset$ and, for every $s^{\prime }@t^{\prime } \in L(G_{CSO})$ such that $P^{\prime }(s@t)=P^{\prime }(s^{\prime }@t^{\prime })$, we have two cases:

• (i) If $\delta (I,s^{\prime }) \cap Q_{NS} = \emptyset$, then $\delta ^{\prime }(I,s^{\prime }@t^{\prime }) \cap Q_{NS}^{\prime } = \delta ^{\prime } (\delta ^{\prime }(I,s^{\prime }@)\cap Q^{-}, t^{\prime }) = \delta ^{\prime } (\emptyset , t^{\prime }) = \emptyset$, which shows that G_CSO is not current-state opaque.

• (ii) If $\delta (I,s^{\prime }) \cap Q_{NS} \neq \emptyset$, then $\delta ^{\prime }(I,s^{\prime }@t^{\prime }) \cap Q_{NS}^{\prime } = \delta ^{\prime } (\delta ^{\prime }(I,s^{\prime }@)\cap Q^{-}, t^{\prime }) = \emptyset$, because inserting u to any strict prefix of $t^{\prime }$ may reach $q_{0}^{\star }$ but has to leave it when the rest of $t^{\prime }$ is read, and the rest (neither $P(t^{\prime })$) is not long enough to reach state $q_{K+1}^{\star }$. Therefore, G_CSO is not current-state opaque.

□

We now illustrate the construction.

Example 7

Let G₃ over Σ = {a, b, c} depicted in Fig. 17 (left) be the instance of the K-SO problem from Example 3 with K = 2, the set of secret states Q_S = {2}, and the set of non-secret states Q_NS = {4}. Our transformation of K-SO to CSO then results in the DES $G_{3}^{\prime \prime }$ depicted in Fig. 17 (right) with a new observable event @, a new unobservable event u, the set of secret states $Q_{S}^{\prime }$, and the set of non-secret states $Q_{NS}^{\prime }$. We consider two cases based on the observability status of event c.

Fig. 17

An example of the transformation of the K-SO problem (left) to the CSO problem (right)

If c is unobservable, then G₃ is 2-step opaque, because it is infinite-step opaque as shown in Example 3. The reader can further see that $G_{3}^{\prime \prime }$ is current-state opaque, because it can enter a secret state only after generating a string of the form a@b^k, for $k\in \mathbb {N}$, in which case we have that $\delta ^{\prime }(1,P^{-1}(a@))=\{2^{+},4^{-},5^{-},q_{0}^{\star }\}$ and $\delta ^{\prime }(1,P^{-1}(a@b^{k}))=\{3^{+},5^{-},q_{0}^{\star },\ldots ,q_{i}^{\star }\}$ for k ≥ 1, where $i=\min \limits \{k, 3\}$.

If c is observable, then G₃ is not 2-step opaque, because after generating string ab, the intruder can deduce that the system was in the secret state 2. Similarly, after generating string a@b, system $G_{3}^{\prime \prime }$ ends up in the only state 3⁺, which is a secret state, and hence $G_{3}^{\prime \prime }$ is not current-state opaque.

4.3.3 The case of a single observable event

To preserve the number of observable events, our transformation of K-step opacity to current state opacity relies on Lemma 2. This lemma requires at least two observable events in G_K-SO, and hence it is not applicable to systems with a single observable event. For these systems, we provide a different transformation that requires to add at most a quadratic number of new states.

The problem of deciding K-step opacity for systems with a single observable event consists of a DES G_K-SO = (Q,Σ,δ, I) with Σ_o = {a}, a set of secret states $Q_{S}\subseteq Q$, a set of non-secret states $Q_{NS}\subseteq Q$, and a projection P : Σ^∗→{a}^∗. We denote the number of states of G_K-SO by n, and define a function $\varphi \colon Q \rightarrow \{0,\ldots ,K\}$ that assigns, to every state q, the maximal number k ∈{0,…,K} of observable steps that are possible from state q; formally, $\varphi (q)=\max \limits \left \{ k\in \{0,\ldots ,K\} \mid \delta (q,P^{-1}(a^{k}))\neq \emptyset \right \}$. Notice that if K > n − 1, then a system with a single observable event is K-step opaque if and only if it is infinite-step opaque. Therefore, we may consider only K ≤ n − 1.

From G_K-SO, we construct a DES $G_{CSO}=(Q^{\prime }, {\Sigma }, \delta ^{\prime }, I)$ as illustrated in Fig. 18, where $\delta ^{\prime }$ is initialized as δ and modified as follows. For every state p ∈ Q with φ(p) > 0, we add K new states p₁,…,p_K to $Q^{\prime }$ and K new transitions (p, a, p₁) and (p_i, a, p_i+ 1), for $i=1,\dots , K-1$, to $\delta ^{\prime }$. Finally, we replace every transition (p, a, r) in $\delta ^{\prime }$ by the transition (p_K, a, r). Notice that the transformation requires to add at most n² states, and hence it can be done in polynomial time. Let $Q^{\prime }_{S}=Q_{S}$ and $Q^{\prime }_{NS}=Q_{NS}$. For every state p ∈ Q_S with φ(p) = k > 0, we add the corresponding states p₁,…,p_k to $Q^{\prime }_{S}$ and, for every p ∈ Q_NS with φ(p) = k > 0, we add p₁,…,p_k to $Q^{\prime }_{NS}$.

Fig. 18

Transforming K-SO to CSO for systems with a single observable event

Notice that the transformation can be done in polynomial time, preserves the number of observable events, and determinism. However, whether the transformation can be done in logarithmic space is open.

We show that G_K-SO is K-step opaque if and only if G_CSO is current-state opaque.

Theorem 9

The DES G_K-SO with a single observable event is K-step opaque with respect to Q_S, Q_NS, and P if and only if the DES G_CSO is current-state opaque with respect to $Q^{\prime }_{S}$, $Q^{\prime }_{NS}$, and P.

Proof

Assume that G_K-SO is not K-step opaque, that is, there is st ∈ L(G_K-SO) with |P(t)|≤ K such that δ(δ(I, s) ∩ Q_S, t)≠∅ and δ(δ(I, P^− 1P(s)) ∩ Q_NS, P^− 1P(t)) = ∅. Let f : Σ^∗→Σ^∗ be a morphism such that f(a) = a^K+ 1 and f(b) = b, for a≠b ∈Σ. Then, by construction, $\delta (I,s)= \delta ^{\prime }(I,f(s))$, and hence $\delta ^{\prime }(I,f(s)) \cap Q_{S}^{\prime } \neq \emptyset$. If δ(I, P^− 1P(s)) ∩ Q_NS = ∅, then $\delta ^{\prime }(I,f(P^{-1}P(s)))\cap Q_{NS}^{\prime } = \emptyset$ because $\delta (I,s^{\prime }) = \delta ^{\prime }(I,f(s^{\prime }))$ for any $s^{\prime }\in P^{-1}P(s)$, and G_CSO is not current-state opaque. Otherwise, we denote by q_s ∈ δ(I, s) ∩ Q_S and q_ns ∈ δ(I, P^− 1P(s)) ∩ Q_NS the states with maximal φ(q_s) and φ(q_ns). Since G_K-SO is not K-step opaque, φ(q_s) > φ(q_ns). Then, in G_CSO, q_s has exactly one outgoing observable transition and is followed by φ(q_s) = k secret states, while q_ns is followed by φ(q_ns) < k non-secret states. Therefore, $\delta ^{\prime }(I,f(s)a^{k}) \cap Q_{S}^{\prime }\neq \emptyset$ and $\delta ^{\prime }(I,f(s^{\prime })a^{k}) \cap Q_{NS}^{\prime }=\emptyset$ for any $s^{\prime }\in P^{-1}P(s)$, and hence G_CSO is not current-state opaque.

On the other hand, assume that G_K-SO is K-step opaque, and that $\delta ^{\prime }(I,w)\cap Q_{S}^{\prime }\neq \emptyset$. We show that $\delta ^{\prime }(I,P^{-1}P(w))\cap Q_{NS} \neq \emptyset$. Consider a state $q_{s} \in \delta ^{\prime }(I,w) \cap Q_{S}^{\prime }$ and a path π in G_CSO leading to q_s under w. Denote by p the last state of π that corresponds to a state of G_K-SO; that is, p is not a new state added by the construction of G_CSO. Since $q_{s}\in Q_{S}^{\prime }$, we have, by construction, that p ∈ Q_S. Then the choice of p partitions w = uv, where u, read along the path π, leads to state p, and v = a^ℓ is a suffix of length ℓ ≤ K. Let $u^{\prime }$ be a string such that $f(u^{\prime })=u$. Then $p\in \delta (I,u^{\prime })\cap Q_{S}$. Since φ(p) ≥ ℓ, there exists t such that P(t) = a^ℓ and $\delta (\delta (I,u^{\prime })\cap Q_{S},t) \neq \emptyset$ in G_K-SO. Then K-step opacity of G_K-SO implies that there exists $u^{\prime \prime }$ and $t^{\prime }$ such that $P(u^{\prime })=P(u^{\prime \prime })$, $P(t)=P(t^{\prime })$, and $\delta (\delta (I,u^{\prime \prime })\cap Q_{NS},t^{\prime }) \neq \emptyset$. In particular, there is a state $q_{ns}\in \delta (I,u^{\prime \prime })\cap Q_{NS}$ with φ(q_ns) ≥ ℓ, and $\delta ^{\prime }(I,f(u^{\prime \prime }))\cap Q_{NS}^{\prime } \neq \emptyset$. Therefore, $\delta ^{\prime }(I,f(u^{\prime \prime })a^{\ell })\cap Q_{NS}^{\prime } \neq \emptyset$ and $P(f(u^{\prime \prime })a^{\ell }) = P(uv) = P(w)$, which completes the proof. □

We now illustrate the construction.

Example 8

Let G₄ over Σ = {a, u} depicted in Fig. 19 (left) be the instance of the K-SO problem from Example 4 with K = 2, a single observable event Σ_o = {a}, the set of secret states Q_S = {1}, and the set of non-secret states Q_NS = {3}. Then, φ(1) = φ(3) = 2, and our transformation of K-SO to CSO results in the DES $G_{4}^{\prime \prime }$ depicted in Fig. 19 (right) with the set of secret states $Q_{S}^{\prime }$ and the set of non-secret states $Q_{NS}^{\prime }$. Analogously to Example 4, we consider two cases based on the presence of the unobservable transition (1,u,3) in G₄.

Fig. 19

An example of the transformation of the K-SO problem with a single observable event (left) to the CSO problem (right)

If the transition (1,u,3) exists in G₄, then G₄ is 2-step opaque, since it is infinite-step opaque as shown in Example 4. The reader can see that $G_{4}^{\prime \prime }$ is current-state opaque, because a secret state is reachable only under a string of the form a^k for k ∈{0,1,2}, and for any such string there is an indistinguishable string ua^k reaching a non-secret state.

If the transition (1,u,3) does not exist in G₄, then G₄ is not 2-step opaque, because it is neither current-state opaque and, obviously, neither $G_{4}^{\prime \prime }$ is current-state opaque.

4.3.4 Improving the algorithmic complexity of deciding K-step opacity

Let G = (Q,Σ,δ, I, F) be a DES. We design an algorithm deciding K-step opacity in time O((K + 1)2ⁿ(n + ℓ²m)), where ℓ = |Σ_o| is the number of observable events, n is the number of states of G, and m is the number of transitions of P(G), m ≤ ℓn².

To decide whether G is K-step opaque with respect to $Q_{S},Q_{NS}\subseteq Q$, and $P\colon {\Sigma }^{*} \to {\Sigma }_{o}^{*}$, we proceed as follows:

• 1. We compute the observer $\mathcal G^{obs}$ of G in time O(ℓ2ⁿ);

• 2. We compute the projected automaton P(G) of G in polynomial time O(m + n);

• 3. We compute a DFA $\mathcal D$ accepting the language ${{\Sigma }_{o}^{K}}$; then $\mathcal D$ has K + 1 states and is constructed in time O(ℓ(K + 1));

• 4. We compute the product automaton $\mathcal C = P(G) \times \mathcal G^{obs}$ in time O((m + n) ⋅ ℓ2ⁿ); – states of $\mathcal C$ are of the form Q × 2^Q;

• 5. For every reachable state X of $\mathcal G^{obs}$, we compute X_S = X ∩ Q_S and X_NS = X ∩ Q_NS;

  • (a) If X_S≠∅ and X_NS = ∅, then G is not K-step opaque;

  • (b) Otherwise, for every state x ∈ X_S, we add a transition from X under @ to state (x, X_NS) of $\mathcal C$, and we add the state (x, X_NS) to set Y;

• 6. We set Y to be the set of initial states of $\mathcal C$, and compute $\mathcal G = \mathcal C \times \mathcal D$;

  • (a) If $\mathcal G$ contains a reachable state of the form (q, ∅, d), then G is not K-step opaque; otherwise, G is K-step opaque.

Informally, we make use of the algorithm designed for deciding infinite-step opacity of Section 4.2.4 with the modification that we take an intersection of $\mathcal C$ with the automaton recognizing ${{\Sigma }_{o}^{K}}$. This modification ensures that any computation of $\mathcal {C}$ ends after K steps, and hence we check at most K subsequent steps.

Lemma 4

The DES G is K-step opaque if and only if G is current-state opaque and no state of the form (q, ∅, d) is reachable in $\mathcal G$.

Proof

The algorithm works as that deciding infinite-step opacity. The only modification is that we intersect $\mathcal C$ with $\mathcal D$, recognizing ${{\Sigma }_{o}^{K}}$. This modification ensures that the algorithm checking infinite-step opacity is blocked after K subsequent steps, and hence it decides K-step opacity. □

Since our algorithm constructs and searches the NFA $\mathcal G$ with O((K + 1)n2ⁿ) states and O((K + 1)ℓm2ⁿℓ) transitions, the time complexity of our algorithm is O((K + 1)2ⁿ(n + ℓ²m)).

5 Conclusions

We studied the transformations among the notions of language-based opacity, current-state opacity, initial-state opacity, initial-and-final-state opacity, K-step opacity, and infinite-step opacity. In particular, we provided a general transformation from language-based opacity to initial-state opacity, and constructed transformations between infinite-step opacity and current-state opacity, and between K-step opacity and current-state opacity. Together with the transformations of Wu and Lafortune (2013), we have a complete list of transformations between the discussed notions of opacity. The transformations are computable in polynomial time, preserve the number of observable events, and determinism. We further applied the transformations to improve the algorithmic complexity of deciding language-based opacity, infinite-step opacity, and K-step opacity, and to obtain the precise computational complexity of deciding the discussed notions of opacity.