Assessing the Effects of Holling Type-II Treatment Rate on HIV-TB Co-infection

Abstract

In this paper, a HIV-TB co-infection model is explored which incorporates a non-linear treatment rate for TB. We begin with presenting a HIV-TB co-infection model and analyze both HIV and TB sub-models separately. The basic reproduction numbers corresponding to HIV-only, TB-only and the HIV-TB full model are computed. The disease-free equilibrium point of the HIV sub-model is shown to be locally as well as globally asymptotically stable when its corresponding reproduction number is less than unity. The HIV-only model exhibits a transcritical bifurcation. On the other hand, for the TB sub-model, the disease-free equilibrium point is locally asymptotically stable but may not be globally asymptotically stable. We have also analyzed the full HIV-TB co-infection model. Numerical simulations are performed to investigate the effect of treatment rate in the presence of resource limitation for TB infected individuals, which emphasize the fact that to reduce co-infection from the population programs to accelerate the treatment of TB should be implemented.

1 Introduction

Mathematical modeling is a process of representing a real-world problem in mathematical terms, so as to have an idea about real-world solutions. Epidemiological modeling is a branch of mathematical modeling which describes the transmission dynamics of infectious diseases among individuals. From epidemiological modeling, we are able to predict the macroscopic behavior by using the microscopic description of an infectious disease in a population. Recently some infectious diseases, such as HIV which can lead to AIDS and TB (due to bacterial infection) have become an important concern for both developing and developed countries. The Human Immunodeficiency Virus (HIV) weakens people’s defence against infections by targeting an individual’s immune system. It was first reported in June 1981 (De Cock et al. 2012). The most advanced stage of HIV infection is AIDS, which can take from 2 to 15 years to develop depending on an individual. There are multiple modes of transmission for HIV such as sharing needles with infected people, breastfeeding or anything which transfers contaminated blood. As reported by the World Health Organisation, 1.7 million people became newly infected in 2018 and there were approximately 37.9 million people living with HIV at the end of 2018 (https://www.who.int/news-room/fact-sheets/detail/hiv-aids). In 2018, 770,000 people died from HIV-related causes globally. According to WHO, currently, only 70% of HIV-infected individuals know their status.

Tuberculosis (TB) is a bacterial disease caused by Mycobacterium tuberculosis, which most often affects the lungs. TB transmission occurs by infectious droplets in the air and through interactions with infected individuals. About one-third of the total world population is infected with TB. People infected with TB bacteria have a 5 to 15% lifetime risk of falling ill with TB. Both HIV and TB accelerate the progression of each other (https://www.tbfacts.org/tb-hiv/). Immunity declines as HIV infection progresses and this makes infected individuals more vulnerable to opportunistic infections like TB. TB is the most opportunistic infection for HIV infected individuals. Worldwide TB is one of the top 10 causes of death among individuals and the leading cause of death for people living with HIV. Between 2000 and 2016 diagnosis and treatment of TB saved almost 53 million from the disease (http://www.who.int/mediacentre/factsheets/fs104/en/). Globally people living with HIV were 20 times more likely to fall ill with TB than those without HIV in 2017. According to WHO, 10.4 million people fell ill with TB and 1.7 million died from the disease (including 0.4 million among people living with HIV) in 2016. TB is curable and preventable, but there is no effective vaccine for HIV which can treat infected individuals permanently. Therefore, it is essential to pay adequate attention to study the dynamics of the co-infection to control its spread.

Many mathematicians are working on HIV-TB co-infection models and a lot of work has already been done in this field (Agusto and Adekunle 2014; Denysiuk et al. 2017; Naresh and Tripathi 2005; Sharomi et al. 2008; Tanvi and Aggarwal 2020). West and Thompson (1997) proposed a model to explore the effect of HIV infection on TB infection. The purpose of their work was to investigate the duration and magnitude of the effect that the HIV epidemic may have on TB. Naresh et al. (2009) developed a HIV-TB co-infection model to study the effect of tuberculosis on the transmission dynamics of HIV in a logistically growing human population instead of taking constant recruitment rate. Bhunu et al. (2009) developed a HIV-AIDS and TB co-infection model by considering both latent and active forms of TB and by incorporating re-infection for recovered cases. They concluded that the treatment of HIV along with both latent and active forms of TB infectives results in delayed onset of the AIDS stage of HIV infection. Treatment also had a great impact in decreasing the infected population. Roeger et al. (2009) proposed a model to explore the consequences of the joint dynamics of HIV and TB on the prevalence of both. Gakkhar and Chavda (2012) formulated a simple non-linear HIV-TB co-infection model to show the non-existence of a co-infection equilibrium point. Since currently no cure exists for the HIV disease, we believe that the detection of HIV infection and subsequent counseling can be effective in controlling its spread amongst the population. Based on this, Kaur et al. (2014) developed a simple HIV-TB co-infection model by incorporating screening for both HIV and TB infectives and treatment for screened individuals. Silva and Torres (2015) proposed a HIV-TB co-infection model in which optimal control theory is applied to discuss the optimal treatment strategies for co-infected individuals with HIV and TB. Kumar and Jain (2018) analyzed a HIV-TB co-infection model to explore the effect of early and late HIV treatment on disease-induced deaths during the TB treatment course.

It is obvious that in any (sufficiently large) community there is a limited capacity for the treatment of a disease. Till now authors have used a constant removal rate (that is, constant recovery from the infected population per unit time) which is described as follows (with I denoting the density of infected individuals):

$$\begin{aligned} h(I)= {\left\{ \begin{array}{ll} r,&{} I>0,\\ 0, &{} I=0. \end{array}\right. } \end{aligned}$$

This is called a Holling type-I functional response. There are different types of functional responses, that is, Holling type-II, type-III and type-IV (Dubey et al. 2013), to consider limited treatment capacity.

Many researchers are working with Holling type functions as treatment rates for their models. Dubey et al. (2013) explored the effect of Holling type-III and IV functional response as the treatment rate for infectives in a SEIR epidemic model. Dubey et al. (2015) proposed a SIR model with non-linear incidence rate and Holling type-II function as the treatment rate. It may be noted that although various types of HIV-TB models have been studied and analyzed, HIV-TB models with different types of removal rates, that is, Holling type-II, type-III and type-IV, are yet to be studied. Also along with the high burden countries that are facing problems with the supply of anti-tuberculosis drugs, in the United Kingdom, almost two thirds of hospital pharmacy departments reported problems with accessing anti-tuberculosis treatment (https://www.tbfacts.org/tb-treatment/]. In view of this, we propose a HIV-TB co-infection model with Holling type-II function as the treatment rate for TB infected individuals, which is given as

$$\begin{aligned} h(I) = \frac{\alpha I}{1+\omega I}, \end{aligned}$$

where $\alpha \geqslant 0$ is the initial per capita treatment rate for TB infectives and $\omega >0$ denotes the limitation on resources for the treatment of TB. In this paper, the Holling type-II function depicts the condition when the number of TB infected individuals is very large and the treatment capacity reaches to its maximum value due to limited treatment resources. To study the qualitative behavior of the model we use the stability theory of non-linear differential equations (Perko 1991).

The content of this paper is organized as follows. A deterministic non-linear mathematical model is proposed in the second section, together with the discussion of positivity and boundedness of its solutions. In the third section the HIV sub-model is considered and analyzed. The fourth section deals with the analysis of the TB-only model. Then the full model is discussed in the fifth section. In the sixth section, the system is solved numerically to illustrate the analytical results and to gain more insights into the system. In the last section we conclude the paper with a brief discussion.

2 Model Formation

In this section we propose a deterministic non-linear mathematical model for the transmission dynamics of HIV and TB co-infection with non-linear treatment rate. Here we use a Holling type-II function as treatment rate for TB. We are making a few assumptions in formulating the model. We assume that the susceptibles are recruited into the population at a constant rate. We divide the total population density N(t), that is, no. of individuals per unit area, into ten sub-populations, which are as follows

• (1) S(t)—the class of individuals susceptible to both the diseases.

• (2) $L_T(t)$—the class of individuals latently infected with tuberculosis.

• (3) $I_T(t)$—the class of individuals actively infected with tuberculosis only.

• (4) $R_T(t)$— the class of individuals recovered from TB with temporal immunity.

• (5) $I_H(t)$—the class of individuals infected with HIV only.

• (6) $A_H(t)$—the class of individuals infected with AIDS.

• (7) $L_{T_H}(t)$—the class of individuals co-infected with HIV and latent TB.

• (8) $I_{T_H}(t)$—the class of individuals co-infected with HIV and TB.

• (9) $L_{A_T}(t)$—the class of individuals co-infected with AIDS and latent TB.

• (10) $A_{T_H}(t)$—the class of individuals co-infected with AIDS and TB.

The total population is divided in such a way that,

$$\begin{aligned} N(t) = S(t)+L_T(t)+I_T(t)+R_T(t)+I_H(t)+A_H(t)+L_{T_H}(t)+I_{T_H}(t)+ L_{A_T}(t)+A_{T_H}(t). \end{aligned}$$

Further we assume that in a given compartment all individuals are identically infectious, which might ignore the effects caused due to variation among individuals. Susceptible individuals acquire HIV infection due to effective contact with HIV-infected individuals at a rate $\lambda _H$, where $\lambda _H$ is the force of infection associated with HIV infection and is given as

$$\begin{aligned} \lambda _H= \frac{\beta _H\left( I_H+ I_{T_H}+L_{T_H}+\gamma \left( A_H+L_{A_T}+A_{T_H}\right) \right) }{N}, \end{aligned}$$

where $\gamma > 1$ is a modification parameter which accounts for the fact that individuals infected with AIDS are more likely to spread HIV infection. Susceptibles become TB infectives following effective contact with TB-infected individuals at a rate $\lambda _T$. The force of infection associated with TB infection, denoted by $\lambda _T$ is given by

$$\begin{aligned} \lambda _T=\frac{\beta _T(I_T+I_{T_H}+A_{T_H})}{N}. \end{aligned}$$

HIV-infected individuals and AIDS patients may acquire TB at the rate $\eta _1 \lambda _T$ and $\eta _2 \lambda _T$, respectively. Here, $\eta _1 > 1$ and $\eta _2 > 1$ are the modification parameters which correspond to the fact that HIV-infected and AIDS-infected individuals have a weakened immune system and hence are more prone to get a TB infection than susceptibles. AIDS-infected individuals after getting anti-retroviral therapy at the rate $\tau$ live a healthy life but are still infected with HIV and enter into the HIV-infected class. TB-infected individuals are getting TB treatment at the rate $h(I) = \frac{\alpha I}{1+\omega I}$, $\alpha \geqslant 0,\ \omega > 0,\ I \geqslant 0 ,$ which is a Holling type-II function. The term $\frac{1}{1+\omega I}$ represents the effect of inhibition in the treatment of TB. It can be clearly seen that h(I) is a continuously differentiable, increasing function of I and

• (i) $h(0)=0,$

• (ii) $h'(I)>0,$ $h''(I)<0,$

• (iii) $\underset{I \rightarrow \infty }{\lim }h(I)=\frac{\alpha }{\omega }$,

where $\frac{\alpha }{\omega }$ is the maximum treatment capacity of some community.

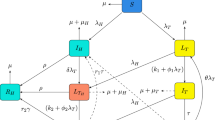
From the assumptions, definition of variables, parameter description (Table 1) and the above-mentioned facts, the mathematical model is formulated according to the schematic diagram given in Fig. 1. The equations representing the model are given as

$$\begin{aligned} \begin{aligned}&\frac{dS}{dt}= \Lambda -\lambda _T S-\lambda _H S -dS+rR_T,\\&\frac{dL_T}{dt}= \lambda _T S -\lambda _H L_T -h(L_T)-(k_1+d )L_T,\\&\frac{dI_T}{dt}= k_1 L_T - \lambda _H I_T -h(I_T)-(d +d_T) I_T,\\&\frac{dR_T}{dt}= h(L_T)+h(I_T)- \lambda _H R_T -(r+d) R_T,\\&\frac{dI_H}{dt}= \lambda _H S- \eta _1 \lambda _T I_H+h(I_{T_H})+h(L_{T_H})+\lambda _H R_T+\tau A_H-(\rho _1 +d) I_H, \\&\frac{dA_H}{dt}= \rho _1 I_H-\eta _2 \lambda _T A_H+h(L_{A_T})+h(A_{T_H})-(d+d_A+\tau ) A_H ,\\&\frac{dL_{T_H}}{dt}= \eta _1 \lambda _T I_H- h(L_{T_H})+\lambda _H L_T-(\rho _2+k_2+d)L_{T_H}+\tau L_{A_T}, \\&\frac{dI_{T_H}}{dt}= k_2 L_{T_H}+\lambda _H I_T- h(I_{T_H})-(\rho _3+d+d_T)I_{T_H}+\tau A_{T_H}, \\&\frac{dL_{A_T}}{dt}= \eta _2 \lambda _T A_H+\rho _2 L_{T_H}-h( L_{A_T}) -(k_3+d+d_A+\tau ) L_{A_T}, \\&\frac{dA_{T_H}}{dt}= k_3 L_{A_T}+\rho _3 I_{T_H}-h( A_{T_H}) -(d+d_{A_T}+\tau ) A_{T_H}. \end{aligned} \end{aligned}$$

(2.1)

The initial conditions of the model (2.1) are given as

$$\begin{aligned}&S(0)=S_0\geqslant 0,\quad L_T(0)= L_{T_0}\geqslant 0, \quad I_T(0)=I_{T_0}\geqslant 0,\quad R_T(0)=R_{T_0}\geqslant 0,\nonumber \\&I_H(0)=I_{H_0}\geqslant 0,\quad A_H(0)= A_{H_0}\geqslant 0, \quad L_{T_H}(0)=L_{T_{H_0}}\geqslant 0,\\&I_{T_H}(0)=I_{T_{H_0}}\geqslant 0 ,\quad L_{A_T}(0)=L_{A_{T_0}}\geqslant 0\ \ \text { and }\ \ A_{T_H}(0)=A_{T_{H_0}}\geqslant 0.\nonumber \end{aligned}$$

(2.2)

Table 1 Parameter description

Fig. 1

Schematic Diagram of the Model

2.1 Positivity and Boundedness of Solutions

Based on biological considerations, the region under consideration is:

$$\begin{aligned} \begin{aligned} G =\left\{ (S,L_T,I_T,R_T,I_H,A_H,L_{T_H},I_{T_H},L_{A_T},A_{T_H})\in \mathbb {R}_+^{10}:N(t)\leqslant \frac{\Lambda }{d}\right\} . \end{aligned} \end{aligned}$$

(2.3)

It is necessary to show that all the variables $S(t),\ L_T(t),\ I_T(t),\ R_T(t),\ I_H(t),\ A_H(t),\ L_{T_H}(t), \ I_{T_H}(t),$ $\ L_{A_T}(t)$ and $\ A_{T_H}(t)$ are positive for all time $t\geqslant 0$, as all of them describe human sub-populations. Hence, we state the following theorem:

Theorem 2.1

For the initial conditions given by (2.2), the solution components S(t),  $\ L_T(t),\ I_T(t),\ R_T(t),$ $\ I_H(t),\ A_H(t),\ L_{T_H}(t), \ I_{T_H}(t),\ L_{A_T}(t)$ and $\ A_{T_H}(t)$ for the model system (2.1) are positive for $t\geqslant 0$ and the region G is positively invariant, that is, all the solutions starting in G remain in G.

Proof

First, we prove that, under the given initial conditions, all the components of the model system (2.1) are positive. For proving this, on the contrary, we assume that there exists a first time $t_1>0$ such that

$$\begin{aligned}&min\{S(t_1),\ L_T(t_1),\ I_T(t_1),\ R_T(t_1),\ I_H(t_1),\ A_H(t_1),\ L_{T_H}(t_1), \ I_{T_H}(t_1),\ L_{A_T}(t_1),\ A_{T_H}(t_1)\}=0 \ \ \text{ and }\\&min\{S(t),\ L_T(t),\ I_T(t),\ R_T(t),\ I_H(t),\ A_H(t),\ L_{T_H}(t), \ I_{T_H}(t),\ L_{A_T}(t),\ A_{T_H}(t)\} > 0, \text{ for } \text{ all } t \in [0,t_1). \end{aligned}$$

In view of our assumption, let,

$$\begin{aligned} min\{S(t_1),\ L_T(t_1),\ I_T(t_1),\ R_T(t_1),\ I_H(t_1),\ A_H(t_1),\ L_{T_H}(t_1), \ I_{T_H}(t_1),\ L_{A_T}(t_1),\ A_{T_H}(t_1)\}= S(t_1). \end{aligned}$$

Hence, $S(t_1) = 0$ and $S(t) > 0$ for all $t \in [0,t_1)$. But,

$$\begin{aligned} \frac{dS(t)}{dt}&= \Lambda -\lambda _T S(t)-\lambda _H S(t) -dS(t)+rR_T(t)\\&\geqslant -(\lambda _H+\lambda _T+d) S(t), \end{aligned}$$

from which we get that

$$\begin{aligned} S(t) \geqslant S_0 e^{-\int _{0}^{t}(\lambda _H+\lambda _T+d)\, dz} > 0. \end{aligned}$$

This implies that $S(t_1)>0$, contradicting the assumption that $S(t_1)=0$. Therefore, our assumption is not true. Hence, $S(t) > 0$ for all $t \geqslant 0$. Similarly, for all other cases we can prove that all the solution components are positive for $t \geqslant 0$.

Table 2 Parameter values

Now,

$$\begin{aligned} N'(t) =&\ \Lambda -dN(t) -d_T (I_T(t)+I_{T_H}(t)) -d_A (A_H(t)+L_{A_T}(t))-d_{A_T} A_{T_H}(t)\nonumber \\ \leqslant&\ \Lambda -dN(t), \end{aligned}$$

which gives

$$\begin{aligned} \frac{dN}{dt} + dN \leqslant \Lambda . \end{aligned}$$

Thus, we get

$$\begin{aligned} N(t) \leqslant N(0) e^{-dt}+\frac{\Lambda }{d}(1-e^{-dt}). \end{aligned}$$

In particular, $0 < N(t) \leqslant \frac{\Lambda }{d}$ if, $N(0) \leqslant \frac{\Lambda }{d}$. Thus, N(t) is bounded and all the solutions starting in G remain in G. Therefore, the model system (2.1) can be considered as a well-posed model both epidemiologically and mathematically.

3 HIV Sub-model

We obtain the HIV sub-model from the equations in (2.1) when $L_T=I_T=R_T=L_{T_H}=I_{T_H}=L_{A_T}=A_{T_H}=0$, which is given by

$$\begin{aligned}&\frac{dS}{dt}= \Lambda -\lambda _H S -dS,\nonumber \\&\frac{dI_H}{dt}= \lambda _H S-(\rho _1+d) I_H+\tau A_H,\\&\frac{dA_H}{dt}= \rho _1 I_H-(d+d_A+\tau ) A_H,\nonumber \end{aligned}$$

(3.1)

with the initial conditions $S(0)=S_0\geqslant 0,\ I_H(0)=I_{H_0}\geqslant 0,\ A_H(0)=A_{H_0}\geqslant 0$ and $\lambda _H=\frac{\beta _H}{N} (I_H+\gamma A_H)$ as the force of infection.

Based on biological considerations, the region of attraction for this sub-model is:

$$\begin{aligned} G_H = \left\{ (S,I_H,A_H)\in \mathbb {R}_+^{3}:0 < N(t)\leqslant \frac{\Lambda }{d}\right\} . \end{aligned}$$

(3.2)

3.1 The Basic Reproduction Number

The disease-free equilibrium point for the HIV sub-model is given by

$$\begin{aligned} E_{H_0}=&(S_0,I_{H_0},A_{H_0}) = \biggl (\frac{\Lambda }{d},0,0\biggr ). \end{aligned}$$

(3.3)

Mathematically, the basic reproduction number is the threshold quantity which counts the number of secondary infections generated by a single infected individual in a completely susceptible population (Jones 2007). For calculating the basic reproduction number we use the next-generation matrix approach (van den Driessche and Watmough 2002) and compute the matrices F and V corresponding to the new infection terms and the remaining transfer terms, respectively. The matrices F and V are given as

$$\begin{aligned} F = \begin{bmatrix} \beta _H &{} \gamma \beta _H \\ 0 &{} 0 \end{bmatrix} \text { and } V = \begin{bmatrix} \rho _1+d &{} -\tau \\ -\rho _1 &{} \tau +d+d_A \end{bmatrix}. \end{aligned}$$

Therefore, using $FV^{-1}$ we get the basic reproduction number for HIV as

$$\begin{aligned} \mathcal {R}_H = \dfrac{\beta _H(\tau +d+d_A+\gamma \rho _1) }{(\rho _1+d)(\tau +d+d_A)-\rho _1 \tau } . \end{aligned}$$

(3.4)

3.2 Stability Analysis of the Disease-Free Equilibrium

In this section we discuss the local stability of the disease-free equilibrium point to see whether small perturbations away from the equilibrium point will grow or shrink in time.

Theorem 3.1

The disease-free equilibrium point $E_{H_0}$ for the model system (3.1) is locally asymptotically stable if $\mathcal {R}_H<1$, and is a saddle point if $\mathcal {R}_H>1$.

Proof

The Jacobian matrix for the model system (3.1), evaluated at $E_{H_0}$ is given by

$$\begin{aligned} J_{H_0}= \begin{bmatrix} -d &{} -\beta _H &{} -\gamma \beta _H\\ 0 &{} \beta _H-(\rho _1+d) &{} \gamma \beta _H+\tau \\ 0 &{} \rho _1 &{} -(d+d_A+\tau ) \end{bmatrix}. \end{aligned}$$

The characteristic equation of $J_{H_0}$ is:

$$\begin{aligned}&(d+\lambda )\left( \lambda ^2+\lambda \left( 2 d+d_A+\tau +\rho _1-\beta _H \right) -\beta _H \left( d+d_A+\tau +\gamma \rho _1 \right) + \left( \rho _1+d\right) \left( d+d_A+\tau \right) -\tau \rho _1\right) =0. \end{aligned}$$

One eigenvalue of the matrix $J_{H_0}$ is $\lambda _1=-d$ and the remaining factor is $\lambda ^2 + a_1 \lambda +a_0=0$ where,

$$\begin{aligned} a_1=&\ 2 d+d_A+\tau +\rho _1-\beta _H,\\ a_0=&-\beta _H \left( d+d_A+\tau +\gamma \rho _1 \right) + \left( \rho _1+d\right) \left( d+d_A+\tau \right) -\tau \rho _1. \end{aligned}$$

Here, $a_1$ and $a_0$ are positive if $\mathcal {R}_H<1$. Therefore, by Routh-Hurwitz criterion all the eigenvalues of $J_{H_0}$ have a negative real part if $\mathcal {R}_H<1$. Hence, the disease-free equilibrium point is locally asymptotically stable if $\mathcal {R}_H<1$, and is a saddle point if $\mathcal {R}_H>1$.

We now list two conditions which are sufficient to guarantee the global stability of the disease-free equilibrium point.

For that, following (Castillo-Chavez et al. 1999), we rewrite the model system (3.1) as

$$\begin{aligned}&\frac{dU}{dt} = F(U,I),\nonumber \\&\frac{dI}{dt} = G(U,I),\\&G(U,0) = 0,\nonumber \end{aligned}$$

(3.5)

where U denotes the number of uninfected individuals and I denotes the number of infected individuals. According to (Castillo-Chavez et al. 1999), the disease-free equilibrium point $(U_0,0)$ is globally asymptotically stable if the following conditions are satisfied:

• (H1) For $\frac{dU}{dt} = F(U,0)$, $U_0$ is globally asymptotically stable,

• (H2) $G(U,I) = AI - \hat{G}(U,I),$   $\hat{G}(U,I)\geqslant 0$ for $(U,I)\in G'$,

where $A = D_IG(U_0,0)$ is an M-matrix and $G'$ is the region where the HIV sub-model model makes biological sense, that is, where all the components of the HIV sub-model are positive.

Theorem 3.2

The equilibrium point $E_{H_0}=(U_0,0)$ for the model system (3.1) is globally asymptotically stable, provided $\mathcal {R}_H<1$ and the conditions (H1) and (H2) are satisfied.

Proof

For an equilibrium point to be globally stable in a given region, it is necessary for the equilibrium point to be locally asymptotically stable in that region. In the previous theorem, it has been proved that $E_{H_0}$ is locally asymptotically stable for $\mathcal {R}_H<1$. Thus, the global stability of $E_{H_0}$ can be studied in the region where $\mathcal {R}_H<1$. For the region where $\mathcal {R}_H<1$, we consider $U= S\in \mathbb {R}_+$ as the number of uninfected individuals and $I = (I_H,A_H)^T\in \mathbb {R}_+^2$ as a vector whose coordinates represent the two classes $I_H$ and $A_H$ of infected individuals. Here, $E_{H_0} = (U_0,0)$, with $U_0 = \frac{\Lambda }{d}$.

For our model system given by (3.1), F(U, I) and G(U, I) in Eq. (3.5) are given as

$$\begin{aligned} F(U,I) = \Lambda -\lambda _H S -dS\ \ \text { and }\ \ G(U,I) = \begin{bmatrix} \lambda _H S-(\rho _1+d) I_H+\tau A_H\\ \rho _1 I_H-(d+d_A+\tau ) A_H \\ \end{bmatrix}. \end{aligned}$$

Therefore,

$$\begin{aligned} F(U,0) = \begin{bmatrix} \Lambda - dS \end{bmatrix}. \text { Clearly, } U_0=\frac{\Lambda }{d}\hbox { is globally asymptotically stable for }F(U,0). \end{aligned}$$

Now, for condition (H2) we consider the equation

$$\begin{aligned} G(U,I) = AI - \hat{G}(U,I),\ \ \text { where}\ \ A = D_IG(U_0,0) \end{aligned}$$

from which we get that

$$\begin{aligned} \hat{G}(U,I)= \begin{bmatrix} \beta _H(I_H+\gamma A_H)\left( 1-\frac{S}{N}\right) \\ 0\\ \end{bmatrix}. \end{aligned}$$

It can be clearly seen that $\hat{G}(U,I)\geqslant 0$ (as $S/N \leqslant 1$). Hence, the equilibrium point $E_{H_0}$ is globally asymptotically stable for $\mathcal {R}_H<1$.

3.3 Existence and Bifurcation Analysis of the Endemic Equilibrium Point

In this section we compute the non-trivial equilibrium point of the HIV sub-model and discuss its stability.

The non-trivial equilibrium point for the model system (3.1) is given by

$$\begin{aligned}&S^*= \frac{N^*}{\mathcal {R}_H} , \end{aligned}$$

(3.6)

$$\begin{aligned}&I_H^*=\frac{d+d_A+\tau }{\rho _1+d+d_A+\tau }\left( 1-\frac{1}{\mathcal {R}_H}\right) N^*,\end{aligned}$$

(3.7)

$$\begin{aligned}&A_H^*=\frac{\rho _1}{d+d_A+\tau } I_H^*. \end{aligned}$$

(3.8)

The value of $N^*$ can be determined by substituting the values of $I_H^*$ and $A_H^*$ from Eqs. (3.7) and (3.8), respectively in equation $\frac{dN^*}{dt}=\Lambda -dN^*-d_A A_H^*=0$. Thus, we get

$$\begin{aligned} N^*=\frac{\Lambda (\rho _1+d+d_A+\tau )\mathcal {R}_H}{d (\rho _1+d+d_A+\tau )\mathcal {R}_H+ d_A \rho _1 (\mathcal {R}_H-1)}. \end{aligned}$$

Therefore, the non-trivial equilibrium point for the HIV sub-model is given by

$$\begin{aligned} E_H^*=(S^*,I_H^*,A_H^*), \end{aligned}$$

(3.9)

where $S^*, I_H^*$ and $A_H^*$ are given by Eqs. (3.6), (3.7) and (3.8), respectively. It is clear, that the non-trivial equilibrium point $E_H^*$ exists if $\mathcal {R}_H>1$.

On introducing $S=x_1, I_H=x_2$ and $A_H=x_3$ such that $N=x_1+x_2+x_3$, the model system (3.1) becomes

$$\begin{aligned}&\frac{dx_1}{dt}=f_1= \Lambda -\lambda _H x_1 -dx_1,\nonumber \\&\frac{dx_2}{dt}= f_2=\lambda _H x_1-(\rho _1+d) x_2+\tau x_3,\\&\frac{dx_3}{dt}= f_3=\rho _1 x_2-(d+d_A+\tau ) x_3,\nonumber \end{aligned}$$

(3.10)

where

$$\begin{aligned} \lambda _H=\frac{\beta _H(x_2+\gamma x_3)}{x_1+x_2+x_3}. \end{aligned}$$

The linearization matrix of system (3.10) evaluated at the disease-free equilibrium point $E_{H_0}$ is given by

$$\begin{aligned} J_{H_0}= \begin{bmatrix} -d &{} -\beta _H&{} - \gamma \beta _H\\ 0 &{} \beta _H-(d+\rho _1) &{} \gamma \beta _H+\tau \\ 0 &{} \rho _1 &{} -(d+d_A+\tau )\\ \end{bmatrix}. \end{aligned}$$

Clearly, it has a zero eigenvalue which is simple when $\mathcal {R}_H=1$, and the other eigenvalues have negative real part, with $\beta _H=\beta ^*=\dfrac{(\rho _1+d)(\tau +d+d_A)-\rho _1 \tau }{d+d_A+\tau +\gamma \rho _1}$. Therefore, the system has a non-hyperbolic critical point. The Center manifold theory (Carr 1981) can be used to determine the local stability of the non-hyperbolic critical point.

We use Theorem 4.1 of Castillo-Chavez and Song (2004) to prove the local asymptotic stability of the non-hyperbolic critical point for the HIV sub-model. For convenience, the theorem in Castillo-Chavez and Song (2004) is stated here:

Theorem 3.3

Consider the following general system of ordinary differential equations with a parameter $\phi$:

$$\begin{aligned} \begin{aligned}&\frac{dx}{dt}=f(x,\phi ),\\&f:\mathbb {R}^n \times \mathbb {R} \rightarrow \mathbb {R} \text { and } C^2(\mathbb {R}^n \times \mathbb {R}), \end{aligned} \end{aligned}$$

(3.11)

where 0 is an equilibrium point of the system (that is, $f(0,\phi )=0$ for all $\phi$) and assume

• (1) $A= D_x f(0,0)=\bigl (\frac{df_i}{dx_j}(0,0)\bigr )$ is the linearization matrix of system (3.11) at the equilibrium 0 and $\phi$ evaluated at 0. Zero is a simple eigenvalue of A and all other eigenvalues of A have a negative real part.

• (2) Matrix A has a right eigenvector w and a left eigenvector v (each corresponding to the zero eigenvalue). Let $f_k$ be the $k^{th}$ component of f and

  $$\begin{aligned} a= \sum _{k,j,i=1} ^n {v_kw_iw_j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0)}, \ \ b= \sum _{k,i=1} ^n {v_kw_i \frac{\partial ^2 f_k}{\partial x_i \partial \phi }(0,0)}. \end{aligned}$$

  (3.12)

  The local dynamics of the system around 0 is totally determined by the signs of a and b.

  • (a) $a>0 , b>0$. When $\phi <0$ with $|\phi |<<1,0$ is locally asymptotically stable and there exists a positive unstable equilibrium; when $0<\phi<<1$, 0 is unstable and there exists a negative, locally asymptotically stable equilibrium point.

  • (b) $a<0, b<0$. When $\phi <0$ with $|\phi |<<1,0$ is unstable; when $0<\phi<<1$, 0 is locally asymptotically stable and there exists a positive, unstable equilibrium point.

  • (c) $a>0, b<0$. When $\phi <0$ with $|\phi |<<1,0$ is unstable and there exists a negative, locally asymptotically stable equilibrium; when $0<\phi<<1$, 0 is stable and a positive unstable equilibrium appears.

  • (d) $a<0, b>0$. When $\phi$ changes sign from negative to positive, 0 changes its stability from stable to unstable. Correspondingly, a negative unstable equilibrium becomes positive and locally asymptotically stable.

Following Theorem 3.3, we now compute left and right eigenvectors of the Jacobian matrix $J_{H_0}$. The right eigenvector of the matrix $J_{H_0}$ associated with the disease-free equilibrium point is given as $w=[w_1,w_2,w_3]$, where

$$\begin{aligned} w_1=- \frac{\beta ^*(d+d_A+\tau +\gamma \rho _1)}{d(d+d_A+\tau )},\quad w_2=1\ \ \text { and } \ \ w_3=\frac{\rho _1}{d+d_A+\tau }. \end{aligned}$$

The left eigenvector satisfying $v J_{H_0} = 0$ is given by $v=[v_1,v_2,v_3]$, where

$$\begin{aligned} v_1=0,\quad v_2=1\ \ \text { and } \ \ v_3=\frac{\beta ^*-(\rho _1+d)}{\rho _1}. \end{aligned}$$

Computation of a and b. To compute a and b, we have to compute the partial derivatives of $f_1,f_2 \text { and } f_3$ with respect to $x_1,x_2,x_3 \text { and } \beta ^*$. As $v_1=0$, it is not required to compute the partial derivative of $f_1$ with respect to any variable. The remaining non-zero second order partial derivatives associated with the system (3.10) evaluated at the disease-free equilibrium are given as

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 f_2}{\partial x_2^2}=-\frac{2 \beta ^* d}{\Lambda } ,\quad \frac{\partial ^2 f_2}{\partial x_2 \partial x_3}=-\frac{\beta ^*d(1+\gamma )}{\Lambda },\quad \frac{\partial ^2 f_2}{\partial x_3^2}=-\frac{2 \beta ^*\gamma d}{\Lambda }, \\&\frac{\partial ^2 f_2}{\partial x_2 \partial \beta ^*}= 1 \ \ \text{ and } \ \ \frac{\partial ^2 f_2}{\partial x_3 \partial \beta ^*}= \gamma . \end{aligned} \end{aligned}$$

(3.13)

Now, using the expressions given by Eq. (3.13), we get

$$\begin{aligned} a =&\ \sum _{k,j,i=1} ^3 { v_k w_iw_j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0)}\\ =&\ v_2 w_2^2\frac{\partial ^2 f_2}{\partial x_2^2}(0,0)+v_2 w_2 w_3 \frac{\partial ^2 f_2}{\partial x_2 \partial x_3}(0,0)+v_2 w_3^2\frac{\partial ^2 f_2}{\partial x_3^2}(0,0) \\ =&- 2\frac{ \beta ^* d}{\Lambda }\left( 1 + (1+\gamma ) w_3 + \gamma w_3^2 \right) <0.\\ b=&\sum _{k,i=1} ^3 {v_k w_i \frac{\partial ^2 f_k}{\partial x_i \partial \beta ^*}(0,0)}\\ =&\ v_2 w_2 \frac{\partial ^2 f_2}{\partial x_2 \partial \beta ^*}(0,0)+ v_2 w_3 \frac{\partial ^2 f_2}{\partial x_3 \partial \beta ^*}(0,0) \\ =&\ 1+ \gamma w_3 > 0. \end{aligned}$$

We can see that $a<0$ and $b>0$. Therefore, by Theorem (3.3) the unique endemic equilibrium point for the model system (3.10) is locally asymptotically stable when $\mathcal {R}_H>1$ and $\beta ^*<\beta _H,$ with $\beta _H$ close to $\beta ^*$. The system undergoes a supercritical transcritical bifurcation at $\beta _H = \beta ^*$. This can be summarized in the following theorem:

Theorem 3.4

The endemic equilibrium point $E^*_H$ is locally asymptotically stable for $\mathcal {R}_H>1$ and the system exhibits a supercritical transcritical bifurcation at $\mathcal {R}_H=1,$ with $\beta _H = \beta ^*$ as bifurcation parameter.

Theorem 3.5

The unique endemic equilibrium point $E_H^*$ is globally asymptotically stable for $\mathcal {R}_H>1$.

Proof

The unique endemic equilibrium point $E_H^*$ exists and is locally asymptotically stable if $\mathcal {R}_H>1$. To prove the global stability in the region $\mathcal {R}_H>1$, we have to show that all the solution trajectories approach $E_H^*$ as $t \rightarrow \infty$. To prove this, we first show that there does not exist any periodic orbit for the HIV sub-model. Consider a real valued function H in the interior of the positive region of $\mathbb {R}^3$ defined as

$$\begin{aligned} H(S,I_H,A_H)=\frac{1}{S I_H A_H}. \end{aligned}$$

Now, let us consider

$$\begin{aligned}&h_1(S,I_H,A_H)=\Lambda -\frac{\beta _H}{S+I_H+A_H}(I_H+\gamma A_H)S-dS,\\&h_2(S,I_H,A_H)=\frac{\beta _H}{S+I_H+A_H}(I_H+\gamma A_H)S -(\rho _1+d)I_H+\tau A_H,\\&h_3(S,I_H,A_H)= \rho _1 I_H-(d+d_A+\tau )A_H. \end{aligned}$$

Thus, we have

$$\begin{aligned} div(Hh_1,Hh_2,Hh_3)&=\frac{\partial }{\partial {S}}\left( Hh_1\right) +\frac{\partial }{\partial {I_H}}\left( Hh_2\right) +\frac{\partial }{\partial {A_H}}\left( Hh_3\right) \\&=-\frac{\Lambda }{S^2 I_H A_H}-\frac{\tau }{S I_H^2}-\frac{\rho _1}{S A_H^2}-\frac{\beta _H \gamma }{N I_H^2}\ < \ 0. \end{aligned}$$

It can be seen that $div(Hh_1,Hh_2,Hh_3)$ is not equal to zero and will not change its sign in the positive region of $\mathbb {R}^3$. Therefore, by Dulac’s criterion (Strogatz 2014), the existence of any periodic orbit for the HIV sub-model can be ruled out. Now, if $\mathcal {R}_H>1$, the disease-free equilibrium point is a saddle point with the S-axis as stable manifold. Any solution starting at $I_H(0)= 0$ and $A_H(0)=0$ will remain on the S-axis and will converge towards the disease-free equilibrium point, as the S-axis is a stable manifold. On the other hand, if $I_H(0) > 0$ and $A_H(0)> 0$, the solution will be repelled by the disease-free equilibrium point and gets closer to the HIV endemic equilibrium point due to the absence of any periodic orbit. Once the solution gets close to the endemic equilibrium point, this equilibrium point will attract the solution since it is locally asymptotically stable for $\mathcal {R}_H>1$. Thus, it attracts all the solution trajectories starting from any initial point satisfying $I_H(0) > 0$ and $A_H(0)> 0$. Therefore, the unique HIV endemic equilibrium point $E_H^*$ is globally asymptotically stable for $\mathcal {R}_H>1$.

4 TB Sub-model

The TB sub-model can be obtained from the full model system given by (2.1) when $I_H=A_H=L_{T_H}=I_{T_H}=L_{A_T}=A_{T_H}=0$, which is given by

$$\begin{aligned} \begin{aligned}&\frac{dS}{dt}= \Lambda -\lambda _T S -dS+rR_T,\\&\frac{dL_T}{dt}= \lambda _T S -h(L_T)-(k_1+d )L_T,\\&\frac{dI_T}{dt}= k_1 L_T-h(I_T)- (d +d_T) I_T,\\&\frac{dR_T}{dt}= h(L_T)+ h(I_T) -d R_T-r R_T,\end{aligned} \end{aligned}$$

(4.1)

with the initial conditions

$$\begin{aligned} S(0)=S_0\geqslant 0,\quad L_T(0)=L_{T_0}\geqslant 0,\quad I_T(0)=I_{T_0}\geqslant 0 \quad \text{ and } \quad R_T(0)=R_{T_0}\geqslant 0, \end{aligned}$$

(4.2)

where

$$\begin{aligned} \lambda _T=\frac{\beta _T I_T}{N} \text { is the force of infection. } \end{aligned}$$

The TB sub-model is studied in the following positively invariant region

$$\begin{aligned} G_T = \left\{ (S,L_T,I_T,R_T)\in \mathbb {R}_+^{4}:0 < N(t)\leqslant \frac{\Lambda }{d}\right\} . \end{aligned}$$

4.1 Stability Analysis of the Disease-Free Equilibrium Point

The disease-free equilibrium point of the TB sub-model is given by

$$\begin{aligned} E_{T_0}=\biggl (\frac{\Lambda }{d},0 ,0,0\biggr ). \end{aligned}$$

(4.3)

The basic reproduction number obtained using the next-generation matrix approach is given as

$$\begin{aligned} \mathcal {R}_T=\frac{\beta _T k_1}{(k_1+d+\alpha )( d+d_T+\alpha )}. \end{aligned}$$

(4.4)

Now, we analyze the local and global asymptotic stability of the disease-free equilibrium point given by Eq. (4.3).

Theorem 4.1

The disease-free equilibrium point $E_{T_0}$ for the model system (4.1) is locally asymptotically stable if $\mathcal {R}_T<1$, and is a saddle point if $\mathcal {R}_T>1$.

Proof

The Jacobian matrix evaluated at $E_{T_0}$ is given as

$$\begin{aligned} J_{T_0} = \begin{bmatrix} -d &{} 0 &{} -\beta _T &{} r \\ 0 &{} -(k_1+d+\alpha ) &{} \beta _T &{} 0\\ 0 &{} k_1 &{} -(d+d_T+\alpha ) &{} 0\\ 0 &{} \alpha &{} \alpha &{} -(d+r)\\ \end{bmatrix}. \end{aligned}$$

The characteristic equation of the matrix $J_{T_0}$ is:

$$\begin{aligned}&(\lambda +d)(\lambda +d+r)(\lambda ^2+\lambda \left( k_1+2 d+2\alpha +d_T \right) +\left( k_1+d+\alpha \right) \left( d+d_T+\alpha \right) - \beta _T k_1)=0 \end{aligned}$$

The first two factors of the characteristic equation give $\lambda _1=-d$ and $\lambda _2 = -(d+r)$ as eigenvalues and the remaining factor is $\lambda ^2 + b_1 \lambda +b_0=0,$ where

$$\begin{aligned} b_1=&\ k_1+2 d+2\alpha +d_T > 0,\\ b_0=&\left( k_1+d+\alpha \right) \left( d+d_T+\alpha \right) -\beta _T k_1. \end{aligned}$$

Here, $b_0$ is positive if and only if $\mathcal {R}_T<1$. Therefore, by the Routh-Hurwitz criterion all the eigenvalues of $J_{T_0}$ have a negative real part if $\mathcal {R}_T<1$. Hence, the disease-free equilibrium point is locally asymptotically stable if $\mathcal {R}_T<1$, and is a saddle point if $\mathcal {R}_T>1$.

Theorem 4.2

The equilibrium point $E_{T_0}=(\frac{\Lambda }{d},0,0,0)$ for the model system (4.1) is globally asymptotically stable, provided $\mathcal {R}_T<1$ and the conditions (H1) and (H2) given in Sect. 3.2 are satisfied.

Proof

We know that the disease-free equilibrium point $E_{T_0}$ for the TB sub-model exists and is locally asymptotically stable for $\mathcal {R}_T<1$. Thus, the global stability of $E_{T_0}$ can be proved in the region where $\mathcal {R}_T<1$. For proving this, let $U= (S,R_T) ^T\in \mathbb {R}_+^2$ be the vector whose coordinates represent the uninfected class of the population and let $I = (L_T,I_T)^T\in \mathbb {R}_+^2$ be the vector whose coordinates represent the two classes $L_T$ and $I_T$ of TB-infected individuals. Here, $E_{T_0}=(U_0,0)$, with $U_0=\left( \frac{\Lambda }{d},0\right) .$ For our model system in Eq. (4.1), F(U, I) and G(U, I) of Eq. (3.5) are given by

$$\begin{aligned} F(U,I) = \begin{bmatrix} \Lambda -\lambda _T S -dS+r R_T\\ h(L_T)+h(I_T)-(d+r) R_T\\ \end{bmatrix} \text { and } G(U,I) = \begin{bmatrix} \lambda _T S-h(L_T) -( k_1+d )L_T\\ k_1 L_T-h(I_T)-(d+d_T) I_T\\ \end{bmatrix}. \end{aligned}$$

Now, for condition (H2) we consider the expression

$$\begin{aligned} G(U,I) = AI - \hat{G}(U,I),\ \ \text{ where } A=D_I G(U_0,0). \end{aligned}$$

Thus, we get

$$\begin{aligned} \hat{G}(U,I)= \begin{bmatrix} \beta _T I_T(1-\frac{S}{N})- \dfrac{\alpha \omega L_T^2}{1+\omega L_T}\\ - \dfrac{\alpha \omega I_T^2}{1+\omega I_T}\\ \end{bmatrix}. \end{aligned}$$

It can be clearly seen that $\hat{G}(U,I)\geqslant 0$, if $\omega =0$. This implies that the disease-free equilibrium point is globally asymptotically stable for $\mathcal {R}_T<1$ in the absence of resource limitation. Epidemiologically, if there is no limitation on resources for the treatment of TB then the disease will die out in the long run.

Remark 4.3

If $\omega \ne 0$, the disease-free equilibrium point may not be globally asymptotically stable. Hence, a transcritical bifurcation may occur near $\mathcal {R}_T=1$.

4.2 Existence and Stability of the Endemic Equilibrium Point

In this section we shall compute the endemic equilibrium point for the TB sub-model.

The endemic equilibrium point for the TB sub-model is given as $\hat{E}_T=(\hat{S},\hat{L}_T,\hat{I}_T,\hat{R}_T)$ with

$$\begin{aligned}&\hat{S} = \frac{(k_1+d+\alpha )\hat{L}_T+\omega (k_1+d)\hat{L}_T^2}{\lambda _T(1+\omega \hat{L}_T)},\end{aligned}$$

(4.5)

$$\begin{aligned}&\hat{L}_T=\frac{(\alpha +d+d_T)\hat{I}_T+\omega (d+d_T)\hat{I}_T^2}{k_1(1+\omega \hat{I}_T)},\end{aligned}$$

(4.6)

$$\begin{aligned}&\hat{R}_T=\frac{1}{d+r}\left( \frac{\alpha \hat{I}_T}{1+\omega \hat{I}_T}+\frac{\alpha (\alpha +d+d_T)\hat{I}_T+\alpha \omega (d+d_T) \hat{I}_T^2}{k_1+\omega (\alpha +k_1+d+d_T)\hat{I}_T+\omega ^2(d+d_T)\hat{I}_T^2}\right) , \end{aligned}$$

(4.7)

where $\hat{I}_T$ can be determined by substituting the values of $\hat{S}$ and $\hat{R}_T$ in equation

$$\begin{aligned} \Lambda = (\lambda _T+d) \hat{S}-r \hat{R}_T \end{aligned}$$

(4.8)

and $\lambda _T$ can be computed using the expression

$$\begin{aligned} \lambda _T ( \hat{S}+\hat{L}_T+\hat{I}_T+\hat{R}_T)=\beta _T \hat{I}_T. \end{aligned}$$

(4.9)

The endemic equilibrium point exists if $\hat{S} > 0$, $\hat{L}_T > 0$, $\hat{I}_T > 0$ and $\hat{R}_T > 0$. Further the endemic equilibrium point $\hat{E}_T$ is unique if $\hat{I}_T$ and the corresponding value of $\lambda _T$ can be uniquely obtained from Eqs. (4.8) and (4.9), respectively.

Let us assume $S=x_1, L_T=x_2, I_T=x_3$ and $R_T=x_4$, such that $N=x_1+x_2+x_3+x_4$. With this, the TB sub-model can be expressed as

$$\begin{aligned} \begin{aligned}&\frac{dx_1}{dt}=f_1= \Lambda -\lambda _T x_1 -dx_1+rx_4,\\&\frac{dx_2}{dt}=f_2= \lambda _T x_1 -h(x_2)-(k_1+d )x_2,\\&\frac{dx_3}{dt}=f_3= k_1 x_2-h(x_3)- (d +d_T) x_3,\\&\frac{dx_4}{dt}=f_4= h(x_2)+ h(x_3) -(d+r) x_4, \end{aligned} \end{aligned}$$

(4.10)

with $\lambda _T=\frac{\beta _T x_3}{N}$.

Now, $\mathcal {R}_T= 1$ gives $\beta _T = \beta ^* = \dfrac{(k_1+d+\alpha )(d+d_T+\alpha )}{k_1}$. The Jacobian matrix evaluated at the disease-free equilibrium point $E_{T_0}$ is given as

$$\begin{aligned} J_{T_0} = \begin{bmatrix} -d &{} 0 &{} -\beta _T &{} r \\ 0 &{} -(k_1+d+\alpha ) &{} \beta _T &{} 0\\ 0 &{} k_1 &{} -(d+d_T+\alpha ) &{} 0\\ 0 &{} \alpha &{} \alpha &{} -(d+r)\\ \end{bmatrix}. \end{aligned}$$

Clearly, this matrix has zero as a simple eigenvalue when $\mathcal {R}_T=1$. The remaining eigenvalues of the matrix $J_{T_0}$ have a negative real part. Therefore, the system (4.10) has a non-hyperbolic critical point. We use Theorem (3.3), which along with determining the local stability of the non-hyperbolic critical point also gives condition for the occurrence of a transcritical bifurcation. We calculate left and right eigenvectors for the Jacobian matrix $J_{T_0}$. The left eigenvector is computed as $v=[v_1,v_2,v_3,v_4]$, where

$$\begin{aligned} v_1 = 0, \ \ v_2=\frac{k_1}{k_1+d+\alpha }, \ \ v_3=1, \ \ v_4=0. \end{aligned}$$

The right eigenvector is $w=[w_1,w_2,w_3,w_4]$, where

$$\begin{aligned}&w_1=\frac{r \alpha (k_1+d+\beta _T+\alpha )-\beta _T(d+r)(k_1+d+\alpha )}{d (d+r) (k_1+d+\alpha )}, \ \ w_2=\frac{\beta _T}{k_1+d+\alpha },\\&\ w_3=1 \quad \hbox {and} \quad w_4=\frac{\alpha (k_1+d+\beta _T+\alpha )}{(d+r)(k_1+d+\alpha )}. \end{aligned}$$

By evaluating all the partial derivatives of $f_i$ with respect to $x_i$, for $i=1,2,3,4$, and $\beta ^*$, at the disease-free equilibrium point, we get

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 f_2}{\partial x_2^2}=2 \alpha \omega ,\quad \frac{\partial ^2 f_2}{\partial x_2 \partial x_3}=-\frac{\beta ^*d}{\Lambda },\quad \frac{\partial ^2 f_2}{\partial x_3^2}=-\frac{2 \beta ^*d}{\Lambda },\\&\frac{\partial ^2 f_2}{\partial x_3 \partial x_4}=-\frac{\beta ^*d}{\Lambda } \quad \frac{\partial ^2 f_3}{\partial x_3^2}=2 \alpha \omega \ \ \text{ and } \ \ \frac{\partial ^2 f_2}{\partial x_3 \partial \beta ^*}= 1. \end{aligned} \end{aligned}$$

(4.11)

The remaining second derivatives appearing in the formula for a and b are all zero. Hence, we get

$$\begin{aligned} a =&\ \sum _{k,j,i=1} ^3 { v_k w_iw_j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0)}\\ =&\ \frac{1}{(k_1+d+\alpha )^2} M,\quad \text{ where }\\&M = \frac{2 \alpha \omega }{k_1+d+\alpha } \left( \left( k_1+d+\alpha \right) ^3+k_1 \beta ^{*^2}\right) -\frac{2\beta ^* k_1 d}{\Lambda (d+r)}(\beta ^*+k_1+d+\alpha )(d+r +\alpha ).\\ b=&\sum _{k,i=1} ^3 {v_k w_i \frac{\partial ^2 f_k}{\partial x_i \partial \beta ^*}(0,0)}\\ =&\ v_2 > 0. \end{aligned}$$

We observe that $a<0$ if $M<0$. Also we can clearly see that $b>0$. Therefore, by Theorem (3.3) the endemic equilibrium point for the model system (4.1) is locally asymptotically stable when $\mathcal {R}_T>1$, $\beta ^*<\beta _T$, with $\beta _T$ close to $\beta ^*$ and $M<0$. The system undergoes a supercritical transcritical bifurcation at $\beta _T = \beta ^*$. We summarize this in the form of the following theorem:

Theorem 4.4

The endemic equilibrium point $\hat{E}_T$ is locally asymptotically stable for $\mathcal {R}_T>1$ if $M<0$. Further the system exhibits a supercritical transcritical bifurcation at $\mathcal {R}_T=1,$ with $\beta _T = \beta ^*$ as bifurcation parameter for $M<0$, and undergoes a subcritical transcritical bifurcation for $M>0$.

Remark 4.5

If $\alpha =0$, that is, there are no treatment options available for TB, then for $\mathcal {R}_T<1$ the disease-free equilibrium point is globally asymptotically stable, and for $\mathcal {R}_T>1$ the system exhibits a supercritical transcritical bifurcation. Hence, for $\alpha =0$ the endemic equilibrium point for the TB sub-model is locally asymptotically stable (if it exists) when $\mathcal {R}_T>1$.

5 Analysis of the Full Model

In this section we analyze the full HIV-TB co-infection model given by Eq. (2.1). The full model will have four endemic equilibrium points, namely, a disease-free equilibrium point $E_0$, a HIV endemic equilibrium point $E_H$, a TB endemic equilibrium point $E_T$ and an interior endemic equilibrium point $E_{T_H}$.

5.1 Stability Analysis of the Disease-Free Equilibrium Point

The disease-free equilibrium point for the full model is given by

$$\begin{aligned} E_0 = \left( \frac{\Lambda }{d},0,0,0,0,0,0,0,0,0\right) . \end{aligned}$$

(5.1)

The associated basic reproduction number $\mathcal {R}_0$ calculated using the next-generation matrix approach is given as

$$\begin{aligned} \mathcal {R}_0=\text {max}\{\mathcal {R}_H,\mathcal {R}_T\}. \end{aligned}$$

(5.2)

Here, $\mathcal {R}_H$ and $\mathcal {R}_T$ are the reproduction numbers corresponding to HIV and TB given by Eqs. (3.4) and (4.4), respectively.

Theorem 5.1

The disease-free equilibrium point for the full HIV-TB model (2.1) given by $E_0$ is locally asymptotically stable if $\mathcal {R}_0<1$, and unstable otherwise.

Proof

The Jacobian matrix for the system (2.1) evaluated at the disease-free equilibrium point given by Eq. (5.1) is

$$\begin{aligned} J_0= \begin{bmatrix} -d &{} 0 &{}-\beta _T &{} r&{} -\beta _H &{}-\gamma \beta _H &{} -\beta _H&{} -\beta _T-\beta _H &{}-\gamma \beta _H &{} -\beta _T-\gamma \beta _H\\ 0 &{} g_1 &{} \beta _T &{} 0 &{} 0 &{} 0 &{} 0 &{} \beta _T &{} 0 &{} \beta _T \\ 0 &{} k_1 &{} g_2 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \alpha &{} \alpha &{} -(r+d) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{}0\\ 0 &{} 0 &{} 0 &{}0 &{}g_3 &{} \gamma \beta _H+\tau &{} \beta _H+\alpha &{} \beta _H+\alpha &{} \gamma \beta _H &{} \gamma \beta _H\\ 0 &{} 0 &{} 0 &{} 0 &{} \rho _1 &{} g_4 &{} 0 &{} 0 &{} \alpha &{} \alpha \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} g_5 &{} 0 &{} \tau &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} k_2 &{} g_6 &{} 0 &{} \tau \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \rho _2 &{} 0 &{} g_7 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \rho _3 &{} k_3 &{} g_8\\ \end{bmatrix}, \end{aligned}$$

where $g_1= -(k_1+\alpha +d)$, $g_2=-(\alpha +d+d_T)$, $g_3=\beta _H-(\rho _1+d)$, $g_4=-(d+d_A+\tau )$, $g_5=-(\alpha +\rho _2+k_2+d)$, $g_6=-(\alpha +\rho _3+d+d_T)$, $g_7= -(\alpha +k_3+d+d_A+\tau )$ and $g_8=-(\alpha +\tau +d+d_{A_T}).$

The characteristic equation for the matrix $J_0$ is given by

$$\begin{aligned}&(\lambda +d)(\lambda +d+r)(\lambda ^2+\lambda (2d+ 2 \alpha +\tau +\rho _3+d_{A_T})+d_{A_T}(d+\alpha +\rho _3)+(d+\alpha )(d+\alpha +\tau +\rho _3))\\&(\lambda ^2+\lambda (2d +2\alpha +\tau +d_A+k_2+k_3+\rho _2)+(d+\alpha +k_2)(d+d_A+\alpha +\tau +k_3)+\rho _2(d+d_A+\alpha +k_3))\\&(\lambda ^2+\lambda (2d +\tau +d_A+\rho _1-\beta _H)+(d+\rho _1)(d+d_A+\tau )-\beta _H(d+d_A+\tau +\gamma \rho _1)-\tau \rho _1)\\&(\lambda ^2+\lambda (2d+ 2\alpha +d_T+k_1)+(d+\alpha +d_T)(d+\alpha +k_1)-k_1 \beta _T) =0. \end{aligned}$$

In the first four factors of the characteristic equation, all coefficients of $\lambda$ and the constant terms are positive. Therefore, by the Routh-Hurwitz criterion all the roots corresponding to the first four factors have a negative real part. Whereas in the fifth factor the coefficient of $\lambda$, which is $2d +\tau +d_A+\rho _1-\beta _H$, and the constant term $(d+\rho _1)(d+d_A+\tau )-\beta _H(d+d_A+\tau +\gamma \rho _1)-\tau \rho _1$ are positive if $\mathcal {R}_H<1$. Thus, both the roots of the fifth factor have a negative real part if $\mathcal {R}_H<1$.

In the sixth factor, the coefficient of $\lambda$, which is $2d+ 2\alpha +d_T+k_1$ is always positive. The constant term in the sixth factor is $(d+\alpha +d_T)(d+\alpha +k_1)-k_1 \beta _T$. Now,

$$\begin{aligned} (d+\alpha +d_T)(d+\alpha +k_1)-k_1 \beta _T>0 \ \ \text{ if } \text{ and } \text{ only } \text{ if } \ \ \frac{k_1 \beta _T}{(d+\alpha +d_T)(d+\alpha +k_1)}<1, \end{aligned}$$

that is, if $\mathcal {R}_T<1$. Thus, both the roots of the sixth factor have negative real part if $\mathcal {R}_T<1$.

Therefore, if $\mathcal {R}_H<1$ and $\mathcal {R}_T<1$, that is, $\max \{\mathcal {R}_H,\mathcal {R}_T\}=\mathcal {R}_0<1$ then all the roots of the characteristic equation corresponding to the matrix $J_0$ have a negative real part. Hence, $E_0$ is locally asymptotically stable if $\mathcal {R}_0<1$, and unstable otherwise.

Theorem 5.2

For the model system (2.1), the disease-free equilibrium point $E_0$ is globally asymptotically stable provided $\mathcal {R}_0<1$ and the conditions (H1) and (H2) given in Sect. 3.2 are satisfied.

Proof

In the previous theorem it has been proved that $E_0$ is locally asymptotically stable for $\mathcal {R}_0<1$. Thus, we can check the global stability of $E_0$ in the region where $\mathcal {R}_0<1$. Let us consider $U= (S,R_T)^T \in \mathbb {R}_+^2$ as the vector whose coordinates represent the uninfected class of population, and $I = (L_T,I_T,I_H,A_H,L_{T_H},I_{T_H},L_{A_T},A_{T_H})^T$ $\in \mathbb {R}_+^8$ as an $8-$dimensional vector in which each coordinate represents a class of infected individuals. Here $E_0 = (U_0,0)$, with $U_0 = \frac{\Lambda }{d}$.

For our model system in equation (2.1)

$$\begin{aligned} \hat{G}(U,I)= \begin{bmatrix} \beta _T(I_T+I_{T_H}+A_{T_H})\left( 1-\frac{S}{N}\right) +\lambda _H L_T-\frac{\alpha \omega L_T^2 }{1+\omega L_T}\\ \lambda _H I_T-\frac{\alpha \omega I_T^2 }{1+\omega I_T}\\ \eta _1 \lambda _T I_H+ \beta _H C \left( 1-\frac{S}{N}\right) -\lambda _H R_T+ \frac{\alpha \omega L_{T_H}^2}{1+ \omega L_{T_H}}+ \frac{\alpha \omega I_{T_H}^2}{1+ \omega I_{T_H}}\\ \eta _2 \lambda _T A_H+\frac{\alpha \omega L_{A_T}^2}{1+\omega L_{A_T}}+\frac{\alpha \omega A_{T_H}^2}{1+\omega A_{T_H}}\\ - \eta _1 \lambda _T I_H-\frac{\alpha \omega L_{T_H}^2}{1+\omega L_{T_H}}-\lambda _H L_T\\ -\lambda _H I_T-\frac{\alpha \omega I_{T_H}^2}{1+\omega I_{T_H}}\\ -\frac{\alpha \omega L_{A_T}^2}{1+\omega L_{A_T}} - \eta _2 \lambda _T A_H\\ -\frac{\alpha \omega A_{T_H}^2}{1+\omega A_{T_H}} \end{bmatrix}, \end{aligned}$$

where $C = I_H+I_{T_H}+L_{T_H}+\gamma (A_H+L_{A_T}+A_{T_H})$. Clearly, it can be seen that $\hat{G}(U,I)\ngeq 0$, which means that the condition (H2) is not satisfied. Thus, the fixed point $E_0=(U_0,0)$ may not be globally asymptotically stable.

Fig. 2

Global stability of the equilibrium points for the HIV sub-model

Fig. 3

Local stability of $E^2_T$

Fig. 4

Local stability of $E_T$

5.2 Endemic Equilibrium Points

We have computed three more equilibrium points corresponding to HIV, TB and HIV-TB co-infection which are given as follows:

• (1) The HIV endemic equilibrium point is given by

  $$\begin{aligned} E_H=(S^*,0,0,0,I^*_H,A^*_H,0,0,0,0), \end{aligned}$$

  where $S^*, I^*_H, A^*_H$ are given by Eqs. (3.6), (3.7) and (3.8), respectively. The HIV endemic equilibrium point $E_H$ exists if $\mathcal {R}_H>1$.

• (2) The TB endemic equilibrium point is given as

  $$\begin{aligned} E_T=(\hat{S},\hat{L}_T,\hat{I}_T,\hat{R}_T,0,0,0,0,0,0), \end{aligned}$$

  where $\hat{S}, \hat{L}_T,\hat{I}_T$ and $\hat{R}_T$ take the values as given by Eqs. (4.5), (4.6), (4.8) and (4.7), respectively. The TB endemic equilibrium point $E_T$ exists when $\hat{S} > 0$, $\hat{L}_T > 0$, $\hat{I}_T > 0$ and $\hat{R}_T > 0.$

• (3) The interior endemic equilibrium point for the system (2.1) exists when both diseases are present in the population and is given by

  $$\begin{aligned} E_{T_H}=(\tilde{S},\tilde{L}_T,\tilde{I}_T,\tilde{R}_T,\tilde{I}_H,\tilde{A}_H,\tilde{L}_{T_H},\tilde{I}_{T_H},\tilde{L}_{A_T},\tilde{A}_{T_H}), \end{aligned}$$

  which exists if all the components of $E_{T_H}$ are positive.

6 Numerical Simulations

In this section numerical simulations are performed, by taking into account the initial conditions $S(0)=9080,\ L_T(0)= 2080,\ I_T(0)= 354, \ R_T(0)= 0,$ $I_H(0)= 1500, \ A_H(0)= 420,\ L_{T_H}(0)=1095,\ I_{T_H}(0)=137, \ L_{A_T}(0)= 325,$ and $A_{T_H}(0)= 29$, together with the estimated value of parameters. Due to limitation on resources, approximately $70\%$ of TB infected population will initially get the treatment facility, which enforced to estimate the value of $\alpha$ as 0.7. In this paper, the value of $k_1$ is taken as 0.213 due to the fact that a latent TB infected individual takes on an average about 4.69 years to become actively infected with TB. Since, HIV infectives have a weak immune system, therefore $\eta _1$ is chosen as 1.02 which implies that they are more prone to catch TB than the susceptibles. Also, AIDS infectives have a weaker immune system than HIV infectives, therefore, $\eta _2$ is taken as 1.04 which indicates that they can be affected by TB faster than the susceptibles. The remaining initial conditions have been taken as per the reviewed literature, mentioned in Table (2).

Fig. 5

Local stability of $E^w_0$

Fig. 6

Local stability of $E^w_T$

Fig. 7

Local stability of $E^w_H$

Fig. 8

Effect of the treatment and resource limitation on infected and uninfected classes

We begin with illustrating the stability of the disease-free and the endemic equilibrium point for the HIV sub-model numerically. By using the prescribed parameter values, the disease-free equilibrium point is obtained as $E_{H_0}=(12500,0,0)$ corresponding to the reproduction number $\mathcal {R}_H=0.881842<1$. In Fig. 2a it can be seen that in the long run every solution trajectory with different initial conditions approach towards $E_{H_0}$. This justifies the global stability of the disease-free equilibrium point $E_{H_0}$ for $\mathcal {R}_H<1$. If we choose $\beta _H=0.075$, we obtain $\mathcal {R}_H=1.20251$, which is greater than unity. Thus, the HIV-endemic equilibrium point computed as $E^*_H=(7653.96,1352.06,197.959)$ becomes locally asymptotically stable. Figure 2b illustrates the stability of $E^*_H$, in which solution trajectories started from different initial values are approaching towards the components of $E^*_H$.

Fig. 9

Effect of $\omega$ on the population

Fig. 10

Effect of $\alpha$ on the population

As the full model is a ten-dimensional system of non-linear differential equations, only limited analytical results are obtained for the full model in comparison to the HIV and the TB sub-models. Hence, we try to investigate some results for the full model system numerically with the parameter values given in Table 2 and the initial conditions as described above. With those parameter values it is found that $\mathcal {R}_0<1$ ($\mathcal {R}_H=0.881842$ and $\mathcal {R}_T=0.29233$). In this case along with the locally stable disease-free equilibrium point $E_0= (12500,0,0,0,0,0,0,0,0,0)$, two TB endemic equilibrium points exist, namely, $E^1_T=(12338.1,29.9981,13.21,52.6293,0,0,0,0,0,0)$ which is unstable and $E^2_T=(467.153,1067.72,1812.53$ , 89.9535, 0, 0, 0, 0, 0, 0) which is stable. In Fig. 3a, b it can be seen that the susceptibles are approaching towards 467.153, individuals infected with latent TB are approaching towards 1067.72, TB infectives approach towards 1812.53, individuals recovered from TB approach towards 89.9535 and the remaining solution trajectories corresponding to $I_H, A_H, L_{T_H}, I_{T_H}, L_{A_T}$ and $A_{T_H}$ are approaching toward zero. This justifies the local stability of $E^2_T$. Using XPPAUT (Ermentrout 2002), phase portraits are formed (see Fig. 3c, d), from which it can be seen that all the nearby solution trajectories are approaching toward the components of $E^2_T$, which also justifies the local stability of $E^2_T$. The existence of TB endemic equilibrium points $E^1_T$ and $E^2_T$ for $\mathcal {R}_0<1$ illustrate the fact that under resource limitation conditions reducing the reproduction number below one is not enough to control the disease. Next, the case when $\mathcal {R}_H=0.881842<1$ and $\mathcal {R}_T=1.03012>1$ (for $\beta _H=0.055$ and $\beta _T=3.7$, respectively) is considered. In this case two equilibrium points are found, one is the disease-free equilibrium point $E_0$ which is unstable and the other is the locally asymptotically stable TB endemic equilibrium point $E_T=(122.162,1097.34,1865.09,89.9794,0,0,0,0,0,0),$ which can be seen in Fig. 4. Our numerical calculations show interesting aspects under the setting when $\mathcal {R}_H=1.20251$ and $\mathcal {R}_T=0.29233$ (for $\beta _H=0.075$ and $\beta _T=1.05$, respectively). In this case five equilibrium points are computed, namely, a disease-free equilibrium point $E_0$ which clearly is unstable, a HIV endemic equilibrium point $E_H(7653.96,0,0,0,1352.06,197.959,0,0,0,0)$, two TB endemic equilibrium points $E^1_T$ and $E^2_T$ and an interior endemic equilibrium point $E^1_{T_H}=(7530.02,35.9683,16.9064,54.0949,1324.85,$ 194.153, 3.66679, 1.29311, 0.486523 , 0.323809). This shows that under resource limitation conditions both diseases HIV and TB can co-exist, even if the reproduction number corresponding to TB is less than one.

The effect of the reproduction number on infected individuals by considering a linear treatment rate for HIV-TB co-infection can be seen in Kumar and Jain’s paper (Kumar and Jain 2018). This paper (Kumar and Jain 2018) is different from our paper from biological point of view as they have taken a linear treatment rate for infected individuals, which signifies an infinite capacity for the treatment of a disease. To make the model more realistic, a Holling type-II function for the treatment for TB has been considered in our paper. In the Kumar and Jain’s paper (Kumar and Jain 2018) single disease treatment was studied, that is, treatment for TB-only and HIV-only patients. They showed that no epidemic can last forever when there is no limitation on resources. But according to our model, HIV and TB can co-exist in the population when the amount of resources for the treatment of TB is limited.

Our model has also been investigated for the case when there is no resource limitation, that is, $\omega =0$. In this case, for $\mathcal {R}_0<1$ ($\mathcal {R}_H=0.881842$ and $\mathcal {R}_T=0.29233$) only the disease-free equilibrium point $E^w_0=(12500,0,0,0,0,0,0,0,0,0)$ exists, which is locally asymptotically stable, as shown in Fig. 5. If $\mathcal {R}_H=0.881842<1$ and $\mathcal {R}_T=1.03012>1$, two equilibrium points exist, an unstable disease-free equilibrium point $E^w_0$ and a stable TB endemic equilibrium point $E^w_T= (12047.7,68.8717,17.8898,276.059,0,0,0,$ 0, 0, 0). Local stability of $E^w_T$ can be seen in Fig. 6. On the other hand, if $\mathcal {R}_H=1.20251$ and $\mathcal {R}_T=0.29233$, an unstable disease-free equilibrium point $E^w_0$ and a stable HIV endemic equilibrium point $E^w_H= (7653.96,0,0,0,1352.06,197.9590,0,0,0,0)$ (see Fig. 7) exist. If $\mathcal {R}_H=1.20251>1$ and $\mathcal {R}_T=1.03012>1$ (for $\beta _H=0.075$ and $\beta _T=3.7$, respectively), four equilibrium points are obtained, namely, $E^w_0$, $E^w_T$, $E^w_H$ and an endemic equilibrium point $E^w_{T_H}=(7318.28,76.329,19.5362,288.999,1283.6,188.212,$ 13.2656, 3.89858, 1.96221,  1.0649). This shows that for $\omega =0$ both diseases can co-exist in the population if both $\mathcal {R}_H$ and $\mathcal {R}_T$ are greater than one.

Furthermore, the effect of treatment rate and resource limitation on total infected ($L_T(t)+I_T(t)+I_H(t)+A_H(t)+L_{T_H}(t)+I_{T_H}(t)+ L_{A_T}(t)+A_{T_H}(t)$) individuals and uninfected individuals ($S(t)+R(t)$) can be seen when both the disease are endemic, that is, when $\mathcal {R}_H=1.20251>1$ and $\mathcal {R}_T=1.03012>1$. From Fig. 8a it can be seen that the total infectives initially increase to a higher level and then settle down when both the treatment rate and the resource limitation term are zero in comparison to the case when treatment for TB is available with very small limitation on resources. On the other hand, if treatment for TB is available without the limitation on resources, infected individuals start decreasing. Figure 8b shows that the uninfected class of population increases to a higher level when treatment is provided without any limitation on resources. Whereas they start decreasing either if there is no treatment or if the treatment is available with limitation on resources for infected individuals. This happened because more and more individuals became infected and entered into the infected class in this case.

In Fig. 9, the effect of a non-linear treatment rate by changing the amount of limitation on resources ($\omega$) can be observed by taking the remaining parameter values from Table (2) and initial conditions as described in the beginning of the section to obtain $\mathcal {R}_H=1.20251$ and $\mathcal {R}_T=0.03012$. We have plotted the graphs of the population against time for four different values of the resource limitation term: $\omega =0$, $\omega =0.01$, $\omega =0.07$ and $\omega =5$. From Fig. 9a, b it can be noticed that the number of infected individuals reduces to zero with respect to time if there is no limitation on resources for treatment. However, for $\omega >0$, the population in each class $L_T$ and $I_T$ initially rises and then each starts diminishing and reduces to a fixed value for each $\omega >0$. It can also be seen that increase in population is proportional to the increase in $\omega$, that is, higher limitation on resources causes more infectives. From Fig. 9c it can be observed that if $\omega =0$, that is, if there is no limitation on resources for the treatment of TB, then the population recovered from TB rises initially and then approaches zero as individuals become susceptible again. As the limitation on resources becomes large, improvement in the recovered population reduces significantly. The population in class $R_T$ approaches zero for $\omega =5$. The dynamics of the population in each of the class $L_{T_H}$ and $L_{A_T}$ is slightly different, which can be seen in Fig. 9d, f. If the limitation on resources for treatment is zero, then the population in the classes $L_{T_H}$ and $L_{A_T}$ diminishes to zero with respect to time. If $\omega$ rises, then initially the infected population increases proportional to the limitation on resources and then starts diminishing inversely proportional to the limitation on resources with respect to time, because of transfer of individuals infected with latent TB to the class of individuals actively infected with TB. Now from Fig. 9e, g it can be seen that if there is no resource limitation, that is, $\omega =0$, then the population numbers in the classes $I_{T_H}$ and $A_{T_H}$ approach zero. On the other hand, if $\omega$ increases, then the number of individuals in the classes $I_{T_H}$ and $A_{T_H}$ also start increasing. Hence, to eradicate the disease from the population, proper treatment without limitation on resources has to be provided.

The impact of the initial per capita treatment rate for TB infectives over the population can be visualized in Fig. 10 by keeping the remaining parameter values same as given in Table (2). We have plotted graphs for four different values of the initial per capita treatment rate: $\alpha =6$, $\alpha =4$, $\alpha =2$ and $\alpha =0$ (see Fig. 10). Corresponding to them $\mathcal {R}_H=1.20251$ and the reproduction numbers for TB are obtained as $\mathcal {R}_T=0.0206601$, $\mathcal {R}_T=0.0451893$, $\mathcal {R}_T=0.166478$ and $\mathcal {R}_T=28.1867$, respectively. From Fig. 10a, b it can be seen, as $\alpha$ increases, then the population in the classes $L_T$ and $I_T$ also increase initially, but with a rate which is inversely proportional to $\alpha$. This means that a higher initial per capita treatment rate implies a lower rate of increase for these classes. After some time interval, population in the class $I_T$ starts decreasing proportionally to $\alpha$ as a result of treatment, whereas population in the class $L_T$ diminishes inversely proportional to $\alpha$ as its individuals are entering into the class of active TB infected individuals more rapidly for a lower value of $\alpha$. From Fig. 10c it can be observed that the population in class $R_T$ increases proportional to $\alpha$, that is, for a higher initial per capita treatment rate more individuals are recovering from TB. Now Fig. 10d, f show the behaviour of individuals in the classes $L_{T_H}$ and $L_{A_T}$. Population in the classes $L_{T_H}$ and $L_{A_T}$ start rising as $\alpha$ decreases and after some interval of time the number of individuals in both classes start diminishing inversely proportional to $\alpha$ because of the progression of latently infected individuals into the active class of TB infection. Also, from Fig. 10e, g it can be observed that the population in the classes $I_{T_H}$ and $A_{T_H}$ start increasing as $\alpha$ decreases.

Our numerical results suggest that to reduce the prevalence of HIV-TB co-infection, improvement in TB treatment programs are required. Although, this may not be easy due to the lack of effective medication facilities. However, significant reductions may be obtained by increasing resources for treatment.

7 Conclusion

In this paper, a HIV-TB co-infection model which incorporates a non-linear treatment rate for TB has been discussed, by taking into consideration the Holling type-II function as a treatment rate for TB infected classes, with the inhibition effect $\frac{1}{1+\omega I}$. The term $\omega$ which indicates the limitation of resources for the treatment of TB negatively influences the initial per capita treatment rate $\alpha$. The HIV sub-model has been shown to exhibit a supercritical transcritical bifurcation, with bifurcation parameter $\beta _H=\beta ^*$. When $\beta _H=\beta ^*$, the globally stable disease-free equilibrium point changes its stability from stable to unstable and an endemic equilibrium point comes into existence. On the other hand, for the TB sub-model, the disease-free equilibrium point is locally asymptotically stable when its corresponding reproduction number is less than unity. It is determined that the disease-free equilibrium point for the TB sub-model is globally asymptotically stable only when there is no limitation on the resources for TB treatment. The endemic equilibrium point for the TB sub-model, if it exists, is locally asymptotically stable under certain conditions on the parameters. The full HIV-TB co-infection model has been shown to have a locally asymptotically stable disease-free equilibrium point. In literature, some authors have introduced a mathematical model with linear treatment rate on infected individuals, which signifies that the disease can not remain forever, if there is no restriction on the availability of resources. However, in this paper we justify that the disease may remain in the community due to the limitation on resources.

Numerical simulations have provided many interesting insights about the dynamical interactions between HIV and TB and have shown the impact of TB on the prevalence of HIV. The existence and stability of the equilibrium points with a linear treatment rate as well as under resource limitation conditions have been verified. We derived the existence of a HIV-TB co-endemic equilibrium point even if $R_T<1$ under resource limitation conditions, which shows that reducing the basic reproduction number below one is not sufficient enough to eradicate the disease from the community. Thus, investing more in increasing the treatment rate for TB can be considered as a better approach to control HIV-TB co-infection prevalence. The effects of the resource limitation term ($\omega$) and the initial per capita treatment rate for TB ($\alpha$) on infected individuals have also been investigated, which justify the fact that efforts toward increasing the treatment rate and diminishing the factors that cause limitation on the availability of resources for the treatment are required to control the disease. Hence, it has been concluded that controlling the TB infection can be an asset in controlling the HIV-TB co-infection.