A fractional order HIV-TB co-infection model in the presence of exogenous reinfection and recurrent TB

Abstract

In this article, a novel fractional order model has been introduced in Caputo sense for HIV-TB co-infection in the presence of exogenous reinfection and recurrent TB along with the treatment for both HIV and TB. The main aim of considering the fractional order model is to incorporate the memory effect of both diseases. We have analyzed both sub-models separately with fractional order. The basic reproduction number, which measures the contagiousness of the disease, is determined. The HIV sub-model is shown to have a locally asymptotically stable disease-free equilibrium point when the corresponding reproduction number, $\mathcal {R}_H$, is less than unity, whereas, for $\mathcal {R}_H>1$, the endemic equilibrium point comes into existence. For the TB sub-model, the disease-free equilibrium point has been proved to be locally asymptotically stable for $\mathcal {R}_T<1$. The existence of TB endemic equilibrium points in the presence of reinfection and recurrent TB for $\mathcal {R}_T<1$ justifies the existence of backward bifurcation under certain restrictions on the parameters. Further, we numerically simulate the fractional order model to verify the analytical results and highlight the role of fractional order in co-infection modeling. The fractional order derivative is shown to have a crucial role in determining the transmission dynamics of HIV-TB co-infection. It is concluded that the memory effect plays a significant role in reducing the infection prevalence of HIV-TB co-infection. An increment in the number of recovered individuals can also be observed when the memory effect is taken into consideration by introducing fractional order model.

1 Introduction

Mathematical modeling is a process of developing a mathematical model to describe and analyze a physical problem using the mathematical concepts. From a mathematical and biological point of view, many diseases are there that require adequate attention such as COVID-19, dengue, HIV and tuberculosis (TB). Among these, HIV and TB are two diseases which have a synergistic relation between them and we will be examining the dynamics of their co-infection in this article.

TB is a contagious disease generated due to a rod-shaped bacteria called mycobacterium tuberculosis, which was first discovered in 1882. Around $90\%$ of people infected with latent TB remains latently infected and does not develop active TB disease [1]. Progression from latent TB to active TB can occur in two ways that are endogenous reactivation and exogenous reinfection [2]. Endogenous infection describes a situation in which an individual is already harboring the causative agent, mycobacterium tuberculosis bacteria, which is under control due to a healthy immune system and reactivates to cause active TB due to the destabilization of Immune system, whereas exogenous reinfection in latent TB infectives occurs through the recent exposure to some external infectious sources, generally through contact with infectious individuals.

The human immunodeficiency virus weakens an individual’s immune system by attacking the immune system cells such as helper T cells, dendritic cells and macrophages. Even if HIV/AIDS is not permanently curable, antiretroviral therapy is used to improve the health of HIV-infected individuals and to fight against the opportunistic infections. HIV and TB are strongly interrelated to each other and accelerates the progression of each other. Due to the deficiency in immunity, HIV-infected individuals are at a higher risk of developing TB. In 2018, the number of individuals who died from HIV-TB co-infection was estimated to be 251, 000 [3]. Collaborative anti-TB and HIV activities such as HIV testing, antiretroviral therapy and TB preventive measures are required for the reduction in HIV-TB co-infection prevalence. The emergent requirement by the healthcare authorities led many researchers to work upon various infectious diseases including HIV-TB co-infection with an aim to provide strategies and control policies which reduce the transmission of HIV-TB co-infection [4,5,6,7,8,9,10,11,12,13,14].

Fractional calculus is an extension of ordinary calculus, which is an emerging field in the area of applied mathematics such as modeling of complex phenomena, neural networks and signal processing [15]. Kang et al. [16,17,18] have also worked on several physical phenomena of dynamical systems using the fractional order derivatives. It is a powerful tool that has been recently used by various researchers to model the complex dynamical systems such as modeling of infectious diseases that consist of nonlinear behavior and involvement of memory effect. The main advantage of fractional calculus is the inclusion of memory concepts. The memory features in fractional derivatives explore hidden dynamics of the infection which is not feasible to obtain with integer order derivatives. In case of disease modeling, memory effect also involves hereditary properties of an individual and prior knowledge of the disease which may come due to a previous exposure of the disease. As the study of fractional order derivatives incorporates memory effect of the disease (if any) and the hereditary properties, the use of fractional order differential equations proves to be more realistic during the study of infectious diseases rather than classical integer order models as integer order models do not take these properties into consideration. It is also known that individuals recovered from TB may not gain permanent immunity and suffer through the recurrence of TB either by the reinfection with a new strain of mycobacterium tuberculosis or relapse of original strain. This emergence of the second episode of TB after the successful recovery from the first episode of TB is termed as recurrent TB [19]. Hence, fractional order derivatives provide an excellent way to model the infectious diseases such as HIV/AIDS and TB.

Recently, many researchers have started working on the fractional order models to study the transmission dynamics of HIV and TB [20,21,22,23,24,25,26,27]. Pinto and Carvalho [28] proposed a fractional order HIV-TB co-infection model in the presence of multidrug-resistant TB strains and shows different dynamics of the model for various orders of fractional derivatives $\alpha \in (0,1]$, with biologically relevant parameters. Zafar et al. [29] presented a fractional order model in Caputo sense to describe the transmission dynamics of HIV with an aim to help the researchers and policy makers in targeting, prevention and treatment resources for maximum effectiveness. A fractional order derivative model has been proposed by Arshad et al. [30] by focusing on the degree of T cell depletion to study the transmission dynamics of HIV infection.

Directed by the aforementioned articles and the need of including memory effects to analyze the dynamics of HIV and TB, we have formulated and analyzed a fractional order HIV-TB co-infection model in Caputo sense by incorporating the effect of exogenous reinfection and recurrent TB. In this article, a nonlinear mathematical model has been formulated in the third section, together with the verification of existence and uniqueness of positive solutions. The HIV sub-model has been analyzed in the fourth section. The fifth section deals with the analysis of TB sub-model along with determining the conditions under which endemic equilibrium point exists. The full model has been analyzed in the sixth section. Sensitivity analysis of the reproduction number to the parameters has been done in the seventh section. In the eight section the system is solved numerically for distinct values of the order of fractional derivatives with biologically relevant parameters. Finally, in the last section, we conclude the study with a brief discussion.

In this article, the quantitative and qualitative analyses of the proposed model have been performed by following [31, 32].

2 Preliminaries

In this section, we will discuss some of the basic definitions describing the Caputo fractional order derivative.

Definition 2.1

[15] The fractional integral of order $\alpha >0$ for a function $h: \mathbb {R}^+ \rightarrow \mathbb {R}$ is defined as

$$\begin{aligned} I_t^{\alpha } h(t)= \frac{1}{\Gamma (\alpha )} \int _0^t (t-\chi )^{\alpha -1} h(\chi ) d \chi , \end{aligned}$$

where $\Gamma (.)$ denotes the gamma function.

Definition 2.2

[15] The Caputo fractional order derivative for a function $h \in C^n$ of order $\alpha$ is given as:

$$\begin{aligned} D_t^{\alpha } (h(t))&= I^{n-\alpha } D^n h(t)\\&= \frac{1}{\Gamma (n-\alpha )} \int _0^t \frac{h^n(\chi )}{(t-\chi )^{\alpha +n-1}}d\chi , \end{aligned}$$

which is defined for absolutely continuous functions and $(n-1)< \alpha <n$, where $n \in \mathbb {N}$.

Definition 2.3

[33] The constant $x^*$ is called an equilibrium point of the Caputo fractional dynamical system given below

$$\begin{aligned} D_t^{\alpha } x(t)=h(t,x(t)) , \ \ \alpha \in (0,1], \end{aligned}$$

if and only if, $h(t,x^*)=0$.

3 Model formation

In this section, we formulate a mathematical model to describe the transmission dynamics of HIV-TB co-infection by assimilating the treatment for both diseases along with the incorporation of exogenous reinfection and recurrent TB infection. We all know that co-infection of HIV and TB is considered as a very serious stage in an individual’s life regardless of the stage of HIV. Thus, in this paper, we do not differentiate between HIV and AIDS, which are the two clinical stages of HIV. However, we have considered both the forms of TB, that is, latent and active TB. In order to formulate the model, it is assumed that the population is entering into the susceptible class with a constant recruitment rate $\Lambda$. It is also assumed that susceptibles cannot become HIV-TB co-infected at the same time. Further, we have assumed that the co-infected individuals continuing HIV treatment after getting recovered from TB will follow certain precautionary measures to keep themselves away from TB-infected individuals in order to avoid TB reinfection.

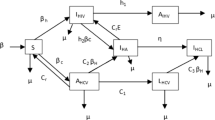
Different disease stages can be described by dividing the total population N(t) into eight mutually exclusive compartments, namely, the class of population susceptible to both diseases (S(t)), latent TB-infected individuals $(L_T(t))$, tuberculosis-infected individuals $(I_T(t))$, individuals recovered from TB $(R_T(t))$, only HIV-infected individuals $(I_H(t))$, individuals co-infected with latent TB and HIV $(L_{T_H}(t))$, individuals actively infected with TB and HIV $(I_{T_H}(t))$, individuals recovered from TB and under treatment of HIV $(R_H(t))$ in such a manner that

$$\begin{aligned} \begin{aligned} N(t)&= S(t)+L_T(t)+I_T(t)+R_T(t)\\&\quad +I_H(t)+L_{T_H}(t)\ +I_{T_H}(t)+R_H(t). \end{aligned} \end{aligned}$$

Individuals infected with TB and those who are co-infected with HIV and TB can spread TB among susceptible individuals with the force of infection, given as

$$\begin{aligned} \lambda _T=\frac{\beta _T}{N}(I_T+I_{T_H}). \end{aligned}$$

(3.1)

Further, HIV can be acquired by susceptible individuals after coming in contact with HIV infectives, HIV-TB co-infectives and individuals recovered from TB but still continuing antiretroviral therapy. Thus, the force of infection associated with HIV is given as

$$\begin{aligned} \lambda _H= \frac{\beta _H}{N}\left( I_H+L_{T_H}+ I_{T_H}+\eta R_H\right) . \end{aligned}$$

(3.2)

The modification parameter considered in $\lambda _H$, that is, $\eta <1$, accounts for the fact that the class of individuals undergoing antiretroviral therapy has a restored immune system and hence lesser viral load of HIV due to which they spread HIV at a lower rate. At the rate $\lambda _T$ and $\lambda _H$, susceptibles switch to the class of latent TB and HIV infectives, respectively. Individuals latently infected with TB progress to the class of active TB infectives at the rate $k_1 L_T$, with $k_1$ as the progression coefficient. Further, latent TB infectives also move into the class of active TB infectives due to the occurrence of exogenous reinfection at the rate $\phi _1 \lambda _T$, which may result from the recent exposure of latent TB infectives with actively infected individuals. Individuals actively infected with TB headway to the class of recovered individuals after getting completely recovered from TB at the rate $\tau$. Individuals from the recovered class again move to the class of latent TB infectives at the rate $\theta \lambda _T$, where $0 \leqslant \theta \leqslant 1$ describes the modification parameter accounting for the effectiveness of anti-TB treatment. Also, individuals suffering from latent TB and active TB acquire HIV infection at the rate $\lambda _H$. HIV infectives become co-infected with latent TB at the rate $\delta \lambda _T$, with the modification parameter $\delta >1$, justifying the fact that HIV-infected individuals are more prone to acquire TB infection due to weak immune system. Further, individuals co-infected with HIV and latent TB progress to the class of HIV-TB co-infected individuals at the rate $(k_2+\phi _2\lambda _T)$. The progression rate $k_2$ is considered in such a way that $k_2>k_1$, due to the fact that the risk of progression from latent to active TB class is estimated to be twenty times higher among HIV-positive individuals than HIV negative individuals [3] (Table 1).

Some co-infectives may not get detected with HIV and TB simultaneously. Thus, individuals in $I_{T_H}$ class who do not get detected with HIV start taking TB treatment only and enter in $I_H$ class after getting recovered from TB at the rate $r_1 \tau$. However, as advised by the healthcare authorities, individuals detecting from the co-infection burden of HIV and TB start taking TB treatment first and then commence HIV treatment either after the completion of TB treatment or after few weeks of the commencement of TB treatment on the basis of CD4+ cell count and move to $R_H$ class at the rate $r_2 \gamma$, where $r_2$ is the fraction of individuals detected both HIV and TB simultaneously. From the $I_H$ class, HIV infectives move to the $R_H$ class at the rate $\rho$. Using the schematic diagram given in Fig. 1, the differential equations describing the dynamics of population in all the classes can be expressed as

Table 1 The description of parameters

Fig. 1

Schematic diagram describing the transmission of HIV-TB Co-infection

$$\begin{aligned} \begin{aligned}&\frac{d^{\alpha } S}{dt^{\alpha }}=\Lambda -\lambda _T S-\lambda _H S-\mu S\\&\frac{d^{\alpha }L_T}{dt^{\alpha }}=\lambda _T S +\theta \lambda _T R_T \\&\quad -\lambda _H L_T-(k_1+\phi _1 \lambda _T) L_T-\mu L_T\\&\frac{d^{\alpha }I_T}{dt^{\alpha }}=(k_1+\phi _1 \lambda _T) L_T \\&\quad -\lambda _H I_T-(\tau +\mu +\mu _T) I_T\\&\frac{d^{\alpha }R_T}{dt^{\alpha }}=\tau I_T-\theta \lambda _T R_T-\lambda _H R_T-\mu R_T\\&\frac{d^{\alpha }I_H}{dt^{\alpha }}=\lambda _H S+\lambda _H R_T\\&\quad -\delta \lambda _T I_H+r_1 \tau I_{T_H}-(\rho +\mu +\mu _H) I_H\\&\frac{d^{\alpha } L_{T_H}}{dt^{\alpha }}=\lambda _H L_T +\delta \lambda _T I_H \\&\quad -(k_2+\phi _2 \lambda _T) L_{T_H}-(\rho +\mu +\mu _H) L_{T_H}\\&\frac{d^{\alpha } I_{T_H}}{dt^{\alpha }}=\lambda _H I_T +(k_2+\phi _2 \lambda _T) L_{T_H}\\&\quad -r_1 \tau I_{T_H}-(r_2 \gamma +\mu +\mu _{T_H}) I_{T_H}\\&\frac{d^{\alpha }R_H}{dt^{\alpha }}=r_2 \gamma I_{T_H}+\rho (I_H+L_{T_H})-\mu R_H,\\ \end{aligned} \end{aligned}$$

(3.3)

with the initial conditions given as

$$\begin{aligned} \begin{aligned}&S(0)=S_0\geqslant 0,\ L_T(0)= L_{T_0}\geqslant 0, \\&\quad I_T(0)=I_{T_0}\geqslant 0,\ R_T(0)=R_{T_0}\geqslant 0, \\&I_H(0)=I_{H_0}\geqslant 0,\ L_{T_H}(0)=L_{T_{H_0}} \geqslant 0, \\&\quad I_{T_H}(0)=I_{T_{H_0}}\geqslant 0\ \text{ and } \ R_H(0)=R_{H_0}\geqslant 0. \end{aligned} \end{aligned}$$

(3.4)

3.1 Basic properties of the model

All the variables $S(t),\ L_T(t),\ I_T(t), R_T(t),\ I_H(t), L_{T_H}(t),$ $I_{T_H}(t)$ and $R_H(t)$ describe human population. Thus, it is necessary to prove that all the variables are positive for all time $t\geqslant 0$. To establish the positivity of the model solutions in Caputo sense, we first discuss some of the essentials that will be required for this proposed study.

Lemma 3.1

[34] (Generalized mean value theorem) Suppose that $h(x) \in C[a,b]$ and $D_t^{\alpha }h(x) \in C[a,b]$, for $0 < \alpha \leqslant 1$, then we have

$$\begin{aligned} h(x)=h(a)+ \frac{1}{\Gamma (\alpha )} (D_t^{\alpha }h) (\zeta ) (x-a)^{\alpha } \end{aligned}$$

(3.5)

with $a \leqslant \zeta \leqslant x, \forall x \in [a,b]$ and $\Gamma (.)$ denoting the gamma function.

Lemma 3.2

[34] Suppose that $h(x) \in C[a,b]$ and $D_t^{\alpha }h(x) \in C[a,b]$, for $0 < \alpha \leqslant 1$. Then, the following conditions hold true:

• (1) If $D_t^{\alpha }h(x) \geqslant 0$, for all $x \in [a,b],$ then h(x) is non-decreasing for each $x \in [a,b]$.

• (2) If $D_t^{\alpha }h(x) \leqslant 0$, for all $x \in [a,b],$ then h(x) is non-increasing for each $x \in [a,b]$.

Lemma 3.3

[35] Assume that the vector function $h : \mathbb {R}^+ \times \mathbb {R}^n \rightarrow \mathbb {R}^n$ satisfies the following conditions:

• (1) Function h(t, X(t)) is Lebseque measurable with respect to t on $\mathbb {R}^+$.

• (2) Function h(t, X(t)) is continuous with respect to X(t) on $\mathbb {R}^n$.

• (3) $\frac{\partial h(t,X)}{\partial X}$ is continuous with respect to X(t) on $\mathbb {R}^n$.

• (4) $|| h(t,X) || \leqslant \nu +\kappa ||X||$, for $t \in \mathbb {R}^+$ and $X \in \mathbb {R}^n$, where $\nu$ and $\kappa$ are positive constants.

Then, the initial value problem

$$\begin{aligned} \begin{aligned}&D_t^{\alpha } X(t)=h(t,X(t))\\&X(t_0)=X_0, \ \ \ \alpha \in (0,1] \end{aligned} \end{aligned}$$

(3.6)

has a unique solution.

Based on biological considerations, the following bounded region will be considered for the rest of the analysis

$$\begin{aligned} \begin{aligned} \Delta =&\bigg \{(S,L_T,I_T,R_T,I_H,L_{T_H},I_{T_H},R_H)\in \bigg .\\&\bigg . \mathbb {R}_+^{8} : N(t) \leqslant \frac{\Lambda }{\mu }\bigg \}. \end{aligned} \end{aligned}$$

(3.7)

Thus, with the region $\Delta$, we have the following result:

Theorem 3.4

There exists a unique solution $X(t)=(S(t),\ L_T(t),\ I_T(t), R_T(t),\ I_H(t),\ L_{T_H}(t),$ $\ I_{T_H}(t),\ R_H(t) )$ for the model system (3.3), with the initial conditions given by (3.4) in the positively region $\Delta$.

Proof

The existence and uniqueness of the $X(t)=(S(t),\ L_T(t),\ I_T(t), R_T(t),\ I_H(t),\ L_{T_H}(t),\ I_{T_H}(t),$

$R_H(t))$ corresponding to the model system (3.3) can be easily verified by using Lemma 3.3 stated above and Theorem 3.1 given by Huo et al. [36].

Now, in order to prove that the region $\Delta$ considered in equation (3.7) is positively invariant, we have to show that every solution trajectory starting in $\Delta$ remains in $\Delta$ for all $t \geqslant 0$. First of all, we observe that

$$\begin{aligned} \begin{aligned}&D_t^{\alpha }S_{|S=0}\ \ \ \ \ =\ \Lambda >0\\&D_t^{\alpha }{L_T}_{|L_T=0}\ \ =\ \frac{\beta _T}{N} (I_T+ I_{T_H}) S + \theta \lambda _T R_T \geqslant 0\\&D_t^{\alpha }{I_T}_{|I_T=0}\ \ \ \ =\ k_1 L_T +\phi _1 \frac{\beta _T}{N}L_T I_{T_H} \geqslant 0\\&D_t^{\alpha }{R_T}_{|R_T=0}\ \ =\ \tau I_T \geqslant 0\\&D_t^{\alpha }{I_H}_{|I_H=0}\ \ \ =\ \frac{\beta _H}{N}(L_{T_H}+I_{T_H}\\&\quad +\eta R_H)(S+R_T)+ r_1 \tau I_{T_H} \geqslant 0\\&D_t^{\alpha }{L_{T_H}}_{|L_{T_H}=0}=\ \frac{\beta _H}{N}(I_H+I_{T_H}+\eta R_H)L_T \\&\quad + \delta \frac{\beta _T}{N} (I_T+ I_{T_H}) I_H \geqslant 0\\&D_t^{\alpha }{I_{T_H}}_{|I_{T_H}=0}\ =\ \frac{\beta _H}{N}(I_H+L_{T_H} \\&\quad +\eta R_H)I_T + \phi _2 \frac{\beta _T}{N} I_T L_{T_H}+k_2 L_{T_H} \geqslant 0\\&D_t^{\alpha }{R_H}_{|R_H=0}\ \ =\ r_2 \gamma I_{T_H} + \rho (I_H+L_{T_H}) \geqslant 0.\\ \end{aligned} \end{aligned}$$

Thus, Lemma 3.2 establishes the positivity of all the solution components. Further, for proving the boundedness of the solution components, it can be observed that the rate of change of total population corresponding to the model system (3.3) is

$$\begin{aligned} D_t^{\alpha } N =&\ \Lambda -\mu _T I_T(t)-\mu _H (I_H+L_{T_H}) \nonumber \\&\ -\mu _{T_H} I_{T_H}-\mu N(t) \leqslant \Lambda -\mu N(t). \end{aligned}$$

After solving for N(t), we obtain

$$\begin{aligned} N(t) \leqslant N(0) E_{\alpha }(-\mu t^{\alpha })+\frac{\Lambda }{\mu }(1-E_{\alpha }(-\mu t^{\alpha })). \end{aligned}$$

Thus, in particular, if $N(0) \leqslant \frac{\Lambda }{\mu }$, then $0 < N(t) \leqslant \frac{\Lambda }{\mu }$ for all $t \geqslant 0$. Therefore, the total population N(t) is bounded between 0 and $\frac{\Lambda }{\mu }$. This in turn proves the boundedness of all the solution components. Therefore, the region $\Delta$ is positively invariant and the model system (3.3) is mathematically as well as epidemiologically well-posed. $\square$

4 The HIV sub-model

In this section, we analyze the model system (3.3) by considering that TB is not present in the population. Thus, by substituting $L_T=I_T=R_T=L_{T_H}=I_{T_H}=0$, the HIV sub-model is obtained as

$$\begin{aligned} \begin{aligned}&\frac{d^{\alpha } S}{dt^{\alpha }}= \Lambda - \frac{\beta _H}{N} (I_H+\eta R_H) S -\mu S\\&\frac{d^{\alpha }I_H}{dt^{\alpha }}= \frac{\beta _H}{N} (I_H+\eta R_H) S -\rho I_H-(\mu +\mu _H) I_H\\&\frac{d^{\alpha }R_H}{dt^{\alpha }}= \rho I_H-\mu R_H, \end{aligned} \end{aligned}$$

(4.1)

with the nonnegative initial conditions as $S(0)=S_0\geqslant 0,\ I_H(0)=I_{H_0}\geqslant 0$ and $R_H(0)=R_{H_0}\geqslant 0$.

The feasible region for HIV sub-model is considered as

$$\begin{aligned} \Delta _H = \left\{ (S,I_H,R_H)\in \mathbb {R}_+^{3}:0 < N(t)\leqslant \frac{\Lambda }{\mu }\right\} . \end{aligned}$$

Analogous to Theorem 3.4, $\Delta _H$ can be easily proved to be positively invariant.

4.1 Basic reproduction number

For the HIV sub-model, the disease-free equilibrium point is computed as

$$\begin{aligned} E_0^H= \left( \frac{\Lambda }{\mu },0,0\right) . \end{aligned}$$

(4.2)

The basic reproduction number is defined as the average number of secondary infection cases generated by a single infected individual in a completely susceptible population [37]. It is used to measure the contagiousness of a disease. For models with more compartments, the next-generation matrix approach [38] is used to calculate the basic reproduction number. Following the next-generation matrix approach, the matrices F corresponding to the new infection terms and V corresponding to the transfer terms are computed as

$$\begin{aligned} F= \begin{bmatrix} \beta _H &{} \eta \beta _H\\ 0 &{} 0\\ \end{bmatrix} \text{ and } V= \begin{bmatrix} \rho + \mu +\mu _H &{} 0\\ -\rho &{} \mu \\ \end{bmatrix}. \end{aligned}$$

Therefore, the basic reproduction number for the HIV sub-model, defined as the spectral radius of $FV^{-1}$, is determined as

$$\begin{aligned} \mathcal {R}_H = \frac{\beta _H}{\mu (\rho +\mu +\mu _H)}(\rho \eta +\mu ), \end{aligned}$$

(4.3)

which gives the number of secondary infection cases introduced into the population by a single HIV-infected individual.

4.2 Stability analysis of the disease-free equilibrium

Now, we determine the conditions under which small disturbances away from the disease-free equilibrium point dissipate in time, that is, when the disease-free equilibrium point is asymptotically stable. The following lemma will be used to prove the local asymptotic stability of the disease-free equilibrium point $E_0^H$.

Lemma 4.1

[34] Let $\alpha \left( = \frac{p}{q} \right)$ where $p,q \in Z^+$ and $gcd(p,q)=1$. Define $M=q,$ then the disease-free equilibrium point of the nonlinear system (4.1) is asymptotically stable if $|arg(\lambda )|> \frac{\pi }{2M}$ for all roots $\lambda$ of the following equation

$$\begin{aligned} det(diag[\lambda ^p \ \lambda ^p \ \lambda ^p]-M_3)=0, \end{aligned}$$

where $M_3$ is the matrix of linearization of the model system (4.1) around the disease-free equilibrium point.

Theorem 4.2

The disease-free equilibrium point $E_0^H$ for the HIV sub-model given by (4.1) is locally asymptotically stable, if $\mathcal {R}_H<1$ and is unstable for $\mathcal {R}_H>1$.

Proof

The linearization matrix for the model system (4.1) evaluated at $E_0^H$ is given as

$$\begin{aligned} J_0^H= \begin{bmatrix} -\mu &{} -\beta _H &{} -\eta \beta _H\\ 0 &{} \beta _H-(\rho +\mu +\mu _H) &{} \eta \beta _H\\ 0 &{} \rho &{} -\mu \\ \end{bmatrix}. \end{aligned}$$

The characteristic equation of the matrix $(\lambda ^p I_3-J_0^H)$ is computed as

$$\begin{aligned} \begin{aligned}&(\lambda ^p+\mu ) ( \lambda ^{2p}+(\rho +2 \mu +\mu _H -\beta _H)\lambda ^p \\&\quad +\, \,\mu (\rho +\mu +\mu _H) -\beta _H(\rho \eta +\mu ))=0. \end{aligned} \end{aligned}$$

(4.4)

The argument of each root of the first factor $(\lambda ^p+\mu )$ is given as

$$\begin{aligned} arg(\lambda _s)=\frac{\pi }{p}+s \frac{2\pi }{p} \geqslant \frac{\pi }{p}> \frac{\pi }{M}> \frac{\pi }{2M}, \end{aligned}$$

for $s=0,1,2, \dotsc ,(p-1)$.

For the remaining quadratic factor, the coefficient of $\lambda ^p$ and the constant term both are positive only if $\mathcal {R}_H<1$. Thus, by Routh–Hurwitz stability criterion for fractional derivatives [39], all the roots of the quadratic factor have argument greater than $\frac{\pi }{2M}$, if $\mathcal {R}_H<1$. Hence, the disease-free equilibrium point is locally asymptotically stable if $\mathcal {R}_H<1$. However, for $\mathcal {R}_H>1$, there exists at least one root of the quadratic factor given in equation (4.4) having argument less than $\frac{\pi }{2M}$, which justifies the unstability of $E_0^H$ for $\mathcal {R}_H>1$.

Now, consider a function $h : \Omega \rightarrow \mathbb {R}^n$, $\Omega \subset \mathbb {R}^n$, and an autonomous system of fractional order differential equations given by

$$\begin{aligned} \begin{aligned}&D_t^{\alpha } x(t)= \ h(x)\\&x(0)= \ _0, \end{aligned} \end{aligned}$$

(4.5)

where $\alpha \in (0,1]$. For a continuously differentiable function $\mathcal {V}: B \rightarrow \mathbb {R}$, we define the $\alpha$ order derivative of $\mathcal {V}(x(t))$ along the solution of the system (4.5) in the following form

$$\begin{aligned} \begin{aligned} D_t^{\alpha } \mathcal {V}(x(t))=I^{1-\alpha } D \mathcal {V} (x(t))= I^{1-\alpha } \left( \frac{d\mathcal {V}}{dx} \frac{dx}{dt} \right) . \end{aligned} \end{aligned}$$

(4.6)

To prove the global asymptotic stability of the disease-free equilibrium point, Huo et al. [36] have proposed the following Lyapunov LaSalle’s Principle for fractional order derivatives.

Lemma 4.3

[36] (Lyapunov LaSalle’s Principle) Let $\Omega \subset B$ be a bounded closed set that is positively invariant. Let $\mathcal {V}: B \rightarrow \mathbb {R}$ be a continuously differentiable function and assume that $D_t^{\alpha }\mathcal {V}(x(t))\leqslant 0$ for all $x(t) \in \Omega$. Let D be the set of all points in $\Omega$ where $D_t^{\alpha }\mathcal {V}(x(t)) =0$. Let M be the largest invariant set in D. Then, every bounded solution starting in $\Omega$ approaches M as $t \rightarrow \infty$, that is, for every $x(0) \in \Omega$, $x(t) \rightarrow M$ as $t \rightarrow \infty$. Particularly, when $M=x^*$, then $x \rightarrow x^*$ as $t \rightarrow \infty$.

Using this lemma, we will prove the global stability of the disease-free equilibrium point in the following theorem.

Theorem 4.4

The disease-free equilibrium point $E_0^H$ for the model system (4.1) is globally asymptotically stable, if $\mathcal {R}_H<1$.

Proof

Consider a positively invariant function

$$\begin{aligned} \begin{aligned} \mathcal {V}= \frac{\beta _H (\rho \eta +\mu )}{\mu (\rho +\mu +\mu _H)} I_H+\frac{\eta \beta _H}{\mu } R_H. \end{aligned} \end{aligned}$$

(4.7)

After taking $\alpha$ order derivative of the function V along the solution of the model system (4.1), we get,

$$\begin{aligned} \begin{aligned} D_t^{\alpha } \mathcal {V}=&\ \frac{\beta _H (\rho \eta +\mu )}{\mu (\rho +\mu +\mu _H)} D_t^{\alpha } I_H+\frac{\eta \beta _H}{\mu } D_t^{\alpha } R_H\\ =&\ \frac{\beta _H (\rho \eta +\mu )}{\mu (\rho +\mu +\mu _H)}\\&\quad \left( \beta _H (I_H+\eta R_H)\frac{S}{N} -(\rho +\mu +\mu _H) I_H \right) \\&\ + \frac{\eta \beta _H \rho }{\mu } I_H- \eta \beta _H R_H \\ \leqslant&\ \frac{\beta _H^2(I_H+\eta R_H)}{\mu (\rho +\mu +\mu _H)} - \beta _H (I_H +\eta R_H)\\ =&\ \beta _H (I_H+\eta R_H) (\mathcal {R}_H-1)\\ \leqslant&\ 0, \ \text{ if } \ \mathcal {R}_H \leqslant 1. \end{aligned} \end{aligned}$$

Therefore, $D_t^{\alpha } \mathcal {V} \leqslant 0$ if $\mathcal {R}_H \leqslant 1$ and $D_t^{\alpha } \mathcal {V}=0$ if and only if, $E_0^H=\left( \frac{\Lambda }{\mu },0,0 \right)$. Thus, the largest invariant set on which $D_t^{\alpha } \mathcal {V}=0$ is singleton $\{ E_0^H\}$. Hence, by the Lyapunov LaSalle’s Principle, it can be concluded that the disease-free equilibrium point $E_0^H$ is globally asymptotically stable whenever $\mathcal {R}_H<1$. However, it can be observed $D_t^{\alpha } \mathcal {V}>0$ in a neighborhood of the disease-free equilibrium point if $\mathcal {R}_H>1$. Thus, by Lyapunov stability theory the disease-free equilibrium point becomes unstable for $\mathcal {R}_H>1$.

4.3 The endemic equilibrium point

In this section, we compute the non-trivial endemic equilibrium point for the HIV sub-model, by considering the system of equations given as

$$\begin{aligned} \begin{aligned}&\Lambda - \frac{\beta _H}{N} (I_H+\eta R_H)S -\mu S=0\\&\frac{\beta _H}{N} (I_H+\eta R_H) S -\rho I_H-(\mu +\mu _H) I_H=0\\&\rho I_H-\mu R_H=0. \end{aligned} \end{aligned}$$

(4.8)

Using (4.8) the endemic equilibrium point is obtained as

$$\begin{aligned} \hat{E}_H=(\hat{S},\hat{I}_H,\hat{R}_H), \end{aligned}$$

where the components of $\hat{E}_H$ are computed as

$$\begin{aligned} \begin{aligned}&\hat{S} = \frac{\hat{N}}{\mathcal {R}_H}\\&\hat{I}_H = \frac{\mu \hat{N}}{\rho +\mu } \left( 1-\frac{1}{\mathcal {R}_H} \right) \\&\hat{R}_H = \frac{\rho \hat{N}}{\rho +\mu } \left( 1-\frac{1}{\mathcal {R}_H} \right) . \end{aligned} \end{aligned}$$

(4.9)

Here, $\hat{N}$ is given by

$$\begin{aligned} \begin{aligned} \hat{N}= \frac{\Lambda (\mu +\rho ) \mathcal {R}_H^2}{\beta _H (\mathcal {R}_H-1)(\mu +\rho \eta )+\mu (\mu +\rho ) \mathcal {R}_H}. \end{aligned} \end{aligned}$$

(4.10)

It can be clearly observed that the HIV endemic equilibrium point exists if $\mathcal {R}_H>1$.

Now to determine the conditions under which the HIV endemic equilibrium point is locally asymptotically stable, we compute the linearization matrix corresponding to the HIV sub-model and evaluate it at the endemic equilibrium point to obtain

$$\begin{aligned} R= \begin{bmatrix} r_{11} &{} r_{12} &{} r_{13}\\ r_{21} &{} r_{22} &{} r_{23}\\ 0 &{} r_{32} &{} r_{33} \end{bmatrix}, \end{aligned}$$

where the entries of the matrix R are given as

$$\begin{aligned} \begin{aligned}&r_{11}=-\frac{\beta _H (\hat{I}_H+\eta \hat{R}_H)}{\hat{N}^2} (\hat{I}_H+ \hat{R}_H)-\mu , \\&\quad \ r_{12}= \frac{\beta _H}{\hat{N}} \left( \frac{\hat{I}_H+\eta \hat{R}_H}{\hat{N}}-1\right) \hat{S},\\&r_{13}= \frac{\beta _H}{\hat{N}} \left( \frac{\hat{I}_H+\eta \hat{R}_H}{\hat{N}}-\eta \right) \hat{S}, \\&\quad \ r_{21}= \frac{\beta _H (\hat{I}_H+\eta \hat{R}_H)}{\hat{N}^2} (\hat{I}_H+ \hat{R}_H), \\&r_{22}= \frac{\beta _H}{\hat{N}^2} (\hat{S}+(1-\eta ) \hat{R}_H) \hat{S}-(\rho +\mu +\mu _T),\\&\quad \ r_{23}= -\frac{\beta _H}{\hat{N}} \left( \frac{\hat{I}_H+\eta \hat{R}_H}{\hat{N}}-\eta \right) \hat{S},\\&r_{32}=\rho \ \text{ and } \ r_{33}=-\mu . \end{aligned} \end{aligned}$$

The characteristic equation of the matrix R is given as

$$\begin{aligned} \lambda ^3 +R_2 \lambda ^2+R_1 \lambda +R_0=0, \end{aligned}$$

(4.11)

where

$$\begin{aligned} \begin{aligned}&R_2=-(r_{11}+r_{22}+r_{33})\\&R_1=r_{11}(r_{22}+r_{33})-r_{12} r_{21}-r_{23} r_{32}+r_{22} r_{33}\\&R_0=r_{21}(r_{12} r_{33}-r_{13} r_{32})+ r_{11}(r_{23} r_{32}-r_{22} r_{33}). \end{aligned} \end{aligned}$$

Now, the discriminant of the polynomial $\chi (\lambda )$ given by

$$\begin{aligned} \chi (\lambda )=\lambda ^3+R_2 \lambda ^2+R_1 \lambda +R_0, \end{aligned}$$

(4.12)

can be written as

$$D(\chi )= 18 R_0 R_1 R_2+(R_2 R_1)^2-4 R_0 R_2^3-4 R_1^3-27 R_0^2.$$

Thus, following Ahmed et al. [39], the next theorem provides the conditions under which the TB endemic equilibrium point $\hat{E}_H$ is locally asymptotically stable.

Theorem 4.5

For the endemic equilibrium point $\hat{E}_H$ and $\alpha \in (0,1]$, all the roots of equation (4.11) satisfy $arg(\lambda ) > \frac{\alpha \pi }{2}$ if the following conditions hold true:

• (1) $R_0>0$, $R_2>0$ and $R_1 R_2> R_0$.

• (2) $D(\chi )<0$, $R_2 \geqslant 0$, $R_1 \geqslant 0$, $R_0>0$, $R_1 R_2 < R_0$ and $\alpha < \frac{2}{3}$.

• (3) $D(\chi )<0$, $R_2>0$, $R_1>0$ and $R_1 R_2=R_0$.

Corollary 4.6

If any one of the condition given in Theorem 4.5 is satisfied, then the endemic equilibrium point $\hat{E}_H$ is locally asymptotically stable.

5 The TB sub-model

In this section, the TB sub-model will be analyzed separately by considering that HIV is not present in the population. Thus, by setting $I_H=L_{T_H}=I_{T_H}=R_H=0$, in the model system (3.3), the TB sub-model is obtained as

$$\begin{aligned} \begin{aligned}&\frac{d^{\alpha }S}{dt^{\alpha }}= \Lambda -\lambda _T S -\mu S\\&\frac{d^{\alpha }L_T}{dt^{\alpha }}= \lambda _T S +\theta \lambda _T R_T-(k_1+\phi _1 \lambda _T)L_T-\mu L_T\\&\frac{d^{\alpha }I_T}{dt^{\alpha }}= (k_1+\phi _1 \lambda _T) L_T-\tau I_T- (\mu +\mu _T) I_T\\&\frac{d^{\alpha }R_T}{dt^{\alpha }}= \tau I_T- \theta \lambda _T R_T -\mu R_T, \end{aligned} \end{aligned}$$

(5.1)

along with the nonnegative initial conditions given as

$$\begin{aligned} \begin{aligned}&S(0)=S_0\geqslant 0,\ \ L_T(0)=L_{T_0}\geqslant 0,\\&I_T(0)=I_{T_0}\geqslant 0 \ \text{ and } \ R_T(0)=R_{T_0}\geqslant 0. \end{aligned} \end{aligned}$$

(5.2)

The transmission of TB occurs with the force of infection $\lambda _T$, given as $\lambda _T=\dfrac{\beta _T }{N} I_T.$ The following feasible region will be considered for the TB sub-model

$$\begin{aligned} \Delta _T = \left\{ (S,L_T,I_T,R_T)\in \mathbb {R}_+^{4}:0 < N(t)\leqslant \frac{\Lambda }{\mu }\right\} . \end{aligned}$$

5.1 Stability analysis of the disease-free equilibrium

The disease-free equilibrium point for the TB sub-model given by

$$\begin{aligned} E_0^T=\biggl (\frac{\Lambda }{\mu },0 ,0,0\biggr ). \end{aligned}$$

(5.3)

The basic reproduction number computed in accordance with the next-generation matrix approach is given as

$$\begin{aligned} \mathcal {R}_T=\frac{\beta _T k_1}{(k_1+\mu )(\tau + \mu +\mu _T)}. \end{aligned}$$

(5.4)

Now to qualitatively analyze the solution corresponding to the TB sub-model, the following lemma is stated:

Lemma 5.1

[34] Let $\alpha \left( = \frac{p}{q} \right)$ where $p,q \in Z^+$ and $gcd(p,q)=1$. Define $M=q,$ then the disease-free equilibrium point for the TB sub-model given by (5.1) is locally asymptotically stable if $|arg(\lambda )|> \frac{\pi }{2M}$ for all roots $\lambda$ of the following equation

$$ det(diag[\lambda ^p \ \lambda ^p \ \lambda ^p \ \lambda ^p]-M_4)=0,$$

where $M_4$ is the linearization matrix of the model system (5.1) in the neighborhood of the disease-free equilibrium point.

Using the above lemma, we establish the local stability of the disease-free equilibrium point.

Theorem 5.2

The disease-free equilibrium point $E_0^T$ for the TB sub-model given by (5.1) is locally asymptotically stable, if $\mathcal {R}_T<1$ and is a saddle point for $\mathcal {R}_T>1$.

Proof

The linearization matrix for the TB sub-model given in (5.1) evaluated at the disease-free equilibrium point $E_0^T$ is computed as

$$\begin{aligned} J_0^T = \begin{bmatrix} -\mu &{} 0 &{} -\beta _T &{} 0 \\ 0 &{} -(k_1+\mu ) &{} \beta _T &{} 0\\ 0 &{} k_1 &{} -(\tau +\mu +\mu _T) &{} 0\\ 0 &{} 0 &{} \tau &{} -\mu \\ \end{bmatrix}. \end{aligned}$$

Expanding $det(\lambda ^p I_4-J_0^T)$, with $I_4$ as a $4 \times 4$ identity matrix, we obtain

$$\begin{aligned}&\left( \lambda ^p+\mu )^2(\lambda ^{2p}+\lambda ^p\left( k_1+\tau +2 \mu +\mu _T \right) \right. \\&\quad \left. + \left( k_1+\mu \right) \left( \tau +\mu +\mu _T\right) - \beta _T k_1\right) =0. \end{aligned}$$

The argument of each root of the first two factors $\left( \lambda ^p+\mu \right) ^2$ satisfies

$$\begin{aligned} arg(\lambda _s)=\frac{\pi }{p}+s \frac{2\pi }{p} \geqslant \frac{\pi }{p}>\frac{\pi }{M}> \frac{\pi }{2M}, \end{aligned}$$

for $s=0,1,2, \dotsc ,(p-1).$

However, for the next quadratic factor the constant term is positive only if $R_T<1$. Thus, by the Routh–Hurwitz stability criterion for fractional order derivatives [39], all the roots of the remaining quadratic factor have a negative real part, if $\mathcal {R}_T<1$. Hence, the disease-free equilibrium point is locally asymptotically stable for $\mathcal {R}_T<1$ and is unstable for $\mathcal {R}_T>1$.

Following Lemma 4.3 discussed in sect. 4, we now prove the global asymptotic stability of the disease-free equilibrium point $E_0^T$.

Theorem 5.3

The disease-free equilibrium point $E_0^T$ for the TB sub-model is globally asymptotically stable, if $\mathcal {R}_T<1$ and the population is free from exogenous reinfection and recurrent TB.

Proof

Consider a Lyapunov Function

$$\begin{aligned} \mathcal {V}=\frac{\beta k_1}{(k_1+\mu )(\tau +\mu +\mu _T)} L_T +\frac{\beta }{(\tau +\mu +\mu _T)} I_T. \end{aligned}$$

By computing $\alpha$ order derivative of the Lyapunov function $\mathcal {V},$ we obtain

$$\begin{aligned} D_t^{\alpha } \mathcal {V}&= \ \frac{\beta _T k_1}{(k_1+\mu )(\tau +\mu +\mu _T)} D_t^{\alpha }L_T\\&\quad +\frac{\beta _T}{(\tau +\mu +\mu _T)}D_t^{\alpha }I_T \\&= \ \frac{\beta _T k_1}{(k_1+\mu )(\tau +\mu +\mu _T)} \\&\quad \left( \beta _T \frac{ S I_T }{N} +\theta \lambda _T R_T-(k_1+\phi _1 \lambda _T)-\mu L_T \right) \\&\quad +\frac{\beta _T}{(\tau +\mu +\mu _T)}\\&\quad \left( (k_1+\phi _1 \lambda _T) L_T-\tau I_T- (\mu +\mu _T) I_T \right) \\&\leqslant \ \frac{\beta _T^2 k }{(k_1+\mu )(\tau +\mu +\mu _T)}I_T- \\&\quad \frac{\beta \phi _1 \lambda _T}{(\tau +\mu +\mu _T)} \left( \frac{k_1}{k_1+\mu }-1 \right) L_T\\&\quad + \frac{\beta _T \theta k_1 \lambda _T}{(k_1+\mu )(\tau +\mu +\mu _T)} R_T- \beta _T I_T\\&= \beta _T (\mathcal {R}_T-1) I_T+\theta \lambda _T R_T \mathcal {R}_T- \frac{\phi _1 \beta \lambda _T}{\tau +\mu +\mu _T}\\&\quad \left( \frac{k}{k+\mu }-1 \right) \\&\leqslant \ 0, \ \text{ if } \mathcal {R}_T<1, \theta =0 \text{ and } \phi _1=0. \end{aligned}$$

Further, $D_t^{\alpha } \mathcal {V}(x(t))=0$ for $E_0^T=\left( \frac{\Lambda }{\mu },0,0,0 \right)$. Thus, singleton $\{ E_0^T\}$ is the largest invariant set on which $D_t^{\alpha } \mathcal {V}(x(t))=0$. Therefore, by Lyapunov LaSalle’s Principle, the disease-free equilibrium point for the TB sub-model is globally asymptotically stable in the absence of exogenous reinfection and recurrent TB when the corresponding reproduction number $\mathcal {R}_T$ is less than unity.

5.2 The endemic equilibrium point

The steady state in which TB is endemic in the population gives rise to TB endemic equilibrium point which can be computed by solving the following system of equations:

$$\begin{aligned} \begin{aligned}&\Lambda -\lambda _T S -\mu S=0\\&\lambda _T S +\theta \lambda _T R_T-(k_1+\phi _1 \lambda _T)L_T-\mu L_T=0\\&(k_1+\phi _1 \lambda _T) L_T-\tau I_T- (\mu +\mu _T) I_T=0\\&\tau I_T- \theta \lambda _T R_T -\mu R_T=0. \end{aligned} \end{aligned}$$

(5.5)

Solving (5.5), the TB endemic equilibrium point in terms of the force of infection $\lambda _T$ is calculated as $\check{E}_T=(\check{S},\check{L}_T,\check{I}_T,\check{R}_T)$, where

$$\begin{aligned}&\check{S} = \frac{\Lambda }{\lambda _T +\mu } \nonumber \\&\check{L}_T= \frac{\Lambda \lambda _T (\tau +\mu +\mu _T) (\theta \lambda _T +\mu ) }{\left( \lambda _T + \mu \right) \left( (k_1+\phi _1 \lambda _T+\mu )(\theta \lambda _T +\mu )(\tau +\mu +\mu _T)- (\tau \theta \lambda _T) (k_1+\phi _1 \lambda _T) \right) } \nonumber \\&\check{I}_T= \frac{\Lambda \lambda _T (k_1+\phi _1 \lambda _T) (\theta \lambda _T +\mu ) }{\left( \lambda _T + \mu \right) \left( (k_1+\phi _1 \lambda _T+\mu )(\theta \lambda _T +\mu )(\tau +\mu +\mu _T)- (\tau \theta \lambda _T) (k_1+\phi _1 \lambda _T) \right) }\nonumber \\&\check{R}_T= \frac{\Lambda \tau \lambda _T (k_1+\phi _1 \lambda _T) }{\left( \lambda _T + \mu \right) \left( (k_1+\phi _1 \lambda _T+\mu )(\theta \lambda _T +\mu )(\tau +\mu +\mu _T)- (\tau \theta \lambda _T) (k_1+\phi _1 \lambda _T) \right) }. \end{aligned}$$

(5.6)

The force of infection $\lambda _T$ can be obtained by using the expressions of the components of $\check{E}_T$ given by (5.6). Thus, by the expression of $\lambda _T$ given as

$$\begin{aligned} \lambda _T = \frac{\beta _T \check{I}_T}{N}, \end{aligned}$$

we obtain

$$\begin{aligned} \lambda _T \left( 1- \frac{\beta _T \mu (k_1+\phi _1 \lambda _T) (\theta \lambda _T +\mu ) }{\left( \lambda _T + \mu \right) \left( (k_1+\phi _1 \lambda _T+\mu )(\theta \lambda _T +\mu )(\tau +\mu +\mu _T)- (\tau \theta \lambda _T) (k_1+\phi _1 \lambda _T) \right) } \right) =0. \end{aligned}$$

After simplifying for $\lambda _T$, we get

$$\begin{aligned} \lambda _T = 0 \text{ or } A_3 \lambda ^3_T+ A_2 \lambda _T^2 +A_1 \lambda _T +A_0=0,\nonumber \\ \end{aligned}$$

(5.7)

where the coefficients $A_3$, $A_2$, $A_1$ and $A_0$ are computed as

$$\begin{aligned}&A_3=\ \theta \phi _1 (\mu +\mu _T) \\&A_2=\ \mu \theta \phi _1 (\beta _2-\beta _T)\\&A_1=\ \mu (\theta k_1+\mu \phi _1) (\beta _1 -\beta _T)\\&A_0=\ \mu k_1^2 (\beta _0-\beta _T). \end{aligned}$$

The terms $\beta _2,\ \beta _1$ and $\beta _0$ are given by

$$\begin{aligned} \begin{aligned}&\beta _2= \frac{\mu (\tau +\mu +\mu _T)(\theta (1+\phi _1)+\phi _1)+\theta k_1(\mu +\mu _T)-\mu \theta \phi _1 \tau }{\mu \theta \phi _1},\\&\beta _1=\frac{\mu (1+\theta )(\tau +\mu +\mu _T)(k_1+\mu )+\mu ^2 \phi _1 (\tau +\mu +\mu _T)-\mu \theta \tau k_1}{\mu (\theta k_1+\mu \phi _1)},\\&\beta _0=\frac{(\mu +k_1)(\tau +\mu +\mu _T)}{k_1}. \end{aligned} \end{aligned}$$

(5.8)

In equation (5.7), the term $\lambda _T = 0$ corresponds to the disease-free equilibrium point $E_0^T$ and $\lambda _T > 0$ satisfying the cubic equation

$$\begin{aligned} A_3 \lambda _T^3 + A_2 \lambda _T^2 +A_1 \lambda _T +A_0=0 \end{aligned}$$

(5.9)

give rise to one or more endemic equilibrium points existing simultaneously. It can be observed that $A_3$ is always positive. Now, to identify and locate the TB endemic equilibrium point we consider the following scenario:

5.2.1 Without exogenous reinfection and recurrent TB:

First, we examine the case when exogenous reinfection rate is zero and individuals recovered from TB got permanent immunity from TB infection, that is, $\phi _1=0$

and $\theta =0$. In this case equation (5.9) can be expressed as

$$\begin{aligned} \begin{aligned} A_1 \lambda _T +A_0=0, \end{aligned} \end{aligned}$$

(5.10)

where

$$\begin{aligned}&A_1=\mu (k_1+\mu )(\tau +\mu +\mu _T),\\&A_0= \mu k_1^2 (\beta _0-\beta _T). \end{aligned}$$

It can be easily observed that $A_1>0$ for all time $t\geqslant 0$. From equation (5.10), we obtain $\lambda _T=-\frac{A_0}{A_1}$, where $\lambda _T$ is positive only if, $A_0<0$, that is, if $\beta _T>\beta _0$,

which is possible if $\mathcal {R}_T>1$. Therefore, for $\mathcal {R}_T>1$ a unique TB endemic equilibrium point exists. However, for $\mathcal {R}_T \leqslant 1$ only disease-free equilibrium point exists, corresponding to $\lambda _T=0$. Thus, the following theorem has been proved.

Theorem 5.4

For the TB sub-model, if $\phi _1=0$ and $\theta =0$, that is, reinfection of TB does not occur and the treatment from TB gives permanent immunity, then there exists a unique TB endemic equilibrium point if $\mathcal {R}_T>1.$

5.2.2 In the absence of exogenous TB reinfection:

Next, we investigate the case when latent TB infectives do not enter into the class of active TB infectives after getting re-infected from TB, that is, $\phi _1=0$ and $\theta \ne 0$.

For $\phi _1=0$ equation (5.9) takes the form of a quadratic equation given as

$$\begin{aligned} A_2 \lambda _T^2+A_1 \lambda _T+A_0=0, \end{aligned}$$

(5.11)

where

$$\begin{aligned}&\ \ \ \ \ A_2 = \theta k_1 (\mu +\mu _T), \nonumber \\&\ \ \ \ A_1= \mu \tau k_1 (1-\theta ) +\mu (\mu +k_1) (\mu +\mu _T) +\mu ^2 \tau \nonumber \\&\qquad + \mu \theta \left( (\mu +k_1)(\tau +\mu +\mu _T)-\beta _T k_1 \right) ,\nonumber \\&\ \ \ \ A_0= \mu k^2 (\beta _0-\beta _T). \end{aligned}$$

(5.12)

It can be easily observed that $A_2>0$, whereas $A_0$ and $A_1$ are positive, if $\mathcal {R}_T<1$. Thus, for $\mathcal {R}_T<1$, there does not exist any positive root of equation (5.11) and hence TB endemic equilibrium point does not exist for $\mathcal {R}_T<1.$ For $\mathcal {R}_T=1,$ the parameter $\beta _T$ coincides with $\beta _0$ and gives $A_0=0.$ Thus, equation (5.11) takes the form

$$\begin{aligned} \lambda _T (A_2 \lambda _T+A_1)=0, \end{aligned}$$

(5.13)

which gives $\lambda _T = -\frac{A_1}{A_2}$ which is negative as $A_1>0$ for $\mathcal {R}_T=1$. Therefore, TB endemic equilibrium point does not exist in this case.

Further, for $\mathcal {R}_T>1$, the transmission rate $\beta _T$ exceeds $\beta _0$ which gives $A_0<0$. Hence, by Descartes’ rule of sign a unique positive root of equation (5.11) exists, corresponding to which a unique TB endemic equilibrium point exists for $\mathcal {R}_T>1$. We can summarize the above analysis in form of the following theorem.

Theorem 5.5

For the TB sub-model, if $\phi _1=0$, that is, reinfection from TB does not occur, then there exists a unique TB endemic equilibrium point for $\mathcal {R}_T>1.$

5.2.3 In the absence of recurrent TB:

Now, we examine the case when recovery from TB gives permanent immunity, that is, $\theta =0$ and $\phi _1 \ne 0$. As $\theta$ does not appear in the expression of the basic reproduction number, the reproduction number $\mathcal {R}_T$ remains uninfected. Thus, for $\theta =0$ equation (5.9) takes the form

$$\begin{aligned} A_2 \lambda _T^2+A_1 \lambda _T +A_0=0, \end{aligned}$$

(5.14)

where

$$\begin{aligned}&A_2= \mu \phi _1 (\tau +\mu +\mu _T),\\&A_1= \phi _1 \mu ^2 (\bar{\beta }_1-\beta _T), \\&A_0= \mu k_1^2 (\beta _0-\beta _T). \end{aligned}$$

The parameter $\bar{\beta }_1$ is given as

$$\begin{aligned} \bar{\beta }_1=\frac{(\tau +\mu +\mu _T)(k_1+\mu )+\phi _1 \mu (\tau +\mu +\mu _T)}{\phi _1 \mu }. \end{aligned}$$

It can be seen that $A_2>0$ for all time $t \geqslant 0$ and $A_0$ also becomes positive, whenever $\mathcal {R}_T<1$. Further, if $\bar{\beta }_1> \beta$, we get $A_1>0$, corresponding to which no positive root exist for equation (5.14). Hence, no TB endemic equilibrium point exist in this case. However, for $\bar{\beta }_1< \beta$, $A_1$ reduces below 0. Therefore, if $A_1^2-4 A_2 A_0>0$, equation (5.14) has two positive roots, corresponding to which two TB endemic points exist for $\bar{\beta }< \beta _T$. Thus, backward bifurcation may occur for $\mathcal {R}_T<1$, whenever $\theta =0$ and $\phi _1 \ne 0$.

Also, for $\mathcal {R}_T=1$, we observe that $A_0=0$. Thus, equation (5.14) gives rise to a unique endemic equilibrium point corresponding to $\lambda _T=-\frac{A_1}{A_2}$, whenever $A_1<0$ and no endemic equilibrium point, if $A_1 \geqslant 0.$ Further, for $\mathcal {R}_T>1$, $A_0$ becomes negative. Hence, by Descartes’ rule of sign, a unique TB endemic equilibrium point exists corresponding to the positive root of equation (5.14). The above discussion can be summarized in the form of the following theorem.

Theorem 5.6

In the absence of recurrent TB, the TB sub-model given by (5.1) has

• (1) a unique endemic equilibrium point, if $\mathcal {R}_T>1$.

• (2) a unique endemic equilibrium point, if $\mathcal {R}_T=1$ and $A_1<0$.

• (3) two equilibrium points, if $\mathcal {R}_T < 1$ and $A_1<0$ with $A_1^2-4 A_2 A_0>0$.

• (3) no positive endemic equilibrium point, if $\mathcal {R}_T \leqslant 1$ and $A_1 \geqslant 0$.

5.2.4 In the presence of exogenous reinfection and recurrent TB:

Further, we examine the case when TB treatment does not give permanent immunity and exogenous reinfection occurs in latent TB infectives, that is, $\theta \ne 0$ and $\phi _1 \ne 0$.

For $\mathcal {R}_T=1$, the transmission rate $\beta _T$ coincides with $\beta _0$, corresponding to which the constant term $A_0$ in equation (5.9) vanishes. Thus, equation (5.9) becomes

$$\begin{aligned} A_3 \lambda _T^3+A_2 \lambda _T^2+A_1 \lambda _T=0. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \lambda _T = 0 \text{ or } A_3 \lambda _T^2+A_2 \lambda _T+A_1=0. \end{aligned}$$

Here, $\lambda _T>0$ satisfying the equation

$$\begin{aligned} A_3 \lambda _T^2+A_2 \lambda _T+A_1=0, \end{aligned}$$

(5.15)

gives rise to the TB endemic equilibrium point. Also, as $A_3>0$, the following cases arise:

• (1) If $\beta _2< \beta _T$ and $\beta _1< \beta _T$, then $A_2<0$ and $A_1<0$. By Descrate’s rule of sign, the equation (5.15) has one positive root $\lambda _T$ corresponding to which a unique endemic equilibrium point exists. Also, if $\beta _1< \beta _T < \beta _2$, then $A_2>0$ and $A_1<0$ which also justifies the existence of a unique endemic equilibrium point for the TB sub-model.

• (2) If $\beta _2< \beta _T < \beta _1$, we get $A_2<0$ and $A_1>0$. In this case, equation (5.15) has two positive roots say, $\lambda _{T_1}$ and $\lambda _{T_2}$, if $A_2^2> 4 A_1 A_3$, corresponding to which two endemic equilibrium points exist.

• (3) If $\beta _T< \beta _2$ and $\beta _T< \beta _1$, then both the expressions $A_2$ and $A_1$ are positive. Thus, no positive root of equation (5.15) exists in this case, which shows that endemic equilibrium point cannot exist in this case.

The above discussion can be summarized as

Theorem 5.7

At $\mathcal {R}_T=1$, when $\beta _T=\beta _0$, along with the disease-free equilibrium point the model has:

• (1) one positive endemic equilibrium point, if $\beta _2 < \beta _0$ and $\beta _1 < \beta _0$ or $\beta _1< \beta _0< \beta _2$, which indicates the occurrence of backward bifurcation.

• (2) two positive endemic equilibrium points, if $\beta _2< \beta _0< \beta _1$ and $A_2^2> 4 A_1 A_3$.

• (3) no positive endemic equilibrium point, if $\beta _0 < \beta _2$ and $\beta _0 < \beta _1$.

6 Analysis of the full model

In this section, we analyze the full HIV-TB co-infection model given in (3.3) by computing all the equilibrium points. Further, to identify the behavior of solution trajectories near the disease-free equilibrium point, stability analysis will be done.

6.1 Basic reproduction number

For calculating the basic reproduction number for the full model using the next generation matrix approach, the matrices F and V are computed as

$$\begin{aligned} F= & {} \begin{bmatrix} 0 &{} \beta _T &{} 0 &{} 0 &{} 0 &{} \beta _T &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \beta _H &{} \beta _H &{} \beta _H &{} \eta \beta _H\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{bmatrix} \text{ and } \\ V= & {} \begin{bmatrix} -g_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0\\ k_1 &{} -g_2 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} -\tau &{} \mu &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -g_3 &{} 0 &{} -g_4 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -g_5 &{} 0&{} 0\\ 0 &{} 0 &{} 0 &{}0&{} -k_2&{} -g_6 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\rho &{} -\rho &{} -r_2 \gamma &{} \mu \\ \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&g_1=-(k_1+\mu ),\ \ g_2=-(\tau +\mu +\mu _T),\\&\quad g_3=(\alpha +\mu +\mu _H),\ \ g_4= r_1 \tau , \\&g_5=-(k_2+\alpha +\mu +\mu _H) \text{ and } \\&\quad g_6=-(r_1 \tau +r_2 \gamma + \mu + \mu _{T_H}). \end{aligned} \end{aligned}$$

(6.1)

The basic reproduction number given by the spectral radius of $FV^{-1}$ is computed as

$$\begin{aligned} \mathcal {R}_0=\text {max}\{\mathcal {R}_H,\mathcal {R}_T\}, \end{aligned}$$

(6.2)

where $\mathcal {R}_H$ and $\mathcal {R}_T$ are the reproduction numbers corresponding to HIV and TB, given in equation (4.3) and equation (5.4), respectively. In the expression of $\mathcal {R}_0$, the term $\text {max}\{\mathcal {R}_H,\mathcal {R}_T\}$ represents the number of secondary cases introduced in the population by a single individual infected suffering from the dominant disease.

6.2 Equilibrium points

Biologically, four types of equilibrium points exist for the full co-infection model system (3.3), which are given as follows:

• (1) The disease-free equilibrium point:

  $$\begin{aligned} E_0 = \left( \frac{\Lambda }{\mu },0,0,0,0,0,0,0\right) . \end{aligned}$$

  (6.3)

  It describes the state in which neither HIV nor TB is present in the population.

• (2) The TB endemic equilibrium point:

  $$\begin{aligned} E_T=(\check{S},\check{L}_T,\check{I}_T,\check{R}_T,0,0,0,0), \end{aligned}$$

  (6.4)

  where the nonzero components of $E_T$ can be obtained from equation (5.6). It corresponds to the steady state in which only TB is endemic in the population.

• (3) The HIV endemic equilibrium point:

  $$\begin{aligned} E_H=(\hat{S},0,0,0,\hat{I}_H,0,0,\hat{R}_H), \end{aligned}$$

  (6.5)

  where the nonzero components of $E_H$, that is, $\hat{S}, \hat{I}_H$ and $\hat{R}_H$ are given by equation (4.9) that exist, if $\mathcal {R}_H>1$. It represents a steady state in which only HIV is endemic in the population.

• (4) The interior endemic equilibrium point:

  $$\begin{aligned} \begin{aligned} E_{T_H}{=}(\tilde{S},\tilde{L}_T,\tilde{I}_T, \tilde{R}_T,\tilde{I}_H,\tilde{L}_{T_H},\tilde{I}_{T_H},\tilde{R}_H). \end{aligned} \end{aligned}$$

  (6.6)

  The components of $E_{T_H}$ are determined by using the equations given in (3.3) and are computed as

  $$\begin{aligned} \begin{aligned}&\tilde{S} = \frac{\Lambda }{\lambda _T+\lambda _H+\mu }\\&\tilde{L}_T=\frac{\lambda _T (\theta \lambda _T+\mu +\lambda _H) \tilde{S}+ \tau \lambda _T I_T}{(\lambda _H+\theta \lambda _T+\mu )(\lambda _H+ k_1+\mu +\phi _1 \lambda _T)}\\&\tilde{I}_T=\frac{(k_1+\phi _1 \lambda _T)(\lambda _H+\theta \lambda _T+\mu ) \lambda _T}{(\lambda _H +\tau +\mu +\mu _T)(\lambda _H+\theta \lambda _T +\mu )(k_1+\phi _1 \lambda _T+\lambda _H +\mu )-\tau (k_1+\phi _1 \lambda _T) \lambda _T} \tilde{S}\\&\tilde{R}_T=\frac{\tau (k_1+\phi _1 \lambda _T) \lambda _T}{(\lambda _H +\tau +\mu +\mu _T)(\lambda _H+\theta \lambda _T +\mu )(k_1+\phi _1 \lambda _T+\lambda _H +\mu )-\tau (k_1+\phi _1 \lambda _T) \lambda _T} \tilde{S}\\&\tilde{I}_H= \frac{\lambda _H (\tilde{S}+\tilde{R}_T)+ r_1 \tau \tilde{I}_{T_H}}{\delta \lambda _T+\rho +\mu +\mu _H}\\&\tilde{L}_{T_H}=\frac{\lambda _H L_T(\delta \lambda _T+\rho +\mu +\mu _H)+\delta \lambda _T \lambda _H (\tilde{S}+\tilde{R}_H+\delta \lambda _T r_1 \tau \tilde{I}_{T_H})}{(\delta \lambda _T+\rho +\mu +\mu _H)(k_2+\phi _2 \lambda _T+\rho +\mu +\mu _H)}\\&\tilde{I}_{T_H}=\frac{\lambda _H \tilde{I}_T+(k_2+\phi _2 \lambda _T) \tilde{L}_{T_H}}{r_1 \tau +r_2 \gamma +\mu +\mu _{T_H}}\\&\tilde{R}_H = \frac{r_2 \gamma \tilde{I}_{T_H}+\rho (\tilde{I}_H+\tilde{L}_{T_H})}{\mu }, \end{aligned} \end{aligned}$$

  where $\lambda _T$ and $\lambda _H$ satisfy equation (3.1) and equation (3.2), respectively. The HIV-TB co-endemic equilibrium point exists, if all the components of $E_{T_H}$ are positive. It represents the steady state in which both diseases are endemic in the population.

6.3 Stability analysis of the disease-free equilibrium point

The following lemma establishes the conditions under which the disease-free equilibrium point for the full model given by (6.3) is locally asymptotically stable.

Lemma 6.1

[34] Let $\alpha \left( = \frac{p}{q} \right)$ where $p,q \in Z^+$ and $gcd(p,q)=1$. Define $M=q,$ then the disease-free equilibrium point of the nonlinear system (3.3) is asymptotically stable if $|arg(\lambda )|> \frac{\pi }{2M}$ for all roots $\lambda$ of the equation

$$\begin{aligned} det(diag[\lambda ^p \ \lambda ^p \ \lambda ^p \dotsc \lambda ^p]-M_8)=0, \end{aligned}$$

(6.7)

where $M_8$ is an $8 \times 8$ linearization matrix of the model system (3.3), evaluated at the disease-free equilibrium point.

Theorem 6.2

The disease-free equilibrium point $E_0$ for the full HIV-TB model system (3.3) is locally asymptotically stable, if $\mathcal {R}_0<1$ and unstable otherwise.

Proof

The linearization matrix for the model system (3.3) evaluated at $E_0$ is given as

$$\begin{aligned} J_0= \begin{bmatrix} -\mu &{} 0 &{} -\beta _T &{} 0 &{} -\beta _H &{} -\beta _H &{} -(\beta _H+\beta _T) &{} -\eta \beta _H\\ 0 &{} g_1 &{} \beta _T &{} 0 &{} 0 &{} 0 &{} \beta _T&{} 0\\ 0&{} k_1 &{} g_2 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \tau &{} -\mu &{} 0 &{} 0 &{} 0 &{} 0\\ 0&{} 0 &{} 0 &{} 0 &{} \beta _H+g_3 &{} \beta _H &{} \eta \beta _H+g_4 &{} \eta \beta _H \\ 0&{} 0 &{} 0 &{} 0 &{} 0 &{} g_5 &{} 0&{} 0\\ 0&{} 0 &{} 0 &{} 0 &{}0&{} k_2&{} g_6 &{} 0 \\ 0&{} 0 &{} 0 &{} 0 &{} \rho &{} \rho &{} r_2 \gamma &{} -\mu \\ \end{bmatrix}, \end{aligned}$$

where each $g_i$ for $i=1,2,3,4,5,6$ is given by equation (6.1). After solving equation (6.7) with the linearization matrix $J_0$, we obtain

$$\begin{aligned} \begin{aligned}&(\lambda ^p+\mu )^2(\lambda ^p+r_1 \tau +r_2 \gamma +\mu +\mu _{T_H})\\&\quad (\lambda ^p+\alpha +k_2+\mu +\mu _H)\\&\left( \lambda ^{2p}+\lambda ^p \left( k_1+\tau +2 \mu +\mu _T \right) \right. \\&\quad \left. + \left( k_1+\mu \right) \left( \tau +\mu +\mu _T \right) - \beta _T k_1\right) \\&\left( \lambda ^{2p}+\lambda ^p(\rho +2\mu +\mu _H-\beta _H)\right. \\&\quad \left. +\left( \mu (\rho +\mu +\mu _H)-\beta _H(\rho \eta +\mu )\right) \right) =0. \end{aligned} \end{aligned}$$

(6.8)

Clearly, the argument of each root of the first four factors is greater than $\frac{\pi }{2M}$. However, in the fifth quadratic factor given by

$$\begin{aligned}&\lambda ^{2p}+\lambda ^p \left( k_1+\tau +2 \mu +\mu _T \right) \\&\quad + \left( k_1+\mu \right) \left( \tau +\mu +\mu _T \right) - \beta _T k_1, \end{aligned}$$

the constant term is positive only if $R_T<1$. Thus, by the Routh–Hurwitz criterion for fractional derivatives, argument of all the roots of the quadratic equation is greater than $\frac{\pi }{2M}$. Similarly, for the remaining factor given by

$$\begin{aligned}&\lambda ^{2p}+\lambda ^p(\rho +\mu +\mu _H-\beta _H)\\&\quad +\mu (\rho +\mu +\mu _H)-\beta _H(\rho \eta +\mu ), \end{aligned}$$

the coefficient of $\lambda ^p$ and the constant term both are positive if $\mathcal {R}_H<1$. Thus, argument of each root of the above-mentioned factor is greater than $\frac{\pi }{2 M}$, if $\mathcal {R}_H<1.$ Hence, if $\mathcal {R}_0=\text {max}\{\mathcal {R}_H,\mathcal {R}_T\}<1$, then the disease-free equilibrium point $E_0$ is locally asymptotically stable and is unstable otherwise.

7 Sensitivity analysis

This section determines the significance of various parameters on the proposed nonlinear mathematical model. We highlight the impact of various parameters on the threshold quantity, $\mathcal {R}_0$. The sensitivity analysis of the reproduction number is required to determine the relative importance of various parameters in reducing the disease case fatality rate of the human population and also the consequences of the various parameters that cause transmission and prevalence. In view of this, the ratio of the relative change in a variable to the relative change in a parameter provides the normalized forward sensitivity index. The sensitivity index can also be defined using partial derivatives, provided that a variable is a differentiable function of a parameter. The occurrence of errors in using presumed values and collecting data may affect the significance of mathematical model. Thus, the sensitivity analysis also helps to acknowledge the vitality of parameters value in model prediction.

Definition 7.1

[42] The normalized forward sensitivity index of a variable, v, that depends differentiably on a parameter p is defined as:

$$\begin{aligned} \Upsilon _p^v := \frac{\partial v}{\partial p} \frac{p}{v}. \end{aligned}$$

(7.1)

The sensitivity index of $\mathcal {R}_0$ helps to determine the parameters (which appears in the basic reproduction number) imposing an immense impact on the reproduction number $\mathcal {R}_0$. We can obtain the sensitivity indices by using the parameters value given in Table 2 as

$$\begin{aligned} \Upsilon _\beta ^{R_T} :=&\ \frac{\partial \mathcal {R}_T}{\partial \beta _T} \frac{\beta _T}{\mathcal {R}_T} = \ +1. \end{aligned}$$

The remaining values of the sensitivity index are given in Table 3. The positive value of sensitivity index implies that an increase in the parameter value will lead to increase in the basic reproduction number, whereas a negative value of sensitivity index shows that an increase in the parameters value decreases the basic reproduction number. From $\Upsilon _{\beta _T}^{\mathcal {R}_T} =+1$ and $\Upsilon _{\beta _H}^{\mathcal {R}_H} =+1$ it can be observed that $\mathcal {R}_0=\text {max}\{\mathcal {R}_H,\mathcal {R}_T\}$ is directly proportional to the transmission rates corresponding to TB and HIV. If the transmission rate corresponding to the dominant disease, that is, HIV or TB, increases by $10\%,$ the reproduction number $\mathcal {R}_{0}$ also increases by $10\%$, which may lead to an epidemic. Therefore, the transmission rate must be significantly decreased in order to reduce the reproduction number by following proper preventive measures and treatment.

From Table 3, it can be concluded that sensitivity indices play a vital role in analyzing the mathematical model with the data taken into consideration.

Table 2 Parameters value used in numerical simulations

Table 3 Sensitivity indices of $\mathcal {R}_T$ and $\mathcal {R}_H$ to the parameters

Fig. 2

Graphs showing the solution trajectories converging toward the disease-free equilibrium point $E_0=(12500,0,0,0,0,0,0,0)$ when the reproduction number $\mathcal {R}_0$ corresponding to HIV and TB is less than unity; a Susceptibles b TB infectives c HIV infectives d HIV-TB co-infectives

Fig. 3

Graphs justifying the local asymptotic stability of the TB endemic equilibrium point $E_T=(35.0784, 113.731, 2050.01, 51.1209,0,0,0,0)$; a Susceptibles b Latent TB infectives c TB infectives d Individuals recovered from TB e HIV infectives f HIV-TB co-infectives

Fig. 4

Graphs showing the local asymptotic stability of the HIV endemic equilibrium point $E_H=(2430.56, 0, 0, 0, 592.32, 0, 0, 3553.92)$ when the reproduction number $\mathcal {R}_H$ is greater than unity; a Susceptibles b TB infectives c HIV infectives d HIV-TB co-infectives e Individuals under treatment of HIV

Fig. 5

Graphs illustrating the local asymptotic stability of the co-endemic equilibrium point $E_{T_H}^2=(45.1281,121.822, 1481.14, 47.474,2.59682, 3.53903, 178.078, 48 2.01)$ when the reproduction number $\mathcal {R}_0$ is greater than unity; a Susceptibles b TB infectives c Individuals recovered from TB d HIV infectives e HIV-TB co-infectives f Individuals under treatment of HIV

Fig. 6

Graphs illustrating the local stability of the TB endemic equilibrium point $E_T^1=(222.89, 673.56, 1884.25, 298.063, 0, 0,0,0),$ when the reproduction numbers corresponding to both HIV and TB are less than unity; a Susceptibles b Latent TB infectives c TB infectives d Individuals recovered from TB e HIV infectives f HIV-TB co-infectives

Fig. 7

Graphs showing the solution trajectories converging toward the locally asymptotically stable HIV endemic equilibrium point $E_H=(2430.56, 0, 0, 0, 592.32, 0 , 0, 3553.92)$; a Susceptibles b TB infectives c HIV infectives d HIV-TB co-infectives e Individuals under treatment of HIV

8 Numerical simulations

The model is numerically simulated for the existence and local asymptotic stability of the endemic equilibrium points as, due to an eight dimensional model, it is difficult for the full model to determine all the results analytically. Thus, the existence and local asymptotic stability of the endemic equilibrium points for the full model will be illustrated numerically. In this section, the numerical simulations are performed by taking the parameters value as described in Table 2. In Table 2, certain parameter values have been chosen from previously published articles and for the remaining values we have used the facts provided by other researches and the World Health Organization. In our model, we have assumed $\mu _{T_H}=0.3$, by taking into consideration the fact that the death rate due to HIV-TB co-infection is more than the death rate induced due to HIV and TB only, which we have taken as 0.2 and 0.1, respectively. Also, $\eta <1$ is a modification parameter, which is taken into account by considering the fact that the class of individuals taking antiretroviral therapy have lesser viral load due to a restored immune system and hence chosen as $\eta =0.6$. The initial conditions are chosen as $S(0)=1400,\ L_T(0)= 850,\ I_T(0)= 170, \ R_T(0)= 30,\ I_H(0)= 40,\ L_{T_H}(0)=60,\ I_{T_H}(0)=30$ and $R_H(0)=20$. The numerical simulations are performed using the predictor–corrector method [43] in MATLAB by considering four different values of the order of differential equations, which are $\alpha =1, 0.9, 0.8, 0.7$.

From the sensitivity indices given in Table 3, it can be observed that the transmission rates corresponding to HIV and TB have an immense impact on the reproduction number $\mathcal {R}_0$ and hence on the equilibrium points. Thus, with the chosen parameters, various equilibrium points can be obtained by varying the value of transmission rates corresponding to HIV and TB, that is, $\beta _H$ and $\beta _T$, respectively.

• (1) By choosing $\beta _H=0.07$ and $\beta _T=0.8$, the associated reproduction numbers are obtained as $\mathcal {R}_H=0.947059$ and $\mathcal {R}_T=0.152796,$ both of which are less than unity and hence, $\mathcal {R}_0 =\max \{\mathcal {R}_H, \mathcal {R}_T \}$ is less than unity. Therefore, only a locally asymptotically stable disease-free equilibrium point $E_0=(12500,0,0,0,0,0,0,0)$ exists in this case. The local asymptotic stability of the disease-free equilibrium point can be seen in Fig. 2, where all the solution trajectories are approaching toward the respective components of the disease-free equilibrium point for different values of the order of differential equations $(\alpha )$. It can be observed from Fig. 2 that as the order of differential equations changes from fractional to integer value, that is, when $\alpha$ increases from 0.7 to 1, susceptibles start approaching the equilibrium value 12500 more rapidly. It can also be visualized from Fig. 2b,c and d that when $\alpha$ takes fractional value, that is, 0.9, 0.8 and 0.7 instead of integer value, the number of infectives approaches toward zero in slightly higher time, which seems to be more realistic as far as a real world problem is considered.

• (2) If the transmission rate corresponding to TB increases from $\beta _T = 0.8$ to 7.8, with $\beta _H$ same as defined in Table 2, the reproduction number corresponding to TB exceeds unity and takes the value $\mathcal {R}_T=1.48976$. Thus, TB becomes endemic in the population corresponding to which two equilibrium points come into existence, namely, an unstable disease-free equilibrium point $E_0=(12500,0,0,0,0,0,0,0)$ and a locally asymptotically stable TB endemic equilibrium point $E_T=(35.0784, 113.731,2050.01, 51.1209,0,0,0,0).$ The local asymptotic stability of the TB endemic equilibrium point $E_T$ can be visualized in Fig. 3 with four different values of $\alpha$ that are $\alpha =1, 0.9, 0.8, 0.7$. It can be seen from Fig. 3c that the TB infectives are rising with a lower rate for $\alpha =0.7$, whereas the rate of increment of infectives increases as $\alpha$ increases. Further, from Fig. 3d, it can be observed that the individuals recovered from TB are more for fractional values of $\alpha$ rather than an integer value of $\alpha$. This may happen due to the fact that, as $\alpha$ reduces from 1 to 0.7, memory effects come under consideration and individuals having a previous history of the disease start taking more precautionary measures which leads to lower incremental rate of infectives and higher rate of recovery. However, the rate of convergence toward the equilibrium point is higher for a larger value of $\alpha$.

• (3) By increasing the value of $\beta _H$ from 0.07 to 0.2 with the value of $\beta _T$ same as 0.8, the reproduction number corresponding to HIV exceeds unity. Thus, along with an unstable disease-free equilibrium point $E_0$, a locally asymptotically stable HIV endemic equilibrium point $E_H=(2430.56, 0, 0, 0, 592.32, 0 , 0, 3553.92)$ exists. Fig. 4 justifies the local asymptotic stability of the HIV endemic equilibrium point $E_H$ for $\mathcal {R}_0=2.70588$. From Fig. 4, it can be visualized that the solution trajectories are approaching the respective components of the equilibrium point $E_H$ with a faster rate of convergence for higher value of $\alpha$. It can be observed from Fig. 4a that the number of susceptibles is less when $\alpha =1$ for initial few days; however, they start increasing for $\alpha =0.7$, due to the incorporation of memory effects. Also, since the memory effect of the system increases as $\alpha$ decreases, HIV infectives having previous knowledge of the disease start taking the antiretroviral therapy soon. Thus, HIV infectives increase with a smaller rate for fractional values of $\alpha$ as compared to the case when $\alpha$ assumes integer value (see Fig. 4c).

• (4) If we choose $\beta _H=0.2$ and $\beta _T=7.8$, the reproduction numbers corresponding to HIV and TB are obtained as $\mathcal {R}_H=2.70588$ and $\mathcal {R}_T=1.48976,$ respectively, both of which are greater than unity. Thus, in this case, both diseases coexist in the population. Hence, along with the disease-free equilibrium point $E_0$ and single disease equilibrium points $E_T$ and $E_H$, we obtain two interior endemic equilibrium points that are an unstable co-endemic equilibrium point $E_{T_H}^1=(2170.11,241.479,6.6578,9.34821,508. 647,77.726,3.82626,3527.8)$ and a locally asymptotically stable co-endemic equilibrium point $E_{T_H}^2=(45.1281,121.822, 1481.14, 47.474, 2.59682, 3.53903, 178.078, 482.01).$ The local asymptotic stability of the co-endemic equilibrium point $E_{T_H}^2$ can be observed in Fig. 5.

Now, we further vary the transmission rates to verify the existence of backward bifurcation when the reproduction number corresponding to TB is less than unity but greater than the critical value. In this scenario, we will illustrate the following two cases:

• (1) When $\beta _H=0.07$, $\beta _T=1.8$ and the remaining values same as given in Table 2, we obtain $\mathcal {R}_H=0.947059<1$ and $\mathcal {R}_T=0.34379<1$. In this case, along with the disease-free equilibrium point $E_0$, the existence of two more TB endemic equilibrium points, namely a locally asymptotically stable TB endemic equilibrium point $E_T^1=(222.89, 673.56, 1884.25, 298.063, 0,0,0,0)$ and an unstable TB endemic equilibrium point $E_T^2=(10038.3, 2039.1, 33.6027, 220. 217, 0, 0,0, 0)$, is verified numerically, which justifies the occurrence of backward bifurcation. The local asymptotic stability of the TB endemic equilibrium point $E_T^1$ can be visualized from Fig. 6. In this case also, the rate of increment in TB-infected individuals is less for a fractional value of $\alpha$ rather than an integer value, with a faster rate of convergence for a higher value of $\alpha$.

• (2) When the transmission rate of HIV increases to 0.2, the reproduction numbers corresponding to HIV and TB are computed as $\mathcal {R}_H=2.70588>1$ and $\mathcal {R}_T=0.34379<1$, respectively. In this case, HIV and TB both exist in the population, corresponding to which four equilibrium points are obtained—an unstable disease-free equilibrium point $E_0=(12500,0,0,0,0,0,0,0)$, an unstable TB endemic equilibrium point $E_T^1=(222.89, 673.56, 18 84.25, 298.063, 0,0,0,0)$, an unstable TB endemic equilibrium point $E_T^2=(10038.3, 2039.1, 33.6027, 220.217, 0, 0,0, 0)$ and a locally asymptotically stable HIV endemic equilibrium point $E_H=(2430.56, 0, 0, 0, 592.32, 0 , 0, 3553.92).$ The local asymptotic stability of the HIV endemic equilibrium point $E_H$ for different values of $\alpha$ can be observed from Fig. 7.

In our model, we have shown the trajectories corresponding to HIV and TB for four different values of the order of derivatives ($\alpha$), to represent the role that memory plays in the treatment and recovery from HIV and TB infection and also in the stability of the equilibrium points. The different behaviors of solution trajectories, corresponding to the HIV-TB model for different values of the order of derivatives, indicate the novelty of this article over other papers on HIV-TB co-infection[14, 44].

The results obtained in other papers on HIV-TB co-infection have been proved for integer order only rather than fractional order. Tanvi et al. [14] and Kumar and Jain [44] have considered HIV-TB co-infection models with integer order derivatives. They have shown the trajectories corresponding to HIV and TB co-infection for integer order. In the model by Kumar and Jain [44], they have shown that the disease-free equilibrium point is locally asymptotically stable when the corresponding reproduction number is less than unity. Also, the endemic equilibrium point has been shown to be locally asymptotically stable if the corresponding reproduction number is greater than unity in both analytical and numerical ways. In our model, however, along with the stability of the disease-free and the endemic equilibrium point corresponding to the reproduction number, the convergence rate of solution trajectories toward the components of equilibrium points can also be visualized by taking into consideration the different value for fractional order derivatives. In our model, it has been shown that the solution trajectories converge more rapidly to the components of equilibrium points if the order of derivatives is higher; that is, the rate of convergence toward the steady state is higher for higher value of which cannot be observed in case of integer order models.

Thus, it can be observed that the fractional order model plays a significant role in reducing the number of infectives and visualizing the convergence rate of the solution trajectories toward the steady state.

9 Conclusion

In this paper, we have proposed a fractional order differential equation model to study the transmission dynamics of HIV-TB co-infection by incorporating the reinfection from tuberculosis in both TB and HIV-TB co-infected individuals along with the occurrence of recurrent TB. The reproduction number corresponding to both HIV and TB has been computed. The analysis of both HIV and TB sub-models has been performed separately for $\alpha \in (0,1]$. The disease-free equilibrium point for the full model is shown to be locally asymptotically stable for $\mathcal {R}_0<1$. It has been concluded that if exogenous reinfection occurs and the effectiveness of TB treatment is low, then the system exhibits backward bifurcation. Thus, reducing the reproduction number, $\mathcal {R}_0$, below unity is not enough to eradicate the disease from the population. However, the results show that, by reducing the reproduction number below unity, both HIV and TB can be eradicated from the population, if reinfection from TB does not occur in latently infected individuals and recovery from TB gives permanent immunity. Further, the existence of HIV-TB co-endemic equilibrium point has been illustrated numerically when the corresponding reproduction number $\mathcal {R}_0$ is greater than unity.

The model is numerically simulated to investigate the Caputo fractional order model for different values of $\alpha$. Numerical results justify the local asymptotic stability of the equilibrium points for $\alpha =1, 0.9, 0.8, 0.7$ and show that the rate of convergence toward the equilibrium points is more for higher order of derivatives in comparison to the smaller order derivatives. Thus, to achieve faster convergence toward an equilibrium point a higher order system should be considered. The graphical results show a lower increment rate in the number of HIV and TB infectives for a smaller fractional order parameter. It is observed that $\alpha$ can play the role of precautionary measures against infection prevalence, as by reducing the value of $\alpha$, a lower rate increment in the number of infectives can be observed due to the incorporation of memory effect. Thus, the present work is a novel analysis to describe the transmission dynamics of HIV-TB co-infection that can be useful for the readers and healthcare authorities and policy makers.