1 Introduction

The main objectives of mathematical modeling of infectious diseases are to identify and study the factors that influence the spread of the disease and to predict the future dynamics of a particular disease or combination of diseases under consideration. Furthermore, mathematical modeling is significantly used in formulating and evaluating strategies to control and prevent their spread in the susceptible population. Throughout the world, more so in the developing world, there are a number of deadly infectious diseases that are severely affecting the lifespan of the human population. Acquired Immuno Deficiency Syndrome (AIDS) is one of such deadly diseases that is a seriously life threatening condition caused by the Human Immuno-deficiency Virus (HIV). This infection causes a progressive decrease in the body’s natural inbuilt immunity to fight against infections. It was first reported in June 1981 and since then AIDS has become one of the history’s worst pandemics. HIV/AIDS epidemic continues its deadly expansion across the globe with approximately 14,000 new infections per day. Till date, there is no vaccine to protect an individual from this dreadful virus. The HIV is transmitted predominantly via sexual contact or needle sharing. Moreover, vertical transmission is also a mode of transmission for HIV. AIDS is the last stage of HIV infection resulting in death.

Tuberculosis (TB) is an infectious disease and in humans it is mainly caused by Mycobacterium tuberculosis. The most important source of infection is the patient with TB of the lung, or pulmonary TB (PTB). The two diseases (HIV and TB) differ in their modes of transmission. TB is an airborne disease and is described as a slow disease because of its long and variable latency period distribution and its short infectious period [1, 2]. Tuberculosis (TB) and Human immuno deficiency syndrome (HIV) are well-known mortality and morbidity resulting diseases worldwide. As HIV infection causes a decrease in the immunity level of individuals, so people infected with HIV are more likely to get opportunistic infections. Amongst the HIV cases, TB is the most common opportunistic infection. These two diseases exhibit a special bond, where each accelerates the progression of the other. In a HIV/TB co-infected person, the immune response to TB bacilli increases HIV replication. As a result of the increase in the number of viruses in the body, there is rapid progression of HIV infection. The viral load can increase by six–seven fold. As a result, there is a rapid decline in the count of CD4 cells, which carry the CD4 glycoprotein and are also called T-helper cells and the patient starts developing symptoms of various opportunistic infections. Thus the health of the patient who has dual infection deteriorates much faster than a patient with a single infection. The mortality due to TB in AIDS cases is also high. The risk of developing TB has been estimated to be between 21–34 times greater in people living with HIV than among those without HIV infection. TB increases the rate of progression from HIV to AIDS and shortens the life span of patients with HIV infection. In 2010, 1.8 million HIV infectives have died due to HIV among which 350, 000 were due to TB and of the 1.1 million people who died from TB. TB represents a serious health risk and is a leading cause of morbidity and mortality among people living with HIV [2–4].

Since currently no cure exists for the HIV disease, only prevention is effective in controlling its spread amongst the population. We believe that the detection of HIV infection and subsequent counseling can be treated as a control measure. In India, HIV counseling and testing services started in 1997. Currently, there are numbers of Integrated Counseling and Testing Centers (ICTCs)/Prevention of Parent to Child Transmission (PPTCTs) and Surveillance Centres under NACO (National AIDS Control Organization) that are actively working in screening and providing counseling to HIV infectives. The government of India has opened many Anti-retroviral Therapy (ART) centres, to provide anti-retroviral therapy to all the AIDS patients in the country. In addition to this several NGOs such as The Naz Foundation (India), Desire Society and SAATHII, etc. are working to bring better awareness and knowledge regarding HIV, AIDS and TB to the Indian population.

In recent years, mathematical modeling of HIV, TB and HIV/TB co-infections have been reported by several researchers, [for details see 4–14]. However, most of these models do not incorporate the effects of screening of infectives in the transmission dynamics of these diseases. In [15, 16], the authors incorporated the effect of screening of HIV infectives but they did not incorporate the treatment. Most of the researchers, who have incorporated the screening of infectives, have made separate classes for aware and unaware infectives. Hence, the extension of these models to HIV-TB co-infection is very difficult as the number of variables in the mathematical model will increase, making analysis of the model very complicated.

In the present paper, we consider a simple mathematical model for the dynamics of HIV/TB co-infection by incorporating both screening and treatment of infectives. As our approach of mathematical modeling is different, so incorporation of both the treatment and screening does not complicate the analysis of the model. It is assumed that the screening is associated with proper counseling. And, further we assume that the screened HIV infectives are not taking part in the transmission of HIV. However, some screened HIV infectives can contribute in the transmission of the HIV virus but in this work we ignore those individuals as if they are not screened. We consider only the adult sexually active population in the model formulation as the majority of HIV transmissions are due to hetero-sexual transmissions.

The remaining of this paper is organized as follows: Section 2 presents the mathematical model, Section 3 is devoted to the analysis of the sub-models, Section 4 deals with the analysis of the full model, Section 5 presents the numerical simulations to illustrate analytical findings and to see the effect of various parameters on the transmission dynamics of HIV and Section 6 concludes the paper with a brief discussion.

2 The model

We formulate a deterministic HIV/AIDS-TB co-infection model to investigate the effect of screening (with proper counseling) and treatment of infectives. The total sexually active human population N (t) is subdivided into six sub-populations i.e., susceptible individuals (S), active TB individuals who are capable of transmitting the disease (I 1), HIV-infected individuals (I 2), individuals dully infected with HIV and TB (I 3), AIDS patients (I 4) and AIDS individuals dually infected with TB (I 5). Hence the total sexually active human population N is given by:

N = S + I 1 + I 2 + I 3 + I 4 + I 5.

It is assumed that the human population is recruited into the population at a constant rate Λ. Susceptible individuals acquire HIV infection due to effective contact with HIV-infected individuals at a rate λ H and acquire TB infection following effective contact with TB-infected individuals at a rate λ T . The force of infection associated with TB infection, denoted by λ T is given by:

$$\lambda_{T} =\frac{\beta_{T} (I_{1} +I_{3} +I_{5} )}{N}$$
(1)

In (1), β T is the effective contact rate for TB infection. HIV-infected individuals and AIDS patients may acquire TB at rate β T . The force of infection associated with HIV infection is denoted by λ H and is given by:

$$\lambda_{H} =\frac{\beta_{H} \{{(1-\alpha_{1} )I_{2} +(1-\alpha_{2})\eta_{1} I_{3} +(1-\alpha_{3})I_{4} +(1-\alpha_{4}) \eta_{2} I_{5}}\}}{N}$$
(2)

where, β H is the effective contact rate for HIV infection.

The parameters (η 1 ≥ 1 and η 2 ≥ 1) are the modification parameters that correspond to the assumption that the dually infected individuals transmit HIV infection with a higher rate as compared to HIV-only infectives. Similarly, ϕ 1, ϕ 2 ≥ 1 are modification parameters that correspond to the fact that HIV or AIDS infected individuals are more prone to acquire TB infection than the susceptibles. It is assumed that TB patients may recover after treatment at a rate γ and will enter the susceptible class. μ is the natural death rate for all the individuals in different subgroups. Further μ i for i = 1, 2, 3, 4, 5 account for the disease related death rate in the respective class. η is considered as the rate of screening for TB and it is assumed that the individuals who are screened of TB are keeping themselves away from HIV infection. Here, α i for i = 1, 2, 3, 4 are the rates of screening for HIV, HIV-TB co-infected individuals, AIDS and AIDS-TB co-infected individuals respectively. The parameters δ 1 and δ 2 are the disease progression rates to AIDS by HIV treated and untreated individuals respectively. Similarly δ 3 and δ 4 are the disease progression rates to AIDS-TB dual infection by HIV-TB dually infected treated and untreated individuals respectively. The rate of treatment for HIV is denoted by ν, under the assumption that the disease progression rate will be slow in the individuals who are taking treatment. Combining the different rates mentioned above τ 1 is considered as the progression rate to AIDS by HIV-infected individuals and τ 2 is the progression rate to the AIDS-TB dually infected class by HIV-TB dually infected individuals. Here τ 1 and τ 2 are given by:

τ 1 = α 1 {δ 1 ν + δ 2 (1 − ν)} + δ 2 (1 − α 1)

τ 2 = α 2 {δ 3 v + δ 4 (1− ν)} + δ 4 (1 − α 2).

Combining all the above mentioned facts, the mathematical model can be formulated as follows:

$$\begin{array}{@{}rcl@{}} \frac{dS}{dt}&=&\Lambda -\lambda_{T} S-\lambda_{H} S-\mu S+\gamma \eta I_{1} \notag\\ \frac{dI_{1} }{dt}&=&\lambda_{T} S-\lambda_{H} (1-\eta )I_{1} -\mu I_{1} -\mu_{1} I_{1} -\gamma \eta I_{1} \notag\\ \frac{dI_{2} }{dt}&=&\lambda_{H} S-\phi_{1} \lambda_{T} I_{2} +\alpha_{2} \gamma I_{3} -(\mu +\mu_{2} +\tau_{1} )I_{2} \notag\\ \frac{dI_{3} }{dt}&=&\lambda_{H} (1-\eta )I_{1} +\phi_{1} \lambda_{T} I_{2} -\alpha_{2} \gamma I_{3} -(\mu +\mu_{3} +\tau_{2} )I_{3} \notag\\ \frac{dI_{4} }{dt}&=&\tau_{1} I_{2} -\phi_{2} \lambda_{T} I_{4} -(\mu +\mu_{4} )I_{4} +\gamma \alpha_{4} I_{5} \notag\\ \frac{dI_{5} }{dt}&=&\phi_{2} \lambda_{T} I_{4} +\tau_{2} I_{3} -(\mu +\mu_{5} )I_{5} -\gamma \alpha_{4} I_{5} \end{array}$$
(3)

Here S > 0, I 1 ≥ 0, I 2 ≥ 0, I 3 ≥ 0, I 4 ≥ 0, I 5 ≥ 0. Model system (3) governs the human population, hence all the variables and parameters used in the model formulation are non-negative. We consider a biologically-feasible region:

$$\Omega =\left\{ {(S, I_{1} , I_{2} , I_{3} , I_{4} , I_{5} )\in R_{+}^{6} :N\le \frac{\Lambda }{\mu }} \right\}$$

We adhere to the following steps to show the positive invariance of Ω i.e., all the solutions of (3) that initiate in Ω remain in the region Ω:

We have N(t) = S(t) + I 1(t) + I 2(t) + I 3(t) + I 4(t) + I 5(t). The rate of change of the total population by adding all the equations considered in (3) is:

$$\frac{dN}{dt}=\Lambda -\mu N-\mu_{1} I_{1} -\mu_{2} I_{2} -\mu_{3} I_{3} -\mu_{4} I_{4} -\mu_{5} I_{5}$$

Clearly, whenever N > Λ/μ, dN/dt < 0. Notice that dN/dt is bounded by Λ − μN. By using the standard comparison theorem [17] it can be shown that, 0 ≤ N(t) ≤ \(\frac {\Lambda }{\mu }(1-e^{-\mu t}) + N(0)e^{-\mu t}\). In particular, N (t) ≤ \(\frac {\Lambda }{\mu }\) if N (0) ≤ \(\frac {\Lambda }{\mu }\). Hence, the region \(\Omega =\left \{ {(S, I_{1} , I_{2} , I_{3} , I_{4} , I_{5} )\in R_{+}^{6} :N\le \frac {\Lambda }{\mu }} \right \}\) is positively invariant for system (3).

It is also necessary to prove that all the variables of model (3) are non-negative so that the solution of the system with positive initial conditions remains positive for all t > 0. The following lemma describes this fact.

Lemma 1

If S(0) ≥ 0, I i (0) ≥ 0 for i = 1, 2 . . . 5, the solutions S(t), I 1(t), I 2(t), I 3(t), I 4(t), I 5(t) of system (3) are positive for all t > 0.

Proof

We shall prove this lemma using a contradiction by assuming that the total population N (t) ≠ 0 for all t ≥ 0.

We assume that there exists a first time t 1 such that:

$$S(t_{1}) = 0, S^{\prime}(t_{1}) < 0, I_{1} (t)\ge 0, I_{2} (t)\ge 0, I_{3} (t)\ge 0, I_{4} (t)\ge 0, I_{5} (t)\ge 0, 0\le t\le t_{1} ,$$
(4)

there exists a first time t 2 such that:

$$I_{1} (t_{2} ) = 0, I_{1}^{\prime} (t_{2} ) < 0, S(t)\ge 0, I_{2} (t)\ge 0, I_{3} (t)\ge 0, I_{4} (t)\ge 0, I_{5} (t)\ge 0, 0\le t\le t_{2} ,$$
(5)

there exists a first time t 3 such that:

$$I_{2} (t_{3} ) = 0, I_{2}^{\prime} (t_{3} ) < 0, S(t)\ge 0, I_{1} (t)\ge 0, I_{3} (t)\ge 0, I_{4} (t)\ge 0, I_{5} (t)\ge 0, 0\le t\le t_{3} ,$$
(6)

there exists a first time t 4 such that:

$$I_{3} (t_{4} ) = 0, I_{3}^{\prime} (t_{4} ) < 0, S(t)\ge 0, I_{1} (t)\ge 0, I_{2} (t)\ge 0, I_{4} (t)\ge 0, I_{5} (t)\ge 0, 0\le t\le t_{4} ,$$
(7)

there exists a first time t 5 such that:

I 4(t 5) = 0, I′4(t 5) < 0, S(t) ≥ 0, I 1(t) ≥ 0, I 2(t) ≥ 0, I 3 (t) ≥ 0, I 5 (t) ≥ 0, 0 ≤ t ≤ t 5   (8)

and there exists a first time t 6 such that:

$$I_{5} (t_{6}) = 0, I_{5}^{\prime} (t_{6} ) < 0, S(t)\ge 0, I_{1} (t)\ge 0, I_{2} (t)\ge 0, I_{3} (t)\ge 0, I_{4} (t)\ge 0, 0\le t\le t_{6}.$$
(9)

□

From (4) S′(t 1) = Λ +γ η I 1(t 1) > 0, which is a contradiction, meaning that S(t) ≥ 0, t ≥ 0. From (5), we get:

$$I_{1}^{\prime} (t_{2} ) = \left. {\lambda_{T} } \right|_{t=t_{2} } S(t_{2} ) = \frac{\beta_{T} [ {I_{1} (t_{2} ) + I_{3} (t_{2} ) + I_{5} (t_{2} )} ]}{N(t_{2} )}S(t_{2} )\ge 0,$$

which is again a contradiction, meaning that I 1(t) ≥ 0, t ≥ 0.

Again from (6), we get:

$$\begin{array}{@{}rcl@{}} I_{2}^{\prime} (t_{3} )&=&\left.\lambda_{H}\right|_{t=t_{3}} S(t_{3} ) + \alpha_{2} \gamma I_{3} (t_{3})\notag \\ &=&\frac{(1-\alpha_{2})\eta_{1} I_{3} (t_{3} ) + (1-\alpha_{3} )I_{4} (t_{3} ) + (1-\alpha_{4} )\eta_{2} I_{5} (t_{3} )}{N(t_{3} )}S(t_{3} ) + \alpha_{2} \gamma I_{3} (t_{3} )\ge 0, \notag \end{array}$$

which is a contradiction, implying I 2(t) ≥ 0, t ≥ 0.

Similarly, using the assumptions in Eqs. (7)–(9), we get the following contradictions respectively:

$$\begin{array}{@{}rcl@{}} I_{3}^{\prime} (t_{4} )&=&\left. {\lambda_{H} } \right|_{t=t_{4} } (1-\eta )I_{1} (t_{4} ) + \left. {\phi_{1} \lambda_{T} } \right|_{t=t_{4} } I_{2} (t_{4} )\notag \\ &=&\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2} (t_{4} ) + (1-\alpha_{3} )I_{4} (t) + (1-\alpha_{4} )\eta_{2} I_{5} (t_{4} )} \right\}}{N(t_{4} )}(1-\eta) I_{1} (t_{4} )\notag\\ &&+\;\phi_{1} \frac{\beta_{t} I_{1} (t_{4}) + I_{5} (t_{4} )}{N(t_{4} )}I_{2} (t_{4} )\ge 0, \notag \\ I_{4}^{\prime} (t_{5} )&=&\tau_{1} I_{2} (t_{5} ) + \gamma \alpha_{4} I_{5} (t_{5} )\ge 0, \notag \\ I_{5}^{\prime} (t_{6} )&=&\left. {\phi_{2} \lambda_{T} } \right|_{t=t_{6} } I_{4} (t_{6} ) + \tau_{2} I_{3} (t_{6} ) = \phi_{2} \beta_{T} \frac{I_{1} (t_{6} ) + I_{3} (t_{6} )}{N(t_{6} )}I_{4} (t_{6} ) + \tau_{2} I_{3} (t_{6} )\ge 0.\notag \end{array}$$

Hence we conclude that I 3(t) ≥ 0, I 4(t) ≥ 0, I 5(t) ≥ 0, for t ≥ 0. Thus the solutions S(t) , I i (t) , i = 1, 2…5 of system (3) remain positive for all t > 0.

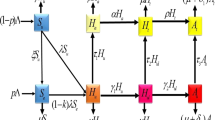
The schematic flow diagram in Fig. 1 describes the flow of individuals from one to another compartment with the possibility of acquiring TB, HIV or HIV/TB co-infection.

Fig. 1
figure 1

The schematic flow diagram of HIV/TB model system (3)

Full size image

3 Analysis of the sub-models

The analysis of the full model will be followed by analyzing the dynamics of the sub-models with TB-only and HIV-only.

3.1 TB-only model

The TB-only model is obtained by setting I 2 = I 3 = I 4 = 0 = I 5 and is given by:

$$\begin{array}{@{}rcl@{}} \frac{dS}{dt}&=&\Lambda -\lambda_{T} S-\mu S+\gamma \eta I_{1}, \notag \\ \frac{dI_{1}}{dt}&=&\lambda_{T} S-\mu I_{1} -\mu_{1} I_{1} -\gamma \eta I_{1}. \end{array}$$
(10)

Here \(\lambda _{T} =\frac {\beta _{T} I_{1} }{N}\). The basic reproduction number for the above model is calculated as:

$$R_{T} =\frac{\beta_{T} }{\mu +\mu_{1} +\gamma \eta }$$

The region of attraction for this sub-model is given by:

$${\Omega}_{1} =\left\{ {(S, I_{1} )\in {{R}_{+}^{2}} :{S+I}_{1} =N\le \frac{\Lambda }{\mu }} \right\}.$$

3.1.1 Stability of disease-free equilibrium (DFE)

Model (10) has a DFE, obtained by setting the right-hand side of the equations in the model to zero and is given by:

$$\mathcal{E}_{T0} =\left({S^{0}, {I_{1}^{0}} } \right) = \left({\frac{\Lambda }{\mu }, 0} \right)$$

Theorem 1

The disease-free equilibrium Ɛ T0 of system (10) is locally asymptotically stable when R T < 1.

Proof

To study the stability of the DEF we calculated the variational matrix at Ɛ T0, which gives two eigenvalues −μ, −(1 − R T )(μ + μ 1 + γ η), which are negative for R T < 1 that ensures that the DFE Ɛ T0 is locally asymptotically stable. □

Theorem 2

If R T < 1, then the disease-free steady state Ɛ T0 of (10) is globally asymptotically stable in the region Ω1.

Proof

Define the Lyapunov-LaSalle function U : {(S, I 1) ∈ Ω1 : S > 0} → ℝ by:

$$U(S, I_{1} ) = \frac{1}{2}{I_{1}^{2}} .$$

□

The time derivative of U computed along solutions of (10) is:

$$\begin{array}{@{}rcl@{}} U^{\prime} ({S, I_{1} } )&=&\left({\frac{\beta_{T} I_{1} S}{S+I_{1} }-({\mu +\mu_{1} +\gamma \eta } )I_{1} } \right)I_{1}\notag \\ &=&\frac{{I_{1}^{2}} }{({S+I_{1} } )}\{ {\beta_{T} S-({\mu +\mu_{1} +\gamma \eta } )({S+I_{1} } )} \}\notag \\ &=&({\mu +\mu_{1} +\gamma \eta } )\frac{{I_{1}^{2}} }{({S+I_{1} } )}\left\{ {\left({\frac{\beta_{T} }{\mu +\mu_{1} +\gamma \eta }-1} \right)S-I_{1} } \right\}\notag \\ &=&-({\mu +\mu_{1} +\gamma \eta } )\frac{{I_{1}^{2}} }{({S+I_{1} } )}\{ {({1-R_{T} } )S+I_{1} } \}\notag \end{array}$$

Since all the model parameters are positive and variables are non-negative, it follows that U′(S, I 1) ≤ 0 for R T ≤1 with U′(S, I 1) = 0 if and only if I 1 = 0. Hence the largest invariant set contained in {(S, I 1)∈Ω1, U′ = 0} is the singleton {Ɛ T0}. Thus the global asymptotic stability of Ɛ T0 for R T < 1 follows from LaSalle’s invariance Principle [18].

3.1.2 Existence and stability of the endemic equilibrium point

The unique endemic equilibrium point of system (10) is given by:

$$\mathcal{E}_{1} =({S^{\ast} , I_{1}^{\ast} } ) = \left({\frac{\Lambda }{({\mu +\mu_{1} } )({R_{T} -1} ) + \mu }, \frac{\Lambda ({R_{T} -1} )}{({\mu +\mu_{1} } )({R_{T} -1} ) + \mu }} \right),$$

which exists whenever R T > 1. The local stability of this equilibrium point is summarized in the following theorem.

Theorem 3

The TB-only endemic equilibrium Ɛ 1 of system (10) is locally asymptotically stable if R T > 1.

Proof

The Jacobian of system (10) evaluated at the equilibrium point (Ɛ 1) is given by:

$$J({\mathcal{E}_{1} } ) = \left({{\begin{array}{*{20}c} {-\mu -\frac{\beta_{T} \left({I_{1}^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}} & {-\frac{\beta_{T} \left({S^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}+\gamma \eta } \\ {\frac{\beta_{T} \left({I_{1}^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}}& {\frac{\beta_{T} \left({S^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}-\left({\mu +\mu_{1} +\gamma \eta } \right)} \\ \end{array} }} \right)$$

Using the steady state, we take into account the following identity:

$$\gamma \eta +\mu_{1} +\mu =\frac{\beta_{T} S^{\ast} }{S^{\ast} +I_{1}^{\ast} }$$

and the above Jacobian matrix can be rewritten as:

$$J({\mathcal{E}_{1} }) = \left({{\begin{array}{*{20}c} {-\mu -\frac{\beta_{T} \left({I_{1}^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}} & {\frac{\beta_{T} S^{\ast} I_{1}^{\ast} }{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}-\left({\mu +\mu_{1} } \right)} \\ {\frac{\beta_{T} \left({I_{1}^{\ast} } \right)^{2}}{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}} & {-\frac{\beta_{T} S^{\ast} I_{1}^{\ast} }{\left({S^{\ast} +I_{1}^{\ast} } \right)^{2}}} \\ \end{array} }} \right)$$

The trace of Ɛ 1 is:

$$tr(J(\mathcal{E}_{1})) = -\left\{ {\mu +\frac{\beta_{T} I_{1}^{\ast} }{({S^{\ast} +I_{1}^{\ast} } )}} \right\} < 0.$$

Further,

$$det(J(\mathcal{E}_{1})) = \frac{\mu\beta_{T} {S}^{\ast} {I}_{1}^{\ast}}{(S^{\ast} + {I}_{1}^{\ast})}^{2}+\frac{(\mu +\mu_{1})\beta_{T} {{I}^{\ast}}_{1}^{2}}{{(S^{\ast} + {I}_{1}^{\ast})}^{2}}>0.$$

□

Hence, the eigenvalues of the Jacobian matrix J(Ɛ 1) have negative real parts. This establishes the result that the endemic equilibrium is locally asymptotically stable whenever it exists.

The global stability of TB-only endemic equilibrium Ɛ 1 is proved using the method of Lyapunov and is stated in the following theorem.

Theorem 4

If R T > 1, then the unique TB-only endemic equilibrium Ɛ 1 of (10) is globally asymptotically stable.

Proof

Define L : {(S, I 1) ∈ Ω1 : S, I 1 > 0} → ℝ by:

$$\begin{array}{@{}rcl@{}} L(S, I_{1} )&=&\left[ {({S-S^{\ast}}) + ({I_{1} +I_{1}^{\ast}})-({S^{\ast} +I_{1}^{\ast}})\ln \left({\frac{S+I_{1}}{S^{\ast} +I_{1}^{\ast} }}\right )} \right] \notag\\ &&+\frac{(2\mu +\mu_{1})(S^{\ast}+I_{1}^{\ast})}{\beta_{T}}\left(\ln \frac{I_{1}}{I_{1}^{\ast}}+\frac{I_{1}^{\ast} }{I_{1}}-1 \right).\notag \end{array}$$

□

Here, L is C 1 on the interior of Ω1, Ɛ 1 is the global minimum of L on Ω1 and L(S ∗, I 1 ∗) = 0. Computing the time derivative of the above function along the solutions of (10), we get:

$$\begin{array}{@{}rcl@{}} L^\prime (S,I_{1} )&=&\frac{\left[ {( {S-S^{\ast}})+\left( {I_{1} -I_{1}^{\ast}}\right)} \right]}{S+I_{1} }\frac{d( {S+I_{1} })}{dt}+\frac{( {2\mu +\mu_{1} } )\left( {S^{\ast}+I_{1}^{\ast} } \right)}{\beta_{T} }\frac{\left( {I_{1} -I_{1}^{\ast} } \right)}{I^{2}}\frac{dI_{1} }{dt},\notag \\ &=&\frac{\left[ {( {S-S^{\ast} } )+\left( {I_{1} -I_{1}^{\ast} } \right)} \right]}{S+I_{1}}( {\Lambda -\mu ( {S+I_{1} } )-\mu_{1} I_{1} } )\notag \\ &&+\frac{( {2\mu +\mu_{1} } )\left( {S^{\ast} +I_{1}^{\ast} } \right)}{\beta_{T} }\frac{( {I_{1}}-{I_{1}^{\ast} } )}{{I_{1}^{2}}}\left( {\frac{\beta_{T} SI_{1} }{S+I_{1}}-({\mu +\mu_{1} +\gamma \eta })I_{1} } \right), \notag\\ &=&\frac{\left[ {\left( {S-S^{\ast} } \right)+\left( {I_{1} -I_{1}^{\ast} } \right)} \right]}{S +I_{1}}\left\{ {-\mu ( {S-S^{\ast}})-( {\mu +\mu_{1} } )\left( {I_{1} -I_{1}^{\ast} } \right)} \right\}\notag\\ &&+( {2\mu +\mu_{1} } )\left( {S^{\ast} +I_{1}^{\ast} } \right)\frac{\left( {I_{1} -I_{1}^{\ast} } \right)}{I_{1} }\left( {\frac{S}{S +I_{1}}-\frac{S^{\ast} }{S^{\ast} +I_{1}^{\ast} }} \right).\notag \end{array}$$

Using,

$$\begin{array}{c} \frac{S}{S+I_{1}}-\frac{S^{\ast}}{S^{\ast} +I_{1}^{\ast}}=\frac{I_{1} ({S-S^{\ast}})-S\left({I_{1} -I_{1}^{\ast}} \right)}{({S+I_{1}} )\left({S^{\ast} +I_{1}^{\ast} } \right)}\\ L^{\prime} (S, I_{1} ) = -\mu \frac{({S-S^{\ast} })^{2}}{S+I_{1} }-\left\{ {({\mu +\mu_{1} }) + ({2\mu +\mu_{1} } )\frac{S}{I_{1} }} \right\}\frac{\left({I_{1} -I_{1}^{\ast} } \right)^{2}}{({S+I_{1} } )}. \end{array}$$

Clearly, L′(S, I 1) < 0 always holds except at the TB-only endemic equilibrium, Ɛ 1. Also, L(S, I 1) → ∞ as S→∞ and L(S, I 1) → ∞ as I 1 → 0 or I 1 → ∞. Therefore, we may conclude that function L(S, I 1) is a Lyapunov function for system (10) and that, by the Lyapunov asymptotic stability theorem [19], the endemic steady state is globally asymptotically stable in the interior of Ω1, when it exists and this proves Theorem 4.

The dynamics of the HIV-only model is explored below.

3.2 HIV-only model

The HIV-only model is obtained by setting I 1 = I 3 = 0 = I 5 and is given by:

$$\begin{array}{@{}rcl@{}} \frac{dS}{dt}&=&\Lambda -\lambda_{H} S-\mu S, \notag \\ \frac{dI_{2}}{dt}&=&\lambda_{H} S-({\mu +\mu_{2} +\tau_{1} } )I_{2}, \notag \\ \frac{dI_{4}}{dt}&=&\tau_{1} I_{2} -({\mu +\mu_{4} } )I_{4}, \end{array}$$
(11)

where \(\lambda _{H} =\frac {\beta _{H}\{ {(1-\alpha _{1} )I_{2} +(1-\alpha _{3} )I_{4} }\}}{N}\)

3.2.1 Local stability of DFE

The HIV-only model (11) has a DFE given by:

$$\mathcal{E}_{H0} =\left({S^{0}, {I_{2}^{0}} , {I_{4}^{0}} } \right) = \left({\frac{\Lambda }{\mu }, 0, 0} \right)$$

. The linear stability of Ɛ H0 is carried out by the basic reproduction number R H . The stability of the equilibrium is further investigated using the next generation matrix operator [22]. The F and V matrices corresponding to new infection terms and remaining transfer terms are respectively given as follows:

$$F=\left({{\begin{array}{*{20}c} {\beta_{H} (1-\alpha_{1} )} & {\beta_{H} (1-\alpha_{3} )} \\ 0 & 0 \\ \end{array} }} \right); V=\left({{\begin{array}{*{20}c} {(\mu +\mu_{2} +\tau_{1} )} & 0 \\ {-\tau_{1} } & {(\mu +\mu_{4} )} \\ \end{array} }} \right)$$

. From this, it follows that:

$$R_{H} =\rho (FV^{-1}) = \frac{\beta_{H} \left\{ {(1-\alpha_{1} )(\mu +\mu_{4} ) + \tau_{1} (1-\alpha_{3} )} \right\}}{(\mu +\mu_{2} +\tau_{1} )(\mu +\mu_{4} )}.$$

(Note that S* = N * at the DFE Ɛ H0.) The following result is established using Theorem 2 of [22].

Lemma 2

The disease-free equilibrium of model (11) given by Ɛ H0, is locally asymptotically stable if R H < 1 and unstable if R H > 1.

The local stability analysis can also be viewed by evaluating the Jacobian matrix J (Ɛ H0) at the disease-free equilibrium point Ɛ H0. One eigenvalue of the Jacobian matrix J(Ɛ H0) is evaluated as -μ and the other two eigenvalues are the roots of the following quadratic equation:

λ 2 + {(μ + μ 2 + τ 1) + (μ + μ 4) − (β H (1− α 1))} λ + (μ + μ 2 + τ 1) (μ + μ 4) (1 − R H) = 0.

Clearly for R H < 1, the constant term as well as the coefficient of λ are positive implying the local stability of the disease-free equilibrium point Ɛ H0. Also it is noted that one of the eigenvalues will be zero for R H = 1.

The non-trivial equilibrium Ɛ 2 = (S *, 1 2 *, I 4 *) of system (11), is given by:

$$\begin{array}{@{}rcl@{}} &&{\kern3pc} S^{\ast} =\frac{(\mu +\mu_{2} +\tau_{1} )N^{\ast} }{\beta_{H} \left\{{(1-\alpha_{1}) + (1-\alpha_{3})\frac{\tau_{1}}{\mu +\mu_{4} }} \right\}}, \\ &&I_{2}^{\ast} =\frac{\left({\mu +\mu_{4} } \right)}{\mu +\mu_{4} +\tau_{1} }\left[ {1-\frac{\left({\mu +\mu_{2} +\tau_{1} } \right)}{\beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}}} \right]N^{\ast}, \end{array}$$

\(I_{4}^{\ast } =\frac {\tau _{1}}{(\mu + \mu _{4})}I_{2}^{\ast }\) and N ∗ is given by:

$$N^{\ast} =\frac{\Lambda \beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}}{\left({\frac{\left({\mu +\mu_{4} } \right)}{\mu +\mu_{4} +\tau_{1} }\left[ {\beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}-(\mu {}+{} \mu_{2} {}+{} \tau_{1} )} \right]+\mu } \right)({\mu +\mu_{2} {}+{} \tau_{1} } )}.$$

It is clear that the non-trivial equilibrium point \(\mathcal {E}_{2}\) exists only when R H > 1 and this corresponds to a unique positive equilibrium point associated with the HIV-only model.

3.2.2 Stability and bifurcation analysis for endemic equilibrium point

Let S = x 1, I 2 = x 2 and I 4 = x 3, so that N = x 1 + x 2 + x 3, and model (11) is re-written in the form:

$$\begin{array}{@{}rcl@{}} \frac{dx_{1} }{dt}&=&f_{1} =\Lambda -\lambda_{H} x_{1} -\mu x_{1}, \notag \\ \frac{dx_{2} }{dt}&=&f_{2} =\lambda_{H} x_{1} -({\mu +\mu_{2} +\tau_{1} })x_{2}, \notag \\ \frac{dx_{3} }{dt}&=&f_{3} =\tau_{1} x_{2} -({\mu +\mu_{4} } )x_{3}, \end{array}$$
(12)

where, \(\lambda _{H} =\frac {\beta _{H} \{{({1-\alpha _{1} } )x_{2} +({1-\alpha _{3} } )x_{3} } \}}{({x_{1} +x_{2} +x_{3} } )}\)

The Jacobian of system (12), at DFE \(\left ({\mathcal {E}_{H0} } \right )\) is given by:

$$J({\mathcal{E}_{H0} } ) = J_{\beta}^{\ast} =\left({{\begin{array}{*{20}c} {-\mu } & {-\beta_{H} (1-\alpha_{1} )} & {-\beta_{H} (1-\alpha_{3} )} \\ 0 & {\beta_{H} (1-\alpha_{1} )-(\mu +\mu_{2} +\tau_{1} )} & {\beta_{H} (1-\alpha_{3} )} \\ 0 & {\tau_{1} } & {-(\mu +\mu_{4} )} \\ \end{array} }} \right)$$

Suppose β H is chosen as a bifurcation parameter. Solving the system for the reproduction number given above for R H = 1, we get:

$$\beta_{H} =\beta^{\ast} =\frac{(\mu +\mu_{2} +\tau_{1} )(\mu +\mu_{4} )}{(1-\alpha_{1} )(\mu +\mu_{4} ) + \tau_{1} (1-\alpha_{3} )}.$$

Note that the above linearized system, of transformed system (12) with β H = β*, has a zero eigenvalue that is simple. Hence, the center manifold theory [20] can be used to analyze the dynamics of (12) near β H = β*.

3.3 Eigenvectors of J (Ɛ 0) | β H = β ∗

It can be shown that the Jacobian of (12) at β H = β ∗ (denoted by J β∗) has a right eigenvector (associated with the zero eigenvalue) given by w = [w 1, w 2, w 3]T, where:

$$w_{1} =-\frac{({\beta^{\ast} [ {(1-\alpha_{1} )(\mu +\mu_{4} ) + (1-\alpha_{3} )\tau_{1} } ]})w_{2} }{\mu ({\mu +\mu_{4} } )}$$

w 2 = w 2 > 0 and \(w_{3} =\frac {\tau _{1}}{\mu + \mu _{4}}w_{2}\). Further, J β∗ has a left eigenvector v = [v 1, v 2, v 3] (associated with the zero eigenvalue), where:

$$v_{1} =0, v_{2} =v_{2} > 0, v_{3} =\frac{\beta^{\ast} ({1-\alpha_{3} } )}{({\mu +\mu_{4} } )}v_{2} .$$

For convenience, the theorem in [21] is stated here:

Theorem 5

(Castillo-Chavez and Song) Consider the following general system of ordinary differential equations with a parameter ϕ:

$$\frac{dx}{dt}=f(x, \phi ), f:\mathbb{R}^{n}\times \mathbb{R}\to \mathbb{R}\;\text{and}\;C^{2}(\mathbb{R}^{n} \times \mathbb{R}),$$
(13)

where 0 is an equilibrium point of the system (that is, f (0, ϕ) ≡ 0 for all ϕ and assume

A1 ::

\(\mathrm {A}=D_{x} f(0, 0) = \left ({\frac {\partial f_{i} }{\partial x_{j} }(0, 0)} \right )\) is the linearization matrix of system(13) around the equilibrium 0 and ϕ evaluated at 0. Zero is a simple eigenvalue of A and other eigenvalues of A have negative real parts;

A2 ::

Matrix A has a right eigenvector w and a left eigenvector v (each corresponding to the zero eigenvalue);

Let f k be the k th component of f and:

$$a=\sum\limits_{k, j, i=1}^{n} {v_{k} w_{i} w_{j} } \frac{\partial^{2}f_{k} }{\partial x_{i} \partial x_{j} }(0, 0), \quad b=\sum\limits_{k, i=1}^{n} {v_{k} w_{i} } \frac{\partial^{2}f_{k} }{\partial x_{i} \partial \phi }(0, 0)$$

The local dynamics of the system around 0 is totally determined by the signs of a and b.

  •   i: a > 0, b > 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is locally asymptotically stable and there exists a positive unstable equilibrium; when 0 < ϕ ≪ 1, 0 is unstable and there exists a negative, locally asymptotically stable equilibrium;

  •  ii: a < 0, b < 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is unstable; when 0 < ϕ ≪ 1, 0 is locally asymptotically stable and there exists a positive unstable equilibrium;

  • iii: a > 0, b < 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is unstable and there exists a locally asymptotically stable negative equilibrium; when 0 < ϕ ≪ 1, 0 is stable and a positive unstable equilibrium appears;

  • iv: a < 0, b > 0. When ϕ changes from negative to positive, 0 changes its stability from stable to unstable. Correspondingly a negative unstable equilibrium becomes positive and locally asymptotically stable.

Computation of a and b

For system (12), the associated non-zero partial derivatives of f (at the DFE ) are given by:

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}f_{2}}{\partial x_{2} \partial x_{3}}&=& −\frac{\beta^{\ast} [{(1-\alpha_{1} ) + (1-\alpha_{3} )}]\mu}{\Lambda }, \quad \frac{\partial^{2}f_{2} }{\partial {x_{2}^{2}} }=-\frac{2\beta^{\ast} (1-\alpha_{1} )\mu}{\Lambda }, \notag\\ \frac{\partial^{2}f_{2}}{\partial {x_{3}^{2}}} &=& -\frac{2\beta^{\ast} (1-\alpha_{3} )\mu }{\Lambda}, \quad \frac{\partial^{2}f_{2}}{\partial x_{2} \partial \beta^{\ast}}=(1-\alpha_{1}), \quad \frac{\partial^{2}f_{2}}{\partial x_{3} \partial \beta^{\ast}}=(1-\alpha_{3}).\notag \end{array}$$

It follows from above expressions that:

$$\begin{array}{@{}rcl@{}} a &=& v_{2} \sum\limits_{k,j,i=1}^{3} {w_{i} w_{j} \frac{\partial^{2}f_{k} }{\partial x_{i} \partial x_{j} }(0, 0)}, \notag\\ &=&-2v_{2} \left( {\frac{w_{2} w_{3} \mu }{\Lambda }[ {\beta^{\ast} (1-\alpha_{1} )+\beta^{\ast} (1-\alpha_{3} )} ]+{w_{2}^{2}} \frac{\beta^{\ast} (1-\alpha_{1} )\mu }{\Lambda }+{w_{3}^{2}} \frac{\beta^{\ast} (1-\alpha_{3} )\mu }{\Lambda }} \right) < 0\notag\end{array}$$

and

$$\begin{array}{@{}rcl@{}} b&=&v_{2} \sum\limits_{k, i=1}^{3} w_{i} \frac{\partial^{2}f_{k}}{\partial x_{i} \partial \phi}(0, 0), \notag \\ &=&v_{2} \left[ {(1-\alpha_{1} )w_{2} +(1-\alpha_{3} )\frac{\tau_{1} }{({\mu +\mu_{4} })}w_{2} } \right] > 0.\notag \end{array}$$

We get a < 0 and b > 0. From (iv) of the above theorem it implies that the unique equilibrium point of model system (12), which exists whenever R H > 1, will be locally asymptotically stable when R H > 1 and β ∗ < β H with β H close to β ∗. This establishes the following theorem.

Theorem 6

The unique endemic equilibrium Ɛ 2 is locally asymptotically stable for R H > 1.

4 Analysis of the full model

The full HIV-TB co-infection model has four equilibria, namely, disease-free equilibrium Ɛ 0, TB-only equilibrium Ɛ̂, HIV-equilibrium Ɛ ∗ and endemic equilibrium point Ɛ ∗∗ (associated with the existence of co-epidemics).

The TB-only equilibrium point Ɛ̂ = (Ŝ, Î1, 0, 0, 0, 0) is obtained by setting I 2 = I 3 = I 4 = 0 = I 5 and is given by:

$$\Hat{{\mathcal{E}}}=(\Hat{S}, \Hat{I}_{1} , 0, 0, 0, 0) = \left({\frac{\Lambda }{(\mu +\mu_{1} )(R_{T} -1) + \mu }, \frac{\Lambda (R_{T} -1)}{(\mu +\mu_{1} )(R_{T} -1) + \mu }, 0, 0, 0, 0)} \right).$$

The HIV-only equilibrium point \(\mathcal {E}^{\ast } =\left ({S^{\ast } , 0, I_{2}^{\ast } , 0, I_{4}^{\ast } , 0} \right )\), is obtained by setting I 1 = I 3 = 0 = I 5, where:

$$\begin{array}{@{}rcl@{}} S^{\ast} &=&\frac{({\mu +\mu_{2} +\tau_{1} })N^{\ast} }{\beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}}, \notag \\ I_{2}^{\ast} &=&\frac{({\mu +\mu_{4} } )}{\mu +\mu_{4} +\tau_{1} }\left[ {1-\frac{({\mu +\mu_{2} +\tau } )}{\beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}}} \right]N^{\ast}, \notag \end{array}$$

\(I_{4}^{\ast } =\frac {\tau _{1} }{(\mu +\mu _{4} )}I_{2}^{\ast }\) and N ∗ is given by:

$$N^{\ast} =\frac{\Lambda \beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}}{\frac{\left({\mu +\mu_{4} } \right)}{\mu +\mu_{4} +\tau_{1} }\left[ {\beta_{H} \left\{ {(1-\alpha_{1} ) + (1-\alpha_{3} )\frac{\tau_{1} }{\mu +\mu_{4} }} \right\}-({\mu +\mu_{2} +\tau_{1} } )} \right]+\mu ({\mu +\mu_{2} +\tau_{1} } )}.$$

System (3) has co-existence equilibrium Ɛ∗∗ = (S ∗∗, I 1 ∗∗, I 2 ∗∗, I 3 ∗∗, I 4 ∗∗, I 5 ∗∗), where:

$$\begin{array}{@{}rcl@{}} S^{\ast \ast}&=&\frac{\{ {\lambda_{H} (1-\eta ) + \mu +\mu_{1} +\gamma \eta }\}\Lambda }{(\lambda_{T} +\lambda_{H} +\mu )\{ {\lambda_{H} (1-\eta ) + \mu +\mu_{1}}\}+(\lambda_{H} +\mu )\gamma \eta}, \notag\\ I_{1}^{\ast \ast } &=&\frac{\lambda_{T} \Lambda }{(\lambda_{T} +\lambda_{H} +\mu )\{ {\lambda_{H} (1-\eta ) + \mu +\mu_{1} } \}+(\lambda_{H} +\mu )\gamma \eta }, \notag \\ I_{2}^{\ast \ast } &=&\frac{\lambda_{H} (\alpha_{2} \gamma +\mu +\mu_{3} +\tau_{2} )S^{\ast \ast }+\alpha_{2} \gamma \lambda_{H} (1-\eta )I_{1}^{\ast \ast } }{(\phi_{1} \lambda_{T} +\mu +\mu_{2} +\tau_{1} )(\mu +\mu_{3} +\tau_{2} ) + (\mu +\mu_{2} +\tau 1)\alpha_{2} \gamma}, \notag \\ I_{3}^{\ast \ast } &=&\frac{\lambda_{H} (1-\eta )I_{1}^{\ast \ast } +\phi_{1} \lambda_{T} I_{2}^{\ast \ast } }{\alpha_{2} \gamma +\mu +\mu_{3} +\tau_{2}}, \notag \\ I_{4}^{\ast \ast } &=&\frac{(\mu +\mu_{5} +\gamma \alpha_{4} )\tau_{1} I_{2}^{\ast \ast } +\gamma \alpha_{4} \tau_{2} I_{3}^{\ast \ast } }{(\mu +\mu_{5} +\gamma \alpha_{4} )(\mu +\mu_{4} ) + (\mu +\mu_{5} )\phi_{2} \lambda_{T} }, \notag \\ I_{5}^{\ast \ast } &=&\frac{\tau_{2} I_{3}^{\ast \ast } +\phi_{2} \lambda_{T} I_{4}^{\ast \ast } }{\mu +\mu_{5} +\gamma \alpha_{4} }.\notag \end{array}$$

From the above expressions it is clear that all the variables S ∗∗, I 1 ∗∗, I 2 ∗∗, I 3 ∗∗, I 4 ∗∗, I 5 ∗∗ can be written in terms of λ T and λ H . Now using the expressions for λ T and λ H , the following two equations give the system of two non-linear equations in λ T and λ H , which can be solved for λ T and λ H :

$$\begin{array}{@{}rcl@{}} &&{\kern6pc} \lambda_{T} \left({S^{\ast\ast}, I_{1}^{\ast\ast}, I_{2}^{\ast\ast}, I_{3}^{\ast\ast}, I_{4}^{\ast \ast}, I_{5}^{\ast \ast}} \right) = \beta_{T} \left({I_{1}^{\ast\ast} +I_{3}^{\ast\ast} +I_{5}^{\ast\ast}} \right), \\ &&\lambda_{H} \beta_{T} \left({I_{1}^{\ast\ast } +I_{3}^{\ast\ast } +I_{5}^{\ast\ast}} \right) {}={} \lambda_{T} \beta_{H} \left\{{({1-\alpha_{1}})_{2}^{\ast \ast } {}+{} ({1-\alpha_{2}}) \eta_{1} I_{3}^{\ast \ast} {}+{} ({1-\alpha_{3}})I_{4}^{\ast \ast } +({1-\alpha_{4} } )\eta_{2} I_{5}^{\ast \ast } } \right\}. \\ \end{array}$$

Once we know λ T and λ H , our co-existence equilibrium Ɛ∗∗ = (S ∗∗, I 1 ∗∗, I 2 ∗∗, I 3 ∗∗, I 4 ∗∗, I 5 ∗∗), is completely known.

4.1 Local stability of disease-free equilibrium (DFE)

Model (3) has a DFE given by \(\mathcal {E}_{0} =(S^{0}, 0, 0, 0, 0, 0) = \left ({\frac {\Lambda }{\mu }, 0, 0, 0, 0, 0} \right )\).

Using the next generation matrix method the reproduction number R HT has been calculated for which associated F and V matrices are given as:

$$\begin{array}{@{}rcl@{}} F&=&\left({{\begin{array}{*{20}c} {\beta_{T} } & 0 & {\beta_{T} } & 0 & {\beta_{T} } \\ 0 & {\beta_{H} ({1-\alpha_{1} })} & {\beta_{H} ({1-\alpha_{2} })\eta_{1} } & {\beta_{H} ({1-\alpha_{3} } )} & {\beta_{H} ({1-\alpha_{4}})\eta_{2} } \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array}}} \right)\notag \\ V&=&\left({{\begin{array}{*{20}c} {({\mu +\mu_{1} +\gamma \eta } )} & 0 & 0 & 0 & 0 \\ 0 & {({\mu +\mu_{2} +\tau_{1} } )} & {-\alpha_{2} \gamma } & 0 & 0 \\ 0 & 0 & {\alpha_{2} \gamma +({\mu +\mu_{3} +\tau_{2} } )} & 0 & 0 \\ 0 & {-\tau_{1} } & 0 & {({\mu +\mu_{4} } )} & {-\gamma \alpha_{4} } \\ 0 & 0 & {-\tau_{2} } & 0 & {({\mu +\mu_{5} } ) + \gamma \alpha_{4} } \\ \end{array} }} \right) \notag \end{array}$$

Here, it is shown that the associated reproduction number R HT is given by:

R HT = max{R T , R H }

Again using Theorem 2 in [22] the following result is established.

Lemma 3

The DFE of the full HIV-TB model (3), given by Ɛ 0, is locally asymptotically stable if R HT < 1 and unstable if R HT > 1.

4.2 Local stability of TB-only and HIV-only equilibrium points

The variational matrix corresponding to system (3) at the TB-only equilibrium point is given by:

$$M_{1} =\left({{\begin{array}{*{20}c} {m_{11} } & {m_{12} } & {m_{13} } & {m_{14} } & {m_{15} } & {m_{16} } \\ {m_{21} } & {m_{22} } & {m_{23} } & {m_{24} } & {m_{25} } & {m_{26} } \\ 0 & 0 & {m_{33} } & {m_{34} } & {m_{35} } & {m_{36} } \\ 0 & 0 & {m_{43} } & {m_{44} } & {m_{45} } & {m_{46} } \\ 0 & 0 & {\tau_{1} } & 0 & {m_{55} } & {m_{56} } \\ 0 & 0 & 0 & {\tau_{2} } & {m_{65} } & {m_{66} } \\ \end{array} }} \right),$$

where

$${\begin{array}{*{20}c} {m_{11} =-\left({\frac{\beta_{T} \Hat{{I}}_{1} }{\Hat{{N}}}+\mu } \right) + \frac{\beta_{T} \Hat{{S}}\Hat{{I}}_{1} }{\Hat{{N}}^{2}}=-\left({\frac{\beta_{T} \Hat{{I}}_{1}^{2} }{\Hat{{N}}^{2}}+\mu } \right), } \\ {m_{12} =-\left({\frac{\beta_{T} \Hat{{S}}^{2}}{\Hat{{N}}^{2}}} \right) + \gamma \eta , m_{13} =\frac{\beta_{T} \Hat{{I}}_{1} \Hat{{S}}}{\Hat{{N}}^{2}}-\frac{\beta_{H} \left({1-\alpha_{1} } \right)\Hat{{S}}}{\Hat{{N}}}, } \\ {m_{14} =-\left({\frac{\beta_{T} \Hat{{S}}^{2}}{\Hat{{N}}^{2}}} \right)-\frac{\beta_{H} \left({1-\alpha_{2} } \right)\eta_{1} \Hat{{S}}}{\Hat{{N}}}, m_{15} =\frac{\beta_{T} \Hat{{I}}_{1} \Hat{{S}}}{\Hat{{N}}^{2}}-\frac{\beta_{H} \left({1-\alpha_{3} } \right)\Hat{{S}}}{\Hat{{N}}}, } \\ {m_{16} =\frac{\beta_{T} \Hat{{I}}_{1} \Hat{{S}}}{\Hat{{N}}^{2}}-\frac{\beta_{H} \left({1-\alpha_{4} } \right)\eta_{2} \Hat{{S}}}{\Hat{{N}}}, } \\ {m_{21} =\frac{\beta_{T} \Hat{{I}}_{1}^{2} }{\Hat{{N}}^{2}}, m_{22} =-\frac{\beta_{T} \Hat{{I}}_{1} \Hat{{S}}}{\Hat{{N}}^{2}}, } \\ {m_{23} =-\frac{\beta_{T} \Hat{{S}}\Hat{{I}}_{1} }{\Hat{{N}}^{2}}-\frac{\left({1-\eta } \right)\beta_{H} \left({1-\alpha_{1} } \right)\Hat{{I}}_{1} }{\Hat{{N}}}, m_{24} =\frac{\beta_{T} \Hat{{S}}^{2}}{\Hat{{N}}^{2}}, } \\ {m_{25} =\frac{\beta_{T} \Hat{{S}}\Hat{{I}}_{1} }{\Hat{{N}}^{2}}-\frac{\left({1-\eta } \right)\left({1-\alpha_{3} } \right)\beta_{H} \Hat{{I}}_{1} }{\Hat{{N}}}, m_{26} =\frac{\beta_{T} \Hat{{S}}^{2}}{\Hat{{N}}^{2}}-\frac{\beta_{H} \left({1-\eta } \right)\left({1-\alpha_{4} } \right)\eta_{2} \Hat{{I}}_{1} }{\Hat{{N}}}, } \\ {m_{33} =\frac{\Hat{{S}}\beta_{H} \left({1-\alpha_{1} } \right)}{\Hat{{N}}}-\frac{\phi_{1} \beta_{T} \Hat{{I}}_{1} }{\Hat{{N}}}-\left({\mu +\mu_{2} +\tau_{1} } \right), m_{34} =\frac{\Hat{{S}}\beta_{H} \left({1-\alpha_{2} } \right)\eta_{1} }{\Hat{{N}}}+\alpha_{2} \gamma , } \\ {m_{35} =\frac{\Hat{{S}}\beta_{H} \left({1-\alpha_{3} } \right)}{\Hat{{N}}}, m_{36} =\frac{\Hat{{S}}\beta_{H} \left({1-\alpha_{4} } \right)\eta_{2} }{\Hat{{N}}}, } \\ {m_{43} =\frac{\left({1-\eta } \right)\beta_{H} \left({1-\alpha_{1} } \right)\Hat{{I}}_{1} }{\Hat{{N}}}+\frac{\phi_{1} \beta_{T} \Hat{{I}}_{1} }{\Hat{{N}}}, m_{44} =\frac{\left({1-\eta } \right)\beta_{H} \left({1-\alpha_{2} } \right)\eta_{1} \Hat{{I}}_{1} }{\Hat{{N}}}-\left({\mu +\mu_{3} +\tau_{2} +\alpha_{2} \gamma } \right), } \\ {m_{45} =\frac{\left({1-\eta } \right)\beta_{H} \left({1-\alpha_{3} } \right)\Hat{{I}}_{1} }{\Hat{{N}}}, m_{46} =\frac{\left({1-\eta } \right)\left({1-\alpha_{4} } \right)\eta_{2} \Hat{{I}}_{1} }{\Hat{{N}}}, } \\ {m_{55} =-\frac{\phi_{2} \beta_{T} \Hat{{I}}_{1} }{\Hat{{N}}}-\left({\mu +\mu_{4} } \right), m_{56} =\gamma \alpha_{4} , } \\ {m_{65} =\frac{\phi_{2} \beta_{T} \Hat{{I}}_{1} }{\Hat{{N}}}, m_{66} =-\left({\mu +\mu_{5} +\gamma \alpha_{4} } \right).} \end{array}}$$

It is easy to observe that the eigenvalues of this variational matrix are the roots of the following polynomials:

ψ 2 − (m 11 + m 22) ψ + (m 11 m 22 − m 12 m 21) = 0 and

     ψ 4 + a 3 ψ 3 + a 2 ψ 2 + a 1 ψ + a 0 = 0,

where

$$\begin{array}{@{}rcl@{}} a_{3} &=&-(m_{33} +m_{44} +m_{55} +m_{66})\notag \\ a_{2} &=&m_{33} (m_{44} +m_{55} +m_{66} ) + m_{55} m_{66} -m_{65} m_{56} +m_{44} (m_{55} +m_{66} )-\tau_{2} m_{46} -m_{43} m_{13} -\tau_{1} m_{35} \notag \\ a_{1} &=&-m_{33} \left\{ {m_{55} m_{66} -m_{65} m_{56} +m_{44} (m_{55} +m_{66} )-\tau_{2} m_{46} } \right\}\mathrm{ } \notag\\ &&-m_{44} (m_{55} m_{66} -m_{65} m_{56} ) + \tau_{2} (m_{46} m_{56} -m_{46} m_{55} ) \notag\\ &&+m_{43} m_{13} (m_{55} +m_{66} )\tau_{2} m_{36} -\tau_{1} m_{34} m_{45} +m_{35} (m_{44} +m_{66} )\tau_{1} -\tau_{1} m_{36} m_{65}, \notag\\ a_{0} &=&m_{33} \left\{ {m_{44} (m_{55} m_{66} -m_{65} m_{56} ) + \tau_{2} (m_{45} m_{56} -m_{46} m_{55} )} \right\} \notag\\ &&-m_{43} m_{13} (m_{55} m_{66} -m_{56} m_{65} )-m_{43} \tau_{2} (m_{35} m_{56} -m_{36} m_{55} )\notag \\ &&+\tau_{1} m_{34} (m_{45} m_{66} -m_{46} m_{65} ) + \tau_{1} \tau_{2} m_{35} m_{46} \notag\\ &&-\tau_{1} m_{35} m_{44} m_{66} +\tau_{1} m_{36} (m_{44} m_{65} -\tau_{2} m_{45} ) \notag \end{array}$$

It is easy to visualize that the co-efficient of ψ and the constant term in the first quadratic equation are positive, which implies that the roots of this quadratic are either negative or have negative real parts. Now using Routh-Hurwitz criteria, the biquadratic equation will have roots with negative real parts provided a 3 > 0 and \(a_{1} a_{2} a_{3} -{a_{1}^{2}} -a_{0} {a_{3}^{2}} > 0\). Hence by the Routh-Hurwitz criteria the equilibrium point Ɛ̂ is locally asymptotically stable provided a 3 > 0 and \(a_{1} a_{2} a_{3} -{a_{1}^{2}} -a_{0} {a_{3}^{2}} > 0\).

The variational matrix corresponding to system (3) at the HIV-only equilibrium point Ɛ ∗ is given by:

$$M_{2} =\left({{\begin{array}{*{20}c} {n_{11} } & {n_{12} } & {n_{13} } & {n_{14} } & {n_{15} } & {n_{16} } \\ 0 & {n_{22} } & 0 & {n_{24} } & 0 & {n_{26} } \\ {n_{31} } & {n_{32} } & {n_{33} } & {n_{34} } & {n_{35} } & {n_{36} } \\ 0 & {n_{42} } & 0 & {n_{44} } & 0 & {n_{46} } \\ 0 & {n_{52} } & {n_{53} } & {n_{54} } & {n_{55} } & {n_{56} } \\ 0 & {n_{62} } & 0 & {n_{64} } & 0 & {n_{66} } \\ \end{array} }} \right),$$

where

$${\begin{array}{*{20}l} {n_{11} =-\left[ {\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}+\mu } \right]+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}} \\[8pt] {n_{12} =\frac{S^{\ast} \beta_{T} }{N^{\ast} }+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}+\gamma \eta } \\[10pt] {n_{13} =\frac{-\beta_{H} \left( {1-\alpha_{1} } \right)S^{\ast} }{N^{\ast} }+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}S^{\ast} }{N^{\ast 2}}} \\[10pt] {n_{14} =\frac{-\beta_{T} S^{\ast} }{N^{\ast} }-\frac{\beta_{H} (1-\alpha_{2} )\eta_{1} S^{\ast} }{N^{\ast} }+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}S^{\ast} }{N^{\ast 2}}} \\[10pt] {n_{15} =\frac{\beta_{H} (1-\alpha_{3} )S^{\ast} }{N^{\ast} }+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}S^{\ast} }{N^{\ast 2}}} \\[10pt] {n_{16} =\frac{\beta_{H} (1-\alpha_{4} )\eta_{2} S^{\ast} }{N^{\ast} }+\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}S^{\ast} }{N^{\ast 2}}} \\[10pt] {n_{22} =\frac{\beta_{T} S^{\ast} }{N^{\ast} }-\left[ {\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast}}(1-\eta )+\mu +\mu_{1} +\gamma \eta } \right]} \\[10pt] {n_{24} =\frac{\beta_{T} S^{\ast} }{N^{\ast} }} \\[10pt] {n_{26} =\frac{\beta_{T} S^{\ast} }{N^{\ast} }} \\[10pt] {n_{31} =\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast} }-\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}} \\[10pt] {n_{32} =\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}-\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{33} =\frac{S^{\ast} \beta_{H} (1-\alpha_{1} )}{N^{\ast} }-\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}+\alpha_{2} \gamma -\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{34} =\frac{S^{\ast} \beta_{H} (1-\alpha_{2} )\eta_{1} }{N^{\ast} }-\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}} \\[10pt] {n_{35} =\frac{S^{\ast} \beta_{H} (1-\alpha_{3} )}{N^{\ast} }-\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}} \\[10pt] {n_{36} =\frac{S^{\ast} \beta_{H} (1-\alpha_{4} )\eta_{2} }{N^{\ast} }-\frac{S^{\ast} \beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}}{N^{\ast 2}}-\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{42} =\frac{\beta_{H} \left\{ {(1-\alpha_{1} )I_{2}^{\ast} +(1-\alpha_{3} )I_{4}^{\ast} } \right\}(1-\eta )}{N^{\ast} }+\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{44} =\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }-(\mu +\mu_{3} +\tau_{2} +\alpha_{2} \gamma )} \\[10pt] {n_{46} =\frac{\phi_{1} I_{2}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{52} =-\frac{\phi_{2} I_{4}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{53} =\tau_{1} } \\[10pt] {n_{54} =-\frac{\phi_{2} I_{4}^{\ast} \beta_{T} }{N^{\ast} }} \\[10pt] {n_{55} =-(\mu +\mu_{4} )} \\[10pt] {n_{56} =-\frac{\phi_{2} I_{4}^{\ast} \beta_{T} }{N^{\ast} }+\gamma \alpha_{4} } \end{array} }$$
$$\begin{array}{@{}rcl@{}} n_{62} &=&\frac{\phi_{2} I_{4}^{\ast} \beta_{T} }{N^{\ast}} \\ n_{64} &=&\frac{\phi_{2} I_{4}^{\ast} \beta_{T} }{N^{\ast}}+\tau_{2} \\ n_{66} &=& -(\mu +\mu_{5} +\gamma \alpha_{4}) \end{array}$$

The eigenvalues of this variational matrix are the roots of following two cubic equations:

ψ 3 + g 1 ψ 2 + g 2 ψ + g 3 = 0,

ψ 3 + f 1 ψ 2 + f 2 ψ + f 3 = 0,

where

$$\begin{array}{@{}rcl@{}} g_{1} &=& -(n_{22} +n_{44} +n_{66}) \\ g_{2} &=& n_{44} n_{66} +n_{22} (n_{44} +n_{66} )-n_{64} n_{46} -n_{24} n_{42} \\ g_{3} &=& n_{22} n_{64} n_{46} +n_{24} n_{42} n_{66} -n_{24} n_{62} n_{46} -n_{22} n_{44} n_{66} \\ f_{1} &=& -(n_{11} +n_{33} +n_{55}) \\ f_{2} &=& n_{33} n_{55} +n_{11} (n_{33} +n_{55} )-n_{13} n_{31} -n_{35} n_{53} \\ f_{3} &=& n_{31} n_{13} n_{55} +n_{11} n_{35} n_{53} -n_{11} n_{33} n_{55} -n_{31} n_{15} n_{53}. \end{array}$$

Using Routh-Hurwitz’s criteria, this equilibrium is locally asymptotically stable provided g 1 > 0, f 1 > 0, g 1 g 2 − g 3 > 0 and f 1 f 2 − f 3 > 0. Hence we conclude that when both the reproduction numbers are greater than one then the local asymptotic stability of any boundary equilibrium i.e., TB-only or HIV-only equilibrium point is not guaranteed. They are locally asymptotic stable only under some restriction on the parameters.

4.3 Bifurcation analysis of the full HIV-TB model

Consider S = x 1, I 1 = x 2, I 2 = x 3, I 3 = x 4, I 4 = x 5, I 5 = x 6 and N = S + I 1 + I 2 + I 3 + I 4 + I 5. Model system (3) can be rewritten in the following form:

$${\begin{array}{*{20}l} {\frac{dx_{1} }{dt}=f_{1} =\Lambda -\lambda_{T} x_{1} -\lambda_{H} x_{1} -\mu x_{1} +\gamma \eta x_{2} } \\ {\frac{dx_{2} }{dt}=f_{2} =\lambda_{T} x_{1} -\lambda_{H} (1-\eta )x_{2} -\mu x_{2} -\mu_{1} x_{2} -\gamma \eta x_{2} } \\ {\frac{dx_{3} }{dt}=f_{3} =\lambda_{H} x_{1} -\phi_{1} \lambda_{T} x_{3} -\alpha_{2} \gamma x_{4} -(\mu +\mu_{2} +\tau_{1} )x_{3} } \\ {\frac{dx_{4} }{dt}=f_{4} =\lambda_{H} (1-\eta )x_{2} +\phi_{1} \lambda_{T} x_{3} -\alpha_{2} \gamma x_{4} -(\mu +\mu_{3} +\tau_{2} )x_{4} } \\ {\frac{dx_{5} }{dt}=f_{5} =\tau_{1} x_{3} -\phi_{2} \lambda_{T} x_{5} -(\mu +\mu_{4} )x_{5} -\gamma \alpha_{4} x_{6} } \\ {\frac{dx_{6} }{dt}=f_{6} =\phi_{2} \lambda_{T} I_{4} +\tau_{2} x_{4} -(\mu +\mu_{5} +\gamma \alpha_{4} )x_{6} } \end{array} }$$
(14)

To analyze the dynamics of full model (3), we compute the Jacobian of (14) at the DFF Ɛ 0 denoted by J(Ɛ 0).

$${ J({\mathcal{E}_{0}}) = J_{\beta}^{\ast} =\left({{\begin{array}{*{20}c} {-\mu } & {-\beta_{T} +\gamma \eta } & {-\beta_{H} \left({1-\alpha_{1} } \right)} & {K_{1} } & {-\beta_{H} \left({1-\alpha_{3} } \right)} & {K_{2} } \\ 0 & {\beta_{T} -\left({\mu +\mu_{1} +\gamma \eta } \right)} & 0 & {\beta_{T} } & 0 & {\beta_{T} } \\ 0 & 0 & {K_{3} } & {\beta_{H} \left({1-\alpha_{2} } \right)\eta_{1} +\alpha_{2} \gamma } & {\beta_{H} \left({1-\alpha_{3} } \right)} & {K_{4} } \\ 0 & 0 & 0 & {-\alpha_{2} \gamma -\left({\mu +\mu_{3} +\tau_{2} } \right)} & 0 & 0 \\ 0 & 0 & {\tau_{1} } & 0 & {-\left({\mu +\mu_{4} } \right)} & {\gamma \alpha_{4} } \\ 0 & 0 & 0 & {\tau_{2} } & 0 & {K_{5} } \\ \end{array} }} \right) }$$

Here, K 1 = −β T − β H η 1(1 − α 2), K 2 = −β T − β H (1 − α 4) η 2, K 3 = β H (1 − α 1)−(μ + μ 2 + τ 1), K 4 = β H (1 − α 4) η 2, K 5 = −(μ + μ 5)−γ α 4.

The four eigenvalues of this matrix are −[α 2 γ + (μ + μ 3 + τ 2)], −μ, β T − (μ + μ 1 + γ η), −(μ + μ 5 + γ α 4) and the other eigenvalues are the roots of the following quadratic equation:

λ 2 − (β H (1 − α) − (μ + μ 2 + τ 1) − (μ + μ 4)) λ + (μ + μ 2 + τ 1) (μ + μ 4) (1 − R H) = 0,

which has a zero eigenvalue for R H = 1.

Consider the case when R H > R T i.e., R HT = R H and R HT = 1. Choose β H = β* as the bifurcation parameter.

Eigenvectors of \(J_{\beta }^{\ast }\)

For the case when R HT = 1, it is shown that the Jacobian of (14) at β H = β ∗ has a right eigenvector and a left eigenvector given by w = [w 1, w 2, w 3, w 4, w 5, w 6]T and v = [v 1, v 2, v 3, v 4, v 5, v 6], respectively, where,

$$\begin{array}{@{}rcl@{}} w_{1} &=& -\frac{\beta^{\ast} \{ {(1-\alpha_{1} )w_{3} +(1-\alpha_{3} )w_{5} }\}}{\mu }, \\ w_{2} &=& 0=w_{4} =w_{6}, \\ && w_{5} > 0, \\ w_{3} &=& \frac{(\mu +\mu_{4} )w_{5} }{\tau_{1} }. \end{array}$$

\(J_{\beta }^{\ast }\) has a left eigenvector v = [v 1, v 2, v 3, v 4, v 5, v 6], where,

$$\begin{array}{@{}rcl@{}} v_{1} &=& 0=v_{2} , \quad v_{5} =v_{5} > 0, \\ v_{3} &=& \frac{(\mu +\mu_{4} )v_{5} }{\beta^{\ast} (1-\alpha_{3} )}, \\ v_{4} &=& \frac{(\beta^{\ast} (1-\alpha_{2})\eta_{1} + \alpha_{2} \gamma)v_{3} + \tau_{2} v_{6}}{\alpha_{2} \gamma + (\mu +\mu_{3}) + \tau_{2}}, \\ v_{6} &=&\frac{\gamma \alpha_{4} v_{5} +\beta^{\ast} (1-\alpha_{4} )\eta_{2} v_{3} }{(\mu +\mu_{5} +\gamma \alpha_{4})}. \end{array}$$

Computation of a and b

Computing the non-zero partial derivatives associated with F at DFE, the expressions for a and b (defined in Theorem 5) are given as:

$${ \frac{\partial^{2}f_{3} }{\partial {x_{3}^{2}} }=-\frac{2\beta^{\ast} (1-\alpha_{1} )\mu }{\Lambda }, \quad \frac{\partial^{2}f_{3} }{\partial x_{3} \partial x_{5} }=-\frac{\beta^{\ast} [{(1-\alpha_{1} ) + (1-\alpha_{3})}]\mu }{\Lambda }, \quad \frac{\partial^{2}f_{3} }{\partial {x_{5}^{2}} }=-\frac{2\beta^{\ast} (1-\alpha_{3} )\mu }{\Lambda } }$$

and

$$\begin{array}{@{}rcl@{}}\frac{\partial^{2}f_{3}}{\partial x_{3}\partial \beta^{\ast}} {\kern-3pt}&=&{\kern-3pt} (1-\alpha_{1} ),\quad \frac{\partial^{2}f_{3}}{\partial x_{5}\partial \beta^{\ast}}=(1-\alpha_{3}) \\a {\kern-3pt}&=&{\kern-5pt}-2v_{3} \beta^{\ast}{\kern-3pt} \left({\frac{{w_{3}^{2}} (1{\kern-1pt}-{\kern-1pt}\alpha_{1})\Lambda}{\mu}{\kern-1pt}+{\kern-1pt}\frac{w_{3}w_{5} \left[{(1{\kern-1pt}-{\kern-1pt}\alpha_{1})+(1{\kern-1pt}-{\kern-1pt}\alpha_{3} )} \right]\Lambda }{\mu}{\kern-1pt}+{\kern-1pt}\frac{{w_{5}^{2}}(1{\kern-1pt}-{\kern-1pt}\alpha_{3})\Lambda }{\mu}} \right) < 0 \\b &{\kern-1pt}={\kern-1pt}& v_{3} (w_{3}(1-\alpha_{1} )+w_{5}(1-\alpha_{3} )) > 0. \\ \end{array}$$

Again, we get a < 0 and b > 0. From (iv) of Theorem 5, it is clear that the unique non-trivial equilibrium point of model system (3), which exists whenever R H > 1, will be locally asymptotically stable when R H > R T > 1 and β ∗ < β H with β H close to β ∗. This establishes the following theorem.

Theorem 7

The unique endemic equilibrium Ɛ ** is locally asymptotically stable for R H > R T > 1.

4.3.1 Global stability of disease-free equilibrium

Here, we list two conditions that need to be satisfied to guarantee the global asymptotic stability of the disease-free state. Following Castillo-Chavez et al. [23], we rewrite model system (3) as follows:

$$\left\{ {{\begin{array}{*{20}l} {X^{\prime} (t) = F(X, Y), } \\ {Y^{\prime} (t) = G(X, Y), \quad G(X, 0) = 0.} \\ \end{array} }} \right.$$
(15)

where X = S and Y = (I 1, I 2, I 3, I 4, I 5)T with X ∈ ℝ+ denoting the number of uninfected individuals and \(Y\in \mathbb {R}_{+}^{5}\) denoting the number of infected and co-infected individuals. The disease-free equilibrium is denoted here by \(E_{0} =(X_{0} , 0) = \left ({\frac {\Lambda }{\mu }, 0, 0, 0, 0, 0} \right )\).

The conditions (H 1) and (H 2) below must be met to guarantee global asymptotic stability.

H 1::

Fr X′(t) = F(X 0, 0), X 0 is globally asymptotically stable (g.a.s.),

H 2::

G(X, Y) = AY − Ĝ (X, Y), Ĝ (X, Y) ≥ 0 for (X, Y) ∈ 𝒟.

Here A = D Y G(X 0, 0) is an M-matrix (the off-diagonal elements of A are non-negative) and 𝒟 is the region where the model makes biological sense. If model system (15) satisfies the conditions H 1 and H 2, then the following result stated in Theorem 8 holds.

Theorem 8

The fixed point E 0 = (X 0, 0) is the globally asymptotically stable equilibrium of system (3), provided R HT < 1 and the conditions stated in H 1 and H 2 are satisfied.

Proof

In Section 4.1 we have proved that for R HT < 1, Ɛ 0 is locally asymptotically stable.

Consider

F(X, 0) = Λ − μS, G(X, Y) = AY − Ĝ(X, Y),

where

$$A=\left( {{\begin{array}{*{20}c} {\beta_{T} -\left( {\mu +\mu_{1} +\gamma \eta } \right)} & 0 & {\beta_{T} } & 0 & {\beta_{T} } \\ 0 & {\beta_{H}\left( {1-\alpha_{1} } \right)-\left( {\mu +\mu_{2} +\tau_{1} } \right)} & {\beta_{H} \left( {1-\alpha_{2} } \right)\eta_{1} +\alpha_{2} \gamma } & {\beta_{H} \left( {1-\alpha_{3} } \right)} & {\beta_{H} \left( {1-\alpha_{4} } \right)\eta_{2} } \\ 0 & 0 & {-\alpha_{2} \gamma -\left( {\mu +\mu_{3} +\tau_{2} } \right)} & 0 & 0 \\ 0 & {\tau_{1} } & 0 & {-\left( {\mu +\mu_{4} } \right)} & {\gamma \alpha_{4} } \\ 0 & 0 & {\tau_{2} } & 0 & {-\left( {\mu +\mu_{5} } \right)-\gamma \alpha_{4} } \\\end{array} }} \right)$$

Then

$${ \Hat{{G}}(X, Y) = \left({{\begin{array}{*{20}l} {\widehat{G_{1} }(X, Y)} \\ {\widehat{G_{2} }(X, Y)} \\ {\widehat{G_{3} }(X, Y)} \\ {\widehat{G_{4} }(X, Y)} \\ {\widehat{G_{5} }(X, Y)} \\ \end{array} }} \right) = \left({{\begin{array}{*{20}c} {\beta_{T} \left({I_{1} +I_{3} +I_{5} } \right)\left({1-\frac{S}{N}} \right) + \lambda_{H} \left({1-\eta } \right)I_{1} } \\ {\beta_{H} \left[ {\left({1-\alpha_{1} } \right)I_{2} +\left({1-\alpha_{2} } \right)\eta_{1} I_{3} +\left({1-\alpha_{3} } \right)I_{4} +\left({1-\alpha_{4} } \right)\eta_{2} I_{5} } \right]\left({1-\frac{S}{N}} \right) + \lambda_{T} \phi_{1} I_{2} } \\ {-\left({\lambda_{H} \left({1-\eta } \right)I_{1} +\lambda_{T} \phi_{1} I_{2} } \right)} \\ {\phi_{2} \lambda_{T} I_{4} } \\ {-\phi_{2} \lambda_{T} I_{4} } \\ \end{array} }} \right) }$$

Notice that the matrix A is an M-Matrix since all its of-diagonal elements are non-negative, where as to establish the result of global stability of Ɛ 0, we need to prove Ĝ (X, Y) ≥ 0 but here Ĝ 3(X, Y) < 0 and Ĝ 5(X, Y) < 0. This implies that the DFE (Ɛ 0) is not globally stable. □

5 Numerical simulation

Numerical simulations are carried out in XPP [24] to visualize the dynamics of the HIV/TB full model (3) using various sets of parameters. Here Figs. 2 and 3 demonstrate the stability of disease-free equilibrium \(\mathcal {E}_{0} =\left ({\frac {\Lambda }{\mu }, 0, 0, 0, 0, 0} \right )\) for the set of parameters described in Table 1. Here all the parameters are in yr−1. The basic reproduction numbers R T and R H for this set of parameters are 0.8888 and 0.9077 respectively and Ɛ 0(12500, 0, 0, 0, 0, 0). That means the two diseases disappear from the population. The stability of the TB-only equilibrium point is demonstrated in Figs. 4 and 5, where the parameter β T = 0.1 and all other parameters are the same as listed in Table 1. Here R T = 1.1111 and R H = 0.9077 and the TB-only equilibrium point is given by Ɛ̂ = (9782.609, 1086.957, 0, 0, 0, 0). In this case the disease-free equilibrium is unstable and HIV-only and co-infection equilibria do not exist.

Fig. 2
figure 2

S-I 1 phase plane showing the stability of the disease-free equilibrium point \(\mathcal {E}_{0}\) when R T = 0.8888889, R H = 0.9077159

Full size image
Fig. 3
figure 3

S-I 2 phase plane showing the stability of the disease-free equilibrium point \(\mathcal {E}_{0}\) when R T = 0.8888889, R H = 0.9077159

Full size image
Table 1 Description of parameters used in HIV-TB co-infection model system (3)
Full size table
Fig. 4
figure 4

S−I 1 phase plane showing the stability of the TB-only equilibrium point \(\hat {\mathcal {E}}\) when R T = 1.111111, R H = 0.9077159

Full size image
Fig. 5
figure 5

S−I 2 phase plane showing the stability of the TB-only equilibrium point \(\hat {\mathcal {E}}\) when R T = 1.111111, R H = 0.9077159

Full size image

Now system (3) is again simulated by changing the parameter β H as 0.12 and keeping all the other parameters as listed in Table 1. For this set of parameters R T = 0.8888889 and R H = 1.210288. Here TB-only and co-infection equilibria do not exist and the disease-free equilibrium point is unstable. Figures 6 and 7 are demonstrating the stability of the HIV-only equilibrium point Ɛ *, which is (7581.92, 0, 1167.57, 0, 426.81, 0). When both the reproduction numbers R T and R H are greater than one then there is a possibility of stability of co-infection equilibrium Ɛ ∗∗, which is demonstrated in Fig. 8 for the parameter values described in Table 1, except β T = 0.15, β H = 0.12. For this set of parameters R T = 1.666667, R H = 1.210288. The TB-only equilibrium Ɛ̂, the HIV-only equilibrium Ɛ ∗ and the co-infection equilibrium Ɛ ∗∗ are given by (4687.5, 3125.0, 0, 0, 0), (7581.92, 0, 1167.574, 0, 426.8125, 0) and (4067.9, 2166.5, 451.85, 223.72, 148.2, 113.17) respectively. It is observed that whenever the co-infection equilibrium Ɛ ∗ exists it is locally asymptotically stable and in this case the other equilibria become unstable. That means for R H > 1 and R T > 1, both the diseases will co-exist.

Fig. 6
figure 6

S −I 1 phase plane showing the stability of the HIV-only equilibrium point Ɛ ∗ when R T = 0.8888889, R H = 1.210288

Full size image
Fig. 7
figure 7

S−I 2 phase plane showing the stability of the HIV-only equilibrium point Ɛ * when R T = 0.8888889, R H = 1.210288

Full size image
Fig. 8
figure 8

I 1 − I 2 phase plane showing the stability of the co-infection equilibrium point when R T = 1.666667, R H = 1.210288

Full size image

In Fig. 9, the effect of screening TB patients is shown, which shows a significant decrease in the number of TB-infectives with an increase in rate of screening. Similarly the effect of screening in HIV patients is also considerable as the number of HIV infectives is less with the rise in rate of screening. This fact is demonstrated in Fig. 10. The combined effect of rates of screening of TB and HIV is demonstrated in Fig. 11, where both the TB and HIV infectives decrease significantly with the increase in the rates of screening of TB and HIV. The effects of rate of transmission of TB are demonstrated in Fig. 12, where it is observed that with the increase in this parameter the equilibrium levels of the TB infectives and the co-infected population increase. Similarly with the increase in the rate of transmission of HIV, the equilibrium level of HIV infectives and the co-infected population increase, which is demonstrated in Fig. 13.

Fig. 9
figure 9

Variation of I 1 and I 3 with time, showing the effect of rate of screening of TB where all other parameters are as stated for the co-infection equilibrium point

Full size image
Fig. 10
figure 10

Variation of I 2 and I 3 with time, showing the effect of rate of screening of HIV where all other parameters are as stated for the co-infection equilibrium point

Full size image
Fig. 11
figure 11

Variation of I 1 and I 2 with time, showing the combined effect of rate of screening of both TB and HIV where all other parameters are as stated for the co-infection equilibrium point

Full size image
Fig. 12
figure 12

Variation of I 1 and I 3 with time for different β T , showing the effect of rate of transmission of TB where all other parameters are as stated for the co-infection equilibrium point

Full size image
Fig. 13
figure 13

Variation of I 2 and I 3 with time for different β H , showing the effect of rate of rate of transmission of HIV where all other parameters are as stated for the co-infection equilibrium point

Full size image

6 Conclusion

In this paper we formulated and analyzed a mathematical model for HIV/AIDS-TB co-infection with screening and treatment of both HIV and TB infectives. The reproduction numbers corresponding to both TB and HIV were computed. The existence and stability of various equilibria were also discussed. We found that the system always tends to the disease-free equilibrium point if the basic reproduction numbers R T and R H corresponding to TB and HIV respectively, are less than one. We have shown that the coinfection equilibrium point is locally asymptotically stable whenever it exists. Our numerical simulation showed that the screening of HIV infected people plays a very important role in controlling the spread of this disease. From our presented results, it can be easily seen that the rate of screening of TB has a positive impact on the reproduction number (R T ) corresponding to TB, i.e., with an increase in the rate of screening of TB infectives, the reproduction number R T decreases. Thus we concluded that with an increase in the rate of screening of TB, i.e., η, the number of TB-infectives decreases, which is reflected in numerical simulation too. Also it is easy to observe that both the reproduction numbers R T and R H can be reduced below one by increasing the rate of screening for TB and HIV, leading the disease-free equilibrium to be stable. Also numerical simulation suggests that the rates of transmission of both TB and HIV should be decreased, as an increase causes a rise in the number of infectives at the equilibrium level. Hence, we can conclude that a strong coordination between the national TB and AIDS control programs is required for the effective management of HIV-TB patients.