1 Introduction

Electrokinetic has become widely recognized as an alternative flow mechanism for fluid transport in microfluidic channels. To examine electrokinetic flow via capillary slits, Burgreen and Nakache (1964) developed a Debye–Huckel linearized analytical method. Later, Rice and Whitehead (1965) carried out a numerical analysis on a tiny cylindrical capillary, and their results were consistent with approximations. The need for pumping power can be met by integrating this method with peristalsis-lab-on-a-chip devices. To show how electroosmosis may aid peristaltic pumping, Chakraborty (2006) first built a model that included the impacts of both processes. The field of microfluidics has gathered major attention due to its ability for precise manipulation of fluids at the microscale. This has led to a strong interest in exploring and studying this subject in greater detail. For the development of effective and trustworthy microfluidic devices, a thorough understanding of the behavior and properties of electroosmotic flow is essential (Bandopadhyay et al. 2016; Tripathi et al. 2018; Akram et al. 2022).

Peristalsis, in conjunction with electrokinetic transfer, has particular emphasis on its physiological transportation applications. It serves a crucial function in fields such as medicine, where it is used to pump blood and other biological fluids in heart–lung devices. This mechanism also facilitates lymph flow, ovum migration in the fallopian tube, and kidney-to-bladder urine transport. In addition, it participates in the physiological process of phloem translocation by transporting sucrose down the tubules. Peristaltic motion influences the design of medical devices, facilitates the movement of water in lofty trees, and improves the mobility of earthworms. Latham presented the first analysis of peristaltic phenomena (Latham 1966). Later, several theoretical and experimental investigations were performed to fathom the functions of peristalsis in the ureter. Shapiro (1967) and Shapiro et al. (1969) further investigated the reflux phenomenon from biological and medical perspectives, building on Latham’s work. Peristaltic motion, which imitates the cyclic contraction and relaxation of biological muscles, has also become a potential method of controlling fluid in microchannels. Due to the complexity of fluids, scientific literature contains numerous models. Significantly, the current work cites recent studies relevant to the context (Shit et al. 2016; Prakash and Tripathi 2018; Ramesh and Prakash 2019; Aslam et al. 2023; Waheed et al. 2019; Reddy et al. 2021; Gangavathi et al. 2023).

The term micropolar fluid refers to a fluid consisting of particles with random orientations that are suspended in a viscous medium. Eringen (1964) introduced the concept of micropolar fluids. These fluids are characterized by interconnected forces, body couplings, and micro-rotational and micro-inertial phenomena. Eringen himself presented the theory of simple micropolar fluids (Eringen 1966), explaining the hypothesis in detail. Ariman et al. (1974) have provided a comprehensive overview of microcontinuum fluid mechanics and discussed its numerous physiological applications. There are numerous applications for micropolar fluids where the presence of microstructure or additional internal degrees of freedom is pertinent. They have been utilized to examine the flow of biological fluids, including blood flow in microcirculation and synovial fluid flow in joints. A few researchers have investigated peristaltic flow phenomena in micropolar fluids (Muthu et al. 2008; Pandey and Tripathi 2011; Asha and Deepa 2019; Siddiqui and Turkyilmazoglu 2022; Bejawada and Nandeppanavar 2023) since the introduction of the micropolar fluid hypothesis.

The micropolar fluid model has an advantage over other non-Newtonian fluid models because it incorporates the micro-rotation vector, a specific kinematic vector used to determine the spin of fluid particles. Recent research has yielded new insights into fluid dynamics, shedding light on uncharted territory, and opening up new research avenues. Mehta et al. (Mehta et al. 2023) investigated electroosmotic vortices, illuminating the intricate relationship between electrokinetic forces and non-Newtonian fluid behavior. Kumar and Mondal (2023) utilized perturbation methods to analyze the microflow of Carreau fluid, thereby presenting an alternative viewpoint on non-Newtonian fluid dynamics. Kumar et al. (2023) contributed to biomimetics by examining a rhythmic membrane function for the design of a biomimetic micropump. Mansukhani et al. (2022) focused on modulating effective micropumping of non-Newtonian fluids through propagative-rhythmic membrane contraction. Studies (Chakraborty 2007; Vasu and De 2010; Ramesh et al. 2020; Mekheimer 2008; Chaube et al. 2018) are providing practical insights into applications of electroosmotic flows. In fact, addition of electroosmotic flow mechanism to an existing study makes the work novel, as scientific progress is dependent on the accumulation of prior knowledge. As our model extends the earlier theoretical work of Ali and Hayat (2008), we assume that the underlying theory remains coherent. Therefore, we contend that the effects of the electroosmotic mechanism can be understood within this framework. Our goal was to develop a comprehensive theoretical framework that provides insight into fluid behavior under these interconnected mechanisms. Considering the most recent advances, our study explores the interaction between electroosmotic and peristaltic mechanisms within a channel with the aim to fill in the gaps and contribute to the changing microfluidics landscape.

The purpose of this study is to examine the effect of the electroosmotic parameter, fluid parameter, and coupling parameter on electroosmotic peristaltic motion within a channel with sinusoidal and trapezoidal wave forms. Understanding fluid behavior and manipulation in electroosmosis motivates us to study micro-channel fluid dynamic. We thoroughly study how electroosmosis and peristaltic processes impact symmetric channel flow using micropolar fluid characteristics. From precision fluid manipulation to microscale mixing, this research advances basic understanding and has practical applications. This novel technique aims to find untapped potential at the electrokinetic-peristaltic interface. The flow is assumed to be controlled by both peristalsis and an axial electric field. The Debye–Huckel approximation is applicable if the zeta potential is less than 25 mV.

2 Mathematical model

2.1 Flow analysis

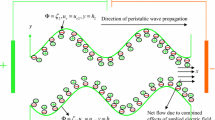
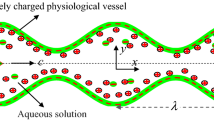
The electroosmotic movement in a symmetric regime via peristaltic wave traveling down the wall is considered and presented in Fig. 1. Wave train stated in Eq. (1) moves down the channel wall at a fixed speed s to create the peristaltic flow. Let \(Y = \pm L\) be upper and lower walls of channel. Flow is subject to body force.

$$\overline{L}\left( {\overline{X},\overline{t}} \right) = d + a\sin \left[ {\frac{2\pi }{\lambda }\left( {\overline{X} - s\overline{t}} \right)} \right] ,$$
(1)

where wavelength is \(\lambda\), time is \(\overline{t}\), wave amplitude is \(a\), wave speed is \(s\), and channel width is \(2d\) (half channel width is \(d\)).

Fig. 1
figure 1

Schematic representation of electroosmotic flow with peristalsis

Full size image

2.2 Governing equations

Fundamental governing equations for the electroosmotic flow (EOF) of an incompressible micropolar fluid, influenced by applied external electric field \(E_{x}\), moving steadily along the channel length (Refs. Ali and Hayat 2008) are provided by

$$\frac{{\partial \overline{F}}}{{\partial \overline{X}}} + \frac{{\partial \overline{G}}}{{\partial \overline{Y}}} = 0,$$
(2)
$$\rho \left( {\overline{F}\frac{{\partial \overline{F}}}{{\partial \overline{X}}} + \overline{G}\frac{{\partial \overline{F}}}{{\partial \overline{Y}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{X}}} + \left( {\mu + k} \right)\left( {\frac{{\partial^{2} \overline{F}}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \overline{F}}}{{\partial \overline{Y}^{2} }}} \right) + k\frac{{\partial \overline{w}}}{{\partial \overline{Y}}} + \rho_{e} E_{x} ,$$
(3)
$$\rho \left( {\overline{F}\frac{{\partial \overline{G}}}{{\partial \overline{X}}} + \overline{G}\frac{{\partial \overline{G}}}{{\partial \overline{Y}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{Y}}} + \left( {\mu + k} \right)\left( {\frac{{\partial^{2} \overline{G}}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \overline{G}}}{{\partial \overline{Y}^{2} }}} \right) - k\frac{{\partial \overline{w}}}{{\partial \overline{X}}},$$
(4)
$$\rho \overline{j}\left( {\overline{F}\frac{{\partial \overline{w}}}{{\partial \overline{X}}} + \overline{G}\frac{{\partial \overline{w}}}{{\partial \overline{Y}}}} \right) = - 2k\overline{w} + k\left( {\frac{{\partial \overline{G}}}{{\partial \overline{X}}} + \frac{{\partial \overline{F}}}{{\partial \overline{Y}}}} \right) + \gamma \left( {\frac{{\partial^{2} \overline{w}}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \overline{w}}}{{\partial \overline{Y}^{2} }}} \right).$$
(5)

Here, \(\overline{F}, \overline{G}, \overline{j}, \overline{p}, \overline{w}, \mu ,\) and \(k{ }\& { }\gamma\) are velocity along \(\overline{X}\) and \(\overline{Y}\) direction, micro-gyration parameter, fluid pressure, micro-rotation vector, viscosity constant for dynamic fluid, and viscosity constants for micropolar fluid, respectively.

2.3 Electrohydrodynamics (EHD)

A binary electrolyte solution \(({\text{Na}}^{ + } {\text{Cl}}^{ - } )\) with a symmetric \(\left( {z:z} \right)\) electric potential distribution is described by Poisson’s equation, which is written as follows (Chakraborty 2007).

$$\nabla^{2} \cdot \overline{\Phi } = - \frac{{\rho_{e} }}{\varepsilon },$$
(6)

where \(\rho_{e}\) represents density of all ionic charges, \(\varepsilon\) represents permittivity and \(\overline{\Phi } = \Phi \zeta\).

The ionic charge density defined in Poisson equation is determined by Boltzmann distribution given as \(\rho_{e} = ez\left( { - n^{ - } + n^{ + } } \right)\), where \(n^{ - }\) and \(n^{ + }\) represent the number of anion and cation densities, respectively. When Debye–Huckel linearization is adopted (Vasu and De 2010), i.e., \(\sinh \Phi \approx \Phi\), Poisson–Boltzmann equation becomes

$$\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} = m_{e}^{2} \Phi ,$$
(7)

where \(m_{e}\) is electroosmotic parameter. Subject to boundary conditions \(\Phi = 1,\) at \(y = L\left( x \right)\) and \(\frac{\partial \Phi }{{\partial y}} = 0,\) at \(y = 0,\) the analytical solution of above equation is obtained as

$$\Phi \left( y \right) = \frac{{\cosh \left( {m_{e} y} \right)}}{{\cosh \left( {m_{e} L} \right)}}.$$
(8)

This study, which takes place in the context of a symmetric micro-channel, focuses mainly on the profound effect of electrohydrodynamics (EHD) on the flow field. The concept is particularly useful and interesting, since it reflects situations that are frequently seen in biological and polymeric fluids. Electric and fluid motion interact dynamically when driven by external applied electric fields. By introducing electroosmotic forces, the emergence of an electric double layer at the fluid–wall boundary modifies the basic fluid behavior. Through the flow field, this EHD-induced transformation cascades, changing the velocity profiles, pressure distributions, and overall flow patterns in various manners.

2.4 Transformation and non-dimensionlization

$$\begin{gathered} \overline{x} = \overline{X} - st,\quad \overline{y} = \overline{Y} \hfill \\ \overline{f} = \overline{F} - s,\quad \overline{g} = \overline{G}. \hfill \\ \end{gathered}$$
(9)

Expression (9) links the velocities and coordinates in both frames, where \(\left( {\overline{F}, \overline{G}} \right)\) is velocity components in fixed frame and \(\left( {\overline{f}, \overline{g}} \right)\) is velocity components in wave frame of reference (Ramesh et al. 2020). In fixed frame of reference, the moving boundary causes the motion to be unsteady. But, in wave frame, the static boundary causes the motion to be steady.

Considering the following non-dimensional parameters and variables for simplification of governing equations.

$$\begin{gathered} x = \frac{{\overline{x}}}{\lambda },\quad y = \frac{{\overline{y}}}{d},\quad f = \frac{{\overline{f}}}{s},\quad g = \frac{{\lambda \overline{g}}}{ds},\quad w = \frac{{d\overline{w}}}{s},\quad L = \frac{{\overline{L}}}{d}, \hfill \\ \phi = \frac{a}{d},\quad \delta = \frac{d}{\lambda },\quad p = \frac{{d^{2} \overline{p}}}{s\lambda \mu },\quad j = \frac{{\overline{j}}}{{d^{2} }}, \quad {\text{Re}} = \frac{\rho sd}{\mu }. \hfill \\ \end{gathered}$$
(10)

where \({\text{Re}} , \zeta , \delta\) are Reynolds number, zeta potential, and wave number, respectively. Employing (9) and (10) in Eqs. (2–5), we get.

$$\frac{\partial f}{{\partial x}} + \frac{\partial g}{{\partial y}} = 0,$$
(11)
$${\text{Re}} \delta \left( {f\frac{\partial f}{{\partial x}} + g\frac{\partial f}{{\partial y}}} \right) = - \frac{\partial p}{{\partial x}} + \frac{1}{1 - R}\left( {R\frac{ \partial w}{{\partial y}} + \delta^{2} \frac{{\partial^{2} f}}{{\partial x^{2} }} + \frac{{\partial^{2} f}}{{\partial y^{2} }}} \right) + m_{e}^{2} \Phi U_{{{\text{HS}}}} ,$$
(12)
$${\text{Re}} \delta^{3} \left( {f\frac{\partial g}{{\partial x}} + g\frac{\partial g}{{\partial y}}} \right) = - \frac{\partial p}{{\partial y}} + \frac{{\delta^{2} }}{1 - R}\left( { - R\frac{\partial w}{{\partial x}} + \delta^{2} \frac{{\partial^{2} g}}{{\partial x^{2} }} + \frac{{\partial^{2} g}}{{\partial y^{2} }}} \right)$$
(13)
$$\frac{{{\text{Re}} j\delta \left( {1 - R} \right)}}{R}\left( {f\frac{\partial w}{{\partial x}} + g\frac{\partial w}{{\partial y}}} \right) = - 2w + \left( {\delta^{2} \frac{\partial g}{{\partial x}} - \frac{\partial f}{{\partial y}}} \right) + \frac{2 - R}{{M^{2} }}\left( {\delta^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right),$$
(14)

where \(M^{2} = \frac{{d^{2} k\left( {2\mu + k} \right)}}{{\gamma \left( {\mu + k} \right)}}\) is micropolar parameter, \(R = \frac{k}{\mu + k}\) is coupling number (\(0 \le R \le 1,\) due to its physical interpretation and the restrictions it represents within the perspective of the model), \(U_{{{\text{HS}}}} = - \frac{{E_{x} \varepsilon \zeta }}{\mu s}\) is dimensionless Helmholtz–Smoluchowski velocity and \(m_{e} = dze\sqrt {\frac{{2n_{0} }}{{\varepsilon T_{{avK_{{\text{B}}} }} }}}\) is electroosmotic parameter. The governing equations have the following form when the lubrication approximation \(\left( {\delta = \frac{d}{\lambda } \simeq 0} \right)\) and the assumption of low Reynold number (Viscous dominated flow) is used:

$$R\frac{\partial w}{{\partial y}} + \frac{{\partial^{2} f}}{{\partial y^{2} }} + \left( {1 - R} \right)m_{e}^{2} \Phi U_{{{\text{HS}}}} = \left( {1 - R} \right)\frac{\partial p}{{\partial x}},$$
(15)
$$\frac{\partial p}{{\partial y}} = 0,$$
(16)
$$- 2w - \frac{\partial f}{{\partial y}} + \left( {\frac{2 - R}{{M^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} = 0.$$
(17)

2.5 Volume flow rate

In laboratory frame (Mekheimer 2008),

$$Q = \mathop \int \limits_{0}^{{\overline{L}\left( {\overline{X}, \overline{t}} \right)}} \overline{F}\left( {\overline{X}, \overline{Y}, \overline{t}} \right){\text{d}}\overline{Y}.$$
(18)

In wave frame, the equation becomes

$$q = \mathop \int \limits_{0}^{{\overline{L}\left( {\overline{x}} \right)}} \overline{f}\left( {\overline{x}, \overline{y}} \right){\text{d}}\overline{y}.$$
(19)

Dimensionless mean flows θ and H in both frames are given by

$$\theta = H + 1,$$
(20)

where

$$\theta = \frac{{\overline{Q}}}{ds}, \quad H = \frac{q}{ds}.$$
(21)

In which

$$q = \mathop \int \limits_{0}^{L} f{\text{d}}y.$$
(22)

Wall surface in dimensionless form is

$$L\left( x \right) = 1 + \phi \sin 2\pi x,$$
(23)

here \(\phi = \frac{a}{d}.\)

Associated boundary conditions are (Chaube et al. 2018),

$$f = - 1,\quad {\text{at}}\quad y = \pm \left( {1 + \phi \sin 2\pi x} \right),$$
(24)
$$w = 0,\quad {\text{at}}\quad y = \pm \left( {1 + \phi \sin 2\pi x} \right).$$
(25)

2.6 Exact solution

Equation (15) can be written in the following form, with the help of Eq. (16),

$$\frac{{\partial^{2} f}}{{\partial y^{2} }} = \frac{\partial }{\partial y}\left[ {\left( {1 - R} \right)\frac{{{\text{d}}p}}{{{\text{d}}x}}y - Rw} \right] - \left( {1 - R} \right)m_{e}^{2} \Phi U_{{{\text{HS}}}} .$$
(26)

The above equation is integrated to get

$$\frac{\partial f}{{\partial y}} = \left( {1 - R} \right)\frac{{{\text{d}}p}}{{{\text{d}}x}}y - Rw - \left( {1 - R} \right)m_{e}^{2} \Phi U_{{{\text{HS}}}} y + C_{1} .$$
(27)

Using the above value of \(\partial f/\partial y\) in Eq. (17), we have

$$\frac{{\partial^{2} w}}{{\partial y^{2} }} - M^{2} w = \chi \left( {1 - R} \right)\frac{{{\text{d}}p}}{{{\text{d}}x}}y - \chi \left( {1 - R} \right)m_{e}^{2} \Phi U_{{{\text{HS}}}} y + \chi C_{1} .$$
(28)

By solving Eq. (28) subject to boundary condition Eq. (25), we get

$$w = A_{1} (( - 1 + R)\chi (\cosh (My) - \sinh (My))(A_{2} A_{3} U_{{{\text{HS}}}} ).$$
(29)

Using the value of \(w\) and the boundary condition Eq. (24), we have

$$f = \frac{1}{{M^{3} }}\left( {A_{4} A_{5} U_{{{\text{HS}}}} } \right).$$
(30)

Stream function is written as

$$f = \frac{\partial \psi }{{\partial y}},\quad g = - \frac{\partial \psi }{{\partial x}},$$
(31)

using the value \(f = \frac{\partial \psi }{{\partial y}}\) in Eq. (30) we derive the expression for \(\psi\).

Using Eq. (22), we can find the expression for pressure gradient as

$$\frac{{{\text{d}}p}}{{{\text{d}}x}} = - A_{6} \left( { - L - q + \frac{1}{{m_{e} M^{2} (m_{e}^{2} - M^{2} )^{2} }}(( - 1 + R)U_{{{\text{HS}}}} A_{7} )} \right),$$
(32)

where the Appendix has values for \(A_{1} - A_{7}\).

The dimensionless pressure rises per wavelength \({\Delta }P_{\lambda }\) as:

$${\Delta }P_{\lambda } = \mathop \int \limits_{0}^{1} \frac{\partial p}{{\partial x}}{\text{d}}x.$$
(33)

The frictional force \({\text{Frict}}_{\lambda }\) is written as:

$${\text{Fric}}_{\lambda } = - L^{2} \mathop \int \limits_{0}^{1} \frac{\partial p}{{\partial x}}{\text{d}}x.$$
(34)

3 Validation of the results

To prove the accuracy of our ongoing research, we compare our analytical solution for the dimensionless velocity to the findings presented in a previous study (Ali and Hayat 2008), focusing on a specific scenario. This special case involves ignoring the Helmholtz–Smoluchowski velocity \(\left( {U_{{{\text{HS}}}} = 0} \right)\) and electroosmotic \(\left( {m_{e} \to 0} \right)\) effects. Figure 2 illustrates the comparison between our model and the results obtained from Ali and Hayat (2008). To make relevant comparisons, we have set \(U_{{{\text{HS}}}} = 0, m_{e} = 0.001, M = 10, \phi = 0.6, R = 0.2\). In the case where the electroosmotic effect is negligible (\(m_{e} \to 0\)), the fluid flow is governed solely by hydrodynamic mechanisms. This represents a purely hydrodynamic flow scenario where the applied electric field does not have a significant impact on the velocity profile. Consequently, the velocity profile in this case follows the typical characteristics of hydrodynamic flow.

Fig. 2
figure 2

A comparison of the axial velocity between the findings of the current study’s special case and the previous study of Ali and Hayat (2008)

Full size image

However, as the value of \(m_{e}\) increases, the electrohydrodynamic effects become more prominent, and the applied electric field begins to influence the velocity profile. With those of (Ali and Hayat 2008), our findings showed excellent agreement in special case.

4 Graphical analysis and discussion

The physical configuration of the problem includes a micro-channel, which serves as a simplified, yet accurate representation of microfluidic systems found in practical applications. In this configuration, the introduction of an external electric field \(E_{x}\) stimulates the development of electroosmotic forces. The unique features of micropolar fluids, which include internal micro-rotational motion, interact with these forces. Furthermore, the magnitude and direction of the electroosmotic flow can be affected by the thickness and charge distribution of the electric double layer. The electroosmotic flow is influenced by the thickness of the double layer as well; thicker double layers have lower flow rates. Physically, the electrical body force varies directly to \(E_{x}\), which demonstrates that thicker EDL results in a large reduction in electrical body force. On average, the wavelength ranges from a few millimeters to 100 µm. Some are known constants like e (electron charge), KB (Boltzmann constant). Wave speed usually falls in the range of 1–10 mm s−1. Typically ranging from 10 to 200 µm, the wave’s amplitude indicates the greatest possible deviation from the mean position. The channel width d that allows the peristaltic flow typically ranges from 1 to 10 mm. k, μ, γ are the material constants. The ranges of these parameters depend on the experimental conditions, microstructure, and rotational dynamics.

Figure 3 shows how the Helmholtz–Smoluchowski velocity, electroosmotic parameter, and micropolar parameter affect the velocity profile. Spin diffusion is explained by the micropolar parameter. For \(k \to \infty ,\) Newtonian fluid model is reduced from micropolar fluid model. The electroosmotic parameter describes thickness of EDL (i.e., for \(m_{e} \to \infty ,\) EDL is so thin, it can be physically inferred that the charge distribution on the wall surface has no impact on fluid flow) and effect of externally applied electric field is characterized by Helmholtz–Smoluchowski velocity. The problem will be peristaltic movement of micropolar fluid through a symmetric channel if there is no electric field \(\left( {U_{{{\text{HS}}}} \to 0} \right)\). Plots of velocity profiles for case of a negative pressure gradient \(({\text{d}}p/{\text{d}}x < 0\; {\text{i}}{\text{.e}}{.}\;p_{x} = - 5)\) are made for axial speed and displacement (transverse), while other parameters are held constant, i.e., \(x = 1\) and \(\phi = 0.6\). It has been observed that toward the transverse direction, velocity for a negative pressure gradient is parabolic, validating our current model even though this is a simple fact. Figure 3a shows impact of electroosmotic parameter on velocity profile. Zeta potential, a measurement of the surface charge density at the fluid–solid interface, is frequently used to represent the electroosmotic parameter. The magnitude, direction, and velocity of the electroosmotic flow are all determined by the zeta potential. The electroosmotic parameter essentially measures a fluid’s capacity to flow along a charged surface when an electric field is present. For \(m_{e} \to 0\), flow is again simply hydrodynamic, and flow is electrohydrodynamic for certain value of \(m_{e}\). The curve for hydrodynamic flow is below the curves of electrohydrodynamic flow, which shows that applied electric field affects the velocity profile. The magnitude of the velocity profile is observed to widen as \(m_{e}\) is increased, which decreases thickness of EDL. Similarly, Fig. 3b shows the effects of Helmholtz–Smoluchowski velocity. Physically, the equilibrium between the electric force acting on the charged particle and the fluid’s frictional forces is represented by the Helmholtz–Smoluchowski velocity. The average particle speed in the absence of additional external forces like gravity or viscous drag is explicitly referred to as the Helmholtz–Smoluchowski velocity. Curve for \(U_{{{\text{HS}}}} \to 0\) illustrates the velocity for purely hydrodynamic flow. It has been found that velocity increases as the electric field intensity increases, which indicates that electroosmosis can increase peristaltic flow. Figure 3c is the display of impact of micropolar parameter on velocity profile and it is found that there is a small increase in velocity profile with a large variation (0–100) in magnitude of micropolar parameter, indicating that the micropolar parameter does not significantly alter the flow characteristics. The physical significance of the micropolar parameter is that it controls how the material reacts to rotational deformation. A material with a smaller micropolar parameter is more rigid and less sensitive to rotational deformations, whereas a material with a greater micropolar parameter is more flexible and more sensitive to rotational deformations.

Fig. 3
figure 3

Velocity profile for \(m_{e} \left( {3a} \right), U_{HS} \left( {3b} \right), and M \left( {3c} \right)\)

Full size image

From Fig. 4, it is possible to observe the effects of electroosmotic parameter, Helmholtz–Smoluchowski velocity, and micropolar parameter on \(\nabla p\) (pressure difference) with \(Q\) (time averaged flow rate). Like findings of Shapiro et al. (1969), a linear relationship between \(\nabla p\) and \(Q\) is found. The maximum flow rate is also noted to be attained at \(\nabla p = 0\). Three regions are distinguished based on the pressure difference: the pumping region for \(\nabla p > 0\), the enhanced pumping region for \(\nabla p < 0\), and the free pumping region for \(\nabla p = 0\). Impact of electroosmotic parameter on pressure rise is displayed in Fig. 4a. For \(m_{e} \to 0\), the flow is hydrodynamic (i.e., no electric field effect). The flow is electrohydrodynamic for certain value of \(m_{e}\). Hence, it has been claimed that in all pumping zones, pressure difference increases as the thickness of EDL is decreased (\(m_{e}\) is increased). Figure 4b shows how pressure difference is affected by Helmholtz–Smoluchowski velocity, and it is noted that pressure difference increases as electric field strength rises. \(\nabla p\) determined by Ali and Hayat (2008) for sinusoidal flow is shown by curve for \(U_{{{\text{HS}}}} \to 0\), which is same as the pressure rise produced by just peristaltic pumping. Figure 4c shows changes in \(\nabla p\) with micropolar parameter. It is noted that there are slight changes as magnitude of \(M\) increases, augmented pumping area increases, pumping area decreases, and free pumping area remains unchanged.

Fig. 4
figure 4

\(\nabla p\) vs. \(Q\) for \(m_{e} \left( {4a} \right), U_{HS} \left( {4b} \right), and M \left( {4c} \right)\)

Full size image

Figure 5 illustrate the effects of electroosmotic parameter, Helmholtz–Smoluchowski velocity, and micropolar parameter on frictional force \(({\text{Fric}}_{\lambda } )\) with \(Q\). The impact of electroosmosis on frictional force is influenced by several variables, including electric field intensity, EDL thickness, and surface charges of the two surfaces. An electric field can cause the frictional force to decrease. The electroosmotic flow, which reduces the thickness of the EDL (\(m_{e}\) is increased), is responsible for this reduction in friction (Fig. 5a). Influence of Helmholtz–Smoluchowski velocity is depicted in Fig. 5b, and it is seen that frictional force decreases as electric field strength rises. Changes in frictional force with micropolar parameter are shown in Fig. 5c. The frictional force increases with increasing micropolar parameter. This is so because the micropolar characteristic makes the material more capable of resisting shear deformation, which increases the contact area between the two surfaces. A bigger frictional force is the result of the increased contact area.

Fig. 5
figure 5

Frictional force \(\left( {Fric_{\lambda } } \right)\) vs. \(Q\) for \(m_{e} \left( {5a} \right), U_{HS} \left( {5b} \right), and M \left( {5c} \right)\)

Full size image

Figure 6 demonstrate the effects of electroosmotic (\(m_{e}\)) and micropolar \(\left( M \right)\) parameters on flow rate vs. axial coordinate. Notably, the flow rate significantly increases with increasing electroosmotic parameter. Increased electroosmotic parameter typically means higher electrokinetic action, which can boost fluid flow. This improved electroosmotic action may increase flow rate by speeding fluid particle migration down the conduit. There is a notable enhancement in the flow rate as well with an increasing micropolar parameter, as seen in Fig. 6b. Fluid microstructure or rotational effects grow with a greater micropolar parameter. By adding particle motion or changing fluid viscosity, this might change flow. These factors may boost flow rate.

Fig. 6
figure 6

Flowrate \(\left( q \right)\) verses axial coordinate for \(m_{e} \left( {6a} \right) {\text{and }}M \left( {6b} \right)\)

Full size image

Through Figs. 7 and 8, two cases of intriguing peristaltic pumping phenomena known as trapping are explored for both sinusoidal and trapezoidal waveforms. These cases are affected by coupling, electroosmotic, and micropolar parameter impacts. Trapping, technique of recirculating the center streamlines at balance between values for peristaltic wave amplitude and average flow rate. In this study, the peristaltic wave amplitude and average flow rate are assumed to be \(\phi = 0.5 {\text{and }}Q = 0.6\), respectively. In first scenario (Fig. 7), electric field is put in opposition to peristaltic pumping \((U_{{{\text{HS}}}} < 0)\) and second scenario (Fig. 8), electric field is put in direction of peristaltic flow \((U_{{{\text{HS}}}} > 0)\). On trapping, when results of adding and removing electric field are compared, it is evident that in first case, center streamlines create the bolus by recirculating, whereas in second case, the middle lines are parallel and shrink at middle of channel and at upper and lower portions of channel, adjacent lines recirculate. According to a physical interpretation, center streamlines form boluses when peristaltic pumping predominates (first case), whereas in second case, where electric field and peristaltic effects are combined, center streamlines straighten up and make parallel and EDL effects trap streamlines toward channel walls. The left panel shows the variations for sinusoidal waveforms. Figure 7a and c demonstrates how micropolar parameter \(\left( {M = 1, 4} \right)\) affected trapping in first scenario. It is noted that minor change occur in the size of bolus as micropolar parameter varies from 1 to 4. Figure 7c and e shows the impact of changing the electroosmotic parameter \(\left( {m_{e} = 5, 10} \right)\) on trapping, and it is shown that as \(m_{e}\) is increased from 5 to 10, more trapping boluses are produced. The effects of both parameters in the second case (Fig. 8) are identical to those in the first case. Likewise, the right panel shows the variations for trapezoidal waveform. Sinusoidal waves provide mathematical simplicity and are more amenable to computational modeling. If the peristaltic activity consists of a series of successive contractions occurring within a tube, it would be more suitable to represent this phenomenon using a trapezoidal wave shape. The utilization of a composite of both wave types can be employed to capture distinct facets of the phenomenon.

Fig. 7
figure 7

Streamlines for sinusoidal (Left panel) and trapezoidal (Right panel) waveforms at \(\phi = 0.5, U_{HS} = - 1\) and \(Q = 0.6\)

Full size image
Fig. 8
figure 8

Streamlines for sinusoidal (left panel) and trapezoidal (right panel) waveforms at \(\phi = 0.5, U_{HS} = 5,\) and \(Q = 0.6\)

Full size image

Micropolar fluid studies examine particular situations to understand the fluid model. The classical Newtonian fluid ignores microstructural influences and acts like a classic Newtonian fluid as the micropolar parameter approaches zero. To compare the behavior of micropolar fluids with that of classical Newtonian fluids, this case is used as a benchmark. For various combinations of the micropolar parameter and coupling number, Table 1 displays the shear stress \(\tau_{xy}\) at the channel walls. Comparing the shear stress values for various combinations, we can see that the shear stress reduces as the micropolar parameter \(\left( M \right)\) and coupling number \(\left( R \right)\) rise. This demonstrates how the presence of micropolar effects and stronger coupling causes the shear stress at the walls to decrease. By examining Table 2, it can be shown that the electrohydrodynamic and hydrodynamic velocity profiles both generally exhibit a rising tendency when the micropolar parameter \(\left( M \right)\) rises. This shows that a larger micropolar parameter has a more profound effect on the velocity distribution inside the symmetric channel. In addition, with respect to a constant micropolar parameter, a drop in the electrohydrodynamic velocity profile is produced by an increase in the coupling number \(\left( R \right).\) In contrast, a rise in the coupling number causes a rise in the velocity profile in the hydrodynamic situation. The insights gained from this study have the potential to considerably advance applications including microfluidic mixing, pumping, and particle manipulation.

Table 1 Comparison of shear stress \(\tau_{xy}\) at walls for different values of micropolar parameter \(M\) and coupling number \(R\) when \(a = 0.5, x = 1, \theta = 1.2, m_{e} = 6, U_{{{\text{HS}}}} = 0.5\)
Full size table
Table 2 Comparison of velocity profile \(f\) for different values of micropolar parameter \(M\) and coupling number \(R\) when \(a = 0.5, x = 1, y = 0.5, \theta = 1.2, m_{e} = 6, U_{{{\text{HS}}}} = 0.5\)
Full size table

5 Conclusion

This study explores the examination of peristaltic movement of micropolar fluids that is regulated by electroosmosis through a symmetric channel. The outcomes provide a comprehensive understanding of the behavior of the system, which is inextricably linked to the physical factors that control it. Particularly, zeta potential, applied voltage, and channel shape are found to be crucial determinants of the velocity of electroosmotic flow. These results offer useful information for developing microfluidic devices that are suited to certain uses where accurate fluid manipulation is essential. Key findings are as follows:

  • The peristaltic movement of a micropolar fluid enhances with electric field and complex interaction between electric field-induced forces and the dynamics of the micropolar fluid, resulting in alterations to peristaltic patterns.

  • Significant fluctuations are observed with an increase in both the electroosmotic parameter and the Helmholtz–Smoluchowski velocity. On the other hand, the range of the micropolar parameter, which spans from 0 to 100, results in little and virtually insignificant modifications to the flow.

  • Pressure rise per wavelength increases as the electroosmotic parameter increases, while Helmholtz–Smoluchowski velocity and micropolar parameter have varied effects on \(\nabla p\), indicating small variations in pumping characteristics while the situation is reversed for frictional forces.

  • The flow rate experiences a significant rise when there is an augmentation in the electroosmotic and micropolar parameters.

  • The process of trapping exhibits a notable level of sensitivity to fluctuations in electroosmotic parameters revealing minor changes in bolus size with varying micropolar parameter.

The theoretical findings might potentially be applicable to physiological flows and commercial applications that use peristaltic pumping driven by electroosmosis that is subjected to fluid particle micro-rotation.