1 Introduction

In recent times, thermal energy systems are the most demandable and emerging fields which are the need of society and sustainability of the environment. With enhancing the demand for thermal systems and improvement in thermal performance, various types of nanoparticles/nanomaterials are being prepared and tested by the scientist and researchers [1, 2]. Various types of potential materials/nanoparticles have already been developed in the last few decades which can store the latent/sensible energy that can be utilized as per their demands. As a need of improving the thermal conductivity of the base fluid/heat transfer fluids, the concept of nanofluids was introduced by Choi [3] and discussed their properties, synthesis, characterization, and applications in detail. Various types of nanoparticles like metals (Cu, Ag, etc.), metal oxides (ZnO, SiO2, TiO2, etc.), carbon materials (CNTs &Diamonds), metal carbides (SiC), metal nitrides (Boron nitride BN, AIN), and hybrid nanomaterials are available in the literature [4]. Each nanoparticle/nanomaterial has unique thermal properties and is utilized as per the requirement of the thermal systems. In the present paper, we have considered the boron nitride nanotubes (BNNTs) which have tremendous thermal performance and are applicable in various thermal systems [5]. It can be used as zero-dimensional "fullerenes", nanoparticles, one-dimensional nanotubes, nanoribbons, and two-dimensional Nanosheets, which are applicable in durable field emitters, UV luminescent materials, anti-oxidation, and anti-corrosive coatings, electrical insulating fillers in composites, and chemistry inert superhydrophobic films.

Boron nitride has a cubic structure and having a layered analog of carbon [6]. BN is considered as a solid-state lubricant since it has exceptionally high thermal stability characteristics. Boron nitride nanosheet (BNNTs) is a unique 2-D crystalline structure that is exfoliated from boron nitride. In the limelight of BNNTs, many mathematical models [7,8,9,10] have been presented, including stretchable piezoelectric materials and induced by micro fluidization. Moreover, BNNTs have the potential to be functionalized with high electrical and thermal conductivity due to electrically insulating. Tan et al. [11] have fabricated the stretchable laminated GNRs nanocomposite-based conductor. This fabricated device performed the thermal conductivity enhancement of 266% that helps to reduce the temperature from 57.4 to 29.2 °C. Since the BNNTs have the characteristic to heat realize due to efficient heat transfer pathway. In this regard, Lee et al. [12] work on “graftingform” polymerization of caprolactone onto BNNTs for thermally conductive polymer composites, Cao et al. [13] have developed the unique BN nanosheet that has the potential to perform uniform diffusion in PI matrix and is capable of emitting heat transfer.

The colloidal suspension of the nano-size particle in the base fluid such as ethylene glycol, water, carbides is known as nanofluid. In particular, nanofluids are exhibited in thermal application like cooling processes, industrial including power generation to improve thermal conductivity [14]. Thermal transfer nanofluid is considered as a bridge in the heat exchange process to the base fluids that is efficient to perform heat dissipation. Few mathematical models in this regard are presented in [15, 16]. The thermophysical characteristic of BNNTs plays an exciting role in nanofluids to analyze the stability, rheology, and thermal properties. In this regard, Gomez-Villarejo et al. [17] have worked for convectional fluids in solar thermal applications. They experimentally observed the stability and measured the \(\zeta\)-potential, got the nanofluids were stable. Continue in BNNTs nanofluids, various experimental [18,19,20] works have been presented on BN nanofluids [18], grafted hexagonal BNNTs [19]. Ramteke et al. [20] have characterized the performance of hexagonal BN on the tribological.

Pumping is a mechanism that can be defined as the transport of the fluids under the external force or internal force, which creates pressure differences to pump the fluids. In this paper, we have used two types of pumping mechanisms. The first one is peristaltic pumping [21], which means the pressure is generated by the wave propulsion by the channel walls. Peristaltic pumping is a traditional pumping mechanism via propagative wave contraction and expansion that is attached from lower pressure to the higher pressure of a distensible tube. The fundamental principle of this mechanism has been exploited in many engineering applications for years. In the context of nanofluid, Akhter et al. [22] have studied the impact of SWCNT on the peristaltic flow of viscous fluid and illustrate the physical property for heat generation & convection. Continue in this work, Nadeem and Akbar [23] have demonstrated the effect of non-Newtonian nanofluid in peristaltic pumping. Another one is electroosmotic pumping [24], which means that pressure difference is generated by the external electric field. In the limelight of electroosmotic, the interface of the solid surface gets ionized due to the polar aqueous solution. Therefore, opposite charge ions to the surface get attracted, and the same charge ions to the surface get repelled. The influence of electroosmotic flow and nano-size particles in MHD fluid [25] and the Williamson fluid [26] have been presented. The peristaltic and electroosmotic are very significant pumping mechanisms to fabricated the microfluidic devices for the physiological systems. In this regard, Akram et al. [27] have illustrated the thermal radiation impact on electroosmosis-driven peristaltic pumping in the bio-microfluidics channel. Some mathematical models [28, 29] were also developed to comprehend the nature of bio-rheological fluids induced by the electroosmotic and peristaltic pumping mechanisms.

Although, many researchers have put their efforts into dealing with various types of non-Newtonian models for understanding the properties of the complex rheological fluid, in the present literature, there are so many nonlinear fluid models that have been studied. Here, another type of fluid model is incorporated due to its viscoelastic nature that is known as Carreau fluid [30]. The characteristic of Carreau fluid is considered as the Weissenberg number, which is essential in a rheological point of view is involved in this flow model. To illustrate, Akram and Akbar [31] have numerically analyzed the momentum and heat transfer of Carreau nanofluid. Studies of two-dimensional [32] and three-dimensional flow [33] of Carreau fluid have been presented by Ahmed and Nadeem [32] in the catheterized arteries and Riaz et al. [33] on nanoparticle phenomena for the thermal condition, respectively. Hussain et al.[34] discussed the Carreau –Yasuda fluid flow near the stagnation point by considering the convectively heated surfaces.

A wide range of mathematical models has been modeled that deals with the straight channel. However, this approach is not valid in the physiological and complex system as most of the arteries and ducts are curved in nature. To fill this gap, Yoon et al. [35] discussed the Bird-Carreau fluid model in the curved microchannel. Analysis of entropy generation of electron magnetohydrodynamic flow through a curved rectangular microchannel has been demonstrated by Liu et al. [36]. Nekoubin et al. [37] & Narla and Tripathi [38] explored the mathematical study of electroosmotic flow in the curved channel for power-law fluid and blood. Fluid rheology has numerical simulation by Javid et al. [39] induced by the magnetic field in the curved peristaltic wall. The biomimetic electroosmotic nanofluid pumping model is discussed by Narla et al. [40] in which they analyzed the entropy generation. In the same line, some of the interesting models [41,42,43,44,45,46] on curved channel flow with various physics have recently been developed and discussed the curvature effects.

In all the above literature, it is noted that the flow analysis for boron nitride nanotubes (BNNTs) under the effects of peristaltic pumping and electroosmotic pumping has not yet been reported. However, the thermophysical properties of boron nitride nanotubes (BNNTs) nanofluids with various base fluids have been investigated, and found that it has good potential and thermal performance. Motivated by these facts, a mathematical model is studied to analyze the thermal analysis of the EG-based BN nanofluids flows in a curved channel driven by both pumping mechanisms. The effects of the magnetic field in the analysis have also been introduced. Furthermore, the halls and ions slip effects are also taken into consideration to discuss the flow and thermal characteristics in a more elaborated form. The effects of various pertinent parameters on the flow and thermal characteristics have further been performed with the aid of numerical computations. The findings of the present analysis may apply to various thermal systems.

2 Problem Formulation

2.1 Peristaltic Pumping

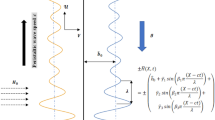
Here the peristaltically driven flow of ionic solution of ethylene glycol (EG)-based boron nitride nanotubes (BNNTs) through a curved channel is conferred. The sinusoidal wave trains with wavelength (λ) are propagated with constant speed (c) along the curved microchannel to generate the peristaltic pumping. The Curvilinear coordinate system \(\left(\tilde{r },\tilde{x }\right)\) is chosen for mathematical formulation of the flow problem in curvilinear flow regime in such a way that \(\tilde{x }\) lies across the channel centerline and \(\tilde{r }\) is perpendicular to it. The deformable wall configuration is represented physically in Fig. 1 and is mathematically expressed as:

$$\tilde{r} = \pm \tilde{H}\left( {\tilde{x},\tilde{t}} \right) = \pm \left( {a + b\sin \left( {\frac{2\pi }{\lambda }\left( {\tilde{x} - c\tilde{t}} \right)} \right)} \right)$$
(1)

In which a represents the half-width of the channel, \(\tilde{t }\) is the time and \(b\) is the amplitude of the peristaltic wave.

Fig. 1
figure 1

Schematic representation of the EG-based BNNTs nanofluid flow induced by peristaltic pumping and electroosmotic pumping

Full size image

2.2 Magnetohydrodynamics

The fluid flow is further controlled by the implication of the radial magnetic field of constant magnitude B0. Here we have considered the peristaltic pumping of EG-based BNNTs nanofluid through a curved channel. It has been experimentally [47] found that ethylene glycol-based BNNTs nanofluid depicts the non-Newtonian shear thinning behavior and can be well described theoretically by employing the Carreau fluid model. Therefore, Carreau fluid model along with the Buongiorno model for nanofluid is utilized for the mathematical formulation of the problem. Xue model for thermal conductivity is incorporated to measure the effective thermal conductivity of boron nitride nanotubes suspension. Moreover, the effect of the applied magnetic field \(\overrightarrow{B}\) =(0, 0, \(\frac{\tilde{R }{B}_{0}}{\tilde{r }+\tilde{R }}\)) is considered and the impact of Hall and ion slip on the fluid phenomenon is also analyzed. The influence of the Joule heating phenomenon occurring due to the applied electric and magnetic field is also included in the heat equation. Introducing the generalized Ohm’s law including the effect of Hall and ion slip effect as [48]:

$$\vec{J} = \sigma_{nf} \left( {\vec{E} + \vec{V}X\vec{B}} \right) - \frac{{\omega_{e} \tau_{e} }}{{\left( {\frac{{\tilde{R}B_{0} }}{{\tilde{r} + \tilde{R}}}} \right)}}\left( {\vec{J}X\vec{B}} \right) + \frac{{\omega_{e} \tau_{e} \beta_{i} }}{{\left( {\frac{{\tilde{R}B_{0} }}{{\tilde{r} + \tilde{R}}}} \right)^{2} }}\left( {\vec{J}X\vec{B}} \right)X\vec{B}$$
(2)

In the above relation, \(\overrightarrow{J}\) designates the current density vector, \(\overrightarrow{E}\) is the induced electric field which is neglected in this investigation, \(\tilde{R }\) is the inner radius of the circle along which flow channel is coiled, \({\beta }_{i}\) is the ion-slip parameter, \({\omega }_{e}\) is the cyclotron frequency, \({\tau }_{e}\) is the collision time of electron, \({\sigma }_{nf}\) is the effective electric conductivity of nanofluid measured by Maxwell–Garnett model and \(\overrightarrow{V}\)= (\(\tilde{v }\),\(\tilde{u }\),0) is the velocity vector. Solving the above equation, the expression for Lorentz force and current density is obtained as:

$$\vec{J}X\vec{B} = \left( { - \frac{{\sigma_{nf} B_{0}^{2} \tilde{R}^{2} \left( {\alpha_{e} \tilde{v} - \beta_{e} \tilde{u}} \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }}, - \frac{{\sigma_{nf} B_{0}^{2} \tilde{R}^{2} \left( {\alpha_{e} \tilde{u} + \beta_{e} \tilde{v}} \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }},0} \right)$$
(3)
$$\frac{{\vec{J}.\vec{J}}}{{\sigma_{nf} }} = \frac{{\sigma_{nf} B_{0}^{2} \tilde{R}^{2} \left( {\tilde{u}^{2} + \tilde{v}^{2} } \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }}$$
(4)

here \({\beta }_{e}\) denotes the Hall parameter and \({\alpha }_{e}=1+{\beta }_{i}{\beta }_{e}.\)

2.3 Governing Equations for Carreau Nanofluids

Subject to various physics involved in the problem, the continuity, momentum, energy, and nanoparticle mass flux equations are modified as [40, 43]:

$$\frac{{\partial \tilde{v}}}{{\partial \tilde{r}}} + \frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \frac{{\tilde{v}}}{{\tilde{r} + \tilde{R}}} = 0$$
(5)
$$\begin{aligned} & \rho_{nf} \left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{t}}} + \tilde{v}\frac{{\partial \tilde{v}}}{{\partial \tilde{r}}} + \frac{{\tilde{R}\tilde{u}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{v}}}{{\partial \tilde{x}}} - \frac{{\tilde{u}^{2} }}{{\tilde{r} + \tilde{R}}}} \right) \\ &\quad= - \frac{{\partial \tilde{p}}}{{\partial \tilde{r}}} + \frac{1}{{\tilde{r} + \tilde{R}}}\frac{\partial }{{\partial \tilde{r}}}\left( {\left( {\tilde{r} + \tilde{R}} \right)\tilde{\tau }_{{\tilde{r}\tilde{r}}} } \right) + \frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{\tau }_{{\tilde{r}\tilde{x}}} }}{{\partial \tilde{x}}}\\ & \quad\quad - \frac{{\tilde{\tau }_{{\tilde{x}\tilde{x}}} }}{{\tilde{r} + \tilde{R}}} + \rho_{e} U_{{E_{{\tilde{r}}} }} - \frac{{\sigma_{nf} B_{0}^{2} \tilde{R}^{2} \left( {\alpha_{e} \tilde{v} - \beta_{e} \tilde{u}} \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }} \end{aligned}$$
(6)
$$\begin{aligned} & \rho_{nf} \left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{t}}} + \tilde{v}\frac{{\partial \tilde{u}}}{{\partial \tilde{r}}} + \frac{{\tilde{R}\tilde{u}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \frac{{\tilde{u}\tilde{v}}}{{\tilde{r} + \tilde{R}}}} \right)\\&\quad = - \frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{p}}}{{\partial \tilde{x}}} + \rho_{e} U_{{E_{{\tilde{x}}} }} + \frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{\tau }_{{\tilde{x}\tilde{x}}} }}{{\partial \tilde{x}}} \\&\qquad+ \frac{1}{{\left( {\tilde{r} + \tilde{R}} \right)^{2} }}\frac{\partial }{{\partial \tilde{r}}}\left( {\left( {\tilde{r} + \tilde{R}} \right)^{2} \tilde{\tau }_{{\tilde{r}\tilde{x}}} } \right) - \frac{{\sigma_{nf} B_{0}^{2} \tilde{R}^{2} \left( {\alpha_{e} \tilde{u} + \beta_{e} \tilde{v}} \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }} \end{aligned}$$
(7)
$$\begin{aligned} & \left( {\rho \zeta } \right)_{{{\text{nf}}}} \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{t}}} + \tilde{v}\frac{{\partial \tilde{T}}}{{\partial \tilde{r}}} + \frac{{\tilde{u}\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{x}}}} \right) \\ &\quad= K_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{r}^{2} }} + \frac{1}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{r}}} + \left( {\frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}} \right)^{2} \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{x}^{2} }}} \right) \\&\qquad + \sigma_{{{\text{nf}}}} U_{{E_{{\tilde{x}}} }}^{2} + \left( {\rho \zeta } \right)_{s} D_{B} \left( {\nabla {\tilde{\Phi }}.\nabla \tilde{T}} \right) + \frac{{D_{T} }}{{\tilde{T}_{0} }}\left( {\rho \zeta } \right)_{s} \left( {\nabla \tilde{T}.\nabla \tilde{T}} \right) \\&\qquad + \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} \tilde{R}^{2} \left( {\tilde{u}^{2} + \tilde{v}^{2} } \right)}}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {\tilde{r} + \tilde{R}} \right)^{2} }} \end{aligned}$$
(8)
$$\begin{aligned} & \left( {\frac{{\partial \tilde{\Phi }}}{{\partial \tilde{t}}} + \tilde{v}\frac{{\partial \tilde{\Phi }}}{{\partial \tilde{r}}} + \frac{{\tilde{u}\tilde{R}}}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{\Phi }}}{{\partial \tilde{x}}}} \right)\\&\quad = D_{B} \left( {\frac{{\partial^{2} \tilde{\Phi }}}{{\partial \tilde{r}^{2} }} + \frac{1}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{\Phi }}}{{\partial \tilde{r}}} + \left( {\frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}} \right)^{2} \frac{{\partial^{2} \tilde{\Phi }}}{{\partial \tilde{x}^{2} }}} \right) \\&\qquad+ \frac{{D_{T} }}{{\tilde{T}_{0} }}\left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{r}^{2} }} + \frac{1}{{\tilde{r} + \tilde{R}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{r}}} + \left( {\frac{{\tilde{R}}}{{\tilde{r} + \tilde{R}}}} \right)^{2} \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{x}^{2} }}} \right) \end{aligned}$$
(9)

where \(\rho_{{{\text{nf}}}} ,\tilde{p},{ }U_{{E_{{\tilde{r}}} }} ,U_{{E_{{\tilde{x}}} ,{ }}} \left( {\rho \zeta } \right)_{{{\text{nf}}}} ,K_{{{\text{nf}}}} ,\left( {\rho \zeta } \right)_{s} ,\tilde{T},\tilde{\Phi }D_{T} ,D_{B} ,{ }\tilde{\tau }_{{\tilde{r}\tilde{x}}} ,{ }\tilde{\tau }_{{\tilde{x}\tilde{x}}} ,\tilde{\tau }_{{\tilde{r}\tilde{r}}}\)\(and {\tilde{T }}_{0}\) designate the effective density of nanofluid, the pressure force, the electric body force in radial and axial direction, the specific heat of nanofluid, the effective thermal conductivity of nanofluid, the specific heat of boron nitride nanotubes, the fluid temperature, the nanoparticle mass flux, the thermophoretic diffusion parameter, the Brownian diffusion parameter, the stress components of Carreau fluid model and the temperature at lower wall of the microchannel, respectively.

The stress tensor for Carreau fluid model is expressed by [47]

$$\tilde{\tau } = \mu_{nf } A_{1}$$
(10)

where

$$\mu_{nf } = \frac{1}{{\left( {1 - \Phi_{0} } \right)^{2.5} }}\left( {\mu_{\infty } + \frac{{\left( {\mu_{0} - \mu_{\infty } } \right)}}{{\left( {1 + \left( {\Gamma \dot{\gamma }} \right)^{2} } \right)^{\frac{n}{2}} }}} \right)$$
(11)

and \({A}_{1}\) the first Rivlin-Erickson tensor is given by:

$$\dot{\gamma } = \sqrt {\frac{1}{2}tr\left( {A_{1}^{2} } \right)}$$
(12)
$$A_{1} = {\text{grad}}\left( {\vec{V}} \right) + \left( {{\text{grad}}\left( {\vec{V}} \right)} \right)^{t}$$
(13)

In which \({\mu }_{0}\) and \({\mu }_{\infty }\) show the viscosities at zero and infinite shear rates, respectively, \(\Gamma\) is the time constant and n is the power-law index. The values of \({\mu }_{0}, {\mu }_{\infty }\) and n for BNNTs-EG nanofluid with different volume fractions are experimentally calculated in [45] and are utilized in this investigation accordingly.

From the general mixture rule, the density and the specific heat of BNNTs-EG nanofluid are calculated as [49]:

$$\rho_{{{\text{nf}}}} = \left( {1 - \Phi_{0} } \right)\rho_{{{\text{bf}}}} + \Phi_{0} \rho_{{{\text{NT}}}}$$
(14)
$$\left( {\rho \zeta } \right)_{{{\text{nf}}}} = \left( {1 - \Phi_{0} } \right)\left( {\rho \zeta } \right)_{{{\text{bf}}}} + \Phi_{0} \left( {\rho \zeta } \right)_{{{\text{NT}}}}$$
(15)

The effective thermal conductivity of boron nitride nanotubes suspension in ethylene is predicted by Xue model [49] and Brinkmann’s model which is employed for effective viscosity of nanofluid as:

$$\frac{{K_{{{\text{nf}}}} }}{{K_{{{\text{bf}}}} }} = \left( {\frac{{\left( {1 - \Phi_{0} } \right) + 2\Phi_{0} \frac{{K_{{{\text{NT}}}} }}{{K_{{{\text{NT}}}} - K_{{{\text{bf}}}} }}\ln \left( {\frac{{K_{{{\text{NT}}}} + K_{{{\text{bf}}}} }}{{2K_{{{\text{bf}}}} }}} \right)}}{{\left( {1 - \Phi_{0} } \right) + 2\Phi_{0} \frac{{K_{{{\text{bf}}}} }}{{K_{{{\text{NT}}}} - K_{{{\text{bf}}}} }}\ln \left( {\frac{{K_{{{\text{NT}}}} + K_{{{\text{bf}}}} }}{{2K_{{{\text{bf}}}} }}} \right)}}} \right) = K_{r}$$
(16)
$$\frac{{ \mu_{{{\text{nf}}}} }}{{\mu_{{{\text{bf}}}} }} = \frac{1}{{\left( {1 - \Phi_{0} } \right)^{2.5} }} = \mu_{r}$$
(17)

In the above equations, the subscript “NT” specifies the properties of boron nitride nanotubes, subscript “bf” and “nf” are used for ethylene glycol properties (base fluids) and nanofluids, respectively, and \({\Phi }_{0}\) is the nanoparticle volume fraction.

The Maxwell–Garnett model for electrical conductivity is defined by:

$$\sigma_{{{\text{nf}}}} = \sigma_{{{\text{bf}}}} \left( {1 + \frac{{\left( {\frac{{\sigma_{{{\text{NT}}}} }}{{\sigma_{{{\text{bf}}}} }} - 1} \right)\Phi_{0} }}{{\left( {\frac{{\sigma_{{{\text{NT}}}} }}{{\sigma_{{{\text{bf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{NT}}}} }}{{\sigma_{{{\text{bf}}}} }} - 1} \right)\Phi_{0} }}} \right)$$
(18)

2.4 Electroosmotic Pumping

Further, the electroosmotic phenomenon is also mobilized within the fluid medium by introducing an electric field across the electric double layer (EDL). Due to the presence of electrolyte solution within the curved microchannel, the walls of the channel are negatively charged so they attract the counterions and repel the coions which result in the formation of EDL. This EDL has an excess of counterions i.e., cations and relatively fewer coions. When an electric field is applied across EDL, the ionic species are dragged toward respective electrodes, dragging the rest of the fluid particles with them. The electric potential established in the fluid medium due to the application of the external electric field is governed by the Poisson equation:

$$\nabla^{2} U_{E} = - \frac{{\rho_{e} }}{{\varepsilon_{0} \varepsilon }}$$
(19)

where \({U}_{E}\) denotes the electric potential, ε is the relative permittivity for the fluid medium,\({\varepsilon }_{0}\) is the dielectric constant for vacuum and \({\rho }_{e}=ez\left({n}^{+}-{n}^{-}\right)\) is the net charge number density in terms of the local density of ionic species having bulk concentration n0, symmetric valence z, and the electric charge \(e.\)

2.5 Transformation and Non-dimensionalization

In order to observe a steady flow phenomenon, a frame of reference \(\left(\dot{r},\dot{x}\right)\) is selected such that it is moving with the peristaltic wave speed c. The transformations between the laboratory and the moving frames of reference are defined as:

$$\dot{x} = \tilde{x} - c\tilde{t},\dot{r} = \tilde{r},\dot{v} = \tilde{v}, \dot{u} = \tilde{u} - c,\dot{p}\left( {\dot{r},\dot{x}} \right) = \tilde{p}\left( {\tilde{r},\tilde{z},\tilde{t}} \right)$$
(20)

The following dimensionless numbers are introduced to facilitate the non-dimensional analysis:

$$\begin{aligned} & x = \frac{{\dot{x}}}{\lambda }, r = \frac{{\dot{r}}}{a}, p = \frac{{\dot{p}d^{2} }}{{\mu_{{{\text{bf}}}} c\lambda }},u = \frac{{\dot{u}}}{c},v = \frac{{\dot{v}}}{c}, n = \frac{{\tilde{n}}}{{n_{0} }},\hfill \\ & \beta_{e} = \omega_{e} \tau_{e} , \alpha_{e} = 1 + \beta_{e} \beta_{i} \phi = \frac{b}{a}, h = \frac{{\tilde{H}}}{a} = 1 + \sin \left( {2\pi x} \right),\hfill \\ & \Pr = \frac{{\mu_{{{\text{bf}}}} \zeta_{{{\text{bf}}}} }}{{k_{{{\text{bf}}}} }} , \delta = \frac{a}{\lambda }, \theta = \frac{{\tilde{T} - \tilde{T}_{0} }}{{\overline{{\tilde{T}_{1} - \tilde{T}_{0} }} }}, Ha^{2} = \frac{{\sigma_{{{\text{bf}}}} l^{2} B_{0}^{2} }}{{\mu_{{{\text{bf}}}} }} \hfill \\& \Phi = \frac{{\tilde{\Phi } - \Phi_{0} }}{{\Phi_{0} }} ,U_{E} = \frac{{ez\tilde{U}_{E} }}{{k_{B} \hat{T}_{{{\text{avg}}}} }},{\text{Re}} = \frac{{\rho_{{{\text{bf}}}} {\text{cl}}}}{{\mu_{{{\text{bf}}}} }}, S = \frac{{\sigma_{{{\text{bf}}}} U_{{E_{x} }}^{2} a^{2} }}{{K_{{{\text{bf}}}} \left( {\hat{T}_{1} - \hat{T}_{0} } \right)}},\hfill \\& \Psi = \frac{{\tilde{\Psi }}}{{{\text{ca}}}} U_{{{\text{hs}}}} = - \frac{{\varepsilon_{0} \varepsilon k_{B} \hat{T}_{{{\text{avg}}}} U_{{E_{{\tilde{x}}} }} }}{{{\text{ez}}\mu_{{{\text{bf}}}} c}}, m = \sqrt {\frac{{2n_{0} e^{2} z^{2} l^{2} }}{{\varepsilon_{0} \varepsilon k_{B} \hat{T}_{{{\text{avg}}}} }}} = \frac{l}{{\lambda_{d} }},\hfill \\& N_{t} = \frac{{D_{{\tilde{T}}} \tau^{ * } \rho_{{{\text{bf}}}} \left( {\tilde{T}_{1} - \tilde{T}_{0} } \right)}}{{\tilde{T}_{0} \mu_{{{\text{bf}}}} }} N_{b} = \frac{{D_{B} \tau^{ * } \rho_{{{\text{bf}}}} \Phi_{0} }}{{\mu_{{{\text{bf}}}} }}, \tau^{ * } = \frac{{\left( {\rho \zeta } \right)_{p} }}{{\left( {\rho \zeta } \right)_{{{\text{bf}}}} }},\\&{\text{Ec}} = \frac{{c^{2} }}{{\zeta_{{{\text{bf}}}} \left( {\overline{T}_{1} - \overline{T}_{0} } \right)}}, {\text{Br}} = {\text{Ec}} \Pr ,\beta = \frac{{\mu_{\infty } }}{{\mu_{0} }} \hfill \\& {\text{We}} = \frac{\Gamma c}{a},u = - \frac{\partial \Psi }{{\partial r}}, v = \delta \frac{\kappa }{r + \kappa }\Psi_{x} , \kappa = \frac{{\tilde{R}}}{a} \hfill \\ \end{aligned}$$
(21)

In the above relation, the following dimensionless parameters are defined as: \(\phi\) is the amplitude ratio. \(Ha\) is the Hartmann number, S is the Joule heating parameter, Ec is the Eckert number, Br is the Brinkmann number, Re is the Reynolds number, \(\kappa\) is the non-dimensional curvature parameter, \({N}_{t}\) is the dimensionless thermophoretic diffusion parameter, \({U}_{hs}\) is the Helmholtz–Smoluchowski velocity parameter also termed as electroosmotic velocity parameter, We is the Weissenberg number, \({N}_{b}\) is the dimensionless Brownian diffusion parameter, m is the Debye length parameter, \(\delta\) is the wavenumber, Pr is the Prandtl number, \(\beta\) is the viscosity ration, and \(\theta\) is the dimensionless temperature parameter.

Transforming the system of Eqs. (5–10), and (19) from laboratory frame to moving frame of reference using Eq. (20) and non-dimensionalizing using Eq. (21) and then applying the lubrication linearization principle i.e., inertial effects are neglected along the microchannel, the continuity equation is identically justified and Eqs. (6–10), and (19) are simplified to:

$$\begin{aligned} \frac{\kappa }{r + \kappa }\frac{\partial p}{{\partial x}} & = \frac{1}{{\left( {r + \kappa } \right)^{2} }}\frac{{\partial \left( {\left( {r + \kappa } \right)^{2} \tau_{{{\text{rx}}}} } \right)}}{\partial r} + U_{{{\text{hs}}}} m^{2} U_{E}\\&\quad - \frac{{M^{2} \kappa^{2} \sigma_{r} \alpha_{e} }}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {r + \kappa } \right)^{2} }}\left( {1 - \frac{\partial \Psi }{{\partial r}}} \right) \end{aligned}$$
(22)
$$\frac{\partial p}{{\partial r}} = 0$$
(23)
$$\begin{aligned} & K_{r} \left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{\partial \theta }{{\partial r}}} \right) + \Pr N_{b} \frac{\partial \theta }{{\partial r}}\frac{\partial \Phi }{{\partial r}} + \Pr N_{t} \left( {\frac{\partial \theta }{{\partial r}}} \right)^{2}\\ &\quad + \sigma_{r} S + \frac{{M^{2} \kappa^{2} \sigma_{r} \alpha_{e} }}{{\left( {\alpha_{e}^{2} + \beta_{e}^{2} } \right)\left( {r + \kappa } \right)^{2} }}\left( {1 - \frac{\partial \Psi }{{\partial r}}} \right)^{2} = 0 \end{aligned}$$
(24)
$$\left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{\partial \Phi }{{\partial r}}} \right) + \frac{{N_{t} }}{{N_{b} }}\left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{\partial \theta }{{\partial r}}} \right) = 0$$
(25)
$$\tau_{{{\text{rx}}}} = \mu_{r } \left( {\beta + \left( {1 - \beta } \right)\left( {1 - \frac{n}{2}{\text{We}}^{2} \left( { - \frac{{\partial^{2} \Psi }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\left( {\frac{\partial \Psi }{{\partial r}} - 1} \right)} \right)^{2} } \right)} \right)\left( { - \frac{{\partial^{2} \Psi }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\left( {\frac{\partial \Psi }{{\partial r}} - 1} \right)} \right)$$
(26)
$$\tau_{{{\text{xx}}}} = \tau_{{{\text{rr}}}} = 0$$
(27)
$$\frac{{\partial^{2} U_{E} }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{{\partial U_{E} }}{\partial r} = m^{2} \left( {\frac{{n^{ - } - n^{ + } }}{2}} \right)$$
(28)

Utilizing the Boltzmann distribution function defined below as:

$$n^{ \pm } = e^{{ \mp \widetilde{{U_{E} }}}} = e^{{ \mp \frac{{ezU_{E} }}{{k_{B} \hat{T}}}}}$$
(29)

Equation (28) can be expressed in terms of a linearized Poisson-Boltzmann equation describing the electric potential distribution in the fluid medium as:

$$\frac{{\partial^{2} U_{E} }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{{\partial U_{E} }}{\partial r} = m^{2} \sinh \left( {U_{E} } \right)$$
(30)

This Poisson-Boltzmann equation can be further simplified subject to the Debye-Hückel linearization approximation assuming a lower zeta potential of up to 25 mV at both walls i.e., \(\mathrm{sinh}\left({U}_{E}\right)\approx {U}_{E}\), Eq. (30) becomes

$$\frac{{\partial^{2} U_{E} }}{{\partial r^{2} }} + \frac{1}{r + \kappa }\frac{{\partial U_{E} }}{\partial r} = m^{2} U_{E}$$
(31)

Equation (31) is a well-known modified Bessel’s equation, which can be executed analytically by imposing suitable boundary conditions for electric potential on both walls. Here we have assumed that the same electric potential is maintained at both walls and it can be mathematically described as:

$$U_{E} |_{r = h} = \xi , U_{E} |_{r = - h} = \xi$$
(32)

Solving Eq. (31) along with Eq. (32), we get electric potential functions in terms of modified Bessel’s functions of the first and second kind as:

$$U_{E} = \xi \frac{{\begin{array}{*{20}c} {\left( { - I_{0} \left[ {m\left( {\kappa - \eta } \right)} \right] + I_{0} \left[ {m\left( {\kappa + \eta } \right)} \right]} \right)K_{0} \left[ {m\left( {\kappa + r} \right)} \right] + I_{0} \left[ {m\left( {\kappa + r} \right)} \right]} \\ {\left( {K_{0} \left[ {m\left( {\kappa - \eta } \right)} \right] - K_{0} \left[ {m\left( {\kappa + \eta } \right)} \right]} \right)} \\ \end{array} }}{{I_{0} \left[ {m\left( {\kappa + \eta } \right)} \right]K_{0} \left[ {m\left( {\kappa - \eta } \right)} \right] - I_{0} \left[ {m\left( {\kappa - \eta } \right)} \right]K_{0} \left[ {m\left( {\kappa + \eta } \right)} \right]}}$$
(33)

2.6 Boundary Conditions

The no-slip boundary conditions for velocity and convective boundary conditions for heat and mass transfer are prescribed as:

$$\begin{gathered} \Psi = - \frac{q}{2}, \frac{\partial \Psi }{{\partial r}} = 1,\frac{\partial \theta }{{\partial r}} + {\text{Bi}}_{1} \left( {1 - \theta } \right) = 0,\frac{\partial \Phi }{{\partial r}} - {\text{Bi}}_{2} \Phi = 0, {\text{at}} r = \eta \hfill \\ \Psi = \frac{q}{2},\frac{\partial \Psi }{{\partial r}} = 1,\theta = 0,\Phi = 0, {\text{at}} r = - \eta \hfill \\ \end{gathered}$$
(34)

here \({Bi}_{1}\) represents the thermal Biot number, \({Bi}_{2}\) the mass transfer Biot number and q is the dimensionless mean flow rate occurring in moving frame i.e., wave frame defined in terms of mean flow rate in fixed frame Q as:

\(q = Q - 2\).

2.7 Solution Methodology

The transmuted set of Eqs. (22–26) is highly nonlinear and coupled. Also due to the involvement of Bessel functions, it seems quite difficult to get the closed-form solutions for the flow properties. Therefore, Eqs. (22–26) along with boundary conditions given in Eq. (34) are treated numerically through the numerical algorithm in mathematical software Maple 17. A built-in routine dsolve is employed to get the solution of the nonlinear boundary value problem which utilizes the finite difference technique along with Richardson extrapolation and provides a numerical solution of the problem with considerable accuracy. The graphical results are prepared from the computed result to observe the salient attributes of the fluid flow phenomenon. The motion of fluid particles is visualized through the contour plot of the stream function. Also, graphs are plotted for Nusselt number to study the heat transfer attributes of conventional heat transfer fluid.

3 Numerical Results and Discussion

The section aims to explore the alteration in flow characteristics for change in various important physical parameters through graphical results and a physical description is provided for the obtained results. For numerical simulation, the thermophysical properties of base fluid i.e., ethylene glycol and the boron nitride nanotubes are calculated at 298 K and are presented in Table 1. The nanoparticle fraction of 0.05 of boron nitride nanotubes is initially dispersed in the base fluid. However, the behavior of various fluid properties is also observed by varying nanoparticle volume fractions over 0.05, 0.1, 0.15, and 0.2. The values of viscosities at lower and upper shear rates and the power-law index for different volume fractions of nanotubes are calculated experimentally in [45] and are utilized here. Based on the thermophysical attributes given in Table 1, the dimensionless Brownian diffusion and thermophoretic diffusion are found to be \({N}_{b}=3.533\times {10}^{-7}\) and \({N}_{t}=3.992\times {10}^{-7}\), respectively. The range of the Debye length parameter in this investigation is 1 ≤ m ≤ 2. The electroosmotic velocity parameter varies over -1 ≤ Uhs ≤ 1, where negative values of the electroosmotic parameter correspond to an electric field aligned in the direction of the peristaltic wave i.e., assisting the motion of the fluid, for a zero value of Uhs signifies the absence of applied and a positive value represent an electric field, which retards the motion of the fluid generated by the peristaltic waves. The average diameter of the boron nitride nanotubes is chosen to be 30 nm. A comparison of numerical results obtained for velocity in this investigation is compared with the results presented by Narla and Tripathi [36]. A very close agreement between the results is obtained which assures the validity of the present computation (see Table 2).

Table 1 Thermophysical properties of boron nitride nanotubes, and ethylene glycol [50] nanoparticles
Full size table
Table 2 Results for velocity profile w(r) along radial axis r
Full size table

3.1 Flow Analysis

In Figs. 2, 3, 4, 5, 6, 7, 8, the velocity profile is plotted versus radial distance for multiple values of Carreau fluid parameters, electroosmotic parameter, Hall and ion slip parameters, curvature parameter, and the nanoparticle volume fraction. Figure 2 depicts that fluid motion is retarded by enhancement in the Weissenberg parameter. As from the definition, the Weissenberg number is directly proportional to the relaxation time of the fluid particle, therefore rising values of we produce a decline in velocity. The impact of the curvature parameter on the velocity profile is outlined in Fig. 3. As larger values of curvature parameter represent a relatively flatter channel and a smaller value means a channel with stronger curvature. In this investigation, κ is chosen to be 2.5 i.e., a strongly curved microchannel. Increasing values of the curvature parameter diminish the velocity profile at the lower wall of the channel; however, an increment in velocity is noticed near the upper wall. The alterations in the velocity profile for varying values of Hall and the ion slip parameter are indicated in Figs. 4 and 5, respectively. A rise in the velocity near the centerline is generated for both parameters. As both Hall and ion slip parameters inversely affect the strength of resistive Lorentz forces due to enhancement in the cyclotron frequency, therefore, fluid is accelerated. It can be concluded from Fig. 6 that there is a significant uplift in the velocity profile for increment in the Debye length parameter. As Debye length parameter is the measure of the electric double layer thickness i.e., a larger m corresponds to a thinner electric double layer. For a thin EDL, the electric potential is nonuniformly distributed throughout the fluid medium, which causes a rapid motion of ionic species. Consequently, a substantial increment in velocity is observed in Fig. 6. The impression of the electroosmotic velocity parameter on the fluid motion is inspected in Fig. 7. The electroosmotic velocity parameter evaluates the strength as well as the direction of the applied electric field. For positive values of the HS parameter, the electric field is oriented in the direction opposite to the main flow direction and retards the motion of the fluid due to propagating waves. The zero value of the HS parameter means the absence of an electric field, i.e., flow is occurring only due to the peristaltic pumping. Therefore, it can be clearly noticed that the velocity profile is higher in the case of zero electric fields when it is compared with the case of the opposing electric field. However, in the case of a negative HS velocity parameter, peristaltic pumping is assisted by electroosmotic velocity, and an uplift in the velocity profile is obtained. For a further rise in the negative HS parameter, peak velocities are attained more rapidly. Figure 8 demonstrates a diminishing trend in velocity profile via a rise in the volume fraction of boron nitride nanotube in the base fluid. From [45], it is clear that for a larger concentration of BN, a considerable increment in zero shear rate viscosity of nanofluid is produced along with a rise in the power-law index, which produces a decline in the shear-thinning aspect of BNNTs-EG nanofluid. Due to comparatively stronger viscous forces experienced by the fluid, fluid velocity drops for growth in the concentration of nanotubes in EG.

Fig.2
figure 2

Velocity versus radial distance for Weissenberg number

Full size image
Fig. 3
figure 3

Velocity versus radial distance for the curvature parameter

Full size image
Fig. 4
figure 4

Velocity versus radial distance for the hall parameter

Full size image
Fig. 5
figure 5

Axial velocity versus radial distance for the ion slip parameter

Full size image
Fig. 6
figure 6

Axial velocity versus radial distance for the debye length parameter

Full size image
Fig. 7
figure 7

Velocity versus radial distance for electroosmotic velocity parameter

Full size image
Fig. 8
figure 8

Velocity versus radial distance for nanotube volume fraction

Full size image

3.2 Trapping Analysis

In this section, streamline contours are exhibited to manifest the variations in fluid flow pattern for escalating values of various embedded parameters such as curvature parameter, Hall parameter, Weissenberg number, and the nanotubes volume fraction. Figure 9a–c reveals that there is a marginal depression in the size trapping bolus for growing values of Weissenberg number and a decrease in the number of circulated streamlines is noticed. As the Weissenberg number accounts for the relaxation time of the working fluid, fluid motion slows down for increment in We, which results in the reduction in the trapping phenomenon. The evolution in the streamline pattern for alteration in the Hall parameter is depicted in Fig. 10a–c. A minute decrease in the size of bolus at the upper wall occurred; however, there is a considerable decrease in the number of closed streamlines in the vicinity of the lower wall. Figure 11a–c describes that for a smaller curvature parameter, a large number of streamlines are circulated, however, for a gradual rise in curvature parameter, less fluid particles are deflected from their original path to follow an elliptical path and enclose a volume of the fluid. Figure 12a–c displays the streamline pattern for several values of BN nanotube volume fraction. A very minute alteration in the circulation structure is observed for increasing the volume fraction of nanotubes up to 0.2 at both walls of the channel. Figure 13a–c discloses that for electric body forces acting in the backward direction, closed streamlines occur near both walls of the curved channel, and the volume of the circulation flow pattern is large. It is due to the backward motion of ionic species diverting the motion of the fluid particles. In the absence of an electric field (see Fig. 13b), a fewer number of streamlines are trapped near the upper walls, however, an expansion in the side size of the trapped bolus is observed near the lower wall. In the case of electroosmotic velocity in the forwarding direction, only one streamline bolus is trapped near the upper wall, however, the volume of circulatory flow slightly rises at the lower half of the microchannel.

Fig. 9
figure 9

Streamline pattern for Weissenberg number

Full size image
Fig. 10
figure 10

Streamline pattern for hall parameter

Full size image
Fig. 11
figure 11

Streamline pattern for curvature parameter

Full size image
Fig. 12
figure 12

Streamline pattern for nanotubes volume fraction

Full size image
Fig. 13
figure 13

Streamline pattern for electroosmotic velocity parameter

Full size image

3.3 Thermal Analysis

The development in the radial thermal distribution versus radial distance for multiple values of involved physical quantities is explored through Figs. 14, 15, 16, 17, 18, 19, 20. The advancements in temperature distribution via a larger Joule heating parameter are visualized in Fig. 14. Clearly, Joule heating is the phenomenon of the transformation of electric energy into heat energy due to the resistance experienced by an electric current to flow through the fluid medium. An uplift in the Joule heating parameter physically corresponds to a stronger electric current passing through the working fluid hence more heat is generated and augmentation in the thermal profile is noticed. A decline in the temperature profile is produced for growth in the Hall parameter as manifested in Fig. 15. As mentioned earlier, the Hall parameter facilitates overcoming the resistive nature of Lorentz forces, so less heat is dissipated when more Hall currents are produced. A similar influence of the ion slip parameter on thermal distribution is displayed in Fig. 16. A considerable augmentation in nanofluid temperature is observed for evolution in the Hartmann number (see Fig. 17). Hartmann number is the measure of magnetic field strength and the strength of resistive Lorentz forces. An augmentation in Hartmann's number physically means the presence of more effective Lorentz forces which strongly control the fluid motion and consequently, more heat is generated. Figure 18 presents the amendments in temperature of the nanofluid for the dispersed volume fraction of BN nanotubes in the EG. It is found that the temperature of the fluid drops for a larger volume fraction. Although the viscosity of the fluid enhances for the larger volume fraction of nanotubes, there is a tremendous uplift in the thermal conduction performance of working fluid due to the nanotube structure and larger thermal conductivity of the BN nanotube which assist the rapid removal of heat from the system. Due to this fact, the temperature of the fluid reduces for a larger volume fraction. The influence of thermal Biot number on temperature profile is elaborated in Fig. 19. As a larger Biot number implies a reduction in the process of thermal conductance at channel boundaries, so a very significant growth in temperature is found at the upper wall of the channel for enhancement in the thermal Biot number. It is evident from Fig. 20 that for increment in the curvature parameter, the temperature of the fluid drops. So it can be concluded that heat can be removed with great ease in the case of the planar channel when compared with the case of the curved channel and higher thermal efficiency is achieved in the case of the relatively planar channel.

Fig. 14
figure 14

Temperature profile versus radial distance for the Joule heating parameter

Full size image
Fig. 15
figure 15

Temperature profile versus radial distance for the hall parameter

Full size image
Fig. 16
figure 16

Temperature profile versus radial distance for the Ion slip parameter

Full size image
Fig. 17
figure 17

Temperature profile versus radial distance for the Hartmann number

Full size image
Fig. 18
figure 18

Temperature profile versus radial distance for the curvature parameter

Full size image
Fig. 19
figure 19

Temperature profile versus radial distance for the nanoparticle volume fraction

Full size image
Fig. 20
figure 20

Temperature profile versus radial distance for the thermal biot number

Full size image

3.4 Nusselt Number

Introducing the dimensionless Nusselt number to calculate the heat transfer rate at the upper wall of the channel:

$${\text{Nu}} = K_{r} \left( {\frac{ - \partial \theta }{{\partial r}}} \right)_{r \to \eta }$$
(35)

Nusselt number quantifies the rate of convective heat transfer relative to the heat transferred by conductance. The influence of nanoparticle volume fraction, curvature parameter, Joule heating parameter, and temperature difference on the magnitude of Nusselt number is perceived through Figs. 21, 22, 23, 24. Figure 21 captures the response of the Nusselt number toward growing values of nanoparticle volume fraction. A very strong decline in the magnitude of the Nusselt number is noticed in the resulting panel. As Nusselt number is inversely related to the transfer of heat due to conductance and larger BN nanotube volume fraction in the base fluid significantly identify the thermal conductivity of the base fluid which results in the reduction of the Nusselt number. Figure 22 is sketched to visualize the influence of the curvature parameter on the Nusselt number. As increasing curvature parameter means a decrease in the curvature of the flow regime and considering a comparably planar channel and it is already mentioned that more cooling effect is caused by larger curvature parameter, therefore, rate of convective heat transfer tends to rise. Consequently, the magnitude of the Nusselt number drops. The outcomes of thermal Biot number on Nusselt number distribution are manifested in Fig. 23. A depression in Nusselt number is found for evolution is Biot number. As for the larger Biot number, the overall process of heat transfer is resisted as it is inversely proportional to the heat transfer ability of the channel boundary therefore there is a decrease in the Nusselt number. Figure 24 depicts the variation in the Nusselt number for enlargement in the Joule heating parameter. It is revealed that there is an increment in the magnitude of the Nusselt number for enhancement in the Joule heating parameter. As the amount of heat produced due to the passage of electric current is directly associated with the strength of the applied electric field which boosts the electroosmotic phenomenon in the flow regime, therefore, A rise in the Joule heating parameter improves the convective transfer of heat and the magnitude of Nusselt number is elevated.

Fig. 21
figure 21

Nusselt number for nanotubes volume fraction

Full size image
Fig. 22
figure 22

Nusselt number for the curvature parameter

Full size image
Fig. 23
figure 23

Nusselt number for the thermal biot number

Full size image
Fig. 24
figure 24

Nusselt number for the Joule heating parameter

Full size image

4 Conclusions

Here an analysis is performed on the heat transfer capability of ethylene glycol-based boron nitride nanofluid which is moving by electroosmosis as well as propagation of peristaltic waves along the walls of curved microchannel. The shear-thinning rheology of BN-EG nanofluid is modeled by Carreau fluid model. Hall and ion slip effects generated by the applied radial magnetic field are also taken into consideration. The simplified set of equations for the flow problem is solved numerically to obtain the graphical representation of various flow properties and to study the influence of various important physical quantities on fluid velocity, temperature, and heat transfer characteristics. The major findings of the investigation are highlighted as:

  • Fluid motion is strongly retarded by increasing the relaxation time of the nanofluid.

  • An uplift in the curvature parameter causes a reduction in velocity at the lower wall and accelerates the flow at the upper wall; however ,temperature profile declines everywhere for larger curvature of the microchannel.

  • The process of streamline circulation is strongly obstructed by an increment in the curvature effect.

  • Velocity profile grows for larger Hall and ion slip parameters, however, they leave a reverse impact on the temperature profile.

  • The temperature of the fluid ascends when the process of Joule heating is boosted and for an increase in the strength of the applied magnetic field.

  • An improvement in the cooling process within the flow regime is noticed when the volume fraction of BN nanotubes is increased.

  • For smaller nanotubes volume fraction, nanofluid exhibits more shear-thinning behavior therefore velocity is higher for less concentration of nanotubes. However, a reduction in velocity is observed for higher volume fractions which is due to a reduction in shear-thinning ability and increment in the viscosity of the fluid.