Electroosmotically induced alterations in peristaltic microflows of power law fluids through physiological vessels

Abstract

A mathematical model to analyze the effects of electric double layer and applied external electric field on peristaltic transport of non-Newtonian aqueous solution through a microchannel is presented. Ostwald–de Waele power law model is employed to describe the non-Newtonian fluid, in an effort to capture the essential biofluid dynamics. The governing equations of physical problem are simplified using low Reynolds number and long wavelength approximations. Poisson Boltzmann equations are also solved under Debye Hückel linearization. Following non-dimensional transformation of the linearized boundary value problem, closed-form analytical solutions are presented for the velocity components, pressure gradient, average flow rate, and stream function subject to physically appropriate boundary conditions. Validation with existing results is also made. A comparative discussion between shear thinning fluid and shear thickening fluids under the influences of Debye length and Helmholtz–Smoluchowski velocity are presented numerically. Trapping phenomenon for dilatant fluids and pseudoplastic fluids under the electrokinetic phenomenon is also computed. This model can help toward designing artificial biomedical devices based on microfluidic devices which can also be applicable to control the physiological transport.

1 Introduction

In colloid science, the electrically driven flow and particle motion in aqueous solution have been studied in last few decades. The movement of one phase relative to another phase under the effect of applied external electric field or a due to negative potential gradient is termed as electrokinetic phenomenon. Electrophoresis and electroosmotic are first type of electrokinetic phenomenon; however, sedimentation and streaming potential are second type of electrokinetic phenomenon. Recently, electrokinetic phenomenon has been receiving wide applications in microfluidics, and it has also application in lab-on-a-chip systems (low hydrodynamic dispersion, no moving parts, electrical actuation and sensing, and easy integration with microelectronics), biology (vesicle motion, membrane fluctuations, electroporation) and electrochemistry (porous electrode charging, desalination dynamics, dendritic growth). Considering the importance of electrokinetic phenomenon, Levine et al. [1] studied the electrokinetic flow at high zeta potential through capillaries. Mala et al. [2] discussed the electrokinetic effects during the water flow through parallel microchannels. Patankar and Hu [3] simulated numerically the electroosmotic flow. Hu et al. [4] presented a numerical model to compute the flow characteristics in capillary electrophoresis. Keh and Tseng [5] reported time-dependent electrokinetic flow through capillary. Hsu et al. [6] investigated the electrokinetic flow through elliptical microchannel. Ghosal [7] examined the electrokinetic flow and dispersion in capillary electrophoresis. Berli and Olivares [8] extended for non-Newtonian fluids. Xuan [9] discussed the joule heating effects on electrokinetic flow. Berry et al. [10] explored a multiphase flow model to discuss electrokinetic phenomenon. Li et al. [11] employed a Lattice Boltzmann method for electroosmotic-driven flow in nanoporous media. Biscombe et al. [12] presented circuit modeling for microfluidics and membranes. In continuation of these models, some authors [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] recently extended for different applications of the electrokinetically driven steady and unsteady flow of Newtonian and non-Newtonian fluids through capillary and microchannels: DNA motion [13]; thermally developing pressure-driven flow [14]; effects of ionic concentration gradient [15]; micropolar fluid flow [16]; magnetohydrodynamic of Maxwell fluids [17]; electromagnetohydrodynamic (EMHD) micropump of Jeffrey fluids [18]; micro- and nanochannel deformation [19]; thermal transport characteristics [20]; thermo-fluidic transport [21]; time periodic electroosmotic flow of micropolar fluids [22]; microtube with sinusoidal roughness [23]; effect of heat transfer on rotating channel flow [24]; two-layered flow [25]; MHD flow and heat transfer [26]; two-phase blood flow and thermal transport [27].

In above investigations, the power law fluid model has not been considered; however, the power law fluid is a non-Newtonian model of fluids which covers the wide range of shear properties of fluids (from shear thinning to shear thickening). Inspired by the wide applications of non-Newtonian fluids, Chen [28] studied the thermal transport power law fluid flow driven by electroosmotic and pressure. Zhao and Yang [29] analyzed the Joule heating effects of electroosmotic flow of power law fluid through capillary. Xie and Jian [30] investigated the rotating electroosmotic flow of power law fluid at high zeta potential. Ng and Qi [31] extended for non-uniform microchannel. Goswami et al. [32] discussed the entropy generation minimization in electroosmotic flow of power law fluids. Qi and Ng [33] further generalized their work for an asymmetrical slit microchannel with gradually varying wall shape and wall potential. Srinivas [34] also explored the electroosmotic flow of power law fluid for elliptic microchannel. Shit et al. [35] discussed the joule heating effects and thermal radiation on electroosmotic flow of power law fluid.

In continuation of investigations in electroosmotic flow, some authors [36,37,38,39,40,41] reported the electrokinetically modulated peristaltic transport to cover the biomedical engineering applications of electrokinetic phenomenon. Peristalsis is physiological word that means the physiological fluids are being transported by continuous wave propagations generated by rhythmic contraction and relaxation of muscular walls. Nowadays, the concept of peristalsis is also being used mechanically to transport the industrial fluids using peristaltic pumps. Shit et al. [36] studied the electromagnetohydrodynamics of couple stress fluids in the presence of peristalsis and observed that formation of the trapping bolus strongly depends on electroosmotic parameter and magnetic field strength. Bandopadhyay et al. [37] presented a theoretical model on electroosmosis-modulated peristaltic transport and discussed the future scope of this model in biomedical engineering where natural mechanisms and processes have been central in driving the study of peristalsis-on-chip devices which aim to mimic the same functionality, for example: a kidney filtration process or digestive system, on a miniature device. Tripathi et al. [38] extended these models for viscoelastic fluids through capillary and found that the viscoelastic nature of fluids alters the electrokinetic phenomenon. Tripathi et al. [38] further discussed the effects of transverse magnetic field on electroosmotically induced peristaltic transport. In view of above studies on electroosmosis-modulated peristaltic transport, none of the studies reported for power law fluids; however, the applications power law fluid is broad in electrodynamics. Filling this gap of the literature, Goswami et al. [40] investigated the electrokinetically modulated peristaltic transport of power law fluids in two-layered (core layer and peripheral) flow model. They have analyzed their model under the restriction of lubrication theory and thin electric double-layer (EDL) approximation where the diameter of flow regime is considered much larger than the EDL thickness. However, the electrokinetic phenomenon is not much effective in the case of thin EDL approximation. Improving electrokinetically modulated peristaltic flow model for power law fluid, we analyze the effect of EDL thickness on electroosmosis-modulated peristaltic transport in present model.

2 Mathematical formulation and analytical solution

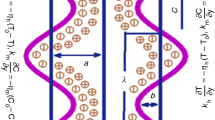
We consider the electrokinetically augmented peristaltic flow of power law fluid in a microchannel under no-slip boundary condition. Let the motion of the walls of the channel be governed by sinusoidal wave which is mathematically modeled as:

$$h = a + b\sin \frac{2\pi }{\lambda }(x - ct),$$

(1)

where $h,a,\,b,\,\lambda ,x,t,c$ are transverse vibration of the wall, half width of the channel, amplitude, wavelength axial displacement, time and wave velocity, respectively (Fig. 1).

Fig. 1

Schematic representation of peristaltic flow of aqueous solution

It is observed that the peristaltic transport problem can be solved using wave frame (steady flow) for simplicity [41] if the microchannel length is finite but equal to an integral number of wavelengths, and if the pressure difference between the ends of the tube is constant.

$$x = X - ct,y = Y,\quad u(x,y) = U(X - ct,Y) - c,\,\,v(x,y) = V(X - ct,Y)$$

(2)

where $\left( {x,y,u,v} \right)$ and $\left( {X,Y,U,V} \right)$ are coordinates and velocity components in wave and laboratory frames, respectively. With the above assumptions, the governing equations for steady, two-dimensional, incompressible flow with an applied electrokinetic body force in the axial (longitudinal) direction through the microchannel can be shown to take the form:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(3)

$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \frac{\partial p}{\partial x} + \frac{{\partial \tau_{xx} }}{\partial x} + \frac{{\partial \tau_{yx} }}{\partial y} + \rho_{e} E_{x} ,$$

(4)

$$\rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) = - \frac{\partial p}{\partial y} + \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \tau_{yy} }}{\partial y},$$

(5)

where $\tau_{xx}$, $\tau_{xy}$, $\tau_{yy}$ are the shear stress components, $\rho ,u,v,y,p$ and $\,E_{x}$ are the fluid density, axial velocity, transverse velocity, transverse coordinate, pressure, and electrokinetic body force. The positive ions $n_{ + }$ and negative ions $n_{ - }$ are both assumed to have bulk concentration (number density) $n_{0}$ and a valency of $z_{ + }$ and $z_{ - }$, respectively. For simplicity, we consider the electrolyte to be a $z:z$ symmetric electrolyte. The charge number density is related to the electrical potential $\left(\Phi \right)$ in the transverse direction via the Poisson equation:

$$\nabla^{2}\Phi = - \frac{{\rho_{e} }}{\varepsilon },$$

(6)

where $\varepsilon$ is the permittivity and $\rho_{e} = ez(n_{ + } - n_{ - } )$ is the electrical charge density, $e$ represents elementary charge. Further, in order to determine the potential distribution, charge number density must also be described. For this, the ionic number distributions of the individual species are given by the Nernst–Planck equation for each species as:

$$u\frac{{\partial n_{ \pm } }}{\partial x} + v\frac{{\partial n_{ \pm } }}{\partial y} = D\left( {\frac{{\partial^{2} n_{ \pm } }}{{\partial x^{2} }} + \frac{{\partial^{2} n_{ \pm } }}{{\partial y^{2} }}} \right) \pm \frac{Dze}{{k_{\text{B}} T}}\left( {\frac{\partial }{\partial x}\left( {n_{ \pm } \frac{\partial \varPhi }{\partial x}} \right) + \frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial \varPhi }{\partial y}} \right)} \right),$$

(7)

where $D$ represents the diffusivity of the chemical species, $T$ is the averaged temperature of the electrolytic solution and $k_{\text{B}}$ Boltzmann constant.

The constitutive relation for the power law fluid given by Ostwald–de Waele is as:

$$\tau = \mu \left\{ {\left| {\frac{1}{2}\left( {W:W} \right)} \right|^{{\left( {n - 1} \right)/2}} } \right\}W$$

(8)

where $\tau$ is the stress tensor, $W$ is the symmetric velocity gradient, $\mu$ is the flow consistency index, $n$ is the fluid behavior index and

$$\frac{1}{2}\left( {W:W} \right) = 2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}} \right)^{2} = \varPi ,$$

(9)

$$\tau_{xx} = 2\mu \left| \varPi \right|^{(n - 1)/2} \frac{\partial u}{\partial x},\tau_{yy} = 2\mu \left| \varPi \right|^{(n - 1)/2} \frac{\partial v}{\partial y},\tau_{xy} = \mu \left| \varPi \right|^{(n - 1)/2} \left( {\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}} \right)$$

(10)

Introducing the following dimensionless parameters:

$$x^{\prime } = \frac{x}{\lambda },y^{\prime } = \frac{y}{a},u^{\prime } = \frac{u}{c},v^{\prime } = \frac{v}{c\delta },\delta = \frac{a}{\lambda },h^{\prime } = \frac{h}{a},\varphi = \frac{b}{a},p^{\prime } = \frac{{pa^{n + 1} }}{{\mu c^{n} \lambda }},\Phi ^{\prime } = \frac{\Phi }{\zeta }$$

(11)

where $c,\,\delta ,\,\,\varphi ,\,\,\mu ,\,\,\zeta$ are the wave velocity, wave number, amplitude ratio, flow consistency index, zeta potential, respectively, and n is the fluid behavior index (i.e., $n < 1$ is pseudoplastic and $n > 1$ is the dilatant fluid and $n = 1$ is the Newtonian fluid). The nonlinear terms in the Nernst–Planck equations are $O\left( {Pe\,\delta^{2} } \right)$, where $Pe = Re\,Sc$ represents the ionic Peclet number and $Sc = {\mu \mathord{\left/ {\vphantom {\mu {\rho D}}} \right. \kern-0pt} {\rho D}}$ denotes the Schmidt number. Therefore, the nonlinear terms may be dropped in the limit that Re, Pe, δ ≪ 1. We also drop the prime of the non-dimensional variables for convenience. After above assumptions, Poisson equation is reduced to:

$$\frac{{\partial^{2}\Phi }}{{\partial y^{2} }} = - m^{2} \left( {\frac{{n_{ + } - n_{ - } }}{2}} \right),$$

(12)

where $m = aez\sqrt {\frac{{2n_{0} }}{{\varepsilon \,K_{\text{B}} T}}} = \frac{a}{{\lambda_{\text{d}} }}$, is known as the electroosmotic parameter and $\lambda_{\text{d}} \propto \frac{1}{m}$ is Debye length or characteristic thickness of electrical double layer (EDL).

The ionic distribution may be determined by means of the simplified Nernst–Planck equations:

$$0 = \frac{{\partial^{2} n_{ \pm } }}{{\partial y^{2} }} \pm \frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial \varPhi }{\partial y}} \right),$$

(13)

subjected to $n_{ \pm } = 1$ at $\varPhi = 0$ and ${{\partial n_{ \pm } } \mathord{\left/ {\vphantom {{\partial n_{ \pm } } {\partial y}}} \right. \kern-0pt} {\partial y}} = 0$ where ${{\partial \varPhi } \mathord{\left/ {\vphantom {{\partial \varPhi } {\partial y}}} \right. \kern-0pt} {\partial y}} = 0$ (bulk conditions). These yield the much celebrated Boltzmann distribution for the ions:

$$n_{ \pm } = e^{ \mp \varPhi } .$$

(14)

Combining Eqs. (12) and (13), we obtain the Poisson–Boltzmann paradigm for the potential determining the potential distribution:

$$\frac{{\partial^{2}\Phi }}{{\partial y^{2} }} = m^{2} \sinh \left(\Phi \right).$$

(15)

In order to make further analytical progress, we must simplify Eq. (15). Equation (15) is linearized under the low-zeta potential approximation. This assumption is not ad hoc since for a wide range of pH, the magnitude of zeta potential is less than 25 mV. Therefore, Eq. (15) reduces to:

$$\frac{{\partial^{2}\Phi }}{{\partial y^{2} }} = m^{2}\Phi ,$$

(16)

which may be solved subjected to $\left. {\frac{{\partial\Phi }}{\partial y}} \right|_{y = 0} = 0$ and $\left.\Phi \right|_{y = h} = 1$, the potential function is obtained as:

$$\Phi = \frac{\cosh (my)}{\cosh (mh)},$$

(17)

Under the assumptions of long wave length and low Reynolds number, the governing conservation Eqs. (3)–(5) reduce to:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(18)

$$\frac{\partial p}{\partial x} = \left( {{\text{sign}}\frac{\partial u}{\partial y}} \right)\frac{\partial }{\partial y}\left( {\left| {\frac{\partial u}{\partial y}} \right|^{n} } \right) + m^{2}\Phi U_{\text{HS}} ,$$

(19)

$$\frac{\partial p}{\partial y} = 0,$$

(20)

where $U_{\text{HS}} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}$ is the Helmholtz–Smoluchowski velocity or maximum electroosmotic velocity. Imposing the boundary conditions: $\left. {\frac{\partial u}{\partial y}} \right|_{y = 0} = 0,\,$ and $\left. u \right|_{y = \pm h} = - 1$ and solving Eq. (18), the axial velocity is obtained as:

$$u = \int\limits_{0}^{h} {\left\{ { - y\frac{{{\text{d}}p}}{{{\text{d}}x}} + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y - \int\limits_{0}^{y} {\left\{ { - y\frac{{{\text{d}}p}}{{{\text{d}}x}} + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y - 1.$$

(21)

The volumetric flow rate through each section [41] in the wave frame is, a constant, independent of $t$, given by

$$q = \int\limits_{0}^{h} {u(x,y)} {\text{d}}y,$$

(22)

The instantaneous volume flow rate in laboratory frame is defined as:

$$Q(X,t) = \int\limits_{0}^{h} {U(X,Y,t)} {\text{d}}Y,$$

(23)

From Eq. (2) $U = u + 1$(dimensionless) and Eq. (3), instantaneous volume flow rate can be expressed as:

$$Q = q + h.$$

(24)

Averaging volumetric flow rate along one time period, we get:

$$\bar{Q} = \int\limits_{0}^{1} {Q{\text{d}}t} = \int\limits_{0}^{1} {(q + h){\text{d}}t} ,$$

(25)

which, on integration, yields

$$\bar{Q} = q + 1 = Q + 1 - h.$$

(26)

In this model, pressure gradient is induced by the peristaltic pumping which generates the peristaltic flow from high pressure (contraction of the muscle) to low pressure (relaxation of the muscles). We know that pressure gradient is a gradual change in pressure from one point to another point. In this model, we have considered the pressure gradient as change in pressure from inlet (x = 0) to outlet (x = 1). In most of the peristaltic models [37,38,39,40,41], pressure rise per wavelength due to peristaltic pumping is defined as:

$$\Delta p = \int\limits_{0}^{1} {\frac{{{\text{d}}p}}{{{\text{d}}x}}} {\text{d}}x = p\left( 1 \right) - p\left( 0 \right).$$

(27)

It is not possible to get explicit expression for induced pressure gradient for the present nonlinear problem. We have approximated the pressure rise across the one wavelength of microchannel which is defined as:

$$\frac{{{\text{d}}p}}{{{\text{d}}x}} \approx \frac{\Delta p}{\Delta x} = \frac{p\left( 1 \right) - p\left( 0 \right)}{1} = \Delta p.$$

(28)

The volume flow rate in wave frame is obtained as:

$$q = \overline{Q} - 1 = \int\limits_{0}^{h} {\int\limits_{0}^{h} {\left\{ { - y\,\Delta p + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y{\text{d}}y} - \int\limits_{0}^{h} {\int\limits_{0}^{y} {\left\{ { - y\,\Delta p + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y} {\text{d}}y - h.$$

(29)

Using Eq. (17), the stream function in the wave frame (obeying the Cauchy–Riemann equations, $u = \frac{\partial \psi }{\partial y}$ and $v = - \frac{\partial \psi }{\partial x}$) takes the form:

$$\psi = \int\limits_{0}^{y} {\int\limits_{0}^{h} {\left\{ { - y\,\Delta p + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y{\text{d}}y} - \int\limits_{0}^{y} {\int\limits_{0}^{y} {\left\{ { - y\,\Delta p + \frac{m\,\sinh (my)}{\cosh (mh)}U_{\text{HS}} } \right\}}^{{\frac{1}{n}}} {\text{d}}y} {\text{d}}y - y.$$

(30)

The all above-obtained results reduce for particular case at $n = 1$, i.e., electroosmotic-induced peristaltic microflows of Newtonian fluid. The whole analysis is also for peristaltic flow of Power law fluid for $U_{\text{HS}} = 0$. All double integrations are numerically solved by using Simpson 1/3rd rule.

3 Validation with existing results

The validation of present model with existing model [37] is computed graphically using Figs. 2 and 3. Figure 2 illustrates that velocity profile at $\varphi = 0.5,\,\Delta p = - \;2,$ $x = 0.5,U_{\text{HS}} = 1,m = 2$ for different value of flow behavior index ($n > 1$, i.e., Dilatant fluids, $n = 1$, i.e., Newtonian fluids [37], and $n < 1$, i.e., pseudoplastic fluids). It is found that the nature of non-Newtonian fluids on velocity profile is similar to Newtonian fluid model presented in Ref [37]. Figure 3 shows that the variation of averaged flow rate against the pressure gradient at $\phi = 0.6,x = 1,U_{\text{HS}} = 1,m = 2$ for different value of flow behavior index. It is observed that the relation is linear for $n = 1$ [37]; however, it moves toward curvilinear for $n < 1$ and $n > 1$.

Fig. 2

Velocity profiles at $\varphi = 0.5,\Delta p = - \;2,x = 0.5,U_{\text{HS}} = 1,m = 2$ for different value of fluid index

Fig. 3

Flow rate versus pressure gradient at $\phi = 0.6,x = 1,U_{\text{HS}} = 1,m = 2$ for different value of fluid index

4 Computational illustrations and discussion

In this section, the effects of electric double-layer thickness (Debye length i.e. $\lambda_{\text{d}} = \frac{1}{m} = ez\sqrt {\frac{{2n_{0} }}{{\varepsilon \,K_{\text{B}} T}}}$) and Helmholtz–Smoluchowski velocity ($U_{\text{HS}} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}$) on velocity profile, flow rate and stream lines are illustrated in Figs. 4, 5, and 6. Two cases on the basis of the flow behavior index ($n > 1$ and $n < 1$) are also computed to see the electrokinetic phenomenon for Dilatant fluids and Pseudoplastic fluids.

Fig. 4

Velocity profiles at $\varphi = 0.5,\Delta p = - \;2,x = 0.5$ for a $n < 1,\,U_{\text{HS}} = 1$ and various values of parameter $m = 1,2,3$. b $n < 1,\,m = 1$ and various values of parameter $U_{\text{HS}} = 0,1,2$. c $n > 1,\,U_{\text{HS}} = 1$ and various values of parameter $m = 1,2,3$. d $n > 1,\,m = 1$ and various values of parameter $U_{\text{HS}} = 0,1,2$

Fig. 5

Flow rate versus pressure gradient at $\varphi = 0.6,x = 1$ for a $n < 1,U_{\text{HS}} = 1$ and various values of parameter $m = 1,\,2,\,3$. b $n < 1,\,m = 1$ and various values of parameter $U_{\text{HS}} = 0,1,2$. c $n > 1,\,U_{\text{HS}} = 1$ and various values of parameter $m = 1,2,3$. d $n > 1,\,m = 1$ and various values of parameter $U_{\text{HS}} = 0,1,2$

Fig. 6

Streamlines in wave frame at $\varphi = 0.6,\,\Delta p = - 1$ for a $n < 1\,( = 0.8),m = 1,U_{\text{HS}} = 0$, b $n < 1\,( = 0.8),m = 1,U_{\text{HS}} = 1$, c $n < 1\,( = 0.8),m = 2,U_{\text{HS}} = 1$, d $n > 1\,( = 1.2),m = 1,U_{\text{HS}} = 0$, e $n > 1\,( = 1.2),m = 1,U_{\text{HS}} = 1$, f $n > 1( = 1.2),m = 2,U_{\text{HS}} = 1$

Figure 4a, b shows the velocity profile for pseudoplastic fluids ($n < 1$), and Fig. 4c, d illustrates velocity profile for Dilatant fluids at $\varphi = 0.5,\,\Delta p = - 2,\,x = 0.5$. It is pointed out that the velocity profile is parabolic and when we increase the electrokinetic effects, the parabolic nature takes the form as trapezoidal shape. In Fig. 4a, the effect of Debye length ($m = 1,2,3$) on velocity profile at $U_{\text{HS}} = 1$ is presented. It is revealed that velocity profile expands with reducing the thickness of electric double layer (increasing the value of m from 1 to 3). In Fig. 4b, the effect of Helmholtz–Smoluchowski velocity ($U_{\text{HS}} = 0,1,2$) on velocity profile is computed at $m = 1$. It is noticed that velocity profile enlarges with increasing the magnitude of Helmholtz–Smoluchowski velocity. It is also noticed that the velocity profile for $U_{\text{HS}} = 0$ is the special case of this model which studies the peristaltic flow power law fluid without electrokinetic effects. The effects of Debye length and Helmholtz–Smoluchowski velocity on velocity profile for Dilatant fluids are shown in Fig. 4c, d. It is inferred that the effects of both parameters for Dilatant fluids are similar to that of the Pseudoplastic fluids.

In many previous studies [37,38,39,40,41], pumping characteristics are discussed using pressure rise and averaged volumetric flow relation. In present model, we also analyzed the variations of averaged flow rate with changes in pressure gradient (pressure difference between inlet and outlet). Figure 5a–d shows the variation of averaged flow rate against the pressure rise at $\varphi = 0.6,x = 1$. It is revealed that the maximum flow rate occurs at zero pressure increase and vice versa. In Fig. 5a, the effect of Debye length $\left( {m = 1,2,3} \right)$ on averaged flow rate at $U_{\text{HS}} = 1$ for pseudoplastic fluids ($n < 1$). It is noted that averaged flow rate diminishes with increasing the thickness of electric double layer. In Fig. 5b, the effect of Helmholtz–Smoluchowski velocity $\left( {U_{\text{HS}} = 0,1,2} \right)$ on averaged flow rate is illustrated at $m = 1$. It is observed that averaged flow rate enhances with increasing the effects of applied external electric filed (i.e., magnitude of Helmholtz–Smoluchowski velocity). The graph for $U_{\text{HS}} = 0$ is a particular case of this model which studies the peristaltic flow of Newtonian fluids without electrokinetic phenomenon. The effects of Debye length and Helmholtz–Smoluchowski velocity on averaged flow rate for dilatant fluids ($n > 1$) are depicted in Fig. 5c, d. The effects are found similar as case pseudoplastic fluids ($n < 1$).

Trapping is an inherent phenomenon of peristaltic transport where the center stream lines starts to trap in circular form at a combination of magnitudes of averaged flow rate and amplitude of peristaltic wave. To discuss the effects of Debye length and Helmholtz–Smoluchowski velocity on trapping phenomenon for Pseudoplastic fluids ($n < 1$) as well as Dilatant fluids ($n > 1$) are shown in Fig. 6a–f. Figure 6a–c is plotted for pseudoplastic fluids ($n < 1$) at $\varphi = 0.6,\,\Delta p = - 1$. It is observed that there is no trapped bolus for $U_{\text{HS}} = 0$; however, with increasing the effect of electric field (the value of $U_{\text{HS}}$ from 0 to 1), center stream lines start to trap. It is also inferred that with reducing the thickness of electric double layer, i.e., Debye length, the size of trapped boluses increases. Figure 6e, f shows the trapping phenomenon for Dilatant fluids ($n > 1$). It is again reported that there is no trapping at $U_{\text{HS}} = 0$ (without electrokinetic phenomenon). It is further revealed that number of trapped boluses enhances with increasing the Helmholtz–Smoluchowski velocity; however, it reduces with increase in the Debye length.

5 Conclusions

The influences of electric double-layer phenomenon and applied external electric field on peristaltic transport of power law fluid are discussed. This model is very much applicable in electro-biofluid-dynamic and biomedical engineering where biomedical electronic devices like peristalsis lab-on-chip and microperistaltic pumps may be engineered. This model revealed that the applied electric field play important role in peristaltic transport process (i.e., physiological transport phenomenon). It is also concluded that physiological flows may be controlled with ionic properties of physiological fluids and negative charge or positive charge of surface walls (physiological vessel) which causes the electric double-layer formation. It is further reported that the Helmholtz–Smoluchowski velocity and Debye length alter the trapping phenomenon. The outcomes of present model can be applicable in fabricating the microperistaltic pumps which can be useful to control the physiological flows.