1 Introduction

Peristaltic pumping is form of a fluid propagation that arises due to regular contraction and expansion of smooth walls along a length of the distensible channel/duct. It is well-known to physiologists as one of the most important phenomena for the propagation of fluid in different biological system such as spermatozoa transport, cilia motion, embryonic lung morphogenesis, bat wing vasomotion, intestinal pumping, medical endoscope design and phloem translocation in botany etc. Furthermore, peristaltic pumping finds its place in different practical applications including biomechanical systems i.e. finger and roller pumps. During recent years, many authors analyzed the peristaltic flow by means of experimental and theoretical techniques with different physiological fluid models, wall properties, and boundary conditions. Initially, Latham [1] introduced the peristaltic pumping phenomena with the help of viscous and incompressible fluid model. Haroun [2] analyzed the nonlinear peristaltic phenomena by means of a fourth-grade fluid model through an asymmetric inclined channel. He observed that the pressure rise is maximum when the fluid behaves as a non-Newtonian as compared to Newtonian fluid. Kothandapani and Srinivas [3] addressed the peristaltic motion using Jeffrey fluid model in the presence of magnetic field through an asymmetric channel. They found the exact solutions with the help of stream functions by means of the integral method. The peristaltic flow of Williamson fluid towards an asymmetric channel was examined by Nadeem and Akram [4]. They used the regular perturbation expansion method to obtain the solution of nonlinear governing equations. Moreover, they observed that pressure rise is not linear due to a higher impact of Weissenberg number; however, pressure rise is linear as Weissenberg number tends to zero. Munir et al. [5] investigated the peristaltic motion in the presence of Joule heating and convective boundary conditions towards an asymmetric channel. Tripathi and Bég [6] studied the peristaltic flow using nanofluids and presented an application for drug delivery system. They considered a Newtonian fluid model and presented the exact solutions for velocity, temperature and concentration profile. Tripathi et al. [7] considered the peristaltic motion of Oldroyd-B viscoelastic rheological model through an asymmetric porous medium and presented digestive transport model. He used the Differential transform method (DTM) to simulate the governing flow problem. Sinha et al. [8] analyzed the peristaltic magnetized flow with heat transfer by considering the variable viscosity, temperature jump, and velocity slip. Ellahi and Hussain [9] discussed the three-dimensional peristaltic motion of Jeffrey fluid model in the presence of slip condition and presented the exact solutions. Some more interesting studies are available in the references [10,11,12,13].

Nowadays, Electrokinetic is considered to be a major part of modern fluid dynamics. It occurs in different applications of medical science, such as microfluidics, blood flow (“Hemodynamics”), plasma separation, colloidal suspension manipulation, and fabrication. Electrokinetic deals with an interaction among heterogeneous fluids connecting to charged particles and static/alternating electric fields. This process is important in the transportation of ionic solutions in a neighborhood of electrically charged interface. Multiple numbers of phenomena occur in electrokinetics such as zeta potential, diffusiophoresis, capillary osmosis, electro-osmosis, dielectrics, streaming current/potential sedimentation potential etc. The concept of Nano-scaled- and micro-scaled devices in bioengineering played a significant role in electrokinetics. Nowadays, computational and mathematical models are an essential tool for experimental studies. Furthermore, they allow optimizing the new designs which are difficult for sustained performance in different areas of medicine, aerospace and nuclear engineering etc. Paul et al. [14] studied the applications of an electrokinetic pump in micro-total analysis systems. He considered the flow through a porous media and presented the experimental and model results for frequency response due to the electrokinetic pump. Kang et al. [15] analyzed the fabrication of electro-kinetic micro-pumps. El-Sayed et al. [16] determined the EHD effects on the peristaltic propulsion of dielectric Oldroyd viscoelastic fluid model propagating through a flexible channel. Sinha and Shit [17] considered the EMHD effects with radiative heat transfer on blood flow (“Hemodynamics”) through capillary. EMHD and heat transfer effects on the non-Newtonian third-grade fluid model through two micro-parallel plates were analyzed by Wang et al. [18]. Recently, Tripathi et al. [19] discussed the transverse magnetic field effect induced by a peristaltic wave in the presence EDL (“electrical double layer”) effects. Few more interesting studies on the current topic are available in Refs [20,21,22,23,24].

According to the above discussion and applications, the main focus of the present study is to examine the electrokinetic transport through an asymmetric channel induced by a peristaltic wave. A long wavelength of a peristaltic wave has been considered whereas as the inertial forces have been neglected. Exact solution for velocity profile is presented whereas numerical integration has been used to evaluate the pressure rise. The physical behavior of all the emerging parameters is discussed for velocity profile, pressure rise, trapping and volume flow rate. The present study is also associated with the imitation of real fluids in electromagnetic biomimetic microscale pumps by means of peristalsis [25]. Such type of pumps is beneficial to achieve better efficiency and longevity, reduce the maintenance and avoid the contamination problems. These pumps have extremely large potential in bio-inspired intravenous drip systems for a medical treatment.

2 Mathematical model

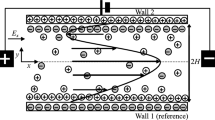
We consider the motion of an incompressible viscous fluid between two parallel microplates (see Fig. 1) induced by peristaltic wave trains propagating with travelling with velocity \(c\) along the walls to have different amplitudes \(\left( {a_{1} ,\,a_{2} } \right)\) and phase \(\left( \varphi \right)\):

$$\bar{h}_{2} = b_{1} + a_{1} \cos \left( {\frac{2\pi }{\lambda }\left( {\bar{x} - c\bar{t}} \right)} \right),\quad {\text{upper wall}}$$
(1a)
$$\bar{h}_{1} = - b_{2} - a_{2} \cos \left( {\frac{2\pi }{\lambda }\left( {\bar{x} - c\bar{t}} \right) + \varphi } \right),\quad {\text{lower wall}}$$
(1b)

where \(b_{1} + b_{2}\), \(\lambda\), \(x\), \(\bar{t}\) are the channel width, wavelength, axial coordinate, and time respectively. The phase difference \(\varphi\) varies in the range \(0 \le \varphi \le \pi\). When \(\varphi = 0\), a symmetric channel with waves out of phase can be described while for \(\varphi = \pi\), the waves are in phase. Moreover, \(a_{1} ,\,\,a_{2}\), \(b_{1} ,b_{2}\) and \(\varphi\) satisfy the condition \(a_{1}^{2} + a_{2}^{2} + 2a_{1} a_{2} \cos \varphi \le b_{1}^{2} + b_{2}^{2}\).

Fig. 1
figure 1

Physical model for peristaltic pumping through asymmetric microchannel altered by applied external electric field

Full size image

The governing equations for unsteady, two-dimensional, viscous, incompressible flow with an axially-applied electrokinetic body force in the \(\left( {\bar{x},\bar{y}} \right)\) coordinate system, are given as:

$$\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\partial \bar{v}}}{{\partial \bar{y}}} = 0,$$
(2)
$$\rho \left( {\frac{\partial }{{\partial \bar{t}}} + \bar{u}\frac{\partial }{{\partial \bar{x}}} + \bar{v}\frac{\partial }{{\partial \bar{y}}}} \right)\bar{u} = - \frac{{\partial \bar{p}}}{{\partial \bar{x}}} + \mu \left( {\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{u}}}{{\partial \bar{y}^{2} }}} \right) + \bar{\rho }_{e} \,E_{x} ,$$
(3)
$$\rho \left( {\frac{\partial }{{\partial \bar{t}}} + \bar{u}\frac{\partial }{{\partial \bar{x}}} + \bar{v}\frac{\partial }{{\partial \bar{y}}}} \right)\bar{v} = - \frac{{\partial \bar{p}}}{{\partial \bar{y}}} + \mu \left( {\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{v}}}{{\partial \bar{y}^{2} }}} \right),$$
(4)

in which \(\rho ,\bar{u},\bar{v},\bar{p},\mu ,\) and \(E_{x}\) denote the fluid density, axial velocity, transverse velocity, pressure, fluid viscosity, and electrokinetic body force. The Poisson–Boltzmann equation for electric potential distribution is employed due to the presence of EDL in the micro-channel and is defined by:

$$\nabla^{2} \bar{\varPhi } = - \frac{{\bar{\rho }_{e} }}{\varepsilon },$$
(5)

where \(\rho_{e}\) is the density of the total ionic change and \(\varepsilon\) is the permittivity.

For a symmetric (z:z) electrolyte, the density of the total ionic energy, \(\rho_{e}\) is given as:

$$\rho_{e} = ez\left( {n^{ + } - n^{ - } } \right),$$
(6)

here \(n^{ + }\) and \(n^{ - }\) are the number of densities of cat-ions and anions respectively.

Boltzmann distribution (considering no EDL overlap) is defined as:

$$n^{ \pm } = n_{0} Exp\left[ { \mp \;\frac{{ez\bar{\varPhi }}}{{K_{B} T}}} \right],$$
(7)

where \(n_{0}\) represents the concentration of ions at the bulk, which is independent of surface electro-chemistry, \(e\) is the electronic charge, \(z\) is the charge balance, \(K_{B}\) is the Boltzmann constant, \(T\) is the average temperature of electrolytic solution.

Applying Debye–Hückel linearization approximation, Poisson–Boltzmann equation reduces to

$$\frac{{\partial^{2} \varPhi }}{{\partial y^{2} }} = - \kappa \,\varPhi ,$$
(8)

where \(\kappa = b_{1} ez\sqrt {\frac{{2n_{0} }}{{\varepsilon \,K_{B} T}}} = \frac{{b_{1} }}{{\lambda_{d} }}\), is known as the electro-osmotic parameter and \(\lambda_{d} \propto \frac{1}{\kappa }\) is Debye length or characteristic thickness of electrical double layer (EDL).

Integrating twice Eq. (8) and deploying the boundary conditions \(\left. \varPhi \right|_{{y = h_{1} }} = \zeta_{1}\) and \(\left. \varPhi \right|_{{y = h_{2} }} = \zeta_{2}\), the electrical potential function emerges in terms of transcendental hyperbolic functions:

$$\varPhi = C_{1} e^{\kappa y} + C_{2} e^{ - \kappa y} ,$$
(9)

where \(C_{1} = \frac{{e^{{h_{2} \kappa }} \zeta_{2} - e^{{h_{1} \kappa }} \zeta_{1} }}{{e^{{2h_{2} \kappa }} - e^{{2h_{1} \kappa }} }}\) and \(C_{2} = \frac{{e^{{h_{1} \kappa + h_{2} \kappa }} \left( {e^{{h_{1} \kappa }} \zeta_{2} - e^{{h_{2} \kappa }} \zeta_{1} } \right)}}{{e^{{2h_{1} \kappa }} - e^{{2h_{2} \kappa }} }}\).

By using the non-dimensional parameters in above governing equations: \(x = \frac{{\bar{x}}}{\lambda },y = \frac{{\bar{y}}}{{b_{1} }},t = \frac{{\bar{t}c}}{\lambda },\) \(u = \frac{{\bar{u}}}{c},v = \frac{{\bar{v}}}{kc},p = \frac{{\bar{p}b_{1}^{2} }}{\mu c\lambda },h_{1} = \frac{{\bar{h}_{1} }}{{b_{1} }},\bar{h}_{2} = \frac{{h_{2} }}{{b_{1} }},\) \(\phi_{1} = \frac{{a_{1} }}{{b_{1} }},\phi_{2} = \frac{{a_{2} }}{{b_{1} }},\) \(b = \frac{{b_{2} }}{{b_{1} }}\), where the nonlinear terms in the momentum equation are found to be \(O\left( {Re\,k^{2} } \right)\), \(Re = \frac{c\lambda }{{{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0pt} \rho }}}\) being the Reynolds number and \(k = \frac{{b_{1} }}{\lambda }\) denotes the ratio of the transverse length scale to the axial length scale, the governing equations reduce to

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(10)
$$\text{Re} k\left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)u = - \frac{\partial p}{\partial x} + \left( {k^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + \kappa^{2} u_{e} \varPhi ,$$
(11)
$$\text{Re} k^{3} \left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)v = - \frac{\partial p}{\partial y} + k^{2} \left( {k^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right),$$
(12)

where \(u_{e} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}\) is the Helmholtz–Smoluchowski velocity or characteristic electro-osmotic velocity. Applying long wavelength and low Reynolds number approximations (\(Re,k \ll 1\)), as is customary for peristaltic hydrodynamics, the Eqs. (10–12) reduce to the following linearized group of coupled partial differential equations:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(13)
$$\frac{\partial p}{\partial x} = \frac{{\partial^{2} u}}{{\partial y^{2} }} + \kappa^{2} u_{e} \varPhi ,$$
(14)
$$\frac{\partial p}{\partial y} = 0.$$
(15)

The associated normalized boundary conditions are:\(\left. u \right|_{{y = h_{1} }} = u_{e1} = - \frac{{E_{x} \varepsilon \zeta_{1} }}{\mu \,c}\), Helmholtz–Smoluchowski slip velocity at lower wall, \(\left. u \right|_{{y = h_{2} }} = u_{e2} = - \frac{{E_{x} \varepsilon \zeta_{2} }}{\mu \,c}\), Helmholtz–Smoluchowski slip velocity at upper wall.

Integrating Eq. (14) and imposing the above boundary conditions, the axial velocity yields:

$$u = - u_{e} (C_{1} e^{y\kappa } + C_{2} e^{ - y\kappa } ) + \frac{\partial p}{\partial x}\frac{{y^{2} }}{2} + C_{3} + C_{4} y,$$
(16)

where

$$C_{3} = \frac{1}{{h_{2} - h_{1} }}\left\{ {h_{1} \left( {\frac{{h_{2}^{2} }}{2}\frac{\partial p}{\partial x} - u_{e2} - C_{2} e^{{ - h_{2} \kappa }} u_{e} - C_{1} e^{{ - h_{2} \kappa }} u_{e} } \right) - h_{2} \left( {\frac{{h_{1}^{2} }}{2}\frac{\partial p}{\partial x} - u_{e1} - C_{2} e^{{ - h_{1} \kappa }} u_{e} - C_{1} e^{{h_{1} \kappa }} u_{e} } \right)} \right\},$$
$$\begin{aligned} C_{4} = & - \frac{{h_{1} }}{2}\frac{\partial p}{\partial x} + \frac{1}{{h_{1} }}\left( {u_{e1} + C_{2} e^{{ - h_{1} \kappa }} u_{e} + C_{1} e^{{h_{1} \kappa }} u_{e} } \right) + \frac{1}{{h_{1} \left( {h_{1} - h_{2} } \right)}}\left\{ {h_{2} \left( { - \frac{{h_{1}^{2} }}{2}\frac{\partial p}{\partial x} + u_{e1} + C_{2} e^{{ - h_{1} \kappa }} u_{e} + C_{1} e^{{h_{1} \kappa }} u_{e} } \right)} \right. \\ & \left. { + h_{1} \left( {\frac{{h_{2}^{2} }}{2}\frac{\partial p}{\partial x} - u_{e2} - C_{2} e^{{ - h_{2} \kappa }} u_{e} - C_{1} e^{{ - h_{2} \kappa }} u_{e} } \right)} \right\}. \\ \end{aligned}$$

The volumetric flow rate in laboratory frame of reference is defined as:

$$Q = \int\limits_{{h_{1} }}^{{h_{2} }} {u\,\,dy} ,$$
(17)

which, by virtue of Eq. (16), yields

$$\begin{aligned} Q = & C_{3} (h_{2} - h_{1} ) + \frac{{C_{4} }}{2}(h_{2}^{2} - h_{1}^{2} ) + \frac{1}{6}\frac{\partial p}{\partial x}\left( {h_{2}^{3} - h_{1}^{3} } \right). \\ & - \frac{{C_{2} \left( {e^{{ - h_{1} \kappa }} - e^{{ - h_{2} \kappa }} } \right)u_{e} }}{\kappa } + \frac{{C_{1} \left( {e^{{h_{1} \kappa }} - e^{{h_{2} \kappa }} } \right)u_{e} }}{\kappa } \\ \end{aligned}$$
(18)

The transformations between a wave frame \((x_{w} ,y_{w} )\) moving with velocity \(c\) and the fixed frame (\(x,y\)) are given by:

$$x = x_{w} - ct,\quad y = \,y_{w} ,\quad u = \,u_{w} + c,\quad v = \,v_{w} ,$$
(19)

where \((u_{w} ,\,v_{w} )\) and \((u,v)\) are the velocity components in the wave and fixed frame respectively.

The volumetric flow rate in the wave frame is given by

$$q_{w} = \int\limits_{{h_{1} }}^{{h_{2} }} {u_{w} d} y_{w} = \int\limits_{{h_{1} }}^{{h_{2} }} {(u - 1)dy_{w} } ,$$
(20)

which, on integration, yields:

$$q_{w} = Q + h_{1} - h_{2} .$$
(21)

Averaging volumetric flow rate along one time period, we get

$$\bar{Q} = \int\limits_{0}^{1} {Qdt} = \int\limits_{0}^{1} {(q_{w} + h_{2} - h_{1} )dt} ,$$
(22)

or

$$\bar{Q} = q_{w} + 1 + b = Q + 1 + b + h_{1} - h_{2} .$$
(23)

Rearranging the terms of Eq. (18) and using Eq. (23), the pressure gradient is obtained as:

$$\begin{aligned} \frac{\partial p}{\partial x} = & \frac{1}{{\left( {h_{1} - h_{2} } \right)^{3} \kappa }}6e^{{ - \left( {h_{1} + h_{2} } \right)\kappa }} \left( {C_{2} u_{e} } \right.\left( {e^{{h_{1} \kappa }} \left( { - 2} \right.} \right. + h_{1} \kappa - h_{2} \left. \kappa \right) + e^{{h_{2} \kappa }} \left( 2 \right. + h_{1} \kappa - h_{2} \left. {\left. \kappa \right)} \right) \\ & + e^{{\left( {h_{1} + h_{2} } \right)\kappa }} \left( {\left( {2(\bar{Q} - 1 - b + h_{2} - h_{1} ) + \left( {h_{1} - h_{2} } \right)\left( {u_{e1} - u_{e2} } \right)} \right)\kappa } \right. \\ & + C_{1} u_{e} \left( {e^{{h_{1} \kappa }} \left( { - 2} \right.} \right. + h_{1} \kappa - h_{2} \left. \kappa \right) + e^{{h_{2} \kappa }} \left( 2 \right. + h_{1} \kappa - h_{2} \left. {\left. {\left. {\left. \kappa \right)} \right)} \right)} \right). \\ \end{aligned}$$
(24)

The pressure difference across one wavelength \(\left( {\Delta p} \right)\) is defined as follows:

$$\Delta p = \int\limits_{0}^{1} {\frac{\partial p}{\partial x}dx} ,$$
(25)

Using Eq. (16), the stream function in the wave frame (obeying the Cauchy–Riemann equations, \(u_{w} = \frac{\partial \psi }{{\partial y_{w} }}\) and \(v_{w} = - \frac{\partial \psi }{{\partial x_{w} }}\)) takes the following form:

$$\begin{aligned} \psi = & \frac{1}{{\left( {h_{1} - h_{2} } \right)^{3} \kappa }}e^{{ - \left( {h_{1} + h_{2} + y} \right)\kappa }} \left( {e^{{\left( {h_{1} + h_{2} + y} \right)\kappa }} } \right.y\left( { - h_{2}^{3} u_{e1} + h_{1}^{3} u_{e2} + h_{2}^{2} \left( {2u_{e1} + u_{e2} } \right)y} \right. + 2Qy^{2} \\ & - h_{2} y\left( {3Q + \left( {u_{e1} + u_{e2} } \right)y} \right) + h_{1}^{2} \left( {h_{2} \left( {2u_{e1} + u_{e2} } \right) - \left( {u_{e1} + 2u_{e2} } \right)y} \right) \\ & + h_{1} \left( { - h_{2}^{2} \left( {u_{e1} + 2u_{e2} } \right) + h_{2} \left( {6Q + \left( { - u_{e1} + u_{e2} } \right)y} \right) + y\left( { - 3Q + \left( {u_{e1} + u_{e2} } \right)y} \right)} \right)\kappa \\ & + C_{2} u_{e} \left( {e^{{\left( {h_{1} + h_{2} } \right)\kappa }} \left( {h_{1} - h_{2} } \right)^{3} - } \right.e^{{\left( {h_{2} + y} \right)\kappa }} y\left( { - 2y^{2} + h_{2}^{3} \kappa - 2h_{2}^{2} y\kappa + h_{1}^{2} \left( { - 2h_{2} + y} \right)\kappa } \right) \\ & + h_{2} y\left( {3 + y\kappa } \right) + h_{1} \left( {h_{2}^{2} \kappa + y\left( {3 - y\kappa } \right) + h_{2} \left( { - 6 + \left. {y\kappa } \right)} \right)} \right) + \,e^{{\left( {h_{1} + y} \right)\kappa }} y\left( {h_{1}^{3} } \right.\kappa + h_{1}^{2} \left( {h_{2} - 2y} \right)\kappa \\ & + y\left( { - 2y + h_{2}^{2} \kappa + h_{2} \left( {3 - y\kappa } \right)} \right) + h_{1} \left( { - 2h_{2}^{2} \kappa + h_{2} \left( { - 6 + y\kappa } \right) + y\left( {3 + \left. {\left. {y\kappa } \right)} \right)} \right)} \right) \\ & + C_{1} u_{e} \left( { - e^{{\left( {h_{1} + h_{2} + 2y} \right)\kappa }} \left( {h_{1} - h_{2} } \right)^{3} + } \right.e^{{\left( {h_{1} + 2h_{2} + y} \right)\kappa }} y(h_{1}^{3} \kappa + h_{1}^{2} \left( {h_{2} - 2y} \right)\kappa \\ & + y\left( {2y + h_{2}^{2} \kappa - h_{2} \left( {3 + y\kappa } \right)} \right) + h_{1} \left( { - 2h_{2}^{2} \kappa + y\left( { - 3 + y\kappa } \right) + h_{2} \left( {6 + y\kappa } \right)} \right) + e^{{\left( {2h_{1} + h_{2} + y} \right)\kappa }} y \\ & \quad \left( { - 2y^{2} - h_{2}^{3} \kappa + h_{1}^{2} \left( {2h_{2} - y} \right)\kappa + 2h_{2}^{2} y\kappa + h_{2} y\left( {3 - y\kappa } \right)\left( { - h_{1} \left( {h_{2}^{2} \kappa - y\left( {3 + y\kappa } \right)} \right.\left. { + h_{2} \left( {6 + y\kappa } \right)} \right)} \right)} \right) \\ \end{aligned}$$
(26)

where \(h_{1} = 1 + \phi_{1} \cos 2\pi (x - t)\) for lower wall and \(h_{2} = - b - \phi_{2} \cos (2\pi (x - t) + \varphi )\) for upper wall.

3 Results and discussion

This section contributes to graphical results for all the governing parameters involved in the governing flow problem. A symbolic computational software “Mathematica” has been used to visualize the behavior of potential function \(\varPhi\), velocity profile \(u\), volume flow rate \(Q\), pressure rise \(\Delta p\) trapping phenomena. For this purpose, Figs. 2, 3, 4, 5 and 6 have been sketched to analyze the behavior of electro-osmotic parameter \(\kappa\), Phase difference \(\varphi\), and Helmholtz–Smoluchowski velocity \(u_{e}\).

Fig. 2
figure 2

Potential profile (potential field vs. transverse coordinate) at \(\phi_{1} = 0.5,\phi_{2} = 1.2,b = 1,\) \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) and (a) \(\varphi = \pi /2\), (b) \(\kappa = 1\)

Full size image
Fig. 3
figure 3

Velocity profile (axial velocity vs. transverse coordinate) at \(\phi_{1} = 0.5,\phi_{2} = 1.2,b = 1,\) \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) \(u_{e1} = 0.5,u_{e2} = 1,\) and (a) \(u_{e} = 1,\varphi = \pi /2\), (b) \(\kappa = 2,\varphi = \pi /2\), (c) \(u_{e} = 1,\kappa = 2\)

Full size image
Fig. 4
figure 4

Volumetric flow rate versus channel length at \(\phi_{1} = 0.5,\phi_{2} = 1.2,b = 1,\) \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) \(u_{e1} = 0.5,u_{e2} = 1,\) and (a) \(u_{e} = 1,\varphi = \pi /2\), (b) \(\kappa = 2,\varphi = \pi /2\), (c) \(u_{e} = 1,\kappa = 2\)

Full size image
Fig. 5
figure 5

Pressure difference across one wavelength versus time averaged volumetric flow rate at \(\phi_{1} = 0.3,\) \(\phi_{2} = 0.7,\) \(b = 1,\) \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) \(u_{e1} = 0.5,u_{e2} = 1,\) and (a) \(u_{e} = 1,\varphi = \pi /2\), (b) \(\kappa = 2,\varphi = \pi /2\), (c) \(u_{e} = - 1,\kappa = 5\)

Full size image
Fig. 6
figure 6figure 6

Stream lines in wave form at \(\phi_{1} = 0.7,\,\,\phi_{2} = 1.5,\) \(\bar{Q} = 1.5\), \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) \(u_{e} = - \;0.5,\) \(u_{e} = - 1\) for (a) \(b = 3,\varphi = \pi /2,\kappa = 1,u_{e} = 0\), (b) \(b = 3,\varphi = \pi /2,\kappa = 1,u_{e} = - 1\), (c) \(b = 3,\varphi = \pi /2,\kappa = 1,u_{e} = - 5\), (d) \(b = 3,\varphi = \pi /2,\kappa = 2,u_{e} = - 5\), (e) \(b = 3,\varphi = \pi /2,\kappa = 3,u_{e} = - 5\), (f) \(b = 3,\varphi = 0,\kappa = 1,u_{e} = - 5\), (g) \(b = 3,\varphi = \pi /4,\kappa = 1,u_{e} = - 5\), (h) \(b = 2,\varphi = \pi /2,\kappa = 1,u_{e} = - 5\)

Full size image

Figure 2(a, b) reveals the variation of potential function \(\varPhi\) against electro-osmotic parameter \(\kappa\) and phase difference \(\varphi\), respectively. In Fig. 2a one can see that electro-osmotic parameter \(\kappa\) does not cause any significant effect on potential function in the region \(y \in \left[ { - \;1,1} \right]\) and remains uniform in this region. The Electro-osmotic parameter \(\kappa = \frac{{b_{1} }}{{\lambda_{d} }}\) is itself directly proportional to Debye length \(\left( {\lambda_{d} } \right)\). On the other hand, potential function becomes significantly increased when \(y < - \;1\) or \(y > 1\) and due to the increment in electro-osmotic parameter \(\kappa\) a similar behavior has been observed. Figure 2b depicts the behavior of phase difference \(\varphi\) on potential function \(\varPhi\). Phase difference \(\varphi = 0\) represents a symmetric channel having waves out of phase and \(\varphi = \pi\) represents the waves are in phase whereas it varies in the range \(0 \le \varphi \le \pi .\) In Fig. 2b, it is found that the phase difference significantly enhances the potential function \(\varPhi\). An increment in phase difference produces a strong acceleration in the potential function. However, when \(y > 1\) then the phase difference does not cause any impact on potential function and the behavior remains same against the rest of all values of phase difference.

Figure 3(a–c) shows the velocity curves against all the pertinent parameters. Figure 3a depicts the variation of the electro-osmotic parameter \(\kappa\) on velocity profile. In this figure, we can notice that the electro-osmotic pressure tends to reduce the axial fluid velocity along the walls of the channel, however, there is no substantial impact in the middle of the channel and remains same in the interval \(y \in \left[ { - \;1,1.5} \right]\). Figure 3b presents the attitude of Helmholtz–Smoluchowski velocity \(u_{e} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}\)(or “characteristic electro-osmotic velocity”), since Helmholtz–Smoluchowski velocity is directly proportional to the electric field. This figure reveals that higher values of Helmholtz–Smoluchowski velocity tend to diminish the axial velocity greatly and axial velocity becomes negative. Moreover, we can see that when the values of Helmholtz–Smoluchowski velocity \(u_{e} \le 0\) then the axial velocity profile is symmetric and for \(u_{e} = 0\), then Eq. (14) reduces to the similar equation obtained by Latham [1]. It is depicted from Fig. 3c that phase difference \(\varphi\) produces a wavy impact on axial velocity and tends to enhance the axial velocity in the middle of the channel and reveals opposite impact near the walls of the channel.

Figure 4(a–c) demonstrates the behavior of volume flow rate \(Q\) along the axial coordinates for multiple values of the electro-osmotic parameter \(\kappa\), Phase difference \(\varphi\), and Helmholtz–Smoluchowski velocity \(u_{e}\). The irregularity in profiles is relevant due to a complex dual amplitude of peristaltic wave propagating through the asymmetric microchannel. In Fig. 4a we can see that there is a significant increment in volume flow rate for higher values of electro-osmotic parameter \(\kappa .\) There is a damping in an axial flow due to an increment in Debye length. The acceleration occurs due to electrokinetic body force in Eq. (14) i.e., \(\kappa u_{e} \varPhi\). From Fig. 4b one can notice that when Helmholtz–Smoluchowski velocity \(u_{e}\) becomes positive then the axial flow accelerates while the behavior is converse for negative values of Helmholtz–Smoluchowski velocity \(u_{e}\). However there is no electric field for \(u_{e} = 0.\) It is depicted from Fig. 4c that when the phase difference \(\varphi\) increases then the axial flow tilts backward, however, higher values of phase difference tend to diminish the volume flow rate when \(Q < 0.8\) nevertheless no change has been observed for higher values of volume flow rate.

Figure 5(a–c) portrays the variation of pressure rise \(\Delta p\) (“peristaltic pumping”) against averaged volume flow rate \(\overline{Q}\) for different values of the electro-osmotic parameter \(\kappa\), Phase difference \(\varphi\), and Helmholtz–Smoluchowski velocity \(u_{e}\). In Fig. 5a one can notice that there is consistently an increment in pressure rise with an increment (“decrement in Debye length”) in the electro-osmotic parameter \(\kappa\). From Fig. 5b, is seen that the higher values of Helmholtz–Smoluchowski velocity \(u_{e}\) markedly enhance the pressure rise. From Fig. 5c it is found that an increment in phase difference \(\varphi\) significantly tends to diminish the pressure rise. Moreover, in all these figures we notice that there is no crossover of profiles i.e., the impact of an electro-osmotic parameter \(\kappa\), phase difference \(\varphi\) and Helmholtz–Smoluchowski velocity \(u_{e}\) remains to sustain against all the values of pressure rise.

The next engrossing part of this section is trapping which can be visualized by drawing streamlines. It is the establishment of an internally moving bolus bounded by streamlines. For this purpose Fig. 6(a–h) have been sketched for multiple values of the electro-osmotic parameter \(\kappa\), phase difference \(\varphi\), and Helmholtz–Smoluchowski velocity \(u_{e}\). It is revealed from Fig. 6(a–c) that a negative increment in Helmholtz–Smoluchowski velocity \(u_{e}\) from − 1 to − 5, yields an accumulation in the formulation of a bolus in the lower and upper zone. However, in the absence of the electric field \(\left( {u_{e} = 0} \right)\) (see Fig. 6a), there are less boluses in the trapped zones. Figure 6(d, e) illustrates the variation of the electro-osmotic parameter \(\kappa\) with all the other parameters remains constant. We can see that the higher values of electro-osmotic parameter \(\kappa\) significantly enhance the trapping bolus in the upper and lower zone. Moreover, trapped boluses also increase in magnitude more in the horizontal direction as compared to the vertical direction. It is clear from Fig. 6(g, h) that when the phase difference \(\varphi\) increases up to \(\varphi = \frac{\pi }{4}\), then the number of trapped bolus remains same, however, the magnitude of the trapped bolus increases vertically. Moreover, when \(\varphi = \frac{\pi }{2}\)(see Fig. 6h) then the trapped bolus disappears in the lower zone and the trapped bolus remains same in the upper zone.

4 Conclusions

A theoretical and mathematical study on peristaltic pumping with electrokinetic effects through an asymmetric channel is presented. An irrotational, incompressible and viscous fluid is considered to model the continuity and momentum equations. Further, Debye linearization has also been used to model the governing equations. The exact solution for velocity function with electrokinetic effects has been derived by considering the long wavelength and the inertial forces have been ignored. However, numerical computations have been utilized to analyze the pressure rise. It is observed that with the increment in electro-osmotic parameter the potential function elevates whereas it opposes the velocity of the fluid. Phase difference reveals converse behavior on velocity profile whereas it significantly enhances the potential function. For positive values of Helmholtz–Smoluchowski velocity significantly reduces the velocity profile while for negative values, the velocity profile is symmetric. Higher values of the electro-osmotic parameter and Helmholtz–Smoluchowski velocity increase the volume flow rate evidently. Subsequent increment in electro-osmotic parameter and Helmholtz–Smoluchowski velocity leads to increase in pressure rise whereas the opposite behaviour in pressure rise has been observed for higher values of phase difference. Trapping boluses increase significantly for higher negative values of Helmholtz–Smoluchowski velocity and electro-osmotic parameter.

The present study reveals different engrossing behaviour that warrants further study on peristaltic flow with electro-kinetic effects. The present study has ignored non-Newtonian fluid models and it will be addressed in near future.