1 Introduction

Emulsions, i.e., metastable dispersions of two immiscible liquids, are used in a variety of industrial, engineering and biomedical applications (Leal-Calderon et al. 2007). Examples include end products in the cosmetic and food industries, dynamical templates for the production of colloidal suspensions, capsules or liposomes in material science and microreactors in high-throughput biomicrofluidic assays. All of these applications require to control the drop size distribution as the physical properties of these materials are highly size dependent. Hence, drop breakup is a central topic in emulsion science. For any drop breakup experiment, the key issues are to identify the experimental conditions for breaking a mother drop and to predict the size of the daughter droplets as a function of the parameters at play.

Since the pioneering studies of the deformation and rupture of an isolated drop in bulk by Taylor (1932, 1934), the topic has been widely studied for many flow configurations such as linear two-dimensional flows (Bentley and Leal 1986), simple shear flows (Janssen and Meijer 1993) and extensional flows (Stone 1994). For low Reynolds numbers and Newtonian fluids, it is known that drop breakup is mainly controlled by two dimensionless parameters: the capillary number \(\mathcal {C}\) defined as the ratio between viscous and capillary forces and p the viscosity ratio between dispersed and continuous phases. Drop breakup usually occurs when the capillary number exceeds a threshold \(\mathcal {C}_{\scriptstyle b}\) that varies with p and the nature of the flow (Grace 1982). Under shear flow, for instance, an isolated droplet adopts an ellipsoidal shape when \(\mathcal {C}<\mathcal {C}_{\scriptstyle b}\). At \(\mathcal {C}_{\scriptstyle b}\), the droplet draw ratio, defined as the drop length needed for breakup over the original droplet diameter, is a non-monotonic function of p: it is either decreasing (\(p<10^{-1}\)) or increasing (\(p>10^{-1}\)) with p (Grace 1982). At either very small (\(p<10^{-5}\)) or very large (\(p>3\)) viscosity ratios, the droplet draw ratio approaches one hundred, a breaking drop is then a very long thread that breaks because of the growth of a capillary-wave instability (Rayleigh 1878), or other processes, e.g., tip streaming (Torza et al. 1972; Grace 1982) or end pinching (Stone and Leal 1989). In all cases, smaller droplets with a broad size distribution are produced. Around \(p=10^{-1}\), the droplet draw ratio is minimum and the size of a drop at breakup is only a few times the original one. This drop then breaks into smaller ones having a narrow size distribution centered around a mean size \(\sim \mathcal {C}^{-1}\). When \(p>4\), the droplet deformation remains small and breakup is never observed. These results strongly depend on the rheological properties of the two-phase fluid. For instance, for fluids having a viscoelastic component, breakup can occur in shear flows when \(p>4\) (Mighri et al. 1998). Also, when shearing alters the microstructure of the two-phase fluid, the response of sheared drops may become non-stationary and sustained droplet size oscillations can be observed (Courbin et al. 2004a). For this class of fluids, the breakup of drops may even occur without elongation (Courbin et al. 2004b). In confined flows, \(\mathcal {C}_{\scriptstyle b}\) does not only depend on p but also on the degree of confinement. This parameter tends to increase the threshold for breakup at low viscosity ratios, whereas \(\mathcal {C}_{\scriptstyle b}\) decreases with the confinement at large p (Vananroye et al. 2006, 2007). For sufficiently confined sheared flows, Vananroye et al. (2006) have even shown that breakup can occur when \(p>4\). Also, Newtonian drops in viscoelastic matrix break at very small values of \(\mathcal {C}_{\scriptstyle b}\) in confined conditions (Cardinaels and Moldanaers 2011; Guido 2011). By contrast, in the case of viscoelastic drops, \(\mathcal {C}_{\scriptstyle b}\) may either increase or decrease depending on the drop viscoelasticity (Gupta and Sbragaglia 2014).

Recent advances in microfluidics for material science (Chu et al. 2007; Shah et al. 2008; Engl et al. 2008), biotechnology and chemistry (Teh et al. 2008; Trivedi et al. 2010; Seeman et al. 2012) have inspired investigations of the breakup of confined drops in various microfluidic geometries. For instance, one can actively break microfluidic drops using an electric field (Link et al. 2006) or an optical approach (Baroud et al. 2007). However, most studies exploit passive (geometry-based) methods that solely rely on the flow geometry. Examples include cross-flow microchannels (Tan et al. 2008; Cubaud 2009; Che et al. 2011), T-junctions (Link et al. 2004; de Menech 2006; Leshansky and Pismen 2009; Afkhami et al. 2011; Bedram and Moosavi 2011; Samie et al. 2013; Salkin et al. 2013; Wang and Yu 2015), Y-junctions (Ménétrier-Deremble and Tabeling 2006; Abate and Weitz 2011; Bedram et al. 2015; Zheng et al. 2016) and micro-obstacles (Link et al. 2004; Protière et al. 2010; Chung et al. 2010; Salkin et al. 2012; Li et al. 2014). The earliest work by Link et al. (2004) has shown that breaking a drop or a bubble into two daughter droplets or bubbles of different sizes can be achieved by drop impact either against an off-centered micro-obstacle in a channel or at a T-junction, i.e., the inlet node of a loop having two arms of different lengths: other governing parameters being fixed, the volume fraction \(\phi _{i}\) (\(i=1\) or 2) of the two daughter droplets or bubbles is controlled either by the distance between obstacle and axis of a channel or by the ratio of the lengths of the two arms of a loop. Similar to bulk experiments, for these two microfluidic configurations, breakup also occurs when the capillary number is larger than a threshold \(\mathcal {C}_{\scriptstyle b}\). Many of the works cited above combine experiments and theory to understand how \(\mathcal {C}_{\scriptstyle b}\) and \(\phi _{i}\) vary with the geometrical, hydrodynamical and physicochemical variables at play. In particular cases, \(\phi _{i}\) solely depends on the geometry and can be explained using simple physical arguments (Link et al. 2004; Salkin et al. 2013). In most cases, however, modeling experimental findings is a challenging task since the number of governing parameters is large. For drop impact against micro-obstacles, Salkin et al. (2012) have shown that the use of a rectangular obstacle allows one to establish a theoretical framework that provides a full description of the experiments. Notably, the model introduced by Salkin et al. (2012) has been successfully employed to rationalize non-trivial experimental results such as the either monotonic or non-monotonic evolution of \(\mathcal {C}_{\scriptstyle b}\) with a drop size depending on the sign of the viscosity contrast, that is, the difference between the viscosities of dispersed and continuous phases divided by the latter one. Salkin et al. (2013) have also used their theoretical framework to explain the variations of \(\phi _{i}\) with numerical simulations, \(\phi _{i}\) being in this case a complex function of the size and speed of a mother drop, p, the surface tension between liquid phases, and the geometrical variables.

Here, we investigate the volume fraction \(\phi _{i}\) of the daughter droplets formed upon breakup of a mother drop against an off-centered rectangular obstacle as a function of the viscosity ratio p and capillary number \(\mathcal {C}\). We present a model that provides an analytical expression for \(\phi _{i}\) as a function of these controlling parameters and the geometrical variables. We find that the threshold in capillary number \(\mathcal {C}_{\scriptstyle b}\) decreases monotonically with \(p=0.2\)–2 and its value is three orders of magnitude smaller than previous results for shear flows in bulk.

2 Experiments: setup, materials and methods

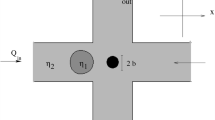
Our microchannels are made in poly-dimethylsiloxane (PDMS) using standard soft lithography (McDonald et al. 2000). They have a rectangular cross section with height \(h=50\,\upmu \hbox {m}\) and width \(w=130\,\upmu \hbox {m}\) (see Fig. 1). We generate a periodic train made of monodisperse drops using a flow-focusing geometry (Anna et al. 2003). Two syringe pumps (PHD 2000, Harvard Apparatus) inject the dispersed (aqueous solution) and continuous (oil) phases at controlled flow rates which are adjusted independently until a steady flow of monodisperse drops with volume \({\varOmega }=1140\) pL is obtained. We herein refer to these flattened drops that are larger than w as “slugs.” Details about the fluid system are given further in the text. Typical flow rates of dispersed and continuous phases are \(q_{w}=5\)–200 \(\upmu \hbox {L}/\hbox {h}\) and \(q_{o}^{f}=5\)–500 \(\upmu \hbox {L}/\hbox {h}\), respectively. The drops are then directed toward a rectangular obstacle (length \(L=500\,\upmu \hbox {m}\) and width \(30\,\upmu \hbox {m}\)) parallel to the walls of the channel and off-centered. As shown in Fig. 1, the two gaps (1) and (2) on both sides of an obstacle have different widths \(w_{1}=70\,\upmu \hbox {m}\) and \(w_{2}=30\,\upmu \hbox {m}\). A dilution module (Prat et al. 2006; Sessoms et al. 2010) allows for an additional injection of oil at constant flow rate \(q_{o}^{d}=0\)–1000 \(\upmu \hbox {L}/\hbox {h}\) to vary the drop velocity v while \({\varOmega }\) is unchanged. This module is far upstream from the obstacle so that the flow is steady near the obstacle (see Fig. 1) and the distance \(\lambda \) between two consecutive drops is large enough to prevent drop-to-drop interactions that are known to affect drop breakup (Belloul et al. 2011; Schmit et al. 2015).

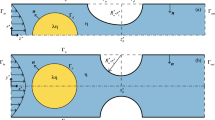
We record videos of the flow nearby the obstacle with a high-speed camera (Phantom V7) working at 1000 frames/s for a resolution of \(64 \times 512\) pixels\(^{2}\). The production rate f of the drops, \({\varOmega }\), v, their size \(L_{\scriptstyle d}\) and the sizes \(L_{\scriptstyle 1}\) and \(L_{\scriptstyle 2}\) of the two daughter droplets, respectively, flowing the gaps (1) and (2) are obtained from image processing using a custom-written MATLAB software. The volume of a mother drop, \({\varOmega }=\frac{q_{w}}{f}\), is first determined by measuring the droplet production rate f. One then computes the effective droplet size \(L_{\scriptstyle d}=220\pm 20\,\upmu \hbox {m}\) according to \(L_{\scriptstyle d}=\frac{{\varOmega }}{hw}\). The volumes \({\varOmega }_{\scriptstyle 1}\) [gap (1)] and \({\varOmega }_{\scriptstyle 2}\) [gap (2)] of the daughter drops are deducted from the measurements of their surface areas by using the formulae predicting the volume of a confined droplet (see Fig. 2). These formulae are valid provided that the capillary number at play is sufficiently small so that the droplet shape is only set by its degree of confinement. Note that we have neglected the thickness of the lubrication films that always exist between a non-wetting droplet and the microchannel walls. Such lubrication films are expected to be much smaller than the characteristic sizes of the channels we use (Huere et al. 2015). Once the volumes mentioned above are obtained, the two daughter droplets effective lengths \(L_{\scriptstyle 1}\) and \(L_{\scriptstyle 2}\) are, respectively, determined using the two relationships \(L_{\scriptstyle 1}=\frac{{\varOmega }_{\scriptstyle 1}}{w_{1}h}\) and \(L_{\scriptstyle 2}=\frac{{\varOmega }_{\scriptstyle 2}}{w_{2}h}\). These effective lengths correspond to the lengths of cuboids having similar volumes to those of the considered droplets. As we will see further in the text, these quantities are useful parameters to model our experiments.

Fig. 1
figure 1

Middle panel: Image of the photomask of the microfluidic device used in our study; defined are the flow rate of the dispersed phase \(q_{w}\) and the oil flow rates in the production and dilution modules, \(q_{o}^{f}\) and \(q_{o}^{d}\), respectively. Top panel: Photographs showing the flow-focusing geometry that produces periodic trains of monodisperse drops and the dilution module. The bottom panel which consists of a photograph of the flow downstream of the dilution module and a combination of a photograph and a schematic nearby the obstacle defines the geometrical, hydrodynamical and physicochemical variables at play. Scale bar \(100\,\upmu \hbox {m}\)

Full size image
Fig. 2
figure 2

This figure depicts the shape that a droplet seeks when it is confined in a microfluidic channel having a rectangular cross section. In this qualitative picture, the capillary number is sufficiently small so that the droplet shape only depends on its degree of confinement. Three possible cases can be obtained depending on the ratio between a drop size and channel geometry. The last column shows the surface, length and volume of a drop in these three cases

Full size image

We use hexadecane (Sigma-Aldrich) for the continuous phase and solutions of glucose (0–38 wt%) in water for the dispersed phase. We add 15 g/L of a surfactant [sodium dodecyl sulfate (SDS), Sigma] in the aqueous solutions to hinder droplet coalescence. In our experiments, the Reynolds and capillary numbers are small and span the ranges \(10^{-2}\)–\(10^{-1}\) and \(10^{-3}\)–\(10^{-2}\), respectively. The Reynolds number \(\mathcal {R}\) and the capillary number \(\mathcal {C}\) correspond to the ratios between inertial and viscous forces and between viscous and capillary forces, respectively. They are defined in our system as \(\mathcal {R}=\frac{\rho _{c}v h}{\eta _{c}}\) and \(\mathcal {C}=\frac{\eta _{c}v}{\gamma }\), \(\rho _{c}\) being the density of the continuous phase. We measure the viscosity of each liquid with an Anton Paar MCR 301 rheometer. Table 1 describes the properties of each water/SDS/glucose mixture with dynamic viscosity \(\eta _{d}\), the viscosity of hexadecane being \(\eta _{c}=3\,\hbox {mPa}\,\hbox {s}\). For the prepared mixtures, the interfacial tension between continuous and dispersed phases determined with pendant drop tensiometry is \(\gamma =5\)–6.5 \(\hbox {mN}/\hbox {m}\). In what follows, we investigate the variations of the volume fraction of the daughter droplet in the narrow gap (2), \(\phi _{2} = {\varOmega }_{\scriptstyle 2}/{\varOmega }\); the volume fraction of the drops in the large gap is simply \(\phi _{1} = {\varOmega }_{\scriptstyle 1}/{\varOmega }= 1 - \phi _{2}\).

Table 1 Composition and viscosities of the water/SDS/glucose mixtures used in our study
Full size table

3 Experiments: results

In our experiments, we vary v while maintaining all other variables fixed. In agreement with foregoing results in the literature, when v becomes larger than threshold velocity \(v_{\scriptstyle b}\), a slug breaks in two daughter droplets when its rear edge meets the obstacle (see Fig. 1). These drops then flow in gaps (1) and (2). By contrast, when \(v<v_{\scriptstyle b}\), a slug does not break and flows in the larger gap. As depicted in Fig. 1, the volume \({\varOmega }_{\scriptstyle 2}\) of the droplet created in the narrow gap is smaller that that of the drop formed in gap (1). Figure 3 shows that \({\varOmega }_{\scriptstyle 2}\) is an increasing function of \(v>v_{\scriptstyle b}\) and that it increases with \(\eta _{d}\) for a given speed.

Fig. 3
figure 3

Variations of the volume \({\varOmega }_{2}\) of the daughter drops produced in gap (2) with the velocity of the mother drop v for different viscosities of the dispersed phase: (circles) 1, (squares) 2.1 and (diamonds) 4.1 mPa s. The lines are guides for the eyes

Full size image

4 Discussion and model

We now discuss the variations of \(\phi _{\scriptstyle 2}\) with the dimensionless parameters controlling the problem, \(\mathcal {C}=\frac{\eta _{c}v}{\gamma }\) and \(p=\frac{\eta _{d}}{\eta _{c}}\). We will rationalize our findings with a theoretical framework recently introduced to describe the breakup dynamics of drops impacting a micro-obstacle (Salkin et al. 2012 and Schmit et al. 2015). We describe below the basic elements of this framework.

We assume that the speed v of a slug flowing in a channel of constant cross section \(S=hw\) varies as q / S with \(q=q_{w}+q_{o}^{f}+q_{o}^{d}\) the total flow rate. We consider that the flows of the slug and the continuous phase satisfy Darcy’s law, with an effective viscosity \(\eta _{d}^{s}\) for the slug. \(\eta _{d}^{s}\) is a free parameter that accounts for viscous dissipation inside the slug, in the thin lubrication films of oil between the slug and the channel walls and in the corners of the rectangular geometry. Thus, the pressure drop \(\Delta p\) over a portion \(\ell \) of the slug reads

$$ \Delta p_{visc}= \frac{\eta _{d}^{s}\ell q}{h^{3}w} f\left( \frac{w}{h}\right), $$
(1)

with

$$ f\left( x\right) = \frac{\pi ^{2}}{4x^{2}}\left[ \sum _{j=1}^{\infty } \sum _{k=1}^{\infty } \frac{[1-(-1)^{j}]^{2}[1-(-1)^{k}]^2}{jk[j^{2}+ k^{2}x^{2}]}\right] ^{-1} $$
(2)

a dimensionless function which can be written \(f\approx 12\)[1–0.63 \(x^{-1}]^{-1}\) for \(1<x\) (Bruus 2008). We write an estimate of the pressure drop across the front edge of the slug due to the curved two-fluid interface

$$ \Delta p_{curv}=\frac{2 \gamma }{w} \left( 1+\frac{w}{h}\right). $$
(3)

This contribution to the pressure accounts for the presence of curved interfaces in our model. We next consider flat interfaces rather than curved for simplicity’s sake. Using these assumptions, we are able to rationalize the breakup dynamics starting at time \(t=0\) when the drop collides with the obstacle. The time at which the rear edge of a slug of length \(L_{\scriptstyle d}\) meets the obstacle is \(t_{f}=L_{\scriptstyle d}/v\). We next work with the dimensionless time \(T=\frac{t}{t_{f}}\).

Fig. 4
figure 4

Top-view schematic of a drop colliding with an obstacle defining the variables used in our model which describes the propagation of two-liquid interfaces in the two gaps

Full size image

Since we work at constant flow rates, a two-fluid interface always invades gap (1) at \(t=0\). Then, it begins to move forward at a speed \({\hbox {d}}\ell _{\scriptstyle 1}/{\hbox {d}}t\) (see Fig. 4 defining the variables used in our model). A two-fluid interface invades the narrow gap (2) only when the pressure drop \(\Delta p\) between the two ends of the obstacles overcomes the Laplace pressure \(\frac{2 \gamma }{w_{2}} \left( 1+\frac{w_{2}}{h}\right) \) required to accommodate a curved interface in this gap. Prior to the invasion of the narrower gap (2) by a fluid–fluid interface, the position of the interface in the large gap at T, \(\ell _{\scriptstyle 1}(T)=X_{\scriptstyle 1}(T)L\), is obtained by conservation of the total flow rate in Eq. (4): \(X_{\scriptstyle 1}(T)=\alpha T\) with \(\alpha =\frac{L_{\scriptstyle d}w}{Lw_{1}}\). We now consider the situation for which the interface which has entered gap (1) has not yet reached the extremity of the obstacle, that is, \(X_{\scriptstyle 1}(T)<1\). Using Eq. (1), we write the pressure drop over L in gap (1), \(\Delta p=\frac{\eta _{c}L q}{h^{3}w_{1}} f_{\scriptstyle 1}[(1+{\Delta \eta }^{s}X_{\scriptstyle 1})+ \frac{2Z}{\mathcal {C}}\left( 1+\frac{w_{1}}{h}\right) ]\), where \({\Delta \eta }^{s}=(\eta _{d}^{s}-\eta _{c})/\eta _{c}\) and \(Z=(f_{\scriptstyle 1}h^{-2} w L)^{-1}\) with \(f_{\scriptstyle 1}=f\left( \frac{w_{1}}{h}\right) \) are two dimensionless parameters. The condition for the invasion of the narrow gap can be mathematically expressed as \(1+{\Delta \eta }^{s}X_{\scriptstyle 1}>\frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}\), where \(\mathcal {C}_{\scriptstyle \star }=2 Z \frac{1-W}{W}\), which provides insights into the importance of the sign of \({\Delta \eta }^{s}\). Indeed, when \({\Delta \eta }^{s}<0\), the term on the left-hand side of the inequality, \(1+{\Delta \eta }^{s}X_{\scriptstyle 1}\), decreases with T, so that the time \(T_{\scriptstyle p}\) at which an interface begins to propagate in gap (2) is \(T_{\scriptstyle p}=0\) whenever \(\mathcal {C}>\mathcal {C}_{\scriptstyle \star }\). By contrast, when \({\Delta \eta }^{s}>0\), this term increases with T so that \(T_{\scriptstyle p}=\frac{1}{\alpha {\Delta \eta }^{s}}\left( \frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}-1\right) \ge 0\). Using the two conditions to be fulfilled to allow propagation in gap (2), \(T_{\scriptstyle p}< 1\) and \(X_{\scriptstyle 1}(T_{\scriptstyle p})\le 1\), one finds that invasion occurs when \(\mathcal {C}> \frac{\mathcal {C}_{\scriptstyle \star }}{1+\alpha {\Delta \eta }^{s}}\) (\(\alpha \le 1\)) or \(\mathcal {C}>\frac{\mathcal {C}_{\scriptstyle \star }}{1+{\Delta \eta }^{s}}\) (\(\alpha \ge 1\)). Note that the extra condition to fulfill, \(T_{\scriptstyle p}\ge 0\), gives \(T_{\scriptstyle p}=0\) whenever \(\mathcal {C}>\mathcal {C}_{\scriptstyle \star }\). For both positive and negative \({\Delta \eta }^{s}\), if those conditions are not fulfilled when the two-fluid interface exits gap (1), the pressure drop in this gap suddenly decreases and remains constant over time, \(\Delta p=\frac{\eta _{c}L q}{h^{3}w_{1}} f_{\scriptstyle 1}[(1+{\Delta \eta }^{s})\). Then, the pressure drop can no longer become larger that the Laplace pressure mentioned above and the invasion of the narrow gap never occurs.

When \(T\ge T_{\scriptstyle p}\), the dynamics of the interfaces present in both gaps are controlled by a set of two coupled first-order ordinary equations whose solutions are \(X_{\scriptstyle 1}\) and \(X_{\scriptstyle 2}=\ell _{\scriptstyle 2}(T)/L\). The conservation of the total flow rate gives

$$ \frac{{\hbox {d}}X_{\scriptstyle 1}}{{\hbox {d}}T}+W\frac{{\hbox {d}}X_{\scriptstyle 2}}{{\hbox {d}}T}=\alpha. $$
(4)

The second one is obtained by the equality of pressure drops over both gaps

$$ (1+{\Delta \eta }^{s}X_{\scriptstyle 1})\frac{{\hbox {d}}X_{\scriptstyle 1}}{{\hbox {d}}T}-FW(1+{\Delta \eta }^{s}X_{\scriptstyle 2})\frac{{\hbox {d}}X_{\scriptstyle 2}}{{\hbox {d}}T}=\alpha \frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}} $$
(5)

for \(X_{\scriptstyle 1}\le 1\) and \(X_{\scriptstyle 2}\le 1\) and where \(W=\frac{w_{2}}{w_{1}}\) and \(F=f\left( \frac{w_{2}}{h}\right) /\left[ W f\left( \frac{w_{2}}{Wh}\right) \right] \).

As we work with a slug size \(L_{\scriptstyle d}=220\pm 20\,\upmu m\) that is constant within experimental errors, we consider that \(\alpha =\frac{L_{\scriptstyle d}w}{L w_{1}}=0.82\pm 0.07<1\) is constant. Assuming that \({\Delta \eta }^{s}>0\), we now discuss the two cases \(\mathcal {C}> \mathcal {C}_{\scriptstyle \star }\) and \(\mathcal {C}\le \mathcal {C}_{\scriptstyle \star }\).

  • The case \(\mathcal {C}> \mathcal {C}_{\scriptstyle \star }\): We have previously shown that this situation corresponds to \(T_{\scriptstyle p}=0\). By integrating Eqs. (4) and (5) between \(T=0\) and \(T=1\) with the initial conditions \(X_{\scriptstyle 1}(0)=X_{\scriptstyle 2}(0)=0\), one easily shows that \(X_{\scriptstyle 2}(1)\) is the positive solution of the quadratic equation

    $$ X_{\scriptstyle 2}(1)^{2}W(W-F)\frac{{\Delta \eta }^{s}}{2}-X_{\scriptstyle 2}(1)W(1+F+\alpha {\Delta \eta }^{s})+\alpha \left( 1+\frac{\alpha {\Delta \eta }^{s}}{2}-\frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}\right) =0. $$
    (6)

  • The case \(\mathcal {C}\le \mathcal {C}_{\scriptstyle \star }\): We integrate Eqs. (4) and (5) between \(T_{\scriptstyle p}=\frac{1}{\alpha {\Delta \eta }^{s}}\left( \frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}-1\right) \) and \(T=1\) with \(X_{\scriptstyle 1}(T_{\scriptstyle p})=\alpha T_{\scriptstyle p}\) and \(X_{\scriptstyle 2}(T_{\scriptstyle p})=0\) as initial conditions. One readily finds that \(X_{\scriptstyle 2}(1)\) is the positive solution of the following equation

    $$\begin{aligned} X_{\scriptstyle 2}(1)^{2}W(W-F)\frac{{\Delta \eta }^{s}}{2}-X_{\scriptstyle 2}(1)W(1+F+\alpha {\Delta \eta }^{s})+ \\ \frac{1}{2{\Delta \eta }^{s}}\left( 1+\alpha {\Delta \eta }^{s}-\frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}\right) ^{2}=0. \end{aligned} $$
    (7)

Since we consider that the slugs have flat interfaces in our modeling work, we estimate \({\varOmega }=L_{\scriptstyle d}w h\) and \({\varOmega }_{\scriptstyle 2}= L_{2} w_{2}h = X_{2}(1)L w_{2}h\) so that \(X_{\scriptstyle 2}(1)=\frac{\alpha \phi _{\scriptstyle 2}}{W}\). Using this relationship between \(X_{\scriptstyle 2}(1)\) and \(\phi _{\scriptstyle 2}\) in Eqs. (6) and (7), one finds that \(\phi _{\scriptstyle 2}\) is the positive solution of the quadratic equation

$$ \phi _{\scriptstyle 2}^{2}\frac{(F-W)\zeta }{2W}+\phi _{\scriptstyle 2}(1+F+\zeta )-A(\zeta ,\mathcal {C},\mathcal {C}_{\scriptstyle \star })=0 $$
(8)

with \(\zeta =\alpha {\Delta \eta }^{s}\) and where

  • \(\circ \) \(A(\zeta ,\mathcal {C},\mathcal {C}_{\scriptstyle \star })= 1+\frac{\zeta }{2}-\frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}\) when \(\mathcal {C}> \mathcal {C}_{\scriptstyle \star }\);

  • \(\circ \) \(A(\zeta ,\mathcal {C},\mathcal {C}_{\scriptstyle \star })=\frac{1}{2\zeta }\left( 1+\zeta -\frac{\mathcal {C}_{\scriptstyle \star }}{\mathcal {C}}\right) ^{2}\) when \(\mathcal {C}\le \mathcal {C}_{\scriptstyle \star }\).

One then easily shows that

$$ \phi _{\scriptstyle 2}= \frac{W(1+F+\zeta )}{(F-W)\zeta }\left( -1+\sqrt{1+\frac{2A(F-W)\zeta }{W(1+F+\zeta )^{2}}}\right) . $$
(9)
Fig. 5
figure 5

Variations of the volume fraction \(\phi _{2}\) of the daughter drops formed in gap (2) with the capillary number \(\mathcal {C}\) for different aqueous solutions; the symbols are identical to those in Fig. 3. The lines correspond to the prediction of \(\phi _{2}\) given by Eq. (9) with the following values of the free parameter \(\zeta =\alpha {\Delta \eta }^{s}\): (circles) 2.04, (squares) 3.68 and (diamonds) 7.35

Full size image

As discussed above, the outcome of our model is Eq. (9) that gives an analytical expression for the variations of \(\phi _{\scriptstyle 2}\) with \(\mathcal {C}\) and other dimensionless parameters describing the geometry; finding an expression of \(\phi _{1}\) is then immediate as \(\phi _{1}=1-\phi _{\scriptstyle 2}\). As shown in Fig. 5, the theoretical prediction provided by Eq. (9) describes remarkably well our experimental data considering there is only one free parameter, \(\zeta \), in the model (Fig. 6).

Fig. 6
figure 6

Evolution of \(\mathcal {C}_{\scriptstyle b}\) with the viscosity ratio p. The symbols stand for different viscosities of the dispersed phase: (up-pointing triangles) 2.7, (down-pointing triangles) 3.5 and (times sign) 5.2 mPa s and as indicated in Table 1. The line is a guide for the eyes

Full size image
Fig. 7
figure 7

Variations of \(\zeta \) with p. The symbols are identical to those of figure and the line is a guide of the eyes

Full size image

For the discussed case \({\Delta \eta }^{s}>0\) and \(\alpha <1\), Salkin et al. (2012) have shown that breakup occurs whenever an interface enters the narrow gap. In other words, the threshold \(\mathcal {C}_{\scriptstyle b}\) corresponds to the capillary number \(\frac{\mathcal {C}_{\scriptstyle \star }}{1+\zeta }\) above which an interface propagates in the gap (2). In Fig. 6, we report the variations of \(\mathcal {C}_{\scriptstyle b}=\frac{\mathcal {C}_{\scriptstyle \star }}{1+\zeta }\) with p determined by using the best fits to our data shown in Fig. 5. Figure 6 shows that that \(\mathcal {C}_{\scriptstyle b}\) takes values that are surprisingly much smaller (\(\propto 10^{-3}\)) than those required to break a drop under shear flow in bulk (\(\propto 1\)). We also note that in our microfluidic experiments, \(\mathcal {C}_{\scriptstyle b}\) is a decreasing function of p in the investigated range [0.2–2].

In Fig. 7, we report the values found for the free parameter \(\zeta \) as a function of p. Since \(\alpha =0.82\pm 0.07\) is constant within experimental errors in our study, our analysis allows us to estimate the free parameter \({\Delta \eta }^{s}\) characterizing the effective viscosity introduced by the flow of slugs. We find that \({\Delta \eta }^{s}=2.5-6.5>0\) for our experiments which validates the assumption made when modeling \(\phi _{\scriptstyle 2}\). We also note that \({\Delta \eta }^{s}\), thus \(\eta _{d}^{s}\), increases with p (Fig. 7). The values we found for this system for \(\eta _{d}^{s}=(1+{\Delta \eta }^{s})\eta _{c}=10.5\)–22.5 are larger than \(\eta _{c}\) in agreement with previous results by Salkin et al. (2012) also conducted with an aqueous solution in oil system.

5 Conclusion

We have studied the breakup of drops flowing against a rectangular obstacle placed off-center in a microchannel. In agreement with earlier works, we have shown that breakup requires that the capillary number \(\mathcal {C}\) exceeds a threshold \(\mathcal {C}_{\scriptstyle b}\). We have characterized the role of the viscosity ratio p between dispersed and continuous phases on drop breakup by investigating the experimental variations of the volume fraction \(\phi _{\scriptstyle 2}\) of the smaller daughter droplet formed upon breakup of a mother drop with \(\mathcal {C}\) and p. We have presented a single free parameter model that gives an analytical expression of \(\phi _{\scriptstyle 2}\) which captures these variations and allows us to determine \(\mathcal {C}_{\scriptstyle b}\). We find a threshold for breakup that is three orders of magnitude smaller than typical values found under shear flow in bulk experiments. In addition, our results show that \(\mathcal {C}_{\scriptstyle b}\) is decreasing with p in the that studied range of the viscosity ratio [0.2–2].