Breakup a droplet passing through an obstacle in an orthogonal cross-section microchannel

Abstract

In this work, the breakup of a droplet passing through an obstacle in an orthogonal cross section is numerically investigated. The relevant boundary data of the velocity field is numerically computed by solving the depth-averaged Brinkman equation via a self-consistent integral equation using the boundary element method. To study the dependence of the droplet breakup on the obstacle shape, two different shapes of obstacle, circular and elliptical, are considered in the present work. We investigate the effect of obstacle size, obstacle position, and capillary number on the breakup treatment of the droplet. Numerical results indicate that the critical capillary number depends on the obstacle shape, obstacle position and droplet size. In the elliptical obstacle, in addition, the results also show that the area ratio of daughter droplets depends on the capillary number. Results show that the area ratio of daughter droplets depends on the capillary number, obstacle shape, and obstacle position. Our results is in a good agreement with the previous studies.

1 Introduction

Due to the widespread application of microfluidics in various fields such as biology, industry, and medicine, many researchers have focused on this field in the recent years [1,2,3,4,5,6,7]. Microfluidics is used to study the structure and behavior of fluids at the micro-level. Useful information on the dynamics of droplets can be obtained by investigating the dynamics of droplet motion [8,9,10,11], droplet deformation [12,13,14,15,16,17,18], droplet coalescence [19,20,21], droplet sorting [22,23,24], and droplet breakup [25,26,27,28].

Droplet breakup is widely in operations and control of droplet size in lab-on-a-chip applications. Droplet breakup in a T-junction, Y-junction, and cross-section channels have been experimentally and numerically studied in recent years. By using lubrication analysis, Leshansky and Pismen proposed a two-dimensional theory for droplet breakup in symmetric T-junction [29]. Droplet breakup in microfluidic T-junction at small capillary numbers has been experimentally studied by Jullien et al. [30]. Their experimental results indicate that there are two different regimes depending whether droplets obstruct or not the T-junction. A numerical study of droplet breakup in a microfluidic T-junction has been presented by Afkhami et al. [31]. Droplet breakup at asymmetric T-junction has been experimentally and numerically studied by Samie et al. [32]. Their results indicate that the daughter droplets volume ratio depends on the width ratio of bifurcations. The dynamics of droplet breakup in an asymmetric bifurcation has been experimentally and numerically studied by Wang et al. [33, 34]. They have investigated the effect of droplet length and capillary number on the evolution of the neck thickness.

Schütz et al. have experimentally and numerically studied the interaction and breakup of droplet pairs in a microfluidic Y-junction by using 3-D boundary element method [35]. By adjusting the hydrostatic pressure on the carrier phase, Liang et al. have investigated the effect of hydrostatic pressure on the splitting of droplets into two daughter droplets at a T-junction [36]. Radcliffe has studied the breakup of ferromagnetic droplet in a rotating magnetic field by coupling the finite element method and boundary element method. He has found that a critical value for droplet viscosity which depends on the magnetic field strength and field rotation speed [37]. The deformation and breakup of a double-core compound droplet in an axisymmetric microfluidic by using front-tracking method have been numerically investigated by Vu et al. [38]. Their numerical results indicate that the compound droplet can only experience the finite deformation and stay at the center. The role of Rayleigh instability on the breakup of charged droplet has been experimentally and numerically studied by Singh et al. [39]. Their numerical simulation was carried out using the boundary element method in the Stokes flow. The hydrodynamics behavior of a single droplet passing through a microfluidic T-junction using phase-field multiphase lattice Boltzmann model has been studied by Cheng and Deng [40]. Their numerical results indicate that the vortex flow formed inside droplet plays an important role in determining whether droplet breaks up or not.

The dynamics study of the droplet passing through an obstacle has been an interesting topic for researchers. The geometrically mediated droplet breakup has been experimentally studied by Link et al [25]. They have proposed two methods for breaking of a large droplet into smaller droplets in a simple microfluidic configurations: (a) using T-shaped junction and (b) using flow passing obstacle [25]. Chung et al. have numerically investigated the deformation and breakup a droplet passing through a cylinder obstacle in a straight microchannel by using the finite element-front tracking method [41]. They have found the daughter droplet size depends on the capillary number [41]. In their subsequent work, Chung et al. have also studied the effect of obstacle shape (cylinder and square), droplet size, and capillary number on the droplet breakup [42]. Lee et al. have numerically investigated the breakup a droplet past an obstacle by using the VOF method of the commercial code FLUENT [43].

Salkin et al. have theoretically and experimentally studied the breakup dynamics of droplets and bubbles passing a linear micro-obstacle [44]. The breakup a droplet passing through an obstacle by using sharp-interface level-set method have been presented by Lee and Son [45]. They have investigated the effect of obstacle length, obstacle width, obstacle location, and obstacle inclination on the droplet breakup in a straight microfluidic channel [45]. Li et al. presented a numerical study of the breakup treatment of a droplet past through a circular cylinder obstacle by employing the lattice Boltzmann method [46]. They have investigated the effect of eccentric ratio, viscosity ratio of droplet phase to carrier phase, and Bond number on the dynamics of droplet breakup. The effect of droplet velocity on the breakup treatment of a droplet passing through a circular obstacle in a straight microchannel has been investigated by Protière et al. [47]. The motion and breakup of viscous droplet past through a spherical obstruction by using the two-phase lattice Boltzmann method have been studied by Bhardwaj et al. [48].

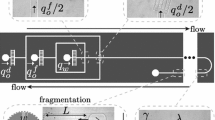
In this work, the droplet breakup by the use of an obstacle is numerically presented. Figure 1 presents the schematic geometry of our work. The microchannel consists an orthogonal intersection having two inlets and two outlets. We consider an obstacle located in the cross section. The width of inlet channel and outlet are equal to W. In this study, we consider a two-phase flow which consists of two fluids separated by an interface. We assume that a flow past two-dimensional droplet containing a droplet phase labeled, 2, and suspended in continuous phase labeled, 1. Viscosity of continuous phase is $\eta _1$ and viscosity of droplet phase is $\eta _2$. In this work, we apply the Brinkman equation to describe the droplets dynamics in the Hele–Shaw limit. In this way, the Brinkman partial differential equation is converted to boundary integral equation and solved by using the boundary element method as well. Finally, the dynamics of droplet motion and droplet breakup are discussed as function of droplet size, capillary number and obstacle size.

This paper is structured as follows: In Sect. 2, we will formulate Brinkman equation and boundary conditions for the velocity field and normal component of stress tensor at the droplet-continuous phase interface as well as at channel walls. Finally, we systematically derive non-dimensionalized boundary integral equation for velocity field. The numerical implementation to solve the boundary integral representation equation for the velocity field as well as for local droplet velocity are also contained in Sect. 2.3. The results of our numerical solutions, including the dynamics of droplet deformation and droplet breakup are reported in Sect. 3. Finally, in Sect. 4, we summarize our findings, conclude, and give an outlook on possible future work in this field.

Fig. 1

Sketch of the microfluidic channel considered

2 Governing equations

The present study is based on the boundary integral equation of interface dynamics for depth-averaged Brinkman equation. The flows are taken to be two-dimensional. The fluid viscosity, $\eta$, and density, $\rho$, are assumed to be constant in two phases. The subscript 1 is used for the carrier phase, and the subscript 2 is chosen for the droplet phase. In order to report data with dimensionless numbers, we use length scale W, time scale $\eta _1 W/\gamma$, pressure scale $\gamma /W$, velocity scale $\gamma /\eta _1$ and modified capillary number $Ca^* = H^2 \eta _1 V_0 /(W^2\gamma )$ where W is channel width, $V_0$ is average velocity of the continuous phase at the midpoint of the straight channel, H is channel height, and $\gamma$ is surface tension. At the low Reynolds number, the flows are explained by the Brinkman equation for the two phases as the following equation [17]:

$$\begin{aligned} \varvec{\nabla }P^{(i)}=\alpha _i \left( \varvec{\nabla }^2{\mathbf {V}}^{(i)}-k^2 {\mathbf {V}}^{(i)}\right) \qquad \mathrm{on} \quad \Omega _i \quad \mathrm{with} \quad i \in \{ \mathrm{1},\mathrm{2} \}~, \end{aligned}$$

(1)

where P(x, y) is the dimensionless pressure, ${\mathbf {V}}$ is the depth averaged dimensionless velocity, $k=\sqrt{12}/H$, and $\alpha _i=\eta _i/\eta _1$.

2.1 Boundary conditions

2.1.1 On the droplet surface

On the droplet surface, because of surface tension, the normal component of stress tensor is discontinuous across the droplet-continuous phase interface. The discontinuity condition on the normal stress at the two-phase interface is given by

$$\begin{aligned} {\varvec{\sigma }}^{\mathbf{(2)}}\cdot \mathbf{n}-{\varvec{\sigma }}^{\mathbf{(1)}}\cdot \mathbf{n}=\gamma \left( \frac{\pi }{4}\, \kappa _{\parallel }+\kappa _{\perp }\right) {\mathbf {n}}, \end{aligned}$$

(2)

where $\varvec{\sigma }$ is stress tensor and $\varvec{\sigma }\cdot {\mathbf {n}}$ is normal component of stress tensor, $\gamma$ is surface tension, ${\mathbf {n}}$ is unit normal vector pointing from the interior of the droplet phase into the continuous phase, $\kappa _{\parallel }$ is local curvature in-plane, and $\kappa _{\perp }$ is curvature in the thin direction. Prefactor $\pi /4$ corresponds to non-wetting condition at the top and bottom walls of the Hele-Shaw cell [49].

The other boundary condition on the droplet-continuous phase interface apples on the normal and tangential components of velocity. According to continuity equation, there is no mass transfer through the two-phase interface. Therefore, the normal and tangential components of fluid velocity is continuous across the droplet-continuous phase interface. This boundary condition reads

$$\begin{aligned} {\mathbf {V}}^{(1)}={\mathbf {V}}^{(2)}\ne 0 \qquad \mathrm{on} \qquad \Gamma _\mathrm{12}~, \end{aligned}$$

(3)

where $\Gamma _\mathrm{12}$ is the two-dimensional droplet contour.

2.1.2 On the channel walls

We apply the no-slip boundary condition on the channel walls and obstacle surface. Therefore, the normal and tangential components of the carrier fluid velocity are zero on the channel walls and obstacle surface.

We assume that the channel length is much larger that the width of cross section. We also assume that the channel inlets and outlets are placed sufficiently far from the cross section. According to Fig. 1, the inlet channels are along the x-axis and the outlet channels are along the y-axis. Therefore, at the channel inlets and outlets, we can apply the solution of Brinkman equation in a straight channel with width W as follows [50]:

$$\begin{aligned} V_{in} (y)= & {} \frac{Ca^*W^2}{H^2}\frac{\cosh (kW/2)-\cosh (ky)}{\cosh (kW/2)-1},\nonumber \\ V_{out} (x)= & {} \frac{Ca^*W^2}{H^2}\frac{\cosh (kW/2)-\cosh (kx)}{\cosh (kW/2)-1}, \end{aligned}$$

(4)

where $Ca^*$ is the modified capillary number. It is important to mention that the outlet fluxes are controlled by total flux of the left-flow and right-flow inlets.

2.2 Integral representation

In order to investigate the droplet shape under the extensional flow, we have to compute the velocity components of the droplet interface including the $V_x$ and $V_y$ on the droplet surface. One way to obtain the relevant boundary data of the velocity field is to numerically compute a self-consistent integral equation for velocity field V on the liquid–liquid boundary and channel walls. Following the formulation of Pozrikidis [51], the jth component of velocity field at point (${\mathbf {r}}_0)$ that lies in the continuous fluid satisfies a self-consistent integral equation of the following form

$$\begin{aligned} V_j({\mathbf {r}}_0)= & {} \frac{1}{C_l} \oint _{\Gamma _\mathrm{w},\Gamma _\mathrm{o}} [V_i({\mathbf {r}})T^B_{ijk} ({\mathbf {r}},{\mathbf {r}}_0)n_k- \sigma ^{(1)} n_i G^B _{ij}({\mathbf {r}},{\mathbf {r}}_0)] \mathrm{d}\ell \nonumber \\&\qquad +\frac{1}{C_l}\oint _{\Gamma _\mathrm{12}} [ (\alpha _2-1) V_i ({\mathbf {r}}) T^B _{ijk} ({\mathbf {r}},{\mathbf {r}}_0)n_k - \gamma (\frac{\pi }{4}\, \kappa _{\parallel }+\kappa _{\perp }) n_i G^B _{ij}({\mathbf {r}},{\mathbf {r}}_0)] \mathrm{d}\ell , \end{aligned}$$

(5)

where ${\mathbf {r}}=(x,y)$, ${\mathbf {r}}_0=(x_0,y_0)$ are the field and the singular points, respectively. When integration point ${\mathbf {r}}$ approaches the evaluation point $\mathbf {r_0}$, the integrands exhibit a singularity. When the singular point $\mathbf {r_0}$ is placed on the channel domain the coefficient $C_l=\frac{1}{2}$, and if it is placed on the liquid–liquid interface, $C_l=\frac{1+\alpha _2}{2}$. $\Gamma _\mathrm{w}$ is the channel wall contour and $\Gamma _o$ is a straight line cutting through the open ends of the microfluidic channel. The channel wall contours ($\Gamma _\mathrm{w}$), open end contours ($\Gamma _\mathrm{o}$), and droplet contour ($\Gamma _{12}$) are presented in Fig. 2. The first term of Eq. 5 includes the two boundary integrals along the $\Gamma _\mathrm{w}$ and $\Gamma _o$. $G^B _{ij}$ and $T^B _{ijk}$ are velocity and stress tensor Green’s functions of Brinkman’s equation, respectively. Free-space Green’s functions of Brinkman’s equation are given by [51, 52]

$$\begin{aligned} G^B _{ij} ({\mathbf {r}},\mathbf {r_0})= & {} -\delta _{ij}A(kR)+\frac{{\hat{R}}_i{\hat{R}}_j}{R^2}B(kR), \end{aligned}$$

(6)

$$\begin{aligned} T^B _{ijk}= & {} \delta _{ij}\frac{{\hat{R}}_j}{R^2}2[B(kR)-1]+\frac{\delta _{ij}{\hat{R}}_k+\delta _{kj}{\hat{R}}_i}{R^2}C(kR)\nonumber \\&\quad -4\frac{{\hat{R}}_i{\hat{R}}_j{\hat{R}}_k}{R^4}D(kR), \end{aligned}$$

(7)

where

$$\begin{aligned} A(R)= & {} 2\left[ \frac{1}{k^2R^2}-\frac{K_1(kR)}{kR}-K_0(kR)\right] ,\nonumber \\ B(R)= & {} 2\left[ \frac{2}{k^2R^2}-2\frac{K_1(kR)}{kR}-K_0(kR)\right] ,\nonumber \\ C(R)= & {} \frac{8}{k^2R^2}-4K_0(kR)-2(kR+\frac{4}{kR})K_1(kR)\nonumber \\ D(R)= & {} C(kR)+kR K_1(kR). \end{aligned}$$

(8)

${{\hat{\mathbf{R}}}}={\mathbf {r}}-\mathbf {r_0}$, $R=|{{\hat{\mathbf{R}}}}|$, and $K_0(kR)$, $K_1(kR)$ are modified Bessel functions.

One may calculate the boundary integral on the right-hand side of Eq. ( 5) either directly by domain discretization followed by numerical integration, or indirectly by the method of approximate particular solutions or the dual reciprocity method. In the next subsection, we will discuss the numerical procedure to solve the integral representation equation.

Fig. 2

Schematic discretization, channel domain, and droplet domain of the present work. Boundary integration is performed in the counter-clockwise direction around the boundaries

2.3 Boundary element discretization

The first step in the implementation of the boundary element method is to discretize the boundary into finite numbers of elements which are defined boundary elements. We discretize fixed boundaries like walls and open ends into a collection of N straight segments defined by the element end-points or nodes, whereas the droplet is discretized by using the cubic-spline method. The boundary integration is performed in the counter-clockwise direction around the boundaries. The advantage of cubic spline method is that slope and curvature of each cubic spline at the end point of elements are continuous. On the other hand, the cubic spline elements improve the accuracy of boundary element method solutions. The coordinates of each cubic spline element are presented in parametric form by the cubic polynomial. Because the droplet is closed surface, we used the periodic cubic-spline which periodicity conditions for the first and second derivative at the first and last nodes are imposed.

The grid independence study was performed by calculation of the droplet area as function of time. According to continuity equation, the droplet area is constant over the travel time. We have found that 98 points for droplet contour and 450 straight elements for fixed boundaries are satisfactory and any increase beyond this mesh size would lead to insignificant changes in results.

The boundary integrals of Brinkman equation are discretized over contours with sums of integrals over the boundary elements. The integrals over each boundary element should be computed accurately by the Gauss–Legendre quadrature with 12 nodes. In this way, the integral of a nonsingular function over the interval $[-1,1]$ is approximated with a weighted sum of the values of the integrand at selected points. However, when the field point ${\mathbf {r}}$ approaches the singular point $\mathbf {r_0}$, the integrands of the Eq. 5 exhibit the weak (logarithmic) and strong (high-order) singularities of the Green’s functions. The logarithmic singularity should be integrated analytically. The high-order singularity disappears as the field point ${\mathbf {r}}$ approaches the singular point $\mathbf {r_0}$. In this case, the normal unit vector is perpendicular to $({\mathbf {r}}-\mathbf {r_0})$.

After computing the local velocity at the collection points, we update the position of the points by using an explicit Euler method. Using the explicit Euler, the interface droplet is advanced in discrete time steps:

$$\begin{aligned} x^{(n+1)}= & {} \int _{t=n} ^{t=n+1} V_x {\mathrm {d}}t+x^{(n)} \approx V_x \Delta t + x^{(n)} ,\nonumber \\ y^{(n+1)}= & {} \int _{t=n} ^{t=n+1} V_y {\mathrm {d}}t+y^{(n)} \approx V_y \Delta t + y^{(n)} , \end{aligned}$$

(9)

where ${\mathbf {V}}$ is the velocity field obtained by solving the boundary integral Eq. 5 at the each collection point, n is the step number of simulation, and $\Delta t$ is the time step. The stability of the numerical algorithm is important in assuring dependably accurate results. The explicit Euler method is unstable for large values of time step. If the time step is too large, one can observe that small perturbations on the droplet interface grow, causing non-physical mesh distortions. The numerical instability depends not only on the mesh size, but also on the time step chosen. Totally, the time step depends on the surface tension, viscosity and smallest mesh length ($l_{min}$), $\Delta t= \eta _1l_{min}/\gamma$. We have found that for the present mesh size, $\Delta t=0.0004$ is a good chosen. Since relative positions of the points on the droplet contour are changed over time, we have to remesh the splines at each time step. When the relative position of two adjacent nodes on the interface is twice as big or twice as small as the initial size, the points are remeshed equidistantly using a cubic interpolation [22]. Since the boundary element method is only implemented for boundaries which are discretized, it is unnecessary to remesh the whole domain as the interface evolves.

3 Results

In this study, the effect of rigid body shape, size and position on the droplet breakup is numerically studied. In this way, we consider a flat microfluidic channel which consists an orthogonal cross-intersection having two inlets and two outlets. We define the x-axis and y-axis along the inlet and outlet channels, respectively . An obstacle is placed on the x-axis in the cross-intersection. Figure 1 presents the channel geometry of the present study. The width of inlets and outlets are equal to W. The channel height, H, is assumed to be much smaller than the channel width, $W/H=6$. The channel length of inlets and outlets are kept fixed to 6W. The carrier fluid is flowed through the left and right channels. The outlet flux is well-controlled by total flow rate at the two ends of the outlet channels. In this way, the inlet and outlet flow rates are labeled with $Q_{in}$ and $Q_{out}$, respectively. From the left channel inlet, a mother droplet with a dimensionless area $a_m$ and viscosity $\eta _2$ is flowed into the carrier fluid of viscosity $\eta _1$.

The droplet flows through the left inlet channel and approaches the cross-junction. By approaching the droplet to the cross-junction, the droplet starts to deform when it is still outside the cross-junction. When a droplet approaches the obstacle, the droplet velocity decreases and the droplet front interface experiences a stronger hydrodynamics force due to hyperbolic flow field around the obstacle. Therefore, its tip becomes elongated perpendicular to the direction of travel. As the droplet approaches closer to obstacle, its tip and rear becomes more elongated parallel to y-axis. In the low capillary number, when the droplet reaches close to the obstacle surface, front and rear of the droplet contour start taking a concave shape. Therefore, the radius of curvature of the front and rear becomes negative. By passing time, a parabolic-like neck is formed at the vicinity of the obstacle surface. Figure 3 illustrates the dimensionless neck thickness, $\delta$, as a function of dimensionless time. As shown in Fig. 3, the neck thickness monotonically decreases as the droplet approaches the obstacle. As shown in Fig. 3, the decrease rate of the neck thickness slows down when the rear surface of the droplet reaches close to the obstacle surface. It is clear that the droplet deformation depends on the capillary number, droplet size, and obstacle size [16, 17, 43]. By increasing the capillary number and droplet size, the droplet deformation increases until the droplet shape is no longer and droplet breakup takes place at a critical value of capillary number and droplet size. Therefore, depending on the droplet size and capillary number, a single droplet may breakup into two smaller daughter after colliding with obstacle (See the Supplementary Material).

Figure 4 shows subsequent snapshots in time of the droplet deformation and droplet breakup in the vicinity of the disk-shaped obstacle. At the low capillary number, the droplet collides with the obstacle but it does not break as its rear surface reaches the obstacle and droplet randomly chooses one branch of the intersection due to random flow fluctuations (see Fig. 4.a and Supplementary Material, Movie1). By increasing the capillary number, the droplet deformation increases and mother droplet breaks up into two daughter droplets (see Fig. 4.b and Supplementary Material, Movie2). Figure 5 presents the droplet velocity as a function of its dimensionless distance from the obstacle surface, $|r|=\sqrt{x^2+y^2}$. As one can see, the droplet velocity decreases as the droplet approaches to the obstacle surface. At the breakup position, the droplet velocity approaches zero at the breakup position.

Fig. 3

Time evolution of dimensionless neck thickness of the droplet. The circle obstacle is located at the center of the intersection zone. The numerical parameters are: $a_m=0.502$, $Ca^*=0.35$ and $a_o=0.0706$

Fig. 4

Subsequent snapshots of droplet dynamics for two different capillary numbers. a Droplet area $a_m=0.282$, capillary number $Ca^*=0.194$, and obstacle radius $b=0.15 (a_o=0.0706)$ (Supplementary Material, Movie 1). b Droplet area $a_m=0.282$, capillary number $Ca^*=0.20$, and obstacle radius $b=0.15$. (Supplementary Material, Movie 2)

Fig. 5

Droplet velocity as a function of droplet distance from the obstacle surface, |r|. The circle obstacle is located at the center of the intersection zone. The numerical parameters are: $a_m=0.502$, $Ca^*=0.35$ and $a_o=0.0706$

The experimental observations and numerical studies indicate that the dynamics of droplet breakup strongly depends on the capillary number, droplet size, obstacle shape and obstacle size [31, 41, 46]. Therefore, we define a critical capillary number below which droplet does not breakup and above which droplet splits into two daughter droplets and the flow into the upward and downward outlets. In this work, we will investigate the dynamics of droplet breakup in the present of circular and elliptical obstacle. In the two following subsections, we will study the collision of droplet with the circular and elliptic obstacle, respectively. We will investigate the effect of droplet size, capillary number, obstacle size and obstacle position on the dynamics of droplet breakup.

Fig. 6

Diagram mapping the breakup dynamics as a function of droplet size and modified capillary number. Symbols indicate the critical modified capillary number for each given value of droplet size. The solid-dashed curves are drawn only to guide the eye. The solid line indicates transition from the no breakup regime to breakup regime

3.1 Droplet splitting by a circular obstacle

We first perform computations to investigate the effect of droplet size on the droplet breakup dynamics. A circular obstacle with a dimensionless radius b and dimensionless area $a_o$ is placed on the x-axis in the cross section. In this way, the obstacle size and obstacle position were kept fix, and we have varied the capillary number at given value of droplet size. For each given value of droplet size, we have found a critical modified capillary number above which the droplet breakup occurs. Figure 6 indicates the various regimes of breakup and non-breakup on the modified capillary number-droplet radius diagram. The symbols represent the critically modified capillary number for a given value of droplet size which above that the mother droplet splits into two daughter droplets. Our numerical results indicate that the critical capillary number decreases by increasing the dimensionless droplet area. The physical reason for this is that droplet deformation and droplet breakup depend on the interfacial forces. The droplet deformation increases with the decrease in the interfacial forces. The interfacial force that resist the droplet deformation is proportional to the curvature of the droplet interface. On the other hand, by increasing the droplet size, the curvature of droplet interface decreases.

As shown in Fig. 6, the critical capillary number depends on the obstacle size, $a_o$. To investigate the effect of obstacle area, $a_o$, on the breakup dynamics, several simulations were carried out for obstacle area varying from 0.05 to 0.4, in which the droplet area is set to be constant. Figure 7 shows the effect of obstacle size on the breakup dynamics of droplet. The numerical prediction for critically modified capillary number indicates that by increasing the obstacle area, the critical modified capillary number decreases. Indeed, the shear force acting on the droplet surface increases as the obstacle area decreases. Therefore, when a droplet passes the large obstacle, a high diverging external flow is experienced by droplet, while a droplet passing the small circle obstacle experiences a low shear force.

Fig. 7

Effect of obstacle area on the critical modified capillary number for given value of droplet size, $a_m=0.6$. Symbols indicate the critical modified capillary number for each given value of obstacle area. The solid-dashed curves are drawn only to guide the eye. The solid line indicates transition from the no breakup regime to breakup regime

In order to investigate the effect of obstacle position on the breakup treatment, the obstacle area was kept fixed, and several simulations were performed for three different values of obstacle position. In this way, the obstacle center coordinate was moved along the x-axis with the y and y positions maintained constant at zero. At each given value of obstacle position, the droplet area was varied from 0.05 to 0.64. Figure 8 shows the effect of obstacle position on the droplet splitting. When the circular obstacle is located on the center of cross section, the velocity field around the obstacle is symmetric. However, as the obstacle is moved close to the left inlet channel, the shear force exerted on the droplet increases. Therefore, the critical capillary number decreases by moving the circular obstacle toward the left inlet channel.

Fig. 8

Critical modified capillary number as a function of mother droplet size for three given values of obstacle location. Symbols indicate the critical modified capillary number for each given value of x position of obstacle center

3.2 Droplet breakup by an elliptical obstacle

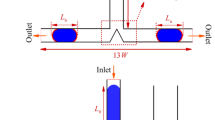
Experimental studies indicate that the breakup phenomenon depends on obstacle shape. In this subsection, we investigate the effect of obstacle shape on the droplet breakup and the size of daughter droplets. In this way, an elliptical obstacle is located at the center of cross section. Figure 9 illustrates the channel geometry of the present study in this subsection. The elliptical obstacle is located at the center of cross-section. The angle between the major axis of elliptical obstacle and x-axis is called $\theta$. As same as previous subsection, the deformable droplet flows through the left inlet channel and approaches the elliptical obstacle. Our numerical results indicate the critical modified capillary number and area ratio of the split daughter droplets depends on the orientation of elliptical obstacle.

Fig. 9

Sketch of the microfluidic channel considered. The elliptical obstacle is located at the center of cross section. The angle between major axis of the elliptical obstacle and the x-axis is called $\theta$

In order investigate the effect of droplet size on the critical capillary number, we kept fix the elliptical obstacle area $a_o$ and the elliptical orientation, $\theta$. Figure 10 illustrates the various regimes of breakup and no-breakup of a droplet colliding with elliptical obstacle which is oriented at the angle of $\pi /6$ with respect to x-axis. Our numerical results indicate that the critical capillary number decreases with increasing droplet size.

Fig. 10

Diagram mapping the breakup dynamics for elliptical obstacle as a function of droplet size and capillary number. Symbols indicate the critical capillary number for each given value of droplet size. The solid-dashed curves are drawn only to guide the eye. The solid line indicates transition from the no breakup regime to breakup regime

As we discussed in the previous subsection, as mother droplet collides with a circular obstacle located at the center of cross section, it may split into two equal daughter droplets. However, when a mother droplet collides with an elliptical obstacle, the area ratio of daughter droplets depends on the capillary number and obstacle orientation. We now study the effect of capillary number on the area ratio of daughter droplets. To investigate the influence of the capillary number on the area ratio of daughter droplets, we keep the mother droplet size and obstacle orientation fixed and vary the capillary number. The capillary number was selected above the critical capillary number where the droplet splits when colliding with the elliptical obstacle. Figure 11 illustrates the effect capillary number on the area ratio of daughter droplets with orientation angle $\theta =\pi /6$, given value of mother droplet sizes $a_m$, two different values of elliptic obstacle area $a_o=0.085$ and $a_o=0.123$. We have found that by increasing the capillary number, the area ratio of daughter droplets increases. However, at high capillary numbers, the area ratio of daughter droplets is independent of capillary number. This result is in a good agreement with the previous studies [41].

Fig. 11

Effect of modified capillary number on the area ratio of daughter droplets for given value of droplet size, $a_m=0.282$ and obstacle orientation $\theta =\pi /6$. Symbols indicate the critical capillary number for each given value of obstacle area. The solid-dashed curves are drawn only to guide the eye

Fig. 12

Subsequent snapshots of droplet splitting at three different values of elliptical obstacle orientation: a $\theta =\pi /4$, b $\theta =\pi /2$, and c) $\theta =3\pi /4$

Fig. 13

Stream line pattern of the flow around the droplet and elliptical obstacle

Fig. 14

Effect of orientation angle ( in degree) of elliptical obstacle on the area ratio of daughter droplets for given value of droplet size, $a_m=0.282$ and obstacle area $a_o=0.085$. The solid-dashed curves are drawn only to guide the eye

Fig. 15

Droplet splitting by an elliptical obstacle at a $\theta =\pi /4$, and b $\theta =3\pi /4$

It is clear that when an elliptical obstacle is located at the center of cross section with orientation angle $\theta =0$ or $\theta =\pi /2$, the velocity field of carrier fluid is symmetric with respect to the x-axis. Therefore, the mother droplet tends to split into two equal daughter droplets. Figure 12 illustrates the sequence of snapshot of droplet motion and droplet breakup in the present of the elliptical obstacle at the three different values of orientation angle. Figure 12a and c shows the time evolution of the droplet past an elliptic obstacle at $\theta =\pi /4$ and $\theta =3\pi /4$, respectively. As shown in Fig. (12a, c), the mother droplet splits into two unequal daughter droplets, while as a mother droplet collides with elliptical obstacle at $\theta =\pi /2$, it breakups into two equal daughter droplets (see Fig. 12b). In this way, we now investigate the effect of orientation angle on the area ratio of daughter droplets, $a_d/a_u$ where $a_d$ and $a_u$ are the droplet area of daughter droplet flows through the down and up outlet channel, respectively. Figure 14 illustrates the effect of orientation angle on the area ratio of daughter droplets. As one can see, the area ratio of daughter droplets at the three values of orientation angle 0, $\pi /2$, $\pi$ is equal to one. In order to better understanding, we define the length distance between the elliptic surface and down/up left corner of cross section by $D_u$ and $D_d$. It is clear that when the orientation angle is smaller than the $\pi /2$, the $D_d$ is smaller than the $D_u$. Therefore, the area ratio of the down daughter droplet to up daughter droplet is smaller than one. At the orientation angle 0, $\pi /2$, and $\pi$, the $D_u$ is equal to $D_d$ and the area ratio of daughter droplets is equal to one (see Fig. 15a, b). As shown in Fig. 14, the area ratio of down daughter droplet to up daughter droplet, $a_d/a_u$, has the minimum value at the orientation angle $\pi /4$. To better understanding, the streamline pattern of the flow around the droplet and elliptical obstacle is shown in Fig. 13.

4 Conclusion

The splitting a droplet past through an obstacle in am orthogonal cross section was investigated numerically by solving the depth-averaged Brinkman equation and employing the boundary element method. The effect of the capillary number, droplet size, obstacle shape and obstacle position on the dynamics of droplet breakup has been studied. Numerical results indicate that the critical capillary number decreases by increasing the droplet size and obstacle size. We have found that the area ratio of daughter droplets depends on the obstacle shape and obstacle position. Understanding of dynamics of droplet breakup might be helpful to control the size distribution of droplets in microfluidics. We hope that this study helped for development of drug delivery and oil recovery processes.