Effects of topological changes in microchannel geometries on the asymmetric breakup of a droplet

Abstract

Passive asymmetric breakups of a droplet could be done in many microchannels of various geometries. In order to study the effects of different geometries on the asymmetric breakup of a droplet, four types of asymmetric microchannels with the topological equivalence of geometry are designed, which are T-90, Y-120, Y-150, and I-180 microchannels. A three-dimensional volume of fluid multiphase model is employed to investigate the asymmetric rheological behaviors of a droplet numerically. Three regimes of rheological behaviors as a function of the capillary numbers Ca and the asymmetries As defined by As = (b1 − b2)/(b1 + b2) (where b1 and b2 are the widths of two asymmetric sidearms) have been observed. A power law model based on three major factors (Ca, As and the initial volume ratio r ₀) is employed to describe the volume ratio of two daughter droplets. The analysis of pressure fields shows that the pressure gradient inside the droplet is one of the major factors causing the droplet translation during its asymmetric breakup. Besides the above similarities among various microchannels, the asymmetric breakup in them also have some slight differences as various geometries have different enhancement or constraint effects on the translation of the droplet and the cutting action of flows. It is disclosed that I-180 microchannel has the smallest critical capillary number, the shortest splitting time, and is hardest to generate satellite droplets.

1 Introduction

Droplet-based microfluidics that could generate and control uniform droplets of sizes in micron scale for some special applications through the interaction of immiscible phases in microchannels, has drawn much attention in recent years (Teh et al. 2008; Wang et al. 2011; Seemann et al. 2012). This fantastic technology has been employed in many fields such as the chemical synthesis through reactions (Song et al. 2006), the generation of drug delivery systems (Xu et al. 2009), the fabrication of micro-particles (Dendukuri et al. 2005), protein crystallization (Zheng et al. 2004), and so on.

The breakup of droplets plays an important role in the emulsion industries, chemical processes involving immiscible phases, and droplet-based microfluidics due to its severe effects on the droplet size distribution, especially for the asymmetric breakup of droplets. In industrial processes involves the mixing of two immiscible phases, the breakup of mother drops is generally an asymmetric process as the flow around it is almost impossible to be symmetric. In addition, the controlled asymmetric breakup of mother drops through microfluidics is able to provide groups of droplets with different sizes but of same numbers. The mixing of these droplets might generate emulsions of some specific droplet size distribution. Thus, it is necessary and desirable to investigate the breakup of a droplet, especially the asymmetric breakup.

The pioneer work on the rheology of a droplet was done by Taylor (1934) who used four-roll mills to generate outer flow fields. After that, the investigation on the deformation and breakup of a droplet has been done by many researchers. In the early works, they mainly focus on the rheological behaviors of droplets in well-defined infinite flows such as the linear two-dimensional flows (Bentley and Leal 1986), simple shear flows (Janssen and Meijer 1993), and extensional flows (Stone 1994; Navot 1999). The critical capillary numbers Ca _cr are specified in their works to determine the critical condition of breakups. In the recent works, the investigation of the deformation and breakup of droplets concentrates on the confined spaces such as the microchannels of various geometries. Diverse microfluidic devices like cross-like microchannels (Tan et al. 2008; Cubaud 2009; Che et al. 2011), T-junctions (Link et al. 2004; Leshansky and Pismen 2009; Afkhami et al. 2011; Samie et al. 2013), Y-junctions (Ménétrier-Deremble and Tabeling 2006; Carlson et al. 2010; Abate and Weitz 2011), microchannels with obstacles (Protière et al. 2010; Salkin et al. 2012; Li et al. 2014), and microchannels of other geometries (Galinat et al. 2007; Sharma and Fang 2014) have been designed to study the symmetric and asymmetric breakup of drops.

As the asymmetric breakups of drops always occur naturally in industrial processes and daily lives, they attracted more attention from researchers lately. Link et al. (2004) successfully introduced two microfluidic devices, T-junctions with unequal arms and straight channels with isolated obstacles to break up droplets asymmetrically. After that, Ménétrier-Deremble and Tabeling (2006) studied the asymmetric breakup of drops in microchannels with branches of various angles experimentally. Salkin et al. (2012) investigated the breakup dynamics of droplets in microchannels with a linear obstacle through experiments and theoretical analyses. They found out that the critical capillary number to break a drop as a function of its size is nonmonotonic when the viscosity contrast between dispersed and continuous phases is greater than zero; but when the viscosity contrast is less than or equal to zero, the critical capillary number versus the size of the drop is monotonic. Bedram et al. (2015) introduced a novel micro-device with valves to generate unequal-sized droplets. Their method reduced the dependence of the droplets volume ratio on the inlet velocity of the system significantly.

In microfluidics, the geometry of microchannels will severely impact and change the flow patterns which could be generated in micro-devices (Wang et al. 2012; Guan et al. 2015). Due to the passive asymmetric breakup of droplets through microfluidics mainly rely on the outer flows which are severely dependent on the geometries of the microchannels, the geometrical design of microchannels to enhance the control of droplet breakups is very important. All the previous works, through theoretical, experimental, and numerical studies, have designed many types of microfluidic devices to complete the asymmetric breakup of droplets according to demands. However, most of these works only discussed one particular type of microchannels. The comparison of microchannels with various geometries has not been done, and the differences and similarities among diverse microchannels have not been discussed systematically. Thus, in this paper, four types of asymmetric microchannels with the topological equivalence of geometry are designed, which are T-90, Y-120, Y-150, and I-180 microchannels, in order to study the effects of different geometries on the asymmetric breakup of a droplet.

Recently, Wang and Yu (2015) investigated numerically the asymmetric breakup of droplets suspended in axisymmetric extensional flows generated in a cross-like micro-device by using a three-dimensional (3D) VOF model. They presented a power law model to predict the volume ratio of two unequal-sized daughter droplets, which is based on the analysis of three major factors: the cutting speed of the continuous phase (proportional to the capillary number Ca), the translation speed of the droplet (proportional to the asymmetry As), and the initial volume ratio r ₀. Based on their works, the asymmetric breakups of a droplet in the designed four types of microchannels will be investigated numerically in this paper by using 3D VOF model. The similarities and differences of the breakup processes in these different microchannels will be discussed carefully and systematically.

2 Mathematical formulations

2.1 The geometry of microchannels

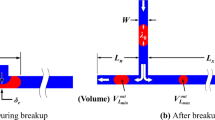
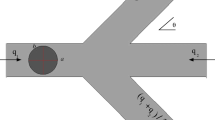
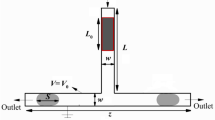
The geometries of various microchannels, which will be employed to study the dynamics of the asymmetric breakup of drops, are shown in Fig. 1. The first microchannel is a T-junction with two asymmetric arms, whose 3D sketch is shown in Fig. 1a. The main channel, through which the fluid enters the micro-device, has a square cross section, and the two equal-length arms, through which the fluid flows out of the device, have rectangle cross sections with different widths. Figure 1b presents the details of the asymmetric geometry of the T-junction from its top view, in which the unit is μm. Here the widths of sub-channels b1 and b2 are 52 and 48 μm, respectively, but the width values could be changed in our investigation in order to get various asymmetries. However, their sum must equal to the width b of the main channel. Based on this T-junction, all other microchannels are obtained by changing topologically the geometry of the T-junction. The angle between the main channel and two arms is 90° for T-junction (Fig. 1-c1). By increasing this angle to 120°, 150°, and 180°, we get different microchannels of Y shapes (Fig. 1-c2, c3) and I shape (Fig. 1-c4), respectively. The microchannel of a I-180 shape is just like a straight rectangular microchannel with a linear obstacle of an infinite length. Here, the obstacle is ideal and like straight line with a width approaching zero. Thus, these four somehow related microchannels are asymmetric since they all have two downstream sub-channels with different widths. Naturally, the drop which enters the main channel will be broken into two unequal daughter droplets in the junction of the two downstream sub-channels.

Fig. 1

a The sketch of a 3D T-junction. b The size (in μm) of the geometry of T-junction from the top view. c The topological changes from microchannel with T shape to microchannel with Y shapes and I shape. C1-C4: T-90, Y-120, Y-150, and I-180 microchannel

2.2 Numerical model

Volume of fluid (VOF) model, one of numerical methods which have the high accuracy in the calculation of three-dimensional flows, has been successfully used to simulate the droplet generation, breakup and merging in microchannels (Sang et al. 2008; Afkhami et al. 2011). This model could be used to study the two-phase flow system by solving the governing equations including the equation of continuity, the equation of motion, and the volume fraction equation simultaneously for each phase. These governing equations are

$$\frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \varvec{v}) = 0,$$

(1)

$$\frac{{\partial (\rho \varvec{v}\text{)}}}{\partial t} + \nabla \cdot (\rho \varvec{vv}) = - \nabla \varvec{p} + \nabla \cdot [\mu (\nabla \varvec{v} + \nabla \varvec{v}^{T} )] + \rho \varvec{g} + \varvec{F},$$

(2)

$$\frac{{\partial a_{\text{d}} }}{\partial t} + \varvec{v} \cdot \nabla a_{\text{d}} = 0.$$

(3)

In these equations, ρ denotes the volume averaged density defined by Eq. (4), μ is the volume averaged viscosity defined by Eq. (5), and F represents the continuum surface force (CSF) (Brackbill et al. 1992) which is added to the momentum equation in order to include the interfacial tension and defined by Eq. (6),

$$\rho = a_{\text{d}} \rho_{\text{d}} + (1 - a_{\text{d}} )\rho_{\text{c}} ,$$

(4)

$$\mu = a_{\text{d}} \mu_{\text{d}} + (1 - a_{\text{d}} )\mu_{\text{c}} ,$$

(5)

$$\varvec{F}\text{ = }\varvec{\sigma}\frac{{\rho k_{\text{d}} \nabla a_{\text{d}} }}{{\frac{1}{2}(\rho_{\text{d}} + \rho_{\text{c}} )}},$$

(6)

where d and c are densities of the dispersed and continuous phase, respectively, a_d is the volume fraction of the dispersed phase, μ _d and μ _c are viscosities of the dispersed and continuous phase, respectively, σ is the interfacial tension, and k _d is the curvature calculated from the divergence of the unit surface normal vector (Eq. 7),

$$k_{\text{d}} = {\mathbf{\nabla }} \cdot \hat{\varvec{n}} = {\mathbf{\nabla }} \cdot \frac{\varvec{n}}{{\left| \varvec{n} \right|}} = {\mathbf{\nabla }} \cdot \frac{{{\mathbf{\nabla }}a_{\text{d}} }}{{\left| {{\mathbf{\nabla }}a_{\text{d}} } \right|}}{\kern 1pt} {\kern 1pt} .$$

(7)

Here, we employ a transient, three-dimensional multiphase model from the commercial software FLUENT to track the deformation of free interfaces and use the pressure-implicit with splitting of operations (PISO) algorithm for pressure–velocity coupling. Spatial discretization terms are set as the followings: PRESTO! method for the pressure term, the second order upwind for the momentum equation, and the Geo-Reconstruction scheme for the volume fraction.

In order to neglect the influence of the buoyancy-driven velocity in a typical oil–water microfluidic system (De Menech et al. 2008), the densities of the droplet and continuous phase are set equal. The surface tension is 5 mN/m. The droplet and continuous phase are both Newtonian fluids, whose viscosities are 0.0005 and 0.001 Pa s, respectively, and the initial volume of the mother droplet is fixed to 1.149 × 10⁶ μm³. The inlet of the main channel is the velocity inlet and the condition at the outlets is the pressure outlet. Assuming that the wall is completely wet, the wall is a no-slip stationary wall with the contact angle 180°.

The volume ratio of two unequal daughter droplets is closely associated with the ratio of the volume flow rates of two asymmetric sub-channels. Assuming that we have a microchannel of length l, whose cross section is rectangular with width w and height h, the flow rate q _v passing through it is calculated by

$$\begin{aligned} q_{v} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {u_{x} } } (y,z){\text{d}}y{\text{d}}z \\ & = - \frac{\Delta p}{\mu l}\left( {\frac{hw}{24}(h^{2} + w^{2} ) - \frac{8}{{\pi^{5} }}\sum\limits_{n = 1}^{\infty } {\frac{1}{{(2n - 1)^{5} }}\left[ {h^{4} {\text{th}}\left( {\frac{2n - 1}{2h}\pi w} \right){ + }w^{4} {\text{th}}\left( {\frac{2n - 1}{2w}\pi h} \right)} \right]} } \right), \\ \end{aligned}$$

(8)

where Δp is the pressure drop in the channel.

2.3 Validation of the numerical method

The numerical model is first verified for Newtonian fluids by comparing our calculated results to those obtained by Stone and Leal (1989) for the deformation at the equilibrium of a droplet suspended in an axisymmetric extensional flow. The extensional flow is defined by

$$\varvec{u}^{\infty } = \frac{Ca}{2}\left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & { - 2} \\ \end{array} } \right)x,$$

(9)

where the capillary number Ca = Gaμ _c/σ, G is the shear rate, and a is the radius of the initial spherical droplet. Deformation parameter D = (L − S)/(L + S) is utilized to describe the deformation degree of a droplet, where L and S are the half-length and half-width of the droplet, respectively.

As shown in Fig. 2, the calculated results (square and circle) are perfectly consistent to those obtained by Stone and Leal (1989) for both λ = μ _d/μ _c = 1.0 and 0.1, which could verify the validity of the numerical model.

Fig. 2

D versus Ca for the drop deformation at the equilibrium in an axisymmetric extensional flow. The open circle and square represent our calculated results through VOF method, and the solid line and dashed line represent the results of Stone and Leal (1989)

3 Results and discussions

Rheological behaviors of the droplet under the action of asymmetric flows generated in the microchannels with four different geometries (see Fig. 1) have been investigated in this section. As shown in Fig. 3, the asymmetric geometries of microchannels could generate asymmetric flow fields near the junction, and sequentially could deform and breakup the droplet trapped at the junction asymmetrically. The asymmetric breakup of a droplet is much more complicated than the symmetric case. For the latter, generally, only the capillary number Ca is important, and the critical capillary number Ca _cr is determined to check whether the droplet will break or not. However, for the asymmetric breakup of a droplet, not only Ca but also the asymmetry As of flow fields play very important roles. Here, Ca is defined by Ca = μ _c U/σ, where U is the average velocity of the continuous phase at the inlet of the main channel. In this paper, as the asymmetry of flow fields is generated due to the different widths of two sub-channels, and as the ratio of volume flow rates through two sub-channels is proportional to the width ratio Q1/Q2 = (b1/b2)^2.570, the asymmetry As could be defined by As = (b1 − b2)/(b1 + b2). The range of As is from 0 to 1. The value 0 means that the flow field is symmetric, and the value 1 means an extremely huge asymmetry for which the width of the narrow sub-channel b2 is zero in our system and the droplet always moves out of the micro-device through the wide sub-channel without any breakup.

Fig. 3

Asymmetric flow fields near the junctions in T-90 (a), Y-120 (b), Y-150 (c), and I-180 (d) microchannels, respectively

3.1 The asymmetric breakup of a droplet in T-90 microchannel

3.1.1 Droplet breakup regimes

The rheological behaviors of a droplet at an asymmetric T-junction are investigated in this section. Various responses of the droplet have been observed at the junction when it moves into the main channel with different volume flow rates of the continuous phase (CP). If the volume flow rate Q ₀ of CP is small, no breakup will occur and the droplet will move out of the micro-device through the wide sub-channel; if Q ₀ is sufficiently large, an asymmetric breakup of the droplet will occur and two daughter droplets with unequal sizes will move out of the device separately through different sub-channels. These various behaviors could be divided into three categories: no-breakup (NB, Fig. 4a), retraction breakup (RB, Fig. 4b), and direct breakup (DB, Fig. 4c).

Fig. 4

Three regimes for the asymmetric breakup of a droplet in T-90 microchannel with As = 0.08. a No-breakup (NB) for Ca = 3.50 × 10⁻³, b retraction breakup (RB) for Ca = 3.60 × 10⁻³, c direct breakup (DB) for Ca = 3.84 × 10⁻³

As for the asymmetric T-junction with As = 0.08, the mother droplet arriving at the T-junction will penetrate into the two sub-channels with different widths (Fig. 4). Due to the resistance difference of the two sub-channels, the half moving into the sub-channel with a bigger width is relatively larger than the other half. When Ca is very low (Ca = 3.50 × 10⁻³), the mother droplet could not be broken. The smaller part moving into the narrow sub-channel will retreat under the drag of the bigger part due to the surface tension when it reaches its maximum extension. Eventually, the entire droplet will penetrate into the wide sub-channel and move out of the device without a breakup (NB, Fig. 4a). Along with the increase of Ca (Ca = 3.60 × 10⁻³), although the flow gets stronger gradually, it still could not break the mother droplet directly. Nevertheless, the droplet is elongated more and the neck bridge connecting the small and large half gets much thinner. Due to the relatively strong surface tension, the smaller part moving into the narrow sub-channel begins to recoil when it reaches its maximum extension and almost at the same time the thin neck is broken due to the increase of the upstream pressure. Then, two daughter droplets move out of the micro-device from the two different sub-channels, respectively. This process is called retraction breakup (RB, Fig. 4b). When Ca is elevated to 3.84 × 10⁻³, the mother droplet is elongated continuously and finally obstructs the two sub-channels. As the gutters are small, which leads to a high local hydrodynamic resistance, eventually the droplet breaks up into two unequal daughter droplets due to the increase of the upstream pressure. Then, they move out of the micro-device from their own sub-channels, respectively. This case is called direct breakup (DB, Fig. 4c).

In order to study the dynamic of asymmetric breakup of a droplet deeply, three regimes of the asymmetric breakup of a droplet in the T-90 microchannel as a function of Ca and As are shown in Fig. 5. Different regimes are marked by different symbols. When As is fixed, rheological behaviors of the mother droplet will vary from NB to RB and to DB along with the increment of Ca. When Ca is fixed, the transition from NB to RB and to DB will occur along with the decrease of the asymmetry As of the microchannel. Thus, in the regime (NB zone marked by triangles) with low Ca or high As, the mother droplet could not break up and will move out of the micro-device from the wide sub-channel due to the relatively weak viscous stress or the quick translation of the droplet caused by the large asymmetry of the flow. Along with the increase of Ca or the decrease of As, the regime transits into RB zone (marked by circles), and there is a boundary (the dash curve) to distinguish the zones of NB and RB. This important curve is the critical capillary number (Ca _cr) as a function of the asymmetry. When As increases, the value of Ca _cr increases as well, which means that the faster translation requires a bigger flow to break the droplet up. As a critical zone, the width of RB is very narrow and gets wider gradually along with the increase of As. In this regime, the mother droplet breaks up when a retraction occurs for its smaller half. Along with the increase of Ca or the decrease of As, the cutting action becomes stronger and plays a principal role, compared to the oriented displacement of the droplet caused by the asymmetry. In this case, the droplet breaks up directly to generate two unequal daughter droplets without any retraction for the smaller half. When As = 0, which means a symmetric case, the regime is just divided into two zones of NB and DB by the critical capillary number. From the above description, it could be concluded that the competition between the cutting action of flow in the T-junction and the oriented movement of the droplet from the narrow sub-channel to the wide caused by the asymmetry could decide whether the mother droplet will break up asymmetrically or not in this micro-device.

Fig. 5

Regimes of the asymmetric rheological responses of a droplet as a function of Ca and As (triangle NB, open circle RB, and square DB) in T-90 microchannels. The dash curve is the critical capillary number (Ca _cr) as a function of the asymmetry

3.1.2 The power law model

One of the most important purposes in droplet manipulations in microchannels is to determine whether the droplet will break up or not when it arrives at the asymmetric T-junction. Another important goal is to predict the volume ratios (r _s = V1/V2) of the two unequal daughter droplets. Comparing the physical behaviors of the asymmetric breakup of a droplet in T-90 microchannels to those in a cross-like micro-device studied by Wang and Yu (2015), it could be seen that there are many similarities. Thus, in this paper, the similar analysis for the rheological behaviors and the similar model to predict the volume ratio could be employed.

In the previous section, the effects of Ca and As on the asymmetric breakup of a droplet in T-90 microchannels are discussed generally. As for the symmetric breakup, the value of Ca does not change r _s (r _s = 1), but will change the time needed to break the extending droplet. However, in the asymmetric breakup process, the deformed droplet will shift in the direction perpendicular to the cutting direction due to the asymmetry, which will affect the final volume ratios of the daughter droplets. The translation speed should be proportional to As. Thus, the translation distance is proportional to the product of the translation speed and the time needed to break up the droplet, i.e., As × (a/Ca), where a is the characteristic thickness of the extending droplet. Thus, r _s is proportional to As, but inversely proportional to Ca. When Ca is too huge, the droplet would have no time to shift from the narrow sub-channel to the wide one. Thus, in this case, r _s should be closed to the initial volume ratio r ₀ very much. r ₀ is a volume ratio of two parts of a droplet when the droplet is moving in the main channel and far from the junction, which could be calculated through the ratio of initial volume flow rates of the two sub-channels. From the above analysis, it is natural to know that the power law model (Wang and Yu 2015) to predict the volume ratio r _s of unequal daughter droplets generated in a cross-like micro-device could also work here. Thus, the model calculating r _s as a function of Ca and As is

$$r_{\text{s}} = \frac{{eAs^{\alpha } }}{{(Ca - Ca_{\text{cr}} )^{\beta } }} + r_{0} ,$$

(10)

where the three parameters e, α, and β are all fitted from the data of numerical calculations, and Ca _cr can be obtained from Fig. 5. The critical capillary numbers are 2.16 × 10⁻³, 2.77 × 10⁻³, 3.54 × 10⁻³, 4.34 × 10⁻³, and 5.20 × 10⁻³ for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively. The precise calculation of the initial volume ratio r ₀ is not so straightforward. Fortunately, it is known that r ₀ is proportional to the ratio of initial volume flow rates of the two sub-channels. Thus, Eq. (11) is introduced to calculate r ₀.

$$r_{0} = k(Q1/Q2) = k\left( {\frac{1 + As}{1 - As}} \right)^{2.570} ,$$

(11)

where Q1 and Q2 are the initial volume flow rates through the wide and narrow sidearm, respectively, when the droplet is moving in the main channel and far from the junction, and k is a parameter which could be fitted from the data of numerical calculations.

The results of the simulation data and fitted lines are shown in Fig. 6 which is the volume ratio r _s versus Ca for various asymmetries. When Ca approaches to Ca _cr, r _s will goes to infinity. Along with the increase of Ca, r _s decreases and gradually approaches a constant. This is consistent to our qualitative analysis in the second paragraph of this section. Comparing the simulation data and the fitted lines of the power law model, it is clear that the power law model could describe very well the volume ratio of two unequal daughter droplets generated in the asymmetric T-90 microchannels. The fitted parameters e, α, and β are 1.240, 1.160, and 0.3937, respectively. When Ca goes to infinity, r _s will be the initial volume ratio r ₀. Through fitting, it is specified that r ₀ are 1.181, 1.293, 1.419, 1.560, and 1.722 for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively. Thus, the corresponding parameters k are 0.9617, 0.9500, 0.9416, 0.9324, and 0.9273, respectively.

Fig. 6

Volume ratios r _s of two daughter droplets versus Ca in T-90 microchannels

3.1.3 Analysis of pressure fields during the asymmetric breakup

In the asymmetric breakup of a droplet, the asymmetry of the flow system results in the translation of droplet. The translation of the droplet could be caused by two mechanisms: one is the asymmetric drag of CP on the droplet, and the other is the asymmetric pressure fields inside and outside the droplet. In this section, the pressure fields during the asymmetric breakup of a droplet are analyzed systematically. The pressure difference Δp between two sides of the droplet might cause the bulk displacement of the droplet, and the inhomogeneous pressure inside the drop due to the difference of interface curvatures might generate an internal circulation which causes the displacement of the droplet mass center. Thus, the pressure distribution around and inside the droplet should be investigated.

The analyses of pressure fields for a droplet moving in an asymmetric T-junction (As = 0.08) when Ca is low (Ca = 3.20 × 10⁻³) are shown in Fig. 7a–c. The pressures shown in Fig. 7, b are measured on the central axes (a, b and a′, b′) of two sub-channels. As the widths of sub-channels are different, X coordinates of point b and b’ are a little bit different, but Y coordinates of them are the same and equal to zero. Pressures at different time during the movement of the droplet are exhibited in Fig. 7a, b. Before this mother droplet arrives at the junction, the pressure distributions in the two sub-channels at 0.07204 s are the same. When it begins to penetrate into the two sub-channels, the pressure curve is divided into three segments due to the pressure jump caused by the curved interface of the droplet. The pressure inside the droplet is much higher than those outside as shown in the figures. Due to the smaller part penetrating into the narrow sub-channel has a bigger interface curvature than the other part penetrating into the wide sub-channel, inside the droplet, the pressure near the end of the small half is higher and decrease gradually toward the other end. However, outside the droplet, the situation is just opposite. The pressure in sub-channel near the end of the small half is lower than that near the big half. Thus, the pressure gradient inside the droplet will be one of the major factors causing the translation of the mass center of the droplet, while the outside pressure difference between two ends of the droplet will not. During the process after time t = 0.08637 s, the pressure near the end of the small half is always higher than that near the other end, and the pressure difference increases along with time before the small half retracts out of the narrow sub-channel, which is shown clearly in Fig. 7c. Eventually, the mother droplet will move into the wide sub-channel entirely.

Fig. 7

Analyses of pressure fields for a droplet moving in an asymmetric T-junction with As = 0.08 and Ca = 3.20 × 10⁻³. Pressures on the central axes (a, b, and a′, b′) of the two sub-channels at time = 0.07204, 0.08245, 0.08637, and 0.08816 s (a), and at time = 0.07204, 0.08816, 0.088917, 0.08956, and 0.09325 s (b). c Pressure fields of the droplet and the entire microchannel at time = 0.08367, 0.08816, 0.08735, 0.08917, 0.08956, and 0.08983 s

Figure 8a–c exhibits the pressure fields for a droplet moving in an asymmetric T-junction (As = 0.08) for Ca = 3.60 × 10⁻³. Under this condition, the mother droplet will break up during its retraction. Similar to the process shown in Fig. 7a–c, the pressure distributions in the two sub-channels are the same at time = 0.07204 s when the mother droplet is still in the main channel. When it reaches the asymmetric T-junction and begins to penetrate into the two sub-channels, the pressure curve is also divided into three segments due to the pressure jump caused by the curved interface of the droplet. Inside the droplet, the pressure near the end of the small half is higher than that near the other end; outside the droplet, the pressure in sub-channel near the end of the small half is lower than that near the big half. The difference between NB and RB process occurs at time = 0.08059 s when the front end of the small half in the narrow sub-channel is retracting and the neck connecting the small and big half is breaking at the junction (Fig. 8b, c). At this moment, the pressure in the neck increases rapidly (Fig. 8c) and a peak appears in the pressure curve shown in Fig. 8b. After the breakup of the droplet, its daughter droplets are driven by the continuous phase and move out of the micro-device separately. As shown in Fig. 8b, c, the small daughter droplet has a relatively higher pressure than the big one due to its larger interface curvature.

Fig. 8

Analyses of pressure fields for a droplet moving in an asymmetric T-junction with As = 0.08 and Ca = 3.60 × 10⁻³. Pressures on the central axes (a, b, and a′, b′) of the two sub-channels at time = 0.06029, 0.07202, 0.07754, and 0.08009 s (a), and at time = 0.06029, 0.08009, 0.08059, and 0.08194 s (b). c Pressure fields of the droplet and the entire microchannel at time = 0.07754, 0.07841, 0.07926, 0.08009, 0.08059, and 0.08084 s

Along with the increase of Ca (Ca = 2.40 × 10⁻²), the mother droplet will break up directly under the high upstream pressure. Figure 9a, b exhibits the pressure fields for this process of DB at different time. The most significant difference between DB and the previous two cases is that there is always a peak in the pressure curve during the entire process (Fig. 9b). As shown in Fig. 9b, inside the droplet, the pressure around the junction (the neck zone) is always the highest, which causes the continuous elongation and direct breakup of the droplet. Comparing Figs. 8b, 9a, the exact location of the peak point or, in other words, the asymmetric breakup point of RB is a little closer to the wide sub-channel than that of DB. This is an indirect proof that the droplet translation (from the narrow sub-channel to the wide one) perpendicular to the cutting direction will occur for a RB process, hardly for a DB process.

Fig. 9

Analyses of pressure fields for a droplet moving in an asymmetric T-junction with As = 0.08 and Ca = 2.40 × 10⁻². a Pressures on the central axes (a, b, and a′, b′) of the two sub-channels at time = 0.01022, 0.01122, 0.01170, and 0.01202 s. b Pressure fields of the droplet and the entire microchannel at time = 0.1162, 0.01170, 0.01182, 0.01202, 0.01222, and 0.01234 s

3.2 The asymmetric breakup of a droplet in Y-120 and Y-150 microchannel

3.2.1 Droplet breakup regimes

The asymmetric Y-120 and Y-150 microchannels are designed based on the topological change of T-90 microchannel to study the asymmetric breakup of a droplet in this section. Similar to those shown in Fig. 4, three typical regimes of the asymmetric breakup of a droplet in each of them have also been observed (Figs. 10, 11).

Fig. 10

Three regimes for the asymmetric breakup of a droplet in Y-120 microchannel with As = 0.08. a No-breakup (NB) for Ca = 2.40 × 10⁻³, b retraction breakup (RB) for Ca = 2.48 × 10⁻³ and c direct breakup (DB) for Ca = 2.64 × 10⁻³, respectively

Fig. 11

Three regimes for the asymmetric breakup of a droplet in Y-150 microchannel with As = 0.08. a No-breakup (NB) for Ca = 1.84 × 10⁻³, b retraction breakup (RB) for Ca = 1.97 × 10⁻³, and c direct breakup (DB) for Ca = 2.05 × 10⁻³

As for the asymmetric Y-120 junction with As = 0.08, the mother droplet arrives at the Y-120 junction and then penetrates into the two sub-channels (Fig. 10). When Ca = 2.40 × 10⁻³, due to the flow is too weak, the mother droplet cannot break up and will move out of this micro-device from the wide sub-channel (Fig. 10a, NB). When Ca is increased continuously (Ca = 2.48 × 10⁻³), the mother droplet will break up with some retraction of the end of the smaller half from the narrow sub-channel to the wide (Fig. 10b, RB). Along with the increase of Ca (Ca = 2.64 × 10⁻³), the mother droplet is elongated continuously until it breaks up into two unequal daughter droplets due to the increase of the upstream pressure (Fig. 10c, DB).

Similarly, in the Y-150 microchannel with As = 0.08, when Ca is very low (Ca = 1.84 × 10⁻³), the mother droplet does not break up and just moves out of the microchannel from the wide sub-channel (Fig. 11a, NB). When Ca is elevated to 1.97 × 10⁻³, the mother droplet breaks up with some retraction of the end of the smaller half from the narrow sub-channel to the wide (Fig. 11b, RB). When Ca is increased to 2.05 × 10⁻³, mainly due to the increase of the upstream pressure, the mother droplet directly breaks up without any retraction. Then, the two unequal daughter droplets move out of the micro-device from the different sub-channels (Fig. 11c, DB).

By changing As and Ca systematically, three regimes of the asymmetric breakup of a droplet are observed and shown in Fig. 12a (for Y-120 microchannel) and in Fig. 12b (for Y-150 microchannel), just similar to those shown in Fig. 5. Due to the asymmetry of the flow system, the mother droplet might either break up asymmetrically or move out of the micro-device, which are decided by the competition between the cutting action of the flow and the oriented translation of the droplet in the microchannels. Along with the increase of Ca or decrease of As, the rheological response of the mother droplet transits from NB to RB and then to DB. In NB region, due to the relatively strong surface tension or the quick movement of the droplet caused by the large As, the mother droplet cannot break up. In RB region, compared to those in NB region, the little increase of Ca or little decrease of As makes the droplet break up with some retraction. In DB region, the strong cutting action of flow or the low translation speed makes the droplet break up directly without any retraction. Moreover, the boundary (the dash curve) between NB and RB zone is the curve of the critical capillary number as a function of As. When As increases, the value of the critical capillary number increases as well. When As = 0, the droplet will break up in a symmetric Y-120 microchannel when Ca ≥ 6.0 × 10⁻⁴; while, it will break up in a symmetric Y-150 microchannel just when Ca ≥ 4.0 × 10⁻⁴. Thus, the mother droplet is easier to break up in Y-150 than in Y-120 microchannel. Comparing the two curves of the critical capillary number in Y-120 and Y-150 microchannel, it is obvious that Ca _cr for the droplet breakup in Y-120 microchannel is bigger than that in Y-150 microchannel when As is fixed. Thus, the bigger the angle between the main channel and sub-channels is, the easier the mother droplet breaks up asymmetrically. For both Y-120 and Y-150 microchannels, the width of RB gets wider gradually along with the increase of As. The width of RB for Y-120 microchannel is a little wider than that for Y-150 microchannel with a fixed As. The reason might be that the geometry of Y-120 microchannel has a less hindrance to the translation of the mother droplet than that of Y-150 microchannel.

Fig. 12

Regimes of the asymmetric rheological responses of a droplet as a function of Ca and As (triangle NB, open circle RB, and square DB) in Y-120 microchannels (a), and Y-150 microchannels (b). The dash curve is the critical capillary number Ca _cr as a function of the asymmetry

3.2.2 The power law model

The effects of Ca and As on the asymmetric breakup of a droplet in Y-120 and Y-150 microchannel are very similar to that in T-90 microchannel. Thus, Eq. (10) based on the power law model could also be applied for the description of the volume ratio of the two daughter droplets in Y-type microchannels. The critical capillary numbers can be obtained in Fig. 12. Ca _cr are 1.46 × 10⁻³, 2.00 × 10⁻³, 2.44 × 10⁻³, 3.04 × 10⁻³, and 3.74 × 10⁻³ for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12) in Y-120 microchannnel, respectively. Also, Ca _cr are 1.14 × 10⁻³, 1.48 × 10⁻³, 1.92 × 10⁻³, 2.40 × 10⁻³, and 2.96 × 10⁻³ for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12) in Y-150 microchannnel, respectively. As both Y-120 and Y-150 microchannel are generated from the topological changes of T-90 microchannel, the initial volume ratio r ₀ of them could also be calculated by Eq. (11). Figure 13 shows the result of the simulation data and the fitted lines (by Eqs. 10, 11) of r _s as a function of Ca for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively, for Y-120 (Fig. 13a) and for Y-150 (Fig. 13b) microchannel. Comparing the simulation data to the fitted lines of the power law model, it is clear that there is a quite good agreement between the data and the lines for both Y-120 and Y-150 microchannel. The fitted parameters e, α, and β are 0.6808, 1.007, and 0.4118 for Y-120 microchannel, respectively, and they are 0.6317, 1.022, and 0.4410 for Y-150 microchannel, respectively. When Ca goes to infinity, r _s will be the initial volume ratio r ₀. In addition, r ₀ for Y-120 and Y-150 microchannel equal to the one for T-90 microchannel when As is the same, which is due to the fact that these microchannels are actually topological equivalent. Thus, r ₀ are 1.181, 1.293, 1.419, 1.560, and 1.722 for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively, and the corresponding parameter k are 0.9617, 0.9500, 0.9416, 0.9324, and 0.9273, respectively.

Fig. 13

Volume ratios r _s of two daughter droplets versus Ca in Y-120 microchannels (a) and Y-150 microchannels (b)

3.2.3 Analysis of pressure fields during the asymmetric breakup

The mechanisms of the translation of the mother droplet in Y-120 and Y-150 microchannel are similar to that in T-90 microchannel. Thus, the pressure distributions around and inside the droplet in Y-120 and Y-150 microchannel are discussed in this section. Figure 14 exhibits the pressure fields in an asymmetric Y-120 microchannel for the rheological behaviors of the mother droplet at different time in NB, RB, and DB zone, respectively. When Ca is low (Ca = 2.40 × 10⁻³), the pressure near the end of the small half is always higher than that near the other end, and the pressure difference increases along with time before the small half retracts out of the narrow sub-channel (Fig. 14a). Similar to NB process, in RB process the pressure near the end of the small half is higher than that near the other end before the droplet break occurs. At time = 0.0019 s, the pressure in the neck increases rapidly to cause the breakup of the droplet (Fig. 14b). When Ca is increased to 2.40 × 10⁻², the droplet breaks up directly, and the significant difference between DB and the previous two cases in Y-120 microchannel is that the pressure around the junction (the neck zone) is always the highest during the entire process (Fig. 14c). This pressure distribution causes the continuous elongation of the droplet until its direct breakup.

Fig. 14

Analyses of pressure fields for a droplet moving in an asymmetric Y-120 junction with As = 0.08 at different times for Ca = 2.40 × 10⁻³ (a), Ca = 2.56 × 10⁻³ (b) and Ca = 2.40 × 10⁻² (c)

Similarly, Fig. 15a–c exhibit the pressure fields in an asymmetric Y-150 microchannel for the rheological behaviors of the mother droplet at different time in NB, RB, and DB zone, respectively. The changing processes and their corresponding analyses of the pressure distribution in Y-150 microchannel are very similar to those in Y-120 microchannel.

Fig. 15

Analyses of pressure fields for a droplet moving in an asymmetric Y-150 junction with As = 0.08 at different times for Ca = 1.92 × 10⁻³ (a), Ca = 2.00 × 10⁻³ (b), and Ca = 2.40 × 10⁻² (c)

3.3 The asymmetric breakup of a droplet in I-180 microchannel

3.3.1 Droplet breakup regimes

In order to study the asymmetric breakup of a droplet in a straight channel with a linear obstacle, I-180 microchannel is designed. Similar to those in the previous three types of microchannels, three regimes for the asymmetric breakup of a droplet in the asymmetric I-180 microchannel are also observed (Fig. 16). The mother droplet moves toward the downstream of the asymmetric I-180 microchannel with As = 0.08. After reaching the front end of the obstacle, it penetrates into the two sub-channels with different widths. For a low Ca (Ca = 1.60 × 10⁻³), it will retreat under the drag of the bigger part due to the surface tension when the smaller part moving into the narrow sub-channel reaches its maximum extension. As the flow is too weak to break the mother droplet, the latter just moves out of the micro-device from the wide sub-channel (NB, Fig. 16a). Along with the increase of Ca (Ca = 1.69 × 10⁻³), the mother droplet breaks up with some retraction of the front end of the small half from the narrow to the wide sub-channel (RB, Fig. 16b). When Ca is increased to 1.78 × 10⁻³, the mother droplet penetrates continuously into two sub-channels and obstructs them. Finally, it splits into two daughter droplets due to the increase of the upstream pressure (DB, Fig. 16c).

Fig. 16

Three regimes for the asymmetric breakup of a droplet in I-180 microchannel with As = 0.08. a No-breakup (NB) for Ca = 1.60 × 10⁻³, b retraction breakup (RB) for Ca = 1.69 × 10⁻³, and c direct breakup (DB) for Ca = 1.78 × 10⁻³

Regimes of the asymmetric breakup of a droplet in I-180 microchannel as a function of Ca and As are shown in Fig. 17, just similar to those shown in Figs. 5, 12. The rheological behavior of a droplet in an asymmetric I-180 microchannel is also affected by the interaction of the cutting action of the flow and the translation of the droplet. In NB zone, the mother droplet will not break up due to the low Ca or high As. In RB zone, the mother droplet will break up with a retraction of its small half in the narrow sub-channel. In DB zone, the mother droplet will break up directly due to the large Ca or low As. The width of RB region is very narrow for I-180 microchannel due to the hindrance of the linear obstacle to the translation of the droplet. The critical capillary number curve for the asymmetric breakup of a droplet increases along with the asymmetry of the microchannels.

Fig. 17

Regimes of the asymmetric rheological responses of a droplet as a function of Ca and As (triangle NB, open circle RB, and square DB) in I-180 microchannels. The dash curve is the critical capillary number Ca _cr as a function of the asymmetry

3.3.2 The power law model

The asymmetric breakup of a droplet in I-180 microchannel is also similar to that in T-90 microchannel and has the same three major factors. Thus, the power law model (Eq. 10) could also be employed to describe the volume ratio of the two unequal daughter droplets in this section. Here, Ca _cr are 9.60 × 10⁻⁴, 1.30 × 10⁻³, 1.69 × 10⁻³, 2.10 × 10⁻³, and 2.63 × 10⁻³ for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively, which are obtained from Fig. 17. As I-180 microchannel is generated from the topological change of T-90 microchannel, the initial volume ratio r ₀ could also be calculated by Eq. (11). The results of the simulation data and fitted lines are shown in Fig. 18 which exhibits the volume ratio r _s versus Ca for various asymmetries. Comparing the simulation data to the fitted lines, it is clear that the power law model could describe very well the volume ratio of two unequal daughter droplets generated in the asymmetric I-180 microchannel. The fitted parameters e, α, and β are 0.9341, 1.213, and 0.4622 for I-180 microchannel, respectively. When Ca goes to infinity, r _s will be the initial volume ratio r ₀, and r ₀ for I-180 microchannel equal to those for T-90 microchannel when As is the same. Thus, r ₀ are 1.181, 1.293, 1.419, 1.560, and 1.722 for various asymmetries (As = 0.04, 0.06, 0.08, 0.10, and 0.12), respectively, and the corresponding parameters k are 0.9617, 0.9500, 0.9416, 0.9324, and 0.9273, respectively.

Fig. 18

Volume ratios r _s of two daughter droplets versus Ca in I-180 microchannels

3.3.3 Analysis of pressure fields during the asymmetric breakup

Similar to the analysis of pressure fields in T-90, Y-120, and Y-150 microchannels during the asymmetric breakup of a droplet, the pressure distribution at different times for three processes in NB, RB and DB zone are shown in Fig. 19a–c, respectively. In NB zone, the droplet does not breakup (Fig. 19a), and the pressure near the end of the small half is always higher than that near the other end. In RB zone, the droplet breaks up with some retraction (Fig. 19b). The pressure near the end of the small half is higher than that near the other end initially (from 0.1258 to 0.1620 s), and then the pressure in the neck increases rapidly to cause the breakup (0.1622 s) of the droplet. In DB zone, the region with the highest pressure is always around the front end of the obstacle (Fig. 19c). Thus, the droplet will elongate continuously and break up directly.

Fig. 19

Analyses of pressure fields for a droplet moving in an asymmetric I-180 junction with As = 0.08 at different times for Ca = 1.60 × 10⁻³ (a), Ca = 1.69 × 10⁻³ (b), and Ca = 2.40 × 10⁻² (c)

3.3.4 Effects of λ on the asymmetric breakup of a droplet

In the next section (Sect. 3.4), the comparisons among the four types of microchannels with various geometries show that I-180 microchannel is the most promising for the asymmetric breakup of a droplet. Thus, effects of the viscosity ratio λ which is another important factor besides Ca for the deformation and breakup of a droplet will be discussed particularly for I-180 microchannel in this section.

The dimensionless parameter λ plays an important role in the asymmetric breakup of a droplet in microchannels. Thus, the asymmetric breakups of droplets with two different viscosity ratios in I-180 microchannel with a fixed As = 0.08 are investigated to disclose the effects of λ. The simulation data and relevant fitted lines of r _s as a function of Ca for two different λ (λ = 0.5 and 0.2) are shown in Fig. 20. It could be seen that λ only changes the critical capillary numbers (Ca _cr) for the two different cases. Ca _cr is 1.90 × 10⁻³ for λ = 0.2 and 1.69 × 10⁻³ for λ = 0.5, which means that a droplet of a bigger λ is easier to break up. The change of λ does not vary r _s when Ca is far beyond Ca _cr, which could be seen from the two overlapping curves for large capillary numbers. Furthermore, it almost does not affect the three fitting parameter e, α, and β of the power model.

Fig. 20

Volume ratios r _s of two daughter droplets versus Ca in I-180 microchannels for two different λ

3.3.5 Universality of Ca

The capillary number (Ca = μ _c U/σ) and the ratio of the viscosity (λ = μ _d/μ _c) are the two crucial parameters to the rheological behaviors of a droplet. The capillary number Ca shows the ratio of viscous forces to interfacial tensions and is always chosen to represent the flow feature. Traditionally, the generic parameter Ca is always employed to study the droplet deformation and breakup in most of previous works (Bentley and Leal 1986; Janssen and Meijer 1993; Stone 1994; Navot 1999). When λ is fixed, if Ca is bigger than Ca _cr, the droplet will break up. It does not matter what is μ_c and what is σ, which means only if Ca is fixed, the change of μ _c and the change of σ are equivalent. In Sect. 3.3.4, the effect of the viscosity ratio λ of the disperse phase to the continuous phase on the asymmetric breakup of a droplet has been discussed. It is found that λ only change the critical capillary numbers.

Next, λ = 0.5 is fixed in order to check the universality of Ca. As shown in Fig. 21, for a specific value of Ca, when μ_c/σ is fixed, r _s of case I (μ _c = 0.001 Pa s and σ = 5 mN/m) is almost equal to that of case II (μ _c = 0.002 Pa s and σ = 10 mN/m). From Fig. 21, it could be seen that the results of two cases are almost the same. The Ca _cr for the asymmetric breakup of droplets are the same and equal to 1.69 × 10⁻³. The volume ratios r _s of two daughter droplets are almost equal in two cases for different Ca. Therefore, the parameter Ca is universal for the droplet breakup in microchannels. Although the physical parameters (μ _d = 0.0005 Pa s, μ _c = 0.001 Pa s, and σ = 5 mN/m) is fixed to do the investigation in this paper, the obtained results are not only valid for this special set of parameters but also valid for more situations.

Fig. 21

Volume ratios r _s of two daughter droplets versus Ca in I-180 microchannels for μ _c/σ = 0.2 s/m

3.4 Effect of topological changes of microchannel geometries

From the above discussion in Sect. 3, it could be asserted that the rheological behaviors of a droplet moving through different asymmetric microchannels (T-90, Y-120, Y-150, and I-180 microchannel) have many similarities. At first, all regimes of them could be partitioned into three zones: NB, RB, and DB. Secondly, the asymmetric breakups of a droplet in all types of microchannels have a similar mechanism which is the competition between the cutting action and the oriented translation of the droplet from the narrow sub-channel to the wide one. Third, the volumes ratios r _s of two daughter droplets for all four cases could be described by employing the power law model based on the three important factors Ca, As, and r ₀. When Ca goes to infinity, r _s in all four types of microchannels will approach the initial volume ratio r ₀. As for the asymmetric breakup of a droplet in various microchannels with a fixed asymmetry As = 0.08, the volume ratios r _s versus Ca are shown in Fig. 22 for comparisons. As the asymmetry As are the same for all four types of microchannels, which means that the initial volume ratio r ₀ will be the same, it could be seen that all r _s approach a value almost the same for various microchannels when Ca is sufficiently large. For example, when Ca = 4.8 × 10⁻², r _s are 1.590, 1.601, 1.586, and 1.599 for I-180, Y-150, Y-120, and T-90 microchannels, respectively. The relative error is lower than 0.7 %. This consistence proves further the topological equivalence of geometries of these four types of microchannels. All above similarities in the processes of the asymmetric breakup of a droplet in various microchannels are due to the topological equivalence of geometries of the microchannels. However, the four types of microchannels are different after all. There are still some slight differences among these processes, which will be discussed in the following.

Fig. 22

Volume ratios r _s of two daughter droplets versus Ca in four different microchannels with a fixed asymmetry As = 0.08 (inverted triangle T-90, diamond Y-120, square Y-150, open circle I-180)

3.4.1 Critical capillary numbers and time of the droplet breakup

As shown in Fig. 22, it is obvious that the critical capillary numbers (Ca _cr) for the asymmetric breakup of a droplet in various confined microchannels with a fixed asymmetry (As = 0.08) are different. The smallest Ca _cr is generated in I-180 microchannel, and they increase gradually from Y-150 to Y-120, and to T-90 microchannel. This tendency means that the droplets with the same initial volume break up more easily in I-180 than in other microchannels. The bigger the angle between the sub- and main channel is, the easier the droplet breaks up.

As Ca _cr is relatively small for I-180 microchannel, the curve of the critical capillary numbers in its regime (Fig. 17) is located slightly more left than other microchannels. Besides this, by comparing Figs. 5, 12, and 17, it also could be seen that the width of RB for I-180 is the smallest. The width of RB becomes wider gradually from I-180 to Y-150, to Y-120, and to T-90. This phenomenon might mean that the retraction effect of a droplet during its asymmetric breakup will get stronger when the angle between the sub- and main channel becomes smaller gradually from 180° to 90°.

During the zone of DB, the droplet will be elongated continuously and eventually break up. As for a droplet with a fixed initial volume, when Ca is large enough, the droplet will be broken into two unequal daughter droplets with almost the same r _s for all four types of asymmetric microchannels with the same asymmetry As, as shown in Fig. 22. However, the time needed to complete the breakup is different. The shortest is in I-180 microchannel, and the longest is in T-90. When Ca = 4.80 × 10⁻², for instance, the splitting time is 0.00402, 0.00404, 0.00409, and 0.00448 s for I-180, Y-150, Y-120, and T-90 microchannel with a fixed As = 0.08 (see Fig. 22), respectively. This tendency might mean that the cutting effect during the asymmetric breakup of a droplet will get stronger when the angle between the sub- and main channel becomes larger gradually from 90° to 180°.

3.4.2 Satellite droplets

It seems that the bigger the capillary number Ca is, the easier to cut a droplet into two daughter droplets is. However, the continuous increase of Ca will cause a new problem. Many satellite droplets will be generated during the breakup when Ca is too big, which should be avoided since the droplet size distribution will be disturbed severely. The phenomenon that some satellite droplets appear during the breakup of a droplet is first observed in T-90 microchannel along with the increase of Ca (Fig. 23). During the breakup process, a severe trailing occurs due to the high upstream pressure, which eventually produces many satellite droplets due to the instability of the slim tails. Then, these unexpected tiny droplets are observed in Y-120 and Y-150 microchannels when Ca is increased continuously. The last one is I-180 microchannel in which satellite droplets are observed under the biggest capillary number. When As = 0.08 and Ca = 8 × 10⁻², the extended droplet in T-90 microchannel splits with some satellite droplets (Fig. 23a), while the droplets in Y-120, Y-150, and I-180 microchannels are broken without any satellites (Fig. 23b–d). When Ca is increased to 1.04 × 10⁻¹, the droplet in T-90 microchannel breaks up with more generated satellites (Fig. 23e). In Y-120 microchannel, when Ca = 1.28 × 10⁻¹, the droplet breakup begins to generate some satellite droplets (Fig. 23f), while this phenomenon is observed in Y-150 microchannel when Ca = 1.36 × 10⁻¹ (Fig. 23g). Further, until Ca is increased to 1.36 × 10⁻¹, the asymmetric breakup of a droplet with many satellites has not been clearly observed at the front end of the obstacle (Fig. 23h). However, the big daughter droplet in the wide sub-channel cannot retain its stability forever. Its tail will breakup to generate several satellite droplets due to Rayleigh instability in the downstream of the sub-channel.

Fig. 23

Appearance of satellite droplets in various asymmetric microchannels with a fixed As = 0.08 when Ca is too big. The droplet breakup for Ca = 8 × 10⁻² in T-90 (a), Y-120 (b), Y-150 (c), and I-180 (d). e The droplet breakup in T-90 for Ca = 1.04 × 10⁻¹. f The droplet breakup in Y-120 for Ca = 1.28 × 10⁻¹. g The droplet breakup in Y-150 for Ca = 1.36 × 10⁻¹. h The droplet breakup in I-180 for Ca = 1.36 × 10⁻¹

3.4.3 Geometrical analysis of various microchannels

Similarities among the asymmetric breakups of a droplet in various microchannels come from the topological equivalence of geometries of these microchannels. While, the slight differences discussed in the previous two sub-sections are all due to the different effects of the microchannels walls on the translation and cutting process of the mother droplet. In T-90 microchannel, the two sub-channels are connected smoothly without any bend. Thus, the oriented displacement of the droplet from the narrow sub-channel to the wide one is relatively smooth without any obstruction of the wall. However, in Y-120, Y-150, and I-180 microchannels, the two sub-channels are connected with a break angle, blunt angle for Y-120, acute angle for Y-150, and zero angle for I-180. Thus, the oriented translation of the droplet need overcome a hindrance of the break walls, and the hindrance gets stronger gradually from Y-120 to Y-150 and to I-180. The above analysis is consistent to the obtained results in Sect. 3.3. The numerator term e × As ^α in the power law model reflects the effect of the droplet translation, whose fitted values decrease from T-90 to Y-120 to Y-150 and to I-180 microchannels for the same As. For example, when As = 0.08, the values of e × As ^α are 0.06606, 0.05371, 0.04712, and 0.04215 for T-90, Y-120, Y-150, and I-180 microchannels, respectively. While, according to our analysis in previous sections, the numerator term just reflects the effects of the translation of the mother droplet. Moreover, the geometries of walls affect not only the drop translation, but also the cutting action. As shown in Fig. 24, the points A in Y-120, Y-150, and I-180 microchannels are like the blades of knives. Certainly, the blade of Y-120 is blunt, of Y-150 is sharper, and of I-180 is the sharpest. When a droplet approaches the point A under the driving action of the flow, the break point of the wall will cut the droplet like a knife together with the high upstream pressure. In addition, the droplet approaching point A will be bended in Y-120 and Y-150 microchannels, and folded in I-180 microchannel, which will generate an addition pressure against the break point of the wall. All these factors will enhance the cutting action and accelerate the breakup process. However, in T-90 microchannel, the wall connecting two sub-channels is smooth and does not provide any assists to the cutting action. The droplet is only stretched into a cylindrical shape and is broken only by the high upstream pressure. Thus, the enhanced cutting action caused by the geometry features will get stronger and stronger along when the angle between the sub- and the main channel become larger and larger from 90° to 180°. The above analysis is consistent to the obtained results in Sect. 3.3. The denominator term (Ca–Ca _cr)^β in the power law model reflects the strength of the cutting process. The higher β is, the stronger the cutting action is. It could be seen from Sect. 3.3 that the fitted values of β increase from T-90 to Y-120 to Y-150 and to I-180 microchannels. They are 0.3937, 0.4118, 0.4410, and 0.4622, respectively. This means that the curve of r _s = f(Ca) decays faster for I-180 microchannel than others.

Fig. 24

Geometry features of various asymmetric microchannels

In the four designed asymmetric microchannels, the geometry feature of I-180 microchannel will enhance the cutting action and hinder the translation process. It is the reason that I-180 microchannel has the smallest critical capillary number, the shortest splitting time and the narrowest RB zone, and is hardest to generate satellite droplets, while the geometry features of T-90 microchannel make the breakup of a droplet in it only through the high upstream pressure and make it have no constraints on the droplet translation. Thus, T-90 microchannel has the largest critical capillary number, the longest splitting time and the widest RB zone, and is easy to generate satellite droplets.

3.5 Multistep consecutive asymmetric breakups of a droplet

The consecutive application of T-junction, Y-junction, and I-junction can all achieve the multistep asymmetric breakup of a droplet successfully. However, from the analysis in Sect. 3.4.3, it is known that I-180 microchannel is the most promising to do the asymmetric breakup of a droplet since it is relatively easier to break up the droplet and hardest to generate satellite droplets. Thus, the consecutive asymmetric breakup of a droplet to generate multiple unequal daughter droplets is better to be executed in the consecutive I-180 microchannel. Figure 25 shows the geometry of the cascade microchannel and the process to generate four unequal droplets from a mother droplet. The asymmetry As of each stage of the microchannel is fixed and equal to 0.08. The volume ratios of the four daughter droplets are 1: 1.718: 1.309: 2.051 from the left to right. If the process could be done for many mother droplets and all the unequal daughter droplets could be collected, emulsions with an expected and specific droplet size distribution could be produced. This type of emulsions might have some special applications in some field in the future.

Fig. 25

Geometry of the cascade I-180 microchannel and the consecutive asymmetric breakups of a droplet

4 Conclusions

Four types of asymmetric microchannels are designed to break up a droplet asymmetrically. The asymmetries of the microchannels are all due to the different widths of two sub-channels. Also, these microchannels are topologically equivalent as their geometries could be generated by increasing continuously (the angle between the main- and the sub-channel) from 90° to 180°. Thus, the processes of asymmetric breakups of a droplet in these microchannels have some significant similarities and certainly also have some slight differences, both of which have been discussed in this paper.

All the processes of the asymmetric breakup of a droplet in these four types of microchannels have similar breakup mechanisms. They all have three zones of the rheological behaviors (NB, RB, and DB zone) and have three common major factors: the cutting speed of the continuous phase (proportional to the capillary number Ca), the translation speed of the droplet (proportional to the asymmetry As), and the initial volume ratio r ₀. Thus, the power law model based on the effects of Ca, As, and r ₀ could be employed to describe the volume ratio of the two unequal daughter droplets for all types of microchannels. Through the analysis of the pressure fields during the asymmetric breakup in these designed microchannels, it could be seen that the pressure gradient inside the droplet will be one of the major factors causing the translation of the mass center of the droplet, while the outside pressure difference between two ends of the droplet will not. For all asymmetric microchannels investigated in this paper, when Ca is too big, satellite droplets will appear during the breakup process, which should be avoided.

Although there are many similarities in the general processes, the geometrical differences of these microchannels also cause some slight differences in some details. For example, I-180 microchannel has the smallest critical capillary number, the shortest splitting time, and the narrowest RB zone and is hardest to generate satellite droplets. While, T-90 microchannel has the largest critical capillary number, the longest splitting time, and the widest RB zone, and is easy to generate satellite droplets. Thus, I-180 microchannel might be more promising in order to generate emulsions with a specific droplet size distribution by breaking up mother droplets passively in microchannels. Although I-180 microchannel is an ideal design which does not consider the wall thickness, it is still useful to guide the design of the microchannels with linear obstacles.

The asymmetric breakup of an isolated droplet has been studied in this paper. However, generally in experiments, a train of droplets will be asymmetrically broken up in microchannels, and the interaction among droplets might lead to complex periodical breakup regimes. The presence of droplets will change the hydrodynamics resistance of a microchannel when a train of droplets impact a micro-obstacle, and thus the behavior of the preceding ones in a train of droplets might influence the breakup of the following droplet (Schmit et al. 2015). Thus, the results obtained in this paper are exact only for an isolated droplet, but approximate for a train of droplets.

In this paper, although only four types of asymmetric microchannels have been studied, the general way of analyses might be applicable for many asymmetric microchannels of other geometries. The obtained results might be helpful to establish a more general framework of the asymmetric breakup of droplets by many different ways, and this paper is meaningful in the standardization of the microchannel design.