Long-wave interface instabilities of a two-liquid DC electroosmotic system for thin films

Abstract

Instabilities of the interface between two thin liquid films under DC electroosmotic flow are investigated using linear stability analysis followed by an asymptotic analysis in the long-wave limit. The two-liquid system is bounded by two rigid plates which act as substrates. The Boltzmann charge distribution is considered for the two electrolyte solutions and gives rise to a potential distribution in these liquids. The effect of van der Waals interactions in these thin films is incorporated in the momentum equations through the disjoining pressure. Marginal stability and growth rate curves are plotted in order to identify the thresholds for the control parameters when instabilities set in. If the upper liquid is a dielectric, the applied electric field can have stabilizing or destabilizing effects depending on the viscosity ratio due to the competition between viscous and electric forces. For viscosity ratio equal to unity, the stability of the system gets disconnected from the electric parameters like interface zeta potential and electric double-layer thickness. As expected, disjoining pressure has a destabilizing effect, and capillary forces have stabilizing effect. The overall stability trend depends on the complex contest between all the above-mentioned parameters. The present study can be used to tune these parameters according to the stability requirement.

1 Introduction

Lab-on-a-chip microtechnologies have shown considerable promise in revolutionizing the fields of clinical and biology research (Sackmann et al. 2014). In such devices, electroosmosis is used to transport the target species (Park et al. 2007). However, in order to transport a non-conductive liquid, a system of two immiscible liquids is formed with the other liquid being conductive. The conductive liquid experiences an electroosmotic flow (EOF), while the non-conductive liquid placed on top of the conductive liquid gets dragged by the shear forces at the interface (Brask et al. 2003). A system of two immiscible electrolyte solutions is also possible in which both liquids experience EOF. The interface between these two immiscible electrolyte solutions has been studied by Samec et al. (1985) and Senda et al. (1991). It can be described using the modified Verwey–Niessen (MVN) model, which represents the interface as a double layer with excess positive space charge in one phase and equal negative space charge in the other phase separated by an inner or compact layer of oriented solvent molecules (Samec et al. 1985).

To ensure steady and laminar flow for such an application, the interfacial instabilities are required to decay in time. On the other hand, if the aim is to achieve chaotic mixing of two miscible liquids, the exact opposite is required (Moctar et al. 2003). In both cases, an understanding of the dependence of the interfacial instabilities on different physicochemical parameters is needed.

In the presence of an externally applied electric field, the liquid experiences an electric field-generated stress named as the Maxwell stress. Previous works on interfacial instabilities for two-liquid EOF did not consider the Maxwell stress in the momentum equations (Shankar and Sharma 2004; Thaokar and Kumaran 2005, Uguz et al. 2008; Gao et al. 2005). Also, these studies did not take into account the van der Waals interaction forces manifesting in the form of disjoining pressure and which cannot be neglected in the case of thin films. The interfacial electrostatics is an important factor which affects the stability behavior of the two-liquid system. Choi et al. (2011) have provided the base state of the system along with complete interfacial electrostatics by incorporating the Maxwell stress but have not considered the stability analysis of the interface. A complete study of instabilities at a free surface (Mayur et al. 2012) and the base state of an air–liquid interface in 3D microchannels (Mayur et al. 2014a) has been developed in the case of a DC electric field. Also the base state of a time-dependent electric field (AC field) of a free surface has been given in (Mayur et al. 2014b). However, the full stability analysis for a liquid–liquid interface is still required for a time-dependent electric field as instability may lead to rupture and eventually to liquid–liquid droplet formation as in the case of a DC field (Ozen et al. 2006).

The stability of the interface depends on the Maxwell stress which appears due to the net charge distribution in the presence of an applied electric field, on capillary forces appearing due to the curvature of the interface, on viscous forces, and on van der Waals interaction forces. Linear stability analysis is used to obtain the Orr–Sommerfeld equations. These equations are then solved with the asymptotic analysis in the long-wave limit. This paper is divided into four sections. The first section describes the physical system under consideration. The electric potential distribution and the base state velocity profile are derived in the second section. The third section presents the linear stability analysis with the long-wave approximation. Finally, the growth rate and the marginal stability curves are presented with a focus on the case of transporting a dielectric liquid.

2 Mathematical formulation

2.1 Electric potential due to ionic charge distribution

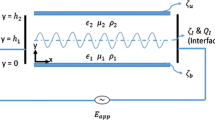
The physical system under consideration consists of thin films of two immiscible liquids having constant density $\rho_{i},$ viscosity μ _i , and electric permittivity ɛ _i , where i = 1 and 2 corresponds to the lower and upper liquids, respectively. The system is confined between two infinite parallel plates at y = 0 and y = h ₂ (see Fig. 1). The interface is represented by $y = h\left( {x,t} \right).$

Fig. 1

Schematics of two-liquid DC EOF system

The zeta potential of the substrate at the upper and lower walls is represented by $\zeta_{u}$ and $\zeta_{b},$ respectively; $\zeta_{I}$ and Q _I are the zeta potential and the surface charge density present at the interface, respectively, (Choi et al. 2011) and are taken as independent parameters. In the experimental studies of the interface between two immiscible electrolyte solutions (ITIES), Samec et al. (1985) showed that for a given interface zeta potential ($\zeta_{I}$), the surface charge density (Q _I) can be varied by varying the electrolyte concentrations. The water/nitrobenzene interface with LiCl in water and tetrabutylammonium tetraphenylborate (TBATPB) can be considered as an example of ITIES (Senda et al. 1991). The liquids are considered to have a low concentration of ions in order to ignore the Joule heating effect (Tang et al. 2004), and hence it ensures that the properties of the liquids remain constant even if large electric fields are applied. It is usually assumed that the ionic distributions are not affected by the fluid flow for an EOF in straight microchannel which results in the Boltzmann charge distribution (Park et al. 2007). For a symmetric electrolyte, combining the Boltzmann charge distribution, the net charge density can be written as,

$$\rho_{e,i} = - 2 z_{i} e \rho_{0,i} \sinh \left( {\frac{{ez_{i} \phi_{{{\text{sc}},i}} }}{{k_{B} T}}} \right)$$

(1)

and the Poisson equation for the potential distribution,

$$\frac{{\hbox{d}^{2} \phi_{{{\text{sc}},i}} }}{{\hbox{d}y^{2} }} = - \frac{{\rho_{e,i} }}{{\varepsilon_{i} }}$$

(2)

The Poisson–Boltzmann equation for the potential field can thus be written as,

$$\frac{{\hbox{d}^{2} \phi_{{{\text{sc}},i}} }}{{\hbox{d}y^{2} }} = \frac{{2z_{i} e\rho_{0,i} }}{{\varepsilon_{i} }}\text{Sinh} \left( {\frac{{ez_{i} \phi_{{{\text{sc}},i}} }}{{k_{B} T}}} \right)$$

(3)

where $\phi_{{{\text{sc}},i}}$ is the electric potential due to the space charge distribution for liquid “i” and ρ _0,i , z _i , k _B , T,  and e are, respectively, the bulk ionic density, the valence of the ions in the aqueous phase for liquid “i”, the Boltzmann constant, the temperature, and the electron charge.

Using the non-dimensional parameters $\varPhi_{{{\text{sc}},i}} = \frac{{\phi_{{{\text{sc}},i}} }}{{\zeta_{b} }},\quad Y = \frac{y}{{h_{1} }}$, Eq. (3) can be written as,

$$\frac{{\hbox{d}^{2} \varPhi_{{{\text{sc}},i}} }}{{d{\text{Y}}^{2} }} = \beta {\text{Sinh}}\left( {\chi \varPhi_{{{\text{sc}},i}} } \right)$$

(4)

where $\beta = \frac{{h_{1}^{2} }}{{\chi \lambda_{{D_{i} }}^{2} }},\quad \chi = \frac{{ez_{i} \zeta_{b} }}{{k_{B} T}}$ is the ionic energy parameter and $\lambda_{Di} = \sqrt {\frac{{\varepsilon_{i} k_{B} T}}{{2z_{i}^{2} e^{2} \rho_{0,i} }}}$ is the Debye length. For χ < 1, which corresponds to $\zeta_{\text{b}} < 25\;{\text{mV}}$ at 25 °C, the Debye–Huckel linearization can be applied and Eq. (4) can be written as,

$$\frac{{\hbox{d}^{2} \varPhi_{{{\text{sc}},i}} }}{{d{\text{Y}}^{2} }} = \frac{{\varPhi_{{{\text{sc}},i}} }}{{De_{i}^{2} }}$$

(5)

where $De_{i} = \frac{{\lambda_{Di} }}{{h_{1} }}$ is the Debye number which represents the relative extent of the electric double layer with respect to the characteristic length scale h ₁. Equation (5) represents two second-order homogeneous linear differential equations, one for each liquid. The four non-dimensional boundary conditions required to solve this set of equations are,

$$\varPhi_{{{\text{sc}},1}} (0) = 1$$

(6)

$$\varPhi_{{{\text{sc}},2}} \left( {H_{2} } \right) = \bar{\zeta }_{u}$$

(7)

$$\varPhi_{{{\text{sc}},1}} (1) - \varPhi_{{{\text{sc}},2}} (1) = \bar{\zeta }_{I}$$

(8)

$$\frac{{d\varPhi_{sc,1} \left( 1 \right)}}{\hbox{d}Y} - \varepsilon_{R} \frac{{d\varPhi_{sc,2} \left( 1 \right)}}{\hbox{d}Y} = \bar{Q}_{I}$$

(9)

where $\bar{\zeta }_{u} = \zeta_{u} /\zeta_{b} , \bar{\zeta }_{I} = \zeta_{I} /\zeta_{b} ,\bar{Q}_{I} = \left( {Q_{I} h_{1} } \right)/\left( {\varepsilon_{1} \zeta_{b} } \right),\varepsilon_{R} = \varepsilon_{2} /\varepsilon_{1}$ and $H_{2} = h_{2} /h_{1}$. The expressions for $\varPhi_{{{\text{sc}},1}}$ and $\varPhi_{{{\text{sc}},2}}$ are given in “Appendix 1”.

2.2 Electric potential due to applied electric field

An external electric field (E _app) is applied to both the liquids and can be written in terms of the gradient of an externally applied potential $\left( {\phi_{\text{app}} } \right)$ as,

$$- \frac{{\hbox{d}\phi_{\text{app}} }}{\hbox{d}x} = E_{\text{app}}$$

(10)

Upon using non-dimensional parameters as $\varPhi_{\text{app}} = \phi_{\text{app}} /\zeta_{b} ;X = x/h_{1} ,$ Eq. (10) can be written as,

$$\frac{{\hbox{d}\varPhi_{\text{app}} }}{\hbox{d}X} = - \frac{1}{{E_{R} }}$$

(11)

where $E_{R} = \zeta_{b} /\left( {E_{\text{app}} h_{1} } \right)$ is the relative strength of the zeta potential to the applied electric field. Therefore, the solution of $\varPhi_{\text{app}} \left( X \right)$ with the boundary condition Φ _app(0) = 0 is obtained as,

$$\varPhi_{\text{app}} \left( X \right) = - \frac{X}{{E_{R} }}$$

(12)

The external electric field does not affect the space charge distribution Φ _sc,i (Y), and hence, superposition principle can be applied. The total electric potential for the i-th liquid can thus be written as,

$$\varPhi_{i} \left( {X,Y} \right) = \varPhi_{\text{app}} \left( X \right) + \varPhi_{{{\text{sc}},i}} \left( Y \right)$$

(13)

where Φ _i is the dimensionless total electric potential for i = 1 and 2.

3 Hydrodynamic equations

3.1 Governing equations

When subjected to an externally applied electric field, the liquid experiences Maxwell stress ($\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}}$) along with the hydrodynamic stress ($\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}}$). The total stress corresponding to the sum of both stresses can be written as,

$$\varvec{\varSigma}_{\varvec{i}}^{\varvec{T}} =\varvec{\varSigma}_{\varvec{i}}^{\varvec{H}} +\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}} = - \left( {p_{i} + \frac{{\varepsilon_{i} \left| {\varvec{E}_{\varvec{i}} } \right|^{2} }}{2}} \right)\varvec{I} + \mu_{i} \left( {\nabla \varvec{u}_{\varvec{i}} + {\mathbf{\nabla }}\varvec{u}_{\varvec{i}}^{\varvec{T}} } \right) + \varepsilon_{i} \varvec{E}_{\varvec{i}} \otimes \varvec{E}_{\varvec{i}}$$

(14)

where $\varvec{E}_{\varvec{i}} = - \nabla \varPhi_{i}$ is the electric field vector, $\varvec{u}_{\varvec{i}} = u_{i} \varvec{i} + v_{i} \varvec{j}$ is the fluid velocity vector, p _i is hydrostatic pressure in the liquid, and I is the unit tensor. Now, in the case of thin films, the intermolecular van der Waals interactions cannot be ignored, and it manifests in the form of a disjoining pressure (Mayur et al. 2012) given by,

$$p_{d,i} = - \frac{{a_{i} }}{{6\pi d_{i}^{3} }}$$

(15)

where a _i is the Hamaker’s constant for liquid “i” and d _i is film thickness. Hence, for lower film, d ₁ = h ₁ and for upper film d ₂ = h ₂ − h ₁. For an incompressible flow, the conservation of mass and momentum leads to the following equations,

$$\nabla \cdot \varvec{u}_{\varvec{i}} = 0$$

(16)

$$\rho_{i} \left( {\frac{{\partial \varvec{u}_{\varvec{i}} }}{\partial t} + \left( {\varvec{u}_{\varvec{i}} \cdot \nabla } \right)\varvec{u}_{\varvec{i}} } \right) = \nabla p_{d,i} - \nabla p_{i} + \mu_{i} \nabla^{2} \varvec{u}_{\varvec{i}} + \nabla \cdot\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}}$$

(17)

The substrate plates at Y = 0 and y = h ₂ are assumed to be rigid and impermeable, and hence, we impose the conditions of no slip and no penetration,

$$u_{1} \left( 0 \right) = v_{1} \left( 0 \right) = u_{2} \left( {h_{2} } \right) = v_{2} \left( {h_{2} } \right) = 0$$

(18)

The perturbed form of the interface between the two liquids is represented by y = h(x, t). At the interface, the continuity of tangential and normal components of the velocity leads to the following equations,

$$\varvec{u}_{1} \cdot\varvec{\tau}= \varvec{u}_{2} \cdot\varvec{\tau},\varvec{ }\quad \varvec{u}_{1} \cdot \varvec{n} = \varvec{u}_{2} \cdot \varvec{n }$$

(19)

Here, n and $\varvec{\tau}$ are unit vectors along the normal and tangential directions, respectively, at the interface:

$$\varvec{n} = \frac{{\frac{\partial h}{\partial x}\varvec{i} - \varvec{j}}}{{\sqrt {1 + \left( {\frac{\partial h}{\partial x}} \right)^{2} } }},\quad\varvec{\tau}= - \frac{{\left( {\varvec{i} + \frac{\partial h}{\partial x}\varvec{j}} \right)}}{{\sqrt {1 + \left( {\frac{\partial h}{\partial x}} \right)^{2} } }}$$

Considering the force balance at the interface, there is a continuity of shear stress in the tangential direction, and the capillary forces create a jump of the normal stresses,

$$\left[ {\varvec{\tau}\cdot\varvec{\varSigma}^{\varvec{T}}_{\varvec{i}} \cdot\varvec{\tau}} \right]_{1}^{2} = 0$$

(20)

$$\left[ {\varvec{n} \cdot\varvec{\varSigma}_{\varvec{i}}^{\varvec{T}} \cdot \varvec{n}} \right]_{1}^{2} = \gamma \kappa$$

(21)

where $\left[ \right]_{1}^{2}$ denotes the jump in variables at the interface, y is the surface tension coefficient and $\kappa = \nabla \cdot \varvec{n}$ is the curvature of the interface.

Since the two liquids are immiscible, there is no mass transfer across the interface; hence the fluid velocity at the interface is equal to the velocity of the interface. This is given by the following kinematic condition,

$$\frac{\partial h}{\partial t} + u_{i} \frac{\partial h}{\partial x} = v_{i}$$

(22)

By using the non-dimensional parameters, $X = \frac{x}{{h_{1} }},\; Y = \frac{y}{{h_{1} }},\;U_{i} = \frac{{u_{i} }}{{U_{\text{ref}} }},\;V_{i} = \frac{{v_{i} }}{{U_{\text{ref}} }}, \;\theta = \frac{{tU_{ref} }}{{h_{1} }},\;P_{i} = \frac{{p_{i} h_{1} }}{{\mu_{1} U_{\text{ref}} }} ,\; H\left( {x,t} \right) = \frac{{h\left( {x, t} \right)}}{{h_{1} }},\; H_{i} = \frac{{h_{i} }}{{h_{1} }},\; \mu_{R} = \frac{{\mu_{2} }}{{\mu_{1} }},$ the corresponding non-dimensional conservation of mass and momentum equations can be written as,

$$\frac{{\partial U_{i} }}{\partial X} + \frac{{\partial V_{i} }}{\partial Y} = 0$$

(23)

For liquid 1,

$${\text{Re}}_{1} \left( {\frac{{\partial U_{1} }}{\partial \theta } + U_{1} \frac{{\partial U_{1} }}{\partial X} + V_{1} \frac{{\partial U_{1} }}{\partial Y}} \right) = - \frac{{\partial P_{1} }}{\partial X} + \frac{{3A_{1} }}{{H^{4} }}\frac{\partial H}{\partial X} + \frac{{\partial^{2} U_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{1} }}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right)$$

(24)

$${\text{Re}}_{1} \left( {\frac{{\partial V_{1} }}{\partial \theta } + U_{1} \frac{{\partial V_{1} }}{\partial X} + V_{1} \frac{{\partial V_{1} }}{\partial Y}} \right) = - \frac{{\partial P_{1} }}{\partial Y} + \frac{{\partial^{2} V_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} V_{1} }}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right)$$

(25)

For liquid 2,

$${\text{Re}}_{2} \left( {\frac{{\partial U_{2} }}{\partial \theta } + U_{2} \frac{{\partial U_{2} }}{\partial X} + V_{2} \frac{{\partial U_{2} }}{\partial Y}} \right) = - \frac{1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial X} - \frac{{3A_{2} }}{{\left( {H_{2} - H} \right)^{4} }}\frac{\partial H}{\partial X} + \frac{{\partial^{2} U_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{2} }}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right)$$

(26)

$${\text{Re}}_{2} \left( {\frac{{\partial V_{2} }}{\partial \theta } + U_{2} \frac{{\partial V_{2} }}{\partial X} + V_{2} \frac{{\partial V_{2} }}{\partial Y}} \right) = - \frac{1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial Y} + \frac{{\partial^{2} V_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} V_{2} }}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right)$$

(27)

The dimensionless boundary conditions are as follows: no slip and no penetration at the two walls,

$$\left. {U_{1} (0} \right) = \left. {U_{2} (H_{2} } \right) = \left. {V_{1} (0} \right) = \left. {V_{2} (H_{2} } \right) = 0$$

(28)

And at the interface, the continuity of normal velocity,

$$\left( {U_{1} - U_{2} } \right)\frac{\partial H}{\partial X} - \left( {V_{1} - V_{2} } \right) = 0$$

(29)

and the continuity of tangential velocity,

$$\left( {U_{1} - U_{2} } \right) + \left( {V_{1} - V_{2} } \right)\frac{\partial H}{\partial X} = 0$$

(30)

The kinematic condition can be written as,

$$\frac{\partial H}{\partial \theta } + U_{i} \frac{\partial H}{\partial X} = V_{i}$$

(31)

And finally the continuity of shear stress,

$$\begin{aligned} \left( {\frac{{\partial U_{1} }}{\partial Y} + \frac{{\partial V_{1} }}{\partial X}} \right)\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - 4\frac{\partial H}{\partial X}\frac{{\partial U_{1} }}{\partial X} + \gamma_{R,1} E_{R} \left( {\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial \varPhi_{1} }}{\partial Y}\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - \frac{\partial H}{\partial X}\left( {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)^{2} } \right)} \right) = \hfill \\ \mu_{R} \left\{ {\left( {\frac{{\partial U_{2} }}{\partial Y} + \frac{{\partial V_{2} }}{\partial X}} \right)\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - 4\frac{\partial H}{\partial X}\frac{{\partial U_{2} }}{\partial X} + \gamma_{R,2} E_{R} \left( {\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial \varPhi_{2} }}{\partial Y}\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - \frac{\partial H}{\partial X}\left( {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)^{2} } \right)} \right)} \right\} \hfill \\ \end{aligned}$$

(32)

and normal stress balance,

$$\begin{aligned} \left\{ { - \left( {P_{1} + \frac{{\gamma_{R,1} E_{R} }}{2}\left( {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)^{2} } \right)} \right) + \frac{2}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\frac{{\partial U_{1} }}{\partial X}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} - 1} \right) - \frac{\partial H}{\partial X}\left( {\frac{{\partial U_{1} }}{\partial Y} + \frac{{\partial V_{1} }}{\partial X}} \right)} \right) + \frac{{\gamma_{R,1} E_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} \left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)^{2} - 2\frac{\partial H}{\partial X}\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)} \right\} \hfill \\ - \left\{ { - \left( {P_{2} + \frac{{\mu_{R} \gamma_{R,2} E_{R} }}{2}\left( {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)^{2} } \right)} \right) + \frac{{2\mu_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\frac{{\partial U_{2} }}{\partial X}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} - 1} \right) - \frac{\partial H}{\partial X}\left( {\frac{{\partial U_{2} }}{\partial Y} + \frac{{\partial V_{2} }}{\partial X}} \right)} \right)} \right\} \hfill \\ + \frac{{\mu_{R} \gamma_{R,2} E_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} \left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)^{2} - 2\frac{\partial H}{\partial X}\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial \varPhi_{2} }}{\partial Y}} \right) =\,\frac{{\frac{{\partial^{2} H}}{{\partial X^{2} }}}}{{{\text{Ca}}\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)^{\frac{3}{2}} }} \hfill \\ \end{aligned}$$

(33)

In addition to the above-mentioned control parameters ($\mu_{R} , \varepsilon_{R} , H_{2} , De_{i} , \bar{Q}_{I} , \bar{\zeta }_{I} , \bar{\zeta }_{u}$), the problem is now described by the following additional eight control parameters,

$$\gamma_{R,i} = \frac{{\varepsilon_{i} \zeta_{b} E_{\text{app}} }}{{\mu_{i} U_{\text{ref}} }},\quad Re_{i} = \frac{{\rho_{i} U_{\text{ref}} h_{1} }}{{\mu_{i} }},\quad A_{i} = \frac{{a_{i} }}{{6\mu_{i} \pi h_{1}^{2} U_{\text{ref}} }}, \quad E_{R} = \frac{{\zeta_{b} }}{{E_{\text{app}} h_{1} }}, \quad Ca = \frac{{\mu_{1} {\text{U}}_{\text{ref}} }}{\gamma }$$

Here γ _R,i is the electroosmotic number, Re _i is the Reynolds number, A _i is the disjoining pressure parameter, E _R is the relative strength of the zeta potential to the applied electric field, and Ca is the capillary number.

3.2 Basic state solution

The basic state solution is obtained by assuming the flow to be uniform, steady and, only in the X-direction (V _i  = 0) without a pressure-driven component. Hence, there is no velocity gradient in the X-direction. Initially the interface is flat and is represented by the equation Y = 1. Since there is no curvature of the interface, there are no capillary forces at the interface. These assumptions result in the following base state equations for i = 1 and 2,

$$\frac{{\partial U_{i,b} }}{\partial X} = 0$$

(34)

$$\frac{{\partial^{2} U_{i,b} }}{{\partial Y^{2} }} + \gamma_{R,i} E_{R} \frac{{\partial \varPhi_{i} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{i} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{i} }}{{\partial Y^{2} }}} \right) = 0$$

(35)

$$0 = - \frac{{\partial P_{1} }}{\partial Y} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right)$$

(36)

$$0 = \frac{ - 1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial Y} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right)$$

(37)

The corresponding boundary conditions to the base state take the following form,

$$U_{1,b} \left( 0 \right) = 0, U_{2,b} \left( {H_{2} } \right) = 0$$

(38)

$$U_{1,b} \left( 1 \right) = U_{2,b} \left( 1 \right)$$

(39)

$$\frac{{\partial U_{1,b} }}{\partial Y} - \gamma_{R,1} \frac{{\partial \varPhi_{1} }}{\partial Y} = \mu_{R} \left\{ {\frac{{\partial U_{2,b} }}{\partial Y} - \gamma_{R,2} \frac{{\partial \varPhi_{2} }}{\partial Y}} \right\}$$

(40)

Equation (33) is solved with the above boundary conditions, and the analytical solution of the base state velocity is given in the “Appendix 2”.

4 Linear stability analysis

Small perturbations in flow variables are introduced as follows,

$$U_{i} = U_{i,b} + \tilde{U}_{i} , \quad V_{i} = \tilde{V}_{i} ,\quad P_{i} = P_{i,b} + \tilde{P}_{i} , \quad H = 1 + \tilde{H}$$

(41)

where the variables with a tilde correspond to perturbation variables. It has to be noted that the perturbation in the electric potential field (see Eq. 13) is not considered in the present work. Such a simplifying assumption has been used to facilitate an analytical solution of the resulting system of equations as a first-order approximation of a rather detailed and nonlinear charge transport such as Poisson–Nernst–Planck equation. The higher-order contribution to the system instability due to the perturbation in the ionic charge distribution requires a detailed numerical analysis and will be considered in a future work. In order to reduce the number of dependent variables, velocity components are converted to their corresponding stream function representation as $\tilde{U}_{i} = \frac{{\partial \tilde{\varPsi }_{i} }}{\partial Y}$ and $\widetilde{{V_{i} }} = - \frac{{\partial \tilde{\varPsi }_{i} }}{\partial X}$. The normal modes approach is then used to represent the perturbations,

$$\tilde{\varPsi }_{i} \left( {X,Y,\theta } \right) = \bar{\varPsi }_{i} \left( Y \right){\text{e}}^{{{i}\alpha \left( {{\text{X}} - {\text{C}}\theta } \right)}} , \;\tilde{H}\left( {X,\theta } \right) = \bar{H}{\text{e}}^{{{i}\alpha \left( {{\text{X}} - {\text{C}}\theta } \right)}} ,\;\tilde{P}_{i} \left( {X,Y,\theta } \right) = \bar{P}_{i} \left( Y \right){\text{e}}^{{{i}\alpha \left( {{\text{X}} - {\text{C}}\theta } \right)}}$$

(42)

where α is the wave number, C is the velocity of the wave, and θ is the dimensionless time. Upon substitution of the perturbed variables and linearization, the base state equations are subtracted from the perturbed equations. The pressure term is eliminated by taking derivative of X-momentum and Y-momentum equations with respect to Y and X, respectively, and subtracting one from the other. The following Orr–Sommerfeld equations for the stream function are then obtained,

$$\left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} - \alpha^{2} } \right)^{2} \bar{\varPsi }_{i}(Y) + i\alpha {\text{Re}}_{i} \left[ {\left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} - \alpha^{2} } \right)\left( {C - U_{i,b} } \right) + \frac{{\hbox{d}^{2} U_{i,b} }}{{\hbox{d}Y^{2} }}} \right]\bar{\varPsi }_{i} (Y) = 0$$

(43)

The boundary conditions at the interface are to be applied at $Y = 1 + \tilde{H}$ and can be written as Taylor series expansion around Y = 1, as follows:

$$\bar{\varPsi }_{1} \left( 0 \right) = 0, \frac{{d\bar{\varPsi }_{1} }}{\hbox{d}Y}\left( 0 \right) = 0, \bar{\varPsi }_{1} \left( {H_{2} } \right) = 0, \frac{{d\bar{\varPsi }_{1} }}{\hbox{d}Y}\left( {H_{2} } \right) = 0$$

(44)

$$\bar{\varPsi }_{1} \left( 1 \right) = \bar{\varPsi }_{2} \left( 1 \right)$$

(45)

$$\bar{H}\left[ {\frac{{dU_{1,b} \left( 1 \right)}}{\hbox{d}Y} - \frac{{dU_{2,b} \left( 1 \right)}}{\hbox{d}Y}} \right] + \frac{d}{dy}\left( {\bar{\varPsi }_{1} - \bar{\varPsi }_{2} } \right) = 0$$

(46)

$$\bar{\varPsi }_{1} - \left( {C + U_{1,b} \left( 1 \right)} \right)\bar{H} = 0$$

(47)

$$\begin{aligned} \left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} + \alpha^{2} } \right)\bar{\varPsi }_{1} \left( 1 \right) + \bar{H}\frac{{\hbox{d}^{2} U_{1,b} \left( 1 \right)}}{{\hbox{d}Y^{2} }} + \gamma_{R,1} E_{R} \bar{H}\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} - {i}\alpha \gamma_{R,1}\,E_{R} \bar{H}\left[ {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right] = \left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} + \alpha^{2} } \right)\mu_{R} \bar{\varPsi }_{2} \left( 1 \right) + \mu_{R} \bar{H}\frac{{\hbox{d}^{2} U_{2,b} \left( 1 \right)}}{{\hbox{d}Y^{2} }} + \mu_{R} \gamma_{R,2} \hfill \\ E_{R} \bar{H}\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }} - i\alpha \mu_{R} \gamma_{R,2}\,E_{R} \bar{H}\left[ {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right] \hfill \\ \end{aligned}$$

(48)

$$\begin{aligned} - i\alpha \left\{ {\text{Re}_{1} \left( {C\frac{{d\bar{\varPsi }_{1} \left( 1 \right)}}{\hbox{d}y} - U_{1,b} \frac{{d\bar{\varPsi }_{1} \left( 1 \right)}}{\hbox{d}y} + \bar{\varPsi }_{1} \left( 1 \right)\frac{{dU_{1,b} }}{\hbox{d}Y}} \right) - \mu_{R} \left\{ {\text{Re}_{2} \left( {C\frac{{d\bar{\varPsi }_{2} \left( 1 \right)}}{\hbox{d}y} - U_{2,b} \frac{{d\bar{\varPsi }_{2} \left( 1 \right)}}{\hbox{d}y} + \bar{\varPsi }_{2} \left( 1 \right)\frac{{dU_{2,b} }}{\hbox{d}Y}} \right)} \right\} + \left[ {3A_{1} \bar{H} + \mu_{R} \frac{{3A_{2} \bar{H}}}{{\left( {H_{2} - 1} \right)}} - \alpha^{2} \frac{{\bar{H}}}{Ca}} \right]} \right\} \hfill \\ = \left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} - 3\alpha^{2} } \right)\frac{{d\bar{\varPsi }_{1} \left( 1 \right)}}{\hbox{d}y} - \mu_{R} \left( {\frac{{\hbox{d}^{2} }}{{\hbox{d}y^{2} }} - 3\alpha^{2} } \right)\frac{{d\bar{\varPsi }_{2} \left( 1 \right)}}{\hbox{d}y} \hfill \\ \end{aligned}$$

(49)

The stability information of thin film systems can be recovered without solving the complete set of equations. Yih’s method (Yih 1963) (long-wave expansion method) can be used to expand the dependent variables $\overline{\varPsi }_{1} \left( Y \right),\overline{\varPsi }_{2} \left( Y \right)$ and C in powers of iα:

$$\begin{aligned} \bar{\varPsi }_{i} \sim\bar{\varPsi }_{i,0} + i\alpha \bar{\varPsi }_{i,1} \hfill \\ C\;\sim\;C_{0} + i\alpha C_{1} \hfill \\ \end{aligned}$$

(50)

The lengthy equations corresponding to zeroth and first order in iα are given in the “Appendix 3”. These equations are solved with an assumption that the capillary forces are large, i.e., $\alpha^{2} /Ca \sim O\left( 1 \right)$ (Mayur et al. 2012). Since the inertial forces are much weaker than the other forces in play, Re ₁ = Re ₂ ∼ 0. Upon substituting the expansion of wave velocity (Eq. 48) in the perturbation $\widetilde{\varPsi }_{i} \left( {X,Y,\theta } \right)$ and ignoring the higher powers of α, the expression for the real part of the growth rate, σ _R , is found to be α ² C ₁, and the critical wave number can then be obtained by equating the growth rate to zero which in turn gives the marginal stability curves for the system.

5 Results

5.1 Base state profiles

Let us first define some of the dimensionless parameters in order to see the effects of some important physical parameters which act on the system of the two liquids. By assuming the electroosmotic number in liquid 1, γ _R,1 = γ _R ; this number in liquid 2 is then: $\gamma_{R,2} = \frac{{\varepsilon_{R} }}{{\mu_{R} }}\gamma_{R}.$ We assume here that the heights of the two liquid layers are the same and so H ₂ = 2. Moreover, the disjoining pressure parameters are supposed to be the same: A ₁ = A ₂ = A. The quantity $\frac{{\gamma_{R} }}{{E_{R} }}$ represents the applied electric field, and γ _R E _R represents the wall zeta potential (at y = 0). Also, the present analysis is valid only for low electric pressure as compared to the capillary pressure. Thus, the stabilizing effect of the polarization forces (Melcher and Schwarz 1968) can be neglected as the electric pressure does not compete with the capillary pressure.

Figure 2a shows the electric potential profile due to space charge distribution $(\varPhi_{\text{sc}} )$ as a function of the vertical axis Y for different values of the zeta potential at the interface $\overline{\zeta }_{I}$. The other parameters are assumed to have the following values: ${\text{De}}_{1} = {\text{De}}_{2} = {\text{De}} = 0.1, \overline{ Q}_{I} = 0$ and $\varepsilon_{R} = 2$. As expected, for $\overline{\zeta }_{I} = 0$, the profile is continuous and shows a typical potential field profile with symmetric gradients near the top and bottom walls (EDL zones) for identical value of the wall zeta potential ($\overline{\zeta }_{u} = 1$). Moreover, a discontinuous potential field appears at the interface for nonzero values of interface zeta potential ($\overline{\zeta }_{I} = 1$ and $\overline{\zeta }_{I} = - 1$).

Fig. 2

a Electric potential profile, Φ_SC for different values of zeta potential at interface, $\overline{\zeta }_{I}$, and for De₁ = De₂ = De = 0.1, $\bar{Q}_{I} = 0,$ ε _R = 2, $\overline{\zeta }_{u} = 1,$ μ _R = 2, b Base state velocity for the present study and the one calculated by Choi et al. (2011)

Figure 2b represents the base state velocity profile for different values of the interface zeta potential ($\overline{\zeta }_{I} = 0,\;\overline{\zeta }_{I} = 1,$ and $\overline{\zeta }_{I} = - 1$), and all the other dimensionless parameters are the same as in Fig. 2a. For $\overline{\zeta }_{I} = 0,$ it shows a plug-type profile for the considered Debye numbers. For a sufficiently large ($\left| {\overline{\zeta }_{I} } \right| = 1$), flow reversal can occur due to electrostatics at the interface. As the viscous ratio (μ _R ) is equal to 2, the viscous force is larger on the top layer (liquid 2) than the bottom layer (liquid 1) and counteracts the electric force, and hence the magnitude of the velocity is higher on liquid 1. The excellent agreement between the velocity profiles obtained from the present model and the one derived by Choi et al. (2011) as reported in Fig. 2b validates the present Maxwell stress model used in these thin EDL systems.

5.2 Growth rate

The most important case from the viewpoint of practical applications is the case when the liquid at the lower layer is an electrolyte (conductive) and the one at the top layer is a dielectric (non-conductive). A parametric study of the real part of the growth rate is undertaken. In this case, the following parameters are considered: $\varepsilon_{R} \ll 1$ and $\overline{\zeta }_{I} = 0.$ Moreover, as the concentration of ions decreases and vanishes for a dielectric fluid, the corresponding Debye number De ₂ → ∞ so that Eq. (5) for liquid 2 reduces to Laplace equation $\frac{{\hbox{d}^{2} \varPhi_{{{\text{sc}},2}} }}{{d{\text{Y}}^{2} }} = 0.$

In order to convert the liquid–liquid interface problem to a liquid–air interface problem, it is essential that the second liquid should not only be dielectric but also non-viscous. If the upper media is also inviscid, our problem is converted to a liquid–air one, and the interface can be treated as a free surface (Thaokar and Kumaran 2005). A comparison of the growth rate, σ _R , as a function of the wave number, α, for the present work and the work performed by Thaokar and Kumaran (2005) is presented in Fig. 3. The small deviation at $\mu_{\text{R}} = 0.01$ vanishes by decreasing the viscosity ratio by ten times ($\mu_{\text{R}} = 0.001$).

Fig. 3

Real part of growth rate with wave number derived from present study and the one derived by Mayur et al. (2012) for De = 0.1, Ca = 1, A = 0, ε _R = 0, $\overline{\zeta }_{u} = 0,\;\overline{\zeta }_{I} = 0,$ E _R= 1, γ_R = 1 and a μ _R = 0.01, b μ _R = 0.001

Figure 4 shows the growth rate as a function of the wave number for different magnitudes of the electric field, γ _R /E _R , all other parameters being fixed and given. Two extreme values of the viscosity ratio are considered $\left( {\mu_{\text{R}} = 0.1} \right)$ and $\left( {\mu_{\text{R}} = 10} \right)$ in order to study the effect of viscous force over the electric force. For lower values of viscosity ratio $\left( {\mu_{\text{R}} = 0.1} \right),$ the behavior is classical, e.g., the instability increases as the value of the electric field magnitude increases. But as the viscosity ratio increases, the opposite is seen: The system becomes more stable as the magnitude of electric field increases. This is mainly due the competition between the electric force which is directed from right to left (same direction as the velocity field) and the viscous force which opposes the motion and is thus directed from left to right. As the value of electric field diminishes, the viscous force dominates and hence the high viscous jump of the stress at the interface increases the instability for lower values of electric force. The increase in the magnitude of the electric field force counteracts the viscous force, and hence, the stability of the system increases. This result is quite important as the stability of the system can be tuned with the electric field through the Maxwell stress and the viscosity ratio through the viscous stress.

Fig. 4

Variation of the real part of growth rate with the wave number for different values of applied electric field and with De = 0.1, Ca = 0.01, A = 0.1, $\overline{\zeta }_{I} = 0$ and a μ _R = 0.1, b μ _R = 10

This competition between the viscous and electric forces can be better understood by taking a closer look at the momentum equations. The non-dimensional X-momentum equations for liquids 1 and 2, respectively, with an assumption that liquid 2 is dielectric $\left( {\varepsilon_{R} \sim0} \right)$ and Re ₁ = Re ₂ ∼ 0 can be written as,

$$0 = - \frac{{\partial P_{1} }}{\partial X} + \frac{{3A_{1} }}{{H^{4} }}\frac{\partial H}{\partial X} + \frac{{\partial^{2} U_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{1} }}{{\partial Y^{2} }} - \gamma_{R} \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}$$

(51)

$$0 = - \frac{{\partial P_{2} }}{\partial X} - \frac{{3A_{2} \mu_{R} }}{{\left( {H_{2} - H} \right)^{4} }}\frac{\partial H}{\partial X} + \mu_{R} \left( {\frac{{\partial^{2} U_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{2} }}{{\partial Y^{2} }}} \right)$$

(52)

In Eq. (51), the coefficient of the viscous force and electric force term is of the order of one and-γ _R , respectively. In Eq. (52), there is only viscous force and its order of magnitude is μ _R . For μ _R  = 10 and γ _R  < 1, the force experienced by the lower liquid is then much lower than the viscous force exerted by the upper liquid. Since the lower liquid drives the flow in the upper liquid through the interfacial shear stress, a high viscosity ratio would result in a higher jump in the velocity gradient at the interface. Consequently, an increase in electric field increases the driving force experienced by the lower fluid and in turn tries to compensate for the high viscous forces exerted on it by the upper fluid. This leads to an increase in the stability of the system.

Figure 5 shows the growth rate variation as a function of the wave number for different values of the viscosity ratio and two values of the disjoining pressure, A. From these figures, it is observed [as in the case of a liquid–gas interface with a DC field (Mayur et al. 2012)] that upon increasing the disjoining pressure, the system is more unstable. This phenomenon can be explained by the fact that increasing the disjoining pressure pushes the system away from the mechanical equilibrium of the thin film hence making the system more unstable. Moreover, the same kind of behavior as in the previous figure is seen here where there exists a competition between the viscous force and the disjoining pressure force. For lower values of A, the stability of the system is decreased for extreme values of viscosity ratio ($\mu_{\text{R}} = 0.1,\quad \mu_{\text{R}} = 10$). For intermediate values of $\mu_{\text{R}}$ ($\mu_{\text{R}} = 1$), the system is quasi-stable. The same behavior is seen for higher values of A, except that at the crossover point, the instability is higher for $\mu_{\text{R}} = 1$ than $\mu_{\text{R}} = 0.1.$ The overall stability of the proposed system can be tuned with respect to the disjoining pressure by fixing the other two parameters, i.e., the viscosity ratio and the electric field.

Fig. 5

Variation of the real part of the growth rate with wave number for different viscosity ratio and with De = 0.1, Ca = 0.01, ε _R = 1, γ_R = 1, $\overline{\zeta }_{I} = 0$ and a A = 0.1, b A = 1

Figure 6 represents the stability curve (growth rate as a function of the wave number) for different values of the capillary number Ca. The instability is always suppressed by the capillary forces. And, as expected, the instability grows for non-vanishing values of the zeta potential of the interface which states that the Maxwell stress experienced by the interfacial potential inherently destabilizes the system.

Fig. 6

Variation of the real part of the growth rate with wave number for different Capillary number and with De = 0.1, μ_R  = 2, ε _R = 1, γ_R = 1, A = 0.1 and a $\overline{\zeta }_{I} = 0,$ b $\overline{\zeta }_{I} = 1$

5.3 Marginal stability curves

The marginal stability curve gives an idea of the threshold value of the wavenumber, e.g., the zones of stable and unstable regions for a given system. Figure 7 shows the critical wave number (or the threshold value) as a function of the capillary number for different values of the electric field and two extreme values of the disjoining pressure number (A = 0.1 and A = 1). The critical wavenumber increases when the magnitude of the electric field diminishes and when the capillary number increases which is consistent with the previous analysis. For higher values of A, the differences in the threshold values of the wavenumber are barely noticeable. This result means that for high values of A, the threshold of the wavenumber does not change with respect to the values of the electric field (γ _R /E _R  < 1) and regardless the value of the capillary number. The inserts in the Fig. 7 show the variation of critical wave number with γ _R /E _R for a particular value of capillary number (Ca = 0.4). The decline of critical wavenumber number with increase in γ _R /E _R shows that the system is becoming more stable. The critical wavenumber increases when the disjoining pressure increases.

Fig. 7

Marginal stability curve showing critical wave number as a function of capillary number, Ca for different values of applied electric field with De = 0.1, μ_R = 2 and $\overline{\zeta }_{I} = 0$ a A = 0.1, b A = 1

Figure 8 presents the results of the marginal stability curve for the two-liquid system as a function of the disjoining pressure coefficient for liquid 2, A ₂, fixing A ₁ = 1 (Fig. 8a) and Debye number ratio De _R  = De ₂/De ₁ (Fig. 8b) for different values of the viscosity ratio. In Fig. 8a, when A ₂ increases (or the ratio A ₂/A ₁ increases), the instability increases for all values of the viscosity ratio as for the case for a free surface (Thaokar and Kumaran 2005). In Fig. 8b, the effect of Debye number ratio (De _R  = De ₂/De ₁) on the stability of the system is presented in which both the liquids are conductive. The Debye number (representing the EDL thickness) affects the stability of the system differently depending on the viscosity ratio. For $\mu_{\text{R}} = 10,$ the instability increases with the increase in De _R . For $\mu_{\text{R}} = 0.1,$ there is significant decline in stability for De _R  < 3. In both cases, there is very little or no effect on marginal stability if the Debye number ratio is increased beyond a limiting value (De _R  > 10). On the other hand, the stability threshold remains constant whatever the value of the Debye number ratio for $\mu_{\text{R}} = 1.$

Fig. 8

Marginal stability curve showing the critical wave number as a function of (a) the dimensionless Hamaker’s constant, A₂ for different values of viscosity ratio, μ_R with De₁ = De₂ = 0.1, E _R = 1, γ_R = 0.1 and $\overline{\zeta }_{I} = 1,$ Ca = 0.01, A₁ = 1 (b) the Debye number ratio (De₂/De₁), De_R for different values of viscosity ratio, μ_R with De₁ = 0.1, A₁ = A₂ = 1, ε _R = 10, γ_R = 1 and $\overline{\zeta }_{I} = 1$, Ca = 0.1, ε _R = 0.1, $\overline{Q}_{I} = 1$

Figure 9 shows the marginal stability curve as a function of the zeta potential at the interface and for different values of the viscosity ratio. For the case of equal viscosity of the two liquids, the stability does not change irrespective of the value of zeta potential at the interface. Nevertheless, the behavior of the stability of the system is opposite for the extreme values of viscosity ratio (μ _R  = 10, μ _R  = 0.1): It is observed that the stability increases with $\bar{\zeta }_{I}$ (irrespective of the polarity) for μ _R  = 0.1 and vice versa for μ _R  = 10. In other words, the stability of the two-liquid system increases when the magnitude of zeta potential of the interface increases for highly viscous bottom fluid layer.

Fig. 9

Marginal stability curve showing the critical wave number as a function of the non-dimensional interface zeta potential, $\overline{\zeta }_{I}$ for different values of viscosity ratio with De = 0.1, ε _R = 1, γ_R = 0.1 and A = 0.1, Ca = 0.001

The interesting change in the stability behavior with viscosity ratio as observed in Fig. 4 is reiterated in Fig. 10. There is a crossover of the curves at μ _R  = 1. For μ _R  < 1, the stability decreases with the increase in the applied electric field, and the exact opposite happens for μ _R  > 1. Although one may feel that the viscosity is a stabilizing force which should damp any growth of perturbations in this two-liquid system where the upper fluid is dielectric, the viscous force, here, acts as a driving force in the form of interface shear stress and hence can destabilize the system.

Fig. 10

Marginal stability curve showing the critical wave number as a function of the viscosity ratio, μ_R for different values of applied electric field with $\overline{\zeta }_{I} = 0,$ De = 0.1, ε _R = 1, γ_R = 0.1 and A = 0.1, Ca = 0.01

All the above results (except Fig. 8b) were focused on the particularly useful case of the two-liquid EOF system in which the upper fluid is dielectric. However, if both the fluids are considered conductive, interesting stability patterns are also observed. The effect of permittivity ratio ($\varepsilon_{R}$) on the growth rate depends on the viscosity ratio if all other parameters are kept constant. In Fig. 11a, since $\overline{\zeta }_{I}$ and $\bar{Q}_{I}$ are assumed to be zero, electrostatics at the interface are not playing any role in the stability at the interface. In case of high viscosity ratio, the instability increases with an increase in the permittivity ratio. This generic behavior is because of the increased force on the more viscous upper fluid. However, in case of low viscosity ratio, if $\varepsilon_{R}$ is small then the bottom liquid, with higher viscosity and permittivity, acts like a driver liquid, and the shear stress at the interface causes instability. When the permittivity ratio is increased, the upper fluid gets driven by the applied electric field decreasing the effect of shear stress at the interface and hence making the system more stable. However, as soon as an interface zeta potential is present, then the stability behavior is changed significantly (see Fig. 11b). In this case the Maxwell stress at the interface plays an important role in deciding the stability regions.

Fig. 11

Marginal stability curve showing the critical wave number as a function of the permittivity ratio, ε _R in case of both the fluids are conductive for different values of viscosity ratio with, μ_R De = 0.1, ε _R = 1, γ_R = 1 and A = 0.1, Ca = 0.01, $\overline{\zeta }_{u} = 1,$ $\overline{Q}_{I} = 0,$ a $\overline{\zeta }_{I} = 0$, b $\overline{\zeta }_{I} = 1$

6 Conclusion

The analysis of growth rate and marginal stability curves showed an interesting interplay between the viscous forces, electric forces, disjoining pressure, and capillary forces in order to decide the stability of the system. Interfacial electrostatics and EDL thickness also alter the stability behavior significantly. If the upper liquid is considered to be a dielectric, the applied electric field can have stabilizing or destabilizing effects depending on the viscosity ratio because of the competition between viscous and electric forces. Similarly viscous forces, although dissipative in nature, will not always stabilize the system. For viscosity ratio equal to unity, the stability of the system gets disconnected from the electric parameters such as interface zeta potential and EDL thickness. Disjoining pressure has a destabilizing effect, and capillary forces have stabilizing effect. The overall stability trend depends on the complex contest between all the above-mentioned parameters, and the present study can be used to tune these parameters according to the stability requirement.

Appendices

Appendix 1

The electric potential $\varPhi_{{{\text{sc}},i}}$ (i = 1, 2) due the space charge distribution can be written as follows,

$$0 < Y < 1: \varPhi_{sc,1} = A_{1} e^{{\frac{Y}{{De_{1} }}}} + B_{1} e^{{ - \frac{Y}{{De_{1} }}}}$$

(53)

$$1 < Y < H_{2} : \varPhi_{sc,2} = A_{2} e^{{\frac{Y}{{De_{2} }}}} + B_{2} e^{{ - \frac{Y}{{De_{2} }}}}$$

(54)

$$A_{1} = \frac{{\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{2} \left( {1 + {\text{e}}^{{\frac{1}{{{\text{De}}_{1} }}}} {\text{De}}_{1} Q_{i} } \right) + {\text{De}}_{1} \varepsilon_{R} \left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} - 2{\text{e}}^{{\frac{1}{{{\text{De}}_{1} }} + \frac{{1 + H_{2} }}{{{\text{De}}_{2} }}}} \left( {{\text{Cosh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]\overline{\zeta }_{i} + \overline{\zeta }_{u} } \right)} \right)}}{{\left( {1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{1} \varepsilon_{R} }}$$

$$B_{1} = \frac{{{\text{e}}^{{\frac{1}{{De_{1} }}}} \left( {\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} \left( {{\text{e}}^{{\frac{1}{{De_{1} }}}} - De_{1} \overline{Q}_{I} } \right) - De_{1} \varepsilon_{R} \left( {{\text{e}}^{{\frac{1}{{De_{1} }}}} \left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right) - 2{\text{e}}^{{\frac{{1 + H_{2} }}{{De_{2} }}}} \left( {Cosh\left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\overline{\zeta }_{i} + \overline{\zeta }_{u} } \right)} \right)} \right)}}{{\left( {1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }}$$

$$A_{2} = \frac{{2{\text{e}}^{{\left( {\frac{1}{{De_{1} }} + \frac{1}{{De_{2} }}} \right)}} De_{2} \left( {1 + Sinh\left[ {\frac{1}{{De_{1} }}} \right]De_{1} \overline{Q}_{I} - Cosh\left[ {\frac{1}{{De_{1} }}} \right]\overline{\zeta }_{i} } \right) - {\text{e}}^{{\frac{{H_{2} }}{{De_{2} }}}} \left( {De_{2} - De_{1} \varepsilon_{R} + {\text{e}}^{{\frac{2}{{De_{1} }}}} \left( {De_{2} + De_{1} \varepsilon_{R} } \right)} \right)\overline{\zeta }_{u} }}{{\left( {1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }}$$

$$B_{2} = \frac{{{\text{e}}^{{\frac{{1 + H_{2} }}{{{\text{De}}_{2} }}}} \left( {2{\text{e}}^{{\frac{1}{{{\text{De}}_{1} }} + \frac{{H_{2} }}{{{\text{De}}_{2} }}}} {\text{De}}_{2} \left( {1 + {\text{Sinh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]{\text{De}}_{1} \overline{Q}_{I} - {\text{Cosh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]\overline{\zeta }_{i} } \right) - {\text{e}}^{{\frac{1}{{{\text{De}}_{2} }}}} \left( {{\text{De}}_{2} + {\text{De}}_{1} \varepsilon_{R} + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} \left( {{\text{De}}_{2} - {\text{De}}_{1} \varepsilon_{R} } \right)} \right)\overline{\zeta }_{u} } \right)}}{{ - \left( {1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{2} + \left( { - 1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{1} \varepsilon_{R} }}$$

Appendix 2

The expression of the base state velocity in both liquids are derived as follows,

$$\begin{aligned} U_{1,b} = & \left\{ {4e^{{\frac{1}{{De_{1} }} + \frac{{1 + H_{2} }}{{De_{2} }}}} \left( {De_{1} \varepsilon_{R} \left( {H_{2} \gamma_{R1} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\left( {\text{Sinh} \overline{{\left[ {\frac{Y - 1}{{De_{1} }}} \right] + \text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right] - \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]\zeta }}_{i} } \right)} \right.} \right.} \right.} \right. \\ & \left. { - \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]\overline{\zeta }_{u} } \right) + \gamma_{R1} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\left( {\text{Sinh} \left[ {\frac{Y - 1}{{De_{1} }}} \right] + \text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right] - \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]\overline{\zeta }_{i} } \right)} \right. \\ & \left. { - \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]\overline{\zeta }_{u} } \right)\left( { - 1 + \mu_{R} } \right) + Y\text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right]\left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\gamma_{R1} \left( { - 1 + \overline{\zeta }_{i} } \right)} \right. \\ & \left. {\left. {\left. { + \left( {\gamma_{R1} + \left( { - 1 + \text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]} \right)} \right)\gamma_{R2} } \right)\overline{\zeta }_{u} } \right)\mu_{R} } \right) + \text{Sinh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]De_{2} \left( {H_{2} \left( {\text{Cosh} \left[ {\frac{Y - 1}{{De_{1} }}} \right] - \text{Cosh} \left[ {\frac{1}{{De_{1} }}} \right]} \right.} \right. \\ & \left. { + \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]De_{1} \overline{Q}_{I} } \right)\gamma_{R1} + \left( {\text{Cosh} \left[ {\frac{Y - 1}{{De_{1} }}} \right] - \text{Cosh} \left[ {\frac{1}{{De_{1} }}} \right] + \text{Sinh} \left[ {\frac{Y}{{De_{1} }}} \right]De_{1} \overline{Q}_{I} } \right)\gamma_{R1} \left( { - 1 + \mu_{R} } \right) \\ & \left\{ {\left. {\left. {\left( { - \gamma_{R1} + \gamma_{R2} + \text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right]De_{1} \overline{Q}_{I} \left( { - \gamma_{R1} + \gamma_{R2} } \right) + \text{Cosh} \left[ {\frac{1}{{De_{1} }}} \right]\left( {\gamma_{R1} - \gamma_{R2} \left( {\overline{\zeta }_{i} + \overline{\zeta }_{u} } \right)} \right)} \right)\mu_{R} } \right)} \right)} \right\} \\ & /\left\{ {\left( {\left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} } \right)\left( {H_{2} + \left( { - 1 + \mu_{R} } \right)} \right)} \right\} \\ \end{aligned}$$

(55)

$$\begin{aligned} U_{2,b} = & \left\{ {{\text{e}}^{{ - \frac{Y + 1}{{{\text{De}}_{2} }}}} \left( {2{\text{e}}^{{\frac{{Y + 2 + H_{2} }}{{{\text{De}}_{2} }}}} \left( { - 1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right){\text{De}}_{1} \left( {{\text{De}}_{2} \overline{Q}_{I} \left( { - {\text{Sinh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]\left( {Y - H_{2} } \right)\left( {\gamma_{{{\text{R}}1}} - \gamma_{{{\text{R}}2}} } \right)} \right.} \right.} \right.} \right. \\ & \left. { + {\text{Cosh}}\left[ {\frac{{H_{2} }}{{{\text{De}}_{2} }}} \right]{\text{Sinh}}\left[ {\frac{Y}{{{\text{De}}_{2} }}} \right]\gamma_{{{\text{R}}2}} \left( {H_{2} + \left( { - 1 + \mu_{R} } \right)} \right) - {\text{Cosh}}\left[ {\frac{Y}{{{\text{De}}_{2} }}} \right]{\text{Sinh}}\left[ {\frac{{H_{2} }}{{{\text{De}}_{2} }}} \right]\gamma_{{{\text{R}}2}} \left( {H_{2} + ( - 1 + \mu_{R} )} \right)} \right) \\ & + \varepsilon_{R} (\left( {Y - H_{2} } \right)\gamma_{{{\text{R}}1}} \left( {{\text{Cosh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]\left( { - 1 + \overline{\zeta }_{\text{i}} } \right) + \overline{\zeta }_{u} } \right) + \gamma_{{{\text{R}}2}} \overline{\zeta }_{u} \left( {Y\left( { - 1 + {\text{Cosh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right)} \right. \\ & \left. {\left. {\left. { - \left( { - 1 + {\text{Cosh}}\left[ {\frac{Y - 1}{{{\text{De}}_{2} }}} \right]} \right)H_{2} - \left( {{\text{Cosh}}\left[ {\frac{Y - 1}{{{\text{De}}_{2} }}} \right] - {\text{Cosh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right)\left( { - 1 + \mu_{R} } \right)} \right)} \right)} \right) \\ & + {\text{e}}^{{\frac{Y + 1}{{{\text{De}}_{2} }}}} {\text{De}}_{2} (\left( { - 1 + {\text{e}}^{{\frac{1}{{{\text{De}}_{1} }}}} } \right)^{2} \left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right)\left( {Y - H_{2} } \right)\gamma_{{{\text{R}}1}} + 4{\text{e}}^{{\frac{1}{{{\text{De}}_{1} }} + \frac{{1 + H_{2} }}{{{\text{De}}_{2} }}}} \gamma_{{{\text{R}}2}} \left( { - \left( {Y{\text{Sinh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right.} \right. \\ & \left. { + \left( {{\text{Sinh}}\left[ {\frac{{Y - H_{2} }}{{{\text{De}}_{2} }}} \right] - {\text{Sinh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right)H_{2} } \right)\left( { - 1 + {\text{Cosh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]\overline{\zeta }_{\text{i}} } \right) - {\text{Cosh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]\left( {Y{\text{Sinh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right. \\ & \left. {\left. { + {\text{Sinh}}\left[ {\frac{Y - 1}{{{\text{De}}_{2} }}} \right]H_{2} } \right)\overline{\zeta }_{u} \left. {\left. {\left. { - \left( {{\text{Sinh}}\left[ {\frac{{Y - H_{2} }}{{{\text{De}}_{2} }}} \right]\left( { - 1 + {\text{Cosh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]\overline{\zeta }_{\text{i}} } \right) + {\text{Cosh}}\left[ {\frac{1}{{{\text{De}}_{1} }}} \right]\left( {{\text{Sinh}}\left[ {\frac{Y - 1}{{{\text{De}}_{2} }}} \right] + {\text{Sinh}}\left[ {\frac{{1 - H_{2} }}{{{\text{De}}_{2} }}} \right]} \right)\overline{\zeta }_{u} } \right)\left( { - 1 + \mu_{R} } \right)} \right)} \right)} \right)} \right\} \\ & /\left\{ {\left( {1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{{\text{De}}_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{{\text{De}}_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{{\text{De}}_{2} }}}} } \right){\text{De}}_{1} \varepsilon_{R} } \right\} \\ \end{aligned}$$

(56)

Appendix 3

The set of equations with iα ⁰ order are as follows:

$$D^{4} \bar{\varPsi }_{1,0} = 0, D^{4} \bar{\varPsi }_{2,0} = 0$$

(57)

with the corresponding boundary conditions, No slip and no penetration:

$$\frac{{d\left( {\bar{\varPsi }_{1,0} } \right)}}{dY}\left( 0 \right) = 0, \quad \bar{\varPsi }_{1,0} \left( 0 \right) = 0, \quad \frac{{d\left( {\bar{\varPsi }_{2,0} } \right)}}{dY}\left( {H_{2} } \right) = 0,\quad \bar{\varPsi }_{2,0} \left( {H_{2} } \right) = 0$$

(58)

Shear stress balance:

$$D^{2} \bar{\varPsi }_{1,0} + \bar{H}\frac{{\hbox{d}^{2} U_{1,b} \left( 1 \right)}}{{\hbox{d}y^{2} }} + \gamma_{R,1} E_{R,1} \bar{H}\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} = \mu_{R} \left\{ {D^{2} \bar{\varPsi }_{2,0} + \bar{H}\frac{{\hbox{d}^{2} U_{2,b} \left( 1 \right)}}{{\hbox{d}y^{2} }} + \gamma_{R,2} E_{R} \bar{H}\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }}} \right\}$$

(59)

Normal stress balance:

$$D^{3} \bar{\varPsi }_{1,0} \left( 1 \right) - \mu_{R} D^{3} \bar{\varPsi }_{2,0} \left( 1 \right) = 0$$

(60)

Continuity of normal and tangential velocity:

$$\bar{\varPsi }_{1,0} \left( 1 \right) = \bar{\varPsi }_{2,0} \left( 1 \right), D\left( {\bar{\varPsi }_{1,0} - \bar{\varPsi }_{2,0} } \right)\left( 1 \right) + \bar{H}\left( {\frac{{dU_{1,b} \left( 1 \right)}}{dY} - \frac{{dU_{2,b} \left( 1 \right)}}{dY}} \right) = 0$$

(61)

Kinematic conditions:

$$\left( {U_{1,b} \left( 1 \right) - C_{0} } \right)\bar{H} = - \bar{\varPsi }_{1,0} \left( 1 \right),\quad \left( {U_{2,b} \left( 1 \right) - C_{0} } \right)\bar{H} = - \overline{\varPsi }_{2,0} \left( 1 \right)$$

(62)

The set of equations with iα ¹ order are as follows:

$$D^{4} \bar{\varPsi }_{1,1} = - {\text{Re}}_{1} \left( {C_{0} D^{2} \bar{\varPsi }_{1,0} - U_{1,b} D^{2} \bar{\varPsi }_{1,0} + \frac{{\hbox{d}^{2} U_{1,b} }}{{\hbox{d}y^{2} }}\bar{\varPsi }_{1,0} } \right)$$

(63)

$$D^{4} \bar{\varPsi }_{2,1} = - {\text{Re}}_{2} \left( {C_{0} D^{2} \bar{\varPsi }_{2,0} - U_{2,b} D^{2} \bar{\varPsi }_{2,0} + \frac{{\hbox{d}^{2} U_{2,b} }}{{\hbox{d}y^{2} }}\bar{\varPsi }_{2,0} } \right)$$

(64)

with the following boundary conditions:

No slip and no penetration:

$$\frac{{d\left( {\bar{\varPsi }_{1,1} } \right)}}{dY}\left( 0 \right) = 0, \bar{\varPsi }_{1,1} \left( 0 \right) = 0, \frac{{d\left( {\bar{\varPsi }_{2,1} } \right)}}{dY}\left( {H_{2} } \right) = 0, \bar{\varPsi }_{2,1} \left( {H_{2} } \right) = 0$$

(65)

Shear stress balance:

$$D^{2} \bar{\varPsi }_{1,1} \left( 1 \right) - \gamma_{R,1} E_{R,1} \bar{H}\left( {\left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right) = \mu_{R} \left\{ {D^{2} \bar{\varPsi }_{2,1} \left( 1 \right) - \gamma_{R,2} E_{R} \bar{H}\left( {\left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right)} \right\}$$

(66)

Normal stress balance:

$$D^{3} \bar{\varPsi }_{1,1} \left( 1 \right) - \mu_{R} D^{3} \bar{\varPsi }_{2,1} \left( 1 \right) + \text{Re}_{1} \left[ {\left( {C_{0} - U_{1,b} } \right)D\bar{\varPsi }_{1,0} \left( 1 \right) + \frac{{dU_{1,b} \left( {H_{1} } \right)}}{dY}\bar{\varPsi }_{1,0} \left( {H_{1} } \right)\left] { - \mu_{R} \text{Re}_{2} } \right[\left( {C_{0} - U_{2,b} } \right)D\bar{\varPsi }_{2,0} \left( 1 \right) + \frac{{dU_{2,b} \left( 1 \right)}}{dY}\bar{\varPsi }_{2,0} \left( 1 \right)} \right] + \left\{ {\frac{{3A_{1} \bar{H}}}{{H_{1} }} + \mu_{R} \frac{{3A_{2} \bar{H}}}{{\left( {H_{2} - 1} \right)}} - \alpha^{2} \frac{{\bar{H}}}{Ca}} \right\} = 0$$

(67)

Continuity of normal and tangential velocity:

$$\bar{\varPsi }_{1,1} \left( 1 \right) = \bar{\varPsi }_{2,1} \left( 1 \right), D\left( {\bar{\varPsi }_{1,1} - \bar{\varPsi }_{2,1} } \right)\left( 1 \right) = 0$$

(68)

Kinematic conditions:

$$C_{1} \bar{H} = \bar{\varPsi }_{1,1} \left( 1 \right), C_{1} \bar{H} = \bar{\varPsi }_{2,1} \left( 1 \right)$$

(69)

Thus C ₁ can be obtained from this last kinematic condition as:

$$C_{1} = \bar{\varPsi }_{1,1} \left( 1 \right)/\bar{H}$$

(70)