Introduction

Precise point positioning (PPP) is an absolute positioning technology for global navigation satellite system (GNSS) and is widely used in scientific research and civilian applications (Malys and Jensen 1990; Zumberge et al. 1997; Kouba and Héroux 2001; Montenbruck et al. 2017). Since its development, PPP and its applications quickly became a hot topic in the GNSS community and developed into one of the most representative technologies in GNSS precise positioning. However, there are still some unresolved difficulties in high-precision PPP applications, such as multi-frequency and multi-GNSS PPP with successful ambiguity resolution (AR), inconsistencies in the satellite attitude model between network and user ends, together with the inter-frequency clock bias (IFCBs) of the GPS L5 signal in multi-frequency PPP.

With the rapid development and modernization of GNSS, its users can benefit from multi-frequency and multi-GNSS satellites, such as carrier phase multipath extraction, cycle slip processing, high-order ionosphere mitigation, and efficient AR in particular (Zhang and Li 2016; Li et al. 2018, 2019; Zhou et al 2019). A higher PPP performance can be achieved with AR than ambiguity-float PPP (Laurichesse et al. 2009; Ge et al. 2008; Collins et al. 2008). Traditionally, PPP AR can be achieved by adopting integer recovery clocks (IRCs) or uncalibrated phase delays (UPDs), which are estimated by using dual-frequency ionosphere-free (IF) combination observations through reference network and then issued to PPP users. The corresponding relationship and equivalence of these two methods are investigated and proved by Geng et al. (2010) as well as Shi and Gao (2014). Unfortunately, unlike the classic dual-frequency model, IFCBs exist between GPS L1/L2 and L1/L5 IF observations, which are primarily caused by large variations in the GPS L5 phase hardware delay (Montenbruck et al. 2012). The existence of such pronounced IFCBs makes it impossible or inappropriate to use one set of satellite clock products in data processing for all frequencies (Guo and Geng 2018; Pan et al. 2017).

On the other hand, to obtain more accurate PPP solutions, the consistency of satellite attitude models between network and user ends must be ensured. During satellites maneuver periods, how to accurately model the non-nominal yaw attitudes and eliminate their effect is of particular interest to many researchers (Kouba 2009; Dilssner et al. 2011; Wang et al. 2018; Montenbruck et al. 2017). The impact of satellite reverse yaw maneuvers on BeiDou precise orbit determination (POD) has been assessed, and phase residuals of nearly 40 cm can be caused with the yaw attitude model previously established by Wuhan University (Xia et al. 2019). International GNSS Service (IGS) Analysis Centers (ACs) employ various strategies in non-nominal yaw attitude treatment. However, most of the PPP users are not concerned with how these orbit and clock products are generated and directly use them, which causes centimeter-level errors in the kinematic PPP solutions, since an inconsistent attitude model is applied with respect to the ACs (Lou et al. 2015; Loyer et al. 2017). Therefore, to ensure consistency between network and user ends is a critical issue for reducing positioning errors. Because of this reason, exchanging satellite attitude information in the ORBit EXchange (ORBEX) format among ACs is being tested (Banville et al. 2020; Loyer et al. 2017).

To address the above issues and be compatible with multi-frequency PPP AR, a new phase bias model compatible with Bias Solution INdependent EXchange Format (Bias-SINEX) format has been presented by Centre National d’Etudes Spatiales (CNES) (Laurichesse and Privat 2015; Schaer 2016). The post-processed phase biases, which are estimated based on the GeoForschungs Zentrum (GFZ) satellites rapid orbit and clock products, are saved as files available on the CNES website (www.ppp-wizard.net/products/POST_PROCESSED). Considering the inconsistency of satellite attitude model between CNES and GFZ, satellite attitude files with attitude quaternions of GNSS satellites are provided by CNES. Nevertheless, only initial studies on these phase biases have been given by Banville et al. (2020) and Liu et al. (2020). In their research, the performance of the dual-frequency PPP model was studied, but ambiguity fixing should be extended with more than dual frequencies. Moreover, the impact of GPS L5 IFCBs and attitude model inconsistency errors are rarely investigated by using these phase biases, especially in the conditions of satellite maneuvers and low sun elevation. Hence, we believe that it is still necessary to carry out a detailed and deep research on these topics to better understand the characteristics of phase biases and their application in multi-GNSS and multi-frequency PPP AR.

By using a modified version of the Precise Point Positioning with Integer and Zero-difference Ambiguity Resolution Demonstrator (PPP-WIZARD, Laurichesse and Privat 2015), the temporal characteristics of post-processed phase biases are assessed, and the position performance is evaluated in static, kinematic PPP AR. Following the introduction, the undifferenced and uncombined GPS/Galileo/BeiDou multi-frequency PPP observation model is presented through applying GFZ rapid orbit, clock products, and CNES satellite attitude files. We then introduce the transformation between phase biases and IRC model in the case of multi-frequency. Meanwhile, the reason GPS L5 IFCBs and satellite attitude model inconsistency errors can be absorbed into phase biases is also explained. Furthermore, the impact of phase biases on the carrier phase residual for multi-frequency PPP is analyzed in low sun elevation and satellite maneuver periods, and the positioning accuracy is assessed during the reverse yaw maneuver period. Finally, conclusions and perspectives are summarized.

Multi-frequency and multi-GNSS PPP model

With GFZ rapid clock, orbit products, and CNES satellite attitude files, the raw observation equations of multi-frequency GNSS PPP for code \(P\) and carrier phase \(L\) observations at a particular epoch can be expressed as follows:

$$P_{r,i}^{sys,s} \; = D_{r,i}^{sys,s} + c\left( {dt_{r}^{sys} - dt_{GFZ}^{sys,s} } \right) + \gamma_{i}^{sys} \cdot I_{1}^{sys,s} + T_{r} + b_{{r,P_{i} }}^{sys} - b_{{P_{i} }}^{sys,s} + yaw_{i,CNES - GFZ}^{sys,s}$$
(1)
$$\lambda_{i}^{sys} L_{r,i}^{sys,s} = D_{r,i}^{sys,s} + c\left( {dt_{r}^{sys} - dt_{GFZ}^{sys,s} } \right) - \gamma_{i}^{sys} \cdot I_{1}^{sys,s} + T_{r} + \lambda_{i}^{sys} \cdot \left( {N_{r,i}^{sys,s} + b_{{r,L_{i} }}^{sys} - b_{{L_{i} }}^{sys,s} } \right) + yaw_{i,CNES - GFZ}^{sys,s} + \varepsilon_{r,i}^{s}$$
(2)

where \(i = 1,2,3,4\) refers to the carrier frequency; \(s\) and \(r\) denote the satellite and receiver, respectively; \(sys\) denotes different satellite systems, which could be G (GPS), E (Galileo), or C (BeiDou); \(\lambda_{i}^{sys}\) denotes the wavelength of carrier phase observations at frequency \(f_{i}^{sys}\), and \(D_{r,i}^{sys,s}\) is the geometric distance between satellite and receiver antennas. \(dt_{GFZ}^{sys,s}\) and \(dt_{r}^{sys}\) are the GFZ satellite code clock (satellite code clock is available from the IGS convention) and receiver clock, respectively; \(c\) is the speed of light in vacuum; \(I_{1}^{sys,s}\) represents the slant ionospheric delay at the first frequency \(f_{1}^{sys}\); \(\gamma_{i}^{sys} = \left( {{{f_{1}^{sys} } \mathord{\left/ {\vphantom {{f_{1}^{sys} } {f_{i}^{sys} }}} \right. \kern-\nulldelimiterspace} {f_{i}^{sys} }}} \right)^{2}\) is a corresponding coefficient; \(T_{r}\) is the slant tropospheric delay; \(N_{i}^{s}\) denotes the integer ambiguity for each frequency. \(b_{{r,P_{i} }}^{sys}\) and \(b_{{r,L_{i} }}^{sys}\) are the receiver code and phase hardware delay, respectively. \(b_{{P_{i} }}^{sys,s}\) and \(b_{{L_{i} }}^{sys,s}\) are the satellite code and phase hardware delay, respectively. The variation in the GPS L5 phase hardware delay is large at low sun elevation (Montenbruck et al. 2012; Pan et al. 2017); hence, the GPS L5 satellite phase hardware delay \(b_{{L_{5} }}^{G,s} { + }\delta b_{{L_{5} }}^{G,s}\) should be divided into time-invariant parts \(b_{{L_{5} }}^{G,s}\) and time-dependent parts \(\delta b_{{L_{5} }}^{G,s}\). Since the satellite attitude files from CNES are used, to obtain more higher accuracy, the yaw attitude errors \(yaw_{i,CNES - GFZ}\) (such as phase center offsets (PCO) and phase wind-up) caused by inconsistent satellite attitude model between the GFZ and CNES must be considered (Loyer et al. 2017; Lou et al. 2015). The CNES provided satellite attitude is presented in the form of four quaternion elements (\(q_{0} ,q_{1} ,q_{2} ,q_{3}\)), and the unit vectors (\(e_{x} ,e_{y} ,e_{z}\)) in the satellite-fixed coordinate system can be defined as (Loyer et al. 2017):

$$e_{x} = \left[ {\begin{array}{*{20}c} {q_{0}^{2} + q_{1}^{2} - q_{2}^{2} - q_{3}^{2} } \\ {2 \cdot \left( {q_{1} q_{2} - q_{0} q_{3} } \right)} \\ {2 \cdot \left( {q_{1} q_{3} + q_{0} q_{2} } \right)} \\ \end{array} } \right]\;\;e_{y} = \left[ {\begin{array}{*{20}c} {2 \cdot \left( {q_{1} q_{2} + q_{0} q_{3} } \right)} \\ {q_{0}^{2} - q_{1}^{2} + q_{2}^{2} - q_{3}^{2} } \\ {2 \cdot \left( {q_{2} q_{3} - q_{0} q_{1} } \right)} \\ \end{array} } \right]\;\;e_{z} = \left[ {\begin{array}{*{20}c} {2 \cdot \left( {q_{1} q_{3} - q_{0} q_{2} } \right)} \\ {2 \cdot \left( {q_{2} q_{3} + q_{0} q_{1} } \right)} \\ {q_{0}^{2} - q_{1}^{2} - q_{2}^{2} + q_{3}^{2} } \\ \end{array} } \right]$$
(3)

If rapid satellite orbit and clock products from GFZ are applied in the multi-frequency undifferenced and uncombined observation equations (Liu et al. 2020), the GPS-only (\(sys = G\)) narrow-lane \(\overline{N}_{1}^{s}\), wide-lane (WL) \(\overline{N}_{W}^{s}\), and extra-wide-lane (EWL) \(\overline{N}_{E}^{s}\) ambiguities can be formulated as:

$$\left\{ \begin{gathered} \begin{array}{*{20}l} \begin{gathered} \lambda_{1} \cdot \overline{N}_{1}^{s} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \lambda_{1} \cdot \left( {N_{1}^{s} + b_{{r,L_{1} }} - b_{{L_{1} }}^{s} } \right) + b_{{P_{IF} }}^{s} - b_{{r,P_{IF} }} + \beta_{12} \left( {DCB_{r,12} + DCB_{12}^{s} } \right) \hfill \\ \lambda_{2} \cdot \left( {\overline{N}_{W}^{s} + \overline{N}_{1}^{s} } \right)\;\;\;\;\;\;\;\;\; = \lambda_{2} \cdot \left( {N_{2}^{s} + b_{{r,L_{2} }} - b_{{L_{2} }}^{s} } \right) + b_{{P_{IF} }}^{s} - b_{{r,P_{IF} }} + \gamma_{2} \beta_{12} \left( {DCB_{r,12} + DCB_{12}^{s} } \right) \hfill \\ \end{gathered} \hfill \\ {\lambda_{5} \cdot \left( {\overline{N}_{E}^{s} + \overline{N}_{W}^{s} + \overline{N}_{1}^{s} } \right)\;\; = \lambda_{5} \cdot \left( {N_{5}^{s} + b_{{r,L_{5} }} - b_{{L_{5} }}^{s} } \right) + b_{{P_{IF} }}^{s} - b_{{r,P_{IF} }} + \gamma_{5} \beta_{12} \left( {DCB_{r,12} + DCB_{12}^{s} } \right)} \hfill \\ \end{array} \hfill \\ DCB_{r,12} = b_{{r,P_{1} }} - b_{{r,P_{2} }} \;\;\;\;\;\;\;\;\;\;\;DCB_{12}^{s} = b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} \hfill \\ b_{{P_{IF} }}^{s} = \alpha_{12} \cdot b_{{P_{1} }}^{s} + \beta_{12} \cdot b_{{P_{2} }}^{s} \;\;\;\;\;\;\;\;b_{{r,P_{IF} }} = \alpha_{12} \cdot b_{{r,P_{1} }} + \beta_{12} \cdot b_{{r,P_{2} }} \hfill \\ \alpha_{12} = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}\;\;\;\;\;\;\;\;\;\;\;\beta_{12} = {{ - f_{2}^{2} } \mathord{\left/ {\vphantom {{ - f_{2}^{2} } {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \hfill \\ \end{gathered} \right.$$
(4)

where \(DCB_{12}^{s}\) and \(DCB_{r,12}\) denote the difference code biases at satellite \(s\) and receiver \(r\), respectively. Since satellite and receiver hardware delays are highly correlated with integer ambiguity, the integer property of the estimated ambiguity parameter \(\overline{N}_{1}^{s} ,\overline{N}_{W}^{s} ,\overline{N}_{E}^{s}\) will be lost. Note that time-dependent parts \(\delta b_{{L_{5} }}^{G,s}\) of the GPS L5 phase hardware delays are not compensated by the precise code satellite clocks \(dt_{GFZ}^{s}\), which are estimated based on dual-frequency (L1 and L2) measurement observations, and these time-dependent parts \(\delta b_{{L_{5} }}^{G,s}\) will have an influence on the GPS L5 phase residuals (Cao et al. 2018). Moreover, due to the mixed application of GFZ rapid orbit, clock products, and CNES yaw attitude model, the inconsistent yaw attitude errors \(yaw_{i,CNES - GFZ}\) will also cause systematic errors during satellite maneuver period (Lou et al. 2015; Loyer et al. 2017; Kouba 2009). Finally, the phase residuals symbolized as \(v_{{L_{i} }}^{s}\) in each GPS frequency can be expressed as follows:

$$\left[ {\begin{array}{*{20}c} {v_{{L_{1} }}^{G,s} } \\ {v_{{L_{2} }}^{G,s} } \\ {v_{{L_{5} }}^{G,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varepsilon_{r,1}^{G,s} + yaw_{1,CNES - GFZ}^{G} } \\ {\varepsilon_{r,2}^{G,s} + yaw_{2,CNES - GFZ}^{G} } \\ {\varepsilon_{r,5}^{G,s} + yaw_{5,CNES - GFZ}^{G} + \delta b_{{L_{5} }}^{G,s} } \\ \end{array} } \right]$$
(5)

while for Galileo and BeiDou system (\(sys = E,C\)), phase residuals can be expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{{L_{1} }}^{E,s} } \\ \end{array} } \\ {v_{{L_{{5}} }}^{E,s} } \\ {v_{{L_{{7}} }}^{E,s} } \\ {v_{{L_{{6}} }}^{E,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{r,1}^{E,s} + yaw_{1,CNES - GFZ}^{E,s} } \\ \end{array} } \\ {\varepsilon_{{r,{5}}}^{E,s} + yaw_{{{5},CNES - GFZ}}^{E,s} } \\ {\varepsilon_{{r,{7}}}^{E,s} + yaw_{{{7},CNES - GFZ}}^{E,s} } \\ {\varepsilon_{{r,{6}}}^{E,s} + yaw_{{{6},CNES - GFZ}}^{E,s} } \\ \end{array} } \right]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{{L_{2} }}^{C,s} } \\ \end{array} } \\ {v_{{L_{7} }}^{C,s} } \\ {v_{{L_{6} }}^{C,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{r,2}^{C,s} + yaw_{2,CNES - GFZ}^{C,s} } \\ \end{array} } \\ {\varepsilon_{r,7}^{C,s} + yaw_{7,CNES - GFZ}^{C,s} } \\ {\varepsilon_{r,6}^{C,s} + yaw_{6,CNES - GFZ}^{C,s} } \\ \end{array} } \right]$$
(6)

Due to the smaller effect of time-dependent parts on Galileo E5b, E6 and BeiDou B3 phase hardware delays with the current GFZ rapid products (Cao et al. 2018; Li et al. 2018), these errors will not be considered for the multi-frequency and multi-GNSS PPP model in this study.

Transformation between the phase bias and IRC model for multi-frequency PPP

AR at the PPP user end can be implemented by applying the IRC model (Laurichesse et al. 2009). Different from the IRC model, PPP user end can use phase biases and code satellite clocks to recover the integer properties of ambiguities. Taking GPS as an example, the phase biases \(\overline{b}_{{L_{i} }}^{s}\) are estimated by using the integer phase clock \(dt_{IRC}^{s}\), code satellite clock \(dt_{GFZ}^{s}\), and triple-frequency IF phase combination \(L_{{IF_{3} }}\) (Liu et al. 2020). The precise code satellite clocks \(dt_{GFZ}^{s}\) can be obtained with dual-frequency IF phase combination:

$$cdt_{GFZ}^{s} = cdt^{s} + b_{{P_{IF} }}^{s} = cdt^{s} + \frac{{\gamma_{2} \cdot b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)}}$$
(7)

Based on the GFZ rapid orbit products and CNES satellite yaw attitude model, the inconsistent yaw attitude error \(yaw_{i,CNES - GFZ}\) will be absorbed into integer phase clocks \(dt_{IRC}^{s}\) during the satellite maneuver period (Lou et al. 2015; Loyer et al. 2017). Therefore, the integer phase clocks \(dt_{IRC}^{s}\) can be presented as follows:

$$cdt_{IRC}^{s} = cdt^{s} + \frac{{\gamma_{2} \cdot \lambda_{1} \cdot b_{{L_{1} }}^{s} - \lambda_{2} \cdot b_{{L_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)}} + \frac{{\gamma_{2} \cdot yaw_{1,CNES - GFZ}^{s} - yaw_{2,CNES - GFZ}^{s} }}{{\left( {\gamma_{2} - 1} \right)}}$$
(8)

To make multi-frequency phase biases \(\overline{b}_{{L_{i} }}^{s}\) compatible with code satellite clocks \(dt_{GFZ}^{s}\), the difference \(cd_{IRC}^{s} - cdt_{GFZ}^{s}\) should be assimilated into phase biases \(\overline{b}_{{L_{i} }}^{s}\). Combining (7) and (8), the estimated phase biases \(\overline{b}_{{L_{1} }}^{s} ,\overline{b}_{{L_{2} }}^{s}\) can be determined by \(cd_{IRC}^{s} - cdt_{GFZ}^{s}\):

$$\frac{{\gamma_{2} \cdot \lambda_{1} \cdot \overline{b}_{{L_{1} }}^{s} - \lambda_{2} \cdot \overline{b}_{{L_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)}} = cdt_{IRC}^{s} - cdt_{GFZ}^{s}$$
(9)

The phase biases \(\overline{b}_{{L_{i} }}^{s}\) for each frequency cannot be resolved due to rank deficiency of (9). In the multi-frequency case, using GFZ rapid orbit, clock products and the CNES satellite yaw attitude model, the phase bias difference among \(\overline{b}_{{L_{1} }}^{s} ,\overline{b}_{{L_{2} }}^{s} ,\overline{b}_{{L_{5} }}^{s}\) can be obtained by applying triple-frequency IF phase combination \(L_{{IF_{3} }}\) (Liu et al. 2020):

$$\begin{gathered} L_{{IF_{3} }} = \frac{{f_{1} \cdot \lambda_{{WL_{L1L2} }} \cdot \left( {L_{1} - L_{2} } \right)}}{{f_{1} - f_{5} }}\; - \frac{{f_{5} \cdot \lambda_{{WL_{L2L5} }} \cdot \left( {L_{2} - L_{5} } \right)}}{{f_{1} - f_{5} }}\; \hfill \\ \;\;\;\;\; = D_{r}^{s} + T_{r} + \overline{d}t_{r} - cdt_{GFZ}^{s} + \frac{{f_{1} \cdot \lambda_{{WL_{L1L2} }} \cdot \overline{N}_{W}^{s} }}{{f_{1} - f_{5} }} - \frac{{f_{5} \cdot \lambda_{{WL_{L2L5} }} \cdot \overline{N}_{E}^{s} }}{{f_{1} - f_{5} }} \hfill \\ \end{gathered}$$
(10)

with

$$\lambda_{{WL_{L1L2} }} = \frac{c}{{f_{1} - f_{2} }}\;\;\;\;\;\;\;\;\;\lambda_{{WL_{L2L5} }} = \frac{c}{{f_{2} - f_{5} }}$$
(11)

where \(\lambda_{{W_{L1L2} }}\) and \(\lambda_{{W_{L2L5} }}\) are the WL and EWL wavelengths, respectively. In Eq. (10), WL ambiguities can be obtained from IRC model, \(D_{r}^{s}\) and \(cdt_{GFZ}^{s}\) are fixed, while \(\overline{N}_{E}^{s}\), \(\overline{N}_{W}^{s}\) are estimated as completely independent between epochs. Therefore, the GPS L5 time-dependent parts \(\delta b_{{L_{5} }}^{G,s}\) and yaw attitude error \(yaw_{i,CNES - GFZ}\) will be absorbed into \(\overline{N}_{W}^{s} ,\;\overline{N}_{E}^{s}\):

$$\begin{gathered} \overline{N}_{W}^{s} = N_{W}^{s} + \frac{{\gamma_{2} \cdot b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)\lambda_{{WL_{L1L2} }} }} - \frac{{yaw_{1,CNES - GFZ}^{s} }}{{\lambda_{1} }} + \frac{{yaw_{2,CNES - GFZ}^{s} }}{{\lambda_{2} }} - b_{{L_{1} }}^{s} + b_{{L_{2} }}^{s} \hfill \\ \overline{N}_{E}^{s} = N_{E}^{s} + \frac{{\gamma_{2} \cdot b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)\lambda_{{WL_{L2L5} }} }} - \frac{{yaw_{2,CNES - GFZ}^{s} }}{{\lambda_{{2}} }} + \frac{{yaw_{5,CNES - GFZ}^{s} }}{{\lambda_{{5}} }} - b_{{L_{2} }}^{s} + b_{{L_{5} }}^{s} + \delta b_{{L_{5} }}^{G,s} \hfill \\ \end{gathered}$$
(12)

The phase bias difference among \(\overline{b}_{{L_{1} }}^{s} ,\overline{b}_{{L_{2} }}^{s} ,\overline{b}_{{L_{5} }}^{s}\) can then be expressed as fractional parts of \(\overline{N}_{W}^{s}\) and \(\overline{N}_{E}^{s}\):

$$\begin{gathered} \mu_{12}^{s} = \overline{b}_{{L_{1} }}^{s} - \overline{b}_{{L_{2} }}^{s} = \overline{N}_{W}^{s} - \left\langle {\overline{N}_{W}^{s} } \right\rangle = \frac{{\gamma_{2} \cdot b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)\lambda_{{WL_{L1L2} }} }} - \frac{{yaw_{1,CNES - GFZ}^{s} }}{{\lambda_{1} }} + \frac{{yaw_{2,CNES - GFZ}^{s} }}{{\lambda_{2} }} - b_{{L_{1} }}^{s} + b_{{L_{2} }}^{s} \hfill \\ \mu_{25}^{s} = \overline{b}_{{L_{2} }}^{s} - \overline{b}_{{L_{5} }}^{s} = \overline{N}_{E}^{s} - \left\langle {\overline{N}_{E}^{s} } \right\rangle = \frac{{\gamma_{2} \cdot b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} }}{{\left( {\gamma_{2} - 1} \right)\lambda_{{WL_{L2L5} }} }} - \frac{{yaw_{2,CNES - GFZ}^{s} }}{{\lambda_{2} }} + \frac{{yaw_{5,CNES - GFZ}^{s} }}{{\lambda_{5} }} - b_{{L_{2} }}^{s} + b_{{L_{5} }}^{s} + \delta b_{{L_{5} }}^{G,s} \hfill \\ \end{gathered}$$
(13)

where \(\left\langle * \right\rangle\) means to round the real value to the nearest integer value and \(\mu_{12}^{s} ,\mu_{25}^{s}\) are the fractional parts of \(\overline{N}_{W}^{s} ,\overline{N}_{E}^{s}\). Combining (9) and (13), the estimated phase bias parameters \(\overline{b}_{{L_{1} }}^{s} ,\overline{b}_{{L_{2} }}^{s} ,\overline{b}_{{L_{5} }}^{s}\) can be determined with the 3*3 matrix in the triple-frequency case:

$$\left( {\begin{array}{*{20}c} {\overline{b}_{{L_{1} }}^{s} } \\ \begin{gathered} \overline{b}_{{L_{2} }}^{s} \hfill \\ \overline{b}_{{L_{5} }}^{s} \hfill \\ \end{gathered} \\ \end{array} } \right) = \frac{1}{{\gamma_{2} \lambda_{1} - \lambda_{2} }}\left( {\begin{array}{*{20}c} { - \lambda_{2} } & 1 & {\;\;0} \\ \begin{gathered} - \gamma_{2} \lambda_{1} \hfill \\ - \gamma_{2} \lambda_{1} \hfill \\ \end{gathered} & \begin{gathered} 1 \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} \;\;0 \hfill \\ - 1 \hfill \\ \end{gathered} \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\mu_{12}^{s} } \\ \begin{gathered} \left( {\gamma_{2} - 1} \right)\left( {cdt_{IRC}^{s} - cdt_{IGS}^{s} } \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu_{25}^{s} \hfill \\ \end{gathered} \\ \end{array} } \right)$$
(14)

among which \(\mu_{12}^{s} ,\;\mu_{25}^{s} ,\;cdt_{IRC}^{s} ,\;cdt_{GFZ}^{s}\) are represented by \(b_{{P_{IF} }}^{s} ,\;b_{{L_{i} }}^{s} ,\;yaw_{i,CNES - GFZ}^{s}\), so that we can simplify the above transformation as:

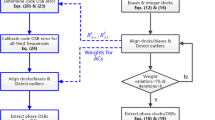
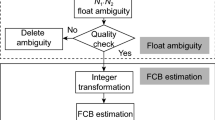
$$\left( {\begin{array}{*{20}c} {\overline{b}_{{L_{1} }}^{s} } \\ \begin{gathered} \overline{b}_{{L_{2} }}^{s} \hfill \\ \overline{b}_{{L_{5} }}^{s} \hfill \\ \end{gathered} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{1}{{\lambda_{1} }} \cdot b_{{P_{IF} }}^{s} - b_{{L_{1} }}^{s} - \frac{1}{{\lambda_{1} }} \cdot yaw_{1,CNES - GFZ}^{s} } \\ \begin{gathered} \;\;\;\;\frac{1}{{\lambda_{2} }} \cdot b_{{P_{IF} }}^{s} - b_{{L_{2} }}^{s} - \frac{1}{{\lambda_{2} }} \cdot yaw_{2,CNES - GFZ}^{s} \hfill \\ \frac{1}{{\lambda_{5} }} \cdot b_{{P_{IF} }}^{s} - b_{{L_{5} }}^{s} - \frac{1}{{\lambda_{5} }} \cdot yaw_{5,CNES - GFZ}^{s} - \delta b_{{L_{5} }}^{G,s} \hfill \\ \end{gathered} \\ \end{array} } \right)$$
(15)

This transformation can be described in Fig. 1:

Fig. 1
figure 1

Estimation of phase biases in the multi-frequency case

Full size image

Considering that the code biases \(\overline{b}_{{P_{i} }}^{s}\) are standardized in Bias-SINEX format V1.00 (Schaer 2016; Banville et al. 2020), these biases can be expressed as follows:

$$\left( {\begin{array}{*{20}c} {\overline{b}_{{P_{1} }}^{s} } \\ {\overline{b}_{{P_{2} }}^{s} } \\ {\overline{b}_{{P_{5} }}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\beta_{12} \left( {b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} } \right)} \\ { - \alpha_{12} \left( {b_{{P_{1} }}^{s} - b_{{P_{2} }}^{s} } \right)} \\ {b_{{P_{IF} }}^{s} - b_{{P_{5} }}^{s} } \\ \end{array} } \right)$$
(16)

The PPP user end applies code and phase biases to raw measurements with the GFZ code satellite clock \(dt_{GFZ}^{s}\) and CNES satellite attitude, the integer properties of ambiguities can then be recovered, GPS L5 IFCBs and yaw-attitude errors \(yaw_{i,CNES - GFZ}\) can also be mitigated at the PPP user end. The reparameterization of (4) for GPS, as an example, can be conducted as:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{1}^{{}} \cdot \overline{N}_{1}^{,s} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \lambda_{1}^{{}} \cdot \left( {N_{1}^{s} + b_{{r,L_{1} }}^{{}} } \right) - b_{{r,P_{IF} }}^{{}} + \beta_{12}^{{}} DCB_{r,12}^{{}} } \hfill \\ \begin{gathered} \lambda_{2}^{{}} \cdot \left( {\overline{N}_{W}^{s} + \overline{N}_{1}^{s} } \right)\;\;\;\;\;\;\;\;\; = \lambda_{2}^{{}} \cdot \left( {N_{2}^{,s} + b_{{r,L_{2} }}^{{}} } \right) - b_{{r,P_{IF} }}^{{}} + \gamma_{2}^{{}} \beta_{12}^{{}} DCB_{r,12}^{{}} \hfill \\ \lambda_{5}^{{}} \cdot \left( {\overline{N}_{E}^{s} + \overline{N}_{W}^{s} + \overline{N}_{1}^{s} } \right) = \lambda_{5}^{{}} \cdot \left( {N_{5}^{s} + b_{{r,L_{5} }}^{{}} } \right) - b_{{r,P_{IF} }}^{{}} + \gamma_{5}^{{}} \beta_{12}^{{}} DCB_{r,12}^{{}} \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$
(17)

The carrier phase residual errors \(v_{{L_{i} }}^{s}\) in the multi-frequency case can be expressed as follows:

$$\left[ {\begin{array}{*{20}c} {v_{{L_{1} }}^{G,s} } \\ {v_{{L_{2} }}^{G,s} } \\ {v_{{L_{5} }}^{G,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varepsilon_{r,1}^{G,s} } \\ {\varepsilon_{r,2}^{G,s} } \\ {\varepsilon_{r,5}^{G,s} } \\ \end{array} } \right]\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{{L_{1} }}^{E,s} } \\ \end{array} } \\ {v_{{L_{{5}} }}^{E,s} } \\ {v_{{L_{{7}} }}^{E,s} } \\ {v_{{L_{{6}} }}^{E,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{r,1}^{E,s} } \\ \end{array} } \\ {\varepsilon_{{r,{5}}}^{E,s} } \\ {\varepsilon_{{r,{7}}}^{E,s} } \\ {\varepsilon_{{r,{6}}}^{E,s} } \\ \end{array} } \right]\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{{L_{2} }}^{C,s} } \\ \end{array} } \\ {v_{{L_{7} }}^{C,s} } \\ {v_{{L_{6} }}^{C,s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{r,2}^{C,s} } \\ \end{array} } \\ {\varepsilon_{r,7}^{C,s} } \\ {\varepsilon_{r,6}^{C,s} } \\ \end{array} } \right]$$
(18)

These post-processed GPS/Galileo/BeiDou multi-frequency phase biases and satellite attitude files have been uploaded to the CNES website since June 4, 2019.

Data description and process schemes

In the process of multi-frequency and multi-GNSS PPP, GFZ rapid orbit and clock products as well as CNES post-processed phase biases were used. We applied attitude quaternion elements from attitude files to obtain the same satellite attitude model as CNES network end. Considering that CNES did not estimate BeiDou GEO and BeiDou-3 satellite phase biases in 2019, these satellites were excluded from our experiment. The satellite PCO and phase center variation (PCV) corrections provided by ‘igs_2084.atx’ were applied for GPS L1/L2, Galileo E1/E5a/E5b/E6 and BeiDou B1/B2/B3 frequencies. For the third GPS frequency (L5), the same PCO and PCV corrections for the second frequency (L2) are used (Li et al. 2018). Since receiver PCO and PCV corrections for Galileo and BeiDou were not available, we use GPS correction for Galileo and BeiDou signals during the experiment. In addition, for L5, E5b, E6, and B3 frequency observables, the receiver PCO and PCV corrections for the second frequency were used (Li et al. 2018, 2019).

The EWL and WL ambiguities were fixed by rounding averaged strategy with several epochs. After fixing EWL and WL ambiguities successfully, the optimal integer solution of N1 ambiguity can be searched using least squares ambiguity decorrelation adjustment (LAMBDA). The ratio threshold was set to 2.0 (Teunissen 1995; Geng et al. 2019). Instead of fixing full ambiguities, partial AR method was applied to find a subset of integers that can be fixed (Li et al. 2018). Standard deviation of ambiguities larger than 0.8 cycles, satellite elevations of less than 10°, or short tracking arcs (EWL, WL< 150 s and N1 <180 s) were not attempted to fix. We keep float solutions for these low-quality ambiguities and try to fix a subset of high-quality ambiguities. To avoid negative effects from possible incorrectly fixed ambiguities in the last epoch, float solutions were introduced into the next update of the filter.

The positioning errors were defined as the difference between the PPP solution and the reference coordinate from IGS SINEX weekly solutions. As shown in Fig. 2, observation data from 34 Multi-GNSS Experiment (MGEX) stations were selected, and the detailed strategy for PPP is summarized in Table 1.

Fig. 2
figure 2

Distribution of the MGEX stations in this experiment. All these stations are equipped with Septentrio PolaRx5 and Trimble Alloy receivers, which are able to track GPS L1/L2/L5, Galileo E1/E5a/E5b/E6, and BeiDou B1/B2/B3 signals

Full size image
Table 1 Strategies for GPS/Galileo/BeiDou PPP
Full size table

Impact of phase biases on the IFCBs

As a typical representative, time series for GPS L5, Galileo E5b and E6, BeiDou B3 phase biases in units of cycle on DOY 222, 2019 are shown in Fig. 3. The values of phase biases are offset for clarity purposes. As shown in (15), the time-dependent parts \(\delta b_{{L_{5} }}^{G,s}\) of GPS L5 are absorbed into L5 phase biases, so it can be found that the periodic variations in the GPS IIF satellites and different amplitudes can be observed in different satellites. Following Montenbruck et al. (2012), the amplitude is related to sun elevation above the satellite orbital plane. On this day, the sun elevations for G03 and G10 are both approximately -0.1°; hence, the amplitudes of L5 phase biases for G03 and G10 are relatively larger than those of the other GPS IIF satellites. In addition, frequent jumps can be found for G03 and G10 phase biases. These are caused by the inconsistent satellite attitude \(yaw_{i,CNES - GFZ}\) between GFZ and CNES in the satellite maneuver periods, which will be proved in the following section. Variations in the phase biases for most Galileo satellites are stable except for E14 and E18, while the phase bias of Beidou shows poorer stability than that of Galileo.

Fig. 3
figure 3

Time series of phase biases on DOY 222, 2019. Different frequency types are shown in different panels. From left to right represents GPS L5, Galileo E5b, Galileo E6, and BeiDou B3, respectively

Full size image

Figure 4 shows the time series of the carrier phase residuals in GPS L5, Galileo E5b and E6, as well as BeiDou B3 at station KIR0 on DOY 222, 2019. Large systematic errors of over 2.5 cm in the.

Fig. 4
figure 4

Residual carrier phase (left panels) and carrier phase + phase biases (right panels) for the KIR0 station on DOY 222, 2019. Different satellites are identified by different colors

Full size image

GPS L5 carrier phase residual can be observed without phase biases. This phenomenon reflects the existence of IFCBs in the GPS L5 observation carrier phase residuals. For comparison, the GPS L5 carrier phase residuals with phase biases are also presented in Fig. 4, and it is clear that the effect of IFCBs can be mitigated at the user end by using phase biases. For Galileo E5b and E6 together with BeiDou B3, we can see that the carrier phase residuals have almost no obvious systematic errors with these two methods.

Impact of phase biases on the satellite maneuver period

Taking GPS as an example, the time series of phase biases, yaw angle, and sun elevation angle for G10 (Block IIF) and G05 (Block IIR) on DOY 222 and 2019 are shown in Fig. 5. The yaw angle is obtained by the satellite attitude file provided by the CNES, and the gray bars indicate the satellite maneuver period. From Fig. 5, we can see that the G10 IIF sun elevation angle is approximately 0°, and pronounced variations can be found for the G10 IIF L1, L2, and L5 phase biases in the maneuver periods, while no obvious variations can be found for the G05 IIR L1 and L2 phase biases. According to (15), the inconsistent yaw attitude errors \(yaw_{i,CNES - GFZ}\) between GFZ and CNES are absorbed into phase biases for each frequency. These also reflect that different attitude models of the GPS IIF satellites are applied between CNES phase biases and GFZ rapid orbit, clock products in the satellite maneuver periods.

Fig. 5
figure 5

Time series of phase bias and yaw angle for the G10 Block IIF (top panels) and G05 Block IIR (bottom panels) satellites. The sun elevation variation is 0.5°to − 0.5° for G10 and − 0.5° to − 1.5° for G05. Gray bars indicate the satellite maneuver period

Full size image

In addition, a cycle bias of approximately 1.0 can be found in the red circle of Fig. 5. The reason for this 1.0 cycle bias is that the CNES and GFZ apply the reverse yaw direction for G10 at the low sun elevation (Dilssner et al. 2011; Kuang et al. 2017). For example, the yaw angle variation range for CNES is 0° to 180°, while it is 0° to -180° for GFZ in the maneuver periods. Because of the reverse yaw direction, approximately 1.0 cycle wind-up errors are mostly absorbed into phase biases. Once introduced, a 1.0 cycle bias remains in the phase biases until the end of the orbit solution arc or the next reverse yaw direction occurs (Kuang et al. 2017). The impact of reverse yaw direction on the static and kinematic PPP accuracy will be investigated in the next section.

To verify the validity of phase biases and satellite attitude file in the maneuver periods, observation of station GRAZ and USN7 was selected. Figure 6 shows the G10 IIF and G05 IIR satellite carrier phase residuals by using the two different methods. It is obvious that large systematic errors of greater than 3 cm can be observed for the G10 IIF L1 carrier phase residual without phase biases. When phase biases are added to the raw measurement, the G10 IIF carrier phase residuals can be significantly reduced.

Fig. 6
figure 6

Residuals of G10 IIF carrier phase (top panels) at station GRAZ station and G05 IIR carrier phase (bottom panels) at station USN7 on DOY 222, 2019. Gray bars indicate the satellite maneuver period

Full size image

The ambiguity residual can be used as an integer property indicator for AR. In our experiment, observations of 34 MGEX stations were used to estimate the EWL, WL, and N1 ambiguities. By using phase biases and CNES satellite attitude, the estimated ambiguities of (17) are still contaminated by receiver hardware delay. To recover the integer property of ambiguity, we select the highest elevation of the satellite as a datum. The ambiguities with float values are rounded to their nearest integers in each epoch. Then, the ambiguity residuals can be expressed by the differences between the float values and their corresponding integer values of ambiguities. Figure 7 shows the ambiguity residual distributions of G10 in the reverse yaw maneuver period (red circle of Fig. 5). It can be seen from this figure that the EWL, WL, and N1 ambiguity residuals follow standard normal distributions. Therefore, we conclude that the integer property of ambiguity can be recovered by using phase biases and CNES satellite attitude in the reverse yaw maneuver period.

Fig. 7
figure 7

Residual distributions of the EWL (left panel), WL (middle panel), and N1 (right panel) ambiguity for G10 in the reverse yaw maneuver period

Full size image

Static and kinematic PPP AR in the reverse yaw maneuver period

To investigate the benefits from phase biases in the case of reverse yaw maneuvers, three data processing strategies are listed in Table 2. The first strategy (NO PHASE BIAS) uses CNES satellite attitude without phase biases, and second strategy (DELETE) deletes the satellite data during maneuver periods. In both strategies, the ambiguities are kept float solutions. The third strategy (WITH PHASE BIAS) uses CNES satellite attitude with phase biases, and the ambiguities will be fixed. We collect information about the reverse yaw maneuver between CNES and GFZ from DOY 152 to 243, 2019, and these results are shown in Table 3.

Table 2 List of the data processing strategies
Full size table
Table 3 Reverse yaw maneuvers of GPS, Galileo, and BeiDou between CNES and GFZ products
Full size table

We take station KIR0 on DOY 222, 2019, as an example. The 1-day kinematic and static positioning errors for different PPP strategies are given in Fig. 8. We observe that the static and kinematic positioning errors in the east (E) direction can be reduced by AR. After filter convergence, the static positioning errors of different strategies are almost the same. However, the kinematic positioning errors of DELETE and NO PHASE BIAS strategies are obviously larger than those of the WITH PHASE BIAS strategy. In the up (U) direction, the NO PHASE BIAS strategy positioning errors can reach up to 15 cm. From Figs. 3 and 8, we notice that the maneuvering satellites including G03 and G10 and that these two satellites have reversed yaw directions during the maneuver periods. At the PPP user end, the reversed yaw direction would cause the approximately 1.0 cycle wind-up errors until the end of the observation arc or the next reverse yaw direction occurs. Therefore, these errors will continue to affect the positioning accuracy after the end of the maneuvering period, even if we delete this satellite during the maneuvering period. In kinematic PPP solutions, these errors will seriously damage the accuracy of epoch-dependent parameters such as station coordinates. As concluded in the above section, the 1.0 cycle wind-up errors are mostly absorbed into phase biases (Fig. 5); the influence of these errors on the PPP user end can be mitigated by using phase biases.

Fig. 8
figure 8

Kinematic (left panels) and static (right panels) PPP for station KIR0 on DOY 222, 2019, by using different strategies. Black lines represent the G03 and G10 satellite maneuver periods, while purple lines represent the G03 and G10 observation arcs for station KIR0

Full size image

The 12-day (Table 3) datasets from 34 MGEX stations were employed for static and kinematic PPP accuracy analysis to further analyze the benefit of phase biases on reverse yaw maneuver. We calculated the root mean square (RMS) in E, north (N) and U directions, as shown in Fig. 9 for both static and kinematic PPP. We can see that three strategies show similar positioning performance in static PPP, and the positioning accuracy of WITH PHASE BIAS strategy can reach approximately 0.9, 0.8, and 1.0 cm in the E, N, U directions, respectively. In kinematic PPP, however, the RMSs of the three strategies are significantly different. Compared with NO PHASE BIAS strategy, the RMS of WITH PHASE BIAS strategy can be reduced by 34.4%, 23.1%, and 37.4% (from 2.38, 1.86, and 4.57 cm to 1.56, 1.43, and 2.86 cm) in the E, N, and U directions, respectively. These results indicate that the positioning performance can be improved by using the phase biases in the reverse yaw maneuver periods.

Fig. 9
figure 9

RMS values in the E, N, and U directions in the kinematic (left panel) and static (right panel) PPP for different strategies

Full size image

The N1 ambiguity fixing rate \(N_{1\_rate}\) is a useful indicator to assess the performance of PPP AR. It is calculated with the following formula:

$$N_{1\_rate} = \frac{{N_{1\_fixed} }}{{N_{1\_total} }} \times 100\%$$
(19)

where \(N_{1\_fixed}\) denotes the number of N1 ambiguities-fixed and \(N_{1\_total}\) denotes the number of total ambiguities-float. Figure 10 shows the fixing rate of GPS, Galileo, and BeiDou in static and kinematic PPP. The fixing rates of GPS are approximately 94.7% and 91.3% in static and kinematic modes, respectively, while Galileo shows almost the same fixing rate as GPS. Through comparing the fixing rate of GPS, Galileo, and BeiDou, it can be seen that fixing rate of GPS and Galileo is higher than that of BeiDou, which may be caused by the lower accuracy of BeiDou orbit and clock products (Steigenberger and Montenbruck 2019).

Fig. 10
figure 10

Fixing rate of N1 ambiguities for the different systems in static and kinematic PPP AR

Full size image

Conclusion and summary

Multi-frequency and multi-GNSS PPP-AR with post-process phase biases and satellite attitude files are implemented by CNES, which are based on GFZ rapid orbit and clock products. By using these products, integer property of ambiguity can be recovered at the user end. In this paper, we introduced the transformation between phase biases and IRC model in the multi-frequency case. The theoretical derivation and experimental results demonstrate that GPS L5 IFCBs and inconsistent satellite attitude errors between CNES and GFZ products will be absorbed into the multi-frequency phase biases.

To assess the performance of phase biases in satellite maneuvers and low sun elevations, the phase residual and positioning performance of static and kinematic PPP AR were evaluated with 34 MGEX tracking stations. We find that through using these phase biases and satellite attitude files, the effect of IFCBs and inconsistent satellite attitude errors can be mitigated at the user end. Under the condition of satellite reverse yaw maneuver, the influence of reverse yaw maneuver on static PPP is not significant. However, the performance of kinematic PPP without phase biases or deleting maneuvering satellites will degrade significantly until the end of satellite observation arc or the next reverse yaw maneuver occurs. By applying phase biases with AR, the kinematic positioning accuracy can be improved by 34.4%, 23.1%, and 37.4% in the E, N, and U directions, respectively.

We conclude that the positioning accuracy, reliability, and availability performance can be improved by applying post-process phase biases with AR. When using GFZ rapid orbit and clock products, it is suggested that PPP users apply phase biases and satellite attitude files that are provided by CNES, especially for satellite maneuvers and low sun elevations.