Introduction

Integer carrier-phase ambiguity resolution (AR) is the key to fast and high-precision GNSS positioning and navigation. For a long time, AR could only be achieved in relative positioning. The integer property of the ambiguity parameter is often ignored in precise point positioning (PPP) (Zumberge et al. 1997) due to the difficulty of separating the fractional cycle bias (FCB) from the ambiguity parameter for a single receiver. As a result, a long observation period of more than 3 h is required to achieve centimeter- to subdecimeter-level positioning precision (Geng et al. 2009). However, the east component of the PPP results is still worse than that of relative positioning even if observations over a day are processed. Therefore, all types of PPP results should be improved by AR.

In recent years, AR techniques relying only on a single station have been developed successfully to further improve the positioning accuracy of PPP. The key to successful AR for PPP is to remove FCB from the ambiguity and then to recover the integer property of the ambiguity parameter, with the additional satellite FCB products estimated in advance.

Specifically, with undifferenced ambiguity estimates derived from a GPS network solution, Ge et al. (2008) separated the FCBs and provided them for PPP users to retrieve the integer property of single-differenced ambiguities. With this method, Ge et al. (2008) and Geng et al. (2009) achieved a significant accuracy improvement in static PPP with daily and hourly observations, respectively, especially in the east component.

Collins et al. (2008) developed a method known as the decoupled clock model, characterized by the separated satellite clocks for code and phase observations, respectively. These satellites clocks were estimated in a network solution and can be used for separating receiver/satellite code/phase biases from PPP ambiguities. By applying the satellite decoupled clock corrections and estimating the receiver decoupled clock parameters, both the undifferenced integer wide-lane and L1 ambiguities can be directly estimated. Laurichesse et al. (2009) also developed an integer phase clock model in which the FCBs are assimilated into receiver and satellite clock estimates of a GPS network solution. This model utilizes the wide-lane satellite FCBs to resolve the integer wide-lane ambiguity, whereas the integer L1 ambiguity was directly estimated. In practice, the horizontal accuracy of epoch-wise position estimates at a static receiver was better than 2 cm (Laurichesse et al. 2009), and that of hourly position estimates was also better than 2 cm (Collins et al. 2008).

Although similar positioning performances have been demonstrated with these methods (Collins et al. 2010; Ge et al. 2008; Geng et al. 2009, 2010; Laurichesse et al. 2009; Shi and Gao 2014), their integer satellite products are not open for PPP users, except for the precise integer-recovered clock (IRC) corrections from CNES (Centre National d’Etudes Spatiales) (Loyer et al. 2012). The IRC corrections from CNES are absorbed by the Groupe de Recherche de Géodésie Spatiale (GRGS) precise satellite clock and can only be used with GRGS precise products. In addition, most of the integer satellite products lack long-term tests with GPS measurement taken under various environments.

AR in PPP has also been investigated by several international commercial corporations such as Trimble (Chen et al. 2013). The corresponding software and hardware products have been developed to offer ambiguity-fixed PPP service for various applications, for instance, precise farming. With AR, the PPP position quality in terms of accuracy and reliability can be dramatically improved. Nevertheless, their corresponding integer satellite products are proprietary, and their PPP AR service is bonded to GPS measurements from their own receiver hardware.

The School of Geodesy and Geomatics at Wuhan University (SGG-WHU) has been involved in the development of PPP technology since 2002. Earlier research includes developing the high-accuracy positioning software “TRIP,” and using it for scientific applications (Zhang and Forsberg 2007). Research specifically about integer AR in PPP began in 2008 (Zhang and Li 2010, 2013; Li et al. 2011; Zhang et al. 2013; Li and Zhang 2014), and routine generation of wide-lane and narrow-lane FCB products for PPP users began on January 1, 2015. We describe SGG’s research about generating FCB products and how they can be used for PPP ambiguity fixing. This will be particularly useful for those who wish to use our products to realize reliable and high-accuracy PPP solutions.

Theoretical background and a detail description on the FCB estimation are given, and then, our FCB products are evaluated using GPS measurements taken in various situations. We also comment on specific properties and applications of the SGG FCB products, followed by conclusions and perspectives.

PPP ambiguity resolution and FCB estimation

We start with the basic GPS observational equations to give a detail description on our PPP AR and FCB estimation system. After a brief discussion on how FCBs at both the receiver and satellite impact PPP AR, our method for satellite FCB estimation and its usage in PPP AR are presented. Finally, the overall design of our computation system is introduced.

Basic observation equations

The functional model describing carrier-phase and code observation is first given. For a satellite s observed by receiver r, the pseudorange and carrier-phase observations can be expressed as:

$$P_{r,j}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r} - {\text{d}}t^{s} ) + T_{r}^{s} + I_{r,j}^{s} + b_{r,j}^{{}} - b_{j}^{s} + e_{r,j}^{s}$$
(1)
$$L_{r,j}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r}^{{}} - {\text{d}}t^{s} ) + T_{r}^{s} - I_{r,j}^{s} + \lambda_{j}^{{}} (N_{r,j}^{s} + B_{r,j}^{{}} - B_{j}^{s} ) + \varepsilon_{r,j}^{s}$$
(2)

where the subscript j refers to a given frequency; ρ is the geometric distance; c is the speed of light; dt r and dt s are the clock errors of receiver and satellite; \(T_{r}^{s}\) is the slant troposphere delay; \(I_{r,j}^{s}\) is the slant ionospheric delay at the jth frequency; \(N_{r,j}^{s}\) is the integer ambiguity; B r,j and \(B_{j}^{s}\) are the receiver-dependent and satellite-dependent FCB at frequency j; λ j is the wavelength of the frequency j; b r,j is the code hardware delay from receiver antenna to the signal correlator in the receiver; \(b_{j}^{s}\) is code hardware delay from satellite signal generator to satellite antenna; e is the pseudorange measurement noise; and ɛ is measurement noise of carrier phase. Other error items such as the phase center offsets and variations (Schmid et al. 2005), phase windup (Wu et al. 1993), relativistic effect, and tide loading are assumed to be precisely corrected with their corresponding models.

Ionospheric-free combination observations are normally used in PPP to eliminate the first-order ionospheric delays in the pseudorange and carrier-phase measurements. The corresponding ionospheric-free observables and ambiguity parameter can be formulated as:

$$P_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r}^{{}} - {\text{d}}t^{s} ) + T_{r}^{s} + b_{{r,{\text{IF}}}}^{{}} - b_{\text{IF}}^{s} + e_{{r,{\text{IF}}}}^{s}$$
(3)
$$L_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r}^{{}} - {\text{d}}t^{s} ) + T_{r}^{s} + \lambda_{\text{IF}} \cdot (N_{{r,{\text{IF}}}}^{s} + B_{{r,{\text{IF}}}}^{{}} - B_{\text{IF}}^{s} ) + \varepsilon_{r,{\text{IF}}}^{s}$$
(4)

with

$$b_{{r,{\text{IF}}}} = \left( {f_{1}^{2} \;b_{r,1} - f_{2}^{2} \;b_{r,2} } \right)/\left( {f_{1}^{2} - f_{2}^{2} } \right)$$
(5)
$$b_{\text{IF}}^{s} = \left( {f_{1}^{2} \;b_{1}^{s} - f_{2}^{2} \;b_{2}^{s} } \right)/\left( {f_{1}^{2} - f_{2}^{2} } \right)$$
(6)
$$N_{{r,{\text{IF}}}}^{s} = c\;\left( {f_{1} \;N_{r,1}^{s} - f_{2} \;N_{r,2}^{s} } \right)/\left( {f_{1}^{2} - f_{2}^{2} } \right)/\lambda_{\text{IF}}$$
(7)
$$B_{{r,{\text{IF}}}} = c\;\left( {f_{1} \;B_{r,1} - f_{2} \;B_{r,2} } \right)/\left( {f_{1}^{2} - f_{2}^{2} } \right)/\lambda_{\text{IF}}$$
(8)
$$B_{\text{IF}}^{s} = c\;\left( {f_{1} \;B_{1}^{s} - f_{2} \;B_{2}^{s} } \right)/\left( {f_{1}^{2} - f_{2}^{2} } \right)/\lambda_{\text{IF}}$$
(9)

For GPS observations, the pseudorange ionospheric-free hardware delay biases \(b_{\text{IF}}^{s}\) are assimilated into the clock offset c·dt s following the IGS analysis convention. Due to the fact that the pseudorange observation in (3) provides the reference to clock parameters, the actual receiver clock estimate would absorb the ionospheric-free combination of the receiver hardware delay \(b_{{r,{\text{IF}}}}\). The carrier-phase hardware delay biases are linearly dependent with the ambiguity parameter and considered stable over time. Thus, they are grouped into the ambiguity in ambiguity-float GPS data processing (Defraigne and Bruyninx 2007; Geng et al. 2010).

After applying the GPS precise satellite clocks, the rewritten versions of Eqs. (3) and (4) can be given as:

$$P_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c{\bar{\text{d}}}t_{r} + T_{r}^{s} + e_{{r,{\text{IF}}}}^{s}$$
(10)
$$L_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c{\bar{\text{d}}}t_{r}^{{}} + T_{r}^{s} + \lambda_{\text{IF}} \cdot \bar{N}_{{r,{\text{IF}}}}^{s} + \varepsilon_{{r,{\text{IF}}}}^{s}$$
(11)

where \({\bar{\text{d}}}t_{r}\) and \(\bar{N}_{{r,{\text{IF}}}}^{s}\) are reparameterized receiver clock and ambiguity as:

$$c\;{\bar{\text{d}}}t_{r} = c\;{\text{d}}t_{r} + b_{{r,{\text{IF}}}}$$
(12)
$$\bar{N}_{{r,{\text{IF}}}}^{s} = N_{{r,{\text{IF}}}}^{s} + d_{{r,{\text{IF}}}} - d_{\text{IF}}^{s}$$
(13)
$$d_{{r,{\text{IF}}}} = B_{{r,{\text{IF}}}} - b_{{r,{\text{IF}}}} /\lambda_{\text{IF}}$$
(14)
$$d_{\text{IF}}^{s} = B_{\text{IF}}^{s} - b_{\text{IF}}^{s} /\lambda_{\text{IF}}$$
(15)

The tropospheric delay may be split into a hydrostatic (dry) part and a nonhydrostatic (wet) part. The zenith dry component of tropospheric delays can be corrected with an a priori model, for example, the Saastamoinen model (Saastamoinen 1972). The zenith wet delay (ZWD) needs to be estimated as an unknown. The global mapping functions (Boehm et al. 2006) can be used to project the slant dry and wet delays to the zenith delays. Although the troposphere gradient parameters are sometimes estimated in high-precision scientific software, to account for the bulk of the asymmetric delay, as reported by Urquhart et al. (2012), these gradients account for only a single main direction of asymmetry, and their estimation reduces the redundancy of the solution. For the sake of simplicity, the estimation of horizontal troposphere gradients is not considered in this study. Therefore, four types of unknown parameters: station position, receiver clock, ZWD, and carrier-phase ambiguities should be estimated in the PPP model above (Juan et al. 2012).

For ambiguity-float PPP solution, the ionospheric-free ambiguity parameter \(\bar{N}_{{r,{\text{IF}}}}^{s}\) is estimated as a real-value constant. This is reasonable because based on (13)–(15) the estimated ambiguity parameter is a combination of the integer ambiguity, the corresponding code hardware delay, and carrier-phase FCB at both receiver and satellite ends. This means that the integer property of the ambiguity parameter is lost (Shi and Gao 2014).

For ambiguity-fixed PPP solution, \(\bar{N}_{{r,{\text{IF}}}}^{s}\) is usually decomposed into the following combination of integer wide-lane and float narrow-lane ambiguities for ambiguity fixing, due to the fact that the L1 and L2 ambiguity cannot be estimated simultaneously in ionospheric-free PPP (Dach et al. 2007),

$$\bar{N}_{{r,{\text{IF}}}}^{s} = \left( {\frac{{c\;f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{{r,{\text{WL}}}}^{s} + \frac{c}{{f_{1} + f_{2} }}\bar{N}_{{r,{\text{NL}}}}^{s} } \right)/\lambda_{\text{IF}}$$
(16)

The wide-lane ambiguity can be resolved with the Hatch–Melbourne–Wübbena (HMW) combination observable (Hatch 1982; Melbourne 1985; Wübbena 1985),

$$\begin{aligned} \bar{N}_{{r,{\text{WL}}}}^{s} & = \left[ {\left( {f_{1} \;L_{r,1}^{s} - f_{2} \;L_{r,2}^{s} } \right)/\left( {f_{1} - f_{2} } \right) - \left( {f_{1} \;P_{r,1}^{s} + f_{2} \;P_{r,2}^{s} } \right)/\left( {f_{1} + f_{2} } \right)} \right]/\lambda_{\text{WL}} \\ & = N_{{r,{\text{WL}}}}^{s} + d_{{r,{\text{WL}}}} - d_{\text{WL}}^{s} \\ \end{aligned}$$
(17)
$$d_{{r,{\text{WL}}}} = B_{r,1} - B_{r,2} - \left( {f_{1} \;b_{r,1} + f_{2} \;b_{r,2} } \right)/\left( {f_{1} + f_{2} } \right)/\lambda_{\text{WL}}$$
(18)
$$d_{\text{WL}}^{s} = B_{1}^{s} - B_{2}^{s} - \left( {f_{1} \;b_{1}^{s} + f_{2} \;b_{2}^{s} } \right)/\left( {f_{1} + f_{2} } \right)/\lambda_{\text{WL}}$$
(19)

As we can see, if the wide-lane ambiguity can be correctly fixed based on (17), then the derived narrow-lane ambiguity observable will have a same structure,

$$\begin{aligned} \bar{N}_{{r,{\text{NL}}}}^{s} & = \lambda_{\text{IF}} \left( {f_{1} + f_{2} } \right)\;\bar{N}_{{r,{\text{IF}}}}^{s} /c - f_{2} /\left( {f_{1} - f_{2} } \right)\;N_{{r,{\text{WL}}}}^{s} \\ & = N_{r,1}^{s} + d_{{r,{\text{NL}}}} - d_{\text{NL}}^{s} \\ \end{aligned}$$
(20)
$$\begin{aligned} d_{{r,{\text{NL}}}} & = \left( {f_{1} + f_{2} } \right)/c\;\left( {B_{{r,{\text{IF}}}} \;\lambda_{\text{IF}} - b_{{r,{\text{IF}}}} } \right) \\ & = f_{1} /\left( {f_{1} - f_{2} } \right)\;\left( {B_{r,1} - b_{r,1} /\lambda_{1} } \right) - f_{2} /\left( {f_{1} - f_{2} } \right)\;\left( {B_{r,2} - b_{r,2} /\lambda_{2} } \right) \\ \end{aligned}$$
(21)
$$\begin{aligned} d_{\text{NL}}^{s} & = \left( {f_{1} + f_{2} } \right)/c\;\left( {B_{\text{IF}}^{s} \;\lambda_{\text{IF}} - b_{\text{IF}}^{s} } \right) \\ & = f_{1} /\left( {f_{1} - f_{2} } \right)\,\left( {B_{1}^{s} - b_{1}^{s} /\lambda_{1} } \right) - f_{2} /\left( {f_{1} - f_{2} } \right)\,\left( {B_{2}^{s} - b_{2}^{s} /\lambda_{2} } \right) \\ \end{aligned}$$
(22)

We note that \(\bar{N}_{r,NL}^{s}\) is a linear combination of \(N_{r,1}^{s}\), the corresponding code hardware delay, and carrier-phase FCB. It is usually named narrow-lane ambiguity because in (16) it is multiplied by the narrow-lane wavelength. For PPP users, usually the receiver-dependent FCBs are not of concern and cannot be corrected in advance. In order to avoid considering the receiver-dependent FCBs, we apply the single difference between satellites and the resulting single-differenced ambiguities can be fixed. Denoting the reference satellite as s 0, the single-differenced wide-lane and narrow-lane float ambiguity and FCB can be expressed as:

$$\Delta \bar{N}_{{r,{\text{WL}}}}^{{s,s_{0} }} = \bar{N}_{{r,{\text{WL}}}}^{s} - \bar{N}_{{r,{\text{WL}}}}^{{s_{0} }} = N_{{r,{\text{WL}}}}^{{s,s_{0} }} - d_{\text{WL}}^{{s,s_{0} }}$$
(23)
$$d_{\text{WL}}^{{s,s_{0} }} = B_{1}^{{s,s_{0} }} - B_{2}^{{s,s_{0} }} + \left( {f_{1} \,b_{1}^{{s,s_{0} }} + f_{2} \,b_{2}^{{s,s_{0} }} } \right)/\left( {f_{1} + f_{2} } \right)/\lambda_{\text{WL}}$$
(24)
$$\Delta \bar{N}_{{r,{\text{NL}}}}^{{s,s_{0} }} = \bar{N}_{{r,{\text{NL}}}}^{s} - \bar{N}_{{r,{\text{NL}}}}^{{s_{0} }} = N_{{r,{\text{NL}}}}^{{s,s_{0} }} - d_{\text{NL}}^{{s,s_{0} }}$$
(25)
$$d_{\text{NL}}^{{s,s_{0} }} = f_{1} /\left( {f_{1} - f_{2} } \right)\,\,\left( {B_{1}^{{s,s_{0} }} - b_{1}^{{s,s_{0} }} /\lambda_{1} } \right) - f_{2} /\left( {f_{1} - f_{2} } \right)\,\left( {B_{2}^{{s,s_{0} }} - b_{2}^{{s,s_{0} }} /\lambda_{2} } \right)$$
(26)

where the double superscripts indicate the differencing operation. According to (23) to (26), one can see that if the satellite wide-lane and narrow-lane fractional bias corrections \(d_{\text{WL}}^{{s,s_{0} }}\) and \(d_{\text{NL}}^{{s,s_{0} }}\) can be determined and delivered to the users, the wide- and narrow-lane ambiguities could be fixed in two sequential steps to recover the integer property of the ionospheric-free ambiguity in PPP. Hence, estimating a series of satellite FCB products of high quality is the key to realizing PPP AR.

FCB estimation algorithm description

The method of FCB estimation proposed by Ge et al. (2008) was modified and then applied in our processing. All involved undifferenced wide-lane and narrow-lane ambiguity estimates, which are derived from the HMW combination and the real-valued PPP ambiguities, are used as input for FCB estimation. Based on the discussion above, it can be seen that for all continuous arcs without cycle slip, the general expressions for the float wide-lane and narrow-lane undifferenced ambiguity can be rewritten by the following equation (Li and Zhang 2012; Loyer et al. 2012)

$$R_{r}^{s} = \bar{N}_{r}^{s} - N_{r}^{s} = d_{r} - d^{s}$$
(27)

where \(R_{r}^{s}\) is the combined fractional part of FCBs from both receiver r and satellite s, \(\bar{N}_{r}^{s}\) denotes float undifferenced ambiguities in the standard model, \(N_{r}^{s}\) denotes the integer part of \(\bar{N}_{r}^{s}\), which is the sum of the original integer ambiguity and the integer part of combined FCBs from both receiver r and satellite s, d r denotes receiver FCB, and d s denotes satellite FCB.

Assuming that m satellites have been tracked in a network of n stations, the undifferenced ambiguity in each continuous arc can be put together to form a set of equations in the form of (27). We apply least-squares estimation to estimate the satellite FCBs. In order to eliminate the rank deficiency, one arbitrarily selected FCB is set to zero. One of the satellite FCBs is chosen because satellite FCBs are more stable than those of the receivers (Zhang and Li 2013). Then, the global FCB products referenced to that satellite can be estimated. The FCB products for all GPS satellites are expected to be generated and provided on a regular basis, accompanied by satellite orbit and clock products to obtain accurate and reliable ambiguity-fixed PPP solutions.

Although in theory the various FCB estimation products are equivalent to each other (Geng et al. 2010; Shi and Gao 2014), some differences still exist because of the specific estimation strategy. Ge’s method determines FCB by averaging the fractional parts of all involved float wide-lane and narrow-lane ambiguity estimates, while our method uses least-squares estimation in an integrated adjustment to enhance the estimates (Zhang and Li 2013; Li and Zhang 2012). In the CNES method, a receiver FCB is selected as the reference to eliminate the rank deficiency of the equations, while we select a more stable satellite FCB. In addition, the FCB product from CNES is absorbed by the GRGS precise satellite clock, so one can only use the GRGS precise product to conduct PPP AR when using the CNES method. In our method, several series of FCB products can be estimated, accompanied with different precise products. Finally, compared with the FCB products of Trimble RTX (Chen et al. 2013), our method is receiver independent and can be used to process the dual-frequency GPS observations from any receiver.

System design

The TRIP software is running at SGG-WHU for research and application with PPP. Recently, a new module TRIP-AR, consisting of a server component for FCB estimation and a client component for PPP ambiguity fixing with FCB products, was developed in C/C++ to implement our modified FCB estimation algorithm. Figure 1 shows the system structure and the data flow.

Fig. 1
figure 1

Flowchart of the GPS satellite FCB estimation

Full size image

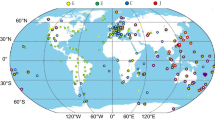
First, all available data needed for FCB generation, including GPS observations, broadcast ephemeris, precise orbits and clocks from different analysis centers, differential code biases, earth rotation parameters, and weekly solution files, are automatically downloaded by the data-downloading tool. The global IGS reference network (Dow et al. 2009), consisting of about 160 stations and denoted by blue dots in Fig. 2, is used for FCB determination.

Fig. 2
figure 2

Distribution of global reference network and user stations. The blue dots denote the reference stations used for FCB estimation; the red stars denote the user stations for investigating the performance of static hourly PPP with and without ambiguity fixing

Full size image

Then, all observations are processed by the TRIP software to generate the AMB_ARC files which contain the transmitting satellite name, phase arc start time, phase arc stop time, estimated float wide-lane ambiguity value, and the estimated ionospheric-free ambiguity value for each arc of each site-satellite pair. In order to reduce the number of estimated parameters and improve the accuracy of ionospheric-free ambiguities, we fix the coordinates of the reference station to those given in IGS weekly solution files.

Third, all the float wide-lane and ionospheric-free ambiguities are used as input to estimate the satellite FCB products. The daily wide-lane FCBs can be estimated precisely from the smoothed HMW combinations owing to its long wavelength feature and insensitivity to measurement errors. However, the narrow-lane ambiguities are more sensitive to biases caused by modeling inaccuracies because of its short wavelength. The biases caused by modeling inaccuracies appear relatively stable over short time intervals but do vary over longer time intervals. This implies that the narrow-lane FCBs appear stable over short intervals, say about 1 h, but do, in fact, change over longer intervals such as 1 day. Thus, the narrow-lane FCB should be estimated for short time interval (15 min in this study, as suggested by Ge et al. (2008)) in order to ensure enough precision. In order to avoid possible biased estimates due to, for example, large multipath effects, undifferenced ambiguities with a high formal sigma or low number of observations are eliminated.

Finally, the estimated wide-lane and narrow-lane FCBs are written in a self-defined format and saved in a single file in our FTP server (ftp://gnss.sgg.whu.edu.cn/). Currently, 14 sets of FCB products corresponding to different precise products such as those from COD, ESA, GFZ, GRGS, IGR, and IGS are estimated every day sequentially. Usually, it takes about 6 h, in total, for all processing work, which is obviously much less than the delay of about 14 days for the final precise orbit and clock. With these FCBs, users are able to do ambiguity-fixed PPP anywhere around the world.

At the user end, PPP AR can be conducted in two sequential steps. In order to form single difference between satellites, the satellite with good-quality observations and the highest elevation angle can be selected as the reference one for PPP AR. First, the single-differenced, wide-lane ambiguities are derived from the HMW combination and then corrected with wide-lane FCB estimates. They can be easily fixed by rounding averaged wide-lane ambiguities over several epochs. After successfully fixing the wide-lane ambiguities, the single-differenced narrow-lane ambiguities are derived from the float ionosphere-free ones and the integer wide-lane ones. Due to the fact that the narrow-lane FCBs at time node t i are calculated with the input ambiguities covering at least half of the time interval (t i , t i+1) (a 15-min session), the float narrow-lane ambiguities between the time interval (t i , t i+1) take the narrow-lane FCBs at t i as corrections. After taking the narrow-lane FCB corrections into consideration, a search strategy based on the Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method is applied to fix the single-differenced narrow-lane ambiguities since the narrow-lane ambiguities are strongly correlated in PPP. An ionosphere-free ambiguity is fixed only when both the related wide- and narrow-lane ones are fixed.

FCB product evaluation and applications

An evaluation of the effectiveness of PPP AR was conducted to demonstrate the quality of the FCB product. GPS measurements taken under various circumstances, i.e., static, dynamic, and on low earth orbit (LEO) satellite, were included in the evaluation. The results are presented in this section.

The static GPS measurements used for this evaluation, recorded at a 30-s sampling rate, were from 35 IGS stations denoted by red stars in Fig. 2 which were not involved in the FCB generation. The daily static observations from DOY 001 to 030 in 2015 were used in this study. For each station, the 24-h observations were divided into 24 1-h sessions to calculate hourly PPP. The IGS weekly solution coordinates were taken as truth.

A kinematic test was conducted in an open-sky area in Wuhan, China, on November 14, 2013. The test started at GPS time 1:22:51 and lasted for about 4000 s, using a land vehicle that carried a NovAtel GNSS dual-frequency receiver. The kinematic data were collected at a 1-s sampling rate. A receiver of the same type was set up within 9.6 km as a base station to help determine the coordinates of the moving vehicle at centimeter-level accuracy using double-differenced RTK. The RTK-derived coordinates were assumed to be truth for the evaluation of the PPP results. The base station was set up at GPS time 22:35:50 on the previous day, and the observation period lasted more than 4 h. We calculated the base station position by using TRIP and three other online precise GPS data-processing software, CSRS-PPP, magicGNSS, and AUSPOS (Guo 2014). The difference of results from these softwares was less than 3 cm in X, Y, and Z components. The averaged result was considered as the reference coordinate of the base station.

The LEO GPS measurements were taken in 10-s intervals on GRACE-A and GRACE-B satellites. The daily observation files from DOY 001 to 030 in 2012 were used in this study. The GRACE-A and GRACE-B coordinates provided by JPL (Case et al. 2010) were taken as truth for the comparison to these PPP results. The reduced dynamic orbit provided with the GRACE level 1B products can serve as a reference for assessing the high-frequency variations in the kinematic PPP orbit because the radial component of reduced dynamic orbits is usually very well determined (Montenbruck et al. 2009) and, even more importantly, it is as smooth as the real GRACE orbit (Weinbach and Schön 2013).

The final GPS satellite orbit and clock products produced by the Center for European Space Agency (ESA) were used, and the corresponding FCB products were employed for the PPP AR test. We applied the absolute antenna-phase center model and the phase windup corrections (Wu et al. 1993). Special concerns should be given on the cycle slip detection and phase center variation correction for LEO satellites (refer to Li et al. (2010), Weinbach and Schön (2013)). The elevation cutoff angle was set to 7°. The elevation-dependent weighting of observations was applied in this research to mitigate the effects of multipath, as well as atmospheric errors. The elevation-dependent variance model quantified the precision of the observations as a function of satellite elevation angle:

$$\sigma^{2} = a^{2} + b^{2} /\sin^{2} \left( {el} \right)$$

where σ is the standard deviation of GPS carrier-phase measurements, a = b = 3 mm, and el is the elevation angle of the satellite. The relative weighting of code and carrier-phase observations was chosen as 1/104. Generally, four types of unknown parameters, i.e., station position, receiver clock, ZWD, and carrier-phase ambiguities, should be estimated in a PPP model. The horizontal troposphere gradients were not estimated in our static and kinematic PPP test because they cannot be determined well with data covering a short time interval less than 90 min. In addition, for the LEO test, the GPS observations recorded by a space-borne GPS receiver were not affected by tropospheric delays, so the troposphere parameter was not estimated.

We applied both the well-known success rate and ratio test to validate the integer ambiguity solution. The success rate is a model-driven index and gives a quantitative assessment of the probability of correct fixing. The bootstrapped success rate which has been proved to be a good approximation of the actual integer least-squares success rate was used here. The ratio test, defined as the ratio of the second minimum quadratic form of the residuals to the minimum quadratic form of the residuals, is a data-driven index of the reliability of AR and frequently applied to assess the closeness of the float solution to its nearest integer vector (Ji et al. 2010). The critical criteria of the ratio value and success rate were set as 2.0 and 0.99, respectively (Seeber 2003).

Quality of FCB products

First, the usage rate, i.e., the percentage of valid float ambiguities observations employed to estimate FCBs, is used to indicate the consistency of FCBs. Figure 3 shows the usage rate of wide-lane and narrow-lane float ambiguities in the 30th session calculated with ESA precise products, on DOY 015, 2015, as a typical example. The min and max rates are 90.3 % for G06 and 97.2 % for G22, respectively, and the average usage rate of all satellites is 93.7 % for wide-lane float ambiguities. With these wide-lane float ambiguities, the standard deviations of wide-lane FCB estimates are usually around 0.006 cycles. The number of input narrow-lane float ambiguities is around 50 for each operable satellite in each session, which is much less than that of wide-lane (around 280). It is found that generally the narrow-lane usage rate is a little lower than the wide-lane one and the min and max rates are 83.3 % for G23 and 95.4 % for G22, respectively, and the average rate of all satellites is 89.9 %. With these narrow-lane float ambiguities, the standard deviations of narrow-lane FCB estimates are usually around 0.017 cycles.

Fig. 3
figure 3

Usage rate of wide-lane and the narrow-lane float ambiguities in the 30th session on DOY 015, 2015

Full size image

Then, the quality of the FCB estimates is evaluated by examining the a posteriori residuals of observations. The histogram of the residuals of wide-lane ambiguities is shown in Fig. 4. The total number of the input wide-lane float ambiguities is about 8600. The absolute values of all residuals are less than 0.3 cycles, and 94.2 % of them are within 0.2 cycles. This indicates a high consistency between all observations and the estimates. Randomly taking the narrow-lane ambiguity residuals results in the 30th session as example, the statistical histogram of the residuals is shown in Fig. 5. The total number of narrow-lane float ambiguities is about 1400. The absolute values of all residuals are within 0.3 cycles, and 93.7 % of them are within 0.2 cycles. Both histograms are very symmetric and nearly centered at zero.

Fig. 4
figure 4

Histogram of a posteriori residuals of the daily wide-lane float ambiguities (DOY 015, 2015)

Full size image
Fig. 5
figure 5

Histogram of a posteriori residuals of the 30th session narrow-lane float ambiguities (DOY 015, 2015)

Full size image

We can find that the quality of narrow-lane FCBs is a little worse than that of wide-lane. This is attributable to the fact that the narrow-lane FCB estimates are easily affected by unmodeled errors.

Furthermore, we compared our FCB estimations with the FCB corrections from the CNES GRGS precise product. The undifferenced wide-lane FCBs of CNES are written in the header of the GRGS precise clock file. The single-differenced FCBs referenced to PRN 10, which is in healthy condition throughout January, 2015, are calculated and compared. For wide-lane FCB, the differences of the two products are very close to zero for some satellites, while for other satellites the differences are close to 1 or −1. This is because the two wide-lane FCB products have different value range. We have limited the FCB corrections to be between −0.5 and 0.5 cycles, while the value range of CNES wide-lane FCB is between 0 and 1 cycles. However, a constant bias of 1 cycle in the wide-lane FCB would be fully absorbed by the narrow-lane FCB of that satellite and does not impact PPP AR at user end (Loyer et al. 2012). After correcting these constant biases, the histogram of the FCB difference between SGG and CNES is shown in Fig. 6. As one can see, almost all the differences are within ±0.05 cycles, which indicates that our wide-lane FCBs are quite consistent with those of CNES.

Fig. 6
figure 6

Histogram of the difference of single-differenced wide-lane FCBs between SGG and CNES (DOY 001-030, 2015). The reference satellite is 10

Full size image

Theoretically, the single-differenced narrow-lane FCBs estimated with the GRGS precise products should be zero, because they have been absorbed by the GRGS satellite clock and corrected in the ionospheric-free combination observation equation. Therefore, the value of our single-differenced narrow-lane FCB itself represents the bias relative to that from CNES. Also the constant bias of 0.47 cycles caused by the 1-cycle wide-lane bias was corrected (Loyer et al. 2012). The histogram of the narrow-lane FCB difference between SGG and CNES is shown in Fig. 7. In total, 87.8 % of the biases are within ±0.05 cycles, and 97.4 % of them are within ±0.075 cycles, which indicates that our narrow-lane FCBs agree well with those from CNES.

Fig. 7
figure 7

Histogram of the difference of single-differenced narrow-lane FCBs between SGG and CNES (DOY 001-030, 2015). The reference satellite is 10

Full size image

Static PPP test

Figure 8 shows the histogram of the positioning biases in east, north, and up directions of all hourly position estimates with respect to the truth benchmarks from the IGS weekly solution for each test station. For ambiguity-float static PPP, the average convergence time is 23.8 min to obtain a 3D positioning error less than 1 decimeter, while for ambiguity-fixed static PPP, the average convergence time is 22.6 min to achieve the first ambiguity-fixed solution. From the left panels of Fig. 8, we can see that the accuracy of the east component is considerably worse than that of the north component for ambiguity-float PPP. Generally speaking, the accuracy of the east component is lower than that of north component for a PPP float solution (Ge et al. 2008). However, with AR, the east accuracy shows the most improvement and is comparable with that of the north component.

Fig. 8
figure 8

Percentage of bias distribution in east, north, and up directions, achieved by ambiguity-float (left) and ambiguity-fixed (right) static PPP

Full size image

The mean RMS of all hourly solutions has improved significantly by AR, from (3.6, 1.4, 3.6) to (2.0, 1.0, 2.7) centimeters in the east, north, and up directions, respectively, with an accuracy improvement of 44.4, 28.6, and 25.0 %. These FCBs significantly improve the accuracy of hourly static position estimates.

To analyze the efficiency of PPP AR, we also compare the 3D positioning bias of ambiguity-float and ambiguity-fixed solutions to identify hourly solutions with incorrect AR. This is meaningful because incorrect integer ambiguity estimates often result in unacceptable positioning errors. An ambiguity-fixed PPP solution is considered to have failed if the 3D bias is larger than 5 cm and, in addition, 1.5 times larger than that of ambiguity-float PPP. The percentage of ambiguity-fixed solution failures using these criteria is 4.8 %. The averaged 3D bias of these failed ambiguity-fixed solutions reaches up to 7.6 cm. While the averaged 3D bias of the ambiguity-float solutions of the same data sets is only 4.5 cm. However, if we employ a stricter ambiguity validation, i.e., increase the threshold of success rate and ratio test to 0.999 and 3.0, respectively, this percentage is significantly reduced to only 1.1 %. This indicates that ambiguity validation is a crucial factor affecting the occurrence of degraded solutions in hourly PPP AR. Ambiguity validation is still an important issue for GNSS positioning and continues to be a topic for study.

Dynamic PPP test

For kinematic PPP, a random walk process is used to model the dynamics of the vehicle in the Kalman filter. The same spectral density values are used as the static case except that a value of 104 m2/s is utilized for position coordinates, instead of a zero value as used in the static processing. The ambiguity-fixed RTK results are adopted as the reference to assess the PPP solutions during the entire test.

Figure 9 shows the positioning errors of the ambiguity-float (top) and the ambiguity-fixed (bottom) PPP solutions with respect to the reference coordinate values in the east, north, and up directions. It is observed that the positioning biases of the ambiguity-fixed PPP are much closer to zero in all directions when compared to the ambiguity-float PPP solutions. It should also be noted that a systematic bias exists in the east and up coordinate components for the ambiguity-float PPP processing. This is because the ambiguity parameters did not converge adequately during such a short observation span. After performing AR in PPP with the provided FCB products, one can see that almost no systematic biases exist in the three coordinate components. With a correct AR, the correlation between ambiguity estimates and other estimates, such as position and ZWD, can be greatly reduced.

Fig. 9
figure 9

Percentage of bias distribution in east, north, and up directions, achieved by ambiguity-float (top) and ambiguity-fixed (bottom) kinematic PPP

Full size image

As given in Table 1, the statistical values using all epochs of data are used to assess the kinematic positioning accuracy. The ambiguity-fixed PPP solutions have RMS values of 2.6, 1.9, and 3.7 cm in the east, north, and up directions. The corresponding improvement of the positioning accuracy is about 78.2, 20.8, and 65.1 % in the three coordinate components with AR. For this experiment test, the ambiguity-fixed GPS kinematic PPP can achieve an accuracy of better than 5 cm at the one-sigma level in all three coordinate components with observation of 80 min.

Table 1 RMS of the epoch-wise position bias of ambiguity-float and ambiguity-fixed dynamic PPP in east, north, up directions (m)
Full size table

LEO POD test

For LEO PPP, the results of GRACE-A/B on DOY 013, 2012, will be shown as a representative example of the impact of AR on positioning accuracy. The epoch-wise coordinate biases in three directions are plotted in Figs. 10 and 11. No obvious biases are evident, and most differences are between −0.1 and 0.1 m, indicating that error sources have been well considered in this procedure. The ambiguity-float results are not very stable occasionally, as in case from epochs 2000th to 4000th (Fig. 11, top), but this can be attributed to poorer GPS satellite coverage, resulting in correspondingly larger PDOPs. Nevertheless, with AR, the positioning accuracy and stability has improved. For each subfigure, the percentage of the 3D biases within 0.05 m increased from 84.2 % for the float results (Fig. 10, top) to 92.4 % for the AR results (Fig. 10, bottom) for GRACE-A, and 76.9 % (Fig. 11, top) to 95.5 % (Fig. 11, bottom) for GRACE-B. The higher percentages indicate that a better consistency between all observations and the estimates can be achieved by the ambiguity-fixed solution.

Fig. 10
figure 10

Ambiguity-float (top) and ambiguity-fixed (bottom) PPP solution positions for GRACE-A on DOY 013, 2012, relative to those provided by JPL

Full size image
Fig. 11
figure 11

Ambiguity-float (top) and ambiguity-fixed (bottom) PPP solution positions for GRACE-B on DOY 013, 2012, relative to those provided by JPL

Full size image

We have calculated the average RMS of the epoch-wise biases on all 30 days. A summary of those is shown in Fig. 12. The RMS has improved by 24.6, 39.5, and 42.5 % (from 29.7, 25.6, and 21.2 mm to 22.4, 15.5, and 12.2 mm) for GRACE-A, and 22.8, 35.6, and 44.1 % (from 37.2, 31.5, and 23.6 mm to 28.7, 20.3, and 13.2 mm) for GRACE-B, in radial, tangential, and normal directions, respectively, when AR was applied to the same data set. Although the positioning accuracy of GRACE-A is better than that of GRACE-B, this is attributable to data quality issues such as the average number of observed GPS satellites, but the PPP results experienced almost the same improvement through by AR.

Fig. 12
figure 12

Averaged RMS of orbit determination bias in radial, tangential, and normal directions, achieved by ambiguity-float and ambiguity-fixed static PPP

Full size image

Conclusions and remarks

On January 1, 2015, the School of Geodesy and Geomatics at Wuhan University (SGG-WHU) started routinely generating wide-lane and narrow-lane FCB products for global PPP users to obtain ambiguity-fixed PPP solutions. Currently, 14 sets of FCB products corresponding to different precise products such as those from COD, ESA, GFZ, GRGS, IGR, and IGS are estimated every day and can be obtained from our FTP server (ftp://gnss.sgg.whu.edu.cn/). An entire algorithm for FCB generation at the server end had been developed. The practical realization of the two-step (wide-lane and narrow-lane) FCB estimation scheme was described in detail. For the PPP users, the averaged single-differenced wide-lane ambiguities could be easily fixed by rounding after they were corrected with the daily wide-lane FCB estimates. The float narrow-lane ambiguities between the time intervals (t i , t i+1) (a 15-min session) took the narrow-lane FCBs at t i as corrections and then could be fixed using the LAMBDA method. An ionosphere-free ambiguity was fixed only when both the related wide- and narrow-lane ones were fixed.

We compared our FCBs with those produced by CNES, and the results indicated that our FCBs had a good consistency with the CNES. For wide-lane FCB, almost all the differences between the two products were within ±0.05 cycles, while for narrow-lane FCB, 97.4 % of the differences were between ±0.075 cycles.

We demonstrated that PPP AR using these FCB products is applicable for GPS measurements taken under various environments. Three examples were provided. Compared with conventional ambiguity-float PPP, the ambiguity-fixed PPP using these FCB products improved the mean position RMS of static PPP results by 44.4, 28.6, and 25.0 % in the east, north, and up, respectively. A kinematic positioning test with observation of 80 min achieved a position accuracy of better than 5 cm at the one-sigma level in all three coordinate components, with an improvement of 78.2, 20.8, and 65.1 % in east, north, and up, respectively, over the ambiguity-float results. The RMS of LEO PPP improved by about 23, 37, and 43 % for GRACE-A and GRACE-B, in radial, tangential, and normal directions, respectively, when the AR is applied to the same data set.