1 Introduction

Precise point positioning ambiguity resolution (PPP-AR) can be achieved by correcting for phase biases (Gabor and Nerem 2002; Zumberge et al. 1997). Phase bias products are conventionally defined in the form of wide-lane and ionosphere-free combinations, and calibrated on PPP ambiguities to recover their integer properties (e.g., Ge et al. 2008; Laurichesse et al. 2009 among others). In recent years, an observable-specific signal bias (OSB) concept has been proposed where each pseudorange and carrier-phase observable (i.e., code and phase OSB) on all tracking channels is paired with its individual bias correction (Schaer 2016). Under this framework, integer ambiguities can be retrieved by applying OSB corrections directly on raw GNSS observables, rather than combination ambiguities (Laurichesse 2015; Odijk et al. 2016; Schaer et al. 2021). The OSB framework is straightforward and extensible for multi-frequency GNSS signals as prescribed observable combinations (e.g., wide-lane, ionosphere-free) are not necessary anymore. Geng et al. (2022a) further introduced the concept of all-frequency OSBs that were able to recover the integer properties of ambiguities regardless of frequency choice, signal prescription and observable combination. The International GNSS Service (IGS) has been encouraging all participating analysis centers (ACs) to provide phase bias products under the OSB framework. Then an ensuing task for the IGS AC coordination is to combine and cross-validate AC-specific phase bias products for the highest robustness, as routinely accomplished for the GPS satellite orbit and clock products (e.g., Griffiths 2019; Seepersad and Bisnath 2017).

Banville et al. (2020) developed a method for the combination of dual-frequency GPS phase bias products. It was exposed that the combination of satellite phase bias products could not be separated from the satellite clock combination. At first, code and phase OSBs had to be converted into wide-lane and ionosphere-free phase biases referring to the Melbourne-Wübbena and the ionosphere-free combinations, respectively. Then the AC-specific wide-lane phase biases were calibrated by a number of integer cycles to be aligned with each other, and as a result, we had to recompute the ionosphere-free phase biases to reconcile them to their calibrated wide-lane counterparts. Finally, the resulting ionosphere-free phase biases were combined with legacy satellite clock products to form integer clocks (Laurichesse et al. 2009), which were then aligned in a similar manner to that for the wide-lane phase biases. Of particular note, it is the integer clocks integrating legacy clocks with phase biases, rather than the ionosphere-free phase biases individually, that can be rigorously and precisely aligned among AC-specific products. Integer clocks are tied to ambiguity-fixed carrier-phase data, and thus also called “phase clocks” in this study (see Banville et al. 2020; Geng et al. 2019a; Loyer et al. 2012). It was found that the GPS combination products outperformed individual AC-specific products in terms of ambiguity fixing rates and positioning precisions. Of particular note, legacy satellite clocks without corresponding phase bias products can also join the combination, but the integer datum for ambiguities in the combination process has to be exclusively determined by phase clocks.

The method for the dual-frequency phase clock/bias combination seems straightforward as the classic wide-lane/ionosphere-free model is a natural choice. However, when generalizing this combination method to multi-frequency GNSS signals, we have rather more, but hard, choices for the extension of the wide-lane/ionosphere-free model. An apparent thought would be just simply introducing more wide-lane phase biases to enable multi-frequency phase clock/bias combination. For instance, a second wide-lane phase bias (e.g., GPS L1/L5) can be formed from original OSBs in addition to its classic wide-lane/ionosphere-free counterparts (e.g., GPS L1/L2). Then a further wide-lane phase bias alignment for L1/L5 can be carried out following the classic dual-frequency phase clock/bias combination for L1/L2. This procedure can be applied to even more extra frequencies of signals, and we can finally accomplish the phase bias combinations for all frequencies. Since the wide-lane phase bias combination is much easier compared to its ionosphere-free counterpart which must involve satellite clocks, the idea of forming only more wide-lane phase biases seems attractive to the multi-frequency phase clock/bias combination. However, the wide-lane phase bias combination involves code OSBs which typically have an error of up to a few tenths of a nanosecond (Villiger et al. 2019). It should thus be investigated whether such an error would propagate through the combination and thus compromise the precision of all third-frequency combined phase OSBs.

Alternatively, instead of combining extra wide-lane phase biases, we can also attempt to combine integer clocks for each eligible ionosphere-free phase bias product derived from AC-specific legacy clocks and multi-frequency OSBs. For instance, after finishing the phase clock/bias combination for GPS L1/L2 OSBs, a second integer clock product can be formed by integrating the legacy satellite clocks with the L1/L5 ionosphere-free phase biases, and the integer clock combination is then performed again. The advantage of this method is that all third-frequency phase OSBs in addition to satellite clocks can be precisely aligned among ACs at a typical precision of less than 10 ps (Banville et al. 2020; Geng et al. 2021). Favorably, all-frequency PPP-AR using such combination products is then able to rigorously ensure high positioning precisions for any eligible dual-frequency signal combination (Geng et al. 2022a). However, aligning each eligible integer clock product among ACs implicates that its corresponding wide-lane phase biases have to be pre-aligned as well to keep consistency between AC-specific wide-lane and ionosphere-free phase biases. In this sense, the method of combining all eligible integer clock products in the case of multi-frequency OSBs is rather cumbersome, not to mention the number of eligible dual-frequency signal combinations among five frequencies of observables (e.g., BDS-3 B1C/B1I/B2a/B2b/B3I).

In addition, a special issue is the combination of the time-variable OSBs on GPS Block IIF L5 carrier-phase signals (Montenbruck et al. 2011). Their peak-to-peak variations within a day can be up to several decimeters, whereas the phase OSBs on the baseline frequencies (e.g., GPS L1/L2, Galileo E1/E5a, etc.) are usually presumed as daily constants in practice. The distinctive temporal behaviors of such GPS L5 phase OSBs make them of particular concern in the multi-frequency phase clock/bias combination task.

Currently, a few IGS ACs are able to provide all-frequency OSB products. Since 2019, Laurichesse (2015) from CNES (Centre national d'études spatiales) has been releasing all-frequency GPS/Galileo/BDS OSB products at http://www.ppp-wizard.net/products/POST_PROCESSED, but based on GFZ (GeoForschungsZentrum) multi-GNSS orbits and clocks. A preliminary experiment showed that the integer properties of GPS L1/L5 wide-lane and narrow-lane ambiguities can be well recovered. Moreover, in the IGS Repro3 task accomplished in 2022 (http://acc.igs.org/repro3/repro3.html), the Graz University of Technology (TUG) contributed all-frequency GPS/Galileo OSBs along with phase clocks, though only dual-frequency satellite products were required in the campaign (Strasser et al. 2019). Since 2023, Wuhan University has also begun to provide all-frequency GPS/Galileo/BDS OSBs as well as phase clocks as announced in IGSMail-8409 (ftp://igs.gnsswhu.cn/pub/whu/phasebias) (Geng et al. 2022a).

Therefore, in this study, we aim at all-frequency, rather than multi-frequency, phase clock/bias combination. This means that the combination products should keep the characteristics of both phase clocks and all-frequency OSBs, or in other words, enable the high robustness of all-frequency PPP-AR in terms of ambiguity fixing rates and positioning precisions. The article is organized as follows: Sect. 2 describes the methods for all-frequency phase clock/bias combination; Sect. 3 introduces the AC-specific products for our combination and the GNSS data for all-frequency PPP-AR validation; Sect. 4 shows all-frequency GPS/Galileo phase clock/bias combination results and the PPP-AR validation; Sect. 5 draws the conclusions.

2 Method

GNSS all-frequency observation equations from satellite \(k\) to station \(r\) in the unit of length can be written as

$$\begin{array}{l}\left\{\begin{array}{l}{P}_{r,1}^{k}={\rho }_{r,1}^{k}+{t}_{r}-{t}^{k}+{g}_{1}^{2}{I}_{r,1}^{k}+{d}_{r,1}+{d}_{1}^{k} \\ {P}_{r,2}^{k}={\rho }_{r,2}^{k}+{t}_{r}-{t}^{k}+{g}_{2}^{2}{I}_{r,1}^{k}+{d}_{r,2}+{d}_{2}^{k} \\ {P}_{r,q}^{k}={\rho }_{r,q}^{k}+{t}_{r}-{t}^{k}+{g}_{q}^{2}{I}_{r,1}^{k}+{d}_{r,q}+{d}_{q}^{k} \\ {L}_{r,1}^{k}={\rho }_{r,1}^{k}+{t}_{r}-{t}^{k}-{g}_{1}^{2}{I}_{r,1}^{k}+{\lambda }_{1}{N}_{r,1}^{k}+{b}_{r,1}+{b}_{1}^{k} \\ {L}_{r,2}^{k}={\rho }_{r,2}^{k}+{t}_{r}-{t}^{k}-{g}_{2}^{2}{I}_{r,1}^{k}+{\lambda }_{2}{N}_{r,2}^{k}+{b}_{r,2}+{b}_{2}^{k} \\ {L}_{r,q}^{k}={\rho }_{r,q}^{k}+{t}_{r}-{t}^{k}-{g}_{q}^{2}{I}_{r,1}^{k}+{\lambda }_{q}{N}_{r,q}^{k}+{b}_{r,q}+{b}_{q}^{k}+\delta {b}_{q}^{k}\end{array}\right.\end{array}$$
(1)

where \({P}_{r,i}^{k}\) and \({L}_{r,i}^{k}\) \((i=1, 2, q)\) are the pseudorange and carrier-phase measurements, respectively, while subscript \(q\) denotes frequencies > 2; \({\rho }_{r,i}^{k}\) denotes the geometric distance between the antenna phase centers of satellite \(k\) and station \(r\) including the troposphere delay; \({t}_{r}\) and \({t}^{k}\) are the receiver and satellite clocks, respectively; \({g}_{i}=\frac{{f}_{1}}{{f}_{i}}\) where \({f}_{i}\) is the signal frequency; \({I}_{r,1}^{k}\) represents the slant ionosphere delay for frequency 1; \({\lambda }_{i}\) is the carrier-phase wavelength and \({N}_{r,i}^{k}\) is the integer ambiguity; \({d}_{i}^{k}\) is assumed as a daily-constant satellite code bias; similarly, \({b}_{i}^{k}\) denotes the daily-constant satellite phase biases; conversely, \(\delta {b}_{q}^{k}\) denotes the time-variable phase bias on frequency \(q\) whenever present (e.g., GPS L5; Montenbruck et al. 2011); in addition, \({d}_{r,i}\) and \({b}_{r,i}\) are those biases at the receiver end.

Note that the biases in Eq. 1 can also be presumed all time-variable, and such a more general model can refer to Odijk et al. (2016). Since daily-constant satellite code/phase bias products are usually provided by the IGS in practice and the resultant PPP-AR performance has been highly qualified (e.g., Geng et al. 2022b; Schaer et al. 2021; Strasser et al. 2019), we thus presume the satellite biases constant within 24 h to simplify the following mathematical derivations in this study. Moreover, time-variable receiver biases can hardly be translated into satellite biases. This is because receiver biases differ among stations, and cannot be easily absorbed by their satellite counterparts. Time-variable receiver biases would become part of observation residuals after a least-squares adjustment.

The code biases in Eq. 1 can be mitigated using the pre-determined code OSBs released by the IGS (Villiger et al. 2019). In this study, \({D}_{1}^{k}\), \({D}_{2}^{k}\) and \({D}_{q}^{k}\) are used to denote the code OSB corrections for \({d}_{1}^{k}\), \({d}_{2}^{k}\) and \({d}_{q}^{k}\), respectively. Since \({D}_{i}^{k}\) \((i=1, 2, q)\) is only a pseudo-absolute correction for \({d}_{i}^{k}\), we cannot simply presume \({D}_{i}^{k}={d}_{i}^{k}\). Rather, it is showed that they should obey the following relations

$$\left\{\begin{array}{l}{D}_{1}^{k}-{D}_{2}^{k}+{\sigma }_{{D}_{12}}^{k}={d}_{1}^{k}-{d}_{2}^{k}\\ {D}_{1}^{k}-{D}_{q}^{k}+{\sigma }_{{D}_{1q}}^{k}={d}_{1}^{k}-{d}_{q}^{k}\end{array}\right.$$
(2)

where we introduce \({\sigma }_{{D}_{12}}^{k}\) and \({\sigma }_{{D}_{1q}}^{k}\) to denote the DCB (differential code bias) errors, which are the key to the method in this study. In addition, we list some relevant definitions

$$\left\{\begin{array}{l}{d}_{0}^{k}=\alpha {d}_{1}^{k}-\beta {d}_{2}^{k}\\ {D}_{0}^{k}=\alpha {D}_{1}^{k}-\beta {D}_{2}^{k}\\ \alpha =\frac{{g}_{2}^{2}}{{g}_{2}^{2}-1}\\ \beta =\frac{1}{{g}_{2}^{2}-1}\end{array}\right.$$
(3)

where \({d}_{0}^{k}\) is the ionosphere-free combination of code biases on baseline frequencies, while analogously \({D}_{0}^{k}\) for code OSBs.

2.1 All-frequency phase OSBs

Due to rank deficiency when estimating all bias unknowns in Eq. 1, we can reformulate it to eliminate the linear dependence of those unknowns, and then introduce code OSBs \({D}_{i}^{k}\) \((i=1, 2, q)\) to correct for \({d}_{i}^{k}\) (see Geng et al. 2022a),

$$\left\{\begin{array}{l}{P}_{r,1}^{k}={\rho }_{r,1}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}+{g}_{1}^{2}{\bar {I}}_{r,1}^{k}\\ {P}_{r,2}^{k}={\rho }_{r,2}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}+{g}_{2}^{2}{\bar {I}}_{r,1}^{k}\\ {P}_{r,q}^{k}={\rho }_{r,q}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}+{g}_{q}^{2}{\bar {I}}_{r,1}^{k}+{\overline{h} }_{r,q}^{k}\\ {L}_{r,1}^{k}={\rho }_{r,1}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}-{g}_{1}^{2}{\bar {I}}_{r,1}^{k}+{\lambda }_{1}{\bar {N}}_{r,1}^{k}\\ {L}_{r,2}^{k}={\rho }_{r,2}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}-{g}_{2}^{2}{\bar {I}}_{r,1}^{k}+{\lambda }_{2}{\bar {N}}_{r,2}^{k}\\ {L}_{r,q}^{k}={\rho }_{r,q}^{k}+{\bar {t}}_{r}-{\bar {t}}^{k}-{g}_{q}^{2}{I}_{r,1}^{k}+{\lambda }_{q}{\bar {N}}_{r,q}^{k}+\delta {b}_{q}^{k}\end{array}\right.$$
(4)

where

$$\left\{\begin{array}{l}{\bar {t}}_{r}={t}_{r}+(\alpha {d}_{r,1}-\beta {d}_{r,2})\\ {\bar {I}}_{r,1}^{k}={I}_{r,1}^{k}-\beta ({d}_{r,1}-{d}_{r,2}+{\sigma }_{{D}_{12}}^{k})\\ {\overline{h} }_{r,q}^{k}={g}_{q}^{2}\beta ({d}_{r,1}-{d}_{r,2}+{\sigma }_{{D}_{12}}^{k})-(\alpha {d}_{r,1}-\beta {d}_{r,2})-({d}_{0}^{k}-{D}_{0}^{k})+{d}_{r,q}+{d}_{q}^{k}-{D}_{q}^{k}\end{array}\right.$$
(5)

\({\overline{h} }_{r,q}^{k}\) is an inter-frequency pseudorange bias on frequency \(q\) with respect to baseline frequencies.

Moreover, the satellite clock and ambiguity terms are reformulated as

$$\left\{\begin{array}{l}{\bar {t}}^{k}={t}^{k}-({d}_{0}^{k}-{D}_{0}^{k})\\ {\bar {N}}_{r,1}^{k}={N}_{r,1}^{k}+\frac{1}{{\lambda }_{1}}\left({b}_{1}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{1}^{2}\beta {\sigma }_{{D}_{12}}^{k}\right)+\frac{1}{{\lambda }_{1}}\left({b}_{r,1}-(\alpha +\beta ){d}_{r,1}+2\beta {d}_{r,2}\right)\\ {\bar {N}}_{r,2}^{k}={N}_{r,2}^{k}+\frac{1}{{\lambda }_{2}}\left({b}_{2}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{2}^{2}\beta {\sigma }_{{D}_{12}}^{k}\right)+\frac{1}{{\lambda }_{2}}\left({b}_{r,2}-2\alpha {d}_{r,1}+(\alpha +\beta ){d}_{r,2}\right)\\ {\bar {N}}_{r,q}^{k}={N}_{r,q}^{k}+\frac{1}{{\lambda }_{q}}\left({b}_{q}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{q}^{2}\beta {\sigma }_{{D}_{12}}^{k}\right)+\frac{1}{{\lambda }_{q}}\left({b}_{r,q}-{g}_{q}^{2}\beta ({d}_{r,1}-{d}_{r,2})-\alpha {d}_{r,1}+\beta {d}_{r,2}\right)\end{array}\right.$$
(6)

where \({\bar {t}}^{k}\) denotes the legacy clock as implemented by the IGS, which is a combination of the physical satellite clock and code biases; \({\bar {N}}_{r,i}^{k}\) \((i=1, 2, q)\) is the de facto frequency-specific ambiguity term to be estimated, which absorbs phase and code biases from both satellite and receiver ends. From Eq. 6, we are able to identify the satellite-specific all-frequency phase bias terms

$$\left\{\begin{array}{l}{\bar {b}}_{1}^{k}={\lambda }_{1}{B}_{1}^{k}+{b}_{1}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{1}^{2}\beta {\sigma }_{{D}_{12}}^{k}\\ {\bar {b}}_{2}^{k}={\lambda }_{2}{B}_{2}^{k}+{b}_{2}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{2}^{2}\beta {\sigma }_{{D}_{12}}^{k}\\ {\bar {b}}_{q}^{k}={\lambda }_{q}{B}_{q}^{k}+{b}_{q}^{k}+\delta {b}_{q}^{k}-{d}_{0}^{k}+{D}_{0}^{k}-{g}_{q}^{2}\beta {\sigma }_{{D}_{12}}^{k}\end{array}\right.$$
(7)

where \({\bar {b}}_{i}^{k}\) \((i=1, 2, q)\) denotes the phase bias on frequencies 1, 2 and \(q\); \({\bar {b}}_{q}^{k}\) also accommodates the time-variable portion of phase biases; of particular note, \({B}_{i}^{k}\) is an ambiguity-related integer denoting a possible arbitrary offset resulting from the process of identifying fractional phase biases out of the raw ambiguity terms in Eq. 6. Note that Eq. 7 contains only the DCB error term \({\sigma }_{{D}_{12}}^{k}\) on baseline frequencies.

2.2 Interoperability between satellite clock and phase bias

Typically, satellite clocks are often computed against a single or an ensemble of atomic clocks to eliminate the linear dependency between satellite and receiver clocks. The choice of such atomic clocks, or timing reference, is up to ACs themselves, implying that the timing reference is likely to differ among AC-specific satellite clock products. Therefore, the offset among the timing references should be removed before the clock combination detailed in the remainder of this study. To be brief, this can be accomplished by aligning the average of clocks for all common satellites from all participating ACs at each epoch (e.g., Chen et al. 2022).

According to Eq. 6, once the AC-specific clock timing offset is removed, the satellite clock from a specific AC \(A\) can be modeled as

$${\bar {t}}_{A}^{k}={t}^{k}-({d}_{0}^{k}-{D}_{A,0}^{k})$$
(8)

where \({D}_{A,0}^{k}\) denotes the ionosphere-free code OSBs employed by AC \(A\). Equation 8 is the basis of legacy clock combination where satellite clock products \({\bar {t}}^{k}\) from all ACs are aligned by identifying their differences caused by individual code bias datum (e.g., Kouba et al. 2001). To be concise, \({t}^{k}\) can be taken as the combined clock unknown, which is computed by shifting the clock products (i.e., \({\bar {t}}_{A}^{k}\)) of all ACs toward a common datum to remove their inter-AC offset originating in the code bias terms (i.e., \({d}_{0}^{k}-{D}_{A,0}^{k}\)). Finally, we achieve the estimate

$${t}^{k}\doteq {\overline{t} }_{{\text{m}},{\text{L}}}^{k}$$
(9)

where \({\overline{t} }_{{\text{m}},{\text{L}}}^{k}\) denotes the combined legacy clock for satellite \(k\); “\(\doteq \)” means “defined as” throughout. The combination precision for legacy clock is usually up to a few tens of picosecond (Griffiths 2019).

Regarding the combination of phase biases, we must integrate them with satellite clocks to form integer clocks as demonstrated by Banville et al. (2020), and it is the integer clocks that are combined to preserve their ability in recovering the integer property of PPP ambiguities. Combining Eqs. 7 and 8 in the case of AC \(A\)’s products, we obtain the fundamental relation

$${\bar {t}}_{A}^{k}-{\bar {b}}_{A,*}^{k}={t}^{k}-{b}_{*}^{k}-{\lambda }_{*}{B}_{A,*}^{k}+{g}_{*}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}$$
(10)

where “*” is a wildcard denoting any raw signal frequency; \({B}_{A,*}^{k}\) is the arbitrary integer offset specific to AC \(A\).

Analogous to Eq. 8, \({t}^{k}-{b}_{*}^{k}\) in Eq. 10 can be taken as the combined integer clock unknown, which is going to be estimated as a whole. Similar to Eq. 9, we define

$${t}^{k}-{b}_{*}^{k}\doteq {\overline{t} }_{{\text{m,I}}_{*}}^{k}$$
(11)

where \({\bar {t}}_{\text{m},{\text{I}}_{*}}^{k}\) denotes the combined integer clock on signal frequency * and is called the “frequency-specific integer clock” in this study. Equation 11 is the basis for integer clock combination on each raw signal frequency. In particular, \({B}_{A,*}^{k}\) is an integer and thus has to be removed by shifting integer clock products at integer step lengths. However, there is still a DCB error term \({\sigma }_{A,{D}_{12}}^{k}\), which is unknown at the moment, in Eq. 11 preventing the integer clock combination on raw signal frequencies.

2.3 Dual-frequency phase clock/bias combination

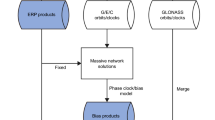
Dual-frequency phase clock/bias combination consists of the DCB combination, wide-lane phase bias combination and integer clock combination, which are elaborated in the following six processing steps (see also Banville et al. 2020) (See also the right side of Fig. 1).

Fig. 1
figure 1

A schematic diagram for dual-frequency and all-frequency phase clock/bias combination. The boxes with solid black arrows denote dual-frequency combination on baseline frequencies, whereas those with blue arrows denote all-frequency combination on all third frequencies. Dashed arrows denote data input/output

Full size image
  1. 1.

    Convert AC-specific code and phase OSB products into DCBs, wide-lane and ionosphere-free phase biases

    $$\left\{\begin{array}{l}{D}_{A,12}^{k}={D}_{A,1}^{k}-{D}_{A,2}^{k} \\ ={d}_{1}^{k}-{d}_{2}^{k}-{\sigma }_{A,{D}_{12}}^{k} \\ \doteq {d}_{12}^{k}-{\sigma }_{A,{D}_{12}}^{k} \\ \begin{array}{l}{\overline{b} }_{A,{\text{w}}}^{k}=\frac{{g}_{2}}{{g}_{2}-1}{\overline{b} }_{A,1}^{k}-\frac{1}{{g}_{2}-1}{\overline{b} }_{A,2}^{k}-\frac{{g}_{2}}{{g}_{2}+1}{D}_{A,1}^{k}-\frac{1}{{g}_{2}+1}{D}_{A,2}^{k}\\ =\left(\frac{{g}_{2}}{{g}_{2}-1}{b}_{1}^{k}-\frac{1}{{g}_{2}-1}{b}_{2}^{k}-\frac{{g}_{2}}{{g}_{2}+1}{d}_{1}^{k}-\frac{1}{{g}_{2}+1}{d}_{2}^{k}\right)\\ +\frac{c}{{f}_{1}-{f}_{2}}\left({B}_{A,1}^{k}-{B}_{A,2}^{k}\right)\\ \doteq {b}_{\text{w}}^{k}+{\lambda }_{\text{w}}{B}_{A,{\text{w}}}^{k}\\ {\overline{b} }_{A\text{,0}}^{k}=\alpha {\overline{b} }_{A,1}^{k}-\beta {\overline{b} }_{A,2}^{k}\\ =\alpha {b}_{1}^{k}-\beta {b}_{2}^{k}-\left({d}_{0}^{k}-{D}_{A,0}^{k}\right)+\alpha {\lambda }_{1}{B}_{A,1}^{k}-\beta {\lambda }_{2}{B}_{A,2}^{k}\\ \doteq {b}_{0}^{k}-\left({d}_{0}^{k}-{D}_{A,0}^{k}\right)+\beta {\lambda }_{2}{B}_{A,{\text{w}}}^{k}+{\lambda }_{\text{n}}{B}_{A,1}^{k}\end{array}\end{array}\right.$$
    (12)

    where

    $$\left\{\begin{array}{l}{d}_{12}^{k}\doteq {d}_{1}^{k}-{d}_{2}^{k} \\ \begin{array}{l}{b}_{\text{w}}^{k}\doteq \frac{{g}_{2}}{{g}_{2}-1}{b}_{1}^{k}-\frac{1}{{g}_{2}-1}{b}_{2}^{k}-\frac{{g}_{2}}{{g}_{2}+1}{d}_{1}^{k}-\frac{1}{{g}_{2}+1}{d}_{2}^{k}\\ {b}_{0}^{k}\doteq \alpha {b}_{1}^{k}-\beta {b}_{2}^{k}\\ {B}_{A,\text{w}}^{k}={B}_{A,1}^{k}-{B}_{A,2}^{k}\\ {\lambda }_{\text{w}}=\frac{c}{{f}_{1}-{f}_{2}}\\ {\lambda }_{\text{n}}=\frac{c}{{f}_{1}+{f}_{2}}\end{array}\end{array}\right.$$
    (13)

    \({D}_{A,12}^{k}\), \({\bar {b}}_{A,\text{w}}^{k}\) and \({\bar {b}}_{A\text{,0}}^{k}\) are the DCB, wide-lane and ionosphere-free phase biases for AC \(A\), respectively; \({\bar {b}}_{A,1}^{k}\), \({\bar {b}}_{A,2}^{k}\), \({D}_{A,1}^{k}\) and \({D}_{A,2}^{k}\) are the phase and code OSBs of AC \(A\); \({\lambda }_{\text{w}}=\frac{c}{{f}_{1}-{f}_{2}}\) and \({\lambda }_{\text{n}}=\frac{c}{{f}_{1}+{f}_{2}}\) are the wide-lane and narrow-lane wavelengths, respectively; \({B}_{A\text{,w}}^{k}\) is defined as an arbitrary integer offset among AC-specific wide-lane phase biases. Note that the error term \({\sigma }_{A,{D}_{12}}^{k}\) in Eq. 7 cancels completely for \({\bar {b}}_{A,\text{w}}^{k}\) and \({\bar {b}}_{A\text{,0}}^{k}\).

  2. 2.

    Compute the combined DCB according to the first line of Eq. 12, that is

    $${d}_{12}^{k}\doteq {D}_{\text{m},12}^{k}$$
    (14)

    where \({D}_{\text{m},12}^{k}\) is defined as the combined DCB for satellite \(k\). The DCB error \({\sigma }_{A,{D}_{12}}^{k}\) can be computed as the difference between the AC-specific \({D}_{A,12}^{k}\) and the combined \({D}_{\text{m},12}^{k}\), which is not precise though due to the high noise of code OSB products. More precise \({\sigma }_{A,{D}_{12}}^{k}\) estimation refers to step 2 in Sect. 2.4.

  3. 3.

    Compute the combined wide-lane phase bias according to the second line of Eq. 12 after calibrating the integer offset \({B}_{A\text{,w}}^{k}\), as demonstrated in Eq. 10, that is

    $${b}_{\text{w}}^{k}\doteq {\overline{b} }_{{\text{m}},{\text{w}}}^{k}$$
    (15)

    where \({\bar {b}}_{\text{m},\text{w}}^{k}\) is defined as the combined wide-lane phase bias for satellite \(k\).

  4. 4.

    Form and combine integer clocks among ACs. Combining Eq. 8 and the third line of Eq. 12, we have the integer clock for AC \(A\),

    $${\bar {t}}_{A}^{k}-{\bar {b}}_{A,0}^{k}-\beta {\lambda }_{2}{B}_{A,\text{w}}^{k}={t}^{k}-{b}_{0}^{k}-{\lambda }_{\text{n}}{B}_{A,1}^{k}$$
    (16)

    Note that the wide-lane integer offset \({B}_{A\text{,w}}^{k}\) has been identified in the previous step and thus moved to left-hand side as a known quantity. Similar to Eq. 11, we define

    $${t}^{k}-{b}_{0}^{k}\doteq {\overline{t} }_{{\text{m, I}}_{0}}^{k}$$
    (17)

    where \({\bar {t}}_{\text{m, }{\text{I}}_{0}}^{k}\) denotes the combined integer clock with respect to ionosphere-free phase biases for satellite \(k\). Differing from \({\bar {t}}_{\text{m},{\text{I}}_{*}}^{k}\) in Eq. 11, \({\bar {t}}_{\text{m, }{\text{I}}_{0}}^{k}\) is called the “ionosphere-free integer clock” in this study. Again, the arbitrary integer offset \({B}_{A\text{,1}}^{k}\) can be calibrated by shifting integer clocks from all ACs toward a common datum.

In addition, the combined integer clocks are computed following an iterative weighting strategy. The weight of each AC is determined by its integer clock residuals in the combination. When the weight of each AC varies within 1% compared to the last iteration or the iterations exceed six, the combination algorithm will stop. The median absolute deviation is used to detect outliers in integer clocks for the highest robustness of combined products.

(5) Extract the combined phase clock and ionosphere-free phase bias from the combined integer clock in Eq. 17 using

$$\left\{\begin{array}{l}{\bar {b}}_{\text{m,0}}^{k}=\frac{1}{n}{\sum }_{j=1}^{n}\left({\bar {t}}_{\text{m,L}}^{k}(j)-{\bar {t}}_{\text{m,}{\text{I}}_{0}}^{k}(j)\right)\\ {\bar {t}}_{\text{m,P}}^{k}(j)={\bar {t}}_{\text{m,}{\text{I}}_{0}}^{k}(j)+{\bar {b}}_{\text{m,0}}^{k}\end{array}\right.$$
(18)

where \(j\) denotes an epoch and \(n\) denotes the total number of epochs for satellite \(k\); \({\bar {b}}_{\text{m,0}}^{k}\) is the combined ionosphere-free phase bias whereas \({\bar {t}}_{\text{m,P}}^{k}\left(j\right)\) is the combined phase clock at epoch \(j\).

(6) Convert the combined DCBs, wide-lane and ionosphere-free phase biases into code and phase OSBs using

$$\left\{\begin{array}{l}{D}_{\text{m},1}^{k}=-\beta \bullet {D}_{\text{m},12}^{k} \\ {D}_{\text{m},2}^{k}=-\alpha \bullet {D}_{\text{m},12}^{k} \\ {\bar {b}}_{\text{m,1}}^{k}=\frac{-1}{{g}_{2}}\bullet {\bar {b}}_{\text{m,w}}^{k}+\frac{1+{g}_{2}}{{g}_{2}}\bullet {\bar {b}}_{\text{m,0}}^{k}-\frac{1}{{g}_{2}+1}\bullet {D}_{\text{m},1}^{k}-\frac{1}{{g}_{2}\left({g}_{2}+1\right)}\bullet {D}_{\text{m},2}^{k} \\ {\bar {b}}_{\text{m,2}}^{k}=-{g}_{2}\bullet {\bar {b}}_{\text{m,w}}^{k}+\left({g}_{2}+1\right)\bullet {\bar {b}}_{\text{m,0}}^{k}-\frac{{g}_{2}^{2}}{{g}_{2}+1}\bullet {D}_{\text{m},1}^{k}-\frac{{g}_{2}}{{g}_{2}+1}\bullet {D}_{\text{m},2}^{k}\end{array}\right.$$
(19)

where \({D}_{\text{m},1}^{k}\) and \({D}_{\text{m},2}^{k}\) denote the combined code OSBs; \({\bar {b}}_{\text{m,1}}^{k}\) and \({\bar {b}}_{\text{m,2}}^{k}\) are the combined phase OSBs on baseline frequencies.

2.4 All-frequency phase clock/bias combination

All-frequency phase clock/bias combination implies combining all third-frequency phase biases in addition to the previous dual-frequency combination. A simple solution is to form extra wide-lane phase biases between each third-frequency OSB and either of the baseline frequency OSBs; then for each of them iterate wide-lane phase bias combination as demonstrated in Eq. 15; finally perform phase clock/bias combination on baseline frequencies in Sect. 2.3 to conclude the entire combination task. We label this method as “MW” standing for “Melbourne-Wübbena”.

However, in this study, we attempt to combine the phase clock/bias products individually for each third-frequency signal, which is labeled as the “UC” method standing for “uncombined”. To be specific, the phase bias products on each third-frequency signal are combined independently without forming wide-lane phase biases, while preceded by the phase clock/bias combination on baseline frequencies as detailed in Sect. 2.3. The key to the UC method is to estimate the DCB error \({\sigma }_{A,{D}_{12}}^{k}\) for the baseline frequencies and introduce the concept of frequency-specific integer clock in Eq. 11. According to Eqs. 10 and 11, we have

$$\left\{\begin{array}{l}{\bar {t}}_{A}^{k}-{\bar {b}}_{A,1}^{k}={\bar {t}}_{\text{m,}{\text{I}}_{1}}^{k}-{\lambda }_{1}{B}_{A,1}^{k}+{g}_{1}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}\\ {\bar {t}}_{A}^{k}-{\bar {b}}_{A,2}^{k}={\bar {t}}_{\text{m,}{\text{I}}_{2}}^{k}-{\lambda }_{2}{B}_{A,2}^{k}+{g}_{2}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}\end{array}\right.$$
(20)

where

$$\left\{\begin{array}{l}{{\overline{t} }_{{\text{m,I}}_{1}}^{k}=t}^{k}-{b}_{1}^{k}\\ {{\overline{t} }_{{\text{m,I}}_{2}}^{k}=t}^{k}-{b}_{2}^{k}\end{array}\right.$$
(21)

In the following, the UC method is divided into four steps in addition to the preceding dual-frequency phase clock/bias combination (See also the left side of Fig. 1).

  1. 1.

    Recover the integer offset \({B}_{A\text{,2}}^{k}\) in Eq. 12. Since \({B}_{A\text{,w}}^{k}\) and \({B}_{A\text{,1}}^{k}\) have already been identified in the dual-frequency phase clock/bias combination, \({B}_{A\text{,2}}^{k}\) can be computed using

    $${B}_{A,2}^{k}={B}_{A,1}^{k}-{B}_{A,\text{w}}^{k}$$
    (22)
  2. 2.

    Compute the DCB error \({\sigma }_{A,{D}_{12}}^{k}\). Thanks to the preceding dual-frequency phase clock/bias combination, the combined phase clock (i.e., \({\overline{t} }_{\text{m,P}}^{k}\)) and the combined phase biases (i.e., \({\overline{b} }_{\text{m,1}}^{k}\) and \({\overline{b} }_{\text{m,2}}^{k}\)) on baseline frequencies have been computed (Eqs. 18 and 19). Therefore, substitute \({\overline{t} }_{\text{m,P}}^{k}-{\overline{b} }_{\text{m,1}}^{k}\) and \({\overline{t} }_{\text{m,P}}^{k}-{\overline{b} }_{\text{m,2}}^{k}\) for \({\bar {t}}_{\text{m},{\text{I}}_{1}}^{k}\) and \({\bar {t}}_{\text{m},{\text{I}}_{2}}^{k}\) in Eq. 20, respectively, and reformuluate Eq. 20 as

    $$\left\{\begin{array}{l}{\overline{t} }_{A}^{k}-{\overline{b} }_{A,1}^{k}+{\lambda }_{1}{B}_{A,1}^{k}-({\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{\overline{b} }_{{\text{m}},1}^{k})={g}_{1}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}\\ {\overline{t} }_{A}^{k}-{\overline{b} }_{A,2}^{k}\text{+}{\lambda }_{2}{B}_{A,2}^{k}-\left({\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{\overline{b} }_{{\text{m}},2}^{k}\right)={g}_{2}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}\end{array}\right.$$
    (23)

    where the DCB error \({\sigma }_{A,{D}_{12}}^{k}\) is the only unknown and can be easily estimated.

  3. 3.

    Correct for the DCB error \({\sigma }_{A,{D}_{12}}^{k}\) on each third-frequency signal. Again according to Eq. 10, for any third-frequency \(q\) we have

    $${\bar {t}}_{A}^{k}-{\bar {b}}_{A,q}^{k}-{g}_{q}^{2}\beta {\sigma }_{A,{D}_{12}}^{k}={t}^{k}-{b}_{q}^{k}-{\lambda }_{q}{B}_{A,q}^{k}$$
    (24)

    after moving the known DCB error term to the left-hand side. We can further define

    $${t}^{k}-{b}_{q}^{k}\doteq {\overline{t} }_{{\text{m}},{\text{I}}_{q}}^{k}$$
    (25)

    where \({\bar {t}}_{\text{m},{\text{I}}_{\text{q}}}^{k}\) denotes the combined integer clocks for frequency \(q\), which can be estimated following the same strategy of Eq. 16. Note that no more iteration is needed this time because we can assign each AC the same weight as that derived from the dual-frequency combination process.

  4. 4.

    Separate all third-frequency phase OSBs from their corresponding combined frequency-specific integer clocks. The epoch-wise combined phase OSB on any third-frequency \(q\) can be obtained using

    $${\overline{b} }_{\text{m,}q}^{k}(j)={\overline{t} }_{\text{m,P}}^{k}(j)-{\overline{t} }_{{\text{m,I}}_{q}}^{k}(j)$$
    (26)

    where \(j\) denotes an epoch. Note that in Eq. 26\({\overline{b} }_{\text{m,q}}^{k}\) is computed epoch by epoch to accommodate time-variable phase OSBs. If a daily-constant phase OSB is presumed, an average operation can be applied on Eq. 26 as analogous to the first line of Eq. 18.

2.5 All-frequency PPP-AR

For PPP-AR, users only need to fix the combined satellite clocks and deduct the combined code/phase OSBs from their corresponding raw pseudorange and carrier-phase observations (e.g., Geng et al. 2022a), that is

$$\begin{array}{l}\left\{\begin{array}{l}{\widehat{P}}_{r,1}^{k}={P}_{r,1}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{D}_{\text{m},1}^{k} \\ {\widehat{P}}_{r,2}^{k}={P}_{r,2}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{D}_{\text{m},2}^{k} \\ {\widehat{P}}_{r,q}^{k}={P}_{r,q}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{D}_{\text{m},q}^{k} \\ {\widehat{L}}_{r,1}^{k}={L}_{r,1}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{\overline{b} }_{{\text{m}},1 }^{k} \\ {\widehat{L}}_{r,2}^{k}={L}_{r,2}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{\overline{b} }_{{\text{m}},2}^{k} \\ {\widehat{L}}_{r,q}^{k}={L}_{r,q}^{k}+{\overline{t} }_{{\text{m}},{\text{P}}}^{k}-{\overline{b} }_{\text{m,}q}^{k}\end{array}\right.\end{array}$$
(27)

Note that users can select any two or more frequencies of pseudorange and carrier-phase from Eq. 27 to carry out PPP-AR.

3 Data and products

The phase clock/bias products for GPS and Galileo from CODE (Center for Orbit Determination in Europe), CNES, TUG and WUM in the year of 2020 were used for the combination validation (Table 1). Since Galileo E5 phase biases were only provided by TUG and WUM and the relevant outlier detection is unachievable, the Galileo E5 signal was excluded in the combination process. GPS/Galileo orbit products from the four ACs were combined according to Chen et al. (2023). We corrected for satellite attitudes in the clock/bias combination where the reference attitudes were computed using GROOPS (Loyer et al. 2021; Mayer-Gürr et al. 2021). Satellite antenna phase center offsets (PCOs) were reconciled among ACs using igs14.atx, and the GPS Block IIF L2 PCOs were duplicated for the L5 signals (Lin et al. 2023). We tested both MW and UC methods to compare their performance in all-frequency phase clock/bias combination. In the following, the combinations based on the MW and UC methods are labeled as “MW-enabled” and “UC-enabled”, respectively, unless noted otherwise.

Table 1 Phase bias products used in the combination of this study
Full size table

A phase clock/bias combination software package, PRIDE ckcom, is developed at Wuhan University to carry out this combination task. It is written in the C +  + environment and is capable of combining either dual-frequency or all-frequency phase clock/bias products. PRIDE ckcom has been dedicated to the third IGS reprocessing campaign (IGS Repro-3, IGSMail-8248) to accomplish the mission of combining dual-frequency phase clock/bias products from all ACs for the past two decades (Lin et al. 2023).

In addition, we experimented on all-frequency daily PPP-AR at about 128 globally-distributed stations using our combined clock/bias products. The open-source software PRIDE PPP-AR was used to enable GPS L1/L2, L1/L5, Galileo E1/E5a, E1/E5b, and E1/E6 PPP-AR (Geng et al. 2019b; Wen et al. 2020). The sequential bias fixing strategy was adopted, and the round-off criteria were 0.25 and 0.15 cycles for wide-lane and narrow-lane ambiguities, respectively (Dong and Bock 1989). More details refer to Table 2.

Table 2 Models and estimation strategies for GPS/Galileo data processing
Full size table

4 Results

4.1 Phase clock/bias combination on baseline frequencies

The phase clock/bias combination on the baseline frequencies is the same for both MW and UC methods. Figure 2 shows the consistency among the GPS L1/L2 (left panel) and Galileo E1/E5a (right panel) wide-lane phase biases from all ACs in the dual-frequency phase bias/clock combination. The horizontal axes denote the day of year in 2020, while the vertical axes the satellite vehicle numbers. The consistency is measured as the RMS (ps) of all ACs’ wide-lane phase bias residuals after datum alignment (Eq. 15), and then color coded according to the rightmost vertical color bar in Fig. 2. It can be seen that the wide-lane phase bias consistency for a number of satellites on many days exceed 40 ps (or 1.2 cm) which equates approximately the statistics reported by Banville et al. (2020) for GPS. In particular, the legacy GPS BLOCK IIA satellite G034, as well as the latest BLOCK IIIA satellites G076 and G077, have wide-lane phase bias consistencies as poor as 80 ps (or 2.4 cm) among ACs, clearly exceeding those of the remaining GPS satellites on average. Since limited data span was used in this study to investigate the three satellites, more in-depth analysis is necessary to elucidate the phenomenon. Likewise, the Galileo IOV satellites (i.e., E101, E102 and E103) and the two FOC satellites on elliptical orbits (i.e., E201 and E202) have clearly worse consistencies compared to other Galileo satellites during the whole year. Overall, GPS and Galileo satellites have similar wide-lane phase bias consistencies, as shown in Table 3 where the mean for GPS L1/L2 and Galileo E1/E5a are 55.1 and 58.2 ps, respectively.

Fig. 2
figure 2

Consistency (ps) among GPS L1/L2 and Galileo E1/E5a wide-lane phase biases from all ACs in 2020. The GPS BLOCK IIA, IIR, IIF and IIIA satellite vehicle numbers are colored in black, blue, red and green, respectively, while the Galileo IOV and FOC satellite vehicle numbers are in black and blue. “GAL” stands for Galileo

Full size image
Table 3 Consistency (ps) among AC-specific wide-lane phase bias and ionosphere-free integer clock products on GPS and Galileo baseline frequencies
Full size table

Moreover, Fig. 3 shows the consistency among the GPS L1/L2 (left panel) and Galileo E1/E5a (right panel) integer clocks (i.e., ionosphere-free integer clocks as indicated in Eq. 17) from all ACs. Again, the consistency here is defined as the RMS (ps) of all ACs’ integer clock residuals after datum alignment (Eq. 16). Note that the integer clocks are the integration of the legacy satellite clocks and the ionosphere-free phase biases. Compared to the wide-lane phase bias consistency in Fig. 2, the integer clock consistencies become much better for both GPS and Galileo where most colored coded RMS are below 15 ps. Table 3 shows that the mean consistencies achieve 9.3 and 10.7 ps for GPS and Galileo, respectively, which are close to the statistics by Banville et al. (2020). Unlike Fig. 2, the GPS BLOCK IIA satellite G034, as well as the BLOCK IIIA satellites G076 and G077, do not exhibit any inferiority in terms of integer clock consistencies compared to other GPS satellites. However, the two Galileo FOC satellites on the elliptical orbits still reveal worse performance in comparison to their counterpart satellites, which is attributed to the relatively poor satellite clock quality from CNES. Of particular note, Table 3 implies the generally large noise or inconsistencies in combining wide-lane phase biases that originate in the Melbourne-Wübbena combination.

Fig. 3
figure 3

Consistency (ps) among GPS L1/L2 and Galileo E1/E5a integer clocks from all ACs in 2020. Refer to Fig. 2 for the colors of satellite vehicle numbers along the vertical axes

Full size image

4.2 All-frequency combination based on the MW method

4.2.1 GPS L1/L5 wide-lane phase bias combination

The MW method to combine all-frequency phase bias/clock products is based on the concept of forming extra wide-lane phase biases using the Melbourne-Wübbena combination. As a typical example, Fig. 4 shows the GPS L1/L5 wide-lane phase biases of four representative BLOCK IIF satellites for day 365 of 2020. Due to the time-variable phase OSBs originating in the GPS BLOCK IIF L5 carrier-phase signals, the GPS L1/L5 wide-lane phase biases manifest semidiurnal variations as expected (Montenbruck et al. 2011), which cannot be found for any other extra wide-lane phase biases in this study (e.g., Galileo E1/E6 and E1/E5b not shown here for brevity). The MW-enabled combined L1/L5 wide-lane phase biases (labeled as CMB) are plotted in red curves, while those from CNES, TUG and WUM are in green, light blue and orange, respectively. We can see that the disagreement among CMB and CNES can be up to 0.2 ns for satellites G03 and G25. On average, the L1/L5 wide-lane phase bias consistencies for both satellites exceed 100 ps among CNES, TUG and WUM. This explains why their resulting CMB product deviates significantly from the contributing AC-specific products in Fig. 4 (i.e., the red curves distanced from the remaining). In Table 4, the MW-enabled mean consistency among AC-specific GPS L1/L5 wide-lane phase biases is as poor as 61.0 ps in 2020, whereas those for Galileo E1/E6 and E1/E5b reach also 60 ps, which all resemble the quantities listed in Table 3 for GPS L1/L2 and Galileo E1/E5a. This result confirms the fact that the wide-lane phase biases recovered through the Melbourne-Wübbena combination can hardly be combined at a high precision level, compared to the integer clock combination which is not subject to code OSB errors.

Fig. 4
figure 4

GPS L1/L5 wide-lane phase biases (ns) for four BLOCK IIF satellites (G03/G08/G10/G25) from CNES/TUG/WUM and their MW-enabled combination (CMB) for day 365 of 2020. The RMS (ps) denote the consistency among all ACs’ L1/L5 wide-lane phase biases

Full size image
Table 4 Consistency (ps) among AC-specific wide-lane phase bias and integer clock products
Full size table

4.2.2 Consistency among MW-enabled ionosphere-free integer clocks

The MW method achieves combined phase clock/bias products on all third-frequencies by introducing extra wide-lane phase biases, rather than extra ionosphere-free integer clocks, into the legacy combination on baseline frequencies. In this case, we cannot directly obtain the consistency statistics for all third-frequency integer clocks from the combination process. Alternatively, we formulate the integer clocks for GPS L1/L5, Galileo E1/E6 and E1/E5b using each AC’s original and the combined phase clock/bias products (see Eq. 12), and then compute the consistency (or RMS errors) among such AC-specific integer clocks against the combined integer clocks. Figure 5 hence shows the resultant consistencies for GPS L1/L5, Galileo E1/E6 and E1/E5b integer clocks throughout the year of 2020. Compared to Fig. 3 with an identical color bar, the three panels of Fig. 5 are obviously redder, especially for Galileo E1/E6, suggesting poor consistencies among the MW-enabled ionosphere-free integer clocks connected to a third-frequency signal. In Table 4, the mean consistencies for GPS L1/L5, Galileo E1/E6 and E1/E5b are 17.3, 34.9 and 16.8 ps, respectively, which are almost all 2–3 times worse than those for the baseline frequencies in Table 3.

Fig. 5
figure 5

Consistency (ps) among GPS L1/L5, Galileo E1/E6 and E1/E5b integer clocks from all ACs in 2020. These integer clocks are computed for each AC-specific products and the MW-enabled combined phase clock/bias products. Refer to Fig. 2 for the colors of satellite vehicle numbers along the vertical axes

Full size image

4.3 All-frequency combination based on the UC method

4.3.1 GPS L5 phase clock/bias combination

In contrast to the MW method, the UC method avoids the Melbourne-Wübbena combination to combine phase biases related to a third-frequency signal. Rather, each third-frequency phase bias is integrated with the phase clock individually to form a frequency-specific integer clock (i.e., Eq. 11) before being conveyed into the combination process. Typically, Fig. 6 shows the detrended GPS L5 integer clocks from CNES/TUG/WUM and their UC-enabled combination (CMB) for day 365 of 2020 for the same four satellites as those in Fig. 4. In contrast to Fig. 4, the disagreements among the AC-specific GPS L5 integer clocks are all smaller than 25 ps, suggesting that their consistency outperforms significantly that among the GPS L1/L5 wide-lane phase biases. In fact, Table 4 shows that the GPS L5, Galileo E6 and E5b integer clocks have mean inter-AC consistencies of 18.7, 14.9 and 15.4 ps, respectively, over all relevant satellites in the year of 2020. This result demonstrates that the UC method is able to combine third-frequency phase biases at a much higher precision level compared to the MW method, since the frequency-specific integer clock concept is employed instead of the Melbourne-Wübbena combination. This fact demonstrates the adverse impact of code OSB errors on the third-frequency phase bias combination.

Fig. 6
figure 6

Detrended GPS L5 integer clocks (ns) for four BLOCK IIF satellites (G03/G08/G10/G25) from CNES/TUG/WUM and their UC-enabled combination (CMB) for day 365 of 2020. The RMS (ps) denote the consistency among all ACs’ L5 integer clocks

Full size image

4.3.2 Consistency among UC-enabled ionosphere-free integer clocks

Since the UC method does not introduce any extra ionosphere-free integer clocks either into the combination, similar to Fig. 5, such integer clocks for GPS L1/L5, Galileo E1/E6 and E1/E5b are formulated for each AC’s original and the UC-enabled combined phase clock/phase products, and then their consistency statistics are computed as plotted in Fig. 7. In contrast to Figs. 3 and 5 with identical color bars, the integer clock consistencies in Fig. 7 for all third-frequencies are comparable to those on the baseline frequencies, and more importantly, much better than those based on the MW method, especially for Galileo E1/E6. The two Galileo satellites on the elliptical orbits (i.e., E201 and E202) have low consistencies, which are imputed to their outlier solutions from CNES. As shown in Table 4, the mean integer clock consistencies for GPS L1/L5, Galileo E1/E6 and E1/E5b are 11.2, 12.8 and 10.9 ps, respectively, which improve dramatically by 35, 63 and 35% compared to those derived from the MW method. These results demonstrate again the superiority of the UC method in combining all-frequency phase clocks/biases compared to the MW method, since the UC method mitigates the impact of code OSB errors.

Fig. 7
figure 7

Consistency (ps) among GPS L1/L5, Galileo E1/E6 and E1/E5b integer clocks from all ACs in 2020. These integer clocks are computed for each AC-specific products and the UC-enabled combined phase clock/bias products. Refer to Fig. 2 for the colors of satellite vehicle numbers along the vertical axes

Full size image

4.4 Positioning validation

Table 5 shows the mean wide-lane/narrow-lane ambiguity fixing rates for typical GPS and Galileo dual-frequency signals (e.g., GPS L1/L2 and L1/L5, Galileo E1/E5a, E1/E6 and E1/E5b). These fixing rates were computed by averaging the wide-lane and narrow-lane ambiguity fixing rates at all 128 stations throughout the year of 2020. Note that only non-Trimble stations were used to carry out GPS L1/L5 PPP-AR as cautioned by Geng et al. (2022a). From Table 5, we can see that the UC method is always able to achieve better, or at least comparable, fixing rates to those of each AC. Although the wide-lane ambiguity fixing rates from both MW and UC are quite similar, the MW-enabled narrow-lane ambiguity fixing rates are clearly lower for GPS L1/L5, Galileo E1/E6 and E1/E5b than those achieved by the UC method. Particularly, in the case of GPS L1/L5 and Galileo E1/E6, the UC method reaches the fixing rates that are about 12 and 40 percentage points more than those of the MW method, respectively. These results corroborate that the UC method outperforms the MW method in achieving the combined all-frequency phase clock/bias products of the high robustness. In addition, the overall performance of the CNES products is relatively poor where the narrow-lane ambiguity fixing rates can drop to 30% on some days. Since the other ACs perform much better, the combination process is able to reject such outlier products and finally achieve a robust combined phase clock/bias product.

Table 5 GPS-only and Galileo-only PPP ambiguity fixing rates (%) at 128 globally-distributed stations in 2020 using the phase clock/bias products from CNES, CODE, TUG and WUM as well as the two combined products (MW-enabled and UC-enabled)
Full size table

Furthermore, Fig. 8 shows the GPS L1/L2 and Galileo E1/E5a daily positioning RMS errors against the IGS weekly solutions for the east, north and up components in the year of 2020. A 7-parameter Helmert transformation has been applied. In Fig. 8, the daily solutions based on the combined products (horizontal axes) are plotted against those based on the AC-specific products (vertical axes). Since the MW and the UC methods share the combination process for baseline frequencies, we do not distinguish between the MW-enabled and UC-enabled combined products in Fig. 8. Every dot in the panels denotes a solution for a particular day, and the dots above the diagonal dashed lines mean better precisions achieved by the combined products. It can be seen that the RMS errors for the combined products are generally the smallest among all solutions, especially compared to the CNES and CODE solutions. The mean RMS errors for the combined solutions in the east, north and up directions are down to 1.6 mm, 1.6 mm and 5.8 mm, respectively, for GPS L1/L2, and 2.5 mm, 2.6 mm and 9.4 mm for Galileo E1/E5a.

Fig. 8
figure 8

GPS L1/L2 and Galileo E1/E5a daily positioning RMS errors (mm) against the IGS weekly solutions for the east, north and up components in the year of 2020. AC-specific solutions are compared against those based on the combined products. Every black dot in the panels denotes a solution for a particular day, and the dots above the diagonal dashed lines mean better precisions achieved by the combined products. Yearly mean RMS are plotted in blue along the axes within each panel. Note that the horizontal components refer to the left vertical axes while the vertical to the right axes

Full size image

Similar to Figs. 8, 9 further shows the daily positioning RMS errors (mm) for GPS L1/L5, Galileo E1/E6 and E1/E5b signals against the IGS weekly solutions for the east, north and up components in the year of 2020. The 7-parameter Helmert transformation has still been applied. Again, from the top three lines of panels, the UC-enabled RMS errors are generally smaller than those based on the AC-specific products, especially compared to CNES, demonstrating the benefit of combining AC-specific phase clock/bias products to improve PPP-AR. More importantly, from the bottom panels of Fig. 9, the RMS errors based on the UC-enabled combined products uniformly outperform those based on the MW-enabled combined products for all dual-frequency signal combinations. In particular, for GPS L1/L5 and Galileo E1/E6, almost 90% of all solutions have smaller RMS errors in the case of UC-enabled combined products, whereas this percentage is still up to 70% in the case of Galileo E1/E5b. The UC-enabled solutions achieve the positioning RMS errors of 2–3 mm in the horizontal directions and 8–10 mm in the vertical, which are generally more than 10% better than those achieved by the MW-enabled combined products.

Fig. 9
figure 9

Daily positioning RMS errors (mm) for GPS L1/L5, Galileo E1/E6 and E1/E5b against the IGS weekly solutions for the east, north and up components in the year of 2020. AC-specific solutions as well as the MW-enabled solutions (along vertical axes) are contrasted against those based on the UC-enabled solutions (along horizontal axes). Every black dot in the panels denotes a solution for a particular day, and the dots above the diagonal dashed lines mean better precisions achieved by the UC-enabled combined products. Yearly mean RMS are plotted in blue along the axes within each panel. Note that the horizontal components refer to the left vertical axes while the vertical to the right axes

Full size image

For completeness, we carried out triple-frequency static PPP-AR and Table 6 shows the mean extra-wide-lane/wide-lane/narrow-lane ambiguity fixing rates for GPS-only L1/L2/L5, Galileo-only E1/E5a/E6 and E1/E5a/E5b signals. These quantities were computed by averaging the extra-wide-lane (i.e., L2/L5, E5a/E6, E5a/E5b), wide-lane and narrow-lane (i.e., L1/L2, E1/E5a) ambiguity fixing rates at all 128 stations from days 300 to 330, 2020. We can see that for all AC-specific and combined products, the extra-wide-lane ambiguities are almost 100% recovered to integers. The wide-lane and narrow-lane ambiguity fixing rates manifest comparable statistics of around 95% to those in Table 5. These results demonstrate the capability of the all-frequency phase clock/bias products in achieving multi-frequency PPP-AR.

Table 6 GPS-only and Galileo-only triple-frequency PPP ambiguity fixing rates (%) at 128 globally-distributed stations from days 300 to 330, 2020 using the phase clock/bias products from CNES, TUG and WUM as well as UC-enabled combined products
Full size table

5 Conclusions

In this study, we develop a combination method for AC-specific all-frequency phase clock/bias products to improve PPP-AR in terms of ambiguity fixing rates and positioning precisions. While the legacy dual-frequency phase clock/bias combination is tied to both wide-lane phase bias and ionosphere-free integer clock, the difficulty challenging all-frequency phase clock/bias combination is how to combine all third-frequency phase biases efficiently and precisely without the cumbersome formulation of Melbourne-Wübbena and ionosphere-free combinations. Therefore, we develop the concept of frequency-specific integer clock and then augment the traditional dual-frequency phase clock/bias combination with integer clock combination for each third-frequency signal individually. In this case, the combination process is quite straightforward, and the combination precision for all third-frequency phase biases can be maintained at the same level as that for the baseline-frequency combination.

The GPS/Galileo all-frequency phase clock/bias products from CNES, CODE, TUG and WUM in the year of 2020 were combined. On the one hand, the mean consistencies among the AC-specific products for all third-frequency phase biases (i.e., on GPS L5, Galileo E6 and E5b) are as high as 10 ps, which reaches the same level as that for GPS/Galileo baseline frequencies. It is also presented that the wide-lane phase bias products based on the Melbourne-Wübbena combination cannot be combined at a high precision, where the consistency can be as low as 100 ps. On the other hand, the combined products achieve better or at least comparable ambiguity fixing rates and daily positioning precisions to those enabled by AC-specific products. This is primarily attributed to the robustness of the combined product, which is more resistant to outliers than any individual AC-specific product. More encouragingly, the ambiguity fixing rates and daily positioning precisions in the case of GPS L1/L5, Galileo E1/E6 and E1/E5b resemble overall those for the legacy GPS L1/L2 and Galileo E1/E5a signals. We have developed a software package PRIDE ckcom to accomplish this all-frequency phase clock/bias combination which has been delivered to the IGS AC coordinator with the goal of serving routine product combination task.