Introduction

Pore geometry and its topology affect multiphase flow in porous media significantly. Network models can simulate the physics of air and fluid flow and mass transport in soil (Berkowitz and Ewing 1998). The coordination number is widely regarded as the main feature of network topology. The mean of the coordination number, the microscopic topology of pore connectivity, and its distribution should be determined using network models (Chatzis and Dullien 1977; Raoof and Hassanizadeh 2010). The soil structure and constriction size distribution (CSD) is one of the methods that can be used to estimate the fluid flow in porous media (Berkowitz and Ewing 1998; Sahimi 2011), permeability (Carman 1937; Fan et al. 2021),and the amount and size of eroded particles from the soil skeleton (Kezdi 1979; Kovacs 1981; Kenney et al. 1985; Indraratna and Vafai 1997).

The transport eventuality of granular media depends on the constriction size and its probability of occurring within the particles or constriction size distribution (Reboul et al. 2010). Transport of fine grains through the pores between the skeleton of coarser particles, under seepage flow, or vibrating force, is the major cause of instabilities of the granular assemblies, causing erosion phenomena (Kenney and Lau 1985). This phenomenon can occur when two basic conditions happen. Firstly, the pore diameter of the solid matrix should be greater than the smallest fine grains (geometrical conditions). If the first condition does not exclude fine-grain movement, then the hydraulic condition (critical velocity or hydraulic gradient) must be studied (Kovacs 1981; Wan and Fell 2008; Tangjarusritaratorn et al. 2022).

Common geometrical criteria for the internal stability assessment of cohesionless soils are a function of grain size and shape of the particle size distribution (Istomina 1957; Kezdi 1979; Kenney and Lau 1985; Burenkova 1993; Wan and Fell 2008; Chapuis 2021).

Furthermore, some geometrical criteria have been established based on soil structure/pore geometry and categorized into constriction size distribution criteria and capillary tube model. These criteria depend mainly on particle size, particle morphology, density, pore size, and pore size distribution (Kezdi 1979; Kovacs 1981; Vafai 1996; Maroof et al. 2021b, a).

When fine particles are transported to the void network formed by a coarser skeleton, grains smaller than the controlling constriction size are likely to be transported (Liang et al. 2017). Thus, the eroded fine grains are controlled by the pore geometry. Numerous network models emphasizing fine-grain transport mechanisms through soil pores can be classified as analytical models, constriction-based criteria, and capillary tube model. The former one is discussed in the next section (“Capillary tube models”).

Analytical and numerical models

The more simple description for the void space in granular materials consists of envisioning it as a set of larger void spheres (pores) linked by throats (tubes) representing pore constrictions (Schuler 1996). Any movement of fine particles within this network is controlled by the constriction sizes and their occurrence in the material (Khilar and Fogler 1998).

Different analytical models were proposed to compute the constriction size distribution. They are all based on a proposal by Silveira (1965) to simplify the complex configurations giving rise to the constrictions by a set of geometrical configurations (Silveira 1965).

There also exist numerical approaches to the problem based on a numerical representation of the granular material. They are processed on the basis of an image of an actual sample obtained by CT-scan (Dong and Blunt 2009; Homberg et al. 2012; Taylor et al. 2016) after segmentation of the pore space. Finally, the CSD can also be obtained for numerical samples built through the discrete element method (DEM) (Reboul et al. 2008; Taylor et al. 2015; Shire et al. 2016; Seblany et al. 2018; Nguyen et al. 2021). Approaches developed based on CT-scan are specifically powerful since they can address any sample composed of particles with irregular shapes with very different sphericities, angularities, or flatness. However, they always need robust post-processing in order to remove artificial entities created by the very discrete nature of the images (set of voxels) (e.g., (Taylor et al. 2016)).

Controlling constriction size

Pore throats control the particle transport mechanism in porous media due to geometrical restrictions and constriction sizes along flow paths. Studies carried out by Kenney et al. (1985) over a wide range of gradations exhibited that the CSDs, for a given compaction, organized a narrow band of similarly shaped curves when normalized by a representative filter thickness (D5 or D15). Therefore, smaller filter particles seem to govern the process of filtration. It was also found by Sherard et al. (1984) and Foster and Fell (2001) and is underlying the filter retention criterion of Terzaghi (Terzaghi et al. 1996). Kenney et al. (1985) revealed the concept of controlling constriction size \({d}_{c}\), where this quantity is related to the maximum particle size that can pass through a pore network. Base particles smaller than \({d}_{c}^{*}\) can pass through the granular filter depending on the seepage conditions. The controlling constriction size has a close relationship with the concept of effective opening size that a fine particle will find on any pathway by Witt (1993). More practically, in all these definitions, the granular filter is associated to a mechanical sieve with an equivalent opening size. Indraratna et al. (2007) found that the controlling constriction size (or equivalent opening size) is close to \({d}_{c}^{35}\) (constriction diameter that is 35% smaller than the cumulative CSD). Seblany et al. (2021) demonstrated that this quantity can be associted to the largest mode of the CSD, the most represented size in the pore network. Some relationships proposed by researchers are shown in Table 1.

Table 1 Proposed relationship for controlling constriction size
Full size table

Due to an over-idealization of the soil skeleton, the proposed analytical technique that anticipates the full distribution of constriction sizes using incircling circles to approximate constriction sizes is often found to poorly estimate the CSD for broadly distributed grading (Shire and O’Sullivan 2016). Furthermore, analytical methods may have specific limitations such as gradation or density. Even if Wu et al. (2012) showed that the analytical CSD (Indraratna et al. 2007; Seblany et al. 2021) mainly developed for spherical materials can be used for granular materials with shapes associated that are not perfectly spherical and smooth, they are not adapted to materials with elongated shapes (see also Taylor et al. 2018). In that case, there are more numerous smaller constrictions and larger constrictions sizes than predicted by these formulas. Moreover, angular and elongated particles tend to have smaller mean pore lengths and an increase in tortuosity, leading to a higher probability of clogging of fine particles than granular filters composed of smooth and spherical-like ones (Maroof et al. 2021a; Deng et al. 2023).

There are more precise grain packings and porous skeletons such as the imprint of pore networks (e.g., Vincens et al. 2015; Maroof et al. 2022a), CT-scan and DEM-based models (Taylor et al. 2015), and pore network models (e.g., Daneshian et al. 2021; Veiskarami et al. 2023). Yet, some particular requirements and specific limitations of these methods (Vincens et al. 2015), and the complexity of the real porous skeleton which can be altered for different soils and even in one soil from pore to pore, make them difficult to utilize in practical applications. The use of capillary tube models may address the limitations of these models while taking into account grading, density, and particle shape.

In previous works, the problem of the void size distribution (Sjah and Vincens 2013; Vincens et al. 2015; Seblany et al. 2018, 2021; Maroof et al. 2022a), particle shape classification (Maroof et al. 2020b), the determination of shape coefficients (Maroof et al. 2020a), and the effect of particle morphology on internal instability (Maroof et al. 2021a) have been investigated. These studies showed that sphericity, roundness, and surface texture affect the susceptibility to suffusion, and spherical rounded particles with smooth surfaces are more prone to internal instability and volume change during suffusion. The concept of the capillary tube model developed by Kovacs (1981) is revisited and extended to characterize the pore network and the susceptibility to internal erosion in order to take into account the influence of grading, density, and particle shape of the granular material. This study improved the Kovacs model that integrates the accurate shape coefficient of particles, and it has been validated through previous research and the new experimental data.

Capillary tube models

Kovacs (1981) characterized the average pore size of the coarser fraction directly in terms of the average pipe diameter of a bundle of capillary tubes (Fig. 1). In this definition, the pore size actually denotes the mean size of the throat linking two adjacent pores (Schuler 1996). Afterward, to evaluate the potential movement of finer loss particles, this characteristic size related to a hydraulic process is compared with the mean opening size of the coarser skeleton.

Fig. 1
figure 1

Bundle of capillary tubes and void size (after Kovacs 1981 and Vafai 1996)

Full size image

This model takes into account the porosity and mean particle shape of the coarser fraction and indirectly the grain size distribution by expanding its effective diameter rather than computing the direct geometric property of the pore space (controlling constriction size).

Effective diameter

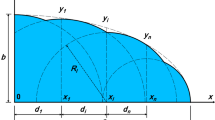
The effective or equivalent mean diameter of a particle, Deff, in a granular medium, is often characterized as the diameter of the smallest circumscribed sphere (D) (Maroof et al. 2020a). In the two-dimensional state, it is defined as the diameter of the encircling circle on the projection plan or the main section of the particle (Kovacs 1981) (Fig. 2).

Fig. 2
figure 2

a 3D-reconstructed particle, b the smallest circumscribed sphere and largest inscribed sphere, c particle projected plan, smallest circumscribed circle, and largest inscribed circle

Full size image

For grain assemblies with randomly mixed particles, the effective particle diameter can be associated with the equivalent diameter of a mono-size mixture with an identical specific surface area as the heterogeneous mixture (Aubertin et al. 2003). The effective particle diameter is then computed on the basis of the particle size distribution (PSD). The PSD is split into classes with frontiers corresponding to different sieves of different opening sizes.

Knowing the mean particle size \({D}_{av,i}\) of a given class i, the effective diameter is determined by (Kozeny 1927; Fair and Hatch 1933; Carman 1937; Loudon 1952; Kovacs 1981; Sperry and Peirce 1995; Dolzyk and Chmielewska 2014; Zheng and Tannant 2017):

$${\mathrm{D}}_{\mathrm{eff}}=\frac{100}{\sum \left({~}^{{\mathrm{fi}}}\!\left/ \!{~}_{{\mathrm{D}}_{{\mathrm{av}},{\mathrm{i}}}}\right.\right)}\;and\;{\mathrm{D}}_{{\mathrm{av}},{\mathrm{i}}}=\sqrt{{\mathrm{D}}_{{\mathrm{li}}\times }{\mathrm{D}}_{\mathrm{si}}}$$
(7)

where \({D}_{{\mathrm{av}}}\) is the average grain size of class i, \({D}_{li}\) and \({D}_{si}\) are the limits of class i, that is to say, the maximum and minimum particle size (adjacent sieve opening sizes) respectively, and fi is the grains percentile (mass) of class i. More recently, on the assumption that in a given class i, grains are log-linearly distributed, Carrier (2003) and Zheng and Tannant (2017) proposed to compute \({d}_{av,i}\) by the relationship:

$${D}_{{\mathrm{av}},{\mathrm{i}}}={\mathrm{D}}_{li}^{b}{\mathrm{D}}_{si}^{1-b}$$
(8)

where b was proposed to be equal to 0.404 for all graded grain sizes (Carrier 2003), 0.68 for poorly graded particles, and 0.90 for gap-graded particle sizes (Zheng and Tannant 2017).

Coarser fraction

In the capillary tube model, the soil is assumed to be composed of two fractions, a finer and a coarser, where fine loose grains can pass through the void formed by the coarser primary fabric (references). Then, PSD is split into a coarser and finer fraction (f) at a given delimitation diameter (D) (Kezdi 1979; Aberg 1992; Li and Fannin 2013; Dallo and Wang 2016).

This latter is supposed to coincide with the point of inflection or (H/F)min for a broadly distributed gradation and the maximum location of the gap in gap-graded soils (Li and Fannin 2013). The value of \({{D_{0} } \mathord{\left/ {\vphantom {{D_{0} } {D_{85}^{{\mathrm{f}}} }}} \right. \kern-0pt} {D_{85}^{{\mathrm{f}}} }}\) at (H/F)min, or the end of the gap in gap-graded soils, is very close to \({{(D_{0} } \mathord{\left/ {\vphantom {{(D_{0} } {D_{85}^{{\mathrm{f}}} }}} \right. \kern-0pt} {D_{85}^{{\mathrm{f}}} }})_{\max }\) (Li and Fannin 2013). Afterward, the coarser fabric void ratio can be expressed in terms of e and f (Kezdi 1979):

$${e}_{c}=\frac{{\mathrm{e}}+f}{1-f}$$
(9)

Furthermore, the porosity of the coarser fraction is assumed:

$${n}_{c}=n+f(1-n)$$
(10)

A threshold of about 35% separates possible loose finer fraction particles from fixed coarse grains. Meanwhile, more fine particles caused floating coarser particles in the matrix of fines (Skempton and Brogan 1994).

Shape factor and specific surface area

Surface roughness and specific surface area of particles (SSA, S0) are key information that can explain phenomena at the microscale (Maroof et al. 2020a). An ideal sphere or cube has the lowest value for SSA defined as the ratio between the surface area and the volume ratio or mass (Chapuis 2012):

$$SSA=\frac{6}{D}$$
(11)

where D denotes the side of a cube or the diameter of a sphere. The SSA of a heterogeneous sample containing irregular particle shapes can be defined as (Heywood 1933; Carman 1939; Loudon 1952; Kovacs 1981):

$${\mathrm{SSA}}=\alpha \mathrm{(}\sum_{i=1}^{n}{\mathrm{x}}_{i}{\mathrm{S}}_{i})=6\sum_{i=1}^{n}{~}^{{\mathrm{x}}_{i}}\!\left/ \!{~}_{{\alpha }_{i}{D}_{xi}}\right.$$
(12)

where \({\alpha }_{i}\) and \({x}_{i}\) denote the mean shape factor and weight percentile of particles in the ith class of the gradation curve, Dxi and Si are the average size and surface area of equivalent spheres in the ith class, respectively.

Indeed, the SSA of particles is controlled by the grain size and shape. As a result, it is defined as the ratio of the shape factor to the effective particle diameter (Kovacs 1981; Maroof et al. 2020a):

$$\frac{\mathrm{A}}{\mathrm{V}}=\frac{\pi}{{\mathrm{D}}_\mathrm{eff}}$$
(13)

Shape factor, \(\alpha\), is a dimensionless coefficient that is only dependent on the shape of the grain which illustrates the differences between actual nonspherical grains and ideal smooth spheres (Fair and Hatch 1933; Loudon 1952; Hunger and Brouwers 2009). Kovacs proposed different values for the shape factor of grains including spheroid, rounded, angular, and laminated grains equal to 6, 7–9, 9–11, and 20, respectively (Kovacs 1981).

Moreover, the shape factor has a strong connection to the particle sphericity, roundness, and roughness and thus to particle shape indicators. Numerous shape coefficients were obtained using various sphericity definitions, such as Wadell’s true sphericity (ѱs) and the inscribed-circumference sphere ratio (see Fig. 2) (\({\psi }_{ic}\)) (Wadell 1933; Maroof et al. 2020b).

The surface texture of the particle, as well as sphericity and roundness, can also affect the pore network. Indeed, the possibility of fine particle blockage in the pore throats increases as roughness increases (Maroof et al. 2021a). Relationships for particle shape factors with different sphericities, rough textures, and smooth surfaces were proposed by Maroof et al. (2020a) (Eqs. 13 and 14). The shape factor of particles with different forms is accounted for in the new model (Eqs. 15 and 17 to 21).

$$\alpha=6.3\psi_{ic}^{-0.85}\;\;\;\;\;\mathrm{rough}\;\mathrm{texture}$$
(14)
$$\alpha=6.0\psi_{ic}^{-0.72}\;\;\;\;\;\mathrm{smooth}\;\mathrm{surface}$$
(15)

Equivalent tube diameter

Due to the complexity of pore network geometry, it is difficult to measure the pore size directly from the grain size distribution (Liang et al. 2017). Within the framework of the capillary tube model, the pore space is modeled as a bundle of straight cylindrical capillary pipes with smooth walls, by an extension of Hagen–Poiseuille law (Carman 1937; Bear 1972).

The surface area to volume of the pores is equal to the ratio of the wetted surface or particle surface (A) to the volume of the conduit (Vp). As a result, the following equation can be used to define the d0, d1, and d2 (see Fig. 1) (Kovacs 1981):

$$\frac{{\pi}_0\Delta l}{\frac{\pi}4\mathrm{d}_0^2\Delta l}=\frac{\mathrm{A}}{{\mathrm{V}}_\mathrm{p}}=\frac{\mathrm{A}}{\frac{\mathrm{nV}}{1-\mathrm{n}}}=\frac{1-\mathrm{n}}{\mathrm{n}}\frac{\mathrm{A}}{\mathrm{V}}=\frac{1-\mathrm{n}}{\mathrm{n}}\frac a{{\mathrm{D}}_\mathrm{eff}},\;\mathrm{then}\;d_0=4\frac n{1-n}\frac{D_{eff}}{\mathrm\alpha}$$
(16)

and

$${d}_{1}=0.67{d}_{0},{d}_{2}=1.25{d}_{0}$$
(17)

where V is the volume of the sample, Δl is the length of the conduit, and d1 and d2 denote the minimum and maximum diameter of the pore channel (see Fig. 1), respectively.

The mean capillary tube diameter is determined by Eq. 15, and it is the basis of the capillary tube model as discussed in the next section.

Proposed capillary tube model

In the capillary tube model, the probability of fine particle movement and suffusion potential is assessed by comparing the smallest pore diameter (\({d}_{1}\)) or the mean diameter of the pores between the coarser fabric (\({d}_{0}\)) when the arching effect and inhomogeneity are considered and the minimum particle diameter (Dmin or \({D}_{85}^{\mathrm{f}}\)) (Kovacs 1981; Kenney et al. 1985; Aberg 1993; Wan and Fell 2008). Some researchers, modifying the Kovacs model, suggested substituting the average pore diameter of the coarser part by the controlling constriction size of the coarser fraction (Li and Fannin 2013; Dallo and Wang 2016)).

Kovacs (1981) criterion considers the influence of particle shape with the shape factor (α). It means that an increase in grain angularity results in an increase in the shape coefficient (Maroof et al. 2020a) and a decrease in the mean diameter of pores. The shape of soil grains also influences the sample porosity (Maroof et al. 2022b) which is also taken into account in the capillary tube model. Table 2 illustrates the proposed capillary tube model and shape coefficient for predicting the suffusion potential.

Table 2 Proposed capillary tube model and shape coefficient
Full size table

Developed capillary tube model

Experimental work

In this study, proposed Kenney and Lau’s (1985, 1986) boundaries between internally stable and unstable soils were examined. Therefore, the internal stability of two ideal particle size distribution curves was evaluated; the Fuller and Thomson (Fuller and Thomson 1907) and the Lubochkov PSD curves (Lubochkov 1969). These new results were utilized both for developing the new model and for comparison with other geometrical criteria.

Fuller and Thomson (1907) depict an ideal gradation for an optimum density represented by:

$${F}_{d}={(d/{d}_{100})}^{m}$$
(23)

if m = 0.5 since mass increment \(H={F}_{4d}-{F}_{d}=F({(4)}^{0.5}-1)=1.0{F}\)

Lubochkov (1969) proposed that suffusion susceptibility depends on the particle size distribution shape and proposed upper and lower boundary curves for internally stable soils (Kovacs 1981), with lower limit (Kenney and Lau 1985):

$${F}_{d}=0.6{({d}_{x}/{d}_{60})}^{0.6}$$
(24)

and H = 1.297F. Kenney and Lau (1985) amended the Lubochkov lower limit to yield a limiting PSD curve H = 1.3F. Comments in the literature (Milligan 1986; Sherard and Dunnigan 1986) and the further test data resulted in the subsequently revised threshold consistent with Fuller and Thompson’s (1907) boundary to (H/F)min ≤ 1.0 (Kenney and Lau 1986).

The previous experimental results show that the Lubochkov lower limit curve is a stable grading (Kenney and Lau 1985). Furthermore, Fuller gradation is also internally stable (Kenney and Lau 1986; Milligan 1986; Li 2008). Particle shape, whole PSD curve, and sample density have been neglected by many geometrical criteria of internal stability assessment. Obviously, constriction sizes reduce as relative densities increase. The Fuller gradation is partially internally stable at higher compaction levels (Rd ≥ 70%) (Indraratna et al. 2015).

Herein, the effect of particle shape on internal stability was evaluated by creating samples where each of them has grains with similar shapes. SSA and shape coefficient for the studied mixtures were evaluated using the analytical formula. The average shape factor for rounded, angular, flat, and elongated particles is 7.2, 9.3, 14, and 23, respectively (Maroof et al. 2020a).

Ten experimental tests were performed in a medium-dense condition (relative density equal to 50 ± 8%). These tests were conducted on Well-graded soils that are similar to the ideal Fuller and Lubochkov PSD curves, with five distinct particle shapes including spherical glass beads, rounded, angular, flaky, and elongated grains. The grading, particle shape, and particle packing properties of the test materials are depicted in Tables 3.

Table 3 General properties of the test materials
Full size table

The experimental results showed that the samples with spherical and medium sphericity/rounded grains were classified as internally unstable, and specimens containing elongated particles were categorized as internally stable, both in Fuller and Lubochkov curves (more details about internal instability occurrence have been elucidated in the Maroof et al. 2021a). The specimen with angular grain in the Lubochkov curve is categorized as transient, and the sample having flaky particles is internally unstable. Furthermore, in the Fuller curve, samples with angular and flaky particles are categorized as samples with internal stability (see Table 5). These findings agree with previous experimental work that spherical/rounded particles are more likely to suffusion (Slangen and Fannin 2017; Hassani 2020; Maroof et al. 2021b, a). Meanwhile, this change in particle form makes them easier to pack and causes lower void ratios (see Table 3 and Maroof et al. 2022b).

Exploring new data

The capillary tube model considers both density and shape as well as particle size. In these methods, particle geometry is characterized based on roundness and sphericity (Kovacs 1981) or roundness (Chang and Zhang 2013; Li and Fannin 2013), and the shape coefficient was estimated by visual comparison. The boundary thresholds proposed by Li and Fannin and Dallo and Wang were established using a database compiling soils and glass bead specimens. In their work, soil samples were assumed to have a shape coefficient of 8 (sub-angular to angular soils) (Li 2008; Li and Fannin 2013; Dallo and Wang 2016).

Maroof et al. (2021a, b) performed 26 suffusion tests on five different gradations and six various shapes. According to Kovacs capillary tube model, the average pore diameter (Eq. 15) and \(D_{85}^{{\mathrm{f}}}\) of the finer fraction were determined. Summary results for the capillary tube model are presented in Table 4.

Table 4 Summary of the relevant results for the capillary tube model
Full size table

Modified capillary tube model

Aside from the binary stable-unstable qualification for the granular material, safety margins are defined to involve uncertainties in the engineering design process. These two boundaries are defined as \({d}_{0}={1.5D}_{85}^{f}\) and \({d}_{0}={D}_{85}^{f}\) for the upper and lower side, respectively (Li and Fannin 2013; Dallo and Wang 2016).

The different prediction in the Kovacs criterion is due to several factors: the variation of the cross-sectional area of the conduit, the tortuosity of the mean hydraulic tube, and the pore interconnectivity (Chatzis and Dullien 1977; Khilar and Fogler 1998; Li 2008).

Li and Fannin (2013) suggested a boundary threshold for a database of 42 suffusion tests (\({d}_{0}={2.3D}_{85}^{f}\)) (Li and Fannin 2013); Nevertheless, Dallo and Wang (2016) proposed a boundary threshold to modify this value to \({d}_{0}={2.75D}_{85}^{f}\) after analyzing a database of 32 tests where the prediction of Kovacs model resulted wrong in four cases among 32. So, the actual threshold margin will need to be adjusted. Exploring suffusion tests performed by Maroof et al. (2021b) and new experimental tests, the upper boundary was shifted to \({d}_{0}={2.8D}_{85}^{f}\) \({\mathrm{d}}_{{0}} { = 2}{\mathrm{.8D}}_{85}^{{\mathrm{f}}}\). The \({\mathrm{d}}_{{0}} { = 2}{\mathrm{.3D}}_{85}^{{\mathrm{f}}}\) is a margin for internal stable soils, and the zone between \({d}_{0}={2.3D}_{85}^{f}\) and \({d}_{0}={2.8D}_{85}^{f}\) is specified as the transient zone. The flowchart assessing the modified model is depicted in Fig. 3. This model incorporates the effective grain size distribution and porosity to the mean pore size, through specific surface area, and the shape factor.

Fig. 3
figure 3

The flowchart assessing the modified capillary tube model

Full size image

The results are given in Fig. 4 and Table 5, including the results derived from experiments performed by Maroof et al. (2021b) and current experiments. The transient zone was suggested because besides the parameters considered in capillary tube models, other factors such as hydrodynamical conditions (hydraulic gradient and seepage flow) and stress conditions (Zhang et al. 2023) also affect internal stability/instability which is usually ignored in geometrical criteria.

Fig. 4
figure 4

The proposed and modified boundary threshold of the capillary tube model

Full size image
Table 5 Summary results of permeameter tests and internal instability assessment using proposed criteria and developed capillary tube mode
Full size table

Verification of the model

The most common geometrical criteria are a function of particle size distribution depending on the shape or slope of the PSD curve (Kezdi 1979; Kenney and Lau 1985; Li and Fannin 2008; Chang and Zhang 2013; Chapuis 2021). In addition to grain size distribution, it is necessary to take into account other factors such as particle shape and density for internal instability assessment.

The current and previous experimental works exhibited that soils with different grain shapes have various levels of internal stability/instability. The angular/low sphericity particles with rough textures are more resistant to suffusion, and these criteria are more conservative for grains with low sphericity, angular particles, or particles with a rough texture (Maroof et al. 2021a). These results showed that soils with the same grain size distribution but different particle shapes exhibit different levels of suffusion susceptibility. As a result, when common geometrical criteria are applied to soil samples with various grain shapes and densities, they have inaccurate predictions.

Previous databases of soil and glass bead samples are presented in Li (2008), Li and Fannin (2013), and Dallo and Wang (2016). Summary results of new and past laboratory permeameter tests (Hassani 2020; Maroof et al. 2021a) and internal instability assessment using proposed criteria and improved capillary tube model are revealed in Table 5.

In this model, particle shape was considered with the shape coefficient. By employing an appropriate shape factor, this model estimates the internal instability of soil with reasonable accuracy. Li and Fannin and Dallo and Wang assumed soil samples sub-angular to angular soils (shape factor = 8); by employing precise shape factor with the Li and Fannin boundary, the results of the internal stability were assessed (Table 5).

This correlation is developed by considering the porosity and grain shape in the formulation of the capillary tube model. Nevertheless, this model originally connects the SSA of the particles with the SSA of a capillary tube and compares its pores with the size of the loose fine grains. The constrictions have a surface in common with the passed grains, when two or more particles enter a pore where the cross-section of the pores is much more than that of a throat. Therefore, modeling distributions of both constriction and pores with a bundle of capillary tubes is more simplified as compared to realistic models. This modified model solved this problem by moving the boundaries of the Kovacs model. Nevertheless, other factors such as porosity variation, hydrodynamic conditions, fluid properties, and applied stress changed pore constriction and particle transport, and the transient zone enables consideration of them by more detailed experimental investigation.

Conclusions

The boundary between internal stable and unstable soils can be conveyed by pore diameter and loose fine particle comparison. The capillary tube model considers particle shape and porosity as well as particle gradation and may be favored in engineering practice. By the way, this model has been rarely validated based on experimental data, and it has not been commonly used.

In the current study, using the previous database of 42 permeameter tests, exploring new data, including 26 data, the validity of the proposed capillary tube models was examined. Furthermore, 10 new suffusion tests with different particle shapes, on the boundary threshold of Kenny and Lau’s criteria, were performed.

The experimental test showed that as particle sphericity, roundness, and smoothness increase, the particle migration in the coarser skeleton facilitates and promotes the internal instability of the soil matrix.

Additionally, based on experimental data, the capillary tube model was developed and enhanced for practical applications. New margins to internal instability have been established as \({d}_{0}={2.3d}_{85}^{f}\) and \({d}_{0}={2.8d}_{85}^{f}\). These threshold boundaries classified soil samples as internally stable, transient zone, or unstable.

The proposed boundaries were found to be reasonably accurate when compared to experimental results. A few wrong predictions were fixed in the safe boundaries, while only one internally unstable soil was predicted to be internally stable.