1 Introduction

Granular soils are commonly encountered in a variety of geotechnical and geoenvironmental engineering applications. It has long been recognized that water and gas transport through the soil skeleton is mainly controlled by pore characteristics (e.g., pore geometry, topology and spatial variability) [4, 14, 24, 40, 60]. Due to the difficulty in detecting and characterizing the microstructural features of granular assemblies by experiments, pore-scale numerical techniques are normally applied to facilitate the understanding of how pore structures can affect the flow properties of granular soils. The pore-scale simulations are dominated by particle-based methods, including the lattice Boltzmann method [32], the immersed boundary method [50], computational fluid dynamics and discrete element method coupling [26, 27], and smooth particle hydrodynamics [63]. However, these methods are usually computationally expensive, and only very limited pore volumes can be addressed. The pore network model (PNM), which can simulate fluid and solute transport processes on a pore-to-pore basis, has drawn much attention for its capacity to incorporate more heterogeneity in modeling larger volumes due to the inherent simplifications of pore spaces [8, 18, 22, 23, 44]. This pore-based approach has been used to upscale a wide range of pore-scale phenomena, including capillarity, displacement, phase exchange, and contaminant transport [9, 36, 54, 56].

The PNM represents the realistic pore space in a porous medium by a network of interconnected pore bodies and pore throats with parameterized geometries. A key focus of using the PNM for simulating multiple processes is the choice of the geometry and topology of pore bodies and pore throats. Many studies have used idealized pore networks to provide insights into macroscopic transport properties through granular soils by varying pore geometry and connectivity parameters [3, 19, 48]. These parameters are usually obtained by judicious estimations, as they are hardly accessible via experiments. For example, the log-normal, normal and uniform distributed pore size distributions and simple cubic, body-centered cubic, and face-centered cubic lattice types have been extensively used to investigate the effects of pore size heterogeneity and pore topology on flow properties, respectively  [15, 28, 34, 53]. Note that the pore networks are closely related to particle geometric features (e.g., particle size, shape and gradation) in natural granular soils. However, these aforementioned idealized pore networks do not necessarily preserve the geometry and spatial allocation of the solid particles and corresponding void spaces. The construction of pore networks directly from solid matrices is therefore required to ensure physical representation.

A process-based approach was pioneered by Bryant et al. [10] and later extended by Øren and Bakke [42] to relate pore structures with granular packings, but this approach can only simulate the geological process for consolidated media and is mostly applied to spherical particles. The discrete element method (DEM) can generate granular soil samples subjected to complex mechanical and geological processes. The soil particles in DEM simulations are idealized entities with spherical or non-spherical shapes [1, 13, 33]. Chareyre et al. and Yuan et al. presented preliminary studies on extracting the pore geometry and simulating the drainage process in DEM samples based on a regular triangulation method [11, 58]. This method divides the pore space into tetrahedrons, with each tetrahedron serving as a pore unit. At present, this method has been successfully implemented into the YADE-DEM. On a basis of this method, Mahmoodlu et al. [37, 38] investigated the effect of compaction and mixing on the pore structure and unsaturated hydraulic properties of uniform and layered sands. However, the regular triangulation method is currently limited to extracting the pore information of sphere packings. The maximal ball method distinguishes between the pore spaces and solid matrices based on digital images of porous media. It characterizes the pore structure by establishing the geometries, volumes and connectivity of pore bodies and pore throats from discrete voxels [46, 47]. Compared with the regular triangulation method, the maximal ball method employs a more explicit pore characterization algorithm, and could be applied to extract the pore formation from samples with more irregular particle arrangements and shapes. Currently, it has been validated by experimental and numerical data, and widely applied in petroleum engineering to extract topologically equivalent pore networks from micro-X-ray computerized tomography images of sand and rock samples [6, 17]. It is desirable to derive pore networks from the imaged DEM soil samples using the maximal ball method and thus establish the relationship between the particle geometric features and the pore characteristics. Subsequently, the extracted pore networks can be used as the input to PNM codes for fast predictions of single and multiphase flow properties such as the water retention curve, which is identified as an indicator of unsaturated flow behavior.

This study aims to investigate the effect of particle gradation and geometry on the pore characteristics and the water retention curves of granular soils using the combined techniques of the DEM and PNM. Two classes of soil specimens with various uniformity coefficients and aspect ratios of particles are generated by three-dimensional (3-D) DEM simulations. The pore networks of these specimens are constructed using the maximal ball method for further analysis of pore characteristics and water retention curves. The results bridge the relationship between the particle geometric features and physically representative pore structures and enhance the fundamental understanding of unsaturated flow properties from the perspective of pore structures.

2 Methodology

2.1 Discrete element method

All the DEM implementations in this study are performed using the open-source DEM code YADE [30]. In DEM simulations, the interaction force Fi between two contacted particles A and B is decomposed into a normal force \({{\varvec{F}}_n}\) and a tangential force \({{\varvec{F}}_s}\), shown as:

$${{\varvec{F}}_n} = {K_n}{U_n}{\varvec{n}},$$
(1)
$${{\varvec{F}}_s}{\text{ = }}{{\varvec{F}}_{s,prev}}+{K_s}\Delta {{\varvec{U}}_s},$$
(2)

where Kn and Ks are the normal and tangential stiffnesses, respectively, Un is the overlap between particles A and B in contact, \({\varvec{n}}\) is the normal contact vector, \(\Delta {{\varvec{U}}_s}\) is the incremental tangential displacement, and \({{\varvec{F}}_{s,prev}}\) is the tangential force from the previous iteration. The tangential contact force is truncated if its absolute value is larger than the maximum value given by Mohr–Coulomb criterion: Fs ≤ Fntanφ, where φ is the internal friction angle.

The stiffness parameters are calculated by:

$${K_n} = {E_c}\frac{{2{R_A}{R_B}}}{{{R_A}+{R_B}}}{\text{ and }}{K_s} = {E_c}{\nu _c}\frac{{2{R_A}{R_B}}}{{{R_A}+{R_B}}},$$
(3)

where Ec and νc are the Young’s modulus and Poisson’s ratio of the particle contact, respectively, and RA and RB are the particle radii of particles A and B, respectively.

The translational and rotational motions of each particle are governed by Newton’s second law of motion as given by:

$$\frac{{d{\varvec{x}}}}{{dt}} = \frac{{\sum {\left( {{{\varvec{F}}_n}+{{\varvec{F}}_s}} \right)} }}{m},$$
(4)
$$\frac{{d\varvec{\omega}}}{{dt}} = \frac{{\sum {\varvec{M}} }}{I},$$
(5)

where \({\varvec{x}}\) and \(\varvec{\omega}\) are the translational and angular velocities of the considered particle, respectively; \({\varvec{M}}\) is the torque acting on the particle by its neighboring particles or the walls; and m and I are the mass and moment of inertia of the particle, respectively.

YADE uses artificial numerical damping to dissipate the kinetic energy of particles and stabilize the computational system. More detailed information about the artificial numerical damping could be found in Šmilauer and Chareyre [49].

To simulate the complex particle shape of granular soils, the multisphere (MS) model is used to generate elliptical particles [39]. The aspect ratio (AR = a/b), defined as the ratio between the major and minor half-lengths of the elongation axes (i.e., a and b, see Fig. 1), is selected to characterize the elongation of particles. The MS model defines an elliptical particle by an arbitrary number of inscribed spheres. The construction of the MS particles relies on the determination of the locations and radii of subspheres. The radius of the smallest subsphere Rn is first defined as:

Fig. 1
figure 1

Sectional geometry of a quarter ellipsoid for the multisphere (MS) model

Full size image
$${R_{min}}={R_n}=\frac{{{b^2}}}{a}.$$
(6)

Thereafter, the location of the smallest subsphere xn is determined as:

$${x_n}=a - {R_n}=a - \frac{{{b^2}}}{a}.$$
(7)

Based on the assumption that subsphere distances vary proportionally to the ellipsoid shape, the following equation can be obtained:

$$\frac{{{y_{i - 1}}\left( {{x_{i - 1}}} \right)}}{{{d_i}}}=\frac{{{y_i}\left( {{x_i}} \right)}}{{{d_{i{\text{+1}}}}}}.$$
(8)

Substituting Eq. (8) into Eq. (7) yields the following nonlinear equation:

$${d_1}+\sum\limits_{{i=2}}^{n} {{d_i}\left( {{d_1}} \right)} =a - \frac{{{b^2}}}{a}.$$
(9)

Finally, the locations of the other subspheres can be obtained by solving Eq. (9) numerically, and their radii can be easily calculated based on the principle that the subspheres are tangent to the ellipsoidal surface.

Elliptical particles consisting of subspheres with varying AR values can be generated by creating clumped particles in YADE. The equivalent radius of an individual particle clump is defined as the radius of a spherical particle with the same volume. Clump members behave as stand-alone particles during simulation for purposes of collision detection and contact resolution, except that they have no contacts created among themselves within one clump. Thus, the stiffness parameters Kn and Ks of clump members are also calculated by Eq. (3). The force Fc and torque Mc acting on a clump are given by:

$${{\varvec{F}}_c} = \sum {{{\varvec{F}}_i}} ,$$
(10)
$${{\varvec{M}}_c} = \sum {{{\varvec{F}}_i} \times {r_i}+} {{\varvec{M}}_i},$$
(11)

where Fi and Mi are the force and torque acting on each clump member, and ri is the relative position of each clump member with regard to the clump’s centroid.

2.2 Pore network model

The maximal ball algorithm developed by Dong [16] is adopted to extract topologically equivalent pore networks from the images of soil specimens generated by DEM simulations. Once a 3-D DEM sample is generated, the sample is discretized into a 3-D binary image consisting of voxels with a value of either 1 or 0, which represent solid particle or void space, respectively, using MATLAB. The maximal balls are voxel assemblies that must touch the particle surface, acting as the basic element in the maximal ball algorithm to define the void space and detect the pore connectivity. This algorithm firstly find maximal balls that are inscribed to the particle surface or the image boundary using a two-step searching method. The maximal balls that are subsets of others are then removed. Thereafter, clustering processes are applied to organize the maximal balls into pore–throat chains according to their sizes and ranks. In a general rule, pore bodies (i.e., pores, hereafter) are the largest spheres centered in the pore spaces of the soil images, and their diameters are defined as pore diameters. Pore throats (i.e., throats, hereafter) are composed of a series of small spheres connecting two pores, and the maximum diameters of the connecting spheres are defined as throat diameters. The irregularity in the geometries of real pores and throats is considered by introducing the dimensionless shape factor G, which is defined as the ratio between the cross-sectional area A and the square of perimeter P, i.e., G = A/P2 [41]. The maximal ball algorithm has been successfully used to extract pore networks from a wide variety of sphere packings and real rock samples [17, 35, 55]. More details about the maximal ball algorithm could be found in Dong and Blunt [17].

The drainage process of air invasion into a water-saturated network is simulated by the the PoreFlow code developed by Valvatne [51] to render the water retention curve, which represents the relationship between the water saturation and the capillary pressure. The PoreFlow is one of the most frequently used PNM codes and its effectiveness has been validated by previous studies [29, 45, 55]. Once the pore networks are extracted from the DEM samples using the maximal ball method, they can be directly input into the PoreFlow code. Then, fluid flow and solute transport under saturated and unsaturated conditions can be simulated using designated algorithms. During the simulations, the input data are translated to MATLAB for the purpose of analysis and postprocessing. After the simulations, the flow and transport properties through these input pore networks, such as intrinsic permeability, water retention curve and relative permeability could be predicted and output. The detailed workflow of the PoreFlow code is given in Raoof et al. [45]. During the drainage process, air will invade a water-filled pore or throat once the pressure difference between the air and water exceeds the capillary entry pressure Pc, which is obtained by calculating the force equilibrium acting on the air-water interface.

$${P_c}=\frac{{\sigma \cos {\theta _r}\left( {1+2\sqrt {\pi G} } \right)}}{r}{F_d}\left( {{\theta _r},G} \right),$$
(12)

where σ and θr are the air–water interfacial tension and contact angle, respectively; r is the radius of the pore or throat; and Fd is a function of the contact angle θr and shape factor G. For a circular pore or throat that has a shape factor of 1/4π, Eq. (12) is simplified into:

$${P_c}=\frac{{2\sigma \cos {\theta _r}}}{r}.$$
(13)

Low air pressure is assigned to the bottom of the extracted pore network to produce the drainage process. The top of the pore network serves as the outlet boundary, and four other surfaces serve as isolated peripheral boundaries. By increasing the air pressure in small increments, the drainage process continues until all the pores and throats are invaded by air. In this study, the air-water interfacial tension is σ = 0.072 N/m, and the contact angle is assumed to be θr = 45°.

3 Simulation details

The numerical procedure in this study includes four consecutive steps: particle insertion, compression, pore network extraction, and pore network modeling for water retention curves. Initially, a random cloud of particles with designated particle size distribution is generated in a rectangular box. As the box width is normally set to be 10–20 times the maximum particle diameter to exclude the potential inhomogeneity in particle packings [21, 26, 57, 61], this study adopts a cubical box of 30 mm × 30 mm × 30 mm to make the box width of 15 times the maximum particle diameter (Dmax = 20 mm). Then, the particle cloud is isotropically compressed to the desired mean effective stress p′ = 10 kPa using a servo-control algorithm. The 10-kPa effective stress is selected to reflect the self-weight conditions for shallow soils. For example, the soils used in landfill covers usually have self-weight effective stresses in a range of 0–30 kPa as most landfill covers are 1.0–2.0 m in thickness [5, 7, 59]. After compression, the sample is then translated to a 3-D array image to serve as the input for subsequent pore extraction. Next, the maximal ball method is utilized to extract the pore network of the sample. Finally, the PoreFlow code is performed to render the water retention curve, which characterizes the unsaturated hydraulic properties.

3.1 Determination of the representative element volume

The representative element volume (REV) is normally intercepted from the interior of the compressed samples to eliminate boundary effects. The side length of the REV should be larger than 5.15 times the maximum particle diameter, as recommended by Clausnitzer and Hopmans [12]. Taking the mono-sized soil specimen as an example, the following illustrates how we determine the REV. First, a compressed soil sample consisting of 14,000 spherical particles of the same diameter D = 1.0 mm is formed under p′ = 10 kPa. To ensure static equilibrium after compression, the unbalanced force ratio needs to be less than 0.001 based on the recommendation of Kuhn et al. [31]. The detailed input parameters are summarized in Table 1. The overlaps within the compressed sample are examined, and it is found the overlaps present a unimodal distribution. The ratio of the overlap over the particle radius (S/R) at the peak is smaller than 1/1000, and the maximum S/R is smaller than 1/100 (see Fig. 2), indicating that the numerical stability in terms of the overlap can be ensured. After compression, the particles are assembled in a domain of 23 mm × 23 mm × 23 mm. The porosity profiles along the three orthogonal directions in the domain are shown in Fig. 3. It is observed that the central cubic portion of 15 mm × 15 mm × 15 mm is free from the boundary effects. The requirement that the size length exceeds 5.15 times the particle diameter can be satisfied as well. It is also found that the boundary effects on porosity decrease as the uniformity coefficient of particle sizes increases; however, we do not show it here with specific figures to save space. Moreover, we performed three random runs on two mono-sized particle packings (D = 1.0 mm) with extreme shapes used in this study (AR = 1.0 and 2.5) to examine the effect of the particle initialization on the pore structure of REV. By comparing the pore information obtained from these compressed samples, it is confirmed that the cubical domain of 30 mm × 30 mm × 30 mm can ensure the reproducibility of the simulation results. Hence, all the soil samples in this study are compressed to have a desired size length close to 23 mm by adjusting the number of particles, and the REVs are obtained by intercepting the central cubic portions with size lengths of 15 mm from the compressed samples. The obtained REVs are then segmented into 3-D array images consisting of 500 × 500 × 500 voxels for subsequent pore network extraction and modeling, with each voxel in a volume of 0.03 mm × 0.03 mm × 0.03 mm.

Fig. 2
figure 2

S/R distribution within a mono-sized sphere packing (D = 1.0 mm, Ec = 7 × 104 kPa)

Full size image
Fig. 3
figure 3

Porosity profiles along the three orthogonal directions in a cubical domain

Full size image
Table 1 Input DEM parameters used in the determination of the REV
Full size table

3.2 Validation of the pore network extracted from the DEM sample

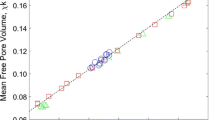
Jiang et al. [29] prepared a packed sample of spherical glass beads with D = 1.0 mm in the laboratory (the porosity of the sample was ~ 0.40) and extracted the pore network of the sample using Dong’s [16] maximal ball method. To validate the pore network extracted from the DEM sample, a sample of glass beads with D = 1.0 mm was first generated in DEM simulations. The DEM sample was then compressed to the same porosity as that of the experimental glass bead sample. The physical parameters of the glass beads in the DEM simulations are shown in Table 2. A comparison of the pore networks extracted from the experimental and DEM samples in terms of the pore geometry and connectivity parameters (including pore diameters, throat diameters, pore spacings, and coordination numbers) is shown in Fig. 4. Figure 4 indicates that good agreement is obtained between the statistical sizes of the pore geometry and connectivity parameters of the networks extracted from the experimental and the DEM samples. Therefore, the DEM simulations are believed to be suitable for representing real particle packings and will be used in this study to generate representative granular samples for pore network extraction and modeling.

Fig. 4
figure 4

Comparison of the pore networks extracted from the experimental and DEM samples in terms of the pore geometry and connectivity parameters: a pore diameter distributions; b throat diameter distributions; c pore spacing distributions; and d coordination number distributions

Full size image
Table 2 Physical parameters of the glass beads in the DEM simulations
Full size table

3.3 Model setup

For the numerical DEM samples used in this study, the Kosugi-type particle size distribution is adopted to replicate real sand gradations [25]. To assess the effect of particle gradation on the pore characteristics and the water retention curves, six particle size distributions with the same average particle diameter D50 = 1.0 mm are investigated in this study, as shown in Fig. 5.

Fig. 5
figure 5

Particle size distributions of the soil samples of spherical particles

Full size image
$$\frac{{f\left( D \right)}}{{100}}=\frac{1}{2}\text {erfc}\left( {\frac{{{D_{50}} - D}}{{\sqrt {2\sigma^*} }}} \right),$$
(14)

where f(D) is the cumulative mass fraction less than diameter D and σ* is a parameter representing the width of the particle size distribution. Additionally, the uniformity coefficient Cu = D60/D10 is used to characterize the particle size distribution. As Cu increases, more particles will be needed when constructing the soil sample to guarantee the size of the REV. The gradation parameters of the particle size distributions used in this study are listed in Table 3.

Table 3 Gradation parameters of the particle size distributions
Full size table

A group of mono-sized elliptical particle assemblies with different AR values ranging from 1.00 to 2.50 are created to investigate the effect of particle geometry. Each assembly consists of 14,000 particles with a designated equivalent diameter of 1.0 mm. The purely geometric effect of the MS approximation may be evaluated by comparing the approximated MS volume with that of the smooth ellipsoid. The volume difference is maintained lower than 5% when determining the numbers of the subspheres to reduce the purely geometric effect. As a consequence, five subspheres are needed for the particles with 1.00 < AR ≤ 1.50, seven subspheres are needed for the particles with 1.50 < AR ≤ 2.00, and nine subspheres are needed for the particles with 2.00 < AR ≤ 2.50. The perpendicular distance from any point on the MS approximation surface to the smooth ellipsoid surface is found to be smaller than 1.50 voxel lengths. The roughness on the MS approximation surface is filtered by employing an exclusion length of 1.75 voxels when extracting the pore networks [43]. Several representative elliptical particles and relevant parameters are shown in Table 4. The other input parameters in the DEM simulations of the particle insertion and compression are the same as those in Table 1.

Table 4 Geometric parameters of elliptical particles
Full size table

4 Results and discussion

4.1 Porosity

Figure 6a, b shows the particle assemblies and extracted pore networks of the compressed soil samples with three different uniformity coefficients Cu = 1.12, 1.47 and 2.16. The relationship between the porosity and Cu is presented in Fig. 6c. It is observed that the porosity decreases as Cu increases. This is reasonable because more small particles can fill the voids among large particles for the specimen with a larger Cu, as shown by the partial cross sections of the samples in Fig. 6c. The porosity decreases from ~ 0.38 to ~ 0.31 as Cu increases from 1.00 to 2.16.

Fig. 6
figure 6

Effect of the uniformity coefficient Cu of particle size distributions on the porosity of soil samples: a particle assemblies, in which the magnitude of particle diameter is identified by different colors; b extracted pore networks using the maximal ball method, in which the pores and throats are depicted in red and cyan, respectively; and c relationship between the porosity and Cu (color figure online)

Full size image

The particle assemblies and extracted pore networks of the compressed soil samples with three different aspect ratios AR = 1.00, 1.75 and 2.50 are shown in Fig. 7a, b, respectively. The variation in the porosity of the soil sample with AR is plotted in Fig. 7c. Figure 7c indicates an interesting phenomenon in which the porosity first decreases and then increases with increasing AR. The minimum porosity is observed at AR = 1.75, representing the most efficient packing. Similar behaviors have also been found in other DEM simulations of ellipsoidal and spherocylindrical particles with slight differences in the values of the minimum porosity and corresponding AR [2, 20, 62]. The axial asymmetry of an elliptical particle enables it to have extra degrees of freedom compared with that of a spherical particle (i.e., AR = 1.00). As AR increases, the degrees of freedom of the particles become more significant. This promotes a more efficient occupation of some irregular gaps among particles by the particle tips and thus reduces the porosity, as identified from the partial cross sections in Fig. 7c. However, once the AR value exceeds 1.75, the steric effects of particle arrangements become more significant and thus enlarge the volume of the interstices, leading to an increase in the porosity. Eventually, the competing effects of these two factors lead to the nonmonotonic variation in the porosity with AR [2].

Fig. 7
figure 7

Effect of the aspect ratio AR of particles on the porosity of soil samples: a particle assemblies; b extracted pore networks using the maximal ball method, in which the pores and throats are depicted in red and cyan, respectively; and c relationship between the porosity and AR (color figure online)

Full size image

4.2 Pore geometry and connectivity

Figures 8a−c shows the statistical sizes of pore geometries, including pore diameters, throat diameters, and pore spacings of the soil samples with different Cu. It is observed that, in general, a larger Cu results in reduced mean values of pore diameters, throat diameters and pore spacings. Figure 8a indicates that the pore diameters exhibit a bimodal distribution for the soil with more uniform particles (i.e., a lower Cu). For instance, the pore diameter distribution of the soil with Cu = 1.12 presents the first and second peaks at pore diameters of 0.28 and 0.44 mm, respectively. Owing to the spatial variabilities of particle arrangement and contacts, the pore diameters of compressed samples present non-uniform distributions. It is deduced that a large pore series and a small pore series can be formed in the soils with a lower Cu (see the illustrated cross sections at Cu = 1.12 in Fig. 6c and at AR = 1.0 in Fig. 7c), and thus lead to a bimodal pore diameter distribution. With the increase in Cu, the pore diameters gradually change from a bimodal to a unimodal distribution due to the occupation of large pore spaces by smaller particles. In addition, the more efficient filling of larger voids reduces the mean value and the distribution range (broadness) of the pore diameters, which is in agreement with the variation in the porosity with Cu in Fig. 6. The inset of Fig. 8a indicates that the mean pore diameter µp can decrease from ~ 0.36 to ~ 0.22 mm as Cu increases from 1.00 to 2.16. The maximum mean pore diameter is ~ 0.36 mm, which is smaller than that of the mean particle diameter D50 = 1.0 mm. The mean pore diameters µp for all specimens are larger than the mean throat diameters µt, with the pore–throat diameter ratio being approximately 2.0. The mean pore spacing is much higher than those of the mean pore and throat diameters and is comparable to the mean particle diameter when Cu ≤ 1.47 (see the inset of Fig. 8c). Figure 8d shows the coordination number (cn) distributions of the soil samples with various Cu values. The coordination number is defined as the number of independent throats linked to a pore and has been widely used to characterize pore connectivity. Figure 8d shows that a larger coordination number is caused by a larger Cu within the investigation range, suggesting that the occupation of voids by small particles contributes to increasing the pore connectivity. All the coordination numbers of the soil samples present typical unimodal distributions with peak values at cn = 5.0–6.0. The mean coordination numbers of all the soil samples vary in a range of 7.7–8.2. Similar results were also reported in Jiang et al. [29] by analyzing the coordination numbers of packings of spherical glass beads with various diameters. Note that the mean coordination numbers of granular soils are much larger than those of rocks; for instance, the mean cn values of the Berea and Fontainebleau sandstones mainly range between 3 and 4 [16]. The lower mean coordination numbers of rocks are mainly attributed to the enhanced connection between particles resulting from complex geological processes such as quartz cementation. It appears that the enhanced connection has the capacity to block part of the pore spaces between particles and thus reduce the pore connectivity, which is different from the mechanism of void occupation by individual small particles in granular soils.

Fig. 8
figure 8

Statistical sizes of pore geometry and connectivity of the soil samples with various Cu values (D50 = 1.0 mm). The inset of each figure shows the variation in the mean value with Cu: a pore diameter distributions; b throat diameter distributions; c pore spacing distributions; and d coordination number distributions

Full size image

Figure 9a shows the pore diameter distributions of the samples with various AR values. The increase in AR can change the pore diameters from a bimodal to a unimodal distribution. The variation in the mean pore diameter with AR is consistent with the variation between the porosity and AR (see Fig. 7). The mean pore diameter continues decreasing as AR increases until the most efficient packing is achieved at AR = 1.75 and then presents an increasing trend due to steric effects. However, this is not the case for the mean throat diameter, as it dramatically decreases as AR increases from 1.00 to 1.75 but varies insignificantly when AR exceeds 1.75. This suggests that steric effects are more likely to affect larger voids than smaller voids. The variation in the mean pore spacing with AR is in agreement with that of the mean pore diameter with AR (see Fig. 9c). In addition, the mean coordination number shows a nonmonotonic variation as AR increases with its minimum (µcn = 7.1) at AR = 1.25 and maximum (i.e., µcn = 8.3) at AR = 2.50. The decrease in coordination number is related to the occupation of voids by ellipsoid particle tips that have high degrees of freedom. This also illustrates the difference in the mechanism of occupying voids by ellipsoid particle tips and individual spherical particles, as the latter case increases the pore connectivity, as shown in Fig. 8d. With the further increase in the occupation of void spaces, some of the void spaces may be converted from pores to throats, thus leading to an increase in the coordination number. This can also explain why the minimum coordination number is observed prior to the occurrence of the most efficient packing at AR = 1.75.

Fig. 9
figure 9

Statistical sizes of pore geometry and connectivity of the soil samples with various AR values (D50 = 1.0 mm). The inset of each figure shows the variation in the mean value with AR: a pore diameter distributions; b throat diameter distributions; c pore spacing distributions; and d coordination number distributions

Full size image

The relationships between the standard deviations and mean values of the pore geometry and connectivity parameters of all samples are plotted in Fig. 10. Affected by the Cu, the standard deviations of these parameters correlate linearly with the corresponding mean values. Larger mean values can lead to higher standard deviations for the pore diameters, throat diameters and pore spacings but a lower standard deviation for the coordination numbers. The relationships between the standard deviations and mean values can be fitted well by the straight lines with the given expressions in Fig. 10. Among the three pore geometry parameters, the throat diameters and pore spacings have the largest and the smallest slopes of the fitting line, respectively. Moreover, the coefficients of variation (i.e., the ratio of the standard deviation over mean value, COV = σ/µ) of pore diameters, throat diameters, and pore spacings decrease as corresponding mean values decrease since the fitting lines have negative y-intercept values. Note that these linear correlations are only applicable to soils with Cu varying from 1.00 to 2.16. The negative y-intercept values suggest that more complicated correlations should be presented for the soils with Cu out of the investigation range based on the inherent nature that the standard deviation of any pore geometry parameter should be a positive value. Overall, the COV of pore and throat diameters, which are key parameters for characterizing pore size heterogeneity, vary in ranges of 0.22–0.31 and 0.34–0.42, respectively, for soils with various Cu. Affected by the AR, different correlations between the standard deviations and mean values of the pore geometry parameters are observed before and after the samples reach the most efficient packing. For the pore diameters, the standard deviation decreases as the mean value decreases for each correlation. However, this is not the case for the throat diameters. Before reaching the most efficient packing, a smaller mean value results in a smaller standard deviation as well. After reaching the most efficient packing, the mean value of throat diameters remains almost constant, but the standard deviation shows a further increase. The COV of the pore and throat diameters vary in ranges of 0.26–0.31 and 0.40–0.48, respectively, for soils with various AR values. For the pore spacings, the standard deviation increases as the mean value increases for each correlation, but a lower standard deviation corresponds to a given mean pore spacing after the sample reaches the most efficient packing (see Fig. 10b). Two distinct correlations between the standard deviation and mean value are also found for the coordination numbers, but the intersection of the two correlations corresponds to the occurrence of the minimum coordination number rather than the most efficient packing. For each correlation, in general, a larger mean value results in a larger standard deviation, as shown in Fig. 10c.

Fig. 10
figure 10

Standard deviation versus mean value for pore geometry and connectivity parameters of the soil samples with various Cu and AR: a pore and throat diameters; b pore spacings; and c coordination numbers

Full size image

4.3 Water retention curve

Drainage processes are employed to all the extracted pore networks to render the water retention curves. The computed data for the soil samples with representative Cu and AR values are shown in Fig. 11 and are fitted to the van Genuchten equation [52] using the least square method. The van Genuchten equation is one of the most commonly used equations to describe the water retention curve of soils as given by:

Fig. 11
figure 11

Water retention curves of the soil samples: a effects of Cu (Cu = 1.12, 1.47, and 2.16); and b effects of AR (AR = 1.00, 1.75, and 2.50)

Full size image
$${P_c}={P_0}{\left[ {{{\left( {\frac{{{S_w} - {S_{rw}}}}{{1 - {S_{rw}}}}} \right)}^{ - \frac{1}{m}}} - 1} \right]^{1 - m}},$$
(15)

where Pc and P0 are the capillary pressure and air entry value (AEV), respectively; Sw and Srw are the water saturation and residual water saturation, respectively; and m is a fitting parameter, and a lower m value represents that the water saturation varies more gradually as the capillary pressure varies.

Figure 11 indicates that the numerical data can be fitted well by the van Genuchten equation. The slight discrepancies may be related to the differences in the particle compositions, arrangements, shapes and contacts between the real soils and the artificial particle packings. Table 5 summarizes the best fitting parameters in the van Genuchten equation for the samples with various Cu and AR. The results indicate that the AEV, m, and Srw all depend on the Cu and AR. The effects of Cu and AR on Srw will not be discussed in this study, as Srw maintains low values of 0.6–4.0%.

Table 5 Best fitting parameters in the van Genuchten equation for the soil samples with various Cu and AR values
Full size table

The AEV increases as Cu increases, and the water saturation at a given capillary pressure also increases, as shown in Fig. 11a. This can be explained by the decreased pore sizes for the soil with a larger Cu according to Eqs. (12) and (13). Similarly, the AEV first increases and then decreases with increasing AR, which is in accordance with the development of pore sizes with AR. To further investigate the abovementioned phenomenon, the relationship between the AEV and the mean pore diameter is plotted in Fig. 12 considering that the pore volumes dominate the soil voids. Figure 12 indicates that the logarithm of AEV decreases linearly as the logarithm of mean pore diameter increases in response to variations in Cu or AR. Note that the linear correlation between the AEV and the mean pore diameter associated with the variation in AR has a steeper slope compared with that of the correlation affected by Cu. This also implies that the correlation between the AEV and the mean pore diameter is independent of the steric effects.

Fig. 12
figure 12

Logarithm of the air entry value versus the logarithm of the mean pore diameter

Full size image

A slight increase in the m value is found as Cu increases. The relationship between the m value and AR is nonmonotonic (see Table 5). The relationships between the COV of pore diameters and m values for all samples are shown in Fig. 13 to identify the influence of pore size variance on the m value. Figure 13 shows that, in terms of the effect of Cu, the m value decreases linearly as the COV of pore diameters increases, and their correlation can be captured by m = − 0.48COVp + 0.99. Based on this correlation, the sample with mono-sized pore diameters (i.e., COVp = 0) can give the largest m value, 0.99, which is approximated as the theoretical upper limit of 1.00. However, the linear correlation is not applicable for the case in which the pore diameter variance is affected by the AR. For soils with various AR values, the maximum m value is approximately observed in the soil with the most efficient packing. Compared with the soil prior to the most efficient packing, a smaller m value can be induced by the same COV for the soil beyond the most efficient packing.

Fig. 13
figure 13

Value of m versus the coefficient of variation of pore diameters

Full size image

5 Conclusions

This study presents a numerical procedure combining the DEM and PNM to relate the particle geometric features and physically representative pore structures, and rapidly predict the macroscopic flow properties of granular assemblies. This procedure is applied to investigate the effects of particle gradation and geometry on the pore characteristics and the water retention curves of granular soils under isotropic compression of effective stress p′ = 10 kPa. A series of DEM simulations are first performed to generate 3-D granular soil samples with various Cu and AR values. The pore networks are then extracted from the imaged DEM soil samples using the maximal ball method, and the corresponding porosities and pore characteristics are analyzed. Finally, the water retention curves of these soil samples are computed using the PNM. Based on the numerical results, the following conclusions can be drawn:

  1. 1.

    A larger Cu results in the more efficient occupation of voids by relatively smaller particles, leading to a reduced porosity. The increasing AR from 1.00 to 2.50 results in a nonmonotonic variation in porosity that first decreases and then increases. The minimum porosity occurs at AR = 1.75 when the soil reaches the most efficient packing.

  2. 2.

    The increase in Cu can change the pore diameters from a bimodal to a unimodal distribution, decrease the mean values of pore geometry parameters, including the pore diameters, throat diameters, and pore spacings, but increase the mean coordination number. Linear correlations between the standard deviations and mean values of these pore geometry and connectivity parameters are observed for soils with various Cu values.

  3. 3.

    The increase in AR can change the pore diameters from a bimodal to a unimodal distribution. The mean pore diameter, mean pore spacing, and mean coordination number first decrease and then increase in response to the variation in AR. The mean throat diameter decreases substantially as AR increases from 1.00 to 1.75 but presents insignificant variation once AR exceeds 1.75. Different correlations between the standard deviations and mean values of the pore geometry parameters before and after the soil reaches the most efficient packing are observed. Two distinct correlations between the standard deviation and mean value of the coordination numbers are also presented but with the intersection of the two correlations occurring at the minimum coordination number.

  4. 4.

    The logarithm of AEV decreases linearly as the logarithm of the mean pore diameter increases for both cases in which the pore diameters are affected by Cu and AR. In terms of the effect of Cu, the best fitting parameter m in the van Genuchten equation for water retention curves decreases linearly as the COV of pore diameters increases, and their correlation can be described by m = − 0.48COVp + 0.99. However, the linear correlation is not applicable for the case with varying AR values. A smaller m value can be induced at the same COV for the soil beyond the most efficient packing compared with that prior to the most efficient packing.

The numerical procedure developed in this study can be easily adopted to simulate more sophisticated particle size and shape scenarios, such as soil specimens consisting of graded particles with various AR values. The regular particle shapes of spheres and ellipsoids are considered in this study. Further extensions of the numerical procedure involving more realistic particle shapes will have great significance. In addition, how particle geometric features affect preferential flows and relative permeability in granular soils is also of interest for further research.