Propagation of semi-infinite crack in an initially stressed dry sandy medium impacted by shear wave

Abstract

This study deals with the propagation of a semi-infinite crack influenced by SH-wave propagation in an initially stressed dry sandy (ISDS) strip. The Fourier integral transforms (FIT) and Wiener–Hopf (WH) approach are used to solve the model analytically. For the cases of concentrated force of constant intensity (CF) and constant load (CL), the stress intensity factor (SIF) is calculated. The effects of sandiness, crack speed/length, and initial stress on the SIF in ISDS strip are numerically elucidated and graphically demonstrated. Comparison of the SIF analysed for differently configured strips influenced by distinct cases of initial stresses is one of the novel features of this study.

1 Introduction

Cracks forming in elastic material, which is perhaps one of the reasons of engineering structural failures, are a common occurrence in the real world. Any engineering structure that cracks is a serious concern that should be taken into account, while designing such systems. To ensure added safety, it is necessary to prevent crack formation as well as nucleation in such structures, if at all possible. Composite materials are gaining rapid popularity due to their numerous uses in mining, structural, mechanical/civil, manufacturing, design engineering, as well as hydrology and geophysics. Crack propagation in engineered materials under alternating or monotonic loads is an essential field of research considering composite materials. Many engineers and scientists have studied the problems related to fracture in elastic media and found the SIF for analysing the strength, stability, rigidity, and safety of constructed structures. Koiter [1] studied the concept of approximate solutions of WH type equations with applications. The role of the WH-technique in dynamic elasticity was discussed by Abrahams [2]. The propagation of wave in an elastic solid with a line of discontinuity or finite crack has been calculated by Sih and Loeber [3]. The propagation of crack subjected to general loading conditions in an elastic solid has been studied by Freund [4], and the concept related to the propagation of wave in elastic solids has been studied by Achenbach [5]. Achenbach et al. [6] found that near a crack tip, the elastodynamic stress field is quickly propagating along with the interface between two dissimilar isotropic elastic solids. The interfacial crack propagation in anisotropic half-space was examined by Karim and Kundu [7]. Ing and Ma [8] investigated the transient impact on the incident shear wave on finite length crack in an unbounded elastic solid. Furthermore, the seismic wave propagation in a porous medium with crack was examined by Pointer et al. [9]. Ing and Ma [10] analysed the dynamic fracture for finite cracks in anisotropic solids due to SH waves. Radi and Mariano [11] examined the dynamic steady‐state crack propagation in quasi‐crystals. The expression of dynamic SIF of multiple cracks in a functionally graded orthotropic half-plane was established by Monfared and Ayatollahi [12]. Under a time-harmonic elastic P-wave, Liu et al. [13] examined the dynamic SIFs of two 3D rectangular cracks in a transversely isotropic elastic material. Wu et al. [14] discussed the transference of multiple parallel cracks in elastic media with anti-plane loading. Singh et al. [15] investigated the effects of porosity, initial stresses, and anisotropy on the transference of crack in a poroelastic media due to a Love wave and derived the mathematical expression of SIF for the case of constant concentrated force. An analytical solution for the transference of interfacial crack in two different transversely isotropic layers was obtained by Yadav et al. [16]. Shear wave propagation due to semi-infinite crack in a dissimilar dry sandy elastic medium under different loading conditions was studied by Singh et al. [17]. Bagheri and Monfared [18] studied the in-plane transient behaviour of two different heterogeneous half-planes with multiple contact cracks. The propagation of SH-wave due to semi-infinite crack in distinct poroelastic strips has been discussed by Negi et al. [19]. Singh and Singh [20] studied the crack propagation in a pre-stressed orthotropic strip with functional gradedness. Oda et al. [21] discussed the thermal SIF of an edge interface crack under arbitrary material combination considering double singular stress fields before and after cracking. The dynamic analysis of interfacial multiple cracks in piezoelectric thin film/substrate was examined by Zhang et al. [22].

Seismology is the discipline of elastic (seismic) waves, which explains how waves propagate through the earth’s interior and how they are executed as earthquakes or explosions. Seismologists are interested in the theory of elastic surface waves in a dry sandy medium, because of its practical uses in geophysical prospecting. Seismic waves are used to study the Earth’s internal structure. The Earth is a complicated natural system that contains a variety of rocks and materials with fascinating properties like sandiness, inhomogeneity, anisotropy, and initial stress, among others. Dry sandy material is widely employed in the construction of bridges, buildings, and other structures. Sandiness of the crustal layers of Earth is an important feature that cannot be overlooked, while modelling geological problems. As a result, both elasticity and sandiness should be taken into account. The layers of the soil in the earth are assumed to be sandier as compared to elastic. A dry sandy layer is a layer consisting of sandy particles which retain no water vapours or moisture. Dey et al. [23, 24] analysed torsional surface waves moving in a dry sandy media with gravity and initial stress. Tomar and Kaur [25] addressed the reflection and transmission problem caused by SH-wave between an anisotropic half-space and a dry sandy half-space. Kumar et al. [26] studied the impact of an impulsive source subjected to the transference of shear wave in a layered structure containing porous, dry sandy, and functionally graded components. Singh and Singh [27] discussed the idea of smooth moving punch in a dry sandy strip under initial stress influenced by shear wave. Analytical study on the transference of Griffith crack in a dry sandy strip due to punch pressure was explored by Singh and Singh [28].

Initial stresses may originate due to applied loads, gravity, atmospheric pressure, creep, or temperature differences. It is commonly recognised that the Earth is an initially stressed medium and that many different types of initial stress can occur within the Earth. Furthermore, the initial stresses have an impact on seismic wave propagation, which can be caused by either a man-made or natural process. As a result, it is vital to investigate the impact of initial stress on the transference of surface seismic waves. Qian et al. [29] discussed the transference of love waves in an initially stressed piezoelectric layered structure. Du et al. [30] investigated the Love wave propagation in layered magneto-electro-elastic structures with initial stress. The influence of initial stresses on guided waves in functionally graded hollow cylinders was examined by Yu and Zhang [31]. The effect of initial stresses and rotation on pyroelectric waves were studied by Yuan [32]. Shams [33] investigated the influence of initial stress on the propagation of Love wave at the boundary between a layer and a half-space. Mahanty et al. [34] studied the impact of initial stress, heterogeneity and anisotropy on the transference of seismic surface waves. Ejaz and Shams [35] explored the concept of Rayleigh wave propagation in compressible hyper elastic materials with initial stress. Said et al. [36] explored  the impact of initial stress and rotation on a nonlocal fibre-reinforced thermoelastic medium with a fractional derivative heat transfer. As per our knowledge, no attempt has been made yet for analysing the propagation characteristics of a crack in a dry sandy isotropic media under initial stress.

The present analysis deals with the propagation  of a semi-infinite crack impacted by the transference of SH-wave in ISDS strip for CF and CL cases. The WH-technique, FIT, Liouville’s, and Abel’s theorem have been implemented to find the expression of SIF. The noteworthy effect of the prevalent physical parameters, viz., crack speed and length, sandiness parameter and horizontal/vertical initial stresses on the SIF are shown through graphs. Further, the comparative study was made for the SIF for distinct values of the sandiness parameter and horizontal/vertical initial stresses, for propagating semi-infinite crack associated with propagating SH-wave in the considered strip.

2 Formulation of the problem

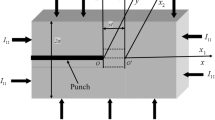
We consider an ISDS elastic strip that is weakened because of the presence of a semi-infinite crack $\left( {x \le 0} \right)$ as shown in Fig. 1. The Cartesian coordinate system is chosen such that the strip is shown as $- \infty < x < \infty ,\; - a \le z \le a$ and it is weakened at $z = 0$ by a crack $\left( {x \le 0} \right).$ The upper and lower surfaces $z = \pm a$ of the strip are assumed to be rigidly clamped. The horizontal and vertical initial stresses $\left( {I_{11} ,\,\,I_{33} } \right)$ act along the x and z-directions, respectively.

Fig. 1

Configuration of the problem

At first, we derive the equations of motion for propagating SH-wave in the undertaken medium. The constitutive equations for the dry sandy medium are as follows: (Mandi et al. [37])

$$\tau_{ij} = \lambda \delta_{ij} e_{kk} + 2\frac{\mu }{\eta }e_{ij} ,\quad \eta > 1,$$

(1)

where the notation $\tau_{ij}$ are the components of stress, $e_{ij}$ represents the strain components, $\lambda \,$ and $\mu$ are Lame’s constants, $\eta$ is dry sandy parameter and$\delta_{ij}$ is defined as Kronecker delta. In the absence of body forces, the governing equations in the considered strip following Biot [38] are as follows

$$\tau_{ij,j} + \frac{\partial }{{\partial x_{j} }}\left( {I_{jk} \hbar_{ik} + I_{ij} e - I_{ik} e_{kj} } \right) = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},$$

(2)

where $i,j,k = 1,2,3;$ $\hbar_{ij} = \frac{1}{2}\left( {u_{i,j} - u_{j,i} } \right);\;e = e_{ij} \delta_{ij}$ and $I_{ij}$ denotes the component of initial stresses, $\rho$ is the medium density, $t$ is the time, and $u_{i}$ denotes the displacement.

Characteristic of SH-wave (propagating in $x$-direction causing non-vanishing displacement in $y$-direction only) may be written in mathematical form in terms of displacement as

$$u = w = 0,\;v = v(x,z,t),$$

(3)

where $u,v,w$ denote the displacement components along $x,y,z$-directions, respectively.

In view of Eqs. (2), and (3), we obtain

$$\frac{{\partial \tau_{21} }}{\partial x} + \frac{{\partial \tau_{23} }}{\partial z} + \frac{{I_{11} }}{2}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{I_{33} }}{2}\frac{{\partial^{2} v}}{{\partial z^{2} }} = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }},$$

(4)

$${\text{where}}\;\tau_{21} = \frac{\mu }{\eta }\left( {\frac{\partial v}{{\partial x}}} \right)\;{\text{and}}\;\tau_{23} = \frac{\mu }{\eta }\left( {\frac{\partial v}{{\partial z}}} \right).$$

(5)

Equation (4) can be further be simplified as

$$R\frac{{\partial^{2} v}}{{\partial z^{2} }} + S\frac{{\partial^{2} v}}{{\partial x^{2} }} = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }},$$

(6)

$${\text{where}}\;R = \left( {\frac{\mu }{\eta } + \frac{{I_{33} }}{2}} \right)\text{and}\ S = \left( {\frac{\mu }{\eta } + \frac{{I_{11} }}{2}} \right).$$

(7)

The frame $\left( {x,y,z} \right)$ is replaced by the convective frame $\left( {x_{1} ,x_{2} ,x_{3} } \right)$ by employing Galilean transformation as

$$x = x_{1} + st,\;y = x_{2} ,\;z = x_{3} ,$$

(8)

where ‘$s$’ denotes the velocity of the motion of the system $\left( {x_{1} ,\,x_{2} ,\,x_{3} } \right).$

With aid of above Galilean transformation (8), Eq. (6) reduces to

$$R\frac{{\partial^{2} v}}{{\partial x_{3}^{2} }} + \left( {S - \rho s^{2} } \right)\frac{{\partial^{2} v}}{{\partial x_{1}^{2} }} = 0,$$

(9)

Also shear stress can be reduces as follows

$$\varphi \left( {x_{1} } \right) = R\frac{\partial v}{{\partial x_{3} }}.$$

(10)

3 Boundary conditions

The following are the boundary conditions of the proposed model:

$$\left. {\begin{array}{*{20}l} {v\left( {x_{1} ,x_{3} } \right) = 0} \hfill & {{\text{for}}\;\left| {x_{1} } \right| < \infty ,} \hfill & {x_{3} = a,} \hfill \\ {v\left( {x_{1} ,x_{3} } \right) = 0} \hfill & {{\text{for}}\;x_{1} > 0,} \hfill & {x_{3} = 0,} \hfill \\ {A\left( {x_{1} ,x_{3} } \right) = R\frac{{\partial v}}{{\partial x_{3} }} = \varphi \left( {x_{1} } \right)} \hfill & {{\text{for}}\;x_{1} < 0,} \hfill & {x_{3} = 0.} \hfill \\ \end{array} } \right\}$$

(11)

Equations (9), (10), and (11) together form a complete  mathematical model  of the problem.

4 Solution

For analytical solution of the problem, we assume FIT, which is defined as

$$P\left( {x_{3} ,\chi } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{\infty } {p\left( {x_{1} ,x_{3} } \right)} e^{{i\chi x_{1} }} {\text{d}}x_{1} ,$$

(12)

$$p\left( {x_{1} ,x_{3} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty + i\delta }^{\infty + i\delta } {P\left( {x_{3} ,\chi } \right)} e^{{ - i\chi x_{1} }} {\text{d}}\chi ,$$

(13)

where $i\delta$ denotes the complex number lie within the common strip of regularity  of the transformation.

Using the properties of regular function, $P\left( {x_{3} ,\chi } \right)$ is expressed as (Titchmarsh [39])

$$P\left( {x_{3} ,\chi } \right) = P\,^{ - } \left( {x_{3} ,\chi } \right) + P\,^{ + } \left( {x_{3} ,\chi } \right),$$

(14)

where

$$\left. \begin{gathered} P^{ - } \left( {x_{3} ,\chi } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {p\left( {x_{1} ,x_{3} } \right)} e^{{i\chi x_{1} }} {\text{d}}x_{1} , \hfill \\ P^{ + } \left( {x_{3} ,\chi } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{0}^{\infty } {p\left( {x_{1} ,x_{3} } \right)} e^{{i\chi x_{1} }} {\text{d}}x_{1} , \hfill \\ \end{gathered} \right\}$$

(15)

is analytic function in the respective half-plane ${\text{imag}}\;\left( \chi \right)\; < \delta_{2} \,\& \,{\text{imag}}\;\left( \chi \right)\;{ < }\delta_{1} .$

With the aid of FIT (14), (15), Eqs. (9) and (10) becomes

$$\frac{{{\text{d}}^{2} V\left( {x_{3} ,\chi } \right)}}{{{\text{d}}x_{3}^{2} }} - \gamma^{2} \chi^{2} V\left( {x_{3} ,\chi } \right) = 0,$$

(16)

$${\text{and}}\;A\left( {x_{3} ,\chi } \right) = \varphi \left( \chi \right) = R\frac{\partial v}{{\partial x_{3} }}.$$

(17)

Solution of Eq. (16) becomes

$$V\left( {x_{3} ,\chi } \right) = C\,_{1} \left( \chi \right)\sinh \left( {\chi \gamma x_{3} } \right) + C_{\,2} \left( \chi \right)cosh\left( {\chi \gamma x_{3} } \right),$$

(18)

where $C_{\,1} \left( \chi \right)\,{\text{and}}\,C_{\,2} \left( \chi \right)$ are arbitrary constants and $\gamma = \left[ {\frac{S}{R} - \frac{{\rho s^{2} }}{R}} \right]^{\frac{1}{2}} .$

In view of Eq. (18), Eq. (17) reduces to

$$A\left( {x_{3} ,\chi } \right) = \left( {\chi \gamma R} \right)\left[ {C_{\,1} \left( \chi \right)cosh\left( {\chi \gamma x_{3} } \right) + C_{\,2} \left( \chi \right)sinh\left( {\chi \gamma x_{3} } \right)} \right].$$

(19)

Applying the FIT (12) into boundary condition (11) and using Eqs. (18) & (19), we get

$$V^{ - } \left( {0,\chi } \right) = - \frac{{\tanh \left( {\chi \gamma a} \right)}}{\chi }\left\{ {\frac{{\varphi \left( \chi \right) + A^{ + } (\chi )}}{\gamma R}} \right\},$$

(20)

$${\text{where}}\;\varphi \left( \chi \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {\varphi \left( {x_{1} } \right)e^{{i\chi x_{1} }} {\text{d}}x_{1} } .$$

(21)

The domain of existence of the Eq. (20) is $- \frac{\pi }{2\gamma a} < - \varepsilon < {\text{imag}}\left( \chi \right){ < 0}$. Now writing the kernel $\left( {F\left( \chi \right) = \frac{{\tanh \left( {\chi \gamma a} \right)}}{\chi }} \right)$ of Eq. (20) in terms of $\Gamma$-function as (Noble [40])

$$F\left( \chi \right) = \frac{\gamma a}{\pi }F^{ + } \left( \chi \right)F^{ - } \left( \chi \right),$$

(22)

$${\text{where}}\,F^{ + } \left( \chi \right) = \frac{{\Gamma \left( {\frac{1}{2} - \frac{i\chi a\gamma }{\pi }} \right)}}{{\Gamma \left( {1 - \frac{i\chi a\gamma }{\pi }} \right)}},\quad F^{ + } \left( { - \chi } \right) = F^{ - } \left( \chi \right).$$

(23)

The functions $\left\{ {\Gamma \left( {1 + \frac{i\chi a\gamma }{\pi }} \right),\Gamma \left( {\frac{1}{2} + \frac{i\chi a\gamma }{\pi }} \right)} \right\}\,{\text{and}}\,\left\{ {\Gamma \left( {1 - \frac{i\chi a\gamma }{\pi }} \right),\Gamma \left( {\frac{1}{2} - \frac{i\chi a\gamma }{\pi }} \right)} \right\}$ are analytic and non-zero in the half-planes ${\text{imag}}\left( \chi \right) < \frac{\pi }{{2\gamma a}}{{\& }}\;{\text{imag}}\left( \chi \right) > \frac{{ - \pi }}{{2\gamma a}},$ , respectively. In light of Eq. (22), Eq. (20) reduces as

$$- \frac{{V^{ - } \left( {0,\chi } \right)\pi R}}{{F^{ - } \left( \chi \right)a}} = F^{ + } \left( \chi \right)A^{ + } \left( \chi \right) + T\left( \chi \right),$$

(24)

$${\text{where}}\;T\left( \chi \right) = F^{ + } \left( \chi \right)\varphi \left( \chi \right).$$

(25)

Using the properties of analytic function in the half-spaces ${\text{imag}}\;\left( \chi \right) > - \varepsilon$ and ${\text{imag}}\left( \chi \right) < 0,$ $T\left( \chi \right)$ is expressed as

$$T\left( \chi \right) = T\,^{ + } \left( \chi \right) - T\,^{ - } \left( \chi \right),$$

(26)

$${\text{where}}\;T^{\, + } \left( \chi \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty - i\tau_{1} }}^{{\infty - i\tau_{1} }} {\frac{T\left( \nu \right)}{{\nu - \chi }}{\text{d}}\nu } ,$$

(27)

$${\text{and}}\;T^{ - } \left( \chi \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty + i\tau_{1} }}^{{\infty + i\tau_{1} }} {\frac{T\left( \nu \right)}{{\nu - \chi }}{\text{d}}\nu } ,$$

(28)

in which $- \tau_{1} < {\text{imag}}\left( \chi \right) < \tau_{2} \,\,{\text{and}}\,\,i\tau_{1} \,\,,i\tau_{2}$ lying in region of analyticity and $T^{ + } \left( \chi \right)\,,T^{ - } \left( \chi \right)$ are analytic in the respective half-planes $imag\left( \chi \right) > \,\frac{ - \pi }{{2\gamma a}}\,\,\& \,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0}{\text{.}}$

Inserting (26) into (24) leads to

$$- \frac{{V^{ - } \left( {0,\chi } \right)\pi R}}{{F^{ - } \left( \chi \right)a}} + T^{ - } \left( \chi \right) = F^{ + } \left( \chi \right)A^{ + } \left( \chi \right) + T^{ + } \left( \chi \right).$$

(29)

Both sides of Eq. (29) are non-zero and analytic in the half-planes $imag\left( \chi \right) > \,\frac{ - \pi }{{2\gamma a}}\,\,\& \,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0}$. Further, with the help of Liouville’s theorem, we obtain $V^{ - } \left( {0,\chi } \right) = \frac{a}{\pi R}T^{ - } \left( \chi \right)F^{ - } \left( \chi \right)$ regular in

$${\text{imag}}\left( \chi \right){ < 0,}$$

(30)

$${\text{and}}\;A^{ + } \left( \chi \right) = - \frac{{T^{ + } \left( \chi \right)}}{{F^{ + } \left( \chi \right)}}\;{\text{regular}}\;{\text{in}}\;imag\left( \chi \right) > \frac{ - \pi }{{2\gamma a}}.$$

(31)

Now considering the functions $T^{ + } \left( \chi \right)$ and $T^{ - } \left( \chi \right)$ are analytic in the region $\,\frac{ - \pi }{{2\gamma a}}\,\, < \,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0}{\text{.}}$ Therefore, functions $T^{ + } \left( \chi \right)$and $T^{ - } \left( \chi \right)$ may be written as

$$T^{ \pm } \left( \chi \right) = - \frac{1}{\chi }\left\{ {Q - \frac{1}{2\pi i}\int\limits_{{ - \infty - i\tau_{1} }}^{{\infty - i\tau_{1} }} {\frac{T\left( \nu \right)}{{\nu - \chi }}{\text{d}}\nu } } \right\},$$

(32)

$${\text{where}}\;Q = \frac{1}{2\pi i}\int\limits_{ - \infty - i\tau }^{\infty - i\tau } {T\left( \nu \right)} {\text{d}}\nu ,\tau_{1} < \tau < \tau_{2}$$

(33)

Now using (Noble [41])

$$\frac{{\Gamma \left( {k_{1} + k_{2} } \right)}}{{\Gamma \left( {k_{1} } \right)}} \simeq k_{1}^{{k_{2} }} ,\,\,\left| {k_{1} } \right| \to \infty$$

(34)

With the virtue of function $T^{ + } \left( \chi \right),$ Eqs. (30), and (31) results in

$$V\,^{ - } \left( {0,\chi } \right) = - \frac{Q}{\chi R}\sqrt {\frac{a}{i\pi \chi \gamma }} ,$$

(35)

$${\text{and}}\;A^{ + } \left( \chi \right) = Q\sqrt { - \frac{ia\gamma }{{\pi \chi }}} .$$

(36)

In view of Abel’s theorem (Noble [40]), Eqs. (35) and (36) gives

$$V\,\left( {0,\chi } \right) = - \frac{2N}{{\gamma R}}\sqrt { - x_{1} } \;{\text{for}}\;x_{1} \to - \varepsilon ,\varepsilon \to 0,$$

(37)

$${\text{and}}\;A\left( {x_{1} } \right) = \frac{N}{{\sqrt {x_{1} } }}\;{\text{for}}\;x_{1} \to + \varepsilon ,\varepsilon \to 0,$$

(38)

where $N = - iQ\sqrt {\frac{2a\gamma }{\pi }}$ represents the rate of energy release at the crack tip and is defined as the stress intensity factor  related to the crack in the undertaken strip.

5 SIF for concentrated force

Let us assume that a force of constant intensity $\left( {J_{0} } \right)$ is loaded on the edge $x_{1} = 0$ at $x_{1} = - d$ where $J_{0}$ is a constant.

$${\text{Suppose}}\;{\text{that}}\;J_{1} \left( {x_{1} } \right) = J_{0} \delta \left( {x_{1} + d} \right),$$

(39)

where $\delta \left( {x_{1} + d} \right)$ denotes the Dirac delta function.

Applying FIT (12) in Eq. (39), we obtain

$$\psi \left( \chi \right) = \frac{{J_{0} }}{{\sqrt {2\pi } }}e^{id\chi } ,$$

(40)

$\psi \left( \chi \right),$ being the FIT of $J\left( {x_{1} } \right).$

In light of Eqs. (22), (26), (33), and (39), we obtain

$$N = - \frac{{J_{0} }}{{\sqrt {a\gamma } }}e^{{ - \frac{\pi d}{{2a\gamma }}}} \frac{1}{2\pi i}\int\limits_{\varepsilon - i\infty }^{\varepsilon + i\infty } {\frac{\Gamma \left( \psi \right)}{{\Gamma \left( {\psi + \frac{1}{2}} \right)}}} e^{{\frac{\pi \psi d}{{a\gamma }}}} {\text{d}}\psi ,$$

(41)

where $0 < \varepsilon < 1/2.$

Now integrating Eq. (41) according as (Erdelyi et al. [41]), we get

$$N = - \frac{{J_{0} }}{{\sqrt {\pi a} }}\frac{{\exp \left( { - \frac{1}{2}\left[ {\pi \left( {H/D(s/\beta )} \right) - 1} \right]} \right)}}{{\sqrt {D(s/\beta )} }},$$

(42)

$${\text{and}}\;D(s/\beta ) = \sqrt {\frac{{S^{\prime } }}{{R^{\prime } }} - \frac{{\left( {s/\beta } \right)^{2} }}{{R^{\prime } }}} = \sqrt {\frac{{1/\eta + S_{11} }}{{1/\eta + S_{33} }} - \frac{{\left( {s/\beta } \right)^{2} }}{{1/\eta + S_{33} }}} ,$$

(43)

where $\beta = \sqrt {\frac{\mu }{\rho }}$ is the speed of shear wave,$\,\,H = \frac{d}{a}$ is the relative crack length,$\,S_{11} = \frac{{I_{11} }}{2\mu }$ and $\,S_{33} = \frac{{I_{33} }}{2\mu }$ are the dimensionless components of horizontal and vertical initial stresses, respectively.

Equation (42) represents the expression of SIF related to the crack in the considered strip for the CF case.

6 SIF for constant load

For the CL case, we assume the edge $x_{1} = 0$ of the crack are loaded at $x_{1} = - d$ by a constant $J_{c}$. With the help of Eqs. (22), (33) and the  expression of $\phi \left( \chi \right)$ in Eq. (21) and $T\left( \chi \right)$ in Eq. (33), we have

$$N^{*} = - J_{c} \sqrt {\frac{{aD\left( {s/\beta } \right)}}{\pi }} .$$

(44)

Equation (44) corresponds to the expression of SIF connected with the crack in the undertaken strip for the CL case.

7 Particular cases

• (1) When $\,S_{11} = 0 = S_{33}$ (i.e. the strip is devoid of initial stresses), Eqs. (43) results in

  $$D(s/\beta ) = \sqrt {1 - \eta \left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s \beta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\beta $}}} \right)^{2} } .$$

  (45)

  Equation (42) together with (45) is the SIF expression for the CF case, and Eq. (44) together with (45) is the SIF expression for the CL case related to the crack in a  dry sandy elastic strip.

• (2) When $\eta = 1$ (i.e. the strip is devoid of sandiness), Eq. (43) results in

  $$D(s/\beta ) = \sqrt {\frac{{\left( {1 + S_{11} } \right)}}{{\left( {1 + S_{33} } \right)}} - \frac{{\left( {s/\beta } \right)^{2} }}{{\left( {1 + S_{33} } \right)}}} .$$

  (46)

  Equation (42) together with (46) shows the SIF expression for the CF case, and Eq. (44), together with (46), shows the SIF expression for the CL case connected with the crack in the initially stressed isotropic strip.

• (3) When $\eta = 1$ and $\,S_{11} = 0 = S_{33}$ (i.e. the strip is devoid of sandiness and initial stresses), Eq. (43) results in

  $$D(s/\beta ) = \sqrt {1 - \left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s \beta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\beta $}}} \right)^{2} } .$$

  (47)

Equation (42) together with (47) demonstrates the SIF expression for the CF case in isotropic elastic strip which matches with the result of Chattopadhyay and Maugin [42]. Further Eqs. (44) and (47) give the SIF expression for the CL case in the isotropic elastic strip. The obtained expression matches with that derived in the work of Chattopadhyay and Bandyopadhyay [43].

8 Results and discussion

In this section, we have carried out numerical computation and graphical demonstrations of the influence of the prevalent parameters on the stress intensity factor  for CF and CL cases in an initially stressed dry sandy strip. For this purpose, we used the following data:

For considered dry sandy elastic medium: $\rho = 3364\,\,\left( {{\text{kg/m}}^{{3}} } \right),$$\mu = 6.34\, \times 10^{10} \,\left( {{\text{N/m}}^{{2}} } \right),$ (Gubbins [44]).

Sandiness parameter $\left( \eta \right) = 1.0,\,1.5,\,2.0,\,2.5$ crack length $\left( {H = {\raise0.7ex\hbox{$d$} \!\mathord{\left/ {\vphantom {d a}}\right.\kern-0pt} \!\lower0.7ex\hbox{$a$}}} \right) = 0.10,\,\,0.11,\,\,0.12$.

Unless otherwise specified:

Dimensionless horizontal initial stress $S_{11} = I_{11} /2\mu = - 0.04,\,\, - 0.02,\,\,0.00,\,\,0.02,\,\,0.04,$

Dimensionless vertical initial stress $S_{33} = I_{33} /2\mu = - 0.04,\,\, - 0.02,\,\,0.00,\,\,0.02,\,\,0.04.$

To describe the impact of numerous influencing parameters such as sandiness parameter $\left( \eta \right),$ horizontal and vertical initial stresses $\left( {S_{11} ,\,\,S_{33} } \right),$ on the SIF against the crack speed $\left( {s/\beta } \right),$ mathematical simulation has been accomplished by taking Eq. (42) into account for CF case and Eq. (44) for CL case.

Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 display the nature of SIF against the crack speed. More precisely, Figs. 2, 3, 4, 5 and 6 show the variation of SIF $\left( { - N\sqrt {\pi a} /J_{0} } \right)$ against the crack speed $\left( {s/\beta } \right)$ for CF case, while Figs. 7, 8, 9, 10, and 11 show the variation of SIF $\left( { - N^{*} \sqrt \pi /J_{c} \sqrt a } \right)$ against the crack speed $\left( {s/\beta } \right)$ for CL case. From the Figs. 2, 3, 4, 5, and 6, it may be noticed that when the crack is moving due to SH-wave propagating in the undertaken strip, with the rise in crack speed, the value of SIF increases, but after reaching a maximum value of the crack speed, the value of SIF falls down. Figures 2 and 3 studied the pronounced effect of $S_{11}$ and $S_{33}$ respectively, on the SIF in the considered strip for CF case. In Fig. 2, curves 1 and 2 represent the horizontal tensile initial stress, curves 4 and 5 represent the horizontal compressive initial stress and curve 3 corresponds to the case when the strip is of without horizontal initial stress. It is found after meticulous examination of Fig. 2 that SIF decreases uniformly when the crack speed $\left( {s/\beta } \right) \le 1.02,$ for increasing values of $S_{11}$ and when the crack speed $\left( {s/\beta } \right) > 1.02,$ then SIF rapidly falls. It is pointed out that the SIF attains maximum value for the case of horizontal tensile initial stress, while it attains minimum for the case of horizontal compressive initial stress; however, when the strip is free of initial stresses, the SIF has a moderate value. Figure 3 shows the effect of vertical initial stress on the SIF in the considered strip. In Fig. 3, curves 1 and 2 represent the vertical tensile initial stress and curves 4 and 5 correspond to the vertical compressive initial stress, while curve 3 represents the case when the medium is free from compressive/tensile initial stresses. Figure 3 shows that when the crack speed $\left( {s/\beta } \right) \le 1.0,$ vertical initial stress have a favourable impact on the SIF i.e. when the value of vertical initial stress increases, the value of SIF also increased but when crack speed $\left( {s/\beta } \right) > 1.0,$ SIF falls and the impact of initial stress becomes negligible. It is remarkably quoted that the SIF has attained the maximum value for vertical compressive initial stress in the undertaken strip compared to vertical tensile initial stress, whereas it attained moderate value when no initial stresses prevailed. The emphatic effect of crack length on the SIF in the undertaken strip has been shown in Fig. 4. This figure manifests that when the crack speed $\left( {s/\beta } \right) \le 1.0,$ the value of SIF decreases uniformly with increasing crack length. Further, it is also observed that when the crack speed $\left( {s/\beta } \right) > 1.0,$ the impact of crack length on the SIF becomes negligible. Figure 5 shows the effect of sandiness parameter on the SIF in the undertaken strip. From meticulous observation of Fig. 5, it is observed that when the crack speed $\left( {s/\beta } \right) \le 1.02,$ the sandiness parameter has a disfavouring impact on the SIF and when the crack speed $\left( {s/\beta } \right) > 1.02,$ the effect of sandiness parameter on the SIF vanishes. Figure 6 represents the comparative study of the SIF in various cases of the considered strip for CF case. In Fig. 6, curve 1 signifies that the strip is dry sandy with initial stress; curve 2 signifies that the strip is isotropic with initial stress and without sandiness; curve 3 signifies that the strip is without sandiness and initial stress. The SIF reaches its highest value when sandiness and initial stresses do not influence the strip, and it reaches its lowest value when the strip is dry sandy with initial stress.

Fig. 2

Scaled SIF against crack speed for distinct values of horizontal initial stress for CF case

Fig. 3

Scaled SIF against crack speed for distinct values of vertical initial stress for CF case

Fig. 4

Scaled SIF against crack speed for distinct values of crack length for CF case

Fig. 5

Scaled SIF against crack speed for distinct values of sandiness parameter for CF case

Fig. 6

Comparative study of SIF for distinct cases for CF case

Fig. 7

Scaled SIF against crack speed for distinct values of horizontal initial stress for CL case

Fig. 8

Scaled SIF against crack speed for distinct values of vertical initial stress for CL case

Fig. 9

Scaled SIF against crack speed for distinct values of crack length for CL case

Fig. 10

Scaled SIF against crack speed for distinct values of sandiness parameter for CL case

Fig. 11

Comparative study of SIF for distinct cases for CL case

Further, from the Figs. 7, 8, 9, 10, and 11, it has been observed that the value of SIF decreases for CL case with increasing values of the crack speed $\left( {s/\beta } \right),$ because increasing crack speed increases the area around the tip. Thus, the effect of CL at the crack tip reduces. Figures 7 and 8 show the pronounced effect of $S_{11}$ and $S_{33}$ respectively, on the SIF in the assumed strip for CL case. In Fig. 7, curves 1 and 2 represent the horizontal tensile initial stress, curves 4 and 5 represent the horizontal compressive initial stress and curve 3 distinctly established the case when the undertaken strip is free from both compressive/tensile initial stresses. After the meticulous examination of Fig. 7, it is found that the value of SIF increases uniformly with an increase in $S_{11} .$ It is pointed out that the value of SIF is minimum for horizontal tensile initial stress, while it is maximum horizontal compressive initial stress; however, the SIF has moderate value when the strip is devoid initial stress. In Fig. 8, curves 1 and 2 represent the vertical tensile initial stress, curves 4 and 5 represent the vertical compressive initial stress, and curve 3 is associated with the case when the strip is free from initial stress. After meticulously examining Fig. 8 it can be concluded that increasing values of vertical initial stress decrease SIF uniformly. It is pointed out that the SIF is maximum for vertical tensile initial stress, while it is minimum for the case of vertical compressive initial stress; however, the SIF has a moderate value when the strip is free from initial stress. Figure 9 shows that as crack length increases for CL case, the value of SIF does not change. Hence, for CL case, the SIF is independent of crack length. Figure 10 shows that the impact of sandiness parameter on the SIF for the case of CL. From the minute observation of Fig. 10, it is evident that the sandiness parameter has a favourable impact on the SIF. Figure 11 represents the comparative study of the SIF in various cases of the considered strip for CL case. In Fig. 11, curve 1 signifies that the strip is dry sandy under initial stress; curve 2 signifies that the strip is isotropic under initial stress without sandiness; curve 3 signifies that the strip is devoid of sandiness and initial stress. The SIF reaches its lowest value sandiness and initial stresses do not affect the strip, and it reaches its highest value when the strip is dry sandy under initial stress.

9 Conclusions

In this study, an exact expression of the stress intensity factor  has been obtained for crack propagation influenced by the transference of SH-wave in an initially stressed  dry sandy strip for CF and CL cases using WH-technique and FIT. The impact of numerous affecting parameters viz. length and speed of the crack, sandiness parameter and horizontal/ vertical tensile initial stresses on the SIF are analysed. The SIF in various cases of the strip has been examined and compared. The major outcomes of the study are highlighted as follows:

• The SIF for both CF and CL cases were determined and compared with pre-existing results.

• For CF case, the value of SIF keeps increasing when crack speed increases in the undertaken strip until it attains a maximum value, past which, it keeps decreasing sharply when crack speed gets closer to the shear wave speed. However, in the case of CL, the value of SIF decreases with increasing crack speed but at a slower rate for the lesser crack speed and steeply when the crack speed approaches towards shear wave speed in the medium.

• It is pointed out that horizontal compressive tensile initial (horizontal tensile initial stress) discourages (encourages) the SIF for CF case, whereas the opposite influence is reported for CL case.

• It is found that the SIF encourages and discourages with the increasing vertical compressive and vertical tensile initial stresses for CF case respectively, whereas for CL case the effect gets reversed. Further, on comparative analysis, it is revealed that cumulative effect of both horizontal and vertical initial stresses are discouraging for CF case and encouraging for CL case, establishing that effect of horizontal initial stresses on the SIF dominates over vertical one in either cases.

• It has been reported that increasing crack length decreases the SIF for the CF case, whereas a negligible effect of crack length on the SIF is reported for the CL case.

• It is noticed that the SIF is disfavoured with the increasing values of strip sandiness for the CF case. In contrast, it is favoured uniformly by the sandiness of the medium for the CL case.

• In the CF case, SIF attains its higher value when the strip is without sandiness and initial stresses, whereas it reaches its lower value when the strip is dry sandy under initial stress. On the contrary, an opposite trend is reported for the CL case.

The outcome of the present study may find its worth in the stability/ structural analysis, fracture initiation, and toughness of materials having sandiness in their characteristics. Moreover, this investigation may have significant contribution towards designing, health monitoring, and maintenance of building, bridges, dams etc. as these involve initially stressed dry sandy material in their construction so fatigue, crack growth rates and fracture toughness for the surface-crack can be better analysed.