Thermal stress intensity factor of an edge interface crack under arbitrary material combination considering double singular stress fields before and after cracking

Abstract

This paper discusses the stress intensity factor (SIF) for an edge interfacial crack in a wide bimaterial plate under uniform temperature change. The results shows that the SIF is controlled by the singular stress field including a constant term appearing at the interface end of the bimaterial plate without the crack. Since the constant term peculiar to thermal loading is necessary to be considered, it is confirmed that the SIF is analyzed by superposing the SIF under tension and the SIF under uniform interface stress. Finally, the SIF under thermal stress is systematically calculated and tabulated for arbitrary material combination in the whole range of Dundurs parameters α and β. When α = 2β, the SIF is presented as a function of α ( = 2β) by considering the logarithmic-type edge singularity, which is also peculiar to the thermal loading.

1 Introduction

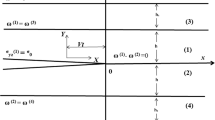
In recent years, electronic components such as semiconductors have become highly integrated, and thermal stress caused by the different expansion coefficient becomes more problematic. Furthermore, the temperature change in automobiles, computers, etc. in a day increases greatly causing many mechanical failures such as reduced strength at the joint interface due to thermal stress, cracking of constituent materials and delamination at the interface of dissimilar materials. Several previous studies have considered the singular stress field at the interface end to evaluate such problems [1,2,3,4,5,6]. Since fracture of the bonding material often occurs from the interface end, the analysis of the edge interface crack is mandatory for evaluating the interface failure. To evaluate the stress intensity factor (SIF) of an edge interface crack, care should be taken for two distinct singular stress fields existing: One is caused by the bonded plate end before cracking and the other is due to the interface crack itself after cracking. Figure 1 illustrates the double singular stress fields whose SIF was clarified by applying the proportional method in the preceding papers [7, 8]. As shown in Sect. 3 and Appendix A, the proportional method may provide exact solutions. Then, the results showed that when the relative crack length $a/W\le 1{0}^{-2}$ (see Fig. 10), the SIF is dominated by the singular stress field in Fig. 1b [8]. Noda and Lan [8] presented a suitable form to express the stress intensity factor for arbitrary material combinations by taking into account the edge singularity.

Fig. 1

Illustration of double singular stress fields: a The stress intensity factor (SIF) controlling the singular stress field of an edge interface crack in a is controlled by b the intensity of the singular stress field (ISSF) controlling the singular stress field of the bonded AB plate without crack in b

However, the singular stress field under thermal loading has some differences compared to the one under tensile loading [3, 9, 10]. First, unlike under mechanical loading, a constant term existing around the interface end peculiar to thermal loading must be taken into account [9, 10]. Due to the constant term before cracking, the thermal SIF becomes more complex compared to mechanical loading. Therefore, to understand the double singular stress fields is more important especially for thermal loading. Second, no analytical thermal loading solution is available for interface edge crack under arbitrary material combinations except for the semi-infinitely long cracks [11, 12]. Third, certain specific material combinations may cause a logarithmic-type singular stress field unlike tensile loading where only a power function-type singular stress field appears [10].

Therefore, in this study, the SIF of the edge interface crack under uniform temperature change will be clarified in comparison with the one under tension. The SIF is controlled by the thermal stress generated when a uniform temperature change is applied. Since the SIF becomes larger especially when the crack length is smaller due to the singular stress before cracking, the problem of small edge crack will be focused. The small edge crack is essential because the SIFs of large edge cracks is quite small under thermal loading (see Table 10 in Appendix B). First, the difference of the singular stress field without crack will be clarified under mechanical and thermal loading. Then the SIF will be analyzed systematically by varying the material combination. Finally, the SIF will be newly provided under arbitrary material combinations. The proposed solution for the edge interface crack will be able to provide SIFs for arbitrary material combinations under mechanical and thermal loads without numerical calculations.

Table 1 Behaviors of the interface stress ${\sigma }_{y}\left(r\right)$ when $r\to 0$ in Fig. 2 under mechanical loading and thermal loading

2 Difference of singular stress field of a bimaterial plate before cracking under tension and thermal loading

To understand the SIF of an edge interface crack under thermal loading, it is necessary to know the singular stress without crack since the double singularities in Fig. 1 must be considered. In the previous studies, Bogy pointed out the existence of logarithmic singularity in dissimilar bonded plates under surface traction without mentioning the equivalent tensile stress of the thermal loading [13]. Chen et al. [6] explained that the stress distribution due to thermal loading can be expressed by the stress distribution under tension and the constant uniform stress without mentioning that the meaning of the constant stress value. Therefore, in this Sect. 2, the interfacial stress distributions under tension and thermal loading will be indicated with the difference of the singular stress distribution. Then, the value of the constant stress will be clarified to understand the edge interface crack problem [6, 13].

2.1 Interface stress distribution under tension when $\boldsymbol{\alpha }\left(\boldsymbol{\alpha }-2{\varvec{\beta}}\right)>0$

Figure 2a shows the stress distribution ${\sigma }_{y}(r)$ at the interface end due to the remote tensile stress ${\sigma }_{y}^{\infty }\left(x\right)={\sigma }_{0}$ when $\alpha =0.8, \beta =0.3.$ Without losing generality, the remote tensile stress can be put as ${\sigma }_{y}^{\infty }\left(x\right)={\sigma }_{y0}$, which will be defined later in Eq. (6) as shown in Fig. 2a. The singular stress distribution near the interface edge ${\sigma }_{y}(r)$ can be expressed in Eq. (1).

$$\sigma_{y} \left( r \right) = \frac{{K_{\sigma } }}{{r^{1 - \lambda } }}$$

(1)

Fig. 2

Interface stress distribution ${\sigma }_{y}\left(r\right)$ under mechanical loading and thermal loading. Those results are obtained when α = 0.8, β = 0.3, (${G}_{A}/{G}_{B}=10.93$, ${\nu }_{A}/{\nu }_{B}=0.0314$, plane stress), ΔT = ${T}_{0}=-$ 100 deg, thermal expansion coefficient ratio ${\eta }_{A}/{\eta }_{B}=10$

Here, ${K}_{\sigma }$ is the intensity of the singular stress field (ISSF) and λ is the edge singularity index whose value is given by the characteristic equation of Eq. (2) [14].

$$\left[ {\sin^{2} \left( {\frac{\pi }{2}\lambda } \right) - \lambda^{2} } \right]^{2} \beta^{2} + 2\lambda^{2} \left[ {\sin^{2} \left( {\frac{\pi }{2}\lambda } \right) - \lambda^{2} } \right]\alpha \beta + \lambda^{2} \left( {\lambda^{2} - 1} \right)\alpha^{2} + \frac{{\sin^{2} (\lambda \pi )}}{4} = 0$$

(2)

In Eq. (2), Dundurs parameters $\alpha$, $\beta$ are determined from the material combination as follows [14].

$$\alpha = \frac{{G_{A} \left( {\kappa_{B} + 1} \right) - G_{B} \left( {\kappa_{A} + 1} \right)}}{{G_{A} \left( {\kappa_{B} + 1} \right) + G_{B} \left( {\kappa_{A} + 1} \right)}}, \beta = \frac{{G_{A} \left( {\kappa_{B} - 1} \right) - G_{B} \left( {\kappa_{A} - 1} \right)}}{{G_{A} \left( {\kappa_{B} + 1} \right) + G_{B} \left( {\kappa_{A} + 1} \right)}},$$

(3)

$$\kappa_{m} = \left\{ {\begin{array}{*{20}c} {\left( {3 - \nu_{m} } \right)/\left( {1 + \nu_{m} } \right)} & {\left( {{\mathrm{plane}}\,{\mathrm{stress}}} \right)} \\ {3 - 4\nu_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{strain}}} \right)} \\ \end{array} } \right.\left( {m = A,B} \right)$$

(4)

The singularity index $\lambda <1$ obtained from Eq. (2) characterizes the presence of the singular stress in Fig. 1b in the following way.

• (1) When $\alpha \left(\alpha -2\beta \right)>0$ (bad pair), $0<\lambda <1$.

• (2) When $\alpha \left(\alpha -2\beta \right)=0$ (equal pair), $\lambda =1$.

• (3) When $\alpha \left(\alpha -2\beta \right)<0 \,$ (good pair), $\lambda >1.$

Table 1 summarizes the characteristic of singular stress fields under mechanical loading in comparison within the case of thermal loading.

2.2 Interface stress distribution under thermal loading when $\boldsymbol{\alpha }\left(\boldsymbol{\alpha }-2{\varvec{\beta}}\right)>0$

The presence or absence of the interface stress singularity was discussed in the previous studies [6, 10]. Table 1 summarizes the behaviors of the interface stress ${\sigma }_{y}\left(r\right)$ when $r\to 0$ in Fig. 2 under mechanical loading and thermal loading. The interface stress behavior varies depending on $\alpha \left(\alpha -2\beta \right)>0$, $\alpha \left(\alpha -2\beta \right)=0,$ $\alpha \left(\alpha -2\beta \right)<0$.

Figure 2b shows the stress distribution ${\sigma }_{y}(r)$ at the interface edge due to the thermal loading by cooling the plate’s temperature uniformly as $\Delta T={T}_{0}<0.$ Fig. 2b is an example when α = 0.8, β = 0.3, ${T}_{0}=-$ 100 deg and thermal expansion coefficient ratio ${\eta }_{A}/{\eta }_{B}=10$. To conform the constant term peculiar to the thermal loading, Fig. 2c shows the subtracted distribution of Fig. 2b from Fig. 2a. As shown in Fig. 2c, a constant interface stress distribution ${\sigma }_{y}^{c}\left(r\right)={\sigma }_{y0}$ is confirmed as can be expressed ${\sigma }_{y}^{c}\left(r\right)={\sigma }_{y}^{a}\left(r\right)-{\sigma }_{y}^{b}\left(r\right)={\sigma }_{y0}$. The dashed line in Fig. 2b is the stress ${\sigma }_{y}$ at the interface due to the uniform temperature change $\Delta T={-T}_{0}<0$ subtracting the constant term ${\sigma }_{y}={\sigma }_{y0}$ in Fig. 2c.

From Fig. 2, it can be confirmed that the singular stress distribution under thermal loading in Fig. 2b at the interface end ${\sigma }_{y}(r)$ can be expressed in Eq. (5).

$$\sigma_{y} \left( r \right) = \frac{{K_{\sigma } }}{{r^{1 - \lambda } }} + \sigma_{y0}$$

(5)

In other words, under the bad pair condition satisfying $\alpha \left(\alpha -2\beta \right)>0$ the power function-type singular stress field ${r}^{1-\lambda }$ occurs in the case of the thermal load as well as in the case of the mechanical load causing ${\sigma }_{y}\left(r\right)\to \infty \, \mathrm{as} \, r\to 0$.

The constant term ${\sigma }_{y0}$ is known as the equivalent remote tensile stress that should be applied to the bimaterial plate (see Fig. 2a) to produce the same ISSF (see Fig. 2b). Under the remote tensile stress ${\sigma }_{y0}$ defined in Eq. (6), the same intensity of the singular stress ${K}_{\sigma }$ due to the uniform temperature change $\Delta T={-T}_{0}<0$ can be obtained [6].

$$\begin{aligned} \sigma_{y0} & = \frac{{8G_{A} G_{B} \left( {\eta_{B}^{*} - \eta_{A}^{*} } \right)\Delta T}}{{G_{A} \left( {\kappa_{B} - 1} \right) - G_{B} \left( {\kappa_{A} - 1} \right) - 2\left( {G_{A} - G_{B} } \right)}} , \\ \eta_{m}^{*} & = \left\{ {\begin{array}{*{20}c} {\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{stress}}} \right)} \\ {\left( {1 + \nu_{m} } \right)\,\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{strain}}} \right)} \\ \end{array} } \right.\left( {m = A,B} \right) \\ \end{aligned}$$

(6)

Here, ${G}_{A}$, ${G}_{B}$ are shear modulus, ${\nu }_{A}$, ${\nu }_{B}$ are Poisson’s ratio and ${\eta }_{A}^{*}$, ${\eta }_{B}^{*}$ are thermal expansion coefficient of material A, B, respectively.

Figure 3 illustrates the idea of the analysis method used later in Sect. 4. The stress distribution in Fig. 3a under thermal loading consists of the one under the tensile loading in Fig. 3b and the constant interface stress in Fig. 3c. The SIF solution in Fig. 3b was analyzed previously. As shown in Fig. 3c, the uniform interface stress in Fig. 3c is expressed by the sum of the compressive remote loading and the thermal loading. In this study, the stress intensity factor of the edge crack in the bimaterial plate under uniform temperature change will be discussed on the basis of the superposition in Fig. 3.

Fig. 3

a Singular interface stress due to uniform thermal loading $\Delta T={T}_{0}<0$ can be expressed by superposing b tensile loading and c constant interface stress when $\alpha \left(\alpha -2\beta \right)>0$. The constant interface stress in c can be obtained from compressive ${\sigma }_{y0}$ and $\Delta T={T}_{0}<0$

2.3 Interface stress distribution under thermal loading when $\boldsymbol{\alpha }\left(\boldsymbol{\alpha }-2{\varvec{\beta}}\right)=0$

It is known that even when $\alpha \left(\alpha -2\beta \right)=0$, which is named equal pair condition under mechanical loading, a logarithmic singularity occurs for thermal loading [10]. In other words, under the equal pair condition $\alpha \left(\alpha -2\beta \right)=0$, ${\sigma }_{y}\left(r\right)\to$ finite as $r\to 0$ in the case of mechanical load, whereas in the case of thermal load, logarithmically singular stress field is generated and ${\sigma }_{y}\left(r\right)\to \infty$ when $r\to 0$. Figure 4 shows an example of logarithmic singular stress distribution under equal pair conditions, and ${\sigma }_{y}\left(r\right)\to \infty$ when $r\to 0$ when $\alpha =0.6, \beta =0.3.$

Fig. 4

Stress distribution near the interface edge in bimaterial plate when $\alpha - 2\beta = 0, \alpha = 0.6, \beta = 0.3, \Delta T = - 100 \deg ,\,{\mathrm{thermal}} \,{\mathrm{expansion}}\,{\mathrm{coefficient}}\,{\mathrm{ratio}} \,\eta_{A} /\eta_{B} = 10.$

2.4 Interface stress distribution under thermal loading when $\boldsymbol{\alpha }\left(\boldsymbol{\alpha }-2{\varvec{\beta}}\right)<0$

Under good pair condition $\alpha \left(\alpha -2\beta \right)<0$, the stress singularity disappears in the case of the thermal load as well as in the case of the mechanical load, and ${\sigma }_{y}\left(r\right)\to 0$ as $r\to 0$. In the case of $\alpha \left(\alpha -2\beta \right)<0$, no singular stress field occurs, so in this sense $\alpha \left(\alpha -2\beta \right)<0$ is a good pair even for thermal loading.

3 Analysis method of interfacial cracks under thermal load and influence of material combination

3.1 Proportional method to analyze thermal interface stress intensity factors

Figure 5 shows a bimaterial plate with an edge interface crack subjected to uniform temperature change $\Delta T$, which is the target problem in this study. In the FEM analysis, a uniform temperature change $\Delta T$ is applied to the entire element in Fig. 5 considering elastic modulus and thermal expansion coefficient. Then, the stress value at the crack tip is calculated. In a similar way, an interface edge crack under heat flow may be solved after analyzing temperature distribution [19]. Since the singular field appears at the interface end of the bonded plate without crack, the discussion in Sect. 2 must be useful for heat flow problems. In this study, the SIF of the interface crack under uniform temperature change $\Delta T$ is focused by applying the proportional method [15,16,17]. As shown in the preceding papers as well as the following explanation in Sects.  3 and 4, the proportional method may provide exact solutions [7, 8, 15,16,17].

Fig. 5

Unknown problem for an edge interface crack in bimaterial rectangular plate subjected to uniform temperature change $\Delta T$. The stress values at the crack tip ${\sigma }_{y0,FEM}$, ${\tau }_{xy0,FEM}$ are calculated by FEM considering the elastic modulus ${G}_{A}$, ${\nu }_{A}$, ${G}_{B}$, ${\nu }_{B}$ and thermal expansion coefficients ${\eta }_{A}$, ${\eta }_{B}$

In the method, stress values at the crack tip node are used and a stress intensity factor is determined by the ratio of the crack tip stress values between an unknown problem in Fig. 5 and the reference problem in Fig. 6. The method gives the singular stress field equal to the unknown problem by adjusting load stress T and S of the reference problem whose stress intensity factor is already known. The single interface crack in a bonded semi-infinite plate subjected to the tension T and shear S is selected as the reference problem because the interface crack tip is always mixed mode state. The stress values at the interface crack tip node calculated by FEM in the reference problem under the tensile stress T = 1 (S = 0) or shear stress S = 1 (T = 0) are written by ${\sigma }_{y0,FEM}^{T=1 *}$, ${\tau }_{xy0,FEM}^{T=1 *}$ and ${\sigma }_{y0,FEM}^{S=1 *}$, ${\tau }_{xy0,FEM}^{S=1 *}$, respectively, in Fig. 6. The crack tip stress values of the unknown problem under the uniform temperature change in Fig. 5 are also denoted by ${\sigma }_{y0,FEM}$, ${\tau }_{xy0,FEM}$. By using the same crack tip stress condition between the reference and the unknown problems, that is, ${\sigma }_{y0,FEM}={\sigma }_{y0,FEM}^{ *}$ and ${\tau }_{xy0,FEM}={\tau }_{xy0,FEM}^{ *}$, the external loading stress T and S in the reference problem can be determined from the next expression.

$$\begin{gathered} \hfill T = \frac{{\sigma_{{y0,{\mathrm{FEM}}}} \cdot \tau_{{xy0,{\mathrm{FEM}}}}^{S = 1 *} - \sigma_{{y0,{\mathrm{FEM}}}}^{S = 1 *} \cdot \tau_{{xy0,{\mathrm{FEM}}}} }}{{\sigma_{{y0,{\mathrm{FEM}}}}^{T = 1 *} \cdot \tau_{{xy0,{\mathrm{FEM}}}}^{S = 1 *} - \sigma_{{y0,{\mathrm{FEM}}}}^{S = 1 *} \cdot \tau_{{xy0,{\mathrm{FEM}}}}^{T = 1 *} }}, \\ \hfill S = \frac{{\sigma_{{y0,{\mathrm{FEM}}}}^{T = 1 *} \cdot \tau_{{xy0,{\mathrm{FEM}}}} - \sigma_{{y0,{\mathrm{FEM}}}} \cdot \tau_{{xy0,{\mathrm{FEM}}}}^{T = 1 *}}}{{\sigma_{{y0,{\mathrm{FEM}}}}^{T = 1 *} \cdot \tau_{{xy0,{\mathrm{FEM}}}}^{S = 1 *} - \sigma_{{y0,{\mathrm{FEM}}}}^{S = 1 *}\cdot \tau_{{xy0,{\mathrm{FEM}}}}^{T = 1 *} }} \\ \end{gathered}$$

(7)

Fig. 6

Reference problem for an interface crack in a bonded semi-infinite plate subjected to tension T and shear S

From the loading stresses T and S obtained by Eq.(7), the stress intensity factor of the interface crack in the reference problem in Fig.6 can be evaluated by

$$K_{1}^{*} + iK_{2}^{*} = \left( {T + iS} \right)\sqrt {\pi a^{*} } \left( {1 + 2i\varepsilon } \right), \, \varepsilon = \frac{1}{2\pi }\ln \left[ {\left( {\frac{{\kappa_{A} }}{{G_{A} }} + \frac{1}{{G_{B} }}} \right)/\left( {\frac{{\kappa_{B} }}{{G_{B} }} + \frac{1}{{G_{A} }}} \right)} \right]$$

(8)

Here, ε is the oscillation singular index, $\kappa_{m} = 3 - 4\nu_{m}$(plane strain), $(3 - \nu_{m} )/(1 + \nu_{m} )$(plane stress). Because the stress intensity factor of Eq. (8) is equal to that of the unknown problem, the stress intensity factors of the unknown problem in Fig. 5 can be obtained as

$$K_{1} = K_{1}^{*} ,\quad K_{2} = K_{2}^{*}$$

(9)

From ${K}_{1}={{K}_{1}}^{*},\hspace{1em}{K}_{2}={{K}_{2}}^{*}$, ($T$, $S$) in Eq. (8) can be regarded as dimensionless SIFs (${F}_{1}$, ${F}_{2}$) of unknown problem [see Eq. (11))]. It is noted that in the proportional method the finite element models of the reference and the unknown problems have the same crack length and the same FEM mesh pattern near the interface crack tip [7, 8, 15,16,17], a = a* and e = e*. The definition of stress intensity factor shown in Eq. (8) is expressed as follows based on the interface crack length 2a^*.

$$\sigma_{y} \left( r \right) + \;i\tau_{xy} \left( r \right) = \frac{{K_{1} + i\;K_{2} }}{{\sqrt {2\pi r} }}\left( {\frac{r}{{2a^{*} }}} \right)^{i\varepsilon }$$

(10)

The detail of the accuracy discussion can be found in previous papers under mechanical loading [8, 15, 16]. The proportional method is useful for analyzing interface cracks by providing mesh-independent interface SIFs ${F}_{1}$, ${F}_{2}$ efficiently. Since those FEM results are mesh-independent, the obtained SIFs ${K}_{1}$, ${K}_{2}$ can be regarded as the exact solution by using the exact reference solution in the bonded infinite plate ${K}_{1}+i{K}_{2}=(T+iS)\sqrt{\pi a}(1+2i\varepsilon )$. For the readers’ convenience, several examples are indicated in Appendix A.

3.2 Importance of edge interface crack under thermal loading compared to internal crack

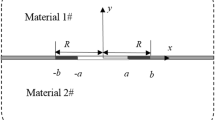
Figure 7 shows an edge interface crack in a bimaterial plate considered in this paper in comparison with a central interface crack in a bimaterial plate. When $a/W\to 0$, those problems are reduced to most fundamental crack problems, that is, a cracked semi-infinite plate and a cracked infinite plate. For example, when the two materials have the same material properties, they correspond to an edge crack in a homogeneous semi-infinite plate and an internal crack in a homogeneous infinite plate. In this study, the dimensionless stress intensity factors F₁, F₂ defined in Eq. (11) will be compared by applying the proportional method in Sect. 3.1.

$$K_{1} + iK_{2} = \left( {F_{1} + iF_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right)$$

(11)

Fig. 7

Comparison between the edge interface crack and the central interface crack by taking an example of the bimaterial plate $\alpha =0.8, \beta =0.3, a/W={10}^{-5}$ subjected to uniform temperature change $\Delta T$= ${T}_{0}=-100 \ \mathrm{deg}$, thermal expansion coefficient ratio ${\eta }_{A}/{\eta }_{B}=10$. Here, the constant term stress ${\sigma }_{y0}$ is defined by Eq. (6)

The thermal stress intensity factors ${K}_{1}$, ${K}_{2}$ depend on the temperature change $\Delta T$, Dunders parameter $\alpha$, $\beta$, thermal expansion coefficient ratio ${\eta }_{A}/{\eta }_{B}$ and relative crack length $a/W$. When uniform temperature change $\Delta T$ = ${T}_{0}$= $-$ 100 deg is applied to the cracked bimaterial plate with $\alpha =$ 0.8, $\beta =$ 0.3 and $a/W={10}^{-5}$, the dimensionless SIFs are obtained as ${F}_{1}=2.568$ and ${F}_{2}=-0.364$ in Fig. 7a. Instead, in Fig. 7b, the dimensionless SIFs are obtained as ${F}_{1}=-0.0214$ and ${F}_{2}=1.7\times {10}^{-5}$, whose values are much smaller than ${F}_{1}=2.568$ in Fig. 7a. Furthermore, when the tensile thermal stress appears at the interface end, the compressive thermal stress occurs at the center of the bimaterial plate. This is because the summation of ${\sigma }_{y}$ along the interface is zero and only at the interface end the singular stress appears. In this way, it may be concluded that regarding thermal stress intensity factors the small edge interface crack is essential and practically important.

3.3 Effect of material combination on the thermal interface stress intensity factors

The thermal stress intensity factors ${K}_{1}$, ${K}_{2}$ depend on the temperature change $\Delta T$, Dunders parameter $\alpha$, $\beta$, thermal expansion coefficient ratio ${\eta }_{A}/{\eta }_{B}$ and relative crack length $a/W$. Table 2 shows the values of ${F}_{1}, {F}_{2}$ of the edge interface crack by varying material constants but under fixed α = 0.8, β = 0.3 with $a/W={10}^{-5}$. Table 2 shows that even if the material constants are different, the values of F₁, F₂ are the same. This is because Dundurs parameters $\alpha$, $\beta$ control ${F}_{1}, {F}_{2}$.

Table 2 Confirmation of the thermal SIFs ${F}_{1}, {F}_{2}$ defined from ${K}_{1}+i{K}_{2}=({F}_{1}+i{F}_{2}){\sigma }_{y0}\sqrt{\pi a}(1+2i\varepsilon )$ that are controlled by $\alpha , \beta$ by taking an example when $\alpha$  = 0.8, $\beta$ = 0.3 and $a/W={10}^{-5}$ in Fig. 5

To clarify the effects of the crack length and the material combination, Fig. 8 shows F₁, F₂ by varying the crack length as a/W = 10^–7 ~ 10^–1 by taking an example when α = 0.5 ~ 0.95 and β = 0.3. When α = 0.5 ~ 0.55 with β = 0.3, the good pair condition $\alpha \left(\alpha -2\beta \right)<0$ can be satisfied; then, the dimensionless SIF ${F}_{1}, {F}_{2}\to \mathrm{finite}$ as a/W $\to$ 0. However, when α = 0.65 ~ 0.95 with β = 0.3, the bad pair condition $\alpha \left(\alpha -2\beta \right)>0$ can be satisfied; then, ${F}_{1},\left|{F}_{2}\right|\to \infty$ as $a/W\to 0$. This is due to the singular stress field at the interface end under the bad pair condition. Due to the singularity, as the crack becomes shorter as $a/W\to 0$, the stress at the crack tip goes to infinity. Figure 8, for the small interface crack, shows that the expression of ${F}_{1}$, ${F}_{2}$ in Eq. (11) is not enough and the double singular stress fields have to be considered. In Fig. 9, the equal pair condition $\alpha \left(\alpha -2\beta \right)>0$ is not considered, the equivalent stress ${\sigma }_{y0} \to \infty$. In Sect. 4, ${F}_{1}$, ${F}_{2}$ in Eq. (11) will be defined in a different way of Eq. (11).

Fig. 8

Relation between normalized SIFs F₁, F₂ and the relative crack length a/W when β = 0.3 in Fig. 7a, [${K}_{1}+i{K}_{2}=({F}_{1}+i{F}_{2}){\sigma }_{y0}\sqrt{\pi a}(1+2i\varepsilon )$]

Fig. 9

a Singular interface stress due to uniform thermal loading $\Delta T={T}_{0}<0$ can be expressed by superposing b tensile loading and c constant interface stress when $\alpha \left(\alpha -2\beta \right)>0$. The constant interface stress in Fig. 10c can be obtained from compressive ${\sigma }_{y0}$ and $\Delta T={T}_{0}<0$

Fig. 10

Values of ${C}_{1}={F}_{1}/(W/a{)}^{1-\lambda }$ and ${C}_{2}={F}_{2}/(W/a{)}^{1-\lambda }$ in Fig. 9b by varying $a/W$ in the range $a/W={10}^{-7}$~${10}^{-1}$ and also by varying α in the range α = 0.5 ~ 0.95 under fixed $\beta$=0.3

Table 3 summarizes the behavior of SIFs under mechanical loading and thermal loading, that is, ${F}_{1},{F}_{2}\to \infty$, ${F}_{1},{F}_{2}\to \mathrm{finite}$ or ${F}_{1},{F}_{2}\to 0\,\mathrm{ as }\,a/W\to 0\,\mathrm{ in }$Fig. 5. Comparison between Table 1 and Table 3 shows that ${\sigma }_{y}\left(r\right)$ and ${F}_{1},{F}_{2}$ have the same behavior; for example, when the singular stress field without crack exists as ${\sigma }_{y}(r)\to \infty$, ${F}_{1},{F}_{2}\to \infty$. In other words, the dimensionless SIFs ${F}_{1},{F}_{2}$ are totally controlled by the interface stress ${\sigma }_{y}(r)$ without crack.

Table 3 Behaviors of dimensionless SIFs ${F}_{1},{F}_{2}$ when $a/W\to 0$ in Fig. 5 under mechanical loading and thermal loading corresponding to the behaviors of the interface stress ${\sigma }_{y}\left(r\right)$ in Table 1. [${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{0}\sqrt{\pi a}\left(1+2i\varepsilon \right)$, where ${\sigma }_{0}$ is the equivalent stress defined by Eq. (6) or Eq. (15)]

4 Stress intensity factor for interfacial edge crack in bimaterial plate based on the principle of superposition

4.1 Stress intensity factor of a small edge crack in bimaterial plate considering the edge singularity of the power function type

In this section, the SIF of a small interface crack in bimaterial plate in Fig. 9a will be analyzed on the basis of the discussion in Sect. 2. As shown in Fig. 9, the singular stress field at the edge of the interface in Fig. 9a due to the thermal loading can be expressed by superposing the tensile loading in Fig. 9b and the constant interface stress in Fig. 9c [6]. In Fig. 9, the uniform stress field at the interface in Fig. 9c is expressed by the sum of the compressive remote loading and the thermal loading.

To express the SIF of the edge interface crack under uniaxial tension in Fig. 9b, the coefficients C₁, C₂ were newly proposed as shown in Eq. (12) [8] considering the interface end singularity without crack. Then, the coefficients C₁, C₂ in Fig. 9b were obtained by the proportional method using FEM confirming more than three digits convergence.

$$K_{1} + iK_{2} = \left( {F_{1} + iF_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right), F_{1} = C_{1} \cdot (W/a)^{1 - \lambda } , F_{2} = C_{2} \cdot (W/a)^{1 - \lambda }$$

(12)

when α(α-2β) ≠ 0 in Fig. 9b

As shown in Fig.16 in Appendix B, as $a/W\to 0,$ F₁, F₂ are not suitable for expressing the SIF since F₁ $\to \infty$, F₂ $\to \infty$. Instead, since C₁, C₂ are always finite, they can be used conveniently. This is similar to the finite value of the SIF that can be used to evaluate cracks instead of the infinite stress value at the crack tip ${\sigma }_{y}\left(r\right)\to \infty$ that cannot be used when $r\to 0$. Figure 10 illustrates the values of C₁, C₂ in Fig. 9b when $a/W={10}^{-7}$~${10}^{-1}$, α = 0.5 ~ 0.95 under fixed $\beta$ = 0.3. Figure 10 shows ${C}_{1}$ and ${C}_{2}$ are insensitive of $a/W$ when $a/W\le 1{0}^{-1}$ and become almost constant more than three significant digits in the range $a/W\le 1{0}^{-3}$. It should be noted that when α = 0.5, α = 0.55 with $\beta$ = 0.3, good pair condition $\alpha \left(\alpha -2\beta \right)<0$ can be satisfied. However, as shown in Fig. 10, the values of C₁, C₂ are also constant for α = 0.5, 0.55. In other words, Eq. (12) can also be used for good pairs where singularity disappears. Table 4 shows ${C}_{1}$, ${C}_{2}$ values with more than three digits accuracy in the range $a/W\le 1{0}^{-3}$ for Fig. 9b under tension ${\sigma }_{y0}$ based on the definition (12) $.$ Note that Noda–Lan [8] used another definition, ${K}_{1}={F}_{1}{\sigma }_{y0}\sqrt{\pi a}$, ${K}_{2}={F}_{2}{\sigma }_{y0}\sqrt{\pi a}$, ${F}_{1}={C}_{1}\cdot (W/a{)}^{1-\lambda }, {F}_{2}={C}_{2}\cdot (W/a{)}^{1-\lambda }$, and their values are therefore different from the values in Table 4.

Table 4 Values of ${C}_{1}$, ${C}_{2}$ in Eq. (12) having more than three digits accuracy in the range $a/W\le 1{0}^{-3}$ subjected to tension ${\sigma }_{y0}$ in Fig. 9(b) [${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{y0}\sqrt{\pi a}\left(1+2i\varepsilon \right), {F}_{1}={C}_{1}\cdot (W/a{)}^{1-\lambda }, {F}_{2}={C}_{2}\cdot (W/a{)}^{1-\lambda }$]

Next, consider the SIF of the interface edge crack under uniform stress field in Fig. 9c. The SIFs in Fig. 9c have been also obtained by the proportional method using FEM confirming more than three digits convergence. Figure 11 shows the dimensionless coefficients ${D}_{1}$ and ${D}_{2}$ in Eq. (13) by varying $a/W$ in the range $a/W={10}^{-7}$~${10}^{-1}$ and also by varying α in the range α = 0.5 ~ 0.95 under fixed $\beta$ = 0.3. As shown in Fig. 11, the values of ${D}_{1}$ and ${D}_{2}$ are insensitive of $a/W$ in the range $a/W\le 1{0}^{-2}$ and coincide with each other more than three significant digits in the range $a/W\le 1{0}^{-3}$.

$$K_{1} + iK_{2} = \left( {D_{1} + iD_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right)$$

(13)

Fig. 11

Values of $D_{1}$, $D_{2}$ in Fig. 9c by varying $a/W$ in the range $a/W = 10^{ - 7}$~$10^{ - 1}$ and also by α in the range α = 0.5~0.95 under fixed $\beta$ = 0.3 in Fig. 9c

Table 5 shows the values of coefficients ${D}_{1}$, ${D}_{2}$ defined in Eq. (13) having more than three digits accuracy in the range $a/W\le {10}^{-3}$ in Fig. 9c by varying α, β. When $\alpha =2\beta$, a logarithmic singularity occurs at the interface end and the equivalent load ${\sigma }_{y0}$ expressed by Eq. (6) becomes infinite, so Eq. (13) cannot be used although ${D}_{1}$, ${D}_{2}$ are indicated in Table 5. Table 5 shows that the value of ${D}_{1}$ is close to the value of edge crack in homogeneous semi-infinite plate ${F}_{I}$ = 1.1215.

Table 5 Values of ${D}_{1}$, ${D}_{2}$ in Eq. (13) having more than three digits accuracy in the range $a/W\le {10}^{-3}$ subjected to $\Delta T$ and ${\sigma }_{y0}$ as shown in Fig. 9c [${K}_{1}+i{K}_{2}=({D}_{1}+i{D}_{2}){\sigma }_{y0}\sqrt{\pi a}(1+2i\varepsilon )$]

As shown in Fig. 9, the SIF${F}_{1}$, ${F}_{2}$ in Fig. 9a can be expressed as Eq. (14) by superposing the problems in Fig. 9b, c. Table 6 indicates ${C}_{1} , {C}_{2}$ in Table 4 and ${D}_{1} , {D}_{2}$ in Table 5 by taking an example when $\alpha$ = 0.8, 0.9, $\beta$ = 0.3. By substituting those values into Eq. (14), the values of${F}_{1}={C}_{1}\cdot (W/a{)}^{1-\lambda }+{D}_{1}$, ${F}_{2}={C}_{2}\cdot (W/a{)}^{1-\lambda }+{D}_{2}$ are estimated and indicated in Table 6 as “${F}_{1}$ in Eq. (14)” and “${F}_{2}$ in Eq. (14).”

$$\begin{aligned} K_{1} + iK_{2} & = \left( {F_{1} + iF_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right), F_{1} = C_{1} \cdot (W/a)^{1 - \lambda } + D_{1} , \\ F_{2} & = C_{2} \cdot (W/a)^{1 - \lambda } + D_{2} , \\ \end{aligned}$$

(14)

when $\alpha \left( {\alpha - 2\beta } \right) > 0,\quad a/W \le 10^{ - 3}$in Fig. 9a

Table 6 Confirmation of ${F}_{1},{F}_{2}$ values estimated from Table 4 and Table 5 coincident with the results obtained by the proportional method [${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{y0}\sqrt{\pi a}\left(1+2i\varepsilon \right)$]

To confirm the validity those values, the proportional method described in Sect. 3.1 is applied and the obtained ${F}_{1}, {F}_{2}$ values are indicated in Table 6 as “Proportional method.” It is seen that ${F}_{1}, {F}_{2}$ values from ${C}_{1} , {C}_{2}, {D}_{1} , {D}_{2}$ and ${F}_{1}, {F}_{2}$ values from proportional method coincide with each other more than three significant digits. In this way, it is confirmed that Table 4 and Table 5 are useful for obtained the SIF in Fig. 9a.

4.2 Stress intensity factor of an edge crack in a wide bimaterial plate considering the logarithmic singular stress field without crack

Regarding the singularity at the joint end, it is known that a logarithmic singular stress field occurs as shown in Fig. 12 when $\alpha -2\beta =0$ in terms of Dundurs parameter [10, 13]. Furthermore, when $\alpha -2\beta =0$, the equivalent tensile stress ${\sigma }_{y0}$ defined in Eq. (6) goes to infinity although ${\sigma }_{y0}$ can be used to express the thermal singular stress field as shown in Fig. 9a when $\alpha -2\beta \ne 0$. Therefore, instead of ${\sigma }_{y0}$, the uniform temperature change is expressed by applying the stress ${\sigma }_{x0}$ defined in Eq. (15) in the x-direction as shown in Fig. 12. As shown in Appendix C, the equivalent stress ${\sigma }_{x0}$ of Eq. (15) can be derived from the condition that the strain ${\varepsilon }_{x}$ at the interface is equal between the upper and lower materials [6, 18].

$$\sigma_{x0} = \frac{{8G_{A} G_{B} \left( {\eta_{B}^{*} - \eta_{A}^{*} } \right)\Delta T}}{{G_{A} \left( {\kappa_{B} + 1} \right) - G_{B} \left( {\kappa_{A} + 1} \right)}}$$

(15)

Fig. 12

Singular interface stress due to thermal loading expressed by the equivalent tensile stress in the x-direction $\sigma_{x0}$when $\alpha - 2\beta = 0$ a the thermal loading in bimaterial plate b tensile loading in the x-direction

The equivalent stress replacement in Fig. 12 by using ${\sigma }_{x0}$ defined in Eq. (15) is useful not only when $\alpha -2\beta =0$, but also for all material combinations $\alpha$, $\beta$ [11]. However, the replacement in Fig. 12 cannot clarify the difference between the tensile load and the thermal load unlike the replacement in Fig. 9 by using ${\sigma }_{y0}$ defined in Eq. (15). Therefore, it is inconvenient to use the replacement in Fig. 12b as well as the direct analysis results of the thermal load in Fig. 12a itself especially in experiments that combine thermal loads and tensile loads conducted previously. In other words, the substitution method in Fig. 9 is more useful than the one in Fig. 12 for the previous experiments combining thermal and tensile loads [5, 6]. Therefore, this paper uses the replacement in Fig. 12 only when $\alpha -2\beta =0$.

Figure 13 shows the stress intensity factors ${F}_{1}$, ${F}_{2}$ vs. log ($a/W$) relation. Figure 13 indicates ${F}_{1}$, ${F}_{2}$ of edge cracks are controlled by interface edge logarithmic singularity when there is no crack. Then, they are proportional to log ($a/W$) when $a/W\le 1{0}^{-3}$. Therefore, as shown in the dashed line in Fig. 13 when $a/W\le 1{0}^{-3}$, F₁, F₂ can be expressed by Eq. (16).

$$\begin{aligned} K_{1} + iK_{2} & = \left( {F_{1} + iF_{2} } \right)\sigma_{x0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right), F_{1} = c_{1} \log (a/W) + d_{1} , \\ F_{2} & = c_{2} \log (a/W) + d_{2} , \\ \end{aligned}$$

(16)

where $\left( {\alpha - 2\beta } \right) = 0, a/W \le 10^{ - 3}$ in Fig. 12a

Fig. 13

Relation between $F_{1}$, $F_{2}$ and the relative crack length a/W in Fig. 12 when $\alpha - 2\beta = 0$

As shown in Fig. 14, the values of ${c}_{1}$, ${c}_{2}$, ${d}_{1}$, ${d}_{2}$ are insensitive of $a/W$ in the range $a/W\le 1{0}^{-2}$ and coincide with each other more than three significant digits in the range $a/W\le 1{0}^{-3}$. Figure 15 shows the values of ${c}_{1}$, ${c}_{2}$, ${d}_{1}$, ${d}_{2}$ obtained by the proportional method in the whole range of $\alpha$. Since those values depend on only α (= 2β), they can be approximated as a function of α as shown in Eq. (17), which can be conveniently used to obtain the values ${c}_{1}$, ${c}_{2}$, ${d}_{1}$, ${d}_{2}$ for any value of α. They are odd functions with respect to $\alpha$. It is confirmed that the calculation formula (17) may provide ${F}_{1}$, ${F}_{2}$ values with less than 1% error.

$$\begin{gathered} c_{1} = 10.7035\alpha^{6} - 20.9471\alpha^{5} + 18.3439\alpha^{4} - 6.6708\alpha^{3} + 3.2555\alpha^{2} - 0.0671\alpha \hfill \\ c_{2} = 0.3721\alpha^{6} - 0.6765\alpha^{5} + 0.5463\alpha^{4} - 0.1638\alpha^{3} + 0.0334\alpha^{2} - 0.0022\alpha \hfill \\ d_{1} = - 25.5432\alpha^{6} - 49.8314\alpha^{5} - 41.8688\alpha^{4} - 15.1837\alpha^{3} - 4.9974\alpha^{2} - 0.1509\alpha \hfill \\ d_{2} = 4.0137\alpha^{6} - 9.6898\alpha^{5} + 9.4712\alpha^{4} - 4.0005\alpha^{3} + 0.8521\alpha^{2} + 0.6590\alpha \hfill \\ \end{gathered}$$

(17a)

where $\alpha = 2\beta \ge 0, a/W \le 10^{ - 3}$

$$\begin{gathered} c_{1} = - 10.7035\alpha^{6} - 20.9471\alpha^{5} - 18.3439\alpha^{4} - 6.6708\alpha^{3} - 3.2555\alpha^{2} - 0.0671\alpha \hfill \\ c_{2} = - 0.3721\alpha^{6} - 0.6765\alpha^{5} - 0.5463\alpha^{4} - 0.1638\alpha^{3} - 0.0334\alpha^{2} - 0.0022\alpha \hfill \\ d_{1} = - 25.5432\alpha^{6} - 49.8314\alpha^{5} - 41.8688\alpha^{4} - 15.1837\alpha^{3} - 4.9974\alpha^{2} - 0.1509\alpha \hfill \\ d_{2} = - 4.0137\alpha^{6} - 9.6898\alpha^{5} - 9.4712\alpha^{4} - 4.0005\alpha^{3} - 0.8521\alpha^{2} + 0.6590\alpha \hfill \\ \end{gathered}$$

(17b)

where $\alpha = 2\beta \le 0, a/W \le 10^{ - 3}$.

Fig. 14

Relation between $c_{1}$, $d_{1} ,{ }$ $c_{2}$, $d_{2}$ and the relative crack length a/W in Fig. 12 when $\alpha - 2\beta = 0$

Fig. 15

Valuses of c₁, c₂, d₁, d₂ in Eq. (17) when $- 0.9 \le \alpha \left( { = 2\beta } \right) \le 0.9$

Finally, Table 7 summarizes suitable expressions considering the double singular stress fields in Fig. 9 under mechanical loading and thermal loading. Even when ${F}_{1},{F}_{2}\to \infty$, the coefficients ${C}_{1}$,${C}_{2}$,${D}_{1}$,${D}_{2}$,${c}_{1}$,${c}_{2}$,${d}_{1}$, ${d}_{2}$ are always finite and suitable to express ${F}_{1}$, ${F}_{2}$. This is similar to the finite value of the stress intensity factors that can be used to evaluate cracks instead of the infinite stress value at the crack tip ${\sigma }_{y}\left(r\right)\to \infty$ that cannot be used when $r\to 0$. In Table 7, the expressions of ${F}_{1}$, ${F}_{2}$ are chosen to express the singular stress fields considering the difference between thermal loading and mechanical loading.

Table 7 Suitable expression of ${F}_{1}$, ${F}_{2}$ in Fig. 9 when $a/W\le 1{0}^{-3 }$ considering the double singular stress fields in Fig. 9 under mechanical loading and thermal loading. [${K}_{1}+i{K}_{2}=({F}_{1}+i{F}_{2}){\sigma }_{0}\sqrt{\pi a}\left(1+2i\varepsilon \right)$, ${\sigma }_{0}$ is the equivalent stress defined by Eq. (6) or Eq. (15)]

5 Conclusions

In recent years, mechanical failures due to thermal stress such as cracking and delamination at the interface of dissimilar materials are becoming more problematic in automobiles, computers, etc. To evaluate such thermal load-induced damage in terms of the singular stress field, it is necessary to consider a constant term as well as the singular term at the interface end, unlike in the case of mechanical loading. In this study, therefore, the stress intensity factors (SIFs) of an interface edge crack in a wide bimaterial plate due to uniform temperature change were analyzed and they were indicated under arbitrary material combination. It was confirmed that the values are independent of the crack length when the crack length is sufficiently small when the relative crack length $a/W\le {10}^{-3}$. The conclusion can be summarized as follows.

Care should be taken for the SIF under thermal loading when $\alpha \left(\alpha -2\beta \right)$ = 0 and $\alpha \left(\alpha -2\beta \right)<0$ (see Table 7). When $\alpha \left(\alpha -2\beta \right)$ = 0, the dimensionless SIF ${F}_{1}, {F}_{2}\to \infty$ as $a/W\to 0$ under thermal loading although ${F}_{1}, {F}_{2}\to \mathrm{finite}$ under mechanical loading. When $\alpha \left(\alpha -2\beta \right)<$ 0, ${F}_{1}, {F}_{2}\to \mathrm{finite}$ as $a/W\to 0$ under thermal loading although ${F}_{1}, {F}_{2}\to 0$ under mechanical loading.

When $\alpha -2\beta \ne$ 0 $\mathrm{and }\ a/W\le {10}^{-3}$ in Fig. 9a, the SIF under uniform temperature change can be expressed by superposing the SIF under tension in Fig. 9b and the SIF due to a uniform interface stress in Fig. 9c as shown in the following equations.

$$K_{1} + iK_{2} = \left( {F_{1} + iF_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right), F_{1} = C_{1} \left( {W/a} \right)^{1 - \lambda } + D_{1,} { }F_{2} = C_{2} \left( {W/a} \right)^{1 - \lambda } + D_{2}$$

$$\begin{aligned} \sigma_{y0} & = \frac{{8G_{A} G_{B} \left( {\eta_{B}^{*} - \eta_{A}^{*} } \right)\Delta T}}{{G_{A} \left( {\kappa_{B} - 1} \right) - G_{B} \left( {\kappa_{A} - 1} \right) - 2\left( {G_{A} - G_{B} } \right)}} , \\ \eta_{m}^{*} & = \left\{ {\begin{array}{*{20}c} {\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{stress}}} \right)} \\ {\left( {1 + \nu_{m} } \right)\,\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{strain}}} \right)} \\ \end{array} } \right.\left( {m = A,B} \right) \\ \end{aligned}$$

In this study, the coefficients ${C}_{1}$,${C}_{2}$, ${D}_{1} ,{D}_{2}$ are tabulated in Tables 4, 5 in the whole range of α, β. The values of ${C}_{1}$,${C}_{2}$, ${D}_{1} ,{D}_{2}$ are insensitive of $a/W$ in the range $a/W\le 1{0}^{-2}$ and coincide with each other more than three significant digits in the range $a/W\le 1{0}^{-3}$. Therefore, the SIFs of the thermal stress field were presented under arbitrary material combinations.

When $\alpha -2\beta$ = 0 $\mathrm{and \ }a/W\le {10}^{-3}$ in Fig. 12a, due to the peculiar logarithmic singularity under thermal loading, the SIF of an interfacial edge crack in a bonded plate under uniform temperature change in Fig. 12a can be expressed in the following equations.

$$K_{1} + iK_{2} = \left( {F_{1} + iF_{2} } \right)\sigma_{x0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right), F_{1} = c_{1} \log \left( {a/W} \right) + d_{1,} { }F_{2} = c_{2} \log \left( {a/W} \right) + d_{2}$$

$$\begin{aligned} \sigma_{y0} & = \frac{{8G_{A} G_{B} \left( {\eta_{B}^{*} - \eta_{A}^{*} } \right)\Delta T}}{{G_{A} \left( {\kappa_{B} + 1} \right) - G_{B} \left( {\kappa_{A} + 1} \right) }} , \\ \eta_{m}^{*} & = \left\{ {\begin{array}{*{20}c} {\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{stress}}} \right)} \\ {\left( {1 + \nu_{m} } \right)\,\eta_{m} } & {\left( {{\mathrm{plane}}\,{\mathrm{strain}}} \right)} \\ \end{array} } \right.\left( {m = A,B} \right) \\ \end{aligned}$$

The values of ${c}_{1}$, ${c}_{2}$, ${d}_{1,}$, ${d}_{2}$ are insensitive of $a/W$ in the range $a/W\le 1{0}^{-2}$ and coincide with each other more than three significant digits in the range $a/W\le 1{0}^{-3}$. In this study, the coefficients ${c}_{1}$, ${c}_{2}$, ${d}_{1,}$, ${d}_{2}$ are expressed in Eq. (17), which can be used conveniently in the whole range of α $(=2\beta )$ with less than 1% error.

Suitable expressions of ${F}_{1},{F}_{2}$ are summarized in Table 7 by considering the double singular stress fields in Fig. 9 under arbitrary material combination. It should be noted that even when ${F}_{1},{F}_{2}\to \infty$, the coefficients ${C}_{1}$, ${C}_{2}$, ${D}_{1}$, ${D}_{2}$, ${c}_{1}$, ${c}_{2}$, ${d}_{1}$, ${d}_{2}$ are always finite and suitable to express${F}_{1}$, ${F}_{2}$. This is similar to the finite value of the stress intensity factors that can be used to evaluate cracks instead of the infinite stress value at the crack tip ${\sigma }_{y}\left(r\right)\to \infty$ that cannot be used when $r\to 0$. In Table 7, the expressions of ${F}_{1}$, ${F}_{2}$ are chosen to express the singular stress fields considering the difference between thermal loading and mechanical loading.

Appendices

Appendix A. Mesh independence of interface stress intensity factor obtained by the proportional method

The proportional method is useful for analyzing interface cracks by providing mesh-independent interface SIFs efficiently. Since the FEM results are mesh-independent, the obtained results can be regarded as the exact solution by using the exact reference solution. The detail of the accuracy discussion can be found in previous papers under mechanical loading [8, 15, 16]. For the readers’ convenience, in this paper, several examples of mesh independence will be shown by varying the minimum element size $e/a$ under thermal and mechanical loading.

Table 8 shows the SIFs ${F}_{1}$, ${F}_{2}$ of the short and long edge cracks in the bimaterial plate when $a/W={10}^{-5}$ and $a/W=$ 0.8. By varying the minimum element size $e/a$ around the crack, the SIFs are indicated under thermal and mechanical loading. The four-node quadrilateral elements are used and the minimum element sizes are $e/a={3}^{-6}/11$, ${3}^{-7}/11$, ${3}^{-8}/11$ for each FE model. The FEM mesh around the crack tip in the reference problem is the same as that of the unknown problem. In the analysis, the elastic parameters are fixed as α = 0.8 and β = 0.3. Table 8 shows that the results of ${F}_{1}$, ${F}_{2}$ are mesh-independent to more than three digits for both short and long cracks. Under the thermal loading, the proportional method provides the same level of accuracy under the mechanical loading. The expression ${F}_{1}={C}_{1}{(W/a)}^{1-\lambda }+{D}_{1,}{ F}_{2}={C}_{2}{(W/a)}^{1-\lambda }+{D}_{2}$ is significant in thermal loading since the SIF of a larger crack is always smaller (see Appendix B).

The coefficients ${C}_{1}$, ${C}_{2}$, ${D}_{1}$, ${D}_{2}$ in Eq. 14 can be analyzed by applying the proportional method on the basis of the illustration in Fig. 9a–c. Table 9 shows that the results of ${F}_{1}$, ${F}_{2}$ are mesh-independent to more than three digits when $a/W={10}^{-5}$ and ${10}^{-7}$. All values of ${C}_{1}$, ${C}_{2}$, ${D}_{1}$, ${D}_{2}$ in Table 4 and Table 5 are obtained by confirming more than three digits accuracy as shown in Table 9. As shown in Table 9, ${C}_{1}$, ${C}_{2}$, ${D}_{1}$, ${D}_{2}$ are useful for expressing short cracks because the constant values can be used for $a/W\le {10}^{-3}$. Instead, ${F}_{1}$, ${F}_{2}$ increase with decreasing $a/W.$

See Tables

Table 8 Mesh− independence of ${F}_{1}$, ${F}_{2}$ obtained by the proportional method in Fig. 9a, b (${K}_{1}+i{K}_{2}=({F}_{1}+i{F}_{2}){\sigma }_{y0}\sqrt{\pi a}(1+2i\varepsilon )$, $\alpha$ = 0.8, $\beta$ = 0.3, $a/W={10}^{-5}\ \mathrm{and}\ a/W=0.8$)

8 and

Table 9 Mesh− independence of ${C}_{1}$, ${C}_{2}$, ${D}_{1}$, ${D}_{2}$ obtained by the proportional method in Fig. 9b , c (${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{y0}\sqrt{\pi a}(1+2i\varepsilon )$, $\alpha$ = 0.8, $\beta$ = 0.3)

9.

Appendix B. Stress intensity factor solution of an edge interface crack in a bimaterial plate under thermal and mechanical loading in the whole range ${\varvec{a}}/{\varvec{W}}$ = 0 ~ 1.0

The stress intensity factor (SIF) was previously analyzed for an edge interface crack in a bimaterial plate subjected to tension ${{{\sigma}}}_{0}$ in Fig. 1 by varying material combinations systematically [7, 8]. Figure 16a shows some examples of ${{{F}}}_{1}$-${{a}}/{{W}}$ relations as well as ${{{K}}}_{1}$-${{a}}/{{W}}$ relations when α = 0.4 ~ 0.95 under fixed β = 0.3. As shown Fig.16a, ${{{F}}}_{1}\to {\infty }$ as ${{a}}/{{W}}\to 0$ when $\alpha (\alpha -2{{\beta}})$> 0. Figure 16b shows the log–log plot of ${{{F}}}_{1}$-${{a}}/{{W}}$ relations to confirm the double singular stress behavior of ${{{F}}}_{1}$ in detail. According to Fig. 16b, it can be seen that ${{{F}}}_{1}$ can be expressed as shown in Eq. (B1) in the range of ${{a}}/{{W}}\le {10}^{-3}$. Here, ${{\lambda}}$ is the singularity index at the interface end without crack.

$${F}_{1}={C}_{1}\cdot{(W/a)}^{1-\lambda }$$

(B1)

In other words, Fig. 16b shows that the dimensionless stress intensity factor ${F}_{1}={C}_{1}{(W/a)}^{1-\lambda }$ is controlled by the singular stress field without crack, which can be expressed as shown in Eq. (1), that is, ${\sigma }_{y}(r)={K}_{\sigma }/{r}^{1-\lambda }$. As shown in Fig. 10, the values of ${C}_{1}$ and ${C}_{2}$ are independent of $a/W$ and coincide with each other more than four significant digits in the range $a/W\le 1{0}^{-3}$. In the previous studies, the SIF solution when $a/W\le 1{0}^{-3}$ in Fig.16 was provided under arbitrary material combinations. The SIFs are expressed by considering the character of the double singular stress field as shown in Eq. (B2).

${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{0}\sqrt{\pi a}\left(1+2i\varepsilon \right)$ in Fig. 1 when $a/W\le 1{0}^{-3}$:

$$ \left\{ {\begin{array}{*{20}l} {{\mathrm{When}}\; \alpha \left( {\alpha - 2\beta } \right) > 0:} \hfill & {F_{1} = C_{1} (W/a)^{{1 - \lambda }} ,F_{2} = C_{2} (W/a)^{{1 - \lambda }} }, C_{1}, C_{2} \rightarrow {\text{finite}} \;(a/W \rightarrow 0), 0<\lambda<1 \hfill \\ {{\mathrm{When}}\;\alpha \left( {\alpha - 2\beta } \right) = 0:} \hfill & {F_{1} = C_{1} = 1.121 + 0.0128\beta - 0.253\beta ^{2} ,F_{2} = C_{2} = 0.029\beta + 0.0526\beta ^{2} }, \lambda =1\hfill \\ {{\mathrm{When}} \;\alpha \left( {\,\alpha - 2\beta } \right) < 0:} \hfill & {F_{1} = C_{1} (W/a)^{{1 - \lambda }} ,F_{2} = C_{2} (W/a)^{{1 - \lambda }} }, C_{1}, C_{2} \rightarrow {\text{finite}} \;(a/W \rightarrow 0), \lambda >1 \hfill \\ \end{array} } \right. $$

(B2)

Figure 16c shows some examples of ${{{K}}}_{1}-{{a}}/{{W}}$ relations subjected to the remote tensile stress ${{{\sigma}}}_{0}=1$ when α = 0.4 ~ 0.95 under fixed β = 0.3. As shown Fig.16c, the stress intensity factor ${{{K}}}_{1}$ increases with increasing the relative crack length ${{a}}/{{W}}$. The value of ${{{K}}}_{2}$ also increases with increasing ${{a}}/{{W}}$ in a similar way of ${{{K}}}_{1}$.

See Fig. 

Fig. 16

${F}_{1}$ in Eq. B1 as ${K}_{1}+i{K}_{2}=\left({F}_{1}+i{F}_{2}\right){\sigma }_{0}\sqrt{\pi a}\left(1+2i\varepsilon \right)$ for an edge interface crack in a bimaterial plate when $\alpha$ = 0.4 ~ 0.95 under fixed β = 0.3

16.

Table 10 shows the SIFs ${F}_{1}$, ${F}_{2}$ of the edge crack in the bimaterial plate subjected to thermal and mechanical loading analyzed for various crack sizes $a/W = 10^{ - 5} \sim 0.8$. For thermal loading, ${F}_{1}$, ${F}_{2}$ decrease rapidly with increasing $a/W$. Therefore, the expression ${F}_{1}={C}_{1}{(W/a)}^{1-\lambda }+{D}_{1,}{ F}_{2}={C}_{2}{(W/a)}^{1-\lambda }+{D}_{2}$ is significant in thermal loading since the SIF of a larger crack is always smaller.

See Table

Table 10 SIFs ${F}_{1}$, ${F}_{2}$ in 9a, b in the range $a/W = 10^{ - 5} \sim 0.8$ ($K_{1} + iK_{2} = \left( {F_{1} + iF_{2} } \right)\sigma_{y0} \sqrt {\pi a} \left( {1 + 2i\varepsilon } \right)$, $\alpha$= 0.8, $\beta$= 0.3)

10.

Appendix C. Derivation of equivalent stress ${{\varvec{\sigma}}}_{{\varvec{y}}0}$ and ${{\varvec{\sigma}}}_{{\varvec{x}}0}$ to express thermal singular stress field

In this study, the equivalent stress is used to express the stress intensity factor of the edge interfacial crack under the thermal loading [6]. Then, the equivalent tensile stress ${\sigma }_{y0}$ acting in the y-direction defined in Eq. (6) is used to express the power-type singularity ${r}^{\lambda -1}$ at the interface end, and the equivalent tensile stress ${\sigma }_{x0}$ acting in the x-direction defined in Eq. (15) is used to express the logarithmic-type singularity at the interface end.

See Fig. 17.

Fig. 17

Singular stress field caused by temperature change is equivalent to that caused by uniaxial tension in the y-direction

Figure 17 illustrates that the stress field due to a uniform temperature change $\Delta T$ in Fig. 17a can be expressed by superposing the stress fields caused by the boundary conditions in Fig. 17d,e. Figure 17a shows a bonded strip subjected to a uniform temperature change of $\Delta T$. As shown in Fig. 17b, if both materials are separated from each other, a difference of thermal strain along the interface, ${\varepsilon }_{x,A}^{T}-{\varepsilon }_{x,B}^{T}$, is produced because of the difference of the thermal expansion coefficients. This difference can be canceled by applying a certain uniform pressure ${\sigma }_{y}=-{\sigma }_{y0}$ to those plates, as shown in Fig. 17c. Assuming that the difference due to the uniform pressure ${\sigma }_{y}=-{\sigma }_{y0}$ is equal to ${\varepsilon }_{x,A}^{\sigma }-{\varepsilon }_{x,B}^{\sigma }$, the condition along the interface in Fig. 17c can be expressed in Eq. (C1).

$${\varepsilon }_{x,A}^{T}-{\varepsilon }_{x,B}^{T}-\left({\varepsilon }_{x,A}^{\sigma }-{\varepsilon }_{x,B}^{\sigma }\right)=0 \to \left({\eta }_{A}^{*}-{\eta }_{B}^{*}\right)\Delta T-\left(-\frac{{\nu }_{A}^{*}}{{E}_{A}^{*}}+\frac{{\nu }_{B}^{*}}{{E}_{B}^{*}}\right){\sigma }_{y0}=0$$

(C1)

As shown in Fig. 17d, two plates have no difference in the width of interface and can be bonded to each other. In order to be the same as the boundary conditions in Fig. 17a, an additional tensile stress ${{\sigma}}_{{y}}={{\sigma}}_{{y}0}$ should be applied in Fig. 17e. Therefore, the equivalent stress ${{\sigma}}_{{{y}}0}$ can be expressed in Eq. (C2).

$${\sigma }_{y0}=\frac{({\eta }_{B}^{*}-{\eta }_{A}^{*})\Delta T}{\frac{{\nu }_{B}^{*}}{{E}_{B}^{*}}-\frac{{\nu }_{A}^{*}}{{E}_{A}^{*}}}$$

(C2)

Equation (C2) can be written as shown in Eq. (C3) by using the relations ${{{E}}}_{{{m}}}=2(1+{{{\nu}}}_{{{m}}}){{{G}}}_{{{m}}}$ and ${{{\kappa}}}_{{{m}}}=(3-{{{\nu}}}_{{{m}}})/(1+{{{\nu}}}_{{{m}}})$ for plane stress, ${{{\kappa}}}_{{{m}}}=3-4{{{\nu}}}_{{{m}}}$ for plane strain (m = A, B).

$${\sigma }_{y0}=\frac{8{G}_{A}{G}_{B}\left({\eta }_{B}^{*}-{\eta }_{A}^{*}\right)\Delta T}{{G}_{A}\left({\kappa }_{B}-1\right)-{G}_{B}\left({\kappa }_{A}-1\right)-2\left({G}_{A}-{G}_{B}\right)},$$

$${\eta }_{m}^{*}=\left\{\begin{array}{c}{\eta }_{m} \mathrm{\quad (plane\,stress)}\\ \left(1+{\nu }_{m}\right){\eta }_{m} \mathrm{\quad (plane\,strain)}\end{array} (m=A, B)\right.$$

(C3)

When $\alpha -2\beta =0$, the logarithmic singularity occurs near the interface end. As shown in Eq. (C4), the denominator of Eq. (C3) becomes zero, and the equivalent stress ${\sigma }_{y0}$ cannot be applied.

$$\alpha -2\beta =0 \to {G}_{A}\left({\kappa }_{B}-1\right)-{G}_{B}\left({\kappa }_{A}-1\right)-2\left({G}_{A}-{G}_{B}\right)=0$$

(C4)

See Fig. 18.

Fig. 18

Singular stress field caused by temperature change is equivalent to that caused by uniaxial tension in the x-direction

Figure 18 illustrates that the stress field due to a uniform temperature change $\Delta T$ in Fig. 18a can be expressed as the one due to the equivalent tensile stress in the x-direction. As shown in Fig. 18b, if both materials are separated from each other, a difference of thermal strain along the interface, ${\varepsilon }_{x,A}^{T}-{\varepsilon }_{x,B}^{T}$, is produced because of the difference of the thermal expansion coefficients. Fig. 18c shows that the same difference can also be produced by applying a certain uniform tension in the x-direction to those plates as shown in Eq. (C5).

$${\varepsilon }_{x,A}^{T}-{\varepsilon }_{x,B}^{T}={\varepsilon }_{x,A}^{\sigma }-{\varepsilon }_{x,B}^{\sigma } \to ({\eta }_{A}^{*}-{\eta }_{B}^{*})\Delta T=\left(\frac{1}{{E}_{A}^{*}}-\frac{1}{{E}_{B}^{*}}\right){\sigma }_{x0}$$

(C5)

Therefore, the equivalent stress ${{{\sigma}}}_{{{x}}0}$ in the x-direction can be expressed in Eq. (C6).

$${\sigma }_{x0}=\frac{({\eta }_{B}^{*}-{\eta }_{A}^{*})\Delta T}{\frac{1}{{E}_{B}^{*}}-\frac{1}{{E}_{A}^{*}}}=\frac{8{G}_{A}{G}_{B}\left({\eta }_{B}^{*}-{\eta }_{A}^{*}\right)\Delta T}{{G}_{A}\left({\kappa }_{B}+1\right)-{G}_{B}\left({\kappa }_{A}+1\right)}$$

(C6)