1 Introduction

Dry sandy materials have a unique resistive character normally used to construct reinforced structures with geosynthetic reinforcement. This type of material is broadly used in bridge construction, buildings construction, and many more. The sandiness in the Earth's crustal layers is of essential characteristics and could not be neglected while modeling the geological problems. Therefore, sandiness is to be taken into account, along with elasticity. In the solid mechanics and fractures mechanics field, problems related to punch is one of the exciting subjects, particularly in possessing diverse dynamic, physical, and technical applications involving ballistic impact, explosives, metal forming, and manufacturing operations punching and blanking. Nowadays, significant consideration was drawn relating to determining the stress and strain fields in elastic solids having finite dimension punches or cracks. In the dynamics case the punch strikes the material with finite velocity; hence, the propagation of waves confounds the mathematical analysis. More specifically, in geophysical prospecting, the propagation of seismic waves shows a significant role in an anisotropic medium. The application of the Wiener–Hopf technique in dynamic elasticity problems has been discovered by Abrahams [1] and Koiter [2]. The solution of a matrix Wiener–Hopf equation connected with a diffraction plane wave by impedance loaded parallel plate waveguide was examined by Büyükaksoy and Çınar [3]. With the help of the Laplace transform technique, Miklowitz [4] discussed the linear problem of plane stress unloading waves emanating from a suddenly punched hole in the stretched elastic plate. Dhaliwal [5] studied the problem related to the punch for an elastic layer. Wave propagation in elastic solids was explored by Achenbach [6]. Keer and Parihar [7] explained the singularity at the corner of a wedge-shaped crack or punch by using Green's function method. The problem of the highly orthotropic elastic layer with the help of WH-technique and integral transforms due to a moving punch was discussed by Georgiadis [8]. The problem of frictional crack and punch in-plane elasticity was explored by Hasebe et al. [9]. Under horizontal impulsive punch loading, the solution for the horizontal displacement at the center of an elastic half-space surface was studied by Jin and Liu [10]. The contact problem of a rigid punch was discussed by Comez and Guler [11] and Çömez [12]. The impact of gravity due to a torsional surface wave in the dry sandy medium was examined by Dey et al. [13]. In a dry sandy medium, the impact of initial stress and gravity due to torsional surface waves was studied by Dey et al. [14]. Naeini and Baziar [15] discussed the effect of fines content on the steady-state strength of mixed and layered samples of sand. The propagation of a crack in bi-material dry sandy medium influenced by an SH-wave under harmonic and non-harmonic loading conditions was studied by Singh et al. [16].

The initial stress is the stress present in a body not due to external forces. It is well known that the Earth is an initially stressed medium. The initial stress might arise due to applied loads, gravity, atmospheric pressure, creep, or temperature differences. Inside the Earth, many kinds of initial stress may exist. Further, the initial stress affects the propagation of seismic waves, which are generated by any artificial process or natural phenomena. Therefore, it is necessary to study the effect of initial stress on surface seismic wave propagation. Du et al. [17] analytically studied the effect of initial stress on layered magneto-electro-elastic structures due to propagating a Love-type wave. The effect of initial stress on guided waves in different material structures was examined by Yu and Zhang [18, 19]. Further, the shear wave propagation in vertically heterogeneous two distinct layers overlying an isotropic half-space with initial stress was studied by Singh et al. [20]. The impact of heterogeneity, initial stress, and anisotropy on propagating seismic surface waves was studied by Mahanty et al. [21]. Ejaz and Shams [22] discussed Rayleigh wave propagation in incompressible hyperelastic materials with initial stress. Plane wave reflection/transmission in imperfectly bonded rotating piezothermoelastic fiber-reinforced half-spaces with initial stress was examined by Guha and Singh [23].

The present work aims to develop a mathematical model for studying the effect of a semi-infinite smooth moving punch on shear wave propagation in an initially stressed dry sandy strip for the case of constant load. The Wiener–Hopf technique and Fourier integral transform have been implemented to obtain the closed-form expression of dynamic stress concentration. Remarkable effects of numerous physical parameters viz. speed of the moving punch, horizontal initial stress, vertical initial stress, and sandiness parameter on the dynamic stress concentration are shown by graphs. Moreover, a comparative study of dynamic stress concentration has also been carried out for different cases of initial stresses and differently configured strips, which is the major highlight of the problem.

2 Formulation and geometry of the problem

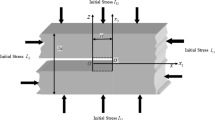
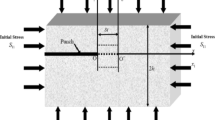
In a rectangular system \(\left( {x,y,z} \right)\) of coordinates, let us consider an infinite strip \(- a \le z \le a\) in which a smooth semi-infinite punch is pressed at \(x \le 0.\) The upper and lower surface i.e., \(z = \pm a\) are rigidly clamped as shown in Fig. 1. The horizontal initial stress \(\left( {I_{11} } \right)\) acts along the \(x -\) direction, and vertical initial stress \(\left( {I_{33} } \right)\) acts along the \(z -\) direction.

Fig. 1
figure 1

Geometrical sketch of the problem

Full size image

The shear stress \(\tau_{23}\) is subjected to the surface of the semi-infinite punch, which is moving with constant speed ‘\(s\)’ in the positive direction of the \(x -\) axis associated with shear wave propagation in the considered strip.

The constitutive equation for a dry sandy elastic model can be written as (Mandi et al. [24])

$$\tau_{ij} = \lambda \delta_{ij} e_{kk} + 2\frac{\mu }{\eta }e_{ij} ,\quad \eta > 1,$$
(1)

where \(\tau_{ij}\) are components of stress, \(e_{ij}\) are components of strain, \(\lambda \,\) and \(\mu\) are Lamé’s constants, \(\eta\) represents the sandiness parameter, and \(\delta_{ij}\) is the Kronecker delta.

The governing equation of motion without body forces is

$$\tau_{ij,j} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},$$
(2)

where \(u_{i}\) are the components of displacement, \(\rho\) denotes the density of the medium, and \(t\) denotes the time.

The governing equations of motion for the strip can be written as by Biot [25],

$$\tau_{ij,j} + \frac{\partial }{{\partial x_{j} }}\left( {I_{jk} \hbar_{ik} + I_{jk} e_{ij} \delta_{ij} - I_{ik} e_{kj} } \right) = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},$$
(3)

where \(\hbar_{ij} = \frac{1}{2}\left( {u_{i,j} - u_{j,i} } \right)\) denote the local angles of rotation components and \(I_{ij} (i,j,k = 1,\,2,\,3)\) represent the components of initial stresses.

If \(u,v,w\) are the displacement components in \(x,y,z\) directions, respectively, then for a shear wave propagating in the \(x -\) direction and causing displacement in the \(y -\) direction only, we assume that

$$u = w = 0\,,\,\,v = v\,\,(x,z,t),\,\frac{\partial }{\partial y} = 0.$$
(4)

In view of Eqs. (4) and (3), we obtain

$$\frac{{\partial \tau_{21} }}{\partial x} + \frac{{\partial \tau_{23} }}{\partial z} + \frac{{I_{11} }}{2}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{I_{33} }}{2}\frac{{\partial^{2} v}}{{\partial z^{2} }} = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }},$$
(5)
$${\text{where}}\;\tau_{21} = \frac{\mu }{\eta }\left( {\frac{\partial v}{{\partial x}}} \right),\;{\text{and}}\;\tau_{23} = \frac{\mu }{\eta }\left( {\frac{\partial v}{{\partial z}}} \right).$$
(6)

With the aid of Eqs. (6), and (5), we have

$$R\frac{{\partial^{2} v}}{{\partial z^{2} }} + S\frac{{\partial^{2} v}}{{\partial x^{2} }} = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }},$$
(7)
$${\text{where}}\;R = \frac{\mu }{\eta } + \frac{{I_{33} }}{2},\,\,S = \frac{\mu }{\eta } + \frac{{I_{11} }}{2}.$$
(8)

For setting the frame of reference using Galilean transformation we replace the frame \(\left( {x,y,z} \right)\) by the convective frame \(\left( {x_{1} ,x_{2} ,x_{3} } \right)\) as

$$x = x_{1} + st,\,\,y = x_{2} ,\,\,z = x_{3} .$$
(9)

In view of the above Galilean transformation (9) and Eq. (6), Eq. (5) reduces to

$$R\frac{{\partial^{2} v}}{{\partial x_{3}^{2} }} + \left( {S - \rho s^{2} } \right)\frac{{\partial^{2} v}}{{\partial x_{1}^{2} }} = 0,$$
(10)

and the shear stress reduces to

$$\tau_{23} \left( {x_{1} ,x_{3} } \right) = R\frac{\partial v}{{\partial x_{3} }} = \left( {\frac{\mu }{\eta } + \frac{{I_{33} }}{2}} \right)\frac{\partial v}{{\partial x_{3} }}.$$
(11)

3 Boundary conditions and solution of the problem

The boundary conditions of the considered problem are defined as

$$\left. \begin{gathered} v\left( {x_{1} ,x_{3} } \right) = 0\,\,\,\,\,\,{\text{for}}\,\left| {x_{1} } \right| < \infty ,\,x_{3} = a, \hfill \\ v\left( {x_{1} ,x_{3} } \right) = \varphi (x_{1} )\,\,{\text{for}}\,x_{1} < 0,\,\,x_{3} = 0, \hfill \\ \tau_{23} \left( {x_{1} ,x_{3} } \right) = 0\,\,{\text{for}}\,\,x_{1} > 0\,,\,\,\,\,x_{3} = 0, \hfill \\ \end{gathered} \right\}$$
(12)

where \(\varphi \left( {x_{1} } \right)\) is the displacement due to the moving punch in the \(x_{1} -\) direction.

Thus, Eqs. (10), (11), and (12) together establish a complete mathematical model for the present problem.

We consider the Fourier integral transform for an analytical solution of the problem, which is defined as

$$P\left( {\chi ,x_{3} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{\infty } {p\left( {x_{1} ,x_{3} } \right)} \,e^{{i\chi x_{1} }} dx_{1} ,$$
(13)
$${\text{and}}\;p\left( {x_{1} ,x_{3} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty + i\delta }^{\infty + i\delta } {P\left( {\chi ,x_{3} } \right)} \,e^{{ - i\chi x_{1} }} d\chi ,$$
(14)

where \(\chi\) denotes the complex transform variable such that the Fourier transform \(P\left( {\chi ,x_{3} } \right)\) is analytic along the integration path and \(i\delta\) represents the purely imaginary number lying in the common strip of regularity of all the transforms appearing in the solution.

With the help of properties of a regular function \(P\left( {\chi ,x_{3} } \right)\) can be written as (Titchmarsh [26])

$$P\left( {\chi ,x_{3} } \right) = P\,^{ - } \left( {\chi ,x_{3} } \right) + P\,^{ + } \left( {\chi ,x_{3} } \right),$$
(15)

where

$$\left. \begin{gathered} P^{ - } \left( {\chi ,x_{3} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {p\left( {x_{1} ,x_{3} } \right)} \,e^{{i\chi x_{1} }} dx_{1} , \hfill \\ {\text{and}}\,\,P^{ + } \left( {\chi ,x_{3} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{0}^{\infty } {p\left( {x_{1} ,x_{3} } \right)} \,e^{{i\chi x_{1} }} dx_{1} , \hfill \\ \end{gathered} \right\}$$
(16)

are regular functions in the half-plane \({\text{imag}}\;\left( \chi \right)\; < \delta_{2} \,{\text{and}}\;\,{\text{imag}}\;\left( \chi \right)\;{ < }\delta_{1} ,\) respectively, and \(i\delta_{1} \,\,{\text{and}}\,\,i\delta_{2}\) represent purely imaginary numbers lying in the common strip of regularity of the transforms \(P^{ - } \left( {\chi ,x_{3} } \right)\,\,{\text{and}}\,\,P^{ + } \left( {\chi ,x_{3} } \right),\) respectively.

With the aid of the Fourier integral transform (15), (16), Eqs. (10) and (11) lead to

$$\frac{{d^{2} V\left( {\chi ,x_{3} } \right)}}{{dx_{3}^{2} }} - \gamma^{2} \chi^{2} V\left( {\chi ,x_{3} } \right) = 0,$$
(17)

and the shear stress is

$$\tau_{23} \left( {\chi ,x_{3} } \right) = \left( {\frac{\mu }{\eta } + \frac{{I_{33} }}{2}} \right)\frac{\partial V}{{\partial x_{3} }}.$$
(18)

The solution of Eq. (17) can be written as

$$V\left( {\chi ,x_{3} } \right) = C_{1} \left( \chi \right)\sinh \left( {\chi \gamma x_{3} } \right) + C_{2} \left( \chi \right)\cosh\left( {\chi \gamma x_{3} } \right),$$
(19)

where \(C_{\,1} \left( \chi \right)\,{\text{and}}\,C_{\,2} \left( \chi \right)\) are arbitrary constants, and \(\gamma = \left( {\frac{S}{R} - \frac{{\rho s^{2} }}{R}} \right)^{\frac {1} {2}}.\)

In view of Eqs. (18) and (19), we obtain

$$\tau_{23} \left( {\chi ,x_{3} } \right) = \left( {\frac{\mu }{\eta } + \frac{{I_{33} }}{2}} \right)\left( {\chi \gamma } \right)\left[ {C_{\,1} \left( \chi \right)\cosh\left( {\chi \gamma x_{3} } \right) + C_{\,2} \left( \chi \right)\sinh\left( {\chi \gamma x_{3} } \right)} \right].$$
(20)

Applying the Fourier integral transform (13) and (14) to the boundary condition (12) and with the help of Eqs. (19) and (20), we get the following Wiener–Hopf equation:

$$\tau_{23}^{ - } \left( {\chi ,\,0} \right) =- \left( {\frac{\mu }{\eta } + \frac{{I_{33} }}{2}} \right)\left( {\gamma \chi } \right)\left\{ {\frac{{\varphi \left( \chi \right) + V^{ + } (\chi ,0)}}{{\tanh \left( {\chi \gamma a} \right)}}} \right\},$$
(21)
$${\text{where}}\;\varphi \left( \chi \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {\varphi \left( {x_{1} } \right)e^{{i\chi x_{1} }} dx_{1} } .$$
(22)

The domain of existence of Eq. (21) is in the range \(- \frac{\pi }{2\gamma a} < - \varepsilon < \;{\text{imag}}\left( \chi \right){ < 0},\) and the kernel of Eq. (21) is

$$F\left( \chi \right) = \frac{\chi }{{\tanh \left( {\chi \gamma a} \right)}},$$
(23)

which can be further expressed in the form of the \(\Gamma -\) function as (Noble, [27])

$$F\left( \chi \right) = \frac{\pi }{\gamma a}F^{ + } \left( \chi \right)F^{ - } \left( \chi \right),$$
(24)
$${\text{where}}\;F^{ + } \left( \chi \right) = \frac{{\,\Gamma \left( {1 - \frac{i\chi a\gamma }{\pi }} \right)}}{{\,\Gamma \left( {\frac{1}{2} - \frac{i\chi a\gamma }{\pi }} \right)}},\,\,{\text{and}}\,\,F^{ + } \left( { - \chi } \right) = F^{ - } \left( \chi \right).$$
(25)

The functions \(\left\{ {\Gamma \left( {1 + \frac{i\chi a\gamma }{\pi }} \right),\Gamma \left( {\frac{1}{2} + \frac{i\chi a\gamma }{\pi }} \right)} \right\}\,\,{\text{and}}\,\,\left\{ {\Gamma \left( {1 - \frac{i\chi a\gamma }{\pi }} \right),\Gamma \left( {\frac{1}{2} - \frac{i\chi a\gamma }{\pi }} \right)} \right\}\) are analytic and free from zeroes in the half-planes \({\text{imag}}\left( \chi \right) < \frac{\pi }{2\gamma a}\,\,{\text{and}}\,\,{\text{imag}}\left( \chi \right) > \frac{ - \pi }{{2\gamma a}}\,,\) respectively.

In view of Eqs. (8), (23), and (24), Eq. (21) takes the form

$$- \frac{{a\,\tau_{23}^{ - } \left( {\chi ,0} \right)}}{{\pi RF^{ - } \left( \chi \right)}} = F^{ + } \left( \chi \right)V^{ + } \left( {\chi ,0} \right) + T\left( \chi \right),$$
(26)
$${\text{where}}\;T\left( \chi \right) = F\,^{ + } \left( \chi \right)\varphi \left( \chi \right).$$
(27)

With the help of properties of the  regular function \(T\left( \chi \right)\) in the corresponding half-planes \({\text{imag}}\left( \chi \right) > - \varepsilon\) and \({\text{imag}}\left( \chi \right) < 0\) can be written as the following system (Titchmarsh, [26]):

$$T\left( \chi \right) = T\,^{ + } \left( \chi \right) - T\,^{ - } \left( \chi \right),$$
(28)
$${\text{where}}\;T^{\, + } \left( \chi \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty - i\tau_{1} }}^{{\infty - i\tau_{1} }} {\frac{T\left( \nu \right)}{{\nu - \chi }}d\nu } ,$$
(29)
$${\text{and}}\;T^{ - } \left( \chi \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty + i\tau_{2} }}^{{\infty + i\tau_{2} }} {\frac{T\left( \nu \right)}{{\nu - \chi }}d\nu } ,$$
(30)

in which, \(- \tau_{1} < {\text{imag}}\left( \chi \right) < \tau_{2} \,\,{\text{and}}\,\,i\tau_{1} ,\,\,i\tau_{2} ,\) lie within the required strip of regularity, and \(T^{ + } \left( \chi \right)\,,T^{ - } \left( \chi \right)\) are regular in the half-planes \({\text{imag}}\left( \chi \right) > \,\frac{ - \pi }{{2\gamma a}},\,\,{\text{and}}\,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0,}\) respectively.

In view of Eq. (28), Eq. (26) can be written as

$$- \frac{{a\,\tau_{23}^{ - } \left( {\chi ,0} \right)}}{{\pi RF^{ - } \left( \chi \right)}} + T\,^{ - } \left( \chi \right) = F^{ + } \left( \chi \right)V^{ + } \left( {\chi ,0} \right) + T\,^{ + } \left( \chi \right).$$
(31)

Both the sides of Eq. (31) are regular and free from zeroes in the respective half-planes \({\text{imag}}\left( \chi \right) > \,\frac{ - \pi }{{2\gamma a}}\,\,{\text{and}}\,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0}{\text{.}}\) Now using Liouville’s theorem, we have

$$V^{ + } (\chi ,0) = - \frac{{T^{ + } \left( \chi \right)}}{{F^{ + } \left( \chi \right)}},\quad {\text{which is regular in}}\,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0,}$$
(32)
$${\text{and}}\;\tau_{23}^{ - } \left( {\chi ,0} \right) = \frac{\pi R}{a}T^{ - } \left( \chi \right)F^{ - } \left( \chi \right),\quad {\text{which is regular in }}{\text{imag}}\left( \chi \right) > \,\frac{ - \pi }{{2\gamma a}}\,.$$
(33)

Now we are considering that the functions \(T^{ + } \left( \chi \right)\,\) and \(T^{ - } \left( \chi \right)\,\) are analytic in the region \(\,\frac{ - \pi }{{2\gamma a}}\,\, < \,\,{\text{imag}}\left( \chi \right)\,{ < }\,{0}\). Therefore, the function \(T^{ + } \left( \chi \right)\,\) and \(T^{ - } \left( \chi \right)\,\) can be written in the following form:

$$T^{ \pm } \left( \chi \right) = - \frac{1}{\chi }\left\{ {Q - \frac{1}{2\pi i}\int\limits_{ - \infty - i\tau }^{\infty - i\tau } {\frac{T\left( \nu \right)}{{\nu - \chi }}d\nu } } \right\},$$
(34)

where

$$Q = \frac{1}{2\pi i}\int\limits_{ - \infty - i\tau }^{\infty - i\tau } {T\left( \nu \right)} \,d\nu ,\quad \tau_{1} < \tau < \tau_{2} .$$
(35)
$${\text{Now using}}\;\frac{{\Gamma \left( {\xi + \zeta } \right)}}{\Gamma \left( \xi \right)} \approx \xi^{\zeta } ,\,\,\left| \xi \right| \to \infty \; \left( {{\text{Noble}}, \, \left[ {{27}} \right]} \right),$$
(36)

and using Eq. (34), the functions \(V^{ + } (\chi ,0)\,\,\,{\text{and}}\,\,\,\tau_{23}^{ - } (\chi ,0)\,\) defined by Eqs. (32) and (33) become

$$V\,^{ + } \left( \chi \right) = \frac{Q}{\chi }\sqrt { - \frac{\pi }{ia\chi \gamma }} ,$$
(37)
$${\text{and}}\;\tau_{23}^{ - } \left( \chi \right) = - QR\sqrt {\frac{i\pi \gamma }{{a\chi }}} .$$
(38)

By mean of Abel’s theorems (Noble, [27]), Eqs. (37) and (38) can be written as

$$\tau_{23} \left( {x_{1} } \right) = \frac{N\gamma R}{{2\sqrt { - x_{1} } }},{\text{for}}\;\,x_{1} \to - \varepsilon ,\,\,\varepsilon \to 0,$$
(39)
$${\text{and}}\;v\left( {x_{1} } \right) = N\sqrt {x_{1} } ,\,{\text{for}}\,x_{1} \to + \varepsilon ,\,\,\varepsilon \to 0,$$
(40)

where \(N = - 2\pi i\sqrt {\frac{2\pi }{{a\gamma }}} .\)

In the above expression \(N\) represents the expression of dynamic stress concentration.

4 Punch  subjected to constant load

In this Section, we consider that the edge \(x_{3} = 0\) of the punch is loaded by a force of intensity \(J_{0} ,\) which is constant, i.e.,

$$\varphi \left( {x_{1} } \right) = J_{0} .$$
(41)

Inserting Eq. (41) into Eq. (22) leads to

$$\varphi (\chi ) = \frac{{J_{0} }}{{i\chi \sqrt {2\pi } }}.$$
(42)

With the help of Eqs. (24), (25), (36), (38), (39), and (42), we get

$$\frac{1}{\sqrt \gamma } = - \frac{{N\sqrt {\pi a} }}{{2J_{0} }},$$
(43)
$${\text{where}}\;\gamma = \left[ {\frac{{S^{^{\prime}} }}{{R^{^{\prime}} }} - \frac{{\left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s \beta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\beta $}}} \right)^{2} }}{{R^{^{\prime}} }}} \right]^{\frac{1}{2}} ,$$
(44)

where \(\,\,S^{^{\prime}} = \left[ {\frac{1}{\eta } + S_{11} } \right],R^{^{\prime}} = \left[ {\frac{1}{\eta } + S_{33} } \right]\,,\,\) \(S_{11} = \frac{{I_{11} }}{2\mu }\,\), and \(S_{33} = \frac{{I_{33} }}{2\mu }\) are the dimensionless horizontal and vertical initial stresses, respectively, and \(\beta = \sqrt {\frac{\mu }{\rho }}\) is the shear wave speed.

The above Eq. (43) represents the expression for dynamic stress concentration due to a smooth moving punch for constant load in an initially stressed dry sandy medium.

5 Special cases

5.1 When \(S_{11} = 0 = S_{33}\) (i.e., the considered strip is free from initial stresses, for which it becomes a dry sandy strip), then Eq. (44) yields

$$\gamma = \sqrt {1 - \eta \left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s \beta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\beta $}}} \right)^{2} } .$$
(45)

Taking Eq. (45) into account, Eq. (43) represents the expression of dynamic stress concentration in the dry sandy isotropic strip for constant load.

5.2 When \(\eta = 1\) (i.e., the considered strip is free from sandiness, for which it becomes an initially stressed isotropic strip), then Eq. (44) can be rewritten as

$$\gamma = \sqrt {\frac{{\left( {1 + S_{11} } \right)}}{{\left( {1 + S_{33} } \right)}} - \frac{{\left( {s/\beta } \right)^{2} }}{{\left( {1 + S_{33} } \right)}}} .$$
(46)

In view of Eq. (46), Eq. (43) leads to the expression of dynamic stress concentration in an initially stressed isotropic strip for constant load.

5.3 When \(S_{11} = 0 = S_{33}\) and \(\eta = 1\) (i.e., the considered strip is free from initial stresses and sandiness, for which it becomes a purely isotropic strip), then Eq. (44) reduces to

$$\gamma = \sqrt {1 - \left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s \beta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\beta $}}} \right)^{2} } .$$
(47)

Equation (43) together with Eq. (47) shows the expression of dynamic stress concentration in the isotropic strip for constant load. This result is found in well agreement with the results (expression for dynamic stress concentration) obtained by Chattopadhyay [28] for reinforced-free case (i.e., \(\mu_{L} = \mu_{T} ,\) where \(\mu_{T}\) represents the shear modulus in transverse shear across the preferred direction, and \(\mu_{L}\) denotes the shear modulus in longitudinal shear in the preferred direction) and also with the results obtained by Singh et al. [29] for the isotropic case without viscoelasticity and initial stress (i.e., \(\,\mu^{\prime} = 0,\,\frac{{S_{11} }}{2\mu } = 0 = \frac{{S_{33} }}{2\mu },\) where \(\mu^{\prime}\) is the parameter responsible for the effect of internal friction).

6 Computational results and discussion

To carry out the numerical calculations and graphical demonstrations of the various affecting parameters on the dynamic stress concentration under constant load in an initially stressed dry sandy strip, we considered the following data:

For dry sandy medium:\(\rho = 3364\,\,\left( {{\text{kg/m}}^{{3}} } \right),\)\(\mu = 6.34\, \times 10^{10} \,\left( {{\text{N/m}}^{{2}} } \right),\) (Gubbins, [30]).

Sandiness parameter \(\left( \eta \right) = 1.0,1.2,\,\,1.4,\,\,1.6,\,1.8,\)

Dimensionless horizontal initial stress \(\left( {S_{11} = I_{11} /2\mu } \right) = - 0.4,\,\, - 0.2,\,\,0.0,\,\,0.2,\,\,0.4,\)

Dimensionless vertical initial stress \(\left( {S_{33} = I_{33} /2\mu } \right) = - 0.4,\,\, - 0.2,\,\,0.0,\,\,0.2,\,\,0.4.\)

In order to describe the effects of various affecting parameters viz. sandiness parameter \(\left( \eta \right),\) horizontal initial stresses \(\left( {S_{11} } \right)\,\), and vertical initial stresses \(\left( {S_{33} } \right)\,\) on the dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against the dimensionless speed \(\left( {s/\beta } \right)\) of the moving punch, the mathematical simulation was accomplished by taking into account Eq. (43) for the case of constant load. Figures 2, 3, 4, 5, 6 graphically demonstrate the variation of dynamic stress concentration against the dimensionless speed of the moving semi-infinite punch. It is observed in Figs. 2, 3, 4, 5, 6 that at first the dynamic stress concentration increases with an increase in the speed of the moving punch associated with the shear wave speed at a slow rate, but after a certain stage it increases abruptly for both initially stressed strips with/without sandiness. Figure 2 shows the impact of the sandiness parameter on the dynamic stress concentration subjected to a moving punch associated with the shear wave propagation in the undertaken strip for constant load. In Fig. 2, curve 1 is associated with the case when the considered strip is free from sandiness, and curves 2, 3, 4, and 5 correspond to the case when the strip is initially stressed dry sandy. It is manifested from Fig. 2 that the dynamic stress concentration decreases when the sandiness parameter increases. It is established that the dynamic stress concentration is maximum when the considered strip is free from sandiness, and it is minimum when the strip is with the considered higher  value of the sandiness parameter.

Fig. 2
figure 2

Variation of dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against dimensionless speed \(\left( {s/\beta } \right)\) of the moving punch for distinct values of the sandiness parameter \(\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Variation of dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against dimensionless speed \(\left( {s/\beta } \right)\) of the moving punch for different values of the horizontal initial stress \(\left( {S_{11} } \right)\)

Full size image
Fig. 4
figure 4

Variation of dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against dimensionless speed \(\left( {s/\beta } \right)\) of moving punch for different values of vertical initial stress \(\left( {S_{33} } \right)\)

Full size image
Fig. 5
figure 5

Comparison of dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against dimensionless speed \(\left( {s/\beta } \right)\) of moving punch for different cases of initial stresses

Full size image
Fig. 6
figure 6

Comparative study of dynamic stress concentration \(\left( { - N\sqrt {\pi a} /2J_{0} } \right)\) against dimensionless speed \(\left( {s/\beta } \right)\) of moving punch for differently configured strip

Full size image

Figures 3 and 4 represent the effects of horizontal initial stresses and vertical initial stresses, respectively, on the dynamic stress concentration in the considered strip for constant load. In Fig. 3, curves 1, 2, 3, 4, and 5 correspond to horizontal initial stresses when the strip is initially stressed dry sandy, and curves 6, 7, 8, 9, and 10 represent horizontal initial stresses when the strip is free from sandiness. It is evident from Fig. 3 that the dynamic stress concentration decreases with an increase in horizontal initial stresses for both the cases separately (i.e., the strip is initially stressed dry sandy and is free from sandiness parameter). It is observed that the dynamic stress concentration attains higher values for the initially stressed dry sandy strip in contrast to the sandiness-free strip when the horizontal initial stress \(\left( {S_{11} } \right)\) takes values -0.4 and -0.2. When \(S_{11} = 0,\) the dynamic stress concentration is found to attain a higher value for the initially stressed dry sandy strip in contrast to the sandiness-free strip, up to a certain value of \(s/\beta ,\) past which the pattern reverses. When \(S_{11}\) increases and takes value 0.2, the pattern reversal occurs at a much earlier stage for a lower value of \(s/\beta .\) Lastly, when \(S_{11} = 0.4,\) it is observed that dynamic stress concentration attains a lower value for the initially stressed dry sandy strip in contrast to the sandiness-free strip for all considered values of \(s/\beta .\) Furthermore, in Fig. 4, curves 1, 2, 3, 4, and 5 correspond to the vertical initial stresses when the strip is initially stressed dry sandy and curves 6, 7, 8, 9, and 10 represent the vertical initial stresses when the strip is free from sandiness. It is noticed from Fig. 4 that the dynamic stress concentration increases with an  increase in vertical initial stresses for both cases when the strip is initially stressed dry sandy and it is free from sandiness. It is observed that the dynamic stress concentration attains a lower value for the initially stressed dry sandy strip in contrast to the sandiness-free strip when the vertical initial stress \(\left( {S_{33} } \right)\) takes values -0.4, -0.2, and 0.0. When \(S_{33} = 0.2,\) the dynamic stress concentration initially attains a higher value for the initially stressed strip with sandiness in contrast to the sandiness-free strip. However, starting from a small value of \(s/\beta ,\) the pattern reverses. Lastly, when \(S_{33} = 0.4,\) the dynamic stress concentration attains a higher value for the initially stressed strip with sandiness in contrast to the sandiness-free strip. However, starting from a moderate value of \(s/\beta ,\) the pattern reverses.

The combined effect of horizontal and vertical initial stresses on the dynamic stress concentration has been discussed in Fig. 5. Curves 1, 2, 3, 4, and 5 correspond to the case when the considered strip is free from sandiness, and curves 6, 7, 8, 9, and 10 represent the case when the strip consists of sandiness. It is reported from Fig. 5 that the dynamic stress concentration decreases for both cases when the initially stressed strip is with/without sandiness for increasing and equal value of horizontal and vertical initial stresses. It is observed that the dynamic stress concentration attains a lower value for the initially stressed dry sandy strip in contrast to the sandiness-free strip when the horizontal and vertical initial stresses \(\left( {S_{11} ,\,S_{33} } \right)\) take values -0.4 and -0.2. When \(S_{11} = S_{33} = 0,\) the dynamic stress concentration is found to attain a lower value for the initially stressed dry sandy strip in contrast to the sandiness-free strip, up to a certain value of \(s/\beta ,\) past which the pattern reverses. When \(S_{11} ,\,S_{33}\) increase and take value 0.2, the pattern reversal occurs at a much earlier stage for a lower value of \(s/\beta .\) Lastly, when \(S_{11} = S_{33} = 0.4,\) it is observed that the dynamic stress concentration attains a higher value for the initially stressed dry sandy strip in contrast to the sandiness-free strip for all considered values of \(s/\beta .\) Furthermore, the effects of horizontal initial stresses, vertical initial stresses, and sandiness parameter on the dynamic stress concentration have been examined in Fig. 6. In Fig. 6, curve 1 is associated with the case when the strip is initially stressed dry sandy, curve 2 corresponds to the case when the strip is initially stressed without sandiness, curve 3 represents the case when the considered dry sandy strip is free from initial stresses, and curve 4 corresponds to the case when the considered strip is free from initial stresses and sandiness. It is evident from Fig. 6 that the dynamic stress concentration is higher when the strip is without initial stresses as compared to the case when the strip is with initial stresses. It is also observed that under the influence of initial stresses the dynamic stress concentration of the strip without sandiness is larger in contrast to the one with sandiness. However, in the absence of initial stresses, the impact of sandiness on the dynamic stress concentration is also negligible.

7 Concluding remarks

The present study is concerned with the analysis of a semi-infinite moving punch associated with propagating shear waves in an initially stressed dry sandy strip for constant load. An exact expression of the dynamic stress concentration has been obtained in closed-form with the help of the Wiener–Hopf technique and Fourier integral transform. The effects of smooth moving punch, horizontal initial stresses, vertical initial stresses, and sandiness parameters on the dynamic stress concentration have been examined by the graphs. The exact solution of dynamic stress concentration under constant load in terms of the said parameters has been established. A comparative study has been accomplished to reveal the effects of initial stresses and sandiness. The salient features of the study are encapsulated as follows:

  • The closed-form expression of dynamic stress concentration for the case of constant load was established and matched with the pre-established results for validation.

  • Initially, the dynamic stress concentration increases with an increase in the speed of the moving punch associated with the shear wave speed at a slow rate but later it increases at a very fast rate and abruptly approaches toward its maximum value in both initially stressed strips with/without sandiness.

  • The dynamic stress concentration decreases with an increase in the sandiness parameter.

  • The dynamic stress concentration decreases with an increase in horizontal initial stresses. The dynamic stress concentration attains a higher value for an initially stressed dry sandy strip in contrast to the sandiness-free strip for low values of horizontal initial stress, and a pattern reversal occurs for higher values of horizontal initial stresses.

  • The dynamic stress concentration increases with an increase in vertical initial stresses. The dynamic stress concentration attains low values for an initially stressed dry sandy strip in contrast to the sandiness-free strip for the smaller values of vertical initial stress, and pattern reversal occurs for larger values of vertical initial stresses.

  • The dynamic stress concentration decreases for both cases when the initially stressed strip is with/without sandiness for increasing and equal value of horizontal and vertical initial stresses.

  • The dynamic stress concentration is higher when the strip is without initial stresses as compared to the case when the strip is with initial stresses. Under the influence of initial stresses, dynamic stress concentration of the strip without sandiness is larger in contrast to the one with sandiness. However, in the absence of initial stresses, the impact of sandiness on the dynamic stress concentration is also negligible.

The outcomes of the present work may aid in the study of structural and stability analysis, fracture initiation, and material toughness. The investigation of dynamic stress concentration for a semi-infinite smooth moving punch associated with a propagating shear wave in an initially stressed dry sandy strip might also lead to some essential contributions in building, bridge construction, and underground structures such as tunnels and pipelines subjected to natural calamities. Also, this study could find applications in many fields of applied sciences, for example, in the analysis of seismic data, soil mechanics, composite materials, civil engineering, and earthquake science.