1 Introduction

1.1 Background

Owing to their electromechanical coupling behavior, piezoelectric materials have been widely used in advanced instruments. However, fractures can cause safety accidents. Therefore, cracks, which represent their main disadvantages, have been extensively investigated [1,2,3,4,5,6,7,8,9,10]. With the emergence of piezoelectric bimaterials, the behavior of interfacial cracks has raised significant concerns [11,12,13].

However, all the above works have focused on static propagation. Recently, many researchers [14, 15] have studied the dynamic fracture of cracks. Narita [16] researched a crack in a piezoelectric layer. The results showed that designing piezoelectric devices was feasible and practical. The DSIF was obtained from Gu [17]. A semi-infinite interfacial crack and permeable cracks between two piezoelectric materials were analyzed [18, 19].

Piezoelectric films and coatings have recently emerged, which allow for the design of more sophisticated materials and devices and expand the range of piezoelectric material applications [20,21,22,23,24,25,26,27,28,29].

Piezoelectric thin-film/substrate materials are widely used in modern life. However, due to mismatched characteristics, piezoelectric thin-film/substrate materials tend to fracture at the interface under in-service loading conditions. Nonetheless, most of the abovementioned studies on the fracture of piezoelectric biomaterials have been focused on large grain sizes, and a few studies have been conducted on the fracture of micrometer-scale piezoelectric thin films, especially the dynamic analysis of multiple cracks in a piezoelectric thin film/ substrate. In addition, stress, thin film thickness, substrate thickness, and impact time play an essential role in the structural safety design of piezoelectric film/substrate. Thus, the investigation of these factors with the dynamic expansion of a piezoelectric film/substrate represents the innovation of the present study.

1.2 Outline

This paper is organized as follows. Section 2 presents in detail the constitutive equations and mixed initial boundary conditions. Section 3 provides the integral equations and calculates the DSIF under anti-plane mechanical stress and electric displacement impact loading. The DSIF under far-field forces and electric impact loading are provided in Sect. 4. The numerical examples are discussed in Sect. 5. The conclusions are provided in Sect. 6.

2 Problem statement and formulation

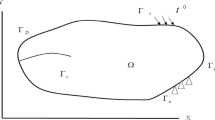
Figure 1 shows that the piezoelectric thin film and substrate occupy the domains \(\Omega_{1}\) and \(\Omega_{2}\), respectively. The film and substrate thicknesses are \(d_{1}\) and \(d_{2}\), respectively. Multiple interface cracks appear in the same direction and belong to this interval (\(a_{k} ,b_{k}\)) (\(k = 1,2, \ldots ,n\)), where \(a_{k}\) and \(b_{k}\) denote the left and right ends of the crack, respectively. We assume that the crack is in static equilibrium when \(t < 0\). The crack propagation velocity is \(v\). The crack tip is located at \(x = vt\) (\(t > 0\)).

Fig. 1
figure 1

Multiple interfacial propagating cracks between the piezoelectric thin film /substrate

Full size image

The dynamic anti-plane equilibrium equations of the piezoelectric thin film/substrate are written as

$$c_{44}^{(m)} \left( {\frac{{\partial^{2} w}}{{\partial X^{2} }} + \frac{{\partial^{2} w}}{{\partial Y^{2} }}} \right) + e_{15}^{(m)} \left( {\frac{{\partial^{2} \phi }}{{\partial X^{2} }} + \frac{{\partial^{2} \phi }}{{\partial Y^{2} }}} \right) = \rho^{(m)} \frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(1)
$$e_{15}^{(m)} \left( {\frac{{\partial^{2} w}}{{\partial X^{2} }} + \frac{{\partial^{2} w}}{{\partial Y^{2} }}} \right) - \varepsilon_{11}^{(m)} \left( {\frac{{\partial^{2} \phi }}{{\partial X^{2} }} + \frac{{\partial^{2} \phi }}{{\partial Y^{2} }}} \right) = 0,$$
(2)

where \(w = w(x,y,t)\) and \(\phi (x,y,t)\) represent the displacement components and the electric dielectric constants, respectively; \(\rho^{(m)}\) is the mass density; and \(m = 1,\)\(2\) signify the upper and lower materials, respectively.

A moving coordinate system is introduced as

$$x = X - vt,\;y = Y.$$
(3)

By using the transformation, Eq. (1) may be expressed as follows:

$$\left[ {1 - \left( {\frac{v}{{\overline{{c_{m} }} }}} \right)^{2} } \right]\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{e_{15}^{(m)} }}{{c_{44}^{(m)} }}\left( {\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right) = \left( {\frac{1}{{\overline{{c_{m} }} }}} \right)^{2} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - 2v\frac{{\partial^{2} w}}{\partial x\partial t}} \right)$$
(4)
$$\frac{{e_{15}^{(m)} }}{{c_{44}^{(m)} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) - \frac{{\varepsilon_{11}^{(m)} }}{{c_{44}^{(m)} }}\left( {\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right) = 0,$$
(5)

where \(\overline{{c_{m} }} = \left( {{{c_{44}^{(m)} } \mathord{\left/ {\vphantom {{c_{44}^{(m)} } {\rho^{(m)} }}} \right. \kern-\nulldelimiterspace} {\rho^{(m)} }}} \right)^{\frac{1}{2}}\) is the shear bulk wave velocity.

3 Anti-plane mechanical stress and electric displacement impact loading

The mixed mechanical boundary conditions of the issues become:

$$\tau_{yz} (x,0^{ + } ,t) = \tau_{yz} (x,0^{ - } ,t) = - \tau_{0} H(t),x \in (a_{k} ,b_{k} ),$$
(6)
$$D_{y} (x,0^{ + } ,t) = D_{y} (x,0^{ - } ,t) = - D_{0} H(t),x \in (a_{k} ,b_{k} ),$$
(7)
$$w(x,0^{ + } ,t) = w(x,0^{ - } ,t),x \notin (a_{k} ,b_{k} ),$$
(8)
$$\phi (x,0^{ + } ,t) = \phi (x,0^{ - } ,t),x \notin (a_{k} ,b_{k} ),$$
(9)
$$\tau_{yz} (x,0^{ + } ,t) = \tau_{yz} (x,0^{ - } ,t),x \notin (a_{k} ,b_{k} ),$$
(10)
$$D_{y} (x,0^{ + } ,t) = D_{y} (x,0^{ - } ,t),x \notin (a_{k} ,b_{k} ),$$
(11)
$$w(x,y^{ + } ,t) = w(x,y^{ - } ,t) = 0,\;x^{2} + y^{2} \to \infty,$$
(12)
$$\phi (x,y^{ + } ,t) = \phi (x,y^{ - } ,t) = 0,\;x^{2} + y^{2} \to \infty,$$
(13)
$$\tau_{yz} (x,d_{1} ,t) = \tau_{yz} (x, - d_{2} ,t) = 0,$$
(14)
$$D_{y} (x,d_{1} ,t) = D_{y} (x, - d_{2} ,t) = 0,$$
(15)

where \(D_{0}\) is the electric displacement, \(\tau_{0}\) is the stress, and \(H(t) = \left\{ {\begin{array}{*{20}c} {0,} \\ {1,} \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {t < 0}, \\ {t > 0}. \\ \end{array}\)

We assume that the piezoelectric biomaterials are at mechanical and electrical rest at \(t = 0\), which is

$$w(x,y,0) = 0,\;\frac{\partial w(x,y,0)}{{\partial t}} = 0,\; - \infty < x,y < + \infty .$$
(16)
$$\phi (x,y,0) = 0,\frac{\partial \phi (x,y,0)}{{\partial t}} = 0, - \infty < x,y < + \infty .$$
(17)

Following Li and Mataga [14, 15], a function is written as

$$\varphi = \phi - \frac{{e_{15}^{(m)} }}{{\varepsilon_{11}^{(m)} }}w.$$
(18)

3.1 Solution to the problem

The Fourier transform on \(x\) and Laplace transform on \(t\), we obtain [30]

$$w^{*} (\zeta ,y,p) = \int_{ - \infty }^{ + \infty } {\int_{0}^{ + \infty } {w(x,y,t)e^{ - pt} {\text{d}}te^{i\zeta x} {\text{d}}x} },$$
(19)
$$\phi^{*} (\zeta ,y,p) = \int_{ - \infty }^{ + \infty } {\int_{0}^{ + \infty } {\phi (x,y,t)e^{ - pt} {\text{d}}te^{i\zeta x} {\text{d}}x} },$$
(20)
$$\varphi^{*} (\zeta ,y,p) = \int_{ - \infty }^{ + \infty } {\int_{0}^{ + \infty } {\phi (x,y,t)e^{ - pt} {\text{d}}te^{i\zeta x} {\text{d}}x} } - \frac{{e_{15}^{(m)} }}{{\varepsilon_{11}^{(m)} }}\int_{ - \infty }^{ + \infty } {\int_{0}^{ + \infty } {w(x,y,t)e^{ - pt} {\text{d}}te^{i\zeta x} {\text{d}}x} },$$
(21)

where \(\zeta = \zeta_{1} + i\zeta_{2}\) is complex.

According to the theory at infinity, we obtain the expression

$$w^{*} (x,y,p) = \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {(A_{1m} e^{{\alpha_{m} y}} + B_{1m} e^{{ - \alpha_{m} y}} )e^{ - i\zeta x} {\text{d}}\zeta },$$
(22)
$$\phi^{*} (x,y,p) = \frac{{e_{15}^{(m)} }}{{\varepsilon_{11}^{(m)} }}w^{*} (x,y,p) + \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {(A_{2m} e^{\left| \zeta \right|y} + B_{2m} e^{ - \left| \zeta \right|y} )e^{ - i\zeta x} {\text{d}}\zeta },$$
(23)

where \(\alpha_{m} (\zeta ) = \sqrt {\frac{{[f_{m} - (\frac{v}{{\overline{{c_{m} }} }})^{2} ]\zeta^{2} + \frac{{p^{2} }}{{\overline{{c_{m} }}^{2} }} + \frac{2vip\zeta }{{\overline{{c_{m} }}^{2} }}}}{{f_{m} }}} = s_{k} \sqrt {\zeta - {{ip} \mathord{\left/ {\vphantom {{ip} {(c_{m} + v)}}} \right. \kern-\nulldelimiterspace} {(c_{m} + v)}}} \sqrt {\zeta + {{ip} \mathord{\left/ {\vphantom {{ip} {(c_{m} - v)}}} \right. \kern-\nulldelimiterspace} {(c_{m} - v)}}} = a_{{m_{ + } }} (\zeta )a_{{m_{ - } }} (\zeta )\), \(s_{m} = \sqrt {1 - {{(v} \mathord{\left/ {\vphantom {{(v} {c_{m} )^{2} }}} \right. \kern-\nulldelimiterspace} {c_{m} )^{2} }}}\), \(f_{m} = 1 + \frac{{e_{15}^{(m)} e_{15}^{(m)} }}{{c_{44}^{(m)} \varepsilon_{11}^{(m)} }}\), \(A_{1m}\) and \(B_{1m}\) are unknown functions satisfying the loading displacement \(w^{*} (x,y,p)\), and \(A_{2m}\) and \(B_{2m}\) are unknown functions satisfying the electric field \(\phi^{*} (x,y,p)\).

The boundary conditions, i.e., Eqs. (6–15), can be assumed to take the form

$$\tau_{yz}^{*} (x,0^{ + } ,p) = \tau_{yz}^{*} (x,0^{ - } ,p) = - \frac{{\tau_{0} }}{p},\;x \in (a_{k} ,b_{k} ),$$
(24)
$$D_{y}^{*} (x,0^{ + } ,p) = D_{y}^{*} (x,0^{ - } ,p) = - \frac{{D_{0} }}{p},\;x \in (a_{k} ,b_{k} ),$$
(25)
$$w^{*} (x,0^{ + } ,p) = w^{*} (x,0^{ - } ,p),\;x \notin (a_{k} ,b_{k} ),$$
(26)
$$\varphi^{*} (x,0^{ + } ,p) = \varphi^{*} (x,0^{ - } ,p),\;x \notin (a_{k} ,b_{k} ),$$
(27)
$$\tau_{yz}^{*} (x,0^{ + } ,p) = \tau_{yz}^{*} (x,0^{ - } ,p),\;x \notin (a_{k} ,b_{k} ),$$
(28)
$$D_{y}^{*} (x,0^{ + } ,p) = D_{y}^{*} (x,0^{ - } ,p),\;x \notin (a_{k} ,b_{k} ),$$
(29)
$$\tau_{yz}^{*} (x,d_{1} ,p) = \tau_{yz}^{*} (x, - d_{2} ,p) = 0,$$
(30)
$$D_{y}^{*} (x,d_{1} ,p) = D_{y}^{*} (x, - d_{2} ,p) = 0.$$
(31)

According to the geometric equation [28], we have:

$$\begin{aligned} \tau_{yz}^{*} (x,y,p) & = c_{44}^{(m)} \frac{\partial w}{{\partial y}} + e_{15}^{(m)} \frac{\partial \phi }{{\partial y}} \\ & = \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {c_{44}^{(m)} (1 + \frac{{e_{15}^{(m)} e_{15}^{(m)} }}{{\varepsilon_{11}^{(m)} }})(A_{1m} \alpha_{m} e^{{\alpha_{m} y}} - B_{1m} \alpha_{m} e^{{ - \alpha_{m} y}} )e^{ - i\zeta x} {\text{d}}\zeta } \\ & \quad + \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {e_{15}^{(m)} (A_{2m} \left| \zeta \right|e^{\left| \zeta \right|y} - B_{2m} \left| \zeta \right|e^{ - \left| \zeta \right|y} )} e^{ - i\zeta x} {\text{d}}\zeta, \\ \end{aligned}$$
(32)
$$D_{y}^{*} (x,y,p) = - \varepsilon_{11}^{(m)} \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {\left( {A_{2m} \left| \zeta \right|e^{\left| \zeta \right|y} - B_{2m} \left| \zeta \right|e^{ - \left| \zeta \right|y} } \right)} e^{ - i\zeta x} {\text{d}}\zeta.$$
(33)

Substituting Eqs. (28–31) into Eqs. (32–33), respectively, we obtain:

$$c_{44}^{(1)} \left( {1 + \frac{{e_{15}^{(1)} e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }}} \right)\alpha_{1} \left( {A_{11} e^{{\alpha_{1} d_{1} }} - B_{11} e^{{ - \alpha_{1} d_{1} }} } \right) + e_{15}^{(1)} \left| \zeta \right|\left( {A_{21} e^{{\left| \zeta \right|d_{1} }} - B_{21} e^{{ - \left| \zeta \right|d_{1} }} } \right) = 0,$$
(34)
$$c_{44}^{(2)} \left( {1 + \frac{{e_{15}^{(2)} e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }}} \right)a_{2} \left( {A_{12} e^{{ - a_{2} d_{2} }} - B_{12} e^{{a_{2} d_{2} }} } \right) + e_{15}^{(2)} \left| \zeta \right|\left( {A_{22} e^{{ - \left| \zeta \right|d_{2} }} - B_{22} e^{{\left| \zeta \right|d_{2} }} } \right) = 0,$$
(35)
$$- \varepsilon_{11}^{(1)} \left| \zeta \right|(A_{21} e^{{\left| \zeta \right|d_{1} }} - B_{21} e^{{ - \left| \zeta \right|d_{1} }} ) = 0,$$
(36)
$$- \varepsilon_{11}^{(2)} \left| \zeta \right|(A_{22} e^{{ - \left| \zeta \right|d_{2} }} - B_{22} e^{{\left| \zeta \right|d_{2} }} ) = 0,$$
(37)
$$\begin{aligned} & c_{44}^{(1)} \left(1 + \frac{{e_{15}^{(1)} e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }}\right)a_{1} (A_{11} - B_{11} ) + e_{15}^{(1)} \left| \zeta \right|(A_{21} - B_{21} ) \\ &\quad = c_{44}^{(2)} \left(1 + \frac{{e_{15}^{(2)} e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }})a_{2} (A_{12} - B_{12}\right ) + e_{15}^{(2)} \left| \zeta \right|(A_{22} - B_{22} ), \\ \end{aligned}$$
(38)
$$- \varepsilon_{11}^{(1)} \left| \zeta \right|(A_{21} - B_{21} ) = - \varepsilon_{11}^{(2)} \left| \zeta \right|(A_{22} - B_{22} ).$$
(39)

According Eqs. (34–39), we have:

$$A_{21} = B_{21} e^{{ - 2\left| \zeta \right|d_{1} }} ,\;B_{22} = A_{22} e^{{ - 2\left| \zeta \right|d_{2} }} ,\;A_{11} = B_{11} e^{{ - 2\alpha_{1} d_{1} }} ,\;B_{12} = A_{12} e^{{ - 2\alpha_{2} d_{2} }},$$
(40)
$$B_{21} = \frac{{\varepsilon_{11}^{(2)} (1 - e^{{2\left| \zeta \right|d_{2} }} )}}{{\varepsilon_{11}^{(1)} (1 - e^{{ - 2\left| \zeta \right|d_{1} }} )}}B_{22} ,\;B_{21} = - \frac{{\varepsilon_{11}^{(2)} (1 - e^{{ - 2\left| \zeta \right|d_{2} }} )}}{{\varepsilon_{11}^{(1)} (1 - e^{{ - 2\left| \zeta \right|d_{1} }} )}}A_{22} .$$
(41)

This problem is solved more efficiently by using the continuous distribution function to simulate collinear cracks. The density function is introduced as follows:

$$h_{w(k)} (x) = \frac{d}{{{\text{d}}x}}\left[ {w_{(k)}^{{}} (x,0^{ + } ,p) - w_{(k)} (x,0^{ - } ,p)} \right],\;k = 1,2, \ldots ,n,$$
(42)
$$h_{\varphi (k)} (x) = \frac{d}{{{\text{d}}x}}\left[ {\varphi_{(k)} (x,0^{ + } ,p) - \varphi_{(k)} (x,0^{ - } ,p)} \right],\;k = 1,2, \ldots ,n.$$
(43)

Substituting Eqs. (26–27) into Eqs. (42–43), respectively, we have [10]:

$$A_{11} + B_{11} - A_{12} - B_{12} = \frac{i}{\zeta }\int_{{a_{k} }}^{{b_{k} }} {h_{w(k)} (s)} e^{i\zeta s} {\text{d}}s = \eta_{1},$$
(44)
$$\frac{{e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }}(A_{11} + B_{11} ) - \frac{{e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }}(A_{12} + B_{12} ) + (A_{21} + B_{21} - A_{22} - B_{22} ) = \frac{i}{\xi }\int_{{a_{k} }}^{{b_{k} }} {h_{{\varphi_{(k)} }} (s)} e^{i\xi s} {\text{d}}s = \eta_{2}.$$
(45)

Solving Eqs. (40–41) and Eqs. (44–45), we obtain:

$$A_{11} = \frac{{R_{1} \eta_{1} + R_{2} \eta_{2} }}{R},\;B_{11} = \frac{{R_{3} \eta_{1} + R_{4} \eta_{2} }}{R},\;A_{12} = \frac{{R_{5} \eta_{1} + R_{6} \eta_{2} }}{R},\;B_{12} = \frac{{R_{7} \eta_{1} + R_{8} \eta_{2} }}{R},$$
(46)
$$A_{21} = \frac{{R_{9} \eta_{1} + R_{10} \eta_{2} }}{R},\;B_{21} = \frac{{R_{11} \eta_{1} + R_{12} \eta_{2} }}{R},\;A_{22} = \frac{{R_{13} \eta_{1} + R_{14} \eta_{2} }}{R},\;B_{22} = \frac{{R_{15} \eta_{1} + R_{16} \eta_{2} }}{R}.$$
(47)

The values of \(R\) and \(R_{n}\) \((n = 1,2, \ldots ,16)\) are given in the Appendix.

The unknown functions \(A_{1m}\), \(A_{2m}\), \(B_{1m}\) and \(B_{2m}\) (\(m = 1,2\)) depend on \(\eta_{1}\), \(\eta_{2}\). If we determine the values of \(\eta_{1}\) and \(\eta_{2}\), then we can obtain the stress and electric displacement expressions. We know that the values of \(\eta_{1}\) and \(\eta_{2}\) rely on the density functions \(h_{w(k)}\), and \(h_{\varphi (k)}\) (\(k = 1,2,3 \ldots ,n\)). Therefore, we need to solve for the density function \(h_{w(k)}\), and \(h_{\varphi (k)}\) (\(k = 1,2,3 \ldots ,n\)).

Using Eqs. (32–33) and Eqs. (42–43), the equation expressions of the upper half plane are:

$$\begin{aligned} & \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {p_{1} \frac{{i\alpha_{1} e^{{\alpha_{1} y}} }}{R\zeta }\left[ {(R_{1} - R_{3} )\int_{{a_{k} }}^{{b_{k} }} {h_{w(k)} } (s)e^{i\zeta s} {\text{d}}s + (R_{2} - R_{4} )\int_{{a_{k} }}^{{b_{k} }} {h_{\varphi (k)} } (s)e^{i\zeta s} {\text{d}}s} \right]} e^{ - i\zeta x} {\text{d}}\zeta \\ & \quad + \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {e_{15}^{(1)} } \frac{{i\left| \zeta \right|e^{{\alpha_{1} y}} }}{R\zeta }\left[ {(R_{9} - R_{11} )\int_{{a_{k} }}^{{b_{k} }} {h_{w(k)} } (s)e^{i\zeta s} {\text{d}}s + (R_{10} - R_{12} )\int_{{a_{k} }}^{{b_{k} }} {h_{\varphi (k)} } (s)e^{i\zeta s} {\text{d}}s} \right]e^{ - i\zeta x} {\text{d}}\zeta \\ & = \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {p_{1} } (R_{1} - R_{3} )\frac{{i\alpha_{1} e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{w(k)} (s){\text{d}}s \\ & \quad + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {p_{1} } (R_{2} - R_{4} )\frac{{i\alpha_{1} e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{\varphi (k)} (s){\text{d}}s \\ & \quad + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {e_{15}^{(1)} } (R_{9} - R_{11} )\frac{{i\left| \zeta \right|e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{w(k)} (s){\text{d}}s \\ & \quad + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {e_{15}^{(1)} } (R_{10} - R_{12} )\frac{{i\left| \zeta \right|e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{\varphi (k)} (s){\text{d}}s \\ & = - \frac{{\tau_{0} }}{p}, \\ \end{aligned}$$
(48)
$$\begin{aligned} & - \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {\varepsilon_{11}^{(1)} (R_{9} - R_{11} )} \frac{{i\left| \zeta \right|e^{\left| \zeta \right|y} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{w(k)} (s){\text{d}}s \\ & - \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {\varepsilon_{11}^{(1)} (R_{10} - R_{12} )} \frac{{i\left| \zeta \right|e^{\left| \zeta \right|y} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]h_{\varphi (k)} (s){\text{d}}s} \\ =& - \frac{{D_{0} }}{p}, \\ \end{aligned}$$
(49)

where \(p_{1} = c_{44}^{(1)} \left( {1 + \frac{{e_{15}^{(1)} e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }}} \right)\)

Now, we transform Eqs. (48) and (49) into the integral Cauchy nuclear equation of the first kind:

$$\begin{aligned} & \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{1} } \frac{{i\alpha_{1} e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{w(k)} (s){\text{d}}s + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{2} } \frac{{i\alpha_{1} e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{\varphi (k)} (s){\text{d}}s \\ & \quad + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{3} } \frac{{i\left| \zeta \right|e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} d\zeta } \right]} h_{w(k)} (s){\text{d}}s + \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{4} } \frac{{i\left| \zeta \right|e^{{\alpha_{1} y}} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{\varphi (k)} (s){\text{d}}s \\ & = - \frac{{\tau_{0} }}{p}, \\ \end{aligned}$$
(50)
$$\begin{aligned} & - \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{5} } \frac{{i\left| \zeta \right|e^{\left| \zeta \right|y} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{w(k)} (s){\text{d}}s - \frac{1}{2\pi }\int_{{a_{k} }}^{{b_{k} }} {\left[ {\int_{ - \infty }^{ + \infty } {H_{6} } \frac{{i\left| \zeta \right|e^{\left| \zeta \right|y} }}{R\zeta }e^{i\zeta (s - x)} {\text{d}}\zeta } \right]} h_{\varphi (k)} (s){\text{d}}s \\ & = - \frac{{D_{0} }}{p}, \\ \end{aligned}$$
(51)

where \(p_{1} (R_{1} - R_{3} ) = H_{1}\), \(p_{1} (R_{2} - R_{4} ) = H_{2}\), \(e_{15}^{(1)} (R_{9} - R_{11} ) = H_{3}\),\(e_{15}^{(1)} (R_{10} - R_{12} ) = H_{4}\), \(\varepsilon_{11}^{(1)} (R_{9} - R_{11} ) = H_{5}\), \(\varepsilon_{11}^{(1)} (R_{10} - R_{12} ) = H_{6}\).

On the crack surface, we have:

$$ \int_{{a_{k} }}^{{b_{k} }} {\left( {\int_{ - \infty }^{ + \infty } {\frac{{H_{1}^{*} }}{{R^{*} }}\frac{1}{s - x} + h_{1} (x,s)} } \right)} h_{w(k)} (s){\text{d}}s + \int_{{a_{k} }}^{{b_{k} }} {\left( {\int_{ - \infty }^{ + \infty } {\frac{{H_{2}^{*} }}{{R^{*} }}\frac{1}{s - x} + h_{2} (x,s)} } \right)} h_{\varphi (k)} (s){\text{d}}s = - \pi \frac{{\tau_{0} }}{p},$$
(52)
$$\int_{{a_{k} }}^{{b_{k} }} {\left( {\int_{ - \infty }^{ + \infty } {\frac{{H_{3}^{*} }}{{R^{*} }}\frac{1}{s - x} + h_{3} (x,s)} } \right)} h_{w(k)} (s){\text{d}}s + \int_{{a_{k} }}^{{b_{k} }} {\left( {\int_{ - \infty }^{ + \infty } {\frac{{H_{4}^{*} }}{{R^{*} }}\frac{1}{s - x} + h_{4} (x,s)} } \right)} h_{\varphi (k)} (s){\text{d}}s = - \pi \frac{{D_{0} }}{p},$$
(53)

where

$$H_{1}^{*} = s_{1} p_{1} \left( {s_{2} p_{2} \frac{{\varepsilon_{11}^{(2)} }}{{\varepsilon_{11}^{(1)} }} - \frac{{e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }}\frac{{e_{15}^{(2)} \varepsilon_{11}^{(2)} - e_{15}^{(1)} \varepsilon_{11}^{(1)} }}{{\varepsilon_{11}^{(1)} }}} \right) - e_{15}^{(1)} \frac{{\varepsilon_{11}^{(2)} }}{{\varepsilon_{11}^{(1)} }}\left( {s_{2} p_{2} \frac{{e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }} + s_{1} p_{1} \frac{{e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }}} \right),$$
$$H_{2}^{*} = - s_{1} p_{1} \frac{{e_{15}^{(2)} \varepsilon_{11}^{(1)} - e_{15}^{(1)} \varepsilon_{11}^{(2)} }}{{\varepsilon_{11}^{(1)} }} - e_{15}^{(1)} \frac{{\varepsilon_{11}^{(2)} }}{{\varepsilon_{11}^{(1)} }}(s_{2} p_{2} + s_{1} p_{1} ),$$
$$H_{3}^{*} = \varepsilon_{11}^{(2)} \left( {s_{2} p_{2} \frac{{e_{15}^{(1)} }}{{\varepsilon_{11}^{(1)} }} + s_{1} p_{1} \frac{{e_{15}^{(2)} }}{{\varepsilon_{11}^{(2)} }}} \right),$$
$$H_{4}^{*} = \varepsilon_{11}^{(2)} (s_{2} p_{2} + s_{1} p_{1} ),$$
$$R^{*} = - \frac{{(e_{15}^{(1)} \varepsilon_{11}^{(2)} - e_{15}^{(2)} \varepsilon_{11}^{(1)} )^{2} }}{{\varepsilon_{11}^{(1)} \varepsilon_{11}^{(1)} \varepsilon_{11}^{(2)} }} + \frac{{\varepsilon_{11}^{(2)} }}{{\varepsilon_{11}^{(1)} }}(s_{2} p_{2} + s_{1} p_{1} ),$$
(54)
$$h_{1} (x,s) = \int_{0}^{\infty } {\left( {\frac{{H_{1} + H_{3} }}{R} - \frac{{H_{1}^{*} }}{{R^{*} }}} \right)\sin (\zeta (s - x))} {\text{d}}\zeta ,$$
$$h_{2} (x,s) = \int_{0}^{\infty } {\left( {\frac{{H_{2} + H_{4} }}{R} - \frac{{H_{2}^{*} }}{{R^{*} }}} \right)\sin (\zeta (s - x)} ){\text{d}}\zeta ,$$
$$h_{3} (x,s) = \int_{0}^{\infty } {\left( {\frac{{H_{5} }}{R} - \frac{{H_{3}^{*} }}{{R^{*} }}} \right)\sin (\zeta (s - x)} ){\text{d}}\zeta ,$$
$$h_{4} (x,s) = \int_{0}^{\infty } {\left( {\frac{{H_{6} }}{R} - \frac{{H_{4}^{*} }}{{R^{*} }}} \right)\sin (\zeta (s - x))} {\text{d}}\zeta .$$

Considering the boundary conditions and superposition principle, Eqs. (52) and (53) can be expressed as:

$$\begin{aligned} & \sum\limits_{k = 1}^{n} {\left( {\int_{{a_{k} }}^{{b_{k} }} {\left( {\frac{{H_{1}^{*} }}{{R^{*} }}\frac{1}{{s_{k} - x_{j} }} + h_{1} (x_{j} ,s_{k} } \right)h_{w(k)} (s_{k} )ds_{k} }+\int_{{a_{k} }}^{{b_{k} }} {\left( {\frac{{H_{2}^{*} }}{{R^{*} }}\frac{1}{{s_{k} - x_{j} }} + h_{2} (x_{j} ,s_{k} )} \right)h_{\varphi (k)} (s_{k} ){\text{d}}s_{k} } } \right) } \\ & \quad = - \pi \frac{{\tau_{0} }}{p},\;x_{j} \in (a_{j} ,b_{j} ),j,k = 1,2, \ldots ,n, \\ \end{aligned}$$
(55)
$$\begin{aligned} & \sum\limits_{k = 1}^{n} {\left( {\int_{{a_{k} }}^{{b_{k} }} {\left( {\frac{{H_{3}^{*} }}{{R^{*} }}\frac{1}{{s_{k} - x_{j} }} + h_{5} (x_{j} ,s_{k} } \right)h_{w(k)} (s_{k} )ds_{k} }+\int_{{a_{k} }}^{{b_{k} }} {\left( {\frac{{H_{4}^{*} }}{{R^{*} }}\frac{1}{{s_{k} - x_{j} }} + h_{6} (x_{j} ,s_{k} )} \right)h_{\varphi (k)} (s_{k} ){\text{d}}s_{k} } } \right) } \\ & \quad = - \frac{1}{{\varepsilon_{11}^{(1)} }}\frac{{D_{0} }}{p},\;x_{j} \in (a_{j} ,b_{j} ),j,k = 1,2, \ldots ,n. \\ \end{aligned}$$
(56)

By transforming, we have:

$$h_{w(k)} (x) = g_{1(k)} (x),$$
$$h_{\varphi (k)} (x) = g_{2(k)} (x),$$
$$h_{i} (x,s) = P_{i} (f,l),\;(i = 1,2,3,4).$$

For the convenience and accuracy of numerical calculation, the normalized quantities are defined as:

$$m_{{o_{k} }} = \frac{{b_{k} - a_{k} }}{2},\;n_{{o_{k} }} = \frac{{b_{k} + a_{k} }}{2}\;(k = 1,2, \ldots ,n),$$
(57)
$$f_{k} = \frac{{x_{k} - n_{{0_{k} }} }}{{m_{{0_{k} }} }},\;l_{k} = \frac{{s_{k} - n_{{0_{k} }} }}{{m_{{0_{k} }} }}\;(k = 1,2, \ldots ,n).$$
(58)

Using equations (57) and (58), the integral equations (55) and (56) can be expressed as follows:

$$\begin{aligned} & \sum\limits_{k = 1}^{n} {\int_{ - 1}^{1} ({\frac{{H_{1}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{k} + n_{{0_{k} }} - m_{{0_{j} }} f_{j} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{1} (f_{j} ,l_{k} ))g_{1(k)} (l_{k} ){\text{d}}l_{k} } } \\ & \quad + \sum\limits_{k = 1}^{n} {\int_{ - 1}^{1} ({\frac{{H_{2}^{*} }}{{R^{*} }}\frac{{m_{{0_{j} }} }}{{m_{{0_{k} }} l_{k} + n_{{0_{k} }} - m_{{0_{j} }} f_{j} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{2} (f_{j} ,l_{k} ))g_{2(k)} (l_{k} ){\text{d}}l_{k} } } = - \pi \frac{{\tau_{0} }}{p}, \\ \end{aligned}$$
(59)
$$\begin{aligned} & \sum\limits_{k = 1}^{n} {\int_{ - 1}^{1} ({\frac{{H_{3}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{k} + n_{{0_{k} }} - m_{{0_{j} }} f_{j} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{3} (f_{j} ,l_{k} ))g_{1(k)} (l_{k} ){\text{d}}l_{k} } } +\\ & \sum\limits_{k = 1}^{n} {\int_{ - 1}^{1} ({\frac{{H_{4}^{*} }}{{R^{*} }}\frac{{m_{{0_{j} }} }}{{m_{{0_{k} }} l_{k} + n_{{0_{k} }} - m_{{0_{j} }} f_{j} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{4} (f_{j} ,l_{k} ))g_{2(k)} (l_{k} ){\text{d}}l_{k} } } = - \frac{{\pi D_{0} }}{p}. \\ \end{aligned}$$
(60)

To obtain the dislocation densities on the surface of the interface crack, we need to solve the Cauchy singular integral equation. We can observe that the dominant part of the integral equation has a Cauchy kernel. We find that the dislocation density functions \(g_{1(k)} (l_{k} )\) and \(g_{2(k)} (l_{k} )\) (\(k = 1,2,...,n\)) in Eqs. (59) and (60) have square-root type singularities. We can express that \(g_{1(k)} (l_{k} ) = (1/\sqrt {1 - l_{k}^{2} } ) \cdot h_{1(k)} (l_{k} )\pi \tau_{0} \cdot (1/p)\), where \(h_{1(k)} (l_{k} )\) is a continuous function defined in the interval \([ - 1,1]\). Therefore, the following equations are obtained:

$$g_{1(k)} (l_{k} ) = \frac{{h_{1(k)} (l_{k} )}}{{\sqrt {1 - l_{k}^{2} } }}\pi \frac{{\tau_{0} }}{p},$$
(61)
$$g_{2(k)} (l_{k} ) = \frac{{h_{2(k)} (l_{k} )}}{{\sqrt {1 - l_{k}^{2} } }}\pi \frac{{D_{0} }}{p}.$$
(62)

According to the Chebyshev point method, Eqs. (59) and (60) can be transformed into the following algebraic equation:

$$\begin{aligned} & \frac{1}{N}\sum\limits_{Q = 0}^{N} {\chi_{Q} } \sum\limits_{k = 1}^{n} (({\frac{{H_{1}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{kQ} + n_{{0_{k} }} - m_{{0_{j} }} f_{jq} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{1} (f_{jq} ,l_{kQ} )}) h_{1(k)} (l_{kQ} )+({\frac{{H_{2}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{kQ} + n_{{0_{k} }} - m_{{0_{j} }} f_{jq} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{2} (f_{jq} ,l_{kQ} )}) h_{2(k)} (l_{kQ} )) = - 1, \\ \end{aligned}$$
(63)
$$\begin{aligned} & \frac{1}{N}\sum\limits_{Q = 0}^{N} {\chi_{Q} } \sum\limits_{k = 1}^{n} (({\frac{{H_{3}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{kQ} + n_{{0_{k} }} - m_{{0_{j} }} f_{jq} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{3} (f_{jq} ,l_{kQ} )}) h_{1(k)} (l_{kQ} )+({\frac{{H_{4}^{*} }}{{R^{*} }}\frac{{m_{{0_{k} }} }}{{m_{{0_{k} }} l_{kQ} + n_{{0_{k} }} - m_{{0_{j} }} f_{jq} - n_{{0_{j} }} }} + m_{{0_{k} }} P_{4} (f_{jq} ,l_{kQ} )}) h_{2(k)} (l_{kQ} )) = - 1, \\ \end{aligned}$$
(64)
$$\sum\limits_{Q = 0}^{N} {\chi_{Q} h_{1(k)} (l_{kQ} )} = 0,\;\sum\limits_{Q = 0}^{N} {\chi_{Q} h_{2(k)} (l_{kQ} )} = 0,\;j = 1,2, \ldots n,q = 1,2, \ldots N,$$
(65)

where \(\chi_{0} = \chi_{N} = \frac{1}{2}\), \(\chi_{1} = \cdots = \chi_{N - 1} = 1\),

$$f_{jq} = \cos \frac{(2q - 1)\pi }{{2N}},\;l_{kQ} = \cos \frac{Q\pi }{N}.$$

\(N\) is the number of nodes in the quadrature formula. \(f_{jq}\) and \(l_{kQ}\) are zero points of Chebyshev polynomials of the first and second kinds, respectively. According to Eqs. (63–65), we can find the solutions of \(h_{1(k)} (l_{k} )\) and \(h_{2(k)} (l_{k} )\), so that the stress and electrical displacement are obtained.

3.2 Intensity factors

According to fracture theory, when the DSIF reaches the fracture toughness, the crack will expand, otherwise, the crack will not expand or stop growing. Therefore, it is essential to calculate the DSIF accurately.

According to [31, 32], the DSIF \(K_{{\text{III}}}\) and electric displacement intensity factors \(K_{IV}\) are expressed as

$$K_{{\text{III}}}^{*} (a_{k} ) = \sqrt {2\pi (a_{k} - x)}_{{x \to a_{k} - 0}} \tau_{yz} (x,0,p),$$
(66)
$$K_{{\text{IV}}}^{*} (a_{k} ) = \sqrt {2\pi (a_{k} - x)}_{{x \to a_{k} - 0}} D_{y} (x,0,p),$$
(67)
$$K_{{\text{III}}}^{*} (b_{k} ) = \sqrt {2\pi (x - b_{k} )}_{{x \to b_{k} + 0}} \tau_{yz} (x,0,p),$$
(68)
$$K_{{\text{IV}}}^{*} (b_{k} ) = \sqrt {2\pi (x - b_{k} )}_{{x \to b_{k} + 0}} D_{y} (x,0,p).$$
(69)

According to Eqs. (59–62), we have:

$$\mathop {\lim }\limits_{{x \to a_{k}^{ - } }} \tau_{yz} (x,0,p) = \frac{{\tau_{0} H_{1}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{1(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{0} H_{2}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{2(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(70)
$$\mathop {\lim }\limits_{{x \to a_{k}^{ - } }} D_{y} (x,0,p) = \frac{{D_{0} H_{3}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{1(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{D_{0} H_{4}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{2(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(71)
$$\mathop {\lim }\limits_{x \to b + } \tau_{yz} (x,0,p) = \frac{{\tau_{0} H_{1}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{1(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{0} H_{2}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{2(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(72)
$$\mathop {\lim }\limits_{x \to b + } D_{y} (x,0,p) = \frac{{D_{0} H_{3}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{1(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{0} H_{4}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{2(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }}.$$
(73)

Using the inverse Laplace transform, we have:

$$K_{{\text{III}}} (a_{k} ) = \tau_{0} \sqrt {\pi a_{k} } (Z_{1k} (t) + Z_{2k} (t)),$$
(74)
$$K_{{\text{IV}}} (a_{k} ) = D_{0} \sqrt {\pi a_{k} } (Z_{3k} (t) + Z_{4k} (t)),$$
(75)
$$K_{{\text{III}}} (b_{k} ) = - \tau_{0} \sqrt {\pi b_{k} } (Z_{5k} (t) + Z_{6k} (t)),$$
(76)
$$K_{{\text{IV}}} (a_{k} ) = - D_{\infty } \sqrt {\pi b_{k} } (Z_{7k} (t) + Z_{8k} (t)),$$
(77)

where

$$Z_{1k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)e^{pt} {\text{d}}p} ,\;Z_{2k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)e^{pt} {\text{d}}p},$$
$$Z_{3k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)} e^{pt} {\text{d}}p,\;Z_{4k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{4}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)} e^{pt} {\text{d}}p,$$

\(Z_{5k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} (1)e^{pt} dp}\), \(Z_{6k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} (1)e^{pt} dp}\), \(Z_{7k} (t) = \frac{1}{2\pi i}\int_{Br} \frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)}\break (1) e^{pt} dp\), \(Z_{8k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{4}^{*} }}{{pR^{*} }}h_{2(k)} (1)} e^{pt} dp\).

When \(t \to \infty\), according to Eqs. (74–77), we have:

$$K_{{{\text{III}}}} (a_{k} ) = \tau_{0} \sqrt {\pi a_{k} } \left[ {\frac{{H_{1}^{*} }}{{R^{*} }}h_{1(k)} ( - 1) + \frac{{H_{2}^{*} }}{{R^{*} }}h_{2(k)} ( - 1)} \right],$$
(78)
$$K_{{{\text{IV}}}} (a_{k} ) = D_{0} \sqrt {\pi a_{k} } \left[ {\frac{{H_{3}^{*} }}{{R^{*} }}h_{1(k)} ( - 1) + \frac{{H_{4}^{*} }}{{R^{*} }}h_{2(k)} ( - 1)} \right],$$
(79)
$$K_{{{\text{III}}}} (b_{k} ) = - \tau_{0} \sqrt {\pi b_{k} } \left[ {\frac{{H_{1}^{*} }}{{R^{*} }}h_{1(k)} (1) + \frac{{H_{2}^{*} }}{{R^{*} }}h_{2(k)} (1)} \right],$$
(80)
$$K_{{{\text{IV}}}} (b_{k} ) = - D_{0} \sqrt {\pi b_{k} } \left[ {\frac{{H_{3}^{*} }}{{R^{*} }}h_{1(k)} (1) + \frac{{H_{4}^{*} }}{{R^{*} }}h_{2(k)} (1)} \right].$$
(81)

The nondimensional DSIF and electric displacement factors can be expressed as

$$f(v) = {{K_{{{\text{III}}}} (t,v)} \mathord{\left/ {\vphantom {{K_{{{\text{III}}}} (t,v)} {K_{{{\text{III}}}} (t,0)}}} \right. \kern-\nulldelimiterspace} {K_{{{\text{III}}}} (t,0)}}$$
(82)
$$g(v) = {{K_{{{\text{IV}}}} (t,v)} \mathord{\left/ {\vphantom {{K_{{{\text{IV}}}} (t,v)} {K_{{{\text{IV}}}} (t,0)}}} \right. \kern-\nulldelimiterspace} {K_{{{\text{IV}}}} (t,0)}}$$
(83)

where \(K_{{{\text{III}}}} (t,v)\) and \(K_{{{\text{IV}}}} (t,v)\) are the universal function for the DSIF and electric displacement intensity factor, respectively; \(K_{{{\text{III}}}} (t,0)\) and \(K_{{{\text{IV}}}} (t,0)\) are the DSIF and electric displacement intensity factor for a stationary crack, respectively.

4 Far-field forces and electric impact loading

For piezoelectric media, the boundary conditions of the crack are well-known. The solution to a piezoelectric crack problem involves a geometrically and physically discontinuous problem, and the actual electrical boundary condition should be that the normal electrical displacement of the media is equal to the nondimensional electrical displacement of the defect interface. However, few solutions can be obtained under these boundary conditions. Therefore, according to different defects, they can be divided into impermeable cracks and permeable cracks after approximate treatment.

The nondimensional electrical displacements on the upper and lower surfaces of the crack are considered permeable cracks. The surface charge of an impermeable crack is considered to be zero, which is defined as the D-P boundary condition.

The crack growth problem under stress and electric displacement impact loading (\(\tau_{\infty } H(t)\) and \(D_{\infty } H(t)\)) at infinity is investigated. The boundary conditions of Eqs. (6) and (7) are changed into

$$\tau_{yz} (x,0^{ + } ,t) = \tau_{yz} (x,0^{ - } ,t) = - \tau_{\infty } H(t),\;x \in (a_{k} ,b_{k} ),$$
(84)
$$D_{y} (x,0^{ + } ,t) = D_{y} (x,0^{ - } ,t) = D^{*} - D_{\infty } H(t),\;x \in (a_{k} ,b_{k} ),$$
(85)

where \(H(t) = \left\{ {\begin{array}{*{20}c} {0,} \\ {1,} \\ \end{array} } \right.\begin{array}{*{20}l} {} \\ {} \\ \end{array} \begin{array}{*{20}l} {t < 0,} \\ {t > 0,} \\ \end{array}\) \(D^{*}\) is the electrical displacement in the crack plane.

Taking the Laplace transform of Eqs. (84) and (85), we obtain

$$\tau_{yz}^{*} (x,0^{ + } ,p) = \tau_{yz}^{*} (x,0^{ - } ,p) = - \frac{{\tau_{\infty } }}{p},\;x \in (a_{k} ,b_{k} ),$$
(86)
$$D_{y}^{*} (x,0^{ + } ,p) = D_{y}^{*} (x,0^{ - } ,p) = - \frac{{D_{\infty } - D^{*} }}{p},\;x \in (a_{k} ,b_{k} ).$$
(87)

According to the above derivation method, the DSIF and electric displacement intensity factor of \(a_{k}\) and \(b_{k}\) are expressed as

$$\mathop {\lim }\limits_{{x \to a_{k}^{ - } }} \tau_{yz} (x,0,p) = \frac{{\tau_{\infty } H_{1}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{1(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{\infty } H_{2}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{2(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(88a)
$$\mathop {\lim }\limits_{{x \to a_{k}^{ - } }} D_{y} (x,0,p) = \frac{{D_{\infty } H_{3}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{1(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{D_{\infty } H_{4}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to - 1^{ - } }} \frac{{h_{2(k)} ( - 1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(88b)
$$\mathop {\lim }\limits_{x \to b + } \tau_{yz} (x,0,p) = \frac{{\tau_{\infty } H_{1}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{1(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{\infty } H_{2}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{2(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }},$$
(88c)
$$\mathop {\lim }\limits_{x \to b + } D_{y} (x,0,p) = \frac{{D_{\infty } H_{3}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{1(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }} + \frac{{\tau_{\infty } H_{4}^{*} }}{{pR^{*} }}\mathop {\lim }\limits_{{l_{k} \to 1^{ + } }} \frac{{ - h_{2(k)} (1)}}{{\sqrt {l_{k}^{2} - 1} }}.$$
(88d)

4.1 Impermeable cracks (D-P boundary condition)

For impermeable cracks, the electrical displacement within the crack is negligible because the dielectric constant of the piezoelectric material is 3–4 orders of magnitude larger than that of air or vacuum. \(D^{*}\) in Eq. (85) satisfies the following condition [5]:

$$D^{*} = 0.$$
(89)

We have

$$K_{{\text{III}}} (a_{k} ) = \tau_{\infty } \sqrt {\pi a_{k} } (Z_{1k} (t) + Z_{2k} (t)),$$
(90a)
$$K_{{\text{IV}}} (a_{k} ) = D_{\infty } \sqrt {\pi a_{k} } (Z_{3k} (t) + Z_{4k} (t)),$$
(90b)
$$K_{{\text{III}}} (b_{k} ) = - \tau_{\infty } \sqrt {\pi b_{k} } (Z_{5k} (t) + Z_{6k} (t)),$$
(90c)
$$K_{{\text{IV}}} (a_{k} ) = - D_{\infty } \sqrt {\pi b_{k} } (Z_{7k} (t) + Z_{8k} (t)),$$
(90d)

where \(Z_{1k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)e^{pt} {\text{d}}p}\), \(Z_{2k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)e^{pt} {\text{d}}p}\), \(Z_{3k} (t) = \frac{1}{2\pi i}\int_{Br}\break {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)} e^{pt} {\text{d}}p\), \(Z_{4k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{4}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)} e^{pt} {\text{d}}p\), \(Z_{5k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} (1)e^{pt} dp}\), \(Z_{6k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} (1)e^{pt} dp}\), \(Z_{7k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} (1)} e^{pt} dp\), \(Z_{8k} (t) = \frac{1}{2\pi i}\int_{Br} \frac{{H_{4}^{*} }}{{pR^{*} }}\break h_{2(k) (1)} e^{pt} dp\).

According to Eqs. (90a–90d) and the virtual crack closure technique, we can obtain the energy release rate [33]

$$G(a_{k} ) = \frac{{\pi a_{k} }}{4}(\varpi_{1} K_{{{\text{III}}}}^{2} + \varpi_{2} K_{{{\text{III}}}} K_{{{\text{IV}}}} + \varpi_{3} K_{{{\text{IV}}}}^{2} ),$$
(91)

where \(\varpi_{1} = \frac{{Z_{4k} (t)}}{\Xi }\),

$$\varpi_{2} = - \frac{{Z_{3k} (t) + Z_{2k} (t)}}{\Xi },$$
$$\varpi_{3} = \frac{{Z_{1k} (t)}}{\Xi },$$
$$\Xi = \left| {\begin{array}{*{20}c} {Z_{1k} (t)} & {Z_{2k} (t)} \\ {Z_{3k} (t)} & {Z_{4k} (t)} \\ \end{array} } \right|.$$

One can see

$$K_{{{\text{III}}}} (a_{k} ) = \tau_{\infty } \sqrt {\pi a_{k} } Y_{1k} (t),$$
(92a)
$$K_{{{\text{IV}}}} (a_{k} ) = D_{\infty } \sqrt {\pi a_{k} } Y_{2k} (t),$$
(92b)
$$K_{{{\text{III}}}} (b_{k} ) = - \tau_{\infty } \sqrt {\pi b_{k} } Y_{3k} (t),$$
(92c)
$$K_{{{\text{IV}}}} (a_{k} ) = - D_{\infty } \sqrt {\pi b_{k} } Y_{4k} (t),$$
(92c)

where

$$Y_{1k} (t) = \frac{1}{2\pi i}\int_{Br} {\left[ {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1) + \frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)} \right]} e^{pt} {\text{d}}p,$$
$$Y_{2k} (t) = \frac{1}{2\pi i}\int_{Br} {\left[ {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1) + \frac{{H_{4}^{*} }}{{pR^{*} }}h_{2(k)} ( - 1)} \right]} e^{pt} {\text{d}}p,$$
$$Y_{3k} (t) = \frac{1}{2\pi i}\int_{Br} {\left[ {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} (1) + \frac{{H_{2}^{*} }}{{pR^{*} }}h_{2(k)} (1)} \right]} e^{pt} {\text{d}}p,$$
$$Y_{4k} (t) = \frac{1}{2\pi i}\int_{Br} {\left[ {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} (1) + \frac{{H_{4}^{*} }}{{pR^{*} }}h_{2(k)} (1)} \right]} e^{pt} {\text{d}}p.$$

4.2 Permeable cracks

The joint degree of electromechanical load can be expressed as

$$e_{15} D_{\infty } /\varepsilon_{11} \tau_{\infty } = \lambda,$$
(93)

where \(\lambda\) is a parameter.

For permeable cracks, the electric potential on the upper and lower surfaces of the crack is continuous:

$$h_{\varphi (k)} (x) = 0.$$
(94)

By applying the inverse Laplace transform, the DSIF and dynamic electric displacement intensity factor are written as

$$K_{{{\text{III}}}} (a_{k} ) = \sqrt {2\pi (a_{k} - x)}_{{x \to a_{k} - 0}} \tau_{yz} (x,0,t) = \sqrt {\pi a_{k} } \tau_{\infty } S_{1k} (t),$$
(95)
$$K_{{{\text{IV}}}} (a_{k} ) = \sqrt {2\pi (a_{k} - x)}_{{x \to a_{k} - 0}} D_{y} (x,0,t) = \frac{{\lambda \varepsilon_{11} }}{{e_{15} }}\sqrt {\pi a_{k} } \tau_{\infty } S_{2k} (t),$$
(96)
$$K_{{{\text{III}}}} (b_{k} ) = \sqrt {2\pi (x - b_{k} )}_{{x \to b_{k} + 0}} \tau_{yz} (x,0,t) = \sqrt {\pi b_{k} } \tau_{\infty } S_{3k} (t),$$
(97)
$$K_{{{\text{IV}}}} (b_{k} ) = \sqrt {2\pi (x - b_{k} )}_{{x \to b_{k} + 0}} D_{y} (x,0,t) = \frac{{\lambda \varepsilon_{11} }}{{e_{15} }}\sqrt {\pi b_{k} } \tau_{\infty } S_{4k} (t),$$
(98)

where \(S_{1k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)} e^{pt} {\text{d}}p\), \(S_{2k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} ( - 1)} e^{pt} {\text{d}}p\),

\(S_{3k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{1}^{*} }}{{pR^{*} }}h_{1(k)} (1)} e^{pt} {\text{d}}p\), \(S_{4k} (t) = \frac{1}{2\pi i}\int_{Br} {\frac{{H_{3}^{*} }}{{pR^{*} }}h_{1(k)} (1)} e^{pt} {\text{d}}p\).

From the previous results, we find that the DSIF and dynamic electrical-displacement intensity factors are related to the applied impact stress and material properties. The singularity of the electrical displacement is derived from the electromechanical coupling effect. This conclusion is consistent with that in [31].

5 Numerical examples

This section consists of three parts. In the first part, numerical validation is performed with previous work to verify the correctness of the theoretical derivation. In the second part, numerical examples of double- and triple-interface cracks are presented. The influence of material constants, \(v\) and \(t/t_{0}\) are discussed. Our research yields some new conclusions. The crack length is \(2a\), and the thickness of the single material is denoted by \(d\). The value of \(t_{0}\) is \(1\,\upmu {\text{s}}\), and the unit of \(t/t_{0}\) is \({\text{ms}}\). The electromechanical coupling coefficient is represented by \(k\). In the third part, the influence of \(\tau_{\infty }\) and \(D_{\infty }\) on the dynamic energy release rate are discussed.

5.1 Numerical validation with the previous results

Some numerical validations are performed with previous results [17]. We choose \(PZT - 4/PZT - 5H\) and \({\text{BaTiO}}_{3} /PZT65/35\) for our research. The corresponding analysis diagram is presented in Fig. 2. We show the change in the nondimensional function \(f(v)\) with two different piezoelectric film thicknesses. Each is plotted against \({v \mathord{\left/ {\vphantom {v c}} \right. \kern-\nulldelimiterspace} c}\) for two different piezoelectric thin film/substrate materials. The larger the ratio of the crack size to material thickness is, the more significant the nondimensional function \(f(v)\). In other words, the thinner the film is, the higher the nondimensional function \(f(v)\). We also find that the smaller the electromechanical coupling coefficient is, the larger is nondimensional function \(f(v)\). This result is consistent with the result in Ref. [17].

Figure 3a–d show the change in the nondimensional function \(f(v)\) at five different piezoelectric film thicknesses. Each is plotted against \({v \mathord{\left/ {\vphantom {v c}} \right. \kern-\nulldelimiterspace} c}\) for four different piezoelectric thin film/substrate materials. When the film thickness is smaller, the nondimensional function \(f(v)\) increases. The nondimensional function \(f(v)\) is controlled by the piezoelectric film thickness, i.e., the thinner the film thickness is, the greater its influence on the nondimensional DSIF. In addition, the variation law of crack growth is consistent with that in Refs. [14] and [15].

Fig. 2
figure 2

The nondimensional function \(f(v)\) versus \({v \mathord{\left/ {\vphantom {v c}} \right. \kern-\nulldelimiterspace} c}\) for the following piezoelectric thin film/substrate materials: a \({\text{PZT}} - 4/{\text{PZT}} - 5H\) and b \({\text{BaTiO}}_{3} /{\text{PZT}}65/35\)

Full size image

Figure 4a shows the nondimensional function \(f(v)\) of a \({\text{PVDF}}\) thin film/\(PZT - 5H\) substrate and the ratio of the piezoelectric film thickness to crack length. Figure 4b shows the nondimensional function \(f(v)\) of a \({\text{PVDF}}\) thin film/\(PZT - 4\) substrate and the ratio of the piezoelectric film thickness to crack length. Under four different conditions, the normalized stress intensity factor increases with the decrease in \({{d_{1} } \mathord{\left/ {\vphantom {{d_{1} } {2a}}} \right. \kern-\nulldelimiterspace} {2a}}\). When the substrate thickness is constant, the thinner the film is, the more pronounced the effect. By comparing the two figures, we can observe that when the ratio of the film thickness to the substrate is constant, the influence of a smaller electromechanical coupling coefficient on \(f(v)\) becomes more apparent.

Fig. 3
figure 3figure 3

The \(f(v)\) versus the nondimensional velocity \({v \mathord{\left/ {\vphantom {v c}} \right. \kern-\nulldelimiterspace} c}\) for the following piezoelectric thin film/substrate materials: a PZT-4/PZT-5H; b PZT-4/BaTiO3; c PZT65/35/PZT-5H; d BaTiO3/PZT65/35

Full size image

Figure 5a shows the nondimensional function \(f(v)\) of a \({\text{PVDF}}\) thin film/PZT-4 substrate and the ratio of \(t\) to \(t_{0}\). Figure 5b shows the nondimensional function \(f(v)\) of a \({\text{PVDF}}\) thin film/\(PZT - 5H\) substrate and the ratio of \(t\) to \(t_{0}\). We can observe that \(f(v)\) increases as the dimensionless time increases. We can clearly see that when the film thickness is constant, the thicker the substrate is, the lesser its influence on the nondimensional function \(f(v)\). The dynamic nondimensional stress intensity factor reaches a peak and then tends to static values.

Fig. 4
figure 4

Variations of \(f(v)\) verses \(d_{1} /(2a)\) for different piezoelectric thin film/substrate materials PVDF thin film/PZT-5H substrate and PVDF thin film/PZT-4 substrate

Full size image

5.2 The double- and triple-interface cracks

We now focus on the multiple-fracture solution: On this basis, the interaction behavior of interfacial cracks under impact loading is investigated in detail. Figures 6 and 7 show the numerical results.

Fig. 5
figure 5

Variations in \(f(v)\) versus \(t/t_{0}\) for different piezoelectric thin film/substrate materials a \({\text{PVDF}}\) thin film/\({\text{PZT}} - 4\) substrate and b \({\text{PVDF}}\) thin film/\({\text{PZT}} - 5H\) substrate

Full size image
Fig. 6
figure 6

Variations of \(f(v)\) with versus for different piezoelectric thin film/substrate materials PZT-4 thin film/PZT-4 substrate and PVDF thin film/PZT-4 substrate

Full size image

Under dynamic loading, \(f(v)\) of the piezoelectric thin film/substrate with double interface cracks is obviously different from that of a single crack. The variations in the nondimensional DSIF against \(d_{1} /(2a)\) as a function of crack distance \(d_{1} /(2a)\) are computed.

In the case of multiple cracks, according to their mutual effects, the nondimensional DSIF inside the crack tip is more significant than that outside the crack tip, regardless of the number of cracks. Figure 6a shows that when the film thickness is constant, the larger the crack size is, the larger its influence on the nondimensional function \(f(v)\). We can clearly see that when the film thickness is constant, the thicker the substrate is, the lesser its influence on the nondimensional function \(f(v)\) in Fig. 7. Figure 6b shows that when the substrate thickness is constant, the film thickness is small, and the change in the nondimensional stress intensity factor is large, which indicates that under appropriate circumstances, a thinner film thickness is more conducive to safe design.

5.3 Impermeable and permeable cracks

According to Eq. (91), the dynamic nondimensional energy-release rate can be expressed \(G/G_{r}\) (\(G_{r}\) is the dynamic energy-release rate for a stationary crack). According to Eq. (95), the nondimensional DSIF can be defined as \(F_{0}\).

Figure 8 shows the effect of stress on the nondimensional energy-release rate at different values (\(PZT - 5\) thin film/\(PZT - 5\) substrate). Figure 8 shows that when \(\tau_{\infty }\) increases from zero, \(G/G_{r}\) always increases. However, when \(\tau_{\infty }\) decreases from zero, \(G/G_{r}\) will first decrease and then increase. The stress loading pushes or interferes with the crack growth.

Fig. 7
figure 7

Variations of \(f(v)\) with versus \(t/t_{0}\) for different piezoelectric thin-film/substrate materials PZT-4 thin film/PZT-4 substrate and PVDF thin film/PZT-4 substrate

Full size image

Figure 9 shows the effects of the electrical displacement and stress on the nondimensional energy-release rate at different values. As a result, their effects on the energy-release rate take the form of a parabola at different values. Figure 9 shows that when \(D_{\infty }\) decreases from zero, \(G/G_{r}\) decreases. However, when \(D_{\infty }\) increases (\(a > 0\)), \(G/G_{r}\) first increases and then decreases. The result suggests that when the electrical displacement is negative, crack growth can be hindered. However, positive electric-displacement loads can promote or hinder crack growth. This is discussed by Pak [5].

Fig. 8
figure 8

Influence of stress on the energy-release rate at different values \(a/d_{1}\)

Full size image

To better investigate dynamic crack propagation under mechanical and electrical impacts. Figure 10 shows the nondimensional dynamic intensity factors under different values of \(\lambda\). As shown, when \(ct/(2a)\) proceeds, \(F_{0}\) first increases, peaks and finally flattens, which is similar to the result presented by Wang [32].

Fig. 9
figure 9

Influence of electric displacement on energy release rate at different values \(a/d_{1}\) a: PZT-5 thin film/PZT-5 substrate; b: PZT-4 thin film/PZT-4 substrate

Full size image
Fig. 10
figure 10

The variation in the nondimensional DSIF under different values \(\lambda\)

Full size image

6 Conclusions

The dynamic fracture characteristics of mode-III cracks are investigated. The theoretical solution to this problem is described using the integral-transform method (Laplace and Fourier transforms) and the Chebyshev point method. By analysis, the following conclusions are presented: (1) When the film thickness is thinner, the nondimensional functions increase. The nondimensional functions are controlled by the piezoelectric film thickness. (2) The nondimensional DSIF increases with decreasing \({{d_{1} } \mathord{\left/ {\vphantom {{d_{1} } {(2a}}} \right. \kern-\nulldelimiterspace} {(2a}})\). (3) When the thickness of the film is constant, the thinner the substrate is, the more apparent the effect. When the ratio of the film thickness to substrate remains constant, the influence of the smaller electromechanical coupling coefficient on the nondimensional DSIF becomes more evident. (4) The nondimensional DSIF increases as the dimensionless time increases. We can observe that when the thickness of the substrate is constant, the thinner the film is, the more significant the influence on the nondimensional functions. (5) The nondimensional DSIF of multiple cracks is clearly more significant than that of a single crack when the film thickness is the same. (6) The nondimensional DSIF of the crack tip inside is more significant than that outside the crack tip of the dimensionless DSIF, irrespective of the number of cracks. (7) Stress loading can promote or prevent crack propagation. (8) Negative electrical displacement loads always prevent crack propagation, whereas positive electric-displacement loads can promote or prevent crack propagation.

It is believed that the stress intensity factor is related to crack size, component geometry, and loading. According to the analysis in the current work, the larger crack size is, the more significant the nondimensional DSIF is. The smaller the electromechanical coupling coefficient is, the larger the nondimensional DSIF is. The thinner the film thickness is, the larger the nondimensional DSIF is. The larger the nondimensional DSIF at the crack tip is, the more pronounced the stress concentration at the crack tip is. If the nondimensional DSIF exceeds the critical value, then the crack will expand and fracture. Therefore, under appropriate conditions, the thinner the film is, the safer is the structure design.