Upscaling coupled heterogeneous diffusion reaction equations in porous media

Abstract

In this work, the periodic homogenization method is applied to a system of two equations of diffusion coupled through heterogeneous chemical reactions at the solid–fluid interface. This upscaling is discussed according to the order of magnitude of the Damköhler number. For large values of Damköhler number, a new homogenized diffusion reaction model coupling chemical reaction and diffusion is obtained. The homogenized diffusion and co-diffusion tensors are function of the heterogeneous reaction rate coefficients. The relevance of this homogenized model is analysed with respect to the order of magnitude of the Damköhler number. Some numerical simulations using this homogenized model are carried out and compared to numerical simulations at pore scale.

1 Introduction

The study of multi-species transport coupled to chemical reaction is crucial to a variety of domains, among which are geomechanics, petroleum reservoirs, environmental contaminants, hydro-geology, geochemistry, nuclear industry and civil engineering [22, 23, 25, 43]. The common point in all these domains is that the reactive mass transport is in the majority of cases a multi-scale and multi-physics problem. The knowledge of the transport properties at the macro-scale (the structure scale) is fundamental for engineers to perform accurate predictions on the global behaviour. The modelling of the reactive mass transport by Pore Scale Simulation (PSS) requires the detailed knowledge of the pore geometry which is seldom available. To overcome these limitations, the homogenization techniques are alternative solutions to describe the macroscopic transport model from the pore scale description. They enable also to determine accurately the transport properties only from the knowledge of the microstructure of an elementary representative cell (see for instance [4, 8, 13, 14, 20, 21, 42]).

The reactive mass transport has been the subject of several works based on upscaling techniques, which include the periodic homogenization method (PHM), the method of moment and the volume averaging method (VAM). The PHM, whose foundations are due to [8, 36], has been applied by numerous authors for diffusion/adsorption/advection problems [6], for ionic transfers in cementitious materials [10, 11, 27] or in clays [28], for coupled problems in heterogeneous media [4], for diffusion–reaction [17], dispersion/convection [35] or dispersion/convection/reaction [26] in porous media and many others. The VAM, of which the pioneer is Whitaker [42], consists in averaging the balance equations on the domain considered. This method has been applied to dispersion and reaction [19] and to diffusion, dispersion and reaction in porous media [38, 39], to reactive and solute transport in porous media [32, 33], or to analyse the role of tortuosity [40]. The method of moment has been also applied to transport problem to obtain homogenized macroscopic models for mass transport in porous media [18, 37].

For the study of the upscaling of the reactive transport with VAM, we refer to a non-exhaustive list of references. In [31], the authors applied VAM to the diffusion equation coupled to an heterogeneous first-order chemical reaction at pore scale, highlighting that the diffusivity tensor is decoupled from the chemical reaction rate coefficient. In [39], the VAM is applied to diffusion problem with homogeneous chemical reaction. It is found that the diffusivity tensor depends on the reaction rate coefficient through a boundary value problem at the elementary scale; the effective reaction rate coefficient is nonlinear with respect to microscopic chemical reaction rate one. In [38], the authors extended the study to diffusion and diffusion-advection problems coupled to heterogeneous chemical reactions. They confirmed that the diffusivity tensor and effective reaction rate coefficient depend on the microscopic reaction rate one. The authors highlighted that when the Thiele modulus¹ is arbitrarily large, corresponding to high chemical reaction effect, the relevance of the obtained macroscopic model is hindered. To improve this point, a revisited model of diffusion coupled to heterogeneous reaction is proposed in [41]. In this model, corrective terms were considered in the diffusivity tensor and in the effective reaction rate expressions. The corresponding macroscopic diffusion reaction model was validated by comparison with PSS under steady and transient conditions. In [24, 30], using VAM, the authors investigated the upscaling of a diffusion problem coupled to nonlinear and nonlinear homogeneous chemical reactions, respectively. Recently, diffusion of multicomponent with coupled heterogeneous chemical reaction was investigated using VAM in [34]. Authors pointed out that at the macro-scale, diffusion reaction equations are obtained with additional co-diffusion terms that appear with a co-diffusivity tensor. The diffusivity, co-diffusivity tensors and effective reaction rates are function of chemical reaction rates. Authors give the similar conclusion in [38,39,40,41]

Auriault et al. focused on the diffusion coupled with heterogeneous chemical reaction in [5] and with advection in [6]. They concluded that the homogenized parameters of diffusion and reaction are decoupled. Diffusion-advection problem coupled with heterogeneous chemical reaction is addressed in [26]. The obtained macroscopic homogenized models were discussed according to order of magnitude of Damköhler and Peclet numbers. In the case of high values of Damköhler number, the authors highlight the coupling between diffusion tensor and reaction rate at the micro-scale. In [18, 37], the authors upscaled a diffusion-convection problem coupled to first-order heterogeneous chemical reaction, using the method of moment. They found that for a large value of Damköhler number the homogenized diffusion tensor depends on the local reaction rate coefficient. Homogenization by two scale convergence with drift was also applied to upscale diffusion-advection problem with heterogeneous chemical reaction in case of predominant advection and reaction [1,2,3]. The homogenized dispersion tensor obtained in that case is function of the local reaction rate. In [7], authors applied the periodic homogenization method to upscale diffusive and advective transport coupled to a nonlinear heterogeneous chemical reaction. With respect to the order of magnitude of Damköhler’s and Peclet’s numbers, several models have been obtained. For comparable diffusion and reaction order of magnitude, the homogenized diffusion tensor depends only on the microstructure of the considered porous media. In [9], the periodic homogenization method is applied to the multi-species diffusion and advection problem coupled with linear and nonlinear homogeneous and heterogeneous chemical reactions. For a Damköhler number of order of unity, corresponding to the comparable diffusion and reaction order of magnitude, authors obtain a decoupled homogenized diffusion reaction model. In that case, the homogenized diffusion tensors are purely geometric and the effective chemical reaction rate is a linear function of the local one.

This paper focuses on the upscaling of a system of two equations of diffusion coupled through heterogeneous chemical reactions at the solid–fluid interface. A similar study has already been addressed in the case of a single diffusive equation with heterogeneous chemical reaction by PHM [15]. The main difficulty is to manage the periodic homogenization process for high Damköhler number using a relevant change of variable. The limits of classical homogenization procedure for coupled diffusion heterogeneous reactions for high Damköhler numbers have been highlighted in [16]. The same model has been investigated using VAM in [34], relying on a complex and coupled localization rule which needs to introduce supplementary physical assumptions.

In this work, we propose to generalize the relevant homogenization procedure used in [15] to a system of two coupled diffusion reaction equations. The problem revealed to be much more complex as in [15] and the numerical simulations put in a prominent position some unexpected very interesting diffuse/reactive behaviours. The results obtained are of great interest for the community with numerous applications in the domain of porous media. In the case of high values of Damköhler number (model III), we rewrite easily the coupled problem on the form of a single diffusion equation without reaction, coupled with another one with chemical reaction. The homogenization of these equations is then performed using the approach proposed in [26] and already applied in [15, 29].

It is important to notice that the results obtained here are fundamentally different from those obtained with VAM in [34]. Indeed, the boundary value problems required to the determination of the homogenized transport parameters and the expressions of diffusion and co-diffusion tensors are very different.

The second section of this work is devoted to numerical simulations on 2D elementary cells. It is important to underline that the homogenized diffusion (respectively co-diffusion) tensors obtained in our study are decreasing (respectively increasing) functions of local heterogeneous reaction rate coefficients and Damköhler number, unlike in the results obtained in [34]. Finally, we compare the macroscopic models obtained by PHM and by VAM to the Pore Scale Simulation (PSS) model for porous media whose microstructure is composed of the periodic repetition of a single 2D elementary cell constituted of circular inclusion. Another comparison is carried out between PHM and PSS models in the case of more complex microstructure (randomly porous media).

2 Pore scale diffusion reaction problem

2.1 Governing equations

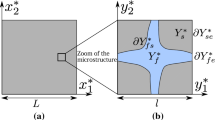
Let us consider that the macroscopic porous medium occupies a domain $\varOmega ^{*}$ whose characteristic length is L composed of an immobile fluid phase $\varOmega _f^{*}$ and of a rigid solid phase $\varOmega _s^{*}$ separated by the solid–fluid interface $\varGamma ^{*}_{sf}$. The microstructure of $\varOmega ^{*}$ is assumed to be constituted of the repetition of a periodic elementary cell $Y^{*}$ of characteristic length l. The macroscopic spatial coordinates in $\varOmega ^{*}$ are noted ${\textbf{x}}^{*}=\left( x^{*}_1,~x^{*}_2,~ x^{*}_3\right)$ and the microscopic spatial coordinates in $Y^{*}$ are noted ${\textbf{y}}^{*} = \left( y^{*}_1,~ y^{*}_2,~ y^{*}_3\right)$. The condition of scale separation ($l \ll L$) allows to introduce the small parameter $\varepsilon =\dfrac{l}{L}$, ratio of the micro-scale l to the macro-scale L.

Fig. 1

Schema of the considered porous medium

The elementary cell of the porous media $Y^{*}=Y^{*}_f\cup Y^{*}_s$ is composed of a fluid phase $Y^{*}_{f}$ and of a solid phase $Y^{*}_s$. Let $\partial Y^{*}=\partial Y^{*}_{sf} \cup \partial Y^{*}_{ff}$ represent the boundary of $Y^{*}$, where $\partial Y^{*}_{sf}$ denotes the solid–fluid interface assumed to be impermeable and where $\partial Y^{*}_{ff}$ denotes the fluid-fluid interface separating fluid phases of two juxtaposed elementary cells (Fig. 1).

In this study, we consider multicomponent transfer coupled to reversible heterogeneous chemical reaction. The governing equations and associated boundary conditions at the pore scale can be described by the following dimensional system of equations:

$$\begin{aligned}{} & {} \frac{\partial C_a^{*}}{\partial t^{*}}+\mathbf {\nabla ^{*} \cdot }\left( -D^{*}\mathbf {\nabla ^{*} } C_a^{*}\right) =0\qquad \text {in }\qquad \varOmega ^{*} _{f} \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{\partial C_b^{*}}{\partial t^{*}}+\mathbf {\nabla ^{*} \cdot }\left( -D^{*}\mathbf {\nabla ^{*} } C_b^{*}\right) =0\qquad \text {in }\qquad \varOmega ^{*} _{f} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \left( -D^{*}\mathbf {\nabla ^{*} }C_a^{*}\right) \cdot {\textbf{n}} = k^{*}_{a}C_a^{*}-k^{*}_{b}C_b^{*} \qquad \text {on }\qquad \varGamma ^{*} _{sf} \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \left( -D^{*}\mathbf {\nabla ^{*} }C_b^{*}\right) \cdot {\textbf{n}} = k^{*}_{b}C_b^{*}-k^{*}_{a}C_a^{*}\qquad \text {on }\qquad \varGamma ^{*} _{sf} \end{aligned}$$

(4)

where $C_a^{*}$ (respectively $C_b^{*}$) is the molar concentration, $k^{*}_a$ (respectively $k^{*}_b$) is the rate of heterogeneous chemical reaction of chemical component A (respectively B ), $D^*$ is the molecular diffusion coefficient assumed to be a same for components A and B, and ${\textbf{n}}$ represents the outward normal vector to the fluid phase on $\varGamma _{sf}^{*}$. Moreover, initial conditions are given at the macroscopic domain $\varOmega ^{*}$ to supplement the system of Eqs. (1)–(4):

$$\begin{aligned} C_a^{*}(t=0)=C_{a_{init}}^{*}, \quad C_b^{*}(t=0)=C_{b_{init}}^{*} \end{aligned}$$

2.2 Dimensionless analysis

The dimensional analysis performed here is similar to that developed in [4, 12]. The reference quantities (with index (ref)) are used to define the dimensionless ones (without $^*$) of order ${\mathscr {O}}(1)$:

$$\begin{aligned} t=\frac{t^{*}}{t_\textrm{ref}};\; C_a=\frac{C_a^{*}}{C_\textrm{ref}}; \; C_b=\frac{C_b^{*}}{C_\textrm{ref}};\; D=\frac{ D^{*}}{D_\textrm{ref}};\; k_a=\frac{k_a^{*}}{k_\textrm{ref}}; \; k_b=\frac{k_b^{*}}{k_\textrm{ref}} \end{aligned}$$

(5)

The following characteristic times can be defined:

$$\begin{aligned} t^{dif}_{l}= & {} \frac{l^{2}}{D_\textrm{ref}};\quad t^{dif}_{L} =\frac{L^{2}}{D_\textrm{ref}} \end{aligned}$$

(6)

$$\begin{aligned} t^{reac}_{l}= & {} \frac{l}{k_\textrm{ref}};\quad t^{reac}_{L}=\frac{L}{k_\textrm{ref}} \end{aligned}$$

(7)

where $t^{dif}_{l}$ $\left( \text {or}~t^{dif}_{L}\right)$ are characteristic time associated with diffusion and where $t^{reac}_{l}$ $\left( \text {or}~t^{reac}_{L}\right)$ are characteristic time associated with reaction at micro-scale and macro-scale, respectively. In what follows, the characteristic time of diffusion at macro-scale is considered as reference time: $t_\textrm{ref}=t^{dif}_{L}$. In addition, the macroscopic characteristic length L is assumed to be the reference length used for the normalization of the spatial variables. Accordingly, the dimensionless diffusion reaction equations are given by:

$$\begin{aligned}{} & {} \frac{\partial C_a}{\partial t}+\mathbf {\nabla \cdot }\left( -D\mathbf {\nabla } C_a\right) =0\qquad \text {in }\qquad \varOmega _{f} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \frac{\partial C_b}{\partial t}+\mathbf {\nabla \cdot }\left( -D\mathbf {\nabla } C_b\right) =0\qquad \text {in }\qquad \varOmega _{f} \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \left( -D\mathbf {\nabla }C_a\right) \cdot {\textbf{n}} = Da _{L}\left( k_{a}C_a-k_{b}C_b\right) \qquad \text {on }\qquad \varGamma _{sf} \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \left( -D\mathbf {\nabla }C_b\right) \cdot {\textbf{n}} = Da _{L}\left( k_{b}C_b- k_{a}C_a\right) \qquad \text {on }\qquad \varGamma _{sf} \end{aligned}$$

(11)

where $Da _{L}$ is the dimensionless Damköhler number for components A and B, which represent the ratio of the diffusion characteristic time to the reaction characteristic one at the macro-scale:

$$\begin{aligned} Da_{L}=\dfrac{L k_\textrm{ref}}{D_\textrm{ref}}=\dfrac{t^{dif}_{L}}{t^{reac}_{L}} \end{aligned}$$

3 Multi-scale homogenization procedure

The concentration fields $C_a \left( {\textbf{x}},{\textbf{y}},t\right)$ and $C_b \left( {\textbf{x}},{\textbf{y}},t\right)$ are assumed to be functions depending of time t and of two independent space variables: ${\textbf{x}} = {\textbf{x}}^{*}/L$ and ${\textbf{y}} = {\textbf{y}} ^{*}/l$. Moreover, the concentrations $C_a \left( {\textbf{x}},{\textbf{y}},t\right)$ and $C_b \left( {\textbf{x}},{\textbf{y}},t\right)$ are assumed to admit an asymptotic expansion with respect to $\varepsilon$:

$$\begin{aligned} C_a \left( {\textbf{x}},{\textbf{y}},t\right)= & {} \sum _{i=0}^{\infty }\varepsilon ^{i} C_{a_{i}}\left( {\textbf{x}},{\textbf{y}},t\right) \quad \text {with} \quad \left( i \in {\mathbb {N}} \right) \end{aligned}$$

(12)

$$\begin{aligned} C_b \left( {\textbf{x}},{\textbf{y}},t\right)= & {} \sum _{i=0}^{\infty }\varepsilon ^{i} C_{b_{i}}\left( {\textbf{x}},{\textbf{y}},t\right) \quad \text {with} \quad \left( i \in {\mathbb {N}} \right) \end{aligned}$$

(13)

where $C_{a_{i}}$ and $C_{b_{i}}$ are y-periodic variables. According to the separation of scales, the gradient $\mathbf {\nabla }$ and divergence $\mathbf {\nabla \cdot }$ operators may be expressed as:

$$\begin{aligned} \mathbf {\nabla }= & {} \mathbf {\nabla }_{{\textbf{x}}}+\varepsilon ^{-1} \mathbf {\nabla }_{{\textbf{y}}} \end{aligned}$$

(14)

$$\begin{aligned} \mathbf {\nabla } \cdot= & {} \mathbf {\nabla }_{{\textbf{x}}} \cdot +\varepsilon ^{-1} \mathbf {\nabla }_{{\textbf{y}}} \cdot \end{aligned}$$

(15)

Let us define the local averages of the quantity $f \left( {\textbf{x}},~{\textbf{y}},~t\right)$, that will be used in the sequel:

$$\begin{aligned} \left\langle f \right\rangle =\dfrac{1}{\vert Y \vert } \int _{Y_f} f d{\textbf{y}}, \quad \left\langle f \right\rangle ^f =\dfrac{1}{\vert Y_f \vert } \int _{Y_f } f d{\textbf{y}},\quad \left\langle f \right\rangle ^{sf} =\dfrac{1}{\vert \partial Y_{sf} \vert } \int _{\partial Y_{sf} } f d{\textbf{y}} \end{aligned}$$

(16)

where $\left\langle f \right\rangle$, $\left\langle f \right\rangle _{Y_f }$ and $\left\langle f \right\rangle ^{sf}$ represent the average over the domain Y, over the fluid phase $Y_f$ and over the boundary $\partial Y_{sf}$, respectively.² Let us quote that we have obviously $\left\langle f \right\rangle =\varphi \left\langle f \right\rangle ^f$ where $\varphi = \vert Y_f \vert / \vert Y \vert$ denotes the porosity of the porous medium.

In the sequel, we assume that the order of magnitude of the Damköhler number is:

$$\begin{aligned} Da_L=\varepsilon ^{\beta } \end{aligned}$$

(17)

with $\beta \in {\mathbb {Z}}$. Different values of $\beta$ will be considered in the sequel. The homogenization technique then proceeds as follows. The concentrations $C_a$ and $C_b$ are replaced by their asymptotic expansions (12) in the diffusion reaction Eqs. (8)–(11). In addition, the derivative operators given by (14)–(15) are also used in (8)–(11). The collected factors of the same powers of $\varepsilon$ are equated to zero. This way, we obtain a cascade of coupled problem to be solved, leading to the search homogenized model at the leading order.

3.1 Diffusion model

In that case, we consider that diffusion is predominant compared to the chemical reaction, which is equivalent to $Da_L={\mathscr {O}}\left( \varepsilon ^2 \right)$. In that case, the homogenized diffusion models obtained at the macroscopic scale are given by the following result:

Case 1

For predominant diffusion at the macroscopic scale, corresponding to the Damköhler number of the order of $Da_L={\mathscr {O}} \left( \varepsilon ^2 \right)$, at the leading order the associated homogenized models are diffusive ones

$$\begin{aligned} \varphi \frac{\partial C^{*}_a}{\partial t^{*}}+\mathbf {\nabla }^{*}_{x^{*}} \cdot \left( -\mathbf {D^{\hom *}} \mathbf {\nabla ^{*}}_{x^{*}} C^{*}_a\right)= & {} 0 \quad \text {in} \quad \varOmega ^{*} \; \text {(Model I)} \end{aligned}$$

(18)

$$\begin{aligned} \varphi \frac{\partial C^{*}_b}{\partial t^{*}}+\mathbf {\nabla ^{*}}_{x^{*}} \cdot \left( -\mathbf {D^{\hom *}} \mathbf {\nabla ^{*}}_{x^{*}} C^{*}_b\right)= & {} 0 \quad \text {in} \quad \varOmega ^{*} \; \text {(Model I)} \end{aligned}$$

(19)

where $C^{*}_a = C^{*}_a\left( {\textbf{x}}^{*}, t^{*} \right)$ and $C^{*}_b = C^{*}_b\left( {\textbf{x}}^{*}, t^{*} \right)$ are the macroscopic concentrations of components A and B, respectively. $\mathbf {D^{\hom *}}$ is the symmetric and definite positive homogenized diffusion tensor defined by

$$\begin{aligned} \mathbf {D^{\hom *}} =\frac{1}{\left| Y^{*} \right| }\int _{Y^{*}_{f}}\left( D^{*}\left( {\textbf{I}}+(\mathbf {\nabla ^{*} _{y^{*}}\chi ^{*}})^{\textsf{T}} \right) \right) d\mathbf {y^{*}} \end{aligned}$$

(20)

where ${\textbf{I}}$ is the identity tensor and where the superscript ${\textsf{T}}$ denotes the transposition operator. The vector $\mathbf {\chi ^{*}}$ is y-periodic, of zero average on $Y^{*}_f$ and solution of the local problem:

$$\begin{aligned} \left\{ \begin{array}{rcll} \mathbf {\nabla ^{*}}_{y^{*}} \cdot \left( -D^{*}\left( {\textbf{I}}+(\mathbf {\nabla ^{*} _{y^{*}}\chi ^{*}})^{\textsf{T}} \right) \right) &{}=&{}0\qquad \text {in}\qquad &{}Y^{*}_{f}\\ -D^{*}\left( {\textbf{I}}+\mathbf {\nabla ^{*} _{y^{*}} \chi ^{*}} \right) \cdot {\textbf{n}}^{*} &{}=&{}0\qquad \text {on}\qquad &{}\partial Y^{*}_{sf} \\ \mathbf {\chi }^{*} \left( {\textbf{y}}^{*}\right) &{}=&{}\mathbf {\chi }^{*} \left( {\textbf{y}}^{*}+l\right) \qquad \text {on}\qquad &{} \partial Y^{*}_{ff} \\ \left\langle \mathbf {\chi }^{*} \right\rangle &{}=&{}0 \qquad \text {in}\qquad &{} Y^{*}_{f} \end{array} \right. \end{aligned}$$

(21)

Proof

The proof of case 1 is classical and detailed in [4, 6, 7]. It is left to the reader. $\square$

3.2 Decoupled diffusion reaction model

In this second case, we consider that the characteristic times of diffusion and reaction are of the same order of magnitude, which is equivalent to $Da_L = {\mathscr {O}} \left( \varepsilon \right)$. The homogenization procedure then leads to the following result:

Case 2

For diffusion and reaction of the same order at the macroscopic scale, corresponding to $Da_L = {\mathscr {O}} \left( \varepsilon \right)$, at the leading order the associated homogenized model couples diffusion and reaction effects:

$$\begin{aligned}{} & {} \varphi \frac{\partial C^{*}_a}{\partial t^{*}}+\mathbf {\nabla ^{*}}_{x^{*}} \cdot \left( -\mathbf {D^{\hom *}} \mathbf {\nabla }^{*}_{x^{*}} C^{*}_a\right) +{\mathscr {K}}^{*}_{a}C^{*}_a-{\mathscr {K}}^{*}_{b}C^{*}_b=0 \quad \text {in} \quad \varOmega ^{*} \; \text {(Model II)} \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \varphi \frac{\partial C^{*}_b}{\partial t^{*}}+\mathbf {\nabla }^{*}_{x^{*}} \cdot \left( -\mathbf {D^{\hom *}}\mathbf {\nabla }^{*}_{x^{*}} C^{*}_b\right) -{\mathscr {K}}^{*}_{a}C^{*}_a+{\mathscr {K}}^{*}_{b}C^{*}_b=0 \quad \text {in} \quad \varOmega ^{*} \; \text {(Model II)} \end{aligned}$$

(23)

where $C^{*}_a\left( {\textbf{x}}^{*},t^{*}\right)$ and $C^{*}_b\left( {\textbf{x}}^{*},t^{*}\right)$ are the macroscopic concentrations and $\mathbf {D^{\hom *}}$ is the homogenized diffusion tensor given by Eq. (20), where $\mathbf {\chi }^{*}$ solution of the local problem (21).

Furthermore, reactive terms appear in the transport equations as a homogeneous reaction at the macro-scale, where ${\mathscr {K}}^{*}_a$ and ${\mathscr {K}}^{*}_b$ represent the effective reaction rate coefficients given by:

$$\begin{aligned} {\mathscr {K}}^{*}_a={\mathscr {S}}^{*} k^{*}_a; \quad {\mathscr {K}}^{*}_b={\mathscr {S}}^{*} k^{*}_b \end{aligned}$$

(24)

They are functions of the heterogeneous reaction rate coefficients $k^{*}_a$, $k^{*}_b$ at micro-scale and of the porous medium specific area, this is ${\mathscr {S}}^{*} =\vert \partial Y^{*}_{sf} \vert / \vert Y^{*} \vert$.

Proof

The proof of case 2 is classical and detailed for one heterogeneous chemical reaction in [4, 6, 16, 20] and for several chemical reactions in [7]. $\square$

In that case 2, the diffusion and the reaction are comparable at the marco-scale. Despite this, the homogenized diffusion tensor $\mathbf {D^{\hom *}}$ and the homogenized reaction rate coefficients ${\mathscr {K}}^{*}_a$ and ${\mathscr {K}}^{*}_b$ are decoupled at the macro-scale. It is important to notice, that the homogenized diffusion tensor is purely geometric with the same expression and associated boundary value problem as in case 1.

3.3 Predominant reaction

The last case addressed of this work is devoted to the homogenization of the diffusion reaction Eqs. (8)–(11) for predominant reaction effects versus diffusion ones. In that case, the characteristic time of diffusion is larger than the characteristic time of chemical reaction, that leads to $Da_L = {\mathscr {O}} \left( 1\right)$ and $Da_L = {\mathscr {O}} \left( \varepsilon ^{-1}\right)$.

Case 3

For predominating chemical reactions at the macro-scale corresponding to $Da_L = {\mathscr {O}} \left( 1\right)$ and $Da_L = {\mathscr {O}} \left( \varepsilon ^{-1}\right)$, at the leading order the macroscopic concentrations $\left\langle C^{*}_a \right\rangle ^f$ and $\left\langle C^{*}_b \right\rangle ^f$ are solution of the coupled homogenized diffusion reaction equations:

$$\begin{aligned} \varphi \frac{\partial \left\langle C^{*}_a\right\rangle ^f}{\partial t^{*} }+\mathbf {\nabla ^{*} }_{x^{*}} \cdot \left( -\mathbf {D_{aa}^{\hom *}}\mathbf {\nabla ^{*} } _{x^{*}}\left\langle C^{*}_a\right\rangle ^f-\mathbf {D_{ab}^{\hom *}} \mathbf {\nabla ^{*} }_{x^{*}}\left\langle C^{*}_b\right\rangle ^f\right) \nonumber \\ +{\mathscr {K}}^{*}_{a}\left\langle C^{*}_a\right\rangle ^f-{\mathscr {K}}^{*}_{b}\left\langle C^{*}_b\right\rangle ^f =0&\, \text {in} \, \varOmega ^{*}&\end{aligned}$$

(25)

$$\begin{aligned} \varphi \frac{\partial \left\langle C^{*}_b\right\rangle ^f}{\partial t^{*} }+\mathbf {\nabla ^{*} }_{x^{*}} \cdot \left( -\mathbf {D_{ba}^{\hom *}}\mathbf {\nabla ^{*} } _{x^{*}}\left\langle C^{*}_a\right\rangle ^f-\mathbf {D_{bb}^{\hom *}} \mathbf {\nabla ^{*} }_{x*}\left\langle C^{*}_b\right\rangle ^f\right) \nonumber \\ +{\mathscr {K}}^{*}_{b}\left\langle C^{*}_b\right\rangle ^f-{\mathscr {K}}^{*}_{a}\left\langle C^{*}_a\right\rangle ^f =0&\,\text {in} \, \varOmega ^{*}&\end{aligned}$$

(26)

The homogenized diffusion and co-diffusion tensors are defined by:

$$\begin{aligned} \mathbf {D_{aa}^{\hom *}}= & {} \frac{\mathbf {D_{r}^{\hom *}}k^{*}_{a}+\mathbf {D^{\hom *}}k^{*}_{b}}{k^{*}_{a}+k^{*}_{b}},\quad \mathbf {D_{ab}^{\hom *}}=\frac{k^{*}_{b}\left( \mathbf {D^{\hom *}}-\mathbf {D_{r}^{\hom *}}\right) }{k^{*}_{a}+k^{*}_{b}} \end{aligned}$$

(27)

$$\begin{aligned} \mathbf {D_{ba}^{\hom *}}= & {} \frac{k^{*}_{a}\left( \mathbf {D^{\hom *}} -\mathbf {D_{r}^{\hom *}}\right) }{k^{*}_{a}+k^{*}_{b}},\quad \mathbf {D_{bb}^{\hom *}}=\frac{\mathbf {D_{r}^{\hom *}} k^{*}_{b}+\mathbf {D^{\hom *}}k^{*}_{a}}{k^{*}_{a}+k^{*}_{b}} \end{aligned}$$

(28)

where $\mathbf {D^{\hom *} }$ is the purely geometrical homogenized diffusion tensor given by (20); the periodic vector $\mathbf {\chi }^{*}$ is solution of the local problem (21). The reactive homogenized diffusion tensor³$\mathbf {D_r^{\hom *}}$ reads

$$\begin{aligned} \mathbf {D_r^{\hom *} }=\frac{1}{\left| Y^{*} \right| }\int _{Y^{*}_{f}}D^{*}\psi _{\eta } ^{*2}\left( {\textbf{I}}+(\mathbf {\nabla }^{*}_{y^{*}}\mathbf {\chi }^{*}_{r})^{\textsf{T}} \right) d{\textbf{y}}^{*} \end{aligned}$$

(29)

where the y-periodic vector $\mathbf {\chi }^{*}_{r}$ is of null average over the domain fluid $Y^{*}_f$ and solution of the boundary value problem⁴ given by:

$$\begin{aligned} \mathbf {\nabla }^{*}_{y^{*}} \cdot \left( -D^{*}\psi _{\eta } ^{*2}\left( {\textbf{I}}+(\mathbf {\nabla }^{*}_{y^{*}}\mathbf {\chi }^{*}_{r})^{\textsf{T}} \right) \right)= & {} 0\qquad \text {in}\qquad Y ^{*}_{f} \end{aligned}$$

(30)

$$\begin{aligned} \left( -D^{*}\psi _{\eta } ^{*2}\left( {\textbf{I}}+\mathbf {\nabla }^{*}_{y^{*}}\mathbf {\chi }^{*}_r \right) \right) \cdot {\textbf{n}}^{*}= & {} 0\qquad \text {on}\qquad \partial Y^{*}_{sf} \end{aligned}$$

(31)

Moreover, $\psi ^{*}_{\eta } \left( {\textbf{y}}^{*}\right)$ denotes a y-periodic eigenfunction, solution of the following spectral problem:

$$\begin{aligned} \mathbf {\nabla }^{*}_{y^{*} }\cdot \left( -D^{*}\mathbf {\nabla }^{*}_{y^{*}} \psi _{\eta }^{*} \right)= & {} \lambda ^{*} \psi ^{*}_{\eta } \qquad \ \ \textrm{in}\qquad Y^{*}_{f} \end{aligned}$$

(32)

$$\begin{aligned} \left( -D^{*} \mathbf {\nabla }^{*}_{y^{*}} \psi ^{*}_{\eta } \right) \cdot {\textbf{n}}^{*}= & {} k^{*}_{+}\psi ^{*}_{\eta } \qquad \textrm{on}\qquad \partial Y^{*}_{sf} \end{aligned}$$

(33)

$$\begin{aligned} \left\langle \psi _{\eta }^{*2} \right\rangle ^{f}= & {} 1 \end{aligned}$$

(34)

where $k^{*}_{+}$ is the heterogeneous reaction rate coefficient defined as $k^{*}_{+}=k^{*}_a+k^{*}_b$. As $\psi ^{*}_{\eta }$ is defined to within one multiplicative constant, the last condition (34) ensures the uniqueness of the solution. Note also that the problem (32)–(33) is posed in dimensionless form in the unit cell. Finally, ${\mathscr {K}}^{*}_a$ and ${\mathscr {K}}^{*}_b$ are the homogenized reaction rates given by:

$$\begin{aligned} {\mathscr {K}}^{*}_a=\frac{\varphi \, {\tilde{\lambda }}^{*} \, k^{*}_a}{k^{*}_{a}+k^{*}_{b}}, \quad {\mathscr {K}}^{*}_b=\frac{\varphi \, {\tilde{\lambda }}^{*} \, k^{*}_b}{k^{*}_{a}+k^{*}_{b}} \end{aligned}$$

(35)

where ${\tilde{\lambda }}^{*}$ is the dimensional first eigenvalue (the smallest one) of the spectral problem (32)–(33).

Proof

The proof is identical for $Da_L={\mathscr {O}}(1)$ and $Da_L={\mathscr {O}}(\varepsilon ^{-1})$ as soon as the Damköhler number is large enough for the reaction terms to be important. Indeed, the Damköhler number is only contained implicitly in the boundary condition of spectral problem (33) but is not involved in the proof of result 3. In order to simplify the calculations, we consider the auxiliary problem:

$$\begin{aligned} \frac{\partial \rho ^{*} }{\partial t^{*}}+\mathbf {\nabla }^{*} \cdot \left( -D^{*} \mathbf {\nabla }^{*} \rho ^{*} \right)= & {} 0\qquad \text {in} \qquad \varOmega ^{*} _{f} \end{aligned}$$

(36)

$$\begin{aligned} \frac{\partial \eta ^{*} }{\partial t^{*}}+\mathbf {\nabla }^{*} \cdot \left( -D^{*} \mathbf {\nabla }^{*} \eta ^{*} \right)= & {} 0\qquad \text {in}\qquad \varOmega ^{*} _{f} \end{aligned}$$

(37)

$$\begin{aligned} -D^{*} \mathbf {\nabla }^{*} \rho ^{*} \cdot {\textbf{n}}^{*}= & {} 0\qquad \text {on}\qquad \varGamma ^{*} _{sf} \end{aligned}$$

(38)

$$\begin{aligned} -D^{*} \mathbf {\nabla }^{*} \eta ^{*} \cdot {\textbf{n}}^{*}= & {} k^{*} _{+}\eta ^{*} \qquad \text {on}\qquad \varGamma ^{*} _{sf} \end{aligned}$$

(39)

obtained from (1)–(4) by setting $\rho ^{*} =C^{*} _a+C^{*} _b$, $\eta ^{*} =k^{*} _a C^{*} _a- k^{*} _b C^{*} _b$. To determine the searched homogenized models, we will apply the periodic homogenization procedure to problems (36)–(39). Thanks to this change of variables, we only have to upscale decoupled problems⁵ a diffusion problem without chemical reaction (36) and (38) and a diffusion problem with heterogeneous chemical reaction (37) and (39).

After the dimensional analysis, the homogenization procedure of equation⁶ (36) with corresponding boundary condition (38) is very classical and leads to the dimensionless homogenized diffusion equation:

$$\begin{aligned} \varphi \frac{\partial \rho }{\partial t}+\mathbf {\nabla }_{x}.\left( - {\textbf{D}}^{\hom }\mathbf {\nabla }_{x}\rho \right) =0 \end{aligned}$$

where $\rho =C_{a}+C_{b}$ is the dimensionless concentration at the leading order and $\varphi$ is the porosity of the porous medium. This homogenized diffusion equation is written in dimensional form as:

$$\begin{aligned} \varphi \frac{\partial \rho ^{*} }{\partial t^{*} }+\mathbf {\nabla }^{*} _{x^{*} }.\left( - {\textbf{D}}^{\hom *}\mathbf {\nabla }^{*} _{x^{*} }\rho ^{*} \right) =0 \end{aligned}$$

(40)

where ${\textbf{D}}^{\hom *}$ is the purely geometric homogenized diffusion tensor given by (20).

For the homogenization of Eqs. (37) and (39), we follow the approach developed in [1, 15, 26, 29]. The outlines required to obtain the homogenized model are summarized in the sequel.

First, we perform the change of variable:

$$\begin{aligned} \eta ^{*} = \exp \left( -\lambda ^{*} t^{*}\right) \psi ^{*}_{\eta } \left( {\textbf{y}}^{*} \right) u^{*} \left( {\textbf{x}}^{*},{\textbf{y}}^{*},t^{*}\right) \end{aligned}$$

(41)

as in [15, 26, 29] where $\psi ^{*} _{\eta }$ is assumed to be solution of the following eigenvalue problem:

$$\begin{aligned} \mathbf {\nabla ^{*} }.\left( -D^{*} \mathbf {\nabla ^{*} }\psi ^{*} _{\eta }\right)= & {} \lambda ^{*} \psi ^{*} _{\eta } \qquad \text {in}\qquad Y^{*} _{f} \end{aligned}$$

(42)

$$\begin{aligned} -D^{*} \mathbf {\nabla ^{*} }\psi ^{*} _{\eta }.{\textbf{n}}^{*}= & {} k^{*} _{+}\psi ^{*} _{\eta } \qquad \text {on}\qquad \partial Y^{*} _{sf} \end{aligned}$$

(43)

Substituted (41) in Eqs. (37) and (39), we obtain:

$$\begin{aligned} \psi ^{*} _{\eta }\frac{\partial u^{*} }{\partial t^{*} } +{} & {} \psi ^{*} _{\eta }\mathbf {\nabla }^{*}.\left( - D^{*} \mathbf {\nabla }^{*} u^{*} \right) -2D^{*} \mathbf {\nabla }^{*} u^{*} \mathbf {\nabla }^{*} \psi ^{*} _{\eta }+u^{*} \left( \mathbf {\nabla }^{*}.\left( - D^{*} \mathbf {\nabla }^{*} \psi ^{*} _{\eta }\right) -\lambda ^{*} \psi ^{*} _{\eta }\right) =0 \end{aligned}$$

(44)

$$\begin{aligned}{} & {} u^{*} \left( -D^{*} \mathbf {\nabla }\psi ^{*} _{\eta } \cdot {\textbf{n}}^{*} -k^{*} _{+}\psi ^{*} _{\eta }\right) -D^{*} \left( \psi ^{*} _{\eta }\mathbf {\nabla }^{*} u^{*} \right) \cdot {\textbf{n}}^{*} =0 \end{aligned}$$

(45)

Multiplying Eqs. (44) and (45) by $\psi ^{*} _{\eta }$, using the eigenvalue problem (42)–(43), we obtain a non-steady diffusion problem for dimensional variable⁷$u^{*}$:

$$\begin{aligned} \psi _{\eta }^{*2}\frac{\partial u^{*}}{\partial t^{*}}= & {} \mathbf {\nabla }^{*} \cdot \left( D^{*}\psi _{\eta }^{*2}\mathbf {\nabla }^{*} u^{*}\right) \qquad \text {in}\qquad \varOmega ^{*} _{f} \end{aligned}$$

(46)

$$\begin{aligned} -\left( D^{*}\psi _{\eta }^{*2}\mathbf {\nabla }^{*}u^{*}\right) \cdot {\textbf{n}}^{*}= & {} 0 \qquad \text {on}\qquad \varGamma ^{*} _{sf} \end{aligned}$$

(47)

The dimensionless diffusion problem to be homogenized reads:

$$\begin{aligned} \psi _{\eta }^{2}\frac{\partial u}{\partial t}= & {} \mathbf {\nabla } \cdot \left( D\psi _{\eta }^{2}\mathbf {\nabla } u\right) \qquad \text {in}\qquad \varOmega _{f} \end{aligned}$$

(48)

$$\begin{aligned} -\left( D\psi _{\eta }^{2}\mathbf {\nabla }u\right) \cdot {\textbf{n}}= & {} 0 \qquad \text {on}\qquad \varGamma _{sf} \end{aligned}$$

(49)

where u is assumed to admit an asymptotic expansion as in (12). The homogenization procedure is similar to those used for the model of 1. It leads to the homogenized diffusion equation for $u \equiv u_0 \left( {\textbf{x}},t \right)$:

$$\begin{aligned} \varphi \frac{\partial u}{\partial t}=\mathbf {\nabla }_{x}\cdot \left( \mathbf {D _{r}^{\hom } }\mathbf {\nabla }_{x} u\right) \end{aligned}$$

(50)

The homogenized diffusion Eq. (50) is rewritten here after under the dimensional form as:

$$\begin{aligned} \varphi \frac{\partial u^{*}}{\partial t^{*}}=\mathbf {\nabla }^{*}_{x^{*}}\cdot \left( \mathbf {D _{r}^{\hom *} }\nabla ^{*}_{x^{*}} u^{*} \right) \end{aligned}$$

(51)

where $\varphi$ represents the porosity of the porous medium and $\mathbf {D_{r}^{\hom *} }$ denotes the reactive homogenized diffusion tensor given by (29). The y-periodic vector $\mathbf {\chi ^{*}_r}$ of null average on $Y^{*}_f$ is solution of the boundary value problem (30)–(31). It is important to quote that vector $\mathbf {\chi }^{*}_{r}$ depends not only on the geometry of the porous medium but also on the chemical reaction through the eigenfunction $\psi ^{*}_{\eta }$. The reactive homogenized diffusion tensor $\mathbf {D_{r}^{\hom *} }$ is therefore linked to the chemical reaction⁸ via the eigenfunction $\psi ^{*}_{\eta }$. In the case without chemical reaction, corresponding to $\psi ^{*}_{\eta }=1$, problem (30)–(31) becomes identical to the local problem (21) of case 1.

Let us come back to the dimensional variable $\eta ^{*}$, which writes at the leading order:

$$\begin{aligned} \eta ^{*} =\exp \left( -\lambda ^{*} t^{*}\right) \psi ^{*} _{\eta }\left( {\textbf{y}}^{*} \right) u^{*}\left( {\textbf{x}}^{*},t^{*}\right) \end{aligned}$$

Its intrinsic average over fluid phase $Y^{*}_f$ is given by

$$\begin{aligned} \left\langle \eta ^{*} \right\rangle ^f =\exp \left( -\lambda ^{*} t^{*}\right) \left\langle \psi ^{*} _{\eta }\right\rangle ^fu^{*} \left( {\textbf{x}}^{*},t^{*}\right) \end{aligned}$$

(52)

and the temporal derivative of $\left\langle \eta ^{*} \right\rangle ^f$ reads:

$$\begin{aligned} \frac{\partial \left\langle \eta ^{*}\right\rangle ^f}{\partial t^{*}}=\exp \left( -\lambda ^{*} t^{*}\right) \left\langle \psi ^{*} _{\eta }\right\rangle ^f\frac{\partial u^{*}}{\partial t^{*}}-\lambda ^{*}\exp \left( -\lambda ^{*} t^{*}\right) \left\langle \psi ^{*} _{\eta }\right\rangle ^fu^{*} \end{aligned}$$

(53)

Then, multiplying (51) by $\left( \exp \left( -\lambda ^{*} t^{*}\right) \psi ^{*} _{\eta }\right)$ and using (53), we obtain easily the homogenized diffusion reaction equation for $\left\langle \eta ^{*} \right\rangle ^f$:

$$\begin{aligned} \varphi \frac{\partial \left\langle \eta ^{*} \right\rangle ^f}{ \partial t^{*}}+\mathbf {\nabla ^{*} }_{x^{*}}\cdot \left( -{\textbf{D}}_{r}^{\hom *}\mathbf {\nabla }^{*} _{x^{*}}\left\langle \eta ^{*} \right\rangle ^f\right) +\varphi \lambda ^{*} \left\langle \eta ^{*} \right\rangle ^f=0 \end{aligned}$$

(54)

In the last step of this proof, we rewrite the obtained homogenized problems of diffusion (40) and of diffusion reaction (54) with respect to dimensional concentrations $C^{*} _{a}$ and $C^{*} _{b}$. We obtain at the leading order⁹:

$$\begin{aligned} \rho ^{*}= & {} \left\langle C^{*} _{a}\right\rangle ^f+\left\langle C^{*} _{b}\right\rangle ^f \end{aligned}$$

(55)

$$\begin{aligned} \left\langle \eta ^{*} \right\rangle ^f= & {} k^{*}_{a}\left\langle C^{*} _{a}\right\rangle ^f-k^{*} _{b}\left\langle C^{*}_{b}\right\rangle ^f \end{aligned}$$

(56)

with obviously $C^{*} _{a}\left( {\textbf{x}}^{*},t^{*} \right) =\left\langle C^{*}_{a}\right\rangle ^f$ and $C^{*} _{b}\left( {\textbf{x}}^{*},t^{*} \right) =\left\langle C^{*}_{b}\right\rangle ^f$. It is easy to deduce from (55) and (56) the expressions of averaged concentrations of components A and B over $Y_f$:

$$\begin{aligned} \left\langle C^{*}_{a}\right\rangle ^f= & {} \frac{1}{k^{*} _{a}+k^{*} _{b}} \left( k^{*} _{b}\rho ^{*} +\left\langle \eta ^{*} \right\rangle ^f\right) \end{aligned}$$

(57)

$$\begin{aligned} \left\langle C^{*} _{b}\right\rangle ^f= & {} \frac{1}{k^{*} _{a}+k^{*} _{b}} \left( k^{*} _{a}\rho ^{*}-\left\langle \eta ^{*}\right\rangle ^f \right) \end{aligned}$$

(58)

To finish, the sum of Eq. (40) multiplied by $\frac{k^{*} _b}{k^{*} _a+k^{*} _b}$ and of Eq. (54) multiplied by $\frac{1}{k^{*} _a+k^{*} _b}$ leads to the homogenized equation for $\left\langle C^{*}_{a_{0}}\right\rangle ^f$:

$$\begin{aligned} \nonumber \varphi \frac{\partial \left\langle C^{*}_{a}\right\rangle ^f}{ \partial t^{*}}&+\mathbf {\nabla }^{*}_{x^{*}}\cdot \left( -\left( \frac{\mathbf {D_{r}^{\hom *} }k^{*}_{a}+\mathbf {D^{\hom *} }k^{*}_{b}}{k^{*}_{a}+k^{*}_{b}}\right) \mathbf {\nabla }^{*} _{x^{*}}\left\langle C^{*}_{a}\right\rangle ^f \right)&\\ \nonumber&+\mathbf {\nabla }^{*}_{x^{*}}\cdot \left( -\left( \frac{k^{*}_{b}\left( \mathbf {D^{\hom *} }-\mathbf {D_{r}^{\hom *} }\right) }{k^{*}_{a}+k^{*}_{b}}\right) \mathbf {\nabla }^{*}_{x^{*}}\left\langle C^{*}_{b}\right\rangle ^f\right)&\\&+\frac{\varphi {\tilde{\lambda }}^{*} }{k^{*}_{a}+k^{*}_{b}}\left( k^{*}_{a}\left\langle C^{*}_{a}\right\rangle ^f- k^{*}_{b}\left\langle C^{*}_{b}\right\rangle ^f\right) =0&\end{aligned}$$

(59)

Likewise, the sum of Eq. (40) multiplied by $\frac{k^{*}_a}{k^{*}_a+k^{*}_b}$ and of Eq. (54) multiplied by $\frac{-1}{k^{*}_a+k^{*}_b}$ leads to the homogenized equation for $\left\langle C^{*}_{b}\right\rangle ^f$:

$$\begin{aligned} \nonumber \varphi \frac{\partial \left\langle C^{*}_{b}\right\rangle ^f}{ \partial t^{*}}&+\mathbf {\nabla }^{*}_{x^{*}} \cdot \left( -\left( \frac{k^{*}_{a}\left( \mathbf {D ^{\hom *} }-\mathbf {D_{r}^{\hom *} }\right) }{k^{*}_{a}+k^{*}_{b}}\right) \mathbf {\nabla }^{*} _{x^{*}}\left\langle C^{*}_{a}\right\rangle ^f \right)&\\ \nonumber&+\mathbf {\nabla }^{*}_{x^{*}} \cdot \left( -\left( \frac{\mathbf {D _{r}^{\hom *} }k^{*}_{b}+\mathbf {D^{\hom *} }k^{*}_{a}}{k^{*}_{a}+k^{*}_{b}}\right) \mathbf { \nabla }^{*}_{x^{*}}\left\langle C^{*}_{b}\right\rangle ^f\right)&\\&+\frac{ \varphi {\tilde{\lambda }}^{*} }{k^{*}_{a}+k^{*}_{b}}\left( k^{*}_{b}\left\langle C^{*}_{b}\right\rangle ^f-k^{*}_{a}\left\langle C^{*}_{a}\right\rangle ^f\right) =0&\end{aligned}$$

(60)

From Eqs. (59) and (60), we deduce the expressions of the homogenized diffusion tensors and of the homogenized reaction rate coefficients given by (27)–(28) and (35), respectively. Some supplementary macroscopic reaction terms appear in the transport homogenized Eq. (59) (or (25)) for component A, and in Eq. (60) (or (26)) for component B, as homogeneous reactions involving $\left\langle C^{*}_{a}\right\rangle ^f$ and $\left\langle C^{*}_{b}\right\rangle ^f$. Furthermore, supplementary diffusion terms appear in Eqs. (59) and (60) depending on $\left\langle C^{*}_{b}\right\rangle ^f$ and $\left\langle C^{*}_{a}\right\rangle ^f$, respectively. These diffusive terms are new (by comparing to case 2) and reflect the influence of diffusion of component B (respectively A) on the diffusion of component A (respectively B) at the macro-scale.

The homogenized reaction rate coefficients ${\mathscr {K}}^{*}_a$ and ${\mathscr {K}}^{*}_b$ are function of the first eigenvalue ${\tilde{\lambda }}$ determined from the spectral problem (42)–(43). Note that the compatibility equation of Neumann problem leads to

$$\begin{aligned} {\mathscr {K}}^{*}_a= & {} \frac{k^{*}_a\varphi {\tilde{\lambda }}^{*}}{k^{*}_a+k^{*}_b}=k^{*}_a{\mathscr {S}}^{*}\frac{\left\langle \psi _{\eta }^{*}\right\rangle ^{sf} }{\left\langle \psi _{\eta }^{*}\right\rangle ^f} \end{aligned}$$

(61)

$$\begin{aligned} {\mathscr {K}}^{*}_b= & {} \frac{k^{*}_b\varphi {\tilde{\lambda }}^{*}}{k^{*}_a+k^{*}_b}=k^{*}_b{\mathscr {S}}^{*}\frac{\left\langle \psi _{\eta }^{*}\right\rangle ^{sf} }{\left\langle \psi _{\eta }^{*}\right\rangle ^f} \end{aligned}$$

(62)

where ${\mathscr {S}}^{*}$ is the specific area of the porous medium. $\square$

It is important to notice that for low values of Damköhler number $Da_L$, we have $\psi _{\eta }^{*}=1$ and the homogenized reaction rate coefficients are identical to those given by expressions (24) of case 2. In addition, expression (29) of the reactive homogenized diffusion tensor reduces to the purely geometric one given by (20). Moreover, the homogenized diffusion tensors $\mathbf {D_{ab}^{hom*}}$ and $\mathbf {D_{ba}^{hom*}}$ are equal to zero and the homogenized diffusion tensors $\mathbf {D_{aa}^{hom*}}$ and $\mathbf {D_{bb}^{hom*}}$ are identical to $\mathbf {D^{hom*}}$ given by Eqs. (20). For the sake of simplicity, in the sequel of the article the superscript $^{*}$ will be omitted.

4 Numerical study

The aim of this part is the determination of the homogenized diffusion tensors given by (27)–(28) by solving numerically the boundary value problems (21) and (30)–(31). In the case of the reactive diffusion homogenized model of case 3, we begin with solving the spectral problem (32)–(33) to determine the eigenfunctions $\psi _{\eta }$ and the first associated eigenvalue ${\tilde{\lambda }}$. Thereafter, the local variable $\mathbf {\chi }_r$ will be determined by solving problem (30)–(31). Finally, the reactive homogenized diffusion tensor will be computed from $\psi _{\eta }$ and $\mathbf {\chi }_r$ using (29). The knowledge of $\mathbf {D^\textrm{hom}}$, $\mathbf {D_r^\textrm{hom}}$, $k_a$ and $k_b$ allows to calculate the homogenized diffusion tensors given by (27)–(28). The numerical study will carried out by using Comsol Multiphysics 4.4 software. We begin with solving the eigenvalue problem (32)–(33) and then the boundary value problem (30)–(31) where $\psi _{\eta }$ is known. To do this, we use the predefined partial derivative equations (PDE interfaces of Comsol software). To obtain the solution of the eigenvalue problem (32)–(33), Poisson Eq. (63) of Comsol software is solved using the eigenvalue solver with corresponding parameters given hereafter:

$$\begin{aligned} \left\{ \begin{array}{llll} \mathbf {\nabla }\cdot \left( -c\mathbf {\nabla }u\right) =f\quad \text{ in } Y_{f} &{}\\ -{\textbf{n}}\cdot \left( -c\nabla u\right) =g-qu\quad \text{ on } \partial Y_{sf} &{}\\ c=D, u=\psi _{\eta }, f=\lambda \psi _{\eta }, g=0, q=k_{+}&{} \end{array} \right. \end{aligned}$$

(63)

Solving Eq. (63) allows to determine the eigenfunctions and the associated eigenvalues. Thereafter, the general PDE formulation in Comsol software is used with stationary solver to obtain the vector $\mathbf {\chi }_r$, solution of the boundary value problem (30)–(31).

$$\begin{aligned} { \left\{ \begin{array}{ll} e_{a}\dfrac{\partial ^{2}{\textbf{v}}}{\partial t^{2}}+d_{a}\dfrac{\partial {\textbf{v}}}{\partial t}+\nabla \cdot \left( \pmb {\varGamma }\right) ={\textbf{f}}\quad \text { in }Y_{f}&{} \\ -{\textbf{n}} \cdot \pmb {\varGamma } =0\quad \text { on }\partial Y_{sf}&{} \\ e_{a}=0,\; d_{a}=0,\; {\textbf{v}}=\left( \chi _{r1},\chi _{r2}\right) ^{T},\; \pmb {\varGamma =}D\psi _{\eta }^{2}\left( {\textbf{I}}+\mathbf {\nabla v}\right) ,\;\mathbf {f=0} &{} \end{array} \right. } \end{aligned}$$

(64)

Once $\psi _{\eta }$ and $\mathbf {\chi }_r$ determined numerically, the reactive homogenized diffusion tensor $\mathbf {D_r^\textrm{hom}}$ is calculated from (29). However, the determination of the homogenized diffusion and co-diffusion tensors given by (27)–(28) requires also to calculate previously the homogenized diffusion tensor $\mathbf {D^\textrm{hom}}$. For that, the boundary value problem (21) is solved using the general PDE formulation predefined in Comsol software which corresponds to Eq. (64) without the eigenfunction $\psi _{\eta }$.

The numerical procedure was validated in the case of two parallel plans by comparing the numerical results to the analytical solution (see [15] for more details).

4.1 Circular inclusion

Let us consider a 2D elementary cell of size l with a circular inclusion of radius R localized at the centre (see Fig. 2). The eigenvalue problem (32)–(34) and boundary value problem (21) are solved numerically for different value of the Damköhler number¹⁰$Da \in [10^{-6}, 10^2]$. It is important to notice that $Da=k_{+}l/D_\textrm{ref}$ and $k_{+}=k_a+k_b$ with $k_b/k_a=\alpha$. In this case, the porosity of the elementary cell is $\varphi =0.8$ with $l=1$. It is important to emphasize that the solutions of the eigenvalue problem (32)–(34) and boundary value problem (30)–(31) are sensitive to the mesh size h. A numerical parametric study¹¹ according to the mesh size is carried out for the elementary cell of Fig. 2 in order to fix the mesh size for the numerical calculations. Linear triangular elements were chosen for the simulations. The obtained results show that the mean size of elements should be less than l/100 to give constant eigenvalues and homogenized diffusion coefficients with respect to the mesh size. According to the symmetry of the unit cell, the geometric and reactive homogenized diffusion tensors are isotropic $\mathbf {D^\textrm{hom}}=D^\textrm{hom}{\textbf{I}}$ and $\mathbf {D_r^\textrm{hom}}=D_r^\textrm{hom}{\textbf{I}}$. Therefore the homogenized diffusion and co-diffusion tensors are isotropic also. In the sequel, we compare only the coefficients.

Fig. 2

Unit cell with circular inclusion

Figure 3a shows the variation of relative homogenized diffusion tensors as functions of Damköhler number Da for several values of the ratio $\alpha$. We observe that the ratios $D^\textrm{hom}_{aa}/D^\textrm{hom}$ and $D^\textrm{hom}_{bb}/D^\textrm{hom}$ are equal to 1 for $Da<10^{-1}$. In this range, the effects of chemical reactions on the homogenized diffusion tensors can be neglected, that corresponds to model I and II presented above. For $Da>10^{-1}$, $D^\textrm{hom}_{aa}/D^\textrm{hom}$ and $D^\textrm{hom}_{bb}/D^\textrm{hom}$ decrease with the increase in Da. This is due to chemical reactions which slow down the diffusive transfer of components A and B.

We remark that $D^\textrm{hom}_{aa}/D^\textrm{hom}$ (respectively $D^\textrm{hom}_{bb}/D^\textrm{hom}$) is an increasing (respectively decreasing) function of the ratio $\alpha$. Indeed, for a fixed value of Da, the reactive homogenized diffusion coefficient $D^\textrm{hom}_r$ is constant,¹² whereas the heterogeneous reaction rate coefficients $k_b$ and $k_a$ are increasing and decreasing functions of $\alpha$, respectively,¹³ which explain the variation of $D^\textrm{hom}_{aa}$ and $D^\textrm{hom}_{bb}$ according to their definition given by (27)–(28). In other words, the increase in the heterogeneous reaction rate coefficients induces the decrease in the homogenized diffusion tensor for the same component.

Fig. 3

Variation of relative homogenized diffusion coefficients versus Da, for a unit cell with a circular inclusion of porosity of 0.8

The variation of the relative homogenized co-diffusion coefficients $D^\textrm{hom}_{ab}$ and $D^\textrm{hom}_{ba}$ with respect to Da is represented in Fig. 3b. We observe that $D^\textrm{hom}_{ab}$ and $D^\textrm{hom}_{ba}$ are equal to zero for $Da<10^{-1}$ as in that case the reactive and geometric homogenized diffusion coefficient $D^\textrm{hom}_r$ and $D^\textrm{hom}$ are very close. When the Damköhler number is in the range $Da>10^{-1}$, $D^\textrm{hom} _{ab}$ and $D^\textrm{hom}_{ba}$ increase with Da. This is due, on the one hand to the decrease in $D^\textrm{hom}_r$ with Da and on the other, to the increase in $k_a$ and $k_b$ with Da.

We remark also that $D^\textrm{hom}_{ab}/D^\textrm{hom}$ and $D^\textrm{hom}_{ba}/D^\textrm{hom}$ are increasing and decreasing functions of $\alpha$, respectively. It is important to underline that the increase in the homogenized co-diffusion coefficient $D^\textrm{hom}_{ab}$ and $D^\textrm{hom}_{ba}$ implies that a diffusive coupling appears at macro-scale (see Eqs. (25)–(26)).

Let us focus now, on the variation of the homogenized reaction rate coefficients ${\mathscr {K}}^{II}$ and ${\mathscr {K}}^{III}$ given by Eqs. (24) and (35) for model II and III versus Damköhler number Da for different value of ratio $\alpha$ (see Fig. 4). In that case, we remark that for $Da<1$ the homogenized reaction rate coefficients $K^{II}$ and ${\mathscr {K}}^{III}$ are identical; that can be explained from Eqs. (61)–(62) for an eigenfunction $\psi _{\eta }$ equal to 1. Model III can reproduce model II for $Da<1$ and also model I for $Da={\mathscr {O}} \left( \varepsilon ^2 \right)$. For $Da>1$, we observe that the variation of ${\mathscr {K}}^{III}$ becomes nonlinear with Da and ${\mathscr {K}}^{II}>{\mathscr {K}}^{III}$ (in that case, the eigenfunction $\psi _{\eta }<1$). In addition, we remark that ${\mathscr {K}}_a$ and ${\mathscr {K}}_b$ are decreasing and increasing function of $\alpha$, respectively.

Thus, it can be concluded that the increase in the Damköhler number Da induces the increase in the homogenized reaction rate coefficient ${\mathscr {K}}_{a}$ and ${\mathscr {K}}_{b}$, the decrease in homogenized diffusion coefficients $D^\textrm{hom}_{aa}$ and $D^\textrm{hom}_{bb}$ and the increase in the homogenized co-diffusion coefficients $D^\textrm{hom}_{ab}$ and $D^\textrm{hom}_{ba}$ at macro-scale.

Fig. 4

Variation of ${\mathscr {K}}_a$ and ${\mathscr {K}}_b$ versus Da for different value of $\alpha$ and for $\varphi =0.8$

4.1.1 Analysis at the elementary cell scale

In this section, we will focus on the comparison of homogenized parameters obtained here by Periodic Homogenization Method (PHM) to those obtained by Volume Averaging Method¹⁴ (VAM) in [34]. Figure 5 presents the homogenized parameters obtained from PHM and VAM in the case of circular inclusion of porosity $\varphi =0.8$ and for a ratio of heterogeneous reaction rate coefficients of $\alpha =k_b/k_a=2$. First, for $Da<0.1$ (corresponding to model II in our analysis), the homogenized diffusion coefficients $D^\textrm{hom}_{aa}$ and $D^\textrm{hom}_{bb}$ are equal to the geometric one in the case of VAM and of PHM (see Fig. 5a). In the same range of Da, we remark also that the homogenized co-diffusion coefficients $D_{ab}$ and $D_{ba}$ are equal to zero, which corresponds to the absence of diffusive coupling in model II for the PHM and for the VAM (see Fig. 5b). An important point to quote is that for $Da>0.1$, we observe that the relative homogenized diffusion coefficients obtained from VAM are increasing functions of Da, whereas those obtained from PHM are decreasing functions of Da (Fig. 5a).

Fig. 5

Comparison between homogenized parameters obtained by volume average method (VAM) and by periodic homogenization method (PHM), for a unit cell with a circular inclusion of porosity $\varphi =0.8$. a $D^\textrm{hom}_{aa}/D^\textrm{hom}$ and $D^\textrm{hom}_{bb}/D^\textrm{hom}$ versus Da. b $D^\textrm{hom}_{ab}/D^\textrm{hom}$ and $D^\textrm{hom}_{ba}/D^\textrm{hom}$ versus Da. c ${\mathscr {K}}^{III}_a/{\mathscr {K}}^{II}_a$ and ${\mathscr {K}}^{III}_b/{\mathscr {K}}^{II}_b$ versus Da

Moreover, we obtain that the ratios $D^\textrm{hom}_{ab}/ D^\textrm{hom}$ and $D^\textrm{hom}_{ba}/D^\textrm{hom}$ obtained from PHM are positive and increasing functions of Da in the range $Da>0.1$ whereas they are negative and decreasing functions of Da for VAM (Fig. 5b). In that case, the homogenized co-diffusion coefficients reflect the deviation of the reactive homogenized diffusion coefficient $D^\textrm{hom}_r$ from the geometric one $D^\textrm{hom}$ weighted by reaction coefficients $k_b$ for $D^\textrm{hom}_{ab}$ and $k_a$ for $D^\textrm{hom}_{ba}$. This deviation is positive and increases with Da for PHM, whereas it is negative and decreases with Da for VAM. In Fig. 5c, for $Da>0.1$, we observe that the relative homogenized reaction rate coefficients obtained by VAM and PHM follow the similar trends but with a gap between the VAM and PHM homogenized reaction rate coefficients.

It can be concluded that the homogenized parameters obtained by PHM and VAM are very different and generally with opposite tendencies when the Damköhler number Da varies. It seems interesting to quantify the impact of this difference on the associated macroscopic concentrations profiles and fluxes. This is the aim of the next section.

4.1.2 Comparison of the PSS and the PHM model

Fig. 6

Porous media of porosity $\varphi =0.8$ at the macro-scale [15]

The aim of this section is to compare the homogenized coupled diffusion reaction model obtained by PHM (Model III) given by (25)–(26) to the Pore Scale Simulation (PSS) given by (1)–(2) at the pore scale. The homogenized Eqs. (25)–(26) are solved on a continuous homogeneous macroscopic domain of length $L=Nl$, where N is the number of unit cells of size l constituting the macroscopic domain¹⁵ (Fig. 6). The unit cell is those of Fig. 2, constituted of a circular solid inclusion. The variations of the associated homogenized diffusion coefficients are represented in Figs. 3 and 4. On the inlet and outlet, Dirichlet boundary conditions are applied and periodic boundary conditions are considered on the lateral boundary. In addition, boundary conditions (3)–(4) are applied on the solid–fluid interface $\varGamma _{sf}$. The homogenized coupled diffusion reaction Eqs. (25)–(26) are solved on the whole fluid domain $\varOmega _f$ of the N juxtaposed unit cells.

In this numerical study, we consider for the numerical simulations PSS and PHM a value of $D=1$ and $C_{a}(x_1=0)=C_{b}(x_1=0)=1$ at inlet, $C_{a}(x_1=L)=C_{b}(x_1=L)=0$ at outlet as boundary conditions. The Damköhler number Da is considered as the parameter of the simulation with values $Da=0.01,~0.1,~1,~10$ and two values of the ratio $\alpha =0.1,~0.5$.

Fig. 7

Concentration of component A for different values of Da obtained by PSS and PHM

Fig. 8

Concentration of component B for different values of Da obtained by PSS and PHM

Figures 7 and 8 show, for different values of Da, the variation of the average concentrations $\langle C_a \rangle ^f$ and $\langle C_b \rangle ^f$ obtained from homogenized Eqs. (25)–(26) and the variation of the concentrations $C_a$ and $C_b$ obtained by solving the local problem (1)–(2) by PSS. The concentrations of component A and B obtained from the PHM model and PSS are in very good agreement for different values of the Damköhler number.

4.1.3 Comparison of the PHM and the VAM model

In order to analyse in greater depth these results, Fig. 9 compares the variation of the average concentrations $\langle C_a \rangle ^f$ and $\langle C_b \rangle ^f$ obtained from PHM and VAM [34] to average concentrations $\langle C_a \rangle _{y_2}$ and $\langle C_b \rangle _{y_2}$

$$\begin{aligned} \left\langle C_a \right\rangle _{y_2}=\frac{1}{l}\int _{0}^{l} C_a dy_2; \quad \quad \left\langle C_b \right\rangle _{y_2}=\frac{1}{l}\int _{0}^{l}C_bdy_2 \end{aligned}$$

(65)

computed by PSS.

We remark from Fig. 9 that the concentration of component A (reactant species) decreases with $x_1/L$. This tendency increases significantly for high values of Da. We observe also that PHM and VAM concentration profiles are in good agreement with PSS for different value of Da and ratio $\alpha$. It is important to notice that the relative error for concentrations, when PSS solution is considered as the reference one, is less than $2\%$ for both solutions VAM and PHM. For component B (product species), the concentration profile increases and then decreases. This is due to the chemical reaction allowing to the production of component B. From a physical point of view, the chemical reactions at the solid–fluid interface must slow down the diffusive transfer, leading to a decreasing of the homogenized diffusion tensors. This is observed with PHM but not with VAM.

Fig. 9

Average concentration versus $x_1/L$ for different values of $\alpha$ and Da

Let us compare now the diffusive flux of the component A obtained from PHM and VAM with PSS one. The diffusive flux of PHM and VAM is defined as:

$$\begin{aligned} J_{a_{x_1}}=-\left( D^\textrm{hom}_{aa}+D^\textrm{hom}_{ba} \right) \nabla _{x_1} \langle C_a \rangle ^f \end{aligned}$$

(66)

For the PSS model, the diffusive flux is determined by:

$$\begin{aligned} J_{a_{x_1}}=\langle -D \nabla _{y_1} C_a \rangle _{y_2} \end{aligned}$$

(67)

The diffusive fluxes are plotted with respect to $x_1/L$ for different values of Da in Fig. 10. The fluxes decrease with respect to $x_1/L$. Indeed, the component A (reactant) is consummated by chemical reaction on the solid–fluid interface. The decrease in the diffusive flux $J_{a_{x_1}}$ is more significant when Da increases. Afterwards, it reaches a constant value (for $Da>0.1$). The PHM and VAM diffusive fluxes are in good agreement with PSS ones. The diffusion and co-diffusion homogenized tensors obtained by PHM and VAM are different and of opposite tendency with respect to Da (see Fig. 5). However, it is important to notice that the values of $\left( D^\textrm{hom}_{aa}+D^\textrm{hom}_{ba} \right)$ given by PHM and VAM models are very close, which explains the similar results for fluxes and concentrations (see Fig. 9).

Nevertheless, the PHM results seem to be more coherent from a physical point of view. Indeed, the chemical reactions at the solid–fluid interface must slow down the diffusive transfer, leading to a decreasing of the homogenized diffusion tensors.

Fig. 10

Diffusion flux of component A versus $x_1/L$ for different values of Da and for $\alpha =0.1$

4.2 Random porous media

4.2.1 Analysis at the elementary cell scale

Fig. 11

Random elementary cell with porosity $\phi =0.28$

Fig. 12

a, b Variation of relative homogenized diffusion coefficients in direction $y_1$ and $y_2$ versus Da. c Variation of relative homogenized diffusion of Eq. (29) in direction $y_1$ and $y_2$ versus Da. d Variation of the relative homogenized reaction rate coefficients for components A and B versus Da for $\alpha =0.1$

Let us consider a 2D elementary cell containing several circular inclusions whose radii and positions are distributed randomly. On this random elementary cell, we resolve numerically problems (21), (30)–(31) and (32)–(34) for different value of Da to compute $\mathbf {D^\textrm{hom}}$ and $\mathbf {D_r^\textrm{hom}}$ from (20) and (29). Let us notice that in the expression of Da only the local heterogeneous reaction rate coefficients $k_a$ or $k_b$ vary, the microscopic diffusion coefficient D and the size of unit cell l are assumed to be constant. Figure 12a, b shows the variation in directions $y_1$ and $y_2$ (versus Damköhler number Da) of the relative reactive homogenized diffusion coefficients given by (27)–(28) normalized by the purely geometric homogenized ones. We observe that for $Da<0.1$, the relative coefficients $D^\textrm{hom}_{aa_{11}}/D_{11}^\textrm{hom}$ and $D^\textrm{hom}_{bb_{11}}/D_{11}^\textrm{hom}$ are equal to one, whereas $D^\textrm{hom}_{ab_{11}}/D_{11}^\textrm{hom}$ and $D^\textrm{hom}_{ba_{11}}/D_{11}^\textrm{hom}$ are equal to zero. As already observed in the previous example, in this range of Da, the chemical reaction effects are negligible and therefore the reactive homogenized diffusion tensor $\mathbf {D^\textrm{hom}_r}$ given by (29) is equal to geometric homogenized one $\mathbf {D^\textrm{hom}}$ given by (20).

For $0.1<Da<3$, we observe as in the previous case of a circular inclusion, that the relative homogenized diffusion coefficients $D^\textrm{hom}_{aa_{11}}/D_{11}^\textrm{hom}$ and $D^\textrm{hom}_{bb_{11}}/D_{11}^\textrm{hom}$ (respectively the homogenized co-diffusion coefficients $D^\textrm{hom}_{ab_{11}}/D_{11}^\textrm{hom}$ and $D^\textrm{hom}_{ba_{11}}/D_{11}^\textrm{hom}$) are decreasing (respectively increasing) functions of Da. This is due to the decrease in the reactive homogenized diffusion $\mathbf {D^\textrm{hom}_r}$ when Da increases (see Fig. 12c, for more details on the dependency of $\mathbf {D^\textrm{hom}_r}$ with respect to Da see [15]).

For $Da>3$, we observe that all relative homogenized diffusion coefficients are constant. In that case, the reactive homogenized diffusion coefficient $D_{r_{11}}^\textrm{hom}$ tends to zero. Indeed, as we have considered that $\frac{k_b}{k_a}=\alpha$, substituting in (27)–(28) with $D_{r_{11}}^\textrm{hom} \approx 0$ (see Fig. 12c), we obtain that:

$D^\textrm{hom}_{aa_{11}}=D^\textrm{hom}_{ab_{11}}=\frac{D_{11}^\textrm{hom}}{\left( 1+\alpha \right) }; \quad D^\textrm{hom}_{bb_{11}}=D^\textrm{hom}_{ab_{11}}=\frac{\alpha D_{11}^\textrm{hom}}{\left( 1+\alpha \right) }$, that is observed in Fig. 12.

The same observations can be noticed in direction $y_2$. In addition, we observe also that the relative homogenized diffusion coefficients $D^\textrm{hom}_{nm{11}}/D^\textrm{hom}_{11}$ and $D^\textrm{hom}_{nm{22}}/D^\textrm{hom}_{22}$ (with n and m equal to a or b) are very close. In what follow we focus our analysis only in direction $y_1$. Figure 12d shows the variation of the relative homogenized reaction rate coefficients ${\mathscr {K}}^{III}_{a}/k_a$ and ${\mathscr {K}}^{III}_{b}/k_b$, for component A and B, with respect to the Damköhler number Da. We notice that the ratios ${\mathscr {K}}^{III}_{a}/k_a$ and ${\mathscr {K}}^{III}_{b}/k_b$ are increasing functions of Da. For $Da<0.1$, ${\mathscr {K}}^{III}_{a}/k_a$ and ${\mathscr {K}}^{III}_{b}/k_b$ present a linear variation. In this range, the homogenized reaction rate coefficients of model II and model III are identical and the diffusion and reaction are decoupled. For $Da>0.1$, the variation of ${\mathscr {K}}^{III}_{a}/k_a$ and ${\mathscr {K}}^{III}_{b}/k_b$ with Da becomes slightly nonlinear. In that range, the diffusion and reaction are coupled through the homogenized diffusion coefficients, which are function of the chemical reactions rates according to Eqs. (27)–(28).

4.2.2 Comparison of the PSS and the PHM model

Fig. 13

Random porous media of porosity $\varphi =0.28$ at macro-scale

To finish, in this section, we are interested in comparing the homogenized diffusion reaction model III (PHM) given by Eqs. (25)–(26) to the Pore Scale Simulation (PSS) of coupled diffusion reaction equations at microscopic scale (1)–(4). The macroscopic domain of size L is constituted of the juxtaposition of N elementary cells of size l with $L=Nl$ (Fig. 13). The homogenized transfers parameters are those presented by Fig. 12. In this study, we only consider transfer in direction $x_1$, the results in direction $x_2$ are nearly identical, due to the "quasi" isotropy of the elementary cell of Fig. 11. Dirichlet boundary conditions are imposed on the inlet and the outlet for unknowns $\left\langle C_a\right\rangle ^f$ and $\left\langle C_b\right\rangle ^f$, solution of Eqs. (25)–(26). Periodic boundary conditions are imposed on the lateral boundary. The numerical parameters used in this study are summarized in Table 1.

Table 1 Numerical parameters used in the simulations of Fig. 14

Fig. 14

Average concentration fields $\left\langle C_a\right\rangle ^f$, $\left\langle C_b\right\rangle ^f$, $C_a$ and $C_b$ according to $x_1$ obtained from PHM and PSS for different values of Da

Fig. 14 compares the average concentration fields obtained from PHM and the local concentration fields given by PSS for different values of Da and $\alpha$. We remark that the PHM model is in a good agreement with PSS with a very reduced computation time.¹⁶ We notice that the average concentration fields $\left\langle C_a\right\rangle ^f$ and $\left\langle C_b\right\rangle ^f$ are very similar to the local concentration fields $C_a$ and $C_b$.

Fig. 15

Concentration fields versus $x_1/L$ for different values of Da and $\alpha$

Finally, we compare in Fig. 15 the variation of average concentrations $\left\langle C_a\right\rangle ^f$, $\left\langle C_b\right\rangle ^f$ of PHM to average concentrations¹⁷$\left\langle C_a\right\rangle _{y_2}$ and $\left\langle C_b\right\rangle _{y_2}$ of PSS versus $x_1/L$.

We observe that the average concentrations obtained from PHM and from PSS are very close¹⁸ for different values of Da and $\alpha$. Moreover, the concentration of component A decreases (reactant) and the concentration of component B increases (product). This effect becomes all the more important when Da increases and $\alpha$ decreases, which corresponds to a more important contrast of the heterogeneous reaction rate coefficients. Indeed, the concentrations at the inlet of the porous media do not satisfy the chemical equilibrium¹⁹ in the case of PSS and PHM model. This chemical equilibrium is reached in the porous medium after the decrease and the increase in concentrations of components A and B, respectively (nonlinear part of each curve). The distance from the inlet required to achieve the equilibrium depends on the Damköhler number Da. Indeed, this distance decreases with the increase in Da.

5 Conclusion

In this work, we applied the periodic homogenization technique to upscale multi-species diffusion equations coupled with heterogeneous first-order chemical reaction at the solid–fluid interface. Several cases were discussed, according to the order of magnitude of the Damköhler number Da. For small values of Da, the upscaling procedure leads to an homogenized diffusion model, where the homogenized diffusion tensor is purely geometric. For intermediate orders of magnitude of Da, we recovered at the macro-scale a diffusion reaction model where the coupling between species is carried out through the reactive terms. In that intermediate case, the homogenized diffusion tensor is still decoupled from the chemical reactions. For large values of Da, we obtain a non-classical homogenized diffusion reaction model, where co-diffusion terms appear at the macro-scale, involving homogenized co-diffusion tensors $\mathbf {D_{ab}^\textrm{hom}}$ and $\mathbf {D_{ba}^\textrm{hom}}$, in addition to the more classical homogenized diffusion tensors $\mathbf {D_{aa}^\textrm{hom}}$ and $\mathbf {D_{bb}^\textrm{hom}}$. An important point is that all these homogenized diffusion tensors are coupled to heterogeneous reaction rate coefficients. The determination of the homogenized transfer parameters, such as diffusion, co-diffusion tensors and homogenized chemical reaction rate coefficients, requires to solve coupled boundary values problems at unit cell scale.

Numerical studies have then been performed on a simple two-dimensional elementary cell with a circular inclusion in order to highlight the influence of chemical reaction effects on the homogenized diffusion and co-diffusion tensors and on the homogenized diffusion reaction rate coefficients. In this case, it has been found that the homogenized diffusion (respectively co-diffusion) tensors are decreasing (respectively increasing) functions of the local heterogeneous reaction rate coefficients. The chemical reaction slows down the diffusion transfer according to the microscopic heterogeneous reaction rate coefficients. These homogenized parameters were compared to those obtained by VAM.²⁰ It has been underlined that the effective diffusion (respectively co-diffusion) obtained from VAM is increasing (respectively decreasing with negative values) function of Da. The homogenized reaction rate coefficients are increasing functions of Da for both PHM and VAM.

Finally, numerical study on a 2D random elementary cell has been conduced in order to highlight the influence of the chemical reaction effect in the case of a more complex porous media. The variation of transfer parameters (decrease in diffusivity and increase in co-diffusivity) with respect to Da are confirmed in the case of a more complex random elementary cell. The comparison between homogenized diffusion reaction equations obtained from PHM and PSS is in good agreement. Therefore, the homogenized model of case 3 is a good approximation of the global behaviour at macro-scale, including accurately the physics at the micro-scale.

This study could be extended to the case of different diffusion coefficient at micro-scale where the theoretical development seems to be difficult. It could be also considered nonlinear chemical reactions at solid–fluid interface.