Upscaling diffusion–reaction in porous media

Abstract

In this work, we present the outlines of the periodic homogenization of the diffusion equation with chemical reaction at the interface, for different orders of magnitude of the Damköhler number. For large values of the Damköhler number, a non-classical homogenized model is obtained, where the homogenized diffusion tensor is strongly coupled with the chemical reaction rate. This homogenized model is particularly well adapted to describe, at the macroscopic level, diffusion with strong chemical reactions at the pore interfaces. The aim of this article is to highlight the transition between different regimes of diffusion–reaction according to the order of magnitude of the Damköhler number. In the last part of this work, we first consider a simple analytical example between two parallel plates, to understand the transition between the different possible regimes of diffusion–reaction. Finally, numerical simulations are performed on more complex two-dimensional elementary cells.

1 Introduction

The study of mass transport phenomena in porous media is of major interest in several domains, among them civil engineering, mechanics, and geomechanics, petroleum engineering, geochemistry, hydrogeology, and nuclear industry. In all these domains, the knowledge of mass transfer properties at the macro-scale (the scale of the structure), taking into account the multi-physics coupling involved at the micro-scale, is fundamental to derive accurate predictive models for engineers. This would require to know very accurately the geometry of the microstructure of the porous media at different scales and then to solve numerically diffusion–advection or diffusion–reaction (coupled or not with advection) equations in the whole pore network. This is still out of reach of modern imaging techniques and computing devices. To overcome these limitations, an alternative solution is to use homogenization techniques, also known as upscaling methods. They enable to determine very accurately the macroscopic transfer properties from the transfer equations at the micro-scale, knowing only the microstructure in an elementary representative cell [3, 7, 31, 38]. In this work, we derive a homogenized model of diffusion coupled to chemical reaction using the periodic homogenization method [3, 7, 31].

Several works using upscaling methods concern the diffusion transport in porous media coupled to chemical reactions. To quote some examples classified by the upscaling method, let us cite the method of moment [19, 20, 32], the periodic homogenization method [30], the averaging method [18, 34, 38] or the pore network model [16].

The homogenization with asymptotic expansion of an elliptical problem is analysed in several works, for the diffusion problem in [14] and for diffusion with nonlinear chemical reaction models (as Freundlich and Langmuir kinetics) in [15]. Auriault et al. focused on the diffusion transport with adsorption and discussed different cases according to the order of magnitude of the dimensionless number characterizing diffusion and adsorption [4] and diffusion, adsorption, and advection [5]. They found that the transport parameters do not depend on the adsorption rate at the micro-scale. In [23], the authors are interested in the diffusion–advection coupled with heterogeneous chemical reaction taking place at the solid–fluid interface. They discussed the case of higher reaction rate at the micro-scale and its influence on the macroscopic model of diffusion–advection–reaction. The method of moment [19, 32] was used to uspscale the diffusion–convection–reaction and the macro-transport parameters. The results depend on the reaction rate coefficient. Diffusion–advection accounting for heterogeneous reaction has been also considered in [1, 2] using periodic homogenization technique with drift. In the case of predominant reaction and advection, the homogenized diffusion–dispersion tensor obtained decreases when the microscopic reaction rate increases. Battiato and Tartakovsky [6] used also the periodic homogenization to upscale the one species local mass transport equation coupled to nonlinear heterogeneous chemical reaction. They studied several cases comparing diffusion, reaction, and advection according to the order of magnitude of Peclet and Damköhler numbers. They underscored that when diffusion and reaction are comparable, the diffusivity tensor is purely geometric. Boso and Battiato [8] upscaled the multi-species mass transport coupled to nonlinear homogeneous and heterogeneous chemical reactions. Korneek and Battiato [21] used the sequential periodic homogenization technique to upscale the reactive transport equation in idealized polydisperse porous media. They focused on the influence of the porous geometry on the homogenized model obtained with the multi-scale periodic homogenization method. For the study of the reactive mass transport in porous media using the volume averaging method, we refer to the non-exhaustive list of references. Among them, in [38] Whitaker upscaled the diffusion with heterogeneous chemical reaction, showing that the effective diffusion tensor is purely geometric and does not depend on the reaction rate coefficient. Wood and Whitaker [39] investigated diffusion and reaction in biofilms, Porta et al. [27, 28] upscaled multi-component diffusion–dispersion coupled with homogeneous biomolecular reaction. Valdes-Parada and Alvarez-Ramirez [34, 35] studied the diffusion coupled with the first-order homogeneous chemical reaction. They underscored according to Thiele modulus $\phi$ (with $\phi ^2=Da$) that the diffusivity is affected by the reaction. In [33], where the diffusion and diffusion–convection equations are coupled with homogeneous or heterogeneous chemical reactions, the authors pointed out that the effective diffusion tensor is an increasing function of the reaction rate. In addition, when the chemical reaction rate at the micro-scale is relatively large, the capabilities of the upscaled model are hindered. To remedy to this, the model of diffusion and heterogeneous reaction is revisited, and corrective terms are taken into account in the expressions of the diffusivity tensor and of the effective reaction rate [36]. Lugo-Méndez et al. [22] investigated the case of nonlinear chemical reaction coupled to diffusion and explored a linearization approach to solve the closure problem.

Recently, [29] used the volume averaging method to upscale the multi-component mass transfer and heterogeneous reversible reaction at the solid–fluid interface. They investigated the influence of the local reaction rate on the macroscopic transfer parameters and highlighted a similar behaviour as in [33,34,35].

The framework of this synthesis work is focussed on the study of the diffusion problem with linear heterogeneous chemical reaction. We propose to perform periodic homogenization of the diffusion–reaction problem, for different orders of magnitude of the Damköhler number, and to analyse very accurately the dependence of the homogenized diffusion tensor with respect to the reaction rate. We obtain a classification of macroscopic models with respect to the Damköhler number. Moreover, this approach enables one to specify accurately the domain of validity of the models obtained. For small values of the Damköhler number, corresponding to a low chemical reaction rate, we recover classical homogenized diffusive equations (cases 1 and 2), where the homogenized diffusion tensor depends only on the geometry of the microstructure. (It is decoupled from the chemical reaction.) For large values of the Damköhler number, we obtain a diffusion–reaction homogenized model (case 3), where the homogenized diffusion tensor is strongly coupled with the chemical reaction rate. This homogenized model is particularly well adapted to describe, at the macroscopic level, diffusion with strong chemical reactions at the pore interfaces. In the last part of the present work, we first consider a simple example of diffusion–reaction between two parallel plates, where an analytical resolution is possible. This example enables to well understand the transition between the different regimes of diffusion–reaction considered. Finally, the associated homogenized properties in the three possible regimes are computed for more complex 2D elementary cells. A comparison between homogenized diffusion–reaction model and direct numerical simulation is made at the pore scale.

2 The diffusion–reaction problem

2.1 Governing equations

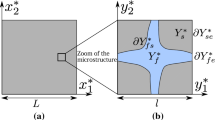
We consider reactive transport in a porous medium ${\mathscr {S}}^{*}$ whose characteristic length is L. We assume that the macroscopic medium ${\mathscr {S}}^{*}$ can be represented microscopically by the repetition of a periodic elementary cell $\varOmega ^{*}$ (Fig. 1) of characteristic length l. The macroscopic variable is denoted ${\mathbf {x}}^{*}=\left( x^{*}_1,~x^{*}_2,~ x^{*}_3\right)$, whereas the microscopic variable is ${\mathbf {y}}^{*} = \left( y^{*}_1,~ y^{*}_2,~ y^{*}_3\right)$. The small parameter $\varepsilon$:

$$\begin{aligned} \varepsilon =\dfrac{l}{L} \end{aligned}$$

is the ratio of the micro-scale l to the macro-scale L. The porous medium $\varOmega ^{*}$ is assumed to be rigid and saturated by a stagnant fluid occupying the domain $\varOmega _f^{*}$. The solid phase $\varOmega _s^{*}$ is considered impermeable to fluid and diffusive solute. The boundary of $\varOmega ^{*}$ is noted $\varGamma ^{*}$ and is composed of the solid–fluid interface $\varGamma ^{*}_{\mathrm{sf}}$ and of the fluid–fluid and solid–solid interfaces $\varGamma ^{*}_{\mathrm{ff}}$ and $\varGamma ^{*}_{\mathrm{ss}}$ separating fluid or solid phases of the neighbouring elementary cells (Fig. 1).

In this work, we consider diffusion with the heterogeneous first-order chemical reaction. The governing equations at the pore scale are given by¹

$$\begin{aligned} \frac{\partial c^{*}}{\partial t^{*}}= & {} \mathbf {\nabla ^{*}} \cdot \left( D^{*}\mathbf {\nabla ^{*}}c^{*}\right) \qquad in \quad \varOmega _f^{*}, \end{aligned}$$

(1)

$$\begin{aligned} -D^{*}\mathbf {\nabla ^{*}}c^{*} \cdot {\mathbf {n}}= & {} k^{*}c^{*} \qquad on \quad \varGamma _{\mathrm{sf}}^{*} \end{aligned}$$

(2)

where $c^{*}$ is the concentration of the chemical species, $D^{*}$ is the molecular diffusion coefficient, $k^{*}$ is the rate of heterogeneous chemical reaction, and ${\mathbf {n}}$ denotes the outward vector normal to the fluid phase on $\varGamma _{sf}^{*}$. In addition to boundary condition (2), the diffusion equation (1) is supplemented by a proper boundary condition on the external boundary $\partial \mathscr {S^{*}}$ of the macroscopic domain $\mathscr {S^{*}}$.

2.2 Dimensionless analysis

The homogenization procedure proposed here is similar to that developed in [3, 9,10,11, 13, 17, 24,25,26]. Equations (1)–(2) are rewritten in a dimensionless form with respect to reference quantities identified by the subscript (ref) in such a manner that the dimensionless quantities are of order ${\mathscr {O}}(1)$:

$$\begin{aligned} t=\frac{t^{*}}{t_{\mathrm{ref}}};\quad c=\frac{c^{*}}{c_{\mathrm{ref}}};\quad D=\frac{ D^{*}}{D_{\mathrm{ref}}};\quad k=\frac{k^{*}}{k_{\mathrm{ref}}}. \end{aligned}$$

(3)

Two characteristic times are associated with diffusion $t^{dif}_{l}$$\left( \text {or}~t^{dif}_{L}\right)$ and with reaction $t^{\mathrm{reac}}_{l}$$\left( \text {or}~t^{\mathrm{reac}}_{L}\right)$ at micro-scale and macro-scale, respectively:

$$\begin{aligned}&t^{dif}_{l} =\frac{l^{2}}{D_{\mathrm{ref}}};\quad t^{dif}_{L} =\frac{L^{2}}{D_{\mathrm{ref}}}, \end{aligned}$$

(4)

$$\begin{aligned}&t^{\mathrm{reac}}_{l}=\frac{l}{k_{\mathrm{ref}}};\quad t^{\mathrm{reac}}_{L}=\frac{L}{k_\mathrm{{ref}}}. \end{aligned}$$

(5)

The reference time is fixed equal to the characteristic time of diffusion at macro-scale: $t_{\mathrm{ref}}=t^{\mathrm{dif}}_{L}$. In addition, the spatial variable will be normalized with respect to the macroscopic characteristic length L. Therefore, we obtain the non-dimensional diffusion–reaction equation:

$$\begin{aligned} \frac{\partial c}{\partial t}= & {} \mathbf {\nabla } \cdot \left( D\mathbf {\nabla } c\right) \qquad \text {in} \quad \varOmega _f, \end{aligned}$$

(6)

$$\begin{aligned} -D\mathbf {\nabla } c \cdot {\mathbf {n}}= & {} Da_{L}kc \qquad \text {on} \quad \varGamma _{\mathrm{sf}}. \end{aligned}$$

(7)

The diffusion–reaction problem (6), (7) introduces the classical non-dimensional Damköhler number, which represents the ratio of the diffusion characteristic time to the reaction characteristic one, at the macro-scale:

$$\begin{aligned} Da_{L}=\dfrac{L k_{\mathrm{ref}}}{D_{\mathrm{ref}}}=\dfrac{t^{\mathrm{dif}}_{L}}{t^{\mathrm{reac}}_{L}}. \end{aligned}$$

3 Multi-scale homogenization procedure

Due to the assumption of scale separation, the concentration field $c \left( {\mathbf {x}},{\mathbf {y}},t\right)$ is assumed to be a function depending on the time t and on two independent space variables: a macroscopic or slow one ${\mathbf {x}} = x^{*}/L$ and a microscopic or rapid one ${\mathbf {y}} = y^{*}/l$. Moreover, we assume that $c \left( {\mathbf {x}},{\mathbf {y}},t\right)$ admits a formal expansion with respect to $\varepsilon$:

$$\begin{aligned} c \left( {\mathbf {x}},{\mathbf {y}},t\right) =\sum _{m=0}^{\infty }\varepsilon ^{m} c _{m}\left( {\mathbf {x}},{\mathbf {y}},t\right) \quad \text {with} \quad \left( m=0,~1,~2,~\ldots \right) \end{aligned}$$

(8)

where $c_{m}\left( {\mathbf {x}},{\mathbf {y}},t\right)$ are y-periodic functions. According for the separation of scales, the operators gradient $\mathbf {\nabla }$ and divergence $\mathbf {\nabla }.$ using the chain rule are written:

$$\begin{aligned} \mathbf {\nabla }= & {} \mathbf {\nabla }_{{\mathbf {x}}}+\varepsilon ^{-1} \mathbf {\nabla }_{{\mathbf {y}}}, \end{aligned}$$

(9)

$$\begin{aligned} \mathbf {\nabla } \cdot= & {} \mathbf {\nabla }_{{\mathbf {x}}} \cdot +\varepsilon ^{-1} \mathbf {\nabla }_{{\mathbf {y}}} \cdot \end{aligned}$$

(10)

We define three types of local averages of the quantity $A \left( {\mathbf {x}},~{\mathbf {y}},~t\right)$ that will be used in the sequel:

$$\begin{aligned} \left\langle A \right\rangle =\dfrac{1}{\vert \varOmega \vert } \int _{\varOmega } A d{\mathbf {y}}, \quad \left\langle A \right\rangle _{\varOmega _f} =\dfrac{1}{\vert \varOmega _f \vert } \int _{\varOmega _f } A d{\mathbf {y}},\quad \left\langle A \right\rangle _{\varGamma } =\dfrac{1}{\vert \varGamma \vert } \int _{\varGamma } A d{\mathbf {y}} \end{aligned}$$

(11)

where $\vert \varOmega \vert$ and $\vert \varOmega _f \vert$ are the volumes of $\varOmega$ and $\varOmega _f$, respectively, and $\vert \varGamma \vert$ is the surface area of $\varGamma$. Here, $\left\langle A \right\rangle$, $\left\langle A \right\rangle _{f}$, and $\left\langle A \right\rangle _{\varGamma }$ denote the average over the domain $\varOmega$, over the fluid phase $\varOmega _f$, and over the boundary $\varGamma$, respectively. $\left\langle A \right\rangle =\varphi \left\langle A \right\rangle _{\varOmega _f}$ and $\varphi = \vert \varOmega _f \vert / \vert \varOmega \vert$ is the porosity of the medium.

Fig. 1

Schematic representation of the porous medium considered

We assumed that the order of magnitude of the Damköhler number is:

$$\begin{aligned} Da_l=\varepsilon ^{\alpha } \quad \text {and} \quad Da_L=\varepsilon ^{\alpha -1}. \end{aligned}$$

(12)

Three cases are discussed in this work according to the value of exponent $\alpha$:

• 1. $Da_L={\mathscr {O}} \left( \varepsilon \right)$ (or equivalently $Da_l={\mathscr {O}} \left( \varepsilon ^2 \right)$) which corresponds to a predominant diffusion at the macroscopic scale. Equivalently, this case corresponds to $t^{dif}_{L}=\varepsilon t^{\mathrm{reac}}_{L}$ (or equivalently $t^{dif}_{l}=\varepsilon ^{2} t^{\mathrm{reac}}_{l}$).

• 2. $Da_L={\mathscr {O}} \left( 1 \right)$ (or equivalently $Da_l={\mathscr {O}} \left( \varepsilon \right)$) which corresponds to diffusion and reaction of the same order of magnitude on the macroscopic scale; this means that $t^{dif}_{L}=t^{\mathrm{reac}}_{L}$ ( or equivalently $t^{dif}_{l}=\varepsilon t^{\mathrm{reac}}_{l}$).

• 3. $Da_L={\mathscr {O}} \left( \varepsilon ^{-1} \right)$ (or equivalently $Da_l={\mathscr {O}} \left( 1 \right)$) which corresponds to a predominant chemical reaction on the macroscopic scale; this is equivalent to $t^{\mathrm{dif}}_{L}=\varepsilon ^{-1}t^{\mathrm{reac}}_{L}$ (or $t^{dif}_{l}= t^{\mathrm{reac}}_{l}$).

The homogenization procedure consists in introducing the asymptotic development (8) for the concentration c into the diffusion–reaction equation (6), (7) and taking into account the order of magnitude of the Damköhler number by its order of magnitude according to the case considered. Also, using derivative operators defined by (9), (10) and equating to zero the factors of successive powers of the parameter $\varepsilon$ lead to the coupled problems to be solved.

3.1 Diffusion model

We consider a characteristic time of diffusion shorter than the reaction one at the macro-scale, which is equivalent to $Da_L={\mathscr {O}} \left( \varepsilon \right)$ (or $Da_l={\mathscr {O}} \left( \varepsilon ^2 \right)$). In that case, the homogenized model obtained at the macroscopic scale is a purely diffusive model given by the following result:

Case 1

For dominant diffusion at the macroscopic scale, such as when the Damköhler number characteristic of the diffusion–reaction transfer is of the order of $Da_L={\mathscr {O}} \left( \varepsilon \right)$ (or $Da_l={\mathscr {O}} \left( \varepsilon ^2 \right)$), the associated homogenized model is a purely diffusive given by:

$$\begin{aligned} \varphi \frac{\partial c}{\partial t}+\mathbf {\nabla }_{x} \cdot \left( -{\mathbf {D}}^{\hom } \mathbf {\nabla }_{x}c\right) = 0 \qquad \text {(model I)} \end{aligned}$$

(13)

where $c = c\left( {\mathbf {x}}, t \right)$ is the macroscopic concentration² and ${\mathbf {D}}^{\hom }$ is the symmetric and positive definite homogenized diffusion tensor:

$$\begin{aligned} {\mathbf {D}}^{\hom } =\frac{1}{\left| \varOmega \right| }\int _{\varOmega _{f}}\left( D\left( {\mathbf {I}}+\mathbf {\nabla _{y}\chi } \right) \right) d\varOmega . \end{aligned}$$

(14)

The vector $\mathbf {\chi }$ is y-periodic, null average, and solution of the closure problem:

$$\begin{aligned} \mathbf {\nabla }_{y} \cdot \left( -D\left( {\mathbf {I}}+\mathbf {\nabla _{y}\chi } \right) \right)= & {} 0\qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(15)

$$\begin{aligned} -D\left( {\mathbf {I}}+\mathbf {\nabla _{y} \chi } \right) \cdot {\mathbf {n}}= & {} 0\qquad \text {on}\qquad \varGamma _{\mathrm{sf}}, \end{aligned}$$

(16)

$$\begin{aligned} \mathbf {\chi } \left( {\mathbf {y}}\right)= & {} \mathbf {\chi } \left( {\mathbf {y}}+l\right) \qquad \text {on}\qquad \varGamma _{\mathrm{ff}}, \end{aligned}$$

(17)

$$\begin{aligned} \left\langle \mathbf {\chi } \right\rangle= & {} 0 \qquad \text {in}\qquad \varOmega _{f}. \end{aligned}$$

(18)

The proof of case 1 is very classical and figures in details in [3, 5, 6, 20].

Therefore, the homogenization procedure leads to a diffusion macroscopic model, where the effects of the very slow reaction are not present at macro-scale. In this case, the homogenized diffusion tensor depends only on the microscopic variable $\mathbf {\chi }$ which is purely geometric.

3.2 Decoupled reaction diffusion model

We analyse now the case where the diffusion and reaction are of the same order of magnitude at the macro-scale, which corresponds to a Damköhler number $Da_L = {\mathscr {O}} \left( 1 \right)$ (or $Da_l={\mathscr {O}} \left( \varepsilon \right)$). The periodic homogenization procedure leads to case 2 detailed as follows.

Case 2

For diffusion and reaction of the same order on the macroscopic scale such as $Da_L={\mathscr {O}} \left( 1 \right)$ (or $Da_l={\mathscr {O}} \left( \varepsilon \right)$), the homogenized diffusion–reaction model reads:

$$\begin{aligned} \varphi \frac{\partial c}{\partial t}+\mathbf {\nabla }_{x} \cdot \left( -{\mathbf {D}} ^{\hom }\mathbf {\nabla }_{x} c\right) +{\mathscr {K}}c=0 \qquad \text {(model II)} \end{aligned}$$

(19)

where $c\left( {\mathbf {x}},t\right)$ is the concentration at the macro-scale and ${\mathbf {D}}^{\hom }$ is the homogenized diffusion tensor given by Eq.  (14):

$$\begin{aligned} {\mathbf {D}}^{\hom } =\frac{1}{\left| \varOmega \right| }\int _{\varOmega _{f}}\left( D\left( {\mathbf {I}}+\mathbf {\nabla _{y}\chi } \right) \right) d\varOmega . \end{aligned}$$

(20)

The vector $\mathbf {\chi }$ is always solution of the same boundary value problem (15)–(18). In addition, a reactive term appears in the transport equation as a homogeneous reaction at the macro-scale, where ${\mathscr {K}}$ represents the effective reaction rate given by:

$$\begin{aligned} {\mathscr {K}}=S_a k, \end{aligned}$$

(21)

which is a function of the heterogeneous reaction rate constant at micro-scale k and the porous medium specific area $S_a =\vert \varGamma _{\mathrm{sf}} \vert / \vert \varOmega \vert$.

The proof of case 2 is classical and detailed in [3, 5, 6, 20]. It is important to underscore that the homogenized equation (19), homogenized diffusion tensor (20), and corresponding closure problem (15)–(18) are similar to those obtained by Whitaker in [38].

It should be stressed that the homogenized diffusion tensor ${\mathbf {D}}^{\hom }$ is purely diffusive and independent of the chemical reaction. In this case, the diffusion and reaction are of the same order of magnitude at the macro-scale, but the respective homogenized parameters of diffusion ${\mathbf {D}}^{\hom }$ and of reaction ${\mathscr {K}}$ are decoupled. For the positiveness and symmetry of the non reactive effective diffusivity tensor (case 1 and case 2), the reader may refer to [3].

3.3 Coupled diffusion–reaction model

The last case considered in this paper corresponds to the homogenization of the diffusion–reaction (6), (7) for dominating reaction effects compared to diffusion ones. In that case, the characteristic time of chemical reaction is less than the characteristic time of diffusion which is equivalent to $Da_L = {\mathscr {O}} \left( \varepsilon ^{-1}\right)$ or equivalently to $Da_l={\mathscr {O}} \left( 1\right)$. Application of the periodic homogenization previous ansatz leads to mathematical difficulties due to the high difference in the order of magnitude between diffusion and reaction characteristic times (very high Damköhler number $Da_L={\mathscr {O}} \left( \varepsilon ^{-1}\right)$). This difficulty will be overcome thanks to a judicious change in variables similar to that proposed by Rubinstein and Mauri [23] or Allaire and Raphael [2](see proof, Eq. (30)).

Case 3

For dominating chemical reactions at the macro-scale corresponding to $Da_L={\mathscr {O}} \left( \varepsilon ^{-1}\right)$ (or $Da_l={\mathscr {O}} \left( 1\right)$), the macroscopic concentration³$\left\langle c \right\rangle _{\varOmega _{f}}$ is solution of the coupled homogenized diffusion–reaction model:

$$\begin{aligned} \varphi \frac{\partial \left\langle c \right\rangle _{\varOmega _{f}}}{\partial t} +\mathbf {\nabla }_{x} \cdot \left( -{\mathbf {D}}_{r}^{\hom }\mathbf {\nabla }_{x}\left\langle c \right\rangle _{\varOmega _{f}}\right) + {\mathscr {K}}\left\langle c \right\rangle _{\varOmega _{f}} =0 \qquad \text {(model III)}. \end{aligned}$$

(22)

The homogenized diffusion tensor ${\mathbf {D}}_r^{\hom }$ reads:

$$\begin{aligned} {\mathbf {D}}_r^{\hom } =\frac{1}{\left| \varOmega \right| }\int _{\varOmega _{f}}D\psi ^{2}\left( {\mathbf {I}}+\mathbf {\nabla }_{y}\mathbf {\chi }_{r} \right) dy \end{aligned}$$

(23)

where the vector $\mathbf {\chi }_{r}$ is y-periodic, of null average over the domain fluid $\varOmega _f$, and solution of the following boundary value problem:

$$\begin{aligned} \mathbf {\nabla }_{y} \cdot \left( -D\psi ^{2}\left( {\mathbf {I}}+\mathbf {\nabla }_{y} \mathbf {\chi }_r \right) \right)= & {} 0\qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(24)

$$\begin{aligned} \left( -D\psi ^{2}\left( {\mathbf {I}}+\mathbf {\nabla }_{y}\mathbf {\chi }_r \right) \right) \cdot {\mathbf {n}}= & {} 0\qquad \text {on}\qquad \varGamma _{\mathrm{sf}}. \end{aligned}$$

(25)

The closure (24, 25) is the homogenization of a diffusive problem with a spatially varying periodic diffusion coefficient $D \psi ^{2}$. Moreover, $\psi \left( {\mathbf {y}}\right)$ denotes a y-periodic eigenfunction, solution of the Sturm–Liouville problem:

$$\begin{aligned} \mathbf {\nabla }_{y} \cdot \left( -D\mathbf {\nabla }_{y} \psi \right)= & {} \lambda \psi \qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(26)

$$\begin{aligned} \left( -D \mathbf {\nabla }_{y} \psi \right) \cdot {\mathbf {n}}= & {} k\psi \qquad \text {on}\qquad \varGamma _{\mathrm{sf}}, \end{aligned}$$

(27)

$$\begin{aligned} \left\langle \psi ^2 \right\rangle= & {} 1 \qquad \text {in}\qquad \varOmega _{f}. \end{aligned}$$

(28)

Finally, ${\mathscr {K}}$ is the homogenized reaction rate given by:

$$\begin{aligned} {\mathscr {K}}=\varphi {\tilde{\lambda }} \end{aligned}$$

(29)

where ${\tilde{\lambda }}$ is the first eigenvalue (the smallest one) of the Sturm–Liouville problem (26), (27).

Proof

The similar model is analysed in [2, 23, 32]. We present only the outlines required to obtain the homogenized problem (22). Let us use the following change in variables, similar to the one proposed in [2, 23] which is still valid in the case of diffusion–reaction without convection:

$$\begin{aligned} c \left( {\mathbf {x}},{\mathbf {y}},t \right) = \exp \left( -\lambda ^{*} t^{*}\right) \theta \left( {\mathbf {x}},{\mathbf {y}},t\right) = \exp \left( -\varepsilon ^{-2}\lambda t\right) \theta \left( {\mathbf {x}},{\mathbf {y}},t\right) \end{aligned}$$

(30)

where $\lambda$ is a real constant to be determined. The concentration c is decomposed into two terms on the time scale. The first one decreases exponentially with t and depends on $\lambda$. The second one is the variable $\theta$ function of ${\mathbf {x}}$, ${\mathbf {y}}$, and t. According to [23], the change in variable (30) allows to make the diffusion and reaction at the same order of magnitude at the macro-scale. As $\lambda$ is the dimensionless eigenvalue of the local problem (26–28), $\lambda ^{*} = \lambda D_{\mathrm{ref}}/l^2$, and using the definition of $t^{*} = t L^2/D_{\mathrm{ref}}$, $\lambda ^{*} t^{*} = \varepsilon ^{-2} \lambda t$.

Substituting (30) in (6), (7), we obtain:

$$\begin{aligned} \frac{\partial \theta }{\partial t}-\varepsilon ^{-2}\lambda \theta + \mathbf {\nabla } \cdot \left( -D \mathbf {\nabla } \theta \right)= & {} 0\qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(31)

$$\begin{aligned} \left( -D \mathbf {\nabla } \theta \right) \cdot {\mathbf {n}}= & {} \varepsilon ^{-1} k \theta \qquad \text {on}\qquad \varGamma _{\mathrm{sf}}. \end{aligned}$$

(32)

According to the approach developed in [37], we search the solution of this problem in the form:

$$\begin{aligned} \theta \left( {\mathbf {x}},{\mathbf {y}},t \right) =\psi \left( {\mathbf {y}}\right) v \left( {\mathbf {x}},{\mathbf {y}},t \right) \end{aligned}$$

(33)

where $\psi \left( {\mathbf {y}}\right)$ is y-periodic. Now, by substitution of the change in variable (33) problem (31), (32) becomes after some algebra:

$$\begin{aligned} \psi \frac{\partial v}{\partial t} +\psi \mathbf {\nabla } \cdot \left( - D\mathbf {\nabla } v\right) -2D\mathbf {\nabla } v\mathbf {\nabla } \psi +v\left( \mathbf {\nabla } \cdot \left( - D\mathbf {\nabla } \psi \right) -\varepsilon ^{-2}\lambda \psi \right)= & {} 0, \end{aligned}$$

(34)

$$\begin{aligned} v\left( -D\mathbf {\nabla } \psi \cdot {\mathbf {n}}-\varepsilon ^{-1}k\psi \right) - \psi \left( D\mathbf {\nabla } v\right) \cdot {\mathbf {n}}= & {} 0. \end{aligned}$$

(35)

Now, we search the particular function $\psi \left( {\mathbf {y}}\right)$ solution of the eigenvalue problem:

$$\begin{aligned} \mathbf {\nabla }_{y} \cdot \left( -D\mathbf {\nabla }_{y} \psi \right)= & {} \lambda \psi \qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(36)

$$\begin{aligned} \left( -D \mathbf {\nabla }_{y} \psi \right) \cdot {\mathbf {n}}= & {} k\psi \qquad \text {on}\qquad \varGamma _{\mathrm{sf}} \end{aligned}$$

(37)

where $\lambda$ is an eigenvalue. It is important to notice that problem (36), (37) is defined up to a multiplicative constant which can be fixed using the condition:

$$\begin{aligned} \left\langle \psi ^2 \right\rangle = 1 \qquad \text {in}\qquad \varOmega _{f}. \end{aligned}$$

(38)

It is important to notice that the determination of the first eigenvalue is sufficient to homogenize the diffusion–reaction problem (6), (7) (see [1, 2, 23, 37]). Combining problems (34), (35) and (36), (37), we obtain the equation for $v\left( {\mathbf {x}},{\mathbf {y}},t \right)$ that corresponds to the problem to be homogenized:

$$\begin{aligned} \psi ^{2}\frac{\partial v}{\partial t}= & {} \mathbf {\nabla } \cdot \left( D\psi ^{2}\mathbf {\nabla } v\right) \qquad \text {in}\qquad \varOmega _{f}, \end{aligned}$$

(39)

$$\begin{aligned} \left( -D \psi ^{2}\mathbf {\nabla } v\right) \cdot {\mathbf {n}}= & {} 0 \qquad \text {on}\qquad \varGamma _{\mathrm{sf}}. \end{aligned}$$

(40)

In this last step of proof of case 3, we carry out the homogenization procedure by considering that the variable v admits an asymptotic expansion with respect to $\varepsilon$ according to Eq.  (8). It is important to notice that the homogenization of the diffusion problem (39), (40) is without difficulty and similar to the homogenization of the diffusion problem of case 1. The homogenized diffusion problem is given by:

$$\begin{aligned} \varphi \frac{\partial v}{\partial t}+\mathbf {\nabla }_{x} \cdot \left( -{\mathbf {D}}_r^{\hom } \mathbf {\nabla }_{x} v\right) =0 \end{aligned}$$

(41)

where $\varphi$ denotes the porosity of the porous medium. ${\mathbf {D}}_r^{\hom }$ denotes the homogenized diffusion tensor (with a subscript r) accounting for the chemical reaction given by (23), where the vector⁴$\mathbf {\chi }_{r}$ is y-periodic, of zero average in the fluid domain $\varOmega _f$, and solution of the boundary value problem (24), (25).

The closure variable $\mathbf {\chi }_{r}$ depends on the geometry of the unit cell and on the eigenfunction $\psi$, accounting for the chemical reaction on the interface solid–fluid $\varGamma _{\mathrm{sf}}$ through the boundary condition (27).

Thus, the variable $\mathbf {\chi }_{r}$ takes into account the geometry of the porous media coupled with the chemical reaction effects. The homogenized diffusion tensor is in this case also function of $\psi$, and ${\mathbf {D}}_r^{\hom }$ is linked to the reaction rate k. For the proof of the positiveness and symmetry of the reactive homogenized diffusion tensor case 3, we can refer to [32]. In this case, the homogenized diffusion tensor is different compared with cases 1 and 2.

Now, Eq. (41) is rewritten for the intrinsic average of concentration $\left\langle c \right\rangle _{\varOmega _{f}}$ defined by:

$$\begin{aligned} \left\langle c \right\rangle _{\varOmega _{f}} =\exp \left( -\lambda t\right) \left\langle \psi \right\rangle _{\varOmega _{f}}v. \end{aligned}$$

(42)

The temporal derivative is given by:

$$\begin{aligned} \frac{\partial \left\langle c \right\rangle _{\varOmega _{f}}}{\partial t} =\exp \left( -\lambda t\right) \left\langle \psi \right\rangle _{\varOmega _{f}}\frac{\partial v}{\partial t}-\lambda \exp \left( -\lambda t\right) \left\langle \psi \right\rangle _{\varOmega _{f}}v. \end{aligned}$$

(43)

Multiplying the homogenized equation (41) by $\left( \exp \left( -\lambda t\right) \left\langle \psi \right\rangle _{\varOmega _{f}} \right)$ and using (43), as $\psi ({\mathbf {y}})$ depends only on the variable ${\mathbf {y}}$, we obtain the homogenized diffusion–reaction equation (22) for the macroscopic concentration $\left\langle c \right\rangle _{\varOmega _{f}}$. The unknown $\left\langle c \right\rangle _{\varOmega _{f}}$, solution of the homogenized diffusion–reaction equation (22), depends on the eigenfunction $\psi$ and on the eigenvalue $\lambda$ determined from problem (26), (27). In this case, the macroscopic concentration $\left\langle c\right\rangle _{\varOmega _{f}}$ and the homogenized diffusion tensor ${\mathbf {D}}_r^{\hom }$ are coupled with the chemical reaction. The macroscopic reaction term in Eq. (22) is a homogeneous reaction term even if at the micro-scale the chemical reaction is heterogeneous (Fig. 2). $\square$

The first eigenvalue ${\tilde{\lambda }}$ plays the role of the homogenized chemical rate. Indeed, by integrating Eq. (26) over $\varOmega _f$ and applying the divergence theorem, the compatibility equation of problem (26), (27) reads:

$$\begin{aligned} {\mathscr {K}}=\varphi {\tilde{\lambda }}=kS_a\frac{\left\langle \psi \right\rangle _{\varGamma _{\mathrm{sf}}} }{\left\langle \psi \right\rangle _{\varOmega _{f}}}. \end{aligned}$$

(44)

For very low value of the Damköhler number, the homogenized chemical reaction rate is identical to the one given by (21). Model III is the richest one as it contains cases 1 and 2 for smaller values of the Damköhler number. This behaviour will be studied in details in the next Section.

Fig. 2

Macroscopic descriptions

4 Numerical study

The aim of this part is to determine the reactive homogenized diffusion tensor ${\mathbf {D}}_{r}^{\hom }$ given by (23) by resolving the numerically closure problems (24)–(27). Firstly, we solve the Sturm–Liouville problem (26), (27) in order to determine the first eigenvector $\psi$ and the first associated eigenvalue ${\tilde{\lambda }}$. Thereafter, the closure problem (24), (25) will be resolved to determine $\mathbf {\chi }_{r}$. From $\psi$ and $\mathbf {\chi }_{r}$, we compute the reactive diffusion tensor ${\mathbf {D}}_{r}^{\hom }$ by expression (23). The reactive homogenized diffusion tensor will be compared to the homogenized diffusion tensor ${\mathbf {D}}^{\hom }$ in the absence of chemical reaction given by (14). Note that the closure problem (15), (16) is the same for dominating diffusion (model I) or diffusion and reaction at the same order (model II)⁵.

4.1 Case of a semi-infinite channel

We consider the simple case of a single pore represented by two parallel planes (the solid–fluid interface $\varGamma _{\mathrm{sf}}$) where the chemical reaction takes place. The distance between the parallel planes is of 2H, and the channel length is much larger than H, which justifies the semi-infinite pore assumption (Fig. 3).

Accounting for symmetry equations (26), (27) reduces to:

$$\begin{aligned} D\frac{d^{2}\psi }{dy_2^{2}}+\lambda \psi= & {} 0\qquad 0<y_2<H, \end{aligned}$$

(45)

$$\begin{aligned} \frac{d\psi }{dy_2}= & {} 0\qquad y_2=0, \end{aligned}$$

(46)

$$\begin{aligned} \qquad -D\frac{d\psi }{dy_2}= & {} k\psi \qquad y_2=H. \end{aligned}$$

(47)

Fig. 3

Schematic description of a semi-infinite channel

The solution of Eq. (45) reads:

$$\begin{aligned} \psi \left( y_2\right) =2\sqrt{\frac{\sqrt{\frac{\lambda }{D}}H}{\left( \sin 2H \sqrt{\frac{\lambda }{D}}+2H\sqrt{\frac{\lambda }{D}}\right) }}\cos \left( \sqrt{\frac{\lambda }{D}}y_2\right) \end{aligned}$$

(48)

where the eigenvalues $\lambda$ of the Sturm–Liouville problem (45)–(47) may be determined from:

$$\begin{aligned} H\sqrt{\frac{\lambda }{D}} \tan \left( \sqrt{\frac{\lambda }{D}} H\right) =\frac{kH}{D}=Da. \end{aligned}$$

(49)

Let us notice that similar results have been obtained by Shapiro and Brenner in [32] that enables to validate the numerical procedure of resolution used. In addition, the Sturm–Liouville problem (45)–(47) will be solved numerically using the eigenvalue solver of Comsol Multiphysics software in the case of a semi-infinite channel.

Fig. 4

Variation of the eigenvalue ${\tilde{\lambda }}$ versus the Damköhler number Da, comparison between numerical and analytical solutions given by (49)

Figure 4 shows the variation of the first eigenvalue ${\tilde{\lambda }}$ determined from Eq. (49) as function of the Damköhler number. It is important to notice that the numerical solution is in good agreement with the analytical solution given by Eq. (49). This validates our numerical procedure implemented in Comsol Multiphysics software.

We observe also that the eigenvalue ${\tilde{\lambda }}$ increases with the Damköhler number Da. We may consider three parts in Fig. 4:

• Firstly, the macroscopic diffusion coefficient in the directions parallel to the plates is constant and equal to $\varphi D$ regardless of the Damköhler number value.

• When Da is in the range of $[10^{-3},~~10^{-1}]$, the variation of ${\tilde{\lambda }}$ is linear. In that case, the reaction does not affect the transfer ($\psi \simeq 1$).

• Nonlinear variation of ${\tilde{\lambda }}$ is observed for Da in the range $[10^{-1},~~10^{2}]$. This case corresponds to dominant reaction.

• For $Da>100$ which corresponds to the strong chemical reaction effect, we observe in this range that the eigenvalue ${\tilde{\lambda }}$ is constant and equal to $\frac{\pi ^2 D}{4 H^2}$.

To well understand the transition (continuous) between model III and model II (of cases 3 and 2), let us analyse the analytical solution obtained in the case of the semi-infinite pore model addressed.

When $Da \rightarrow 0$ (or equivalently $k \rightarrow 0$), the eigenvalue problem (45)–(47) leads to a Neumann problem with homogeneous boundary conditions whose smallest eigenvalue ${\tilde{\lambda }}$ is near zero.

When ${\tilde{\lambda }} \rightarrow 0$, it is obvious from (48) that $A \rightarrow 1$ and $\psi (y)\rightarrow 1$.

Therefore, from (44), we get ${\mathscr {K}}=kS_a$, and we recover expression (21) of ${\mathscr {K}}$ for model II. Moreover, for ${\tilde{\lambda }}=0$ and $\langle \psi \rangle =1$, (42) reduces to $\langle c_0 \rangle _{\varOmega _f}=v_0 \left( x,t\right)$, and the homogenized Eq. (22) corresponds exactly to (19) (model II). This behaviour will be also observed in the more complex examples in 2D presented in Section 4.2, where no simple analytical solution is possible.

4.2 More complex 2D elementary cells

Let us focus on the case of 2D elementary cells containing a circular inclusion of Fig. 5. Problem (26), (27) is solved for different values of the Damköhler number $Da \in [10^{-6},~~ 10^{3}]$, it is important to underscore that in this example the variation of Da is caused only by the variation of the coefficient of reaction k, and the molecular diffusion coefficient D and the size of the elementary cell l are constant. Figure 5 represents the distribution of the eigenfunction $\psi$ on the unit cell of porosity $\varphi =0.6$ and for several values of Da. We notice that the variation of $\psi$ becomes significant with the increase in the Damköhler number Da. We may distinguish three domains of variation of $\psi$. The zone of cool colour for $\psi < 1$ which corresponds to the vicinity of the solid–fluid interface; this zone becomes larger for high values of Da. The second zone of green colour corresponds to $\psi =1$. The last zone of warm colour corresponds to $\psi >1$ far from the solid-fluid interface.

In the case of volume average method, the boundary value problem (11) in [33] seems to be the equivalent to the eigenvalue problem (26), (27). Comparing both problems in the case of a unit cell with a square inclusion, we notice that the eigenfunction $\psi$ is strictly positive and that the closure variable s of [33] can take negative and positive values.

Fig. 5

Variation of $\psi$ for different values of Da and $\varphi =0.6$

Figure 6 shows the distribution of $\chi _r$ in the direction Ox (horizontal direction of the page) on the unit cell of porosity $\varphi =0.6$, for different values of Da. We observe that the value $\chi _r$ becomes higher with the increase in Da. When Da is lower, the variations of $\chi _r$ correspond to those of $\chi$ solution of the boundary value problems (15), (16) of models I and II. For very low values of Da ($Da<10^{-2}$), as in the analytical example addressed in Sect. 4.1, we have ${\tilde{\lambda }} \rightarrow 0$ and $\psi \rightarrow 1$.

Let us focus now on the variation of the homogenized diffusion tensor ${\mathbf {D}}^{\hom }_{r}$ given by Eq. (23), accounting for the chemical reaction which takes place in the unit cell with circular inclusion. ${\mathbf {D}}^{\hom }_{r}$ will be compared to the homogenized diffusion tensor without chemical reaction ${\mathbf {D}}^{\hom }$ given by Eq. (14). According to the symmetry of the considered unit cell, only the coefficients $D^{\hom }_{r}$ and $D^{\hom }$ will be compared.

Fig. 6

Variation of $\chi _r$ for different values of Da and $\varphi =0.6$

Fig. 7

Variation of $D^{\mathrm{hom}}_{r}/D^{\mathrm{hom}}$ versus the Damköhler number for different values of porosity $\varphi$

In the parametric study that follows, the porosity of the cell varies form 0.3 to 0.95 with step of 0.05. For each value of porosity, the Damköhler number Da varies in the range $Da \in [10^{-6}, ~~ 10^{3}]$. Figure 7 presents the variation of the relative homogenized diffusion coefficient $D^{\mathrm{hom}}_{r}/D^{\mathrm{hom}}$ versus the Damköhler number Da for several values of porosity $\varphi$. We observe that $D^{\mathrm{hom}}_{r}/D^{\mathrm{hom}}$ is equal to 1 for $Da<10^{-2}$. In that case, corresponding to models I and II, the effect of chemical reaction on the homogenized diffusion coefficient can be neglected. When the Damköhler number is in the range $Da>10^{-2}$, $D^{\mathrm{hom}}_{r}$ depends on Da by the eigenfunction $\psi$. The ratio $D^{\mathrm{hom}}_{r}/D^{\mathrm{hom}}$ decreases with the increase in Da due to the chemical reaction which takes place on the interface $\varGamma _{sf}$ and slows down the diffusive transfer. This decrease in $D^{\mathrm{hom}}_{r}/D^{\mathrm{{hom}}}$ becomes increasingly significant for lower porosity values corresponding to very close $\varGamma _{\mathrm{sf}}$ interfaces between neighbouring unit cells. Let us notice that in [33] the authors obtain as a result that the homogenized diffusive coefficient increases with Da, whereas it is the opposite here.

Fig. 8

Variation of ${\mathscr {K}}_{II}$ and ${\mathscr {K}}_{III}$ (model II and model III, respectively) versus Da with $\varphi =0.6$ from Eqs.  (21) and (44)

Let us focus now on the homogenized reaction rate given by Eqs.  (21) and (44) for model II and model III, respectively, that will be denoted ${\mathscr {K}}_{II}$ and ${\mathscr {K}}_{III}$, respectively, in the sequel. We remain to compare the homogenized reaction rates ${\mathscr {K}}_{III}$ to ${\mathscr {K}}_{II}$ for a unit cell containing a circular inclusion. Figure 8 shows the respective variations of ${\mathscr {K}}_{III}$ and ${\mathscr {K}}_{II}$ according to Da. The homogenized reaction rates ${\mathscr {K}}_{III}$ and ${\mathscr {K}}_{II}$ increase with the Damköhler number Da. For values of $Da<1$ we observe that the homogenized rates ${\mathscr {K}}_{III}$ and ${\mathscr {K}}_{II}$ are identical. We have noticed from Fig. 5 that for $Da<1$ the eigenfunction $\psi$ is equal to 1 (Fig. 5a and b). For $Da>1$, the variation of ${\mathscr {K}}_{III}$ becomes nonlinear, and ${\mathscr {K}}_{II}>{\mathscr {K}}_{III}$. Indeed, in the expression of ${\mathscr {K}}_{III}$ given by Eq. (44), the ratio $\frac{\left\langle \psi \right\rangle _{\varGamma _{\mathrm{sf}}} }{\left\langle \psi \right\rangle _{\varOmega _{f}}}$ is equal to 1 for $Da<1$ and decreases for $Da>1$. From that, it is important to underscore that model III is able to reproduce the behaviour of model II for $Da<1$ and also model I when $Da={\mathscr {O}}\left( \varepsilon ^2 \right)$.

Let us focus on the relative error on the homogenized chemical reaction rate $e_{K}$ and on the homogenized diffusion coefficient $e_D$. These errors are calculated by considering the homogenized parameters of model II as reference ones:

$$\begin{aligned} e_K= & {} \left| \frac{ K_{III}-K_{II} }{K_{II}}\right| ,\\ e_D= & {} \left| \frac{ D^{\mathrm{hom}}_{r}-D^{\mathrm{hom}} }{D^{\mathrm{hom}}}\right| . \end{aligned}$$

Figure 9 shows the variation of $e_K$ and $e_D$ versus Da for a unit cell of porosity 0.6. For $Da< 10^{-3}$, the reaction term is negligible, which corresponds to model I (predominant diffusion at the macro-scale), with the respective order of magnitude of ${\mathscr {K}}_{II}$ and ${\mathscr {K}}_{III}$ represented in Fig. 9. Thus, the behaviour of model I can be reproduced by model II or model III in the considered range of Da. For $10^{-3}<Da< 1$, the relative errors on the homogenized reaction rate and on the homogenized diffusion coefficient are, respectively, between 0.008 and $8\%$ for $e_K$ and between $0.001\%$ and $3 \%$ for $e_D$. In this range of Da, model III reproduces the behaviour of model II, and both models are quasi-identical (diffusion and reaction are decoupled). Finally, for $Da>1$, we remark that the relative errors are larger than $3\%$ for $e_D$ and larger than $8\%$ for $e_K$. In this range of Da, diffusion and reaction are coupled at the macro-scale, and transfer parameters must be calculated accounting for reaction according to Eqs. (23) and (29). Therefore, model II cannot substitute model III.

Fig. 9

Relative error of ${\mathscr {K}}$ and $D^\mathrm{{{hom}}}$ versus Da for a unit cell with circular inclusion of porosity $\varphi =0.6$

Fig. 10

Variation of $D^{\mathrm{hom}}_{r}/D$ and ${\mathscr {K}}_{III}/{\mathscr {K}}_{II}$ according to Da, for 2D unit cells of porosity of 0.6

Figure 10 shows the variation of the homogenized parameters as function of the Damköhler number Da for 2D unit cells constituted of aligned and staggered circular and square inclusions of porosity $\varphi =0.6$. Figure 10a compares the variation of $D^{\mathrm{hom}}_{r}/D$ for each unit cell versus the Damköhler number Da. It is important to underline that for $Da<0.01$ the effect of the chemical reaction on the transfer parameters is negligible. Moreover, the diffusion coefficient for circular inclusion and staggered circular inclusions is larger than for square inclusion and staggered square inclusions. This difference is due to the inclusion tortuosity, and identical results are obtained for circular and square inclusions in [12]. For $Da>0.01$, we remark that the homogenized diffusion coefficient of circular inclusion and staggered circular inclusions decreases and becomes lower than the one of square inclusion. From this value of Da, the effect of chemical reaction becomes important, and the zone where the eigenfunction $\psi <1$ (important chemical reaction) covers all the cells when Da increases (Fig. 5).

Figure 10b shows the variation of the relative ratio ${\mathscr {K}}_{III}/{\mathscr {K}}_{II}$ for the homogenized reaction rates of model III and model II, respectively. This ratio decreases with increasing Damköhler numbers as noticed in Fig. 10b. The variations ${\mathscr {K}}_{III}/{\mathscr {K}}_{II}$ versus Da are almost identical for all unit cells, with a slight difference for higher Damköhler number. It is important to notice that the coefficient ${\mathscr {K}}_{III}$ for square and circular inclusions is lower than one of staggered array for square and circular inclusions. This is due to the specific area of staggered array which is higher than the case of a unit cell with single inclusion.

4.2.1 Validation

Let us focus now on the comparison between the homogenized models and the pore-scale simulation called here the direct numerical simulation (DNS). This comparison enables to highlight the range of validity of each model (models I, II, III) according to the range of the Damköhler number.

Figure 11 shows the continuous macroscopic domain of length $L=Nl$, where N is the number of unit cells of length l composing the macroscopic domain. The homogenized models (models I, II, and III) will be solved by imposing Dirichlet boundary condition on the inlet $c=1$ at $x_1=0$ and on the outlet $c=0$ at $x_1=L$. On the lateral boundaries, periodicity conditions are imposed. In that case, the three homogenized equations become 1D problems, where the analytical solutions are known. The transfer parameters of the three homogenized model are those given in Fig. 10.

Fig. 11

Porous media with circular inclusion of $\varphi =0.6$ at macro-scale

Figure 12 shows the variation of concentration fields with respect to $x_1/L$ for different values of Da. For $Da<10^{-3}$, we observe that the concentration fields obtained with models I, II, and III are identical to DNS solution. For $10^{-3}<Da<10$, we observe that models II and III give the same solution by comparing to DNS simulations. In this range of Da, the concentration field is nonlinear which corresponds to the reaction term effect, but the diffusion and reaction are still decoupled. In the last range of $Da>10$, we observe that the concentration fields of model III and DNS are very close, unlike model II where the gap with DNS solution becomes more and more important when Da increases. In this range of Da, where the homogenized diffusion coefficient is coupled to the chemical reaction, only model III is valid. It is important to underscore that in all ranges of Da the homogenized model (models I, II or III according to the value Da) is in good agreement with the DNS solution.

Fig. 12

Concentration fields of homogenized and DNS models versus $x_1/L$ for different values of Da

4.3 Random porous media

Let us focus on the case of a 2D elementary cell containing circular inclusions of different size distributed randomly (Fig. 13). Random unit cells are generated by fixing the porosity value and the interval of the radii of circular inclusions. In addition, the positions of circle centres are determined arbitrarily to avoid overlapping between inclusions. For this purpose, we determine for each inclusion the distance between neighbouring ones. This distance must be at least equal to a fixed minimum. In this way, the connectivity of the fluid phase is guaranteed. It is obvious that for a fixed porosity value there is an infinity of unit cells. As in the case of the unit cell with circular inclusion, problem (26), (27) is solved for different values of the Damköhler number $Da \in [10^{-6},~~ 10]$. After that, the vector $\mathbf {\chi }_r$ and the homogenized diffusion tensor ${\mathbf {D}}^{\hom }_{r}$ are determined, respectively, from (24), (25), and (23).

Fig. 13

Unit cells of random porous media. a The number of inclusions is 436. The radii belong to interval $[7.6\,10^{-3} \, 0.14]$ with mean value of $1.54\,10^{-2}$ and standard deviation of $1.42\,10^{-2}$. b The number of inclusions is 189. The radii belong to interval $[7.6\,10^{-3} \, 0.14]$ with mean value of $2.17\,10^{-2}$ and standard deviation of $1.93\,10^{-2}$. All these values are scaled by the size l of the unit cell

Figure 14a shows the variation of $D^{\mathrm{hom}}_{r_{11}}/D$ and $D^{\mathrm{hom}}_{r_{22}}/D$ versus the Damköhler number Da for two elementary cells of porosity 0.4 and 0.5, the choice of this value being arbitrary. As in the previous case, the homogenized diffusion coefficients are constant for low Damköhler number ($Da<10^{-1}$ for $D^{\mathrm{hom}}_{r_{11}}/D$ and $Da<10^{-2}$ for $D^{\mathrm{hom}}_{r_{22}}/D$ for porosity $\varphi =0.5$) and decrease with the increase in Da. Figure 14b presents the variation of the eigenvalue $\lambda$ with respect to the Damköhler number Da for the considered elementary cells of porosity $\varphi =0.4$ and $\varphi =0.5$. In addition, Fig. 14c shows the variation of ratio ${\mathscr {K}}_{III}/{\mathscr {K}}_{II}$ as function of the Damköhler number Da. We observe that the relative homogenized reaction rate is constant for $Da<10^{-2}$. In this range, models II and III give identical results. For $Da>10^{-2}$, the relative homogenized reaction rate strongly decreases with Da (we have ${\mathscr {K}}_{II}>{\mathscr {K}}_{III}$). On other hand, we notice that the homogenized reaction rate increases with porosity for fixed value of Da. This depends on the variation of the eigenfunction $\psi \left( y_1,y_2\right)$ in the fluid domain for the two considered unit cells.

Fig. 14

Homogenized parameters of the elementary cells of Fig. 13

4.3.1 Validation

The aim of this last part is to compare the homogenized diffusion–reaction model (model III) given by Eq. (22) to the direct numerical simulation DNS of the diffusion–reaction equation at microscopic scale given by Eq. (1) at steady state.

Fig. 15

Porous media of porosity $\varphi =0.4$ at the macro-scale

As in the previous case, the homogenized diffusion–reaction model (model III) is solved on the continuous macroscopic domain of Fig. 15a. The homogenized transfer parameters considered are those presented in Fig. 14. Dirichlet boundary conditions are imposed on the inlet $\left( x_1=0 \right)$ where $\left\langle c \right\rangle =1$ and on the outlet $\left( x_1=L \right)$ where $\left\langle c \right\rangle =0$. In a similar manner, we have $\left\langle c \right\rangle =1$ on $x_2=0$ and $\left\langle c \right\rangle =0$ on $x_2=L$ . Periodic boundary conditions are imposed on the lateral boundary.

The direct numerical simulation DNS consists in solving the local diffusion equation (1) on the whole fluid domain $\varOmega _f$ resulting from the juxtaposition of N unit cells (Fig. 15b and c). Similar boundary conditions are imposed: Dirichlet boundary conditions on the inlet and outlet, and periodic ones on lateral boundaries. In addition, boundary condition (2) is applied on the $\varGamma _{\mathrm{sf}}$ solid–fluid interface.

Fig. 16

Average concentration field $\left\langle c \right\rangle$ and $\left\langle c \right\rangle _{y_2}$ according to $x_1$ and $x_2$ obtained from model III and DNS solutions for different values of the Damköhler number Da. Here, $L=1$ and $N=100$

Figure 16 shows the distribution of the average concentration $\left\langle c \right\rangle$ solution of model III and the concentration c solution of the local model obtained by DNS. Both solutions are very similar for different values of the Damköhler number Da. It is important to notice that the DNS solution depends on $y_2$ and $x_1$ (respectively, on $y_1$ and $x_2$), whereas the homogenized solution is function of $x_1$ (respectively, $x_2$) only.

To finish, let us consider $\left\langle c \right\rangle _{y_2}$, the average of c over $y_2$ (we have a similar expression with $\left\langle c \right\rangle _{y_1}$):

$$\begin{aligned} \left\langle c \right\rangle _{y_2}=\frac{1}{l}\int _{0}^{l}cdy_2. \end{aligned}$$

Figure 17a (Fig. 17b, respectively) compares the variation of the concentration field $\left\langle c \right\rangle _{y_2}$ versus $x_1/L$ (respectively, $\left\langle c \right\rangle _{y_1}$ versus $x_2/L$) obtained from model III and DNS. Solutions are in very good agreement. More accurately, Fig. 17c (respectively, Fig. 17d) is a zoom on the concentration field for $Da=10^{-4}$ versus $x_1/L$ (respectively, $x_2/L$). The DNS solution (dot black curve) is very close to the concentration field given by model III (red curve). The same observation for Fig. 17e (respectively, Fig. 17f) in the case of high value of the Damköhler number $Da=10^{-1}$ and $Da=1$. We observe classical periodic oscillations of DNS solution of period l around the mean value given by model III. It is also important to notice that the concentration fields $\left\langle c \right\rangle _{y_1}$ and $\left\langle c \right\rangle _{y_2}$ are very close, due to very similar values of $D^{\mathrm{hom}}_{r_{11}}$ and $D^{\mathrm{hom}}_{r_{22}}$ (Fig. 14a).

Fig. 17

a Concentration field of model III and DNS solutions according to $x_1/L$ for different values of Da and for $\varphi =0.4$. b Concentration field of model III and DNS solutions according to $x_2/L$ for different values of Da and for $\varphi =0.4$. c Zoom on the variation of the concentration field versus $x_1/L$ for $Da=10^{-4}$. d Zoom on the variation of the concentration field versus $x_2/L$ for $Da=10^{-4}$. e Zoom on the variation of the concentration field versus $x_1/L$ for $Da=10^{-1}$ and $Da=1$. f Zoom on the variation of the concentration field versus $x_2/L$ for $Da=10^{-1}$ and $Da=1$

5 Summary and conclusions

In this work, we proposed to perform the periodic homogenization of the diffusion equation with the linear first-order heterogeneous chemical reaction at the interface, for different values of the Damköhler number. For small values of the Damköhler number, corresponding to a low chemical reaction rate, we recover classical homogenized diffusive equations (cases 1 and 2), where the homogenized diffusion tensor depends only on the geometry of the microstructure. (It is decoupled with the chemical reactions.) For large values of the Damköhler number, we obtain a non-classical homogenized model (case 3), where the homogenized diffusion tensor is strongly coupled with the chemical reaction rate. This homogenized model is particularly well adapted to describe, at the macroscopic level, diffusion with strong chemical reactions at the pore interfaces. In addition, the homogenized parameters such as the homogenized diffusion tensor and the homogenized reaction rate can be obtained by solving coupled boundary value problems at the elementary cell scale. The analytical example of coupled diffusion–reaction between two parallel plates allows to well understand the transition between the different possible regimes of reaction, corresponding to different orders of magnitude of the Damköhler number. The relevance of model III (case 3), with a strong coupling between homogenized diffusion tensor and chemical reaction rate at the microscopic level, is put in a prominent position by the numerical simulations performed on different two-dimensional elementary cells. Moreover, numerical simulation performed on 2D random elementary cells highlights the influence of the chemical reaction effect on the homogenized diffusion tensor and on the homogenized reaction rate. In this case, it has been found that the chemical reaction slows down the macroscopic transfer: We have a decrease in the homogenized diffusion tensor with the increase in the Damköhler number Da.

Finally, comparison between homogenized diffusion–reaction equation (model III) and the pore-scale direct numerical simulation (DNS) on porous media with random 2D circular inclusions is made. Model III and DNS solutions are in good agreement with different values of the Damköhler number, which validates the results given by model III, and the associated homogenized transfer properties deduced from the diffusion at the macro-scale.

Following the same approach, this work could be extended to the case of multi-species transfer with taken into account heterogeneous and homogeneous chemical reactions. Another extension would be to take into account the variation of the porosity caused by chemical reaction on the solid–fluid interface.