Effect of inclined load on a functionally graded fiber-reinforced thermoelastic medium with temperature-dependent properties

Abstract

The present research work is concerned with the solution of a problem on thermoelastic interactions in a functionally graded (non-homogeneous), fiber-reinforced, transversely isotropic half-space with temperature-dependent properties under the application of an inclined load in the context of Green-Naghdi theory of type III. Material properties are supposed to be temperature-dependent and are graded along x-direction. Normal mode technique is adopted to obtain the exact expressions for the temperature field, displacement, and stress components. These are computed numerically and limned graphically to observe the disturbances induced in the medium due to fiber reinforcement, non-homogeneity parameter, temperature-dependent properties, and inclination angle of the load and time. Certain particular cases of interest have been deduced from the current investigation.

1 Introduction

The theory of thermoelasticity is concerned with the relationship between elastic properties of a material and its temperature. Although Duhamel [1] presented equations of thermoelasticity with coupling of deformation and temperature fields already in 1837, only research works done 120 years later by Biot [2] and Lessen [3] gave a new impulse to do research in this area. In classic thermoelasticity, a problem regarding temperature was solved first, and then stresses were received from Duhamel–Neumann equations. But both the theoretical assumptions and very simple experiments show that a change of displacements in a material accompanies a change of temperature, and a change of temperature is accompanied by a change of displacements. Thus, treating a dynamic problem of thermoelasticity in stresses requires simultaneous solution of the stress equation of motion and the heat conduction equation in which the time derivative of first stress invariant appears clearly. Thereafter, Weiner [4] presented a proof on uniqueness of solutions of coupled equations of thermoelasticity. A generalization of the theory of thermoelasticity was put forwarded by Lord and Shulman [5], which involves a single relaxation time in the equation for heat conduction. They developed the theory by including a heat flux rate term in the classical Fourier’s equation of thermal conduction. As a result, it ensures the finite speed of heat propagation because the obtained heat equation is hyperbolic.

One other generalization of coupled theory was proposed by Green and Lindsay [6], which contains two relaxation times and amends all the field equations of coupled theory, not the thermal conduction equation only. Later on, by providing sufficient basic modifications in the constitutive equations, Green and Naghdi [7,8,9] produced three alternative theories for thermoelastic materials, namely as GN theory of type I, GN theory of type III and GN theory of type II, respectively. When these theories are linearized, GN theory of type I reduces to the classical heat conduction theory, and GN theories of type III and II permit thermal signals to propagate with finite speed. GN theory of type II does not contain the thermal conductivity parameter, and the internal rate of production of entropy is taken to be identically zero, implying no dissipation of thermal energy. GN theory of type III includes the previous two theories as special cases and admits dissipation of energy in general. However, these theories do not account for the relaxation time. An article of representative theories on the account of generalized thermoelasticity is given by Hetnarski and Ignaczak [10]. Awrejcewicz and Pyryev [11] modeled a dynamic 2-DoF (two degrees of freedom) damper with reference to dry friction and heating processes. In addition, the proposed method of solution may also be applied to model any other nonlinear problem of dynamics of thermoelastic contacting bodies. Krysko et al. [12] described the regular (periodic and quasi-periodic) and chaotic vibrations of flexible beams, plates, cylindrical shells, panels, and sector-type spherical shells under the action of thermal and piezoelectric phenomena. In an another research article, Awrejcewicz and Krysko [13] formulated fundamental assumptions and relations for coupled nonlinear thermoelastic problems similar to those formulated for coupled linear thermoelasticity problems of shallow shells. In addition, they discussed the existence and uniqueness of a solution as well as the convergence of the Bubnov–Galerkin method. A theory of shells with physical nonlinearities and coupling is also outlined by them by discussing variational equations of physically nonlinear coupled problems. Recently, Krysko-jr et al. [14] developed the theory of nonlinear statics and dynamics of flexible plates, taking into account the modified couple stress theory and temperature field and investigated the hyperchaotic vibrations in a mathematical model of rectangular plates obtained based on the modified couple stress theory, subjected to transverse harmonic loads and embedded into a temperature field.

Functionally graded materials (FGMs) are a modern class of smart materials and are defined as diverse and advanced materials whose thermal and elastic characteristics differ slowly and continuously corresponding to variation in spatial coordinates. These types of specifications develop spatial heterogeneity in the materials. FGMs are designed to work in high temperature fields, and as a result, these materials are extremely helpful in aviation, nuclear reactors, and space technology applications. Their applications extend to several other fields, such as material science, geophysics, and magnetic storage, as well as mechanical and thermal engineering. Lagrangian finite element formulations were proposed by Reddy and Chin [15] to analyze the pseudodynamic thermal vibrations induced in functionally graded elastic cylinders. Krysko et al. [16] studied a coupled thermomechanical problem of functionally graded, i.e., non-homogeneous Timoshenko type shells, i.e., shells with variable thickness and variable Young’s modulus. Furthermore, the problem is reduced to a uniformly correct problem in the form of a first order difference operator equation. A problem on one-dimensional transient thermal stresses in nonhomogeneous plates, spheres, and cylinders was solved by Wang and Mai [17] by adopting finite element technique. Abbas and Zenkour [18] examined the electro-magnetic responses of a nonhomogeneous thermoelastic cylinder in the purview of LS theory, with the help of finite element technique. Kirichenko et al. [19] proposed mathematical models to design non-homogeneous thermoelastic shallow shells which define a novel class of boundary problems in the non-classical theory of shallow shells with initial imperfections. Pal et al. [20] investigated magneto-thermoelastic interactions in a rotating functionally graded isotropic medium due to a periodically varying heat source in the context of Green-Naghdi theories of types II and III. The thermomechanical disturbances in a nonhomogeneous isotropic elastic thin annular disk subjected to exponential and periodic types of axisymmetric pressures were examined by Mishra et al. [21]. Krysko et al. [22] defined and solved the problem of topological optimization of the microstructure of a composite aimed at the construction of a material associated with multifunctional requirements with respect to effective characteristics of composites consisting of two components as well as composites with holes or technological inclusions. An analysis of nonlinear functionally graded beams behavior based on the modified couple stress theory was carried out by Awrejcewicz et al. [23]. They defined the deflection curve to simplify the governing equations and then investigated the influence of scale length parameter and the non-homogeneity coefficient on the dynamic characteristics and the scenario of transition from periodic to chaotic beam vibrations. Saeed et al. [24] studied the influence of the magnetic field in non-homogeneous (functionally graded) semiconductor materials in the context of the photo-thermoelasticity theory. Thi [25] analyzed the thermal vibration responses of functionally graded porous plates with varying thickness resting on two-parameter-based elastic foundations adopting finite element method.

Usually, the material properties are supposed to be constant in many important investigations. However, the physical properties of some specific modern engineering materials may vary with temperature. Lomakin [26] proposed that the material characteristics such as coefficient of thermal expansion, elastic constants, and the thermal conductivity are no longer constant, at very high magnitude of temperature. Ezzat et al. [27] analyzed a problem of generalized thermoelasticity with two relaxation times in an isotropic elastic medium with temperature-dependent mechanical properties. Aouadi [28] investigated the effect of elastic modulus temperature dependency on the behavior of two-dimensional solutions in a micropolar thermoelastic model. Othman and Said [29] examined the influence of temperature-dependent properties and magnetic field on the plane waves in a fiber-reinforced thermoelastic medium in the context of Green–Naghdi theory without energy dissipation and three-phase-lag theory. Sheoran et al. [30] obtained numerical results for the thermophysical fields in a rotating nonlocal thermoelastic medium with temperature-dependent properties in the context of GN theory of type II.

Fiber-reinforced composites are now firmly placed in the forefront of advanced materials and are used in a wide number of applications of diverse fields like aerospace, acoustics, geophysics, and automotive fields. These consist of fibers of high strength and modulus embedded in or bonded to a matrix with distinct interfaces between them. The mechanical behavior of the majority of fiber-reinforced composites is appropriately modeled by linearized elasticity theory for transversely isotropic materials, with preferable direction, the same as the direction of fibers. Light weight with better impact resistance, high strength, easy mold proficiency, and excellent corrosion resistance are many remarkable advantages of fiber-reinforced composites over traditional metals/materials. The numerical results of technically salient elastic moduli for fiber-reinforced composites have been acquired by Hashin and Rosen [31]. For the last four decades, the study of strain and stress in composites reinforced by fibers has been a very significant topic in mechanics of solids. Rogers [32] did premier work on this special topic of research. Belfield et al. [33] introduced the continuous self-reinforcement throughout the elastic medium and acquired the veracious solutions for a circular annulus. A problem on propagation of plane waves in a fiber-reinforced magneto-thermoelastic half-space in the context of Lord-Shulman theory was discussed by Abbas et al. [34]. Kalkal et al. [35] examined the reflection and transmission phenomena at the plane interface between an initially stressed fiber-reinforced thermoelastic half-space and a thermoelastic half-space in the context of dual-phase-lag theory. Deswal et al. [36] analyzed the mechanical disturbances induced in an initially stressed fiber-reinforced orthotropic thermoelastic half space due to an inclined load. Hobiny and Abbas [37] investigated the thermoelastic interactions in a fiber-reinforced material with spherical cavities in the purview of Green–Naghdi theory of type III. Recently, Deswal et al. [38] studied the characteristics of various reflected waves in a homogeneous anisotropic fiber-reinforced magneto-thermoelastic diffusive solid under dual-phase-lag theory of generalized thermoelasticity with two-temperatures.

The objective of the present research is to analyze the disturbances induced in a functionally graded fiber-reinforced, transversely isotropic thermoelastic medium with temperature-dependent properties due to an inclined load in the context of GN theory of type III. Although many research problems do exist in a fiber-reinforced thermoelastic medium, as well as in a functionally graded thermoelastic medium, no attempt has been made to access the distributions of various physical fields, i.e., normal displacement, normal stress, shear stress, and temperature distribution in a functionally graded (non-homogeneous), fiber-reinforced, transversely isotropic thermoelastic medium with temperature-dependent properties due to an inclined load. The normal mode technique is applied to obtain the exact expressions of the considered field variables. This model may be very useful in geophysics, marine, automobile field, lightweight beams in construction, aerospace field, pressure pipes, and nuclear reactors.

2 Basic equations

Following Green and Naghdi [8] and Spencer [39], the governing field equations and relations among stress, strain, and temperature in a functionally graded fiber-reinforced transversely isotropic thermoelastic medium are as follows: The constitutive relation:

$$\begin{aligned}&\sigma _{ij}=\lambda e_{kk}\delta _{ij}+2\mu _T e_{ij}+\alpha (a_ka_le_{kl}\delta _{ij}+a_ia_je_{kk}) +\beta a_ka_le_{kl}a_ia_j\nonumber \\&+2(\mu _L-\mu _T)(a_ia_ke_{kj}+a_ja_ke_{ki})-\beta _{ij}\theta \delta _{ij}, \end{aligned}$$

(1)

The equation of motion:

$$\begin{aligned} \sigma _{ji,j}=\rho \ddot{u}_i, \end{aligned}$$

(2)

Heat conduction equation:

$$\begin{aligned}& (K^*_{ij}\theta ,_{j}+ K_{ij}{{\dot{\theta }}},_{j}),_i=\rho C_E\ddot{\theta }+T_0\beta _{ij} \ddot{u}_{i,j}, \end{aligned}$$

(3)

Strain–displacement relation:

$$\begin{aligned}&e_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}), \end{aligned}$$

(4)

where $i, j, k, l=1,2,3$, $\rho$ is the density of the material, $\sigma _{ij}$ are the components of the stress tensor, $e_{ij}$ are the components of the strain tensor, $u_i$ are the components of the displacement vector, $\alpha ,\,\beta ,\,\lambda ,\,\mu _L$ and $\mu _T$ are the elastic constants, $\delta _{ij}$ is the Kronecker delta, $e_{kk}=e$ is the cubical dilatation, $\theta =T-T_0$, T is the absolute temperature, and $T_0$ is the temperature of the material in its natural state assumed to be ${|\frac{\theta }{T_0}|}\ll 1.$ The direction of fiber reinforcement is the normalized vector a$=(a_1,a_2,a_3)$. $\beta _{ij}$ are components of the thermal elastic coupling tensor, $c_E$ is the specific heat at constant strain, $K_{ij}$ is the thermal conductivity such that $K_{ij}=K_i\,\delta _{ij}$, and $K^*_{ij}$ is the material constant such that $K^*_{ij}=K^*_i\,\delta _{ij}$.

Here, a comma denotes material derivative, dot indicates partial temporal derivative, and the summation convention is used.

For a functionally graded, i.e., non-homogeneous medium, the parameters $\lambda$, $\mu _T$, $\mu _L$, $\alpha$, $\beta$, $\beta _{ij}$, $K_{ij}$, and $\rho$ are no longer constant but become space-dependent. Hence, we consider

$$\begin{aligned} \big [\lambda ,\,\mu _T,\,\mu _L,\,\alpha ,\,\beta ,\,\beta _{ij},\,K_{ij},\,K^*_{ij},\,\rho \big ]=f(\pmb {x})\,\big [\lambda ^{'},\,\mu _T^{'},\,\mu _L^{'},\,\alpha ^{'},\,\beta ^{'},\,\beta _{ij}^{'},\,K_{ij}^{'},\,K^{*'}_{ij},\,\rho ^{'}\big ], \end{aligned}$$

(5)

where $\lambda ^{'}$, $\mu _T^{'}$, $\mu _L^{'}$, $\alpha ^{'}$, $\beta ^{'}$, $\beta _{ij}^{'}$, $K_{ij}^{'}$, $K^{*'}_{ij}$, and $\rho ^{'}$ are supposed to be constants, and $f({{\varvec{x}}})$ is a given non-dimensional function of the space variable ${{\varvec{x}}}=(x,\,y,\,z)$.

Using these values of parameters, Eqs. (1)-(3) take the following forms:

$$\begin{aligned}&\sigma _{ij}=f({{\varvec{x}}})\left[ \lambda ^{'}e_{kk}\delta _{ij}+2\mu _T^{'} e_{ij}+\alpha ^{'}(a_ka_le_{kl}\delta _{ij}+a_ia_je_{kk})+\beta ^{'} a_ka_le_{kl}a_ia_j\right. \nonumber \\&\left. +2(\mu _L^{'}-\mu _T^{'})(a_ia_ke_{kj}+a_ja_ke_{ki})-\beta _{ij}^{'}\theta \delta _{ij}\right] , \end{aligned}$$

(6)

$$\begin{aligned}&\sigma _{ji,j}=f({{\varvec{x}}})\rho ^{'}\ddot{u}_{i}, \end{aligned}$$

(7)

$$\begin{aligned}& \left[ f({{\varvec{x}}})(K^{*'}_{ij}\theta ,_{j}+ K^{'}_{ij}{{\dot{\theta }}},_{j})\right] ,_{i}=f({{\varvec{x}}})\left[ \rho ^{'}c_E\ddot{\theta }+\beta _{ij}^{'}T_0\ddot{u_i}_{,j}\right] . \end{aligned}$$

(8)

This research work is proposed with an aim to examine the effect of the temperature-dependent nature of the material. Following Said and Othman [40], one can assume

$$\begin{aligned}&\big [\lambda ^{''},\,\mu _T^{''},\,\mu _L^{''},\,\alpha ^{''},\,\beta ^{''},\,\beta _{ij}^{''}\big ]=\frac{1}{r(\alpha ^{*})}\,\big [\lambda ^{'},\,\mu _T^{'},\,\mu _L^{'},\,\alpha ^{'},\,\beta ^{'},\,\beta _{ij}^{'}\big ], \end{aligned}$$

(9)

where $\alpha ^{*}$ is an empirical material constant such that $r(\alpha ^{*})=1-\alpha ^{*}T_0$, and $r(\alpha ^{*})$ is a dimensionless quantity.

3 Mathematical model

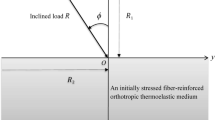
A model made up of a functionally graded fiber-reinforced transversely isotropic thermoelastic half-space ($x\ge 0$, $-\infty \le y \le \infty$) subjected to an inclined load under the purview of GN theory of type III is considered, as shown in Fig. 1. The half-space is assumed to be transversely isotropic in the sense that its elastic and thermal properties are symmetric about the perpendicular to the plane of isotropy. The present formulation is restricted to xy-plane, and thus all the field variables are independent of the space variable z. So, the displacement vector $\pmb {u}$ has the components as

Fig. 1

Geometry of the problem

$$\begin{aligned}& \pmb {u}=(u, v, 0)\,\,\text{ such } \text{ that }\,\,u=u(x, y, t),\,v=v(x, y, t). \end{aligned}$$

The fiber direction is chosen as $\pmb {a}=(1,0,0)$, and the material properties of the model are assumed to be graded in x-direction only, so we take $f(\pmb {x})$ as f(x). In view of Eq. (9) along with these assumptions, the stresses obtained from Eq. (6) can be expressed as

$$\begin{aligned}&\sigma _{xx}=f(x)\left[ H_{11}\frac{\partial u}{\partial x}+H_{12}\frac{\partial v}{\partial y}-r(\alpha ^{*})\beta _{11}^{''}\theta \right] , \end{aligned}$$

(10)

$$\begin{aligned}&\sigma _{yy}=f(x)\left[ H_{12}\frac{\partial u}{\partial x}+H_{13}\frac{\partial v}{\partial y}-r(\alpha ^{*})\beta _{22}^{''}\theta \right] , \end{aligned}$$

(11)

$$\begin{aligned}&\sigma _{xy}=f(x)\left[ H_{14}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) \right] , \end{aligned}$$

(12)

where

$\displaystyle H_{11}=r(\alpha ^{*})[\lambda ^{''}+2(\alpha ^{''}+\mu _T^{''})+4(\mu _L^{''}-\mu _T^{''})+\beta ^{''}],\,\,H_{12}=r(\alpha ^{*})[\lambda ^{''}+\alpha ^{''}],\,\,$

$\displaystyle H_{13}=r(\alpha ^{*})[\lambda ^{''}+2\mu _T^{''}],\,\, H_{14}=r(\alpha ^{*})\mu _L^{''}.$

Also, $\beta _{11}^{''}=(2\lambda ^{''}+3\alpha ^{''}+4\mu _L^{''}-2\mu _T^{''}+\beta ^{''}) \alpha _{11}+(\lambda ^{''}+\alpha ^{''})\alpha _{22},$ $\beta _{22}^{''}=(2\lambda ^{''}+\alpha ^{''})\alpha _{11}+ (\lambda ^{''}+2\mu _T^{''})\alpha _{22},$ and $\alpha _{11}$ and $\alpha _{22}$ are coefficients of linear thermal expansion.

Upon substituting the stresses obtained in Eqs. (10)-(12) into the equation of motion (7), one can obtain the following equations:

$$\begin{aligned}&f(x)\rho ^{'}\frac{\partial ^2 u}{\partial t^2}=f(x)\left[ H_{11}\frac{\partial ^2u}{\partial x^2}+H_{15}\frac{\partial ^2v}{\partial x \partial y}+H_{14} \frac{\partial ^2 u}{\partial y^2}-r(\alpha ^{*})\beta _{11}^{''} \frac{\partial \theta }{\partial x}\right] \nonumber \\&+\frac{\partial f(x)}{\partial x}\left[ H_{11}\frac{\partial u}{\partial x} +H_{12}\frac{\partial v}{\partial y}-r(\alpha ^{*})\beta _{11}^{''}\theta \right] , \end{aligned}$$

(13)

$$\begin{aligned}&f(x)\rho ^{'}\frac{\partial ^2 v}{\partial t^2}=f(x)\left[ H_{14}\frac{\partial ^2v}{\partial x^2}+H_{15}\frac{\partial ^2u}{\partial x \partial y}+H_{13} \frac{\partial ^2 v}{\partial y^2}-r(\alpha ^{*})\beta _{22}^{''} \frac{\partial \theta }{\partial y}\right] \nonumber \\&+\frac{\partial f(x)}{\partial x}\left[ H_{14}\left( \frac{\partial u}{\partial y} +\frac{\partial v}{\partial x}\right) \right] , \end{aligned}$$

(14)

where $\displaystyle H_{15}=H_{12}+H_{14}$.

By using the summation convention and temperature-dependent properties as defined in Eq. (9), the heat conduction equation (8) in the xy-plane takes the form

$$\begin{aligned}&f(x)\left[ K^{*'}_{11}\frac{\partial ^2 \theta }{\partial x^2}+K^{*'}_{22}\frac{\partial ^2 \theta }{\partial y^2}+\frac{\partial }{\partial t}\left( K^{'}_{11}\frac{\partial ^2 \theta }{\partial x^2}+K_{22}^{'}\frac{\partial ^2\theta }{\partial y^2}\right) \right] +\frac{\partial f(x)}{\partial x}\left[ K_{11}^{*'}\frac{\partial \theta }{\partial x}\right. \nonumber \\& \left. +\frac{\partial }{\partial t}\left( K_{11}^{'}\frac{\partial \theta }{\partial x}\right) \right] =f(x)\frac{\partial ^2}{\partial t^2}\left[ \rho ^{'} C_E\theta +T_0\,r(\alpha ^{*})\left( \beta _{11}^{''}\frac{\partial u}{\partial x}+\beta _{22}^{''}\frac{\partial v}{\partial y}\right) \right] . \end{aligned}$$

(15)

To facilitate the solution, one can introduce the following set of dimensionless quantities:

$$\begin{aligned}&(x^{\widehat{}},\,\,y^{\widehat{}},\,\,u^{\widehat{}},\,\,v^{\widehat{}}) =c_0\eta _0\,(x,\,\,y,\,\,u,\,\,v), \,\,\,\,\,t^{\widehat{}}=c_0^2\eta _0\,t, \end{aligned}$$

$$\begin{aligned}&\sigma _{ij}^{\widehat{}}=\frac{\sigma _{ij}}{\rho ^{'} c_0^2},\,\,\,\,\,\theta ^{\widehat{}}=\frac{\beta _{11}^{''}}{\rho ^{'} c_0^2}\,\theta ,\,\,\,\, \end{aligned}$$

(16)

where

$\displaystyle \eta _0=\frac{\rho ^{'} C_E}{K_{11}^{'}},\,\,\,c_0^2=\frac{H_{11}}{\rho ^{'}}\,.$

4 Exponential variation of non-homogeneity

The considered model is made of functionally graded material, i.e., mechanical and thermal properties of the model are non-homogeneous along x-direction. In order to incorporate the non-homogeneity of the model, let us consider $f(x)=e^{-nx}$, where n is the non-homogeneity parameter, and this implies that the material properties of the considered model vary exponentially along the x-direction.

With the help of the dimensionless quantities defined in (16) and the expression of function f(x) as $f(x)=e^{-nx}$, the governing Eqs. (10)-(15) transform to the following non-dimensional forms (while dropping the hats):

$$\begin{aligned}&\sigma _{xx}=e^{-nx}\left[ \frac{\partial u}{\partial x}+I_{2}\frac{\partial v}{\partial y}-r(\alpha ^{*})\theta \right] , \end{aligned}$$

(17)

$$\begin{aligned}&\sigma _{yy}=e^{-nx}\left[ I_{2}\frac{\partial u}{\partial x}+I_3\frac{\partial v}{\partial y}-I_1r(\alpha ^{*})\theta \right] , \end{aligned}$$

(18)

$$\begin{aligned}&\sigma _{xy}=e^{-nx}\left[ I_{4}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) \right] , \end{aligned}$$

(19)

$$\begin{aligned}&\frac{\partial ^2 u}{\partial t^2}=\left[ \frac{\partial ^2u}{\partial x^2}+I_{5}\frac{\partial ^2v}{\partial x \partial y}+I_{4} \frac{\partial ^2 u}{\partial y^2}- r(\alpha ^{*})\frac{\partial \theta }{\partial x}\right] -n\left[ \frac{\partial u}{\partial x} +I_{2}\frac{\partial v}{\partial y}-r(\alpha ^{*})\theta \right] , \end{aligned}$$

(20)

$$\begin{aligned}&\frac{\partial ^2 v}{\partial t^2}=\left[ I_{4}\frac{\partial ^2v}{\partial x^2}+I_{5}\frac{\partial ^2u}{\partial x \partial y}+I_{3} \frac{\partial ^2 v}{\partial y^2}-I_{1}r(\alpha ^{*})\frac{\partial \theta }{\partial y}\right] -n\,\left[ I_{4}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) \right] ,\end{aligned}$$

(21)

$$\begin{aligned}&\left[ I_6\frac{\partial ^2\theta }{\partial x^2}+I_{7}\frac{\partial ^2\theta }{\partial y^2}+\frac{\partial }{\partial t}\left( \frac{\partial ^2\theta }{\partial x^2}+I_{0}\frac{\partial ^2\theta }{\partial y^2}\right) \right] -n\left[ I_6\frac{\partial \theta }{\partial x}+\frac{\partial }{\partial t}\left( \frac{\partial \theta }{\partial x}\right) \right] \nonumber \\&=\frac{\partial ^2}{\partial t^2}\left[ \theta +I_{8}\frac{\partial u}{\partial x}+I_{9}\frac{\partial v}{\partial y}\right] , \end{aligned}$$

(22)

where

$~~~~~~~~~~~~\displaystyle I_{0}=\frac{K_{22}^{'}}{K_{11}^{'}}$,  $\displaystyle I_1=\frac{\beta _{22}^{''}}{\beta _{11}^{''}},$  $\displaystyle [I_2,I_3,I_4,I_5]=\frac{1}{H_{11}}[H_{12},H_{13},H_{14},H_{15}],$   

$\displaystyle I_{6}=\frac{K^{*'}_{11}}{K^{'}_{11}c_0^2\eta _0},\,\,I_{7}=\frac{K^{*'}_{22}}{K^{'}_{11}c_0^2\eta _0},\,\,I_{8}=\frac{T_0\,r(\alpha ^{*})\beta _{11}^{''}\beta _{11}^{''}}{H_{11} K_{11}^{'}\eta _0},$  $\displaystyle I_{9}=\frac{T_0\,r(\alpha ^{*})\beta _{11}^{''}\beta _{22}^{''}}{H_{11} K_{11}^{'}\eta _0}$.

5 Solution methodology

In the current Section, normal mode technique is applied to get the exact solutions without any presumed restrictions on the physical variables. So, the physical variables under consideration and the stresses can be decomposed into terms of normal modes in the following form:

$$\begin{aligned}&[u,\,v,\,\theta ,\,\sigma _{ij}](x,y,t)=[u^*,\,v^*,\,\theta ^*,\,\sigma ^*_{ij}](x)\exp (\omega t+\iota my),\,\,\,\, \end{aligned}$$

(23)

where $\omega$ is the frequency, $\iota$ is the imaginary unit, m is the wave number in y-direction, and $u^*,\,v^*,\,\theta ^*$, and $\sigma ^*_{ij}$ are the amplitudes of the functions $u,\,v,\,\theta$, and $\sigma _{ij}$, respectively.

Introducing expression (23) to Eqs. (20)-(22), one can get

$$\begin{aligned}&(D^2-nD-J_1)u^*(x)+(J_2D-J_3)v^*(x)-r(\alpha ^{*})(D-n)\theta ^*(x)=0, \end{aligned}$$

(24)

$$\begin{aligned}&(J_2D-J_4)u^*(x)+(I_4D^2-J_5D-J_6)v^*(x)-J_7\,\theta ^*(x)=0, \end{aligned}$$

(25)

$$\begin{aligned}&J_{8}D\,u^*(x)+J_{9}\,v^*(x)- (J_{10}D^2-J_{11}D-J_{12})\theta ^*(x)=0, \end{aligned}$$

(26)

where $~~~~~~~~~~~\displaystyle D=\frac{d}{dx},$  $\displaystyle J_1=m^2I_4+\omega ^2,$  $\displaystyle J_2=\iota mI_5,$  $\displaystyle J_3=\iota mnI_2,$  $\displaystyle J_4=\iota mnI_4,$  

$~~~~~~~~~~~\displaystyle J_5=nI_4,$  $\displaystyle J_6=m^2I_3+\omega ^2,$  $\displaystyle J_7=\iota m\,r(\alpha ^{*})I_1,$   $\displaystyle J_8=\omega ^2I_8,$  $\displaystyle J_{9}=\iota m \omega ^2 I_9,$  

$\displaystyle J_{10}=\omega +I_6,$  $\displaystyle J_{11}=nJ_{10},$  $\displaystyle J_{12}=m^{2}(I_7+\omega I_0)+\omega ^2.$

Equations (24)-(26) represent a system of linear differential equations in the physical variables $u^*(x), v^*(x)$, and $\theta ^*(x)$. By adopting elimination procedure, the following differential equation of order six is obtained:

$$\begin{aligned}& \left[ D^6+L_1D^5+L_2D^4+L_3D^3+L_4D^2+L_5D+L_6\right] (u^*,\,v^*,\,\theta ^*)=0, \end{aligned}$$

(27)

where

$$\begin{aligned}&L_1=\frac{A_{11}A_{2}-A_{12}A_{1}-A_{4}A_{7}-A_{0}A_{8}}{A_{11}A_{1}+A_7 A_{0}},\nonumber \\&L_2=\frac{A_{11}A_{3}-A_{12}A_{2}+A_{13}A_{1}+A_{7}A_{5}+A_{8}A_{4}+A_{0}A_{9}}{A_{11}A_{1}+A_7 A_{0}},\\&L_3=\frac{A_{13}A_{2}-A_{12}A_{3}+A_{14}A_{1}-A_{7}A_{6}-A_{8}A_{5}-A_{4}A_{9}+A_{0}A_{10}}{A_{11}A_{1}+A_7 A_{0}},\\&L_4=\frac{A_{13}A_{3}+A_{14}A_{2}-A_{15}A_{1}+A_{8}A_{6}+A_{9}A_{5}-A_{10}A_{4}}{A_{11}A_{1}+A_7 A_{0}},\\&L_5=\frac{A_{14}A_{3}-A_{15}A_{2}-A_{9}A_{6}+A_{10}A_{5}}{A_{11}A_{1}+A_7A_{0}},\,\, L_6=\frac{-A_{15}A_{3}-A_{10}A_{6}}{A_{11}A_{1}+A_7 A_{0}}, \end{aligned}$$

$$\begin{aligned}& A_0=r(\alpha ^{*})I_4,\,\,A_{1}=J_{7}-r(\alpha ^{*})J_{2},\,\,A_{2}=-nJ_7+r(\alpha ^{*})(J_4+nJ_2),\\& A_{3}=-J_{7}J_{1}-n\,r(\alpha ^{*})J_{4},\,\,A_{4}=r(\alpha ^{*})(J_{5}+nI_{4}),\\&A_{5}=r(\alpha ^{*})(-J_{6}+nJ_5)-J_{7}J_2,\,\,A_{6}=-J_{7}J_{3}-n\,r(\alpha ^{*})J_{6},\\&A_{7}=J_{10}J_2,\,\,A_{8}=J_{11}J_{2}+J_{4}J_{10},\,\, A_{9}=J_{11}J_{4}-J_{12}J_{2}-J_7J_8,\\& A_{10}=J_{4}J_{12},\,\,A_{11}=I_4J_{10},\,\,A_{12}=I_4J_{11}+J_5J_{10},\\&A_{13}=-I_4J_{12}+J_5J_{11}-J_{10}J_{6},\,\,A_{14}=J_5J_{12}+J_6J_{11},\,\,A_{15}=-J_6J_{12}+J_7J_9. \end{aligned}$$

The solution of Eq. (27), which is bounded as $x\rightarrow \infty$, is given by

$$\begin{aligned}&(u^*, v^*,\theta ^*)(x)=\sum _{j=1}^{3}(H_j,H'_j,H''_j)(m,\omega ) e^{-\lambda _j x},\,\,\text {for} \,\,\text {Re}(\lambda _j)>0, \end{aligned}$$

(28)

where $H_j,\,H'_j$ and $H''_j$ are expressions which depend upon $\omega$ and m, and the constants $H_j$ will be determined by imposing the proper boundary conditions in the next Section. Making use of the solutions (28) in the system of Eqs. (24)-(26), we get the following simplified expressions:

$$\begin{aligned}& [u^*,\,v^*,\,\theta ^*](x)=\sum _{j=1}^{3}[1,\,N_{1j},\,N_{2j}]H_j(m,\,\omega )e^{-\lambda _j x}, \,\,\text {for} \,\,\text {Re}(\lambda _j)>0, \end{aligned}$$

(29)

where

$$\begin{aligned}& N_{1j}=\frac{-(A_{1}\lambda ^2_j-A_{2}\lambda _j+A_{3})}{(A_{0}\lambda ^3_j+A_{4}\lambda ^2_j+A_{5}\lambda _j+A_{6})},\,\,\, N_{2j}=\frac{(\lambda ^2_j+n\lambda _j-J_{1})+(-J_2\lambda _j-J_3)N_{1j}}{-r(\alpha ^{*})(\lambda _j+n)}. \end{aligned}$$

In view of the solution Eq. (29), the stress components (17) and (19) take the form

$$\begin{aligned}& [\sigma ^*_{xx}, \,\sigma ^*_{xy}](x)=\sum _{j=1}^{3}[N_{3j},\,N_{4j}]H_j(m,\,\omega )e^{-\lambda _j x-nx}, \,\,\text {for} \,\,\text {Re}(\lambda _j)>0, \end{aligned}$$

(30)

where

$$\begin{aligned}& N_{3j}=-\lambda _j+\iota mI_{2}N_{1j}-r(\alpha ^{*})N_{2j},\,\,\,N_{4j}=I_{4}(\iota m-\lambda _j N_{1j}). \end{aligned}$$

6 Application: inclined mechanical load is subjected to the boundary of the half-space

The surface of the functionally graded fiber-reinforced thermoelastic half space, i.e., the plane $x=0$, is subjected to an inclined load $\pmb {R}\,(R_1,R_2,0)$ with an inclination angle $\phi$, defined from the negative x-axis as shown in Fig. 1. The applied load $\pmb {R}$ is decomposed as a normal load $R_1=R\,\cos {\phi }$ and shear load $R_2=R\,\sin {\phi }$, where ${|\pmb {R}|}=R$. The surface of the medium is kept at reference temperature $T_0$; hence, the boundary conditions can be written as

$$\begin{aligned}&\theta (0,y,t)=0, \end{aligned}$$

(31)

$$\begin{aligned}&\sigma _{xx}(0,y,t)=-R_1, \end{aligned}$$

(32)

$$\begin{aligned}&\sigma _{xy}(0,y,t)=-R_2,\,\,\,\,\,\,\,\text {at} \,\,x=0. \end{aligned}$$

(33)

Using expressions of non-dimensional quantities in (16) and normal mode technique defined in (23), the boundary conditions (31)-(33) transform to

$$\begin{aligned}&\theta ^*=0, \end{aligned}$$

(34)

$$\begin{aligned}&\sigma _{xx}^*=-R_1^*, \end{aligned}$$

(35)

$$\begin{aligned}&\sigma _{xy}^*=-R_2^*,\,\,\,\,\,\,\,\text {at} \,\,x=0, \end{aligned}$$

(36)

where $\displaystyle \,R^*_1=R^*\cos {\phi },\,R^*_2=R^*\sin {\phi }$, and $R^*$ is defined by the expression $R=R^*\,\exp (\omega t+{\iota }my)$.

Using expressions (29) and (30), the boundary conditions (34)-(36) yield a non-homogeneous system of three equations, which can be written in matrix form as

$$\begin{aligned} \left[ \begin{array}{rrr} N_{21} &{}N_{22} &{} N_{23} \\ N_{31} &{}N_{32} &{} N_{33} \\ N_{41} &{}N_{42} &{} N_{43} \\ \end{array}\right] \left[ \begin{array}{cc} H_1\\ H_2\\ H_3 \end{array}\right] =\left[ \begin{array}{cc} 0\\ -R_1^*\\ -R_2^* \end{array}\right] . \end{aligned}$$

(37)

The expressions for $H_j, (j=1,2,3)$ obtained by solving the system (37) are

$$\begin{aligned}& H_1=\frac{\Delta _1}{\Delta }, \,\,\, H_2=\frac{\Delta _2}{\Delta }, \,\,\, H_3=\frac{\Delta _3}{\Delta }, \end{aligned}$$

(38)

where

$$\begin{aligned}&\Delta _1=-N_{22}(-R^*_1 N_{43}+R^*_2N_{33})+N_{23}(-R^*_1 N_{42}+R^*_2N_{32}),\\&\Delta _2=N_{21}(-R^*_1 N_{43}+R^*_2N_{33})+N_{23}(-R^*_2 N_{31}+R^*_1N_{41}),\\&\Delta _3=N_{21}(-R^*_2 N_{32}+R^*_1 N_{42})-N_{22}(-R^*_2 N_{31}+R^*_1N_{41}),\\&\Delta =N_{21}(N_{32}N_{43}-N_{42}N_{33})-N_{22}(N_{31}N_{43}-N_{41}N_{33})\\&\quad \qquad +N_{23}(N_{31}N_{42}-N_{32}N_{41}). \end{aligned}$$

Substitution of (38) in (29) and (30) provides us the following expressions of the physical fields:

$$\begin{aligned}&u^*(x)=\frac{1}{\Delta }[\Delta _1 e^{-\lambda _1x}+\Delta _2 e^{-\lambda _2x}+\Delta _3 e^{-\lambda _3x}], \end{aligned}$$

(39)

$$\begin{aligned}&v^*(x)=\frac{1}{\Delta }[N_{11}\Delta _1e^{-\lambda _1 x}+N_{12}\Delta _2e^{-\lambda _2 x}+N_{13}\Delta _3e^{-\lambda _3 x}], \end{aligned}$$

(40)

$$\begin{aligned}&\theta ^*(x)=\frac{1}{\Delta }[N_{21}\Delta _1e^{-\lambda _1x}+N_{22}\Delta _2e^{-\lambda _2x}+ N_{23}\Delta _3e^{-\lambda _3x}], \end{aligned}$$

(41)

$$\begin{aligned}&\sigma ^*_{xx}(x)=\frac{1}{\Delta }[N_{31}\Delta _1e^{-\lambda _1x-nx}+N_{32}\Delta _2e^{-\lambda _2x-nx}+ N_{33}\Delta _3e^{-\lambda _3x-nx}], \end{aligned}$$

(42)

$$\begin{aligned}&\sigma ^*_{xy}(x)=\frac{1}{\Delta }[N_{41}\Delta _1e^{-\lambda _1x-nx}+N_{42}\Delta _2e^{-\lambda _2x-nx}+ N_{43}\Delta _3e^{-\lambda _3x-nx}]. \end{aligned}$$

(43)

7 Particular cases

7.1 Neglecting the non-homogeneity effect

By setting $n=0$ in Eqs. (17)-(22), Eqs. (39)-(43) provide the expressions for various field variables in a homogeneous fiber-reinforced transversely isotropic thermoelastic medium with temperature-dependent properties due to an inclined load under the purview of GN theory of type III. In addition, setting $\phi =0^\circ$ along with this modification, the results obtained match with the limiting case ($g=0,\,\tau _v=\tau _t=\tau _q=0$) of Said and Othman [40].

7.2 Without fiber reinforcement

To discuss the problem in a functionally graded isotropic thermoelastic medium with temperature-dependent properties due to an inclined load in the context of GN theory of type III, it is sufficient to set the values of parameters $\alpha$, $\beta$, and $\mu _L-\mu _T$ as $\alpha =0,$ $\beta =0$, and $\mu _L=\mu _T$. Furthermore, the temperature dependence of the parameters $\lambda$, $\mu _T$, $\mu _L$, $\alpha$, $\beta$, $\beta _{ij}$ can be neglected from the considered model by setting $\alpha ^{*}$ as $\alpha ^{*}=0$; thereafter, we shall be dealing with a functionally graded isotropic thermoelastic half-space due to an inclined load in the context of GN theory of type III. By setting $\phi =0^\circ$ along with these modifications, the results obtained match with the particular case ($\Omega =0,\,H_0=0$) of Gunghas et al. [41].

8 Numerical results and discussion

To illustrate the analytical procedure presented earlier, we now present some numerical results, which are shown by depicting the variations of normal displacement, normal stress, shear stress, and temperature distribution with the help of computer programming using the MATLAB software. For the purpose of simulation, the values of relevant parameters are taken from Abbas et al. [34]:

$\rho ^{'}=2660\, kg\,m^{-3},$  $\lambda ^{''}=5.65\times {10}^{10}\,N\,m^{-2},$  $\mu _T^{''}=2.46\times {10}^{10}\,N\,m^{-2},$  $n=0.1,$  

$K_{11}^{'}=0.0921\times {10}^{3}\,J\, m^{-1} s^{-1}K^{-1},$  $K_{22}^{'}=0.0963\times {10}^{3}\,J\, m^{-1} s^{-1}K^{-1},$  

$K^{*'}_{11}=1.313\times {10}^{2}\,J\, m^{-1} s^{-2}K^{-1}$,  $K^{*'}_{22}=1.540\times {10}^{2}\,J\, m^{-1} s^{-2}K^{-1}$,  $\omega =1.0$,  

$\mu _L^{''}=5.66\times {10}^{10}\,N\,m^{-2},$   $\alpha ^{''}=-1.28\times 10^{10}\,N\,m^{-2},$  $\beta ^{''}=220.90\times 10^{10}\,N\,m^{-2},$  

$\alpha _{11}=0.017\times {10}^{-4}\,K^{-1},$  $\alpha _{22}=0.015\times {10}^{-4}\,K^{-1},$  $c_{E}=0.787\times {10}^{3}\,J\,kg^{-1}K^{-1},$  

$T_0=293\,K,$  $\alpha ^{*}=2.0\,s^{-1},\,\,R^{*}=1,$  $\phi =45^{\circ },$  $m=1.0$.

Utilizing the above numerical values of the parameters, the values of the non-dimensional field variables have been evaluated, and the results are presented in the form of the graphs at different positions of x at $t=0.01s$ and $y=1.0$.

Figures 2, 3, 4, and 5 illustrate the effect of the non-homogeneity parameter n on normal displacement, normal stress, shear stress, and temperature field, respectively, for four different values of $n\,(0.00,\,0.05,\,0.10$,  and 0.20). The influence of fiber reinforcement on displacement component, stress components, and temperature distribution field for the two models, a functionally graded fiber-reinforced thermoelastic medium with temperature-dependent properties due to an inclined load (WFR), and a functionally graded thermoelastic medium with temperature-dependent properties due to an inclined load (NFR) are shown in Figs. 6, 7, 8, and 9, respectively. Figures 10, 11, 12, and 13 exhibit the temperature dependency of the material constants on normal displacement, stress components, and temperature distribution field, respectively, for three different values of the empirical constant $\alpha ^{*}$ ($0.0,\,2.0,\,\text{ and }\,4.0$). Figures 14, 15, 16, and 17 are plotted to observe the effects of the inclination angle of load on the physical fields for four different values of $\phi$ ($0^\circ ,\,45^\circ ,\,60^\circ ,\,\text{ and }\,90^\circ$). Figures 18, 19, 20, and 21 offer the graphic details about the effect of time t on the profiles of normal displacement, normal stress, shear stress, and temperature distribution, respectively, for three different values of t ($0.01,\,0.10,\,\text{ and }\,0.20$).

Fig. 2

Effect of non-homogeneity parameter on normal displacement at y = 1

Fig. 3

Effect of non-homogeneity parameter on normal stress at y = 1

Fig. 4

Effect of non-homogeneity parameter on shear stress at y = 1

Fig. 5

Effect of non-homogeneity parameter on temperature field at y = 1

Fig. 6

Influence of fiber reinforcement on normal displacement at y = 1

Fig. 7

Influence of fiber reinforcement on normal stress at y = 1

Fig. 8

Influence of fiber reinforcement on shear stress at y = 1

Fig. 9

Influence of fiber reinforcement on temperature field at y = 1

Fig. 10

Effect of temperature-dependent properties on normal displacement at y = 1

Fig. 11

Effect of temperature-dependent properties on normal stress at y = 1

Fig. 12

Effect of temperature-dependent properties on shear stress at y = 1

Fig. 13

Effect of temperature-dependent properties on temperature field at y = 1

Fig. 14

Effect of inclination angle of load on normal displacement at y = 1

Fig. 15

Effect of inclination angle of load on normal stress at y = 1

Fig. 16

Effect of inclination angle of load on shear stress at y = 1

Fig. 17

Effect of inclination angle of load on temperature field at y = 1

Fig. 18

Effect of time on normal displacement at y = 1

Fig. 19

Effect of time on normal stress at y = 1

Fig. 20

Effect of time on shear stress at y = 1

Fig. 21

Effect of time on temperature field at y = 1

Figure 2 is drawn to observe the graphical details of normal displacement against the spatial distance x for four different values of the non-homogeneity parameter n ($0.00,\,0.05,\,0.10,\,\text{ and }\,0.20$). The Figure clearly indicates that all the curves of normal displacement start from positive values, and the normal displacement increases significantly with an increase in the value of the non-homogeneity parameter in the initial part of the domain of distance x, while it has a mixed kind of behavior in the later part of the domain. Figure 3 shows that all the curves of normal stress have a coincident starting value $-0.324$, which is due to the presence of resolved component $R_1$ of the inclined load at the surface and hence satisfies the boundary conditions. In addition, all the curves then start to approach the zero value as we move away from the boundary. Also, the solution curves corresponding to $n=0.05, 0.10,\,\text{ and }\,0.20$ follow a similar pattern with difference in magnitudes, while the curve corresponding to $n=0.0$ follows a different path and shows that the physical field in this case is compressive in nature. Figure 4 indicates that an increment in the values of non-homogeneity parameter n has a decreasing effect on the profile of shear stress. Figure 5 shows that the magnitude of the temperature field increases with an increase in the values of the non-homogeneity parameter n. The maximum impact of the temperature distribution with respect to distance is observed as x reaches 0.265, and this impact dies out with the passage of distance.

Figures 6 depicts the space variations of the normal displacement u versus distance x for the two models, WFR and NFR. The fiber reinforcement has a mixed influence on the profile of normal displacement. Figure 7 shows that normal stress starts with a common initial value $-0.324$ for both WFR and NFR, which also satisfies the boundary conditions. In the absence of fiber reinforcement, the normal stress is compressive in nature throughout the domain. Figure 8 shows that the presence of fiber reinforcement has a decreasing effect on shear stress, and Fig. 9 shows that it has an increasing effect on the temperature distribution field.

Figures 10, 11, 12, and 13 illustrate that the temperature dependency of the material constants has a mixed effect on normal displacement and normal stress for three distinct values of the empirical constant $\alpha ^{*},\,0.0,\,2.0,\,\text{ and }\,4.0$; while it has a decreasing effect on the profiles of shear stress and temperature distribution field with an increase in the values of the empirical constant.

Figure 14 shows that the inclination angle of load has an increasing effect on the profile of normal displacement for all considered values of $\phi$ except $\phi =0^{\circ }$. Figure 15 depicts that the solution curves corresponding to $\phi =45^{\circ },\,\phi =60^{\circ }$, and $\phi =90^{\circ }$ follow the same pattern with difference in magnitude, while the curve corresponding to $\phi =0^{\circ }$ follows a different pattern and is compressive in nature. Figures 16 and 17 show that the magnitudes of both shear stress and temperature field increase with an increase in the inclination angle of load, and therefore, the inclination angle of load has an increasing effect on the profiles of both shear stress and temperature distribution field.

Figures 18, 19, 20, and 21 show that time has a prominent increasing effect on the profiles of all the considered physical fields, normal displacement, normal stress, shear stress, and temperature distribution field.

9 Concluding remarks

The present investigation provides a mathematical model to study the behavior of normal displacement, normal stress, shear stress, and temperature field in a functionally graded fiber-reinforced transversely isotropic thermoelastic medium with temperature-dependent properties due to an inclined load within the framework of GN theory of type III, by using normal mode technique. The theoretical and numerical results reveal that the parameters, namely fiber reinforcement, non-homogeneity, temperature dependency of material constants, inclination angle of the load, and time, have significant effects on the physical fields. The following conclusions can be drawn according to the analysis of this study:

• (i) Both the non-homogeneity parameter and fiber reinforcement have a deceasing effect on the shear stress and an increasing effect on the temperature distribution, while these have mixed effects on normal displacement and normal stress.

• (ii) A significant decreasing effect of the empirical constant is clearly seen on shear stress and temperature distribution, while it has mixed effects on normal displacement and normal stress.

• (iii) The inclination angle of load has an increasing effect on the profile of normal displacement for all considered values of $\phi$ except $\phi =0^{\circ }$ and has an increasing effect on the profile of shear stress and temperature distribution for all considered values of $\phi$ including $\phi =0^{\circ }$, while it has a mixed effect on normal stress throughout the domain.

• (iv) Time t has a remarkable increasing effect on all the physical variables, i.e., normal displacement, normal stress, and temperature distribution.

• (v) From all the Figures, it has been observed that all the physical fields have non-zero values only in the bounded region of space, which is in accordance with the notion of generalized thermoelasticity theory and supports the physical facts.

The above study is of geophysical interest and explores applications in the problems related to seismology, as such a model is expected to exist in the interior of the earth. The results discussed in the present research work will prove practicable for designers of new materials, researches in material science as well as for those working on the second sound effect.