Gravitational Effect on a Fiber-Reinforced Thermoelastic Medium with Temperature-Dependent Properties for Two Different Theories

Abstract

A general model of equations of the three-phase-lag model and thermoelasticity without energy dissipation theory was used to study the effect of the gravity field on a fiber-reinforced thermoelastic half-space. The material is a homogeneous isotropic elastic half-space. Normal mode analysis was used to get the exact expressions for the displacement components, force stresses and temperature. The variations of the considered variables with the horizontal distance were illustrated graphically. Comparisons were made with the results of the two theories in the absence and presence of the gravity field as well as the reinforcement. A comparison was also made between the results of the two theories with and without temperature-dependent properties.

1 Introduction

Fiber-reinforced composites are widely used in engineering structures, due to their superiority over the structural materials in applications requiring high strength and stiffness in lightweight components. A continuum model is used to explain the mechanical properties of such materials. A reinforced concrete member should be designed for all conditions of stresses that may occur and in accordance with the principles of mechanics. The characteristic property of a reinforced concrete member is that its components, namely concrete and steel, act together as a single unit as long as they remain in the elastic condition, i.e., the two components are bound together so that there can be no relative displacement between them. In the case of an elastic solid reinforced by a series of parallel fibers, it is usual to assume transverse isotropy. In the linear case, the associated constitutive relations, relating infinitesimal stress and strain components, have five material constants. In the last three decades, the analysis of stress and the deformation of fiber-reinforced composite materials have been an important research area of solid mechanics. Belfield et al. (1983) introduced the idea of continuous self-reinforcement at every point of an elastic solid. One can find some studies on transversely isotropic elasticity in the literature by Sengupta and Nath (2001), Abbas (2012, 2014a; 2015), Zenkour and Abbas (2014) and Othman and Said (2012, 2013, 2015).

The effect of mechanical and thermal disturbances on an elastic body was studied by the theory of thermoelasticity. This theory has two defects. This theory was studied by Biot (1956). He deals with a defect of the uncoupled theory that mechanical causes have no effect on temperature. Noda (1986) reviewed extensive studies on the thermal stresses in materials with temperature-dependent properties. Material properties such as a modulus of elasticity and a thermal conductivity vary with temperature. In the thermal stress analyses of engineering materials and structures, the properties of materials are usually regarded as constants, about correct when the temperature variation from the initial temperature is not very high. In the reactor vessels, turbine engines, space vehicles and refractory industries, the structural components exposed to high temperature changes. In the thermal stress analyses of these components, neglecting the temperature dependence of material properties will usually result in significant errors. Jin and Batra (1998) studied the thermal fracture mechanics of ceramic with temperature-dependent properties. Othman (2001) used Lord–Shulman (L–S) theory under depend the modulus of elasticity on the reference temperature in a two-dimensional generalized thermoelasticity. The state-space approach to the generalized thermoelastic problem with temperature-dependent elastic moduli and internal heat sources was discussed by Othman (2011). The generalized thermoelastic medium with temperature-dependent properties for different theories under the effect of the gravity field was discussed by Othman et al. (2013). Fractional-order theory of thermoelasticity for elastic medium with temperature-dependent properties was discussed by Wang et al. (2015). Many studies in a generalized thermoelasticity with temperature-dependent properties can be found in the literature by Zenkour and Abbas (2014) and Abbas (2014b, c, d).

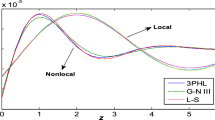
It is well known that the usual theory of heat conduction based on Fourier’s law predicts an infinite heat propagation speed. It is also known that heat transmission at low temperature propagates by means of waves. These aspects have caused intense activity in the field of heat propagation. Extensive reviews on the second sound theories (hyperbolic heat conduction) are given in Hetnarski and Ignaczak (1999, 2000). A two-phase-lag model to both the heat flux vector and the temperature gradient was introduced by Tzou (1995). According to this model, classical Fourier’s law $\varvec{q} = - K{\mathbf{\nabla }}{\rm T}$ was replaced by $\varvec{q}\text{(}P,t\text{ + }\tau_{\text{q}} \text{) = } - K{\mathbf{\nabla }}{\rm T}\text{(}P,t\text{ + }\tau_{\text{T}} \text{)}$, where the temperature gradient ${\mathbf{\nabla }}{\rm T}$ at a point P of the material at time $\text{t }+\tau_{\text{T}}$ corresponds to the heat flux vector $\varvec{q}$ at the same point at time $\text{t + }\tau_{\text{q}}$. Here K is the thermal conductivity of the material. The delay time $\tau_{\text{T}}$ interpreted as that caused by the microstructural interactions and called the phase lag of the temperature gradient. The other delay time $\tau_{\text{q}}$ interpreted as the relaxation time due to the fast transient effects of thermal inertia and called the phase lag of the heat flux. Recently, Choudhuri (2007) has proposed a theory with three-phase lag (3PHL) which is able to contain all the previous theories at the same time. In this case Fourier’s law $\varvec{q} = - K{\mathbf{\nabla }}{\rm T}$ was replaced by $\varvec{q}\text{(}P,t\text{ + }\tau_{\text{q}} \text{) = } - \;[K{\mathbf{\nabla }}{\rm T}\text{(}P,t\text{ + }\tau_{\text{T}} \text{) + }K^{*} {\mathbf{\nabla }}\nu \text{(}P,t\text{ + }\tau_{\nu } \text{)],}$ where ${\mathbf{\nabla }}\nu \;(\dot{\nu } = T)$ is the thermal displacement gradient, $K^{*}$ is the additional material constant, and $\tau_{\nu }$ is the phase lag for the thermal displacement gradient. The purpose of the work of Choudhuri (2007) was to set up a mathematical model that includes 3PHL in the heat flux vector, the temperature gradient and the thermal displacement gradient. For this model, we can consider several kinds of Taylor approximations to recover the previously cited theories. In particular, the thermoelasticity without energy dissipation and thermoelasticity with energy dissipation introduced by Green and Naghdi (1991, 1992, 1993) were recovered. A three-phase-lag model is very useful in the problems of nuclear boiling, exothermic catalytic reactions, phonon–electron interactions, phonon scattering, etc. Quintanilla and Racke (2008), Kar and Kanoria (2009), Kumar et al. (2012), Abbas (2014e) and Kumar and Kumar (2015) have solved different problems applying the 3PHL model.

In the classical theory of elasticity, the gravity effect is generally neglected. The effect of gravity field in the problem of propagation of waves in solids, in particular on an elastic globe, was first studied by Bromwich (1898). Subsequently, an investigation of the effect of the gravity field was discussed by Love (1911), who showed that the velocity of Rayleigh waves increased to a significant extent by gravitational field when wavelengths are large. Abd-Alla et al. (2010, 2011) investigated the effect of the gravity field on an orthotropic elastic medium for different theories. The effect of the gravity field on the plane waves in a rotating thermomicrostretch elastic solid for a mode-I crack with energy dissipation was discussed by Othman et al. (2015).

Our main object in writing this paper is to present a fiber-reinforced thermoelastic medium with temperature-dependent properties due to a thermal shock in the context of generalized thermoelasticity without energy dissipation (G-N II) theory and the three-phase-lag (3PHL) model. The governing equations of the problem were solved by using normal mode analysis. The effect of the gravity field, the temperature-dependent properties and reinforcement on the physical quantities was studied.

2 Formulation of the Problem and Basic Equations

We consider the problem of a thermoelastic half-space $(x \ge 0).$ The surface of a half-space was subjected to a thermal shock which is a function of $y$ and $t.$ Thus, all quantities considered will be the functions of the time variable $t$ and of the coordinates $x$ and $y.$

The constitutive equations for a fiber-reinforced linearly thermoelastic isotropic medium with respect to the reinforcement direction $\varvec{a}$ are discussed by Belfeild et al. (1983)

$$ \sigma_{ij} = \lambda e_{kk} \delta_{ij} + 2\mu_{T} e_{ij} + \alpha (a_{k} a_{m} e_{km} \delta_{ij} + a_{i} a_{j} e_{kk} ) + \,2(\mu_{L} - \mu_{T} )(a_{i} a_{k} e_{kj} + a_{j} a_{k} e_{ki} )\, + \,\beta \,a_{k} a_{m} e_{km} a_{i} a_{j} - \gamma \,\hat{T}\,\delta_{ij\,} , $$

(1)

where $\sigma_{ij}^{{\prime }} s$ are the components of stress, $e_{ij}^{{\prime }} s$ are the components of strain, $e_{kk}$ is the dilatation, $\lambda ,\,\,\mu_{\text{T}} '{\text{s}}$ are the elastic constants, $\alpha ,\beta ,(\mu_{L} - \mu_{T} ),\gamma$ are the reinforcement parameters, $\delta_{ij}$ is the Kronecker delta, $\hat{T} = T - T_{\text{0}} ,$ where $T$ is a temperature above the reference temperature $T_{\text{0}} ,$ and $\varvec{a} \equiv (a_{\text{1}} ,\,a_{2} ,\,\,a_{3} ),$ $a_{\text{1}}^{\text{2}} \text{ + }a_{\text{2}}^{\text{2}} \text{ + }a_{\text{3}}^{\text{2}} \text{ = 1}.$ We choose the fiber direction as $\varvec{a} \equiv (1,0,0).$ The strains can be expressed in terms of the displacement $u_{i}$ as

$$ e_{ij} = \frac{1}{2}(u_{i,\,j} + u_{j,\,i} ),\quad e_{kk} = u_{k,\,k} ,\quad i.j = x,y. $$

(2)

We assume that (Othman et al. 2013)

$$ \begin{aligned} \lambda = \lambda_{1} (1 - \alpha^{ * } T_{0} )\,,\quad \alpha = \alpha_{1} (1 - \alpha^{ * } T_{0} )\,,\quad \mu = \mu_{1} (1 - \alpha^{ * } T_{0} )\,,\quad \mu_{L} = \mu_{L1} (1 - \alpha^{ * } T_{0} )\,,\quad \mu_{T} = \mu_{T1} (1 - \alpha^{ * } T_{0} )\,, \hfill \\ \gamma = \gamma_{1} (1 - \alpha^{ * } T_{0} )\,,\quad \beta = \beta_{1} (1 - \alpha^{ * } T_{0} )\,, \hfill \\ \end{aligned} $$

(3)

where $\lambda_{1} ,\,\alpha_{1} ,\mu_{1} ,\mu_{L1} ,\,\mu_{T1} ,\,\gamma_{1} ,\,\beta_{1}$ are constants of the material and $\alpha^{ * }$ is the linear temperature coefficient.

For plane strain deformation in the $x\, - y$ plane with displacement components $u = u (x ,y ,t ) ,$ $v = v (x ,y ,t ) ,$ $w = 0.$ Using Eq. (3) in Eq. (1), we get

$$ \sigma_{xx} = \frac{1}{{\alpha_{0} }}\left[ {B_{11} u_{ ,x} + B_{ 1 2} v_{ ,y} - {{\upgamma }}_{ 1} \hat{T}} \right], $$

(4)

$$ \sigma_{yy} = \frac{1}{{\alpha_{0} }}[B_{12} u_{ ,x} + B_{ 2 2} v_{ ,y} - {{\upgamma }}_{ 1} \hat{T}], $$

(5)

$$ \sigma_{xy} = \frac{{\mu_{L1} }}{{\alpha_{0} }}\left( {u_{,y} + v_{,x} } \right),\quad \sigma_{xz} = \sigma_{yz} = 0, $$

(6)

where $B_{11} = \lambda_{1} + 2(\alpha_{1} + \mu_{T1} ) + 4(\mu_{L1} - \mu_{T1} ) + \beta_{1} ,$ $B_{12} = \lambda_{1} + \alpha_{1} ,$ $B_{22} = \lambda_{1} + 2\mu_{T1} ,$ $\alpha_{0} = \frac{1}{{(1 - \alpha^{ * } T_{0} )}}.$

2.1 Equation of Motion

The dynamical equations of a fiber-reinforced thermoelastic medium are (Othman et al. 2013)

$$ \rho \,{\ddot{u}}_{i} = \sigma_{ij,\,j} + F_{i} ,\quad i,j = 1,2,3, $$

(7)

where $F_{i}$ is the force due to the gravity field and is given in the form,

$$ F_{1} = \rho \,g\frac{\partial v}{\partial x},\quad F_{2} = - \rho \,g\frac{\partial u}{\partial x},\quad F_{3} = 0. $$

(8)

Substituting Eqs. (4)–(6) and (8) in Eq. (7), then, using the summation convection, we note that the third equation of motion in Eq. (7) is identically satisfied and the first two equations become

$$ \rho \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }} = \frac{1}{{\alpha_{0} }}\left( {B_{ 1 1} \frac{{\partial^{ 2} u}}{{\partial x^{ 2} }} + E_{2} \frac{{\partial^{ 2} v}}{\partial x\partial y} + E_{ 1} \frac{{\partial^{ 2} u}}{{\partial y^{ 2} }} - \gamma_{1} \frac{{\partial \hat{T}}}{\partial x}} \right) + \rho g\frac{\partial v}{\partial x}, $$

(9)

$$ \rho \frac{{\partial^{ 2} v}}{{\partial t^{ 2} }} = \frac{1}{{\alpha_{0} }}\left( {B_{ 2 2} \frac{{\partial^{ 2} v}}{{\partial y^{ 2} }} + E_{2} \frac{{\partial^{ 2} u}}{\partial x\partial y} + E_{ 1} \frac{{\partial^{ 2} v}}{{\partial x^{ 2} }} - \gamma_{1} \frac{{\partial \hat{T}}}{\partial y}} \right) - \rho g\frac{\partial u}{\partial x}, $$

(10)

where $E_{1} = \mu_{L1} ,$ $E_{2} = \alpha_{1} + \lambda_{1} + \mu_{L1} .$

2.2 Heat Conduction Equation

The generalized heat conduction equation in the 3PHL model discussed by Choudhuri (2007) is

$$ K^{*} \nabla^{2} T + \tau_{\nu }^{*} \nabla^{2} \dot{T} + K\tau_{T} \nabla^{2} {\ddot{T}} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\rho C_{E} {\ddot{T}} + \gamma T_{0} {\ddot{e}} } \right), $$

(11)

where $K$ is the coefficient of thermal conductivity, $K^{*}$ is the additional material constant, $\rho \,$ is the mass density, $C_{E}$ is the specific heat at constant strain, $\tau_{T}$ and $\tau_{q}$ are the phase lag of temperature gradient and the phase lag of heat flux, respectively. Also, $\tau_{\nu }^{*} = K + \tau_{\nu } \,K^{*} ,$ where $\tau_{\nu }$ is the phase lag of thermal displacement gradient. In the above equations, a dot denotes partial derivative with respect to time, and a comma followed by a suffix denotes partial derivative with respect to the corresponding coordinates.

Employing Eq. (3) and using Eq. (11), this yields

$$ K^{*} \nabla^{2} T + \tau_{\nu }^{*} \nabla^{2} \dot{T} + K\tau_{T} \nabla^{2} {\ddot{T}} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\,\left( {\rho C_{E} {\ddot{T}} + \frac{{\gamma_{1} }}{{\alpha_{0} }}T_{0} {\ddot{e}} } \right), $$

(12)

Introducing the following non-dimensional quantities:

$$ \begin{aligned} (x^{{\prime }} ,y^{{\prime }} ,u^{{\prime }} ,v^{{\prime }} ) &= c_{1} \eta (x,y,u,v),\quad g^{{\prime }} = \frac{g}{{\eta c_{1}^{3} }},\quad \theta = \frac{{\gamma_{1} \hat{T}}}{{(\lambda_{1} + 2\mu_{T1} )}},\quad (t^{{\prime }} ,\tau_{q}^{{\prime }} ,\tau_{\nu }^{{\prime }} ,\tau_{T}^{{\prime }} ) = c_{1}^{2} \eta \left( {t,\tau_{q} ,\tau_{\nu } ,\tau_{T} } \right), \hfill \\ \sigma_{ij}^{{\prime }}& = \frac{{\sigma_{ij} }}{{\mu_{T1} }},\quad i,j = 1,2. \hfill \\ \end{aligned} $$

(13)

where $\eta = \frac{{\rho \,C_{E} }}{{K^{*} }},$ $c_{1}^{2} = \frac{{(\lambda_{1} + 2\mu_{T1} )}}{\rho }.$

Using the above non-dimensional variables, Eqs. (9), (10) and (12) take the following form (dropping the primes for convenience)

$$ \alpha_{0} \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }} = h_{ 1 1} \frac{{\partial^{ 2} u}}{{\partial x^{ 2} }} + h_{2} \frac{{\partial^{ 2} v}}{\partial x\partial y} + h_{ 1} \frac{{\partial^{ 2} u}}{{\partial y^{ 2} }} - \frac{\partial \theta }{\partial x} + \alpha_{0} g\frac{\partial v}{\partial x}, $$

(14)

$$ \alpha_{0} \frac{{\partial^{ 2} v}}{{\partial t^{ 2} }} = h_{ 2 2} \frac{{\partial^{ 2} v}}{{\partial y^{ 2} }} + h_{ 2} \frac{{\partial^{ 2} u}}{\partial x\partial y} + h_{ 1} \frac{{\partial^{ 2} v}}{{\partial x^{ 2} }} - \frac{\partial \theta }{\partial y} - \alpha_{0} g\frac{\partial u}{\partial x}, $$

(15)

$$ C_{K} \theta_{,ii} + C_{\nu } \dot{\theta }_{,ii} + C_{T} \ddot{\theta }_{,ii} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)(\ddot{\theta } + \varepsilon {\ddot{e}}), $$

(16)

where $(\,\,h_{ 1} ,\,\,h_{2} \,,\,h_{11} ,\,\,h_{ 2 2} ) { } = \frac{{ (\,E_{ 1} ,\,\,E_{ 2} ,\,B_{ 1 1} ,\,B_{22} )}}{{\rho \,c_{1}^{2} }}\,,$ $C_{K} = \frac{{K^{*} }}{{\,\rho \,C_{E} \,c_{1}^{2} }},$ $C_{\nu } = \frac{\eta \,K}{{\,\rho \,\,C_{E} \,}} + C_{K} \,\tau_{\nu } ,$ $C_{T} = \frac{{\eta \,K\tau_{T} }}{{\,\rho \,C_{E} \,}},$ $\varepsilon = \frac{{\gamma_{1T 0}^{2} }}{{\,\rho \,C_{E} \alpha_{0} (\lambda_{1} + 2\mu_{T1} )}}.$

3 Normal Mode Analysis

The solution of the considered physical variable can be decomposed in terms of normal mode in the following form:

$$ [u,v,\theta , \sigma_{ij} ](x,y,t) = [ u^{*} ,v^{*} ,\theta^{*} , \sigma_{ij}^{*} ](x)\exp (\omega t + {\text{i}}my), $$

(17)

where $\omega$ is a complex constant, ${\text{i}} = \sqrt {{\kern 1pt} - 1} ,$ $m$ is the wave number in the $y$-direction, and $u^{*} (x),$ $v^{*} (x),$ $\theta^{*} (x),$ $\sigma_{ij}^{*} (x)$ are the amplitudes of the field quantities.

Substituting Eq. (17) in Eqs. (14–16), we get

$$ [h_{11} \text{D}^{2} - A_{1} ]u^{*} + A_{2} \text{D}v^{*} = \text{D}\theta^{*} , $$

(18)

$$ A_{3} {\text{D}}u^{*} + [h_{1} {\text{D}}^{2} - A_{4} ]\,v^{*} = {\text{i}}m\,\theta^{*} , $$

(19)

$$ A_{5} \text{D}u^{*} + \text{i}m{\kern 1pt} A_{5} \,v^{*} = [A_{6} \text{D}^{\text{2}} - A_{7} ]\,\theta^{*} , $$

(20)

where $A_{1} = \alpha_{0} \omega^{2} + h_{1} m^{2} ,$ $A_{2} = {\text{i}}mh_{2} + \alpha_{0} g,$ $A_{3} = {\text{i}}mh_{2} - \alpha_{0} g,$ $A_{4} = \alpha_{0} \omega^{2} + h_{22} m^{2} ,$ $A_{5} = \varepsilon \omega^{2} \left( {1 + \tau_{q} \omega + \frac{1}{2}\tau_{q}^{2} \omega^{2} } \right),$ $A_{6} = C_{K} + C_{\nu } \omega + C_{T} \omega^{2} ,$ $A_{7} = A_{6} m^{2} + \frac{{A_{5} }}{\varepsilon },$ ${\text{D}} = \frac{\text{d}}{{{\text{d}}x}}.$

Eliminating $v^{ *}$ and $\theta^{*}$ between Eqs. (18–20), we get the sixth-order ordinary differential equation satisfied with $u^{ *}$

$$ [\,{\text{D}}^{ 6} - A\,{\text{D}}^{ 4} + B{\text{ D}}^{ 2} - C{ ]}\,\,u^{ *} (x )= 0 , $$

(21)

where $A = \frac{1}{{h_{1} h_{11} A_{6} }}\left\{ {h_{1} A_{1} A_{6} + h_{11} A_{4} A_{6} \, + h_{1} h_{11} A_{7} + h_{1} A_{5} + A_{2} A_{3} A_{6} } \right\},$

$$ B = \frac{1}{{h_{1} h_{11} A_{6} }}\left\{ {A_{1} A_{4} A_{6} + h_{1} A_{1} A_{7} + h_{11} A_{4} A_{7} h_{11} m^{2}\, A_{5} + A_{4} A_{5} + A_{2} A_{3} A_{7} - 2m^{2} h_{2} A_{5} } \right\},\quad C = \frac{1}{{h_{1} h_{11} \,A_{6} }}\left\{ {A_{ 1} A_{ 4} A_{ 7} + m^{2} A_{1} A_{ 5} } \right\}. $$

In a similar manner, we can show that $v^{ *}$ and $\theta^{*}$ satisfy the equation,

$$ [\,{\text{D}}^{ 6} - A\,{\text{D}}^{ 4} + B{\text{ D}}^{ 2} - \;C{ ]}\,\{ v^{ *} (x ) ,\,\,\theta^{ *} (x ) \} = 0. $$

(22)

Equation (21) can be factored as

$$ (\,{\text{D}}^{ 2} - k_{ 1}^{ 2} )\,(\,{\text{D}}^{ 2} - k_{ 2}^{ 2} )\,(\,{\text{D}}^{ 2} - k_{ 3}^{ 2} )\,\,u^{ *} (x )= 0 , $$

(23)

where $k_{n}^{ 2} \quad (n = 1 ,\,\, 2 ,\,\, 3 )$ are the roots of the characteristic of Eq. (21)

The solution of Eq. (21), bound as $x \to \infty ,$ is given by

$$ \,u^{ *} (x )= \sum\limits_{n = 1}^{ 3} {\;G_{n} } {\text{exp(}} - k_{n} x ). $$

(24)

Similarly,

$$ \,v^{ *} (x )= \sum\limits_{n = 1}^{ 3} {L_{1n} G_{n} } {\text{exp(}} - k_{n} x ) , $$

(25)

$$ \,\theta^{ *} (x )= \sum\limits_{n = 1}^{ 3} {L_{2n} G_{n} } \,{\text{exp(}} - k_{n} x ) , $$

(26)

where $L_{ 1n} = \frac{{\,{\text{i}}\,mA_{ 1} - ({\text{i}}\,mh_{11} - A_{3} )k_{n}^{ 2} }}{{h_{ 1} k_{n}^{ 3} - (A_{ 4} + {\text{i }}mA_{2} )k_{n} }},$ $L_{ 2n} = \frac{{A_{ 1} - \,h_{11} k_{n}^{ 2} \, + A_{2} k_{n} L_{ 1n} }}{{k_{n} }}.$

Using Eqs. (13) and (17) in Eqs. (4) and (6), we get

$$ \sigma_{xx}^{*} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left\{ {B_{11} {\text{D}}\,u^{*} + {\text{i}}\,mB_{ 1 2} v^{*} - (\lambda_{1} + 2\mu_{T1} )\theta^{*} } \right\}, $$

(27)

$$ \sigma_{xy}^{*} = \frac{{\mu_{L1} }}{{\alpha_{0} \mu_{T1} }}\{ \,{\text{i}}\,mu^{*} + {\text{D}}\,v^{*} \} \,. $$

(28)

Introducing Eqs. (24–26) in Eqs. (27) and (28), this yields

$$ \sigma_{xx}^{*} = \sum\limits_{n = 1}^{3} {\,L_{3n} G_{n} } \,\exp ( - k_{n} x), $$

(29)

$$ \sigma_{xy}^{*} (x )= \sum\limits_{n = 1}^{3} {L_{4n} G_{n}} {\text{exp(}} - k_{n} x ) , $$

(30)

where $L_{3n} = \frac{1}{{\alpha_{0} \mu_{T1} }}[ -B_{11} k_{n} + {\text{i}}\,mB_{12} L_{1n} - (\lambda_{1} + 2\mu_{T1} )L_{2n} ],$ $L_{4n} = \frac{{\mu_{L1} }}{{\alpha_{0} \mu_{T1} }}\left[ {{\text{i }}m - k_{n} L_{\ln } } \right].$

4 Boundary Condition

In this section we find the parameters $G_{n} (n = 1,\,2,\,3).$ In the physical problem, we should suppress the positive exponential that unbounded at infinity. The constants $G_{1} ,\,\,G_{2} ,\,\,G_{3}$ have chosen such that the boundary conditions on the surface at $\,x = 0$ take the form:

• 1. A thermal boundary condition that the surface of the half-space subjected to a thermal insulated boundary,

  $$ \frac{\partial \theta }{\partial x} = 0. $$

  (31)

• 2. A mechanical boundary condition that the surface of the half-space subjected to a mechanical force,

  $$ \sigma_{xx} (0 , { }y ,\,t )= - P^{*} \exp (\omega \,t + {\text{i}}\,m\,y). $$

  (32)

• 3. A mechanical boundary condition that the surface of the half-space is a traction free,

  $$ \sigma_{xy} (0 , { }y ,\,t )= 0. $$

  (33)

Substituting the expressions of the variables considered into the above boundary conditions, we can get the following equations satisfied by the parameters:

$$ - \sum\limits_{n = 1}^{ 3} {k_{n} L_{ 2n} G_{n} } = 0,\quad \sum\limits_{n = 1}^{ 3} {L_{ 3n} G_{n} } = - P^{*} ,\quad \sum\limits_{n = 1}^{ 3} {L_{ 4n} G_{n} } = 0. $$

(34)

Invoking Eqs. (34), we get a system of three equations. After applying the inverse of matrix method, we have the values of the three constants $G_{n} (n = 1,2,3).$ Hence, we get the expressions of displacements, temperature distribution and the stress components.

$$ \left( \begin{aligned} G_{1} \hfill \\ G_{2} \hfill \\ G_{3} \hfill \\ \end{aligned} \right) = \left( {\begin{array}{*{20}l} {k_{1} \,L_{21} } \hfill & {k_{2} L_{22} } \hfill & {k_{3} L_{23} } \hfill \\ {L_{31} } \hfill & {L_{32} } \hfill & {L_{33} } \hfill \\ {L_{41} } \hfill & {L_{42} } \hfill & {L_{43} } \hfill \\ \end{array} } \right)^{ - 1} \left( \begin{aligned} 0 \hfill \\ - P^{*} \hfill \\ 0 \hfill \\ \end{aligned} \right). $$

(35)

5 Numerical Results and Discussion

With a view to illustrate the analytical procedure presented earlier, we now consider a numerical example for which computational results are given, and to compare these in the context of 3PHL model and the G-N II theory and to study the effect of the gravity field and temperature-dependent properties on the wave propagation in a conducting fiber reinforced, we now present some numerical results for the physical constants as $\lambda_{1} = 7.59 \times 10^{9} {\text{N}}\;{\text{m}}^{ - 2} ,\quad \mu_{T1} = 0.89 \times 10^{9} {\text{N}}\;{\text{m}}^{ - 2},$ $\mu_{L1} = 2.45 \times 10^{9} {\text{N}}\;{\text{m}}^{ - 2} ,\quad \rho = 7800\;{\text{kg}}\;{\text{m}}^{-3} ,$ $\alpha_{1} = 1.28 \times 10^{9} {\text{N}}\;{\text{m}}^{ - 2}$ $\beta_{1} = 0.32 \times 10^{9} {\text{N}}\;{\text{m}}^{ - 2} ,$ $T_{0} = 253\;{\text{K}},\quad C_{E} = 383.1\;{\text{J}}\;{\text{kg}}^{ - 1} \;{\text{K}}^{ - 1} ,\quad m = 0.3,$ $\tau_{T} = 0.007{\text{s}}, \tau_{q} = 0.009\;{\text{s}},\quad \tau_{\nu } = 0.006\;{\text{s}},$ $\alpha_{t} = 1.78\, \times 10^{ - 3} \,{\text{K}}^{ - 1} ,\,\,\,\,f^{*} = 0.5,\,$ $\mu_{1} = 3.86 \times 10^{11} \;{\text{kg}}\;{\text{m}}^{ - 1} {\text{s}}^{ - 2} ,$ $g = 9.8\;{\text{m}}\;{\text{s}}^{ - 2} ,$ $\omega = \omega_{0} + i\xi ,\,$ $\omega_{0} = - \;0.4,\,\,\,\,\,\xi = 0.07,\,$ $K = 800\;{\text{W}}\;{\text{m}}^{ - 1} \;{\text{K}}^{ - 1} ,\quad K^{*} = 386\;{\text{W}}\;{\text{m}}^{ - 1} \;{\text{K}}^{ - 1} \;{\text{s}}^{ - 1} ,$ $\alpha^{*} = 0.009\;{\text{K}}^{ - 1} .$

The computations were carried out for a value of time $t = 0.9.$ The variations of the thermal temperature $\theta ,$ the displacement components $u,\,v$ and the stress components $\sigma_{xx} ,\,\,\sigma_{xy}$ with distance $x$ in the plane $y = 1.2$ for the problem under consideration were based on the 3PHL model and the G-N II theory. The results are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. The graphs show four curves predicted by the two different theories of thermoelasticity. In these figures, the solid lines represent the solution in the 3PHL model and the dashed lines represent the solution derived using the G-N II theory. Here all the variables were used in non-dimensional forms, and we consider five cases:

Fig. 1

Horizontal displacement distribution $u$ for dependent and independent temperature

Fig. 2

Vertical displacement distribution $v$ for dependent and independent temperature

Fig. 3

Temperature distribution $\theta$ for dependent and independent temperature

Fig. 4

Distribution of stress component $\sigma_{xx}$ for dependent and independent temperature

Fig. 5

Distribution of stress component $\sigma_{xy}$ for dependent and independent temperature

Fig. 6

Horizontal displacement distribution $u$ with and without gravity field

Fig. 7

Vertical displacement distribution $v$ with and without gravity field

Fig. 8

Temperature distribution $\theta$ with and without gravity field

Fig. 9

Distribution of stress component $\sigma_{xx}$ with and without gravity field

Fig. 10

Distribution of stress component $\sigma_{xy}$ with and without gravity field

Fig. 11

Horizontal displacement distribution $u$ in the absence and presence of reinforcement

Fig. 12

Vertical displacement distribution $v$ in the absence and presence of reinforcement

Fig. 13

Temperature distribution $\theta$ in the absence and presence of reinforcement

Fig. 14

Distribution of stress component $\sigma_{xx}$ in the absence and presence of reinforcement

Fig. 15

Distribution of stress component $\sigma_{xy}$ in the absence and presence of reinforcement

• 1. The corresponding equations for a fiber-reinforced linearly thermoelastic isotropic medium with temperature-dependent properties and without the gravity field from the above-mentioned cases by taking $g = 0.$

• 2. The corresponding equations for a fiber-reinforced linearly thermoelastic isotropic medium with the gravity field and without temperature-dependent properties from the above-mentioned cases by taking $\alpha^{*} = 0.$

• 3. The corresponding equations for an isotropic generalized thermoelastic medium with the gravity field and with temperature-dependent properties from the above-mentioned cases by taking the reinforcement parameters $\alpha_{1} ,\,\,\beta_{1} ,\,\,(\,\mu_{L1} - \mu_{T1} )$ vanish.

• 4. Equations of the 3PHL model when $K,\tau_{\text{T}} ,\tau_{\text{q}} ,\tau_{{{\upnu }}} > 0,$ and the solutions are always (exponentially) stable if $\frac{{2K\tau_{\text{T}} }}{{\tau_{\text{q}} }} > \tau_{\nu }^{*} > K^{*} \tau_{\text{q}}$ as in Quintanilla and Racke (2008).

• 5. Equations of the G-N II theory when $K = \tau_{\text{T}} = \tau_{\text{q}} = \tau_{\nu } = 0$.

Figures 1, 2, 3, 4 and 5 show comparisons between the displacement components $u,\,v,$ the temperature $\theta$ and the stress components $\sigma_{xx} ,\sigma_{xy}$ with and without temperature-dependent properties in the effect of the gravitational field.

Figure 1 depicts that distribution of the horizontal displacement $u,$ begins from negative values for temperature-independent properties, but it begins from positive values for temperature-dependent properties. In the context of the two theories and with temperature-dependent properties, $u$ increases to a maximum value, then decreases to a minimum value and moves in a wave propagation. However, in the context of the two theories and without temperature-dependent properties, $u$ increases in the range $0\le x \le 20.$ Figure 2 depicts that distribution of the vertical displacement $v$ begins from positive values. In the context of the two theories and with temperature-dependent properties, $v$ increases to a maximum value, then decreases to a minimum value and moves in a wave propagation. However, in the context of the two theories and without temperature-dependent properties, $v$ increases to a maximum value and then decreases. Figure 3 exhibits distribution of the temperature $\theta$ and demonstrates that it begins from negative values with temperature-dependent properties, but it begins from positive values without temperature-dependent properties. In the context of the two theories and with temperature-dependent properties, $\theta$ decreases to a minimum value, then increases to a maximum value and moves in a wave propagation. However, in the context of the two theories and without temperature-dependent properties, $\theta$ increases to a maximum value and then decreases. Figure 4 exhibits that distribution of the stress component $\sigma_{xx}$ begins from a negative value and satisfies the boundary condition at $x = 0.$ In the context of the two theories and with temperature-dependent properties, $\sigma_{xx}$ decreases to a minimum value, then increases to a maximum value and moves in a wave propagation. However, in the context of the two theories and without temperature-dependent properties, $\sigma_{xx}$ decreases to a minimum value and then increases. Figure 5 depicts distribution of the stress component $\sigma_{xy}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $x = 0.$ In the context of the two theories and with temperature-dependent properties, $\sigma_{xy}$ increases to a maximum value, then decreases to a minimum value and moves in a wave propagation. However, in the context of the two theories and without temperature-dependent properties, $\sigma_{xy}$ decreases to a minimum value and then increases.

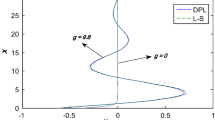
Figures 6, 7, 8, 9 and 10 show comparisons between the displacement components $u,\,v,$ the temperature $\theta$ and the stress components $\sigma_{xx} ,\,\,\sigma_{xy}$ in the absence and presence of the gravitational field with temperature-dependent properties. It is clear from Figs. 6, 7, 8, 9 and 10 that the gravitational field decreases the values of $u,\,v,\,\theta ,\,\sigma_{xx} ,\,\,\sigma_{xy}$, then increases their values, after then decreases and last again increases. There is no difference in the results of $u,$ $v,$ $\theta ,$ $\sigma_{xx} ,\,\,\sigma_{xy}$ for the two theories in the effect of gravitational field.

Figures 11, 12, 13, 14 and 15 show comparisons between the displacement components $u,\,v,$ the temperature $\theta$ and the stress components $\sigma_{xx} ,\,\,\sigma_{xy}$ in the absence (WRF) and presence (NRF) of the reinforcement and with temperature-dependent properties in the effect of the gravitational field. It is clear from Figs. 11, 12, 13, 14 and 15 that the reinforcement parameters increase the values of $u,\,v,\,\,\sigma_{xy}$, then decrease their values, after then increase and last again decrease. However, the reinforcement parameters decrease the values of $\theta ,\,\,\sigma_{xx}$, then increase their values, after then decrease and last again increase.

Figures 16, 17 and 18 are giving 3D surface curves for the physical quantities, i.e., the vertical displacement, and the stress components $\sigma_{xx} ,\,\,\sigma_{xy}$ for a thermal shock problem in the effect of the gravitational field with temperature-dependent properties in the context of the 3PHL model. These figures are very important to study the dependence of these physical quantities on the vertical component of distance. The curves obtained are highly depending on the vertical distance from origin, and all the physical quantities are moving in a wave propagation.

Fig. 16

Vertical component of displacement based on the 3PHL model in the effect of gravity field with temperature dependent

Fig. 17

Distribution of stress component $\sigma_{xx}$ based on the 3PHL model in the effect of gravity field with temperature dependent

Fig. 18

Distribution of stress component $\sigma_{xy}$ based on the 3PHL model in the effect of gravity field with temperature dependent

6 Conclusion

By comparing the figures which obtained under the two thermoelastic theories, important phenomena observed:

• 1. The gravitational field, temperature-dependent properties and reinforcement play a significant role on all the physical quantities.

• 2. Analytical solutions based upon normal mode analysis of the thermoelastic problem in solids were developed and used.

• 3. The method that used in the present article is applicable to a wide range of problems in thermodynamics and thermoelasticity.

• 4. Deformation of the body depends on the nature of the applied force as well as the type of boundary conditions.

• 5. There are significant differences in the field quantities under the G-N II theory and 3PHL model due to the phase lag of temperature gradient and the phase lag of heat flux.

• 6. The three-phase-lag model is useful in the problems of heat transfer, heat conduction, nuclear boiling, exothermic catalytic reactions, phonon–electron interactions and phonon scattering.

• 7. The physical quantities depend on the vertical distance and horizontal distance.