SH surface wave propagating in a strain-gradient layered half-space

Abstract

By employing Mindlin’s Form II gradient elasticity theory (strain gradient elasticity theory), we investigate the SH surface wave propagating in a strain-gradient layered half-space. The dispersion equation of the SH surface wave is derived analytically. For the general case where both the surface layer and the half-space are strain-gradient elastic materials, the dispersion equation involves 10 material constants. The dispersion equation of the general case can degenerate to that of several special cases by dropping some material parameters. The existence regions of the dispersion curves are discussed in detail. The effects of strain-gradient elastic constants on the dispersion curves are examined. It is seen that the features of SH surface waves in strain-gradient elastic materials are much richer than those in classical elastic materials.

1 Introduction

Layer substrate structures are widely used in many engineering fields, such as aerospace engineering, automobile manufacturing, microelectromechanical systems (MEMS), acoustic and optical components, to name a few. In these applications, the materials of the surface layer and the substrate may have micropatterns/microstructures and thus may exhibit size effects when external loads are applied. Due to their inherent size independence, classical elasticity theories cannot describe the size effects of materials with microstructures when the characteristic length of the material’s microstructure is comparable with that of the external load. In contrast, gradient elasticity theories, which incorporate characteristic lengths of material’s microstructures in their formulations, can be employed to describe the size effects of materials with microstructures [1]. Gradient elasticity theories include the couple stress theory originally proposed by Cosserat and Cosserat [2] and later developed by Mindlin and Tiersten [3], the general higher-order gradient elasticity theory proposed by Mindlin [4], the micropolar elasticity theory generalized by Eringen [5] from the couple stress theory, and the nonlocal theory of elasticity proposed also by Eringen [6], etc. A comprehensive review on these theories can be found in Maugin [7].

When the characteristic length of the external load is much larger than that of the material’s microstructure, the influence of the microstructure can be neglected; we can use classical elasticity theories to describe the mechanical behavior of the material. On the contrary, if the characteristic length of the external load is of the same order of magnitude as that of the material’s microstructure, the specific geometric features of the microstructure need to be considered; at this time, we need to use the method of molecular dynamic simulation. Here we choose surface waves as the object of our study. The reason is that the characteristic length of surface waves, i.e., the wave length, can be conveniently controlled to be larger (but not too much larger) than the characteristic length of the material’s microstructure. In this case, generalized continuum theories, for instance, gradient elasticity theories, prevail.

As early as in the 1960s, Graff and Pao [8] and Parfitt and Eringen [9] investigated the reflection of plane elastic waves in a couple-stress elastic half-space and a micropolar elastic half-space, respectively. Their results show that an incident wave gives rise to three reflected waves, instead of the usual two waves predicted by the classical elasticity theory. Later, Gourgiotis et al. [10] showed that, for a dipolar elastic half-space (the half-space is governed by a simplified version of Mindlin’s general gradient elasticity theory), an incident wave can give rise to four reflected waves. Georgiadis and Velgaki [11], Chirita and Ghiba [12], and Georgiadis et al. [13] predicted dispersive Rayleigh waves in a couple-stress elastic half-space, a micropolar elastic half-space, and a dipolar elastic half-space, respectively. While in the classical elastic half-space, the Rayleigh wave is nondispersive. It is well known that the SH and torsional surface waves do not exist in a classical elastic half-space [14], but this is not the case when the half-space is governed by a simplified version of gradient elasticity theory with surface energy [15, 16]. The existence of torsional and SH surface waves in a half-space is also predicted by Gourgiotis and Georgiadis [17] in the context of the complete Mindlin’s theory of gradient elasticity. In addition, Vavva et al. [18] and Sidhardh and Ray [19] studied the propagation of elastic waves in gradient elastic plates, and showed that gradient elasticity significantly changes the dispersion behavior predicted by the classical Lamb wave theory.

For the layer substrate structure, Love [20] predicted the existence of an SH surface wave in a classical elastic layered half-space mathematically (named as Love wave). Fan and Xu [21] and Fan and Long [22] investigated, respectively, the propagation of SH and in-plane surface waves in a classical linear elastic half-space covered by a couple-stress surface layer. Midya [23] studied the propagation of an SH surface wave in a micropolar elastic layered half-space and obtained the dispersion equation when either the surface layer or the half-space or both are micropolar elastic. In the case of isotropic and linear elasticity, the most versatile gradient elasticity theory is Mindlin’s Form II gradient elasticity theory (strain gradient elasticity theory) [4]. In the present paper, we investigate the propagation of an SH surface wave in a layered half-space governed by the strain gradient elasticity theory. As in Midya [23], we consider various situations, i.e., either the surface layer or half-space or both or none of them is gradient elastic. Besides, we also consider the cases that either the surface layer or the half-space is absent, that is, we consider the cases of gradient elastic half-space and gradient elastic waveguide. We would like to perform a complete and systematic study on all the combinations of the material configurations, which will contribute to the research of wave propagation in gradient elastic materials from the theoretical aspect.

The rest of this paper is organized as follows. In Sect. 2, an SH surface wave propagating in a strain-gradient layered half-space is investigated, and the dispersion equation is derived analytically. In Sect. 3, the dispersion equations of several special cases are obtained. In Sect. 4, the existence regions of the dispersion curves are discussed, and the influence of strain-gradient elastic constants on the dispersion curves is examined.

2 SH surface wave propagating in a strain-gradient layered half-space

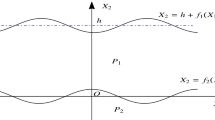
We consider an SH surface wave propagating in an elastic half-space B covered by a surface layer A with the thickness h, as shown in Fig. 1a. Both the surface layer and the half-space are described by the strain gradient elasticity theory. The surface wave propagates in the x₁-direction, and its amplitude decays exponentially in the x₂-direction.

Fig. 1

Schematic diagram of different cases: a SH surface wave propagating in a strain-gradient elastic half-space covered by a strain-gradient elastic surface layer (the general case); b surface layer is strain-gradient elastic, while the half-space is classical elastic; c surface layer is classical elastic while the half-space is strain-gradient elastic; d both the surface layer and the half-space are classical elastic (Love wave); e strain-gradient elastic half-space; f strain-gradient elastic wave guide. Shaded materials are strain-gradient elastic, while non-shaded materials are classical elastic. The arrows indicate the degeneration processes by dropping some material parameters

2.1 SH wave in the surface layer and the half-space

The governing equation of an anti-plane wave in gradient elastic material is given by Mindlin’s Form II gradient elasticity theory (strain gradient elasticity theory):

$$c_{T}^{2} \left( {1 - l_{2}^{2} \nabla^{2} } \right)\nabla^{2} \nabla \times {\mathbf{u}} = \left( {1 - \frac{{d^{2} }}{3}\nabla^{2} } \right)\nabla \times {\ddot{\mathbf{u}}},$$

(1)

where c_T= (μ/ρ)^1/2 is the shear wave velocity of the material. For the readers’ convenient reference, we list some basic equations of Mindlin’s Form II gradient elasticity theory in the “Appendix.”

Based on Eq. (1), the SH wave in the surface layer (− h < x₂ < 0) is given by

$$u_{3}^{A} = \left( {A_{1} \cos px_{2} + A_{2} \sin px_{2} + A_{3} \cosh qx_{2} + A_{4} \sinh qx_{2} } \right)\cos \left( {kx_{1} - \omega t} \right),$$

(2)

where k is the wave number, ω is the circular frequency, A₁–A₄ are four constants to be determined,

$$p^{2} = \frac{1}{{2l_{A}^{2} }}\left[ {\frac{{d_{A}^{2} }}{3}\frac{{\omega^{2} }}{{c_{A}^{2} }} - 1 + \sqrt {\left( {\frac{{d_{A}^{2} }}{3}\frac{{\omega^{2} }}{{c_{A}^{2} }} - 1} \right)^{2} + 4l_{A}^{2} \frac{{\omega^{2} }}{{c_{A}^{2} }}} } \right] - k^{2} ,$$

(3)

$$q^{2} = \frac{1}{{2l_{A}^{2} }}\left[ {1 - \frac{{d_{A}^{2} }}{3}\frac{{\omega^{2} }}{{c_{A}^{2} }} + \sqrt {\left( {\frac{{d_{A}^{2} }}{3}\frac{{\omega^{2} }}{{c_{A}^{2} }} - 1} \right)^{2} + 4l_{A}^{2} \frac{{\omega^{2} }}{{c_{A}^{2} }}} } \right] + k^{2} ,$$

(4)

c_A= (μ_A/ρ_A)^1/2 is the shear wave velocity of the surface layer, μ_A and ρ_A are, respectively, the shear modulus and density of the surface layer, and l and _A and d_A are the characteristic lengths of the surface layer related to the strain energy and kinetic energy, respectively.

It is noted that the requirement of p² > 0 in Eq. (3) posts a constraint on the phase velocity c, that is,

$$c = \frac{\omega }{k} > c_{A} \sqrt {\frac{{1 + l_{A}^{2} k^{2} }}{{1 + d_{A}^{2} k^{2} /3}}} .$$

(5)

The SH wave in the half-space (x₂ > 0) can be written as

$$u_{3}^{B} = \left( {B_{1} e^{{ - ax_{2} }} + B_{2} e^{{ - bx_{2} }} } \right)\cos \left( {kx_{1} - \omega t} \right),$$

(6)

where B₁ and B₂ are two constants to be determined,

$$a^{2} = \frac{1}{{2l_{B}^{2} }}\left[ {1 - \frac{{d_{B}^{2} }}{3}\frac{{\omega^{2} }}{{c_{B}^{2} }} - \sqrt {\left( {\frac{{d_{B}^{2} }}{3}\frac{{\omega^{2} }}{{c_{B}^{2} }} - 1} \right)^{2} + 4l_{B}^{2} \frac{{\omega^{2} }}{{c_{B}^{2} }}} } \right] + k^{2} ,$$

(7)

$$b^{2} = \frac{1}{{2l_{B}^{2} }}\left[ {1 - \frac{{d_{B}^{2} }}{3}\frac{{\omega^{2} }}{{c_{B}^{2} }} + \sqrt {\left( {\frac{{d_{B}^{2} }}{3}\frac{{\omega^{2} }}{{c_{B}^{2} }} - 1} \right)^{2} + 4l_{B}^{2} \frac{{\omega^{2} }}{{c_{B}^{2} }}} } \right] + k^{2} ,$$

(8)

c_B= (μ_B/ρ_B)^1/2 is the shear wave velocity of the half-space, μ_B and ρ_B are, respectively, the shear modulus and density of the half-space, and l_B and d_B are the characteristic lengths of the half-space associated with the strain energy and kinetic energy, respectively.

Similarly, the requirement of a² > 0 in Eq. (7) imposes a restriction on the phase velocity c, i.e.,

$$c = \frac{\omega }{k} < c_{B} \sqrt {\frac{{1 + l_{B}^{2} k^{2} }}{{1 + d_{B}^{2} k^{2} /3}}} .$$

(9)

Combing Eqs. (5) and (9), we have

$$c_{A} \sqrt {\frac{{1 + l_{A}^{2} k^{2} }}{{1 + d_{A}^{2} k^{2} /3}}} < c < c_{B} \sqrt {\frac{{1 + l_{B}^{2} k^{2} }}{{1 + d_{B}^{2} k^{2} /3}}} .$$

(10)

2.2 Boundary conditions and continuity conditions

For the considered anti-plane problem, the displacement components can be written in general forms as

$$\begin{array}{*{20}c} {u_{1} = 0,} & {u_{ 2} = 0,} & {u_{ 3} = u_{3} (x_{1} ,x_{2} ,t)} \\ \end{array} .$$

(11)

By substituting Eq. (11) into Eqs. (39)–(42), (45) and (46), we can obtain the components of auxiliary force traction and auxiliary double force traction as follows:

$$\begin{array}{*{20}c} {P_{1} = 0,} & {P_{2} = 0,} & {P_{3} = \mu u_{3,2} - \mu \left( {2l_{2}^{2} - \bar{a}_{3} } \right)u_{3,112} - \mu l_{2}^{2} u_{3,222} + I\ddot{u}_{3,2} ,} \\ \end{array}$$

(12)

$$\begin{array}{*{20}c} {R_{1} = 0,} & {R_{2} = 0,} & {R_{3} = \mu \bar{a}_{3} u_{3,11} + \mu l_{2}^{2} u_{3,22} } \\ \end{array} ,$$

(13)

where $\bar{a}_{3} \equiv a_{3} /2\mu$, and the comma in the subscript denotes the derivative with respect to the coordinate variables. The material constant $\bar{a}_{3}$ has the unit of m² and can take positive or negative values. To ensure the positive definiteness of the strain energy density, the inequality $|\bar{a}_{3} | < l_{ 2}^{ 2}$ needs to be satisfied [17].

From Eqs. (12) and (13), and by the surface integral in Eq. (44), we can find that, for the anti-plane problem, there are only two energy conjugate pairs appearing on the surface, namely, (P₃, u₃) and (R₃, Du₃). Therefore, for the present problem, we have the following boundary conditions and continuity conditions:

at the free surface (x₂ = −h):

$$P_{3}^{A} (x_{1} , - h,t) = 0,$$

(14)

$$R_{3}^{A} (x_{1} , - h,t) = 0,$$

(15)

along the interface (x₂ = 0):

$$P_{3}^{A} (x_{1} ,0,t) = P_{3}^{B} (x_{1} ,0,t),$$

(16)

$$u_{3}^{A} (x_{1} ,0,t) = u_{3}^{B} (x_{1} ,0,t),$$

(17)

$$R_{3}^{A} (x_{1} ,0,t) = R_{3}^{B} (x_{1} ,0,t),$$

(18)

$$Du_{3}^{A} (x_{1} ,0,t) = Du_{3}^{B} (x_{1} ,0,t),$$

(19)

where $P_{3}^{A}$ and $R_{3}^{A}$ are the components of auxiliary force traction and auxiliary double force traction of the surface layer, and $P_{3}^{B}$ and $R_{3}^{B}$ are the corresponding traction components of the half-space.

2.3 Dispersion equation

Substituting the displacement components of the surface layer and the half-space (Eqs. (2) and (6)) into the non-vanishing components of the auxiliary force traction and the auxiliary double force traction (Eqs. (12) and (13)), and then according to the boundary conditions and continuity conditions (Eqs. (14)–(19)), we can derive six linear algebraic equations for the undetermined constants A₁–A₄, B₁ and B₂ as follows:

$$p\eta_{A} \left( {A_{1} \sin ph + A_{2} \cos ph} \right) - q\xi_{A} \left( {A_{3} \sinh qh - A_{4} \cosh qh} \right) = 0,$$

(20)

$$\xi_{A} \left( {A_{1} \cos ph - A_{2} \sin ph} \right) + \eta_{A} \left( {A_{3} \cosh qh - A_{4} \sinh qh} \right) = 0,$$

(21)

$$\mu_{A} \left( {p\eta_{A} A_{2} + q\xi_{A} A_{4} } \right) = - \mu_{B} \left( {a\eta_{B} B_{1} + b\xi_{B} B_{2} } \right),$$

(22)

$$A_{1} + A_{3} = B_{1} + B_{2} ,$$

(23)

$$\mu_{A} \left( {\xi_{A} A_{1} + \eta_{A} A_{3} } \right) = \mu_{B} \left( {\xi_{B} B_{1} + \eta_{B} B_{2} } \right),$$

(24)

$$pA_{2} + qA_{4} = - aB_{1} - bB_{2} ,$$

(25)

where p, q, a, and b are defined in Eqs. (3), (4), (7), and (8), respectively,

$$\begin{array}{*{20}c} {\xi_{A} = \bar{a}_{3A} k^{2} + l_{A}^{2} p^{2} ,} & {\eta_{A} = \bar{a}_{3A} k^{2} - l_{A}^{2} q^{2} ,} \\ \end{array}$$

(26)

$$\begin{array}{*{20}c} {\xi_{B} = \bar{a}_{3B} k^{2} - l_{B}^{2} a^{2} ,} & {\eta_{B} = \bar{a}_{3B} k^{2} - l_{B}^{2} b^{2} } \\ \end{array} ,$$

(27)

$\bar{a}_{3A}$ and $\bar{a}_{3B}$ are the designations of the material constants $\bar{a}_{3}$ in the surface layer and half-space, respectively.

Constants A₁–A₄, B₁, and B₂ can be determined by solving the algebraic equations (20)–(25). For a non-trivial solution of A₁–A₄, B₁ and B₂, the determinant of the coefficients must vanish, which yields the following dispersion equation of the SH surface wave:

$$\begin{aligned} & 2pq\xi_{A} \eta_{A} \left[ {\xi_{A} \eta_{A} \left( {a - b} \right) - \frac{{\mu_{B} }}{{\mu_{A} }}\left( {\xi_{A} + \eta_{A} } \right)\left( {a\eta_{B} - b\xi_{B} } \right) + \frac{{\mu_{B}^{2} }}{{\mu_{A}^{2} }}\left( {a\eta_{B}^{2} - b\xi_{B}^{2} } \right)} \right] \\ & \quad - pq\left[ {2\xi_{A}^{2} \eta_{A}^{2} \left( {a - b} \right) - 2\frac{{\mu_{B} }}{{\mu_{A} }}\xi_{A} \eta_{A} \left( {\xi_{A} + \eta_{A} } \right)\left( {a\eta_{B} - b\xi_{B} } \right) + \frac{{\mu_{B}^{2} }}{{\mu_{A}^{2} }}\left( {\xi_{A}^{2} + \eta_{A}^{2} } \right)\left( {a\eta_{B}^{2} - b\xi_{B}^{2} } \right)} \right] \\ & \quad \times \cos ph\cosh qh + \left[ {\left( {q^{2} \xi_{A}^{4} - p^{2} \eta_{A}^{4} } \right)\left( {a - b} \right) - 2\frac{{\mu_{B} }}{{\mu_{A} }}\left( {q^{2} \xi_{A}^{3} - p^{2} \eta_{A}^{3} } \right)\left( {a\eta_{B} - b\xi_{B} } \right)} \right. \\ & \quad \left. { +\, \frac{{\mu_{B}^{2} }}{{\mu_{A}^{2} }}\left( {q^{2} \xi_{A}^{2} - p^{2} \eta_{A}^{2} } \right)\left( {a\eta_{B}^{2} - b\xi_{B}^{2} } \right)} \right]\sin ph\sinh qh + \frac{{\mu_{B} }}{{\mu_{A} }}\left( {\xi_{A} - \eta_{A} } \right)\left( {\xi_{B} - \eta_{B} } \right) \\ & \quad \times \left[ {q\left( {p^{2} \eta_{A}^{2} + ab\xi_{A}^{2} } \right)\sin ph\cosh qh + p\left( {q^{2} \xi_{A}^{2} - ab\eta_{A}^{2} } \right)\cos ph\sinh qh} \right] = 0. \\ \end{aligned}$$

(28)

3 Special cases

In Sect. 2, we investigated the general case where both the surface layer and the half-space are strain-gradient elastic materials. Now we study some special cases.

If the surface layer is strain-gradient elastic while the half-space is classical elastic (Fig. 1b), that is, the material constants of the half-space associated with strain-gradient elasticity all equal to zero, i.e., l_B= d_B= $\bar{a}_{3B}$ = 0, then we have a = (k² − ω²/$c_{B}^{2}$)^1/2 = $\tilde{a}$, b = ∞, l_Bb = 1 from Eqs. (7) and (8), and further deduce ξ_B= 0, η_B= − 1, bξ_B= 0 from Eq. (27). In this situation, the dispersion equation of the general case (Eq. (28)) degenerates to

$$\begin{aligned} & 2pq\xi_{A}^{2} \eta_{A}^{2} \left( { 1- \cos ph\cosh qh} \right) + \left( {q^{2} \xi_{A}^{4} - p^{2} \eta_{A}^{4} } \right)\sin ph\sinh qh \\ & \quad - \frac{{\mu_{B} }}{{\mu_{A} }}\tilde{a}\left( {\xi_{A} - \eta_{A} } \right)\left( {q\xi_{A}^{2} \sin ph\cosh qh - p\eta_{A}^{2} \cos ph\sinh qh} \right){ = 0} .\\ \end{aligned}$$

(29)

Conversely, if the surface layer is classical elastic while the half-space is strain-gradient elastic (see Fig. 1c), the material constants of the surface layer related to strain-gradient elasticity all equal to zero, i.e., l_A= d_A= $\bar{a}_{3A}$ = 0, then from Eqs. (3) and (4) we have p = (ω²/ $c_{A}^{2}$ − k²)^1/2 = $\tilde{p}$, q = ∞, l_Aq = 1, and further from Eq. (26) derive ξ_A= 0, η_A= − 1, qξ_A= 0. The dispersion equation of the general case in this situation reduces to

$$\tilde{p}\left( {\xi_{B} - \eta_{B} } \right)\sin \tilde{p}h - \frac{{\mu_{B} }}{{\mu_{A} }}\left( {a\eta_{B}^{2} - b\xi_{B}^{ 2} } \right)\cos \tilde{p}h = 0.$$

(30)

If both the surface layer and the half-space are classical elastic, the case of Love wave [14] is recovered, as illustrated in Fig. 1d. In this case, by dropping the material parameters associated with strain-gradient elasticity, we can derive the dispersion equation from either Eq. (29) or (30) as

$$\tilde{p}\sin \tilde{p}h - \frac{{\mu_{B} }}{{\mu_{A} }}\tilde{a}\cos \tilde{p}h = 0.$$

(31)

If the surface layer is absent, that is, h = 0, the SH surface wave propagates in a strain-gradient elastic half-space (Fig. 1e). In this situation, the dispersion equation of the general case degenerates to

$$a\eta_{B}^{ 2} - b\xi_{B}^{ 2} { = 0,}$$

(32)

which is exactly the solution of Gourgiotis and Georgiadis [17].

At last, if the half-space disappears, i.e., μ_B= 0, an SH surface wave propagates in a strain-gradient elastic wave guide (Fig. 1f). The dispersion equation of the general case in this situation degenerates to

$$2pq\xi_{A}^{ 2} \eta_{A}^{ 2} \left( { 1- \cos ph\cosh qh} \right) + \left( {q^{ 2} \xi_{A}^{ 4} - p^{ 2} \eta_{A}^{ 4} } \right)\sin ph\sinh qh{ = 0} .$$

(33)

The dispersion equations (32) and (33) also can be deduced from Eqs. (30) and (29) by setting h = 0 and μ_B= 0, respectively, as indicated by the dark cyan arrows in Fig. 1.

4 Results and analysis

For the general case where both the surface layer and the half-space are strain-gradient elastic materials, we have two sets of material constants. Each set consists of 5 material parameters, as shown as follows:

$$\begin{aligned} & \mu_{A} ,\quad \rho_{A} ,\quad l_{A} ,\quad d_{A} ,\quad \bar{a}_{3A} , \\ & \mu_{B} ,\quad \rho_{B} ,\quad l_{B} ,\quad d_{B} ,\quad \bar{a}_{3B} . \\ \end{aligned}$$

The parametric study becomes very difficult, if it is not impossible. Our objective in this Section is to gain an overall picture of the dispersion curves. Our study in the following is made in two steps. First, we discuss the existence regions of the dispersion curves. Next, we examine the influence of strain-gradient elastic constants on the dispersion curves.

4.1 Existence regions of the dispersion curves

For the case that both the surface layer and the half-space are classical elastic materials (Love wave), it is well known that the dispersion curves fall in the region of c_A< c<c_B. The introduction of the material characteristic lengths in strain gradient elasticity theory enriches the existence regions of the dispersion curves. Let us refer to Eq. (10), which defines the lower and upper bounds of the dispersion curves, for an easy explanation. It should be pointed out that there are six material parameters involved in the governing equations and the bounds of the dispersion curves, namely,

$$\begin{aligned} & c_{A} ,\quad l_{A} ,\quad d_{A} , \\ & c_{B} ,\quad l_{B} ,\quad d_{B} , \\ \end{aligned}$$

and the other four material parameters are associated with the boundary and continuity conditions (Eqs. (14)–(19)).

It can be found from Eq. (10) that the upper and lower bounds of the dispersion curves are no longer two straight lines as in the classical case of Love wave. The possible shapes of the bounds are schematically shown in Fig. 2, where the short dash line represents the upper bound, and the dash lines denote the lower bounds. Figure 2 only shows the possible five variations of the lower bound of the dispersion curves for different ratios of $\sqrt 3$l_A/d_A under the condition of c_A< c_B. The upper bound also can have 5 variations for different ratios of $\sqrt 3$l_B/d_B. Thus there are 25 combinations when the upper and lower bounds are considered together. If we swap the condition into c_A> c_B, we have another 25 combinations of the upper and lower bounds. Of course, there is quite a number of the combinations of the bounds which lead to no solution of the dispersion curve. For different combinations of material constants, the existence regions of the dispersion curves are defined by the corresponding upper and lower bounds, as illustrated in Figs. 3 and 4.

Fig. 2

Possible shapes of the bounds of the dispersion curves. The upper bound is denoted by short dash line, while the lower bounds are denoted by dash lines. Here we only show the possible 5 variations of the lower bound of the dispersion curves for different ratios of $\sqrt 3$l_A/d_A under the condition of c_A< c_B. The upper bound also can have 5 variations for different ratios of $\sqrt 3$l_B/d_B. Thus there are 25 combinations when the upper and lower bounds are considered together. If we swap the condition into c_A> c_B, we have another 25 combinations of the upper and lower bounds

Fig. 3

Existence regions of the dispersion curves (denoted by the shaded areas) for different combinations of material constants under the condition of l_A= l_B= 0. The SH surface wave: a, b can exist in the whole range of the wave number, c can only exist in the large wave numbers, d can only exist in the small wave numbers, e, f does not exist for any wave number. k_cr is the critical wave number

Fig. 4

Existence regions of the dispersion curves (denoted by the shaded areas) for different combinations of material constants under the condition of d_A= d_B= 0. The SH surface wave: a, b can exist in the whole range of the wave numbers, c can only exist in the large wave numbers, d can only exist in the small wave numbers, e, f does not exist for any wave number. k_cr is the critical wave number

In Fig. 3, we show the existence regions of the dispersion curves (denoted by the shaded areas) for different combinations of material constants under the condition that the material constants related to the strain energy equal zero (l_A= l_B= 0). It can be seen from Fig. 3 that the features of the possible solution of the SH surface wave in strain-gradient elastic materials are much richer than that of the classical Love wave. The SH surface wave can exist in the whole range of the wave number (for c_A≤ c_B, d_A> d_B, Fig. 3a, b), or can only exist in the large wave numbers (for c_A> c_B, d_A> d_B, Fig. 3c), or can only exist in the small wave numbers (for c_A< c_B, d_A< d_B, Fig. 3d), or does not exist for any wave number (for c_A≥ c_B, d_A< d_B, Fig. 3e, f). Under the condition that the material constants related to the kinetic energy equal zero (d_A= d_B= 0), the existence regions of the dispersion curves for different combinations of material constants are depicted in Fig. 4 (denoted by the shaded areas), and similar conclusions can be drawn as those of Fig. 3.

4.2 Influence of strain-gradient elastic constants on the dispersion curves

Now we examine the influence of the material constants introduced by the strain gradient elasticity theory on the dispersion curves of an SH surface wave. First we examine the effects of strain-gradient elastic constants related to the kinetic energy on the dispersion curves of the general case (both the surface layer and the half-space are strain-gradient elastic materials).

we assume that the strain-gradient elastic constants involved in the strain energy and boundary/continuity conditions vanish, that is, l_A= l_B= 0, $\bar{a}_{3A}$ = $\bar{a}_{3B}$ = 0. Then, Eq. (28) reduces to

$$\tan \left( {hk\sqrt {\frac{{c^{2} /c_{A}^{2} }}{{1 - \left( {d_{A}^{2} k^{2} /3} \right)c^{2} /c_{A}^{2} }} - 1} } \right) = \frac{{\mu_{B} }}{{\mu_{A} }}\sqrt {\frac{{1 - \left( {d_{B}^{2} k^{2} /3} \right)c^{2} /c_{B}^{2} }}{{1 - \left( {d_{A}^{2} k^{2} /3} \right)c^{2} /c_{A}^{2} }}} \sqrt {\frac{{1 - \left( {1 + d_{B}^{2} k^{2} /3} \right)c^{2} /c_{B}^{2} }}{{\left( {1 + d_{A}^{2} k^{2} /3} \right)c^{2} /c_{A}^{2} - 1}}} .$$

(34)

Figure 5 demonstrates the dimensionless dispersion curves of this situation, where the short dash lines represent the upper bounds, while the dash lines denote the lower bounds. Figure 5a–d makes correspondence with Fig. 3a–d, respectively. It can be seen from Fig. 5 that, for all the four cases, the dispersion curves of Eq. (34) lie between the upper and lower bounds (in the existence regions of the dispersion curves), and decrease gradually from the upper bounds to the lower bounds with the increase of the wave number.

Fig. 5

Dispersion curves of the general case where both the surface layer and the half-space are strain-gradient elastic materials. Under the conditions of l_A= l_B= 0, $\bar{a}$_3A= $\bar{a}$_3B= 0, dispersion curves are depicted for four cases: a c_A< c_B, d_A> d_B, b c_A= c_B, d_A> d_B, c c_A> c_B, d_A> d_B, and d c_A< c_B, d_A< d_B. The short dash lines represent the upper bounds, while the dash lines denote the lower bounds

Second, we examine the effects of strain-gradient elastic constants involved in the strain energy and boundary/continuity conditions on the dispersion curves of the case that the surface layer is classical elastic, while the half-space is strain-gradient elastic.

Let the strain-gradient elastic constant related to the kinetic energy equal zero, i.e., d_B= 0, then Eq. (30) can be written as

$$\begin{aligned} & \tan \left( {hk\sqrt {c^{2} /c_{A}^{2} - 1} } \right) \\ & \quad = \frac{{\mu_{B} }}{{\mu_{A} }}\frac{{l_{B} k\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } \left( {1 + 2l_{B}^{2} k^{2} - 2\bar{a}_{3B} k^{2} + l_{B} k\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } } \right) - \bar{a}_{3B}^{2} k^{4} }}{{l_{B} k\sqrt {c^{2} /c_{A}^{2} - 1} \left( {1 + 2l_{B}^{2} k^{2} + 2l_{B} k\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } } \right)^{1/2} }}. \\ \end{aligned}$$

(35)

If we only examine the influence of l_B, that is, let $\bar{a}$_3B= 0, Eq. (35) then further reduces to

$$\tan \left( {hk\sqrt {c^{2} /c_{A}^{2} - 1} } \right) = \frac{{\mu_{B} }}{{\mu_{A} }}\frac{{\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } \left( {1 + 2l_{B}^{2} k^{2} + l_{B} k\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } } \right)}}{{\sqrt {c^{2} /c_{A}^{2} - 1} \left( {1 + 2l_{B}^{2} k^{2} + 2l_{B} k\sqrt {1 + l_{B}^{2} k^{2} - c^{2} /c_{B}^{2} } } \right)^{1/2} }}.$$

(36)

Figure 6 shows the dimensionless dispersion curves for three cases (c_A/c_B= 0.5, 1, and 2) under the condition of d_B= 0, $\bar{a}$_3B= 0. For each case, the dispersion curves of Eq. (36) for l_B/h = 6, 4, 2, and 1, as well as the corresponding upper (short dash lines) and lower (dash lines) bounds, are depicted. It can be found that, for all the three cases (Fig. 6a–c), both the dispersion curves and the upper bounds decrease as l_B/h is decreasing; the dispersion curves lie between the upper and lower bounds, and vary gradually from the upper bounds to the lower bounds with the increase of the wave number. For the case c_A< c_B (Fig. 6a), as the decrease of l_B/h, the dispersion curves show three variations as the wave number is increasing: first increase then decrease (l_B/h = 6), first decrease then increase then decrease (l_B/h = 4), decrease in the whole range of the wave number (l_B/h = 2 and 1); and with the decrease of l_B/h, the dispersion curves approach that of a Love wave (l_B/h = 0). For the cases c_A≥ c_B (Fig. 6b, c), the dispersion curves show only one variation, that is, the dispersion curves first increase then decrease with the increase of the wave number. In addition, for the cases c_A≤ c_B (Fig. 6a, b), the dispersion curves exist in the whole range of the wave number; while for the case c_A> c_B (Fig. 6c) the dispersion curves only exist for the large wave numbers.

Fig. 6

Dispersion curves of the case that the surface layer is classical elastic while the half-space is strain-gradient elastic. Under the conditions of d_B= 0, $\bar{a}$_3B= 0, dispersion curves of l_B/h = 6, 4, 2, and 1 are depicted for three cases: a c_A< c_B, b c_A= c_B, and c c_A> c_B. The short dash lines represent the upper bounds, while the dash lines denote the lower bounds

Now we examine the influence of $\bar{a}_{3B}$. Under the condition of d_B= 0, l_B/h = 2, Fig. 7 demonstrates the dimensionless dispersion curves for three cases: c_A/c_B= 0.5, 1 and 2. For each case, the dispersion curves of Eq. (35) for $\bar{a}_{3B} /l_{B}^{2}$ = − 0.9, − 0.5, 0, 0.5, and 0.9, as well as their upper (short dash lines) and lower (dash lines) bounds, are depicted. It can be seen from Fig. 7a–c that, for all the three cases, the dispersion curves decrease with the increase of $\bar{a}_{3B} /l_{B}^{2}$ and almost coincide when $\bar{a}_{3B} /l_{B}^{2}$ ≤ − 0.5. The dispersion curves are located between the upper and lower bounds and gradually vary from the upper bounds to the lower bounds as the wave number is increasing. For the case c_A< c_B (Fig. 7a), as the increase of $\bar{a}_{3B} /l_{B}^{2}$, the dispersion curves show two variations as the wave number is increasing: first decrease then increase then decrease ($\bar{a}_{3B} /l_{B}^{2}$ = − 0.9 and − 0.5), decrease in the whole range of the wave number ($\bar{a}_{3B} /l_{B}^{2}$ = 0, 0.5 and 0.9). For the cases c_A≥ c_B (Fig. 7b, c), the dispersion curves show only one variation: first increase then decrease with the increase of the wave number. Besides, the dispersion curves exist in the whole range of the wave number for the cases c_A≤ c_B (Fig. 7a, b), while only exist in the large wave numbers for the case c_A> c_B (Fig. 7c).

Fig. 7

Dispersion curves of the case that surface layer is classical elastic while the half-space is strain-gradient elastic. Under the conditions of d_B= 0, l_B/h = 2, dispersion curves of $\bar{a}_{3B} /l_{B}^{2}$ = − 0.9, − 0.5, 0, 0.5, and 0.9 are depicted for three cases: a c_A< c_B, b c_A= c_B, and c c_A> c_B. The short dash lines represent the upper bounds, while the dash lines denote the lower bounds

5 Conclusions

In the present paper, we systematically studied the SH surface wave propagating in the strain-gradient elastic materials. Technically, we studied all the material combinations between the surface layer and the half-space. The procedure is straightforward, yet tedious. By introducing strain-gradient material constants, we observed rich dispersion phenomena in comparing with the traditional Love wave. The most attractive phenomenon in the outcome of this paper is that the upper and lower bounds of the SH surface waves are no longer two straight lines. This leads to the fact that SH surface waves no longer exist in all the wave numbers. Instead, SH surface waves exist for certain ranges of the wave number, see Fig. 3c, d, as well as Fig. 4c, d. This new finding hints that a “filter” can be proposed for letting surface waves with big or small wave number pass through and block the rest of the surface waves. Surface layers with microstructures/micropatterns are used more and more widely, and modeling them as gradient elastic materials is increasingly accepted by people. The present study may shed some light on possible engineering applications in this area.

Appendix: Mindlin’s Form II gradient elasticity theory

We introduce some basic equations of Mindlin’s Form II gradient elasticity theory (strain gradient elasticity theory). For the details of this theory, readers can refer to the original paper of Mindlin [4].

For a material composed wholly of unit cells (cubes), the kinetic energy density can be obtained with respect to a Cartesian coordinate system Ox₁x₂x₃ as

$$T = \frac{1}{2}\rho \dot{u}_{j} \dot{u}_{j} + \frac{1}{6}\rho d^{2} \left( {\partial_{i} \dot{u}_{j} } \right)\left( {\partial_{i} \dot{u}_{j} } \right),$$

(37)

where ρ is the density of the material, 2d is the length of edges of a cube, u_j are the components of displacement, ∂_i() ≡ ∂()/∂x_i, and the overhead dot denotes the derivative with respect to time t. The Latin indices span the range (1, 2, 3), and Einstein’s summation convention is applied for repeated indices.

If the material is isotropic, the strain energy density can be written as

$$W = \frac{1}{2}\lambda \varepsilon_{ii} \varepsilon_{jj} + \mu \varepsilon_{ij} \varepsilon_{ij} + a_{1} \kappa_{iik} \kappa_{kjj} + a_{2} \kappa_{ijj} \kappa_{ikk} + a_{3} \kappa_{iik} \kappa_{jjk} + a_{4} \kappa_{ijk} \kappa_{ijk} + a_{5} \kappa_{ijk} \kappa_{kji} ,$$

(38)

where λ and μ are the classical Lamé constants, a₁, …, a₅ are five additional material constants,

$$\varepsilon_{ij} = \frac{1}{2}\left( {\partial_{i} u_{j} + \partial_{j} u_{i} } \right) = \varepsilon_{ji} ,$$

(39)

is the strain tensor, and

$$\kappa_{ijk} = \partial_{i} \varepsilon_{jk} = \kappa_{ikj} $$

(40)

is the strain gradient tensor.

From Eq. (38), the constitutive equations can be derived as

$$\tau_{ij} = \frac{\partial W}{{\partial \varepsilon_{ij} }} = \lambda \delta_{ij} \varepsilon_{kk} + 2\mu \varepsilon_{ij} = \tau_{ji} ,$$

(41)

$$\begin{aligned} & \mu_{ijk} = \frac{\partial W}{{\partial \kappa_{ijk} }} = \frac{1}{2}a_{1} \left( {\delta_{ij} \kappa_{kll} + 2\delta_{jk} \kappa_{lli} + \delta_{ik} \kappa_{jll} } \right) + 2a_{2} \delta_{jk} \kappa_{ill} \\ & \quad + a_{3} \left( {\delta_{ij} \kappa_{llk} + \delta_{ik} \kappa_{llj} } \right) + 2a_{4} \kappa_{ijk} + a_{5} \left( {\kappa_{kij} + \kappa_{jki} } \right) = \mu_{ikj} , \\ \end{aligned}$$

(42)

where τ_ij is the Cauchy stress tensor, μ_ijk is the double stress tensor, and δ_ij is the Kronecker delta. The total stress is defined as

$$\sigma_{jk} = \tau_{jk} - \partial_{i} \mu_{ijk} ,$$

(43)

which is symmetric since both the Cauchy stress tensor τ_jk and the relative stress tensor ∂_iμ_ijk are symmetric according to Eqs. (41) and (42).

We assume that the material occupies a region V bounded by a smooth surface S. In the case of no body forces, the variational form of Hamilton’s principle can be written as

$$\int_{{t_{0} }}^{{t_{1} }} {\left( {\int_{V} {\delta W{\text{d}}V} - \int_{V} {\delta T{\text{d}}V} } \right){\text{d}}t} = \int_{{t_{0} }}^{{t_{1} }} {\left( {\int_{S} {P_{k} \delta u_{k} {\text{d}}S} + \int_{S} {R_{k} D\delta u_{k} {\text{d}}S} } \right){\text{d}}t} ,$$

(44)

where δ denotes the weak variation and acts on the ensuing physical quantities, t₀ and t₁ are two arbitrary instants of time at which the variations δu_k are zero at all points of the material,

$$P_{k} = n_{j} \left( {\tau_{jk} - \partial_{i} \mu_{ijk} } \right) - D_{j} \left( {n_{i} \mu_{ijk} } \right) + \left( {D_{l} n_{l} } \right)n_{i} n_{j} \mu_{ijk} + \frac{1}{3}\rho d^{2} D\ddot{u}_{k} ,$$

(45)

and

$$R_{k} = n_{i} n_{j} \mu_{ijk} ,$$

(46)

are, respectively, the auxiliary force traction and auxiliary double force traction on the surface, n_j are the components of the outward unit vector normal to the surface, D() ≡ n_l∂_l() and D_j() ≡ ∂_j() − n_jD() are, respectively, the normal gradient operator and surface gradient operator, and the overhead two dots denotes the second derivative with respect to time.

From the variational equation of motion (Eq. 44), the stress equations of motion can be derived as

$$\partial_{j} \left( {\tau_{jk} - \partial_{i} \mu_{ijk} } \right) = \rho \ddot{u}_{k} - \frac{1}{3}\rho d^{2} \partial_{j} \left( {\partial_{j} \ddot{u}_{k} } \right).$$

(47)

Substituting Eqs. (39) and (40) into Eqs. (41) and (42) and the latter into Eq. (47), the displacement equation of motion can be obtained as

$$\left( {\lambda { + 2}\mu } \right)\left( {1 - l_{1}^{2} \nabla^{2} } \right)\nabla \nabla \cdot {\mathbf{u}} - \mu \left( {1 - l_{2}^{2} \nabla^{2} } \right)\nabla \times \nabla \times {\mathbf{u}} = \rho {\ddot{\mathbf{u}}} - I\nabla^{2} {\ddot{\mathbf{u}}},$$

(48)

where u is the displacement vector,

$$\begin{array}{*{20}c} {l_{1} = \sqrt {\frac{{2\left( {a_{1} + a_{2} + a_{3} + a_{4} + a_{5} } \right)}}{{\lambda { + 2}\mu }}} ,} & {l_{2} = \sqrt {\frac{{a_{3} + 2a_{4} + a_{5} }}{ 2\mu }} ,} \\ \end{array}$$

(49)

are two characteristic lengths related to the strain energy, I = ρd²/3 is the micro-inertia coefficient, the symbols “$\nabla$” and “$\nabla^{2}$” are, respectively, the gradient operator and Laplacian operator, and “$\cdot$” and “$\times$” denote the dot product and cross product, respectively.