Nonlinear Modulation of Surface SH Waves in a Double Layered Elastic Half Space

Abstract

The nonlinear shear horizontal (SH) surface waves in an elastic half space coated with two different layers of uniform thickness are examined. The half space and both layers are assumed to be homogeneous, isotropic, incompressible, elastic and having different mechanical properties. In the analysis it is assumed that linear shear velocity of the top layer is slower than velocities of the internal layer and the half space. By employing the method of multiple scales, it is shown that nonlinear modulation of SH waves is governed asymptotically by a nonlinear Schrödinger (NLS) equation. The coefficients of this equation depend on, in a complicated way, on linear and nonlinear material parameters of the layered half space, the thicknesses of the layers and also the wave number of the waves. The effect of the existence of a second layer on the existence of solitary waves has been investigated numerically. Also a comparison between the coefficients of the NLS equation for the double layered half space and that of a single layered half space has been made. It is remarked that the existence of the envelope and dark solitons is affected strongly by the nonlinear material parameter of the top layer.

1 Introduction

Linear elastic waves in wave guides made by homogeneous isotropic linear elastic materials are dispersive due to the repeated reflection processes which occur at the boundaries between different media. Dispersive elastic waves have been extensively studied because of their important applications in geophysics, nondestructive testing of materials, electronic signal processing devices, etc. (see, e.g. [2, 6, 7] and references there in). In recent years, connected with these applications, the effect of the constitutional nonlinearities on the propagation characteristics of dispersive elastic waves is investigated by employing the asymptotic perturbation methods previously used in the fields of fluid mechanics, lattice dynamics, plasma physics etc., examining the propagation of weakly nonlinear waves (see, e.g. [1, 4, 10, 28]). In these investigations, as a result of balance between nonlinearity and dispersion several different types of nonlinear evolution equations such as Korteweg–de Vries (K–dV), modified K–dV, NLS and Boussinesq (BE), etc. have been derived to describe the propagation of nonlinear elastic waves in media having boundaries causing dispersion such as rods, plates, layered half spaces, etc., asymptotically. Then several aspects of problems, such as nonlinear stability of modulated waves, steady state solutions, the existence of various types of solitary waves, etc. were discussed on the basis of these equations. (see e.g. [3, 8, 13, 14, 20, 21, 23, 25,26,27]). For an extensive review of most of these works we refer [15,16,17,18,19, 22].

In the present work, the propagation of nonlinear shear horizontal (SH) waves in a half space covered by two homogenous isotropic incompressible elastic layers having different mechanical properties is considered. The corresponding linear problem has been firstly examined by Stoneley and Tillotson [24] since it is a theoretical basis of a method which is developed in order to calculate the thickness of the subcontinental layer. Firstly, [9] calculated the thickness of the subcontinental layer of granite overlying a half space of rock. Stoneley and Tillotson [24] claimed that Jeffrey’s study was inadequate, since the existence of a basalt layer under the granite was not regarded, hence they have constituted a two layered half space model on the assumption that the half space, the internal layer and the top layer consist of rock, basalt and granite, respectively. In this analysis it was assumed that between the linear shear velocities of the top layer $c_1$, the internal layer, $c_2$, and the half space, $c_3$, the inequality $c_1< c_2< c_3$ is valid. If the phase velocity c of the wave satisfies either the condition $c_1< c_2< c < c_3$ or the one $c_1< c< c_2 < c_3$, it is shown that a surface wave propagates. Under these two conditions, the present work extends this study to the nonlinear propagation of the surface SH waves. The constituent materials are assumed to be generalized neo-Hookean materials having different mechanical properties. In the linear limit, the problem reduces to the problem investigated by Stoneley and Tillotson [24]. Then the propagation of small but finite amplitude waves is considered. By employing a multiple scale perturbation method (see, e.g. [10]), an NLS equation is obtained for the nonlinear modulation of the waves. The coefficients of this equation depend on linear and nonlinear material parameters of the layered half space, the thickness ratio of the layers and also the wave number of the waves. It is also observed that when the thickness of the top layer goes to zero, the coefficients of the NLS equation approach to those of the NLS equation for a single layered half space. Then, since the properties of solutions of the NLS equation strongly depend on the sign of the product of its coefficients, the variation of this product with the wave number is evaluated numerically by giving appropriate values to the material constants and to the thickness ratio of the layers. To observe the effect of nonlinearity on the coefficients, consequently on the solutions of the NLS equation, the linear material constants are held fixed while the nonlinear ones are being changed. From the comparison of the coefficients of the NLS equations for a double layered half space and a single layered half space, it is observed that the propagation is affected considerably by the existence of a second layer. Moreover, for relatively long waves the nonlinear properties of the half space dominate the modulation of the waves.

2 Formulation of the Problem

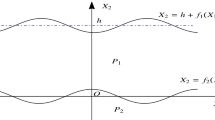
Let $(x_1,x_2,x_3)$ and $(X_1,X_2,X_3)$ be, respectively, the spatial and material coordinates of a point referred to the same rectangular Cartesian system of axes. Consider an elastic half space covered by two different elastic layers each of uniform thickness. In the reference frame $(X_1,X_2,X_3)$, the top layer $(R_1)$, the intermediate layer $(R_2)$ and the half space $(R_3)$ occupy the regions, respectively

$$\begin{aligned} R_{1}= & {} \{(X_1,X_2,X_3)\mid 0< X_2< h_{1} \quad -\infty< X_1< \infty , \quad -\infty< X_3< \infty \} \end{aligned}$$

(1)

$$\begin{aligned} R_{2}= & {} \{(X_1,X_2,X_3)\mid -h_{2}< X_2< 0 \quad -\infty< X_1< \infty , \quad -\infty< X_3< \infty \} \end{aligned}$$

(2)

$$\begin{aligned} R_{3}= & {} \{(X_1,X_2,X_3)\mid -\infty< X_2< -h_{2} \quad -\infty< X_1< \infty , \quad -\infty< X_3< \infty \} \end{aligned}$$

(3)

where $h_{1}$ and $h_{2}$ are positive constants. It is assumed that the free boundary $X_2=h_{1}$ is free of traction, the stresses and displacements are continuous at the interfaces $X_2=0$ and $X_2=-h_{2}$; moreover the displacement in the half space goes to zero as $X_2\rightarrow -\infty$.

Now, we consider a shear horizontal (SH) wave propagating along the $X_1$-axis in this layered half space described by the equations

$$\begin{aligned} x_1=X_1,\quad x_2=X_2, \quad x_3= X_3 +u^{(r)}(X_1,X_2,t) \quad r=1,2,3 \end{aligned}$$

(4)

where t is the time, the superscript r refers to the region $R_{r}$, $u^{(r)}$ is the displacement of a particle in the $X_3$ direction in the region $R_{r}$. Since $det x_{k,K}=1$, the deformation field (4) is isochoric and the density $\rho ^{(r)}$ in motion remains constant. Then in the absence of body forces, the equations of motion in the reference state are written as

$$\begin{aligned} T_{K\beta ,K}^{(r)}= 0, \quad \beta =1,2; \quad \quad T_{K3,K}^{(r)}=\rho ^{(r)}\ddot{u}^{(r)},\quad r=1,2,3 \end{aligned}$$

(5)

where $T_{Kl}^{(r)}$ is the first Piola-Kirchoff stress tensor, Latin and Greek indices take the respective ranges (1, 2, 3) and (1, 2), subscripts preceded by a comma indicate partial differentiation with respect to the material coordinates and an over dot represents the partial differentiation with respect to t.

The assumption of vanishing tractions on the free surface $X_2=h_1$ imposes the boundary condition

$$\begin{aligned} T_{2k}^{(1)}= 0, \quad \hbox {on} \quad X_2=h_1, \end{aligned}$$

(6)

while continuity of stresses and displacements at the interfaces $X_2=0$ and $X_2=-h_2$ is satisfied if

$$\begin{aligned} T_{2k}^{(1)}= T_{2k}^{(2)}, \quad \hbox {and} \quad u^{(1)}=u^{(2)} \quad \hbox {on} \quad X_2=0, \end{aligned}$$

(7)

and

$$\begin{aligned} T_{2k}^{(2)}= T_{2k}^{(3)}, \quad \hbox {and} \quad u^{(2)}=u^{(3)} \quad \hbox {on} \quad X_2=-h_2, \quad k=1,2,3. \end{aligned}$$

(8)

In this work, it is assumed that the constituent materials are homogenous, nonlinear, isotropic, incompressible elastic and their strain energy functions are only the functions of the first invariant of Finger deformation tensor $\mathbf c ^{-1 }=[x_{k,K} x_{l,K}]$, i.e. $\Sigma ^{(r)}=\Sigma ^{(r)}(I^{(r)})$ where $I^{(r)}=tr \mathbf c ^{-1}$, $r=1,2,3$. Namely, the double layered half space is made of generalized neo-Hooken materials (see, e.g. [11]). For the antiplane motion (4), the first invariants $I^{(r)}$ are found to be

$$\begin{aligned} I^{(r)}=3+\mathcal {K}^{(r)} \qquad \mathcal {K}^{(r)}=\left( \frac{\partial u^{(r)} }{\partial X_1}\right) ^2+\left( \frac{\partial u^{(r)}}{\partial X_2}\right) ^2 \quad r=1,2,3 \end{aligned}$$

(9)

Stress constitutive equations for a generalized neo-Hookean medium can be expressed as (see, e.g. [5])

$$\begin{aligned} t _{kl}=-p{\delta }_{kl}+ \Phi c_{kl}^{-1} \qquad \hbox {with}~~\Phi =2\frac{\partial \Sigma }{\partial I} \end{aligned}$$

(10)

where $t_{kl}$ is the components of Cauchy stress tensor and $p(X_K,t)$ is a hydrostatic pressure function. Then, by using the relation $T _{Kl}=j X_{K,k}t _{kl}$, where $j= det(x_{k,K})=1$, the components of the Piola-Kirchoff stress tensor are written as (see [26] for details)

$$\begin{aligned} T_{\alpha \beta }^{(r)}=T_{33}^{(r)}=0~,~~T_{\alpha 3}^{(r)}=T_{3 \alpha }^{(r)}=\Phi ^{(r)}u_{,\alpha }^{(r)} \end{aligned}$$

(11)

Hence the first two equations in (5) are satisfied identically and therefore the anti-plane motion (4) can exist in the double layered elastic half space made of generalized neo-Hooken materials without body forces. Let $X=X_1$, $Y=X_2$, $Z=X_3$, then the third equation in (5) and the boundary conditions of the problem can be written as

$$\begin{aligned} \frac{\partial }{\partial X}\left( \Phi ^{(r)}\frac{\partial u^{(r)}}{\partial X}\right) +\frac{\partial }{\partial Y}\left( \Phi ^{(r)}\frac{\partial u^{(r)}}{\partial Y}\right) =\rho ^{(r)} \frac{\partial ^{2}u^{(r)}}{\partial t^{2}} \quad r=1,2,3 \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial u^{(1)}}{\partial Y}=0 \quad \hbox {on the free boundary} \quad Y=h_{1} \end{aligned}$$

(13)

$$\begin{aligned} u^{(1)}=u^{(2)} \ \ \hbox {and} \ \ \Phi ^{(1)}\frac{\partial u^{(1)}}{\partial Y}=\Phi ^{(2)}\frac{\partial u^{(2)}}{\partial Y} \ \hbox {on} \ \ Y=0\ \text {(the interface between }R_1\text { and }R_2) \end{aligned}$$

(14)

$$\begin{aligned} u^{(2)}=u^{(3)} \ \ \hbox {and} \ \ \Phi ^{(2)}\frac{\partial u^{(2)}}{\partial Y}=\Phi ^{(3)}\frac{\partial u^{(3)}}{\partial Y} \ \ \hbox {on}\ Y=-h_{2}\ \text {(the interface between }R_2\text { and }R_3) \end{aligned}$$

(15)

$$\begin{aligned} u^{(3)} \rightarrow 0 \quad \hbox {as} \quad Y\rightarrow -\infty \ \ \hbox {(the radiation condition)} \end{aligned}$$

(16)

3 Small but Finite Amplitude Waves

We now examine the propagation of small but finite amplitude surface SH waves. To do this we will employ the method of multiple scales by introducing the following new independent variables

$$\begin{aligned} x_{i}=\epsilon ^{i}X, \quad t_{i}=\epsilon ^{i}t, \quad y=Y, \quad i=0,1,2 \end{aligned}$$

(17)

in which $\epsilon >0$ is a small parameter which measures the weakness of the nonlinearity and $(x_{1}, x_{2},t_{1},t_{2})$ are the slow variables describing the slow variations in the problem whereas $(x_{0}, t_{0},y)$ are fast variables describing the fast variations. Then $u^{(r)}$, $r=1,2,3,$ are taken to be functions of these new independent variables and they are expanded in the following asymptotic series in $\epsilon$:

$$\begin{aligned} u^{(r)}=\sum _{n=1}^{\infty }\epsilon ^{n}u_{n}^{(r)}(x_{0},x_{1}, x_{2},y,t_{0}, t_{1}, t_{2}) \end{aligned}$$

(18)

Writing the governing equations and boundary conditions in terms of the new independent variables (17) and then employing the expansions (18) in the resulting expressions and collecting the terms of like powers in $~\epsilon ~$ yield a hierarchy of problems from which it is possible to determine $u_{n}^{(r)}$, successively. Up to third order in $~\epsilon ~$ these are given as below:

$O(\epsilon )$:

$$\begin{aligned} L(u_{1}^{(r)})=\frac{\partial ^{2}u_{1}^{(r)}}{\partial t_{0}^{2}}-c_{r}^{2}\left( \frac{\partial ^{2}u_{1}^{(r)}}{\partial x_{0}^{2}}+\frac{\partial ^{2}u_{1}^{(r)}}{\partial y^{2}}\right) =0 \quad r=1,2,3 \end{aligned}$$

(19)

$$\begin{aligned}&\frac{\partial u_{1}^{(1)}}{\partial y}=0 \quad \hbox {at} \quad y=h_{1}\end{aligned}$$

(20)

$$\begin{aligned}&u_{1}^{(1)}=u_{1}^{(2)}\quad \text{ and }\quad \frac{\partial u_{1}^{(1)}}{\partial y}-\gamma _{1}\frac{\partial u_{1}^{(2)}}{\partial y}=0 \quad \hbox {at}\quad y=0\end{aligned}$$

(21)

$$\begin{aligned}&u_{1}^{(2)}=u_{1}^{(3)}\quad \text{ and } \quad \frac{\partial u_{1}^{(2)}}{\partial y}-\gamma _{2}\frac{\partial u_{1}^{(3)}}{\partial y}=0 \quad \hbox {at }\quad y=-h_{2}\end{aligned}$$

(22)

$$\begin{aligned}&u_{1}^{(3)}\rightarrow 0 \quad \hbox {as} \qquad y\rightarrow -\infty \end{aligned}$$

(23)

$O(\epsilon ^{2})$:

$$\begin{aligned} L(u_{2}^{(r)})=2\left( c_{r}^{2}\frac{\partial ^{2}u_{1}^{(r)}}{\partial x_{0} \partial x_{1}}-\frac{\partial ^{2}u_{1}^{(r)}}{\partial t_{0} \partial t_{1}}\right) \quad r=1,2,3 \end{aligned}$$

(24)

$$\begin{aligned}&\frac{\partial u_{2}^{(1)}}{\partial y}=0 \quad \hbox {at} \quad y=h_{1}\end{aligned}$$

(25)

$$\begin{aligned}&u_{2}^{(1)}=u_{2}^{(2)}\quad \text{ and }\quad \frac{\partial u_{2}^{(1)}}{\partial y}-\gamma _{1}\frac{\partial u_{2}^{(2)}}{\partial y}=0\quad \hbox {at} \quad y=0 \end{aligned}$$

(26)

$$\begin{aligned}&u_{2}^{(2)}=u_{2}^{(3)}\quad \text{ and } \quad \frac{\partial u_{2}^{(2)}}{\partial y}-\gamma _{2}\frac{\partial u_{2}^{(3)}}{\partial y}=0 \quad \hbox {at}\quad y=-h_{2}\end{aligned}$$

(27)

$$\begin{aligned}&u_{2}^{(3)}\rightarrow 0\quad \hbox {as} \qquad y\rightarrow -\infty \end{aligned}$$

(28)

$O(\epsilon ^{3})$:

$$\begin{aligned} L(u_{3}^{(r)})= & {} 2\left( c_{r}^{2}\frac{\partial ^{2}u_{2}^{(r)}}{\partial x_{0} \partial x_{1}}-\frac{\partial ^{2}u_{2}^{(r)}}{\partial t_{0} \partial t_{1}}\right) +c_{r}^{2}\left( \frac{\partial ^{2}u_{1}^{(r)}}{\partial x_{1}^{2}}+2\frac{\partial ^{2}u_{1}^{(r)}}{\partial x_{0}x_{2}}\right) -\frac{\partial ^{2}u_{1}^{(r)}}{\partial t_{1}^{2}}-2\frac{\partial ^{2}u_{1}^{(r)}}{\partial t_{0}t_{2}} \nonumber \\+ & {} n_{r}\left( \frac{\partial }{\partial x_{0}}\left( \frac{\partial u_{1}^{(r)}}{\partial x_{0}}\mathcal {K}_{0}(u_{1}^{(r)})\right) +\frac{\partial }{\partial Y}\left( \frac{\partial u_{1}^{(r)}}{\partial Y}\mathcal {K}_{0}(u_{1}^{(r)})\right) \right) \quad r=1,2,3 \end{aligned}$$

(29)

$$\begin{aligned}&\frac{\partial u_{3}^{(1)}}{\partial y}=0 \quad \hbox {at} \quad y=h_{1}\end{aligned}$$

(30)

$$\begin{aligned}&u_{3}^{(1)}=u_{3}^{(2)}\quad \hbox {and} \nonumber \\&\frac{\partial u_{3}^{(1)}}{\partial y}-\gamma _{1}\frac{\partial u_{3}^{(2)}}{\partial y}=\gamma _{1}\beta _{2}\frac{\partial u_{1}^{(2)}}{\partial y}\mathcal {K}_{0}(u_{1}^{(2)})-\beta _{1}\frac{\partial u_{1}^{(1)}}{\partial y}\mathcal {K}_{0}(u_{1}^{(1)})\quad \hbox {at}\quad y=0 \end{aligned}$$

(31)

$$\begin{aligned}&u_{3}^{(2)}=u_{3}^{(3)}\quad \hbox {and} \nonumber \\&\frac{\partial u_{3}^{(2)}}{\partial y}-\gamma _{2}\frac{\partial u_{3}^{(3)}}{\partial y}=\gamma _{2}\beta _{3}\frac{\partial u_{1}^{(3)}}{\partial y}\mathcal {K}_{0}(u_{1}^{(3)})-\beta _{2}\frac{\partial u_{1}^{(2)}}{\partial y}\mathcal {K}_{0}(u_{1}^{(2)})\quad \hbox {at}\quad y=-h_{2} \end{aligned}$$

(32)

$$\begin{aligned}&u_{3}^{(3)}\rightarrow 0\quad \hbox {as} \quad y\rightarrow -\infty \end{aligned}$$

(33)

where

$$\begin{aligned} \mathcal {K}_{0}(\psi )=\left( \frac{\partial \psi }{\partial x_{0}}\right) ^{2}+\left( \frac{\partial \psi }{\partial y}\right) ^{2}~. \end{aligned}$$

(34)

In the above equations the constants $c_{r}$, $r=1,2,3$ are the linear shear velocities in the top layer, intermediate layer and half space, respectively, and they are defined as $c_{r}^{2}=\mu ^{(r)}/\rho ^{(r)}$ where $\mu ^{(r)}$ are linear shear modulus given as $\mu ^{(r)}=2 d\Sigma ^{(r)}(3)/dI$. $n_r$ defined as $n_r=(2/\rho ^{(r)})d^2 \Sigma ^{(r)}(3)/dI^{2}$ are nonlinear material constants. If $n_r>0$, the relevant medium is hardening in shear, else it is softening. The constants $\gamma _r$ and $\beta _r$ are defined as $\gamma _{r}=\mu ^{(r+1)}/\mu ^{(r)}$, $\beta _{r}=n_{r}/c_{r}^2$. Note that, these perturbation problems, at each step, are linear and first order problem is simply the classic linear wave problem which was first investigated by Stoneley and Tillotson [24]. They showed that between the linear shear velocities of the layers and the half space if the inequalities $~c_1<c_2<c_3$ hold then when the phase velocity  c  of the SH wave satisfies the either inequality

$$\begin{aligned} c_1< c_2<c<c_3\qquad \hbox {or} \qquad c_1<c< c_2<c_3 \end{aligned}$$

(35)

then SH waves are dispersive. We proceed first by assuming that the first inequality is satisfied by the phase velocity c of the surface SH wave.We also assume that the nonexistence of the long waves in the initial disturbances. Hence by using the separation of variables method and also by employing the radiation conditions (23), the solutions of the Eqs. (19) are found to be

$$\begin{aligned} u_{1}^{(1)}= & {} \sum _{l=1}^{\infty }\left\{ A_{1}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{ilkp_{1}y} +B_{1}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{-ilkp_{1}y}\right\} e^{il\theta }+c.c \qquad \qquad \end{aligned}$$

(36)

$$\begin{aligned} u_{1}^{(2)}= & {} \sum _{l=1}^{\infty }\left\{ C_{1}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{ilkp_{2}y} +D_{1}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{-ilkp_{2}y}\right\} e^{il\theta }+c.c \qquad \qquad \end{aligned}$$

(37)

$$\begin{aligned} u_{1}^{(3)}= & {} \sum _{l=1}^{\infty } E_{1}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{lkv_{3}y}e^{il\theta }+c.c \end{aligned}$$

(38)

where

$$\begin{aligned} \theta =kx_0-\omega t_0~,~~p_1=(c^2/c_1^2-1)^{1/2}~,~~p_2=(c^2/c_2^2-1)^{1/2}~,~~ {v}_3=(1-c^2/c_3 ^2)^{1/2}~ \end{aligned}$$

(39)

and  k  is the wave number, $~\omega ~$ is the angular frequency, $~c=\omega / k~$ is the phase velocity, the symbol $~''c.c.''~$ denotes the complex conjugate of the preceding terms, $~A_1^{(l)},~B_1^{(l)},~C_1^{(l)}$, $~D_1^{(l)}~$and $~E_1^{(l)}~$ are the first order slowly varying amplitude functions of the waves to be determined by using the boundary conditions of the first order perturbation problem. Hence the substitution of first order solutions into the boundary conditions of the first order perturbation problem yields

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_1^{(l)}=\mathbf{0}, \quad l=1,2,\ldots , \end{aligned}$$

(40)

where $~\mathbf{W}_l~$ is the dispersion matrix defined as

$$\begin{aligned} \mathbf W _{l}=\left( \begin{array}{ccccc} iklp_{1}e^{ilP_{1}} &{} -iklp_{1}e^{-ilP_{1}} &{} 0 &{} 0 &{} 0 \\ iklp_{1} &{} -iklp_{1} &{} -i\gamma _{1}klp_{2} &{} i\gamma _{1}klp_{2} &{} 0 \\ 1 &{} 1 &{} -1 &{} -1 &{} 0 \\ 0 &{} 0 &{} iklp_{2}e^{-il P_{2}} &{} -iklp_{2}e^{il P_{2}} &{} -\gamma _{2}klv_{3}e^{-lV_{3}} \\ 0 &{} 0 &{} e^{-i lP_{2}} &{} e^{il P_{2}} &{} -e^{-lV_{3}} \\ \end{array} \right) \end{aligned}$$

(41)

and the vectors $~\mathbf{U}_n^{(l)}~,~~n=1,2,\ldots ,$ are defined as

$$\begin{aligned} \mathbf{U}_n^{(l)}=(A_n^{(l)},B_n^{(l)},C_n^{(l)},D_n^{(l)}, E_n^{(l)} )^T~~. \end{aligned}$$

(42)

$\det \mathbf{W}_1=0~$ gives the dispersion relation of the linear waves

$$\begin{aligned} p_{1}p_{2}\tan P_{1}+\gamma _{2}p_{1}v_{3}\tan P_{1}\tan P_{2}-\gamma _{1}\gamma _{2}p_{2}v_{3}+\gamma _{1} p_{2}^{2}\tan P_{2}=0 \end{aligned}$$

(43)

where $P_{1}=k p_1 h_1$, $P_2=k p_2 h_2$, which is first derived by [24]. Note that, when the thickness of the top layer goes to zero, $h_1=0$, this dispersion relation reduces to

$$\begin{aligned} -\gamma _{2}p_{2}v_{3}+ p_{2}^{2}\tan P_{2}=0 \end{aligned}$$

(44)

which is the dispersion relation obtained for the propagation of Love waves in a half space covered by a single layer [12]. In this work, nonlinear self modulation of a group of surface SH-waves centered around a wave number k and corresponding frequency $\omega$ is investigated. Thus the harmonic-resonance phenomena is excluded in the analysis. Then for $~l\ge 2~$

$$\begin{aligned} \det \mathbf{W}_l\ne 0~~. \end{aligned}$$

(45)

Hence, considering (45) the solutions of the homogeneous algebraic systems are found to be

$$\begin{aligned} \mathbf{U}_1^{(1)}= & {} {\mathcal A}_1(x_1,x_2,t_1,t_2)\mathbf{R}~\end{aligned}$$

(46)

$$\begin{aligned} \mathbf{U}_1^{(l)}\equiv & {} \mathbf{0}~~~~\text{ for }~~~~l\ge 2 \end{aligned}$$

(47)

where $~{\mathcal A}_1~$ is a complex function, representing the first order slowly varying amplitude of the self modulation and $~\mathbf{R}~$ is a column vector satisfying

$$\begin{aligned} ~\mathbf{W}_1\mathbf{R}=\mathbf{0}. \end{aligned}$$

(48)

By using (46) and (47) the first order solutions are written explicitly as

$$\begin{aligned} u_{1}^{(1)}= & {} {\mathcal A}_{1}(R_{1}e^{ikp_{1}y}+R_{2}e^{-ikp_{1}y})e^{i\theta }+c.c\end{aligned}$$

(49)

$$\begin{aligned} u_{1}^{(2)}= & {} {\mathcal A}_{1}(R_{3}e^{ikp_{2}y}+R_{4}e^{-ikp_{2}y})e^{i\theta }+c.c \end{aligned}$$

(50)

$$\begin{aligned} u_{1}^{(3)}= & {} {\mathcal A}_{1}R_{5}e^{kv_{3}y}e^{i\theta }+c.c \end{aligned}$$

(51)

where $~R_m~,~m=1,\ldots ,5~$ are the components of $~\mathbf{R}$, their explicit forms are given in the Appendix A.

To complete the first order solutions ${\mathcal A}_{1}$ has to be determined. This has been done by examining the higher order perturbation problems. Using the first order solutions in the differential equations of the second order perturbation problem yields

$$\begin{aligned} L(u_{2}^{(1)})= & {} 2i {M}_{11}^{(1)}(R_{1}e^{ikp_{1}y}+R_{2}e^{-ikp_{1}y})e^{i\theta }+c.c\end{aligned}$$

(52)

$$\begin{aligned} L(u_{2}^{(2)})= & {} 2i {M}_{11}^{(2)}(R_{3}e^{ikp_{2}y}+R_{4}e^{-ikp_{2}y})e^{i\theta }+c.c \end{aligned}$$

(53)

$$\begin{aligned} L(u_{2}^{(3)})= & {} 2i {M}_{11}^{(3)}R_{5}e^{kv_{3}y}e^{i\theta }+c.c \end{aligned}$$

(54)

where

$$\begin{aligned} {M}_{11}^{(\alpha )}=\omega \frac{\partial {\mathcal A}_{1} }{\partial t_{1}}+kc_{\alpha }^{2}\frac{\partial {\mathcal A}_{1} }{\partial x_{1}}, \quad \alpha =1,2,3 \end{aligned}$$

(55)

The solutions $u_{2}^{(r)}$, $r=1,2,3$, of this problem are decomposed as

$$\begin{aligned} u_{2}^{(r)}=\bar{u}_{2}^{(r)}+\tilde{u}_{2}^{(r)} \end{aligned}$$

(56)

where $~{\overline{u}}_2^{(r)}$, $r=1,2,3$, are the particular solutions of the nonhomogeneous differential equations while $~{\widetilde{u}}_2 ^{(r)}$ are the solutions of the corresponding homogeneous equations satisfying the nonhomogeneous boundary conditions derived from the boundary conditions of the second order perturbation problem by considering the decompositions (56). The solutions $~{\overline{u}}_2^{(r)}$ are found by the method of undetermined coefficients. For $~{\widetilde{u}}_2^{(r)}$ the solutions satisfying the radiation condition are written as in the first order problem

$$\begin{aligned} {\widetilde{u}}_{2}^{(1)}= & {} \sum _{l=1}^{\infty }\left\{ A_{2}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{ilkp_{1}y} +B_{2}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{-ilkp_{1}y}\right\} e^{il\theta }+c.c. \end{aligned}$$

(57)

$$\begin{aligned} {\widetilde{u}}_{2}^{(2)}= & {} \sum _{l=1}^{\infty }\left\{ C_{2}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{ilkp_{2}y} +D_{2}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{-ilkp_{2}y}\right\} e^{il\theta }+c.c. \end{aligned}$$

(58)

$$\begin{aligned} {\widetilde{u}}_{2}^{(3)}= & {} \sum _{l=1}^{\infty } E_{2}^{(l)}(x_{1},x_{2},t_{1},t_{2})e^{lkv_{3}y}e^{il\theta }+c.c. \end{aligned}$$

(59)

The second order slowly varying amplitudes $\mathbf{U}_2^{(l)}=(A_2^{(l)},B_2^{(l)},C_2^{(l)},D_2^{(l)},E_2^{(l)})^{T}$ of the waves are determined by employing the nonhomogeneous boundary conditions. Then the use of $~{\widetilde{u}}_2^{(r)}$ together with the solutions $~{\overline{u}}_2^{(r)}$, $r=1,2,3$, in the boundary conditions of the second order problem yields the following systems of algebraic equations

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_2^{(l)}=\mathbf{b}_2^{(l)} \end{aligned}$$

(60)

where

$$\begin{aligned} \mathbf{{b}}_2^{(1)}=-i\left( \frac{\partial {\mathcal {A}}_1}{\partial t_1} \frac{\partial \mathbf{{W}}_1}{\partial {\omega }}-\frac{\partial {\mathcal {A}}_1}{\partial x_1} \frac{\partial \mathbf{{W}}_1}{\partial k}\right) \mathbf{{R}}~~~\text{ and }~~~\mathbf{b}_2^{(l)}\equiv \mathbf{0}~~~\text{ for } \text{ all }~~~l\ne 1~~ \end{aligned}$$

(61)

Since it is assumed that $~\det \mathbf{W}_l\ne 0~$ for $l\ge 2$, for these cases the solutions of (60) are

$$\begin{aligned} \mathbf{U}_2^{(l)}\equiv \mathbf{0}, \quad l\ge 2 \end{aligned}$$

(62)

Since $~\det \mathbf{W}_1=0~$ and $~\mathbf{b}_2^{(1)}\ne \mathbf{0}$, in order that the Eq. (60) to have a solution for $~\mathbf{U}_2^{(1)}~$ the compatibility condition

$$\begin{aligned} \mathbf{L}.\mathbf{b}_2^{(1)}=0 \end{aligned}$$

(63)

must be satisfied, where $~\mathbf{L}~$ is a left vector defined by $~\mathbf {L}\mathbf {W}_1=\mathbf{{0}}$. Then the compatibility condition (63) leads to the result

$$\begin{aligned} \frac{\partial {\mathcal {A}}_1}{\partial t_1}+V_g\frac{\partial {\mathcal {A}}_1}{\partial x_1}=0~~ \end{aligned}$$

(64)

where $V_g=\frac{d{\omega }}{dk}=-\left( \mathbf {L} \frac{\partial \mathbf {W}_{1}}{\partial k}\mathbf {R}\right) /\left( \mathbf {L} \frac{\partial \mathbf {W}_{1}}{\partial \omega }\mathbf {R}\right)$ is the group velocity of the waves. The Eq. (64) implies that the amplitude $~{\mathcal {A}}_1$ remains constant in a frame of reference moving with the group velocity $~V_g$. That is, ${\mathcal {A}}_1={\mathcal {A}}_1(x_1-V_gt_1,x_2,t_2)$. Then $~\mathbf{U}_2^{(1)}~$ is found to be

$$\begin{aligned} \mathbf{U}_2^{(1)}={\mathcal {A}}_2 \mathbf{R}-i\frac{\partial {\mathcal {A}}_1}{\partial x_1}\left( \frac{\partial \mathbf{R}}{\partial k}+V_g\frac{\partial \mathbf{R}}{\partial {\omega }}\right) \end{aligned}$$

(65)

where $~{\mathcal A}_2={\mathcal {A}}_2(x_1,x_2,t_1,t_2)~$ is a complex function representing the second order slowly varying amplitude of the wave modulation, and it can be determined from higher-order perturbation problems. But, since this work is centered around the small but finite amplitude waves, the aim is here to obtain just the uniformly valid first-order solution. Note that, we assume that ${\mathcal {A}}_2$ depends on $x_1$ and $t_1$ through the combination $x_1 - V_g t_1$ as ${\mathcal {A}}_1$, so it is not necessary to evaluate $~{\mathcal {A}}_2$, it is sufficient to determinate $~{\mathcal {A}}_1~$ only to obtain the first order solution, and this will be done at the third order perturbation problem. The substitution of the first and second order solutions into the third order equations (29) gives

$$\begin{aligned} L(u_{3}^{(1)})= & {} (\mathcal {D}_{1}e^{ikp_{1}y}+\mathcal {D}_{2}ye^{ikp_{1}y}+\mathcal {D}_{3}e^{-ikp_{1}y}+\mathcal {D}_{4}ye^{-ikp_{1}y}\nonumber \\&+\mathcal {D}_{5}e^{3ikp_{1}y} +\mathcal {D}_{6}e^{-3ikp_{1}y})e^{i\theta }+ c.c. +\,\text {terms in }\,({e^{\pm 3i\theta }}), \end{aligned}$$

(66)

$$\begin{aligned} L(u_{3}^{(2)})= & {} (\mathcal {D}_{7}e^{ikp_{2}y}+\mathcal {D}_{8}ye^{ikp_{2}y}+\mathcal {D}_{9}e^{-ikp_{2}y}+\mathcal {D}_{10}ye^{-ikp_{2}y}\nonumber \\&+\mathcal {D}_{11}e^{3ikp_{2}y} +\mathcal {D}_{12}e^{-3ikp_{2}y})e^{i\theta }+ c.c. +\,\text {terms in }\,({e^{\pm 3i\theta }}) \end{aligned}$$

(67)

$$\begin{aligned} L(u_{3}^{(3)})= (\mathcal {D}_{13}e^{kv_{3}y}+\mathcal {D}_{14}ye^{kv_{3}y}+\mathcal {D}_{15}e^{3kv_{3}y})e^{i\theta }+ c.c. +\,\text {terms in }\,({e^{\pm 3i\theta }}) \end{aligned}$$

(68)

The explicit forms of the coefficients $\mathcal {D}_{i}$, $i=1,\ldots ,15$ will be given in the Appendix B. The solutions of the third order problem can be sought as in the second order problem. That is we decompose the solutions as

$$\begin{aligned} u_{3}^{(r)}=\bar{u}_{3}^{(r)}+\tilde{u}_{3}^{(r)},\quad r=1,2,3 \end{aligned}$$

(69)

where $~{\overline{u}}_3^{(r)}$, $r=1,2,3$, are the particular solutions found by using the method of undetermined coefficients. ${\widetilde{u}}_3^{(r)}$, $r=1,2,3$, the solutions of the corresponding homogenous equations satisfying the nonhomogeneous boundary conditions (30)–(33) are written as in the second order problem replacing $~\mathbf{U}_2^{(l)}~$ by $~\mathbf{U}_3^{(l)}~$ respectively in (57)–(59). $~\mathbf{U}_3^{(l)}=(A_3^{(l)},B_3^{(l)},C_3^{(l)},D_3^{(l)},E_3^{(l)})^T~$ are third order amplitude functions depending on the slow variables ${x_1,x_2,t_1,t_2}$.

The particular solutions $~{\bar{u}}_3^{(r)}$, $r=1,2,3$, can be expressed as a sum of linearly independent terms of the forms

$$\begin{aligned} \bar{u}_{3}^{(r)}=f_{r}^{(1)}(x_{1},x_{2},t_{1},t_{2})e^{i\theta }+f_{r}^{(3)}(x_{1},x_{2},t_{1},t_{2})e^{3i\theta }+c.c. \quad r=1,2,3 \end{aligned}$$

(70)

where the terms $f_{r}^{(1)}$, $r=1,2,3$, are related with the self-interaction of the waves while the terms $f_{r}^{(3)}$, $r=1,2,3$, are representing the third harmonic interaction effects. Since, we are only interested in the self interaction, the explicit form of term $f_{r}^{(3)}$, $r=1,2,3$, will not be required. Therefore, we only calculate $f_{r}^{(1)}$, $r=1,2,3$. Hence, these solutions are obtained by the method of undetermined coefficients as

$$\begin{aligned} f_{1}^{(1)}= & {} (\mathcal {\varepsilon }_{1}+\mathcal {\varepsilon }_{2}y)ye^{ikp_{1}y}+(\mathcal {\varepsilon }_{3}+\mathcal {\varepsilon }_{4}y)ye^{-ikp_{1}y}+\mathcal {\varepsilon }_{5}e^{3ikp_{1}y}+\mathcal {\varepsilon }_{6}e^{-3ikp_{1}y}+c.c \end{aligned}$$

(71)

$$\begin{aligned} f_{2}^{(1)}= & {} (\mathcal {\varepsilon }_{7}+\mathcal {\varepsilon }_{8}y)ye^{ikp_{2}y}+(\mathcal {\varepsilon }_{9}+\mathcal {\varepsilon }_{10}y)ye^{-ikp_{2}y}+\mathcal {\varepsilon }_{11}e^{3ikp_{2}y}+\mathcal {\varepsilon }_{12}e^{-3ikp_{2}y}+c.c\qquad \end{aligned}$$

(72)

$$\begin{aligned} f_{3}^{(1)}= & {} (\mathcal {\varepsilon }_{13}+\mathcal {\varepsilon }_{14}y)ye^{kv_{3}y}+\mathcal {\varepsilon }_{15}e^{3kv_{3}y}+c.c \end{aligned}$$

(73)

Explicit forms of the $\mathcal {\varepsilon }_{i}$, $i=1,2,\ldots ,15$ are given in the Appendix B. Then, the use of these solutions together with $~{\overline{u}}_1^{(r)}$, and $~{\widetilde{u}}_1^{(r)}$, $r=1,2,3$, in the boundary conditions of the third-order problem yields the following systems of algebraic equations to determine $\mathbf{U}_3^{(l)}$’s;

$$\begin{aligned} \mathbf{W}_l~\mathbf{U}_3^{(l)}=\mathbf{b}_3^{(l)}~~. \end{aligned}$$

(74)

where $\mathbf{b}_3^{(1)}\ne \mathbf{0},$ $\mathbf{b}_3^{(3)}\ne \mathbf{0}$ and $\mathbf{b}_3^{(l)}\equiv \mathbf{0}$ for all $l\ne 1,3$, and $\mathbf{b}_3^{(1)}$ can be written as in the form

$$\begin{aligned}&\mathbf{b}_3^{(1)}=\left[ -i\left( \frac{\partial \mathbf{W}_1}{\partial \omega }\frac{\partial {\mathcal {A}}_1}{\partial {t_2}}-\frac{\partial \mathbf{W}_1}{\partial k}\frac{\partial {\mathcal {A}}_1}{\partial {x_2}} \right) +\frac{1}{2}\left( \frac{{\partial }^2\mathbf{W}_1}{\partial {\omega }^2}\frac{{\partial }^2{\mathcal {A}}_1}{\partial {t_1^2}}-2\frac{{\partial }^2\mathbf{W}_1}{{\partial k}{\partial {\omega }}}\frac{{\partial }^2{\mathcal {A}}_1}{{\partial {x_1}}{\partial {t_1}}}+\frac{{\partial }^2\mathbf{W}_1}{\partial {k^2}}\frac{{\partial }^2{\mathcal {A}}_1}{\partial {x_1^2}}\right) \right] \mathbf{R} \nonumber \\&+\left( \frac{\partial \mathbf{W}_1}{\partial k}\frac{{\partial }^2{\mathcal {A}}_1}{\partial x_1^2}-\frac{\partial \mathbf{W}_1}{\partial {\omega }}\frac{{\partial }^2{\mathcal {A}}_1}{{\partial {x_1}}{\partial {t_1}}}\right) \left( \frac{\partial \mathbf{R}}{\partial k}+V_g\frac{\partial \mathbf{R}}{\partial {\omega }}\right) +\mathbf{F}\mid {\mathcal {A}}_1{\mid }^2{\mathcal A}_1~~. \end{aligned}$$

(75)

where $~\mathbf{F}~$ is a constant vector depending on material parameters and the wave number k, their components are given in Appendix B. The explicit form of the vector $~\mathbf{b}_3^{(3)}~$ is not given, since it is not required for self modulation solution. Since we have assumed that $~\det \mathbf{W}_l\ne 0~$ for $~l\ne 1$ the solutions of (74) are found to be

$$ ~\mathbf{U}_3^{(3)}~=\mathbf{W}^{-1} \mathbf{b}_3^{(3)}\qquad \mathrm {and}\qquad \mathbf{U}_3^{(l)}\equiv 0 \quad \mathrm {for} \quad l\ne 1,3 $$

Since $~\det \mathbf{W}_1= 0$, in order that (74) has a solution for $~\mathbf{U}_3^{(1)}~$ the compatibility condition

$$\begin{aligned} \mathbf{L}.\mathbf{b}_3^{(1)}=0 \end{aligned}$$

(76)

must be satisfied. This compatibility condition yields the following nonlinear Schrödinger (NLS) equation

$$ i\frac{\partial \mathcal {A}}{\partial \tau }+\Gamma \frac{{\partial }^2{\mathcal A}}{\partial {\xi }^2} +\Delta \mid {\mathcal A}\mid ^2{\mathcal A}=0. $$

with the following definitions

$$ \tau =\omega t_2~~,~~\xi =k{\epsilon }^{-1}(x_2-V_gt_2)=k(x_1-V_gt_1)~~,~~{\mathcal A}=k{\mathcal A}_1, $$

$$ {\Gamma }=\frac{k^2}{2\omega }\frac{d^2\omega }{dk^2}, ~~{\Delta }=\frac{1}{\omega k^2}\Big [{-}(\mathbf{L}.\mathbf{F})\Big /[\mathbf{L}(\partial \mathbf{W}_1/\partial \omega )\mathbf{R}]\Big ]. $$

Thus the task is completed, since a solution for $~{\mathcal A}~$ is derived from NLS equation for a given initial value of the form $~{\mathcal A}(\xi ,0)={\mathcal A}_0(\xi )~$ then the first-order solutions $~u_1^{(r)}$ can be obtained from (49)–(51).

This analysis is also carried out for the case in which $c_{1}<c<c_{2}<c_{3}$ and we obtain dispersion relation as

$$\begin{aligned} p_{1}v_{2}\tan P_{1}+\gamma _{2}p_{1}v_{3}\tan P_{1}\tanh V_{2}-\gamma _{1}\gamma _{2}v_{2}v_{3}-\gamma _{1} v_{2}^{2}\tanh V_{2}=0 \end{aligned}$$

(77)

where $V_{2}=k v_{2}h_{1}$. For the nonlinear wave modulation of the waves again an NLS equation is obtained whose coefficients $\Gamma$ and $\Delta$ can be obtained by substituting $p_2=i v_2$ in previous ones.

4 Conclusions

It is known that the sign of the product $\Gamma \Delta$ is important in determining how a given initial data will evolve for long times for the asymptotic wave field governed by the NLS equation. An initial disturbance vanishing as $~\mid \xi \mid \rightarrow \infty ~$ tends to become a series of envelope solitary waves if $~\Gamma \Delta >0$, while it evolves into the decaying oscillations if $~\Gamma \Delta <0$. (see, e.g. [1, 4]). The traveling wave solutions of the NLS equation of the form

$$\begin{aligned} \textit{A}(\xi , \tau )=\phi (\eta )\mathrm {e}^{i(K\xi -\Omega \tau )},\quad \eta =\xi -V_{0}\tau ,\quad V_0: \text {constant} \end{aligned}$$

(78)

also depend on sign of $\Gamma \Delta$. For $\Gamma \Delta >0$, if $\phi \rightarrow 0$ and $d\phi /d\eta \rightarrow 0$ as $|\eta |\rightarrow \infty$, the envelope or bright soliton $\phi$ can be obtained as

$$\begin{aligned} \phi =\phi _{0} sech\left[ \left( \Delta /2\Gamma \right) ^{1/2}\phi _{0}\eta \right] , \end{aligned}$$

(79)

where $V_{0}=2K\Gamma$, $\Omega =\Gamma K^{2}-\Delta \phi _{0}^{2}/2$. For $\Gamma \Delta <0$ and $(\Gamma K^{2}-\Omega )/\Delta \phi _{0}^{2}=1$, if $\phi \rightarrow \phi _{0}$ as $\eta \rightarrow -\infty$, the solution for $\phi$ which represents the propagation of a phase jump can be expressed as

$$\begin{aligned} \phi =\phi _{0}\tanh \left[ \left( -\Delta /2\Gamma \right) ^{1/2}\phi _{0}\eta \right] , \quad V_{0}=2K\Gamma . \end{aligned}$$

(80)

Also for $\Gamma \Delta <0$ dark soliton solutions exist [29]. By taking into account the above review about the effect of the sign of $\Gamma \Delta$ on the properties of the solutions of an NLS equation, the behaviour of the solutions for SH waves propagating in a double layered nonlinear half space is now examined. As the properties of solutions of the NLS equation strongly depend on the sign of the product $~\Gamma \Delta$, the variation of it with respect to the nondimensional wave number $~K=k(h_1+h_2)~$ has to be found out. In this paper, the evaluation of these coefficients is carried out numerically for the lowest branch of the dispersion relation giving appropriate values to the materials constants. Similar calculations may be performed for any other branch of the dispersion relations.

Fig. 1

$\Gamma$ versus K for $h_1/h_2 =1$ and $h_1=0$

Fig. 2

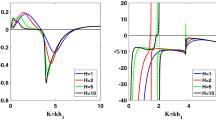
$\Gamma \Delta$ versus K for fixed $\beta _3=2.0$, $\beta _2=2.0$ (hardening half space covered by hardening internal layer) and for $\beta _1={-1,-2}$ (softening top layers), $\beta _1={1,2}$ (hardening top layers). The curve for $\beta _3=2.0$, $\beta _2=2.0$ and $h_1=0$ represents the $\Gamma \Delta$ versus K curve for a single layered half space

The coefficient $\Gamma$ depends only on the linear material constants and the ratio $h_2/h_1$, whereas $\Delta$ also depends on nonlinear material properties. Therefore to observe the variation in the $\Gamma \Delta$ with nonlinearity, in the numerical evaluations of $\Gamma \Delta$, the linear material constants are fixed to be $\rho ^{(1)}=\rho ^{(2)}=\rho ^{(3)}=1$, $\mu _1 =1$, $\mu _2=4$, $\mu _3=9$ while the nonlinear ones $\beta _1= n_1/c_1^2$, $\beta _2=n_2/c_2^2$ and $\beta _3=n_3/c_3^2$ are being changed. In Fig. 1 the variation of $\Gamma$ with respect to K for the first branch of the dispersion relations (43) and (77) is plotted for $h_2/h_1=1$ and also for $h_1 =0$ for a single layered half space. Note that for $h_2/h_1=1$, $\Gamma$ is zero approximately at $K\approx 2.18$ where the related group velocity curve has a minimum. As mentioned before, if $\beta _r>0$ the relevant medium exhibits hardening characteristic, while if $\beta _r<0$ softening characteristic. First we consider the variation of $\Gamma \Delta$ with respect to K for a hardening internal layer and a hardening half space with the nonlinear parameters $\beta _2=\beta _3=2$ in Fig. 2. To observe the effect of the nonlinearity of the top layer on $\Gamma \Delta$; $\beta _2$ and $\beta _3$ are fixed and the variation of $\Gamma \Delta$ with K is computed for $\beta _1=-1$, $\beta _1=-2$ (softening nonlinear layers) and for $\beta _1=1$, $\beta _1=2$ (hardening nonlinear layers). When $\beta _1=1$ and $\beta _1=2$ (i.e. a hardening half space covered by two hardening top layers), $\Delta <0$ for all $K>0$, therefore the sign of $\Gamma \Delta$ will be positive when $K<2.18$ since $\Gamma <0$ then envelope solitary wave solution given by (79) will exist but $\Gamma \Delta$ will be negative for $K>2.18$ as it is seen in Fig. 2, then only the dark solitons exist for this case. When $\beta _1=-1$ and $\beta _1=-2$ (i.e. a hardening half space covered by softening top layer and hardening internal layers) $\Delta <0$ initially and its sign changes with the variation in the nonlinear material parameter of top layer. In Fig. 2 the second zero of each $\Gamma \Delta$ curve is the zero of $\Gamma$ curve and the first one is the zero of $\Delta$ curve. Since the linear material constants and the ratio $h_2/h_1$ are fixed for all nonlinear models, the second zeros are the same for all $\Gamma \Delta$ curves, the other zeros are changing depending on the nonlinear material parameter of the top layer. For softening half space covered by softening internal layer and different top layer models, variations of $\Gamma \Delta$ with respect to K are given in Fig. 3. It is seen that the curves having same absolute $\beta _r$, $r=1,2,3$ values are symmetric with respect to K axis. Therefore the behavior of the solutions of the NLS equation is reversed. In Figs. 2 and 3 the variations of $\Gamma \Delta$ with K for a single layered half space (for $h_1 =0$) are also depicted. From these figures, it can be seen that the wave propagation is affected considerably by the existence of a second (top) layer. As a result of the numerical evaluation of $~\Gamma \Delta ~$ for fixed linear material properties, it is observed that the existence of the envelope solitary waves are affected strongly the nonlinear material parameter of top layer.

Fig. 3

$\Gamma \Delta$ versus K for fixed $\beta _3=-2.0$, $\beta _2=-2.0$ (softening half space covered by softening internal layer) and for $\beta _1={-1,-2}$ (softening top layers), $\beta _1={1,2}$ (hardening top layers). The curve for $\beta _3=-2.0$, $\beta _2=-2.0$ and $h_1=0$ represents the $\Gamma \Delta$ versus K curve for a single layered half space

5 Appendix A

$$\begin{aligned} R_{1}= & {} \frac{1}{2\cos {P_{1}}}e^{-(iP_{1}+V_{3})} \left( \cos P_{2} + \frac{v_{3}\gamma _{2}\sin P_{2} }{p_{2}} \right) , \quad R_{2}=\overline{R_{1}} \end{aligned}$$

(81)

$$\begin{aligned} R_{3}= & {} \frac{1}{2}e^{iP_{2} - V3}\left( 1-i \frac{v_{3}\gamma _{2} }{p_{2}} \right) , \quad R_{4}=\overline{R_{3}}, \quad R_{5}=1 \end{aligned}$$

(82)

6 Appendix B

$$\begin{aligned} \mathcal {D}_{1}= & {} 2 \Lambda _{1}\frac{\partial }{\partial x_{1}}\mathcal {M}_{11}^{(1)}+R_{1}\mathcal {N}^{(1)}+2iR_{1}\mathcal {M}_{12}^{(1)}-\mathcal {P}_{1}^{-} + 2iR_{1}\mathcal {M}_{21}^{(1)} \nonumber \\ \mathcal {D}_{2}= & {} -i\frac{2R_{1}}{p_{1}kc_{1}^{2}}\left( \omega \frac{\partial }{\partial t_{1}}+kc_{1}^{2}\frac{\partial }{\partial x_{1}}\right) \mathcal {M}_{11}^{(1)} \nonumber \\ \mathcal {D}_{3}= & {} 2 \Lambda _{2}\frac{\partial }{\partial x_{1}}\mathcal {M}_{11}^{(1)}+R_{2}\mathcal {N}^{(1)}+2iR_{2}\mathcal {M}_{12}^{(1)}-\mathcal {P}_{1}^{+} + 2iR_{2}\mathcal {M}_{21}^{(1)}\nonumber \\ \mathcal {D}_{4}= & {} \frac{2iR_{2}}{p_{1}kc_{1}^{2}}\left( \omega \frac{\partial }{\partial t_{1}}+kc_{1}^{2}\frac{\partial }{\partial x_{1}}\right) \mathcal {M}_{11}^{(1)} \nonumber \\ \mathcal {D}_{5}= & {} \mathcal {Q}_{1}^{-}\nonumber \\ \mathcal {D}_{6}= & {} \mathcal {Q}_{1}^{+}\nonumber \\ \mathcal {D}_{7}= & {} 2 \Lambda _{3}\frac{\partial }{\partial x_{1}}\mathcal {M}_{11}^{(2)}+R_{3}\mathcal {N}^{(2)}+2iR_{3}\mathcal {M}_{12}^{(2)}-\mathcal {P}_{2}^{-} + 2iR_{3}\mathcal {M}_{21}^{(2)} \nonumber \\ \mathcal {D}_{8}= & {} -\frac{2iR_{3}}{p_{2}kc_{2}^{2}}\left( \omega \frac{\partial }{\partial t_{1}}+kc_{2}^{2}\frac{\partial }{\partial x_{1}}\right) \mathcal {M}_{11}^{(2)} \nonumber \\ \mathcal {D}_{9}= & {} 2 \Lambda _{4}\frac{\partial }{\partial x_{1}}\mathcal {M}_{11}^{(2)}+R_{4}\mathcal {N}^{(2)}+2iR_{4}\mathcal {M}_{12}^{(2)}-\mathcal {P}_{2}^{+} + 2iR_{4}\mathcal {M}_{21}^{(2)} \nonumber \\ \mathcal {D}_{10}= & {} \frac{2iR_{4}}{p_{2}kc_{2}^{2}}\left( \omega \frac{\partial }{\partial t_{1}}+kc_{2}^{2}\frac{\partial }{\partial x_{1}}\right) \mathcal {M}_{11}^{(2)} \nonumber \\ \mathcal {D}_{11}= & {} \mathcal {Q}_{2}^{-} \nonumber \\ \mathcal {D}_{12}= & {} \mathcal {Q}_{2}^{+} \nonumber \\ \mathcal {D}_{14}= & {} \frac{2R_{5}}{v_{3}kc_{3}^{2}}\left( \omega \frac{\partial }{\partial t_{1}}+kc_{3}^{2}\frac{\partial }{\partial x_{1}}\right) \mathcal {M}_{11}^{(3)} \nonumber \\ \mathcal {D}_{15}= & {} n_{3}k^{4}(-3+2v_{3}^{2}+9v_{3}^{4})R_{5}^{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1} \end{aligned}$$

(83)

and

$$\begin{aligned} \mathcal {M}_{\beta \gamma }^{(\alpha )}= & {} \omega \frac{\partial \textit{A}_{\beta } }{\partial t_{\gamma }}+kc_{\alpha }^{2}\frac{\partial \textit{A}_{\beta } }{\partial x_{\gamma }} \nonumber \\ \mathcal {N}^{(\alpha )}= & {} c_{\alpha }^{2}\frac{\partial ^{2}{} \textit{A}_{1} }{\partial x_{1}^{2}}-\frac{\partial ^{2}{} \textit{A}_{1} }{\partial t_{1}^{2}} \nonumber \\ \Lambda _{\alpha }= & {} \left( \frac{\partial R_{\alpha }}{\partial k}+v_{g}\frac{\partial R_{\alpha }}{\partial \omega }\right) \nonumber \\ \mathcal {P}_{1}^{-}= & {} n_{1}k^{4}\left( 9p_{1}^{4}+2p_{1}^{2}+9\right) R_{1}|R_{1}|^{2}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {P}_{1}^{+}= & {} n_{1}k^{4}\left( 9p_{1}^{4}+2p_{1}^{2}+9\right) R_{2}|R_{2}|^{2}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {Q}_{1}^{-}= & {} n_{1}k^{4}\left( 9p_{1}^{4}-2p_{1}^{2}-3\right) R_{1}^{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {Q}_{1}^{+}= & {} n_{1}k^{4}\left( 9p_{1}^{4}-2p_{1}^{2}-3\right) R_{2}^{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {P}_{2}^{-}= & {} n_{2}k^{4}\left( 9p_{2}^{4}+2p_{2}^{2}+9\right) R_{3}^{2}R_{4}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {P}_{2}^{+}= & {} n_{2}k^{4}\left( 9p_{2}^{4}+2p_{2}^{2}+9\right) R_{4}^{2}R_{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {Q}_{2}^{-}= & {} n_{2}k^{4}\left( 9p_{2}^{4}-2p_{2}^{2}-3\right) R_{3}^{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1}\nonumber \\ \mathcal {Q}_{2}^{+}= & {} n_{2}k^{4}\left( 9p_{2}^{4}-2p_{2}^{2}-3\right) R_{4}^{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1} \end{aligned}$$

(84)

where $|\phi |$ denotes the modulus of $\phi$.

$$\begin{aligned} \mathcal {\varepsilon }_{1}= & {} \frac{i\mathcal {D}_{1}}{2kp_{1}c_{1}^{2}}- \frac{\mathcal {D}_{2}}{4k^{2}p_{1}^{2}c_{1}^{2}},\quad \mathcal {\varepsilon }_{2}=\frac{i\mathcal {D}_{2}}{4kp_{1}c_{1}^{2}},\quad \mathcal {\varepsilon }_{3}=-\frac{i\mathcal {D}_{3}}{2kp_{1}c_{1}^{2}}-\frac{\mathcal {D}_{4}}{4k^{2}p_{1}^{2}c_{1}^{2}}\nonumber \\ \mathcal {\varepsilon }_{4}= & {} -i\frac{\mathcal {D}_{4}}{4kp_{1}c_{1}^{2}},\quad \mathcal {\varepsilon }_{5}=\frac{\mathcal {D}_{5}}{8k^{2}p_{1}^{2}c_{1}^{2}},\quad \mathcal {\varepsilon }_{6}=\frac{\mathcal {D}_{6}}{8k^{2}p_{1}^{2}c_{1}^{2}},\quad \mathcal {\varepsilon }_{7}=\frac{i\mathcal {D}_{7}}{2kp_{2}c_{2}^{2}}-\frac{\mathcal {D}_{8}}{4k^{2}p_{2}^{2}c_{2}^{2}}\nonumber \\ \mathcal {\varepsilon }_{8}= & {} \frac{i\mathcal {D}_{8}}{4kp_{2}c_{2}^{2}}\quad \mathcal {\varepsilon }_{9}=-\frac{i\mathcal {D}_{9}}{2kp_{2}c_{2}^{2}}-\frac{\mathcal {D}_{10}}{4k^{2}p_{2}^{2}c_{2}^{2}},\quad \mathcal {\varepsilon }_{10}=-\frac{i\mathcal {D}_{10}}{4kp_{2}c_{2}^{2}}\nonumber \\ \mathcal {\varepsilon }_{11}= & {} \frac{\mathcal {D}_{11}}{8k^{2}p_{2}^{2}c_{2}^{2}},\quad \mathcal {\varepsilon }_{12}=\frac{\mathcal {D}_{12}}{8k^{2}p_{2}^{2}c_{2}^{2}},\quad \mathcal {\varepsilon }_{13}=-\frac{\mathcal {D}_{13}}{2kv_{3}c_{3}^{2}}+\frac{\mathcal {D}_{14}}{4k^{2}v_{3}^{2}c_{3}^{2}}\nonumber \\ \mathcal {\varepsilon }_{14}= & {} -\frac{\mathcal {D}_{14}}{4kv_{3}c_{3}^{2}},\quad \mathcal {\varepsilon }_{15}=-\frac{\mathcal {D}_{15}}{8k^{2}v_{3}^{2}c_{3}^{2}} \end{aligned}$$

(85)

$$\begin{aligned} F_{1}=-\beta _{1}h_{1}\frac{k^{4}(9p_{1}^{4}+2p_{1}^{2}+9)}{8\cos ^{3}P_{1}}\left( \frac{\gamma _{2}v_{3}}{p_{2}}\sin P_{2}+\cos P_{2} \right) ^{3}\mathrm {e}^{-3V_{3}} \end{aligned}$$

(86)

$$\begin{aligned} F_{2}=&\beta _{1}\frac{k^{3}(9p_{1}^{4}+2p_{1}^{2}+9)}{8p_{1}\cos ^{3}P_{1}}\left( \frac{\gamma _{2}v_{3}}{p_{2}}\sin P_{2}+\cos P_{2} \right) ^{3} \sin P_{1}\mathrm {e}^{-3V_{3}} \nonumber \\&-\,\frac{3}{32}\beta _{1}\frac{k^{3}(9p_{1}^{4}-2p_{1}^{2}-3)}{p_{1}\cos ^{3}P_{1}}\left( \frac{\gamma _{2}v_{3}}{p_{2}}\sin P_{2}+\cos P_{2} \right) ^{3} \sin 3P_{1}\mathrm {e}^{-3V_{3}}\nonumber \\&+\,\gamma _{1}\beta _{2}\frac{k^{3}(9p_{2}^{4}+2p_{2}^{2}+9)}{8p_{2}} \left( 1+\frac{\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \left( \sin P_{2}-\frac{\gamma _{2}v_{3}}{p_{2}}\cos P_{2} \right) \mathrm {e}^{-3V_{3}}\nonumber \\&-\,\gamma _{1}\beta _{2}\frac{3k^{3}(9p_{2}^{4}-2p_{2}^{2}-3)}{32p_{2}} \left( 1-\frac{3\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \sin 3P_{2} \mathrm {e}^{-3V_{3}}\nonumber \\&+\,\gamma _{1}\beta _{2}\frac{3k^{3}(9p_{2}^{4}-2p_{2}^{2}-3)}{32p_{2}} \left( 3-\frac{\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \frac{\gamma _{2}v_{3}}{p_{2}}\cos 3P_{2} \mathrm {e}^{-3V_{3}}\nonumber \\&-\,\beta _{1}\frac{k^{3}p_{1}}{\cos ^{3}P_{1}}\left( \frac{\gamma _{2}v_{3}}{p_{2}}\sin P_{2}+\cos P_{2} \right) ^{3}(\sin P_{1}\cos ^{2}P_{1}+3 p_{1}^{2}\sin ^{3} P_{1})\mathrm {e}^{-3V_{3}}\nonumber \\&-\,\gamma _{1}\beta _{2}\frac{k^{3}p_{2}}{4}\left\{ (1+9p_{2}^{2})\left( 1+\frac{\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \left( \sin P_{2}-\frac{\gamma _{2}v_{3}}{p_{2}}\cos P_{2}\right) +\right. \nonumber \\&\left. (1-3p_{2}^{2}) \left[ \left( 1- \frac{3\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \sin 3P_{2}- \left( 3- \frac{\gamma _{2}^{2}v_{3}^{2}}{p_{2}^{2}}\right) \frac{\gamma _{2}v_{3}}{p_{2}}\cos 3P_{2}\right] \right\} \mathrm {e}^{-3V_{3}}\qquad \quad \end{aligned}$$

(87)

$$\begin{aligned} F_{3}=&-\beta _{ 1}\frac{k^{2}\left( 9p_{1}^{4}- 2p_{1}^{2} -3 \right) \left( \frac{v_{3}\gamma _{ 2}}{p_{2}}\sin P_{2}+ \cos P_{2} \right) ^{3}}{32p_{1}^{2}\cos ^{3}P_{1}}\cos 3P_{1}\mathrm {e}^{ - 3V_{3}}\nonumber \\&+\,\beta _{ 2}\frac{k^{2}\left( - 3 - 2p_{2}^{2} + 9p_{2}^{4} \right) }{32p_{2}^{2}}\left( 1-\frac{3v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}} \right) \cos 3P_{2}\mathrm {e}^{ - 3V_{3}}\nonumber \\&+\,\beta _{ 2}\frac{k^{2}\left( 9p_{2}^{4} - 2p_{2}^{2} - 3 \right) }{32p_{2}^{2}}\left( 3-\frac{v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}} \right) \frac{v_{3}\gamma _{ 2}}{p_{2}}\sin 3P_{2}\mathrm {e}^{ - 3V_{3}} \end{aligned}$$

(88)

$$\begin{aligned} F_{4}=&\beta _{2}\frac{k^{3}\left( 9 + 2p_{2}^{2} + 9p_{2}^{4} \right) }{8p_{2}}\left( 1+\frac{v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}}\right) \frac{v_{3}\gamma _{ 2}}{p_{2}}\mathrm {e}^{-3V_{3}}\nonumber \\&+\,\beta _{ 2}\frac{h_{2}k^{4}\left( 9 + 2p_{2}^{2} + 9p_{2}^{4} \right) }{8}\left( 1+\frac{v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}}\right) \mathrm {e}^{-3V_{3}}\nonumber \\&-\,\beta _{2}\frac{3k^{3}\left( -3 -2p_{2}^{2} + 9p_{2}^{4} \right) }{32p_{2}}\left( 3-\frac{v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}}\right) \frac{v_{3}\gamma _{ 2}}{p_{2}}\mathrm {e}^{-3V_{3}}\nonumber \\&-\,\gamma _{2}\beta _{3}\frac{3k^{3}\left( -3+ 2v_{3}^{2} + 9v_{3}^{4} \right) }{8v_{3}}\mathrm {e}^{-3V_{3}}+\gamma _{2}\beta _{3}k^{3}v_{3}(1+3v_{3}^{2})\mathrm {e}^{-3V_{3}}\nonumber \\&-\,\gamma _{2}\beta _{2}k^{3}v_{3}(1+3\gamma _{2}^{2}v_{3}^{2})\mathrm {e}^{-3V_{3}} \end{aligned}$$

(89)

$$\begin{aligned} F_{5}=&-\beta _{2}\frac{h_{2}k^{3}\left( 9 + 2p_{2}^{2} + 9p_{2}^{4} \right) }{8p_{2}}\left( 1+\frac{v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}}\right) \frac{v_{3}\gamma _{ 2}}{p_{2}}\mathrm {e}^{-3V_{3}}\nonumber \\&-\,\beta _{2}\frac{k^{2}\left( -3 - 2p_{2}^{2} + 9p_{2}^{4} \right) }{32p_{2}^{2}}\left( 1-\frac{3v_{3}^{2}\gamma _{ 2}^{2}}{p_{2}^{2}}\right) \mathrm {e}^{-3V_{3}}\nonumber \\&-\,\beta _{3}\frac{k^{2}\left( -3 +2v_{3}^{2} + 9v_{3}^{4} \right) }{8v_{3}^{2}}\mathrm {e}^{-3V_{3}}. \end{aligned}$$

(90)